C13024(100分)答案
石门高考数学试卷真题答案

1. 下列各数中,绝对值最小的是()A. -2B. 3C. -4D. 5答案:A解析:绝对值表示数与0的距离,所以-2的绝对值最小。
2. 若a、b、c是等差数列的前三项,且a+b+c=12,a+c=8,则b的值为()A. 2B. 4C. 6D. 8答案:C解析:由等差数列的性质知,a+c=2b,又a+c=8,所以b=4。
3. 函数f(x)=x^2-2x+1在区间[-1,2]上的最大值为()A. 0B. 1C. 2D. 3答案:C解析:函数f(x)的对称轴为x=1,开口向上,所以最大值在x=2处取得,即f(2)=2^2-22+1=3。
4. 已知等比数列{an}的前三项分别为a、ar、ar^2,且a=2,ar=4,则r的值为()A. 2B. 4C. 1/2D. 1/4答案:C解析:由ar=4,得ar=2r=4,所以r=2。
5. 已知直线l:x-y+1=0,点P(2,3)到直线l的距离为()A. 1B. 2C. 3D. 4答案:B解析:点到直线的距离公式为d=|Ax0+By0+C|/√(A^2+B^2),代入直线l的系数和点P的坐标,得d=|2-3+1|/√(1^2+(-1)^2)=2。
6. 若等差数列{an}的前n项和为Sn,且S10=55,S20=165,则公差d的值为______。
答案:3解析:由等差数列前n项和公式Sn=n(a1+an)/2,得S10=10(a1+a10)/2=55,S20=20(a1+a20)/2=165。
联立方程组,解得a1=1,a10=5,所以公差d=(a10-a1)/(10-1)=3。
7. 函数f(x)=x^3-3x^2+4x在区间[-1,2]上的零点个数为______。
答案:2解析:函数f(x)的导数为f'(x)=3x^2-6x+4,令f'(x)=0,解得x=2或x=2/3。
又f(-1)=-1,f(2)=4,f(2/3)=-8/27,所以f(x)在[-1,2]上有两个零点。
2022一建建筑实务真题 答案(完整版)

2022一建建筑实务真题答案〔完整版〕2022年一级建造师《建筑工程管理与实务》真题一、单项选择题〔共20题,每题1分。
每题的备选项中,只有1个最符合题意〕1.设计使用年限为50年,处于一般环境大截面钢筋混凝土柱,其混凝土强度等级不应低于〔〕。
A.C15B.C20C.C25D.C30 【答案】C【解析】设计使用年限为50年的构件,混凝土强度等级不小于C25。
【考点来源】1A411013建筑结构工程的耐久性2.既有建筑装修时,如需改变原建筑使用功能,应取得〔〕许可。
A.原设计单位B.建设单位C.监理单位D.施工单位【答案】A【解析】装修时不能自行改变原来的建筑使用功能。
如假设必要改变时,应该取得原设计单位的许可。
【考点来源】1A411023荷载对结构的影响 3.以下建筑结构体系中,侧向刚度最大的是〔〕。
A.桁架结构体系B.筒体结构体系C.框架-剪力墙结构体系D.混合结构体系【答案】B【解析】筒体结构便是抵抗水平荷载最有效的结构体系。
【考点来源】1A411024常见建筑结构体系和应用 4.以下水泥品种中,配制C60高强混凝土宜优先选用〔〕。
A.矿渣水泥B.硅酸盐水泥C.火山水泥D.复合水泥【答案】B【解析】此题考查常用水泥的选用,注意和水泥的特性结合起来学习。
高强〔大于C50级〕混凝土宜优先选用硅酸盐水泥,不宜使用火山灰水泥和粉煤灰水泥。
【考点来源】1A412022 水泥的性能和应用5.以下混凝土掺合料中,属于非活性矿物掺和料的是〔〕。
A.石灰石粉B.硅灰C.沸石粉D.粒化高炉矿渣粉【答案】A【解析】混凝土掺合料分为活性矿物掺合料和非活性矿物掺合料。
非活性矿物掺合料根本不与水泥组分起反响,如磨细石英砂、石灰石、硬矿渣等材料。
活性矿物掺合料如粉煤灰、粒化高炉矿渣粉、硅灰、沸石粉等本身不硬化或硬化速度很慢,但能与水泥水化生成的Ca(OH)2起反响,生成具有胶凝能力的水化产物。
【考点来源】1A412022混凝土的性能和应用 6.关于花岗石特性的说法,错误的选项是〔〕。
人教版一年级数学上册《期末考试模拟测试卷》试题及参考答案
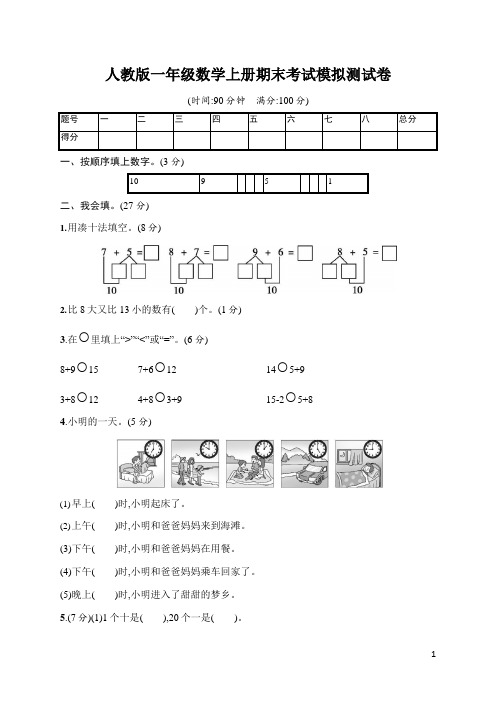
人教版一年级数学上册期末考试模拟测试卷(时间:90 分钟满分:100 分)题号一二三四五六七八总分得分一、按顺序填上数字。
(3 分)10 951二、我会填。
(27 分)1.用凑十法填空。
(8 分)2.比8 大又比13 小的数有( )个。
(1 分)3.在○里填上“>”“<”或“=”。
(6 分)8+9○15 7+6○12 14○5+93+8○12 4+8○3+9 15-2○5+84.小明的一天。
(5 分)(1)早上( )时,小明起床了。
(2)上午( )时,小明和爸爸妈妈来到海滩。
(3)下午( )时,小明和爸爸妈妈在用餐。
(4)下午( )时,小明和爸爸妈妈乘车回家了。
(5)晚上( )时,小明进入了甜甜的梦乡。
5.(7 分)(1)1 个十是( ),20 个一是( )。
(2)20 和16 之间的数有( )、( )、( )。
(3)当分针指向12,时针指向( )的时候,是6 时。
(4)当分针和时针都指向12 的时候,是( ) 时。
三、我会算。
(16 分)四、我会算,我会填。
(6 分)810718108五、我会连。
(12 分)六、我会看时间。
(12 分)1.小猴修表。
(8 分)(1)(2)(3)(4)2.写出2 小时之前的时间。
(4 分)七、我会写算式。
(8 分)1.□○□=□(个)2.□○□=□(本)3.□○□=□(根)4.□○□○□=□(只)八、我会解答。
(16 分)1.一共有多少只小鸡?(4 分)□○□=□(只)2.他们一共剪了多少朵窗花?(4 分)□○□=□(朵)3.一共有几只鸭子?(4 分)□○□=□(只)4.鱼缸里原来有9 条鱼,捞走了2 条,又倒进去3 条。
现在鱼缸里有多少条鱼?(4 分) □○□○□=□(条)答案与解析一、8 7 6 4 3 2二、1.2.43.> > = < = =4.(1)7 (2)10 (3)1 (4)5 (5)95.(1)10 20 (2)17 18 19 (3)6 (4)12三、11 12 15 11 11 16 14 14 17 11 12 12 12 13 18 2四、17 13 16 8 4 4五、六、1.(1)9 9: 00(2)6 时6: 00(3)12 时12: 00(4)3 时3: 002.6 时11 时 1 时8 时七、1.16-3=132.8+7=153.6+5=114.2+7+3=12八、1.7+8=152.6+6=123.5+7=124.9-2+3=10。
C语言程序设计(第3版)第3章习题参考答案

习题三参考答案(1)从键盘输入一个年份值,判断是否闰年。
设iYear为某一年份,iYear为闰年的条件为:iYear可以被4整除且不可以被100整除,或者iYear可以被400整除。
#include "Stdio.h"#include "Conio.h"int main(void){int iYear;printf("please input the year:");scanf("%d",&iYear);if(iYear%400==0||(iYear%4==0&&iYear%100!=0))printf("%d is leap",iYear);elseprintf("%d is not leap",iYear);getch();return 0;}(2)从键盘输入三个整数,按由小到大的顺序输出。
#include "stdio.h"main(){int i,j,k,max;scanf("%d%d%d",&i,&j,&k);max=i>j?i:j;max=max>k?max:k;printf("max=%d",max);getch();}(3)假设星期一至星期五每工作一小时的工资是20元,星期六和星期日每工作一小时的工资是平时的3倍,其中工资的4.5%是税金。
试编一程序从键盘输入星期序号(1,2,3,4,5,6,7,分别表示星期一至星期天)和工作小时数,计算该日的工资及应交税金。
#include "Stdio.h"#include "Conio.h"int main(void){int iWeek,iHours ;float fSalary,fTaxes;printf("please input the week number(1-7):");scanf("%d",&iWeek);printf("please input the work hours(1-12):");scanf("%d",&iHours);switch(iWeek){case 1:case 2:case 3:case 4:case 5:fSalary=20*iHours;fTaxes=fSalary*0.045;break;case 6:case 7:fSalary=3*20*iHours;fTaxes=fSalary*0.045;break;}printf("the salary is %f ,the taxes is %f",fSalary,fTaxes);getch();return 0;}(4)从键盘输入三角形的三条边长,判断是否构成三角形,如能则求出三角形的周长和面积并输出;如不能,输出不能构成三角形的信息。
数学实验梁宝钰版课后答案

数学实验梁宝钰版课后答案1、11.11点40分,时钟的时针与分针的夹角为()[单选题] *A.140°B.130°C.120°D.110°(正确答案)2、已知10?=5,则100?的值为( ) [单选题] *A. 25(正确答案)B. 50C. 250D. 5003、1. 在实数0、-√3?、√2?、-2中,最小的是()[单选题] *A、-2(正确答案)B、-√3C、0D、√24、24.不等式x-3>5的解集为()[单选题] *A. x > 1B. x > 2(正确答案)C. x > 3D. x > 45、42.已知m、n均为正整数,且2m+3n=5,则4m?8n=()[单选题] * A.16B.25C.32(正确答案)D.646、已知直线l的方程为2x-y+7=0,()是直线l上的点[单选题] *A、(2,3)B、(2,4)(正确答案)C、(2,-3)D、(-2,-3)7、46.若a+b=7,ab=10,则a2+b2的值为()[单选题] *A.17B.29(正确答案)C.25D.498、8.数轴上一个数到原点距离是8,则这个数表示为多少()[单选题] *A.8或﹣8(正确答案)B.4或﹣4C.8D.﹣49、14.数﹣在数轴上的位置可以是()[单选题] *A.点A与点B之间(正确答案)B.点B与点O之间C.点O与点D之间D.点D与点E之间10、2.(2020·新高考Ⅱ,1,5分)设集合A={2,3,5,7},B={1,2,3,5,8},则A∩B=( ) [单选题] * A.{1,8}B.{2,5}C.{2,3,5}(正确答案)D.{1,2,3,5,7,8}11、7.如图,数轴上点M表示的数可能是()[单选题] *A.5B.﹣6C.﹣6(正确答案)D.612、以A(3,2),B(6,5),C(1,10)为顶点的三角形是()[单选题] *A、锐角三角形B、锐角三角形C、直角三角形(正确答案)D、无法判断13、点A的坐标为(3,4),点B的坐标为(5,8),则它们的中点坐标是(D)[单选题] *A、(3,4)B、(3,5)C、(8,12)D、(4,6)(正确答案)14、计算(-a)?·a的结果是( ) [单选题] *A. -a?B. a?(正确答案)C. -a?D. a?15、21.|x|>3表示的区间是()[单选题] *A.(-∞,3)B.(-3,3)C. [-3,3]D. (-∞,-3)∪(3,+ ∞)(正确答案)16、已知x-y=3,x2-y2=12,那么x+y的值是( ??) [单选题] *A. 3B. 4(正确答案)C. 6D. 1217、13.如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是() [单选题] *A.(0,4)→(0,0)→(4,0)B.(0,4)→(4,4)→(4,0)C.(0,4)→(3,4)→(4,2)→(4,0)(正确答案)D.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)18、260°是第()象限角?[单选题] *第一象限第二象限第三象限(正确答案)第四象限19、9.如图,下列说法正确的是()[单选题] *A.直线AB与直线BC是同一条直线(正确答案)B.线段AB与线段BA是不同的两条线段C.射线AB与射线AC是两条不同的射线D.射线BC与射线BA是同一条射线20、28、若的三边之长都是整数,周长小于10,则这样的三角形共有()[单选题] *A. 6个,B. 7个,C. 8个,D. 9个(正确答案)21、5.下列结论不正确的是[单选题] *A.若a > 0,b > 0,则a + b > 0B.若a < 0,b < 0,则a + b < 0C.若a > 0,b < 0,且|a| > |b|,则a + b > 0D.若a < 0,b > 0,且|a| > |b|,则a + b > 0(正确答案)22、11.小文买了一支温度计,回家后发现里面有一个小气泡(即不准确了),先拿它在冰箱里试一下,在标准温度是零下7℃时,显示为℃,在36℃的温水中,显示为32℃,那么用这个温度计量得的室外气温是23℃,则室外的实际气温应是()[单选题] *A.27℃(正确答案)B.19℃C.23℃D.不能确定23、北京、南京、上海三个民航站之间的直达航线,共有多少种不同的飞机票?()[单选题] *A、3B、4C、6(正确答案)D、1224、30.圆的方程+=4,则圆心到直线x-y-4=0的距离是()[单选题] *A.√2(正确答案)B.√2/2C.2√2D.225、下列计算正确是()[单选题] *A. 3x﹣2x=1B. 3x+2x=5x2C. 3x?2x=6xD. 3x﹣2x=x(正确答案)26、27.下列各函数中,奇函数的是()[单选题] *A. y=x^(-4)B. y=x^(-3)(正确答案)C .y=x^4D. y=x^(2/3)27、y=k/x(k是不为0的常数)是()。
2024届湖南省常德市高三下学期3月模拟考化学试题及答案

科目:化 学(试题卷)注意事项:1.答题前,考生务必将自己的姓名、准考证号写在答题卡和本试题卷的封面上,并认真核对答题卡条形码上的姓名、准考证号和科目。
2.选择题和非选择题均须在答题卡上作答,在本试题卷和草稿纸上作答无效。
考生在答题卡上按答题卡中注意事项的要求答题。
3.本试卷共6页。
如缺页,考生须及时报告监考老师,否则后果自负。
4.考试结束,将本试题卷和答题卡一并交回。
姓名准考证号祝 你 考 试 顺 利 !2024年常德市高三年级模拟考试化 学可能用到的相对原子质量:H 1 C 12 O 16 Na 23 Cl 35.5 Mg 24 Fe 56一、选择题:本题共14小题,每小题3分,共42分。
在每小题给出的四个选项中,只有一项是符合题目要求。
1.2023年上海科技节以“悦享科技,智创未来”为主题,展示了近年来我国的科技成果。
下列说法错误的是A .冬奥火炬“飞扬”使用的碳纤维复合材料具有强度高、耐高温的特点B .“萌新”机器人的有机高分子材料面罩为纯净物C .“雪龙号”极地破冰船船身由合金钢材料构成,其抗撞击能力强D .直径为300 mm 以上的大硅片首次应用于集成电路,其属于新型无机非金属材料 2.下列说法错误的是 A .汽车尾气中含有氮氧化物是因为燃料的不完全燃烧 B .核苷酸水解得到磷酸和核苷,核苷继续水解得到戊糖和碱基 C .Na 2O 、MgO 、Al 2O 3、SiO 2均属于介于离子晶体与共价晶体之间的过渡晶体D .细胞和细胞器的双分子膜属于一种可以自组装的超分子 3.BrF 3是应用最广的卤素间化合物,是一种很好的溶剂,其熔点、沸点分别为8.8℃、127℃。
常温下,它能与水发生反应:3BrF 3+5H 2O =HBrO 3+Br 2+9HF+O 2↑。
设阿伏加德罗常数值为N A 。
下列说法正确的是A .标准状况下,22.4 L 的BrF 3中含σ键数为3N AB .当反应中转移电子数为4N A 时,可产生1 mol O 2C .将反应生成的1molBr 2溶于水,所得溶液中含溴的微粒总数小于2N AD .若有5mol 水参与反应,则有2molBrF 3被氧化4.下列化学反应表示错误的是 A .Al 2O 3与NaOH 溶液反应:Al 2O 3+2NaOH +3H 2O =2Na[Al(OH)4]B .碱性锌锰电池的正极反应:2MnO 2+2e -+2H 2O =2MnO(OH)+2OH -C .向蓝色CuCl 2溶液中加入浓NaCl 溶液,发生反应:[Cu(H 2O)4]2++4Cl - [CuCl 4]2-+4H 2O D.苯甲酰胺在盐酸中水解:C ONH 2+H 2C O OH +NH 3 5.下列实验操作能达到实验目的的是选项实验操作 实验目的 A 分别称取2gNaClO 与NaHCO 3于盛有10mL 水的两支试管中,充分溶解,用 pH 计测定两溶液的pH 。
2023年河北省普通高中学业水平合格性考试数学真题试卷含详解

2023年3月河北省普通高中学业水平合格性考试数学试卷注意事项:1.本试卷共4页,包括两道大题,36道小题,总分100分,考试时间120分钟.2.所有答案在答题卡上作答,在本试卷和草稿纸上作答无效.答题前,请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题.3.答题时,请用2B 铅笔将答题卡上对应题目的答案标号涂黑.如需改动,请用橡皮将原选涂答案擦拭干净后,再选涂其他答案标号.4.考试结束时,请将本试卷与答题卡一并交回.一、单项选择题(共8小题,每小题2分,共16分)1.设集合{}2,3,4M =,{}3,4,5N =,则M N ⋂=()A.{}2 B.{}5 C.{}3,4 D.{}2,3,4,52.若实数,a b 满足i i(1i)a b +=-,则a b +=()A.2B.2- C.1D.1-3.若实数,,a b c 满足a b >,0c <,则()A .ac bc> B.ac bc < C.a c b c+<+ D.a c b c-<-4.已知向量(2,1)a =- ,(,2)b m = ,若a b ⊥,则实数m =()A.1B.1- C.4D.4-5.设命题p :R α∀∈,sin 1α≥-,则p 的否定是()A.R α∃∈,sin 1α≤-B.R α∃∈,sin 1α<-C.R α∀∈,sin 1α≤-D.R α∀∈,sin 1α<-6.函数()f x =)A.[]0,2 B.[]2,0-C.(][),02,-∞⋃+∞ D.(][),20,-∞-+∞7.魏晋时期刘徽在其撰写的《九章算术注》中提到了“不加借算”2ra a≈+.当a 取正整数且r 最小时,用“不加借算”的方法计算面积为21232m 的正方形区域的边长,其结果是()A.35.1mB.35.3mC.35.5mD.35.7m8.若1sin 4α=,π,π2α⎛⎫∈ ⎪⎝⎭,则cos()α-=()A.34 B.34-C.4-D.4二、单项选择题(共28小题,每小题3分,共84分)9.已知向量,a b满足||1,||2,a b a b ==⋅=r r r r ,a b的夹角为()A.30B.60C.120D.15010.已知函数21,0()log (2),0x x f x x x -≤⎧=⎨+>⎩,则()f x 的最小值是()A.1- B.0C.1D.211.已知m ,n 是两条不同的直线,α是平面,则下列四个结论中正确的是()A.若m α⊥,n α⊥,则//m nB.若//m α,//n α,则//m nC.若m α⊥,m n ⊥,则//n αD.若m ,n 与α所成的角相等,则//m n12.在ABC 中,设3AD DB = ,CA a = ,CB b =uu r r ,则CD =()A.1344a b+ B.1344a b -C.1233a b +D.1233a b- 13.某快递驿站随机记录了7天代收快递的件数,如下表:天/第1234567件数285367463290335719698已知该驿站每代收1件快递收取0.8元服务费,据此样本数据,估计该驿站每月(按30天计算)收取的服务费是(单位:元)()A.8808B.9696C.10824D.1185614.下列函数中,在区间(1,1)-上单调递减的是()A.()1f x x =-+ B.()cos f x x= C.()e e x xf x -=+ D.1()ln 1xf x x+=-15.设,a b R ∈,则“a b >”是“33a b >”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件16.将一块棱长为60cm 的正方体石块,磨制成一个球形石块,则最大球形石块的体积是(取π3=)()A.3864000cm B.3108000cm C.310800cm D.35400cm 17.已知函数()sin()f x x ωϕ=+(0ω>,π0ϕ-<<)的图象如图所示,则ϕ的值是()A.7π10-B.9π10-C.π2-D.π5-18.已知定义在R 上的偶函数()f x 在(],0-∞上是增函数,且()10f -=,则使()0f x >的x 的取值范围是()A.()1,0- B.()0,1 C.()1,1- D.()(),11,-∞-⋃+∞19.若圆锥的底面半径为3,体积为37π,则此圆锥的侧面展开图的圆心角是()A.π2B.2π3C.3π4D.3π220.某旅游爱好者想利用假期去国外的2个城市和国内的3个城市旅游,由于时间所限,只能在这5个城市中选择两个为出游地.若他用“抓阄”的方法从中随机选取2个城市,则选出的2个城市都在国内的概率是()A.35B.12C.13D.31021.已知0.12a -=,0.20.5b =,0.5log 0.2c =,则()A.c a b<< B.c b a<< C.b a c<< D.a b c<<22.已知0a >,0b >,24a b +=,则ab 的最大值是()A.2B.2C.22D.423.将函数sin 2cos 2y x x =+的图象向右平移π4个单位长度,所得图象的函数解析式可以是()A.22y x =B.π224y x ⎛⎫=- ⎪⎝⎭C.π224y x ⎛⎫=- ⎪⎝⎭ D.3π224y x ⎛⎫=+ ⎪⎝⎭24.某足球队进行点球训练,假设守门员不变,球员甲进球的概率为0.9,球员乙、丙进球的概率均为0.8.若3人各踢点球1次,且进球与否相互独立,则至少进2球的概率是()A.0.784B.0.864C.0.928D.0.99325.若3cos 210cos 1αα+=,则cos 2cos αα+=()A.49-B.1-C.109D.126.在ABC 中,若1BC =,3AC =,2cos 3C =,则sin B =()A.306B.155 C.106 D.10527.如图所示的八面体的表面是由2个全等的等边三角形和6个全等的等腰梯形组成,设1111A A A B ==,2AB =,有以下四个结论:①BC ⊥平面12AA A ;②1//AA 平面22BB C C ;③直线1AA 与2CC 成角的余弦值为56④直线11A C 与平面22AA B B 所成角的正弦值为63.其中正确结论的个数是()A.1B.2C.3D.428.河北雄安新区围绕职业培训、岗位开发、岗位对接等一系列工作,制定出台了《河北雄安新区当地劳动力教育培训实施方案(2019—2025年)》等30余项政策文件,截至2022年底,累计开展各项职业培训16.8万人次.雄安新区公共服务局为了解培训效果,对2022年参加职业技能培训的学员进行了考核测试,并从中随机抽取60名学员的成绩(满分100分),进行适当分组后(每组为左开右闭的区间),作出如图所示的频率分布直方图.这批学员技能考核测试成绩的众数的估计值是()A.65B.75C.85D.9529.河北雄安新区围绕职业培训、岗位开发、岗位对接等一系列工作,制定出台了《河北雄安新区当地劳动力教育培训实施方案(2019—2025年)》等30余项政策文件,截至2022年底,累计开展各项职业培训16.8万人次.雄安新区公共服务局为了解培训效果,对2022年参加职业技能培训的学员进行了考核测试,并从中随机抽取60名学员的成绩(满分100分),进行适当分组后(每组为左开右闭的区间),作出如图所示的频率分布直方图.这批学员技能考核测试成绩的中位数的估计值是()A.80.75B.81.25C.82.50D.82.7530.河北雄安新区围绕职业培训、岗位开发、岗位对接等一系列工作,制定出台了《河北雄安新区当地劳动力教育培训实施方案(2019—2025年)》等30余项政策文件,截至2022年底,累计开展各项职业培训16.8万人次.雄安新区公共服务局为了解培训效果,对2022年参加职业技能培训的学员进行了考核测试,并从中随机抽取60名学员的成绩(满分100分),进行适当分组后(每组为左开右闭的区间),作出如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则这批学员技能考核测试成绩的平均数的估计值是()A.79.0B.79.5C.81.0D.82.531.如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PCD 是等边三角形,平面PCD ⊥底面ABCD ,3AD =,四棱锥P ABCD -的体积为183,E 为PC 的中点.线段AB 的长是()A.3B.32C.33D.632.如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PCD 是等边三角形,平面PCD ⊥底面ABCD ,3AD =,四棱锥P ABCD -的体积为183,E 为PC 的中点.平面PAB 与平面ABCD 所成二面角的正切值是()A.2B.3C.2D.133.如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PCD 是等边三角形,平面PCD ⊥底面ABCD ,3AD =,四棱锥P ABCD -的体积为183,E 为PC 的中点.直线DE 与平面PAD 所成角的正弦值是()A.32B.33C.13D.1234.已知函数12()22x x f x a --=-+.若函数()f x 的最大值为1,则实数=a ()A.78-B.78C.98-D.9835.已知函数12()22x x f x a --=-+.关于函数()f x 的单调性,下列判断正确的是()A.()f x 在(),2-∞上单调递增B.()f x 在(),2-∞上单调递减C.()f x 在1,4⎛⎫+∞⎪⎝⎭上单调递增 D.()f x 在1,4⎛⎫+∞⎪⎝⎭上单调递减36.已知函数()1222xx f x a --=-+.若函数()f x 有两个零点1x 、2x ,给出下列不等式:①124x x +>;②()120f x x +<;③()121132f x x +->-;④()1220f x x +->.其中恒成立的个数是()A.1B.2C.3D.42023年3月河北省普通高中学业水平合格性考试数学试卷一、单项选择题(共8小题,每小题2分,共16分)1.设集合{}2,3,4M =,{}3,4,5N =,则M N ⋂=()A.{}2 B.{}5 C.{}3,4 D.{}2,3,4,5【答案】C【分析】根据交集运算法则即可计算得出{}3,4M N ⋂=.【详解】根据列举法表示的集合可知,由{}2,3,4M =,{}3,4,5N =,利用交集运算可得{}3,4M N ⋂=.故选:C2.若实数,a b 满足i i(1i)a b +=-,则a b +=()A.2 B.2- C.1D.1-【答案】A【分析】利用复数相等求出,a b 即可.【详解】因为i i(1i)1i a b +=-=+,所以1,1a b ==,所以2a b +=,故选:A.3.若实数,,a b c 满足a b >,0c <,则()A.ac bc >B.ac bc< C.a c b c+<+ D.a c b c-<-【答案】B【分析】根据题意,利用不等式的性质逐项分析即可.【详解】因为a b >,0c <,所以ac bc <,故A 错误,B 正确,由不等式两边同时加上或减去同一个实数不等号不改变,所以a c b c +>+,a c b c ->-故C ,D 错误,故选:B4.已知向量(2,1)a =- ,(,2)b m = ,若a b ⊥,则实数m =()A.1B.1- C.4D.4-【分析】根据平面向量数量积的运算即可求出结果.【详解】因为a b ⊥ ,则0a b =,又因为向量(2,1)a =- ,(,2)b m = ,所以220a b m =-+=,则1m =,故选:A .5.设命题p :R α∀∈,sin 1α≥-,则p 的否定是()A.R α∃∈,sin 1α≤-B.R α∃∈,sin 1α<-C.R α∀∈,sin 1α≤-D.R α∀∈,sin 1α<-【答案】B【分析】根据含有一个量词命题的否定可知,改变量词符号并否定结论即可.【详解】由题意可知,含有一个量词命题的否定将∀改为∃,并否定结论即可,所以命题p :R α∀∈,sin 1α≥-的否定为“R α∃∈,sin 1α<-”.故选:B6.函数()f x =)A.[]0,2 B.[]2,0-C.(][),02,-∞⋃+∞ D.(][),20,-∞-+∞ 【答案】D【分析】根据函数解析式可得(2)0x x +≥,再利用一元二次不等式解法即可求得定义域.【详解】根据函数定义域可知(2)0x x +≥,解得0x ≥或2x ≤-;所以函数()f x 的定义域为(][),20,-∞-+∞ .故选:D7.魏晋时期刘徽在其撰写的《九章算术注》中提到了“不加借算”2ra a≈+.当a 取正整数且r 最小时,用“不加借算”的方法计算面积为21232m 的正方形区域的边长,其结果是()A.35.1mB.35.3mC.35.5mD.35.7m【答案】A=结合题设公式得出结果.73535.170=≈+=,即用“不加借算”的方法计算面积为21232m 的正方形区域的边长,其结果是35.1m.8.若1sin 4α=,π,π2α⎛⎫∈ ⎪⎝⎭,则cos()α-=()A.34 B.34-C.154-D.154【答案】C【分析】利用三角函数的诱导公式和同角三角函数的基本关系即可求解.【详解】因为1sin 4α=,且π,π2α⎛⎫∈ ⎪⎝⎭,所以15cos 4α==-,又因为cos()cos αα-=,所以15cos()4α-=-,故选:C .二、单项选择题(共28小题,每小题3分,共84分)9.已知向量,a b满足||1,||2,a b a b ==⋅=r r r r ,a b的夹角为()A.30 B.60C.120D.150【答案】D【分析】根据向量的夹角公式运算求解.【详解】由题意可得:3cos ,2a b a b a b ⋅==-r rr r r r ,∵[],0,πa b ∈,∴向量,a b的夹角为150︒.故选:D10.已知函数21,0()log (2),0x x f x x x -≤⎧=⎨+>⎩,则()f x 的最小值是()A.1-B.0C.1D.2【答案】C【分析】求0x ≤时函数()f x 的最小值及0x >时函数()f x 的最小值,最后两个最小值比较,谁最小即为函数()f x 的最小值.【详解】当0x ≤时,函数()1f x x =-在(,0]-∞上单调递减,所以当0x =时,函数()1f x x =-有最小值为(0)1f =,当0x >时,函数2()log (2)f x x =+在(0,)+∞上单调递增,所以2()(0)log 21f x f >==,综上,当0x =时,函数21,0()log (2),0x x f x x x -≤⎧=⎨+>⎩有最小值为1.故选:C11.已知m ,n 是两条不同的直线,α是平面,则下列四个结论中正确的是()A.若m α⊥,n α⊥,则//m nB.若//m α,//n α,则//m nC.若m α⊥,m n ⊥,则//n αD.若m ,n 与α所成的角相等,则//m n【答案】A【分析】根据线面垂直的性质定理以及空间中线线垂直的关系可判断A 正确,C 错误;由线面平行性质定理以及线面角的定义可得BD 均错误.【详解】由线面垂直的性质定理可得垂直于同一平面的两直线平行,即A 正确;若//m α,//n α,可知m ,n 的位置关系可以是平行、相交或异面,即B 错误;若m α⊥,m n ⊥,则直线n 可以在平面α内,所以C 错误;由线面角的定义可知,若m ,n 与α所成的角相等,则m ,n 的位置关系可以是平行、相交或异面,即D 错误.故选:A12.在ABC 中,设3AD DB = ,CA a = ,CB b =uu r r ,则CD =()A.1344a b+ B.1344a b -C.1233a b +D.1233a b-【答案】A【分析】根据平面向量的线性运算法则,用CA 、CB表示出CD 即可.【详解】3313()4444CD CA AD CA AB CA CB CA CA CB =+=+=+-=+,则1344CD a b =+ ,故选:A .13.某快递驿站随机记录了7天代收快递的件数,如下表:天/第1234567件数285367463290335719698已知该驿站每代收1件快递收取0.8元服务费,据此样本数据,估计该驿站每月(按30天计算)收取的服务费是(单位:元)()A.8808B.9696C.10824D.11856【答案】C【分析】求出样本平均数,由此估计30天代收快递件数,并估算出服务费即可.【详解】样本数据7天代收快递的件数的平均数为:()12853674632903357196984517x =⨯++++++=(件),∴每月(按30天计算)代收快递约为4513013530⨯=件,∴该驿站每月(按30天计算)收取的服务费约为135300.810824⨯=元.故选:C.14.下列函数中,在区间(1,1)-上单调递减的是()A.()1f x x =-+B.()cos f x x= C.()e e x xf x -=+ D.1()ln1x f x x+=-【答案】A【分析】根据三角函数及复合函数的单调性逐项判断即可.【详解】对于A:()1f x x =-+在()1,-+∞上单调递减,A 正确;对于B:()cos f x x =在π,02⎛⎫-⎪⎝⎭上单调递增,在π0,2⎛⎫⎪⎝⎭上单调递减,B 错误;对于C:()e e x x f x -=+是1y t t=+,与e x t =复合在一起的复合函数,e xt =在(1,1)x ∈-是单调递增且1,e e t ⎛⎫∈ ⎪⎝⎭,1y t t =+在1,1e t ⎛⎫∈ ⎪⎝⎭是单调递减的,1y t t=+在()1,t e ∈是单调递增的,所以1()ln 1xf x x+=-在(1,0)x ∈-是单调递减的,在(0,1)x ∈是单调递增的,C 错误;对于D:1()ln 1xf x x +=-是ln y t =,与11x t x+=-,复合在一起的复合函数,11x t x+=-在(1,1)x ∈-是单调递增,ln y t =是单调递增的,所以1()ln 1xf x x+=-是在(1,1)x ∈-的单调递增的,D 错误.故选:A.15.设,a b R ∈,则“a b >”是“33a b >”的A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件【答案】C【分析】由“a b >”⇒“33a b >”,“33a b >”⇒“a b >”,即可得最后结果.【详解】∵函数()3f x x =在(),-∞+∞上单调递增,∴当a b >时,()()f a f b >,即33a b >,反之亦成立,∴“a b >”是“33a b >”的充分必要条件,故选C.【点睛】本题主要考查必要条件、充分条件、充分必要条件的性质和应用,属于基础题.16.将一块棱长为60cm 的正方体石块,磨制成一个球形石块,则最大球形石块的体积是(取π3=)()A.3864000cmB.3108000cm C.310800cm D.35400cm 【答案】B【分析】由题可得当球形石块半径等于正方体石块棱长时体积最大,根据球的体积公式计算可得结果.【详解】由题意可得,该问题相当于求正方体内切球体积,易知当石块直径等于正方体棱长时其体积最大,即最大球形石块的半径为30cm ,根据球的体积公式可得33334π430cm 108000cm 3V r ==⨯=.故选:B17.已知函数()sin()f x x ωϕ=+(0ω>,π0ϕ-<<)的图象如图所示,则ϕ的值是()A.7π10-B.9π10-C.π2-D.π5-【答案】A【分析】由图可得函数的最小正周期,从而可得ω,再利用待定系数法即可得解.【详解】由图可知π5ππ266T =-=,所以5π2π3T ω==,所以65ω=,则6()sin 5f x x ϕ⎛⎫=+⎪⎝⎭,把π,06⎛⎫⎪⎝⎭代入得,πsin 05ϕ⎛⎫+= ⎪⎝⎭,所以ππ2π,Z 52k k ϕ+=-+∈,则7π2π,Z 10k k ϕ=-+∈,又因π0ϕ-<<,所以7π10ϕ=-.故选:A.18.已知定义在R 上的偶函数()f x 在(],0-∞上是增函数,且()10f -=,则使()0f x >的x 的取值范围是()A.()1,0- B.()0,1 C.()1,1- D.()(),11,-∞-⋃+∞【答案】C【分析】使用函数的奇偶性和单调性进行求解即可.【详解】∵()f x 是定义在R 上的偶函数,在区间(],0-∞上单调递增,且(1)0f -=,∴()f x 在区间()0,∞+上单调递减,且()()110f f =-=,∴当(],0x ∈-∞时,()()()00110f x f f x x >⇔=-<⇔-<≤,当()0,x ∈+∞时,()()0()1001f x f x f x >⇔>=⇔<<,综上所述,x 的取值范围是()1,1-.故选:C.19.若圆锥的底面半径为3,体积为,则此圆锥的侧面展开图的圆心角是()A.π2B.2π3C.3π4D.3π2【答案】D【分析】根据圆锥底面半径和体积可计算出圆锥的母线,再根据侧面展开图的特征利用弧长公式即可得出圆心角.【详解】设圆锥的高为h ,母线为l ;将半径3r =代入体积公式21π3V r h ==可得,h =则母线长4l ==,设此圆锥的侧面展开图的圆心角为α,则其侧面展开图的半径为4R l ==,弧长为圆锥底面周长2π6πr =,所以圆心角6π3π42α==.故选:D20.某旅游爱好者想利用假期去国外的2个城市和国内的3个城市旅游,由于时间所限,只能在这5个城市中选择两个为出游地.若他用“抓阄”的方法从中随机选取2个城市,则选出的2个城市都在国内的概率是()A.35B.12C.13D.310【答案】D【分析】列举出所有的基本事件,得到基本事件的总数,找出满足条件的事件数,由概率公式求解即可.【详解】设国外的2个城市和国内的3个城市分别为:12123,,,,A A B B B ,则随机选取2个城市的基本事件为:()()()()()1211121321,,,,,,,,,A A A B A B A B A B ,()()()()()2223121323,,,,,,,,,A B A B B B B B B B 共10种,选出的2个城市都在国内的情况为:()()()121323,,,,,B B B B B B 共3种,故所求概率310P =.故选:D.21.已知0.12a -=,0.20.5b =,0.5log 0.2c =,则()A.c a b << B.c b a<< C.b a c<< D.a b c<<【答案】C【分析】根据指数函数、对数函数的性质,将a ,b ,c 与0和1进行比较即可.【详解】由已知0.12a -=,0.20.20.210.522b -⎛⎫=== ⎪⎝⎭∵指数函数()2xf x =在R 上单调递增,且值域为()0,∞+,∴()()()00.20.10f f f <-<-<,∴0.20.1002221--<<<=,即01b a <<<又∵对数函数()0.5log g x x =在区间()0,∞+单调递减,∴()()0.20.5g g >,即0.50.5log 0.2log 0.51>=,即1c >.综上所述,a ,b ,c 的大小关系为b a c <<.故选:C.22.已知0a >,0b >,24a b +=,则ab 的最大值是()A.B.2C. D.4【答案】B【分析】使用基本不等式求解即可【详解】∵0a >,0b >,24a b +=,∴由基本不等式有:22112142222222a b ab a b +⎛⎫⎛⎫=⋅⋅≤⋅=⋅= ⎪⎪⎝⎭⎝⎭,当且仅当2a b =,即2a =,1b =时,等号成立.∴当且仅当2a =,1b =时,ab 的最大值为2.故选:B.23.将函数sin 2cos 2y x x =+的图象向右平移π4个单位长度,所得图象的函数解析式可以是()A.2y x=B.π24y x ⎛⎫=- ⎪⎝⎭C.π24y x ⎛⎫=- ⎪⎝⎭ D.3π24y x ⎛⎫=+ ⎪⎝⎭【答案】B【分析】利用辅助角公式将函数写成π24y x ⎛⎫=+ ⎪⎝⎭,再根据平移规则即可得出相应的解析式.【详解】由sin 2cos 2y x x =+可得π24y x ⎛⎫=+ ⎪⎝⎭,将其图象向右平移π4个单位长度可得πππ22444y x x ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.故选:B24.某足球队进行点球训练,假设守门员不变,球员甲进球的概率为0.9,球员乙、丙进球的概率均为0.8.若3人各踢点球1次,且进球与否相互独立,则至少进2球的概率是()A.0.784B.0.864C.0.928D.0.993【答案】C【分析】利用相互独立事件的概率公式,求出3人都进球和3人中恰有2人进球的概率即可计算求解.【详解】由题意知:由相互独立事件的概率公式得,3人都进球的概率为0.90.80.80.576⨯⨯=,3人中恰有2人进球的概率0.90.80.20.90.80.20.10.80.80.352⨯⨯+⨯⨯+⨯⨯=,故至少进2球的概率为0.5760.3520.928+=,故选:C .25.若3cos 210cos 1αα+=,则cos 2cos αα+=()A.49-B.1-C.109D.1【答案】A【分析】由倍角公式结合换元法得出cos α,继而得出cos 2cos αα+的值.【详解】由题意可知()232cos 110cos 1αα-+=,令cos ,[1,1]t t α=∈-,则23520t t +-=解得1,23t t ==-(舍),故22cos 2cos 2cos 1cos 21t t αααα+=-+=+-2341999=+-=-.故选:A26.在ABC 中,若1BC =,3AC =,2cos 3C =,则sin B =()A.306B.155 C.106 D.105【答案】A【分析】根据余弦定理可计算出c =,再利用正弦定理即可得出30sin 6B =.【详解】由题意可得1BC a ==,3AC b ==,AB c =,由余弦定理可得2222cos 6c a b ab C =+-=,即c =又()2cos ,0,π3C C =∈可得5sin 3C =;利用正弦定理可知sin sin b c B C=,所以53sin 303sin 6b C B c ⨯===.故选:A27.如图所示的八面体的表面是由2个全等的等边三角形和6个全等的等腰梯形组成,设1111A A A B ==,2AB =,有以下四个结论:①BC ⊥平面12AA A ;②1//AA 平面22BB C C ;③直线1AA 与2CC 成角的余弦值为56④直线11A C 与平面22AA B B 所成角的正弦值为63.其中正确结论的个数是()A.1B.2C.3D.4【答案】C【分析】对于①.如图所示,连接12A A ,取BC 中点,D 取11B C 中点E .连接1,,A E AD DE ,证明1BC AA ⊥,2,BC AA ⊥即可判断;对于②③④,取AB 中点O ,建立如图所示的空间直角坐标系,设1O 是111A B C △的中心,2O 是ABC 的中心.过1A 作1AG AD ⊥,过E 作EH AD ⊥,再利用向量法计算即可判断得解.【详解】对于①.如图所示,连接12A A ,取BC 中点,D 取11B C 中点E .连接1,,A E AD DE .由等边三角形的性质得BC AD ⊥,由等腰梯形的性质得BC DE ⊥.又,,AD DE D AD DE =⊂ 平面1ADEA ,所以BC ⊥平面1ADEA .所以1BC AA ⊥.同理2,BC AA ⊥又1212,,AA AA A AA AA =⊂ 平面12AA A ,所以BC ⊥平面12AA A ,所以该结论正确;对于②,首先计算等腰梯形的高2213=1()22-=,再计算几何体111ABC A B C -的高.取AB 中点O ,建立如图所示的空间直角坐标系,设1O 是111A B C △的中心,2O 是ABC 的中心.过1A 作1AG AD ⊥,过E 作EH AD ⊥.2231333326DH O D O H =-=-⨯=.22336()()263HE =-=.所以几何体111ABC A B C -的高为63.所以()()()121361361,0,0,,,,1,0,0,3,0,,,263263A A B C B ⎛⎫⎛⎫--- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭.所以12136136(,,(1,3,0),(,,)263263AA BC BB ==-=-- ,设平面22BB C C 的法向量为111(,,)m x y z =,则112111·302,(3,1,1362·0263m BC x m m BB x y z ⎧=-=⎪∴=-⎨=-+-=⎪⎩,所以11362331()026323m AA =+-=≠,所以1//AA 平面22BB C C 不正确;对于③,由题得2226363,),(0,)3333C CC -∴=- .所以直线1AA 与2CC 336|()|5639613616436939⨯--=++⋅+,所以该结论正确;对于④,由题得11126133,),((2,0,0),3322C A C AB ∴== .2136(,,263BB =-- .设平面22AA B B 的法向量为222(,,)n x y z = ,则22222·20,(0,22,1)136·0263n AB x m n BB x y z ⎧==⎪∴=⎨=-+-=⎪⎩,所以直线11A C 与平面22AA B B 所成角的正弦值为3|22|623138144=+⋅+.所以该结论正确.故选:C28.河北雄安新区围绕职业培训、岗位开发、岗位对接等一系列工作,制定出台了《河北雄安新区当地劳动力教育培训实施方案(2019—2025年)》等30余项政策文件,截至2022年底,累计开展各项职业培训16.8万人次.雄安新区公共服务局为了解培训效果,对2022年参加职业技能培训的学员进行了考核测试,并从中随机抽取60名学员的成绩(满分100分),进行适当分组后(每组为左开右闭的区间),作出如图所示的频率分布直方图.这批学员技能考核测试成绩的众数的估计值是()A.65 B.75C.85D.95【答案】C【分析】根据频率分布直方图求众数的方法求解即可.【详解】根据频率分布直方图中频率值最大的组为(]80,90,则众数为8090852+=故选:C.29.河北雄安新区围绕职业培训、岗位开发、岗位对接等一系列工作,制定出台了《河北雄安新区当地劳动力教育培训实施方案(2019—2025年)》等30余项政策文件,截至2022年底,累计开展各项职业培训16.8万人次.雄安新区公共服务局为了解培训效果,对2022年参加职业技能培训的学员进行了考核测试,并从中随机抽取60名学员的成绩(满分100分),进行适当分组后(每组为左开右闭的区间),作出如图所示的频率分布直方图.这批学员技能考核测试成绩的中位数的估计值是()A.80.75 B.81.25C.82.50D.82.75【答案】B【分析】根据频率分布直方图进行中位数的估计即可.【详解】根据频率分布直方图可知前四组的频率分别为0.005100.05,0.015100.15,0.025100.25,0.040100.40⨯=⨯=⨯=⨯=,前三组频率之和为0.050.150.250.450.5++=<,所以中位数在(]80,90组,设中位数为x ,则()0.450.040800.5x +⨯-=,解得81.25x =.故这批学员技能考核测试成绩的中位数的估计值是81.25.故选:B.30.河北雄安新区围绕职业培训、岗位开发、岗位对接等一系列工作,制定出台了《河北雄安新区当地劳动力教育培训实施方案(2019—2025年)》等30余项政策文件,截至2022年底,累计开展各项职业培训16.8万人次.雄安新区公共服务局为了解培训效果,对2022年参加职业技能培训的学员进行了考核测试,并从中随机抽取60名学员的成绩(满分100分),进行适当分组后(每组为左开右闭的区间),作出如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则这批学员技能考核测试成绩的平均数的估计值是()A.79.0B.79.5C.81.0D.82.5【答案】B【分析】由频率分布直方图求平均数可将每一组数据的中点值乘以其对应的频率相加求和即可得出其平均数.【详解】根据题意可得,平均数的估计值为:()550.005650.015750.025850.04950.0151079.5⨯+⨯+⨯+⨯+⨯⨯=故选:B31.如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PCD 是等边三角形,平面PCD ⊥底面ABCD ,3AD =,四棱锥P ABCD -的体积为,E 为PC 的中点.线段AB 的长是()A.3B.C.D.6【答案】D【分析】设2AB a =,作出四棱锥的高,并用2AB a =求出高,再用体积解出a 即可.【详解】由已知,设2AB CD a ==,则矩形ABCD 的面积326ABCD S a a =⨯=,取CD 中点F ,连接PF ,∵PCD 是等边三角形,2PC PD CD a ===,∴PF CD ⊥,且PF =,∵平面PCD ⊥平面ABCD ,平面PCD 平面ABCD CD =,PF ⊂平面PCD ,∴PF ⊥平面ABCD ,即PF 是四棱锥P ABCD -的高,∴四棱锥P ABCD -的体积11633P ABCD ABCD V S PF a -=⋅=⨯=∴解得,3a =,∴26AB a ==.故选:D.32.如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PCD 是等边三角形,平面PCD ⊥底面ABCD ,3AD =,四棱锥P ABCD -的体积为,E 为PC 的中点.平面PAB 与平面ABCD 所成二面角的正切值是()A.2B.C.D.1【答案】B【分析】由PG ⊥底面ABCD 得出6CD =,进而由PF AB ⊥,FG AB ⊥得出平面PAB 与平面ABCD 所成二面角的正切值.【详解】分别取,CD AB 的中点为,G F ,连接,,,,G P FG P AG F B G ,设()2,0CD a a =>,则PG =.因为PCD 是等边三角形,所以PG CD ⊥,又因为平面PCD ⊥平面ABCD ,平面PCD 平面ABCD CD =,PG ⊂平面PCD ,PG ⊥底面ABCD ,因为四棱锥P ABCD -的体积为,所以1(32)3a ⨯=3a =.则PG FG ⊥,,PG AG PG BG ⊥⊥,所以PA PB =,PF AB ⊥,又因为底面ABCD 为矩形,所以FG AB ⊥,所以PFG ∠为平面PAB 与平面ABCD 所成二面角的平面角,33tan3PG PFG FG ∠===故选:B33.如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PCD 是等边三角形,平面PCD ⊥底面ABCD ,3AD =,四棱锥P ABCD -的体积为,E 为PC 的中点.直线DE 与平面PAD 所成角的正弦值是()A.2B.33C.13D.12【答案】D【分析】根据面面关系建立空间直角坐标系,由四棱锥P ABCD -的体积可得DC 长,从而可利用空间向量的坐标运算求得直线DE 与平面PAD 所成角的正弦值.【详解】取CD 中点为O ,AB 中点为M ,连接,OP OM ,因为PCD 是等边三角形,O 为CD 中点,所以OP CD ⊥,因为平面PCD ⊥底面ABCD ,平面PCD 底面ABCD CD =,OP ⊂平面PCD ,所以OP ⊥平面ABCD ,又,OM OC ⊂平面ABCD ,则,OP OM OP OC ⊥⊥,如图,以O 为原点,,,OM OC OP 分别为,,x y z轴建立空间直角坐标系,又1133332P ABCD V AD DC OP DC DC -=⋅⋅=⨯⋅⋅=,所以6DC =,则()()()(33,3,0,0,3,0,0,3,0,,0,,22A C D P E ⎛⎫-- ⎪ ⎪⎝⎭,所以90,,22DE ⎛⎫= ⎪ ⎪⎝⎭,设平面PAD 的法向量为(),,n x y z =,又()(3,0,0,DA DP == ,则3000300x x DA n y y DP n ⎧==⎧⎧⋅=⎪⎪⎪⇒⇒⎨⎨⎨+==⎪⎪⋅=⎪⎩⎩⎩,令1z =,则()0,n = ,所以9333122cos ,2n DE n DE n DE-+⋅===-⋅ ,则直线DE 与平面PAD 所成角的正弦值是12.故选:D .34.已知函数12()22x x f x a --=-+.若函数()f x 的最大值为1,则实数=a ()A.78-B.78C.98-D.98【答案】B【分析】令2x t -=,由指数函数的单调性以及二次函数的性质得出a .【详解】()2()222x xf x a --=-+,令()0,2xt -∈=+∞,则22112248y t t a t a ⎛⎫=-++=--++ ⎪⎝⎭,当1,24t x ==时,max 118y a =+=,解得78a =.故选:B35.已知函数12()22x x f x a --=-+.关于函数()f x 的单调性,下列判断正确的是()A.()f x 在(),2-∞上单调递增B.()f x 在(),2-∞上单调递减C.()f x 在1,4⎛⎫+∞⎪⎝⎭上单调递增 D.()f x 在1,4⎛⎫+∞⎪⎝⎭上单调递减【答案】A【分析】利用换元法,结合二次函数和指数函数的单调性,最后利用复合函数的单调性即可求解.【详解】令2(0)x t t -=>,函数12()22x x f x a --=-+可化为为22(0)y t t a t =-++>,因为函数22(0)y t t a t =-++>开口向上,对称轴为14t =,即2x =.当104t <<时,函数22(0)y t t a t =-++>单调递增;当14t >时,函数22(0)y t t a t =-++>单调递减,又因为2xy -=在R 上单调递减,由复合函数的单调性可得,函数()f x 在(,2)-∞上单调递增.故选:A .36.已知函数()1222xx f x a --=-+.若函数()f x 有两个零点1x 、2x ,给出下列不等式:①124x x +>;②()120f x x +<;③()121132f x x +->-;④()1220f x x +->.其中恒成立的个数是()A.1 B.2C.3D.4【答案】D【分析】分析可知12x -、22x -是关于t 的二次方程220t t a --=的两根,根据函数()22g t t t a =--有两个不等的正零点可求得1,08a ⎛⎫∈- ⎪⎝⎭,分析可得()1222x x a-+-=,利用指数函数的单调性可判断①;利用二次函数的基本性质可判断②③④的正误.【详解】()()12222222x x xx a f x a -----⨯=-++=,令()0f x =,则()22220x x a --⨯--=,令20x t -=>,可得220t t a --=,令()22g t t t a =--,则函数()g t 有两个不同的正零点,所以,()Δ18010400a g a =+>⎧⎪⎪>⎨⎪=->⎪⎩,解得108a -<<,由题意可知,12x -、22x -是关于t 的二次方程220t t a --=的两根,由韦达定理可得121212220,216x x x x a ----⎛⎫⋅==-∈ ⎪⎝⎭,所以,()12412216x x -+-<=,所以,()124x x -+<-,可得124x x +>,①对;由韦达定理可得()1222x x a -+-=,则()12122,08x xa -+⎛⎫=-⨯∈- ⎪⎝⎭,所以,()()()12122221222220222x x x x a a a a f x x a -+-+-⎛⎫+=-⨯+=-⨯-=< ⎪⎝⎭,②对;()()()()()()121212121221121132321212222282x x x x x x x x x x a f x x a a -+-+--+-+-+⎛⎫+-=-+=-+=-=-⋅- ⎪⎝⎭212,032a ⎛⎫=-∈- ⎪⎝⎭,③对;()()()()()121212212252212222228810x x x x x x f x x a a a a a a a -+-+--++-=-+=--+=--=-+>,④对.故选:D.。
2019-2020学年江西省九江市石门楼中学高三化学测试题含解析

2019-2020学年江西省九江市石门楼中学高三化学测试题含解析一、单选题(本大题共15个小题,每小题4分。
在每小题给出的四个选项中,只有一项符合题目要求,共60分。
)1. 2011年2月15日,备受全球关注的苹果股份有限公司,首次承认此前发生中毒事件的联建科技和运恒五金是其供应商,以及这两家工厂违规使用有毒原料对工人造成的危害的事实。
据了解此次中毒事件的“杀手”是一种分子式为C6H14的有机物。
已知C6H14有多种同分异构体,则其同分异构体中沸点最高的分子的一氯取代物的种数是A.2 B.3 C.4 D.5参考答案:B略2. 在一定条件下,某化合物X受热分解:2XA↑+2B↑+4C↑,测得反应后生成的混合气体对O2的相对密度为1.05,在相同条件下,X的相对分子质量是A.11.43B.117.6C.80.01D.160.02参考答案:B3. 室温下,CH3COOH的K a=1.7×10-5mol?L-1,NH3·H2O的K b=1.7×10-5 mol?L-1,下列说法不正确的是()A、室温下,相同浓度的CH3COOH与NH3·H2O的电离程度相同B、温度改变后,K a、K b都会发生改变C、室温下,CH3COOH溶液中的[H+]与NH3·H2O 中的[OH—]相等D、室温下,相同物质的量浓度时,CH3COOH溶液中的[H+]与NH3·H2O 中的[OH--]相等参考答案:略4. 某有机物的结构简式如图所示,有关该有机物的叙述不正确的是()A.在一定条件下,能发生取代、氧化、酯化和加聚反应B.该物质分子中最多可以有9个碳原子在同一平面上C.1 mol该物质最多可与4 mol H2发生加成反应D.1 mol该物质完全氧化最多可消耗13 mol氧气参考答案:B考点:有机物的结构和性质.专题:有机物的化学性质及推断.分析:由结构简式可知,分子中含﹣COOH、碳碳双键,结合羧酸、烯烃的性质以及苯环、烯烃的结构来解答.解答:解:A.含有羧基,可发生取代、酯化反应,含有碳碳双键,可发生氧化和加聚反应,故A正确;B.与苯环直接相连的原子在同一个平面上,且与碳碳双键直接相连的原子也在同一个平面上,则该物质分子中最多可以有11个碳原子在同一平面上,故B错误;C.能与氢气发生加成反应的为苯环和碳碳双键,则1 mol该物质最多可与4 mol H2发生加成反应,故C正确;D.有机物分子式为C9H12O2,1 mol该物质完全氧化最多可消耗氧气的物质的量为(11+﹣1)mol=13mol,故D正确.故选B.点评:本题考查有机物的结构与性质,为高频考点,把握官能团与性质的关系为解答的关键,侧重烯烃、羧酸性质的考查,题目难度不大.5. 使用化学手段可以消除某些环境污染。
