2015-2016学年辽宁省大连市庄河高中高一(上)期末数学试卷含答案

合集下载

辽宁省大连市高一数学上学期期末试卷(含解析)

辽宁省大连市2014-2015学年高一上学期期末数学试卷一．选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知点A（﹣3，1，5）与点B（0，2，3），则A，B之间的距离为（）A．B．2C．D．2．（5分）集合A={（x，y）|y=ax+1}，B={（x，y）|y=x+3}，且A∩B={（2，5）}，则（）A．a=3 B．a=2 C．a=﹣3 D．a=﹣23．（5分）a，b，c为空间中三条直线，若a⊥b，b⊥c，则直线a，c的关系是（）A．平行B．相交C．异面D．以上都有可能4．（5分）直线ax+by+c=0经过第一、第二、第四象限，则a，b，c应满足（）A．ab＞0，bc＞0 B．ab＞0，bc＜0 C．ab＜0，bc＞0 D．ab＜0，bc＜05．（5分）两条平行线l1：3x﹣4y﹣1=0与l2：6x﹣8y﹣7=0间的距离为（）A．B．C．D．16．（5分）若一个圆柱的侧面展开图是一个正方形，则这个圆柱的全面积与侧面积的比是（）A．B．C．D．7．（5分）若a=20.5，b=logπ3，c=log20.3，则（）A．b＞c＞a B．b＞a＞c C．c＞a＞b D．a＞b＞c8．（5分）若一个水平放置的图形的斜二测直观图是一个底角为45°且腰和上底均为1的等腰梯形，则原平面图形的面积是（）A．B．C．2+D．1+9．（5分）已知圆C：x2+y2=10，过点P（1，3）作圆C的切线，则切线方程为（）A．x+3y﹣10=0 B．x﹣3y+8=0 C．3x+y﹣6=0 D．3x﹣y+10=010．（5分）如图所示，已知三棱柱ABC﹣A1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥B1﹣ABC1的体积为（）A．B．C．D．11．（5分）已知函数f（x）=3﹣2|x|，g（x）=x2，构造函数F（x）=，那么函数y=F（x）（）A．有最大值1，最小值﹣1 B．有最小值﹣1，无最大值C．有最大值1，无最小值D．有最大值3，最小值112．（5分）若半径均为2的四个球，每个球都与其他三个球外切，另有一个小球与这四个球都外切，则这个小球的半径为（）A．B．﹣2 C．﹣3 D．2﹣2二．填空题（本大题共4小题，每小题5分，共20分，把答案填在答卷卡的相应位置上）13．（5分）计算（lg2）2+lg20•lg5=．14．（5分）一个几何体的三视图如图所示，俯视图为等边三角形，若其体积为8，则a=．15．（5分）已知两圆相交于两点（1，3）和（m，1），且两圆的圆心都在直线上，则m+c的值是．16．（5分）过点（2，3）且与圆（x﹣1）2+y2=1相切的直线方程．三．解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）17．（10分）如图，平面α⊥平面β，在α与β的交线l上取线段AB=4，AC、BD分别在平面α和平面β内，它们都垂直于交线l，并且AC=3，BD=12，求CD的长．18．（12分）设，其中a为常数；（1）f（x）为奇函数，试确定a的值；（2）若不等式f（x）+a＞0恒成立，求实数a的取值范围．19．（12分）圆C过点A（6，0），B（1，5），且圆心在直线l：2x﹣7y+8=0上．（1）求圆C的方程；（2）P为圆C上的任意一点，定点Q（8，0），求线段PQ中点M的轨迹方程．20．（12分）如图，菱形ABCD的边长为6，∠BAD=60°，对角线AC，BD相交于点O，将菱形ABCD沿对角线AC折起，得到三棱锥B﹣ACD，点M是棱BC的中点，DM=3．求证：（1）OM∥平面ABD；（2）平面ABC⊥平面MDO．21．（12分）已知函数f（x）=log4（ax2+2x+3）（1）若f（1）=1，求f（x）的单调区间；（2）是否存在实数a，使f（x）的最小值为0？若存在，求出a的值；若不存在，说明理由．22．（12分）在平面直角坐标系xOy中，点A（0，3），直线l：y=2x﹣4．（1）求以点A为圆心，以为半径的圆与直线l相交所得弦长；（2）设圆C的半径为1，圆心在l上．若圆C上存在点M，使|MA|=2|MO|，求圆心C的横坐标a的取值范围．辽宁省大连市2014-2015学年高一上学期期末数学试卷参考答案与试题解析一．选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知点A（﹣3，1，5）与点B（0，2，3），则A，B之间的距离为（）A．B．2C．D．考点：空间两点间的距离公式．专题：直线与圆．分析：根据空间两点间的距离公式进行计算即可．解答：解：∵A（﹣3，1，5），B（0，2，3），∴|AB|===，故选：C点评：本题主要考查空间两点间的距离的计算，比较基础．2．（5分）集合A={（x，y）|y=ax+1}，B={（x，y）|y=x+3}，且A∩B={（2，5）}，则（）A．a=3 B．a=2 C．a=﹣3 D．a=﹣2考点：交集及其运算．专题：集合．分析：根据A，B，以及两集合的交集，确定出a的值即可．解答：解：联立得：，把x=2，y=5代入得：5=2a+1，解得：a=2，故选：B．点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．3．（5分）a，b，c为空间中三条直线，若a⊥b，b⊥c，则直线a，c的关系是（）A．平行B．相交C．异面D．以上都有可能考点：空间中直线与直线之间的位置关系．专题：空间位置关系与距离．分析：根据空间直线垂直的位置关系进行判断即可．解答：解：如图满足a⊥b，b⊥c，则a，c的关系可能平行，可能相交，可能异面，故选D．点评：本题主要考查空间直线的位置关系的判断，比较基础．4．（5分）直线ax+by+c=0经过第一、第二、第四象限，则a，b，c应满足（）A．ab＞0，bc＞0 B．ab＞0，bc＜0 C．ab＜0，bc＞0 D．ab＜0，bc＜0考点：直线的一般式方程．专题：直线与圆．分析：直线ax+by+c=0化为：，利用斜率与截距的意义即可得出．解答：解：直线ax+by+c=0化为：，∵直线ax+by+c=0经过第一、第二、第四象限，∴，＜0，∴ab＞0，bc＜0．故选：B．点评：本题考查了直线斜率与截距的意义，属于基础题．5．（5分）两条平行线l1：3x﹣4y﹣1=0与l2：6x﹣8y﹣7=0间的距离为（）A．B．C．D．1考点：两条平行直线间的距离．专题：直线与圆．分析：把两直线的方程中x、y的系数化为相同的，然后利用两平行线间的距离公式，求得结果．解答：解：两条平行线l1：3x﹣4y﹣1=0，即6x﹣8y﹣2=0，与它平行的直线l2：6x﹣8y﹣7=0，故它们之间的距离为 d==，故选A．点评：本题主要考查两平行线间的距离公式的应用，要注意先把两直线的方程中x、y的系数化为相同的，然后才能用两平行线间的距离公式，属于中档题．6．（5分）若一个圆柱的侧面展开图是一个正方形，则这个圆柱的全面积与侧面积的比是（）A．B．C．D．考点：旋转体（圆柱、圆锥、圆台）．专题：空间位置关系与距离．分析：设侧面展开正方形边长为a，可得底面半径r满足：2πr=a，得r=，从而算出底面圆面积S底=，由此加以计算即可算出这个圆柱的全面积与侧面积的比．解答：解：∵圆柱的侧面展开图是一个正方形，∴设正方形的边长为a，可得圆柱的母线长为a，底面周长也等于a底面半径r满足：2πr=a，得r=，因此，该圆柱的底面圆面积为S底=πr2=，圆柱的全面积与侧面积的比为=，点评：本题给出侧面展开为正方形的圆柱，求全面积与侧面积之比．着重考查了圆柱的侧面展开和圆的周长、面积公式等知识，属于基础题．7．（5分）若a=20.5，b=logπ3，c=log20.3，则（）A．b＞c＞a B．b＞a＞c C．c＞a＞b D．a＞b＞c考点：对数值大小的比较．专题：函数的性质及应用．分析：利用对数函数与指数函数的单调性即可得出．解答：解：∵a=20.5＞1，1＞b=logπ3＞0，c=log20.3＜0，∴a＞b＞c．故选：D．点评：本题考查了对数函数与指数函数的单调性，属于基础题．8．（5分）若一个水平放置的图形的斜二测直观图是一个底角为45°且腰和上底均为1的等腰梯形，则原平面图形的面积是（）A．B．C．2+D．1+考点：斜二测法画直观图．专题：空间位置关系与距离．分析：水平放置的图形为直角梯形，求出上底，高，下底，利用梯形面积公式求解即可．解答：解：水平放置的图形为一直角梯形，由题意可知上底为1，高为2，下底为1+，S=（1++1）×2=2+．故选：C点评：本题考查水平放置的平面图形的直观图斜二测画法，也可利用原图和直观图的面积关系求解．属基础知识的考查．9．（5分）已知圆C：x2+y2=10，过点P（1，3）作圆C的切线，则切线方程为（）A．x+3y﹣10=0 B．x﹣3y+8=0 C．3x+y﹣6=0 D．3x﹣y+10=0考点：圆的切线方程．专题：计算题；直线与圆．分析：判断出P在圆上即P为切点，根据圆的切线垂直于过切点的直径，由圆心和P的坐标求出CP确定直线方程的斜率，根据两直线垂直时斜率乘积为﹣1，求出切线的斜率，根据P 坐标和求出的斜率写出切线方程即可．解答：解：由点P（1，3），圆x2+y2=10，得到P在圆上，则过P作圆的切线与CP所在的直线垂直，因为CP所在直线的斜率为3，所以切线的斜率为﹣，则切线方程为：y﹣3=﹣（x﹣1）即x+3y﹣10=0．点评：此题考查学生掌握点与圆的位置关系及直线与圆的位置关系，掌握两直线垂直时斜率所满足的关系，会根据一点的坐标和直线的斜率写出直线的方程，是一道综合题．10．（5分）如图所示，已知三棱柱ABC﹣A1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥B1﹣ABC1的体积为（）A．B．C．D．考点：直线与平面垂直的性质；棱柱、棱锥、棱台的体积．专题：计算题；空间位置关系与距离．分析：根据题意，三棱柱ABC﹣A1B1C1是棱长均为1的正三棱柱，算出它的体积V=．再根据锥体的体积公式得三棱锥A﹣A1B1C1、三棱锥C1﹣ABC的体积都等于三棱柱ABC﹣A1B1C1体积的，由此用三棱柱ABC﹣A1B1C1体积减去两个三棱锥的体积，即可算出三棱锥B1﹣ABC1的体积．解答：解：∵三棱柱ABC﹣A1B1C1的所有棱长均为1，∴底面△ABC为正三角形，面积S△ABC==又∵AA1⊥底面AB C，AA1=1∴三棱柱ABC﹣A1B1C1的体积V=S△ABC•AA1=∵三棱锥A﹣A1B1C1、三棱锥C1﹣ABC与三棱柱ABC﹣A1B1C1等底等高∴V=V=V=由此可得三棱锥B1﹣ABC1的体积V=V﹣V﹣V=故选：A点评：本题给出棱长均为1的正三棱柱，求其中的三棱锥B1﹣ABC1体积．着重考查了正三棱柱的性质、柱体和锥体的体积公式等知识，属于中档题．11．（5分）已知函数f（x）=3﹣2|x|，g（x）=x2，构造函数F（x）=，那么函数y=F（x）（）A．有最大值1，最小值﹣1 B．有最小值﹣1，无最大值C．有最大值1，无最小值D．有最大值3，最小值1考点：函数的最值及其几何意义．专题：计算题；作图题；函数的性质及应用．分析：由g（x）﹣f（x）=x2﹣3+2|x|≥0得|x|≥1，从而可得F（x）=，作函数图象求解．解答：解：由g（x）﹣f（x）=x2﹣3+2|x|≥0得，|x|≥1；故F（x）=；故作F（x）=的图象如下，故有最大值1，没有最小值．故选C．点评：本题考查了函数的图象的应用，属于中档题．12．（5分）若半径均为2的四个球，每个球都与其他三个球外切，另有一个小球与这四个球都外切，则这个小球的半径为（）A．B．﹣2 C．﹣3 D．2﹣2考点：球的体积和表面积．专题：计算题；空间位置关系与距离；球．分析：将这四个球的球心连接成一个正四面体，并根据四球外切，得到四面体的棱长为2，求出外接球半径，由于这四个球之间有一个小球和这四个球都外切，则小球的球心与四面体外接球球心重合，进而再由小球与其它四球外切，球心距（即正四面体外接球半径）等于大球半径与小球半径之和，得到答案．解答：解：连接四个球的球心，得到一个棱长为4的正四面体，可将该正四面体补成一个正方体，设正方体的边长为a，则有4=a，由正方体的对角线长即为球的直径，可得a=2r，则该正四面体的外接球半径为，若这四个球之间有一个小球和这四个球都外切，则小球的球心与四面体的外接球球心重合，因为由小球与其它四球外切，所以球心距（即正四面体外接球半径）等于大球半径与小球半径之和，所以小球的半径为﹣2．故选B．点评：本题考查棱锥的结构特征，球的结构特征，其中根据已知条件求出四个半径为2的球球心连接后所形成的正四面体的棱长及外接球半径的长是解答本题的关键．二．填空题（本大题共4小题，每小题5分，共20分，把答案填在答卷卡的相应位置上）13．（5分）计算（lg2）2+lg20•lg5=1．考点：对数的运算性质．专题：函数的性质及应用．分析：利用对数的运算法则、lg2+lg5=1即可得出．解答：解：原式=（lg2）2+（lg2+1）•lg5=lg2（lg2+lg5）+lg5=lg2+lg5=1．故答案为：1．点评：本题考查了对数的运算法则、lg2+lg5=1，属于基础题．14．（5分）一个几何体的三视图如图所示，俯视图为等边三角形，若其体积为8，则a=2．考点：棱柱、棱锥、棱台的体积．专题：空间位置关系与距离．分析：由三视图可知：该几何体为正三棱柱，底面正三角形的边上的高为2，棱柱的高为a，即可得出该几何体的体积．解答：解：由三视图可知：该几何体为正三棱柱，底面正三角形的边上的高为2，棱柱的高为a，∴底面正三角形的边长=4，∴该正三棱柱的体积V==，解得a=2．故答案为：2．点评：本题主要考查了正三棱柱的三视图及其体积计算公式、等边三角形的边角关系等基础知识，考查空间想象能力、推理论证能力、运算求解能力、化归与转化能力，属于中档题．15．（5分）已知两圆相交于两点（1，3）和（m，1），且两圆的圆心都在直线上，则m+c的值是3．考点：相交弦所在直线的方程；直线的一般式方程与直线的垂直关系．专题：计算题．分析：两圆的公共弦的方程与两圆连心线垂直，求出公共弦的方程，然后求出m，利用中点在连心线上，求出c，即可求出结果．解答：解：已知两圆相交于两点（1，3）和（m，1），且两圆的圆心都在直线上，所以公共弦方程为：y﹣3=﹣1（x﹣1），所以x+y﹣4=0，因为（m，1）在公共弦上，m=3；中点在连心线上，即（2，2）在连心线上，所以c=0，所以m+c=3；故答案为：3．点评：本题是基础题，考查两圆的位置关系，公共弦的方程与连心线方程的关系，考查计算能力，逻辑推理能力．16．（5分）过点（2，3）且与圆（x﹣1）2+y2=1相切的直线方程4x﹣3y+1=0或 x=2．考点：圆的切线方程．专题：计算题；分类讨论．分析：当切线的斜率不存在时，写出切线的方程；当切线的斜率存在时，设出切线的方程，由圆心到切线的距离等于半径求出斜率，从而得到切线的方程．解答：解：当切线的斜率不存在时，切线的方程为 x=2，当切线的斜率存在时，设切线的斜率为 k，则切线的方程为 y﹣3=k（x﹣2），即 kx﹣y+3﹣2k=0，由圆心（1，0）到切线的距离等于半径得∴k=，此切线的方程 4x﹣3y+1=0，综上，圆的切线方程为 x=2或4x﹣3y+1=0，故答案为：x=2或4x﹣3y+1=0．点评：本题考查求圆的切线方程的方法，点到直线的距离公式的应用，体现了分类讨论的数学思想．三．解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）17．（10分）如图，平面α⊥平面β，在α与β的交线l上取线段AB=4，AC、BD分别在平面α和平面β内，它们都垂直于交线l，并且AC=3，BD=12，求CD的长．考点：与二面角有关的立体几何综合题；平面与平面垂直的性质．专题：空间位置关系与距离．分析：连接BC．由AC⊥l，利用勾股定理可得BC=．利用面面垂直与线面垂直的判定及其性质定理可得BD⊥BC．再利用勾股定理可得CD=，即可得出．解答：解连接BC．∵AC⊥l，∴BC===5．又∵BD⊥l，α⊥β，α∩β=l，∴BD⊥α．又∵BC⊂α，∴BD⊥BC．∴CD===13．∴CD长为13cm．点评：本题考查了面面垂直与线面垂直的判定及其性质定理、勾股定理，考查了空间想象能力，考查了推理能力与计算能力，属于中档题．18．（12分）设，其中a为常数；（1）f（x）为奇函数，试确定a的值；（2）若不等式f（x）+a＞0恒成立，求实数a的取值范围．考点：函数恒成立问题；函数奇偶性的性质．专题：综合题；函数的性质及应用．分析：（1）由奇函数定义可得f（﹣x）=﹣f（x）恒成立，由此可得a值；（2）f（x）+a＞0恒成立，可化为2a＞恒成立，等价于2a＞（）max，利用基本函数的性质可求得（）max；解答：解：（1）∵f（x）为奇函数，∴f（﹣x）=﹣f（x），即a﹣=﹣a+，∴2a=+=+=2，∴a=1；（2）f（x）+a＞0恒成立，即a﹣+a＞0，2a＞恒成立，等价于2a＞（）max，而2x＞0，2x+1＞1，∴0＜＜2，故2a≥2，解得a≥1，故实数a的取值范围可得函数f（x）=log4（﹣x2+2x+3）∵真数为﹣x2+2x+3＞0⇒﹣1＜x＜3∴函数定义域为（﹣1，3）令t=﹣x2+2x+3=﹣（x﹣1）2+4可得：当x∈（﹣1，1）时，t为关于x的增函数；当x∈（1，3）时，t为关于x的减函数．∵底数为4＞1∴函数f（x）=log4（﹣x2+2x+3）的单调增区间为（﹣1，1），单调减区间为（1，3）（2）设存在实数a，使f（x）的最小值为0，由于底数为4＞1，可得真数t=ax2+2x+3≥1恒成立，且真数t的最小值恰好是1，即a为正数，且当x=﹣=﹣时，t值为1．∴⇒⇒a=因此存在实数a=，使f（x）的最小值为0．点评：本题借助于一个对数型函数，求单调性与最值的问题，着重考查了函数的单调性与值域和二次函数的图象与性质等知识点，属于中档题．22．（12分）在平面直角坐标系xOy中，点A（0，3），直线l：y=2x﹣4．（1）求以点A为圆心，以为半径的圆与直线l相交所得弦长；（2）设圆C的半径为1，圆心在l上．若圆C上存在点M，使|MA|=2|MO|，求圆心C的横坐标a的取值范围．考点：直线和圆的方程的应用．专题：直线与圆．分析：（1）设直线l：y=2x﹣4与圆A相交的弦为线段BC，求出圆心到直线l的距离，利用垂径定理求解即可．（2）设圆C的方程为（x﹣a）2+2=1．设点M（x，y），通过|MA|=2|MO|，化简，利用点M（x，y）在圆C上，推出|2﹣1|≤|CD|≤2+1，求解即可．解答：解：（1）设直线l：y=2x﹣4与圆A相交的弦为线段BC则圆心到直线l的距离．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）由题意知，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）解得．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）（2）因为圆心在直线y=2x﹣4上，所以圆C的方程为（x﹣a）2+2=1．设点M（x，y），因为|MA|=2|MO|，所以，化简得x2+y2+2y﹣3=0，即x2+（y+1）2=4，所以点M在以D（0，﹣1）为圆心，2为半径的圆上．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）由题意，点M（x，y）在圆C上，所以M 是圆C与圆D的公共点，则|2﹣1|≤|CD|≤2+1，所以．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）即得所以点C的横坐标a的取值范围为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）点评：本题考查圆的方程的应用，直线与圆的位置关系，考查分析问题解决问题的能力．。

[精品]辽宁省大连市高一上期末数学试卷有答案

2016-2017学年辽宁省大连市高一（上）期末数学试卷一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）设集合A={﹣1，0}，B={0，1，2}，则A∪B=（）A．{0} B．{﹣1，0} C．{1，2} D．{﹣1，0，1，2}2．（5分）在空间直角坐标系中，点P（3，﹣2，1）关于x轴的对称点坐标为（）A．（3，2，﹣1）B．（﹣3，﹣2，1）C．（﹣3，2，﹣1）D．（3，2，1）3．（5分）若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中的真命题是（）A．若m⊂β，α⊥β，则m⊥αB．若α∩γ=m，β∩γ=n，m∥n，则α∥βC．若m⊥β，m∥α，则α⊥βD．若α⊥γ，α⊥β，则β⊥γ4．（5分）如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A．（2+）πB．4π C．（2+2）πD．6π5．（5分）设f（x）=3x+3x﹣8，用二分法求方程3x+3x﹣8=0在x∈（1，2）内近似解的过程中得f（1）＜0，f（1.5）＞0，f（1.25）＜0，则方程的根落在区间（）A．（1，1.25） B．（1.25，1.5）C．（1.5，2）D．不能确定6．（5分）过点（0，3）且与直线2x+y﹣5=0垂直的直线方程为（）A．2x+y﹣3=0 B．x+2y﹣6=0 C．x﹣2y+6=0 D．2x﹣y+3=07．（5分）函数y=x﹣的图象大致为（）A．B．C．D．8．（5分）已知圆：C1：（x+1）2+（y﹣1）2=1，圆C2与圆C1关于直线x﹣y﹣1=0对称，则圆C2的方程为（）A．（x﹣2）2+（y﹣2）2=1 B．（x+2）2+（y+2）2=1 C．（x+2）2+（y﹣2）2=1 D．（x﹣2）2+（y+2）2=19．（5分）已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是（）A．B．C．D．10．（5分）已知a=log23，b=20.5，，则a，b，c从大到小的顺序为（）A．c＞b＞a B．b＞c＞a C．a＞b＞c D．c＞a＞b11．（5分）对于每个实数x，设f（x）取，y=|x﹣2|两个函数中的较小值．若动直线y=m与函数y=f（x）的图象有三个不同的交点，它们的横坐标分别为x1、x2、x3，则x1+x2+x3的取值范围是（）A．（2，）B．（2，）C．（4，）D．（0，）12．（5分）已知两点A（0，0），B（2，2）到直线l的距离分别为1和2，这样的直线l条数为（）A．1条B．2条C．3条D．4条二．填空题（本大题共4小题，每小题5分，共20分，把答案填在答卷卡的相应位置上）13．（5分）已知正四棱锥的底面边长为4cm，高与侧棱夹角为45°，则其斜高长为（cm）．14．（5分）已知圆C：x2+y2=9，过点P（3，1）作圆C的切线，则切线方程为．15．（5分）若函数f（x）=lg（x2+ax﹣a﹣1）在区间[2，+∞）上单调递增，则实数a的取值范围是．16．（5分）已知正三棱柱的棱长均为2，则其外接球体积为．三．解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）．17．（10分）已知函数f（x）=．（I）求f（0），f（1）；（II）求f（x）值域．18．（12分）△ABC三个顶点坐标为A（0，1），B（0，﹣1），C（﹣2，1）．（I）求AC边中线所在直线方程；（II）求△ABC的外接圆方程．19．（12分）已知正方体ABCD﹣A1B1C1D1，O是底ABCD对角线的交点．求证：（1）C1O∥面AB1D1；（2）A1C⊥面AB1D1．20．（12分）如图，有一个正三棱锥的零件，P是侧面ACD上的一点．过点P作一个与棱AB 垂直的截面，怎样画法？并说明理由．21．（12分）已知函数f（x）=．（Ⅰ）证明：f（x）为奇函数；（Ⅱ）判断f（x）单调性并证明；（III）不等式f（x﹣t）+f（x2﹣t2）≥0对于x∈[1，2]恒成立，求实数t的取值范围．22．（12分）平面内有两个定点A（1，0），B（1，﹣2），设点P到A、B的距离分别为d，1，且=d2（ I）求点P的轨迹C的方程；（ II）是否存在过点A的直线l与轨迹C相交于E、F两点，满足（O为坐标原点）．若存在，求出直线l的方程；若不存在，请说明理由．2016-2017学年辽宁省大连市高一（上）期末数学试卷参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）设集合A={﹣1，0}，B={0，1，2}，则A∪B=（）A．{0} B．{﹣1，0} C．{1，2} D．{﹣1，0，1，2}【解答】解：∵A={﹣1，0}，B={0，1，2}，∴A∪B={﹣1，0，1，2}，故选：D．2．（5分）在空间直角坐标系中，点P（3，﹣2，1）关于x轴的对称点坐标为（）A．（3，2，﹣1）B．（﹣3，﹣2，1）C．（﹣3，2，﹣1）D．（3，2，1）【解答】解：∵在空间直角坐标系中，点（x，y，z）关于x轴的对称点的坐标为：（x，﹣y，﹣z），∴点P（3，﹣2，1）关于x轴的对称点的坐标为：（3，2，﹣1）．故选：A3．（5分）若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中的真命题是（）A．若m⊂β，α⊥β，则m⊥αB．若α∩γ=m，β∩γ=n，m∥n，则α∥βC．若m⊥β，m∥α，则α⊥βD．若α⊥γ，α⊥β，则β⊥γ【解答】解：对于A，m⊂β，α⊥β，则m与α的关系有三种，即m∥α、m⊂α或m与α相交，选项A错误；对于B，α∩γ=m，β∩γ=n，若m∥n，则α∥β或α与β相交，选项B错误；对于C，m⊥β，m∥α，则α内存在与m平行的直线与β垂直，则α⊥β，选项C正确；对于D，α⊥γ，α⊥β，则β与γ可能平行，也可能相交，选项D错误．故选：C．4．（5分）如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A．（2+）πB．4π C．（2+2）πD．6π【解答】解：由已知的三视图可得：该几何体是一个半球与一个圆锥组合而成的几何体，半球的半径为1，故半球面面积为：2π，圆锥的底面半径为1，高为2，故母线长为，故圆锥的侧面积为：π，故组合体的表面积是：（2+）π，故选：A5．（5分）设f（x）=3x+3x﹣8，用二分法求方程3x+3x﹣8=0在x∈（1，2）内近似解的过程中得f（1）＜0，f（1.5）＞0，f（1.25）＜0，则方程的根落在区间（）A．（1，1.25） B．（1.25，1.5）C．（1.5，2）D．不能确定【解答】解析：∵f（1.5）•f（1.25）＜0，由零点存在定理，得，∴方程的根落在区间（1.25，1.5）．故选B．6．（5分）过点（0，3）且与直线2x+y﹣5=0垂直的直线方程为（）A．2x+y﹣3=0 B．x+2y﹣6=0 C．x﹣2y+6=0 D．2x﹣y+3=0【解答】解：设与直线2x+y﹣5=0垂直的直线方程为x﹣2y+c=0，把点（0，3）代入，得0﹣6+c=0，解得c=6，∴过点（0，3）且与直线2x+y﹣5=0垂直的直线方程是x﹣2y+6=0．故选C．7．（5分）函数y=x﹣的图象大致为（）A．B．C．D．【解答】解：令y=f（x）=x﹣x，∵f（﹣x）=﹣x+=﹣（x﹣）=﹣f（x），∴y=f（x）=x﹣x为奇函数，∴其图象关于原点成中心对称，故可排除C，D；又x=1时，y=1﹣1=0，当x＞1时，不妨令x=8，y=8﹣8=6＞0，可排除B，故选A．8．（5分）已知圆：C1：（x+1）2+（y﹣1）2=1，圆C2与圆C1关于直线x﹣y﹣1=0对称，则圆C2的方程为（）A．（x﹣2）2+（y﹣2）2=1 B．（x+2）2+（y+2）2=1 C．（x+2）2+（y﹣2）2=1 D．（x﹣2）2+（y+2）2=1【解答】解：在圆C2上任取一点（x，y），则此点关于直线x﹣y﹣1=0的对称点（y+1，x﹣1）在圆C1：（x+1）2+（y﹣1）2=1上，∴有（y+1+1）2+（x﹣1﹣1）2=1，即（x﹣2）2+（y+2）2=1，∴答案为（x﹣2）2+（y+2）2=1．故选：D．9．（5分）已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是（）A．B．C．D．【解答】解：由已知作出梯形ABCD是直角梯形，如右图：∵按照斜二测画法画出它的直观图A′B′C′D′，A′D′=2，B′C′=4，A′B′=1，∴直角梯形ABCD中，AB⊥BC，AD=A′D′=2，BC=B′C′=4，AB=2A′B′=2，过D作DE⊥BC，交BC于E，则DE=AB=2，EC=BC﹣AD=4﹣2=2，∴直角梯形DC边的长度为：=2．故选：B．3，b=20.5，，则a，b，c从大到小的顺序为（）10．（5分）已知a=log2A．c＞b＞a B．b＞c＞a C．a＞b＞c D．c＞a＞b3==＜=c，【解答】解：∵a=log2=＞b=20.5，∴c＞a＞b．故选：D．11．（5分）对于每个实数x，设f（x）取，y=|x﹣2|两个函数中的较小值．若动直线y=m与函数y=f（x）的图象有三个不同的交点，它们的横坐标分别为x1、x2、x3，则x1+x2+x3的取值范围是（）A．（2，）B．（2，）C．（4，）D．（0，）【解答】解：由2=|x﹣2|，平方得4x=x2﹣4x+4，即x2﹣8x+4=0，解得x=4+2或x=4﹣2，设x1＜x2＜x3，作出函数f（x）的图象如图：则0＜x1＜4﹣2，x2与x3，关于x=2对称，则x2+x3=4，则x1+x2+x3=x1+4，∵0＜x1＜4﹣2，∴4＜4+x1＜8﹣2，即x1+x2+x3的取值范围为（4，8﹣2 ），故选：C12．（5分）已知两点A（0，0），B（2，2）到直线l的距离分别为1和2，这样的直线l条数为（）A．1条B．2条C．3条D．4条【解答】解：到点A（0，0）距离为1的直线，可看作以A为圆心1为半径的圆的切线，同理到点B（2，2）距离为2的直线，可看作以B为圆心2为半径的圆的切线，故所求直线为两圆的公切线，又|AB|=2，所以2﹣1＜|AB|＜1+2，故两圆相交，公切线有2条，故选：B．二．填空题（本大题共4小题，每小题5分，共20分，把答案填在答卷卡的相应位置上）（5分）已知正四棱锥的底面边长为4cm，高与侧棱夹角为45°，则其斜高长为（cm）．13．【解答】解：如图所示：∠SBO=45°，OE=2cm，SO=OB=2，∴斜高为SE=﹣，故答案为．14．（5分）已知圆C：x2+y2=9，过点P（3，1）作圆C的切线，则切线方程为x=3或4x+3y ﹣15=0 ．【解答】解：圆心坐标为（0，0），半径为3，∵点P（3，1）在圆外，∴若直线斜率k不存在，则直线方程为x=3，圆心到直线的距离为3，满足相切．若直线斜率存在设为k，则直线方程为y﹣1=k（x﹣3），即kx﹣y+1﹣3k=0，则圆心到直线kx﹣y+1﹣3k=0的距离等于半径1，即d==1，解得k=﹣，此时直线方程为4x+3y﹣15=0，综上切线方程为x=3或4x+3y﹣15=0，故答案为：x=3或4x+3y﹣15=015．（5分）若函数f（x）=lg（x2+ax﹣a﹣1）在区间[2，+∞）上单调递增，则实数a的取值范围是（﹣3，+∞）．【解答】解：令t=x2+ax﹣a﹣1，外函数y=lgt为增函数，要使复合函数f（x）=lg（x2+ax﹣a﹣1）在区间[2，+∞）上单调递增，则，解得a＞﹣3．∴实数a的取值范围是：（﹣3，+∞）．故答案为：（﹣3，+∞）．16．（5分）已知正三棱柱的棱长均为2，则其外接球体积为．【解答】解：取三棱柱ABC﹣A′B′C′的两底面中心O，O′，连结OO′，取OO′的中点D，连结BD则BD为三棱柱外接球的半径．∵△ABC是边长为2的正三角形，O是△ABC的中心，∴BO=．又∵OD=1，∴BD=．∴三棱柱外接球的体积V=π×BD3=．故答案为．三．解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）．17．（10分）已知函数f（x）=．（I）求f（0），f（1）；（II）求f（x）值域．【解答】解：（I） f（0）=1，；（II）这个函数当x=0时，函数取得最大值1，当自变量x的绝对值逐渐变大时，函数值逐渐变小并趋向于0，但永远不会等于0，于是可知这个函数的值域为集合．18．（12分）△ABC三个顶点坐标为A（0，1），B（0，﹣1），C（﹣2，1）．（I）求AC边中线所在直线方程；（II）求△ABC的外接圆方程．【解答】解：（ I）由于AC的中点为（﹣1，1），B（0，﹣1），故AC边中线所在直线方程为2x+y+1=0．﹣﹣﹣﹣﹣﹣（6分）（ II）（方法一）设△ABC的外接圆方程为x2+y2+Dx+Ey+F=0，﹣﹣﹣﹣﹣﹣（8分）则把A，B，C的坐标代入可得，﹣﹣﹣﹣﹣（10分）求得，故要求的圆的方程为 x2+y2+2x﹣1=0．﹣﹣﹣﹣﹣（12分）（方法二）因为AC⊥BA，所以△ABC的外接圆是以Rt△ABC的斜边BC为直径的圆，﹣﹣﹣﹣（8分）则圆心坐标为BC中点（﹣1，0），半径为|BC|的一半是，﹣﹣﹣﹣﹣（10分）所以△ABC的外接圆方程是（x+1）2+y2=2．﹣﹣﹣﹣﹣（12分）19．（12分）已知正方体ABCD﹣A1B1C1D1，O是底ABCD对角线的交点．求证：（1）C1O∥面AB1D1；（2）A1C⊥面AB1D1．【解答】证明：（1）连接A1C1，设A1C1∩B1D1=O1，连接AO1，∵ABCD﹣A1B1C1D1是正方体，∴A1ACC1是平行四边形，∴A1C1∥AC且A1C1=AC，又O1，O分别是A1C1，AC的中点，∴O1C1∥AO且O1C1=AO，∴AOC1O1是平行四边形，∴C1O∥AO1，AO1⊂面AB1D1，C1O⊄面AB1D1，∴C1O∥面AB1D1；（2）∵CC1⊥面A1B1C1D1∴CC1⊥B1D!，又∵A1C1⊥B1D1，∴B1D1⊥面A1C1C，即A1C⊥B1D1，∵A1B⊥AB1，BC⊥AB1，又A1B∩BC=B，AB1⊥平面A1BC，又A1C⊂平面A1BC，∴A1C⊥AB1，又D1B1∩AB1=B1，∴A1C⊥面AB1D120．（12分）如图，有一个正三棱锥的零件，P是侧面ACD上的一点．过点P作一个与棱AB 垂直的截面，怎样画法？并说明理由．【解答】解：（方法一）画法：过点P在面ACD内作EF∥CD，交AC于E点，交AD于F点．过E作EG⊥AB，连接FG，平面EFG为所求．﹣﹣﹣﹣（4分）理由：取CD中点M，连接AM，BM．∵A﹣BCD为正三棱锥，∴AC=AD，BC=BD，∴BM⊥CD，AM⊥CD，﹣﹣﹣﹣（6分）AM∩BM=M，AM⊂平面ABM，BM⊂平面ABM，∴CD⊥平面ABM．﹣﹣﹣﹣（8分）∵AB⊂平面ABM，∴CD⊥AB．∵EF∥CD，∴EF⊥AB．﹣﹣﹣﹣（10分）过E作EG⊥AB，连接FG，∵EF∩EG=E．EF⊂面EFG，EG⊂面EFG，∴AB⊥面EFG．﹣﹣﹣﹣（12分）（方法二）画法：过C在平面ABC内M作CE⊥AB，垂足为E．连接DE．过点P作MN∥CD，交AC于M，AD于N．过M作MH∥CE，交AE于H，连接HN，平面HMN为所求．﹣﹣﹣﹣（4分）理由：∵△ABC≌△ABD，∴DE⊥AB．﹣﹣﹣﹣（6分）∵，，∴，∴HN∥DE，﹣﹣﹣﹣（8分）∴AB⊥HN．由画法知，AB⊥HM，∵HM∩HN=H，HM⊂面MNH，HN⊂面MNH，∴AB⊥平面MNH．﹣﹣﹣﹣（12分）21．（12分）已知函数f（x）=．（Ⅰ）证明：f（x）为奇函数；（Ⅱ）判断f（x）单调性并证明；（III）不等式f（x﹣t）+f（x2﹣t2）≥0对于x∈[1，2]恒成立，求实数t的取值范围．【解答】解：（Ⅰ）证明：对于函数f（x）=，其定义域为R，关于原点对称，∵，∴f（x）为奇函数．（ II）f（x）在R上为增函数．证明：根据题意，，在R内任取x1，x2，△x=x2﹣x1＞0，则，∵x2＞x1∴2x2＞2x1∴，∵，∴△y＞0．∴f（x）在R上为增函数．（ III）根据题意，f（x﹣t）+f（x2﹣t2）≥0⇔f（x﹣t）≥﹣f（x2﹣t2），又由f（x）为奇函数，∵f（x﹣t）≥﹣f（x2﹣t2）=f（t2﹣x2），又∵f（x）在R上为增函数，∴当x∈[1，2]时，x﹣t≥t2﹣x2恒成立，即x2+x≥t2+t恒成立，=2，而x∈[1，2]时，（x2+x）min则x2+x≥t2+t恒成立⇔t2+t≤2，解得﹣2≤t≤1，即t的取值范围是[﹣2，1]．22．（12分）平面内有两个定点A（1，0），B（1，﹣2），设点P到A、B的距离分别为d，1，且=d2（ I）求点P的轨迹C的方程；（ II）是否存在过点A的直线l与轨迹C相交于E、F两点，满足（O为坐标原点）．若存在，求出直线l的方程；若不存在，请说明理由．【解答】（本小题12分）（Ⅰ）设P（x，y），=，则，d2∵，∴，﹣﹣﹣﹣（2分）整理得：（x﹣1）2+（y+4）2=8，∴点P的轨迹C的方程为（x﹣1）2+（y+4）2=8．﹣﹣﹣﹣（4分）=．（ II）存在过点A的直线l，l与轨迹C相交于E，F两点，且使三角形S△OEF理由如下：①当直线l的斜率不存在时，直线l的方程为x=1，直线过圆心，，点O到直线l的距离为1，此时，，所以成立．﹣﹣﹣﹣（6分）②当直线l斜率存在时，设l方程为：y=k（x﹣1）．点C到l的距离，利用勾股定理，得：．﹣﹣﹣﹣（8分）点O到l的距离，∴，﹣﹣﹣﹣（10分）整理得3k2=﹣1，无解．所以直线斜率存在时满足题意的直线不存在．综上，存在过点A的直线l：x=1，满足题意．﹣﹣﹣﹣（12分）（其它做法相应给分）。

辽宁省庄河市高级中学上册期末精选单元测试卷附答案

辽宁省庄河市高级中学上册期末精选单元测试卷附答案一、第一章运动的描述易错题培优（难）1．A、B、C三个物体同时在同一地点沿同一方向做直线运动，如图为他们的位移﹣﹣时间图象，由图象可知，物体在t o时间内（）A．A物体的平均速度最大B．三个物体的平均速度一样大C．三个物体的平均速率一样大D．三个物体的平均速率关系为V A＞V B=V C【答案】BD【解析】由图象看出，在0～t0时间内，三个物体的位移△x相同，所用时间相同，则平均速度都相同，故A错误、B正确；由图象看出，在0～t0时间内，A的路程最大，BC路程相等，故三个物体的平均速率关系为v A＞v B=v C，故C错误，D正确；故选BD.点睛：本题关键抓住位移图象的斜率大小等于速度、纵坐标的变化量表示位移来分析图象的意义；注意理解BC的运动特点．2．一物体做加速度不变的直线运动,某时刻速度的大小为4 m/s, 1 s后速度的大小变为5m/s,则在这1 s内该物体( )A．速度变化的大小可能为3m/s B．速度变化的大小可能为9m/sC．加速度的大小可能为3m/s2D．加速度的大小可能为1m/s2【答案】BD【解析】【分析】【详解】取v1的方向为正方向，则v1=4m/s，若v2 =5m/s，速度的变化为v2-v1=1m/s，即速度变化大小为1m/s，加速度为1m/s2，加速度大小为1 m/s2，若v2 =-5m/s，速度的变化为v2-v1 =-9m/s，即速度变化大小就为9m/s了，加速度为-9m/s2，加速度大小为9m/s2．所以选BD．3．如图所示为某质点的速度-时间图象，则下列说法中正确的是（）A ．在0～6s 内，质点做匀变速直线运动B ．在t =12s 末，质点的加速度为-1m /s 2C ．在6～10s 内，质点处于静止状态D ．在4s 末，质点运动方向改变【答案】B 【解析】在0～4s 内，质点的加速度为64v a t ∆==∆ =1.5（m/s 2），在4-6s 内质点的加速度为：4-62v a t ∆==∆=-1（m/s 2），两段时间内的加速度不同，所以在0～6s 内，质点做非匀变速直线运动，故A 错误；在t=12s 末，质点的加速度为a=044v a t ∆-==∆=-1（m/s 2），故B 正确．在6s ～10s 内，质点以4m/s 的速度做匀速运动，故C 错误；在0-14s 内，质点的速度都为正，一直沿正方向运动，故在4s 末速度方向没有改变，故D 错误；故选B.点睛：本题考查学生对v-t 图象的认识，记住图象的斜率表示加速度，图象与时间轴围成的面积表示这段时间内物体通过的位移．4．甲、乙、丙三个物体同时同地出发做直线运动,它们的位移一时间图象如图所示,在20s 内它们的平均速度和平均速率的大小关系是( )A ．平均速度大小相等，平均速率v v v >=甲乙丙B ．平均速度大小相等，平均速率v v v >>甲乙丙C ．平均速度v v v >>甲乙丙，平均速率相等D ．平均速度和平均速率大小均相等【答案】A 【解析】【分析】平均速度等于位移与所用时间的比值．平均速率等于路程与所用时间的比值．根据位移图象确定出位移关系，分析物体的运动情况，确定出路程关系，再进行判断平均速度和平均速率的关系．【详解】由图看出，三个物体的起点与终点相同，位移相同，所用时间也相同，则三个物体的平均速度大小相同．由图得知，甲先沿正方向运动，后沿负方向返回，而乙、丙都一直沿正方向运动，三个物体的位移相同，则甲的路程最大，乙丙的路程相等，所以甲的平均速率最＞，故选A．大，乙丙的平均速率相等，即v v v甲乙丙【点睛】由位移图象纵坐标的变化量等于位移，能判断出物体的位移关系．根据位移图象的斜率等于速度分析物体的运动情况，确定路程关系，是本题解答的基本思路．5．2015年的股市经历了暴涨急跌，犹如过山车，目前在国家的积极救市下，正逐步回稳．如果将股价的“上涨”类比成运动学中的“加速”，将股价的“下跌”类比成运动学中的“减速”，你认为“股价下跌出现减缓趋势”可以类比成运动学中的（）A．速度增加，加速度减小B．速度增加，加速度增大C．速度减小，加速度减小D．速度减小，加速度增大【答案】C【解析】【分析】把股价类比成速度，股价下跌快慢类比成加速度，根据加速度与速度关系进行分析．【详解】股价类比成速度，股价下跌快慢类比成加速度，股价下跌出现减缓趋势，相当于加速度减小，但仍然在下跌，相当于加速度与速度方向相反，速度仍然减小．故C正确．【点睛】加速度决定于物体所受合力和物体的质量，与速度没有直接的关系，加速席减小，速度不一定减小．6．下列说法中正确的是（）A．研究短跑运动员的起跑动作时，可将运动员看做质点B．研究汽车在上坡时有无翻倒的危险时，可将汽车看做质点C．“两岸猿声啼不住，轻舟已过万重山”是以“万重山”为参考系的D．升国旗时，观察到国旗冉冉升起，观察者是以“国旗”为参考系的【答案】C【解析】【分析】【详解】A．研究短跑运动员的起跑动作时，运动员看成质点，否则的话就没有人的动作可言了，A 错误；B．研究汽车在上坡时有无翻倒的危险时，汽车的大小和形状不能忽略，故不能看作质点，B错误；C．“两岸猿声啼不住，轻舟已过万重山“是描述轻舟相对于“万重山”在运动，是以“万重山”为参考系的，C 正确；D ．升国旗时，观察到国旗冉冉升起，观察者是以大地为参考系的，D 错误。

15—16学年上学期高一期末考试化学试题(附答案)(2)

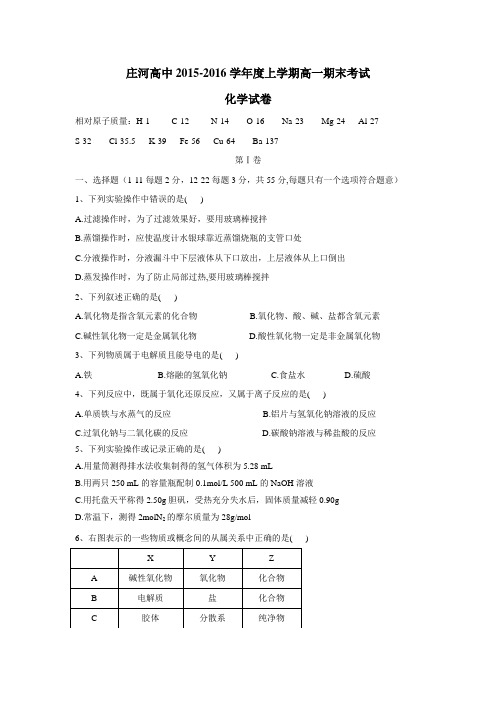
庄河高中2015-2016学年度上学期高一期末考试化学试卷相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27S-32 Cl-35.5 K-39 Fe-56 Cu-64 Ba-137第Ⅰ卷一、选择题（1-11每题2分，12-22每题3分，共55分,每题只有一个选项符合题意）1、下列实验操作中错误的是( )A.过滤操作时，为了过滤效果好，要用玻璃棒搅拌B.蒸馏操作时，应使温度计水银球靠近蒸馏烧瓶的支管口处C.分液操作时，分液漏斗中下层液体从下口放出，上层液体从上口倒出D.蒸发操作时，为了防止局部过热,要用玻璃棒搅拌2、下列叙述正确的是( )A.氧化物是指含氧元素的化合物B.氧化物、酸、碱、盐都含氧元素C.碱性氧化物一定是金属氧化物D.酸性氧化物一定是非金属氧化物3、下列物质属于电解质且能导电的是( )A.铁B.熔融的氢氧化钠C.食盐水D.硫酸4、下列反应中，既属于氧化还原反应，又属于离子反应的是( )A.单质铁与水蒸气的反应B.铝片与氢氧化钠溶液的反应C.过氧化钠与二氧化碳的反应D.碳酸钠溶液与稀盐酸的反应5、下列实验操作或记录正确的是( )A.用量筒测得排水法收集制得的氢气体积为5.28 mLB.用两只250 mL的容量瓶配制0.1mol/L 500 mL的NaOH溶液C.用托盘天平称得2.50g胆矾，受热充分失水后，固体质量减轻0.90gD.常温下，测得2molN2的摩尔质量为28g/mol6、右图表示的一些物质或概念间的从属关系中正确的是( )7、为了配制100mL1 mol/L的NaOH溶液，其中有下列几个操作,错误的是( )①NaOH用称量纸盛装进行称量；②选刚用蒸馏水洗净的100mL容量瓶进行配制；③NaOH在烧杯里刚完全溶解时，立即将溶液转移到容量瓶；④用蒸馏水洗涤烧杯内壁两次，洗涤液都移入容量瓶；⑤使蒸馏水沿着玻璃棒注入容量瓶，直到溶液的凹液面恰好跟刻度线相切。

辽宁省庄河市高级中学2016-2017学年高一上学期期末考试数学(理)试题含答案

庄河高中2016-2017学年度高一（上）期末考试理科数学试卷一、选择题：本大题共12个小题，每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合{1,2,3}M =，{2,3,4}N =，则下列式子正确的是（ )A ．M N ⊆B ．N M ⊆C ．{2,3}M N =∩D ．{1,4}M N =∪2.下列各组函数表示同一函数的是（） A ．()f x =2()g x =B ．()f x =()g x x =C ．()1f x =，9()g x x = D ．()1f x x =-，21()1x g x x -=+3。

已知0ab <，0bc <，则直线ax by c +=通过( ）A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限 4。

已知两条直线,m n ,两个平面,αβ，给出下面四个命题: ①//m n ,m n αα⊥⇒⊥；②//αβ，m α⊂，//n m n β⊂⇒； ③//m n ，////m n αα⇒；④//αβ，//m n ，m n αβ⊥⇒⊥ 其中正确命题的序号是（）A ．①④B ．②④ C. ①③ D ．②③ 5.已知()()()2f x x m x n =--+，并且,αβ是方程()0f x =的两根,则实数,,,m n αβ的大小关系可能是（）A ．a m n β<<<B ．m n αβ<<< C. m n αβ<<< D ．m n αβ<<< 6.若函数()log(01)af x x a =<<,在区间[,2]a a 上的最大值是最小值的3倍，则a 等于（）A ．14B ．22C 。

12D ．247。

已知三棱锥S ABC -的三条侧棱两两垂直，且24SA SB SC ===，，则该三棱锥的外接球的半径为（ )A ．3B ．6 C.36 D ．98.已知某几何体的俯视图是如图所示的边长为2的正方形，主视图与左视图是边长为2的正三角形,则其侧面积（）A ． 4B ．43C 。

辽宁省大连市高一上学期数学期末考试试卷

辽宁省大连市高一上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2018高二下·凯里期末) 已知集合，则（）A .B .C .D .2. （2分）直线经过点A（2，1），B（1，m2）两点（m∈R），那么直线l的倾斜角取值范围是（）A .B .C .D .3. （2分） (2017高三上·湖北开学考) 偶函数f（x）在（0，+∞）上递增，a=f（log2 ）b=f（）c=f （log32），则下列关系式中正确的是（）A . ＜b＜cB . a＜c＜bC . c＜a＜bD . c＜b＜a4. （2分） (2016高一下·老河口期中) 在棱长为1的正方体ABCD—A1B1C1D1中，M和N分别为A1B1和BB1的中点，那么直线AM与CN所成角的余弦值是（）A .B .C .D .5. （2分） (2016高一下·鹤壁期末) 若直线与直线2x+3y﹣6=0的交点位于第一象限，则直线l的倾斜角的取值范围（）A .B .C .D .6. （2分）若，则下列不等式成立的是（）A .B .C .D .7. （2分）已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4，则实数a的值是（）A . -10B . -8C . -4D . -28. （2分） (2016高一下·大连开学考) 已知正四棱柱ABCD﹣A1B1C1D1的底面边长为2，侧棱长为底面边长的2倍，E点为AD的中点，则三棱锥D﹣BEC1的体积为（）A .B . 4C .D . 89. （2分） (2016高一上·辽宁期中) 若x0是函数f（x）=2 的一个零点，x1∈（0，x0），x2∈（x0 ，+∞），则（）A . f（x1）＜0，f（x2）＜0B . f（x1）＞0，f（x2）＞0C . f（x1）＞0，f（x2）＜0D . f（x1）＜0，f（x2）＞010. （2分）(2013·山东理) 过点（3，1）作圆（x﹣1）2+y2=1的两条切线，切点分别为A，B，则直线AB 的方程为（）A . 2x+y﹣3=0B . 2x﹣y﹣3=0C . 4x﹣y﹣3=0D . 4x+y﹣3=011. （2分）已知正三棱锥P-ABC的主视图和俯视图如图所示,则此三棱锥的外接球的表面积为（）A . 4πB . 12πC .D .12. （2分）已知函数f（x）=，则关于x的方程f（x+﹣2）=a的实根个数不可能为（）A . 5个B . 6个C . 7个D . 8个二、填空题 (共4题；共4分)13. （1分） (2018高一上·台州期末) 函数的定义域是________.14. （1分） (2015高三上·务川期中) 我们称满足下面条件的函数y=f（x）为“ξ函数”：存在一条与函数y=f（x）的图象有两个不同交点（设为P（x1 ， y1）Q（x2 ， y2））的直线，y=（x）在x= 处的切线与此直线平行．下列函数：①y= ②y=x2（x＞0）③y= ④y=lnx，其中为“ξ函数”的是________ （将所有你认为正确的序号填在横线上）15. （1分） (2016高二上·平阳期中) 过点P（1，﹣2）且垂直于直线x﹣3y+2=0的直线方程为________16. （1分）过边长为2的正方形的中心作直线l将正方形分成两部分，将其中的一个部分沿直线l翻折到另一个部分上．则两个部分图形中不重叠的面积的最大值是________三、解答题 (共6题；共55分)17. （5分）在平面直角坐标系中，已知A（﹣1，2），B（2，1），C（1，0）．（Ⅰ）判定三角形ABC形状；（Ⅱ）求过点A且在x轴和在y轴上截距互为倒数的直线方程；（Ⅲ）已知l是过点A的直线，点C到直线l的距离为2，求直线l的方程．18. （15分） (2016高二上·武邑期中) 如图，在正方体ABCD﹣A1B1C1D1中，点M、N分别是面对角线A1B 与B1D1的中点，设 = ， = ， = ．（1）以{ ，， }为基底，表示向量；（2）求证：MN∥平面BCC1B1；（3）求直线MN与平面A1BD所成角的正弦值．19. （15分） (2017高二下·淮安期末) 已知函数f（x）=loga （a＞0且a≠1）是奇函数．（1）求实数m的值；（2）判断函数f（x）在区间（1，+∞）上的单调性并说明理由；（3）当x∈（n，a﹣2）时，函数f（x）的值域为（1，+∞），求实数n，a的值．20. （5分）如图，在三棱柱ABC﹣A1B1C1中，AA1⊥底面ABC，且△ABC为正三角形，AA1=AB=6，D为AC的中点．（1）求证：直线AB1∥平面BC1D；（2）求证：平面BC1D⊥平面ACC1A；（3）求三棱锥C﹣BC1D的体积．21. （10分） (2017高一上·嘉峪关期末) 圆M：x2+y2﹣4x﹣2y+4=0（1）若圆M的切线在x轴上的截距是y轴上的截距的2倍，求切线的方程；（2）从圆外一点P（a，b），向该圆引切线PA，切点为A，且PA=PO，O为坐标原点，求证：以PM为直径的圆过异于M的定点，并求该定点的坐标．22. （5分）已知函数f（x）=lnx﹣x+a有且只有一个零点．（1）求a的值；（2）若对任意的x∈（1，+∞），有2f（x）＜﹣x+2恒成立，求实数k的最小值；（3）设h（x）=f（x）+x﹣1，对任意x1 ，x2∈（0，+∞）（x1≠x2），证明：不等式>恒成立．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共55分)17-1、18-1、18-2、18-3、19-1、19-2、19-3、20-1、21-1、21-2、22-1、。

辽宁省庄河市高级中学2015-2016学年高一数学上学期期末考试试题

庄河高中2021 -2021学年度上学期高一期末考试数学试题答案一、选择题： CBDBA CCBAA DD二、填空： 13.lg 214.415.1或 216.81 0, 10三、解答题：17．〔 1〕x1x22(m1)0x1 x22m 603m1〔 2〕设f()x22(m1)x26x m那么 f (2)0m 118.解： (1) 证明：在三棱柱ABC- A1B1C1中，BB1⊥底面ABC，所以BB1⊥AB.又因为 AB⊥ BC，所以 AB⊥平面 B1BCC1，又因为 C1F?平面 B1BCC1，所以 AB⊥ C1F。

(2)证明：取AB的中点 G，连接 EG， FG.因为，，分别是 1 1，，的中点，所以∥，且＝1，1＝1 11.E F G A C BC AB FG AC FG2AC EC2A C因为∥ 11，且＝ 1 1，所以∥1，且＝1，所以四边形 1 为平行四边形，所以CF∥ EG.AC AC AC AC FG EC FG EC FGEC 1又因为?平面， 1?平面，所以1∥平面.EG ABE CF ABE CF ABE2 2(3)因为 AA1＝ AC＝2， BC＝1， AB⊥ BC，所以 AB＝ AC－BC＝3.1113所以三棱锥 E - ABC的体积 V＝3S△ABC· AA1＝3×2×3×1× 2＝3 .19．解：A x2x7， B y3y5〔1〕A B x2x5，①假设C ，那么m12m1m2 m12m1②假设C ，那么m122m 3 2m15综上： m3〔2〕A B x3x76m17m14PA AD面 PAD 面 ABCD 20．〔 1〕PA 面ABCD面 PAD 面 ABCD AD PA 面 PAD同理可证： AB 面 PAD〔 2〕BE // AD 面BEF // 面PADEF // PDAB // CD〔 3〕CD 面 PADCD 面 BEF面 PCDAB面 PADCD面 PCD面 BEF // 面 PAD21．解：f (x)log 4 x 2 log 2 (16a x 3 ) log 2 x (log 2 24 a log 2 x 3)log 2 x(4a 3log 2 x) (x 0) ) 1〔 1〕假设a1，那么( ) log ( 4 3logf x2 x2 x令 tlog 2 x ，那么方程为t (4 3t )1解得： t1或 t13那么 log 2x 1 x 1或 log 23 13 41 x 23或 x22方程的解集为3 4 , 122yx2 , 4log 2 x 1 , 2〔 2〕，令 t log 2 x1 , 2那么 f (t )t(3t4a) , t1 ,2 ，对称轴为t2 a3①当2a 1，即 a3时，12 32f min (t) f (1) 4a 3②当 12 a 2 ，即3 a 3 时 y3 2a)4 a 2 2f min (t) f (33③当2 a 2，即 a3 时0 123f min (t) f (2)8a 12y012面 BEFttt54a 3 , a32综上： f min ( x)4 a 2, 3 a 3 328a 12 , a 322．解：〔 1〕由g(0) 0 得 a1，那么 g( x)4x1g ( x) 是奇函数，2x ，经检验11x ，经检验 f ( x) 是偶函数由 f (1) f (1) 得 b，那么 f( x)lg(10 x1)22ab12〔 2〕g( x) 4x1 2x1 ，且 g (x) 在 ( ,) 单调递增，且 g (x) 为奇函数。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2015-2016学年辽宁省大连市庄河高中高一（上）期末数学试卷一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5.00分）已知集合M={x|﹣1＜x＜3}，N={﹣1，0，1，2，3}，则M∩N=（）A．{0，1，2}B．{﹣1，0，1，2} C．{﹣1，0，1，2，3}D．{﹣1，3} 2．（5.00分）函数y=ln（1﹣x）的定义域为（）A．（0，1） B．[0，1） C．（0，1]D．[0，1]3．（5.00分）设a=0.23，b=30.2，c=log30.2，则a，b，c的大小关系是（）A．c＜a＜b B．a＜c＜b C．a＜b＜c D．b＜c＜a4．（5.00分）函数f（x）=lnx﹣的零点所在的大致区间是（）A．（1，2） B．（2，3） C．（1，）D．（e，+∞）5．（5.00分）设α，β是两个不同的平面，l，m是两条不同的直线，且l⊂α，m⊂β，（）A．若l⊥β，则α⊥βB．若α⊥β，则l⊥m C．若l∥β，则α∥βD．若α∥β，则l∥m6．（5.00分）设函数f（x）=，则f（﹣2）+f（log212）=（）A．3 B．6 C．9 D．127．（5.00分）设偶函数f（x）在[0，+∞）单调递增，则使得f（x）＞f（2x﹣1）成立的x的取值范围是（）A．（，1）B．（﹣∞，）∪（1，+∞）C．（﹣，）D．（﹣∞，﹣）∪（，+∞）8．（5.00分）某几何体的三视图如图所示，则该几何体的表面积等于（）A．8+2B．11+2C．14+2D．159．（5.00分）正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A．B．16πC．9πD．10．（5.00分）已知指数函数f（x）=a x﹣16+7（a＞0且a≠1）的图象恒过定点P，若定点P在幂函数g（x）的图象上，则幂函数g（x）的图象是（）A． B．C．D．11．（5.00分）已知函数，若方程f（x）﹣a=0有三个不同的实数根，则实数a的取值范围是（）A．（1，3） B．（0，3） C．（0，2） D．（0，1）12．（5.00分）对于实数x，符号[x]表示不超过x的最大整数，例如[π]=3，[﹣1.08]=﹣2，如果定义函数f（x）=x﹣[x]，那么下列命题中正确的序号有（）①f（x）的定义域为R，值域为[0，1]②f（x）在区间[0，1）上单调递增③f（x）既不是奇函数也不是偶函数④函数f（x）与g（x）=log5（﹣x）图象有5个交点．A．①②③B．②③C．①②③④D．②③④二、填空题：本大题共4小题，每小题5分.13．（5.00分）已知，则f（2）=．14．（5.00分）已知函数=．15．（5.00分）幂函数的图象与坐标轴没有公共点，则m的值为．16．（5.00分）已知函数，若关于x的方程f（x）=a有四个根x1，x2，x3，x4，则这四个根之和x1+x2+x3+x4的取值范围是．三、解答题：解答应写出文字说明、证明过程或演算步骤.17．（10.00分）求实数m的取值范围，使关于x的方程x2+2（m﹣1）x+2m+6=0（1）有两个正实数根；（2）有两个实数根，且一个比2大，一个比2小．18．（12.00分）如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1=AC=2，BC=1，E，F分别是A1C1，BC的中点．（1）求证：AB⊥C1F；（2）求证：C1F∥平面ABE；（3）求三棱锥E﹣ABC的体积．19．（12.00分）已知集合A={x|≤2x≤128}，B={y|y=log2x，x∈[，32]．（1）若C={x|m+1≤x≤2m﹣1}，C⊆（A∩B），求实数m的取值范围．（2）若D={x|x＞6m+1}，且（A∪B）∩D=∅，求实数m的取值范围．20．（12.00分）如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点，求证：（1）PA⊥底面ABCD；（2）平面BEF∥平面PAD；（3）平面BEF⊥平面PCD．21．（12.00分）已知函数（1）若a=1，求方程f（x）=﹣1的解集．（2）当x∈[2，4]时，求函数f（x）的最小值．22．（12.00分）已知函数是奇函数，f（x）=lg（10x+1）+bx是偶函数．（1）求a+b的值．（2）若对任意的t∈[0，+∞），不等式g（t2﹣2t）+g（2t2﹣k）＞0恒成立，求实数k的取值范围．（3）设，若存在x∈（﹣∞，1]，使不等式g（x）＞h[lg（10a+9）]成立，求实数a的取值范围．2015-2016学年辽宁省大连市庄河高中高一（上）期末数学试卷参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5.00分）已知集合M={x|﹣1＜x＜3}，N={﹣1，0，1，2，3}，则M∩N=（）A．{0，1，2}B．{﹣1，0，1，2} C．{﹣1，0，1，2，3}D．{﹣1，3}【解答】解：集合M={x|﹣1＜x＜3}，N={﹣1，0，1，2，3}，则M∩N={0，1，2}．故选：A．2．（5.00分）函数y=ln（1﹣x）的定义域为（）A．（0，1） B．[0，1） C．（0，1]D．[0，1]【解答】解：由题意，自变量满足，解得0≤x＜1，即函数y=的定义域为[0，1）故选：B．3．（5.00分）设a=0.23，b=30.2，c=log30.2，则a，b，c的大小关系是（）A．c＜a＜b B．a＜c＜b C．a＜b＜c D．b＜c＜a【解答】解：由指数函数的性质可知：0＜0.23＜1，30.2＞1由对数函数的性质可得：log30.2＜0，∴log30.2＜0.23＜30.2，即c＜a＜b故选：A．4．（5.00分）函数f（x）=lnx﹣的零点所在的大致区间是（）A．（1，2） B．（2，3） C．（1，）D．（e，+∞）【解答】解：函数的定义域为：（0，+∞），有函数在定义域上是递增函数，所以函数只有唯一一个零点．又∵f（2）﹣ln2﹣1＜0，f（3）=ln3﹣＞0∴f（2）•f（3）＜0，∴函数f（x）=lnx﹣的零点所在的大致区间是（2，3）．故选：B．5．（5.00分）设α，β是两个不同的平面，l，m是两条不同的直线，且l⊂α，m⊂β，（）A．若l⊥β，则α⊥βB．若α⊥β，则l⊥m C．若l∥β，则α∥βD．若α∥β，则l∥m【解答】解：对于A，∵l⊥β，且l⊂α，根据线面垂直的判定定理，得α⊥β，∴A正确；对于B，当α⊥β，l⊂α，m⊂β时，l与m可能平行，也可能垂直，∴B错误；对于C，当l∥β，且l⊂α时，α与β可能平行，也可能相交，∴C错误；对于D，当α∥β，且l⊂α，m⊂β时，l与m可能平行，也可能异面，∴D错误．故选：A．6．（5.00分）设函数f（x）=，则f（﹣2）+f（log212）=（）A．3 B．6 C．9 D．12【解答】解：函数f（x）=，即有f（﹣2）=1+log2（2+2）=1+2=3，f（log212）==2×=12×=6，则有f（﹣2）+f（log212）=3+6=9．故选：C．7．（5.00分）设偶函数f（x）在[0，+∞）单调递增，则使得f（x）＞f（2x﹣1）成立的x的取值范围是（）A．（，1）B．（﹣∞，）∪（1，+∞）C．（﹣，）D．（﹣∞，﹣）∪（，+∞）【解答】解：因为f（x）为偶函数，所以f（x）＞f（2x﹣1）可化为f（|x|）＞f（|2x﹣1|）又f（x）在区间[0，+∞）上单调递增，所以|x|＞|2x﹣1|，即（2x﹣1）2＜x2，解得＜x＜1，所以x的取值范围是（，1），故选：A．8．（5.00分）某几何体的三视图如图所示，则该几何体的表面积等于（）A．8+2B．11+2C．14+2D．15【解答】解：根据三视图可判断该几何体是底面为直角梯形，高为2的直四棱柱，底面的梯形上底1，下底2，高为1，∴侧面为（4）×2=8，底面为（2+1）×1=，故几何体的表面积为8=11，故选：B．9．（5.00分）正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A．B．16πC．9πD．【解答】解：设球的半径为R，则∵棱锥的高为4，底面边长为2，∴R2=（4﹣R）2+（）2，∴R=，∴球的表面积为4π•（）2=．故选：A．10．（5.00分）已知指数函数f（x）=a x﹣16+7（a＞0且a≠1）的图象恒过定点P，若定点P在幂函数g（x）的图象上，则幂函数g（x）的图象是（）A． B．C．D．【解答】解：指数函数f（x）=a x﹣16+7（a＞0且a≠1）的图象恒过定点P，令x﹣16=0，解得x=16，且f（16）=1+7=8，所以f（x）的图象恒过定点P（16，8）；设幂函数g（x）=x a，P在幂函数g（x）的图象上，可得：16a=8，解得a=；所以g（x）=，幂函数g（x）的图象是A．故选：A．11．（5.00分）已知函数，若方程f（x）﹣a=0有三个不同的实数根，则实数a的取值范围是（）A．（1，3） B．（0，3） C．（0，2） D．（0，1）【解答】解：由题意可知：函数f（x）的图象如下：由关于x的方程f（x）﹣a=0有三个不同的实数解，可知函数y=a与函数y=f（x）有三个不同的交点，由图象易知：实数a的取值范围为（0，1）．故选：D．12．（5.00分）对于实数x，符号[x]表示不超过x的最大整数，例如[π]=3，[﹣1.08]=﹣2，如果定义函数f（x）=x﹣[x]，那么下列命题中正确的序号有（）①f（x）的定义域为R，值域为[0，1]②f（x）在区间[0，1）上单调递增③f（x）既不是奇函数也不是偶函数④函数f（x）与g（x）=log5（﹣x）图象有5个交点．A．①②③B．②③C．①②③④D．②③④【解答】解：∵符号[x]表示不超过x的最大整数，∴0≤x﹣[x]＜1，∴f（x）的定义域为R，值域为[0，1），故①不正确；故排除A，C；作函数f（x）与g（x）=log5（﹣x）图象如下，结合图象可知，有5个交点，故④正确；故选：D．二、填空题：本大题共4小题，每小题5分.13．（5.00分）已知，则f（2）=lg2．【解答】解：令+1=2解得，x=2；则f（2）=lg2，故答案为：lg2．14．（5.00分）已知函数=4．【解答】解：∵f（a）=a+lg+5=6，∴a+lg=1，f（﹣a）=﹣a+lg+5=﹣（a+lg）+5=﹣1+5=4，故答案为：4．15．（5.00分）幂函数的图象与坐标轴没有公共点，则m的值为1或2．【解答】解：幂函数的图象与坐标轴没有公共点，∴，解得，即m=1或m=2．故答案为：1或2．16．（5.00分）已知函数，若关于x的方程f（x）=a有四个根x1，x2，x3，x4，则这四个根之和x1+x2+x3+x4的取值范围是．【解答】解：作函数的图象如下，，结合图象可知，当0＜a＜1时，方程有四个不同的解，如图中的四个交点，故x1+x2=﹣2，x3x4=1且1＜x4＜10；故2＜x3+x4＜10+，故0＜x1+x2+x3+x4＜8+，即x1+x2+x3+x4的取值范围是，故答案为：．三、解答题：解答应写出文字说明、证明过程或演算步骤.17．（10.00分）求实数m的取值范围，使关于x的方程x2+2（m﹣1）x+2m+6=0（1）有两个正实数根；（2）有两个实数根，且一个比2大，一个比2小．【解答】解：（1）由题意可得，解得：﹣3＜m＜﹣1；（2）设f（x）=x2+2（m﹣1）x+2m+6，则由题意可得f（2）=6m+6＜0，解得：m＜﹣1．18．（12.00分）如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1=AC=2，BC=1，E，F分别是A1C1，BC的中点．（1）求证：AB⊥C1F；（2）求证：C1F∥平面ABE；（3）求三棱锥E﹣ABC的体积．【解答】（1）证明：∵BB1⊥底面ABC，AB⊂平面ABC∴BB1⊥AB．又∵AB⊥BC，BC⊂平面B1BCC1，BB1⊂平面B1BCC1，BC∩BB1=B，∴AB⊥平面B1BCC1，又∵C1F⊂平面B1BCC1，∴AB⊥C1F．（2）证明：取AB的中点G，连接EG，FG．∵F，G分别是BC，AB的中点，∴FG∥AC，且FG=AC，∵AC A1C1，E是A1C1的中点，∴EC1=A1C1．∴FG∥EC1，且FG=EC1，∴四边形FGEC1为平行四边形，∴C1F∥EG．又∵EG⊂平面ABE，C1F⊄平面ABE，EG⊂平面ABE，∴C1F∥平面ABE．（3）解：∵AA1=AC=2，BC=1，AB⊥BC，∴AB==．•AA1=×××1×2=．∴三棱锥E﹣ABC的体积V=S△ABC19．（12.00分）已知集合A={x|≤2x≤128}，B={y|y=log2x，x∈[，32]．（1）若C={x|m+1≤x≤2m﹣1}，C⊆（A∩B），求实数m的取值范围．（2）若D={x|x＞6m+1}，且（A∪B）∩D=∅，求实数m的取值范围．【解答】解：A={x|﹣2≤x≤7}，B={y|﹣3≤y≤5}（1）A∩B={x|﹣2≤x≤5}，①若C=φ，则m+1＞2m﹣1，∴m＜2；②若C≠φ，则，∴2≤m≤3；综上：m≤3；（2）A∪B={x|﹣3≤x≤7}，∴6m+1≥7，∴m≥1．20．（12.00分）如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点，求证：（1）PA⊥底面ABCD；（2）平面BEF∥平面PAD；（3）平面BEF⊥平面PCD．【解答】证明：（1）∵平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，∴PA⊥底面ABCD．（2）∵AB∥CD，CD=2AB，E是CD的中点，∴AB∥DE，且AB=DE，∴ABCD是平行四边形，∴AD∥BE，∵BE⊄平面PAD，AD⊂平面PAD，∴BE∥平面PAD，∵E和F分别是CD和PC的中点，∴EF∥PD，∵EF⊄平面PAD，PD⊂平面PAD，∴EF∥平面PAD，∵BF∩BE=B，AD∩PD=D，∴平面BEF∥平面PAD．（3）∵AB⊥AD，ABED是平行四边形，∴BE⊥CD，AD⊥CD，由（1）知PA⊥底面ABCD，∴PA⊥CD，∴CD⊥平面PAD，∴CD⊥PD，∵E和F分别是CD和PC的中点，∴PD∥EF，∴CD⊥EF，∴CD⊥平面BEF，∵CD⊂平面PCD，∴平面BEF⊥平面PCD．21．（12.00分）已知函数（1）若a=1，求方程f（x）=﹣1的解集．（2）当x∈[2，4]时，求函数f（x）的最小值．【解答】解：=log2x （4a+3log2x），（x＞0），（1）若a=1，则f（x）=log2x（4+3log2x）=﹣1，令t=log2x，则方程为t（4+3t）=﹣1，解得：或t=﹣1，则或log2x=﹣1，∴或∴方程的解集为．（2）∵x∈[2，4]，∴log2x∈[1，2]，令t=log2x∈[1，2]，则f（t）=t（3t+4a），t∈[1，2]，对称轴为，①当，即时，f min（t）=f（1）=4a+3②当，即时，③当，即a≤﹣3时f min（t）=f（2）=8a+12，综上：．22．（12.00分）已知函数是奇函数，f（x）=lg（10x+1）+bx是偶函数．（1）求a+b的值．（2）若对任意的t∈[0，+∞），不等式g（t2﹣2t）+g（2t2﹣k）＞0恒成立，求实数k的取值范围．（3）设，若存在x∈（﹣∞，1]，使不等式g（x）＞h[lg（10a+9）]成立，求实数a的取值范围．【解答】解：（1）由g（0）=0得a=1，则，经检验g（x）是奇函数．由f（﹣1）=f（1）得，则，经检验f（x）是偶函数，∴．（2）∵，且g（x）在（﹣∞，+∞）单调递增，且g（x）为奇函数．∴由g（t2﹣2t）+g（2t2﹣k）＞0恒成立，得g（t2﹣2t）＞﹣g（2t2﹣k）=g（﹣2t2+k），∴t2﹣2t＞﹣2t2+k，t∈[0，+∞）恒成立，即3t2﹣2t＞k，t∈[0，+∞）恒成立，令F（x）=3t2﹣2t，在[0，+∞）上F（x）的最小值为，∴．（3）h（x）=lg（10x+1），h（lg（10a+9））=lg[10lg（10a+9）+1]=lg（10a+10），则由已知得，存在x∈（﹣∞，1]，使不等式g（x）＞lg（10a+10）成立，而g（x）在（﹣∞，1]单增，∴，∴，∴．又，∵，∴，∴．。