苏州市2015届高三调研数学考试
苏州市2015届高三数学必过关题(逐题解析)——立体几何

高三必过关题9 立体几何一、填空题例1给出下列命题:①棱柱的侧棱都相等,侧面都是全等的平行四边形; ②用一个平面去截棱锥,棱锥底面与截面之间的部分是棱台; ③若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直; ④存在每个面都是直角三角形的四面体; ⑤棱台的侧棱延长后交于一点 其中正确命题的序号是________. 【答案】: ③④⑤【提示】考点:空间几何体的结构特征①不正确,根据棱柱的定义,棱柱的各个侧面都是平行四边形,但不一定全等;②不正确,用平行于棱锥底面的平面去截棱锥,棱锥底面与截面之间的部分才是棱台;③正确,若三棱锥的三条侧棱两两垂直,则三个侧面构成的三个平面的面角都是直二面角;④正确,如正方体AC 1中的四棱锥C 1ABC ,四个面都是直角三角形;⑤正确,由棱台的概念可知.例2给出下列命题:①若平面α内的直线a 与平面β内的直线b 为异面直线,直线c 是α与β的交线,那么直线c 至多与a 、b 中的一条相交;②若直线a 与b 为异面直线,直线b 与c 平行,则直线a 与c 异面; ③一定存在平面α和异面直线a 、b 同时平行; ④若直线a 、b 异面,b 、c 异面,则a 、c 异面 其中正确命题的序号是__________. 【答案】:③【提示】考点:空间两直线的位置关系①错,c 可以与a 、b 均相交;②错,因为a 与c 可能相交;③对,可以将两异面直线a 与b 平移到空间内任意一点处,确定一个平面,该平面可以与a 、b 同时平行,并且这样的平面有无数多个.④错,a 、c 的位置关系可以平行、相交、异面。
例3与正方体1111ABCD A BC D -的三条棱AB 、1CC 、11A D 所在直线的距离相等的点有 个. 【答案】:无数个【提示】:本题考查了空间想象能力.∵到三条两垂直的直线距离相等的点在以三条直线为轴,以正方体边长为半径的圆柱面上,∴三个圆柱面有无数个交点.例4过正方体1111D C B A ABCD -的顶点A 作直线L ,使L 与棱AB ,AD ,1AA 所成的角都相等,这样的直线L 可以作 条. 【答案】:4条【提示】:考查空间感和线线夹角的计算和判断,重点考查学生分类、划归转化的能力。
2015年江苏省苏锡常镇四市高三教学情况调研(一)数学(一模)试题及答案
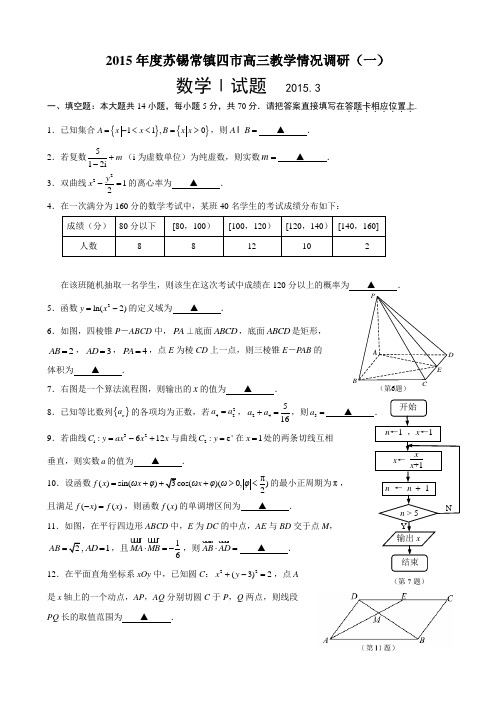
(第6题)EPDCBA2015年度苏锡常镇四市高三教学情况调研(一)数学Ⅰ试题2015.3一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1.已知集合{}{}11,0A x x B x x =-<<=>,则A B = ▲ .2.若复数512im +-(i 为虚数单位)为纯虚数,则实数m = ▲ . 3.双曲线2212y x -=的离心率为 ▲ .4.在一次满分为160分的数学考试中,某班40名学生的考试成绩分布如下:在该班随机抽取一名学生,则该生在这次考试中成绩在120分以上的概率为 ▲ .5.函数2ln(2)y x =-的定义域为 ▲ .6.如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,底面ABCD 是矩形,2AB =,3AD =,4PA =,点E 为棱CD 上一点,则三棱锥E -P AB 的体积为 ▲ .7.右图是一个算法流程图,则输出的x 的值为 ▲ .8.已知等比数列{}n a 的各项均为正数,若242a a =,24516a a +=,则5a9.若曲线321:612C y ax x x =-+与曲线2:e x C y =在1x =垂直,则实数a 的值为 ▲ .10.设函数π()sin())(0,)2f x ωx φωx φωφ=++><且满足()()f x f x -=,则函数()f x 的单调增区间为 ▲ .11.如图,在平行四边形ABCD 中,E 为DC 的中点,AE 与BD 交于点AB 1AD =,且16MA MB ⋅=-,则AB AD ⋅= ▲ . 12.在平面直角坐标系xOy 中,已知圆C :22(3)2x y +-=,点A 是x 轴上的一个动点,AP ,AQ 分别切圆C 于P ,Q 两点,则线段 PQ 长的取值范围为 ▲ .(第7题)13.已知直线1y kx =+与曲线11()f x x x x x=+--恰有四个不同的交点,则实数k 的取值 范围为 ▲ .14.已知实数,x y 满足0x y >>,且2x y +…,则213x y x y++-的最小值为 ▲ .二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证 明过程或演算步骤. 15.(本题满分14分)已知向量πsin(),36α⎛⎫=+ ⎪⎝⎭a ,(1,4cos )a =b ,(0,π)α∈.(1)若a ⊥b ,求tan α的值;(2)若a ∥b ,求α的值.16.(本题满分14分)如图,四边形11AA C C 为矩形,四边形11CC B B 为菱形,且平面11CC B B ⊥平面11AA C C ,D ,E 分别为边11A B ,1C C 的中点.(1)求证:1BC ⊥平面1AB C ; (2)求证:DE ∥平面1AB C .C 1B 1A 1(第16题)ECBAD17.(本题满分14分)如图,有一段河流,河的一侧是以O为圆心,半径为OCD ,河的另一侧是一段笔直的河岸l ,岸边有一烟囱AB (不计B 离河岸的距离),且OB 的连线恰好与河岸l 垂直,设OB 与圆弧CD 的交点为E .经测量,扇形区域和河岸处于同一水平面,在点C ,点O 和点E 处测得烟囱AB 的仰角分别为45︒,30︒和60︒. (1)求烟囱AB 的高度;(2)如果要在CE 间修一条直路,求CE 的长.18.(本题满分16分)在平面直角坐标系xOy 中,已知椭圆C :22221x y a b+=(0)a b >>,过椭圆的左顶点A 作直线l x ⊥轴,点M 为直线l 上的动点,点B 为椭圆右顶点,直线BM 交椭圆C 于P . (1)求椭圆C 的方程; (2)求证:AP OM ⊥;(3)试问OP OM ⋅是否为定值?若是定值,请求出该定值;若不是定值,请说明理由.(第17题)l19.(本题满分16分)已知函数2()e (0)x f x x a a =-…. (1)当1a =时,求()f x 的单调减区间;(2)若方程()f x m =恰好有一个正根和一个负根,求实数m 的最大值.20.(本题满分16分)已知数列{}n a 的前n 项和为n S ,设数列{}n b 满足112()()()n n n n n n b S S S n S S n *++=--+∈N . (1)若数列{}n a 为等差数列,且0n b =,求数列{}n a 的通项公式;(2)若11a =,23a =,且数列{}21n a -,{}2n a 都是以2为公比的等比数列,求满足不等式221n n b b -<的所有正整数n 的集合.D(第21A 题)2014-2015学年度苏锡常镇四市高三教学情况调研(一)数学ⅠI (附加题)试题21.A .如图,AB 为圆O 的切线,A 为切点,C 为线段AB 中点,过C 作圆O 的割线CED (E 在C ,D 之间), 求证:∠CBE =∠BDE .B . 求曲线1x y +=在矩阵M 10103⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦对应的变换作用下得到的曲线所围成图形的面积.C .在极坐标系中,曲线C 的极坐标方程为2cos 2sin rq q =+,以极点为坐标原点,极轴为x 轴的正半轴建立平面直角坐标系,直线l 的参数方程为1,x t y =+⎧⎪⎨=⎪⎩ (t 为参数),求直线l 被曲线C所截得的弦长.D .求函数y =(第22题)22.如图,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,底面ABCD 60︒,PA =M 为PC 的中点.(1)求异面直线PB 与MD 所成的角的大小;(2)求平面PCD 与平面P AD 所成的二面角的正弦值.23.若存在n 个不同的正整数12,,,n a a a ,对任意1i jn <剟,都有i j i ja a a a +∈-Z ,则称这n 个不同的正整数12,,,n a a a 为“n 个好数”. (1)请分别对2n =,3n =构造一组“好数”;(2)证明:对任意正整数(2)n n …,均存在“n 个好数”.苏锡常镇四市高三教学情况调研(一)数学参考答案一、填空题1.{}01x x << 2.1- 3 4.0.3 5.((),2,-∞+∞6.4 7.16 8.1329.13e - 10.π[π,π],()2k k k -+∈Z11.34 12. 13.11{,0,}88- 14 二、解答题15.解:(1)因为a ⊥b ,所以πsin()12cos 06αα++=, ……………………………2分1cos 12cos 02ααα++=25cos 02αα+=, …………………4分又cos 0α≠,所以tan α=. ………………………………………………6分 (2)若a ∥b ,则π4cos sin()36αα+=, ……………………………………………8分即14cos cos )32ααα+=,2cos22αα+=, ………………………………………………………10分所以πsin(2)16α+=, ………………………………………………………………11分因为(0,π)α∈,所以ππ13π2(,)666α+∈, ………………………………………13分 所以ππ262α+=,即π6α=. ……………………………………………………14分 16.证明:(1)∵四边形11AA C C 为矩形,∴AC ⊥1C C ,………………………………2分 又平面11CC B B ⊥平面11AA C C ,平面11CC B B平面11AA C C =1CC ,∴AC ⊥平面11CC B B , ……………………………………………………………3分 ∵1C B ⊂平面11CC B B ,∴AC ⊥1C B , ……………………………………………4分 又四边形11CC B B 为菱形,∴11B C BC ⊥, …………………………………………5分 ∵1B CAC C =,AC ⊂平面1AB C ,1B C ⊂平面1AB C ,∴1BC ⊥平面1AB C .…………………………………………………………………7分(2)取1AA 的中点F ,连DF ,EF ,∵四边形11AA C C 为矩形,E ,F 分别为1C C ,1AA 的中点, ∴EF ∥AC ,又EF ⊄平面1AB C ,AC ⊂平面1AB C ,∴EF ∥平面1AB C , ………………………………………………………………10分 又∵D ,F 分别为边11A B ,1AA 的中点,∴DF ∥1AB ,又DF ⊄平面1AB C ,1AB ⊂平面1AB C , ∴DF ∥平面1AB C ,∵EFDF F =,EF ⊂平面DEF ,DF ⊂平面DEF ,∴平面DEF ∥平面1AB C ,…………………………………………………………12分 ∵DE ⊂平面DEF ,∴DE ∥平面1AB C .…………………………………………14分 17.解:(1)设AB 的高度为h ,在△CAB 中,因为45ACB ∠=︒,所以CB h =, ………………………………1分 在△OAB 中,因为30AOB ∠=︒,60AEB ∠=︒, ………………………………2分所以OB =,EB =, ………………………………………………………4分-=15h =. ………………………………………6分 答:烟囱的高度为15米. ……………………………………………………………7分(2)在△OBC 中,222cos 2OC OB BC COB OC OB+-∠=⋅56==, …………………10分所以在△OCE 中,2222cos CE OC OE OC OE COE =+-⋅∠ 53003006001006=+-⨯=. …………………13分答:CE 的长为10米. ……………………………………………………………14分18.解:(1)∵椭圆C :22221x y a b+=(0)a b >>,∴222a c =,则222a b =,又椭圆C 过点,∴221312a b+=.…………2分∴24a =,22b =,则椭圆C 的方程22142x y +=. …………………………………………………4分(2)设直线BM 的斜率为k ,则直线BM 的方程为(2)y k x =-,设11(,)P x y ,将(2)y k x =-代入椭圆C 的方程22142x y +=中并化简得:2222(21)4840k x k x k +-+-=,………………………………………………………6分解之得2124221k x k -=+,22x =,∴1124(2)21ky k x k -=-=+,从而222424(,)2121k k P k k --++.………………………………8分令2x =-,得4y k =-,∴(2,4)M k --,(2,4)OM k =--. ………………………9分又222424(2,)2121k k AP k k --=+++=22284(,)2121k kk k -++, …………………………………11分∴2222161602121k k AP OM k k -⋅=+=++,∴AP OM ⊥. ………………………………………………………………………13分 (3)222424(,)(2,4)2121k k OP OM k k k --⋅=⋅--++ =2222284168442121k k k k k -+++==++.∴OP OM ⋅为定值4. …………………………………………………………16分19.解:(1)当1a =时,221,e (1),()1,e (1),x x x xf x x x ⎧>-⎪=⎨-⎪⎩… …………………………………1分 当1x >时,2()e (21)x f x x x '=+-,由()0f x '…,解得1x --,所以()f x 的单调减区间为[11]--, ………………………………………3分 当1x …时,2()e (21)x f x x x '=-+-,由()0f x '…,解得1x -…x -…所以()f x 的单调减区间为[-, ……………………………………………5分综上:()f x 的单调减区间为[-,[11]--. ………………………6分 (2) 当0a =时,2()e x f x x =⋅,则2()e 2e e (2)x x x f x x x x x '=⋅+⋅=+,令()0f x '=,得0x =或2x =-,所以()f x 有极大值24(2)e f -=,极小值(0)0f =,…………………………………7分当0a>时,22e(),()e(),xxxx af xa x x⎧>-⎪=⎨-⎪⎩…同(1)的讨论可得,()f x在(,1)-∞上增,在(1,上减,在(1)上增,在1上减,在)+∞上增,……………8分且函数()y f x=有两个极大值点,1(1)2e1)f==,…………………………9分11)1)f==,……………………………10分且当1x a=+时,12(1)e(1)1)af a a a++=++>>所以若方程()f x m=恰好有正根,则1)m f>(否则至少有二个正根).……………………………………11分又方程()f x m=恰好有一个负根,则(1)m f=.………………………12分令()e(1),1xg x x x-=+…,则()e0xg x x-'=-<,所以()e(1)xg x x-=+在1x…时单调减,即2()(1)eg x g=…,………………………13分等号当且仅当1x=时取到.所以22(1)()ef…,等号当且仅当0a=时取到.且此时11)1)0f==,………………………………………14分即(1)f>1)f,…………………………………………………15分所以要使方程()f x m=恰好有一个正根和一个负根,m的最大值为24e.………16分20.解:(1)设等差数列{}n a的公差为d,所以11na a nd+=+,1(1)2nn nS na d-=+,…………………………………………1分由112()()()n n n n n nb S S S n S S n*++=--+∈N,得112(2)n n n n nb a S n S a++=-+,及由0nb=,又由0nb=,得[]1111(1)2()2(1)02n na nd na d n na n n d a nd-⎡⎤++-+-++=⎢⎥⎣⎦对一切n*∈N都成立,………………………………………………………………3分即()222211111(32)20d d n a d d a n a a d a-+--+--=对一切n*∈N都成立.令1n=,2n=,解之得10,0,da=⎧⎨=⎩或11,1,da=⎧⎨=⎩经检验,符合题意,所以{}n a 的通项公式为0n a =或n a n =. …………………………………………5分 (2)由题意得1212n n a --=,1232n n a -=⨯,2213(21)424n n n n S =-+-=⨯-,11212242432524n n n n n n S S a ---=-=⨯--⨯=⨯-.…………………………………6分 221222122(2)n n n n n b a S n S a ++=-+22(424)2(8282)n n n n n =⨯⨯⨯--⨯-+122(294)16n n n n ++=--+. ……………………………………………………7分 212212122(21)(2)n n n n n b a S n S a ---=--+111162(524)(21)(102832)n n n n n ----=⨯⨯⨯---⨯-+⨯112(3022611)168n n n n --=⨯--+-. ………………………………………8分12112212(294)16[2(3022611)168]n n n n n n b b n n n n ++----=--+-⨯--+-121552(25)8282(5)22n n n n n n --=--+=+-+. ………………………9分记215282)()2(5n n n f n -=+-+,即15()2[2(5)]228n n f n n =⨯-++, ……………10分记15()2(5)22n g n n =⨯-+,则111515(1)()2(5)252222n n g n g n n n ++-=⨯-+-⨯++1252n =⨯-,当1n =,2,3时,(1)()0g n g n +-<,当*n ∈N 时,4n ≥,(1)()g n g n +-12502n =⨯->, …………………………12分因为1n =时,13(1)02g =-<,所以(4)0g <;且1(6)02g =-<;53(7)02g =>. 所以15()2[2(5)]228n n f n n =⨯-++在7(*)n n ∈≥N 时也是单调递增, …………14分1n =时,(1)50f =-<; 2n =时,(2)340f =-<; 3n =时,(3)1000f =-<; 4n =时,(4)2240f =-<; 5n =时,(5)3600f =-<; 6n =时,(6)240f =-<; 7n =时,(7)34000f =>,所以满足条件的正整数n 的集合为{1,2,3,4,5,6}.………………………16分21、A .证明:因为CA 为圆O 的切线,所以2CA CE CD =⋅, ………………………………………………………………3分 又CA CB =,所以2CB CE CD =⋅,即CB CDCE CB=, …………………………5分 又BCD BCD ∠=∠,所以BCE D ∽DCB D , …………………………………8分 所以∠CBE =∠BDE . ………………………………………………………………10分B . 解:设点00(,)x y 为曲线1x y +=上的任一点,在矩阵10103M ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦对应的变换作用下得到的点为(,)x y '',则由0010103x x y y ⎡⎤'⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎢⎥⎣⎦,………………………………………………………………3分得:00,1,3x x y y '=⎧⎪⎨'=⎪⎩ 即00,3,x x y y '=⎧⎨'=⎩ ………………………………………………………5分 所以曲线1x y +=在矩阵10103M ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦对应的变换作用下得到的曲线为31x y +=, ………………………………………………………………………………8分所围成的图形为菱形,其面积为1222233⨯⨯=. …………………………………10分C .解:曲线C 的直角坐标方程为22220x y x y +--=,圆心为(1,1)…………………………………………………………3分0y -=, ………………………………………5分所以圆心到直线的距离为12d ==, ………………………………8分所以弦长== ………………………………………………………10分 D .选修4—5:不等式选讲解:因为22= 120(3332)(1)33x x -+++=≤, ……………………………………………3分所以y=.………………………………………………5分等号当且仅当3332113x x-+=,即712x=时成立.………………………………8分所以y…………………………………………………………10分22.解:(1)设AC与BD交于点O,以O为顶点,向量OC,OD为x,y轴,平行于AP且方向向上的向量为z轴建立直角坐标系.………………………………………………1分则(1,0,0)A-,(1,0,0)C,(0,B,D,(P-,所以M,MD=,(1,PB=,……………………3分cos,0MD PAMD PAMD PA⋅<>===.…………………………………4分所以异面直线PB与MD所成的角为90︒.…………………………………………5分(2)设平面PCD的法向量为1111(,,)x y z=n,平面P AD的法向量为2222(,,)x y z=n,因为(CD=-,(1PD=,(0,0,PA=,由11111110,0,CD xPD x⎧⋅=-=⎪⎨⋅=+=⎪⎩nn令11y=,得1=n,……………………7分由22222260,0,PAPD x z⎧⋅=-=⎪⎨⋅=-=⎪⎩nn令21y=-,得21,0)=-n,…………………8分所以121212cos,⋅<>===n nn nn n12sin,<>=n n10分23.解:(1)当2n=时,取数11a=,22a=,因为21312+=-∈-Z,…………………1分当3n=时,取数12a=,23a=,34a=,则12125a aa a+=-∈-Z,23237a aa a+=-∈-Z,13133a aa a+=-∈-Z,…………………………………………………3分即12a=,23a=,34a=可构成三个好数.………………………………………4分(2)证:①由(1)知当2,3n =时均存在,②假设命题当(2,)n k k k Z=≥∈时,存在k个不同的正整数12,,,ka a a,其中12ka a a<<<,使得对任意1i j k<剟,都有i ji ja aa a+∈-Z成立,…………………………………5分则当1n k=+时,构造1k+个数12,,,,kA A a A a A a+++,,(*)其中123k A a =⨯⨯⨯⨯,若在(*)中取到的是A 和()i A a i k +…,则21i i iA A a AA A a a ++=--∈--Z ,所以成立,若取到的是()i A a i k +…和()j A a j k +…,且i j <, 则2+i j i j i ji j i j A a A a a a AA a A a a a a a ++++=+----,由归纳假设得i j i ja a a a +∈-Z ,又j i k a a a -<,所以j i a a -是A 的一个因子,即2i jAa a ∈-Z , 所以2+i j i j i ji j i jA a A a a a A A a A a a a a a ++++=∈+----Z , ………………………………………8分 所以当1n k =+时也成立. ………………………………………………………9分 所以对任意正整数(2)n n …,均存在“n 个好数” ……………………………10分。
2018届江苏省苏州市2015级高三上学期调研考试数学(理)试卷及解析

2018届苏州市2015级高三上学期调研考试数学(理)试卷2018.1★祝考试顺利★注意事项考生在答题前请认真阅读本注意事项及各题答题要求.1.本试卷共4页,包含填空题(第1题第14题)、解答题(第15题第20题).本卷满分160分,考试时间为120分钟.考试结束后,请将答题卡交回.2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在答题卡的规定位置.3.请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚.4.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.5.请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔.参考公式:球的表面积公式S=4πr2,其中r为球的半径.一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请把答案直接填在答题卡相应位置上.........1.已知i为虚数单位,复数的模为_____.【答案】【解析】,故答案为.2.已知集合,,且,则正整数______.【答案】2【解析】,,且,,故答案为.3.在平面直角坐标系xOy中,抛物线的焦点坐标为_________.【答案】【解析】抛物线方程为,抛物线方程为的焦点坐标为,故答案为.4.苏州轨道交通1号线每5分钟一班,其中,列车在车站停留0.5分钟,假设乘客到达站台的时刻是随机的,则该乘客到达站台立即能乘上车的概率为______.【答案】【解析】每分钟一班列车,其中列车在车站停留分钟,根据几何概型概率公式可得,该乘客到达站台立即能乘上车的概率为,故答案为.5.已知,,则正实数______.【答案】【解析】,则,得,故答案为.6.秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.右边的流程图是秦九韶算法的一个实例.若输入n,x的值分别为3,3,则输出v的值为_________.。
江苏省12市2015届高三上学期期末考试数学试题分类汇编:复数与算法初步

江苏省12市2015届高三上学期期末考试数学试题分类汇编复数与算法初步一、复数1、(常州市2015届高三)设复数3i 1im z m +=+(0m >,i 为虚数单位),若z z =,则m 的值为 ▲ 2、(连云港、徐州、淮安、宿迁四市2015届高三)设复数z 满足()i 432i z -=+(i 是虚数单位),则z 的虚部为 ▲3、(南京市、盐城市2015届高三)若复数a i z i+=(其中i 为虚数单位)的实部与虚部相等,则实数a = ▲ 4、(南通市2015届高三)已知复数z 满足()341(i z i +=为虚数单位),则z 的模为5、(苏州市2015届高三上期末)已知23(,,i a bi a b R i i+=+∈为虚数单位),则a b += 6、(泰州市2015届高三上期末)复数z 满足i z 34i =+(i 是虚数单位),则z = ▲ 7、(无锡市2015届高三上期末)已知复数z 满足()11i z i -=+,则z 的模为8、(扬州市2015届高三上期末)已知i 是虚数单位,则21(1)i i +-的实部为____ 参考答案1、-3 3、-1 4、15 5、1 6、43i - 7、1 8、12-二、算法初步1、(常州市2015届高三)右图是一个算法流程图,则输出的a 的值是 ▲2、(连云港、徐州、淮安、宿迁四市2015届高三)如图是一个算法的流程图,若输入x的值为2,则输出y的值为▲3、(南京市、盐城市2015届高三)运行如图所示的程序后,输出的结果为▲4、(南通市2015届高三)有图是一个算法流程图,则输出的x的值是5、(苏州市2015届高三上期末)运行如图所示的流程图,如果输入1,2a b ==, 则输出的a 的值为6、(泰州市2015届高三上期末)执行如右图所示的流程图,则输出的n 为 ▲7、(无锡市2015届高三上期末)根据如图所示的流程图,则输出的结果i为8、(扬州市2015届高三上期末)如图是一个算法流程图,输出的结果为_____参考答案1、1272、73、424、595、96、47、78、15、。
2015届江苏省苏州高三数学调研测试试题

2015届江苏省苏州高三数学调研测试试题(满分150)一.填空题(14×5分)1. 已知集合{}11,cos ,,1,2A B θ⎧⎫==⎨⎬⎩⎭若,A B =则锐角θ=▲ 2. 若复数122,1,z a i z i =+=-且12z z 为纯虚数则实数a 的值为 ▲ 3. 右图是小王所做的六套数学附加题得分(满分40)的茎叶图则其平均得分为▲4. 已知函数()2log 1a xf x x-=+为奇函数则实数a 的值为 ▲ 5. 已知等比数列{}n a 的各项均为正数3614,,2a a ==则45a a += ▲6. 一只口袋内装有大小相同的5只球其中3只白球2只黑球从中一次性随机摸出2只球则恰好有1只是白球的概率为 ▲7. 右图是一个算法的流程图则最后输出W 的值为 ▲8. 已知双曲线2215x y m -=的右焦点与抛物线212y x =的焦点相同则9. 已知函数()sin 0,0,2y A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的图象上有一个最高点的坐标为(,由这个最高点到其右侧相邻最低点间的图像与x 轴交于点()6,0,则此解析式为▲10.若圆柱的底面直径和高都与球的直径相等圆柱、球的表面积分别记为1S 、2,S 则有12:S S = ▲11.已知圆()()2210C y a a +-=>与直线3y x =相交于,P Q 两点则当CPQ ∆的面积最大时此时实数a 12.函数()32122132f x ax ax ax a =+-++13.如图AB 是半径为3的圆O 的直径P 是圆O 上异于,A B 的一点 Q 是线段AP 上靠近A 的三等分点且4,AQ AB ⋅= 则BQ BP ⋅的 值为 ▲14.已知函数()()2,f x x ax b a b R =++∈与x 轴相切若直线y c =与5y c =+分别交()f x 的图象于,,,A B C D 四点且四边形ABCD 的面积为25则正实数c 的值为 ▲YN3π2-3130.614x 84y x π⎛⎫=+ ⎪⎝⎭3:2244二.解答题(3×14分+3×16分)15.如图在平面直角坐标系xOy 中点,,A B C 均在单位圆上已知点A 在第一象限用横坐标是3,5点B 在第二象限点()1,0.C(1)设,COA θ∠=求sin 2θ的值; (2)若AOB ∆为正三角形求点B 的坐标16.如图在四面体ABCD 中,,AB AC DB DC ===点E 是BC 的中点点F 在AC 上,且.AFACλ=(1)若//EF 平面,ABD 求实数λ的值; (2)求证:平面BCD ⊥平面AED17.如图有两条相交直线成060角的直路,,X X Y Y ''交点是,O 甲、乙两人分别在,OX OY 上,甲的起始位置距离O 点3,km 乙的起始位置距离O 点1,km 后来甲沿X X '的方向乙沿Y Y '的方向两人同时以4/km h 的速度步行(1)求甲乙在起始位置时两人之间的距离;(2)设th 后甲乙两人的距离为(),d t 写出()d t 的表达式;当为何值时甲乙两人的距离最短并求出此时两人的最短距离18.如图,,A B 是椭圆()2222:10x y C a b a b+=>>的左右顶点,M 是椭圆上异于,A B 的任意一点直线是椭圆的右准线(1)若椭圆C 的离心率为1,2直线:4,l x =求椭圆C 的方程; (2)设直线AM 交于点,P 以MP 为直径的圆交MB 于,Q 若直线PQ 恰好过原点求椭圆C 的离心率()241625分()214B 分()1162λ= 分()214 证明略分(14分()12132t = 当时,分19.已知数列{}n a 共有2k 项()*2,k N ≤∈数列{}n a 的前n 项的和为,n S 满足12,a =()()1121,2,3,,21,n n a p S n n +=-+=- 其中常数1p >(1)求证:数列{}n a 是等比数列; (2)若2212,k p -=数列{}n b 满足()()2121log 1,2,,2,n n b a a a n n n == 求数列{}n b 的通项公式 (3)对于(2)中的数列{},n b 记3,2n n c b =-求数列{}n c 的前2k 项的和20.设函数()()xf x ax ea R =+∈(1)若函数()f x 有且只有两个零点()1212,,x x x x <求实数a 的取值范围; (2)当1a =时若曲线()f x 上存在横坐标成等差数列的三个点,,A B C ①证明:ABC ∆为钝角三角形;②试判断ABC ∆能否为等腰三角形并说明理由()2211643x y += 分()216e =分()15 证明略分()121921n n b k -=+- 分()2231621k k T k =- 所求和分()()1,6a e ∈-∞- 分()()12,10a e ∈-∞- 分216ABC ∆不可能是等腰三角形分。
苏州市2015届高三第一次调研测试数学试卷(精)

苏州市 2015 届高三调研测试数学Ⅱ试题 2015.1 参考答案与评分标准21. A .解:设⊙O 半径为 r,由切割线定理得, 2 即 12 ,解得 r=9.2 (4)分 (7)分…………………………………………10 分连结 OA,则有,又 CD ,所以 OA∥CD.所以,即 C. OA PO 15 5.解:解:设,由得:,分,,.分 C .解:,圆的普通方程为:即, 24 …………………………………………………3 分…………………6 分直线的普通方程为:,又圆与直线相切,所以解得:..解:∵∴≥ ……………10 分………………………4 分……………………………7 分 18 y z ,当且仅当时取等号, 7 2 3 3 6 9 ∵,∴. 7 7 7 ∴的最小值为 18 3 6 9 ,此时.……………………………………10 分 7 7 7 7 高三数学答案第 5页,共 6 页22.解:(1)如图,以 CD , CB , CE 为正交基底建立空间直角坐标系,则 E (0,0,1 , D( 2,0,0 , B (0, 2,0 , uuu r uur uu u r F ( 2, 2,1 .( 2,0,1 .,∴分平面 ADF 的法向量,,设平面 DFB 法向量,则,∴.从而令,得,2 ,……………………………………………………………………4 分,显然二面角为锐角,故二面角的大小为 60 .………………………………………………6 分(2)由题意,设 P(a, a,0 (0≤a≤ 2 ,则,.∵PF 与 BC 所成的角为,,∴或(舍), 2 2 所以点 P 在线段 AC 的中点处.……………………………………………………10 分 23.解: (1依题意,X 的可能取值为 1,0,-1,………………………………………2 分 X 的分布列为解得-1 1 2 1 4 1 4 ………………………………4 分 1 11 …………………………………………………………………5 分. 3 4 4 (2设 Y 表示 10 万元投资乙项目的收益,则 Y 的分布列为:Y P 2 α -2 β ……………………8 分 E(Y=2α-2β=4α-2,依题意要求4α-2≥ 1 9 ,∴≤α≤1.………………… 10 分 4 16 高三数学答案第 6页,共 6 页。
苏州市2015届高三调研测试(三)

苏州市2015届高三调研测试(三)化 学2015.2本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分120分,考试时间100分钟。
可能用到的相对原子质量:H —1 C —12 N —14 O —16 S —32 Fe —56 Ba —137第Ⅰ卷(选择题 共40分)单项选择题:本题包括10小题,每小题2分,共20分。
每小题只有一个选项符合题意。
1. 下列说法不符合人与自然和谐相处的是( )A. 用电动汽车代替燃油汽车B. 将聚乙烯等塑料垃圾深埋或倾入海中C. 用沼气、太阳能、风能等新型能源替代化石燃料D. 大力实施矿物燃料的脱硫脱硝技术以减少SO 2、NO x 的排放2. 下列有关化学用语表示正确的是( )A. CO 2的电子式:··O ······C ······O ······ B. Cl -的结构示意图:C. 乙醇的结构式:C 2H 6OD. 中子数为53、质子数为78的碘原子:131 53I3. 常温下,下列各组离子在指定溶液中一定能大量共存的是( )A. 在0.01 mol·L -1Ba(OH)2溶液中:Al 3+、NH +4、NO -3、HCO -3B. 在加入甲基橙显红色的溶液中:Mg 2+、Fe 2+、Cl -、NO -3C. 在含有苯酚的溶液中:K +、NH +4、Br -、Fe 3+D. 在0.01 mol·L -1HCl 溶液中:K +、Na +、I -、SO 2-44. 下列物质性质与相应结果或应用的对应关系正确的是( )A. 酸性越强的含氧酸跟铁片反应产生氢气越快B. 将草木灰和硫铵混合施用,可使肥效更高C. Mg(OH)2和Al(OH)3受热易分解,常用它们作阻燃剂D. 某地雨水经过一段时间,其pH 由4.68降为4.28,因为水中溶解了较多的CO 25. 下列关于各实验装置与对应现象或结论的叙述均正确的是 ( )A. 图1装置:可用于分离石油,分别得到汽油、煤油和柴油等各种纯净物B. 图2装置:可用于吸收NH 3或HCl 气体,并防止倒吸C. 图3装置:如果“a 进b 出”可用于收集NO 2,如果“b 进a 出”可用于收集NH 3D. 图4装置:持续通入CO 2气体,现象是先出现白色沉淀,后变澄清6. 设N 0表示阿伏加德罗常数的值。
苏州市2015届高三数学必过关题(逐题解析)——平面向量

高三必过关题7 平面向量一、填空题例1 给出下列命题,其中不正确的序号是 .① 0a = 0;② 对于实数m 和向量,a b (m ∈R ),若m m =a b ,则=a b ; ③ 若≠a 0,⋅=⋅a b a c ,则=a c ;④ ()()⋅=⋅a b c a b c 对任意,,a b c 向量都成立;⑤对任意向量a,有a .答案:①②③④例2 与a = (3,-4)平行的单位向量是_________;答案: (35 ,-45 )或(-35 ,45).例3 平面向量a 与b 的夹角为60°,(,),||==201a b ,则|2|+=a b 答案:例4已知a 与b 为两个不共线的单位向量,k 为实数,若向量a +b 与向量ka -b 垂直,则k=_______ 答案: 1k =.例5 如图,正方形ABCD 内有一个正ABE △,设,AB AD ==i j ,则DE 等于 .(用i 、j 表示) 答案:12i j . 例6 定义*a b 是向量a 和b 的“向量积”,它的长度||||sin ,*=⨯⨯θa b a b 其中θ为 向量a 和b的夹角,若(2,0),(1,=-=u u v 则|()|*+u u v = .答案:.例7 如图,在△ABC 中,AN =31NC ,P 是BN 上的一点,若 AP =m AB +112AC ,则实数m 的值为___________. 解析: 123,.41144AP AC NP mAB AC NP mAB AC =+=+=-BD()3144NB NC CB AC AB AC AB AC =+=+-=-,设,NP NB λ=则14AB AC λλ-=344mAB AC -,3.11m λ==例8. 已知直角梯形ABCD 中,AD //BC ,090ADC ∠=,2,1AD BC ==,P 是腰DC 上的动点,则3PA PB +的最小值为____________.答案:5例9 如图,设P 、Q 为△ABC 内的两点,且2155AP AB AC =+, AQ =23AB +14AC ,则△ABP 的面积与△ABQ 的面积之比为 . 解析:设25AM AB =,15AN AC =,则AP AM AN =+,由平行四边形法则,知NP ∥AB ,所以ABP ABC S AN S AC∆∆==15,同理可得14ABQ ABC S S ∆∆=, 故45ABP ABQ S S ∆∆=.例10 如图,在ABC ∆中,120,2,1,BAC AB AC D ∠=︒==是边BC 上一点,2,DC BD = 则AD BC ⋅=__________.解析:1()()3AD BC AB BD BC AB BC BC ⋅=+⋅=+⋅=121[()]()()333AB AC AB BC AB AC AC AB +-⋅=+⋅-2221183333AB AC AB AC =-++⋅=-.例11 设函数()2x f x x x =⋅+,0A 为坐标原点,n A 为函数()y f x =图像上横坐标n ()n N *∈的点,向量11,(1,0)nn k k k A A -===∑a i ,设n n θ为与a i 的夹角,则1tan nk k θ==∑ .解析:0(,2)n n n A A n n n ==⋅+a ,n θ即为向量0n A A 与x 轴的夹角,所以tan 21n n θ=+,所以211tan (222)22nn n k k n n θ+==++⋅⋅⋅++=+-∑.例12 已知20=≠a b ,且关于x 的函数3211()()32f x x x x =++⋅a a b 在R 上有极值,则a 与b 的夹角范围为 .DCABC N MQ P BA解析:()y f x =在R 上有极值⇔方程2()||f x x x '=++⋅a a b =0在R 上有两个不同的实数根,则22||||404∆=-⋅>⇒⋅<a a a b a b ,设向量,a b 的夹角为θ,则221||14cos 1||||2||2θ⋅=<=a a b a b a ,所以(,]3πθπ∈.例13已知A 、B 、C 是直线l 上的不同的三点,O 是外一点,向量OA 、OB 、OC 满足:23(1)[ln(23)]02OA x OB x y OC -+⋅-+-⋅=,记()y f x =,则函数()y f x =的解析式为 .解析:23(1)[ln(23)]02OA x OB x y OC -+⋅-+-⋅=,∴23(1)[ln(23)]2OA x OB x y OC =+⋅++-⋅.又A 、B 、C 在同一条直线上,∴1])32[ln()123(2=-+++y x x , ∴223)32ln(x x y ++=. 即223)32ln()(x x x f ++=. 例14 已知O 是锐角ABC ∆的外接圆的圆心,且A θ∠=,若cos cos sin sin B CAB AC C B+=2mAO ,则m = 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏州市2015届高三调研考试数学试题一、填空题1.已知集合{|22},{|1}A x x B x x =-<<=≤,则A B = .2.已知23(,,ia bi ab R i i+=+∈为虚数单位),则a b += . 3.已知函数()sin()5f x kx π=+的最小正周期是3π,则正数k 的值为 . 4.某课题组进行城市空气质量监测,按地域将24个城市分成甲、乙、丙三组,对应区域城市数分别为4、12、8.若用分层抽样抽取6个城市,则乙组中应该抽取的城市数为 .5.已知等差数列{}n a 中,4610a a +=,若前5项的和55S =,则其公差为 .6.运行如图所示的流程图,如果输入1,2a b ==, 则输出的a 的值为 .7.以抛物线24y x =的焦点为顶点,顶点为中心, 离心率为2的双曲线标准方程为 . 8.设{1,1},{2,0,2}x y ∈-∈-,则以(,)x y 为坐标 的点落在不等式21x y +≥所表示的平面区域内的 概率为 . 9.已知函数()lg(1)2x a f x =-的定义域是1(,)2+∞, 则实数a 的值为 .10.已知一个圆锥的母线长为2,侧面展开是半圆,则该圆锥的体积为 . 11.如图,在ABC ∆中,已知4,6,60AB AC BAC ==∠=︒, 点,D E 分别在边,AB AC 上,且2,3AB AD AC AE ==, 点F 为DE 中点,则BF DE 的值为 .12.已知函数24,()43,f x x x ⎧=⎨+-⎩,.x m x m ≥<若函数()()2g x f x x =-恰有三个不同的零点,则实数m 的取值范围是 .13.已知圆22:(1)(1)4M x y -+-=,直线:60,l x y A +-=为直线l 上一点,若圆M 上存在两点,B C ,使得60BAC ∠=︒,则点A 的横坐标的取值范围是 .A DFEB C14.已知,a b 为正实数,且2a b +=,则2221a b a b +++的最小值为 . 二、解答题15.已知向量(sin ,2),(cos ,1)a b θθ==,且,a b 共线,其中(0,)2πθ∈.(1)求tan()4πθ+的值;(2)若5cos(),02πθϕϕϕ-=<<,求ϕ的值.16.如图,在正方体1111ABCD A BC D -中,,E F 分别是1,AD DD 中点. 求证:(1)EF ∥平面1C BD ; (2)1AC ⊥平面1C BD .17.如图,某生态园将一三角形地块ABC 的一角APQ 开辟为水果园种植桃树,已知角A 为120,,AB AC ︒的长度均大于200米,现在边界AP ,AQ 处建围墙,在PQ 处围竹篱笆.(1)若围墙AP ,AQ 总长度为200米,如何围可使得三角形地块APQ 的面积最大?(2)已知AP 段围墙高1米,AQ 段围墙高1.5米,造价均为每平方米100元.若围围墙用了A B C D A 1B 1C 1D 1APQC20000元,问如何围可使竹篱笆用料最省?18.如图,已知椭圆22:1124x y C +=,点B 是其下顶点,过点B 的直线交椭圆C 于另一点A (A 点在x 轴下方),且线段AB 的中点E 在直线y x =上.(1)求直线AB 的方程;(2)若点P 为椭圆C 上异于A 、B 的动点,且直线AP ,BP 分别交直线y x =于点M 、N ,证明:OM ON 为定值.19.已知函数()(1)xf x e a x =--,其中,a R e ∈为自然对数底数. (1)当1a =-时,求函数()f x 在点(1,(1))f 处的切线方程; (2)讨论函数()f x 的单调性,并写出相应的单调区间;(3)已知b R ∈,若函数()f x b ≥对任意x R ∈都成立,求ab 的最大值.20.已知数列{}n a 中1111,33n n n a n a a a n+⎧+⎪==⎨⎪-⎩((n n 为奇数)为偶数).(1)是否存在实数λ,使数列2{-}n a λ是等比数列?若存在,求λ的值;若不存在,请说明理由;(2)若n S 是数列{}n a 的前n 项和,求满足0n S >的所有正整数n .数 学数学Ⅱ 附加题部分注意事项1.本试卷共2页,均为解答题(第21题~第23题,共4题).本卷满分为40分,考试时间为30分钟。
考试结束后,请将本试卷和答题卡一并交回.2.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其它位置作答一律无效. 21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题.......,并在相应的答题区域内作...........答..若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .选修4-1:几何证明选讲(本小题满分10分)如图,过圆O 外一点P 作圆O 的切线PA ,切点为A ,连结OP 与圆O 交于点C ,过C 作AP 的算线,垂足为D ,若PA =12cm ,PC =6cm ,求CD 的长。
B .选修4-2:矩阵与变换(本小题满分10分)已知矩阵,A =1211⎡⎤⎢⎥⎣⎦,向量21β⎡⎤=⎢⎥⎣⎦,求向量α,使得2A αβ=.C .选修4-4:坐标系与参数方程(本小题满分10分)在极坐标系中,已知圆3cos ρθ=与直线2cos 4sin 0a ρθρθ++=相切,求实数a 的值.D .选修4-5:不等式选讲(本小题满分10分)设实数x ,y , z 满足,的最小值,并求此时x ,y ,z 的值。
【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)如图,已知正方形ABCD 和矩形ACEF 所在的平面互相垂直,1AB AF =. (1)求二面角A-DF-B 的大小;(2)试在线段AC 上确定一点P ,使PF 与BC 所成角为60︒.23、(10分)某公司有10万元资金用于投资,如果投资甲项目,根据市场分析知道:一年后可能获利10%,可能损失10%,可能不陪不赚,这三种情况发生的概率分别为111 ,, 244;如果投资乙项目,一年后可能获利20%,可能损失20%,这两种情况发生的概率分别为α和β(α+β=1).(1)如果把10万元投资甲项目,用X表示投资收益(收益=回收资金-投资资金),求X的概率分布列及数学期望E(X).(2)若10万元资金投资乙项目的平均收益不低于投资甲项目的平均收益,求α的取值范围.ABCDE FA 1B 1C 1D 1苏州市2015届高三调研测试 数学Ⅰ试题 2015.1 参考答案与评分标准1.(-2,1]2.13.6 4.3 5.26.97.2213y x -= 8.12 910π 11.4 12.(]1,2 13.14.33+ 15.解 (1)∵a ∥b ,∴sin 2cos 0θθ-=,即tan 2θ=. ………………………………4分 ∴π1tan 12tan()341tan 12θθθ+++===---. ………………………………………………7分 (2)由(1)知tan 2θ=,又π(0,)2θ∈,∴sin θθ==, …………9分∴5cos()θϕϕ-=,∴5(cos cos sin sin )θϕθϕϕ+=ϕϕϕ+=, ∴cos sin ϕϕ=,即tan 1ϕ=, ………………………………………………………12分 又02πϕ<<,∴4πϕ=. ……………………………………………………………14分16.证明:(1)连结A1D ,∵ E ,F 分别是AD 和DD1的中点,∴ EF ∥AD 1. …………………………………2分 ∵ 正方体ABCD -A1B1C1D1, ∴ AB ∥D1C1,AB=D1C1.∴ 四边形ABC1D1为平行四边形,即有A1D ∥BC1 ………………………………………4分 ∴ EF ∥BC1.又EF ⊄平面C1BD ,BC1⊂平面C1BD ,∴ EF ∥平面AB1D1. ……………………………………7分 (2)连结AC ,则AC ⊥BD .∵ 正方体ABCD -A1B1C1D1,∴AA1⊥平面ABCD , ∴ AA1⊥BD .又1AA AC A =I ,∴BD ⊥平面AA1C ,∴ A1C ⊥BD . ……………………………………………11分 同理可证A1C ⊥BC1.又1BD BC B =I ,∴A1C ⊥平面C1BD . ……………………………………………… 14分17.解 设AP x =米,AQ y =米. (1)则200x y +=,APQ ∆的面积1sin12024S xy xy =︒=. …………………………………………………………3分∴S 2()2x y += 当且仅当100x y ==时取“=”. …………………………………………………………6分 (注:不写“=”成立条件扣1分)(2)由题意得100(1 1.5)20000x y ⨯⋅+⋅=,即 1.5200x y +=. …………………8分 要使竹篱笆用料最省,只需其长度PQ 最短,所以2222cos120PQ x y xy =+-︒22x y xy =++22(200 1.5)(200 1.5)y y y y =-++-21.7540040000y y =-+(40003y <<) ………………………………………11分当8007y =时,PQ ,此时2007x =. …………………………13分答:(1)当100AP AQ ==米时,三角形地块APQ 的面积最大为 (2)当2007AP =米800,7AQ =米时,可使竹篱笆用料最省.……………………… 14分18.解:(1)设点E (m ,m ),由B (0,-2)得A (2m ,2m+2). 代入椭圆方程得224(22)1124m m ++=,即22(1)13m m ++=, 解得32m =-或0m =(舍). ………………………………………………3分 所以A (3-,1-),故直线AB 的方程为360x y ++=. …………………………………………………6分 (2)设00(,)P x y ,则22001124x y +=,即220043x y =-.设(,)M M M x y ,由A ,P ,M 三点共线,即AP AM uu u r uuu rP ,∴00(3)(1)(1)(3)M M x y y x ++=++,又点M 在直线y=x 上,解得M 点的横坐标000032M y x x x y -=-+, (9)分设(,)N N N x y ,由B ,P ,N 三点共线,即BP BN u u r u u u rP ,∴00(2)(2)N N x y y x +=+,点N 在直线y=x 上,,解得N 点的横坐标00022N x x x y -=--. (12)分所以OM ·0|0|M N x x --=2||||M N x x ⋅=200003||2y x x y --+0002||2x x y -⋅--=2000200262||()4x x y x y ---=2000220000262||23x x y x x x y ---=2000200032||3x x y x x y --=6.…………………… 16分19.解:(1)当1a =-时,()'e 1xf x =+,()'1e 1f =+,()1e f =, (2)分∴函数()f x 在点()()1,1f 处的切线方程为()()e e 11y x -=+-,即()e 11y x =+-. ……………………………………………………………………4分 (2)∵()'e xf x a =-,①当0a ≤时,()'0f x >,函数()f x 在R 上单调递增;………………………………6分 ②当0a >时,由()'e 0xf x a =-=得ln x a =,∴(),ln x a ∈-∞时,()'0f x <,()f x 单调递减;()ln ,x a ∈+∞时,()'0f x >,()f x 单调递增.综上,当0a ≤时,函数()f x 的单调递增区间为(,)-∞+∞;当0a >时,函数()f x 的单调递增区间为()ln ,a +∞,单调递减区间为(),ln a -∞. ……………………………………9分(3)由(2)知,当0a <时,函数()f x 在R 上单调递增,∴()f x b ≥不可能恒成立; ………………………………………………………………10分当0a =时,0b ≤,此时0ab =; ………………………………………………………11分 当0a >时,由函数()f x b ≥对任意x ∈R 都成立,得()min b f x ≤,∵()()min ln 2ln f x f a a a a ==-,∴2ln b a a a -≤ ………………………………13分 ∴222ln ab a a a -≤,设()()222ln 0g a a a a a =->,∴ ()()'42ln 32ln g a a a a a a a a =-+=-,由于0a >,令()'0g a =,得3ln 2a =,32e a =, 当320,e a ∈⎛⎫ ⎪⎝⎭时,()'0g a >,()g a 单调递增;32e ,a ∈+∞⎛⎫ ⎪⎝⎭时,()'0g a >,()g a 单调递减.∴()3max e 2g a =,即ab 的最大值为3e 2,此时33221e ,e 2a b ==. ………………………………………………………………… 16分20.解:(1)设2n n b a λ=-,因为()21122221213n n n n n n a n b a b a a λλλλ+++++--==--()()222211621133n n n n a n n a a a λλλλ-++-+-==--. …………………………………2分若数列{}2n a λ-是等比数列,则必须有22113n n a q a λλ+-=-(常数), 即()211103n q a q λ-+-+=⎛⎫⎪⎝⎭,即()103110q q λ-=-+=⎧⎪⎨⎪⎩⇔1332q λ==⎧⎪⎪⎨⎪⎪⎩, …………………5分此时1213131102326b a a =-=+-=-≠,所以存在实数32λ=,使数列{}2n a λ-是等比数列………………………………………6分 (注:利用前几项,求出λ的值,并证明不扣分)(2)由(1)得{}n b 是以16-为首项,13为公比的等比数列, 故123111126323n n n n b a -⎛⎫⎛⎫=-=-⋅=-⋅ ⎪⎪⎝⎭⎝⎭,即2113232nn a ⎛⎫=-⋅+ ⎪⎝⎭,…………………8分由()2211213n n a a n -=+-,得()1212111533216232n n n a a n n --⎛⎫=--=-⋅-+⎪⎝⎭,……10分 所以12121111692692333n n nn n a a n n --⎡⎤⎛⎫⎛⎫⎛⎫+=-⋅+-+=-⋅-+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,()()()21234212n n n S a a a a a a -=++++++L()211126129333nn n ⎡⎤⎛⎫⎛⎫=-+++-++++⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦L L 11133(1)2691213nn n n ⎡⎤⎛⎫-⎢⎥⎪⎝⎭+⎢⎥⎣⎦=-⋅-⋅+-()221113631233n n n n n ⎛⎫⎛⎫=--+=--+ ⎪ ⎪⎝⎭⎝⎭,………………………………………………………………12分 显然当*n N ∈时,{}2n S 单调递减, 又当1n =时,2703S =>,当2n =时,4809S =-<,所以当2n ≥时,20n S <; 2212231536232nn n n S S a n n -⎛⎫=-=⋅--+ ⎪⎝⎭,同理,当且仅当1n =时,210n S ->.综上,满足0n S >的所有正整数n 为1和2.…………………………………………… 16分。
