第1章作业
1线性代数第一章作业

2x + y − z + ω = 1 3 x − 2 y + z − 3ω = 4 x + 4 y − 3 z + 5ω = −2
1 −1 3 − 4 3 0 2 − 3 1 1 3 −3 5 4 1. A = 0 3 − 4 3 ;2. B = ; 2 −2 3 −2 0 0 4 − 7 − 1 3 − 3 4 − 2 − 1
R( A) _____ R( B) ;
那么该方程组有无穷多个解的充分必 3.设一个 m × n 齐次线性方程组的系数矩阵为 A , 要条件是_______________;仅有零解的充分必要条件是 ;
x1 + 2 x 2 + x3 = 1 4.已知方程 2 x1 + 3 x 2 + ( a + 2) x3 = 3 无解,则 a = x + ax − 2 x = 4 1 2 3
λx1 + x 2 + x3 = 1 五、 λ 取何值时,非齐次线性方程组 x1 + λx 2 + x3 = λ x + x + λx = λ2 2 3 1
1.有唯一解;2.无解;3.有无穷多个解.
Hale Waihona Puke x1 + 2 x 2 − 2 x3 = 1 2 x1 + (5 − λ ) x 2 − 4 x3 = 2 ,问 λ 为何值时,此方程组有唯一解,无解或有 六、设 − 2 x − 4 x + (5 − λ ) x = −λ − 1 1 2 3
无穷解. 七、求下列矩阵的标准形:
1 1 − 1 0 3 1 1. ; 4 4 1 1 − 2 1
大学物理第一章作业

at d v / d t g t / v g t 法向加速度方向与 at 垂直,大小为
2 2 0
2 2
an g a
2
2 1/2 t
2 v0 g / v0 g 2t 2
2.一质点沿半径为R的圆周运动.质点所经过的 S bt ct 2 2 ,其中b、c是 弧长与时间的关系为 大于零的常量,求从 t 0 开始到切向加速度与法 向加速度大小相等时所经历的时间. ds 解: v b ct dt 2 则有 dv v 2 at c an b ct / R dt R 根据题意,当 at an 时有 2 c b ct / R 可解得
d r a 2 (1)i (2t ) j dt
2 x 2 y
2
a
-1
y -arctan4 4 ay
则加速度的大小为
ax
x
at 2 s a a 1 4t 17 4.12m s 2
加速度的方向
ay
2 arctan(1 4) y
dv 2 v 2 6x dx
v d v (2 6x )d x
2
两边同时积分,即
可得
v
0
vd v 2 6 x 2 d x
x 0
1 2 v 2 x 2 x3 2
v 2 x x
3
1
2
一 选择题 质点作半径为R的变速圆周运动时的加速度大 小为(v表示任一时刻质点的速率) 2 d (A) v d t . (B) v R .
a
ay
4 arctan arctan arctan(4) 104 ax 1
第一章作业及答案(学生版)

习题1-21. 选择题(1) 设随机事件A ,B 满足关系A B ⊃,则下列表述正确的是( ). (A) 若A 发生, 则B 必发生. (B) A , B 同时发生. (C) 若A 发生, 则B 必不发生. (D) 若A 不发生,则B 一定不发生.解 应选(D).(2) 设A 表示“甲种商品畅销, 乙种商品滞销”, 其对立事件A 表示( ). (A) 甲种商品滞销, 乙种商品畅销. (B) 甲种商品畅销, 乙种商品畅销. (C) 甲种商品滞销, 乙种商品滞销.(D) 甲种商品滞销, 或者乙种商品畅销. 解 应选(D).2. 写出下列各题中随机事件的样本空间:(1) 一袋中有5只球, 其中有3只白球和2只黑球, 从袋中任意取一球, 观察其颜色;(2) 从(1)的袋中不放回任意取两次球, 每次取出一个, 观察其颜色; (3) 从(1)的袋中不放回任意取3只球, 记录取到的黑球个数; (4) 生产产品直到有10件正品为止, 记录生产产品的总件数. 解 (1) {黑球,白球}; (2) {黑黑,黑白,白黑,白白}; (3) {0,1,2};(4) 设在生产第10件正品前共生产了n 件不合格品,则样本空间为{10|0,1,2,n n += }.3. 设A, B, C 是三个随机事件, 试以A, B, C 的运算关系来表示下列各事件:(1) 仅有A 发生;(2) A , B , C 中至少有一个发生; (3) A , B , C 中恰有一个发生; (4) A , B , C 中最多有一个发生; (5) A , B , C 都不发生;(6) A 不发生, B , C 中至少有一个发生. 解 (1) ABC ; (2) A B C ; (3) ABC ABC ABC ;(4) ABC ABC ABC ABC ; (5) ABC ; (6) ()A B C .4. 事件A i 表示某射手第i 次(i =1, 2, 3)击中目标, 试用文字叙述下列事件: (1) A 1∪A 2; (2) A 1∪A 2∪A 3; (3)3A ; (4) A 2-A 3; (5)23A A ; (6)12A A . 解 (1) 射手第一次或第二次击中目标;(2) 射手三次射击中至少击中目标;(3) 射手第三次没有击中目标;(4) 射手第二次击中目标,但是第三次没有击中目标;(5) 射手第二次和第三次都没有击中目标;(6) 射手第一次或第二次没有击中目标.习题1-31. 选择题(1) 设A, B 为任二事件, 则下列关系正确的是( ).(A)()()()P A B P A P B -=-. (B)()()()P A B P A P B =+ . (C)()()()P AB P A P B =. (D)()()()P A P AB P AB =+.解 应选(D).(2) 若两个事件A 和B 同时出现的概率P (AB )=0, 则下列结论正确的是 ( ).(A) A 和B 互不相容. (B) AB 是不可能事件. (C) AB 未必是不可能事件. (D) P (A )=0或P (B )=0. 解 应选(C).2. 设P (AB )=P (AB ), 且P (A )=p ,求P (B ). 解 ()1.P B p =-3. 已知()0.4P A =,()0.3P B =,()0.4P A B = , 求()P AB . 解 ()()()0.1.P AB P A P AB =-=4. 设A , B 为随机事件,()0.7P A =,()0.3P A B -=, 求()P AB . 解 ()0.6P AB =.5. 已知1()()()4P A P B P C ===,()0P AB =, 1()()12P AC P BC ==, 求A , B , C 全不发生的概率.解 有()P ABC =0.7().12P A B C =5()()1()12P ABC P A B C P A B C ==-=.习题1-41. 选择题在5件产品中, 有3件一等品和2件二等品. 若从中任取2件, 那么以0.7为概率的事件是( ).(A) 都不是一等品. (B) 恰有1件一等品. (C) 至少有1件一等品. (D) 至多有1件一等品.解113225C C C ⨯+023225C C C ⨯. 答案为(D ).2. 从由45件正品、5件次品组成的产品中任取3件. 求: (1) 恰有1件次品的概率; (2) 恰有2件次品的概率; (3) 至少有1件次品的概率; (4) 至多有1件次品的概率; (5) 至少有2件次品的概率.解 (1) 12545350C C C ;(2) 21545350C C C ; (3 ) 1-03545350C C C ; (4) 03545350C C C +12545350C C C ; (5)21545350C C C +30545350C C C . 3. 袋中有9个球, 其中有4个白球和5个黑球. 现从中任取两个球. 求: (1) 两个球均为白球的概率;(2) 两个球中一个是白的, 另一个是黑的概率; (3)至少有一个黑球的概率. 解(1) 2924C C ;(2) 115429C C C ;(3) 12924C C -.习题1-51. 选择题(1) 设随机事件A , B 满足P (A |B )=1, 则下列结论正确的是( )(A) A 是必然事件. (B) B 是必然事件. (C) AB B =. (D)()()P AB P B =. 解 选(D).(2) 设A , B 为两个随机事件, 且0()1P A <<, 则下列命题正确的是( ).(A) 若()()P AB P A =, 则A , B 互斥. (B) 若()1P B A =, 则()0P AB =.(C) 若()()1P AB P AB +=, 则A , B 为对立事件. (D) 若(|)1P B A =, 则B 为必然事件. 解 选(B ).2. 从1,2,3,4中任取一个数, 记为X , 再从1,2,…,X 中任取一个数, 记为Y ,求P {Y =2}.解 P {Y =2}=4813. 3. 甲、乙、丙三人同时对某飞机进行射击, 三人击中的概率分别为0.4, 0.5, 0.7. 飞机被一人击中而被击落的概率为0.2, 被两人击中而被击落的概率为0.6, 若三人都击中, 飞机必定被击落. 求该飞机被击落的概率.解 由全概率公式得到3()()(|)0.360.20.410.60.1410.458.i i i P A P B P A B ===⨯+⨯+⨯=∑4. 在三个箱子中, 第一箱装有4个黑球, 1个白球; 第二箱装有3个黑球, 3个白球; 第三箱装有3个黑球, 5个白球. 现任取一箱, 再从该箱中任取一球. (1) 求取出的球是白球的概率;(2) 若取出的为白球, 求该球属于第二箱的概率.解 (1)由全概率公式知P (A )=112233()(|)()(|)()(|)P H P A H P H P A H P H P A H ++=12053. (2) 由贝叶斯公式知 P (2|H A )=222()()(|)20()()53P AH P H P A H P A P A ==5. 某厂甲、乙、丙三个车间生产同一种产品, 其产量分别占全厂总产量的40%, 38%, 22%, 经检验知各车间的次品率分别为0.04, 0.03, 0.05. 现从该种产品中任意取一件进行检查.(1) 求这件产品是次品的概率;(2) 已知抽得的一件是次品, 问此产品来自甲、乙、丙各车间的概率分别是多少?解(1) 由全概率公式可得112233()(|)()(|)()(|)()P A P A B P B P A B P B P A B P B =++0.40.040.380.030.20.0384.=⨯+⨯+⨯=.(2) 由贝叶斯公式可得111(|)()0.40.045(|)()0.038412P A B P B P B A P A ⨯===, 222(|)()0.380.0319(|)()0.038464P A B P B P B A P A ⨯===, 333(|)()0.220.0555(|)()0.0384192P A B P B P B A P A ⨯===.习题1-61. 选择题(1) 设随机事件A 与B 互不相容, 且有P (A )>0, P (B )>0, 则下列关系成立的是( ).(A) A , B 相互独立. (B) A , B 不相互独立. (C) A , B 互为对立事件. (D) A , B 不互为对立事件.解 应选(B).(2) 设事件A 与B 独立, 则下面的说法中错误的是( ). (A) A 与B 独立. (B) A 与B 独立. (C) ()()()P AB P A P B =. (D) A 与B 一定互斥.解 应选(D).(3) 设事件A 与 B 相互独立, 且0<P (B )<1, 则下列说法错误的是( ).(A) (|)()P A B P A =. (B) ()()()P AB P A P B =. (C) A 与B 一定互斥. (D)()()()()()P A B P A P B P A P B =+- .解 应选(C).2. 设三事件A , B 和C 两两独立, 满足条件:,ABC =∅1()()()2P A P B P C ==<, 且9()16P A B C = ,求()P A .解 29()3()3[()]16P A B C P A P A =-=,1()4P A =.3. 甲、乙两人各自向同一目标射击, 已知甲命中目标的概率为 0.7, 乙命中目标的概率为0.8. 求:(1) 甲、乙两人同时命中目标的概率; (2) 恰有一人命中目标的概率; (3) 目标被命中的概率. 解(1) ()()()0.70.80.56;P AB P A P B ==⨯=(2) ()()0.70.20.30.80.38;P AB P AB +=⨯+⨯=(3) ()()()()()0.70.80.560.94.P A B P A P B P A P B =+-=+-=总 习 题 一1. 选择题:设,,A B C 是三个相互独立的随机事件, 且0()1P C <<, 则在下列给定的四对事件中不相互独立的是( ).(A)A B 与C . (B)AC 与C .(C) A B -与C . (D) AB 与C . 解 选项(B).2. 一批产品由95件正品和5件次品组成, 先后从中抽取两件, 第一次取出后不再放回.求: (1) 第一次抽得正品且第二次抽得次品的概率; (2) 抽得一件为正品, 一件为次品的概率.解 (1)9551910099396⨯=⨯.(2) 95559519.10099198⨯+⨯=⨯3. 设有一箱同类型的产品是由三家工厂生产的. 已知其中有21的产品是第一家工厂生产的, 其它二厂各生产41. 又知第一、第二家工厂生产的产品中有2%是次品, 第三家工厂生产的产品中有4%是次品. 现从此箱中任取一件 产品, 求取到的是次品的概率.解 由全概率公式得P (A )=P (B 1)P (A |B 1)+P (B 2)P (A |B 2)+P (B 3)P (A | B 3)=100441100241100221⨯+⨯+⨯=0.025. 4. 某厂自动生产设备在生产前须进行调整. 假定调整良好时, 合格品为90%; 如果调整不成功, 则合格品有30%. 若调整成功的概率为75%, 某日调整后试生产, 发现第一个产品合格. 问设备被调整好的概率是多少?解 由贝叶斯公式可得()0.750.9(|)0.9()0.75()(|)()P AB P A B P B P A P B A P B ⨯====.5. 将两份信息分别编码为A 和B 传递出去. 接收站收到时, A 被误收作B的概率为0.02, 而B 被误收作A 的概率为0.01, 信息A 与信息B 传送的频繁程度为2:1. 若接收站收到的信息是A , 问原发信息是A 的概率是多少?解 由贝叶斯公式知()()()196()()197()()()()P R D P D P DR P D R P R P R D P D P R D P D ===+.。
第1-3章作业作业题(分组用)

第1章作业1.(10分)分析三大材料的结合键类型并由此归纳其导电性、强度和塑性特点。
金属材料:以金属键为主,具有良好的导电性,较高的强度和良好的塑性和韧性。
无机非金属材料:以离子键和共价键为主,具有良好的绝缘性,较高的强度和低塑性和高脆性。
有机高分子材料:以共价键为主,氢键和范德瓦尔斯键为辅,优良的电绝缘性,强度低,塑性较低。
2. (10分)为什么单晶体具有各向异性而多晶体在一般情况下不显示各向异性?“因为单晶体中不同晶面和晶向上的原子排列密度不同,造成原子间结合力不同,因而在不同方向上的性能各异;而多晶体是由很多个位向不同的单晶体所组成,各个晶粒在整块金属内的空间位向是任意的,整个晶体各个方向上的性能则是大量位向各不相同的晶粒性能均值因而一般不显示各向异性。
”3.(10分) 金属常见的晶格类型有哪几种?画出它们的晶胞,每个晶胞内分别有几个原子?配位数是几?如何计算原子半径金属常见的晶格类型有3种,分别是体心立方晶格,面心立方晶格,密排六方晶格。
4.4. (5分)在立方晶胞中画出下列晶面和晶向:(110)(101)、(111)、[011]、[111]。
(110) [011] 5.(5分)写出六方晶系的}1110{晶面族中所有晶面的密勒指数。
在六方晶胞中画出]0111[]0211[、晶向和)1110(晶面。
6.(10分)分别在一个体心立方和面心立方晶胞内画出所有穿过该晶胞(不含顶点)的(111)和(110)晶面,并由此(不直接用晶面间距计算公式)计算(111)和(110)晶面的晶面间距。
(设晶格常数为a)(111) (111) (110) (110)体心立方晶胞(111)晶面间距为根号3a/6 (110)晶面间距为根号3a/3面心立方晶胞(111)晶面间距为根号3a/3 (110)晶面间距为根号3a/67. (10分)α-Fe原子间距最小的3个方向是哪三个晶向族?分别计算它们的原子间距。
晶面间距最大的3个晶面是哪3个晶面族?分别计算它们的晶面间距。
第一次作业及参考答案

第一次作业:第一章一.名词解释:1.饱和空气2.未饱和空气3.制冷4.露点温度5.含湿量6.绝对湿度7. 相对湿度二.简答题:1.空气调节的定义与客车空调装置的任务2.说明制冷与空调的区别和联系3.空气的干球温度、湿球温度和露点温度有什么区别?三者之间的关系如何?4.确定空调装置外气计算参数的方法是什么?5.空气的相对湿度与含湿量有何区别?空气的枯燥程度与吸湿能力大小由那个参数反映?6.白天空气的温度为30℃,相对湿度为50%,夜间温度下降至20℃,夜间会出现结露吗?夜间的相对湿度是多少?7.冷却、冷藏、冷冻都有什么区别?8.焓湿图由哪几种线群组成?9.列车空调系统主要由哪几个根本局部组成?各局部的用作是什么?第一次作业参考答案一.名词解释:1.饱和空气:干空气和饱和水蒸汽的混合物称为饱和空气。
2.未饱和空气:干空气和过热水蒸汽的混合物称为过饱和空气。
3.制冷:用一定的方法使某物体或空间的温度低于周围环境介质的温度,并且使其维持在某一范围内,这个过程称为制冷。
4.露点温度:指某一状态的空气,在含湿量不变时,降温至饱和状态时的温度。
5.含湿量:随一公斤干空气同时存在的水蒸汽质量,称为湿空气的含湿量〔g〕。
6.绝对湿度:每立方米湿空气中所含水蒸汽的质量,称为空气的绝对湿度。
7.相对湿度:一立方米湿空气中所含水蒸汽的质量,与同一温度下饱和空气中所含水蒸汽质量的比值称为相对湿度。
二.简答题:1. 空气调节的定义与客车空调装置的任务答:空气调节:把经过一定处理后的空气,以一定的方式送入室内,使室内空气的温度、相对湿度、气流速度和干净度等控制在适当范围内的专门技术。
客车空调装置的任务是将一定量的车外新鲜空气和车内再循环空气混合后,经过过滤、冷却或加热、减湿或加湿等处理,以一定的流速送入车内,并将车内一定量的污浊空气排出车外。
答:制冷:用人工的方法在一定时间和空间内将某物体或流体冷却,使其温度低于周围环境介质的温度,并保持这个低温的过程。
第一章 作业答案

解: 1)
I = I 0 e δ l I 1 δ l 0.01×100 ∴ =e =e = ≈ 0.3679=376.79% I0 e
2)由题意知
不 考 虑 损 耗
2 I 0 = I 0 eGZ I ∴ = 2 = eGZ = eG I0 G ≈ ln 2 = 0.6931m -1
考 虑 损 耗
λ
习题八> ※<习题八 习题八 如果受激辐射爱因斯坦系数B 试计算在( ) = 如果受激辐射爱因斯坦系数 10=1019m3s-1w-1,试计算在(1)λ=6um(红外 ( 光);(2)λ=600nm(可见光);( )λ=60nm(远紫外光);( )λ= );( ) = (可见光);(3) = (远紫外光);(4) = );( );( 0.60nm(x射线),自发辐射跃迁几率 10和自发辐射寿命.又如果光强 = 射线),自发辐射跃迁几率A ( 射线),自发辐射跃迁几率 和自发辐射寿命.又如果光强I= 10W/mm2,试求受激跃迁几率 10. 试求受激跃迁几率W 解: 8π hv 3 8π h 1 = Bul 3 Aul = B ul τ = Aul λ c3 1)λ=6um ) =
解:1)
Aul = Bul
∴ B ul
8π hv 3
c3
3 c3 5 λ = Aul = 10 ≈ 6.0022 × 1015 s 1 8π h 8π hv 3
2)
c3 24π hv 3 ∴ρ = c3 Aul = Bul
8π hv 3 1 Bul ρ 3 24π h = ≈ 4.9981 × 10-11Jms 3 =
※<习题九 习题九> 习题九 由两个全反射镜组成的稳定光学谐振腔,腔长为0.5m, 由两个全反射镜组成的稳定光学谐振腔,腔长为 , 腔内振荡光的中心波长为6328A,试求该光的频带宽度 腔内振荡光的中心波长为 , λ的近似值. 的近似值. 的近似值 习题十> ※<习题十 习题十 (1)一光束入射到长为 )一光束入射到长为10cm,增益系数为 ,增益系数为0.5cm-1的工 作物质中,求出射光强对入射光强的比值;( ;(2) 作物质中,求出射光强对入射光强的比值;( )一初始 光强为I 波长为λ的光束入射到长为 的工作物质中, 的光束入射到长为L的工作物质中 光强为 0波长为 的光束入射到长为 的工作物质中,如果 它的增益系数为G= ),式中 它的增益系数为 =Acos2kz(0≤z ≤ L),式中 和k为 ( ),式中A和 为 常数.试求从工作物质出射的光强I的表达式 的表达式. 常数.试求从工作物质出射的光强 的表达式. 习题十一> ※<习题十一 习题十一 试证明,由于自发辐射,原子在E 试证明,由于自发辐射,原子在 2能级的平均寿命 τs=1/A21
数据结构的作业

第五章作业: 第五章作业: 1.假设有二维数组 假设有二维数组a:array[1..6,0..7] of elemtp; 每个数据元 假设有二维数组 素占6个字节 存储器按字节编址 的基地址为1000,则: 素占 个字节,存储器按字节编址。a的基地址为 个字节 存储器按字节编址。 的基地址为 则 (1) 数组 的体积; 数组a的体积 的体积; (2)数组 的最后一个元素的第一个字节的地址; 数组a的最后一个元素的第一个字节的地址 数组 的最后一个元素的第一个字节的地址; (3)按行存储时,a[2,4]的第一个字节的地址; 按行存储时, 的第一个字节的地址; 按行存储时 的第一个字节的地址 (4)按列存储时,a[5,7]的第一个字节的地址; 按列存储时, 的第一个字节的地址; 按列存储时 的第一个字节的地址
7.写出下列各树的先根序列 后根序列 并且画出对应的二 写出下列各树的先根序列,后根序列 写出下列各树的先根序列 后根序列,并且画出对应的二 叉树. 叉树 A A A A B C D B C B C I 8.画出第 题的森林相应的二叉树 画出第7题的森林相应的二叉树 画出第 题的森林相应的二叉树. 9.画出和下列已知序列对应的树 画出和下列已知序列对应的树T: 画出和下列已知序列对应的树 树的先根次序访问序列为:GFKDAIEBCHJ,而且 而且 树的先根次序访问序列为 树的后根次序访问序列为:DIAEKFCJHBG。 。 树的后根次序访问序列为 E F J G H K
3.用单链表实现 用单链表实现Locate(L,x)函数。(可参考 函数。(可参考P26算法 算法2.5) 用单链表实现 函数。(可参考 算法 4.上机题:设单链表Va中的数据元素递增有序。试编 上机题:设单链表 中的数据元素递增有序 中的数据元素递增有序。 上机题 写程序,将数据X插入单链表 插入单链表Va, 写程序,将数据 插入单链表 ,要求插 入后保持该表的有序性。 入后保持该表的有序性。 5.写出双向链表删除第i个结点的算法 5.写出双向链表删除第i个结点的算法。 写出双向链表删除第 个结点的算法。 6.写出求双向循环链表长度的算法。(注:头结点 写出求双向循环链表长度的算法。(注 写出求双向循环链表长度的算法。( 不算) 不算)
“电路原理”第1-6章作业
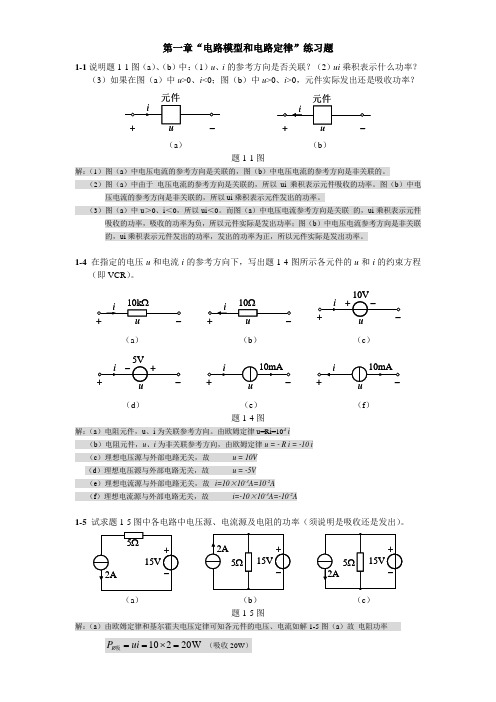
第一章“电路模型和电路定律”练习题1-1说明题1-1图(a )、(b )中:(1)u 、i 的参考方向是否关联?(2)ui 乘积表示什么功率?(3)如果在图(a )中u >0、i <0;图(b )中u >0、i >0,元件实际发出还是吸收功率?(a ) (b )题1-1图解:(1)图(a )中电压电流的参考方向是关联的,图(b )中电压电流的参考方向是非关联的。
(2)图(a )中由于 电压电流的参考方向是关联的,所以ui 乘积表示元件吸收的功率。
图(b )中电压电流的参考方向是非关联的,所以ui 乘积表示元件发出的功率。
(3)图(a )中u >0、i <0,所以ui <0。
而图(a )中电压电流参考方向是关联 的,ui 乘积表示元件吸收的功率,吸收的功率为负,所以元件实际是发出功率;图(b )中电压电流参考方向是非关联的,ui 乘积表示元件发出的功率,发出的功率为正,所以元件实际是发出功率。
1-4 在指定的电压u 和电流i 的参考方向下,写出题1-4图所示各元件的u 和i 的约束方程(即VCR )。
(a ) (b ) (c )(d ) (e ) (f )题1-4图解:(a )电阻元件,u 、i 为关联参考方向。
由欧姆定律u=Ri=104 i (b )电阻元件,u 、i 为非关联参考方向,由欧姆定律u = - R i = -10 i (c )理想电压源与外部电路无关,故 u = 10V (d )理想电压源与外部电路无关,故 u = -5V(e )理想电流源与外部电路无关,故 i=10×10-3A=10-2A(f )理想电流源与外部电路无关,故i=-10×10-3A=-10-2A1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a ) (b ) (c )题1-5图解:(a )由欧姆定律和基尔霍夫电压定律可知各元件的电压、电流如解1-5图(a )故 电阻功率10220WR P u i ==⨯=吸(吸收20W )电流源功率 I 5210WP ui ==⨯=吸(吸收10W ) 电压源功率U 15230WP ui ==⨯=发(发出30W )(b )由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(b )故 电阻功率12345WR P =⨯=吸(吸收45W ) 电流源功率 I 15230WP =⨯=发(发出30W ) 电压源功率U 15115WP =⨯=发(发出15W )(c )由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(c )故 电阻功率15345WR P =⨯=吸(吸收45W )电流源功率 I 15230WP =⨯=吸(吸收30W ) 电压源功率U 15575WP =⨯=发(发出75W )1-16 电路如题1-16图所示,试求每个元件发出或吸收的功率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.
Linux有两种版本,一个是内核(kernel)版,一个是发行(distribution)版。
核心版的序号由三部分数字构成,其形式为:major.minor.patchlevel,其中,majoro为主版本号,minor为次版本号,二者共同构成了当前核心版本号。
patchlevel表示对当前版本的修订次数。
Linux内核的发展过程中,一些社区组织或厂家将Linux系统的内核与一些实用程序软件和文档包装起来,并提供一些系统安装界面和系统配置、设定与管理工具,就构成了一种发行版本,Linux的发行版本其实就是Linux核心再加上外围的实用程序组成的一个大软件包而已。
相对于Linux操作系统内核版本,发行版本的版本号随发布者的不同而不同,与Linux系统内核的版本号是相对独立的。
10.
硬盘分区实质上是对硬盘的一种格式化,然后才能使用硬盘保存各种信息。
创建分区时,就已经设置好了硬盘的各项物理参数,指定了硬盘主引导记录和引导记录备份的存放位置。
分区允许在一个磁盘上有多个文件系统,易于我们管理。
在一个MBR分区表类型的硬盘中最多只能存在4个主分区。
如果一个硬盘上需要超过4个以上的磁盘分块的话,那么就需要使用扩展分区了。
如果使用扩展分区,那么一个物理硬盘上最多只能3个主分区和1个扩展分区。
扩展分区不能直接使用,它必须经过第二次分割成为一个一个的逻辑分区,然后才可以使用。
一个扩展分区中的逻辑分区可以任意多个。
Linux既可以安装在主分区上,也可以安装在逻辑分区上。
11.
多操作系统中每个操作系统独占硬盘一个分区,每个时刻只能运行一个系统,在系统切换时需要重启机器。
虚拟机系统中在主系统上运行多个不同操作系统,各操作系统就像应用程序那一可以随意切换。
每个操作系统都可以进行虚拟分区、配置而不影响真实硬盘的数据。
VMWare安装Linux主要步骤:
启动VMWare,选择New Virtual Machine,然后根据安装向导创建虚拟机。
启动Linux虚拟机,插入选定的Linux光盘,虚拟系统将根据用户选择安装方式安装Linux 系统。
安装VMware Tools。
