Theory of magnetic short-range order for itinerant electron systems
PACS number(s): 75.10.-b, 71.28.+d, 71.45.-d
1
Introduction
In the theory of strongly correlated itinerant electron systems two topics are of continued interest, namely (i) the localized–itinerant complementarity and (ii) the competition between magnetic long–range order (LRO) and short–range order (SRO). In particular, the concept of magnetic SRO and its interrelation to itinerant properties was investigated in the context of both narrow–band magnetism of transition metals and their compounds [1–6] and of the unconventional magnetic behaviour of high–Tc copper oxides [7–12]. In the cuprates, neutron scattering [13] and nuclear magnetic resonance experiments [14] reveal pronounced antiferromagnetic spin correlations within the CuO2 planes which persist even in the superconducting phase. Moreover, measurements of the spin susceptibility χ(T, δ) in the normal metallic state of La2−δ Srδ CuO4 (LSCO) [15, 16] show a maximum in the doping dependence as well as (for δ< ∼ 0.21) in the temperature dependence and give further evidence for strong SRO effects at low temperatures, where the SRO decreases with increasing doping and temperature. Thus the experiments on cuprates bring out the importance of electron correlations as compared with the situation in traditional band magnetism, and therefore yield a new challenge for a microscopic theory of SRO in itinerant electron systems. Such a theory has to provide a self–consistent description of strong SRO (in the absence of LRO) down to zero temperature. The previous theoretical approaches to the problem of SRO in transition metals and cuprates are mostly based on Hubbard–type models [1, 2, 4–6, 8–12, 17]. For example, to explain the normal–state susceptibility of LSCO in terms of SRO, the three–band Hubbard model was used [9]. In connection with the study of SRO some general problems have gained a renewed interest, such as the stability of various magnetic LRO phases against paraphases with and without SRO as well as the question of phase separation in strong correlation models [18, 12]. From the methodical point of view, the SRO theories for itinerant systems are preferentially formulated within functional–integral representations of the one–band Hubbard model using the static approximation. Thereby, various Hubbard–Stratonovich two–field methods, often combined with the single–site coherent potential approximation (CPA) [1, 2, 5, 6, 8] and,
Theory of magnetic short–range order for itinerant el/9609014v1 2 Sep 1996
U. Trapper(1) , D. Ihle(1) and H. Fehske(2)
(1)
Institut f¨ ur Theoretische Physik, Universit¨ at Leipzig, D–04109 Leipzig, Germany
(2)
Physikalisches Institut, Universit¨ at Bayreuth, D–95440 Bayreuth, Germany
February 1, 2008
Abstract On the basis of the one–band t–t′ –Hubbard model a self–consistent renormalization theory of magnetic short–range order (SRO) in the paramagnetic phase is presented combining the four–field slave–boson functional–integral scheme with the cluster variational method. Contrary to previous SRO approaches the SRO is incorporated at the saddle–point and pair–approximation levels. A detailed numerical evaluation of the theory is performed at zero temperature, where both the hole– and electron–doped cases as well as band–structure effects are studied. The ground–state phase diagram shows the suppression of magnetic long–range order in favour of a paramagnetic phase with antiferromagnetic SRO in a wide doping region. In this phase the uniform static spin susceptibility increases upon doping up to the transition to the Pauli paraphase. Comparing the theory with experiments on high–Tc cuprates a good agreement is found.
2
in the context of high–Tc ’s, the scalar four–field slave–boson approach [19, 9, 12] where employed. Those theories are designed to describe the formation and ordering of local magnetic moments in an itinerant system on a time scale large compared to the electron hopping time. In the mode–mode coupling theory of spin fluctuations (SF) by Moriya et al. [1, 2] interpolating between the weakly magnetic (local SF in q –space) and local moment (local SF in real space) limits, the SRO is reflected in the spatial correlation of thermal SF (with an amplitude increasing with temperature) and is appreciable even above the Curie temperature. Starting from the local moment limit and using the two–vector–field Hubbard–Stratonovich/CPA approach, the SRO is taken into account by an expansion in pairwise terms (within the bilinear approximation) around the single–site CPA saddle–point. The lack of self–consistency in this approach may be justified when the SRO is weak. Note that, at T = 0, the theory by Moriya et al. [1, 2] reduces to the Hartree–Fock approximation in both the weak– and strong–coupling limits, and the SRO is lost. The neglect of important correlations at zero temperature may be the reason for the absence of a maximum in the calculated spin susceptibility. Contrary, the phenomenological version of the interpolation theory given in Ref. [2] incorporates the SRO at the saddle point, and in the weakly magnetic limit the results of the classical approximation to the self–consistent renormalization theory of SF are recovered. In the local–band theory of ferromagnetism [3, 4], where the fluctuations of the local magnetizations with a fixed amplitude are considered to be local in q –space, the SRO is described by an expansion around the Stoner saddle point [4] and turns out to be strong near the Curie temperature. As in Ref. [1], the SRO–induced renormalization of the saddle point is disregarded. The non–self consistency is also inherent in the SRO theories taking the SF to be local in real space and employing various cluster methods [5, 6, 8, 9]. For example, in the approaches of Refs. [6] and [9] resulting in an effective Ising free–energy functional, where the exchange energy is evaluated beyond the bilinear approximation used in Ref. [1] and is nearly independent on temperature, the SRO is treated by an expansion around the single–site CPA saddle–point and by the Bethe–Peierls approximation [20].
磁共振(磁谐振耦合)无线充电技术鼻祖级文章-英文原文
Wireless Power Transfer via Strongly Coupled Magnetic ResonancesAndré Kurs,1* Aristeidis Karalis,2 Robert Moffatt,1 J. D. Joannopoulos,1 Peter Fisher,3Marin Soljačić11Department of Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. 2Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. 3Department of Physics and Laboratory for Nuclear Science, Massachusetts Institute of Technology, Cambridge, MA 02139, USA.*To whom correspondence should be addressed. E-mail: akurs@Using self-resonant coils in a strongly coupled regime, we experimentally demonstrate efficient non-radiative power transfer over distances of up to eight times the radius of the coils. We demonstrate the ability to transfer 60W with approximately 40% efficiency over distances in excess of two meters. We present a quantitative model describing the power transfer which matches the experimental results to within 5%. We discuss practical applicability and suggest directions for further studies. At first glance, such power transfer is reminiscent of the usual magnetic induction (10); however, note that the usual non- resonant induction is very inefficient for mid-range applications.Overview of the formalism. Efficient mid-range power transfer occurs in particular regions of the parameter space describing resonant objects strongly coupled to one another. Using coupled-mode theory to describe this physical system (11), we obtain the following set of linear equationsIn the early 20th century, before the electrical-wire grid, Nikola Tesla (1) devoted much effort towards schemes to a&m(t)=(iωm-Γm)a m(t)+∑iκmn a n(t)+F m(t)n≠m(1)transport power wirelessly. However, typical embodiments (e.g. Tesla coils) involved undesirably large electric fields. During the past decade, society has witnessed a dramatic surge of use of autonomous electronic devices (laptops, cell- phones, robots, PDAs, etc.) As a consequence, interest in wireless power has re-emerged (2–4). Radiative transfer (5), while perfectly suitable for transferring information, poses a number of difficulties for power transfer applications: the efficiency of power transfer is very low if the radiation is omnidirectional, and requires an uninterrupted line of sight and sophisticated tracking mechanisms if radiation is unidirectional. A recent theoretical paper (6) presented a detailed analysis of the feasibility of using resonant objects coupled through the tails of their non-radiative fields for mid- range energy transfer (7). Intuitively, two resonant objects of the same resonant frequency tend to exchange energy efficiently, while interacting weakly with extraneous off- resonant objects. In systems of coupled resonances (e.g. acoustic, electro-magnetic, magnetic, nuclear, etc.), there is often a general “strongly coupled” regime of operation (8). If one can operate in that regime in a given system, the energy transfer is expected to be very efficient. Mid-range power transfer implemented this way can be nearly omnidirectional and efficient, irrespective of the geometry of the surrounding space, and with low interference and losses into environmental objects (6).Considerations above apply irrespective of the physical nature of the resonances. In the current work, we focus on one particular physical embodiment: magnetic resonances (9). Magnetic resonances are particularly suitable for everyday applications because most of the common materials do not interact with magnetic fields, so interactions with environmental objects are suppressed even further. We were able to identify the strongly coupled regime in the system of two coupled magnetic resonances, by exploring non-radiative (near-field) magnetic resonant induction at MHzfrequencies. where the indices denote the different resonant objects. The variables a m(t) are defined so that the energy contained in object m is |a m(t)|2, ωm is the resonant frequency of thatisolated object, and Γm is its intrinsic decay rate (e.g. due to absorption and radiated losses), so that in this framework anuncoupled and undriven oscillator with parameters ω0 and Γ0 would evolve in time as exp(iω0t –Γ0t). The κmn= κnm are coupling coefficients between the resonant objects indicated by the subscripts, and F m(t) are driving terms.We limit the treatment to the case of two objects, denoted by source and device, such that the source (identified by the subscript S) is driven externally at a constant frequency, and the two objects have a coupling coefficient κ. Work is extracted from the device (subscript D) by means of a load (subscript W) which acts as a circuit resistance connected to the device, and has the effect of contributing an additional term ΓW to the unloaded device object's decay rate ΓD. The overall decay rate at the device is therefore Γ'D= ΓD+ ΓW. The work extracted is determined by the power dissipated in the load, i.e. 2ΓW|a D(t)|2. Maximizing the efficiency η of the transfer with respect to the loading ΓW, given Eq. 1, is equivalent to solving an impedance matching problem. One finds that the scheme works best when the source and the device are resonant, in which case the efficiency isThe efficiency is maximized when ΓW/ΓD= (1 + κ2/ΓSΓD)1/2. It is easy to show that the key to efficient energy transfer is to have κ2/ΓSΓD> 1. This is commonly referred to as the strongcoupling regime. Resonance plays an essential role in thisDS S D'' power transfer mechanism, as the efficiency is improved by approximately ω2/ΓD 2 (~106 for typical parameters) compared to the case of inductively coupled non-resonant objects. Theoretical model for self-resonant coils. Ourexperimental realization of the scheme consists of two self- resonant coils, one of which (the source coil) is coupled inductively to an oscillating circuit, while the other (the device coil) is coupled inductively to a resistive load (12) (Fig. 1). Self-resonant coils rely on the interplay between distributed inductance and distributed capacitance to achieve resonance. The coils are made of an electrically conducting wire of total length l and cross-sectional radius a wound into Given this relation and the equation of continuity, one finds that the resonant frequency is f 0 = 1/2π[(LC )1/2]. We can now treat this coil as a standard oscillator in coupled-mode theory by defining a (t ) = [(L /2)1/2]I 0(t ).We can estimate the power dissipated by noting that the sinusoidal profile of the current distribution implies that the spatial average of the peak current-squared is |I 0|2/2. For a coil with n turns and made of a material with conductivity σ, we modify the standard formulas for ohmic (R o ) and radiation (R r ) µ0ω l a helix of n turns, radius r , and height h . To the best of our knowledge, there is no exact solution for a finite helix in the literature, and even in the case of infinitely long coils, the solutions rely on assumptions that are inadequate for our R o = 2σ 4πa µ πωr 42 ωh 2 (6)system (13). We have found, however, that the simple quasi- R =0 n 2 + (7)static model described below is in good agreementr ε 12 c3π3 c(approximately 5%) with experiment.We start by observing that the current has to be zero at the ends of the coil, and make the educated guess that the resonant modes of the coil are well approximated bysinusoidal current profiles along the length of the conducting wire. We are interested in the lowest mode, so if we denote by s the parameterization coordinate along the length of the conductor, such that it runs from -l /2 to +l /2, then the time- dependent current profile has the form I 0 cos(πs /l ) exp(i ωt ). It follows from the continuity equation for charge that the linear charge density profile is of the form λ0 sin(πs /l ) exp(i ωt ), so the two halves of the coil (when sliced perpendicularly to its axis) contain charges equal in magnitude q 0 = λ0l /π but opposite in sign.As the coil is resonant, the current and charge density profiles are π/2 out of phase from each other, meaning that the real part of one is maximum when the real part of the other is zero. Equivalently, the energy contained in the coil is 0The first term in Eq. 7 is a magnetic dipole radiation term(assuming r << 2πc /ω); the second term is due to the electric dipole of the coil, and is smaller than the first term for our experimental parameters. The coupled-mode theory decay constant for the coil is therefore Γ = (R o + R r )/2L , and its quality factor is Q = ω/2Γ.We find the coupling coefficient κDS by looking at the power transferred from the source to the device coil,assuming a steady-state solution in which currents and charge densities vary in time as exp(i ωt ).P =⎰d rE (r )⋅J (r ) =-⎰d r (A&S (r )+∇φS (r ))⋅J D (r ) at certain points in time completely due to the current, and at other points, completely due to the charge. Usingelectromagnetic theory, we can define an effective inductance L and an effective capacitance C for each coil as follows:=-1⎰⎰d r d r ' µJ &S(r ')+ρS(r ') 4π |r -r |ε0≡-i ωMI S I Dr '-r|r '-r |3⋅J D (r )(8)L =µ04π |I 0 |⎰⎰d r d r 'J (r )⋅J (r ')|r -r '|where the subscript S indicates that the electric field is due to the source. We then conclude from standard coupled-mode theory arguments that κDS = κSD = κ = ωM /2[(L S L D )1/2]. When 1 1 ρ(r )ρ(r ') the distance D between the centers of the coils is much larger= C 4πε 0 |q 0 | ⎰⎰d r d r ' |r -r '|(4)than their characteristic size, κ scales with the D -3dependence characteristic of dipole-dipole coupling. Both κ and Γ are functions of the frequency, and κ/Γ and the where the spatial current J (r ) and charge density ρ(r ) are obtained respectively from the current and charge densities along the isolated coil, in conjunction with the geometry of the object. As defined, L and C have the property that the efficiency are maximized for a particular value of f , which is in the range 1-50MHz for typical parameters of interest. Thus, picking an appropriate frequency for a given coil size, as we do in this experimental demonstration, plays a major role in optimizing the power transfer.1 2Comparison with experimentallydeterminedU =2 L |I 0 |parameters. The parameters for the two identical helical coils built for the experimental validation of the power 1 2 transfer scheme are h = 20cm, a = 3mm, r = 30 cm, and n = =2C|q 0 | (5)5.25. Both coils are made of copper. The spacing between loops of the helix is not uniform, and we encapsulate theuncertainty about their uniformity by attributing a 10% (2cm) uncertainty to h . The expected resonant frequency given these22dimensions is f0 = 10.56 ± 0.3MHz, which is about 5% off from the measured resonance at 9.90MHz.The theoretical Q for the loops is estimated to be approximately 2500 (assuming σ = 5.9 × 107 m/Ω) but the measured value is Q = 950±50. We believe the discrepancy is mostly due to the effect of the layer of poorly conductingcopper oxide on the surface of the copper wire, to which the current is confined by the short skin depth (~20μm) at this frequency. We therefore use the experimentally observed Q and ΓS= ΓD= Γ = ω/2Q derived from it in all subsequent computations.We find the coupling coefficient κ experimentally by placing the two self-resonant coils (fine-tuned, by slightly adjusting h, to the same resonant frequency when isolated) a distance D apart and measuring the splitting in the frequencies of the two resonant modes. According to coupled-mode theory, this splitting should be ∆ω = 2[(κ2-Γ2)1/2]. In the present work, we focus on the case where the two coils are aligned coaxially (Fig. 2), although similar results are obtained for other orientations (figs. S1 and S2).Measurement of the efficiency. The maximum theoretical efficiency depends only on the parameter κ/[(L S L D)1/2] = κ/Γ, which is greater than 1 even for D = 2.4m (eight times the radius of the coils) (Fig. 3), thus we operate in the strongly- coupled regime throughout the entire range of distances probed.As our driving circuit, we use a standard Colpitts oscillator whose inductive element consists of a single loop of copper wire 25cm in radius(Fig. 1); this loop of wire couples inductively to the source coil and drives the entire wireless power transfer apparatus. The load consists of a calibrated light-bulb (14), and is attached to its own loop of insulated wire, which is placed in proximity of the device coil and inductively coupled to it. By varying the distance between the light-bulb and the device coil, we are able to adjust the parameter ΓW/Γ so that it matches its optimal value, given theoretically by (1 + κ2/Γ2)1/2. (The loop connected to the light-bulb adds a small reactive component to ΓW which is compensated for by slightly retuning the coil.) We measure the work extracted by adjusting the power going into the Colpitts oscillator until the light-bulb at the load glows at its full nominal brightness.We determine the efficiency of the transfer taking place between the source coil and the load by measuring the current at the mid-point of each of the self-resonant coils with a current-probe (which does not lower the Q of the coils noticeably.) This gives a measurement of the current parameters I S and I D used in our theoretical model. We then compute the power dissipated in each coil from P S,D=ΓL|I S,D|2, and obtain the efficiency from η = P W/(P S+ P D+P W). To ensure that the experimental setup is well described by a two-object coupled-mode theory model, we position the device coil such that its direct coupling to the copper loop attached to the Colpitts oscillator is zero. The experimental results are shown in Fig. 4, along with the theoretical prediction for maximum efficiency, given by Eq. 2. We are able to transfer significant amounts of power using this setup, fully lighting up a 60W light-bulb from distances more than 2m away (figs. S3 and S4).As a cross-check, we also measure the total power going from the wall power outlet into the driving circuit. The efficiency of the wireless transfer itself is hard to estimate in this way, however, as the efficiency of the Colpitts oscillator itself is not precisely known, although it is expected to be far from 100% (15). Still, the ratio of power extracted to power entering the driving circuit gives a lower bound on the efficiency. When transferring 60W to the load over a distance of 2m, for example, the power flowing into the driving circuit is 400W. This yields an overall wall-to-load efficiency of 15%, which is reasonable given the expected efficiency of roughly 40% for the wireless power transfer at that distance and the low efficiency of the Colpitts oscillator.Concluding remarks. It is essential that the coils be on resonance for the power transfer to be practical (6). We find experimentally that the power transmitted to the load drops sharply as either one of the coils is detuned from resonance. For a fractional detuning ∆f/f0 of a few times the inverse loaded Q, the induced current in the device coil is indistinguishable from noise.A detailed and quantitative analysis of the effect of external objects on our scheme is beyond the scope of the current work, but we would like to note here that the power transfer is not visibly affected as humans and various everyday objects, such as metals, wood, and electronic devices large and small, are placed between the two coils, even in cases where they completely obstruct the line of sight between source and device (figs. S3 to S5). External objects have a noticeable effect only when they are within a few centimeters from either one of the coils. While some materials (such as aluminum foil, styrofoam and humans) mostly just shift the resonant frequency, which can in principle be easily corrected with a feedback circuit, others (cardboard, wood, and PVC) lower Q when placed closer than a few centimeters from the coil, thereby lowering the efficiency of the transfer.When transferring 60W across 2m, we calculate that at the point halfway between the coils the RMS magnitude of the electric field is E rms= 210V/m, that of the magnetic field isH rms= 1A/m, and that of the Poynting vector is S rms=3.2mW/cm2 (16). These values increase closer to the coils, where the fields at source and device are comparable. For example, at distances 20cm away from the surface of the device coil, we calculate the maximum values for the fields to be E rms= 1.4kV/m, H rms= 8A/m, and S rms= 0.2W/cm2. The power radiated for these parameters is approximately 5W, which is roughly an order of magnitude higher than cell phones. In the particular geometry studied in this article, the overwhelming contribution (by one to two orders of magnitude) to the electric near-field, and hence to the near- field Poynting vector, comes from the electric dipole moment of the coils. If instead one uses capacitively-loaded single- turn loop design (6) - which has the advantage of confining nearly all of the electric field inside the capacitor - and tailors the system to operate at lower frequencies, our calculations show (17) that it should be possible to reduce the values cited above for the electric field, the Poynting vector, and the power radiated to below general safety regulations (e.g. the IEEE safety standards for general public exposure(18).) Although the two coils are currently of identical dimensions, it is possible to make the device coil small enough to fit into portable devices without decreasing the efficiency. One could, for instance, maintain the product of the characteristic sizes of the source and device coils constant, as argued in (6).We believe that the efficiency of the scheme and the power transfer distances could be appreciably improved by silver-plating the coils, which should increase their Q, or by working with more elaborate geometries for the resonant objects (19). Nevertheless, the performance characteristics of the system presented here are already at levels where they could be useful in practical applications.References and Notes1. N. Tesla, U.S. patent 1,119,732 (1914).2.J. M. Fernandez, J. A. Borras, U.S. patent 6,184,651(2001).3.A. Esser, H.-C. Skudelny, IEEE Trans. Indust. Appl. 27,872(1991).4.J. Hirai, T.-W. Kim, A. Kawamura, IEEE Trans. PowerElectron. 15, 21(2000).5.T. A. Vanderelli, J. G. Shearer, J. R. Shearer, U.S. patent7,027,311(2006).6.A. Karalis, J. D. Joannopoul os, M. Soljačić, Ann. Phys.,10.1016/j.aop.2007.04.017(2007).7.Here, by mid-range, we mean that the sizes of the deviceswhich participate in the power transfer are at least a few times smaller than the distance between the devices. For example, if the device being powered is a laptop (size ~ 50cm), while the power source (size ~ 50cm) is in thesame room as the laptop, the distance of power transfer could be within a room or a factory pavilion (size of the order of a fewmeters).8. T. Aoki, et al., Nature 443, 671 (2006).9.K. O’Brien, G. Scheible, H. Gueldner, 29th AnnualConference of the IEEE 1, 367(2003).10.L. Ka-Lai, J. W. Hay, P. G. W., U.S. patent7,042,196(2006).11.H. Haus, Waves and Fields in Optoelectronics(Prentice- Supporting Online Material/cgi/content/full/1143254/DC1SOM TextFigs. S1 to S530 March 2007; accepted 21 May 2007Published online 7 June 2007; 10.1126/science.1143254 Include this information when citing this paper.Fig. 1. Schematic of the experimental setup. A is a single copper loop of radius 25cm that is part of the driving circuit, which outputs a sine wave with frequency 9.9MHz. S and D are respectively the source and device coils referred to in the text. B is a loop of wire attached to the load (“light-bulb”). The various κ’s represent direct couplings between the objects indicated by the arrows. The angle between coil D and the loop A is adjusted to ensure that their direct coupling is zero, while coils S and D are aligned coaxially. The direct couplings between B and A and between B and S are negligible.Fig. 2. Comparison of experimental and theoretical values for κ as a function of the separation between coaxially aligned source and device coils (the wireless power transfer distance.) Fig. 3. Comparison of experimental and theoretical values for the parameter κ/Γ as a function of the wireless power transfer distance. The theory values are obtained by using the theoretical κ and the experimentally measured Γ. The shaded area represents the spread in the theoretical κ/Γ due to the 5% uncertainty in Q.Fig. 4. Comparison of experimental and theoretical efficiencies as functions of the wireless power transfer distance. The shaded area represents the theoretical prediction for maximum efficiency, and is obtained by inserting theHall, Englewood Cliffs, NJ, 1984).12.The couplings to the driving circuit and the load donot theoretical values from Fig. 3 into Eq. 2 [with Γκ2/Γ2 1/2 W /ΓD= (1 +have to be inductive. They may also be connected by awire, for example. We have chosen inductive coupling in the present work because of its easier implementation. 13.S. Sensiper, thesis, Massachusetts Institute of Technology(1951).14.We experimented with various power ratings from 5W to75W.15.W. A. Edson, Vacuum-Tube Oscillators (Wiley, NewYork,1953).16.Note that E ≠cμ0H, and that the fields are out of phaseand not necessarily perpendicular because we are not in a radiativeregime.17.See supporting material on Science Online.18.IEEE Std C95.1—2005 IEEE Standard for Safety Levelswith Respect to Human Exposure to Radio FrequencyElectromagnetic Fields, 3 kHz to 300 GHz (IEEE,Piscataway, NJ,2006).19. J. B. Pendry, Science 306, 1353 (2004).20. The authors would like to thank John Pendry forsuggesting the use of magnetic resonances, and Michael Grossman and Ivan Čelanović for technical assistance.This work was supported in part by the Materials Research Science and Engineering Center program of the National Science Foundation under Grant No. DMR 02-13282, by the U.S. Department of Energy under Grant No. DE-FG02-99ER45778, and by the Army Research Officethrough the Institute for Soldier Nanotechnologies under Contract No. DAAD-19-02-D0002.) ]. The black dots are the maximum efficiency obtained from Eq. 2 and the experimental values of κ/Γ from Fig. 3. The red dots present the directly measured efficiency,as described in thetext.。
磁学 径向克尔 英文 kerr effect
IntroductionThe Kerr effect, also known as the magneto-optic Kerr effect (MOKE), is a phenomenon that manifests the interaction between light and magnetic fields in a material. It is named after its discoverer, John Kerr, who observed this effect in 1877. The radial Kerr effect, specifically, refers to the variation in polarization state of light upon reflection from a magnetized surface, where the change occurs radially with respect to the magnetization direction. This unique aspect of the Kerr effect has significant implications in various scientific disciplines, including condensed matter physics, materials science, and optoelectronics. This paper presents a comprehensive, multifaceted analysis of the radial Kerr effect, delving into its underlying principles, experimental techniques, applications, and ongoing research directions.I. Theoretical Foundations of the Radial Kerr EffectA. Basic PrinciplesThe radial Kerr effect arises due to the anisotropic nature of the refractive index of a ferromagnetic or ferrimagnetic material when subjected to an external magnetic field. When linearly polarized light impinges on such a magnetized surface, the reflected beam experiences a change in its polarization state, which is characterized by a rotation of the plane of polarization and/or a change in ellipticity. This alteration is radially dependent on the orientation of the magnetization vector relative to the incident light's plane of incidence. The radial Kerr effect is fundamentally governed by the Faraday-Kerr law, which describes the relationship between the change in polarization angle (ΔθK) and the applied magnetic field (H):ΔθK = nHKVwhere n is the sample's refractive index, H is the magnetic field strength, K is the Kerr constant, and V is the Verdet constant, which depends on the wavelength of the incident light and the magnetic properties of the material.B. Microscopic MechanismsAt the microscopic level, the radial Kerr effect can be attributed to twoprimary mechanisms: the spin-orbit interaction and the exchange interaction. The spin-orbit interaction arises from the coupling between the electron's spin and its orbital motion in the presence of an electric field gradient, leading to a magnetic-field-dependent modification of the electron density distribution and, consequently, the refractive index. The exchange interaction, on the other hand, influences the Kerr effect through its role in determining the magnetic structure and the alignment of magnetic moments within the material.C. Material DependenceThe magnitude and sign of the radial Kerr effect are highly dependent on the magnetic and optical properties of the material under investigation. Ferromagnetic and ferrimagnetic materials generally exhibit larger Kerr rotations due to their strong net magnetization. Additionally, the effect is sensitive to factors such as crystal structure, chemical composition, and doping levels, making it a valuable tool for studying the magnetic and electronic structure of complex materials.II. Experimental Techniques for Measuring the Radial Kerr EffectA. MOKE SetupA typical MOKE setup consists of a light source, polarizers, a magnetized sample, and a detector. In the case of radial Kerr measurements, the sample is usually magnetized along a radial direction, and the incident light is either p-polarized (electric field parallel to the plane of incidence) or s-polarized (electric field perpendicular to the plane of incidence). By monitoring the change in the polarization state of the reflected light as a function of the applied magnetic field, the radial Kerr effect can be quantified.B. Advanced MOKE TechniquesSeveral advanced MOKE techniques have been developed to enhance the sensitivity and specificity of radial Kerr effect measurements. These include polar MOKE, longitudinal MOKE, and polarizing neutron reflectometry, each tailored to probe different aspects of the magnetic structure and dynamics. Moreover, time-resolved MOKE setups enable the study of ultrafast magneticphenomena, such as spin dynamics and all-optical switching, by employing pulsed laser sources and high-speed detection systems.III. Applications of the Radial Kerr EffectA. Magnetic Domain Imaging and CharacterizationThe radial Kerr effect plays a crucial role in visualizing and analyzing magnetic domains in ferromagnetic and ferrimagnetic materials. By raster-scanning a focused laser beam over the sample surface while monitoring the Kerr signal, high-resolution maps of domain patterns, domain wall structures, and magnetic domain evolution can be obtained. This information is vital for understanding the fundamental mechanisms governing magnetic behavior and optimizing the performance of magnetic devices.B. Magnetometry and SensingDue to its sensitivity to both the magnitude and direction of the magnetic field, the radial Kerr effect finds applications in magnetometry and sensing technologies. MOKE-based sensors offer high spatial resolution, non-destructive testing capabilities, and compatibility with various sample geometries, making them suitable for applications ranging from magnetic storage media characterization to biomedical imaging.C. Spintronics and MagnonicsThe radial Kerr effect is instrumental in investigating spintronic and magnonic phenomena, where the manipulation and control of spin degrees of freedom in solids are exploited for novel device concepts. For instance, it can be used to study spin-wave propagation, spin-transfer torque effects, and all-optical magnetic switching, which are key elements in the development of spintronic memory, logic devices, and magnonic circuits.IV. Current Research Directions and Future PerspectivesA. Advanced Materials and NanostructuresOngoing research in the field focuses on exploring the radial Kerr effect in novel magnetic materials, such as multiferroics, topological magnets, and magnetic thin films and nanostructures. These studies aim to uncover newmagnetooptical phenomena, understand the interplay between magnetic, electric, and structural order parameters, and develop materials with tailored Kerr responses for next-generation optoelectronic and spintronic applications.B. Ultrafast Magnetism and Spin DynamicsThe advent of femtosecond laser technology has enabled researchers to investigate the radial Kerr effect on ultrafast timescales, revealing fascinating insights into the fundamental processes governing magnetic relaxation, spin precession, and all-optical manipulation of magnetic order. Future work in this area promises to deepen our understanding of ultrafast magnetism and pave the way for the development of ultrafast magnetic switches and memories.C. Quantum Information ProcessingRecent studies have demonstrated the potential of the radial Kerr effect in quantum information processing applications. For example, the manipulation of single spins in solid-state systems using the radial Kerr effect could lead to the realization of scalable, robust quantum bits (qubits) and quantum communication protocols. Further exploration in this direction may open up new avenues for quantum computing and cryptography.ConclusionThe radial Kerr effect, a manifestation of the intricate interplay between light and magnetism, offers a powerful and versatile platform for probing the magnetic properties and dynamics of materials. Its profound impact on various scientific disciplines, coupled with ongoing advancements in experimental techniques and materials engineering, underscores the continued importance of this phenomenon in shaping our understanding of magnetism and driving technological innovations in optoelectronics, spintronics, and quantum information processing. As research in these fields progresses, the radial Kerr effect will undoubtedly continue to serve as a cornerstone for unraveling the mysteries of magnetic materials and harnessing their potential for transformative technologies.。
物理学名词
absorption spectroscopy absorption spectrum absorptive optical bistability absorptive power absorptivity abukumalite abundance accelerated motion
又称钇硅磷灰石
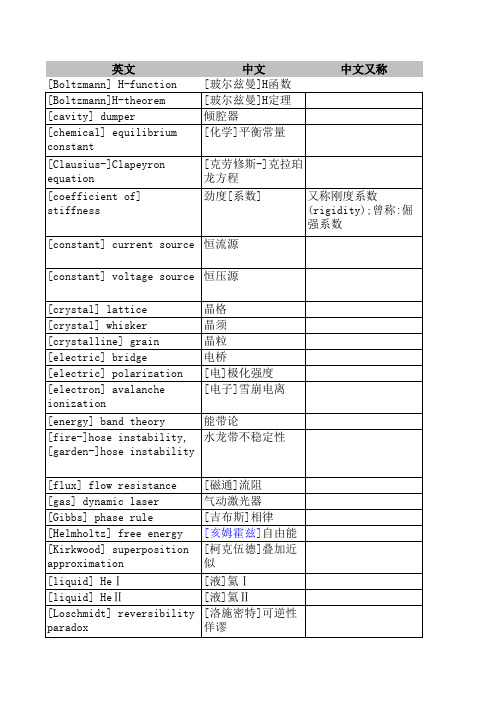
[energy] band theory 能带论 [fire-]hose instability, 水龙带不稳定性 [garden-]hose instability [flux] flow resistance [gas] dynamic laser [Gibbs] phase rule [Helmholtz] free energy [Kirkwood] superposition approximation [liquid] HeⅠ [liquid] HeⅡ [Loschmidt] reversibility paradox [磁通]流阻 气动激光器 [吉布斯]相律 [亥姆霍兹]自由能 [柯克伍德]叠加近 似 [液]氦Ⅰ [液]氦Ⅱ [洛施密特]可逆性 佯谬
英文 [Boltzmann] H-function [Boltzmann]H-theorem [cavity] dumper [chemical] equilibrium constant [Clausius-]Clapeyron equation
中文 [玻尔兹曼]H函数 [玻尔兹曼]H定理 倾腔器 [化学]平衡常量 [克劳修斯-]克拉珀 龙方程
abrupt junction abscissa absolute acceleration absolute activity absolute ampere, Abamper absolute black body absolute coulomb, Abcoulomb absolute cross-section absolute deviation absolute electrostatic unit absolute absolute absolute absolute elsewhere entropy error future
Chapter6 凝聚态物理导论(中科院研究生院)
Chapter 6 Magnetism of MatterThe history of magnetism dates back to earlier than 600 B.C., but it is only in the twentieth century that scientists have begun to understand it, and develop technologies based on this understanding. Magnetism was most probably first observed in a form of the mineral magnetite called lodestone, which consists of iron oxide-a chemical compound of iron and oxygen. The ancient Greeks were the first known to have used this mineral, which they called a magnet because of its ability to attract other pieces of the same material and iron.The Englishman William Gilbert(1540-1603) was the first to investigate the phenomenon of magnetism systematically using scientific methods. He also discovered that Earth is itself a weak magnet. Early theoretical investigations into the nature of Earth's magnetism were carried out by the German Carl Friedrich Gauss(1777-1855). Quantitative studies of magnetic phenomena initiated in the eighteenth century by Frenchman Charles Coulomb(1736-1806), who established the inverse square law of force, which states that the attractive force between two magnetized objects is directly proportional to the product of their individual fields and inversely proportional to the square of the distance between them.Danish physicist Hans Christian Oersted(1777-1851) first suggested a link between electricity and magnetism. Experiments involving the effects of magnetic and electric fields on one another were then conducted by Frenchman Andre Marie Ampere(1775-1836) and Englishman Michael Faraday(1791-1869), but it was the Scotsman, James Clerk Maxwell(1831-1879), who provided the theoretical foundation to the physics of electromagnetism in the nineteenth century by showing that electricity and magnetism represent different aspects of the same fundamental force field. Then, in the late 1960s American Steven Weinberg(1933-) and Pakistani Abdus Salam(1926-96), performed yet another act of theoretical synthesis of the fundamental forces by showing that electromagnetism is one part of the electroweak force. The modern understanding of magnetic phenomena in condensed matter originates from the work of two Frenchmen: Pierre Curie(1859-1906), the husband and scientific collaborator of Madame Marie Curie(1867-1934), and Pierre Weiss(1865-1940). Curie examined the effect of temperature on magnetic materials and observed that magnetism disappeared suddenly above a certain critical temperature in materials like iron. Weiss proposed a theory of magnetism based on an internal molecular field proportional to the average magnetization that spontaneously align the electronic micromagnets in magnetic matter. The present day understanding of magnetism based on the theory of the motion and interactions of electrons in atoms (called quantum electrodynamics) stems from the work and theoretical models of two Germans, Ernest Ising and Werner Heisenberg (1901-1976). Werner Heisenberg was also one of the founding fathers of modern quantum mechanics.Magnetic CompassThe magnetic compass is an old Chinese invention, probably first made in China during the Qin dynasty (221-206 B.C.). Chinese fortune tellers used lodestonesto construct their fortune telling boards.Magnetized NeedlesMagnetized needles used as direction pointers instead of the spoon-shaped lodestones appeared in the 8th century AD, again in China, and between 850 and 1050 they seemto have become common as navigational devices on ships. Compass as a Navigational AidThe first person recorded to have used the compass as a navigational aid was Zheng He (1371-1435), from the Yunnan province in China, who made seven ocean voyages between 1405 and 1433.有关固体磁性的基本概念和规律在上个世纪电磁学的发展史中就开始建立了。
凝聚态物理相关诺贝尔奖Word版
凝聚态物理相关诺贝尔化学奖1970-凝聚态物理相关诺贝尔物理学奖1970-约翰·巴丁美国美国约翰·罗伯特·施里弗美国日本“发现"for their experimental discoveriesregarding tunneling phenomena insemiconductors and superconductors,respectively"挪威英国“他理论上预测出通过隧道势垒的超电流的性质，特别是那些通常被称为象”"for his theoretical predictions of the properties of a supercurrent through a tunnel barrier, in particular those phenomena which are generally known as the Josephson effect"美国英国美国年彼得·列昂尼多维奇·卡皮苏联美国“对与相转变有关的临界现象理论的贡献”"for his theory for critical phenomena inconnection with phase transitions"克劳斯·冯·克利青德国“发现"for the discovery of thequantized Hall effect"德国德国瑞士约翰内斯·贝德诺尔茨德国卡尔·米勒瑞士法国美国美国美国若雷斯·阿尔费罗夫俄罗斯“发展了用于高速电子学和半导体异质结构"for developing semiconductorheterostructures used in high-speed-and optoelectronics"德国美国“在发明"for his part in the invention of theintegrated circuit"美国“在碱性原子稀薄气体的聚态质的早期基础性研究”"for the achievement of Bose-Einsteincondensation in dilute gases of alkaliatoms,of美国德国美国俄罗斯“对性贡献”"for pioneering contributions to thesuperfluids"俄罗斯英国美国法国德国英国美国[110]美国美国荷兰俄罗斯“在二维"for groundbreaking experiments regarding the two-dimensional material graphene"康斯坦丁·诺沃肖洛夫英国俄罗斯（注：可编辑下载，若有不当之处，请指正，谢谢!）。
基于磁屏蔽设计的磁吻合环建立大鼠胃旁路手术的实验研究
19FEATURES中国医疗设备 2021年第36卷 05期 V OL.36 No.05引言胃肠道吻合是重建消化道连续性的重要方法。
胃旁路手术通过对消化道进行改道，是经典的减重代谢手术方式[1]。
有关胃旁路手术改变机体代谢功能的机制虽有大量研究但仍未明确。
SD 大鼠是研究代谢性疾病的常用动物模型，但大鼠胃肠道较细，利用手工缝线对大鼠进行胃肠道吻合重建制备动物模型学习曲线较长，模型制备成功率较低[2]。
套管法[3]、激光焊接法[4]用于肠道吻合已有报道，但技术尚不成熟。
基于磁屏蔽设计的磁吻合环建立大鼠胃旁路手术的实验研究张苗苗1a,1b ，李恒1b,2，吝怡1b,2，魏欣怡1b,2，李美豫1b,2，刘俊杰1b,2，吕毅1a,1b ，严小鹏1a,1b1. 西安交通大学第一附属医院 a. 肝胆外科；b. 精准外科与再生医学国家地方联合工程研究中心，陕西 西安 710061；2. 西安交通大学 启德书院，陕西 西安 710061[摘 要] 目的 探讨基于磁屏蔽理论设计的磁吻合环用于大鼠胃旁路手术模型制备的可行性。
方法 根据磁屏蔽理论自行设计加工了适用于大鼠胃肠道吻合重建的坡莫合金外壳与钕铁硼内核组成的壳核结构磁吻合环。
以12只SD 大鼠为动物模型，开腹后在屈氏韧带远端16 cm 离断空肠，利用磁屏蔽结构的磁吻合环按照胃旁路手术方式依次完成胃肠吻合、肠肠吻合。
术后行正侧位片观察磁体位置、记录磁体排出时间，观察动物术后存活情况。
结果 12只SD 大鼠，除1只因麻醉意外死亡外，其余11只大鼠均顺利完成了磁吻合胃肠旁路手术，手术操作顺利，手术时间（49.73±6.34）min 。
术后动物存活良好，所有磁体均经消化道顺利排出，排出时间（9.14±1.89）d ，术后大鼠均存活良好。
结论 基于磁屏蔽理论设计的壳核结构的磁吻合环可有效避免狭小空间内多个磁体间的非计划相吸，可用于大鼠胃旁路术动物模型制备，具有操作简单、成功率高等优点。
一维磁性原子链系统中的Majorana费米子态
一维磁性原子链系统中的Majorana费米子态杨双波【摘要】对处于螺旋形磁场及横向均匀磁场的一维磁性原子链模型,在平均场近似下通过自洽地求解Bogoliubov-de-Genes方程我们计算了系统的能谱.我们发现在一定参数值的范围内能谱随螺旋形磁场振幅值演化呈现能量为零的Majorana 费米子态.我们计算了局域态密度发现对Majorana费米子其态密度的峰值出现在链的两端(或中点)位置.我们计算了波函数其空间分布,发现它与局域态密度的结果一致.%For a model of one dimensional magnetic atomic chain in both a helical magnetic field and a transverse uniform magnetic field,we calculate its energy spectrum by solving Bogoliubov-de-Genes equation selfconsistently in the mean field approximation. We find that for a certain parameter setting,energy spectrum evolving with amplitude of helical magnetic field,appears Majorana fermion eigenstates. We calculate local density of states,and find that the local density of states for Majorana fermion shows peaks at the both ends(or at middle)of the magnetic atomic chain. We calculate wave function,and its spatial distribution agrees with local density of states.【期刊名称】《南京师大学报（自然科学版）》【年(卷),期】2017(040)003【总页数】8页(P110-117)【关键词】Majorana费米子;磁性原子链;BdG方程;局域态密度【作者】杨双波【作者单位】南京师范大学物理科学与技术学院,江苏省大规模复杂系统数值模拟重点实验室,江苏南京210023【正文语种】中文【中图分类】O413.1Majorana fermion[1] which is a particle of the same as its own antiparticle,has been attracting great attention. Firstly,because of Majorana fermion being connected with topological phase concept,secondly because of its topological character,it provides a platform of potential application in topological quantum computing and quantum storing[2-4]. So experimentally and theoretically search for physical system of Majorana fermion has been a very hot research topic. The purpose of all these researches is to generate a topological superconductor,so that the Majorana fermion appears as a single excitation at the boundary. Recently,Majorana fermion has been studied for a model of an atomic chain in a helical magnetic field in close proximity to a s-wave superconductor[5-7],and the result shows that at a certain parameter setting,the Majorana fermion is localized at the both end of the magnetic atomic chain. This is a spatially uniform system,after a gauge transformation,the Hamiltonian of the system will become an invariant form for space displacement. In this paper we modified this system by adding a new Zeeman term in the original Hamiltonian,which correspondsto a uniform magnetic field h perpendicular to the atomic chain being applied to the original system. Because of the new Zeeman term,the system is nonuniform spatially,we will study the structure of the Majorana fermion for the system of h≠0.In this paper,we get the system eigenenergies and eigenvectors by numerically solving BdG equation,and then we study the birth and the localization in space of the Majorana fermion by calculating the spatially resolved local density of states and wave function. The structure of the paper is as the following,the Model and theory is in section 1,the result of numerical calculation and discussion is in section 2,the summary of the paper is in section 3.Consider a N-atom atomic chain in a helical magnetic filed or magnetic structure. The magnetic filed at site n is =B0(cosnθ+sinnθ),where θ is the angle made by the magnetic fields at the adjacent sites of the atomic chain,the whole atomic chain is in proximity to the surface of a s-wave superconductor,and in the transverse direction of the atomic chain a uniform magnetic field h is applied. The Hamiltonian of this magnetic atomic chain in mean field approximation is given byH=tx(cn+1α+h.c.)-μcnα+(cnβ+Δ(n)(+h.c.)+h(σz)ααcnα,where tx is the jumping amplitude for electron between two adjacent sites,μ is chemical potential,Δ(n)is the superconductor pairing potential or order parameter at sit n,h is the weak uniform magnetic field for tuning system energy spectrum. or cnα is the operator to creat or annihilate an electron of spin α respectively at site n, is pauli matrix vec tor,and h.c. standfor complex conjugate. By introducing Nambu spinor representationψi=(ci↑,ci↓,,-)T,then Hamiltonian(1)can be written as BdG form,i.e.H=Hijψj,where Hij is the BdG Hamiltonian at site i,which can be written as where Kij=tx(δi+1,j+δi-1,j)-μδij,γij=(h-B0cosiθ)δij. This is a 4N×4N matrix,whose energy eigenvalue εn and eigenfunctionψn(i)=(un(↑,i),un(↓,i),vn(↓,i),vn(↑,i))T, for i=1,2,…,N,is determined by eigenvalue equationand boundary condition. In mean field approximation the order parameter at site i takes the form[8]and the mean number of electron at site i iswhere fn=1/(1+eεn/kBT) is the Fermi distribution,T is temperature in Kelvin. The total number of electron isincluding spin up and spin down electrons. To determine eigenenergy,eigenfunction,order parameter,we need to selfconsistently solve eigenvalue equation(3)with(4)-(6). In this paper,we deal with the case of temperature T=0,then the order parameter and the mean number of electron in site i are given bySpecial case:h=0 and Δ(i)=Δ0,a constant. The Hamiltonian in(1)can be transformed into spatially unform form by a gauge transformation. The topologically nontrivial region of the parameter set is given bywhere Majorana fermion corresponds to εn=0. As |h|≠0,Hamiltonian in(1)is nonuniform in space,and the nontrivial region of parameter set can not be obtained analytically.In this paper we deal with open boundary condition with and without themiddle magnetic domain wall,and at the magnetic domain wall we replace θ by -θ. We have also studied under the periodic boundary condition,and found the result has no significant changes.We first study the character of the Majorana fermion as the order parameter Δ and chemical potential μ are constants,then we study the influence of nonuniform Δ(i)on the result of Majorana fermion by doing selfconsistent calculation. In calculation,we choose the number of site N for the atomic chain according to the angle θ,so that the magnetic field at the both ends of the atomic chain points to the same direction.2.1 Energy Spectrum and Wave FunctionsFor a one-dimensional magnetic atomic chain with magnetic domain wall in the middle,the parameter set is chosen asΔ0=1.0,tx=1.0,μ=2.5,h=0.1,θ=π/2,and length of the chain is chosen asN=81 sites. For every value of B0 in the interval[1.0,4.0],we diagonalize the 4N×4N BdG Hamiltonian matrix(2),we get 4N energy eigenvalues and 4N eigenvectors. In open boundary condition,the energy spectrum is shown in Fig.1. For B0 in the interval[1.486 6,3.996 8],we can see that thereexists eigenstates whose eigenenergy εn=0,and these eigenstates are Majorana fermions. The interval for the existense of Majorana fermion in the case of h=0.1 is very close to the interval[1.476,4.039]calculatedfrom(9)for the h=0 case. For Majorana fer mion at B0=2.1,εn=0,shown in red dot in Fig.1,we calculate its wave functionun(↑,i),un(↓,i),vn(↑,i),vn(↓,i),the result is shown in Fig.2(a-d). We can see that the amplitude of the wave function concentrates on the both ends and themiddle of the atomic chain. In Fig.3,we show wave function for the same magnetic atomic chain without magnetic domain wall in the middle,the amplitude of the wave function concentrates on both ends of the magnetic atomic chain. This is similar to the previous result for the 1-dimensional magnetic atomic chain without uniform magnetic field,h=0.2.2 Local Density of States and Total Density of StatesIn this subsection,we study the space distribution of density ofstates(DOS),which is called local density of states(LDOS)and is defined as ρ(ε,i)is a function of energy and space position,and the total density of states(TDOS)can be written as,i.e.,the arithmetic mean of local density of states,a function of energy only. In numerical calculation,we replace δ by a Lorentz function. Fo r parameter setting h=0.1,tx=1.0,Δ=1.0,μ=2.5,θ=π/2,N=81,and B0=2.1,the local density of states for a Majorana fermion and the mean number of electrons on each site are shown in Fig.4(a-d)for the magnetic atomic chain with magnetic domain wall in the middle. Fig.4(a)shows the local density of states ρ(ε,i)in a 3D-plot;Fig.4(b)shows the local density of states ρ(ε,i)in a 2D contour plot;Fig.4(c)shows the local density of states for Majorana fermion ρ(ε=0,i);Fig.4(d)shows the mean number of electron on each si te of atomic chain<n(i)>. We can see from the Fig.4 that the Majorana fermion is localized at two ends and middle for the magnetic atomic chain with magnetic domain wall in the middle. The mean number of electrons on each site of the atomic chain is around 1.5. In Fig.5(a-d)we show theresult for the same magnetic atomic chain without magnetic domain wall in the middle,then we see density of states for Majorana fermion is peaked only at both ends of the magnetic atomic chain.2.3 The Self-consistent ResultAs the order parameter Δ(i)is space position i dependent,we calculate the energy spectrum and local density of states by selfconsistently solving the eigenvalue equation(3)with equations(7)and(8). For parameter seth=0.1,tx=1.0,μ=2.5,U0=4.0,θ=π/2,N=81,the selfconsistently calculated energy spectrum is shown in Fig.6,the Majorana fermion region can be seen,is still there,but the interval is shorten. The local density of states and mean numbers of electron on each site for Majorana fermion at B0=1.57 are shown in Fig.7(a-d)and Fig.9(a-d). By comparison with Fig.4(a-d),we find the main characters are same,but peak position for selfconsistent result moved inside a little bit. We calculate the selfconsistent wave function for Majorana fermion,and the results are shown in Fig.8(a-d)and Fig.10(a-d). The amplitude is significiently large at both ends for magnetic atomic chain without magnetic domain wall,and significiently large at both ends and middle for a magnetic chain with magnetic domain wall in the middle. This agrees with the result of local density of states.In mean field approximation,and by numerically solving Bogoliubov-de-Genes(BdG)equation,this paper studies the birth,and the localization in space of the Majorana fermion in a one dimensional atomic chain in helical magnetic field,and a uniform magnetic field h which is perpendicular to the atomic chain. Studies find that at a certain parameter setting,theevolution of the energy spectrum with helical magnetic field amplitude B0 appears the zero energy eigenstates,which corresponding to the Majorana fermion. We calculate the local density of states,and find that the local density of states for the Majorana fermion has two peaks on the both end of the magnetic atomic chain. When a magnetic domain wall is applied at the middle of the maqgnetic atomic chain,the Majorana fermion shows peaks at both ends and the middle of the magnetic chain. As the order parameter is a function of space coordinate,we do selfconsistent calculation,and find that by comparing with the result of nonselfconsistent calculation,the energy spectrum and the shape of the local density of states are changed a little bit,but the main character does not change. [1] MAJORANA E. Symmetric theory of electron and positrons[J]. Nuovo Cimento,1937,14(1):171-181.[2] WILCZEK F. Majorana returns[J]. Nat Phys,2009,5(9):614-618.[3] NAYAK C,SIMON S H,STERN A,et al. Non-Abelian anyons and topological quantum computation[J]. Rev Mod Phys,2008,80(3):1 083-1 159.[4] ALICEA J. New directions in the persuit of Majorana fermions in solid state system[J]. Rep Prog Phys,2012,75(7):076501-1-36.[5] NADJ-PERGE S,DROZDOV I K,BERNEVIG B A,et al. Proposal for realizing Majorana fermions in chain of magnetic atoms on a superconductor [J]. Phys Rev B,2013,88(2):020407-1-5(R).[6] PÖYHÖNEN K,WESTSTRÖM A,RÖNTYNEN J,et al. Majorana state in helical shiba chain and ladders[J]. Phys Rev B,2014,89(11):115109-1-7.[7] VAZIFEH M M,FRANZ M. Self-organized topological state with Majorana fermions[J]. Phys Rev Lett,2013,111(20):206802-1-5.[8] SACRAMENTO P D,DUGAEV V K,VIEIRA V R. Magnetic impurities in a superconductors:effect of domainwall and interference[J]. Phys RevB,2007,76(1):014512-1-21.[9] EBISU H,YADA K,KASAI H,et al. Odd frequency pairing in topological superconductivity in a one dimensional magnetic chain[J]. Phys RevB,2015,91(5):054518-1-15.【相关文献】Received data:2016-11-17.Corresponding author:Yang Shuangbo,professor,majored in nonlinear physics and low dimensionalsystem.E-mail:*********************.cndoi:10.3969/j.issn.1001-4616.2017.03.016CLC number:O413.1 Document codeA Article ID1001-4616(2017)03-0110-08。
FDTD Solutions资料集锦专题资料(四)
defined local structures.
Numerical study of natural convection in porous media (metals)
using Lattice Boltzmann Method (LBM).pdf 自然对流多孔介质(金属)用晶格玻尔兹曼方法加快的数值研究
The use of latent heat storage, microencapsulated phase change
materials (MEPCMs), is one of the most efficient ways of storing thermal energy and it has received a growing attention in the past
评价的线性和非线性光学聚合物的二次电光系数衰减全反射技术
The impact of local resonance on the enhanced transmission and dispersion of surface resonances.pdf 局部表面共振对传输和分散增强的影响
We investigate the enhanced transmission through the square array
decade.
Plasmonic Nanoclusters Near Field Properties of the Fano
Resonance Interrogated with SERS.pdf 近场法诺共振制备电浆的性能研究
Review on thermal transport in high porosity cellular metal
科技英语词汇
科技英语词汇数学absolute value 绝对值acute angle 锐角aggregate集合algebra 代数；代数学algorithm 算法analysis 分析analysis of variance 方差分析analytic function分析函数；解析函数analytic geometry 分析几何analytic number theory 分析数论angle 角angular 角的area 面积arithmetic 算术axiomatic set theory 公理集合论calculus of finite difference 有限差演算calculus of variations 变分法cardinal number 基数category 范畴central limit theorem 中心极限定理circle 圆circular points at infinity 圆点class field theory 类域论classical group 典型群common factor公因数complex function 复变函数complex number 复数cone 圆锥体congruence 同余conjugate function 共轭函数constant 常数convolution 卷积coordinate system 坐标系correlation analysis 相关分析curve 曲线curve of second degree 二次曲线cylinder 圆柱体data anlysis 数据分析decimal 小数decision analysis 决策分析denominator 分母derivative 导数determinant 行列式developable surface 可展曲面differential 微分differential and integral calculus 微积分学differential calculus 微分学differential coefficient 导数differential topology 微分拓扑学dimension 维数divisibility 整除elementary function 初等函数elimination method 消元法ellipse 椭圆elliptic function 椭圆函数entropy 熵equal sign 等号equation 等式；方程式error 误差even number 偶数extract roots开方；求根extremum 极值field 域figure 图形finite field 有限域formula (pl. formulae) 公式function 函数functional 泛函数fuzzy logic 模糊逻辑game theory 博弈论generalized inverse matrix 广义逆矩阵geometry 几何学golden section 黄金分割harmonic function 调和函数hyperbola 双曲线improper integral 广义积分incenter 内心indeterminate 不定方程inequality 不等式infinitesimal 无穷小infinity无穷大integral 积分integral calculus 积分学integral equation 积分方程integration 积分法interval analysis 区间分析limit 极限linear 线性的；一次的linear algebra 线性代数linear operator 线性算子line segment 线段logical calculus 逻辑演算mapping 映射matrix 矩阵maximum function 极大函数minimal surface 极小曲面minus减去；负号model logic 模态逻辑moment矩nomogram 算图normal distribution 正态分布numerator分子numerical analysis 数值分析obtuse angle 钝角odd number 奇数optimization 最优化optimization method 优选学origin 原点parabola 抛物线paradox 悖论parallel 平行；平行线parallel algorithm 并行算法parallelogram平行四边形parameter 参数parity 奇偶性partial derivative 偏导数perpendicular bisector中垂线plane 平面polygon 多边形polyhedron 多面体polynomial 多项式positive sign 正号power 幂probability 概率quadratic 二次的radical sign根号random variable 随机变量real number 实数rectangle 长方形；矩形recursion theory 递归论right angle 直角rotundity圆形semicircle 半圆形series 级数set集；集合side 边simple equation 一次方程式sphere 球体；球面square 正方形；平方；直角尺straight line 直线supplementary 互补surface 曲面symmetry 对称taper 圆锥（形）trapezoid / trapezium 梯形triangle 三角形trigonometry 三角学unknown （未知）元；未知数variable 变量variance变方差vector 向量volume 体积物理absolute zero 绝对零度absorption 吸收acceleration 加速；加速度acoustics 声学activator 激活剂alkaline 碱的；碱性的alloy 合金alternating current (AC) 交流电ampere 安培ampere-meter 安培计annealing 退火antiparticle 反粒子atom原子atomic原子的atomic beam 原子束atmosphere 大气层beam splitter 分光膜boson 玻色子calorie 卡calorimetry 量热术cell 电池Celsius temperature 摄氏温度centripetal force 向心力centre of gravity 重心centre of mass 质心centrifugal force 离心力charge 电荷coating 涂层；覆盖collision 碰撞collider 对撞机compass 指南针conservation of energy能量守恒constraint 约束continuum 连续体；连续介质convex 凸起的cosmic ray 宇宙射线coulomb 库伦coupling 耦合critical state 临界状态cross section 截面crystal 晶体crystallization 结晶crystallography 晶体学cyclotron 回旋加速器damping 阻尼decay 衰变diamagnetism 抗磁性dielectrics 电介质；绝缘体diffraction 衍射diffusion 扩散direct current (DC) 直流电discharge 放电dislocation 位错dispersion 色散displacement 位移distortion 畸变divergence发散Doppler effect 多普勒效应drag 阻力drift 漂移dynamics 动力学eddy current 涡电流elastic force 弹性力elasticity 弹性力学electromagnetic 电磁的electret 驻极体electric circuits 电路electric current 电流electric field 电场electricity 电学electric polarization 电极化electric potential 电位electric power 电功率electroacoustics 电声学electrocaloric effect 电热效应electrolytic 电解的electromagnetic 电磁的electromagnetic induction 电磁感应electromagnetic radiation 电磁辐射electromagnetic shielding 电磁屏蔽electromagnetic wave 电磁波electromagnetism 电磁学electron 电子electroscope 验电器electrostatic field 静电场elementary particle 基本粒子energy 能量enthalpy 焓；热函entropy 熵exciton 激子；激发子farad 法拉ferroelectricity 铁电性fiber optics 纤维光学first cosmic velocity第一宇宙速度fission裂变fluctuation 波动fluid mechanics 流体力学fluorescence 荧光；荧光性force 力free nergy 自由能friction 摩擦fusion聚合galvanometer 电流计gaseous discharge 气体放电generator 发电机；发生器gluon 胶子grating 光栅gravitational interaction 引力相互作用graviton 引力子gravity wve 重力波hadron 强子heat transfer 热传递heavy lepton 重轻子helium 氦holography 全息摄影术humidity 湿度hydrogen 氢hyperon 超子impulse 冲量incandescent lamp 白炽灯inductance 电感inertia 惯性inertial force 惯性力infrared ray 红外线insulator绝缘体ion 离子ionic离子的ionize 电离；使离子化isotope 同位素jet 喷注joule 焦耳kinetic energy 动能laser 激光latent heat 潜热lever 杠杆lens 透镜magnet 磁体；磁铁magnetic field 磁场magnetics 磁学magnetization 磁化（强度）mass 质量meson 介子microscope 显微镜molecule 分子moment 力矩momentum 动量multimeter 万用（电）表neucleon 核子neucleus 原子核neutrino 中微子neutron 中子nuclide 核素ohm欧姆ohmmeter欧姆计optics 光学ozone 臭氧层parity 宇称phase 相phosphor 荧光粉photon 光子plasma 等离子体pulley 滑轮pyrometer高温计quark 夸克quartz 石英quenching 淬火reacting force反作用力radar 雷达radiation 辐射radioactivity 辐射性raodiocarbon dating 碳定年recoil反冲reflection 反射resistance 电阻resonance 共振（态）reverberation 混响rolling 轧制screw 螺旋semi-conductor 半导体shock wave 激波；冲击波soild 固体sonar 声呐spectrum 光谱spin 自旋stress 应力superconductivity 超导电性swing振幅synchronizer 同步装置telescope 望远镜temperature 温度tension 张力transistor 晶体管ultrasonic 超声的ultraviolet ray 紫外线universal gravitation万有引力uranium 铀vacuum 真空velocity 速度vibration 振动viscosity 粘性急volt 伏特voltage 电压voltmeter 伏特计vortex 涡旋weld 焊接work 功X ray X射线化学acid 酸absorbate 吸附质aerosol 气溶胶alkali 碱alkaline 碱（性）的amino acid 氨基酸anode 阳极base 碱boiling point 沸点bubble point 泡点calorimetric entropy量热熵capillarity 毛细现象carbonification 碳化作用catalyst催化剂cathode 阴极chemical affinity 化学亲合势chemical potential 化学势clone 克隆（无性系繁殖）compound 化合物composite reaction复合反应condensation in capillary 毛细管凝结condensed state 凝聚态conductivity 电导率conductance电导consecutive reaction连串反应coulometer电量计；库伦计critical parameter临界参数cyclic process 循环过程decomposition voltage分解电压demulsification 胶凝作用dew point露点dispersion phase 分散相electrode potential 电极电势electrolytic cell 电解池electromotive force 电动势electrophoresis 电泳embryo 胚胎energy level能级entropy 熵enzyme 酶equilibrium state平衡态ethane 乙烷ethanol 乙醇eutectic point 低共熔点excess pressure 附加压力extensive property 广延性质ferment 发酵；酵素freezing point凝固点gelatin凝胶gene 基因genome 基因组half cell 半电池heat of dissociation 离解热heat of neutralization 中和热heat pump 热泵ionic strength离子强度internal energy内能intermolecular force 分子间力latent heat 潜热macromolecular solution高分子溶液mechanical equivalent of heat热功当量metabolism 新陈代谢methane 甲烷microstate 微态molecular distillation 分子蒸馏negative pole 负极negative adsorption 负吸附overheated liquid 过热液体oxidation 氧化（作用）oxidation-reduction 氧化还原partial pressure 分压pascal 帕斯卡phase change 相变photoreaction 光反应photosensitized reaction 光敏反应photosynthesis 光合作用polarization极化作用polyelectrolyte 聚（合）电解质polyethylene 聚乙烯polymer 聚合物rectify精馏reduced temperature 对比温度relative viscosity 相对粘度relative volatility 相对挥发度reversible process 可逆过程salting out 盐析saturated vapor饱和蒸气sedimentation 沉降solid phase line 固相线solid solution 固态混合物solution 溶液straight chain reactions 单链反应surface excess表面吸附量thermodynamics 热力学transgenic 转基因的triple point 三相点unimolecular reaction单分子反应vaporization 气化work content 功函yield 产率计算机专业access arm 磁头臂；存取臂access time 存取时间adder 加法器address 地址alphanumeric 字母数字的analog computer 模拟计算机analyst 分析员area 区域array 数组；阵列ASCII 美国信息交换标准码assembler 汇编程序audio音频band 区band width带宽batch processing 成批处理BBS 电子布告栏系统binary code 二进制码binary digit 二进制位；二进制数字bit 比特,二进制的一位branch 分支,支线browser 浏览器brush 电刷buffer storage 缓冲存储器byte 字节calculator 计算器call instruction 呼叫指令cancel 取消card punch 卡片穿孔机card reader 卡片阅读机；读卡机cell 单元channel 通道；信道character 字符check digit 校验数位chip 芯片circuit 电路；线路click 点击clear 清除；清零clock 时钟code 代码；编码coder 编码员；编码器command 指令；命令compact disk (CD)光盘compatible兼容的compatibility兼容性compiler 编译程序computer language 计算机语言control unit 控制器core storage, core store 磁心存储器counter 计数器CPU 中央处理器cybernetics 控制论cycle 循环cursor 光标data 数据data processing 数据处理debugging 调试decision 制定delete 删除desktop桌面display 显示屏dialog box 对话框digit 数字,数位,位digital computer 数字计算机disc, disk 磁盘display unit 显示装置driver驱动器drop-down menu 下拉菜单edit 编辑EMS memory 内存encode 编码erase 擦除；清洗；抹除feed 馈送；供给feedback 反馈field 字段；信息组,域file 文件fire wall 防火墙floppy disk软盘flush left 左对齐folder 文件夹font 字体format 格式frame 帧hack 黑客hard disk 硬盘help 帮助highlight 突出显示icon图标identifier 标识符index 索引information 信息inline processing 内处理input 输入inquiry 询问insert 插入interactive 交互式instruction 指令item 项目；项jump 转移key 键,关键码keyboard 键盘latency time 等待时间library 库,程序库linkage 连接line spacing single 单倍行距load 装入；寄存；写入；加载location 存储单元logger 登记器,记录器log in/on注册；登录loop 循环machine language 机器语言magnetic storage 磁存储器magnetic tape 磁带main frame主机matrix 矩阵memory 存储器menu 菜单message 信息；报文microcomputer 微型计算机module 组件；模块modify 修改monitor 监视器；监督程序；管程motherboard主板mouse 鼠标multimedia 多媒体nanosecond 毫微秒network 网络；网numeric, numerical 数字的；数值的octet 八位位组；八位字节operator 操作员optical character reader 光符阅读机optical scanner 光扫描器output 输出overflow 溢出；上溢panel 平板parameter 参数；参量perforator 穿孔机peripheral equipment 外围设备；外部设备personal computer 个人计算机printed circuit 印制电路printer 打印机printout 打印输出process 处理processor 微处理器processing unit 处理部件program 程序program 程序编制programmer 程序设计员programming 程序设计；程序编制punch 穿孔punch 穿孔punched card, punch card 穿孔卡片punch hole 孔；穿孔punched tape, punch tape 穿孔纸带random access 随机存取read 读取reader 阅读程序reading 阅读read-only file 只读文件real time 实时record, register 记录redundancy 冗余right-click 右击routine 例行程序selector 选择器,选择符sentinel 标记sequence 序列,顺序sequential 顺序的serial 串行的.连续的server 服务器shift 移位,移数signal 信号simulation 模拟simulator 模拟器；模拟程序software 软件；软设备sort 分类,排序sorter 分类人员；分类机；分类程序；排序程序sound box 音箱storage 存储器store 存储subroutine, subprogram 子程序switch 开关symbol 符号symbolic language 符号语言system 系统table 表格tabulator 制表机teleprinter 电传打字机terminal 终端terminal unit 终端设备timer 时钟；精密计时器time sharing 分时timing 定时toolbar 工具按钮track 磁道transducer 传感器；翻译机translator 翻译程序：翻译器tools 工具update保更新view 视图virus 病毒visual 视频window 窗口经贸acceptance 承兑acquisition 收购ad valorem duty 从价税after-sales service 售后服务amortization 分期偿还（欠款本息）anti-dumping 反倾销appreciation 升值arbitration 仲裁assessment 估价auction 拍卖auditing 审计average 海损bad debt 呆帐bail out 财政援助balance of payment 国际收支差额balance sheet 资产负债表bank credit 银行信贷bankrupt 破产bar chart 柱形图bar code 条形码bargain 讨价还价benchmark 基准beneficiary 受益人bill of entry 报关单bill of exchange 汇票bill of lading 提单blue chip 蓝筹股board 董事会bonded warehouse 保税仓库bonus 红利brainstorming 集思广益brand loyalty 品牌忠诚度break-even point 收支相抵点broker 经纪人budget 预算bulk goods 散装货byproduct 副产品telegraphic transfer 电汇capital gains 资本收益capital stock 股本carriage 运费certificate of origin 原产地证明chamber of commerce 商会claim 索赔commission 佣金consignee 收货人consumer durables 耐用消费品customize 定制dealer 经销商debit card 借记卡decision-making 决策declaration of income 收入申报deficit 赤字deflation 通货紧缩delivery note 交货单differentiation 产品差异化distribution 分销diversification 经营多样化Dow Jones Industrial Average 道琼斯工业平均指数down payment 首付；定金economic indicator 经济指数endorsement 背书enquiry 寻盘exchange control 外汇管制face value 面值floating rate 浮动汇率foreign exchange 外汇franchise 特许经营freelance 自由职业者free on board 离岸价futures market 期货市场gross domestic/national product 国内/国民生产总值hedging 套期保值idle money 闲置资金import licence 进口许可证industrial tribunal 劳资仲裁庭inflation 通货膨胀infrastructure 基础设施insurance policy 保险单interest rate 利率investment trust 投资信托公司joint venture 合资公司legal expense 诉讼费用letter of credit 信用证liquidation 清算management buyout 管理层够入全部股权marginal cost 边际成本marine insurance 海运保险marketing mix 营销组合market segmentation 市场细分merger 合并mortgage 抵押贷款net asset value 净资产值offer 报盘off-season 淡季的option 期权order 定单overdraft 透支overhead 经常费用patent 专利payoff 回报，赢利performance 业绩price discrimination 价格歧视portfolio 投资组合product life cycle 产品生命周期promotion 促销public relations 公共关系quotation 报价rate of returns 收益率rationalization 合理化改革real estate 房地产refund 退款retail price 零售价securities 证券stock exchange 股票交易所subsidy 补贴surplus 过剩tariff 关税trade deficit 贸易赤字transactions velocity of circulation 货币流通速度underwriter 承保人value added tax 增值税医学albomycin 白霉素allergen过敏原allergy过敏allergic reaction 过敏反应allergic rhinitis过敏性鼻炎anaphylactic shock过敏性休克anatomy解剖学anemia贫血anorexia厌食症apoplexy 中风arthritis 关节炎beriberi脚气病blood pressure 血压blood test 验血blood type A A血型；A型血brainwave脑波bronchitis 支气管炎cancer癌症cerebral apoplexy 脑溢血cholera霍乱circulatory system循环系统clinic 诊所color blindness 色盲common cold感冒computerized tomography CT扫描contraceptive避孕用具cough咳嗽dentin牙质dentist 牙科医生dermatologist 皮肤科医生detoxification解毒作用diabetes 糖尿病dialysis 透析diarrhea 痢疾dissection解剖eardrum / tympanic membrane鼓膜electrocardiogram (ECG) 心电图electroencephalogram (EEG) 脑电图ENT (ear-nose-throat) doctor 耳鼻喉科医生epilepsy癫痫erythromycin 红霉素gastric ulcers 胃溃疡glucose葡萄糖gynaecologist 妇科医生gynecology妇科学head nurse 护士长heat stroke 中暑hormone激素house surgeon 住院外科医生hospitalization 住院治疗immune system免疫系统infectious disease 传染病infertility不孕injection 注射in-patient住院病人in-patient department 住院部intern 实习医生in vitro fertilization试管内受精leukemia白血病life expectancy预期寿命lymph淋巴malnutrition营养不良me asles 麻疹migraine偏头痛nutrition营养obesity 肥胖症obstetrician 产科医生oculist 眼科医生oligocardia 心动徐缓oligoocholia 胆汁过少oligospermia 精子减少oligopnea 呼吸迟缓oligosideremia 血铁减少oligochromimia 血红蛋白过少oligocythmia 红细胞减少oligosteatosis 皮脂减少oncologist 肿瘤科医生ophthalmologist眼科专家ophthalmology眼科学ophthalmic眼炎orthopedist 骨科医生out-patient 门诊病人out-patient department 门诊部ovulation排卵paediatrician 儿科医生paralysis 瘫痪penicillin 青霉素perspiration排汗plastic surgeon 整形外科医生pneumonia 肺炎radiologist 放射科医生register / registration 挂号rejection排斥反应resident physician 住院内科医生resistance抵抗力rheumatoid arthritis类风湿性关节炎saturated fat饱和脂肪scarlatina 猩红热scurvy坏血病sinus窦sinusitis鼻窦炎skin test 皮试smallpox 天花sphygmomanometer 血压计stethoscope听诊器streptomycin 链霉素student nurse实习护士syphilis梅毒total lung capacity总肺活量transplant operation 移植手术tuberculosis (TB) 结核病tumor肿瘤typhoid fever伤寒ultrasonic diagnosis B B超urinalysis 尿检urologist 泌尿科医生vaccine 疫苗venous injection 静脉注射vomit 呕吐ward 病房生物学chrom颜色chromophore生色团chromosome染色体chromatography色谱法melan, melano, nigr 黑melanoma黑素瘤melanin黑色素melanophore黑色素细胞xantho, flavo, fla, flavi, lute黄xanthophyl叶黄素xanthous黄色的，黄色人种xathine黄嘌呤flavin(e)黄素flavone黄酮letein黄体素，叶黄素flavin adenine dinucleotide(FAD)黄素腺嘌呤二核苷酸erythro, rub, rubrm, ruf 红erythrocyte红细胞erythromycin红霉素erythropoitin(EPO)促红细胞生成素chloro, chlor绿，氯chlorophyll叶绿素chloride氯化物chloramphenicol氯霉素cyan, cyano 蓝，青紫色，氰cyanophyceae 蓝藻纲cyanobacteria蓝细菌cyanide氰化物aur, glid, chrys金色aureomycin金霉素chrysose 金藻淀粉chrysanthemum菊花glidstone 金沙石glid 镀金leu, leuco, leuk, leuko, blan, alb无色，白色leucine亮氨酸albomycin白霉素cephal, capit, cran 头，头颅cyte 细胞carn, my, mya, myo,肉，肌肉haem, haemat, hem, aem, sangul 血soma, corp 体，身体some, plast 体，颗粒hepa, hepat 肝heparin 肝素hepatopancreas肝胰腺hepatocyte 肝细胞hepatoma肝癌ren, nephr 肾adrnal肾上腺的nephridia肾管nephron肾单位card, cord 心cardiotoxin 心脏毒素cardiovascular center 心血管中枢electrocardiogram心电图concord一致，和谐ophthalm, ocell, ocul 眼bronchi 鳃filibranch丝鳃lamellibrnch瓣鳃sencondary branchium次生鳃brac, brachi 腕，手臂brachiolaria 短腕幼虫brachionectin臂粘连蛋白bracelet手镯dent, odont 牙齿dentin牙质odontphora 齿舌odontoblast成牙质细胞plum羽plumatus 羽状的plumule绒毛plumage （鸟的）羽毛foli, foil 叶follicle滤泡foiling叶形foliage 叶子foliose 多叶的Haplodermatitis 单纯皮炎haplolichen 单纯苔藓haploid 单倍体Haplomycosis 单孢子囊菌病pan agglutination 全凝集ultra micron 超微粒ultrasonic 超声波的ultraviolet 紫外线ultrasound 超声Subabdominal 腹下的subarchinoid 蛛网膜下腔的subaural 耳下的subscapular 肩胛下的subcapduloperiosteal 关节囊骨膜下的subclavicular 胸骨下的substratum 下层hypoderm 皮下组织cranium颅cranial bone颅骨cranial cavity 颅腔hip 髋coax bone / hip bone 髋骨hip girdle 髋带hip replacement 髋置换base pair盐基对base盐基hydrochloric acid 盐酸salts 盐类tooth decay龋齿dental caries 龋齿palatine bone 腭骨patella髌骨pulp cavity 髓腔medulla 髓质medulla 髓质myelin 髓磷脂cellulose纤维素fibrin 纤维蛋白fibrinogen 纤维蛋白原fibrous cartilage纤维软骨农业land, soil 土壤arable land, tilled land 耕地dry soil 旱田fertile soil 沃土，肥沃的土壤humus 腐殖质irrigable land 水浇地lean soil, poor soil 贫瘠土壤wasteland, barren land 荒地grassland 草地meadow 草甸prairie 大草原pasture land 牧场fallow 休闲地stubble, stubble field 亩茬地straw, hay 稿杆rural population 农村人口rural exodus 农村迁徙land reform, agrarian reform 土地改革mechanization of farming 农业机械化mechanized farming 机械化耕作cattle farm 奶牛场ranch 大农场，牧场hacienda 庄园holding 田产plot, parcel, lot 地块cooperative farm 合作农场collective farm集体农场country, countryside 农村countryman 农民，农夫countrywoman 农民，农妇agronomist 农学家latifundium, large landed estate 大农场主farmer 农户producer 农业工人landowner 地主，土地拥有者absentee landlord 外居地主smallholder, small farmer 小农rancher 牧场主tenant farmer, leaseholder 土地租用人sharecropper 佃农ploughman 农夫，犁田者farm labourers 农场工人，农业工人（美作：farm laborers）farm hand 农场短工cattle farmer 牧场工人cowherd, cowboy 牛仔shepherd 牧人fruit grower 果农vinegrower 葡萄栽植者vintager 采葡萄者farming, husbandry 农业animal husbandry, animal breeding 畜牧业dairy farming 乳品业，乳牛业horticulture 园艺market gardening 商品蔬菜种植业fruit growing 果树栽培vinegrowing, viticulture 葡萄栽培olive growing 油橄榄栽培arboriculture树艺silviculture 造林学agricultural products, farm products 农产品foodstuffs 食品dairy produce, dairy products 乳制品dairy industry 乳品加工业crop year, farming year农事年season 季节agricultural, commodities market 农业市场livestock 牲畜alfalfa 紫苜蓿apple 苹果apricot 杏子aquiculture 水产养殖asparagus 芦笋banana 香蕉barley 大麦bean 豆bee-keeping 养蜂beeswax 蜂蜡branch 树枝breed 繁殖，生育，饲养buffalo 水牛，野牛cabbage 洋白菜calf 小牛，仔camel 骆驼carp 鲤鱼carrot 胡萝卜cassava 木薯castor—bean 蓖麻籽castor—O¨蓖麻油cat fish 鲇鱼cattle 牛(总称)cauliflower 菜花chemical fertilizer 化学肥料cherry 樱桃chicken 小鸡chlorophyll 叶绿素cock 公鸡coconut 椰子cocoon 蚕茧cod 鳕鱼colony 蜂群compost 堆肥，混合肥料corn 玉米cotton 棉花COW 母牛cowboy 牛仔crop 农作物cross—breeding 杂交dairy farm 奶牛场desert 沙漠donkey 驴duck 鸭子egg 鸡蛋fertilizer 肥料fiber 纤维fig 无花果fish 鱼forest 森林fruit 水果game bird 可猎取的鸟garlic 大蒜gene—altered food(crop) 转基因食物(作物) gene—engineered food(crop) 转基因食物(作物)ginseng 人参GM(gene—modified) food(crop) 转基因食物(作物)goat 山羊graft 嫁接grain 谷物grape 葡萄hay 干草hen 母鸡herbicide 除草剂hive 蜂箱honey 蜂蜜honeycomb 蜂巢horse 马incubate 孵化insect pest 病虫，害虫insecticide 杀虫剂irrigation 灌溉lamb 羔羊leaf 树叶levee 大堤，堤livestock (总称)牲畜lobster 龙虾locust 蝗虫log 圆木．1umbering 伐木maize 玉米mating 交配milk 牛奶mink 水貂mule 骡mushroom 蘑菇mustard 芥末nectar 花蜜nitric acid 硝酸oat 燕麦onion 洋葱orange 广柑，橙子organic fertilizer 有机肥料ox 牛parched field 焦干的土地peach 桃peanut 花生persimmon 柿子pesticide 杀虫剂pet 供玩赏的动物，爱畜，宠物photosynthesis 光合作用pineapple 菠萝plum 李子pollen 花粉potato 土豆poultry farming 养鸡场queen wasp 蜂王raise 饲养ram 公羊ranch 牧场rattan 藤reservoir 水库root 树根royal jelly 王浆seed 种子silage 青贮饲料silk 丝silkworm 蚕soybean 大豆squash 南瓜stem 茎，树干straw 稻草strawberry 草莓sugarcane 甘蔗tangerine 红皮桔till 耕作tillable 可耕作的tillage 耕作tomato 西红柿trawler 拖网渔船turkey 火鸡vegetable 蔬菜wasp 黄蜂watermelon 西瓜weed 杂草well 井wheat 小麦石油化工oil field 油田wildcat 盲目开掘的油井percussive drilling 冲击钻探rotary drilling 旋转钻探offshore drilling 海底钻探well 井，油井derrick 井架Christmas tree 采油树crown block 定滑轮travelling block 动滑轮drill pipe, drill stem 钻杆drill bit钻头roller bit 牙轮钻头diamond bit 钻石钻头swivel 泥浆喷嘴turntable, rotary table 轮盘pumping station 泵站sampling 取样sample 样品，样本core sample 矿样storage tank 储油罐pipeline 油管pipe laying 输油管线oil tanker 油轮tank car, tanker （铁路）罐车，槽车tank truck, tanker （汽车）运油罐车，油罐车refining 炼油refinery 炼油厂cracking 裂化separation 分离fractionating tower 分馏塔fractional distillation 分馏distillation column 分裂蒸馏塔polymerizing, polymerization 聚合purification 净化hydrocarbon 烃，碳氢化合物crude oil, crude 原油petrol 汽油（美作：gasoline）LPG, liquefied petroleum gas 液化石油气LNG, liquefied natural gas 液化天然气octane number辛烷数，辛烷值vaseline 凡士林paraffin 石蜡kerosene, karaffin oil 煤油gas oil 柴油lubricating oil 润滑油asphalt 沥青benzene 苯fuel 燃料natural gas 天然气olefin 烯烃high-grade petrol 高级汽油plastic 塑料机械assembly line组装线layout布置图conveyer流水线物料板rivet table拉钉机rivet gun拉钉枪screw driver起子electric screw driver电动起子pneumatic screw driver气动起子worktable 工作桌OOBA开箱检查fit together组装在一起fasten锁紧(螺丝)fixture 夹具(治具)pallet栈板barcode条码barcode scanner条码扫描器fuse together熔合fuse machine热熔机repair修理QC品管cosmetic inspect外观检查inner parts inspect内部检查thumb screw大头螺丝lbs. inch镑、英寸EMI gasket导电条front plate前板rear plate后板chassis 基座bezel panel面板power button电源按键reset button重置键hi-pot test of SPS高源高压测试voltage switch of SPS 电源电压接拉键sheet metal parts 冲件plastic parts塑胶件SOP制造作业程序material check list物料检查表work cell工作间trolley台车carton纸箱sub-line支线left fork叉车planning department企划部QC Section品管科stamping factory冲压厂painting factory烤漆厂molding factory成型厂common equipment常用设备uncoiler and straightener整平机punching machine 冲床robot机械手hydraulic machine油压机lathe车床planer 'plein?刨床miller铣床grinder磨床driller铣床linear cutting线切割electrical sparkle电火花welder电焊机staker=reviting machine铆合机general manager总经理be put in storage入库pack packing包装to apply oil擦油to file burr 锉毛刺final inspection终检to connect material接料to reverse material 翻料wet station沾湿台Tiana天那水cleaning cloth抹布to load material上料to unload material卸料to return material/stock to退料scraped 'skr?pid报废scrape ..v.刮;削deficient purchase来料不良manufacture procedure制程deficient manufacturing procedure制程不良oxidation ' ksi'dei?n氧化scratch刮伤dents压痕defective upsiding down抽芽不良defective to staking铆合不良embedded lump镶块feeding is not in place送料不到位stamping-missing漏冲production capacity生产力education and training教育与训练proposal improvement提案改善spare parts=buffer备件forklift叉车trailer=long vehicle拖板车compound die合模die locker锁模器pressure plate=plate pinch压板bolt螺栓automatic screwdriver电动启子thickness gauge厚薄规gauge(or jig)治具power wire电源线buzzle蜂鸣器defective product label不良标签identifying sheet list标示单screwdriver holder起子插座pedal踩踏板stopper阻挡器flow board流水板hydraulic handjack油压板车forklift叉车pallet栈板band-aid创可贴iudustrial alcohol工业酒精alcohol container沾湿台sweeper扫把mop拖把vaccum cleaner吸尘器rag 抹布garbage container灰箕garbage can垃圾箱garbage bag垃圾袋chain链条jack升降机production line流水线chain链条槽magnetizer加磁器lamp holder灯架to mop the floor拖地to clean the floor扫地to clean a table擦桌子air pipe 气管packaging tool打包机packaging打包missing part漏件wrong part错件excessive defects过多的缺陷critical defect极严重缺陷major defect主要缺陷minor defect次要缺陷not up to standard不合规格dimension/size is a little bigger尺寸偏大(小) cosmetic defect外观不良slipped screwhead/slippery screw head螺丝滑头slipped screwhead/shippery screw thread滑手speckle斑点mildewed=moldy=mouldy发霉rust生锈deformation变形burr(金属)flash(塑件)毛边poor staking铆合不良excesssive gap间隙过大grease/oil stains油污shrinking/shrinkage缩水mixed color杂色scratch划伤poor processing 制程不良poor incoming part事件不良fold of pakaging belt打包带折皱painting make-up补漆discoloration羿色water spots水渍polishing/surface processing表面处理exposed metal/bare metal金属裸露lack of painting烤漆不到位delivery deadline交货期cost成本engineering工程die repair模修die worker模工to start a press开机classification整理regulation整顿cleanness清扫qualified products, up-to-grade products良品defective products, not up-to-grade products 不良品waste废料board看板feeder送料机sliding rack滑料架defective product box不良品箱die change 换模to fix a die装模to take apart a die拆模to repair a die修模packing material包材plastic basket胶筐isolating plate baffle plate; barricade隔板carton box纸箱to pull and stretch拉深to put material in place, to cut material, to input落料to impose lines压线to compress, compressing压缩character die字模to feed, feeding送料transportation运输。
海森伯格法则
J Supercond Nov Magn(2013)26:1451–1454DOI10.1007/s10948-012-2038-7O R I G I NA L PA P E RHeisenberg-Like Critical Properties and Magnetocaloric Effect in Lead Doped NdMnO3Single CrystalNilotpal GhoshReceived:4November2012/Accepted:1December2012/Published online:5January2013©Springer Science+Business Media New York2013Abstract Static magnetization for single crystals of Nd0.7Pb0.3MnO3has been studied around the ferromagnetic-to-paramagnetic transition temperature T C.The results of mea-surements carried out in the critical range|(T−T C)/T C|≤0.1are reported.The critical exponentsβandγfor thethermal behavior of magnetization and susceptibility havebeen obtained both from the modified Arrott plots and theKouvel–Fisher method.The exponentδ,independently ob-tained from the critical isotherm,was found to satisfy theWidom scaling relationδ=γ/β+1.The values of expo-nents are consistent with those expected for isotropic mag-nets belonging to the Heisenberg universality class withshort-range exchange in three dimensions.The maximummagnetic entropy change is found at around T C.We found auniversal scaling behavior in the relative change of magneticentropy( S M).The rescaled curves of the magnetic entropychange for different appliedfields are observed to collapseonto a single curve,which validates the second order natureof the phase transition in Nd0.7Pb0.3MnO3.Keywords Critical point phenomena·Magnetocaloriceffect·Universal scaling1IntroductionIn rare earth manganites,the most attractive phenomenonis the colossal magneto resistance(CMR)[1]which usu-ally appears at metal–insulator(MI)transition associatedN.Ghosh( )VIT University,Vellore,Tamilnadu,Indiae-mail:ghosh.nilotpal@N.Ghoshe-mail:nilotpal@vit.ac.in with ferromagnetic–paramagnetic(FM–PM)phase transi-tion.Hence,it is interesting to know how the interaction is renormalized near the critical point and which univer-sality class governs the magnetic phase transition.Criti-cal phenomena in the double exchange(DE)model have beenfirst described within mean-field theory[2].Later,Mo-tome and Furukawa[3]predicted that the FM–PM transi-tion in manganites should belong to the short-range Heisen-berg universality class.A number of experimental studies of critical phenomena and scaling laws across the FM–PM phase transition have been previously made on manganites [4].In this context,it should be mentioned that the FM–PM phase transition is also very important for the inves-tigation of the magnetocaloric effect(MCE)in rare earth manganites.MCE is connected to change of magnetic en-tropy( S M)and it is a parameter which achieves rela-tively high value at the PM to FM transition.The MCE is often determined for any material by measuring magnetic isotherms at different temperatures across the T C and by determining S M with the help of Maxwell relations.Re-cently,V.Franco et al.have described the universal behavior for S M in materials with a second order phase transition [5–7].Rare earth manganites(A1−x B x MnO3)are potential candidates for MCE.[8].In the perovskite manganite fam-ily,lead(Pb)doped NdMnO3is a comparatively less studied member[9,10].Nd1−x Pb x MnO3system shows a second order FM-to-PM phase transition and belongs to the univer-sality class of the three dimensional Heisenberg ferromagnet [11,12].In the present paper,we report precise estimation of the critical exponents and validity of scaling laws for an Nd0.7Pb0.3MnO3single crystal.We have reported the study of MCE from determination of magnetic entropy by record-ing the magnetization isotherms as a function of magnetic field.A universal scaling behavior in normalized magneticentropy( S M/ S peakM )with respect to rescaled temperature(θ)is also investigated.2ExperimentSingle crystals are grown by the high temperature solutiongrowth method using PbO/PbF2flux[10].The DC magne-tization measurement is carried out at H=0.3T by Quan-tum Design SQUID ter,extensive magne-tization data M(T,H)are collected in external static mag-neticfields H up to4.8T using the SQUID magnetometer[11,12].The sample has been measured in the temperaturerange135K≤T≤186K(T C∼148.5K)near the PM–FM phase transition with a step of1K.The M(T,H)ver-sus H data are corrected by a demagnetization factor thathas been determined by a standard procedure from low-fieldDC-susceptibility measurements[12].3Results and DiscussionsFigure1(a)shows the magnetic isotherms for Nd0.7Pb0.3MnO3over afield range0–4.8T at135–155K.It is seenthatFig.1(a)The magnetization isotherms of Nd0.7Pb0.3MnO3sin-gle crystal measured at temperatures between135and155K with 1K step.The inset shows magnetization as a function of tempera-ture for Nd0.7Pb0.3MnO3single crystal at0.3T.(b)Arrott plot of Nd0.7Pb0.3MnO3which shows that the system undergoes a second or-der phase transition the magnetization increases rapidly at the lowfield range ∼0.05T and then it increases steadily over thisfield.How-ever,the saturation is not achieved even at4.8T due to thepossible canted magnetic structure of Nd moments with re-spect to Mn sublattice[13].The inset shows the result ofmagnetization measurement as a function of temperature atH=0.3T.The FM-to-PM phase transition is clearly ob-served.According to the scaling hypothesis,a second-orderphase transition near the Curie point T C is characterized bya set of interrelated critical exponents,α,β,γ,δ,etc.,anda magnetic equation of state[11,12].The magnetic phasetransition has been analysed by means of the so-called Arrotplots(M2vs H/M)based on Landau theory of phase transi-tion(Fig.1(b)).The positive slope in Arrot plots means thatthe magnetic transition from the FM-to-PM phase is of thesecond order type[14].This also shows that the mean-fieldtheory does not describe the critical behavior for the presentsystem.Therefore,the magnetic phase transition is analysedwith the modified Arrott plots(Fig.2(a)).As trial values,we have chosenβ =0.365andγ =1.336,the critical ex-ponents of the3D Heisenberg model.As these plots resultin nearly straight lines,we have extracted spontaneous mag-netization M S(T)and inverse susceptibilityχ−10(T)fromthem.These values are plotted with respect to temperaturein Fig.2(b),and the continuous curves show the indepen-dent power lawfits to M S(T)andχ−10(T)[12].The valuesof T C obtained from thefits are close to the original value.Alternatively,the values of T C,βandγhave also been ob-tained by Kouvel–Fisher(KF)method(Fig.3(a))[12].TheFig.2(a)Modified Arrott plots with critical exponents of3D Heisenberg universality class.(b)Plots of M S(T)andχ−10(T)of Nd0.7Pb0.3MnO3Fig.3(a)Kouvel–Fisher plots(b)M S(T=T c,H)versus H plots ofNd1−x Pb x MnO3for x=0.3in log–log scale for Nd0.7Pb0.3MnO3value ofδhas been found directly by plotting M(T C,H)versus H on the log–log scale(Fig.3(b)).The critical ex-ponentsβ,γandδare related through the Widom ScalingRelation(δ=1+γ/β)which is verified with the values ob-tained from our measurements.In order to check whetherour data in the critical region obey the magnetic equationof state equation,M/εβas a function of H/εβ+γwhereε=T−T C/T C is plotted in Fig.4for Nd0.7Pb0.3MnO3.It can be clearly seen that all the points fall on two curves,one for T<T C and the other for T>T C.Thus the obtainedvalues of the critical exponents and T C are reliable and inagreement with the universal scaling hypothesis.The magnetic entropy change S M was calculated frommagnetization isotherms(see Fig.5(a))following the stan-dard procedure based on Maxwell equations[15,16].Fig-ure5(b)describes the variation of− S M with temperature(T)at1.2,2.2,and4.8T.The maximum of− S M is ob-served to appear at around T C,which is quite broad,indi-cating the second order transition.In order to study the uni-versal scaling behavior of S M,we have tofind a universalcurve.Hence,the peak entropy change, S peakM,has beentaken as reference in order to normalize S M(T,H)curvesforfinding equivalent points.For each value of the appliedfield,two reference temperatures T r1<T C and T r2>T C areselected.The collapse of the normalized curves ofentropyFig.4Scaled isotherms of Nd0.7Pb0.3MnO3below and above thetransition temperature usingβandγas defined in thetextFig.5(a)The magnetization isotherms of Nd0.7Pb0.3MnO3singlecrystal measured at temperatures between135and186K with1Kstep.(b)Magnetic entropy change(− S M)as a function of temper-ature at H=1.2,2.2,and4.8T for Nd0.7Pb0.3MnO3(Colorfigureonline)Fig.6Normalized entropy change ( S M / S peakM )as a function of the rescaled temperature (θ)for Nd 0.7Pb 0.3MnO 3.The existence of a universal curve shows that the phase transition is of second order (Color figure online)changes can be obtained by defining a new variable for the temperature axis,θ,given by the following expression [17]:θ=−(T −T C )/(T r 1−T C )T ≤T C ,−(T −T C )/(T r 2−T C )T >T C .(1)Figure 6describes the change of the normalized entropyS M / S peakM as a function of rescaled temperature θfor Nd 0.7Pb 0.3MnO 3.We have considered T r 1=T r 2=T rwhere S M / S peakM is approximately 0.74.It is observed that all the three experimental curves measured at 1.2,2.2,and 4.8T collapse onto a unique curve.The collapse of all these data into a unique curve in a wide range of temperature supports the validity of the second order phase transition and universal scaling for Nd 0.7Pb 0.3MnO 3.4ConclusionsWe have studied the magnetization property of Nd 0.7Pb 0.3MnO 3single crystal at low temperature.The magnetiza-tion measurement as a function of magnetic field up to 4.8T has been carried out at several constant tempera-tures around the T C .We have determined the critical expo-nents by modified Arrott plot and the K–F ing Maxwell’s relations,the magnetic entropy is calculated at H =1.2,2.2,and 4.8T.The maximum magnetic entropy change is observed at around T C .We have found a univer-sal scaling behavior in normalized S M as a function of rescaled temperature.Acknowledgements N.G.thanks the SFB 463Project funded by DFG for financial support during his work in IFW Dresden and Dr.K.Nenkov for measurements.References1.Coey,J.M.D.,Viret,M.,von Molnar,S.:Adv.Phys.48,167(1999)2.Kubo,K.,Ohata,N.:J.Phys.Soc.Jpn.33,21(1972)3.Motome,Y .,Furukawa,N.:J.Phys.Soc.Jpn.70,1487(2001)4.Ghosh,K.,Lobb,C.J.,Greene,R.L.,Karabashev,S.G.,Shulyatev,D.A.,Arsenov,A.A.,Mukovskii,Y .:Phys.Rev.Lett.81,4740(1998)5.Franco,V .,Blázquez,J.,Conde,A.:Appl.Phys.Lett.89,222512(2006)6.Dong,Q.Y .,Zhang,H.W.,Sun,J.R.,Shen,B.G.,Franco,V .:J.Appl.Phys.103,116101(2006)7.Franco,V .,Conde,C.,Blázquez,J.,Conde,A.:J.Appl.Phys.101,093903(2007)8.Phan,M.-H.,Yu,S.-C.:J.Magn.Magn.Mater.308,325(2007)9.Kusters,R.M.,Singleton,J.,Keen, D.A.,McGreevy,R.,Hayes,W.:Physica B 155,362(1989)10.Ghosh,N.,Elizabeth,S.,Bhat,H.L.,Subanna,G.N.,Sahana,M.:J.Magn.Magn.Mater.256,286(2003)11.Sahana,M.,Roessler,U.K.,Ghosh,N.,Elizabeth,S.,Bhat,H.L.,Doerr,K.,Eckert,D.,Wolf,M.:Phys.Rev.B 68,144408(2003)12.Ghosh,N.,Roessler,S.,Roessler,U.K.,Nenkov,K.,Elizabeth,S.,Bhat,H.L.,Doerr,K.,Mueller,K.-H.:J.Phys.Condens.Matter 18,557(2006)13.Ghosh,N.:J.Magn.Magn.Mater.323,405(2011)14.Banerjee,S.K.:Phys.Lett.12,16(1964)15.Amaral,J.S.,Amaral,V .S.:J.Magn.Magn.Mater.1552,322(2010)16.Pekala,M.,Pekala,K.,Drozd,V .,Fagnard,J.F.,Vanderbem-den,P.:J.Magn.Magn.Mater.322,3460(2010)17.Franco,V .,Conde,A.,Romero-Enrique,J.M.,Blazquez,J.S.:J.Phys.Condens.Matter 20,285207(2008)。