基本初等函数
基本初等函数

基本初等函数包括以下几种:(1)常数函数y = c(c 为常数)(2)幂函数y = x^a(a 为非0 常数)(3)指数函数y = a^x(a>0, a≠1)(4)对数函数y =log(a) x(a>0, a≠1)(5)三角函数:主要有以下6 个:正弦函数y =sin x余弦函数y =cos x正切函数y =tan x余切函数y =cot x正割函数y =sec x余割函数y =csc x此外,还有正矢、余矢等罕用的三角函数。
(6)反三角函数:主要有以下6 个:反正弦函数y = arcsin x反余弦函数y = arccos x反正切函数y = arctan x反余切函数y = arccot x反正割函数y = arcsec x反余割函数y = arccsc x初等函数是由基本初等函数经过有限次的有理运算和复合而成的函数。
基本初等函数和初等函数在其定义区间内均为连续函数幂函数简介形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
当a取非零的有理数时是比较容易理解的,而对于a取无理数时,初学者则不大容易理解了。
因此,在初等函数里,我们不要求掌握指数为无理数的问题,只需接受它作为一个已知事实即可,因为这涉及到实数连续统的极为深刻的知识。
特性对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性:首先我们知道如果a=p/q,且p/q为既约分数(即p、q互质),q和p都是整数,则x^(p/q)=q 次根号下(x的p次方),如果q是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。
当指数a是负整数时,设a=-k,则y=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞)。
因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道:排除了为0与负数两种可能,即对于x>0,则a可以是任意实数;排除了为0这种可能,即对于x<0或x>0的所有实数,q不能是偶数;排除了为负数这种可能,即对于x为大于或等于0的所有实数,a就不能是负数。
(整理)基本初等函数.

函数的概念1.函数的概念:设A 、B 是非空的数集,如果按照某个确定的对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有唯一确定的数f (x )和它对应,那么就称f :A →B 为从集合A 到集合B 的一个函数。
记作:y =f (x ),x ∈A 。
其中,x 叫做自变量,x 的取值范围A 叫做函数的定义域;与x 的值相对应的y 值叫做函数值,函数值的集合{f (x )| x ∈A }叫做函数的值域。
注意:(1)“y =f (x )”是函数符号,可以用任意的字母表示,如“y =g(x )”;(2)函数符号“y =f (x )”中的f (x )表示与x 对应的函数值,一个数,而不是f 乘x 。
2.构成函数的三要素:定义域、对应关系和值域 3.两个函数的相等:函数的定义含有三个要素,即定义域A 、值域C 和对应法则f 。
当函数的定义域及从定义域到值域的对应法则确定之后,函数的值域也就随之确定。
因此,定义域和对应法则为函数的两个基本条件,当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数。
4.区间(1)区间的分类:开区间、闭区间、半开半闭区间;(2)无穷区间;(3)区间的数轴表示。
5.映射一般地,设A 、B 是两个非空的集合,如果按某一个确定的对应法则f ,使对于集合A 中的任意一个元素x ,在集合B 中都有唯一确定的元素y 与之对应,那么就称对应f :A →B 为从集合A 到集合B 的一个映射。
记作“f :A →B ”。
映射和函数的区别:映射是两个集合之间的对应关系,集合A 所有元素在B 中有元素对应,集合B 中的元素在A 中不一定有对应的元素。
但是函数,自变量x 所有的值在因变量y 里面都有对应,而因变量y 的所有元素在自变量x 中也有对应; 6.分段函数若一个函数的定义域分成了若干个子区间,而每个子区间的解析式不同,这种函数又称分段函数; 7.复合函数若y =f (u),u=g(x ),x ∈(a ,b ),u ∈(m,n),那么y =f [g(x )]称为复合函数,u 称为中间变量,它的取值范围是g(x )的值域。
基本初等函数

基本初等函数初等函数是由基本初等函数经过有限次的四则运算和复合运算所得到的函数。
基本初等函数和初等函数在其定义区间内均为连续函数。
不是初等函数的函数,称为非初等函数,如狄利克雷函数和黎曼函数。
有两种分类方法:数学分析有六种基本初等函数,高等数学只有五种。
基本初等函数包括以下几类:(1)常数函数y=c(c为常数)(2)幂函数y=x^a(a为常数)(3)指数函数y=a^x(a>0,a≠1)(4)对数函数y=log(a)x(a>0,a≠1,真数x>0)(5)三角函数和反三角函数(如正弦函数:y=sinx反正弦函数:y=arcsinx等)幂函数定义:一般来说,形状如y=xα(α具有理数的函数,即以底数为自变量,幂为变量,指数为常数的函数称为幂函数。
例如函数y=x0、y=x1、y=x2、y=x-1(注:y=x-1=1/xy=x0时x ≠0)等等都是幂函数。
一般形式如下:(α它是常数,可以是自然数、有理数,也可以是任复数。
指数函数定义:指数函数是数学中的一个重要函数。
应用于值e的函数写为exp(x)。
也可以等价写作ex,e是数学常数,是自然对数的底数,近似等于2.718281828,又称欧拉数。
一般形式如下:(a>0,a≠1)对数函数定义:一般来说,函数y=logax(a>0,且a≠1)称为对数函数,即以幂(真数)为自变量,指数为因变量,底数为常量函数,称为对数函数。
x是自变量,函数定义域为(0、∞),即x>0.它实际上是指数函数的反函数,可以表示为x=ay。
因此,指数函数中对a的规定也适用于对数函数。
一般形式如下:(a>0,a≠1,x>0,特别当α=e时,记为y=lnx)常见的三角函数主要有以下六种:正弦函数:y=sinx余弦函数:y=cosx正切函数:y=tanx余切函数:y=cotx正割函数:y=secx余割函数:y=cscx此外,还有正矢、余矢等罕见的三角函数。
基本初等函数的定义

基本初等函数的定义基础初等函数是指构成大多数数学模型的基本函数。
它们也被称为标准函数,因为必须具备某些特定的属性和构成,才能被认定为基础初等函数。
它们通常被用来描述或推断各种自然现象,比如流体运动、声学波动、光学表象。
二、基础初等函数的类型1、指数函数指数函数是由一个“基数”乘以一个“指数”组成的函数,经常用于描述指数增长的现象。
指数函数可以使用形如y = a x^b的方程来表示,其中a是基数,而b是指数。
2、对数函数对数函数是指将一个函数的指数变换成自变量的函数。
许多实际情况都以对数函数的形式表示,比如音量与频率的关系、气温与加热量的关系等。
常见的对数函数有以自然对数e为底,以10为底等。
3、幂函数幂函数是一类指数函数,它将自变量的指数变换成函数的指数。
常见的幂函数有平方函数、立方函数、开平方函数等。
此外,也可以将任意的指数变换成幂函数。
4、三角函数三角函数是一类函数,在计算机科学中使用得比较多。
它们可以使用三角形的角度和边长来求出自变量的值,或者将一个值映射到复平面的三角函数曲线上,通常也被称为极坐标函数。
常见的三角函数包括正弦函数、余弦函数、正切函数等。
5、指数型函数指数型函数是一类特殊的指数函数,它们的结构比普通的指数函数更加复杂,可以呈现出更多的曲线形状。
指数型函数可以用来描述不同种类的物理运动模型,比如速度-距离关系、物体受重力运动的轨迹等。
6、微积分函数微积分函数是用来描述微分表达式的一类特殊的函数。
它们十分复杂,可以更准确的描述不同的现象,比如热力学图、普朗克振动等。
微积分函数可以用来描述连续函数,比如平滑函数、抛物函数等。
7、微分函数微分函数是对复杂函数求微分的一类特殊函数。
它们可以用来描述不断变化的现象,比如速度的变化、温度的变化等。
微分函数也可以用来求多元函数的驻点、极值等级。
三、基础初等函数的应用基础初等函数在许多学科领域都有着广泛的应用。
1、工程领域在工程领域,基础初等函数可以用来描述力学、振动学、热学等物理性质以及材料特性,以求得最佳的工程设计结果。
基本初等函数图像及性质
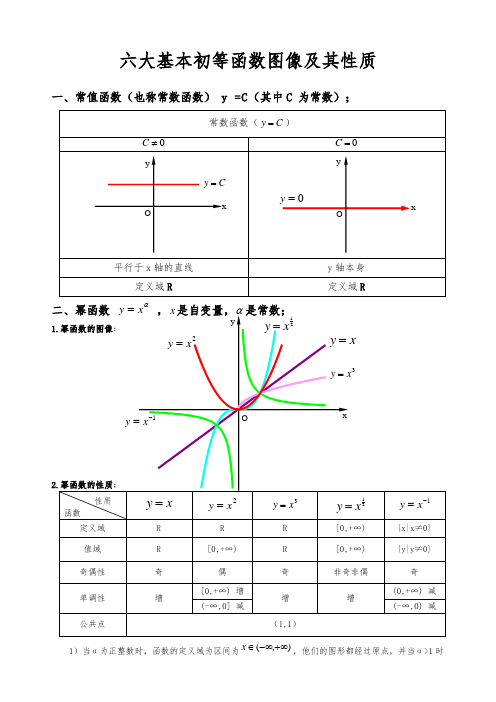
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数1(yf (xx a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nmnm aaa ==(4) ()n n n b a ab=b.根式的性质;(1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂; (1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,f xxxx g ⎪⎫⎛=1)(记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质
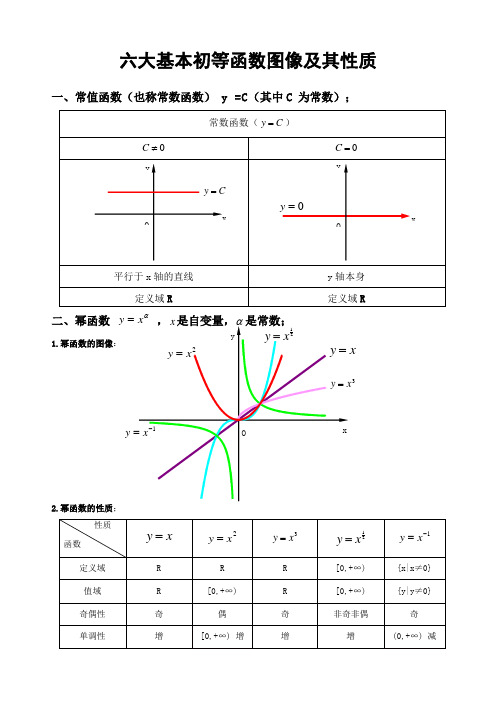
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;3y1)当α为正整数时,函数的定义域为区间为,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnm aaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
基本初等函数定义

基本初等函数定义
1基本初等函数定义
基本初等函数是数学中的一个概念,它也可以称为基本函数,Primary functions,或基础函数。
它被用来定义和描述许多不同的数学模型。
它的定义是:具有某种形式的函数,可以用对数、指数函数、三角函数或其他几何函数组合而成,用来分析某类特定问题。
基本初等函数主要有三种:偶函数、奇函数和其他函数。
偶函数是指在其定义域上,它的取值在坐标轴的对称轴上是对称的,例如二次函数、sinx函数和cosx函数。
奇函数的取值则保持对称,但对称轴不是坐标轴,而是原点,例如tanx函数和cotx函数。
最后,还有一些特殊的函数,例如圆函数、非偶函数和非奇函数,它们可以组合在一起构造特殊的数学模型。
基本初等函数不仅用于模型建构,还可以用来分析数学函数在定义域上的取值规律,以便预测它们在实际问题中的行为。
在几何学中,它常常用于描述和表示不同几何形状的性质,例如点、线、圆、矩形、多边形等。
此外,它还可以用于描述空间几何形状的性质,例如平面、球体等。
因此,基本初等函数在数学和几何学的应用是非常重要的,它们为我们理解数学和几何学中的复杂概念和问题提供了方便的工具和实用的方法。
六大初等函数

六大初等函数
在数学中,初等函数是指可以用有限次基本运算与求导来表示的函数。
在高中数学中,常见的六大初等函数包括:
1. 常数函数:y = c (c为常数)
2. 幂函数:y = x^n (n为正整数)
3. 指数函数:y = a^x (a>0,且a≠1)
4. 对数函数:y = loga(x) (a>0,且a≠1)
5. 三角函数:y = sin(x)、y = cos(x)、y = tan(x) (x为弧度)
6. 反三角函数:y = arcsin(x)、y = arccos(x)、y = arctan(x) (x为实数)
这六大初等函数在数学中应用广泛,是数学学习的基础。
其中,常数函数和幂函数是最基本的函数,指数函数和对数函数则在科学计算、物理学、化学等领域中被广泛应用,三角函数和反三角函数则在几何学、物理学、信号处理等领域中有重要作用。
了解和掌握这些初等函数的概念、性质和应用,对于进一步学习高等数学和应用数学都至关重要。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.已知x=ln π,y=log 52,21-=ez ,则A.x <y <zB.z <x <yC.z <y <xD.y <z <x2.已知2012120121ln ,2011120111ln ,2010120101ln-=-=-=c b a ,则c b a ,,的大小关系为3.设,,a b c 均为正数,且11222112log ,log ,log 22b ca abc ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,请比较三者大小__________4.()f x 设是定义在实数集R 上的函数,满足条件的()1y f x =+是偶函数,且当1x ≥时,()21x f x =-,则请比较231,,323f ff ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的大小关系_________________5.若--y 1,log log x a a a a y a x >+<+且,则正实数x,y 之间的关系适合A. x y <B. x y >C. x y =D.随a 的不同取值,大小关系不定6.已知函数()1lg 2xf x x ⎛⎫=- ⎪⎝⎭有两个零点12,x x ,则有 ( )A .120x x <B .121x x =C .121x x >D .121110x x <<7.不论a 为何值时,函数()122xay a =--恒过定点,则这个定点的坐标为_______________8.已知O 为坐标原点,过点O 的直线与函数x y 3=的图象交于A,B 两点,点A 在线段OB 上,过点A 作y 轴的平行交函数x y 9=的图象于C 点,当BC 平行于x 轴时,点A 的横坐标是9.设函数⎩⎨⎧>-≤=-1,log 11,2)(21x x x x f x ,则满足2)(≤x f 的x 的取值范围是A .1[-,2]B .[0,2]C .[1,+∞]D .[0,+∞]10.若31x xa a -+=+,则33x xxxa a a a ----的值等于______________11.若函数()2log 1a y x ax =-+有最小值,则a 的取值范围是______________12.已知定义在区间[]0,1上的函数()y f x =的图像如图所示,对于满足1201x x <<<的 任意1201x x <<<的任意12,x x ,给出下列结论正确的是____________○1()()2121f x f x x x ->- ○2()()2112x f x x f x > ○3()()121222f x f x x x f ++⎛⎫<⎪⎝⎭13..若[](),xy ex a b =∈的值域为21,e⎡⎤⎣⎦,则点(),a b 的轨迹是右图中的 ( )A,线段BC 和OCB.线段AB 和BCC.线段AB 和OAC.线段OA 和OC14.设函数的集合211()log (),0,,1;1,0,122P f x x a b a b ⎧⎫==++=-=-⎨⎬⎩⎭,平面上点的集合11(,),0,,1;1,0,122Q x y x y ⎧⎫==-=-⎨⎬⎩⎭,则在同一直角坐标系中,P 中函数()f x 的图象恰好..经过Q 中两个点的函数的个数是 (A )4 (B )6 (C )8 (D )1015.已知点P 在曲线y=41xe +上,a 为曲线在点P 处的切线的倾斜角,则a 的取值范围是 A.[0,4π) B.[,)42ππC.3(,]24ππD. 3[,)4ππ16.函数()x x e x x f cos sin 2sin ++=的最大值与最小值之差等于17.对于函数()x f 与()x g 和区间E ,如果存在E x ∈0,使()()100<-x g x f ,则我们称函数()x f 与()x g 在区间E 上“互相接近”.那么下列所给的两个函数在区间()+∞,0上“互相接近”的是A.()()32,2-==x x g x x fB.()()2,+==x x g x x fC.()()xx g e x f x1,-==- D.()()x x g x x f ==,ln18.()f x R 若函数是定义在上的奇函数,且当()1012x x f x -<≤=时 当()()()111.2x f x f x f x x >=--时,则函数y=的零点有________个19.当()()21,21log a x x x ∈-<时,不等式恒成立,则a 的取值范围是______________20.已知函数()()2log 3a f x x ax =-+()0,1a a >≠且满足:对任意实数12x x ,,当122ax x <≤时,总有()()120f x f x ->,求实数a 的取值范围_______________21.已知两条直线1l :y =m 和2l : y=821m +(m >0),1l 与函数2log y x =的图像从左至右相交于点A ,B ,2l 与函数2log y x =的图像从左至右相交于C,D .记线段AC 和BD 在X 轴上的投影长度分别为a ,b ,当m 变化时,ba的最小值为 A .162 B.82 C.84 D.4422.已知函数f (x )=|lg x |.若0<a<b,且f (a )=f (b ),则a+2b 的取值范围是 A.(22,)+∞ B.[22,)+∞ C.(3,)+∞ D.[3,)+∞23.已知函数()[]()⎩⎨⎧+∞∈∈=,1,log 1,0,sin 2011x x x x x f π,若满足()()()c f b f a f ==(c b a ,,互不相等),则c b a ++的取值范围是24.已知函数()⎩⎨⎧>+-≤<=5,1050,ln x x x e x f x ,若方程()k x f =有三个不同的实数根c b a ,,,且c b a <<,则c b a ++的取值范围是25.设实数y x ,满足条件⎪⎩⎪⎨⎧≤≤-≤≤2lg 12lg 122y xxy ,则43lg y x 的最大值为26.已知函数()139139+++⋅+=xx x x k x f ,若对任意的实数321,,x x x ,均存在以()()()321,,x f x f x f 为三边长的三角形,则实数k 的取值范围是27.已知函数()⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫⎢⎣⎡⎪⎭⎫⎢⎣⎡∈+=-2,21,221,0,211x x x x f x ,若存在21,x x ,当2021<<≤x x 时,()()21x f x f =,则()21x f x 的取值范围是28.在平面直角坐标系xoy 中,已知点P 是函数()xf x e =(0x >)的图像上的动点,该图像在点P 处的切线l 交y 轴于点M ,过点P 做l 的垂线交y 轴于点N ,设线段MN 的中点的纵坐标为t,则t 的最大值为29.已知()2f x x =,1()2xg x m ⎛⎫=- ⎪⎝⎭若对于任意的[]11,3x ∈-,总有[]20,2x ∈,使得()()12f x g x ≥成立,则实数m 的取值范围是___________30.设定义域为R 的函数()2lg ,02,0x x f x x x x ⎧>⎪=⎨--≤⎪⎩若关于x 的函数()()2221y f x bf x =++有8个不同的零点,则实数b 的取值范围是_______________31.已知函数()x f x x e =-(其中e 为自然对数的底数),()1g x mx =-若对于任意的[]11,1x ∈-,总存在[]01,1x ∈-,使得()01()g x f x =成立,实数m 的取值范围为___________32.函数()))(2(log 1++∈+=N n n n f n ,定义:使()()()()k f f f f ⋅⋅⋅⋅⋅321为整数的数()+∈N k k 叫做期盼数,则在区间[]10,1内这样的期盼数共有33.已知函数()()()⎩⎨⎧<<-+-<<-+=)31(,12)11(,1log x a x f x x x f a ,(1,0≠>a a 且),若21x x ≠,且()()21x f x f =,则21x x +的值A.恒小于2B.恒大于2C.恒等于2D.与a 相关34.已知函数f x ()=log (0a 1).a x x b a +-≠>,且当2<a <3<b <4时,函数f x ()的零点*0(,1),,n=x n n n N ∈+∈则35.定义在R 上的奇函数()f x ,当()[)[)1213,1,0log (1),0,1x x x f x x x ⎧--∈+∞⎪≥=⎨+∈⎪⎩时则关于x 的方程()()11f x a a =-<<的所有解之和为_____________(用a 表示)36.定义:对函数()y f x =,x D ∈。
若存在常数C ,对于任意的1x D ∈,存在唯一的2x D ∈,使得()()122f x f x C +=则称函数()y f x =在D 上的“均值”为C 。
已知 ()[]lg ,10,100f x x x =∈,则函数()lg f x x =在[]10,100的均值为________________37.定义:区间[]12,x x ()12x x <的长度为21x x -.已知函数12log y x =的定义域为[],a b ,值域为[]0,2,则区间[],a b 的长度的最大值为________________38.对于任意实数x ,[]x 符号表示x 的整数部分,即[]x 是不超过x 的最大整数。
在实数轴R (箭头向右)上[]x 是定在点x 左侧的第一个整数点,当x 是整数时[]x 就是x 。
这个函数叫做“取整函数”。
它在数学本身和生产实践中有广泛的应用,那么[][][][][]33333log 1log 2log 3....log 242log 243+++++=_____________39.()f x R 函数是定义在上的最小正周期为2的周期函数,且当02x ≤<时,()3f x x x =-,则函数()y f x =的图像在区间[]0,6上与x 轴的交点个数为_______个40.函数11y x=-的图像与函数2sin y x π=的图像在[]4,2-所有交点的横坐标之和等于41.已知函数211x y x -=-的图像与函数2y kx =-的图像恰有两个交点,则实数k 的取之范围是____________42.对于实数a 和b ,定义运算“*”: 22,,a ab a ba b b ab a b⎧-≤⎪*=⎨->⎪⎩设()()()211f x x x =-*-,且关于x 的方程()()f x m m R =∈恰有三个互不相同的实数根123,,x x x ,则123x x x 取值范围是__________43.设函数()f x R 的定义域为,若存在常数0k >,使()2010kf x x ≤对一切实数x 均成立,则称()f x 为“海宝”函数。
