高中六大基本初等函数
高中基本初等函数完全归纳总结版

初等函数1、基本初等函数及图形基本初等函数为以下五类函数:(1) 幂函数 μx y =,μ是常数;1.当u 为正整数时,函数的定义域为区间),(+∞-∞∈x ,他们的图形都经过原点,并当u>1时在原点处与X 轴相切。
且u 为奇数时,图形关于原点对称;u 为偶数时图形关于Y 轴对称;2.当u 为负整数时。
函数的定义域为除去x=0的所有实数。
3.当u 为正有理数m/n 时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞+∞)。
函数的图形均经过原点和(1 ,1).如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n 均为奇数时,跟原点对称.4.当u 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数.(2) 指数函数 xa y =(a 是常数且01a a >≠,),),(+∞-∞∈x ;1. 当a>1时函数为单调增,当a<1时函数为单调减.2. 不论x 为何值,y 总是正的,图形在x 轴上方.3. 当x=0时,y=1,所以他的图形通过(0,1)点.(3) 对数函数x y alog =(a是常数且01a a >≠,),(0,)x ∈+∞;(4) 三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,1. 他的图形为于y 轴的右方.并通过点(1,0)2. 当a>1时在区间(0,1),y 的值为负.图形位于x 的下方,在区间(1, +∞),y 值为正,图形位于x 轴上方.在定义域是单调增函数.a<1在实用中很少用到/正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;(5) 反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数 x y cot arc =,),(+∞-∞∈x ,),0(π∈y .选校网专业大全历年分数线上万张大学图片大学视频院校库(按ctrl 点击打开)。
高中数学基本初等函数图形及其性质
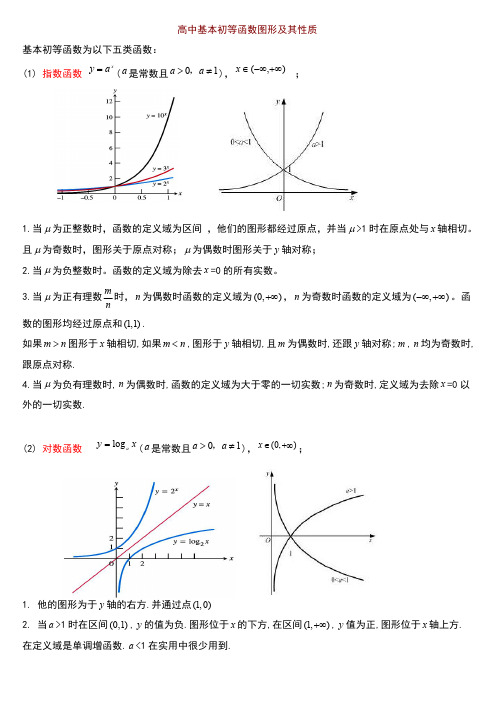
高中基本初等函数图形及其性质基本初等函数为以下五类函数:(1)指数函数x a y =(a 是常数且01a a >≠,),),(+∞-∞∈x ;1.当μ为正整数时,函数的定义域为区间,他们的图形都经过原点,并当μ>1时在原点处与x 轴相切。
且μ为奇数时,图形关于原点对称;μ为偶数时图形关于y 轴对称;2.当μ为负整数时。
函数的定义域为除去x =0的所有实数。
3.当μ为正有理数m n时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1).如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称.4.当μ为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x =0以外的一切实数.(2)对数函数x y a log =(a 是常数且01a a >≠,),(0,)x ∈+∞;1.他的图形为于y 轴的右方.并通过点(1,0)2.当a >1时在区间(0,1),y 的值为负.图形位于x 的下方,在区间(1,)+∞,y 值为正,图形位于x 轴上方.在定义域是单调增函数.a <1在实用中很少用到.(3)幂函数,y x μμ=是常数;1.当μ为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当μ>1时在原点处与x 轴相切。
且μ为奇数时,图形关于原点对称;μ为偶数时图形关于y 轴对称;2.当μ为负整数时。
函数的定义域为除去x =0的所有实数。
3.当μ为正有理数m n时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1).如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称.4.当μ为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x =0以外的一切实数.(4)三角函数正弦函数xy sin =1.定义域:R;2.值域:[-1,1].3.单调性:在区间[2,2]()22k k k Z ππππ-++∈内,函数单调递增;在区间3[2,2]()22k k k Z ππππ++∈()k Z ∈内,函数单调递减;4.对称性:对称轴2x k ππ=+,对称中心(,0),k k Z π∈.5.周期性:2T π=;6.奇偶性:由sin()sin x x -=-知,正弦函数是奇函数;余弦函数xy cos = 1.定义域:R.2.值域:[-1,1].3.单调性:在区间[]2,2()k k k Z πππ-∈内,函数单调递增;在区间[]2,2()k k k Z πππ+∈内,函数单调递减;4.对称性:对称轴x k π=,对称中心(,0),2k k Z ππ+∈.5.周期性:π=T ;6.奇偶性:由cos()cos x x -=知,余弦函数是偶函数;正切函数x y tan = 1.定义域:⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππ;2.值域:R 3.单调性:在开区间z k k k ∈⎪⎭⎫ ⎝⎛++-ππππ2,2内,函数单调递增。
基本初等函数.定义

五类基本初等函数·定义在高中数学中,无论文科理科,函数都占据了所考内容的半壁江山。
总的来说,高中所要解决的函数问题主要是基本初等函数问题与初等函数问题。
高中基本初等函数包括五类:多项式函数(一次函数、二次函数)、指数函数、对数函数、幂函数与三角函数;而所谓的初等函数只是基本初等函数经过有限次的有理运算(÷⨯-+、、、等)与复合,生成的有解析式表示的函数。
①多项式函数一次函数(直线):形如()()R x a b ax x f y ∈≠+==,0的函数,叫做一次函数; 二次函数(抛物线):形如()()R x a c bx ax x f y ∈≠++==,02的函数,叫做二次函数。
②指数函数形如()()R x a a a x f y x ∈≠>==,1,0的函数,叫做指数函数。
函数13213+⋅=+x y 是否为指数函数;指出使函数b a c y n m x +⋅=+为指数函数时,满足条件的n m c b a ,,,,。
③对数函数形如()()0,1,0log >≠>==x a a x x f y a 的函数,叫做对数函数。
函数()113log 23++⋅=x y 是否为对数函数;指出使函数()b n mx c y a ++⋅=log 为对数函数时,满足条件的n m c b a ,,,,。
④幂函数形如()()0,≠∈==x R x x f y αα的函数,叫做幂函数。
函数()113221++⋅=x y 是否为幂函数;指出使函数()b n mx a y ++⋅=α为幂函数时,满足条件的n m b a ,,,。
⑤三角函数正弦函数()x x f y sin ==;余弦函数()x x f y cos ==;正切函数()x x f y tan ==。
函数()12sin 2++⋅=πx y 是否为正弦函数;我们把()ϕω+=x A y cos 称为什么函数。
高中基本初等函数

单调性〔1〕函数的单调性①定义及断定方法单调性是与“区间〞严密相关的概念,对于一个函数,它在某区间上可能有单调性,也可能没有单调性,例如函数y=x+ ,它在区间〔- ,0]上没有单调性,而在[0,+ 〕上是增函数。
有的函数不具备单调性,如函数y= ,它的定义域为R,但它不具备单调性;再如函数y=x+1,x Z,它的定义域不是区间,也不能说它在定义域上具有单调性。
函数的单调性具有可逆性,即在区间D上单调递增,那么,且,有;反之亦然。
②复合函数的单调性:在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数。
对于复合函数[()]u g x=为增,那么[()]y f g x==为增,()y f uy f g x=,令()u g x=,假设()为增;假设()y f u =为减,()u g x =为减,那么[()]y f g x =为增;假设()y f u =为增,()u g x =为减,那么[()]y f g x =为减;假设()y f u =为减,()u g x =为增,那么[()]y f g x =为减.最大〔小〕值定义①一般地,设函数()y f x =的定义域为I ,假如存在实数M 满足:〔1〕对于任意的x I ∈,都有()f x M ≤;〔2〕存在0x I ∈,使得0()f x M =.那么,我们称M 是函数()f x 的最大值,记作max()f x M =.②一般地,设函数()y f x =的定义域为I ,假如存在实数m 满足:〔1〕对于任意的x I ∈,都有()f x m ≥;〔2〕存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max()f x m =.奇偶性函数的奇偶性 ①定义及断定方法函数的奇偶性假如对于函数f(x)定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)叫做奇函数.〔1〕利用定义〔要先判断定义域是否关于原点对称〕〔2〕利用图象〔图象关于原点对称〕假如对于函数f(x)定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)叫做偶函数.〔1〕利用定义〔要先判断定义域是否关于原点对称〕〔2〕利用图象〔图象关于y轴对称〕②假设函数()f x为奇函数,且在0x=处有定义,那么(0)0f=.③奇函数在y轴两侧相对称的区间增减性一样,偶函数在y轴两侧相对称的区间增减性相反.用定义判断函数奇偶性的方法幂函数〔1〕幂函数的定义一般地,函数y xα=叫做幂函数,其中x为自变量,α是常数.(2)幂函数的图象〔3〕幂函数的性质①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于y 轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.②过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1). ③单调性:假如0α>,那么幂函数的图象过原点,并且在[0,)+∞上为增函数.假如0α<,那么幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.④奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数.⑤图象特征:幂函数,(0,)y x x α=∈+∞,当1α>时,假设01x <<,其图象在直线y x =下方,假设1x >,其图象在直线y x =上方,当1α<时,假设01x <<,其图象在直线y x =上方,假设1x >,其图象在直线y x =下方.指数函数对数函数 〔1〕对数的定义①假设(0,1)x a N a a =>≠且,那么x 叫做以a 为底N 的对数,记作log ax N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数. ③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>.〔2〕几个重要的对数恒等式〔3〕常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log eN 〔其中 2.71828e =…〕.(4)对数的运算性质反函数设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.假如对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y f x -=.〔7〕反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=;③将1()x fy -=改写成1()y fx -=,并注明反函数的定义域.反函数的性质①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域.③假设(,)P a b 在原函数()y f x =的图象上,那么'(,)P b a 在反函数1()y fx -=的图象上.。
高中基本初等函数总结归纳.doc

第二章基本初等函数(I)£2.13指数函数【2.1.1】指数与指数幂的运算(1)根式的概念① 如果,n./?e N + ,那么x 叫做的n 次方根.当n 是奇数时,《的次方根用符号&表示;当是偶数时,正数的正的n 次方根用符号 表示,负的n 次方根用符号-表示;0的n 次方根是0;负数6T 没有n 次方根.② 式子叫做根式,这里n 叫做根指数,6?叫做被开方数.当/2为奇数时,为任 意实数;当/?为偶数吋,tz>0.③ 根式的性质:(‘)当n 为奇数时,= a ;当/?.为偶数时,(2)分数指数幂的概念① 正数的正分数桁数幂的意义是0的正分 数指数幂等于0.- 2 1 - / 1② 正数的负分数指数幂的意义是:“"=(一广=彳(一广0/〉0,爪,託乂,且 a V aZ2>1). 0的负分数指数¥没有意义.注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质① W = a r+s (a>0,r,sE R)(§)(</)、-a rs {a >0, r,5G R)③(ab)r= a r b r(a 〉0,b 〉0,re R)【2.1.2】指数函数及其性质指数函数y z y = a xy = a xyJ = 1J = 1(04)(0,1)0 X 0Xy/a" =| a \=a —a (^/>0) (tz<0)K2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①苦¥ = ;7(6/〉0,且《矣1),则叫做以tz为底7V的对数,id作x = log u/V,其屮0叫做底数,2V叫做真数.②负数和零没有对数.③对数式与指数式的互化:x二log, N^a x => 0,6/1, > 0).(2)几个重要的对数恒等式log w 1 = 0, log w 6Z = 1, \og a a h = b .(3)常用对数与自然对数常用对数:IgN,即log m7V;自然对数:\nN,即log^yV (其中£> = 2.71828…).(4)对数的运算性质如果〉0,7V〉0,那么M①加法:log w M + log^ N = log rt{MN)②减法:log n M - log^ N = \og a—n⑤ log h M n=-\og a M(b^^nER)⑥ 换庖公式(l blog; TV lQgz? N (b〉0,且/?弇1)1 log/, “【2.2.2】对数函数及其性质(5)对数函数(6)设函数y = /(幻的定义域为A,值域为C,从式子y = /(x)中解出X,得式子义二炉(>,)•如果对于y在C屮的任何一个位,通过式子x = x在A屮都科唯一确定的值和它对应,那么式子x = ^(y)表示x是y的函数,函数x = 叫做函数j = ,(x)的反函数,记作又二/—1。
基本初等函数导数公式

基本初等函数导数公式基本初等函数导数公式还有同学记得吗?不记得的话,快来小编这里瞧瞧。
下面是由小编为大家整理的“基本初等函数导数公式”,仅供参考,欢迎大家阅读。
基本初等函数导数公式C'=0、(x^n)'=nx^(n-1)、(a^x)'=a^x*lna、(e^x)'=e^x、(loga(x))'=1/(xlna)、(lnx)'=1/x、(sinx)'=cosx、(cosx)'=-sinx。
初等函数是由基本初等函数经过有限次的四则运算和复合运算所得到的函数。
基本初等函数和初等函数在其定义区间内均为连续函数。
不是初等函数的函数,称为非初等函数,如狄利克雷函数和黎曼函数。
拓展阅读:高一数学必修一知识点总结高一数学集合有关概念集合的含义集合的中元素的三个特性:元素的确定性如:世界上最高的山元素的互异性如:由HAPPY的字母组成的集合{H,A,P,Y}元素的无序性: 如:{a,b,c}和{a,c,b}是表示同一个集合集合的表示:{ … } 如:{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋}用拉丁字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}集合的表示方法:列举法与描述法。
注意:常用数集及其记法:非负整数集(即自然数集) 记作:N正整数集 N*或 N+ 整数集Z 有理数集Q 实数集R列举法:{a,b,c……}描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。
{x(R| x-3>2} ,{x| x-3>2}语言描述法:例:{不是直角三角形的三角形}Venn图:集合的分类:有限集含有有限个元素的集合无限集含有无限个元素的集合空集不含任何元素的集合例:{x|x2=-5}高一数学集合间的基本关系1.“包含”关系—子集注意:有两种可能(1)A是B的一部分,;(2)A与B是同一集合。
反之: 集合A不包含于集合B,或集合B不包含集合A,记作AB或BA2.“相等”关系:A=B (5≥5,且5≤5,则5=5)实例:设 A={x|x2-1=0} B={-1,1} “元素相同则两集合相等”即:① 任何一个集合是它本身的子集。
高中数学知识点:基本初等函数的单调性

第 1 页 共 1 页 高中数学知识点:基本初等函数的单调性
1.正比例函数(0)y kx k =≠
当k>0时,函数y kx =在定义域R 是增函数;当k<0时,函数y kx =在定义域R 是减函数.
2.一次函数(0)y kx b k =+≠
当k>0时,函数y kx b =+在定义域R 是增函数;当k<0时,函数y kx b =+在定义域R 是减函数.
3.反比例函数(0)k y k x =≠
当0k >时,函数k y x =的单调递减区间是()(),0,0,-∞+∞,不存在单调增区间;
当0k <时,函数k y x
=的单调递增区间是()(),0,0,-∞+∞,不存在单调减区间.
4.二次函数2(0)y ax bx c a =++≠
若a>0,在区间(]2b a -∞-
,,函数是减函数;在区间[)2b a -∞,+,函数是增函数;
若a<0,在区间(]2b a -∞-
,,函数是增函数;在区间[)2b a -∞,+,函数是减函数.。
函数类型细分辨,一目了然方法现——高中常见函数的分类

函数类型细分辨,一目了然方法现——高中常见函数的分类
高中阶段,学生们开始研究函数。
因为函数的概念难以理解,种类繁多,课本又没有系统地讲解,许多老师也只是泛泛而谈,所以很多学生更是稀里糊涂,无所适从。
因函数类型的不同,处理方式也大不一样,所以函数类型是题目的一个重要标志,找到了标志,方法、步骤大致确定。
其实,只要能分辨清楚函数的类型,则对应的方法、技巧是一目了然的。
这里就给出分类标准,以供参考:
基本初等函数:包括6种
其它的函数,基本上都是由以上基本初等函数进行有限次组合或有限次复合而成的。
组合函数:
复合函数:将基本初等函数的自变量x换成另外一个基本初等函数(自身也行)就得到一个复合函数。
通俗地说,复合函数就是函数套函数,是把几个简单的函数复合为一个较为复杂的函数。
例如:
具体函数:给出了具体的解析式的函数叫具体函数。
抽象函数:没给出具体解析式的函数就是抽象函数。
抽象函数不是没有解析式,只是说题目没有给出来,仅以一个符号y=f(x)或f(x)来体现。
我们可以理解为“有这么一个函数存在,具体的解析式是什么样子的暂时还不知道”
至于其它的一些函数类型,因为高一新生接触不到,这里先不讲了!
函数的种类不同,使用到的方法、步骤大不相同(在以后的发文中我会一一讲解),所以要仔细区分函数的类型,必须达到一眼就能识别的程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中六大基本初等函数
函数在数学中具有重要的地位,它是研究数学问题的基本工具。
在高中数学中,有六大基本初等函数,它们分别是常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数。
下面我们将逐个介绍这六大函数的定义、特点和应用。
常数函数是最简单的函数之一,它的定义域是全体实数集,值域只有一个常数。
常数函数的图像是一条平行于x轴的直线。
常数函数的特点是在定义域内的任何一个点上,函数值都相等。
常数函数在数学中有广泛的应用,例如在物理学中,常数函数可以表示物体的匀速直线运动。
幂函数是形如y=x^n的函数,其中n是一个常数。
幂函数的定义域是正实数集,值域也是正实数集。
幂函数的图像形状随着指数n 的不同而变化,当n>1时,函数图像是上升的开口向上的曲线;当0<n<1时,函数图像是下降的开口向下的曲线。
幂函数在实际问题中有很多应用,例如在经济学中,幂函数可以描述价格与销量之间的关系。
指数函数是形如y=a^x的函数,其中a是一个常数且a>0且a≠1。
指数函数的定义域是全体实数集,值域是正实数集。
指数函数的图像是上升的开口向上的曲线。
指数函数在数学中有许多重要的性质和应用,例如在金融学中,指数函数可以描述复利的增长过程。
对数函数是指数函数的反函数,它的定义域是正实数集,值域是全体实数集。
对数函数的图像是一条上升的曲线,它与指数函数的图像关于y=x对称。
对数函数在实际问题中有广泛的应用,例如在工程学中,对数函数可以描述信号的衰减过程。
三角函数是以单位圆上的点坐标为函数值的函数,它们包括正弦函数、余弦函数和正切函数。
三角函数的定义域是全体实数集,值域是[-1,1]。
三角函数的图像是周期性的波动曲线。
三角函数在物理学、工程学等领域有许多应用,例如在力学中,正弦函数可以描述物体的周期性振动。
反三角函数是三角函数的反函数,它们包括反正弦函数、反余弦函数和反正切函数。
反三角函数的定义域和值域与对应的三角函数相反。
反三角函数在实际问题中也有广泛的应用,例如在导航系统中,反正弦函数可以帮助确定航行方向。
高中六大基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数。
它们各自具有不同的定义域、值域和图像特点,应用于不同的数学和实际问题中。
对这六大函数的理解和掌握,对于高中数学的学习和应用具有重要的意义。
