(完整word)六年级下册数学用比例解决问题练习题(提高)

合集下载

小学六年级数学下册期末总复习----解决问题专项复习题 (三)Microsoft Word 文档

1、淘气从A地向B地驶去，2小时后，笑笑步行从A地向B地走去，笑笑出发2小时后，淘气到达B地，此时笑笑离淘气64千米，淘气在B地休息2.5小时后，按原来返回，1小时后在C处遇到笑笑，AB两地有多远？2、一个圆柱和一个圆锥，底面周长的比是2:3他们的体积比是5:6，圆柱和圆锥高的最简比是多少？3、求下面图形的面积。

12104、一个正方形的棱长减少20%，这个正方形的表面积减少百分之几？体积减少百分之几？5、超市一共有酸奶和纯牛奶630袋，其中酸牛奶占20%，后来卖出一些纯牛奶，这时酸牛奶占总数的30%，卖纯奶多少袋？6、甲乙两车同时从AB两地相对开出，经过5小时相遇，相遇后，按原速度前进，又经过3小时，甲车到达B地，乙车距离A地还有120千米，求AB两地相遇多少千米？7、甲乙两数的和是320，甲数除以乙数的商是1/3，甲乙分别是多少了？8、一个长方形水槽长40厘米，宽20厘米，高15厘米，池内水深12厘米，放入一个底面积为90平方厘米的圆柱零件，池中的水溢出300毫升，圆柱形零件长多少厘米？9、被减数、减数与差的平均数是60，减数是差的1/3，差是多少，减数是多少？10、把160分成三个数，使这三个数分别能被2、3、5整除，而且所得的商都相同，这三个数是多少？11、现在是12时整，时针分针再次重合至少要过多少分钟？12、在一个直径是5米的圆形水池边每隔0.628米放一盆花，一共可以放几盆花？13、在一个长1米、宽60厘米的长方形纸片上，剪一个直径是20厘米的圆，最多可以剪几个？14、学校体育队原有男生人数占男女总人数的3/8,后来又进来20名男生，这是男生的人数占男女生总数的7/12，这个学校体育队现在有学生多少人？15、有一批水果，第一天卖出水果的1/4,第二天卖的是第一天的3/5，还有90筐没有卖，这批水果有多少筐？16、一个圆柱形水桶，里面装了一半的水，倒出了水的1/3，后还剩下60升，已知水桶高8分米，这个水桶的底面积是多少？17、有含糖量为7%的糖水600克，要使其含糖量增大到10%，需要再加入多少克糖？18、丽丽今年的年龄是爸爸的1/3,4年前丽丽的年龄是爸爸的1/4,丽丽今年有多大？19、三个数的平均数是13.5，甲数是乙数的4倍，丙数比甲数大4.5，三个数各是多少？。

六年级数学下册《用比例解决问题》练习题及答案解析

六年级数学下册《用比例解决问题》练习题及答案解析学校:___________姓名：___________班级：_____________一、选择题1．一条2厘米的线段，选用下面比例尺（）画出的平面图最大。

A．1∶200B．1∶5000C．1∶1D．2∶12．老师买了同样数目的田格本、横线本和练习本。

他发给每个同学1个田格本、3个横线本和5个练习本。

这时横线本还剩24个，那么田格本和练习本共剩了（）个。

A．48B．50C．54D．563．把一个圆柱削成一个最大的圆锥，削去的体积是48立方分米，圆柱的体积是（）立方分米。

A．144B．24C．724．一幅地图的比例尺是1∶1000000，下列说法不正确的是（）。

A．这是一个数值比例尺B．说明要把实际距离缩小为11000000后，再画在图纸上C．图上距离相当于实际距离的1 1000000D．图上1厘米相当于实际1000000米5．下列各数中，（）不能与2、8、10组成比例。

A．58B．85C．52D．406．甲乙两个容积相同的瓶子分别装满盐水，已知甲瓶中盐、水的比是2∶3，乙瓶中盐、水的比是3∶5，现在把甲、乙两瓶水混合在一起，则混合盐水中，盐与盐水的比是（）。

A．519B．521C．524D．31807．一个水池有甲乙两个水管。

单独开甲管，2小时可以把空池注满；单独开乙管，3小时可以把空池注满。

如果同时打开甲乙两管，（）小时可以把空池注满。

A．1B．15C．115D．58．希望小学合唱队共有队员108人，则（）一定不是男队员和女队员人数的比。

A．5∶4B．7∶5C．8∶7D．19∶17 9．表示x和y成正比例关系的式子是()．A．x＋y＝9B．y＝1.5x C．＝0D．xy＋1＝510．学校把560棵树的种植任务，按照六年级三个班的人数分配给各班。

一班有47人，二班有45人，三班有48人。

二班应种树（）。

A．192棵B．188棵C．180棵11．在一幅地图上，用20厘米的线段表示50千米的实际距离，那么这幅地图的比例尺是（）。

苏教版数学六年级下册专项～比例解决问题【含答案】

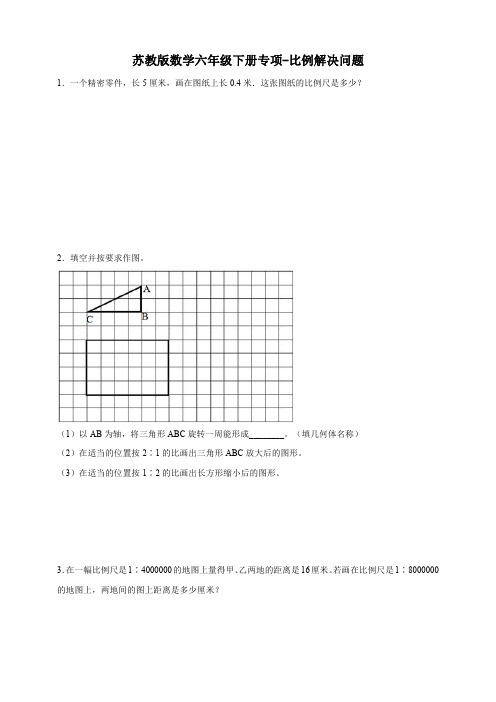
苏教版数学六年级下册专项-比例解决问题1．一个精密零件，长5厘米，画在图纸上长0.4米．这张图纸的比例尺是多少？2．填空并按要求作图。

（1）以AB为轴，将三角形ABC旋转一周能形成________。

（填几何体名称）（2）在适当的位置按2∶1的比画出三角形ABC放大后的图形。

（3）在适当的位置按1∶2的比画出长方形缩小后的图形。

3．在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。

若画在比例尺是1∶8000000的地图上，两地间的图上距离是多少厘米？4．画一画，填一填。

（1）按3∶1的比画出图形A放大后得到的图形B。

（2）按1∶2的比画出图形B缩小后得到的图形C。

我发现：放大或缩小前后的图形（）变了，但（）没有变，而且图形各部分长度是按一定的比变化的。

5．在一张比例尺是1∶150的建筑图纸上，量得一座大楼的长是6分米，这座大楼的实际长与宽的比是3∶1，这座大楼的实际宽是多少米？6．下图中小平行四边形按比放大后得到大平行四边形，求大平行四边形的高。

（单位：分米）12．根据图中提供的信息，完成下列问题。

（1）自来水厂要从水库取水，取水管道怎样铺最短，请在图中画出来。

（2）自来水厂到城区的送水管道经测算最短是2000米，请你测算：自来水厂到水库的取水管道最短需多少米？13．在一幅地图上，用5厘米长的线段表示实际距离100千米，这幅地图的比例尺是多少？如果甲市至乙市的铁路线路长150千米，那么这段铁路线路在这幅地图上的长度是多少厘米？14．江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。

广场绿地面积与铺装面积的比是6∶5，其中铺装面积共5000平方米，绿地面积有多少平方米？15．甲乙两城相距150千米，在一幅地图上量得甲乙两城之间的距离是5厘米，同时在这幅地图上量得乙丙两城之间的距离是8厘米。

乙丙两城之间的实际距离是多少千米？20．下图中A点是游乐场所在的位置，B点是电影院所在的位置，两地实际距离相距2千米。

六年级数学下册《用比例解决问题》练习题

1.小亮半小时能打900个字，照这样的速度，往电脑里输入一篇1500字的文章，小亮需要多长时间？解：设小亮需要x分钟。

半小时＝30分1500：x＝900：30900x＝1500×30x＝50答：小亮需要50分钟。

2.某女裤工厂计划生产6500条女裤，3天已经生产了1500条，按照这样的工作效率，剩下的女裤还需要多少天能生产完？解：设剩下的女裤还需要x天能生产完。

6500－1500＝5000（条）5000：x＝1500：31500x＝5000×3x＝10答：剩下的女裤还需要10天能生产完。

3.100千克黄豆可以榨豆油13千克，按照这样的出油率，要榨豆油6.5吨，需黄豆多少吨？解：设需黄豆x吨。

100：13＝x：6.513x＝100×6.5x＝50答：需黄豆50吨。

4.小明在100m短跑到达终点时领先小刚10m，领先小华15m。

如果小刚和小华按原来的速度继续跑向终点，那么当小刚到达终点时，小华还差多少米到达终点？解：设当小刚到达终点时，小华还差x米到达终点100-10 100-15=100 100-x18 17=100100-xx=50 9答：当小刚到达终点时，小华还差509米到达终点。

5.一张照片长4厘米，宽3厘米，如果按4∶1的比把这张照片放大，放大后照片的长、宽分别是多少厘米？如果要使放大后照片的宽是9厘米，那么放大后照片的长应是多少厘米？4×4＝16（厘米）3×4＝12（厘米）解：设放大后照片的长是x厘米4∶3＝x∶93x＝4×93x＝363x÷3＝36÷3x＝12答：放大后照片的长是16厘米，宽是12厘米。

如果要使放大后照片的宽是9厘米，那么放大后照片的长应是12厘米。

6.客车和货车同时从甲，乙两地相向开出，客车每小时行全程的1 4，货车每小时行60千米，相遇时客车和货车所行路程的比是3∶2。

甲、乙两地相距多少？由分析可得：两车的速度比是3 2客车的速度是：60×32＝90（千米/时）甲、乙两地相距：90÷14＝360（千米）答：甲、乙两地相距360千米。

六年级下册数学2017-2018学年第二学期练习题第4单元比例用比例解决问题含答案)

6.北京到长沙的铁路长大约是1600km 。

一列由北京开往长沙的高铁，9:00出发，11:30到达郑州。

北京到郑州的铁路长大约是700km 。

按照这样的平均速度，从北京到长沙6个小时能到吗？7.一列货车前往灾区运送救灾物资，2小时行驶了30km 。

从出发地点到灾区有90km ，按照这样的速度，全程需要多少小时？8.小林读一本文学名著，如果每天读30页，8天可以读完。

小林想6天读完，那么平均每天要读多少页？9.小明家用收割机割小麦。

如果每小时收割0.3公顷，40小时能完成任务。

（1）现在想用30小时收割完，那么每小时应收割多少公顷？（2）每公顷产小麦8t ，这块地共产小麦多少吨？（3）你能提出其他的数学问题并解答吗？10.一辆运货汽车从甲地到乙地，平均每小时行72km ，10小时到达。

回来时空车原路返回，每小时可行90km 。

多长时间能够返回原地？11.小平的姐姐在上大学，妈妈每个月（按30天算）按每天10元的标准给她一笔零花钱。

（1）如果姐姐每天花6元，一个月的零花钱够用多少天？（2）如果姐姐每天花15元，你能提出数学问题并解答吗？12.小东家的客厅是正方形的，用边长0.6m 的方砖铺地，正好需要100块。

如果改用边长0.5m 的方砖铺地，需要多少块？第4单元比例用比例解决问题练习题（答案） 1. 下面哪个图形是图形A 按2:1放大后得到的图形？2. 自己选定比例画图形，把三角形A放大后得到三角形B，再把三角形B缩小后得到三角形C。

（1）哪些三角形可以由A放大后得到？（2）哪些三角形可以由B缩小后得到？（3）*观察三角形A和B，它们的面积有什么变化？面积与边长是按相同的比变化的吗？解：（1）三角形B和三角形C可以由三角形A放大后得到。

（2）三角形A和三角形C可以由三角形B缩小后得到。

（3）三角形B的面积是三角形A的面积的16倍。

面积与边长不是按相同的比变化的。

3. 小兰的身高1.5m，她的影长是2.4m，如果同一时间、同一地点测得一棵树的影子长4m，这棵树有多高？解：设这棵树高x m。

人教版六年级数学下册第四单元《比例》综合复习练习题(含答案)

人教版六年级数学下册第四单元《比例》综合复习练习题（含答案）考试时间:80分钟满分:100+10分一、填空题。

（每空1分，共18分）1.根据M:N=5:8这个等式，把下面的词语“送回家”。

比值最简整数比互质数比的基本性质比例的基本性质因为5和8是( )，所以M:N的( )是5：8，它们的( )是0.625，根据( )可以推出M:N=10:16,根据( )可以推出8M=5N。

2.在比例中，两个外项互为倒数，一个内项是0.5，另一个内项是( )。

3.笑笑为一家人调制了四杯蜂蜜水，蜂蜜与水的配比情况如表：第一杯第二杯第三杯第四杯蜂蜜/mL 12 12 10 16水/mL 60 48 80 80 其中最甜的一杯是第( )杯，有两杯是同样甜的，这两组数据可以组成一个比例式是( )。

4.若ab=,则a与b成( )比例;若x=y,则x与y成( )比例。

5.一个零件长8mm,工程师绘图时的长度是24cm,这幅图的比例尺是( )。

6.法国巴黎的埃菲尔铁塔高324m,北京“世界公园”里有一座埃菲尔铁塔模型，它的高度与原塔的高度比是1:10,这座模型高( )m。

7.一个长3cm、宽2cm的长方形，按3：1放大，得到的图形的面积是( )cm2,周长是( )cm。

8.在一幅比例尺为1：2000000的地图上，量得A地到B地的图上距离是6 cm,则 A地到B地的实际距离是( )km。

如果甲行完全程需要2小时，乙行完全程需要3小时，甲、乙两人同时从A、B两地相对出发，( )小时可以相遇。

9.爸爸驾驶轿车从A朝阳高速入口北上高速公路，需要经过如图的陡坡，当轿车行驶到日A点时，北斗卫星导航系统显示距80 m100 m离地面40 m,假如陡坡的坡度处处相同，轿车行驶到B点时，北斗卫星导航系统会示距离地面( )m。

(坡度指距离地面的高度与水平长度的比)10.爸爸的平均步长是0.75m,乐乐的平均步长是0.5m,从乐乐家到学校，爸爸走了1200步，乐乐要走( )步。

练习题用比例解决实际问题 (2)

用比例解决问题测试题一、填空．1．两种（）的量，一种量变化，另一种量（），如果这两种量中（）的两个数的（）一定，这两种量就叫做成正比例的量，它们的关系叫做（），关系式是（）．2．两种（）的量，一种量变化，另一种量（），如果这两种量中（）的两个数的（）一定，这两种量就叫做成反比例的量，它们的关系叫做（），关系式是（）．二、下面每题中的两种量是否成比例？如果成比例，成什么比例关系？1.速度一定，路程和时间。

（）2.单价一定，总价和数量。

（）3.学生总人数一定，每行站的人数和站的行数。

（）4.铺地面积一定，方砖面积与所需块数。

（）5.货车的载重量一定，运送货物的总量和辆数。

（）6.小华每天读课外书20页，读书总页数和天数成（）比例关系。

7.长方形的面积一定，长和宽成（）比例关系。

8.李玲的体重与她的年龄（）比例关系。

三、判断．1．一个因数不变，积与另一个因数成正比例．（）2．长方形的长一定，宽和面积成正比例．（）3．大米的总量一定，吃掉的和剩下的成反比例．（）4．圆的半径和周长成正比例．（）5．分数的分子一定，分数值和分母成反比例．（）6．铺地面积一定，方砖的边长和所需块数成反比例．（）7．铺地面积一定，方砖面积和所需块数成反比例．（）8．除数一定，被除数和商成正比例．（）四、选择．1．把一堆化肥装入麻袋，麻袋的数量和每袋化肥的重量．（）A．成正比例B．成反比例C．不成比例2．和一定，加数和另一个加数．（）A．成正比例B．成反比例C．不成比例3．在汽车每次运货吨数，运货次数和运货的总吨数这三种量中，成正比例关系是（），成反比例关系是（）．A．汽车每次运货吨数一定，运货次数和运货总吨数．B．汽车运货次数一定，每次运货的吨数和运货总吨数．C．汽车运货总吨数一定，每次运货的吨数和运货的次数．五、根据条件说出数量关系，并判断成什么比例。

1、食堂买3桶油用了780元，照这样计算，买10桶油需要多少元？因为（）一定，相关联的两种量是（）和（）得数量关系式：所以（）和（）成（）比例关系。

六年级下册解比例练习题

六年级下册解比例练习题解题1：已知2:5和40:100是等比例关系，求未知数。

解答：根据等比例关系的定义，两个比例的比值应该相等。

因此，我们可以设置一个等式来解决这个问题。

2/5 = 40/100在等式两边进行简化运算，消去分子分母中的公共因子。

2/5 = 2/5得到2/5 = 2/5，两边相等。

因此，未知数为2。

解题2：已知3:8和9:24是等比例关系，求未知数。

解答：同样地，根据等比例关系的定义，我们可以得到以下等式：3/8 = 9/24接下来，我们要进行简化运算。

首先，我们可以将3/8和9/24分别化简为最简形式。

3/8 = (3/1)/(8/1) = 3/89/24 = (9/3)/(24/3) = 3/8可以看到，两个比例化简后的结果相等。

因此，未知数为3。

解题3：已知4:7和16:28是等比例关系，求未知数。

解答：利用等比例关系的定义，我们可以得到以下等式：4/7 = 16/28接下来，我们进行简化运算。

首先，我们将4/7化简为最简形式。

4/7 = (4/1)/(7/1) = 4/7然后，我们将16/28化简为最简形式。

16/28 = (16/4)/(28/4) = 4/7可以看到，两个比例化简后的结果相等。

因此，未知数为4。

通过以上练习题的解答，我们可以深入理解和应用等比例关系的概念。

掌握解题方法和技巧，能够帮助我们更好地解决类似的问题。

对于六年级的学生来说，掌握解比例练习题的方法是提高数学能力的重要一步。

希望同学们能够通过多做类似的题目，不断巩固知识，提高成绩。

小学数学比例练习题六年级

小学数学比例练习题六年级在小学六年级数学学习中，比例是一个重要的知识点。

通过练习比例题，不仅可以提高学生的计算能力，还能培养他们的逻辑思维和问题解决能力。

本文将给出一些适合小学六年级的数学比例练习题。

练习题一：果汁配料比例某商店准备生产一种新的果汁，需要调配苹果汁、橙汁和葡萄汁。

根据市场调研，市场对苹果汁、橙汁和葡萄汁的需求比例为3比4比5。

现在要生产300升的果汁，请计算需要调配多少升的苹果汁、橙汁和葡萄汁。

解答：根据需求比例，我们可以得到苹果汁：橙汁：葡萄汁的比例为3:4:5。

将总升数300升按照比例进行分配，得到：苹果汁 = 300 × (3/12) = 75升橙汁 = 300 × (4/12) = 100升葡萄汁 = 300 × (5/12) = 125升因此，调配果汁时，需要用75升苹果汁、100升橙汁和125升葡萄汁。

练习题二：食物中的营养比例下面是某种食物中的营养含量表。

营养成分每100克食物中的含量蛋白质 15克脂肪 10克碳水化合物 30克纤维素 5克请计算蛋白质、脂肪、碳水化合物、纤维素在这种食物中的比例。

解答：根据表格中的数据，我们可以计算出蛋白质、脂肪、碳水化合物、纤维素的比例。

蛋白质比例 = 15 / (15 + 10 + 30 + 5) × 100% = 30%脂肪比例 = 10 / (15 + 10 + 30 + 5) × 100% = 20%碳水化合物比例 = 30 / (15 + 10 + 30 + 5) × 100% = 60%纤维素比例 = 5 / (15 + 10 + 30 + 5) × 100% = 10%因此，蛋白质、脂肪、碳水化合物和纤维素在这种食物中的比例分别为30%、20%、60%和10%。

练习题三：图书馆读者男女比例某图书馆对读者的男女比例进行了调查，结果显示男性读者占总读者数的40%，女性读者占总读者数的60%。

小学数学比例应用题(共6篇)

小学数学比例应用题〔共6篇〕篇1：六年级数学比例应用题练习题六年级数学比例应用题练习题(1)水果店一天运进苹果、香蕉、梨共390千克，苹果的重量是梨的1.5倍，香蕉的重量是梨的3/4，三种水果各运进多少千克?(2)一缸水，用去1/2和5桶，还剩30%，这缸水有多少桶?(3)有一快棱长20厘米的正方体木料，刨成一个底面直径的圆柱体，刨去木料的体积是多少?(4)一根钢管长10米，第一次截去它的7/10，第二次又截去余下的1/3，还剩多少米?(5)两个小组装配收音机，甲组每天装配50台，第一天完成了总任务的10%，这时乙组才开场装配，每天装配40台，完成这批任务时，甲组做了多少天?(6)修筑一条公路，完成了全长的2/3后，离中点16。

5千米，这条公路全长多少千米?(7)师徒两人合做一批零件，徒弟做了总数的2/7，比师傅少做21个，这批零件有多少个?(8)两队修一条公路，甲队每天修全长的1/5，乙队独做7.5天修好。

假如两队合修2天后，其余由乙队独修，还要几天完成?(9)仓库里有一批化肥，第一次取出总数的2/5，第二次取出总数的1/3少12袋，这时仓库里还剩24袋，两次共取出多少袋?(10)前轮在720米的间隔里比后轮多转40周，假如后轮的周长是2米，求前轮的周长。

11、为创立海华公司，张、王、李三人分别投资100万元、120万元和80万元。

在他们三人的共同努力下，到年末，公司共盈利60万元，你认为该如何合理分配这笔钱，每人分别得多少?12、甲乙两地相距360千米，一辆汽车从甲地到乙地方案7小时行完全程，汽车的速度如下表，问能否在规定的时间内行完全程?(计算后简要说明)13、在比例尺是的地图上，量得甲乙两地的间隔为4.5厘米，假如一辆客车和货车同时从甲乙两地相对开出，经过3小时相遇。

客车每小时行65千米，那么这辆货车每小时行多少千米?14、在比例尺是1:3000000的地图上，量得A、B两城之间的间隔是2.4厘米。

(完整word版)2014年六年级数学思维训练：比例解应用题

2014年六年级数学思维训练：比例解应用题一、兴趣篇1．（2014秋•盐城校级期末）圆珠笔和铅笔的单价比是4：3，20支圆珠笔和21支铅笔共71.5元．圆珠笔的单价是多少？2．一段路程分为上坡和下坡两段，这两段的长度之比是4：3．已知阿奇在上坡时每小时走3千米，下坡时每小时走4.5千米．如果阿奇走完全程用了半小时．请问：这段路程一共有多少千米？3．加工一个零件，甲要2分钟，乙要3分钟，丙要4分钟，现有1170个零件，甲、乙、丙三人各加工几个零件，才能使得他们同时完成任务？4．有两块重量相同的铜锌合金．第一块合金中铜与锌的重量比是2：5，第二块合金中铜与锌的重量比是1：3．现在把这两块合金合铸成一块大的．求合铸所成的合金中铜与锌的重量之比．5．（2012•北京模拟）已知甲、乙、丙三个班总人数的比为3：4：2，甲班男、女生的比为5：4，丙班男、女生的比为2：1，而且三个班所有男生和所有女生的比为13：14，请问：（1）乙班男、女生人数的比是多少？（2）如果甲班男生比乙班女生少12人，那么甲、乙、丙三个班各有多少人？6．甲、乙两包糖的重量比是5：3，如果从甲包取出10克放入乙包后，甲、乙两包糖的重量比变为7：5．请问：这两包糖重量的总和是多少克？7．（2012•北京模拟）小明从甲地到乙地，去时每小时走5千米，回来时每小时走7千米，来回共用4小时，小明去时用了多长时间？8．（2012•北京模拟）冬冬从家去学校，平时总是7：50到校，有一天他起晚了，结果晚出发了10分钟，为了不至于迟到，他将速度提高了五分之一，跑步前往学校，最后在7：55到校，请问：冬冬这天是几点出发的？9．一项工程，由若干台机器在规定时间内完成．如果增加2台机器，只需用规定时间的就可完成；如果减少2台机器，就要推迟小时才能完成．请问：（1）在规定时间内完成需几台机器？（2）由1台机器去完成这工程，需要多少小时？10．康师傅加工一批零件，加工720个之后，他的工作效率提高了20%，结果提前4天完成任务；如果康师傅从一开始就把工作效率提高12.5%，那么也可以提前4天完成任务．这批零件共有多少个？二、拓展篇11．学校组织体检，收费标准如下：老师每人3元，女生每人2元，男生每人1元，已知老师和女生的人数比为2：9，女生和男生的人数比为3：7，共收体检费945元．那么老师、女生和男生各有多少人？12．徐福记的巧克力糖每6块包成一小袋，水果糖每15块包成一大袋．现有巧克力糖和水果糖各若干袋，而且巧克力糖比水果糖多30袋．如果巧克力糖的总块数与水果糖的总块数之比为7：10，那么它们各有多少块？13．甲、乙、丙三人合买一台电视机，甲付的钱数等于乙付的钱数的2倍，也等于丙付的钱数的3倍．已知甲比丙多付了680元，请问：（1）甲、乙、丙三人所付的钱数之比是多少？（2）这台电视机售价多少钱？14．一把小刀售价3元．如果小明买了这把小刀，那么小明与小强的钱数之比是2：5；如果小强买了这把小刀，那么两人的钱数之比是8：13．小明原来有多少元钱？15．两根粗细相同、材料相同的蜡烛，长度比为29：26，燃烧50分钟后，长蜡烛与短蜡烛的长度比为11：9，那么较长的那根还能燃烧多少分钟？16．（2008•武汉校级自主招生）某俱乐部男女会员的人数之比是3：2，分为甲、乙、丙三组．已知甲、乙、丙三组的人数比是10：8：7，甲组中男女会员的人数之比是3：1，乙组中男女会员的人数之比是5：3．则丙组中男女会员人数之比是．17．某次数学竞赛设一、二、三等奖，已知：①甲、乙两校获一等奖的人数比为1：2，但它们一等奖人数占各自获奖总人数的百分数之比为2：5；②甲、乙两校获二等奖人数占两校获奖人数总和的25%，其中乙校是甲校的3.5倍；③甲校三等奖获奖人数占该校获奖人数的80%．请问：乙校获三等奖人数占该校获奖人数的百分比是多少？18．（2013•青羊区校级模拟）如果单独完成某项工作，那么甲需要24天，乙需要36天，丙需要48天．现在甲先做，乙后做，最后由丙完成．甲、乙工作的天数比为1：2，乙、丙工作天数比为3：5．问：完成这项工作共用了多少天？19．已知猫跑5步的路程与狗跑3步的路程相同，猫跑7步的路程与兔跑5步的路程相同．而猫跑3步的时间与狗跑5步的时间相同，猫跑5步的时间与兔跑7步的时间相同，求猫、狗和兔的速度之比．20．（2013春•高陵县校级月考）星期天早晨，哥哥和弟弟都要到奶奶家去．弟弟先走5分，哥哥出发后25分追上弟弟．如果哥哥每分多走5米，那么出发后20分就可以追上弟弟．弟弟每分走多少米？21．一支解放军部队从驻地乘车赶往某地抗洪抢险，如果行驶1个小时后，将车速提高五分之一，就可比预定时间提前20分钟赶到；如果先按原速度行驶72千米，再将车速提高三分之一，就可比预定时间提前30分钟赶到，问：这支解放军部队一共需要行多少千米？22．一项工作由甲、乙两人合作，恰可在规定时间内完成，如果甲效率提高三分之一，则只需用规定时间的六分之五即可完成；如果乙效率降低四分之一，那么就要推迟75分钟才能完成，请问：规定时间是小时？三、超越篇23．甲、乙两人分别同时从A、B两地开始，修建一条连接A、B两地的公路，并按修路的距离分配240万元工程款．如果按原计划，甲应分得100万元．而在实际施工的时候，乙每天比原计划多修l千米，结果乙实际分得了150万元，那么乙队实际施工时，每天修多少千米？24．孙悟空有仙桃、机器猫有甜饼、米老鼠有泡泡糖，他们按下面比例互换：仙桃与甜饼为3：5，仙桃与泡泡糖为3：8，甜饼与泡泡糖为5：8．现在孙悟空共拿出39个仙桃分别与其他两位互换，机器猫共拿出甜饼90个与其他两位互换，米老鼠共拿出88个泡泡糖与其他两位互换．请问：米老鼠与孙悟空和机器猫各交换泡泡糖多少个？25．有两包糖，每包糖内装有奶糖、水果糖和巧克力糖．已知：①第一包糖的粒数是第二包糖的；②在第一包糖中，奶糖占25%，在第二包糖中，水果糖占50%；③巧克力糖在第一包糖中所占的百分比是在第二包糖中所占的百分比的两倍，当两包糖混合在一起时，巧克力糖占28%．求第一包与第二包中水果糖占所有糖的百分比．26．某工地用三种型号的卡车运送土方．已知甲、乙、丙三种卡车载重量之比为10：7：6，速度比为3：4：5，运送土方的路程之比为15：14：14，三种车的辆数之比为10：5：7．工程开始时，乙、丙两种车全部投入运输，但甲种车只有一半投入，直到10天后，另一半甲种车才投人工作，又干了15天才完成任务．求甲种车完成的工作量与总工作量之比．27．在一个490米长的圆形跑道上，甲、乙两人从相距50米的A、B两地，相背出发，相遇后，乙返回，甲方向不变，继续前进，甲的速度提高五分之一，乙的速度提高四分之一．当乙回到B地时，甲刚好回到A地，此时他们都按现有速度与方向前进．请问：当甲再次追上乙时，甲（从开始出发算起）一共走了米？28．将A、B两种细菌分别放在两个容器里．在光线亮时A细菌需12小时分裂完毕，B细菌需15小时分裂完毕；在光线暗时，A细菌的分裂速度要下降40%，B细菌的分裂速度反而提高10%．现在两种细菌同时开始分裂并同时分裂完毕，试问：在分裂过程中，光线暗的时间有多少小时？29．如图，A、B、C、D、E、F是六个齿轮．其中A和B相互咬合，B和C相互咬合，D 和E、E和F也都相互咬合；而C和D是同轴的两个齿轮，也就是说C和D转动的圈数始终相同．当A转了7圈时，B恰好转了5圈；当E转了8圈时，F恰好转了9圈；当C转了5圈时，B和E恰好共转了28圈．请问：（1）如果A、E转的总圈数总是和B、F转的总圈数相同，那么当A、F共转了100圈时，D转了多少圈？（注：图片只是示意图，并不代表实际齿数）（2）如果A、E的总齿数和B、F的总齿数相等，D的齿数是C的齿数的2倍，那么当A 转了210圈时，D和F分别转了多少圈？2014年六年级数学思维训练：比例解应用题参考答案与试题解析一、兴趣篇1．（2014秋•盐城校级期末）圆珠笔和铅笔的单价比是4：3，20支圆珠笔和21支铅笔共71.5元．圆珠笔的单价是多少？【分析】根据题干，设圆珠笔的单价是4x元，铅笔的单价是3x元，则根据等量关系：圆珠笔的单价×20+铅笔的单价×21=总价钱71.5，据此列出方程解决问题．【解答】解：设圆珠笔的单价是4x元，铅笔的单价是3x元，根据题意可得方程：4x×20+3x×21=71.5，80x+63x=71.5，143x=71.5，x=0.5，0.5×4=2（元），答：圆珠笔的单价是2元．2．一段路程分为上坡和下坡两段，这两段的长度之比是4：3．已知阿奇在上坡时每小时走3千米，下坡时每小时走4.5千米．如果阿奇走完全程用了半小时．请问：这段路程一共有多少千米？【分析】因为一段路程分为上坡和下坡两段，这两段的长度之比是4：3，设这段路程上坡有x千米，那么下坡为x=0.75x千米，根据路程÷速度=时间，列式为，解答即可．【解答】解：设这段路程上坡有x千米，那么下坡为x（即0.75x），6.75x×2=13.513.5x=13.5x=1下坡：1×0.75=0.75（千米）全程：1+0.75=1.75（千米）答：这段路程一共有1.75千米．3．加工一个零件，甲要2分钟，乙要3分钟，丙要4分钟，现有1170个零件，甲、乙、丙三人各加工几个零件，才能使得他们同时完成任务？【分析】把这批零件个数看作单位“1”，依据工作时间=工作总量÷工作效率，求出三人完成任务需要的时间，再根据工作总量=工作时间×工作效率即可解答．【解答】解：1170÷（）=1170÷=1080（分钟）1080×=540（个）1080×=360（个）1080×=270（个）答：甲加工540个零件，乙加工360个零件，丙加工270个才能使得他们同时完成任务．4．有两块重量相同的铜锌合金．第一块合金中铜与锌的重量比是2：5，第二块合金中铜与锌的重量比是1：3．现在把这两块合金合铸成一块大的．求合铸所成的合金中铜与锌的重量之比．【分析】已知第一块合金中铜与锌的重量比是2：5，其中铜占合金重量的，锌占合金重量的；第二块合金中铜与锌的重量比是1：3．其中铜占合金重量的，锌占合金重量的，两块合铸所成的合金中铜占总重量的（），锌占总重量的（），进而求出它们的重量之比．【解答】解：（）：（）==15：41，答：合铸所成的合金中铜与锌的重量之比是15：41．5．（2012•北京模拟）已知甲、乙、丙三个班总人数的比为3：4：2，甲班男、女生的比为5：4，丙班男、女生的比为2：1，而且三个班所有男生和所有女生的比为13：14，请问：（1）乙班男、女生人数的比是多少？（2）如果甲班男生比乙班女生少12人，那么甲、乙、丙三个班各有多少人？【分析】（1）所有男女比为13：14，13+14=27份，甲乙丙人数比为3：4：2=9：12：6，总份数也是（9+12+6）=27份，对应甲班男、女生的比为5：4，丙班男、女生的比为2：1=4：2，从而对应乙班男、女生人数的比是（13﹣5﹣4）：（14﹣4﹣2）；化成最简整数比即可；（2）由于甲班男、女生的比为5：4，乙班男、女生人数的比是4：8，则甲班男生和乙班女生的比为5：8，差为12人，则相差（8﹣5）份，用12÷（8﹣5）可求出1份的人数，甲乙丙人数比为9：12：6，即甲班有9份，乙班有12份，丙班有6份，然后分别求出即可．【解答】解：（1）所有男女比为13：14，13+14=27份，甲乙丙人数比为3：4：2=9：12：6，甲班男女比5：4，丙班男女比2：1=4：2，则乙班男、女比为（13﹣5﹣4）：（14﹣4﹣2）=1：2；（2）乙班男、女比为（13﹣5﹣4）：（14﹣4﹣2）=1：2=4：8，则甲班男生和乙班女生的比为5：8，差为12人，则相差（8﹣5）份，每份：12÷（8﹣5）=4（人）甲班：4×9=36（人）；乙班：4×12=48（人）；丙班：4×6=24（人）；答：乙班男、女生人数的比是1：2，甲班有36人、乙班有48人、丙班有24人．6．甲、乙两包糖的重量比是5：3，如果从甲包取出10克放入乙包后，甲、乙两包糖的重量比变为7：5．请问：这两包糖重量的总和是多少克？【分析】根据“甲、乙两包糖的重量比是5：3”，可以求出甲包糖原来占总量的，再根据“甲乙两包糖的重量比变为7：5”，知道甲包糖后来占总重量的，由此可知两包糖重量的总和的（﹣）是10克，根据已知一个数的几分之几是多少，求这个数．用除法解答即可．【解答】解：10÷（﹣）=10÷=240（克），答：这两包糖重量的总和是240克．7．（2012•北京模拟）小明从甲地到乙地，去时每小时走5千米，回来时每小时走7千米，来回共用4小时，小明去时用了多长时间？【分析】本题可列方程进行解答，设甲地到乙地为x千米，则去时用时为小时，回来是用时小时，一共用了4小时，由此等量关系可列方程．【解答】解：设甲地到乙地为x千米，则可列方程：12x=140x=11故小明去时用时：11÷5=（小时）；答：小明去时用了小时．8．（2012•北京模拟）冬冬从家去学校，平时总是7：50到校，有一天他起晚了，结果晚出发了10分钟，为了不至于迟到，他将速度提高了五分之一，跑步前往学校，最后在7：55到校，请问：冬冬这天是几点出发的？【分析】原来的速度看成单位“1”，现在的速度就是1+=；原来速度与现在的速度比是5：6，总路程相同，那么它们用的时间比就是6：5；因为现在比原来少用了5分钟，则1份就是5分钟，实际用了5×5=25（分），再从7：55先前推算25分钟即可．【解答】解：1+=；原来速度与现在的速度比是5：6，总路程相同，它们用的时间比就是6：5；7时55分﹣7时50分=5分；6﹣5=1（份）；1份是5分钟，所以现在用的时间就是：5×5=25（分）；7时55分﹣25分=7时30分；答：冬冬这天是7时30分出发．9．一项工程，由若干台机器在规定时间内完成．如果增加2台机器，只需用规定时间的就可完成；如果减少2台机器，就要推迟小时才能完成．请问：（1）在规定时间内完成需几台机器？（2）由1台机器去完成这工程，需要多少小时？【分析】（1）根据“如果增加2台机器，只需用规定时间的就可完成”，那么1÷=，那么原有台数：2÷（﹣1）=14台，解决问题．（2）根据题意，如果增加2台机器，则只需用规定时间的就可做完，设原拥有机器x 台，规定的时间t 小时．则有tx=t（x+2），解得x=14，如果减少2台机器，那么就要推迟小时做完，则14t=（x﹣2）（t+），由此可以求出工作时间，然后根据工作效率×工作时间=工作量解答即可．【解答】解：（1）2÷（1÷﹣1）=2÷（﹣1）=2÷=14（台）答：在规定时间内完成需14台机器．（2）设原拥有机器x台，规定的时间t小时．则有tx=t（x+2）解得x=14，又14t=（x﹣2）（t+）14t=12（t+）14t=12t+814t﹣12t=8t=414×4=56（小时）．答：一台机器去完成这项工程需要56小时．10．康师傅加工一批零件，加工720个之后，他的工作效率提高了20%，结果提前4天完成任务；如果康师傅从一开始就把工作效率提高12.5%，那么也可以提前4天完成任务．这批零件共有多少个？【分析】工作效率提高20%，即工效比5：6，时间比6：5，工效提高12.5%，即工效比8：9，时间比9：8，两者的时间差是一样的：6﹣5=1，9﹣8=1，即1份代表4天，所以求出原来的天数，而加工720个，剩下的按原工作效率进行，那么还需要4×6=24天，即720个用36﹣24=12天，原来1天做720÷12=60个．进而求出这批零件的个数．【解答】解：工作效率提高20%，即工效比为5：6，时间比为6：5，工效提高12.5%，即工效比为8：9，时间比9：8，两者的时间差是一样的：6﹣5=1，9﹣8=1，即1份代表4天，所以原来共有4×9=36（天），而加工720个，剩下的按原工作效率进行，还要4×6=24天，即720个用36﹣24=12天，原来1天做720÷12=60（个）．这批零件共有60×36=2160（个）．答：这批零件共有2160个．二、拓展篇11．学校组织体检，收费标准如下：老师每人3元，女生每人2元，男生每人1元，已知老师和女生的人数比为2：9，女生和男生的人数比为3：7，共收体检费945元．那么老师、女生和男生各有多少人？【分析】已知老师和女生的人数比为2：9，女生和男生的人数比为3：7，首先求出老师、女生、男生人数的连比，又知老师每人3元，女生每人2元，男生每人1元，共收体检费945元．那么老师、女生和男生钱数的比是3：2：1，然后根据按比例分配的方法即可求出老师、女生和男生各有多少人．【解答】解：人数的比：老师：女生：男生2：9：21钱数的比：老师：女生：男生3：2：1945÷（3×2+9×2+21×1）=945÷（6+18+21）=945÷45=21（人），老师：21×2=42（人），女生：21×9=189（人），男生：21×21=441（人），答：老师有42人、女生有189人、男生有441人．12．徐福记的巧克力糖每6块包成一小袋，水果糖每15块包成一大袋．现有巧克力糖和水果糖各若干袋，而且巧克力糖比水果糖多30袋．如果巧克力糖的总块数与水果糖的总块数之比为7：10，那么它们各有多少块？【分析】根据每袋的块数×袋数=总块数，已知巧克力糖比水果糖多30袋．巧克力糖的总块数与水果糖的总块数之比为7：10，设水果糖有x袋，据此列比例解答．【解答】解：设水果糖有x袋，6（x+30）：15x=7：1015x×7=6（x+30）×10105x=60（x+30）105x=60x+180045x=1800x=40水果糖：15×40=600（块），巧克力：6×（30+40）=6×70=420（块），答：水果糖有600块、巧克力有420块．13．甲、乙、丙三人合买一台电视机，甲付的钱数等于乙付的钱数的2倍，也等于丙付的钱数的3倍．已知甲比丙多付了680元，请问：（1）甲、乙、丙三人所付的钱数之比是多少？（2）这台电视机售价多少钱？【分析】甲付的钱数等于乙付的钱数的2倍，也等于丙付的钱数的3倍．把乙付出的钱数设为x，甲付出的钱数是2x，丙付出的钱数是2x÷3，列式2x：x：（2x÷3）求出甲乙丙的比即可，已知甲比丙多付了680元，所以680等于2x﹣2x÷3，求出乙付出的钱数，进一步求出甲丙付出的钱数，然后加在一起就是总钱数．【解答】解：（1）乙付出的钱数设为x，甲付出的钱数是2x，丙付出的钱数是2x÷3甲、乙、丙三人所付的钱数之比2x：x：（2x÷3）=2：1：=6：3：2答：甲、乙、丙三人所付的钱数之比是6：3：2．（2）设乙付出的钱数设为x，甲付出的钱数是2x，丙付出的钱数是2x÷3．2x﹣2x÷3=680x=680x=680×x=510甲付出的钱数：2x=2×510=1020（元）丙付出的钱数：2x÷3=2×510÷3=340（元）510+1020+340=1870（元）答：这台电视机售价1870元．14．一把小刀售价3元．如果小明买了这把小刀，那么小明与小强的钱数之比是2：5；如果小强买了这把小刀，那么两人的钱数之比是8：13．小明原来有多少元钱？【分析】根据条件可知，小明买，小明剩下的钱是两人剩下的钱的，如果小强买，那么小明的钱是两人剩下的钱的因此用除法可求出小明剩下的钱占他自己原来的钱的几分之几；把小明原来的钱看作单位“1”，用1减去小明剩下的钱占他自己原来的钱的几分之几，就得出3元就是几分之几，3除以这个几分之几就算出答案．【解答】解法一：小明买，小明剩下的钱是两人剩下的钱的2÷（2+5）=如果小强买，那么小明的钱是两人剩下的钱的8÷（8+13）=所以小明剩下的钱占他自己原来的钱的÷=．所以小明原来的钱有3÷（1﹣）=12元．答：小明原来有12元．解法二：如果小明买，剩下（8+13）÷（2+5）×2=6份，用掉8﹣6=2份．所以小明有3÷2×8=12元．答：小明原来有12元．15．两根粗细相同、材料相同的蜡烛，长度比为29：26，燃烧50分钟后，长蜡烛与短蜡烛的长度比为11：9，那么较长的那根还能燃烧多少分钟？【分析】设每分钟燃烧x，50分钟燃烧50x，长蜡烛29a，短蜡烛26a，用原来的量减去燃烧的量就是剩下的量，表示出剩下量的比，等于11：9，由此列方程进行解答即可．【解答】解：设每分钟燃烧x，50分钟燃烧50x，长蜡烛29a，短蜡烛26a．（29a﹣50x）：（26a﹣50x）=11：911×（26a﹣50x）=（29a﹣50x）×9286a﹣550x=261a﹣450x100x=25ax=0.25a长蜡烛共能燃烧29a÷（0.25a）=116（分钟）116﹣50=66（分钟）答：那么较长的那根还能燃烧66分钟．16．（2008•武汉校级自主招生）某俱乐部男女会员的人数之比是3：2，分为甲、乙、丙三组．已知甲、乙、丙三组的人数比是10：8：7，甲组中男女会员的人数之比是3：1，乙组中男女会员的人数之比是5：3．则丙组中男女会员人数之比是5：9．【分析】根据甲、乙、丙三组人数的比为10：8：7，可设甲组人数为10x，乙组人数为8x，丙组人数为7x，那么三组共有人数为25x；再根据男女会员的人数之比是3：2，可求得男会员是15x人，女会员是10x人；由甲组中男女会员的人数之比是3：1，求得甲组男会员是7.5x人，女会员是2.5x人；乙组中男女会员的人数比是5：3，求得乙组男会员是5x人，女会员是3x人，那么丙组的男会员就是15x﹣7.5x﹣5x=2.5x人，丙组的女会员就是10x﹣2.5x﹣3x=4.5x人，那么丙组男女会员人数之比是2.5x：4.5x=5：9．【解答】解：设甲组为10x人，乙组为8x人，丙组为7x人，则三组共有会员：10x+8x+7x=25x（人），俱乐部有男会员：25x×=15x（人），俱乐部有女会员：25x×=10x（人），甲组有男会员：10x×=7.5x（人），甲组有女会员：10x﹣7.5x=2.5x（人），乙组有男会员：8x×=5x（人），乙组有女会员：8x﹣5x=3x（人），丙组有男会员：15x﹣7.5x﹣5x=2.5x（人），丙组有女会员：10x﹣2.5x﹣3x=4.5x（人），则丙组中男女会员人数之比：2.5x：4.5x=5：9．答：丙组中男女会员人数之比是5：9．故答案为：5：9．17．某次数学竞赛设一、二、三等奖，已知：①甲、乙两校获一等奖的人数比为1：2，但它们一等奖人数占各自获奖总人数的百分数之比为2：5；②甲、乙两校获二等奖人数占两校获奖人数总和的25%，其中乙校是甲校的3.5倍；③甲校三等奖获奖人数占该校获奖人数的80%．请问：乙校获三等奖人数占该校获奖人数的百分比是多少？【分析】根据题干，可得（1）甲、乙两校获一等奖的人数比为1：2，但他们一等奖人数占各自获奖总人数的百分数之比为2：5，所以甲乙两校获奖总人数的比=5：4；则甲校占两校获奖总数的比等于，乙校占两校获奖总数的比等于；（2）甲、乙两校获二等奖的人数总和占两校获奖人数总和的25%，据此再根据乙校获二等奖的人数是甲校获二等奖人数的3.5倍，进行推算，即可求出甲、乙两校二等奖的人数各占该校总人数的百分数；（3）甲校获三等奖的人数占该校获奖人数的80%，占两校获奖总人数的比=×80%=，所以用甲校获奖人数减去二三等奖即可求出一等奖数，从而求出乙校一等奖人数和乙校三等奖人数占总获奖的分率，再根据甲乙两校总人数之比本题可解．【解答】解：（1）甲、乙两校获一等奖的人数比为1：2，但他们一等奖人数占各自获奖总人数的百分数之比为2：5，所以甲乙两校获奖总人数的比=5：4；则甲校占两校获奖总数的比等于，乙校占两校获奖总数的比等于；解答：（2）甲、乙两校获二等奖的人数总和占两校获奖人数总和的25%，且乙校获二等奖的人数是甲校获二等奖人数的3.5倍，所以，甲校获二等奖的人数占总数的比=（1÷4.5）×25%=；乙校获二等奖占获奖总数的25%﹣=（3）甲校获三等奖的人数占该校获奖人数的50%，占两校获奖总人数的比×80%=；所以，甲校获一等奖的人数占两校获奖总数的比=﹣﹣=，那么，乙校获一等奖的人数占两校获奖总人数的百分比=×2=则乙校获三等奖人数占两校获奖人数的百分比=1﹣﹣﹣﹣=则乙校获三等奖人数占该校获奖人数的×=25%答：乙校获三等奖的人数占该校获奖总人数的百分比是25%．18．（2013•青羊区校级模拟）如果单独完成某项工作，那么甲需要24天，乙需要36天，丙需要48天．现在甲先做，乙后做，最后由丙完成．甲、乙工作的天数比为1：2，乙、丙工作天数比为3：5．问：完成这项工作共用了多少天？【分析】由于甲、乙工作的天数比为1：2，乙、丙工作天数比为3：5，则甲：乙：丙=3：6：10，3+6+10=19，由此可知他们分别工作了全部天数的、、，则他们分别完成了全部工程的×x、×、×x，设完成这项工程共用了x天，可得方程：×x+×x+×x=1．【解答】解：甲：乙=1：2，乙：丙=3：5，则甲：乙：丙=3：6：10．设完成这项工程共用了x天，可得方程：×x+×x+×x=1．x+x+x=1，x=1，x=38．答：完成这项工作共用了38天．19．已知猫跑5步的路程与狗跑3步的路程相同，猫跑7步的路程与兔跑5步的路程相同．而猫跑3步的时间与狗跑5步的时间相同，猫跑5步的时间与兔跑7步的时间相同，求猫、狗和兔的速度之比．【分析】以猫为准，猫跑一步的路程，相当于狗的的路程；相当于兔子的的路程，猫跑一步的时间为1，相当于狗一步的，相当兔子一步的；猫的速度为1，则狗的速度为÷=，兔子的速度为÷=；猫、狗和兔的速度之比为1：：．【解答】解：以猫为准，猫跑一步的路程，相当于狗的的路程；相当于兔子的的路程，猫跑一步的时间为1，相当于狗一步的，相当兔子一步的．猫的速度为1，则狗的速度为÷=，兔子的速度为÷=．猫、狗和兔的速度之比为1：：=1225：441：625．答：猫、狗和兔的速度之比是1225：441：625．20．（2013春•高陵县校级月考）星期天早晨，哥哥和弟弟都要到奶奶家去．弟弟先走5分，哥哥出发后25分追上弟弟．如果哥哥每分多走5米，那么出发后20分就可以追上弟弟．弟弟每分走多少米？【分析】弟弟先走五分钟，哥哥出发后25分钟追上了弟弟，则弟弟5+25=30分钟走的路程等于哥哥25分钟走的路程：哥哥的速度是弟弟的倍哥哥每分钟多走5米，那么出发后20分就可以追上弟弟，则弟弟5+20=25分钟走的路程等于哥哥20分钟走的路程：哥哥的速度是弟弟的倍，所以弟弟的速度=米/分．【解答】解：所以弟弟的速度=（米/分）．答：弟弟每分走100米．21．一支解放军部队从驻地乘车赶往某地抗洪抢险，如果行驶1个小时后，将车速提高五分之一，就可比预定时间提前20分钟赶到；如果先按原速度行驶72千米，再将车速提高三分之一，就可比预定时间提前30分钟赶到，问：这支解放军部队一共需要行多少千米？。

小学六年级下册比例练习题

小学六年级下册比例练习题一、填空题1. 在一本书中，每页有4个插图。

如果这本书共有120页，那么一共有__480__个插图。

2. 一辆汽车每天行驶100公里，已知它行驶了5天，那么它行驶的总里程是__500__公里。

3. 某商品原价为60元，打八折出售。

现在它的价格是__48__元。

4. 甲乙两个学校的比例是4:5，如果甲校有160名学生，那么乙校有__200__名学生。

5. 一辆火车以每小时80公里的速度行驶，已知它行驶了3小时，那么它行驶的距离是__240__公里。

二、选择题1. 甲校共有300名学生，其中男生有200人，那么男生的比例是：A. 1:2B. 2:3C. 3:2D. 2:12. 某商品原价为50元，现在打六折出售，那么现价为：A. 50元B. 30元C. 20元D. 10元3. 一根木棍长12米，已知它被等分为6段，那么每段的长度是：A. 2米B. 4米C. 6米D. 8米4. 某商店为了促销，将原价60元的商品降价到48元，降价的折扣比例是：A. 1:4B. 4:5C. 4:3D. 3:45. 一辆汽车以每小时60公里的速度行驶，已知它行驶了5小时，那么它行驶的总距离是：A. 120公里B. 300公里C. 360公里D. 400公里三、解答题1. 甲乙两个班的男女比例都是3:2，如果甲班有30名男生，那么乙班男生的人数是多少？女生的人数呢？2. 一袋米重5公斤，已知小明买了3袋米共计花费75元，那么他买的米的总重量是多少？3. 某种牛奶原价每瓶20元，现在打八折出售，小明花了80元购买了多少瓶牛奶？4. 一条绳子长420厘米，小明按照1:4的比例分成了几段？每段的长度分别是多少？5. 小红学习时每天花费2小时做作业，已知她连续学习了10天，那么她总共花费多少时间在做作业上？以上是小学六年级下册比例练习题，希望对你的学习有所帮助。

六年级数学下册综合算式专项练习题比例的运算

六年级数学下册综合算式专项练习题比例的运算一、综合算式专项练习题1. 衣物的价格和折扣洛洛买了一件衣服，原价是150元。

商家打了8折，你能帮洛洛计算出打折后的价格吗？解答：原价 = 150元折扣 = 8折 = 80%打折后价格 = 原价 ×折扣= 150元 × 80%= 120元答案：洛洛购买该件衣服的价格是120元。

2. 食材的比例混合小明帮妈妈准备食材，需要将大米和红豆按照1:2的比例混合在一起。

如果小明准备200克红豆，请问他需要准备多少克的大米？解答：大米和红豆的比例为：大米∶红豆 = 1∶2已知红豆的重量为200克。

设大米的重量为x克，则有：1∶2 = x克∶200克根据比例关系，可以通过交叉相乘求解出x克的值：1 × 200 =2 × x200 = 2xx = 100答案：小明需要准备100克的大米。

3. 分钱的比例分配小红、小黄、小蓝三个小朋友在妈妈的帮助下分配了120元的口袋钱。

规定分配比例为小红∶小黄∶小蓝 = 3∶4∶5，请问他们各自分到多少钱？解答：小红∶小黄∶小蓝 = 3∶4∶5总金额为120元。

设小红分到的金额为3x元，小黄分到的金额为4x元，小蓝分到的金额为5x元。

根据比例关系，可以列出方程：3x + 4x + 5x = 120解方程可得：12x = 120x = 10小红分到的金额：3x = 3 × 10元 = 30元小黄分到的金额：4x = 4 × 10元 = 40元小蓝分到的金额：5x = 5 × 10元 = 50元答案：小红分到30元，小黄分到40元，小蓝分到50元。

二、比例的运算在数学中，比例运算是一种重要的数学运算，常用于解决实际生活中涉及到比例关系的问题。

上面的综合算式专项练习题旨在帮助六年级学生巩固对比例运算的理解。

比例是指两个或多个数之间的大小关系。

比如在第一个练习题中，我们计算了打折后的衣物价格。

(完整word版)上海市六年级数学应用提高题21题(含答案)

黄气球总价：（18／3）＊2＝12元，花气球总价：（14／2）＊3＝21元。
16.船的顺水速度：60＋20＝80米／分，船的逆水速度：60－20＝40米／分。
因为船的顺水速度与逆水速度的比为2：1，所以顺流与逆流的时间比为1：2。
这条船从上游港口到下游某地的时间为：
3小时30分＊1／（1＋2）＝1小时10分＝7／6小时。（7/6小时＝70分）
因为甲数＋乙数＝乙数×（商＋1）＋2＝478
因为476＝1×476＝2×238＝4×119＝7×68＝14×34＝17×28，所以“商＋1”＜17
当商＝1时，甲数是240，乙数是238，丙数是236，和就是714
当商＝3时，甲数是359，乙数是119，丙数是39，和就是517
当商＝6时，甲数是410，乙数是68，丙数是11，和就是489
21.甲、乙、丙三台车床加工方形和圆形的两种零件，已知甲车床每加工3个零件中有2个是圆形的；乙车床每加工4个零件中有3个是圆形的；丙车床每加工5个零件中有4个是圆形的.这天三台车床共加工了58个圆形零件，而加工的方形零件个数的比为4：3：3，那么这天三台车床共加工零件几个？
答案：
1.因为3小时客车比货车多行42千米，每小时客车比货车多行42/3=14千米，所以客车速度为14/(7-5)*7=49千米/小时，甲乙相距：49×3×2=245千米
4.购买同款汽车，张叔叔分期付款要多付百分之7，李叔叔用现金一次性付款享受九五折优惠，张叔叔比李叔叔多付7200元，这辆汽车原价多少万元？
5.甲数的3分之2与乙数的5分之3相等，甲数与乙数之和为38，甲数是（）。
6.一个长是4分米的圆柱体，把它截成8个小圆柱体所得表面积的总和，比截成5个小圆柱体所得表面积的总和多180平方厘米，原来圆柱体的体积是（）立方厘米。

用比例解决问题练习题

1、张大妈家上个月用了8吨水，水费是12.8元。

李奶奶家用了10吨水。

李奶奶家上个月的水费是多少钱？2、有一批书，如果每包20本，要捆18包。

如果要捆15包，每包多少本？3、小明买了4枝圆珠笔用了6元。

小刚想买3枝同样的圆珠笔，要用多少钱？4、学校小商店有两种圆珠笔。

小明带的钱刚好可以买4枝单价是1.5元的，如果他想都买单价是2元的，可以买多少枝？5、小兰的身高1.5米，她的影长是2.4米。

如果同一时间、同一地点测得一棵树的影子长4米，这棵树有多高？6、工程队修一条水渠，每天工作6小时12天可以完成。

如果工作效率不变，每天工作8小时，多少天可以完成任务？7、我国发射的科学实验人造地球卫星，在空中绕地球运行6周需要10.6小时，运行14周要用多少小时？8、一个晒盐场用100g海水可以晒出3g盐。

照这样计算，如果一块盐田一次放入585000吨海水，可以晒出多少吨盐？多少吨海水可以晒出9吨盐？1、车队向灾区运送一批救灾物资，去时每小时行60km ，6.5小时到达灾区。

回来时每小时行78km ，多长时间能够返回出发地点？2、王叔叔开车从甲地到乙地，前2小时行了100千米。

照这样的速度，从甲地到乙地一共要用3小时，甲乙两地相距多远？3、在一幅比例尺是1：2000000的地图上，量得甲、乙两个城市之间高速公路的距离是5.5厘米。

在另一幅比例尺是1：5000000的地图上，这条公路的图上距离是多少？4、学校举行团体操表演，如果每列25人，要排24列。

如果每列20人，要排多少列？5、一批零件，共4500个，3天加工900个，照这样的工作效率，几天可以加工完？6、某车间要生产一批零件，计划每天生产80个，15天完成。

实际要10天完成，平均每天应生产多少个？7、一道砖墙，砖的层数是90。

如果量得20层砖的高度为45米，这道砖墙高是多少米？1、王叔叔开车从甲地到乙地一共用了3小时，每小时行50千米，返回时每小时行60千米，返回时用了多长时间？2、机器上有两个相互咬全的齿轮，主动轮有100个齿，每分钟转90转。

六年级下册数学用比例解决问题练习题(提高)

用比例解决问题练习题
姓名：学号：
1.小红使用电脑打字，3分钟打了400个字，照这样计算，打1200个字需要多
少分钟？
2.一列火车经过一座大桥，以每秒3米的速度240秒可以完全通过，如果要在
180秒内通过，速度应该是多少？
3.某制衣有限公司用一批布做服装，如果每套服装用布2米，可以做360套；
如果每套服装用布节约0.2米，现在可以做多少套？
4.一种合金内铜和锌的比是2：3，现在有6克锌，必须用多少铜才能配制成符
合要求的合金？
5.读一本书，每天读30页，20天可以读完，如果每天多读10页，多少天可以
读完？
6.生产一批课桌，每天加工20套，44天可以完成，如果工作效率提高10%，可以提前多少天完成？
7.将55
19
的分子、分母同时加上一个相同的数，所得到的新分数约分后是52，求
分子和分母各加上多少？8.中国古代的“黑火药”配制中硝酸钾、硫磺、木炭的比例为15:2:3，今有木炭50千克，要配制“黑火药”1000千克，还需要木炭多少千克？
9.某厂女工人数与全厂人数的比是3:4，若男、女工人各增加
60人，这时女工
与全厂人数的比是2:3，原来全厂共有多少人？10．A 、B 两个仓库储存粮食重量的比是8:7，如果从A 仓库运走4
1，B 仓库运进8吨，则B 仓库的存粮比A 仓库多17吨，A 仓库存粮多少吨？
11.甲、乙两人二月份存钱比是3:4，三月份甲又存钱300元，乙又存钱500元，这时两人存钱比是5:7，甲、乙二月份各存多少钱？。

【数学】人教版六年级下册比例易错提高练习题

【数学】人教版六年级下册比例易错提高练习题一、比例1．下列说法中，不正确的是（）。

A. 2019年二月份是28天。

B. 零件实际长0.2厘米，画在图纸上长30厘米，这幅图的比例尺是1：150。

C. 9时30分，钟面上时针与分针组成的较小夹角是一个钝角。

D. 两个质数的积一定是一个合数。

【答案】 B【解析】【解答】选项A，2019÷4=504……3，2019年是平年，二月份有28天，此题说法正确；选项B，30cm：0.2cm=（30×10）：（0.2×10）=300：2=（300÷2）：（2÷2）=150：1，原题说法错误；选项C，9时30分，钟面上时针与分针组成的较小夹角是一个钝角，此题说法正确；选项D，质数×质数=合数，此题说法正确。

故答案为：B.【分析】闰年和平年的判断方法：当年份是整百年份时，年份能被400整除的是闰年，不能被400整除的是平年；当年份不是整百年份时，年份能被4整除的是闰年，不能被4整除的是平年，闰年全年366天，平年全年365天，平年2月28天，闰年2月29天，据此解答；比例尺=图上距离：实际距离，据此解答；钟面被12个数字平均分成12大格，每个大格所对的圆心角是360°÷12=30°，角的分类：0°＜锐角＜90°，直角=90°，90°＜钝角＜180°，平角=180°，周角=360°，据此解答；一个数，如果除了1和它本身还有别的因数，这样的数叫做合数，两个质数的积一定是一个合数。

2．把线段比例尺改写成数字比例尺为（）。

A. 1：200B. 1：2000C. 1：20000【答案】 C【解析】【解答】2cm：400m=2cm：40000cm=1：20000故答案：C【分析】通过比例尺的关系式：比例尺=图上距离：实际距离，找出线段比例尺中的图上距离和代表的实际距离，写出它们的比并进行化简。

六年级数学下册解决问题解答应用题练习题50(经典版)带答案解析

六年级数学下册解决问题解答应用题练习题50(经典版)带答案解析一、人教六年级下册数学应用题1．甲、乙两个车间工人的工作时间和耗电量如下表。

工作时间/时123456甲车间耗电量/千瓦∙时40 80 120 160 200 240乙车间耗电量/千瓦∙时4085 130170 205 260（2）根据表中的数据，在下图中描出甲车间工人的工作时间与耗电量所对应的点，再把它们按顺序连接起来。

（3）根据图像估计，甲车间工人工作2.5小时，耗电量大约是________千瓦・时。

2．水果店里西瓜个数与哈密瓜个数的比为7：5，如果每天卖哈密瓜40个，西瓜50个，若干天后，哈密瓜正好卖完，西瓜还剩36个。

水果店里原来有西瓜多少个？3．一个圆柱高8厘米，如果它的高增加2厘米，那么它的表面积增加25.12平方厘米，求原来圆柱的表面积是多少平方厘米？4．一个工厂运来一批煤，计划每天烧8吨，可以烧45天。

实际每天节约用煤10%，这样可以多烧多少天？5．小乐家客厅是长方形的，用边长0.6m的方砖铺地，需要200块，如果改用边长0.5m 的方砖铺地，需用多少块？（用比例解）6．以小强家为观测点，量一量，填一填，画一画。

（1）新城大桥在小强家________方向上________m处。

（2）火车站在小强家________偏________（________）°方向上________m处。

（3）电影院在小强家正南方向上1500m处。

请在图中标出电影院的位置。

（4）商店在小强家北偏西45°方向上2000m处。

请在图中标出商店的位置。

7．甲、乙两种商品，成本共2200元，甲商品按20%的利润定价，乙商品按15%的利润定价。

后来都按定价的90%打折出售，结果仍获利131元，甲种商品的成本是多少元？8．一个底面半径是6cm的圆柱形玻璃器皿里装有一部分水，水中浸没着一个高9cm的圆锥形铅锥，当铅锥从水中取出后，水面下降了0.5cm，这个圆锥的底面积是多少平方厘米？9．爸爸想在网上买一个小家电，A店打八五折销售，B店每满200元减30元。