一模二模第18题--翻折

合集下载

上海中考数学第18题分析(翻折类)

上海中考数学第18题分析（一）——翻折类前言，函数图像的变换和几何图像的变换，我们一般归类为这几类：平移、对称、翻折、旋转、伸缩；而恰恰在初三中考试卷的18题位置，对旋转和翻折的考察更是重中之重，通过旋转和翻折的深入研究，充分的展现学生对几何知识的熟练驾驭能力和对平面图形的变换规律把握能力；一、平移、旋转、翻折知识储备1、运动的性质：运动前、后的图形全等（1）平移的性质：①对应点之间的距离等于平移的距离；②对应点之间的距离相等，对应角大小相等，对应线段的长度相等；③平移前、后的图形全等.（2）旋转的性质：①对应点到旋转中心的距离相等；①对应点与旋转中心所连线段的夹角等于旋转角；③旋转前、后的图形全等．（3）翻折的性质：①对应线段的长度相等，对应角的大小相等，对应点到对称轴的距离相等；②翻折前、后的图形全等二、翻折类题型总结及归纳1. 翻折定义：翻折是指把一个图形按某一直线翻折180º后所形成的新的图形的变化。

2. 翻折特征：平面上的两个图形，将其中一个图形沿着一条直线翻折过去，如果它能够与另一个图形重合，那么说这两个图形关于这条直线对称，这条直线就是对称轴。

3. 翻折总结：解这类题抓住翻折前后两个图形是全等的，弄清翻折后不变的要素。

4. 翻折归纳：翻折在三大图形运动中是比较重要的，考查得较多．另外，从运动变化得图形得特殊位置探索出一般的结论或者从中获得解题启示，这种由特殊到一般的思想对我们解决运动变化问题是极为重要的，值得大家留意。

三、翻折类题型解题策略⑴图形翻折之“翻折边长”题型解题方法与策略：1.寻找翻折直线，即对称轴；2.根据翻折情况，画图，画图是解题的关键；3.寻找翻折相等的线段或角度；4.利用翻折并结合题目中的特殊条件解题；5.部分题目注意分类讨论。

⑵图形翻折之“翻折角度”题型解题方法与策略：1.寻找翻折直线，即对称轴；2.根据翻折情况，画图，画图是解题的关键；3.寻找翻折相等的线段或角度；4.利用翻折并结合题目中的特殊条件解题；5.利用好三角形的内角和外角性质。

上海市历年一模二模18题及解题思路汇总

上海市最新一模二模18题及解题思路汇总作者：***2020.1目录1.类型大纲 (3)2.思路梳理 (3)3.常用技巧 (4)1.黄金三角形2.特殊角正切值3.最新例题1.旋转 (5)2.翻折 (15)3.其他 (17)4.函数 (19)类型大纲一、三角形（伴四边形）背景（46套二模卷中，共出现35次，考察率76%）1．图形运动类1.1-旋转类（46套二模卷中，共出现17次，考察率36%）1.2-翻折类（46套二模卷中，共出现15次，考察率32%）2 . 非图形运动类（46套二模卷中，共出现3次，考察率6%）二、圆背景（46套二模卷中，共出现7次，考察率15%）1. 纯圆2. 伴三角形三、函数背景（46套二模卷中，共出现3次，考察率6%）四、其他（46套二模卷中，共出现2次，考察率4%）思路梳理做题三部曲：①分析背景、分析图形②使用尺规作图③由结论出发，分析出为得到结论所需要的其他量，目标清晰后，再将条件代入求解。

1.黄金三角形⑤18.5°：1/3，71.5°：3⑥26.5°：1/2，63.5°：2⑦74°：24/7，16°：7/24⑧18.5°+26.5°=45°旋转类1.如图，矩形ABCD中，AD=1，AB=k，将矩形ABCD绕着点B顺时针旋转90°得到矩形A’B’C’D’，联结A D’，分别交边C D,A’B于E、F.如果AE=√2D’F，那么k= . (2020松江一模）1.如图，矩形ABCD中，AD=1，AB=k，将矩形ABCD绕着点B顺时针旋转90°得到矩形A’B’C’D’，联结A D’，分别交边C D,A’B于E、F.如果AE=√2D’F，那么k= .（2020松江一模）大致思路：1.判断题目类型：三角形+矩形背景，旋转类2.观察图形，首先找相似，图中平行线众多，相似三角形较多。

2024届上海初三一模数学各区填选题(翻折、旋转)

上海市2024届初三一模数学分类汇编—填选题（翻折、旋转）【2024届·宝山区·初三一模·第18题】（本题满分4分）1.已知AC 和BD 是矩形ABCD 的两条对角线，将ADC 沿直线AC 翻折后，点D 落在点E 处，三角形AEC 与矩形的重叠部分是三角形ACF ，联结DE ．如果6AB ，2BF ，那么BDE 的正切值是．【20242.AD 上的点G ，那么AB 的长为．【20243.如图9，在ABC 中，5AB AC ，tan 4B．点M 在边BC 上，3BM ，点N 是射线BA 上一动点，联结MN ，将BMN 沿直线MN 翻折，点B 落在点'B 处，联结'B C ，如果'//B C AB ，那么BN的长是．图9（本题满分4分）4.如图，在ABC 中，90ACB ，4AC ，3BC ，将ABC 绕点B 旋转到DBE 的位置，其中点D 与点A 对应，点E 与点C 对应．如果图中阴影部分的面积为4.5，那么CBE 的正切值是．5.3:2 16.把矩形ABCD 绕点C 按顺时针旋转90 得到矩形'''A B CD ，其中点A 的对应点'A 在BD 的延长线上，如果1AB ，那么BC ．图7（本题满分4分）7.如图，在ABC 中，AB AC ，3tan 4C，点D 为边BC 上的点，联结AD ，将ABD 沿AD 翻折，点B 落在平面内点E 处，边AE 交边BC 于点F ，联结CE ，如果3AF FE ，那么tan BCE 的值为．【20248.在菱形AFE ，点B 落在点的值为．【20249.如图7为边AD 上一点，将ABP 沿BP 翻折，如果点A 的对应点'A 恰好位于ABE 内，那么AP 的取值范围是．第18题图第17题图（本题满分4分）10.如图，在矩形ABCD 中，3AB ，4AD ．点E 在边AD 上，将CDE 沿直线CE 翻折，点D 的对应点为点G ，延长DG 交边AB 于点F ，如果1BF ，那么DE 的长为．【202411.逆时针旋转，点B 落在'B 处，联结'BB 、'CB 【202412.在点A 的长是．（本题满分4分）13.如图，已知在菱形ABCD 中，1cos 3B，将菱形ABCD 绕点A 旋转，点B 、C 、D 分别旋转至点E 、F 、G ，如果点E 恰好落在边BC 上，设EF 交边CD 于点H ，那么CHDH的值是．【202414.DPC 沿着直线。

2019上海数学初三二模第18题汇编

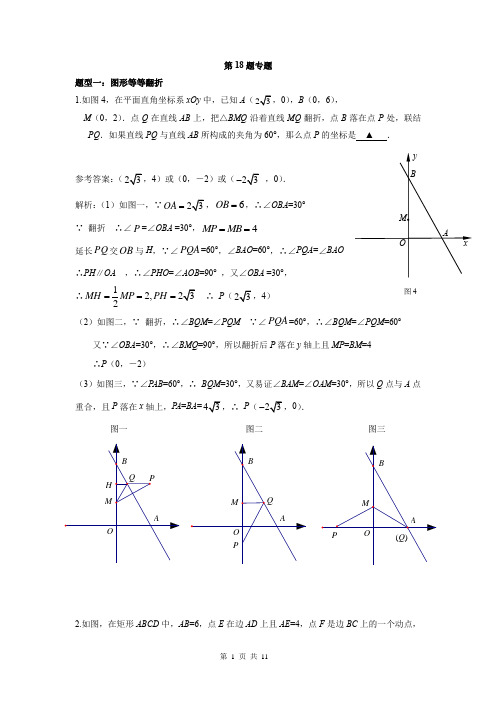
第18题专题题型一：图形等等翻折1.如图4，在平面直角坐标系xOy 中，已知A （23，0），B （0，6），M （0，2）．点Q 在直线AB 上，把△BMQ 沿着直线MQ 翻折，点B 落在点P 处，联结PQ ．如果直线PQ 与直线AB 所构成的夹角为60°，那么点P 的坐标是 ▲ ．参考答案：（23，4）或（0，－2）或（23- ，0）．解析：（1）如图一，∵23OA =，6OB =，∴∠OBA =30° ∵ 翻折 ∴∠P =∠OBA =30°，4MP MB ==延长PQ 交OB 与H ，∵∠PQA =60°，∠BAO =60°，∴∠PQA =∠BAO ∴PH ∥OA ，∴∠PHO =∠AOB =90° ，又∠OBA =30°， ∴12,232MH MP PH === ∴ P （23，4）（2）如图二，∵ 翻折，∴∠BQM =∠PQM ∵∠PQA =60°，∴∠BQM =∠PQM =60°又∵∠OBA =30°，∴∠BMQ =90°，所以翻折后P 落在y 轴上且MP =BM =4 ∴P （0，－2）（3）如图三，∵∠P AB =60°，∴ BQM =30°，又易证∠BAM =∠OAM =30°，所以Q 点与A 点重合，且P 落在x 轴上，P A =BA =43，∴ P （23-，0）．图一图二图三2.如图，在矩形ABCD 中，AB =6，点E 在边AD 上且AE =4，点F 是边BC 上的一个动点，yQ 图4ABOM xQ﹒PQ ABO MP(Q )ABOMH PQMOB A将四边形ABFE 沿EF 翻折，A 、B 的对应点A 1、B 1与点C 在同一直线上，A 1B 1与边AD 交于点G ，如果DG =3，那么BF 的长为 ▲ ．参考答案：658-解析：易证1EGA CGD △∽△，∴11AG A E GD DC=，∴12A E =，∴ EG =25 ∴BC =AD =725+，设BF =x ，则1,725FB x FC x ==+- 易证1FCB CGD △∽△，∴1FB FCDC GC=，GC =35，∴1658FB =-，即658FB =-3.如图，在△ABC 中，AB = AC = 5，25BC = ，D 为边AC 上一点（点D 与点A 、C 不重合）．将△ABC 沿直线BD 翻折，使点A 落在点E 处，联结CE ．如果CE // AB ，那么AD ︰CD =_____参考答案：5：6解析：过A 作AH ⊥BC ，∵AC =AB ，∴ BH=5，过C 作CF ⊥AB ，5cos 5BF BH ABC BC AB ===∠，∴ BF =2，AF =3，C F=4，∵CE // AB ，∴四边形ABCE 为梯形，又因为翻折，所以AB =BE ，所以BE =AC ，所以梯形ABCE 为等腰梯形，所以OA =OB ，C第18题图ABDEABC（第18题图）OE =OC ，过O 作OP ⊥AB ，所以AP =52，因为OP ∥CF ，所以AO AP AC AF =，所以AO =256，OC =OE =56，因为CE // AB ，∴ EC COAB AO=，∴ EC =1，因为翻折，所以DAB DEB =∠∠，又因为CE // AB ，所以DAB ECD =∠∠，所以DEB ECD =∠∠，又∠EDC =∠EDC ，所以△DEO ∽△DCO ，所以56ED EO DC EC ==，又ED =AD ，所以AD ：DC =5:6题型二：图形等等旋转4.如图4，在ABC △中，已知AB AC =，30BAC ∠=︒，将ABC △绕着点A 逆时针旋转30︒，记点C 的对应点为点D ，AD 、BC 的延长线相交于点E .如果线段DE 的长为2，那么边AB 的长为．参考答案．62+解析：如图，过点D 作DH ⊥CE ，∵AB AC =，30BAC ∠=︒∴ ∠ABC =∠ACB =75°，∵ 旋转，∴ ∠CAD =30°，∠ACD =∠ADC =75° ∴∠DCH =30°，∠DEC =45°，∵DE =2，∴ DH =HE =1，∴ CD =2，CH =3 ∴ CE =3+1，∵ ∠E =∠E ，∠DCH =∠CAD =30°，∴ △CDE ∽△ACE ∴CD DEAC CE=，∴ AC =62+，∴ AB =62+BOEDABCH5.如图，在Rt △ABC 中，∠ACB =90°，AB =6，cosB =23，先将△ACB 绕着顶点C 顺时针旋转90°，然后再将旋转后的三角形进行放大或缩小得到△A'CB'（点A'、C 、B'的对应点分别是点A 、C 、B ），联结A'A 、B'B ，如果△AA'B 和△AA'B'相似，那么A C '的长是 ▲ ．参考答案：355-解析：∵∠ACB =90°，AB =6，cosB =23，∴ BC =4，AC =25，∵因为旋转，∴ 1=ABC B ∠∠又∵△AA'B 和△AA'B'相似，∴11BAA CAA =∠∠，过B 作BD ∥AC ，延长1AA 交BD 于点D ，则∠D =1CAA ∠，∴∠D =1BAA ∠，∴ BD =AB =6，因为BD ∥AC ，所以11BA BD AC A C= 即64=25ACAC-，∴AC =355-6.如图3，在ABC ∆中，5==AC AB ，8=BC ，将ABC ∆绕着点C 旋转，点B A 、的对应点分别是点'A 、'B ，若点'B 恰好在线段'AA 的延长线上，则'AA 的长等于 ▲ ．参考答案：145解析：过A 作AE ⊥BC ，所以BE =4,AE =3,因为旋转，所以'8,'5B C BC AC A C ===='B B=∠∠，过C作'CH AA ⊥，3sin 'sin '5CH B B CB ===，所以245CH =，所以2275AH AC CH =-=，所以'145AA =ACBB C D B 1A 1A图3BCH A'B'ABCE7.如图3，在ABC ∆中，90ACB ∠=︒，3sin 5B =，将ABC ∆绕顶点C 顺时针旋转，得到11A B C ∆ ，点A 、B 分别与点1A 、1B 对应，边11A B 分别交边AB 、BC 于点D 、E ，如果点E 是边11A B 的中点，那么1BDB C= ▲ ．【参考答案】35.因为在ABC ∆中，90ACB ∠=︒，3sin 5B =，所以设3AC x =，则5AB x =；4BC x =因为11A B C ∆由将ABC ∆绕顶点C 顺时针旋转得到，所以1190ACB ∠=︒,1B B ∠=∠ 又因为点E 是边11A B 的中点，所以1111115222A EB E CE A B AB x ===== 所以11CEB B ∠=∠;所以1CEB B ∠=∠;所以1//BD B C ;所以11BDB B ∠=∠; 所以1BDB B ∠=∠ 所以542DE BE x x ==-所以15432552x xBD BEB C CEx -===.8.如图，已知Rt △ABC 中，∠ACB=90°，AC =8，BC =6．将△ABC 绕点B 旋转得到△DBE ，点A 的对应点D 落在射线BC 上．直线AC 交DE 于点F ，那么CF 的长为________．【参考答案】3.根据题意得：22228610BD AB AC BC ==+=+=;1064DC DB BC \=-=-=Q 旋转，所以=A D 行，又Q 90ACBDCF ??o\ ACB V ∽DCF V \43DC AC CF BC ==, 3CF \=.9.如图5，矩形ABCD ，AD =a ，将矩形ABCD 绕着顶点B 顺时针旋转，得到矩形EBGF ，顶点A 、D 、C 分别与点E 、F 、G 对应（点D 与点F 不重合）．如果点D 、E 、F 在同一条直线上，那么线段DF 的长是 ▲ ．（用含a 的代数式表示）【参考答案】2a .根据题意，由旋转得到90BEF DAB ??o矩形对角线BD BF = 所以BDF V 是一个等腰三角形所以DE EF a ==（等腰三角形三线合一）所以2DF a =.10.如图7，AD 是△的中线，点E 在边AB 上，且DE ⊥AD ，将△BDE 绕着点D 旋转，使得点B 与点C 重合，点E 落在点F 处，联结AF 交BC 于点G ，如果52AE BE ，那么GFAB的值等于 ▲ ．【参考答案】1063.ABC E 图7联结AF ;因为CFD △由BDE ∆绕点D 旋转得到所以BDE BDE ∆∆≌ 所以DE FD =;B DCF ∠=∠;27CF AB = 所以//AB CF所以27FG AG =;所以29FG AF =在ADE ∆和ADF ∆中90AD AD ADE ADF DE FD o=⎧⎪∠=∠=⎨⎪=⎩；得到ADE ADF ∆∆≌ 所以AE AF =设5AE x =；则5AF x =;7AB x =;109xFG = 所以1063FG AB =.题型三：其他题型：11.我们把满足某种条件的所有点组成的图形，叫做符合这个条件的点的轨迹．如图6，在Rt △ABC 中，∠C =90°，AC =8，BC =12，动点P 从点A 开始沿射线AC 方向以1个单位/秒的速度向点C 运动，动点Q 从点C 开始沿射线CB 方向以2个单位/秒的速度向点B 运动，P 、Q 两点分别从点A 、C 同时出发，当其中一点到达端点时，另一点也随之停止运动，在整个运动过程中，线段PQ 的中点M 运动的轨迹长为．参考答案：35CBAP QM 图6G E DB解析：当t =0时，M 在AC 中点处，即1M 处，当t=6时，Q 运动到B ，此时P 在线段AC 上，且AP=6，CP=2，M 在BP 中点处，即2M 处，过2M 作2M H AC ⊥，交AC 于H ，则26M H =，HP=1，∴ 1HM =3，∴221221()()35M M M H HM =+=，即轨迹长为3512.如图3，点M 的坐标为)2,3(，点P 从原点O 出发，以每秒1个单位的速度沿y 轴向上移动，同时过点P 的直线l 也随之上下平移，且直线l 与直线x y -=平行，如果点M 关于直线l 的对称点落在坐标轴上，如果点P 的移动时间为t 秒，那么t 的值可以是．参考答案：3或2（任意一个都可以）解析：设M 关于直线l 的对称点为点N ，直线l 与x 轴交于点P ，与y 轴交于点F ，易知45?FPO PFO ==∠∠（1）当对称点落在x 轴上时，直线l 垂直平分线段MN ，所以45?MNP PN PM ==∠， ∴45?NMP =∠，∴=90?NPM ∠，∴ P （3,0），∴ OF =OP =3，所以t=3（2）当对称点落在y 轴上时，直线l 垂直平分线段MN ，所以45?,FN=FM MNF =∠ ∴45?NMF =∠，∴ =90?NFM ∠，∴ F （0,2），所以OF =2,所以t =213.如图，在矩形ABCD 中，过点A 的圆O 交边AB 于点E ，交边AD 于点F ，已知AD =5，AE =2，AF =4.如果以点D 为圆心，r 为半径的圆D 与圆O 有两个公共点，那么r 的取值范围是 ▲ .参考答案：105105r -<<+解析：过O 作OH ⊥AD ，OG ⊥AB ，∴AH =2,AG =1，易知四边形AGOH 为矩形，所以OH =1,所以AO =5，易知HD =3，所以OD =10，连接OD 并延长DO ，交圆O 于点P ,Q ，所以PD=105-，DQ=10+5，所以105105r -<<+OFPl N MOPFl NMABCDE F （第18题图）14.定义：如果P是圆O所在平面内的一点，Q是射线OP上一点，且线段OP、OQ的比例中项等于圆O的半径，那么我们称点P与点Q为这个圆的一对反演点。

2019-2021年上海各区数学中考一模压轴题分类汇编18题-图形的翻折含详解

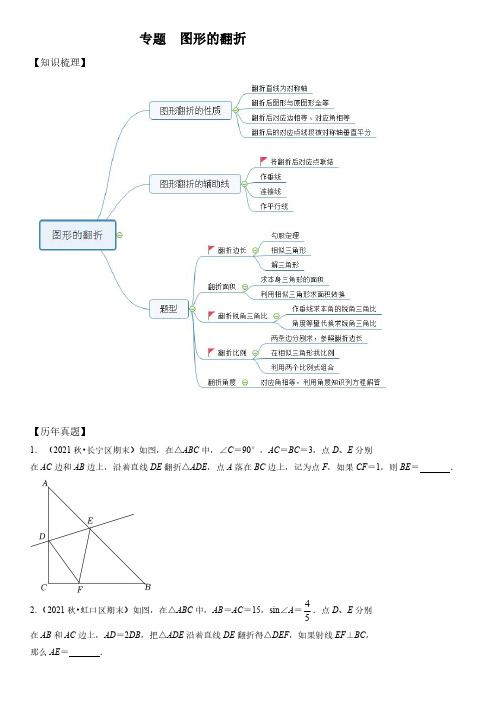
专题图形的翻折【知识梳理】【历年真题】1．（2021秋•长宁区期末）如图，在△ABC中，∠C＝90°，AC＝BC＝3，点D、E分别在AC边和AB边上，沿着直线DE翻折△ADE，点A落在BC边上，记为点F，如果CF＝1，则BE＝．2．（2021秋•虹口区期末）如图，在△ABC中，AB＝AC＝15，sin∠A＝45．点D、E分别在AB和AC边上，AD＝2DB，把△ADE沿着直线DE翻折得△DEF，如果射线EF⊥BC，那么AE＝．3．（2021秋•金山区期末）在△ABC中，AB＝AC＝10，sin B＝45，E是BC上一点，把△ABE沿直线AE翻折后，点B落在点P处，如果PE∥AC，那么BE＝．4．（2021秋•闵行区期末）如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，点P是AC边上一点，将△ACB沿着过点P的一条直线翻折，使得点A落在边AB上的点Q处，联结PQ，如果∠CQB＝APQ，那么AQ的长为．5．（2021秋•徐汇区期末）如图，在Rt△ABC中，∠CAB＝90°，AB＝AC，点D为斜边BC上一点，且BD＝3CD，将△ABD沿直线AD翻折，点B的对应点为B′，则sin∠CB′D＝．6．（2021秋•崇明区期末）如图所示，在三角形纸片ABC中，AB＝9，BC＝6，∠ACB＝2∠A，如果将△ABC沿过顶点C的直线折叠，使点B落在边AC上的点D处，折痕为CM，那么cos∠DMA＝．7．（2021秋•奉贤区期末）如图，在Rt△ABC中，∠C＝90°，sin B＝35．D是边BC的中点，点E在边AB上，将△BDE沿直线DE翻折，使得点B落在同一平面内的点F处．如果线段FD交边AB于点G，当FD⊥AB时，AE：BE的值为．8．（2020秋•崇明区期末）在△ABC中，AB＝2，∠B＝45°，∠C＝60°．点D为线段AB的中点，点E在边AC上，连接DE，沿直线DE将△ADE折叠得到△A′DE．连接AA′，当A′E⊥AC时，则线段AA′的长为．9．（2020秋•长宁区期末17）如图，矩形ABCD沿对角线BD翻折后，点C落在点E处．联结CE交边AD于点F．如果DF＝1，BC＝4，那么AE的长等于．10．（2020秋•虹口区期末）如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8．D是BC的中点，点E在边AB上，将△BDE沿直线DE翻折，使得点B落在同一平面内的点B'处，线段B'D交边AB于点F，联结AB'．当△AB'F是直角三角形时，BE的长为．11．（2020秋•松江区期末）如图，已知矩形纸片ABCD，点E在边AB上，且BE＝1，将△CBE沿直线CE翻折，使点B落在对角线AC上的点F处，联结DF，如果点D、F、E在同一直线上，则线段AE的长为．12．（2020秋•普陀区期末）如图，在▱ABCD中，点E在边BC上，将△ABE沿着直线AE 翻折得到△AFE，点B的对应点F恰好落在线段DE上，线段AF的延长线交边CD于点G，如果BE：EC＝3：2，那么AF：FG的值等于．13．（2019秋•虹口区期末）如图，在等腰梯形ABCD中，AD∥BC，sin C＝45，AB＝9，AD＝6，点E、F分别在边AB、BC上，联结EF，将△BEF沿着EF所在直线翻折，使BF的对应线段B′F经过顶点A，B′F交对角线BD于点P，当B′F⊥AB时，AP的长为．14．（2019秋•青浦区期末）已知，在矩形纸片ABCD中，AB＝5cm，点E、F分别是边AB、CD的中点，折叠矩形纸片ABCD，折痕BM交AD边于点M，在折叠的过程中，如果点A恰好落在线段EF上，那么边AD的长至少是cm．15．（2019秋•闵行区期末）如图，在等腰△ABC中，AB＝AC＝4，BC＝6，点D在底边BC 上，且∠DAC＝∠ACD，将△ACD沿着AD所在直线翻折，使得点C落到点E处，联结BE，那么BE的长为．16．（2019秋•杨浦区期末）在Rt△ABC中，∠A＝90°，AC＝4，AB＝a，将△ABC沿着斜边BC翻折，点A落在点A1处，点D、E分别为边AC、BC的中点，联结DE并延长交A1B 所在直线于点F，联结A1E，如果△A1EF为直角三角形时，那么a＝．17．（2019秋•崇明区期末）如图，在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，D是AC 的中点，点E在边AB上，将△ADE沿DE翻折，使得点A落在点A′处，当A′E⊥AB时，则A′A＝．18．（2019秋•静安区期末）如图，有一菱形纸片ABCD，∠A＝60°，将该菱形纸片折叠，使点A恰好与CD的中点E重合，折痕为FG，点F、G分别在边AB、AD上，联结EF，那么cos∠EFB的值为．专题图形的翻折【历年真题】2．（2021秋•长宁区期末）如图，在△ABC 中，∠C ＝90°，AC ＝BC ＝3，点D 、E 分别在AC 边和AB 边上，沿着直线DE 翻折△ADE ，点A 落在BC 边上，记为点F ，如果CF ＝1，则BE ＝724．【考点】翻折变换（折叠问题）；等腰直角三角形．【专题】平移、旋转与对称；几何直观．【分析】过F 作FG ⊥AB 于点G ．先求出AB ＝3，BF ＝3﹣1＝2．则FG ＝GB ＝BF ，所以AG ＝AB﹣BG ＝﹣＝，设AE ＝x ，则EF ＝x ，EG ＝﹣x ，在Rt △EGF 中，EG 2+FG 2＝EF 2，利用勾股定理解列出（﹣x ）2+（）2＝x 2，解得x ＝524，即求出BE ．【解答】解：过F 作FG ⊥AB 于点G ．∵∠C ＝90°，AC ＝BC ＝3，CF ＝1，∴AB ＝，BF ＝3﹣1＝2．∴FG ＝GB ＝BF ＝，∴AG ＝AB ﹣BG ＝＝，设AE ＝x ，则EF ＝x ，EG ＝﹣x ，在Rt △EGF 中，EG 2+FG 2＝EF 2，即（﹣x ）2+）2＝x 2，解得x ＝524，∴BE ＝AB ﹣AE ＝﹣524＝724．故答案为：724．【点评】本题考查翻折变换，等腰直角三角形的性质等知识，解题的关键是熟练运用勾股定理，属于中考常考题型．2．（2021秋•虹口区期末）如图，在△ABC 中，AB ＝AC ＝15，sin ∠A ＝45．点D 、E 分别在AB 和AC 边上，AD ＝2DB ，把△ADE 沿着直线DE 翻折得△DEF ，如果射线EF ⊥BC ，那么AE ＝510-．【考点】翻折变换（折叠问题）；解直角三角形；等腰三角形的性质．【专题】推理填空题；等腰三角形与直角三角形；平移、旋转与对称；运算能力；推理能力．【分析】先根据折叠得到DE 平分∠AEF ，根据角平分线过D 作∠AEF 两边垂线即可．【解答】过D 作DM ⊥AC 于M ，过B 作BH ⊥AC 于H∵AB ＝AC ＝15，4sin 5A ∠=，AD ＝2DB ∴AD ＝10，DM ＝8，AM=6，BH=12，AH=9，∴CH ＝AC-CH=6∴22tan 2,5BHC BC BH CH CH∠===+过D 作DG ⊥EF 交EF 于N，交AC 于G∵把△ADE 沿着直线DE 翻折得△DEF∴DE 平分∠AEF，∴DM＝DN＝8，EM＝EN，∵EF⊥BC 于点G，∴DH∥BC，∴23DG AD BC AB ==，∠C＝∠NHE，∴23DG BC ==∴8NG DG DN =-=-∵tan tan 2EN C NGE NG∠=∠==∴216EM EN NG ===∴10AE AM EM =+=故答案为：10-【点评】本题难度比较大，综合考查折叠的性质、三角函数、相似三角形的性质与判定，解题的关键是由折叠得到角平分线再根据角平分线作垂线．3．（2021秋•金山区期末）在△ABC 中，AB＝AC＝10，sinB＝45，E 是BC 上一点，把△ABE 沿直线AE 翻折后，点B 落在点P 处，如果PE∥AC，那么BE＝2．【考点】翻折变换（折叠问题）；解直角三角形；平行线的性质；等腰三角形的判定与性质．【专题】等腰三角形与直角三角形；平移、旋转与对称；解直角三角形及其应用；几何直观；应用意识．【分析】过A 作AD ⊥BC 于D ，设AP 交BC 于F ，根据AB ＝AC ＝10，sin B ＝45，AD ⊥BC ，可得AD ＝8，BD ＝CD ＝6，BC ＝12，由△ABE 沿直线AE 翻折后，点B 落在点P 处，即得∠P ＝∠B ＝∠C ，∠BAE ＝∠PAE ，而PE ∥AC ，有∠P ＝∠FAC ，可证得∠AEC ＝∠EAC ，CE ＝AC ＝10，即得BE ＝BC ﹣CE ＝2．【解答】解：过A 作AD ⊥BC 于D ，设AP 交BC 于F ，如图：∵AB ＝AC ＝10，sin B ＝45，AD ⊥BC ，∴4105AD AD AB ==，∴AD ＝8，∴BD ＝CD ＝6，∴BC ＝12，∵△ABE 沿直线AE 翻折后，点B 落在点P 处，∴∠P ＝∠B ＝∠C ，∠BAE ＝∠PAE ，∵PE ∥AC ，∴∠P ＝∠FAC ，∴∠B ＝∠FAC ，∴∠B +∠BAE ＝∠FAC +∠PAE ，即∠AEC ＝∠EAC ，∴CE ＝AC ＝10，∴BE ＝BC ﹣CE ＝2，故答案为：2．【点评】本题考查等腰三角形中的折叠问题，解题的关键是掌握折叠的性质，能熟练运用锐角三角函数解直角三角形．4．（2021秋•闵行区期末）如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，点P是AC边上一点，将△ACB沿着过点P的一条直线翻折，使得点A落在边AB上的点Q处，联结PQ，如果∠CQB＝APQ，那么AQ的长为395．【考点】相似三角形的判定与性质；解直角三角形；勾股定理；翻折变换（折叠问题）．【专题】几何综合题；压轴题；推理填空题；运算能力；推理能力．【分析】利用三角形内角和180°，以及平角180度，推导出PQ平分∠AQC，设CP＝x，则AP＝PQ＝8﹣x，利用三角形等面积法和相似三角形性质求出AQ的长，再利用相似三角形的性质构建方程即可解决问题．【解答】解：根据题意如图所示：在Rt△ABC中，∠C＝90°，∵AC＝8，BC＝6，∴AB＝10，根据折叠的性质可知∠A＝∠PQA，∵∠AQP+∠A+∠APQ＝180°，∠AQP+∠PQC+∠CQB＝180°，∵∠CQB＝∠APQ，∴∠A＝∠AQP＝∠PQC，∴PQ平分∠AQC，设CP＝x，则AP＝PQ＝8﹣x，如图，过点C作CD⊥AB于点D，PE⊥AB于点E，∴S △ABC ＝12⨯AC •BC ＝12⨯AB •CD ，∴10CD ＝6×8，∴CD ＝245，∵CD ⊥AB ，PE ⊥AB ，∴PE ∥CD ，∴△APE ∽△ACD ，∴AP PE AC CD =，∴82485x PE -=，∴PE ＝35（8﹣x ），∴AE=45（8﹣x ），∴AQ ＝2AE ＝85（8﹣x ），∵∠PCQ ＝∠QCA ，∠PQC ＝∠A ∴△PCQ ∽△QCA ，∴CQ CP PQ AC CQ AQ==，∴CQ，88(8)5x x -=-，∴258x =，∴AQ ＝85（8﹣x ）＝395．故答案为：395．【点评】本题属于几何综合题，是中考填空题的压轴题，主要考查了翻折的性质、解直角三角形、相似三角形的判定和性质、勾股定理，三角形等面积法，综合性较强，熟练解直角三角形中线段问题是解题的捷径．5．（2021秋•徐汇区期末）如图，在Rt △ABC 中，∠CAB ＝90°，AB ＝AC ，点D 为斜边BC 上一点，且BD ＝3CD ，将△ABD 沿直线AD 翻折，点B 的对应点为B ′，则sin ∠CB ′D ＝1010．【考点】翻折变换（折叠问题）；平行线分线段成比例；解直角三角形；等腰直角三角形．【专题】平移、旋转与对称；解直角三角形及其应用；运算能力；推理能力．【分析】过点D 作DE ⊥AB 于点E ，由折叠的性质得出AB ＝AB '，∠BAD ＝∠B 'AD ，证出∠CB 'D ＝∠CAD ，由平行线的性质得出∠CAD ＝∠ADE ＝∠CB 'D ，13CD AE BD BE ==，设AE ＝a ，则DE ＝3a ，求出AD＝，由锐角三角函数的定义可得出答案．【解答】解：过点D 作DE ⊥AB 于点E ，∵将△ABD 沿直线AD 翻折，∴AB ＝AB '，∠BAD ＝∠B 'AD ，∵AB ＝AC ，∴AC ＝AB '，∴∠AB 'C ＝∠ACB '，设∠B 'AC ＝x ，∠CB 'D ＝α，∠CAD ＝β，∵AB ＝AC ，∠CAB ＝90°，∴∠B ＝∠ACB ＝∠AB 'D ＝45°，∴2（α+45°）+x ＝180°，∴2α＝90°﹣x ，又∵∠B 'AD +∠BAD ＝∠B 'AC +∠CAB ，∴2（x +β）＝90°+x ，∴2β＝90°﹣x ，∴α＝β，∴∠CB 'D ＝∠CAD ，∵CD ⊥AB ，DE ⊥AB ，∴CA ∥DE ，∴∠CAD ＝∠ADE ＝∠CB 'D ，13CD AE BD BE ==，∵BE ＝DE ，∴13AE BE =，设AE ＝a ，则DE ＝3a ，∴AD =，∴sin ∠CB ′D ＝sin ∠ADE ＝AE DE =＝10．故答案为：1010．【点评】本题考查了折叠的性质，等腰直角三角形的性质，平分线分线段成比例定理，锐角三角函数的定义，熟练掌握折叠的性质是解题的关键．6．（2021秋•崇明区期末）如图所示，在三角形纸片ABC 中，AB ＝9，BC ＝6，∠ACB ＝2∠A ，如果将△ABC 沿过顶点C 的直线折叠，使点B 落在边AC 上的点D 处，折痕为CM ，那么cos ∠DMA ＝3132．【考点】翻折变换（折叠问题）；解直角三角形．【专题】等腰三角形与直角三角形；平移、旋转与对称；运算能力；推理能力．【分析】由折叠的性质可知，CB ＝CD ＝6，∠BCM ＝∠ACM ，证明△BCM ∽△BAC ，由相似三角形的性质得出CD BM CM AB BC AC==，求出BM 和AC 的长，过点D 作DN ⊥AM 于点N ，设MN ＝x ，则AN ＝5﹣x ，由勾股定理求出x ，根据锐角三角函数的定义可得出答案．【解答】解：由折叠的性质可知，CB ＝CD ＝6，∠BCM ＝∠ACM，∵∠ACB ＝2∠A ，∴∠BCM ＝∠A ，∵∠B ＝∠B ，∴△BCM ∽△BAC ，∴CD BM CM AB BC AC ==，∴696BM =，∴BM ＝4，∴AM ＝CM ＝5，∴659AC =，∴AC ＝152，∴AD ＝AC ﹣CD ＝152﹣6＝32，过点D 作DN ⊥AM 于点N ，设MN ＝x ，则AN ＝5﹣x ，∴22223((5)42x x +-=-，解得318x =，∴cos ∠DMA ＝31318432MN DM ==．故答案为：3132．【点评】本题考查了折叠的性质，相似三角形的判定与性质，勾股定理，解直角三角形，证明△BCM ∽△BAC 是解题的关键．7．（2021秋•奉贤区期末）如图，在Rt△ABC中，∠C＝90°，sin B＝35．D是边BC的中点，点E在边AB上，将△BDE沿直线DE翻折，使得点B落在同一平面内的点F处．如果线段FD交边AB于点G，当FD⊥AB时，AE：BE的值为4．【考点】平行线分线段成比例；解直角三角形；翻折变换（折叠问题）．【专题】解直角三角形及其应用；推理能力．【分析】如图，过B点作BH∥DE交GD的延长线于H，如图，利用正弦的定义得到sin B＝35DGBD=，则设DG＝3x，BD＝5x，所以BG＝4x，再根据折叠的性质和平行线的性质得到∠H＝∠DBH，所以DH＝DB＝5x，接着根据平行线分线段成比例定理得到35GE DGBE DH==，则BE＝52x，然后证明△BDG∽△BAC，利用相似比得到BA＝252x，最后计算AE：BE的值．【解答】解：如图，过B点作BH∥DE交GD的延长线于H，如图，∵FD⊥AB，∴∠DGB＝90°，∵sin B＝35DGBD=，∴设DG＝3x，BD＝5x，∴BG4x，∵△BDE沿直线DE翻折得到△FDE，∴∠BDE＝∠FDE，∵DE∥BH，∴∠FDE＝∠H，∠BDE＝∠DBH，∴∠H＝∠DBH，∴DH＝DB＝5x，∵DE∥BH，∴35 GE DGBE DH==，∴BE＝58×4x＝52x，∵∠BGD＝∠C＝90°，∠DBG＝∠ABD，∴△BDG∽△BAC，∴BD BGBA BC=，即5410x xBA x=，∴BA＝252x，∴AE＝AB﹣BE＝252x﹣52x＝10x，∴AE：BE＝10x：52x＝4．故答案为：4．【点评】本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．也考查了折叠的性质和解直角三角形．8．（2020秋•崇明区期末）在△ABC中，AB＝2，∠B＝45°，∠C＝60°．点D为线段AB的中点，点E在边AC上，连接DE，沿直线DE将△ADE折叠得到△A′DE．连接AA′，当A′E⊥AC时，则线段AA′的长为26．【考点】翻折变换（折叠问题）．【专题】等腰三角形与直角三角形；平移、旋转与对称；图形的相似；解直角三角形及其应用；运算能力；推理能力．【分析】画出相应的图形，结合图形通过作高构造直角三角形，求出AM＝BM＝4，进而求出AC，再利用相似三角形的性质和判定求出AE，根据对称在Rt△AEF中求出AF即可．【解答】解：如图，过点A作AM⊥BC，垂足为M，在Rt△ABM中，∠B＝45°，AB＝2，∴AM＝BM＝AB•sin∠B＝4，在Rt△ACM中，AM＝4，∠C＝60°，∴AC＝AM4=sin C sin60∠833，又∵A′E⊥AC，∴∠A′EC＝90°，由折叠得∠AED＝∠A′ED＝12（180°﹣90°）＝45°，AA′⊥DE，∵∠AED＝45°＝∠B，∠DAE＝∠CAB，∴△DAE∽△CAB，∴AE AD=AB DC，∵点D为线段AB的中点，∴AD＝BD＝12AB＝22，AE2242833AE＝3，在Rt△AEF中，AF＝EF＝AE•sin∠AED＝3×226，∴AA′＝2AF＝6，故答案为：6．【点评】本题考查轴对称的性质，相似三角形的判定和性质，解直角三角形，掌握轴对称、相似三角形的性质以及解直角三角形是解决问题的关键．9．（2020秋•长宁区期末17）如图，矩形ABCD 沿对角线BD 翻折后，点C 落在点E 处．联结CE 交边AD 于点F ．如果DF ＝1，BC ＝4，那么AE 的长等于655．【考点】翻折变换（折叠问题）；矩形的性质．【专题】矩形菱形正方形；推理能力．【分析】首先根据题意得到EG ＝CG ，CE ⊥BD ，证明△CDF ∽△BCD 和△CDG ∽△BDC ，可计算CD 和CG 的长，再证明△EFD ∽△AED ，可得AE 的长．【解答】解：由折叠得：CE ⊥BD ，CG ＝EG ，∴∠DGF ＝90°，∴∠DFG +∠FDG ＝90°，∵四边形ABCD 是矩形，∴∠ADC ＝∠BCD ＝90°，∴∠ADG +∠CDG ＝90°，∴∠CDG ＝∠DFG ，∵∠CDF ＝∠BCD ＝90°，∴△CDF ∽△BCD ，∴CD DF =BC CD，∵AB ＝4，DF ＝1，∴CD 1=4CD，∴CD ＝2，由勾股定理得：CF ＝221+2=5，BD 222+45，同理得：△CDG∽△BDC，∴CD CG=BD BCCG4，∴CG ＝455，∴CE＝2CG ＝85 5，∴EF＝CE﹣CF ＝855＝355，∵DF1=ED2，ED21==AD42，且∠EDF＝∠AED，∴△EFD∽△AED，∴EF DF=AE DE ，即15=AE2，∴AE【点评】本题主要考查了几何变换中的翻折变换、相似三角形的性质和判定、矩形的性质、勾股定理；熟练掌握翻折变换和矩形的性质，利用相似三角形列比例式是本题的关键．10．（2020秋•虹口区期末）如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8．D是BC的中点，点E在边AB上，将△BDE沿直线DE翻折，使得点B落在同一平面内的点B'处，线段B'D交边AB于点F，联结AB'．当△AB'F是直角三角形时，BE的长为2或40 17．【考点】翻折变换（折叠问题）；相似三角形的判定与性质；勾股定理．【专题】等腰三角形与直角三角形；平移、旋转与对称；运算能力；推理能力．【分析】分两种情况画出图形，①方法一：如图1，当∠AFB′＝90°时，由相似三角形的性质及直角三角形的性质可求出答案；方法二：过点E作EH⊥BC于点H，设EH＝3a，BE＝5a，则BH＝4a，由BF的长列出方程，解方程求出a即可；②方法一如图2，当∠AB′F＝90°时，由相似三角形的性质及直角三角形的性质可求出答案．方法二：过点E作EG⊥BD于点G，设EG＝3a，BG＝4a，BE＝5a，得出9442a a+=，求出a的值则可得出答案．【解答】解：①方法一：如图1，当∠AFB′＝90°时．在Rt △ABC 中，∵AC ＝6，BC ＝8，∴AB 22226810AC BC +=+=，∵D 是BC 的中点，∴BD ＝CD ＝12BC ＝4，∵∠AFB '＝∠BFD ＝90°，∠ACB ＝90°，∴∠DFB ＝∠ACB ，又∵∠DBF ＝∠ABC ，∴△BDF ∽△BAC ，∴BF BD BC AB =，即4810BF =，解得：BF ＝165，设BE ＝B 'E ＝x ，则EF ＝165﹣x ，∵∠B ＝∠FB 'E ，∴sin ∠B ＝sin ∠FB 'E ，∴'AC EF AB B E =，∴166510x x-=，解得x ＝2．∴BE ＝2．方法二：过点E 作EH ⊥BC 于点H ，设EH ＝3a ，BE ＝5a ，则BH ＝4a ，∵将△BDE 沿直线DE 翻折，∴EF ＝3a ，∴BF ＝8a ＝BD •cos ∠B ＝4×45，∴a ＝25，∴BE ＝5a ＝2；②如图2中，当∠AB ′F ＝90°时，连接AD ，作EH ⊥AB ′交AB ′的延长线于H．∵AD ＝AD ，CD ＝DB ′，∴Rt △ADC ≌Rt △ADB ′（HL ），∴AC ＝AB ′＝6，∵将△BDE 沿直线DE 翻折，∴∠B ＝∠DB 'E ，∵AB '⊥DB '，EH ⊥AH ，∴DB '∥EH ，∴∠DB 'E ＝∠B 'EH ，∴∠B ＝∠B 'EH ，∴sin ∠B ＝sin ∠B 'EH ，设BE ＝x ，则B 'H ＝35x ，EH ＝45x ，在Rt △AEH 中，AH 2+EH 2＝AE 2，∴22234(6)()(10)55x x x ++=-，解得x ＝4017，∴BE ＝4017．则BE 的长为2或4017．方法二：过点E 作EG ⊥BD 于点G ，设EG ＝3a ，BG ＝4a ，BE ＝5a ，∴DG ＝EG ×32＝92a ，∵DG +GB ＝DB ，∴9442a a +=，∴a ＝817，∴BE ＝4017．故答案为：2或4017．【点评】本题考查了翻折变换、勾股定理、解直角三角形、相似三角形的判定与性质、全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想解决问题．11．（2020秋•松江区期末）如图，已知矩形纸片ABCD ，点E 在边AB 上，且BE ＝1，将△CBE 沿直线CE 翻折，使点B 落在对角线AC 上的点F 处，联结DF ，如果点D 、F 、E 在同一直线上，则线段AE 的长为152+．【考点】翻折变换（折叠问题）；矩形的性质．【专题】矩形菱形正方形；平移、旋转与对称；运算能力；推理能力．【分析】根据矩形的性质得到AD ＝BC ，∠ADC ＝∠B ＝∠DAE ＝90°，根据折叠的性质得到CF ＝BC ，∠CFE ＝∠B ＝90°，EF ＝BE ＝1，DC ＝DE ，证明△AEF ∽△DEA ，根据相似三角形的性质即可得到结论．【解答】解：∵四边形ABCD 是矩形，∴AD ＝BC ，AB ＝CD ，∠ADC ＝∠B ＝∠DAE ＝90°，∵把△BCE 沿直线CE 对折，使点B 落在对角线AC 上的点F 处，∴CF ＝BC ，∠CFE ＝∠B ＝90°，EF ＝BE ＝1，∠CEB ＝∠CEF ，∵矩形ABCD 中，DC ∥AB ，∴∠DCE ＝∠CEB ，∴∠CEF ＝∠DCE ，∴DC ＝DE ，设AE＝x，则AB＝CD＝DE＝x+1，∵∠AFE＝∠CFD＝90°，∴∠AFE＝∠DAE＝90°，∵∠AEF＝∠DEA，∴△AEF∽△DEA，∴AF DEEF AE=，∴11x xx+=，解得x＝152+或x＝152（舍去），∴AE＝12．故答案为：15 2．【点评】本题考查了翻折变换（折叠问题），平行线的性质，相似三角形的判定和性质，矩形的性质，正确的识别图形是解题的关键．12．（2020秋•普陀区期末）如图，在▱ABCD中，点E在边BC上，将△ABE沿着直线AE翻折得到△AFE，点B的对应点F恰好落在线段DE上，线段AF的延长线交边CD于点G，如果BE：EC＝3：2，那么AF：FG的值等于214．【考点】相似三角形的判定与性质；平行四边形的性质；翻折变换（折叠问题）．【专题】多边形与平行四边形；平移、旋转与对称；图形的相似；推理能力．【分析】延长BC，AG交于点H，设BE＝3x，EC＝2x，由平行四边形的性质可得AD＝BC＝5x，AD∥BC，由折叠的性质可得∠AEB＝∠AEF，BE＝EF＝3x，通过证明△ADF∽△HEF，△ADG∽△HCG，可求AF＝425y，FG＝AG﹣AF＝85y，即可求解．【解答】解：如图，延长BC，AG交于点H，∵BE：EC＝3：2，∴设BE＝3x，EC＝2x，∵四边形ABCD是平行四边形，∴AD＝BC＝5x，AD∥BC，∴∠DAE＝∠AEB，∵将△ABE沿着直线AE翻折得到△AFE，∴∠AEB＝∠AEF，BE＝EF＝3x，∴∠DAE＝∠AED，∴AD＝DE＝5x，∴DF＝2x，∵AD∥BC，∴△ADF∽△HEF，∴AD DF AFEH EF FH==，∴523x AFEH FH==，∴EH＝152x，AF＝23FH，∴CH＝EH﹣EC ＝x，∵AD∥BC，∴△ADG∽△HCG，∴AD AGCH GH=，∴51011112x AGGHx==，∴设AG＝10y，GH＝11y，∴AH＝21y，∴AF＝215y×2＝425y，∴FG＝AG﹣AF＝85y，∴AF：FG＝21：4＝21 4，故答案为21 4．【点评】本题考查了相似三角形的判定和性质，折叠的性质，平行四边形的性质，灵活运用这些性质进行推理是解题的关键．13．（2019秋•虹口区期末）如图，在等腰梯形ABCD中，AD∥BC，sin C＝45，AB＝9，AD＝6，点E、F分别在边AB、BC上，联结EF，将△BEF沿着EF所在直线翻折，使BF的对应线段B′F经过顶点A，B′F交对角线BD于点P，当B′F⊥AB时，AP的长为24 7．【考点】相似三角形的判定与性质；解直角三角形；等腰梯形的性质；翻折变换（折叠问题）．【专题】图形的相似；解直角三角形及其应用；应用意识．【分析】解直角三角形求出BF，AF，再利用相似三角形的性质求解即可．【解答】解：如图，∵FB′⊥AB，∴∠BAF＝90°，∵四边形ABCD是等腰梯形，∴∠ABC＝∠C，∴sin∠ABC＝sin∠C＝AFBF＝45，设AF＝4k，BF＝5k，则AB＝9＝3k，∴k＝3，∴AF＝12，BF＝15，∵AD∥BF，∴△APD∽△FPB，∴PA AD62=== PF BF155，∴PA＝27AF＝247，故答案为24 7．【点评】本题考查相似三角形的判定和性质，解直角三角形等知识，解题的关键是理解题意，灵活运用所学知识解决问题．14．（2019秋•青浦区期末）已知，在矩形纸片ABCD中，AB＝5cm，点E、F分别是边AB、CD的中点，折叠矩形纸片ABCD，折痕BM交AD边于点M，在折叠的过程中，如果点A恰好落在线段EF上，那么边AD的长至少是532cm．【考点】翻折变换（折叠问题）．【专题】平移、旋转与对称；推理能力．【分析】根据已知条件得到AE＝DF＝BE＝CF，求得四边形AEFD是矩形，得到EF＝AD，∠AEN＝∠BEN＝90°，根据折叠的性质得到BN＝AB，根据直角三角形的性质得到∠BNE＝30°，于是得到EN＝32BN532到结论．【解答】解：如图，∵在矩形纸片ABCD中，点E、F分别是边AB、CD的中点，∴AE＝DF＝BE＝CF，∴四边形AEFD是矩形，∴EF＝AD，∠AEN＝∠BEN＝90°，∵折叠矩形纸片ABCD，折痕BM交AD边于点M，∴BN＝AB，∵BE＝12AB，∴BE＝12BN，∴∠BNE＝30°，∵AB＝5cm，∴EN ＝32BN∴EF≥EN时，点A恰好落在线段EF上，即AD∴边AD的长至少是【点评】本题考查了翻折变换（折叠问题），矩形的性质，直角三角形的性质，正确的识别图形是解题的关键．15．（2019秋•闵行区期末）如图，在等腰△ABC中，AB＝AC＝4，BC＝6，点D在底边BC上，且∠DAC＝∠ACD，将△ACD沿着AD所在直线翻折，使得点C落到点E处，联结BE，那么BE的长为1．【考点】翻折变换（折叠问题）；等腰三角形的性质；勾股定理．【专题】平移、旋转与对称；推理能力．【分析】只要证明△ABD∽△MBE，得AB BDBM BE=，只要求出BM、BD即可解决问题．【解答】解：∵AB＝AC，∴∠ABC＝∠C，∵∠DAC＝∠ACD，∴∠DAC＝∠ABC，∵∠C＝∠C，∴△CAD∽△CBA，∴CA CDCB AC=，∴464CD=，∴CD＝83，BD＝BC﹣CD＝103，∵∠DAM＝∠DAC＝∠DBA，∠ADM＝∠ADB，∴△ADM∽△BDA，∴AD DMBD DA=，即8310833DM=，∴DM＝3215，MB＝BD﹣DM＝65，∵∠ABM＝∠C＝∠MED，∴A、B、E、D四点共圆，∴∠ADB＝∠BEM，∠EBM＝∠EAD＝∠ABD，∴△ABD∽△MBE，（不用四点共圆，可以先证明△BMA∽△EMD，推出△BME∽AMD，推出∠ADB＝∠BEM也可以！）∴AB BD BM BE，∴BE＝BD BMAB＝1．故答案为：1．【点评】本题考查翻折变换、等腰三角形的判定和性质、相似三角形的判定和性质等知识，解题的关键是充分利用相似三角形的性质解决问题，本题需要三次相似解决问题，题目比较难．16．（2019秋•杨浦区期末）在Rt△ABC中，∠A＝90°，AC＝4，AB＝a，将△ABC沿着斜边BC翻折，点A落在点A1处，点D、E分别为边AC、BC的中点，联结DE并延长交A1B所在直线于点F，联结A1E，如果△A1EF为直角三角形时，那么a＝4或【考点】翻折变换（折叠问题）；勾股定理；三角形中位线定理．【专题】平移、旋转与对称；推理能力．【分析】当△A1EF为直角三角形时，存在两种情况：①当∠A1EF＝90°时，如图1，根据对称的性质和平行线可得：A1C＝A1E＝4，根据直角三角形斜边中线的性质得：BC＝2A1B＝8，最后利用勾股定理可得AB的长；②当∠A1FE＝90°时，如图2，证明△ABC是等腰直角三角形，可得AB＝AC＝4．【解答】解：当△A1EF为直角三角形时，存在两种情况：①当∠A1EF＝90°时，如图1，∵△A1BC与△ABC关于BC所在直线对称，∴A1C＝AC＝4，∠ACB＝∠A1CB，∵点D，E分别为AC，BC的中点，∴D、E是△ABC的中位线，∴DE∥AB，∴∠CDE＝∠MAN＝90°，∴∠CDE＝∠A1EF，∴AC∥A1E，∴∠ACB＝∠A1EC，∴∠A1CB＝∠A1EC，∴A1C＝A1E＝4，Rt△A1CB中，∵E是斜边BC的中点，∴BC＝2A1E＝8，由勾股定理得：AB2＝BC2﹣AC2，∴AB=；②当∠A1FE＝90°时，如图2，∵∠ADF＝∠A＝∠DFB＝90°，∴∠ABF＝90°，∵△A1BC与△ABC关于BC所在直线对称，∴∠ABC＝∠CBA1＝45°，∴△ABC是等腰直角三角形，∴AB＝AC＝4；综上所述，AB的长为或4；故答案为：4；【点评】本题考查了翻折变换（折叠问题），三角形的中位线定理、勾股定理、轴对称的性质、等腰直角三角形的判定、直角三角形斜边中线的性质，并利用分类讨论的思想解决问题．17．（2019秋•崇明区期末）如图，在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，D是AC的中点，点E在边AB上，将△ADE沿DE翻折，使得点A落在点A′处，当A′E⊥AB时，则A′A＝5或5．【考点】翻折变换（折叠问题）．【专题】平移、旋转与对称；解直角三角形及其应用．【分析】分两种情形分别求解，作DF⊥AB于F，连接AA′．想办法求出AE，利用等腰直角三角形的性质求出AA′即可．【解答】解：如图，作DF⊥AB于F，连接AA′．在Rt△ACB中，BC＝6，∵∠DAF＝∠BAC，∠AFD＝∠C＝90°，∴△AFD∽△ACB，∴DF AD AFBC AB AC==，∴46108DF AF==，∴DF＝125，AF＝165，∵A′E⊥AB，∴∠AEA′＝90°，由翻折不变性可知：∠AED＝45°，∴EF＝DF＝125，∴AE＝A′E＝125+165＝285，∴AA′＝2825，如图，作DF⊥AB于F，当EA′⊥AB时，同法可得AE＝165﹣125＝45，AA AE＝425．故答案为2825或425．【点评】本题考查翻折变换，相似三角形的判定和性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考填空题中的压轴题．18．（2019秋•静安区期末）如图，有一菱形纸片ABCD，∠A＝60°，将该菱形纸片折叠，使点A恰好与CD的中点E重合，折痕为FG，点F、G分别在边AB、AD上，联结EF，那么cos∠EFB的值为1 7．【考点】翻折变换（折叠问题）；解直角三角形；等边三角形的判定与性质；菱形的性质．【专题】矩形菱形正方形；解直角三角形及其应用．【分析】如图，连接BD ．设BC ＝2a ．在Rt △BEF 中，求出EF ，BF 即可解决问题．【解答】解：如图，连接BD ．设BC ＝2a．∵四边形ABC 都是菱形，∴AB ＝BC ＝CD ＝AD ＝2a ，∠A ＝∠C ＝60°，∴△BDC 是等边三角形，∵DE ＝EC ＝a ，∴BE ⊥CD ，∴BE 22-3BC EC =a ，∵AB ∥CD ，BE ⊥CD ，∴BE ⊥AB ，∴∠EBF ＝90°，设AF ＝EF ＝x ，在Rt △EFB 中，则有x 2＝（2a ﹣x ）2+3a ）2，∴x ＝74a ，∴AF ＝EF ＝74a ，BF ＝AB ﹣AF ＝4a ，∴cos ∠EFB ＝14774a BF a EF ==，故答案为17．【点评】本题考查菱形的性质，解翻折变换，直角三角形等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．。

2022-2023学年上海市松江区中考数学专项突破仿真模拟试题(一模二模)含解析

2022-2023学年上海市松江区中考数学专项突破仿真模拟试题（一模）一、选一选（本大题共6题，每题4分，满分24分）1. 在Rt △ABC 中，∠C=90°，∠A=α，AC=3，则AB 的长可以表示为（）A. B.C. 3sinαD. 3cosα3cos α3sin α2. 如图，在△ABC 中，点D 、E 分别在边BA 、CA 的延长线上，=2，那么下列条件中能判ABAD 断DE ∥BC 的是（）A.B. C. D.12AE EC =2ECAC =12DE BC =2ACAE =3. 将抛物线y=﹣（x+1）2+3向右平移2个单位后得到的新抛物线的表达式为（）A. y=﹣（x+1）2+1 B. y=﹣（x﹣1）2+3C. y=﹣（x+1）2+5D.y=﹣（x+3）2+34. 已知在直角坐标平面内，以点P （﹣2，3）为圆心，2为半径的圆P 与x 轴的位置关系是（）A. 相离 B. 相切C. 相交D. 相离、相切、相交都有可能5. 已知是单位向量，且，那么下列说法错误的是（）e 2,4a e b e =-=A. ∥B. ||=2C. ||=﹣2||D. =﹣ab a b a a 12b6.如图，在四边形ABCD 中，对角线AC 与BD 相交于点O ，AC 平分∠DAB ，且∠DAC ＝∠DBC ，那么下列结论没有一定正确的是（）A. △AOD ∽△BOCB. △AOB ∽△DOCC. CD ＝BCD. BC •CD ＝AC •OA二、填空题（本大题共12题，每题4分，满分48分）7. 若线段a 、b 满足，则的值为_____．12a b =a+b b 8. 正六边形的角等于______度．9. 若抛物线的开口向上，则的取值范围是________．()22y a x =-a 10. 抛物线y=x 2﹣4x+3的顶点坐标为_____．11. 已知与相似，且与的相似比为，若的面积为ABC DEF ABC DEF 2:3DEF ，则的面积等于_______．236cm ABC 12. 已知线段AB=4，点P 是线段AB 的黄金分割点，且AP ＜BP ，那么AP 的长为_____．13. 已知某斜面的坡度为_____度．14. 已知点A （﹣2，m ）、B （2，n ）都在抛物线y=x 2+2x ﹣t 上，则m 与n 的大小关系是m _____n ．（填“＞”、“＜”或“=”）15. 如图，在Rt △ABC 中，∠BAC=90°，点G 是重心，联结AG ，过点G 作DG ∥BC ，DG 交AB于点D ，若AB=6，BC=9，则△ADG 的周长等于_____．16. 已知⊙O 1的半径为4，⊙O 2的半径为R ，若⊙O 1与⊙O 2相切，且O 1O 2=10，则R 的值为_____．17. 如果一个四边形的某个顶点到其他三个顶点的距离相等，我们把这个四边形叫做等距四边形，这个顶点叫做这个四边形的等距点．如图，已知梯形ABCD 是等距四边形，AB ∥CD ，点B 是等距点．若BC=10，CD 的长等于_____．18. 如图，在边长为2的菱形ABCD 中，∠D=60°，点E 、F 分别在边AB 、BC 上．将△BEF 沿着直线EF 翻折，点B 恰好与边AD 的中点G 重合，则BE 的长等于_____．三、解答题（本大题共7题，满分78分）19. 计算：．2cot45cos304sin 45tan60︒-︒︒-︒20. 如图，在△ABC 中，点D 在边AB 上，DE∥BC，DF∥AC，DE 、DF 分别交边AC 、BC 于点E 、F ，且．32AE EC =（1）求的值；BFFC （2）联结EF ，设=，=，用含、的式子表示．BC a ACb a b EF21. 如图，点C 在⊙O 上，联结CO 并延长交弦AB 于点D ，，联结AC 、OB ，若AC BC =CD=40，（1）求弦AB 的长；（2）求sin∠ABO 的值．22. 如图，一栋居民楼AB 的高为16米，远处有一栋商务楼CD ，小明在居民楼的楼底A 处测得商务楼顶D 处的仰角为60°，又在商务楼的楼顶D 处测得居民楼的楼顶B 处的俯角为45°．其中A 、C 两点分别位于B 、D 两点的正下方，且A 、C 两点在同一水平线上，求商务楼CD 的高度．0.1米）23. 如图所示，在△ABC 中，点D 在边BC 上，联结AD ，∠ADB ＝∠CDE ，DE 交边AC 于点E ，DE 交BA 延长线于点F ，且AD 2＝DE •DF ．（1）求证：△BFD ∽△CAD ；（2）求证：BF •DE ＝AB •AD ．24. 在直角坐标平面内，直线y =x +2分别与x 轴、y 轴交于点A 、C ．抛物线12y =﹣+bx +c 点A 与点C ，且与x 轴的另一个交点为点B ．点D 在该抛物线上，且位于直线212x AC 的上方．（1）求上述抛物线的表达式；（2）联结BC 、BD ，且BD 交AC 于点E ，如果△ABE 的面积与△ABC 的面积之比为4：5，求∠DBA的余切值；（3）过点D作DF⊥AC，垂足为点F，联结CD．若△CFD与△AOC相似，求点D的坐标．25. 已知在矩形ABCD中，AB=2，AD=4．P是对角线BD上的一个动点（点P没有与点B、D重合），过点P作PF⊥BD，交射线BC于点F．联结AP，画∠FPE=∠BAP，PE交BF于点E．设PD=x，EF=y．（1）当点A、P、F在一条直线上时，求△ABF的面积；（2）如图1，当点F在边BC上时，求y关于x的函数解析式，并写出函数定义域；（3）联结PC，若∠FPC=∠BPE，请直接写出PD的长．2022-2023学年上海市松江区中考数学专项突破仿真模拟试题（一模）一、选一选（本大题共6题，每题4分，满分24分）1. 在Rt △ABC 中，∠C=90°，∠A=α，AC=3，则AB 的长可以表示为（）A.B.C. 3sinαD. 3cosα3cos α3sin α【正确答案】A【详解】Rt ABC 中，∠C =90°，∴cos = ，∆A ACAB ∵，AC =，A α∠=3∴cosα= ，3AB ∴AB= ，3cos α故选A.考查解直角三角形的知识；掌握和一个角的邻边与斜边有关的三角函数值是余弦值的知识是解决本题的关键．2. 如图，在△ABC 中，点D 、E 分别在边BA 、CA 的延长线上， =2，那么下列条件中能判ABAD 断DE ∥BC 的是（）A.B. C. D. 12AE EC =2ECAC =12DE BC =2ACAE=【正确答案】D【分析】只要证明，可得△BAC ∽△DAE ，证得∠B =∠D ，即可解决问题．AC ABAEAD =【详解】解：A 、，可得AE ：AC =1：1，与已知没有成比例，故没有能判定；12AE EC =2AB AD =B 、，可得AC ：AE =1：1，与已知没有成比例，故没有能判定；2ECAC =2AB AD =C 、即与已知的，可得两组边对应成比例，但夹角没有知是否相等，12DE BC =2BCDE =2AB AD =因此没有一定能判定；12DE BC =D 、，又∠BAC =∠DAE ，∴△BAC ∽△DAE ，∴∠B =∠D ，则DE //BC ，符合题2AC ABAEAD ==意，故选D ．本题考查相似三角形的判定、平行线的判定，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．3. 将抛物线y=﹣（x+1）2+3向右平移2个单位后得到的新抛物线的表达式为（）A. y=﹣（x+1）2+1B. y=﹣（x﹣1）2+3C. y=﹣（x+1）2+5D.y=﹣（x+3）2+3【正确答案】B【详解】解：∵将抛物线y =﹣（x +1）2+3向右平移2个单位，∴新抛物线的表达式为y =﹣（x +1﹣2）2+3=﹣（x ﹣1）2+3．故选B ．4. 已知在直角坐标平面内，以点P （﹣2，3）为圆心，2为半径的圆P 与x 轴的位置关系是（）A. 相离 B. 相切C. 相交D. 相离、相切、相交都有可能【正确答案】A【分析】先求出点P 到x 轴的距离，再根据直线与圆的位置关系得出即可．【详解】解：点P (-2，3)到x 轴的距离是3，3>2，所以圆P 与轴的位置关系是相离，x 故选A.本题考查了坐标与图形的性质和直线与圆的位置关系等知识点，能熟记直线与圆的位置关系的内容是解此题的关键．5. 已知是单位向量，且，那么下列说法错误的是（）e 2,4a e b e =-=A. ∥B. ||=2C. ||=﹣2||D. =﹣aba b a a 12b 【正确答案】C【详解】解：∵是单位向量，且，，e2a e =- 4b e = ∴，，，，//a b 2a = 4b = 12a b =- 故C 选项错误，故选C.6. 如图，在四边形ABCD 中，对角线AC 与BD 相交于点O ，AC 平分∠DAB ，且∠DAC ＝∠DBC ，那么下列结论没有一定正确的是（）A. △AOD ∽△BOCB. △AOB ∽△DOCC. CD ＝BCD. BC •CD ＝AC •OA【正确答案】D【分析】直接利用相似三角形的判定方法分别分析得出答案．【详解】解：∵∠DAC=∠DBC ，∠AOD=∠BOC ，∴∽ ，故A 没有符合题意； AOD ∆BOC ∆∵∽ ，∴AO ：OD=OB ：OC ，∵∠AOB=∠DOC ，∴∽，故B 没有符合AOD ∆BOC ∆AOB ∆DOC ∆题意；∵∽，∴∠CDB=∠CAB，AOB ∆DOC ∆∵∠CAD=∠CAB，∠DAC =∠DBC，∴∠CDB=∠DBC，∴CD=BC；没有条件可以证明，BC CD AC OA ⋅=⋅故选D.本题考查了相似三角形的判定与性质，解题关键在于熟练掌握相似三角形的判定方法①有两个对应角相等的三角形相似；②有两个对应边的比相等，且其夹角相等，则两个三角形相似；③三组对应边的比相等，则两个三角形相似.二、填空题（本大题共12题，每题4分，满分48分）7. 若线段a 、b 满足，则的值为_____．12a b =a+b b 【正确答案】32【分析】由可得b=2a ，然后代入求值.12a b =【详解】解:由可得b=2a ，12a b =所以 =，22a b a a ba ++=32故答案为.32本题考查分式的化简求值，掌握比例的性质是本题的解题关键.8. 正六边形的角等于______度．【正确答案】60°【分析】根据正n 边形角的公式直接求解即可.360n【详解】解：正六边形的圆心角等于一个周角，即为，正六边形有6个角，所以每个角=360360606=故60°本题考查正六边形，解答本题的关键是掌握正六边形的性质，熟悉正六边形的角的概念9. 若抛物线的开口向上，则的取值范围是________．()22y a x =-a 【正确答案】a＞2【分析】利用二次函数图像的性质直接求解.【详解】解:∵抛物线的开口向上，()22y a x =-∴a-2>0，∴a ＞2，故答案为a ＞2.本题考查二次函数图像的性质，掌握二次项系数决定开口方向是本题的解题关键.10. 抛物线y=x 2﹣4x+3的顶点坐标为_____．【正确答案】（2，﹣1）．【详解】先把函数解析式配成顶点式得到y=（x-2）2-1，然后根据顶点式即可得到顶点坐标．解：y=（x-2）2-1，所以抛物线的顶点坐标为（2，-1）．故答案为（2，-1）．“点睛”本题考查了二次函数的性质．二次函数的三种形式：一般式：y=ax 2+bx+c ，顶点式：y=（x-h ）2+k ；两根式：y=a （x-x 1）（x-x 2）．11. 已知与相似，且与的相似比为，若的面积为ABC DEF ABC DEF 2:3DEF ，则的面积等于_______．236cm ABC 【正确答案】216cm 【分析】直接根据相似三角形的性质即可得．【详解】相似三角形的面积比等于它们的相似比的平方，则，224()39ABC DEFS S == ，236DEF cm S = ，4369ABC S ∴= 解得，216()ABC S cm = 故．216cm 本题考查了相似三角形的性质，熟记相似三角形的性质是解题关键．12. 已知线段AB=4，点P 是线段AB 的黄金分割点，且AP ＜BP ，那么AP 的长为_____．【正确答案】（cm ．【分析】根据黄金分割点的定义和AP ＜BP 得出AB ，代入数据即可得出BP 的长度．【详解】解：由于P 为线段AB=4的黄金分割点，且AP ＜BP ，则×4=（-2）cm．∴AP=4-BP=6-故答案为：()cm．6-【点评】本题考查了黄金分割．应该识记黄金分割的公式：较短的线段=较长的线段=原线段的．13. 已知某斜面的坡度为_____度．【正确答案】30°【详解】分析：画出示意图，利用坡角的定义直接得出求出∠A即可．详解：如图所示：∵某坡面的坡比为1:，∴tanA则它的坡角是：30∘.故答案为30.点睛：本题考查三角函数的知识，解题的关键是掌握角度的三角函数值，常见的角的三角函数值包括30°、60°、90°、45°的三角函数值，直接根据角度的三角函数值进行求解即可.14. 已知点A （﹣2，m ）、B （2，n ）都在抛物线y=x 2+2x ﹣t 上，则m 与n 的大小关系是m_____n ．（填“＞”、“＜”或“=”）【正确答案】<【分析】根据二次函数的性质得到抛物线y=x 2+2x-t 的开口向上，有最小值为-t-1，对称轴为直线x=-1，则在对称轴左侧，y 随x 的增大而减小，在对称轴右侧，y 随x 的增大而增大，进而解答即可．【详解】∵y=x 2+2x-t=（x+1）2-t-1，∴a=1＞0，有最小值为-t-1，∴抛物线开口向上，∵抛物线y=x 2+2x-t 对称轴为直线x=-1，∵-2＜0＜2，∴m ＜n ．故＜15. 如图，在Rt △ABC 中，∠BAC=90°，点G 是重心，联结AG ，过点G 作DG ∥BC ，DG交AB 于点D ，若AB=6，BC=9，则△ADG 的周长等于_____．【正确答案】10【详解】延长AG 交BC 于点E ，∵点G 是重心，∴AG ：AE=2：3，BE =BC=4.5，12∵∠BAC=90°，∴AE=BE=4.5，∵DG//BC ，∴△ADG ∽△ABE ，∴AD ：AB=DG ：BE=AG ：AE=2：3，又∵AB=6，∴AD=4，DG=3，AG=3，∴AD+DG+AG=10，故答案为10.16. 已知⊙O 1的半径为4，⊙O 2的半径为R ，若⊙O 1与⊙O 2相切，且O 1O 2=10，则R 的值为_____．【正确答案】6或14cm ．【详解】解：当⊙O 1和⊙O 2内切时，⊙O 2的半径为10+4=14cm ；当⊙O 1和⊙O 2外切时，⊙O 2的半径为10﹣4=6cm ；故答案为6或14cm ．点睛：本题主要是考查两圆相切与数量关系间的联系，一定要考虑两种情况．17. 如果一个四边形的某个顶点到其他三个顶点的距离相等，我们把这个四边形叫做等距四边形，这个顶点叫做这个四边形的等距点．如图，已知梯形ABCD 是等距四边形，AB ∥CD ，点B 是等距点．若BC=10，CD 的长等于_____．【正确答案】16【分析】如图作BM ⊥AD 于M ，DE ⊥AB 于E ，BF ⊥CD 于F ．易知四边形BEDF 是矩形，理由面积法求出DE ，再利用等腰三角形的性质，求出DF 即可解决问题．【详解】连接BD ，过点B 分别作BM ⊥AD 于点M ，BN ⊥DC 于点N ，∵梯形ABCD 是等距四边形，点B 是等距点，∴AB=BD=BC=10，∵ ，cos A=AM AB ∴AM=，∴，∵BM ⊥AD ，∴，∵AB//CD ，∴S △ABD =，11·22AB BN AD BM =⋅∴BN=6，∵BN ⊥DC ，∴，∴CD=2DN=16，故答案为16.18. 如图，在边长为2的菱形ABCD 中，∠D=60°，点E 、F 分别在边AB 、BC 上．将△BEF 沿着直线EF 翻折，点B 恰好与边AD 的中点G 重合，则BE 的长等于_____．【正确答案】75【详解】试题解析：如图，作GH ⊥BA 交BA 的延长线于H ，EF 交BG于O ．∵四边形ABCD 是菱形，∠D=60°，∴△ABC ，△ADC 度数等边三角形，AB=BC=CD=AD=2，∴∠BAD=120°，∠HAG=60°，∵AG=GD=1，∴AH=AG=，，1212在Rt △BHG 中，，∵△BEO ∽△BGH ，∴，BE OB BG BH∴，=∴BE=，75故答案为．75三、解答题（本大题共7题，满分78分）19. 计算：．2cot45cos304sin 45tan60︒-︒︒-︒【详解】试题分析：根据角三角函数值，可得答案．试题解析：解：原式=2=2．20. 如图，在△ABC 中，点D 在边AB 上，DE∥BC，DF∥AC，DE 、DF 分别交边AC 、BC 于点E 、F ，且．32AE EC =（1）求的值；BFFC （2）联结EF ，设=，=，用含、的式子表示．BC a AC b a b EF【正确答案】(1)见解析；（2）=﹣．EF 25b 35a 【分析】（1）由得，由DE//BC 得，再由DF//AC 即可得；32AE EC =25EC AC =25BD EC AB AC ==（2）根据已知可得，，从而即可得.35CF a =- 25EC b = 【详解】（1）∵ ， ∴，32AE EC =25EC AC =∵DE//BC ，∴，25BD EC AB AC ==又∵DF//AC ，∴；25BF BD BC AB ==（2）∵，∴，25BF BC =35FC BC =∵，与方向相反， ∴，BC a =u u u v v CF BC 35CF a =- 同理：，25EC b = 又∵，∴.EF EC CF =+ 2355EF b a =- 21. 如图，点C 在⊙O 上，联结CO 并延长交弦AB 于点D ，，联结AC 、OB ，若AC BC =CD=40，（1）求弦AB 的长；（2）求sin∠ABO 的值．【正确答案】（1）40；（2）35【详解】试题分析：（1）根据，CD 过圆心O ，可得到CD ⊥AB ，AB=2AD=2BD ，在AC BC =Rt △ACD 中利用勾股定理求得AD 长即可得；（2）利用勾股定理求得半径长，然后再根据正弦三角形函数的定义即可求得.试题解析：（1）∵CD 过圆心O ，，AC BC =∴CD ⊥AB ，AB=2AD=2BD ，∵CD=40，，AC =又∵∠ADC=，90∴，AD 20==∴AB=2AD=40；（2）设圆O 的半径为r ，则OD=40-r ，∵BD=AD=20， ∠ODB= ， ∴，090222BD OD OB +=∴，()2222040r r +-=∴r=25，OD=15，∴.OD 153sin ABO OB 255∠===22. 如图，一栋居民楼AB 的高为16米，远处有一栋商务楼CD ，小明在居民楼的楼底A 处测得商务楼顶D 处的仰角为60°，又在商务楼的楼顶D 处测得居民楼的楼顶B 处的俯角为45°．其中A 、C 两点分别位于B 、D 两点的正下方，且A 、C 两点在同一水平线上，求商务楼CD 的高度．0.1米）【正确答案】商务楼的高度为37.9米．CD 【分析】首先分析图形，根据题意构造直角三角形．本题涉及两个直角三角形，即Rt △BED 和Rt △DAC ，利用已知角的正切分别计算，可得到一个关于AC 的方程，从而求出DC ．【详解】过点B 作BE ⊥CD 与点E ，由题意可知∠DBE=，045∠DAC=，CE=AB=16060设AC=x ，则，BE=AC=xCD =∵16DE CD CE =-=-∵∴BE=DE ∴009045BED DBE ∠=∠=，16x =-∴x =∴)81x =+∴2437.9CD ==+≈ 答：商务楼的高度为37.9米.CD 23. 如图所示，在△ABC 中，点D 在边BC 上，联结AD ，∠ADB ＝∠CDE ，DE 交边AC 于点E ，DE 交BA 延长线于点F ，且AD 2＝DE •DF ．（1）求证：△BFD ∽△CAD ；（2）求证：BF •DE ＝AB •AD．【正确答案】（1）见解析；（2）见解析【分析】（1）根据已知条件证明△ADE ∽△FDA ，推出∠DAE =∠F ，依据∠ADB ＝∠CDE ，推出∠FDB =∠ADC ，即可得到结论；（2）根据△BFD ∽△CAD ，推出，∠B =∠C ，得到AB=AC ，由此推出结论．BF AD AC DE =【详解】解：（1）∵AD 2＝DE •DF ．∴，AD DF DEAD =又∵∠ADE =∠FDA ，∴△ADE ∽△FDA ，∴∠DAE =∠F ，∵∠ADB ＝∠CDE ，∴∠FDB =∠ADC ，∴△BFD ∽△CAD ；（2）∵△BFD ∽△CAD ，∴，BF DF AC AD =∵，AD DF DE AD =∴，BF AD AC DE =∵△BFD ∽△CAD ，∴∠B =∠C ，∴AB=AC ，∴，BF AD AB DE =∴BF •DE ＝AB •AD ．此题考查相似三角形的判定及性质，熟记相似三角形的判定及性质定理并熟练应用解决问题是解题的关键．24. 在直角坐标平面内，直线y =x +2分别与x 轴、y 轴交于点A 、C ．抛物线12y =﹣+bx +c 点A 与点C ，且与x 轴的另一个交点为点B ．点D 在该抛物线上，且位于直线212x AC 的上方．（1）求上述抛物线的表达式；（2）联结BC 、BD ，且BD 交AC 于点E ，如果△ABE 的面积与△ABC 的面积之比为4：5，求∠DBA 的余切值；（3）过点D作DF ⊥AC ，垂足为点F ，联结CD ．若△CFD 与△AOC 相似，求点D 的坐标．【正确答案】（1）y =﹣x +2；（2）；（3）（﹣，）或（﹣3，2）．21322x -9832258【分析】（1）由直线得到A 、C 的坐标，然后代入二次函数解析式，利用待定系数法即可得；（2）过点E 作EH ⊥AB 于点H ，由已知可得，从而可得、141252AB EH AB OC =⨯ EH 的长，然后再根据三角函数的定义即可得；HB （3）分情况讨论即可得．【详解】（1）令直线y =x +2中y =0得x +2=01212解得x =-4，∴A (-4，0)，令x =0得y =2，∴C (0，2)把A 、C 两点的坐标代入得，212y x bx c =-++，2840c b =⎧⎨-=⎩∴ ，322b c ⎧=-⎪⎨⎪=⎩∴ ；213222y x x =--+（2）过点E 作EH ⊥AB 于点H，由上可知B （1，0），∵，45ABE ABC S S ∆∆=∴ ，141••252AB EH AB OC =⨯∴，4855EH OC ==将代入直线y =x +2，解得85y =1245x =-∴4855E ⎛⎫- ⎪⎝⎭，∴ ，49155HB =+=∵90EHB ∠=︒∴；995cot 885HB DBA EH ∠===（3）∵DF ⊥AC ，∴，90DFC AOC ∠=∠=︒①若，则CD//AO ，DCF CAO ∠=∠ ∴点D 的纵坐标为2，把y=2代入得x=-3或x=0（舍去），213222y x x =--+∴D (-3，2) ；②若时，过点D 作DG ⊥y 轴于点G ，过点C 作CQ ⊥DG 交x 轴于点Q ，DCF ACO ∠=∠∵ ，90DCQ AOC ∠=∠=︒∴，90DCF ACQ ACO CAO ∠+∠=∠+∠=︒∴，ACQ CAO ∠=∠∴，AQ CQ =设Q (m ，0)，则，4m +=∴ ，32m =-∴，302Q ⎛⎫- ⎪⎝⎭，易证：∽ ，COQ ∆DCG ∆∴ ，24332DG CO GC QO ===设D (-4t ，3t+2)代入得t=0(舍去)或者，213222y x x =--+38t =∴．32528D ⎛⎫- ⎪⎝⎭，综上，D 点坐标为（﹣，）或（﹣3，2）3225825. 已知在矩形ABCD 中，AB=2，AD=4．P 是对角线BD 上的一个动点（点P 没有与点B 、D 重合），过点P 作PF⊥BD，交射线BC 于点F ．联结AP ，画∠FPE=∠BAP，PE 交BF 于点E ．设PD=x ，EF=y ．（1）当点A 、P 、F 在一条直线上时，求△ABF 的面积；（2）如图1，当点F 在边BC 上时，求y关于x 的函数解析式，并写出函数定义域；（3）联结PC ，若∠FPC=∠BPE，请直接写出PD 的长．【正确答案】（1）1；（2）；（3）PD±1或x ≤<【详解】试题分析：（1）根据矩形ABCD ， A 、P 、F 在一条直线上，且PF ⊥BD ，可得，，得一，从而可得ADB BAF ∠=∠ tan tan AB BF ADB BAF AD AB ∠=∠=1BF =ABF S ∆；（2）先证明∽，从而得到，由AD//BC ，可得，BAP ∆FPE∆AB BP PF EF =ADB PBF ∠=∠从而根据三角函数可得，由得，代入12PF BP =BP x =-()12PF x =，即可得；AB BP PF EF =（3）分∠CPF 的∠FPE 的内部与外部两种情况进行讨论即可得.试题解析：（1）∵矩形ABCD ，∴，090BAD ABF ∠=∠=∴ ， ∵A 、P 、F 在一条直线上，且PF ⊥BD ，090ABD ADB ∠+∠=∴ ， ∴，090BPA ∠=090ABD BAF ∠+∠=∴，∵，ADB BAF ∠=∠21tan 42AB ADB AD ∠===∴ ， ∴，1tan 2BF BAF AB ∠==1BF =∴ ；11•21122ABF S AB BF∆==⨯⨯=（2）∵PF ⊥BP ，∴，90BPF ∠=∴ ，∵ ，∴，090PFB PBF ∠+∠=090ABF ∠=090PBF ABP ∠+∠=∴，又∵∠BAP =∠FPE ，ABP PFB ∠=∠∴∽ ，∴ ，BAP ∆FPE ∆AB BP PF EF =∵AD//BC ， ∴，ADB PBF ∠=∠∴，即，1tan tan 2PBF ADB ∠=∠=12PF BP =∵ ， ∴，BP x =()12PF x =，=∴；y x =≤<（3）∠CPF=∠BPE ，①如图所示，当点F 在CE 上时，∵∠BPF=∠FPD=90°，∴∠DPC=∠FPE ，∵∠FPE=∠BAP ，∴∠DPC=∠BAP ，∵AB//CD ，∴∠ABD=∠CDB ，∴△PAB ∽△CPD ，∴PB ：CD=AB ：PD ，∴PB ·PD=CD ·AB ，∴x （）=2×2，x -∴；1±②如图所示，当点F 在EC 延长线上时，过点P 作PN ⊥CD 于点N ，在CD 上取一点M ，连接PM ，使∠MPF=∠CPF ，则有PC ：PM=CH ：MH ，∵∠BPF=∠DPF=90°，∴∠BPC=∠DPM ，∵∠BPE=∠CPF ，∴∠BPE=∠EPF ，∵∠BAP=∠FPE ，∴∠BAP=∠DPM ，∵∠ABD=∠BDC ，∴△PAB ∽△MPD ，∴PB ：MD=AB ：PD ，由PD=x ，tan ∠PDM=tan ∠PFC=2，易得：，，，xxx PH=2x ，，x ，由PB ：MD=AB ：PD 可得，从而可得MN ，在Rt △PCN 中利用勾股定理可得PC ，由PC ：PM=CH ：MH 可得PM ，在在Rt △PMN 中利用勾股定理可得关于x 的方程，解得x=，综上：PD 或.1±本题考查了相似综合题，涉及到的知识点有相似三角形的判定与性质，三角函数的应用，三角形一个角的平分线与其对边所成的两条线段与这个角的两边对应成比例等，解题的关键是根据图形正确地确定相似的三角形，添加适当的辅助线等.2022-2023学年上海市松江区中考数学专项突破仿真模拟试题（二模）一、选一选：（本大题共6题，每题4分，满分24分）1.的为（）；；.2. 下列运算正确的是（）A. B. C. D.235x x x +=235x x x ⋅=()325x x =．623x x x ÷=3. 下列图形中，既是对称又是轴对称图形的为（）A. 正三角形B. 等腰梯形C. 平行四边形D. 菱形．4. 关于反比例函数y=，下列说法中错误的是（）2x A. 它的图象是双曲线B. 它的图象在、三象限C. y 的值随x 的值增大而减小D. 若点（a ，b ）在它的图象上，则点（b ，a ）也在它的图象上5. 将一组数据中的每一个数都加上1得到一组新的数据，那么下列四个统计量中，值保持没有变的是（）A. 方差B. 平均数C. 中位数D. 众数6. 如图，在△ABC 中，∠C=90°，AC=3，BC=4，⊙B 的半径为1，已知⊙A 与直线BC 相交，且与⊙B 没有公共点，那么⊙A 的半径可以是（）A. 4B. 5C. 6D. 7.二、填空题：（本大题共12题，每题4分，满分48分）7. 因式分解：_______________________．34a a -=8.的根是_______．x =9. 函数的定义域是________．32x y x -=10. 已知关于x 的方程x 2﹣4x+m ＝0有两个没有相等的实数根，那么m 的取值范围是_____．11. 把抛物线向左平移1个单位，则平移后抛物线的表达式为________．22y x =-12. 函数的图像如图所示，则当时，的取值范围是________．ykx b =+0y <x 13. 一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数，随机投掷这枚骰子，那么向上一面的点数为合数的概率是________．14. 某区有4000名学生参加学业水平测试，从中随机抽取500名，对测试成绩进行了统计，统计结果见下表：成绩（x ）x ＜6060≤x ＜7070≤x ＜8080≤x ＜9090≤x≤100人数155978140208那么根据上述数据可以估计该区这次参加学业水平测试成绩小于60分的有______人．15. 如图，在△ABC 中，D 是AB 的中点，E 是AC 上一点，且AE=2EC ，如果，AB a = ，那么= ．（用、表示）．AC b = DE a b16. 一个正n 边形的一个内角等于它的角的2倍，则n =___．17. 平面直角坐标系xOy 中，若抛物线y =ax 2上的两点A 、B 满足OA =OB ，且tan ∠OAB =，12则称线段AB 为该抛物线的通径．那么抛物线y =x 2的通径长为______．1218. 如图，已知平行四边形ABCD 中，AC =BC ，∠ACB =45°，将三角形ABC 沿着AC 翻折，点B 落在点E 处，联结DE ，那么的值为________．DEAC 三、解答题：（本大题共7题，满分78分）19. 计算：．031--20. 解没有等式组：并把解集表示在数轴上．2312136x x x x -<⎧⎪+⎨-≤⎪⎩21. 如图，已知△ABC 中，∠B =45°，，BC =6.1tan 2C =（1）求△ABC 面积；（2）AC 的垂直平分线交AC 于点D ，交BC 于点E. 求DE 的长．22. 某条高速铁路全长540公里，高铁列车与动车组列车在该高速铁路上运行时，高铁列车的平均速度比动车组列车每小时快90公里，因此全程少用1小时，求高铁列车全程的运行时间．23. 如图，已知梯形ABCD中，AB∥CD，∠D=90°，BE平分∠ABC，交CD于点E，F是AB 的中点，联结AE、EF，且AE⊥BE．求证：（1）四边形BCEF是菱形；（2）BE•AE=2AD•BC．24. 如图，已知抛物线y＝ax2+bx的顶点为C(1，﹣1)，P是抛物线上位于象限内的一点，直线OP交该抛物线对称轴于点B，直线CP交x轴于点A．(1)求该抛物线的表达式；(2)如果点P的横坐标为m，试用m的代数式表示线段BC的长；(3)如果△ABP的面积等于△ABC的面积，求点P坐标．25. 如图，已知Rt△ABC 中，∠ACB=90°，BC=2，AC=3，以点C为圆心、CB为半径的圆交AB于点D，过点A作AE∥CD，交BC延长线于点E.（1）求CE的长；（2）P是CE延长线上一点，直线AP、CD交于点Q.①如果△ACQ ∽△CPQ ，求CP 的长；②如果以点A 为圆心，AQ 为半径的圆与⊙C 相切，求CP 的长.2022-2023学年上海市松江区中考数学专项突破仿真模拟试题（二模）一、选一选：（本大题共6题，每题4分，满分24分）1.（）；；.【正确答案】B【分析】把A 、B 、D 选项化为最简二次根式，然后根据同类二次根式的定义判断即可．【详解】A ，故本选项错误；=B，故本选项正确；=C ，故本选项错误；D 是同类二次根式，故本选项错误．故选B ．本题考查了同类二次根式的定义：化成最简二次根式后，被开方数相同，这样的二次根式叫做同类二次根式．2. 下列运算正确的是（）A. B. C.D.235x x x+=235x x x⋅=()325x x =．623x x x ÷=【正确答案】B【详解】分析：A.没有是同类项，没有能相加减；B.同底数幂的乘法法则；C.幂的乘方法则；D.同底数幂除法法则.详解：A.与没有是同类项，没有能合并；2x 3x B.，正确；235x x x ⋅=C.，则原计算错误；()326x x =D.，则原计算错误．624x x x ÷=故选B.点睛：本题考查了幂的运算法则和合并同类项法则，同底数幂相乘，底数没有变，指数相加；幂的乘方，底数没有变，指数相乘；同底数幂相除，底数没有变，指数相减；只有同类项才可合并，没有是同类项的没有能合并，合并同类项，只合并系数，字母与字母的指数没有变.3. 下列图形中，既是对称又是轴对称图形的为（）A. 正三角形 B. 等腰梯形C. 平行四边形D. 菱形．【正确答案】D【分析】根据轴对称图形与对称图形的概念求解．【详解】A ．是轴对称图形，没有是对称图形；B ．是轴对称图形，没有是对称图形；C ．没有是轴对称图形，是对称图形；D ．是轴对称图形，也是对称图形．故选D ．掌握好对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，对称图形是要寻找对称，旋转180°后两部分重合．4. 关于反比例函数y=，下列说法中错误的是（）2x A. 它的图象是双曲线B. 它的图象在、三象限C. y 的值随x 的值增大而减小D. 若点（a ，b ）在它的图象上，则点（b ，a ）也在它的图象上【正确答案】C【分析】根据反比例函数y =的图象上点的坐标特征，以及该函数的图象的性质进行分析、解2x 答．【详解】A ．反比例函数的图像是双曲线，正确；2y xB ．k =2＞0，图象位于一、三象限，正确；C ．在每一象限内，y 的值随x 的增大而减小，错误；D ．∵ab =ba ，∴若点（a ，b ）在它的图像上，则点（b ，a ）也在它的图像上，故正确．故选C ．本题主要考查反比例函数的性质．注意：反比例函数的增减性只指在同一象限内．5. 将一组数据中的每一个数都加上1得到一组新的数据，那么下列四个统计量中，值保持没有变的是（）A. 方差 B. 平均数C. 中位数D. 众数【正确答案】A【分析】根据平均数和方差的特点，一组数都加上或减去同一个没有等于0的常数后，方差没有变，平均数改变，即可得出答案．【详解】一组数据x 1，x 2，…x a 的每一个数都加上同一数1，则新数据x 1+1，x 2+1，…x n +1的平均数改变，但是方差没有变．故选A ．本题考查了方差和平均数，一般地设n 个数据，x 1，x 2，…x n 的平均数为，则方差S 2=[（x 1﹣x 1n ）2+（x 2﹣）2+…+（x n ﹣）2]，掌握平均数和方差的特点是本题的关键．x x x 6. 如图，在△ABC 中，∠C=90°，AC=3，BC=4，⊙B 的半径为1，已知⊙A 与直线BC 相交，且与⊙B 没有公共点，那么⊙A 的半径可以是（）A. 4B. 5C. 6D. 7.【正确答案】D【详解】分析：根据勾股定理得AB =5，⊙A 与直线BC 相交，从而求得⊙A 的半径的取值范围；再根据⊙A 与⊙B 没有公共点，则两圆外离或内含，从而求得r 的取值范围．详解：根据勾股定理得：AB =5，根据题意，⊙A 与直线BC 相交，所以⊙A 的半径的取值范围是大于3；又⊙A 与⊙B 没有交点，则 r ＜5-1=4或r ＞5+1=6，∴3＜r ＜4或r ＞6．故选D ．点睛：本题综合考查了直线和圆以及两圆的位置关系与数量之间的联系．本题需注意两圆没有公共点，应分外离和内含两种情况．二、填空题：（本大题共12题，每题4分，满分48分）7. 因式分解：_______________________．34a a -=【正确答案】(2)(2)a a a +-【分析】先提公因式，再用平方差公式分解．【详解】解：()3244(2)(2)a a a a a a a -=-=+-本题考查因式分解，掌握因式分解方法是关键．8. 的根是_______．x =【正确答案】2x =【分析】先把方程两边平方，使原方程化为整式方程，解此一元二次方程得到22x x +=，，二次根式的性质，去掉增根，即可得到答案．12x =21x =-【详解】方程两边平方得：22x x+=∴，12x =21x =-≥0x =≥∴没有符合题意，故舍去21x =-∴原方程的根为2x =故．2x =本题考查了一元二次方程、二次根式的知识；解题的关键是熟练掌握一元二次方程、二次根式的性质，从而完成求解．9. 函数的定义域是________．32x y x -=【正确答案】0x ≠【详解】分析：根据分式有意义的条件，分母2x ≠0，就可以求得x 的范围．详解：根据分式有意义的条件，分母≠0得：2x ≠0，解得：x ≠0．故答案为x ≠0．点睛：函数定义域一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母没有能为0；（3）当函数表达式是二次根式时，被开方数为非负数．10. 已知关于x 的方程x 2﹣4x+m ＝0有两个没有相等的实数根，那么m 的取值范围是_____．【正确答案】m ＜4【分析】由方程有两个没有相等的实数根可得根的判别式△＞0，由此可得关于m 的没有等式，解没有等式即可得出结果．【详解】解：∵关于x 的方程x 2﹣4x +m ＝0有两个没有相等的实数根，∴△＝(﹣4)2﹣4m ＝16﹣4m ＞0，解得：m ＜4．故答案为m ＜4．本题考查的是一元二次方程的根的判别式和一元没有等式的解法，熟知根的判别式与一元二次方程根的关系是求解的关键.11. 把抛物线向左平移1个单位，则平移后抛物线的表达式为________．22y x =-【正确答案】22(1)y x =-+【分析】根据向左平移横坐标减，向上平移纵坐标加求出平移后的抛物线的顶点坐标，然后利用顶点式解析式写出，再展开整理即可．【详解】∵抛物线y =-2x 2向左平移1个单位，∴平移后的抛物线顶点坐标为（﹣1，0），∴平移后抛物线的表达式y =-2（x +1）2．故答案为y =-2（x +1）2．本题考查了二次函数图象与几何变换，平移的规律：左加右减，上加下减，此类题目，利用顶点的变化求解更简便．12. 函数的图像如图所示，则当时，的取值范围是________．y kx b =+0y <x 【正确答案】1x <-【分析】首先找到当y ＜0时，图象所在位置，再根据图象可直接得到答案．【详解】当y ＜0时，图象在x 轴下方．∵与x 交于（﹣1，0），∴y ＜0时，自变量x 的取值范围是x ＜﹣1．故答案为x ＜﹣1．本题主要考查了函数与一元没有等式，关键是能从图象中找到对应的部分．13. 一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数，随机投掷这枚骰子，那么向上一面的点数为合数的概率是________．【正确答案】13【分析】由一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数，掷这枚骰子，向上的一面的点数为合数的有2种情况，直接利用概率公式求解即可求得答案．【详解】∵一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数，掷这枚骰子，向上。

以翻折旋转为背景的几何类比探究压轴问题-2023年中考数学压轴题专项训练(解析版)

以翻折旋转为背景的几何类比探究压轴问题1考向分析1(2023•海安市一模)如图，菱形ABCD中，∠ABC=60°，AB=4，点E是线段BO上一点(不含端点)，将△ABE沿AE翻折，AB的对应边AB′与BD相交于点F．(1)当∠BAE=15°时，求EF的长；(2)若△ABF是等腰三角形，求AF的长；(3)若EF=k•BE，求k的取值范围．【分析】(1)根据菱形的性质以及折叠的性质可得△ABC是等边三角形，AC⊥BD，AO=2，BO= 23，∠BAF=∠FBA=30°，则BF=AF=23-OF，根据勾股定理求出OF，根据等腰直角三角形的性质可得OE=OA=2，即可得EF的长；(2)分三种情况：①当AF=BF时，②当AF=AB时，③当AB=BF时，根据等腰三角形的性质分别求解即可；(3)过点E作EM⊥AB于M，作EN⊥AF于N，根据三角形的面积公式可得ABAF=BEEF，则EF=AF⋅BEAB，由EF=k•BE得k=AFAB，由点F在BD上可得AF的最大值为4，当AF⊥BD，即点F与点O重合时，AF的值最小为OA=2，可得2≤AF≤4，即可得k的取值范围．【解答】解：(1)菱形ABCD中，∠ABC=60°，AB=4，∴△ABC是等边三角形，AC⊥BD，AO=12AC，∠ABD=∠CBD=12∠ABC=30°，∴AO=2，BO=23，由折叠得∠BAE=∠FAE=15°，∴∠BAF=∠FBA=30°，∴BF=AF=23-OF，在Rt△AOF中，OF2+OA2=AF2，∴OF2+22=(23-OF)2，∴OF=233，∵∠BAE=15°，∠FBA=30°，∴∠AEO=45°，∴△AEO是等腰直角三角形，∴OE =OA =2，∴EF =OE -OF =2-233；(2)若△ABF 是等腰三角形，分三种情况：①当AF =BF 时，由(1)知，BF =AF =23-OF ，OF =233，∴AF =23-233=433；②当AF =AB 时，∵AB =4，∴AF =4；③当AB =BF 时，如图1，∵AB =4，∴BF =4，∴OF =BF -OB =4-23，∴AF =OA 2+OF 2=22+(4-23)2=26-22；综上，AF 的长为433或4或26-22；(3)过点E 作EM ⊥AB 于M ，作EN ⊥AF 于N ，由折叠得∠BAE =∠FAE ，∴EM =EN ，∴S △ABES △AFE =12AB ⋅EM 12AF ⋅EN =AB AF ，又∵S △ABE S △AFE=BE EF ，∴AB AF =BE EF ，∴EF =AF ⋅BE AB，∵EF =k •BE ，∴k =AF AB，∵点F 在BD 上，∴AF 的最大值为4，当AF ⊥BD ，即点F 与点O 重合时，AF 的值最小为OA =2，∴2≤AF ≤4，∴12≤AF AB≤1，∴k 的取值范围为12≤k ≤1．【点评】本题是几何变换综合题，考查了折叠的性质，菱形的性质，全等三角形的判定和性质，勾股定理，等腰三角形的性质等，分类思想的运用是解题的关键．2(2023•铁西区模拟)在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连接BD，CE．(1)如图①将△ADE绕点A旋转，在旋转过程中，线段BD与CE总保持相等的数量关系，请说明理由；(2)如图②，∠BAC=∠DAE=90°，AB=8，AD=4，把△ADE绕点A旋转，点P为射线BD与CE的交点，当E在BA延长线上时，求线段CP的长度(只求图中的情况)；(3)在(2)的条件下，在旋转过程中，点P为射线BD与射线CE的交点，当四边形ADPE为正方形时，直接写出线段PB长度的值．【分析】(1)证明△ABD≌△ACE(SAS)，由全等三角形的性质得出BD=CE；(2)证明△ABD≌△ACE(SAS)，得出∠ABD=∠ACE，证明△ABD∽△PCD，由相似三角形的性质得出ABPC=BDCD，求出CD的长，则可得出答案；(3)分两种情况画出图形，由正方形的性质及勾股定理可得出答案．【解答】(1)证明：∵△ABC和△ADE是等腰直角三角形，∠BAC=∠DAE=90°，∴AB=AC，AD=AE，∠DAB=∠CAE，∴△ABD≌△ACE(SAS)，∴BD=CE；(2)解：∵△ABC和△ADE是等腰直角三角形，∠BAC=∠DAE=90°，∴AB=AC，AD=AE，∴△ABD≌△ACE(SAS)，∴∠ABD=∠ACE，∵∠ADB=∠PDC，∴△ABD∽△PCD，∴AB PC=BD CD，又∵AB=8，AD=4，∠BAC=90°，∴CD=AC-AD=AB-AD=8-4=4，BD=AB2+AD2=82+42=45，∴8PC=454，∴PC=855；(3)解：①当四边形ADPE为正方形时，点P在线段BD上，∵∠ADB=90°，AD=4，AB=8，∴BD=AB2-AD2=82-42=43，∴PB=43-4；②如图，当点P在线段BD的延长线上时，同理PB=BD+PD=43+4．综上所述可得PB的长为43+4或43-4．【点评】本题几何变换综合题，主要考查了正方形的判定与性质，等腰直角三角形的性质，旋转的性质，三角形全等的判定与性质，勾股定理等知识，熟练掌握全等三角形的判定与性质是解题的关键．3(2023•南阳一模)在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．问题情景：在矩形ABCD中，点E为AD边上一动点，点F为BC边上一点，连接EF，将四边形CDEF 沿EF折叠，点C、D分别落在点C'、D'处，设∠EFC=α．(1)如图1，若∠EFC=75°，AD=AB，点F为BC的中点，延长D'C'交AB于点P．则PC'与PB的数量关系是PC'=PB，写出图中一个30°的角：∠BFC'；(2)如图2，若点F为BC的中点，AD=2AB，45°<α<90°，延长D'C'交AB于点P．求PC'与PB的数量关系，并说明理由；(3)如图3，若AB=3，AD=6，BF=1，连接C'E，当点E为AD的三等分点时，直接写出EFC'E的值．【分析】(1)证明Rt△PBF≌Rt△PC'F(HL)，由全等三角形的性质得出PB=PC'，由折叠的性质得出∠EFC=∠EFC'=75°，则可得出答案；(2)连接PF，方法同(1)，由全等三角形的性质得出PB=PC'；(3)①若点E为AD的三等分点，且AE=2DE，②若点E为AD的三等分点，且DE=2AE，由勾股定理可得出答案．【解答】解：(1)连接PF，∵F为BC的中点，∴BF=CF，∵四边形ABCD为矩形，AD=AB，∴四边形ABCD是正方形，∴∠B=∠C=90°，∵将正方形CDEF沿EF折叠，∴FC=FC'，∠C=∠D'C'F=90°，∴∠PC'F=90°，BF=C'F，又∵PF=PF，∴Rt△PBF≌Rt△PC'F(HL)，∴PB =PC '，∵∠EFC =75°，将四边形CDEF 沿EF 折叠，∴∠EFC =∠EFC '=75°，∴∠BFC '=180°-∠EFC -∠EFC '=30°，故答案为：PC '=PB ，∠BFC '；(2)PC '=PB ．理由：连接PF ，∵F 为BC 的中点，∴BF =CF ，∵将矩形CDEF 沿EF 折叠，∴FC =FC '，∠C =∠D 'C 'F =90°，∴∠PC 'F =90°，BF =C 'F ，∴Rt △PBF ≌Rt △PC 'F (HL )，∴PB =PC '；(3)①若点E 为AD 的三等分点，且AE =2DE ，∵AD =6，∴AE =4，ED =2，过点E 作EM ⊥BC 于M ，∴四边形ABME 为矩形，∴BM =AE =4，EM =AB =3，∴FM =BM -BF =4-1=3，∴EF =FM 2+EM 2=32+32=32，∵将矩形CDEF 沿EF 折叠，∴ED =ED '=2，C 'D '=CD =3，∠D =∠D '=90°，∴C 'E =C 'D '2+D 'E '2=22+32=13，∴EF C 'E =3213=32613；②若点E 为AD 的三等分点，且DE =2AE ，∴DE =4，EA =2，过点E 作EN ⊥BC 于N ，同理可得FN =1，EN =3，∴EF =FN 2+EN 2=12+32=10，同理由折叠可得ED =ED '=4，C 'D '=CD =3，∠D =∠D '=90°，∴C 'E =D 'E 2+C 'D '2=42+32=5，∴EF C 'E=105，综上所述，EF C 'E的值为105或32613．【点评】本题是几何变换综合题，主要考查了正方形的判定与性质，等腰直角三角形的性质，折叠的性质，三角形全等的判定与性质，勾股定理等知识，熟练掌握折叠的性质是解题的关键．4(2023•沈河区校级模拟)如图1，四边形ABCD中，∠BCD=90°，AC=AD，AF⊥CD于点F，交BD 于点E，∠ABD=2∠BDC．(1)判断线段AE与BC的关系，并说明理由；(2)若∠BDC=30°，求∠ACD的度数；(3)如图2，在(2)的条件下，线段BD与AC交于点O，点G是△BCE内一点，∠CGE=90°，GE=3，将△CGE绕着点C逆时针旋转60°得△CMH，E点对应点为M，G点的对应点为H，且点O，G，H在一条直线上直接写出OG+OH的值．【分析】(1)连接CE，可证得BC∥AF，进而得出DE=BE，运用直角三角形性质可得CE=DE，进而得出∠ECD=∠BDC，推出∠ABD=∠BEC，由平行线的判定定理可得AB∥CE，根据平行四边形的判定和性质可得AE=BC，AE∥BC．(2)根据已知条件可得出△BCE是等边三角形，BC=CE，∠BCE=60°，进而可得四边形ABCE是菱形，利用菱形性质可得∠ACB=12∠BCE=30°，再由∠ACD=∠BCD-∠ACB，即可求得答案；(3)由旋转变换的性质可得：CH=CG，CM=CE，∠GCH=∠ECM=60°，得出△CGH是等边三角形，∠CHG=60°，进而可得四边形BHCO是圆内接四边形，得出∠COH=∠CBH，过点C作CL⊥OH于点L，可证得△COL∽△CBH，利用相似三角形性质和解直角三角形可得OLBH=CL CH=sin∠CHG=sin60°=32，即OL=32BH=332，根据等边三角形性质可得GH=2GL，推出OG+OH=OG+OG+2GL=2(OG+GL)=2OL，即可求得答案．【解答】解：(1)AE=BC，AE∥BC．理由如下：如图1，连接CE，∵AC=AD，AF⊥CD，∴CF=FD，∠AFD=90°，∵∠BCD=90°，∴∠BCD=∠AFD，∴BC∥AF，∴DE BE=DFCF=1，∴DE=BE，∵∠BCD=90°，∴CE=DE，∴∠ECD=∠BDC，∵∠BEC =∠ECD +∠BDC ，∴∠BEC =2∠BDC ，∵∠ABD =2∠BDC ，∴∠ABD =∠BEC ，∴AB ∥CE ，∴四边形ABCE 是平行四边形，∴AE =BC ，AE ∥BC ．(2)∵∠BDC =30°，∠BCD =90°，∴∠CBD =60°，∵CE =BE =DE ，∴△BCE 是等边三角形，∴BC =CE ，∠BCE =60°，∵四边形ABCE 是平行四边形，∴四边形ABCE 是菱形，∴∠ACB =12∠BCE =30°，∴∠ACD =∠BCD -∠ACB =90°-30°=60°；(3)∵将△CGE 绕着点C 逆时针旋转60°得△CMH ，∴CH =CG ，CM =CE ，∠GCH =∠ECM =60°，∴△CGH 是等边三角形，∴∠CHG =60°，由(2)知：△BCE 是等边三角形，∴CB =CE ，∠ECB =60°，∴CE 与CB 重合，点M 与点B 重合，∴BH =EG =3，∠CHB =∠CGE =90°，∵四边形ABCE 是菱形，∴∠BOC =90°，∴∠BOC +∠CHB =90°+90°=180°，∴四边形BHCO 是圆内接四边形，∴∠COH =∠CBH ，如图2，过点C 作CL ⊥OH 于点L ，则∠CLO =90°=∠CHB ，∴△COL ∽△CBH ，∴OL BH =CL CH=sin ∠CHG =sin60°=32，∴OL =32BH =32×3=332，∵△CGH 是等边三角形，CL ⊥OH ，∴GH =2GL ，∵OH =OG +GH =OG +2GL ，∴OG +OH =OG +OG +2GL =2(OG +GL )=2OL ，∴OG+OH=2×332=33．【点评】本题是几何综合题，考查了等腰三角形性质，等边三角形性质，直角三角形性质，平行四边形的判定和性质，菱形的判定和性质，旋转变换的性质，解直角三角形，相似三角形的判定和性质等，解题的关键是学会添加常用辅助线，运用相似三角形的判定和性质解决问题，属于中考压轴题．2压轴题速练1(2023•襄都区校级一模)已知点M，N是直线l上自左向右的两点，且MN=8，点P是MN的中点，点Q是直线l上一点(不与点M，N重合)，直线m经过点Q，MA⊥直线m于点A，NB⊥直线m于点B，连接PA，PB．(1)如图1，当点Q在点P，N之间时，求证：PA=PB；(2)如图2，当点Q在点N的右侧时，若PN=2NQ，且∠AQM=30°，求AB和AP的长度．【分析】(1)过点P作PJ⊥直线m于点J．利用平行线等分线段定理证明即可；(2)过点P作PH⊥AB于点H．分别求出AQ．BQ，可得AB的长，再利用勾股定理求出AP．【解答】(1)证明：过点P作PJ⊥直线m于点J．∵MA⊥直线m，NB⊥直线m，PJ⊥直线m，∴MA∥NB∥PJ，∵PM=PN，∴AJ=JB，∵PJ⊥AB，∴PA=PB；(2)解：过点P作PH⊥AB于点H．∵MA⊥直线m，NB⊥直线m，PH⊥直线m，∴MA∥NB∥PH，∵PM=PN，∴AH=BH，∵MN=8，P是MN的中点，∴PM=PN=4，∵PN=2NQ，∴NQ=2，PQ=6，MQ=8，∵∠AQM=30°，∴PH=12PQ=3，BQ=NQ•cos30=3，AQ=MQ•cos30°=43，∴AB=AQ-BQ=33，∴AH=BH=332，∴PA=AH2+PH2=3322+32=372．【点评】本题属于几何变换综合题，考查了平行线等分线段定理，勾股定理，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题．2(2023•齐齐哈尔一模)综合与实践．旋转是几何图形运动中的一种重要变换，通常与全等三角形等数学知识相结合来解决实际问题，某学校数学兴趣小组在研究三角形旋转的过程中，进行如下探究：如图1，△ABC和△DMN均为等腰直角三角形，∠BAC=∠MDN=90°，点D为BC中点，△DMN绕点D旋转，连接AM、CN．观察猜想：(1)在△DMN旋转过程中，AM与CN的数量关系为AM=CN；实践发现：(2)当点M、N在△ABC内且C、M、N三点共线时，如图2，求证：CM-AM=2DM；拓展延伸：(3)当点M、N在△ABC外且C、M、N三点共线时，如图3，探究AM、CM、DM之间的数量关系是CM+AM=2DM；解决问题：(4)若△ABC中，AB=5，在△DMN旋转过程中，当AM=2且C、M、N三点共线时，DM=　6-22或6+22　．【分析】(1)结论：AM=CN．证明△ADM≌△CDN(SAS)，可得结论；(2)连接AD．利用全等三角形的性质以及等腰直角三角形的性质证明即可；(3)结论：CM+AM=2DM．证明方法类似(2)；(4)分两种情形：利用图2，图3分别求出MN，可得结论．【解答】(1)解：结论：AM=CN．理由：连接AD ．∵AB =AC ，∠BAC =90°，BD =DC ，∴AD ⊥BC ，AD =DB =DC ，∵∠ADC =∠MDN =90°，∴∠ADM =∠CDN ，在△ADM 和△CDN 中，DA =DC ∠ADM =∠CDN DM =DN，∴△ADM ≌△CDN (SAS )，∴AM =CN ．故答案为：AM =CN ；(2)证明：连接AD ．由(1)可知AM =CN ，∵△DMN 是等腰直角三角形，∴MN =2DM ，∴CM -CN =CM -AM =MN =2DM ，即CM -AM =2DM ；(3)解：结论：CM +AM =2DM ．理由：由(1)可知AM =CN ，∵△DMN 是等腰直角三角形，∴MN =2DM ，∴CM +CN =CM +AM =MN =2DM ，即CM +AM =2DM ．故答案为：CM +AM =2DM ；(4)解：如图2中，设AD 交CM 于点O ．∵△ADM ≌△CDN ，∴AM =CN ，∠DAM =∠DCN ，∵∠AOM =∠COD ，∴∠AMO =∠CDO =90°，∵AB =AC =5，AM =2，∴CM =AC 2-AM 2=5-2=3，∴MN =CM -CN =3-2，∴DM =22MN =6-22，如图3中，同法可得DM =6+22．综上所述，DM 的长为6-22或6+22．故答案为：6-22或6+22．【点评】本题属于几何变换综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．3(2023•长安区一模)问题提出：(1)如图，在△ABC中，∠BAC=90°，AO是它的一条中线，则∠COA与∠B的数量关系是：∠COA=2∠B；(2)如图，在△ABC中，∠A=60°，BC=6，CG⊥AB于点G，BH⊥AC于点H，O为BC边上一点，且OG=OB，连接GH，求GH的长；问题解决：(3)某次施工中，工人师傅需要画一个20°的角，但他手里只有一把带刻度的直角尺，工程监理给出了下面简易的作图方法：①画线段OB=15cm，再过它的中点C作m⊥OB；②利用刻度尺在m上寻找点A，使得OA=15cm，再过点A作l∥OB；③利用刻度尺过点O作射线，将射线与AC和l的交点分别记为点F、E，调节刻度尺使FE=□cm时(“□”内的数字被汗渍侵蚀无法看清)，则∠EOB=20°；你认为监理给的方法可行吗？如果可行，请写出“□”内的数字，并说明理由；如果不可行，请给出可行的方案．【分析】(1)利用直角三角形斜边中线的性质以及等腰三角形的性质证明即可．(2)连接OH，证明△OGH是等边三角形可得结论；(3)取EF是中点P，连接AP，证明AP=FP=EP=AO=15，推出∠AEF=∠EAP，∠AOP=∠APO，推出∠AOP=2∠AEF=2∠BOE，可得结论．【解答】解：(1)如图1中，∵∠CAB=90°，AO是中线，∴OA=OB=OC，∴∠OAB=∠B，∵∠COA=∠OAB+∠B，∴∠COA=2∠B，故答案为：2；(2)如图2中，连接OH．∵OG=OB，∴∠GBO=∠BGO，∵∠CGB=90°，∴∠GBO+∠GCO=90°，∠BGO+∠CGO=90°，∴∠GCO=∠CGO，∴OH=BO=OG=OC=3，∴B，C，H，G在以O为圆心，OC为半径的圆上，∵∠A=60°，∴∠ACG=30°，∴∠GOH=60°，∴△GOH是等边三角形，∴GH=OG=3；(3)可行，30．理由：在Rt△ACO中，cos∠AOC=OCOA=12，∴∠AOC=60°，取EF是中点P，连接AP，∵AP∥直线l，AC⊥OB，∴AC⊥AE，∠AEF=∠BOE，∴∠FAE=90°，∵EP=PF，EF=30cm，∴AP=FP=EP=AO=15(cm)，∴∠AEF=∠EAP，∠AOP=∠APO，∴∠AOP=2∠AEF=2∠BOE，∴∠BOE=13∠AOB=20°．【点评】本题属于几何变换综合题，考查了直角三角形斜边中线的性质，平行线的性质，等腰三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．4(2023•南关区校级模拟)如图，在△ABC中，BA=10，BC=3，tan B=3，点D为边BC的中点．动点P从点B出发，沿折线BA-AC向点C运动，在BA、AC上的速度分别为每秒10个单位长度和每秒13个单位长度．连结AD、PD，设点P的运动时间为t秒(t>0)．(1)线段AC的长为　13　；(2)用含t的代数式表示线段AP的长；(3)当∠APD为钝角时，求t的取值范围；(4)做点B关于直线PD的对称点B′，连结B′D，当B′D⊥BC时，直接写出t的值．【分析】(1)如图1中，过点A 作AE ⊥BC 于点E ．解直角三角形求出AE ，BE ，再利用勾股定理求出AC 即可；(2)分两种情形：当0<t ≤1时．当1<t ≤2时，分别根据路程，速度，时间的关系求解；(3)求出两种特殊情形：如图1中，当DP ⊥AB 时，如图2中，当DP ⊥AC 时，t 的值，可得结论；(4)分两种情形：如图3中，当DB ′⊥BC 时，过点P 作PJ ⊥BC 于点J ．解直角三角形求出BP ．如图4中，当DB ′⊥BC 时，过点P 作PJ ⊥BC 于点J ．记住解阿三角形求出CP ，可得结论．【解答】解：(1)如图1中，过点A 作AE ⊥BC 于点E ．∵tan B =AE BE=3，AB =10，∴AE =3，BE =1，∵BC =3，∴EC =2，∴AC =AE 2+CE 2=32+22=13．故答案为：13．(2)当0<t ≤1时，AP =10-10t ．当1<t ≤2时，AP =13(t -1)．综上所述，AP =10-10t (0<t ≤1)13(t -1)(1<t ≤2) ；(3)如图1中，当DP ⊥AB 时，∵12•AB •DP =12•BD •AE ，∴DP =3×3210=91020，∴BP =DB 2-DP 2=32 2-91020 2=31020，此时t =320．如图2中，当DP ⊥AC 时，DP =3×3213=91326，∴CP =CD 2-DP 2=32 2-91326 2=31313，此时t =1+1013=2313，观察图形可知满足条件的t 的值为：320<t <1或1<t <2313．(4)如图3中，当DB ′⊥BC 时，过点P 作PJ ⊥BC 于点J ．设BJ =x ，则PJ =DJ =3x ，∴4x =32，∴x =38，∴PB =3108，∴t =38．如图4中，当DB ′⊥BC 时，过点P 作PJ ⊥BC 于点J ．设DJ =PJ =3y ，则CJ =2y ，∴5y =32，∴y =310，∴PC =PJ 2+CJ 2=910 2+610 2=31310，∴t =1+710=1710．综上所述，满足条件的t 的值为38或1710．【点评】本题属于几何变换综合题，考查了解直角三角形，三角形的面积轴对称变换，等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．5(2023•盐田区二模)操作：如图1，点E 在矩形ABCD 边CD 上，沿AE 折叠，点D 恰落在BC 边上D '处．再将图1对折，使点E 与点A 重合，得多边形AC ′FBNM (图2)，点C 的对应点为点C ′．思考：若AB =6，AD =10．(1)求图1中CE 的长；(2)求证：△AC 'F ≌△ECD '．探究：若用一张A 4(AD =2AB )纸进行上述操作，判断C 'F 与BF 的数量关系，并说明理由．【分析】思考：(1)由折叠的性质得出AD '=AD =10，∠AD 'E =90°，证明△ED 'C ∽△D 'AB ，由相似三角形的性质得出CE BD '=CD 'AB，则可得出答案；(2)由折叠的性质得出∠AED =∠AED '，∠EAC '=∠AEC ，证出∠FAC '=∠CED '，根据ASA 可证明△AC 'F ≌△ECD '；探究：设AB=m，AD=2m，证明△ED'C∽△D'AB，由相似三角形的性质得出ED'D'A=D'CAB，求出ED'=(2-2)m，由全等三角形的性质得出C'F=CD'=(2-1)m，AF=ED'=(2-2)m，则可得出结论．【解答】解：思考：(1)由折叠的性质可得，AD'=AD=10，∠AD'E=90°，∵∠B=90°，AB=6，AD'=10，∴BD'=8，∴CD'=BC-BD'=10-8=2，∵∠AD'B+∠ED'C=90°，∠AD'B+∠BAD'=90°，∴∠ED'C=∠BAD'，∵四边形ABCD是矩形，∴∠B=∠C=90°，∴△ED'C∽△D'AB，∴CE BD'=CD' AB，∴CE8=26，∴CE=83；(2)证明：∵四边形ABCD是矩形，∴AB∥CD，∴∠AED=∠FAE，由折叠的性质得出∠AED=∠AED'，∠EAC'=∠AEC，∴∠FAE=∠AED'，∠EAC'-∠FAE=∠AEC-∠AED'，即∠FAC'=∠CED'，又∵AC'=EC，∠C'=∠C，∴△AC'F≌△ECD'(ASA)；探究：C'F=BF．理由：由AD=2AB，设AB=m，AD=2m，∴BD'=m，CD'=(2-1)m，∴△ED'C∽△D'AB，∴ED' D'A=D'C AB，∴ED'2m =(2-1)mm，∴ED'=(2-2)m，∵△AC'F≌△ECD'，∴C'F=CD'=(2-1)m，AF=ED'=(2-2)m，∴BF=AB-AF=m-(2-2)m=(2-1)m=C'F．【点评】本题是四边形综合题目，考查了相似三角形的判定与性质、翻折变换的性质、全等三角形的判定与性质、矩形的性质和判定，熟练掌握相似三角形的判定与性质是解题的关键．6(2023•白塔区校级一模)已知，在△ABC中，AB=BC，∠ABC=90°，点D在射线CB上，连接DA，将线段DA绕点D逆时针旋转90°后得到DE，过点E作EM⊥BC交直线BC于点M，连接AE，CE ．(1)如图①，若点D 在线段CB 上(且不与点C 、点B 重合)时，求证：①MC =BD ；②∠ACE =90°(2)延长AD 与直线CE 相交于点N ，①当点D 在线段CB 上(且不与点C 、点B 重合)时，如图②所示，若AD 平分∠BAC ，CD =2ME ，且AB =2+22，求线段NE 的长；②当点D 在射线CB 上(且不与点C 、点B 重合)时，若CE NE =37时，直接写出tan ∠MDE tan ∠NAC．【分析】(1)①证明ABD ≌△DME ，进而得出结论；②证明△ABD ∽△ACE ，进而得出结论；(2)①设AC 与DE 交于点F ，证明∠BAD =22.5°，在AB 上取一点T ，使得AT =DT ，证明BD =BT ，设BD =BT =m ，则DT =AT =2m ，可得m +2m =2+22，推出m =2，再证明△ABD ∽△ADF ，利用相似三角形的性质求出AF ，再证明EN =AF 可得结论；②证明∠MDE =∠CAE ，进而在Rt △ACN 和Rt △ACE 中，表示出tan ∠CAN 和tan ∠CAE ，进而求得结果．【解答】(1)证明：①∵∠ADE =90°，∴∠ADB +∠MDE =90°，∵∠ABD =90°，∴∠ADB +∠BAD =90°，∴∠BAD =∠MDE ，在△ABD 和△DME 中，∠B =∠M =90°∠BAD =∠MDE AD =DE，∴△ABD ≌△DME (AAS )，∴AB =DM ，∵AB =BC ，∴BC =DM ，∴MC =BD ；②∵∠BAC=∠DAF，∴∠BAC-∠CAD=∠DAF-∠CAD，即：∠BAD=∠CAE，∵AC AB=AFAD=2，∴△ABD∽△ACE，∴∠ACE=∠B=90°；(2)解：①设AC与DE交于点F，∵△ABD≌△DME，∴AB=DM，BD=EM，∵AB=BC，∴BC=DM，∴MC=BD=EM，∴∠MCE=∠MEC=45°，∴EC=2ME，∵CD=2ME，∴CD=CE，∴∠CDE=∠CED，∵∠MCE=∠CDE+∠CED，∴∠CDE=∠CED=22.5°，∵∠ADE=90°，∴∠ADB=67.5°，∵∠B=90°，∴∠BAD=22.5°，在AB上取一点T，使得AT=DT，∴∠TAD=∠TDA=22.5°，∴∠BTD=∠TAD+∠TDA=45°，∵∠B=90°，∴∠BDT=∠BTD=45°，∴BD=BT，设BD=BT=m，则DT=AT=2m，∴m+2m=2+22，∴m=2，∴BD=2，∴AD=BD2+AB2=22+(2+22)2=16+82，∵AD平分∠BAC，∴∠BAD=∠DAF，∵∠B=∠ADF=90°，∴△ABD∽△ADF，∴AB AD =AD AF，∴2+2216+82=16+82AF，∴AF =42，∵∠DEN =∠DAF =22.5°，DE =AD ，∠EDN =∠ADF =90°，∴△EDN ≌△ADF (ASA )，∴EN =AF =42；②当点D 在线段BC 上时，∵CE NE =37，∴CE CN=34，由上得，∠MDE =∠BAD =∠CAE ，∴tan ∠MDE tan ∠NAC =tan ∠CAE tan ∠NAC =CE AC ：CN AC=CE CN =34．如图，当点D 在CB 的延长线上时，同理可得：tan ∠MDE tan ∠NAC =tan ∠CAE tan ∠NAC =CE AC ：CN AC =CE CN =310综上所述，tan ∠MDE tan ∠NAC=34或310．【点评】本题属于几何变换综合题，考查了等腰直角三角形性质，锐角函数定义，全等三角形判定和性质，相似三角形判定和性质等知识，解决问题的关键是转化线段和角．7(2023•天宁区校级模拟)在平面直角坐标系xOy 中，点A (0，2)，点B 在x 轴正半轴上，点C 在第一象限内．(1)如图1，OB =4．①若△ABC 是以AC 为斜边的直角三角形，且tan ∠BAC =2．请在图(1)中利用圆规、无刻度直尺作出点C 的位置(不写作法，保留作图痕迹)，写出点C 的坐标：(8，8)；②若△ABC 是等边三角形．求点C 的坐标；(2)如图2，△ABC 是等边三角形，点C 在以P (33，6)为圆心，半径为r 的圆上．若存在两个△ABC 满足条件，求r 的取值范围．【分析】(1)①以点B 为圆心，AB 为半径画弧交AB 的延长线于点N ，分别以A 、N 为圆心，大于AB 的长度为半径画弧，交于第一象限内点W ，在射线BW 上截取BC =2AB ，连接AC ，点C 即为所求作的点；设C (x ，y )，过点C 作CE ⊥x 轴于点E ，由tan ∠BAO =tan ∠CBE ，得OB OA=CE BE ，即42=y x -4，得出y =2x -8，即CE =2x -8，由勾股定理得BE 2+CE 2=BC 2，建立方程求解即可；②过点C 作CD ⊥AB 于点D ，作CE ⊥y 轴于点E ，过点D 作FG ⊥x 轴于点G ，交CE 于点F ，设C(a ，b )，则CE =a ，FG =b ，由△DCF ∽△BDG ，可得CF DG =DF BG=CD BD ，即a -21=b -12=3，即可求得答案；(2)以OA 为边作等边三角形OAM ，使点M 落在第一象限，作射线MP 交⊙P 于点C 、C ′，分别以AC 、AC ′为边作等边△ABC 和等边△AB ′C ′，连接AP ，取BB ′的中点Q ，连接AQ 、PQ ，点B 、B ′均在x 轴正半轴上，过点P 作PH ⊥y 轴于点H ，可证得△BAB ′≌△CAC ′(SAS )，△ABQ ≌△ACP (SAS )，推出△PAQ 是等边三角形，可得AP =AQ ，利用勾股定理可求得OQ =39，即可得出0<r ≤39．【解答】解：(1)①如图1-①，点C 即为所求作的点．设C (x ，y )，过点C 作CE ⊥x 轴于点E ，则OE =x ，CE =y ，∴BE =OE -OB =x -4，∵点A (0，2)，∴OA =2，∵OB =4，∴B (4，0)，在Rt △AOB 中，AB =OA 2+OB 2=22+42=25，∵∠AOB =∠BEC =90°，∴∠BAO +∠ABO =90°，∵∠ABC =90°，∴∠CBE +∠ABO =90°，∴∠BAO =∠CBE ，∴tan ∠BAO =tan ∠CBE ，∴OB OA=CE BE ，即42=y x -4，∴y =2x -8，即CE =2x -8，∵tan ∠BAC =2，∴BC AB=2，∴BC =2AB =45，在Rt △BCE 中，BE 2+CE 2=BC 2，∴(x -4)2+(2x -8)2=(45)2，解得：x =0(舍去)或x =8，∴y =2x -8=2×8-8=8，∴点C 的坐标为(8，8)，故答案为：(8，8)；②如图1-②，过点C 作CD ⊥AB 于点D ，作CE ⊥y 轴于点E ，过点D 作FG ⊥x 轴于点G ，交CE 于点F ，设C (a ，b )，则CE =a ，FG =b ，∵△ABC 为等边三角形，CD ⊥AB ，∴AD =DB =12AB =5，∵DG ∥OA ，D 是AB 的中点，∴DG 是△ABO 的中位线，∴OG =BG =2，DG =12OA =1，∴FD =FG -DG =b -1，∵∠EOG =∠OEF =∠FGO =90°，∴四边形EFGO 是矩形，∴EF =OG =2，CF =CE -EF =a -2，在Rt △BCD 中，CD BD=tan ∠ABC =tan60°=3，∵∠DFC =∠BGD =∠BDC =90°，∴∠CDF +∠DCF =∠CDF +∠BDG =90°，∴∠DCF =∠BDG ，∴△DCF ∽△BDG ，∴CF DG =DF BG=CD BD ，即a -21=b -12=3，解得：a =2+3，b =1+23，∴点C 的坐标为(2+3，1+23)；(2)如图2，以OA 为边作等边三角形OAM ，使点M 落在第一象限，作射线MP 交⊙P 于点C 、C ′，分别以AC 、AC ′为边作等边△ABC 和等边△AB ′C ′，连接AP ，取BB ′的中点Q ，连接AQ 、PQ ，点B 、B ′均在x 轴正半轴上，过点P 作PH ⊥y 轴于点H ，则AB =AC ，AB ′=AC ′，∠BAC =∠B ′AC ′=60°，∴∠BAB ′+∠B ′AC =∠B ′AC +∠CAC ′，∴∠BAB ′=∠CAC ′，∴△BAB ′≌△CAC ′(SAS )，∴BB ′=CC ′=2r ，BQ =CP =r ，∠ABQ =∠ACP ，∴△ABQ ≌△ACP (SAS )，∴AQ =AP ，∠BAQ =∠CAP ，∴∠PAQ =∠CAP +∠CAQ =∠BAQ +∠CAQ =∠BAC =60°，∴△PAQ 是等边三角形，∴AP =AQ ，∵AP 2=PH 2+AH 2=(33)2+42=43，AQ 2=OA 2+OQ 2=22+OQ 2，∴22+OQ 2=43，∵OQ >0，∴OQ =39，∴0<r ≤39．【点评】本题是几何变换综合题，考查了勾股定理，等边三角形的判定和性质，直角三角形性质，全等三角形的判定和性质，相似三角形的判定和性质等，添加辅助线构造全等三角形和相似三角形是解题关键．8(2023•长春一模)如图，在Rt △ABC 中，∠C =90°，AB =5，sin A =35．点P 从点A 出发，以每秒2个单位长度的速度向终点B 匀速运动，过点P 作PD ⊥AB 交折线AC -CB 于点D ，连结BD ，将△DBP 绕点D 逆时针旋转90°得到△DEF ．设点P 的运动时间为t (秒)．(1)AC =4．(2)用含t 的代数式表示线段PD 的长．(3)当点E 落在AB 边上时，求t 的值．(4)当△DEF 与△ABC 重叠部分为三角形时，直接写出t 的取值范围．【分析】(1)在△ACB 中，sin A =BC AB =35，可得BC =3，再利用勾股定理求出AC ；(2)分两种情形：如图1-1中，当点D 在线段AC 上时，如图1-2中，当点D 在线段BC 上时，分别求出PD 即可；(3)如图2中，当点E 落在AB 上时，PD =PB =2t ，根据AP +PB =5，构建方程求解即可；(4)当E 或F 在△ABC 内部时，△DEF 与△ABC 重叠部分为三角形，求出几个特殊位置的t 的值，可得结论．【解答】解：(1)在△ACB 中，∠C =90°，AB =5，∴sin A =BC AB=35，∴BC =3，∴AC =AB 2-BC 2=52-32=4．故答案为：4；(2)如图1-1中，当点D 在线段AC 上时，0<t ≤85，∵AP =2t ，∴tan A =DP AP =34，∴PD =32t ．如图1-2中，当点D 在线段BC 上时，85<t ≤52．∵tan B =DP PB =43，∴PD =43(5-2t )，综上所述，PD =32t 0<t ≤85 43(5-2t )85<t ≤52；(3)如图2中，当点E落在AB上时，PD=PB=32t，∵AP+PB=5，∴2t+32t=5，解得t=10 7，∴t=107时，点E落在AB上；(4)如图3中，当点F落在AC边上时，CD+BD=3，∴35×43(5-2t)+53(5-2t)=3，解得，t=7037．观察图象可知当7037<t<52时，点F落在△ABC内部．综合(3)(4)可知，当E或F在△ABC内部时，△DEF与△ABC重叠部分为三角形，当点D与C重合时，2t=4×4 5，解得t=8 5，∴满足条件的t的值为：107≤t≤85或7037≤t<52．【点评】本题属于几何变换综合题，考查了旋转变换，解直角三角形，三角形的面积等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题，属于中考压轴题．9(2023•市中区一模)(1)①如图1，等腰△ABC(BC为底)与等腰△ADE(DE为底)，∠BAC=∠DAE，则BD与CE的数量关系为BD=CE；②如图2，矩形ABCD中，AB=3，AD=4，则sin∠DAC=　35　；(2)如图3，在(1)②的条件下，点E在线段CD上运动，将AE绕点A顺时针旋转得到AF，使∠EAF=∠DAC，连接CF．当AE=32时，求CF的长度；(3)如图4，矩形ABCD中，若AB=23，AD=6，点E在线段CD上运动，将AE绕点A顺时针旋转得到AF，旋转角等于∠BAC，连结CF，AE的中点为G，CF的中点为H，若GH=13，直接写出DE的长．【分析】(1)①证明△BAD≌△CAE(SAS)，由全等三角形的性质得出BD=CE；②由勾股股定理求出AC =5，由正弦的定义可得出答案；(2)连结EF ，延长AD 至M ，使得AM =AC ，连结MC ，证明△AFC ≌△AEM (SAS )，由全等三角形的性质得出CF =ME ，由勾股定理求出ME 的长，则可得出答案；(3)连接CG ，并延长交BA 的延长线于M ，连接MF ，证明△AMG ≌△ECG (AAS )，由全等三角形的性质得出MG =CG ，AM =CE ，由三角形中位线定理得出MF =2GH =213，得出∠BAC =60°，AC =2AB =43，延长AB 至N ，使AB =BN ，连接NF ，过点F 作FP ⊥AN 于点P ，设AN =NF =x ，由勾股定理求出x ，则可得出答案．【解答】解：(1)①∵∠BAC =∠DAE ，∴∠BAC -∠CAD =∠DAE -∠CAD ，即∠BAD =∠CAE ，在△BAD 和△CAE 中，BA =CA∠BAD =∠CAE AD =AE，∴△BAD ≌△CAE (SAS )，∴BD =CE ．故答案为：BD =CE ；②矩形ABCD 中，AB =CD =3，AD =4，∴AC =AD 2+CD 2=5，∴sin ∠DAC =CD AC=35，故答案为：35；(2)连结EF ，延长AD 至M ，使得AM =AC ，连结MC ，∵将AE 绕点A 顺时针旋转得到AF ，∴AE =AF ，又∵∠DAC =∠EAF ，∴∠CAF =∠EAM ，∴△AFC ≌△AEM (SAS )，∴CF =ME ，在Rt △ADE 中，AE =32，AD =4，∴DM =AM -AD =1，DE =AE 2-AD 2=2，∴ME =DE 2+DM 2=3，∴CF =3；(3)43-4．连接CG ，并延长交BA 的延长线于M ，连接MF ，∵AB ∥CE ，G 为AE 的中点，∴∠AMG =∠ECG ，∠MAG =∠ECG ，AE =EG ，∴△AMG ≌△ECG (AAS )，∴MG =CG ，AM =CE ，∵H 是CF 的中点，GH =13，∴GH 是△CMF 的中位线，∴MF =2GH =213，∵矩形ABCD 中，AB =23，DC =AD =6，∴∠BAC =60°，AC =2AB =43，延长AB 至N ，使AB =BN ，连接NF ，∴AN =AC ，∠NAC =∠EAF =60°，同(1)①可知△ANF ≌△ACE ，∴NF =CE ，∠ANF =∠ACE =60°，∵AN =AC ，∠NAC =60°，∴∠ANC =60°，∴∠ANC =∠ANF ，∴点N ，F ，C 三点共线，过点F 作FP ⊥AN 于点P ，设AN =NF =x ，在Rt △PNF 中，∠N =60°，NF =x ，∴PN =12x ，PF =32x ，在Rt △MPF 中，PF 2+MP 2=MF 2，MP =MA +AN +PN =43+12x ，MF =213，∴32x2+43+12x 2=(213)2，解得x =4-23(负值舍去)，∴NF =CE =4-23，∴DE =CD -CE =23-(4-23)=43-4．【点评】本题是几何变换综合题，考查了旋转的性质，矩形的性质，等腰三角形的性质，全等三角形的判定与性质，勾股定理，三角形中位线定理，熟练掌握全等三角形的判定与性质是解题的关键．10(2023•武汉模拟)问题提出：如图，△ABC 为等边三角形，D 为CB 的延长线上一点，∠DAE =∠DEA ，探究BD 与EC 的数量关系．问题探究：(1)现将问题特殊化，如图2，当E 为AC 的中点，DM ⊥AC 于点M ，探究DB 与EC 的数量关系，说明理由；(2)再探究一般情形，如图1，(1)中的结论还成立吗？问题拓展：(3)如图3，若AE =nEC ，AB 与DE 交于点F ，直接写出tan ∠DFB 的值(用含n 的式子表示)．【分析】(1)如图2，过点E 作EH ∥AB ，交BC 于H ，证明△ADB ≌△DEH (AAS )，可得结论；(2)如图1，过点E 作EH ∥AB ，交BC 于H ，同理可得结论；(3)如图3，过点E 作EH ∥AB ，交BC 于H ，过点A 作AG ⊥BC 于G ，则∠DEH =∠DFB ，设CE =a，证明∠ADB=∠DFB，根据三角函数的定义可解答．【解答】解：(1)DB=EC，理由如下：∵△ABC是等边三角形，∴∠ABC=∠BAC=∠C=60°，如图2，过点E作EH∥AB，交BC于H，∴∠CHE=∠ABC=60°，∠CEH=∠BAC=60°，∴∠CHE=∠C=∠CEH=60°，∴EH=CE，∵∠ABC=∠CHE，∴∠ABD=∠DHE，∵∠DAE=∠DEA，∴AD=DE，∵∠DAE=∠BAD+∠BAC，∠AED=∠CDE+∠C，∴∠BAD=∠CDE，∴△ADB≌△DEH(AAS)，∴BD=EH，∴BD=CE；(2)如图1，(1)中的结论还成立，理由如下：如图1，过点E作EH∥AB，交BC于H，同理可得：BD=CE；(3)如图3，过点E作EH∥AB，交BC于H，过点A作AG⊥BC于G，则∠DEH=∠DFB，由(2)知：△ADB≌△DEH，∴∠ADB=∠DEH，∴∠DFB=∠ADB，设CE=a，∵AE=nEC，∴AC=BC=(n+1)a，∵△ABC是等边三角形，AG⊥BC，∴BG=CG=(n+1)a2，∠CAG=30°，∴AG=3CG，Rt△ADG中，tan∠ADB=AGDG=tan∠DFB，∴tan∠DFB=3×(n+1)a2a+(n+1)a2=3(n+1)n+3．【点评】本题是三角形综合题，主要考查了等边三角形的性质和判定，全等三角形的判定与性质，勾股定理，三角函数等知识；熟练掌握全等三角形的判定与性质是解题的关键．11(2023•二道区校级模拟)如图，在Rt△ABC中，∠B=90°，AB=4，sin C=45．点P从点A出发，以每秒4个单位长度的速度向终点B匀速运动，点Q为线段BP的中点．点D与点C在PQ的同侧，且∠DPQ =90°，∠DQP =∠C ．设点P 的运动时间为t (秒)．(1)线段PQ 的长为2-2t (用含t 的代数式表示)；(2)当点D 落在AC 边上时，求PD 的长；(3)当△DPQ 与△ABC 重叠部分是轴对称图形时，求t 的值；(4)当点D 到△ABC 任意两边距离相等时，直接写出t 的值．【分析】(1)根据BP =4-4t ，再利用中点的定义可得答案；(2)首先求得AC =5，BC =3，再根据tan ∠DQP =∠tan C ，求出DP ，从而列出方程即可得出答案；(3)设QD 与AC 交于点E ，由重叠部分是轴对称图形时，则∠QEA =90°，QE =PQ =2-2t ，根据sin A =QE AQ=35，即可解决问题；(4)分点D 到AB 、BC 距离相等或点D 到BC 、AC 距离相等或点D 到AB 、AC 距离相等，分别列出关于t 的方程，解方程即可．【解答】解：(1)由题意知，AP =4t ，∴BP =4-4t ，∵点Q 为BP 的中点，∴PQ =12BP =2-2t ，故答案为：2-2t ；(2)在Rt △ABC 中，∠B =90°，∴sin C =AB AC=45，∴AC =5，由勾股定理得，BC =3，∵∠DQP =∠C ，∴tan ∠DQP =∠tan C ，∴DP QP=43，∴DP =43(2-2t )=8-8t 3，∴PD =AP •tan A =4t ×34=3t ，∴3t =8-8t 3，解得t =817，∴PD =2417；(3)设QD 与AC 交于点E ，当△DPQ 与△ABC 重叠部分是轴对称图形时，则∠QEA =90°，QE =PQ =2-2t ，∴sin A =QE AQ=35，∴2-2t 4t +2-2t =35，解得t =14；(4)当点D 到AB 与BC 距离相等时，则DP =PB ，∴8-8t 3=4-4t ，解得t =1，∵0<t <1，∴t =1舍去，当点D 到BC 与AC 距离相等时，则DG ⊥BC 于G ，DH ⊥AC 于H ，连接DB 、DA 、DC ，则四边形BGDP 是矩形，∴DG =PB =4-4t ，∴S △ABD +S △ACD +S △BCD =S △ABC ，∴12×4×8-8t 3 +12×3×(4-4t )+12×5×(4-4t )=12×3×4，解得t =2332，当点D 到AB 与AC 距离相等时，同理可得12×4×8-8t 3 +12×3×(4-2t )+12×5×8-8t 3 =12×3×4，解得t =23，综上：t =2332或23．【点评】本题是几何变换综合题，主要考查了直角三角形的性质，轴对称图形的性质，三角函数，三角形的面积等知识，运用面积法列方程是解决问题(3)的关键，同时注意分类讨论思想的运用．12(2023•惠水县一模)如图，平行四边形ABCD 中，AB =7，BC =10．点P 是BC 边上的一点，连接AP ，以AP 为对称轴作△ABP 的轴对称图形△AQP ．(1)动手操作当点Q 正好落在AD 边上时，在图①中画出△ABP 的轴对称图形△AQP ，并判断四边形ABPQ 的形状是菱形；(2)问题解决如图②，当点P 是线段BC 中点，且CQ =2时，求AP 的长；(3)拓展探究如图③，当点P 、Q 、D 在同一直线上，且∠PQC =∠PQA 时，求PQ 的长．。

2022闵行二模18、24、25解法分析

2022闵行二模18、24、25解法分析
闵行二模18题解法
解法分析：闵行二模18题是直角三角形背景下的翻折问题。

首先根据题意画出图形，由M是中点，且A'M⊥AB，确定A'的位置，再根据题意分析图形：
通过得到∠B=22.5°，从而有以下两种解法：解法1：利用22.5°的特殊角的三角比进行计算
解法2：利用角平分线分线段成比例定理
模型链接模型1：特殊角的锐角三角比
模型2：角平分线分线段成比例定理
闵行二模24题解法
解法分析：闵行二模24题是二次函数背景下的圆内切问题。

本题的第一问是利用待定系数法求二次函数解析式。

本题的第二问是圆内切问题，找准两圆半径和圆心距，即BG、EF 和EG间的数量关系。

首先需要分类讨论，即GE=GB-EF或GE=EF-GB两种情况，而EB=GB-GE，因此通过作图分析具体情况。

由第①问得到的数量关系，设BD=t，借助锐角三角比，用含t的代数式表示DF 的长度，最后代入抛物线中，求出F点坐标。

同类题链接
闵行二模25题解法
解法分析：闵行二模25题是梯形与圆背景下与比例线段和解三角形相关的问题。

本题的第一问通过作高解梯形求AD的长度。

这也是常见的辅助线的添线方法。

本题的第二问是构造基本图形建立函数关系。

根据AC:CG，联想延长AD、MN构造X型基本图形。

两次利用X型基本图形，建立函数关系。

本题的第三问是求线段长度，但是需要分类讨论，即M在线段BC 或其延长线上两种情况。

根据第二问中构造的基本图形，借助锐角三角比和边的数量关系，从而构造等量关系。

中考翻折问题答案解析

翻折问题---解答题综合1．△AOB在平面直角坐标系中的位置如图所示，其中，A（0，﹣3），B（﹣2，0），O是坐标原点．（1）将△AOB先作其关于x轴的对称图形，再把新图形向右平移3个单位，在图中画出两次变换后所得的图形△AO1B1；（2）若点M（x，y）在△AOB上，则它随上述两次变换后得到点M1，则点M1的坐标是．2．（1）数学课上，老师出了一道题，如图①，Rt△ABC中，∠C=90°，，求证：∠B=30°，请你完成证明过程．（2）如图②，四边形ABCD是一张边长为2的正方形纸片，E、F分别为AB、CD的中点，沿过点D的折痕将纸片翻折，使点A落在EF上的点A′处，折痕交AE于点G，请运用（1）中的结论求∠ADG的度数和AG的长．（3）若矩形纸片ABCD按如图③所示的方式折叠，B、D两点恰好重合于一点O（如图④），当AB=6，求EF的长．3．如图，矩形ABCD中，AB=6，BC=8，点E是射线CB上的一个动点，把△DCE沿DE折叠，点C的对应点为C′．（1）若点C′刚好落在对角线BD上时，BC′=；（2）若点C′刚好落在线段AB的垂直平分线上时，求CE的长；（3）若点C′刚好落在线段AD的垂直平分线上时，求CE的长．4．如图，矩形纸片ABCD，将△AMP和△BPQ分别沿PM和PQ折叠（AP＞AM），点A和点B都与点E重合；再将△CQD沿DQ折叠，点C落在线段EQ上点F处．（1）判断△AMP，△BPQ，△CQD和△FDM中有哪几对相似三角形？（不需说明理由）（2）如果AM=1，sin∠DMF=，求AB的长．5．如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作分、FG∥CD，交AE于点G连接DG．（1）求证：四边形DEFG为菱形；（2）若CD=8，CF=4，求的值．6．如图1，一张菱形纸片EHGF，点A、D、C、B分别是EF、EH、HG、GF边上的点，连接AD、DC、CB、AB、DB，且AD=，AB=；如图2，若将△FAB、△AED、△DHC、△CGB分别沿AB、AD、DC、CB对折，点E、F都落在DB上的点P处，点H、G都落在DB上的点Q处．（1）求证：四边形ADCB是矩形；（2）求菱形纸片EHGF的面积和边长．7．（1）操作发现：如图①，在Rt△ABC中，∠C=2∠B=90°，点D是BC上一点，沿AD折叠△ADC，使得点C恰好落在AB上的点E处．请写出AB、AC、CD之间的关系；（2）问题解决：如图②，若（1）中∠C≠90°，其他条件不变，请猜想AB、AC、CD之间的关系，并证明你的结论；（3）类比探究：如图③，在四边形ABCD中，∠B=120°，∠D=90°，AB=BC，AD=DC，连接AC，点E是CD上一点，沿AE折叠，使得点D正好落在AC上的F处，若BC=，直接写出DE的长．8．如图，现有一张边长为4的正方形纸片ABCD，点P为AD边上的一点（不与点A、点D重合），将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，联结BP、BH．（1）求证：∠APB=∠BPH；（2）求证：AP+HC=PH；（3）当AP=1时，求PH的长．9．如图，折叠矩形纸片ABCD，使点B落在AD边上一点E处，折痕的两端点分别在边AB，BC上（含端点），且AB=6，BC=10，设AE=x．（1）当BF的最小值等于时，才能使点B落在AD上一点E处；（2）当点F与点C重合时，求AE的长；（3）当AE=3时，点F离点B有多远？10．如图，三角形纸片中，AB=8cm，BC=6cm，AC=5cm．沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，求△ADE的周长．11．【问题提出】如果我们身边没有量角器和三角板，如何作15°大小的角呢？【实践操作】如图．第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开，得到AD∥EF∥BC．第二步：再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM．折痕BM 与折痕EF 相交于点P．连接线段BN，PA，得到PA=PB=PN．【问题解决】（1）求∠NBC的度数；（2）通过以上折纸操作，还得到了哪些不同角度的角？请你至少再写出两个（除∠NBC的度数以外）．（3）你能继续折出15°大小的角了吗？说说你是怎么做的．12．已知矩形ABCD中，AB=3cm，AD=4cm，点E、F分别在边AD、BC上，连接B、E，D、F．分别把Rt△BAE 和Rt△DCF沿BE，DF折叠成如图所示位置．（1）若得到四边形BFDE是菱形，求AE的长．（2）若折叠后点A′和点C′恰好落在对角线BD上，求AE的长．13．如图1，矩形纸片ABCD的边长AB=4cm，AD=2cm．同学小明现将该矩形纸片沿EF折痕，使点A与点C重合，折痕后在其一面着色（如图2），观察图形对比前后变化，回答下列问题：（1）GF FD：（直接填写=、＞、＜）（2）判断△CEF的形状，并说明理由；（3）小明通过此操作有以下两个结论：①四边形EBCF的面积为4cm2②整个着色部分的面积为5.5cm2运用所学知识，请论证小明的结论是否正确．14．操作：准备一张长方形纸，按下图操作：（1）把矩形ABCD对折，得折痕MN；（2）把A折向MN，得Rt△AEB；（3）沿线段EA折叠，得到另一条折痕EF，展开后可得到△EBF．探究：△EBF的形状，并说明理由．15．1）如图1，将△ABC纸片沿DE折叠，使点A落在四边形BCDE内点A′的位置，若∠A=40°，求∠1+∠2的度数；（2）通过（1）的计算你发现∠1+∠2与∠A有什么数量关系？请写出这个数量关系，并说明这个数量关系的正确性；（3）将图1中△ABC纸片的三个内角都进行同样的折叠．①如果折叠后三个顶点A、B、C重合于一点O时，如图2，则图中∠α+∠β+∠γ=；∠1+∠2+∠3+∠4+∠5+∠6=；②如果折叠后三个顶点A、B、C不重合，如图3，则①中的关于“∠1+∠2+∠3+∠4+∠5+∠6”的结论是否仍然成立？请说明你的理由．16．如图，长方形纸片ABCD，点E、F分别在边AB、CD上，连接EF，将∠BEF对折，点B落在直线EF上的B′处，得到折痕EC，将点A落在直线EF上的点A′处，得到折痕EN．（1）若∠BEB′=110°，则∠BEC=°，∠AEN=°，∠BEC+∠AEN=°．（2）若∠BEB′=m°，则（1）中∠BEC+∠AEN的值是否改变？请说明你的理由．（3）将∠ECF对折，点E刚好落在F处，且折痕与B′C重合，求∠DNA′．17．如图△ABC中，∠B=60°，∠C=78°，点D在AB边上，点E在AC边上，且DE∥BC，将△ADE沿DE折叠，点A对应点为F点．（1）若点A落在BC边上（如图1），求证：△BDF是等边三角形；（2）若点A落在三角形外（如图2），且CF∥AB，求△CEF各内角的度数．18．如图1，四边形OABC中，OA=a，OC=3，BC=2，∠AOC=∠BCO=90°，经过点O的直线l将四边形分成两部分，直线l与OC所成的角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处（如图1）．（1）若折叠后点D恰为AB的中点（如图2），则θ=；（2）若θ=45°，四边形OABC的直角∠OCB沿直线l折叠后，点B落在点四边形OABC的边AB上的E处（如图3），求a的值．19．在△ABC中，∠C=90°，AC=6，BC=8，D、E分别是斜边AB和直角边CB上的点，把△ABC沿着直线DE折叠，顶点B的对应点是B′．（1）如图（1），如果点B′和顶点A重合，求CE的长；（2）如图（2），如果点B′和落在AC的中点上，求CE的长．20．把一张矩形纸片ABCD按如图方式折叠，使顶点B和D重合，折痕为EF．（1）连接BE，求证：四边形BFDE是菱形；（2）若AB=8cm，BC=16cm，求线段DF和EF的长．21．如图，矩形ABCD中，AB=8cm，BC=6cm，动点P从点A出发，以每秒1cm的速度沿线段AB向点B运动，连接DP，把∠A沿DP折叠，使点A落在点A′处．求出当△BPA′为直角三角形时，点P运动的时间．22．在矩形ABCD中，=a，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．如图1，当DH=DA时，（1）填空：∠HGA=度；（2）若EF∥HG，求∠AHE的度数，并求此时a的最小值；23．如图1，△ABC中，沿∠BAC的平分线AB1折叠，点B落在A1处．剪掉重叠部分；将余下部分沿∠B1A1C 的平分线A1B2折叠，点B1落在A2处．剪掉重叠部分；…；将余下部分沿∠B n A n C的平分线A n B n+1折叠，点B n 与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C 的平分线A1B2折叠，此时点B1与点C重合．（1）情形二中，∠B与∠C的等量关系．（2）若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C的等量关系．（3）如果一个三角形的最小角是4°，直接写出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．答：．24．在矩形纸片ABCD中，AB=6，BC=8，将矩形纸片折叠，使点B与点D重合（如图），（1）求证：四边形BEDF 是菱形；（2）求折痕EF的长．25．如图1，ABCD是一张矩形纸片，AD=BC=1，AB=CD=5．在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK，KB交MN于O．（1）若∠1=80°，求∠MKN的度数；（2）当B与D重合时，画出图形，并求出∠KON的度数；（3）△MNK的面积能否小于2？若能，求出此时∠1的度数；若不能，试说明理由．26．七年级科技兴趣小组在“快乐星期四”举行折纸比赛，折叠过程是这样的（阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为26厘米，回答下列问题：（1）如果长方形纸条的宽为2厘米，并且开始折叠时起点M与点A的距离为3厘米，那么在图②中，BM=厘米；在图④中，BM=厘米．（2）如果信纸折成的长方形纸条宽为2cm，为了保证能折成图④形状（即纸条两端均刚好到达点P），纸条长至少多少厘米？纸条长最小时，长方形纸条面积是多少？（3）如果不但要折成图④的形状，而且为了美观，希望纸条两端超出点P的长度相等，即最终图形是对称图形，假设长方形纸条的宽为x厘米，试求在开始折叠时（图①）起点M与点A的距离（用含x的代数式表示）．（温馨提示：别忘了用草稿纸来折一折哦！）27．将四张形状，大小相同的长方形纸片分别折叠成如图所示的图形，请仔细观察重叠部分的图形特征，并解决下列问题：（1）观察图①，②，③，④，∠1和∠2有怎样的关系？并说明你的依据．（2）猜想图③中重叠部分图形△MBD的形状（按边），验证你的猜想．（3）若图④中∠1=60°，猜想重叠部分图形△MEF的形状（按边），验证你的猜想．28．如图，长方形纸片ABCD中，AB=10，将纸片折叠，使顶点B落在边AD上的E点处，折痕的一端G点在边BC上．（1）如图（1），当折痕的另一端F在AB边上且AE=5时，求AF的长；（2）如图（2），当折痕的另一端F在AD边上且BG=13时，求AF的长．29．矩形ABCD沿EF折叠，使点B落在AD边上的B′处，再沿B′G折叠四边形，使B′D边与B′F重合，且B′D′过点F．已知AB=4，AD=1（1）试探索EF与B′G的位置关系，并说明理由；（2）若四边形EFGB′是菱形，求∠BFE的度数；（3）若点D′与点F重合，求此时图形重叠部分的面积．30．（1）操作发现：如图①，在Rt△ABC中，∠C=2∠B=90°，点D是BC上一点，沿AD折叠△ADC，使得点C恰好落在AB上的点E处，请写出AB、AC、CD之间的关系（2）问题解决：如图②，若（1）中∠C≠90°，其他条件不变，请猜想AB、AC、CD之间的关系，并证明你的结论；（3）类比探究：如图③，在四边形ABCD中，∠B=120°，∠D=90°，AB=BC，AD=DC，连接AC，点E是CD上一点，沿AE折叠，使得点D正好落在AC上的点F处，若BC=3，直接写出DE的长．翻折问题---解答题综合参考答案与试题解析一．解答题（共30小题）1．（2016•安徽模拟）△AOB在平面直角坐标系中的位置如图所示，其中，A（0，﹣3），B（﹣2，0），O是坐标原点．（1）将△AOB先作其关于x轴的对称图形，再把新图形向右平移3个单位，在图中画出两次变换后所得的图形△AO1B1；（2）若点M（x，y）在△AOB上，则它随上述两次变换后得到点M1，则点M1的坐标是（x+3，﹣y）．【分析】（1）首先确定A、B、C三点关于x轴的对称点位置，再向右平移3个单位找到对应点位置，然后再连接即可；（2）根据关于x轴对称的点的坐标特点：横坐标不变，纵坐标相反可得点M（x，y）关于x轴的对称图形上的点的坐标为（x，﹣y），再向右平移3个单位，点的横坐标+3，纵坐标不变．【解答】解：（1）如图所示：（2）点M（x，y）关于x轴的对称图形上的点的坐标为（x，﹣y），再向右平移3个单位得到点M1的坐标是（x+3，﹣y）．故答案为：（x+3，﹣y）．【点评】此题主要考查了作图﹣﹣平移变换和轴对称变换，关键是掌握点的坐标的变化规律．2．（2016•贵阳模拟）（1）数学课上，老师出了一道题，如图①，Rt△ABC中，∠C=90°，，求证：∠B=30°，请你完成证明过程．（2）如图②，四边形ABCD是一张边长为2的正方形纸片，E、F分别为AB、CD的中点，沿过点D的折痕将纸片翻折，使点A落在EF上的点A′处，折痕交AE于点G，请运用（1）中的结论求∠ADG的度数和AG的长．（3）若矩形纸片ABCD按如图③所示的方式折叠，B、D两点恰好重合于一点O（如图④），当AB=6，求EF的长．【分析】（1）Rt△ABC中，根据sinB═=，即可证明∠B=30°；（2）求出∠FA′D的度数，利用翻折变换的性质可求出∠ADG的度数，在Rt△A'FD中求出A'F，得出A'E，在Rt△A'EG 中可求出A'G，利用翻折变换的性质可得出AG的长度．（3）先判断出AD=AC，得出∠ACD=30°，∠DAC=60°，从而求出AD的长度，根据翻折变换的性质可得出∠DAF=∠FAO=30°，在Rt△ADF中求出DF，继而得出FO，同理可求出EO，再由EF=EO+FO，即可得出答案．【解答】（1）证明：Rt△ABC中，∠C=90°，，∵sinB==，∴∠B=30°；（2）解：∵正方形边长为2，E、F为AB、CD的中点，∴EA=FD=×边长=1，∵沿过点D的抓痕将纸片翻折，使点A落在EF上的点A′处，∴A′D=AD=2，∴=，∴∠FA′D=30°，可得∠FDA′=90°﹣30°=60°，∵A沿GD折叠落在A′处，∴∠ADG=∠A′DG，AG=A′G，∴∠ADG===15°，∵A′D=2，FD=1，∴A′F==，∴EA′=EF﹣A′F=2﹣，∵∠EA′G+∠DA′F=180°﹣∠GA′D=90°，∴∠EA′G=90°﹣∠DA′F=90°﹣30°=60°，∴∠EGA′=90°﹣∠EA′G=90°﹣60°=30°，则A′G=AG=2EA′=2（2﹣）；（3）解：∵折叠后B、D两点恰好重合于一点O，∴AO=AD=CB=CO，∴DA=，∵∠D=90°，∴∠DCA=30°，∵AB=CD=6，在Rt△ACD中，=tan30°，则AD=DC•tan30°=6×=2，∵∠DAF=∠FAO=∠DAO==30°，∴=tan30°=，∴DF=AD=2，∴DF=FO=2，同理EO=2，∴EF=EO+FO=4．【点评】本题考查了翻折变换的知识，涉及了含30°角的直角三角形的性质、平行四边形的性质，综合考察的知识点较多，注意将所学知识融会贯通．3．（2016•贵阳模拟）如图，矩形ABCD中，AB=6，BC=8，点E是射线CB上的一个动点，把△DCE沿DE折叠，点C的对应点为C′．（1）若点C′刚好落在对角线BD上时，BC′=4；（2）若点C′刚好落在线段AB的垂直平分线上时，求CE的长；（3）若点C′刚好落在线段AD的垂直平分线上时，求CE的长．【分析】（1）根据点B，C′，D在同一直线上得出BC′=BD﹣DC′=BD﹣DC求出即可；（2）利用垂直平分线的性质得出CC′=DC′=DC，则△DC′C是等边三角形，进而利用勾股定理得出答案；（3）利用①当点C′在矩形内部时，②当点C′在矩形外部时，分别求出即可．【解答】解：（1）如图1，∵点B，C′，D在同一直线上，∴BC′=BD﹣DC′=BD﹣DC=10﹣6=4；故答案为：4；（2）如图2，连接CC′，∵点C′在AB的垂直平分线上，∴点C′在DC的垂直平分线上，∴CC′=DC′=DC，则△DC′C是等边三角形，设CE=x，易得DE=2x，由勾股定理得：（2x）2﹣x2=62，解得：x=2，即CE的长为2；（3）作AD的垂直平分线，交AD于点M，交BC于点N，分两种情况讨论：①当点C′在矩形内部时，如图3，∵点C′在AD的垂直平分线上，∴DM=4，∵DC′=6，由勾股定理得：MC′=2，∴NC′=6﹣2，设EC=y，则C′E=y，NE=4﹣y，故NC′2+NE2=C′E2，即（6﹣2）2+（4﹣y）2=y2，解得：y=9﹣3，即CE=9﹣3；②当点C′在矩形外部时，如图4，∵点C′在AD的垂直平分线上，∴DM=4，∵DC′=6，由勾股定理得：MC′=2，∴NC′=6+2，设EC=z，则C′E=a，NE=z﹣4故NC′2+NE2=C′E2，即（6+2）2+（z﹣4）2=z2，解得：z=9+3，即CE=9+3，综上所述：CE的长为9±3．【点评】此题主要考查了矩形的性质、翻折变换的性质、勾股定理等知识；利用数形结合以及分类讨论得出是解题关键．4．（2015•南充）如图，矩形纸片ABCD，将△AMP和△BPQ分别沿PM和PQ折叠（AP＞AM），点A和点B都与点E重合；再将△CQD沿DQ折叠，点C落在线段EQ上点F处．（1）判断△AMP，△BPQ，△CQD和△FDM中有哪几对相似三角形？（不需说明理由）（2）如果AM=1，sin∠DMF=，求AB的长．【分析】（1）由矩形的性质得∠A=∠B=∠C=90°，由折叠的性质和等角的余角相等，可得∠BPQ=∠AMP=∠DQC，所以△AMP∽△BPQ∽△CQD；（2）先证明MD=MQ，然后根据sin∠DMF==，设DF=3x，MD=5x，表示出AP、BP、BQ，再根据△AMP∽△BPQ，列出比例式解方程求解即可．【解答】解：（1）△AMP∽△BPQ∽△CQD，∵四边形ABCD是矩形，∴∠A=∠B=∠C=90°，根据折叠的性质可知：∠APM=∠EPM，∠EPQ=∠BPQ，∴∠APM+∠BPQ=∠EPM+∠EPQ=90°，∵∠APM+∠AMP=90°，∴∠BPQ=∠AMP，∴△AMP∽△BPQ，同理：△BPQ∽△CQD，根据相似的传递性，△AMP∽△CQD；（2）∵AD∥BC，∴∠DQC=∠MDQ，根据折叠的性质可知：∠DQC=∠DQM，∴∠MDQ=∠DQM，∴MD=MQ，∵AM=ME，BQ=EQ，∴BQ=MQ﹣ME=MD﹣AM，∵sin∠DMF==，∴设DF=3x，MD=5x，∴BP=PA=PE=，BQ=5x﹣1，∵△AMP∽△BPQ，∴，∴，解得：x=（舍）或x=2，∴AB=6．【点评】本题主要考查了相似三角形的判定与性质、矩形的性质、翻折的性质以及锐角三角函数的综合运用，在求AB长的问题中，关键是恰当的设出未知数表示出一对相似三角形的对应边列比例式．5．（2015•漳州）如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作分、FG∥CD，交AE于点G连接DG．（1）求证：四边形DEFG为菱形；（2）若CD=8，CF=4，求的值．【分析】（1）根据折叠的性质，易知DG=FG，ED=EF，∠1=∠2，由FG∥CD，可得∠1=∠3，易证FG=FE，故由四边相等证明四边形DEFG为菱形；（2）在Rt△EFC中，用勾股定理列方程即可CD、CE，从而求出的值．【解答】（1）证明：由折叠的性质可知：DG=FG，ED=EF，∠1=∠2，∵FG∥CD，∴∠2=∠3，∴FG=FE，∴DG=GF=EF=DE，∴四边形DEFG为菱形；（2）解：设DE=x，根据折叠的性质，EF=DE=x，EC=8﹣x，在Rt△EFC中，FC2+EC2=EF2，即42+（8﹣x）2=x2，解得：x=5，CE=8﹣x=3，∴=．【点评】本题主要考查了折叠的性质、菱形的判定以及勾股定理，熟知折叠的性质和菱形的判定方法是解答此题的关键．6．（2015•江西校级模拟）如图1，一张菱形纸片EHGF，点A、D、C、B分别是EF、EH、HG、GF边上的点，连接AD、DC、CB、AB、DB，且AD=，AB=；如图2，若将△FAB、△AED、△DHC、△CGB分别沿AB、AD、DC、CB对折，点E、F都落在DB上的点P处，点H、G都落在DB上的点Q处．（1）求证：四边形ADCB是矩形；（2）求菱形纸片EHGF的面积和边长．【分析】（1）由对折可知∠EAB=∠PAB，∠FAD=∠PAD，利用等角关系可求出∠BAD=90°，同理可求出∠ADC=∠ABC=90°．即可得出四边形ADCB是矩形．（2）由对折可知S菱形EHGF=2S矩形ADCB即可求出EHGF的面积，由对折可得出点A，C为中点，连接AC，得FG=AC=BD．利用勾股定理就可得出边长．【解答】（1）证明：由对折可知∠EAB=∠PAB，∠FAD=∠PAD，∴2（∠PAB+∠PAD）=180°，即∠BAD=∠PAB+∠PAD=90°．同理可得，∠ADC=∠ABC=90°．∴四边形ADCB是矩形．（2）解：由对折可知：△AEB≌△APB，△AFD≌△APD，△CGD≌△CQD，△CHB≌△CQB．∴S菱形EHGF=2S矩形ADCB=．又∵AE=AP=AF，∴A为EF的中点．同理有C为GH的中点．即AF=CG，且AF∥CG，如图2，连接AC，∴四边形ACGF为平行四边形，得FG=AC=BD．∴．【点评】本题主要考查了翻折变换，勾股定理，菱形的性质及矩形的判定，解题的关键是折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．7．（2015•平顶山二模）（1）操作发现：如图①，在Rt△ABC中，∠C=2∠B=90°，点D是BC上一点，沿AD折叠△ADC，使得点C恰好落在AB上的点E处．请写出AB、AC、CD之间的关系AB=AC+CD；（2）问题解决：如图②，若（1）中∠C≠90°，其他条件不变，请猜想AB、AC、CD之间的关系，并证明你的结论；（3）类比探究：如图③，在四边形ABCD中，∠B=120°，∠D=90°，AB=BC，AD=DC，连接AC，点E是CD上一点，沿AE折叠，使得点D正好落在AC上的F处，若BC=，直接写出DE的长．【分析】（1）如图①，设CD=t，由∠C=2∠B=90°易得△ABC为等腰直角三角形，则AC=BC，AB=AC，再根据折叠的性质得DC=DE，∠AED=∠C=90°，又可判断△BDE为等腰直角三角形，所以BD=DE，则BD=t，AC=BC=t+t=（+1）t，AB=•（+1）t=（2+）t，从而得到AB=AC+CD；（2）如图②，根据折叠的性质得DC=DE，∠AED=∠C，AE=AC，而∠C=2∠B，则∠AED=2∠B，根据三角形外角性质得∠AED=∠B+∠BDE，所以∠B=∠BDE，则EB=ED，所以ED=CD，于是得到AB=AE+BE=AC+CD；（3）作BH⊥AC于H，如图③，设DE=x，利用（1）的结论得AC=（2+）x，根据等腰三角形的性质由BA=BC，∠CBA=120°得到∠BCA=∠BAC=30°，且CH=AH=AC=x，在Rt△BCH中，利用30度的余弦得cos30°==，即x=（2+2），然后解方程求出x即可．【解答】解：（1）如图①，设CD=t，∵∠C=2∠B=90°，∴∠B=45°，∠BAC=45°，∴△ABC为等腰直角三角形，∴AC=BC，AB=AC，∵AD折叠△ADC，使得点C恰好落在AB上的点E处，∴DC=DE，∠AED=∠C=90°，∴△BDE为等腰直角三角形，∴BD=DE，∴BD=t，∴AC=BC=t+t=（+1）t，∴AB=•（+1）t=（2+）t，∴AB=AC+CD；故答案为AB=AC+CD；（2）AB=AC+CD．理由如下：如图②，∵AD折叠△ADC，使得点C恰好落在AB上的点E处，∴DC=DE，∠AED=∠C，AE=AC，∵∠C=2∠B，∴∠AED=2∠B，而∠AED=∠B+∠BDE，∴∠B=∠BDE，∴EB=ED，∴ED=CD，∴AB=AE+BE=AC+CD；（3）作BH⊥AC于H，如图③，设DE=x，由（1）的结论得AC=（2+）x，∵BA=BC，∠CBA=120°，∴∠BCA=∠BAC=30°，∵BH⊥AC，∴CH=AH=AC=x，在Rt△BCH中，cos30°==，∴x=（2+2），解得x=，即DE的长为．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了等腰三角形的性质和解直角三角形．8．（2015•潍坊校级一模）如图，现有一张边长为4的正方形纸片ABCD，点P为AD边上的一点（不与点A、点D重合），将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，联结BP、BH．（1）求证：∠APB=∠BPH；（2）求证：AP+HC=PH；（3）当AP=1时，求PH的长．【分析】（1）根据翻折变换的性质得出∠PBC=∠BPH，进而利用平行线的性质得出∠APB=∠PBC即可得出答案；（2）首先证明△ABP≌△QBP，进而得出△BCH≌△BQH，即可得出AP+HC=PH；（3）设QH=HC=x，则DH=4﹣x．在Rt△PDH中，根据勾股定理列出关于x的方程求解即可．【解答】（1）证明：∵PE=BE，∴∠EPB=∠EBP，又∵∠EPH=∠EBC=90°，∴∠EPH﹣∠EPB=∠EBC﹣∠EBP．即∠BPH=∠PBC．又∵四边形ABCD为正方形∴AD∥BC，∴∠APB=∠PBC．∴∠APB=∠BPH．（2）证明：过B作BQ⊥PH，垂足为Q，由（1）知，∠APB=∠BPH，在△ABP与△QBP中，，∴△ABP≌△QBP（AAS），∴AP=QP，BA=BQ．又∵AB=BC，∴BC=BQ．又∵∠C=∠BQH=90°，∴△BCH和△BQH是直角三角形，在Rt△BCH与Rt△BQH中，∴Rt△BCH≌Rt△BQH（HL），∴CH=QH，∴AP+HC=PH．（3）解：由（2）知，AP=PQ=1，∴PD=3．设QH=HC=x，则DH=4﹣x．在Rt△PDH中，PD2+DH2=PH2，即32+（4﹣x）2=（x+1）2，解得x=2.4，∴PH=3.4．【点评】此题主要考查了翻折变换的性质以及全等三角形的判定与性质和勾股定理等知识，熟练利用全等三角形的判定得出对应相等关系是解题关键．9．（2015•江西样卷）如图，折叠矩形纸片ABCD，使点B落在AD边上一点E处，折痕的两端点分别在边AB，BC上（含端点），且AB=6，BC=10，设AE=x．（1）当BF的最小值等于6时，才能使点B落在AD上一点E处；（2）当点F与点C重合时，求AE的长；（3）当AE=3时，点F离点B有多远？【分析】（1）当点G与点A重合时，BF的值最小，即可求出BF的最小值等于6；（2）在RT△CDE中运用勾股定理求出DE，再利用AE=AD﹣DE即可求出答案；（3）作FH⊥AD于点H，设AG=x，利用勾股定理可先求出AG，可得EG，利用△AEG∽△HFE，由=可求出EF，即得出BF的值．【解答】解：（1）点G与点A重合时，如图1所示，四边形ABFE是正方形，此时BF的值最小，即BF=AB=6．当BF的最小值等于6时，才能使B点落在AD上一点E处；故答案为：6．（2）如图2所示，∵在Rt△CDE中，CE=BC=10，CD=6，∴DE===8，∴AE=AD﹣DE=10﹣8=2，（3）如图3所示，作FH⊥AD于点H，AE=3，设AG=y，则BG=EG=6﹣y，根据勾股定理得：（6﹣y）2=y2+9，解得：y=，∴EG=BG=，又△AEG∽△HFE，∴=，∴，∴EF=，∴BF=EF=．【点评】本题主要考查了翻折变换，解题的关键是折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．10．（2015秋•苍溪县期末）如图，三角形纸片中，AB=8cm，BC=6cm，AC=5cm．沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，求△ADE的周长．【分析】根据翻折变换的性质可得DE=CD，BE=BC，然后求出AE，再根据三角形的周长列式求解即可．【解答】解：∵BC沿BD折叠点C落在AB边上的点E处，∴DE=CD，BE=BC，∵AB=8cm，BC=6cm，∴AE=AB﹣BE=AB﹣BC=8﹣6=2cm，∴△ADE的周长=AD+DE+AE，=AD+CD+AE，=AC+AE，=5+2，=7cm．【点评】本题考查了翻折变换的性质，熟记翻折前后两个图形能够完全重合得到相等的线段是解题的关键．11．（2015春•无棣县期末）【问题提出】如果我们身边没有量角器和三角板，如何作15°大小的角呢？【实践操作】如图．第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开，得到AD∥EF∥BC．第二步：再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM．折痕BM 与折痕EF 相交于点P．连接线段BN，PA，得到PA=PB=PN．【问题解决】（1）求∠NBC的度数；（2）通过以上折纸操作，还得到了哪些不同角度的角？请你至少再写出两个（除∠NBC的度数以外）．（3）你能继续折出15°大小的角了吗？说说你是怎么做的．【分析】（1）根据折叠性质由对折矩形纸片ABCD，使AD与BC重合得到点P为BM的中点，即BP=PM，再根据矩形性质得∠BAM=90°，∠ABC=90°，则根据直角三角形斜边上的中线性质得PA=PB=PM，再根据折叠性质由折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM．折痕BM得到PA=PB=PM=PN，∠1=∠2，∠BNM=∠BAM=90°，利用等要三角形的性质得∠2=∠4，利用平行线的性质由EF∥BC得到∠4=∠3，则∠2=∠3，易得∠1=∠2=∠3=∠ABC=30°；（2）利用互余得到∠BMN=60°，根据折叠性质易得∠AMN=120°；（3）把30度的角对折即可．【解答】解：（1）∵对折矩形纸片ABCD，使AD与BC重合，∴点P为BM的中点，即BP=PM，∵四边形ABCD为矩形，∴∠BAM=90°，∠ABC=90°，∴PA=PB=PM，∵折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM．折痕BM，∴PA=PB=PM=PN，∠1=∠2，∠BNM=∠BAM=90°，∴∠2=∠4，∵EF∥BC，∴∠4=∠3，∴∠2=∠3，∴∠1=∠2=∠3=∠ABC=30°，即∠NBC=30°；（2）通过以上折纸操作，还得到了∠BMN=60°，∠AMN=120°等；（3）折叠纸片，使点A落在BM上，则可得到15°的角．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了矩形的性质和直角三角形斜边上的中线性质．12．（2015春•大同期末）已知矩形ABCD中，AB=3cm，AD=4cm，点E、F分别在边AD、BC上，连接B、E，D、F．分别把Rt△BAE和Rt△DCF沿BE，DF折叠成如图所示位置．（1）若得到四边形BFDE是菱形，求AE的长．（2）若折叠后点A′和点C′恰好落在对角线BD上，求AE的长．【分析】（1）由矩形的性质得出∠A=90°，设AE=xcm，则ED=（4﹣x）cm，由菱形的性质得出EB=ED=4﹣x，由勾股定理得出方程，解方程即可；（2）由勾股定理求出BD，由折叠的性质得出A′E=AE，∠EA′B=∠A=90°，A′B=AB=3cm，求出A′D，设AE=A′E=x，则ED=（4﹣x）cm，在Rt△EA′D中，由勾股定理得出方程，解方程即可．【解答】解：（1）∵四边形ABCD是矩形，∴∠A=90°，设AE=xcm，则ED=（4﹣x）cm，∵四边形EBFD是菱形，∴EB=ED=4﹣x，由勾股定理得：AB2+AE2=BE2，即32+x2=（4﹣x）2，解得：x=，∴AE=cm；（2）根据勾股定理得：BD==5cm，由折叠的性质得：A′E=AE，∠EA′B=∠A=90°，A′B=AB=3cm，∴∠EA′D=90°，A′D=5﹣3=2（cm），设AE=A′E=x，则ED=（4﹣x）cm，在Rt△EA′D中，A′E2+A′D2=ED2，即x2+22=（4﹣x）2，解得：x=，∴AE=cm．【点评】本题考查了翻折变换的性质、矩形的性质、勾股定理、菱形的性质；熟练掌握翻折变换和矩形、菱形的性质，并能进行推理计算是解决问题的关键．13．（2015春•廊坊期末）如图1，矩形纸片ABCD的边长AB=4cm，AD=2cm．同学小明现将该矩形纸片沿EF折痕，使点A与点C重合，折痕后在其一面着色（如图2），观察图形对比前后变化，回答下列问题：（1）GF=FD：（直接填写=、＞、＜）（2）判断△CEF的形状，并说明理由；（3）小明通过此操作有以下两个结论：①四边形EBCF的面积为4cm2②整个着色部分的面积为5.5cm2运用所学知识，请论证小明的结论是否正确．【分析】（1）根据翻折的性质解答；（2）根据两直线平行，内错角相等可得∠AEF=∠CFE，再根据翻折的性质可得∠AEF=∠FEC，从而得到∠CFE=∠FEC，根据等角对等边可得CE=CF，从而得解；（3）①根据翻折的性质可得AE=EC，然后求出AE=CF，再根据图形的面积公式列式计算即可得解；②设GF=x，表示出CF，然后在Rt△CFG中，利用勾股定理列式求出GF，根据三角形的面积公式求出S GFC，然后计算即可得解．【解答】解：（1）由翻折的性质，GD=FD；（2）△CEF是等腰三角形．∵矩形ABCD，∴AB∥CD，∴∠AEF=∠CFE，由翻折的性质，∠AEF=∠FEC，∴∠CFE=∠FEC，∴CF=CE，故△CEF为等腰三角形；（3）①由翻折的性质，AE=EC，∵EC=CF，∴AE=CF，∴S四边形EBCF=（EB+CF）•BC=AB•BC=×4×2×=4cm2；②设GF=x，则CF=4﹣x，∵∠G=90°，∴x2+22=（4﹣x）2，解得x=1.5，∴S GFC=×1.5×2=1.5，S着色部分=1.5+4=5.5；综上所述，小明的结论正确．【点评】本题考查了翻折变换的性质，矩形的性质，平行线的性质，等腰三角形的判定，以及勾股定理的应用，熟记翻折前后的两个图形能够完全重合是解题的关键．14．（2015春•娄底期末）操作：准备一张长方形纸，按下图操作：（1）把矩形ABCD对折，得折痕MN；（2）把A折向MN，得Rt△AEB；（3）沿线段EA折叠，得到另一条折痕EF，展开后可得到△EBF．探究：△EBF的形状，并说明理由．【分析】由（1）得出M、N分别是AB、DC的中点，由（2）得出BE=2AP，再由（3）得出BF=2AP，证出BE=BF，因此∠1=∠2，由角的关系求出∠1=60°，即可证出△EBF为等边三角形．【解答】解：△EBF是等边三角形；理由如下：如图所示：由操作（1）得：M、N分别是AB、DC的中点，∴在Rt△ABE中，P为BE的中点，AP是斜边上的中线，∴AP=BP=BE，即BE=2AP，在△EBF中，A是EF的中点，∴AP=BF，即BF=2AP，∴BE=BF，∴∠1=∠2，又∵∠2=∠3，2∠1+∠3=180°，∴3∠1=180°，∴∠1=60°，∴△EBF为等边三角形．【点评】本题考查了矩形的性质、翻折变换的性质、直角三角形斜边上的中线性质、等边三角形的判定；熟练掌握翻折变换和矩形的性质，并能进行推理论证是解决问题的关键．。

新高考数学二轮总复习专题突破练18 立体几何中的翻折问题及探索性问题(含解析)-人教版高三全册数学

专题突破练18 立体几何中的翻折问题及探索性问题1.(2020河北石家庄5月检测,18)如图1,在Rt△ABC中,∠C=90°,BC=AC=4,D,E分别是AC,AB边上的中点,将△ADE沿DE折起到△A1DE的位置,使A1C=A1D,如图2.(1)求证:平面A1CD⊥平面A1BC;(2)求直线A1C与平面A1BE所成角的正弦值.2.(2020贵州贵阳适应性训练,19)如图,在四棱锥P-ABCD中,四边形ABCD为正方形,且平面PAD⊥平面ABCD,F为棱PD的中点.(1)在棱BC上是否存在一点E,使得CF∥平面PAE?并说明理由;(2)若PA=PD=AB,求直线AF与平面PBC所成角的正弦值.3.(2020浙江台州模拟,19)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=3,AA1=2.以AB,BC 为邻边作平行四边形ABCD,连接DA1和DC1.(1)求证:A1D∥平面BCC1B1;(2)在线段BC上是否存在点F,使平面DA1C1与平面A1C1F垂直?若存在,求出BF的长;若不存在,请说明理由.4.(2020云南昆明一中模拟,19)图1是由边长为4的正六边形AEFBCD,矩形DCGH组成的一个平面图形,将其沿AB,DC折起得几何体ABCD-EFGH,使得CG⊥AD,且平面EFGH∥平面ABCD,如图2.(1)证明:在图2中,平面ACG⊥平面BCG;(2)设M为图2中线段CG上一点,且CM=1,若直线AG∥平面BMD,求图2中的直线BM与平面AHB 所成角的正弦值.5.(2020北京通州一模,18)如图1,已知四边形ABCD为菱形,且∠A=60°,取AD中点为E.现将四边形EBCD沿BE折起至EBHG,使得∠AEG=90°,如图2.(1)求证:AE⊥平面EBHG;(2)求二面角A-GH-B的余弦值;(3)若点F 满足AF ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ ,当EF ∥平面AGH 时,求λ的值. 6.如图,在四棱锥P-ABCD 中,PD ⊥平面ABCD ,四边形ABCD 是梯形,且BC ∥AD ,AC=CD=√22AD ,AD=2PD=4BC=4. (1)求证:AC ⊥平面PCD ;(2)求平面PCD 与平面PAB 所成的锐角的余弦值;(3)在棱PD 上是否存在点M ,使得CM ∥平面PAB ?若存在,求PM PD的值;若不存在,说明理由.7.(2020山东省实验中学模拟,19)在矩形ABCD 中,AB=3,AD=2,点E 是线段CD 上靠近点D 的一个三等分点,点F 是线段AD 上的一个动点,且DF ⃗⃗⃗⃗⃗ =λDA ⃗⃗⃗⃗⃗ (0≤λ≤1).如图,将△BEC 沿BE 折起至△BEG ,使得平面BEG ⊥平面ABED. (1)当λ=12时,求证:EF ⊥BG ;(2)是否存在λ,使得FG 与平面DEG 所成的角的正弦值为13?若存在,求出λ的值;若不存在,请说明理由.8.(2020河北衡水中学调研,18)已知,图中直棱柱ABCD-A1B1C1D1的底面是菱形,其中AA1=AC=2BD=4.又点E,F,P,Q分别在棱AA1,BB1,CC1,DD1上运动,且满足BF=DQ,CP-BF=DQ-AE=1.(1)求证:E,F,P,Q四点共面,并证明EF∥平面PQB;(2)是否存在点P使得二面角B-PQ-E的余弦值为√5?如果存在,求出CP的长;如果不存在,请说明理由.5专题突破练18立体几何中的翻折问题及探索性问题1.(1)证明在图1的△ABC中,D,E分别为AC,AB边中点,∴DE∥BC.又AC⊥BC,∴DE⊥AC.在图2中,DE⊥A1D,DE⊥DC,A1D∩DC=D,则DE⊥平面A1CD,又DE∥BC,∴BC⊥平面A1CD.又BC⊂平面A1BC,∴平面A1CD⊥平面A1BC.(2)解由(1)知DE⊥平面A1CD,且DE⊂平面BCDE,∴平面A1CD⊥平面BCDE.又平面A1CD∩平面BCDE=DC,在等边三角形A1CD中过点A1作A1O⊥CD,垂足为O,则O为CD中点,且A1O⊥平面BCDE,分别以DC,梯形BCDE中位线,OA1所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,则A 1(0,0,√3),B (1,4,0),C (1,0,0),E (-1,2,0).A 1C ⃗⃗⃗⃗⃗⃗⃗ =(1,0,-√3),EA 1⃗⃗⃗⃗⃗⃗⃗ =(1,-2,√3),EB ⃗⃗⃗⃗⃗ =(2,2,0).设平面A 1BE 的法向量为n =(x 1,y 1,z 1), 则{EA 1⃗⃗⃗⃗⃗⃗⃗ ·n =x 1-2y 1+√3z 1=0,EB⃗⃗⃗⃗⃗ ·n =2x 1+2y 1=0, 令x 1=1,则y 1=-1,z 1=-√3,∴平面A 1BE 的一个法向量为n =(1,-1,-√3).设直线A 1C 与平面A 1BE 所成角为θ,则sin θ=|cos <A 1C ⃗⃗⃗⃗⃗⃗⃗ ,n >|=|A 1C ⃗⃗⃗⃗⃗⃗⃗⃗ ·n ||A 1C ⃗⃗⃗⃗⃗⃗⃗⃗ |·|n |=√3)√3)|√1+3×√1+1+3=2√55. ∴直线A 1C 与平面A 1BE 所成角的正弦值为2√55.2.解(1)当E 为BC 的中点时,CF ∥平面PAE.理由如下,如图,分别取BC ,PA 的中点E ,G ,连接PE ,AE ,GE ,FG.又F 是PD 的中点,∴FG ∥AD ,FG=12AD.又四边形ABCD 为正方形,则AD ∥BC ,AD=BC ,∴FG ∥BC ,FG=12BC.又E 是BC 的中点,∴FG ∥CE ,FG=CE ,则四边形ECFG 是平行四边形,∴CF ∥EG.又EG ⊂平面PAE ,CF ⊄平面PAE ,∴CF ∥平面PAE.(2)如图,取AD 中点O ,连接PO ,OE ,又PA=PD ,∴PO ⊥AD.∵平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD=AD ,PO ⊂平面PAD ,∴PO ⊥平面ABCD.∴以O 为原点,OA ,OE ,OP 分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系.设AD=2,则A (1,0,0),B (1,2,0),C (-1,2,0),P (0,0,√3),F -12,0,√32,∴AF ⃗⃗⃗⃗⃗ =-32,0,√32,BC ⃗⃗⃗⃗⃗ =(-2,0,0),PB ⃗⃗⃗⃗⃗ =(1,2,-√3), 设平面PBC 的法向量为n =(x ,y ,z ),则{-2x =0,x +2y -√3z =0,令y=3,得x=0,z=2√3,则平面PBC 的一个法向量n =(0,3,2√3),∴|cos <n ,AF ⃗⃗⃗⃗⃗ >|=|n ·AF ⃗⃗⃗⃗⃗ ||n ||AF ⃗⃗⃗⃗⃗ |=|√21×√3|=√77,∴直线AF 与平面PBC 所成角的正弦值为√77.3.(1)证明如图所示,连接B 1C ,∵四边形ABCD 为平行四边形,∴AB CD ,又A 1B 1 AB ,∴A 1B 1 CD ,∴四边形A 1B 1CD 为平行四边形,∴A 1D ∥B 1C. 又B 1C ⊂平面BCC 1B 1,A 1D ⊄平面BCC 1B 1,∴A 1D ∥平面BCC 1B 1.(2)解存在.假设存在点F ,使平面DA 1C 1与平面A 1C 1F 垂直,则平面DA 1C 1与平面A 1C 1F 所成的二面角为直二面角.设平面DA 1C 1与平面A 1C 1F 所成的二面角的平面角为θ,则θ=90°.如图所示,以A 为坐标原点,分别以AD ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ ,AA 1⃗⃗⃗⃗⃗⃗⃗ 为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系.∵∠ACB=90°,AC=BC=3,AA 1=2, ∴A (0,0,0),D (3,0,0),A 1(0,0,2),C 1(0,3,2). ∵点F 在BC 上,∴设点F (m ,3,0).∴A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =(3,0,-2),A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,3,0),A 1F ⃗⃗⃗⃗⃗⃗⃗ =(m ,3,-2).设平面A 1C 1D 的法向量为n 1=(x 1,y 1,z 1), 则{n 1·A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =0,n 1·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0,即{3x 1-2z 1=0,y 1=0,取x 1=2,则y 1=0,z 1=3,∴平面A 1C 1D 的一个法向量n 1=(2,0,3). 设平面A 1C 1F 的法向量为n 2=(x 2,y 2,z 2),则{n 2·A 1F ⃗⃗⃗⃗⃗⃗⃗ =0,n 2·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0, 即{mx 2+3y 2-2z 2=0,y 2=0,取x 2=2,则y 2=0,z 2=m ,∴平面A 1C 1F 的一个法向量n 2=(2,0,m ). 则cos <n 1,n 2>=cos θ=cos90°=0,∴n 1·n 2|n 1||n 2|=0,即4+3m=0,∴m=-43,即CF=43,∴BF=3-43=53.∴在线段BC 上存在点F ,使平面DA 1C 1与平面A 1C 1F 垂直,此时BF=53.4.(1)证明∵四边形DCGH 为矩形,∴CG ⊥CD.又CG ⊥AD ,CD ∩AD=D ,∴CG ⊥平面ADC ,故CG ⊥AC. ∵六边形AEFBCD 为正六边形,∴∠ADC=∠DCB=120°,故∠DCA=30°,∴∠ACB=90°, 即AC ⊥CB.又CG ∩CB=C ,∴AC ⊥平面BCG.∵AC ⊂平面ACG , ∴平面ACG ⊥平面BCG.(2)解设AC 与BD 的交点为N ,连接MN.∵AG ∥平面BMD ,且平面BMD ∩平面ACG=MN ,∴AG ∥MN ,∴CM MG=CN NA=CD AB=48=12.∴MG=2,∴CG=3.由(1)知,AC ⊥CB ,CG ⊥平面ABC ,故以CA ,CB ,CG 分别作为x 轴,y 轴,z 轴建立空间直角坐标系,如图,A (4√3,0,0),B (0,4,0),M (0,0,1),H (2√3,-2,3),∴AB ⃗⃗⃗⃗⃗ =(-4√3,4,0),AH ⃗⃗⃗⃗⃗⃗ =(-2√3,-2,3),BM ⃗⃗⃗⃗⃗⃗ =(0,-4,1),设平面AHB 的法向量为n =(x ,y ,z ),则{n ·AH ⃗⃗⃗⃗⃗⃗ =0,n ·AB ⃗⃗⃗⃗⃗ =0,即{-2√3x -2y +3z =0,-4√3x +4y =0,取x=√3,则y=3,z=4,∴平面AHB 的一个法向量n =(√3,3,4).设直线BM 与平面AHB 所成角为θ,∴sin θ=|cos <BM ⃗⃗⃗⃗⃗⃗ ,n >|=|BM⃗⃗⃗⃗⃗⃗⃗ ·n ||BM⃗⃗⃗⃗⃗⃗⃗ |·|n |=√16+1·√3+9+16=4√119119,即直线BM 与平面AHB 所成角的正弦值为4√119119.5.(1)证明在图1中,△ABD 为等边三角形,E 为AD 中点,∴BE ⊥AD ,∴BE ⊥AE.∵∠AEG=90°,∴GE ⊥AE.∵GE ⊥AE ,BE ⊥AE ,GE ∩BE=E ,∴AE ⊥平面EBHG.(2)解设菱形ABCD 的边长为2,由(1)可知AE ⊥GE ,AE ⊥BE ,GE ⊥BE ,∴以E 为原点,EA ,EB ,EG 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系.可得A (1,0,0),B (0,√3,0),G (0,0,1),H (0,√3,2),∴AG⃗⃗⃗⃗⃗ =(-1,0,1),AH ⃗⃗⃗⃗⃗⃗ =(-1,√3,2).设平面AGH 的法向量为n =(x ,y ,z ),∴{n ·AG ⃗⃗⃗⃗⃗ =0,n ·AH ⃗⃗⃗⃗⃗⃗ =0,即{-x +z =0,-x +√3y +2z =0,令x=√3,则平面AGH 的一个法向量n =(√3,-1,√3).易知平面EBHG 的一个法向量为EA⃗⃗⃗⃗⃗ =(1,0,0).设二面角A-GH-B 的大小为θ,则θ为锐角,∴cos θ=|cos <n ,EA ⃗⃗⃗⃗⃗ >|=|n ·EA ⃗⃗⃗⃗⃗ ||n ||EA ⃗⃗⃗⃗⃗ |=√217. (3)解由AF ⃗⃗⃗⃗⃗ =y AB ⃗⃗⃗⃗⃗ =(-λ,√3y ,0),得EF ⃗⃗⃗⃗⃗ =AF ⃗⃗⃗⃗⃗ −AE⃗⃗⃗⃗⃗ =(-λ,√3y ,0)-(-1,0,0)=(1-λ,√3y ,0).∵EF ∥平面AGH ,则n ·EF ⃗⃗⃗⃗⃗ =0,即1-2λ=0,∴λ=12. 6.(1)证明∵AC=CD=√22AD , ∴AC 2+CD 2=12AD 2+12AD 2=AD 2,∴AC ⊥CD.∵PD ⊥平面ABCD ,AC ⊂平面ABCD ,∴PD ⊥AC.又PD ∩CD=D ,∴AC ⊥平面PCD.(2)解分别以直线DA ,DP 为x 轴,z 轴,建立如图所示的空间直角坐标系,则D (0,0,0),A (4,0,0),B (3,2,0),C (2,2,0),P (0,0,2),∴AB⃗⃗⃗⃗⃗ =(-1,2,0),AP ⃗⃗⃗⃗⃗ =(-4,0,2), 设n =(x ,y ,z )为平面PAB 的一个法向量,由{n ·AB ⃗⃗⃗⃗⃗ =0,n ·AP ⃗⃗⃗⃗⃗ =0,得{-x +2y =0,-4x +2z =0, 取y=1,则n =(2,1,4).由(1)AC ⊥平面PCD ,可知AC⃗⃗⃗⃗⃗ =(-2,2,0)为平面PCD 的一个法向量,设平面PCD 与平面PAB 所成的锐角为θ,则cos θ=|cos <n ,AC⃗⃗⃗⃗⃗ >|=√22+12+42×√(-2)+22+02=√4242.故平面PCD 与平面PAB 所成的锐角的余弦值为√4242.(3)解(方法一)存在.假设在棱PD 上存在点M ,使得CM ∥平面PAB ,则CM⃗⃗⃗⃗⃗⃗ ⊥n ,即CM ⃗⃗⃗⃗⃗⃗ ·n =0.设M (0,0,h ),则CM ⃗⃗⃗⃗⃗⃗ =(-2,-2,h ),由CM ⃗⃗⃗⃗⃗⃗ ·n =0,得2×(-2)+1×(-2)+4h=0,解得h=32.此时,PM PD =2-322=14.故在棱PD 上存在点M ,使得CM ∥平面PAB ,此时PMPD =14. (方法二)存在.在棱PD 上取点M ,使PM PD =14,过M 作MN ∥AD 交PA 于点N ,则MN=14AD.又BC 14AD ,∴BC MN ,∴四边形MNBC 为平行四边形,∴CM ∥BN.∵CM ⊄平面PAB ,BN ⊂平面PAB ,∴CM ∥平面PAB.故在棱PD 上存在点M ,使得CM ∥平面PAB ,此时PM PD =14. 7.(1)证明当λ=12时,F 是AD 的中点.∴DF=12AD=1,DE=13CD=1.∵∠ADC=90°,∴∠DEF=45°.∵CE=23CD=2,BC=2,∠BCD=90°,∴∠BEC=45°.∴BE ⊥EF.又平面GBE ⊥平面ABED ,平面GBE ∩平面ABED=BE ,EF ⊂平面ABED , ∴EF ⊥平面BEG.∵BG ⊂平面BEG ,∴EF ⊥BG.(2)解存在.以C 为原点,CD⃗⃗⃗⃗⃗ ,CB ⃗⃗⃗⃗⃗ 的方向为x 轴,y 轴的正方向建立如图所示空间直角坐标系,则E (2,0,0),D (3,0,0),F (3,2λ,0).取BE 的中点O ,∵GE=BG=2,∴GO ⊥BE ,∴易证得OG ⊥平面BCE.∵BE=2√2,∴OG=√2,∴G (1,1,√2).∴FG ⃗⃗⃗⃗⃗ =(-2,1-2λ,√2),EG⃗⃗⃗⃗⃗ =(-1,1,√2),DG ⃗⃗⃗⃗⃗ =(-2,1,√2). 设平面DEG 的法向量为n =(x ,y ,z ),则{n ·DG ⃗⃗⃗⃗⃗ =-2x +y +√2z =0,n ·EG⃗⃗⃗⃗⃗ =-x +y +√2z =0, 令z=√2,则平面DEG 的一个法向量n =(0,-2,√2).设FG 与平面DEG 所成的角为θ,则sin θ=|cos <FG ⃗⃗⃗⃗⃗ ,n >|=√6×√6+(1-2λ)=13, 解得λ=12或λ=-710(舍去). ∴存在实数λ,使得DG 与平面DEG 所成的角的正弦值为13,此时λ=12.8.(1)证明(方法一)在线段CP ,DQ 上分别取点M ,N ,使得QN=PM=1,易知四边形MNQP 是平行四边形, ∴MN ∥PQ ,连接FM ,MN ,NE ,则AE=ND ,且AE ∥ND ,∴四边形ADNE 为矩形,故AD ∥NE ,同理,FM ∥BC ∥AD 且NE=MF=AD ,故四边形FMNE 是平行四边形,∴EF ∥MN ,∴EF ∥PQ.故E ,F ,P ,Q 四点共面.又EF ∥PQ ,EF ⊄平面BPQ ,PQ ⊂平面BPQ ,∴EF ∥平面PQB.(方法二)∵直棱柱ABCD-A 1B 1C 1D 1的底面是菱形,∴AC ⊥BD ,AA 1⊥底面ABCD. 设AC ,BD 交点为O ,以O 为原点,分别以OA ,OB 及过O 且与AA 1平行的直线为x 轴,y 轴,z 轴建立空间直角坐标系,则有A (2,0,0),B (0,1,0),C (-2,0,0),D (0,-1,0).设BF=a ,a ∈[1,3],则E (2,0,a-1),F (0,1,a ),P (-2,0,a+1),Q (0,-1,a ),EF⃗⃗⃗⃗⃗ =(-2,1,1),QP ⃗⃗⃗⃗⃗ =(-2,1,1), ∴EF ∥PQ ,故E ,F ,P ,Q 四点共面.又EF ∥PQ ,EF ⊄平面BPQ ,PQ ⊂平面BPQ ,∴EF ∥平面PQB.(2)解不存在.理由如下,∵直棱柱ABCD-A 1B 1C 1D 1的底面是菱形,∴AC ⊥BD ,AA 1⊥底面ABCD.设AC ,BD 交点为O ,以O 为原点,分别以OA ,OB 及过O 且与AA 1平行的直线为x 轴,y 轴,z 轴建立空间直角坐标系,则有A (2,0,0),B (0,1,0),C (-2,0,0),D (0,-1,0).设BF=a ,a ∈[1,3],则E (2,0,a-1),F (0,1,a ),P (-2,0,a+1),Q (0,-1,a ),EF ⃗⃗⃗⃗⃗ =(-2,1,1),EQ ⃗⃗⃗⃗⃗ =(-2,-1,1),设平面EFPQ 的法向量为n 1=(x 1,y 1,z 1),则{EF ⃗⃗⃗⃗⃗ ·n 1=0,EQ ⃗⃗⃗⃗⃗ ·n 1=0,即{-2x 1+y 1+z 1=0,-2x 1-y 1+z 1=0,令x 1=1,可得平面EFPQ 的一个法向量n 1=(1,0,2). BP ⃗⃗⃗⃗⃗ =(-2,-1,a+1),BQ ⃗⃗⃗⃗⃗ =(0,-2,a ),设平面BPQ 的法向量为n 2=(x 2,y 2,z 2),则{BP ⃗⃗⃗⃗⃗ ·n 2=0,BQ⃗⃗⃗⃗⃗ ·n 2=0, 即{-2x 2-y 2+(a +1)z 2=0,-2y 2+az 2=0,令y 2=2a ,可得x 2=a+2,z 2=4,∴平面BPQ 的一个法向量n 2=(a+2,2a ,4).若|cos <n 1,n 2>|=|12√5·√(a+2)+4a 2+16=√55, 则(a+10)2=5a 2+4a+20,即有a 2-4a-20=0,a ∈[1,3],解得a=2±2√6∉[1,3],故不存在点P 使之成立.。

2021二模18题解法分析（16区）

2021二模18题解法分析（16区）2021二模18题中的背景围绕着特殊四边形(正方形、等腰梯形)、三角形(直角三角形，或已知某个角的锐角三角比)、二次函数和反比例函数。

题型围绕着图形的翻折(8个区)、图形的旋转(2个区)、新定义(2个区)、求函数解析式(2个区)、等腰三角形存在性(1个区)以及圆与四边形的交点问题(1个区)。

翻折问题涉及到图形的全等、相似以及轴对称的相关知识。

当遇到翻折问题时，往往需要补画出翻折后的图形，在作图时，其关键点在于找准对称轴，画出对应点。

当遇到翻折问题时，需要关注三个问题：①翻折前后的对应线段相等；②翻折前后对应的角(形成的角)相等；③翻折后对应点的连线被折痕垂直平分。

类型1：利用比例线段进行问题解决奉贤18题的背景是带中线的三角形，考查了图形的翻折，解题路径是利用X型基本图形，构建比例关系，从而求得线段的比值。

松江18题的背景是6810的直角三角形，考查了图形的翻折，利用翻折的意义，找出相等的线段，解题路径是利用A型基本图形，构建比例关系，从而求得线段长度。

类型2：借助勾股定理杨浦18题的背景是30°-60°-90°三角形，考查了图形的翻折，本题需要分类讨论，即B’的位置，解题路径是利用勾股定理，从而求得线段长度。

类型3：解三角形黄浦18题的背景是等腰梯形，考查了图形的翻折，画处图形后，即可得到一个菱形和一个等腰三角形，通过解这个等腰三角形即可得到∠C的余切值。

浦东18题的背景是矩形，考查了图形的翻折，通过设元，即可发现一组等角，通过解三角形，利用等角的三角比相等，即可得到线段比值。

类型4：利用直角三角形的性质虹口18题的背景是正方形，考查了图形的翻折，本题需要分类讨论，即N的位置，解题路径是利用平行四边形的性质定理和直角三角形的全等及斜边中点的性质，从而求得线段长度。

新定义问题的关键在于阅读理解，读懂题意再进行问题解决。

当出现多种情况时，可以采取分类讨论；当出现求范围问题时，可以找到临界位置，确定范围。

初二数学翻折练习题及答案

初二数学翻折练习题及答案以下是一些初二数学翻折练习题，以及它们的答案。

希望这些题目能够帮助你巩固数学知识，提高解题能力。

每道题后面都有详细的解答过程，希望你能仔细阅读并理解。

练习题1：三角函数的基本关系1. 求在区间[0, 2π]内，使得sin(x) = cos(x)的解。

答案: 无解解析：根据三角函数的基本关系，我们知道sin(x) = cos(x)只有在x = π/4和x = (5π/4)时成立。

然而，这两个解都不在区间[0, 2π]内，所以该方程在该区间内无解。

练习题2：二次函数的图像2. 给定二次函数f(x) = 2x^2 + 3x - 2，请确定该函数的顶点坐标，并画出函数的图像。

答案：顶点坐标为(-3/4, -25/8)；图像如下所示：（图像展示）解析：为确定二次函数的顶点坐标，我们可以使用公式x = -b/2a来计算顶点横坐标，再将横坐标代入函数表达式求得纵坐标。

代入f(x) = 2x^2 + 3x - 2中，我们可以得到x = -3/4。

将x = -3/4代入f(x)中，我们可以得到f(-3/4) = -25/8，因此顶点坐标为(-3/4, -25/8)。

练习题3：概率3. 在一副标准扑克牌中，抽出两张牌，第一张是红心，第二张是黑桃的概率是多少？答案：13/52解析：一副标准扑克牌中共有52张牌，其中红心有13张，黑桃也有13张。

第一张牌是红心的概率为13/52。

在第一张牌为红心的前提下，剩下的牌中黑桃有13张，所以第二张牌为黑桃的概率是13/51。

因此，第一张是红心且第二张是黑桃的概率为(13/52) * (13/51) = 13/52。

练习题4：平面几何4. 如图所示，ABCD是一个矩形，E是线段AB的中点，DE的延长线与BC相交于点F。

如果AD = 6cm，DE = 3cm，求BC的长度。

答案：BC的长度为9cm。

解析：根据线段中点定理，由于E是线段AB的中点，所以AE = EB。

2024上海初三二模数学试卷分类《翻折、旋转、新定义》

图6图6上海市2024届初三二模数学试卷分类汇编——翻折、旋转、新定义【2024届·宝山区·初三二模·第18题】（本题满分4分）1.如图6，菱形ABCD 的边长为5，4cos 5B =，E 是边CD 上一点（不与点C 、D 重合），把ADE ∆沿着直线AE 翻折，如果点D 落在菱形一条边的延长线上，那么CE 的长为．【2024届·虹口区·初三二模·第18题】（本题满分4分）2.如图6，在扇形AOB 中，105AOB ∠=︒，8OA =，点C 在半径OA 上，将BOC ∆沿着BC 翻折，点O 的对称点D 恰好落在弧AB 上，再将弧AD 沿着CD 翻折至弧1A D （点1A 是点A 的对称点），那么1OA 的长为．【2024届·金山区·初三二模·第17题】（本题满分4分）3.如图，在Rt ABC ∆中，90C ∠=︒，2AC =，D 是AB 的中点，把BCD ∆沿CD 所在的直线翻折，点B 落在点E 处，如果CEAB ⊥，那么BE =．【2024届·普陀区·初三二模·第18题】第17题图图4（本题满分4分）4.如图4，在ABC ∆中，5AB AC ==，4cos 5B =，分别以点B 、C 为圆心，1为半径长作⊙B 、⊙C ，D 为边BC 上一点，将ABD ∆和⊙B 沿着AD 翻折得到'AB D ∆和⊙'B ，点B 的对应点为点'B ，'AB 与边BC 相交，如果⊙'B 与⊙C 外切，那么BD =．【2024届·青浦区·初三二模·第17题】（本题满分4分）5.正方形ABCD 的边长为1，E 为边DC 的中点，点F 在边AD 上，将D ∠沿直线EF 翻折，使点D 落在点G 处，如果BG BC =，那么线段DF 的长为．【2024届·松江区·初三二模·第18题】（本题满分4分）6.如图4，已知ABC ∆中，90C ∠=︒，6BC =，8AC =．D 是边BC 的中点，E 是边AC 上一点，将CDE ∆沿着DE 翻折，点C 落在点F 处，如果DF 与ABC ∆的一边平行，那么AE =．【2024届·徐汇区·初三二模·第17题】（本题满分4分）图4第17题图7.如图，在ABC ∆中，6AB AC ==，4BC =．已知点D 是边AC 的中点，将ABC ∆沿直线BD 翻折，点C 落在点E 处，联结AE ，那么AE 的长是．【2024届·崇明区·初三二模·第17题】（本题满分4分）8.已知在矩形ABCD 中，6AB =，4BC =，将矩形ABCD 绕点B 旋转，AB 的对应边'A B 与边CD 相交于点E ，联结'A C ，当点E 是CD 中点时，tan 'A CD ∠=．【2024届·静安区·初三二模·第18题】（本题满分4分）9.如图，矩形ABCD 中，8AB =，17BC =，将该矩形绕着点A 旋转，得到四边形111AB C D ，使点D 在直线11B C 上，那么线段1BB 的长度是．【2024届·闵行区·初三二模·第18题】（本题满分4分）10.在Rt ABC ∆中，90B ∠=︒，6AB =，3sin 5C =，D 为边AB 上一动点，将DA 绕点D 旋转，使点A 落在边AC 上的点E 处，过点E 作EF DE ⊥交边BC 于点F ，联结DF ，当DEF ∆是等腰三角形时，线段CF 的长为．【2024届·长宁区·初三二模·第17题】（本题满分4分）11.在Rt ABC ∆中，90ACB ∠=︒，AC BC >，将ABC ∆绕着点C 旋转，点A 、点B 的对应点分别是点D 、点E ，如果点A 在DE 的延长线上，且//CE AB ，那么CAE ∠的余弦值为．【2024届·崇明区·初三二模·第18题】（本题满分4分）12.新定义：我们把抛物线2y ax bx c =++（其中0ab ≠）与抛物线2y bx ax c =++称为“关联抛物线”，例如：抛物线223y x x =++的“关联抛物线”为223y x x =++．已知抛物线21:694C y ax ax a =++-（0a >）的“关联抛物线”为2C ，抛物线2C 的顶点为P ，且抛物线2C 与x 轴相交于M 、N 两点，点P 关于x 轴的对称点为Q ，若四边形PMQN 是正方形，那么抛物线1C 的表达式为．【2024届·嘉定区·初三二模·第18题】（本题满分4分）13.定义：如果三角形有两个内角的差为90︒，那么这样的三角形叫做准直角三角形．已知在直角ACB ∆中，第18题图图490C ∠=︒，4AC =，12AB =，如图4，如果点D 在边BC 上，且ADB ∆是准直角三角形，那么CD =．【2024届·浦东新区·初三二模·第18题】（本题满分4分）14.定义：四边形ABCD 中，点E 在边AB 上，联结DE 、EC ，如果DEC ∆的面积是四边形ABCD 面积的一半，且BEC ∆的面积是ADE ∆及DCE ∆面积的比例中项，我们称点E 是四边形ABCD 的边AB 上的一个面积黄金分割点．已知：如图，四边形ABCD 是梯形，且//AD BC ，BC AD >，如果点E 是它的边AB 上的一个面积黄金分割点，那么BCAD 的值是．第18题图。

2022——2023学年天津市红桥区中考数学专项提升仿真模拟试题(一模二模)含答案

2022-2023学年天津市红桥区中考数学专项提升仿真模拟试题（一模）一、选一选：1.拒绝“餐桌浪费”，刻没有容缓．据统计全国每年浪费食物总量约50000000000千克，这个数据用科学记数法表示为A.0.5×1011千克B.50×109千克C.5×109千克D.5×1010千克2.如图，一个放置在水平桌面上的圆柱，它的主（正）视图是（）A. B. C. D.3.下列计算正确的是（）A.=B.=C.4=D.3=-4.将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个没有透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀.随机摸出一球，没有放回；再随机摸出一球.两次摸出的球上的汉字能组成“孔孟”的概率是（）A.18 B.16 C.14 D.125.如图，在平行线a，b之间放置一块直角三角板，三角板的顶点A，B分别在直线a，b上，则∠1+∠2的值为（）A.60°B.80°C.85°D.90°6.若2x +mx+16是一个完全平方式,则m 的取值是（)A.8± B.-8C.8D.4±7.如图，已知矩形OABC，A（4，0），C（0，3），动点P 从点A 出发，沿A﹣B﹣C﹣O 的路线匀速运动，设动点P 的运动时间为t，△OAP 的面积为S，则下列能大致反映S 与t 之间关系的图象是（）A. B. C. D.8.把一块直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（）A.115°B.120°C.145°D.135°9.下列图形中，既是轴对称图形又是对称图形的是()A. B. C. D.10.如图，AB 是⊙O 的直径，==，∠COD=34°，则∠AEO 的度数是（）A.51°B.56°C.68°D.78°11.为了筹备班级元旦联欢晚会，班长打算先对全班同学爱吃什么水果进行民意，再决定买哪种水果.下面的数据中，他最应该关注的是()A.众数B.中位数C.平均数D.加权平均数12.如图，已知抛物线y1=-2x2+2，直线y2=2x+2，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=1时，y1=0，y2=4，y1＜y2，此时M=0．下列判断：①当x＞0时，y1＞y2；②当x＜0时，x值越大，M值越小；③使得M大于2的x值没有存在；④使得M=1的x值是12 或22．其中正确的个数是（）A.1个B.2个C.3个D.4个二、填空题：13.在数：4，5，6，－1中，是没有等式x－2＜3的解的有________．14.如图，已知AC=DB，要使△ABC≌△DCB，则需要补充的条件为_____.15.若函数y=(m﹣3)x+m2﹣9是正比例函数，则m的值为_______．16.分解因式：ab3-ab=_______．17.如图，若▱ABCD的周长为36cm，过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，▱ABCD的面积为_____cm2．18.△ABC 是边长为18的正三角形,点D、E 分别在边AB、BC 上,且BD=BE.若四边形DEFG 是边长为6的正方形时，则点F 到AC 的距离等于__________.三、解答题：19.解方程：2134134x x ---=20.把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.问这个班有多少学生？这些图书共有多少本？21.九年级（1）班开展了为期一周的“敬老爱亲”社会，并根据学生做家务的时间来评价他们在中的表现.老师了全班50名学生在这次中做家务的时间，并将统计的时间（单位：小时）分成5组：A ：0.5≤x ＜1，B ：1≤x ＜1.5，C ：1.5≤x ＜2，D ：2≤x ＜2.5，E ：2.5≤x ＜3，制作成两幅没有完整的统计图（如图）．请根据图中提供的信息，解答下列问题：（1）这次中学生做家务时间的中位数所在的组是____________；（2）补全频数分布直方图；（3）该班的小明同学这一周做家务2小时，他认为自己做家务的时间比班里一半以上的同学多，你认为小明的判断符合实际吗．请用适当的统计知识说明理由．22.已知B 港口位于A 观测点的东向，且其到A 观测点正向的距离BD 的长为16千米，一艘货轮从B 港口以48千米/时的速度沿如图所示的BC 方向航行，15分后到达C 处，现测得C 处位于A 观测点北偏东75 方向，求此时货轮与A 观测点之间的距离AC 的长（大0.1千米）1.41≈ 1.73≈2.24≈ 2.45≈）23.某农户种植一种经济作物，总用水量y（米3）与种植时间x（天）之间的函数关系式如图所示．（1）第20天的总用水量为多少米3？（2）当x≥20时，求y与x之间的函数关系式；（3）种植时间为多少天时，总用水量达到7000米3？24.如图，已知正方形ABCD中，AE∥BD，BE=BD，BE交AD于F.求证：DE=DF.25.如图,⊙O是△ABC的外接圆，AB=AC，BD是⊙O的直径，PA∥BC，与DB的延长线交于点P，连接AD．（1）求证：PA是⊙O的切线；（2）若AD的长．26.在Rt△ABC中，∠ACB=90°，AC=2，BC=4．点D是线段BC上的一个动点．点D与点B、C没有重合，过点D作DE⊥BC交AB于点E，将△ABC沿着直线DE翻折，使点B落在直线BC上的F点．（1）设∠BAC=α（如图①），求∠AEF的大小；（用含α的代数式表示）（2）当点F与点C重合时（如图②），求线段DE的长度；（3）设BD=x，△EDF与△ABC重叠部分的面积为S，试求出S与x之间函数关系式，并写出自变量x的取值范围．2022-2023学年天津市红桥区中考数学专项提升仿真模拟试题（一模）一、选一选：1.拒绝“餐桌浪费”，刻没有容缓．据统计全国每年浪费食物总量约50000000000千克，这个数据用科学记数法表示为A.0.5×1011千克B.50×109千克C.5×109千克D.5×1010千克【正确答案】D【分析】根据科学记数法的定义，科学记数法的表示形式为a×10n，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．在确定n的值时，看该数是大于或等于1还是小于1．【详解】解：50000000000一共11位，从而50000000000=5×1010．故选：D．2.如图，一个放置在水平桌面上的圆柱，它的主（正）视图是（）A. B. C. D.【正确答案】C【详解】试题解析：圆柱的主（正）视图为矩形．故选C．点睛：画物体视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．3.下列计算正确的是（）A.=B.=C.4=D.=-3【分析】根据同类二次根式，二次根式的乘法和化简二次根式逐项计算判断即可．【详解】A没有是同类二次根式，没有能直接加，故该选项错误，没有符合题意；BCD3=，故该选项错误，没有符合题意；故选B．本题考查同类二次根式的判断，二次根式的乘法和化简二次根式．熟练掌握各知识点和运算法则是解题关键．4.将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个没有透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀.随机摸出一球，没有放回；再随机摸出一球.两次摸出的球上的汉字能组成“孔孟”的概率是（）A.18 B.16 C.14 D.12【正确答案】B【分析】根据简单概率的计算公式即可得解.【详解】一共四个小球，随机摸出一球，没有放回；再随机摸出一球一共有12中可能，其中能组成孔孟的有2种，所以两次摸出的球上的汉字能组成“孔孟”的概率是1 6.故选B.考点：简单概率计算.5.如图，在平行线a，b之间放置一块直角三角板，三角板的顶点A，B分别在直线a，b上，则∠1+∠2的值为（）A.60°B.80°C.85°D.90°【分析】过点C 作CD ∥a ，再由平行线的性质即可得出结论．【详解】解：过点C 作CD ∥a ，则∠1=∠ACD ．∵a ∥b ，∴CD ∥b ，∴∠2=∠DCB ．∵∠ACD+∠DCB=90°，∴∠1+∠2=90°．故选D ．本题考查平行线的性质，根据题意作出辅助线，构造出平行线是解题的关键．6.若2x +mx+16是一个完全平方式,则m 的取值是（)A.8± B.-8C.8D.4±【正确答案】A【分析】先根据两平方项确定出这两个数，再根据完全平方公式的乘积二倍项即可确定m 的值．【详解】∵x 2+mx+16=x 2+mx+42，∴mx=±2x ×4，解得m=±8.故选A.本题考查了完全平方式，解题的关键是掌握完全平方式的概念.7.如图，已知矩形OABC，A（4，0），C（0，3），动点P 从点A 出发，沿A﹣B﹣C﹣O 的路线匀速运动，设动点P 的运动时间为t，△OAP 的面积为S，则下列能大致反映S 与t 之间关系的图象是（）A. B. C. D.【正确答案】A【详解】∵A（4，0）、C（0，4），∴OA=AB=BC=OC=4，①当P由点A向点B运动，即0≤t≤4，S=12OA·AP=2t；②当P由点A向点B运动，即4＜t≤8，S=12 OA·AP=8；③当P由点A向点B运动，即8＜t≤12，S=12OA·AP=2（12﹣t）=﹣2t+24；图象可知，符合题意的是A．故选A．8.把一块直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（）A.115°B.120°C.145°D.135°【正确答案】D【分析】由下图三角形的内角和等于180°，即可求得∠3的度数，又由邻补角定义，求得∠4的度数，然后由两直线平行，同位角相等，即可求得∠2的度数．【详解】在Rt△ABC中，∠A=90°，∵∠1=45°（已知），∴∠3=90°-∠1=45°（三角形的内角和定理），∴∠4=180°-∠3=135°（平角定义），∵EF∥MN（已知），∴∠2=∠4=135°（两直线平行，同位角相等）．故选D．此题考查了三角形的内角和定理与平行线的性质．注意两直线平行，同位角相等与数形思想的应用．9.下列图形中，既是轴对称图形又是对称图形的是()A. B. C. D.【正确答案】D【分析】根据轴对称图形和对称图形的定义逐项识别即可，在平面内，把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．【详解】解：A.是轴对称图形，但没有是对称图形，故没有符合题意；B.没有是轴对称图形，是对称图形，故没有符合题意；C.是轴对称图形，但没有是对称图形，故没有符合题意；D.既是轴对称图形又是对称图形，故符合题意．故选D．本题考查了轴对称图形和对称图形的识别，熟练掌握轴对称图形和对称图形的定义是解答本题的关键．10.如图，AB是⊙O的直径，==，∠COD=34°，则∠AEO的度数是（）A.51°B.56°C.68°D.78°【正确答案】A【详解】试题分析：由==，可求得∠BOC=∠EOD=∠COD=34°，继而可求得∠AOE 的度数；然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO的度数．解：如图，∵==，∠COD=34°，∴∠BOC=∠EOD=∠COD=34°，∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=78°．又∵OA=OE，∴∠AEO=∠OAE，∴∠AEO=×（180°﹣78°）=51°．故选A．考点：圆心角、弧、弦的关系．11.为了筹备班级元旦联欢晚会，班长打算先对全班同学爱吃什么水果进行民意，再决定买哪种水果.下面的数据中，他最应该关注的是()A.众数B.中位数C.平均数D.加权平均数【正确答案】A【分析】众数、中位数、平均数从没有同角度反映了一组数据的集中趋势，但该问题应当看吃哪种水果的人至多，故应当用众数．【详解】此问题应当看吃哪种水果的人至多，应当用众数．故选A．本体考查了众数、中位数、平均数的意义，解题时要注意题目的实际意义．12.如图，已知抛物线y1=-2x2+2，直线y2=2x+2，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=1时，y1=0，y2=4，y1＜y2，此时M=0．下列判断：①当x＞0时，y1＞y2；②当x＜0时，x值越大，M值越小；③使得M大于2的x值没有存在；④使得M=1的x值是12 或22．其中正确的个数是（）A.1个B.2个C.3个D.4个【正确答案】B【详解】试题分析：∵当y1=y2时，即-2x2+2=2x+2时，解得：x=0或x=-1，∴当x＜-1时，利用函数图象可以得出y2＞y1；当-1＜x＜0时，y1＞y2；当x＞0时，利用函数图象可以得出y2＞y1；∴①错误；∵抛物线y1=-2x2+2，直线y2=2x+2，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；∴当x＜0时，根据函数图象可以得出x值越大，M值越大；∴②错误；∵抛物线y1=-2x2+2，直线y2=2x+2，与y轴交点坐标为：（0，2），当x=0时，M=2，抛物线y1=-2x2+2，值为2，故M大于2的x值没有存在；∴使得M大于2的x值没有存在，∴③正确；抛物线与x轴的交点为（-1，0）（1，0），由图可知，-1＜x＜0时，M=2x+2，当M=1时，2x+2=1，解得x=-12，x＞0时，M=-2x2+2，当M=1时，-2x2+2=1，解得x=-12，所以，使得M=1的x值是−12或22，故④正确，综上所述，③④都正确．故选B．考点：二次函数的性质；函数的性质．二、填空题：13.在数：4，5，6，－1中，是没有等式x－2＜3的解的有________．【正确答案】4-1【详解】解没有等式x-2＜3得x＜5；∴4、5、6、-1中，4、-1是没有等式的解．故答案是：4,-1.14.如图，已知AC=DB，要使△ABC≌△DCB，则需要补充的条件为_____.【正确答案】AB=DC(答案没有)【分析】本题中有公共边BC=CB，利用SSS来判定全等则只需要添加条件AB=DC即可．【详解】解：由题意可知：AC=DB，BC=CB，∴利用SSS来判定全等则只需要添加条件AB=DC，故答案为：AB=DC(答案没有)．本题考查三角形全等的判定，掌握判定定理是本题的解题关键．15.若函数y=(m﹣3)x+m2﹣9是正比例函数，则m的值为_______．【正确答案】﹣3【详解】∵y=(m﹣3)x+m2﹣9是正比例函数，∴29030 mm-⎧⎨-≠⎩＝解得m=-3．故答案是：-3.16.分解因式：ab3-ab=_______．【正确答案】ab（b+1）（b-1）.【详解】试题解析：ab3-ab，=ab（b2-1），=ab（b+1）（b-1）．考点：提公因式法与公式法的综合运用．17.如图，若▱ABCD的周长为36cm，过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，▱ABCD的面积为_____cm2．【正确答案】40【详解】试题分析：由▱ABCD的周长为36cm，可得AB+BC=18cm①，又由过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，由等积法，可得4AB=5BC②，继而求得答案．解：∵▱ABCD的周长为36cm，∴AB+BC=18cm①，∵过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，∴4AB=5BC②，由①②得：AB=10cm，BC=8cm，∴▱ABCD的面积为：AB•DE=40（cm2）．故答案为40．考点：平行四边形的性质．18.△ABC是边长为18的正三角形,点D、E分别在边AB、BC上,且BD=BE.若四边形DEFG是边长为6的正方形时，则点F到AC的距离等于__________.【正确答案】6【详解】如图，作BL⊥AC于L交DE于H，交FG于K．∵△ABC 是等边三角形，AC=BC=AB=18，∴∠B=90°，∵BE=BD ，∴△BED 是等边三角形，∴BE=BD=DE=6，∵HK=EF=6，∴，∴（），∵∠BED=∠C=60°，∴DE ∥AC ，∵DE ∥FG ，∴FG ∥AC ，∴点F 到AC 的距离-6．故答案是：-6.考查正方形的性质、等边三角形的判定和性质、解直角三角形等知识，解题的关键是学会添加常用辅助线.三、解答题：19.解方程：2134134x x ---=【正确答案】x=-4【详解】解：2134134x x ---=去分母得，4（2x-1）-3（3x-4）=12，去括号得，8x-4-9x+12=12，移项得，8x-9x=12-12+4，合并同类项得，-x=4把x的系数化为1得，x=-4.20.把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.问这个班有多少学生？这些图书共有多少本？【正确答案】见解析【详解】设这个班有x个学生3x+20=4x-25x=45图书：3x+20=3×45+20=155(本)答这个班有45名学生，图书有155本.21.九年级（1）班开展了为期一周的“敬老爱亲”社会，并根据学生做家务的时间来评价他们在中的表现.老师了全班50名学生在这次中做家务的时间，并将统计的时间（单位：小时）分成5组：A：0.5≤x＜1，B：1≤x＜1.5，C：1.5≤x＜2，D：2≤x＜2.5，E：2.5≤x＜3，制作成两幅没有完整的统计图（如图）．请根据图中提供的信息，解答下列问题：（1）这次中学生做家务时间的中位数所在的组是____________；（2）补全频数分布直方图；（3）该班的小明同学这一周做家务2小时，他认为自己做家务的时间比班里一半以上的同学多，你认为小明的判断符合实际吗．请用适当的统计知识说明理由．【正确答案】（1）C组；（2）作图见解析；（3）符合，理由见解析【分析】（1）可根据中位数的概念求值；（2）根据（1）的计算结果补全统计图即可；（3）根据中位数的意义判断．【详解】解：（1）C组的人数是：50×40%=20（人），B 组的人数是：50-3-20-10-2=15（人），把这组数据按从小到大排列为，由于共有50个数，第25、26位都落在1.5≤x ＜2范围内，则中位数落在C 组；故答案为C 组；（2）根据（1）得出的数据补图如下：（3）符合实际．设中位数为m ，根据题意，m 的取值范围是1.5≤m ＜2，∵小明帮父母做家务的时间大于中位数，∴他帮父母做家务的时间比班级中一半以上的同学多．22.已知B 港口位于A 观测点的东向，且其到A 观测点正向的距离BD 的长为16千米，一艘货轮从B 港口以48千米/时的速度沿如图所示的BC 方向航行，15分后到达C 处，现测得C 处位于A 观测点北偏东75 方向，求此时货轮与A 观测点之间的距离AC 的长（大0.1千米）1.41≈ 1.73≈2.24≈ 2.45≈）【正确答案】此时货轮与A 观测点之间的距离AC 约为15.7km．【详解】试题分析：根据在Rt △ADB 中，sin ∠DAB=DB AB ，得出AB 的长，进而得出tan ∠BAH=BH AH，求出BH 的长，即可得出AH 以及CH 的长，进而得出答案．试题解析：BC=48×1560=12，在Rt△ADB中，sin∠DAB=DBAB＝22，∴22=，如图，过点B作BH⊥AC，交AC的延长线于H，在Rt△AHB中，∠BAH=∠DAC-∠DAB=75°-45°=30°，tan∠BAH=BHAH=33，∴，BH2+AH2=AB2，BH2+）2=（）2，∴，∴，在Rt△BCH中，BH2+CH2=BC2，∴CH=4，∴AC=AH-CH=8-4≈15.7km，答：此时货轮与A观测点之间的距离AC约为15.7km．23.某农户种植一种经济作物，总用水量y（米3）与种植时间x（天）之间的函数关系式如图所示．（1）第20天的总用水量为多少米3？（2）当x≥20时，求y与x之间的函数关系式；（3）种植时间为多少天时，总用水量达到7000米3？【正确答案】（1）1000；（2）y=300x﹣5000；（3）40【分析】根据题意得出第20天的总用水量；y与x的函数关系式为分段函数，则需要分两段分别求出函数解析式；将y=7000代入函数解析式求出x的值．【详解】（1）第20天的总用水量为1000米3当0＜x＜20时，设y=mx∵函数图象点（20，1000），（30，4000）∴m=50y与x之间的函数关系式为：y=50x当x≥20时，设y=kx+b∵函数图象点（20，1000），（30，4000）∴100020400030k bk b=+⎧⎨=+⎩解得k300b5000=⎧⎨=-⎩∴y与x之间的函数关系式为：y=300x﹣5000（3）当y=7000时，有7000=300x﹣5000，解得x=40考点：函数的性质24.如图，已知正方形ABCD中，AE∥BD，BE=BD，BE交AD于F.求证：DE=DF.【正确答案】见解析【详解】试题分析：连接AC，交BD于点O，作EG⊥BD于点G，则可知四边形AOGE是矩形，可证得EG=12BD=12E，所以∠EBD=30°，条件可求得∠BED=75°，∠EFD=∠FDB+∠EBD=45+30=75°，故∠DEF=∠DFE，即可得到DF=DE．试题解析：证明：连接AC，交BD于点O，作EG⊥BD于点G．如图所示：∵四边形ABCD是正方形，∴AC⊥BD，∵AE∥BD，∴四边形AOGE是矩形，∴EG=AO=12AC=12BD=12BE，∴∠EBD=30°，∵∠EBD=30°，BE=BD，∴∠BED=75°，∵∠EFD=∠FDB+∠EBD=45+30=75°，∴∠DEF=∠DFE，∴DF=DE．25.如图,⊙O是△ABC的外接圆，AB=AC，BD是⊙O的直径，PA∥BC，与DB的延长线交于点P，连接AD．（1）求证：PA是⊙O的切线；（2）若AD的长．【正确答案】（1）见解析；（2）【详解】试题分析：（1）连接OA交BC于点E，根据垂径定理的推论求得OA⊥BC，然后根据平行线的性质证得∠PAO=90°，即可证得结论．（2）根据勾股定理求得AE，得出tan∠C=12AECE＝，根据∠D=∠C，得出tan∠D=12ABAD=，从而求得AD的长．试题解析：（1）证明：连接OA交BC于点E，如图所示：由AB=AC可得OA⊥BC，∵PA∥BC，∴∠PAO=∠BEO=90°．∵OA为⊙O的半径，∴PA为⊙O的切线．（2）解：根据（1）可得CE=12BC=2．Rt△ACE中，AE1，∴tan∠C=12 AE CE＝∵BD是直径，∴∠BAD=90°，又∵∠D=∠C，∴tan∠D=12 ABAD=，∴AD=2运用了切线的判定、勾股定理、正切函数等；半径的外端且垂直于这条半径的直线是圆的切线．在判定一条直线为圆的切线时，当已知条件中明确指出直线与圆有公共点时，常连接过该公共点的半径，证明该半径垂直于这条直线．26.在Rt△ABC中，∠ACB=90°，AC=2，BC=4．点D是线段BC上的一个动点．点D与点B、C没有重合，过点D作DE⊥BC交AB于点E，将△ABC沿着直线DE翻折，使点B落在直线BC上的F点．（1）设∠BAC=α（如图①），求∠AEF的大小；（用含α的代数式表示）（2）当点F与点C重合时（如图②），求线段DE的长度；（3）设BD=x，△EDF与△ABC重叠部分的面积为S，试求出S与x之间函数关系式，并写出自变量x的取值范围．【正确答案】（1）1800-2α．（2）1；（3）S=221024{34424 4x xx x x≤-+-（＜）（＜＜）【详解】试题分析：（1）首先在Rt△ABC中，判断出∠ABC=90°-∠BAC=90°-α；然后根据翻折的性质，可得∠EFB=∠EBF；根据三角形外角的性质，可得∠AEF=∠EFB+∠EBF，据此解答即可．（2）当点F与点C重合时，BD=CD时，判断出AC∥ED，即可判断出AE=BE；然后根据三角形中位线定理，求出线段DE的长度是多少即可．（3）根据题意，分两种情况：①当点F在AC的右侧时，即0＜x≤2时；②当点F在AC的左侧时，即2＜x＜4时；然后分类讨论，求出S与x之间函数关系式，并写出自变量x的取值范围即可．试题解析：（1）如图①，，在Rt△ABC中，∠ABC=90°-∠BAC=90°-α，∵将△ABC沿着直线DE翻折，使点B落在直线BC上的F点，∴∠EFB=∠EBF，∴∠AEF=∠EFB+∠EBF=2∠EBF=2（900-∠BAC）=1800-2α．（2）如图②，，当点F 与点C 重合时，BD=CD 时，∵ED ⊥BC ，AC ⊥BC ，∴AC ∥ED ，∴AE=BE ，∴DE=12AC=12×2=1．（3）当点F 与点C 重合时，BD=CD=12BC=12×4=2．①如图③，，当点F 在AC 的右侧时，即0＜x≤2时，重叠部分是△EDF ．∵AC ∥ED ，∴△ABC ∽△EDB ，∴ED BDAC BC =，即24ED x=，∴ED=12x ，∴S △EDF =12×ED×DF=12×12x ×x=14x 2，（0＜x≤2）．②如图④，，当点F 在AC 的左侧时，即2＜x ＜4时，设EF 与AC 相交于点M ，则重叠部分是四边形EDCM ．∴FC=FD-CD=x-（4-x ）=2x-4∵∠ACB=∠MCF=90°，∠EFB=∠EBF ，∴△ABC ∽△MFC ，∴MC FCAC BC =，即2424MC x -=，∴MC=x-2，∴S 四边形EDCF =S △EDF -S △EDF =12×x×12x -12×（x-2）×（2x-4）=-34x 2+4x-4，（2＜x ＜4）．综上，可得S=221024{344244x x x x x ≤-+-（＜）（＜＜）考点：函数综合题．2022-2023学年天津市红桥区中考数学专项提升仿真模拟试题（二模）一、（本大题共10小题，每小题3分，共30分）以下各题后面给出的4个选项中，只有1项符合题目要求，请将其选出用2B 铅笔涂抹答题卡对应题目的标号．多选、没有选、错选均没有给分．1.2018的相反数（）A.2018B.-2018C.|-2018|D.12018-2.将一副三角板按如图方式摆放，∠1与∠2没有一定互补的是（）A. B. C. D.3.已知某班有40名学生，将他们的身高分成4组，在160165cm ～区间的有8名学生，那么这个小组的人数占全体的()A.10%B.15%C.20%D.25%4.下列变形中没有正确的是()A.若a>b ，则ac 2>bc 2(c 为有理数)B.由a b ->-得b a >C.由a b >得b a< D.由12x y -<得2x y >-5.二次函数y ＝2x 2﹣8x +m 满足以下条件：当﹣2＜x ＜﹣1时，它的图象位于x 轴的下方；当6＜x ＜7时，它的图象位于x 轴的上方，则m 的值为（）A.8B.﹣10C.﹣42D.﹣246.当A 为锐角，且12＜cos ∠A ＜2时，∠A 的范围是（）A.0°＜∠A ＜30°B.30°＜∠A ＜60°C.60°＜∠A ＜90°D.30°＜∠A＜45°7.八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1名同学植树的棵数没有到8棵若设同学人数为x 人，下列各项能准确的求出同学人数与种植的树木的数量的是()A.()7x 99x 10+-->B.()7x 99x 18+--<C .()()7x 99x 107x 99x 18⎧+--≥⎪⎨+--<⎪⎩ D.()()7x 99x 107x 99x 18⎧+--≥⎪⎨+--≤⎪⎩8.如图，抛物线y=ax 2+bx+c （a≠0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a ﹣b+c ，则P 的取值范围是()A.﹣4＜P ＜0B.﹣4＜P ＜﹣2C.﹣2＜P ＜0D.﹣1＜P ＜09.如图，直线y ＝12x 与双曲线y ＝k x(k>0，x>0)交于点A ，将直线y ＝12x 向上平移4个单位长度后，与y 轴交于点C ，与双曲线y ＝kx(k>0，x>0)交于点B ，若OA ＝3BC ，则k 的值为()A.3B.6C.94D.9210.如图，直线l1∥l2∥l3，直线AC 分别交l1，l2，l3于点A ，B ，C ；直线DF 分别交l1，l2，l3于点D 、E 、F ，AC 与DF 相交于点H ，且AH=2，HB=1，BC=5，则DEEF=（）A.35 B.2 C.25 D.12二、填空题（本大题共6小题，每小题3分，共18分）11.17-的倒数是_____________．12.当x=2的值是_________．13.某学生7门学科考试成绩的平均分是80分，其中=门学科都考了78分，则另外4门学科成绩的平均分是_____________.14.如图，在Rt ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是 CD 上的一个动点，连接AP，则AP的最小值是_____．15.已知，如图，半径为1的⊙M直角坐标系的原点O，且与x轴、y轴分别交于点A、B，点A的坐标为(，0)，⊙M的切线OC与直线AB交于点C.则∠ACO＝________.16.如图，点A（m，6），B（n，1）在反比例函数kyx=的图象上，AD⊥x轴于点D，BC⊥x轴于点C，点E在CD上，CD＝5，△ABE的面积为10，则点E的坐标是_____．三、（本大题共3小题，每小题9分，共27分）17.计算：0112(2018)2sin 60(3π---++︒+18.若没有等式x a 3x 24x 1>⎧⎨+<-⎩的解集是x ＞3，则a 的取值范围是_______．19.先化简，再求值：111)111a a a （-÷+--，其中1a =-．四、（本大题共3小题，每小题10分，共30分）20.如图，在Rt △ABC ，∠ACB =90°，AC =BC ，分别过A 、B 作直线的垂线，垂足分别为M 、N ．（1）求证：△AMC ≌△C ；（2）若AM =3，BN =5，求AB 的长．21.某校开展了“互助、平等、感恩、和谐、进取”主题班会，后，就的个主题进行了抽样（每位同学只选最关注的一个），根据结果绘制了两幅没有完整的统计图．根据图中提供的信息，解答下列问题：（1）这次的学生共有多少名；（2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数；（3）如果要在这个主题中任选两个进行，根据（2）中结果，用树状图或列表法，求恰好选到学生关注至多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A 、B 、C 、D 、E ）．22.某商场用36万元购进A 、B 两种商品，完后共获利6万元，其进价和售价如下表：A B进价(元/件)12001000售价(元/件)13801200（注：获利＝售价－进价）(1)该商场购进A 、B 两种商品各多少件?(2)商场第二次以原进价购进A 、B 两种商品．购进B 种商品的件数没有变，而购进A 种商品的件数是次的2倍，A 种商品按原价出售，而B 种商品打折．若两种商品完毕，要使第二次经营获利没有少于81600元，B 种商品售价为每件多少元?五、（本大题共2小题，每小题10分，共20分）23.如图，O 是△ABC 的内心，BO 的延长线和△ABC 的外接圆相交于D ，连接DC 、DA 、OA 、OC ，四边形OADC 为平行四边形．（1）求证：△BOC ≌△CDA （2）若AB =2，求阴影部分的面积．24.已知：关于x 的一元二次方程：()()2m 1x m 2x 10(m -+--=为实数)．()1若方程有两个没有相等的实数根，求m 的取值范围；()2若12是此方程的实数根，抛物线()()2y m 1x m 2x 1=-+--与x 轴交于A 、B ，抛物线的顶点为C ，求ABC 的面积．六、（本大题共2小题，25题12分，26题13分，共25分）25.如图，在△ABC 中，ABAC ，AE 是∠BAC 的平分线，∠ABC 的平分线BM 交AE 于点M ，点O在AB上，以点O为圆心，OB的长为半径的圆点M，交BC于点G，交AB于点F．（1）求证：AE为⊙O的切线；（2）当BC=4，AC=6时，求⊙O的半径；（3）在（2）的条件下，求线段BG的长．26.如图，抛物线y=–43x2+bx+c过点A（3，0），B（0，2）．M（m，0）为线段OA上一个动点（点M与点A没有重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N．（1）求直线AB的解析式和抛物线的解析式；（2）如果点P是MN的中点，那么求此时点N的坐标；（3）如果以B，P，N为顶点的三角形与△APM相似，求点M的坐标．2022-2023学年天津市红桥区中考数学专项提升仿真模拟试题（二模）一、（本大题共10小题，每小题3分，共30分）以下各题后面给出的4个选项中，只有1项符合题目要求，请将其选出用2B铅笔涂抹答题卡对应题目的标号．多选、没有选、错选均没有给分．1.2018的相反数（）A.2018B.-2018C.|-2018|D.1 2018【正确答案】B【详解】2018的相反数是-2018，故选B.2.将一副三角板按如图方式摆放，∠1与∠2没有一定互补的是（）A. B. C. D.【正确答案】D【详解】A选项：∠1+∠2=360°－90°×2=180°；B选项：∵∠2+∠3=90°，∠3+∠4=90°，∴∠2=∠4，∵∠1+∠4=180°，∴∠1+∠2=180°；C选项：∵∠ABC=∠DEC=90°，∴AB∥DE，∴∠2=∠EFC，∵∠1+∠EFC=180°，∴∠1+∠2=180°；D选项：∠1和∠2没有一定互补.故选D.点睛：本题主要掌握平行线的性质与判定定理，关键在于通过角度之间的转化得出∠1和∠2的互补关系.～区间的有8名学生，那么3.已知某班有40名学生，将他们的身高分成4组，在160165cm这个小组的人数占全体的()A.10%B.15%C.20%D.25%【正确答案】C【分析】用这个小组的人数除以全班人数即可求得结果．÷=．【详解】根据题意得：84020%故选C．本题主要考查了有理数除法的应用，掌握理数除法法则是解题的关键．4.下列变形中没有正确的是()->-得b a>A.若a>b，则ac2>bc2(c为有理数)B.由a bC.由a b >得b a <D.由12x y -<得2x y >-【正确答案】A【详解】分析:根据没有等式的性质进行判断.详解:A 、当c 为0时,没有符合题意；B 、由a b ->-得b a >，正确；C 、由a b >得b a <,正确；D 、由12x y -<得2x y >-，正确；故选A.点睛:考查了没有等式的性质．要认真弄清没有等式的基本性质与等式的基本性质的异同，特别是在没有等式两边同乘以（或除以）同一个数时，没有仅要考虑这个数没有等于0，而且必须先确定这个数是正数还是负数，如果是负数，没有等号的方向必须改变.5.二次函数y ＝2x 2﹣8x +m 满足以下条件：当﹣2＜x ＜﹣1时，它的图象位于x 轴的下方；当6＜x ＜7时，它的图象位于x 轴的上方，则m 的值为（）A.8B.﹣10C.﹣42D.﹣24【正确答案】D【分析】根据抛物线顶点式得到对称轴为直线x 2=，通过顶点坐标位置特征求出m 的范围，将A 选项剔除后，将B 、C 、D 选项带入其中，并根据二次函数对称性和增减性特点判断是否合理．【详解】抛物线22y 2x 8x m 2(x 2)8m =-+=--+的对称轴为直线x 2=，而抛物线在2x 1-<<-时，它的图象位于x 轴的下方；当6x 7<<时，它的图象位于x 轴的上方，m 0∴<，当m 10=-时，则2y 2x 8x 10=--，令y 0=，则22x 8x 100--=，解得1x 1=-，2x 5=，则有当2x 1-<<-时，它的图象位于x 轴的上方；当m 42=-时，则2y 2x 8x 42=--，。

2023年中考数学必考特色题型讲练【选择题】必考重点03 几何变换之翻折问题

【选择题】必考重点03 几何变换之翻折问题几何变换中的折叠问题，是江苏各地中考中常考的题型，难度多为一般或者较难。

几何的翻折问题，本质上考查的是轴对称的性质，常和矩形相结合。

在解题时，首先要明确折叠前后的图形全等，折叠前后的对应边、对应角相等，对称轴垂直平分对应点之间的连线，在结合矩形、菱形、三角形等的性质，运用勾股定理，列出方程，求出相应的线段长度。

【2022·江苏连云港·中考母题】如图，将矩形ABCD 沿着GE 、EC 、GF 翻折，使得点A 、B 、D 恰好都落在点O 处，且点G 、O 、C 在同一条直线上，同时点E 、O 、F 在另一条直线上．小炜同学得出以下结论：①GF ∥EC ；②AB ；③GE DF ；④OC ；⑤△COF ∽△CEG ．其中正确的是（）A ．①②③B ．①③④C ．①④⑤D ．②③④【考点分析】本题主要考查了折叠问题，解题时，我们常常设要求的线段长为x ，然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．【思路分析】由折叠的性质知∠FGE =90°，∠GEC =90°，点G 为AD 的中点，点E 为AB 的中点，设AD =BC =2a ，AB =CD =2b ，在Rt △CDG 中，由勾股定理求得b ，然后利用勾股定理再求得DF =FO =【2021·江苏苏州·中考母题】如图，在平行四边形ABCD 中，将ABC 沿着AC 所在的直线翻折得到AB C '，B C '交AD 于点E ，连接B D '，若60B ∠=︒，45ACB ∠=︒，AC =B D '的长是（）A．1BC D 【考点分析】本题考查翻折变换、等腰三角形的性质、勾股定理、平行四边形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．【思路分析】利用平行四边形的性质、翻折不变性可得△AEC 为等腰直角三角形，根据已知条件可得CE 得长，进而得出ED 的长，再根据勾股定理可得出B D '；1．（2022·江苏苏州·二模）如图把一张矩形纸片ABCD 沿对角线AC 翻折，点B 的对应点为B ′，AB ′与DC 相交于点E ，则下列结论一定正确的是（）A ．BC ＝12ACB ．AE ＝CEC ．AD ＝DE D ．∠DAE ＝∠CAB2．（2022·江苏南京·二模）如图，矩形ABCO ，点A 、C 在坐标轴上，点B 的坐标为()2,4-．将△ABC 沿AC 翻折，得到△ADC ，则点D 的坐标是（）A．612,55⎛⎫⎪⎝⎭B．65,52⎛⎫⎪⎝⎭C．312,25⎛⎫⎪⎝⎭D．35,22⎛⎫⎪⎝⎭3．（2022·江苏泰州·一模）如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平后再次折叠，使点A落在EF上的点A′处，得到折痕BM，BM与EF相交于点N．若直线BA′交直线CD于点O，BC＝11，EN＝2，则FO的长为（）A B C D4．（2022·江苏宿迁·三模）已知长方形纸条ABCD，点E、G在AD边上，点F、H在BC边上．将纸条分别沿着EF、GH折叠，如图，当DC恰好落在EA'上时，1∠与2∠的数量关系是（）A．12135∠+∠=︒B．2115∠-∠=︒C．1290∠+∠=︒D．22190∠-∠=︒5．（2022·江苏苏州·二模）如图①，②，③，④，两次折叠等腰三角形纸片ABC，先使AB与AC重合，折痕为AD，展平纸片：再使点A与点C重合，折痕为EF，展平纸片，AD、EF交于点G．若5cmAB AC==，6cmBC，则DG的长为（）A．3cm4B．7cm8C．1cm D．7cm66．（2022·江苏·苏州中学二模）如图，菱形ABCD中，点E在AD上，将△ABE沿着BE翻折，点A恰好落在CD上的点F处．若∠A=65°，则∠DFE的度数为（）A．85︒B．82.5︒C．65︒D．50︒7．（2022·江苏扬州·二模）如图，在矩形ABCD中，2AB=，BC=E是BC的中点，将ABE△沿直线AE翻折，点B落在点F处，连结CF，则tan ECF∠的值为（）A B C．23D8．（2022·江苏苏州·模拟）如图，在矩形ABCD中，点E在DC上，将矩形沿AE折叠，使点D落在BC 边上的点F处，若3AB=，5BC=，则tan FEC∠的值为（）．A．12B．35C．34D．459．（2022·江苏苏州·一模）如图，在平面直角坐标系中，O为坐标原点，平行四边形ABCD的边AB在x轴上，顶点D在y轴的正半轴上，点C在第一象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处、点B恰好为OE的中点．DE与BC交于点F．若y＝kx（k≠0）图象经过点C．且S△BEF＝1，则k的值为（）A．18B．20C．24D．2810．（2022·江苏·江阴市第一初级中学一模）如图，把三角形纸片ABC沿DE折叠，当点A落在四边形BCDE外部时，则∠A与∠1、∠2之间的数量关系是（）A．2∠A=∠1-∠2B．3∠A=2（∠1-∠2）C．3∠A=2∠1-∠2D．∠A=∠1-∠211．（2022·江苏·无锡市天一实验学校二模）已知：如图，在Rt△ABC中，∠A=90°，AB=8，tan∠ABC=32，点N是边AC的中点，点M是射线BC上的一动点（不与B，C重合），连接MN，将△CMN沿MN 翻折得△EMN，连接BE，CE，当线段BE的长取最大值时，sin∠NCE的值为（）A B C D12．（2022·江苏省南菁高级中学实验学校九年级）如图，在ABC 中，点D 是线段AB 上的一点，过点D 作DE ∥AC 交BC 于点E ，将BDE 沿DE 翻折，得到B DE '，若点C 恰好在线段B D '上，若90BCD ∠=︒，DC ：3CB '=：2，AB =CE 的长度为（）A．B C ．D 13．（2022·江苏·九年级专题练习）如图，在△ABC 中，90ACB ∠=，点D 是AB 的中点，将△ACD 沿CD 对折得△A ′CD ．连接BA '，连接AA ′交CD 于点E ，若14cm AB =，4cm BA '=，则CE 的长为（）A ．4cmB ．5cmC ．6cmD ．7cm14．（2022·江苏·宜兴市树人中学九年级）如图，在△ABC 中，点D 是线段AB 上的一点，过点D 作DE ∥AC 交BC 于点E ，将△BDE 沿翻折，得到△B 'DE ，若点C 恰好在线段B 'D 上，若∠BCD ＝90°，DC ：CB '＝3：2，AB ＝CE 的长度为（）A．B ．4C ．D ．615．（2022·江苏·九年级专题练习）如图①，AB ＝5，射线AM ∥BN ，点C 在射线BN 上，将△ABC 沿AC 所在直线翻折，点B 的对应点D 落在射线BN 上，点P ，Q 分别在射线AM 、BN 上，PQ ∥AB ．设AP ＝x ，QD ＝y ．若y 关于x 的函数图象（如图②）经过点E (9，2)，则cos B 的值等于（）A．25B．12C．35D．71016．（2022·江苏·苏州市吴江区铜罗中学九年级期中）如图，在△ABC中，D是AC边上的中点，连接BD，把△BDC沿BD翻折，得到△BDC′，DC'与AB交于点E，连接AC′，若AD＝AC′＝2，BD＝3，则点D到BC的距离为（）A B C D17．（2022·江苏南通·九年级）如图，AB为⊙O的一条弦，C为⊙O上一点，OC∥AB．将劣弧AB沿弦AB 翻折，交翻折后的弧AB交AC于点D．若D为翻折后弧AB的中点，则∠ABC＝（）A．110°B．112.5°C．115°D．117.5°18．（2022·江苏南京·九年级专题练习）如图，在矩形纸片ABCD中，点E、F分别在矩形的边AB、AD 上，将矩形纸片沿CE、CF折叠，点B落在H处，点D落在G处，点C、H、G恰好在同一直线上，若AB＝6，AD＝4，BE＝2，则DF的长是（）A ．2B ．74C D ．319．（2022·江苏·宿迁青华中学九年级期末）如图，四边形ABCD 内接于O ，AB AD =，3BC =．劣弧BC 沿弦BC 翻折，刚好经过圆心O ．当对角线BD 最大时，则弦AB 的长为（）A B ．C ．32D ．【选择题】必考重点03 几何变换之翻折问题几何变换中的折叠问题，是江苏各地中考中常考的题型，难度多为一般或者较难。

上海中考数学一模二模图形运动专题训练

中考数学填空18题专练———（图形的运动篇之翻折篇）1.已知△ABC 中，∠C=90°，AB=9，32cos =A ，把△ABC 绕着点C 旋转，使得点A 落在点A ’，点B 落在点B ’. 若点A ’在边AB 上，则点B 、B ’的距离为 ▲ （2012.1宝山）．2．如图，在ABC ∆中，MN ∥AC ，直线MN 将ABC ∆分割成面积相等的两部分.将BMN ∆沿直线MN 翻折，点B 恰好落在点E 处，联结AE ，若AE ∥CN ，则:AE NC = . （黄浦）.3．在△ABC 中，AB =AC ，把△ABC 折叠，使点B 与点A 重合，折痕交AB 于点M ，交BC 于点N ．如果△CAN 是等腰三角形，则∠B 的度数为______▲________．（徐汇）4．如图，在ABC Rt ∆中，︒=∠90ACB ，CD 是AB 边上的中线，将ACD ∆沿CD 所在的直线翻折后到达ECD ∆的位置，如果AB CE ⊥，那么=ABAC ．（2009.1徐汇）5.如图，将ABE ∆沿直线AC 翻折，使点B 与AE 边上的点D 重合，若5AB AC ==，9AE =，则CE = ．（第2题图） A B C M N E A C B D E 第4题 A B C D E （第5题图）填空18题专练———（图形的运动篇之旋转篇）1．将等腰△ABC 绕着底边BC 的中点M 旋转30°后，如果点B 恰好落在原△ABC 的边AB 上，那么∠A 的余切值等于 ▲ ．2．如图，在AOB ∆中，已知90AOB ∠=︒，3AO =，6BO =，将AOB ∆绕顶点O 逆时针旋转到A OB ''∆处，此时线段A B ''与BO 的交点E 为BO 的中点，那么线段B E '的长度为 ▲ ．（2013.1崇明）3．如果将一个三角形绕着它一个角的顶点旋转后使这个角的一边与另一边重叠，再将旋转后的三角形进行相似缩放，使重叠的两条边互相重合，我们称这样的图形变换为三角形转似，这个角的顶点称为转似中心，所得的三角形称为原三角形的转似三角形．如图，在△ABC 中，AB =6，BC =7，AC =5，△A 1B 1C 是△ABC 以点C 为转似中心的其中一个转似三角形，那么以点C 为转似中心的另一个转似三角形△A 2B 2C （点A 2、B 2分别与A 、B 对应）的边A 2B 2的长为 ▲ ．4．如图6，已知等腰△ABC ，AD 是底边BC 上的高，AD ：DC =1：3，将△ADC 绕着点D 旋转，得△DEF ，点A 、C 分别与点E 、F 对应，且EF 与直线AB 重合，设AC 与DF 相交于点O ，则:AOF DOC S S ∆∆= ▲ ．（第2题图） A A ′ B O B ′ E A (B 1) B C A 1 （第3题图）图4 DA。

2021上海二模数学压轴题旋转翻折题17或18题分类汇编1

2021年上海16区中考数学二模压轴题汇编难点专题二旋转翻折（填空17或18）【2021年崇明二模】18．（4分）如图，平面直角坐标系中，A （8，0），B （8，4），C （0，4），反比例函数ky x在第一象限内的图象分别与线段AB 、BC 交于点F 、E ，连接EF ．如果点B 关于EF 的对称点恰好落在OA 边上．那么k 的值为．【2021年静安二模】17．已知矩形纸片ABCD 的边AB =10，BC =12（如图），将它折叠后，点D 落在边AB 的中点处，那么折痕的长为 ▲ ．崇明静安宝山金山普陀闵行虹口长宁杨浦松江嘉定奉贤青浦黄埔浦东新区松江（第17题图）A BDC小题考察一题，分值4分18．如图，矩形ABCD 中，AB ＝2．AD ＝5，点E 是BC 边上一点，联结AE ，将AE 绕点E 顺时针旋转90°，点A 的对应点记为点F ，如果点F 在对角线BD上，那么BFDF= ．【举一反三】如图，在矩形ABCD 中，AB=3，BC=5，点E 为BC 边上一个动点，连接AE ，将线段AE 绕点E 顺时针旋转90°，点A 落在点P 处，当点P 在矩形ABCD 外部时，连接PC 、PD.若ADPC 为直角三角形，则BE 的长为____________。

【2021年金山二模】18.如图，在矩形ABCD 中，3=AB ，4=BC ，点E 在对角线BD 上，联结AE ，作AE EF ⊥交边BC 于F ，若1639=BF ，那么=BE ．第18题图AB CDEF18．如图，正方形ABCD中，AB＝4，E为边BC的中点，点F在AE上，过点F作MN⊥AE，分别交边AB、DC于点M、N，联结FC，如果⊥FNC是以CN为底边的等腰三角形，那么FC＝．【举一反三】如图，在矩形ABCD中，AB=3，BC-4，点E在对角线BD上，联结AE，作EF⊥AE交BC于点F，联结AF交BE于点G，那么GE的最小值为_____________。