统计学公式汇总

合集下载

统计学常用公式汇总

统计学常用公式汇总项目三统计数据的整理与显示组距＝上限－下限a)组中值＝（上限 +下限）÷ 2b)缺下限张口组组中值＝上限－邻组组距 /2c)缺上限张口组组中值＝下限 +1/2 邻组组距例按达成净产值分组（万元）10 以下缺下限：组中值 =10— 10/2=510—20组中值 =（10+20） /2=1520—30组中值 =（20+30） /2=2530—40组中值 =（30+40） /2=3540—70组中值 =（40+70） /2=5570 以上缺上限：组中值 =70+30/2=85项目四统计描绘i.相对指标1.构造相对指标＝各组（或部分）总量 / 整体总量2.比率相对指标＝整体中某一部分数值 / 整体中另一部分数值3.比较相对指标＝甲单位某指标值 / 乙单位同类指标值4.动向相对指标＝报告期数值 / 基期数值5.强度相对指标＝某种现象总量指标 / 另一个有联系而性质不一样的现象总量指标6.实质数实质达成程度%计划达成程度相对指标 K＝=计划数计划规定的达成程度 %7.1实质提升百分数计划达成程度（提升率）： K=100%1计划提升百分数1实质提升百分数计划达成程度（降低率）： K=100%1计划提升百分数ii.均匀指标1.简单算术均匀数：2. 加权算术均匀数或iii.变异指标1.全距＝最大标记值－最小标记值2. 标准差 :简单σ =；加权σ=p p(1 p)成数的标准差3.标准差系数 :项目五时间序列的组成剖析一、均匀发展水平的计算方法：(1)由总量指标动向数列计算序时均匀数①由期间数列计算aan②由时点数列计算在连续时点数列的条件下计算（判断标记按日登记）： a af f在中断时点数列的条件下计算（判断标记按月/ 季度 / 年等登记）：若中断的间隔相等，则采纳“首末折半法”计算。

公式为：1a 1 a 2a n 1a n 1a2n12若中断的间隔不等，则应以间隔数为权数进行加权均匀计算。

统计学公式汇总

1 第三章统计整理公式名称数学公式说明组距（最大值-最小值）/组数 — 全距/组数

组中值（上限+下限）/2 — 上限-相邻组的组距/2 开口组只有上限下限+相邻组的组距/2 开口组只有下限

第四章总量指标和相对指标公式名称数学公式说明

相对指标结构相对指标＝总体部分数值/总体全部数值无名数分子分母不可互换

比例相对指标＝总体中某一部分数值/总体中另一部分数值无名数分子分母可互换

比较相对指标＝某条件下某类指标数值/另一条件下的同类指标值无名数分子分母可互换

动态相对指标=报告期水平/基期水平无名数分子分母不可互换

强度相对指标＝某一总量指标数值/另一个有联系而性质不同的总量指标数值有名数或无名数分子分母有的可互换、有的

不可互换

计划完成程度相对指标＝实际完成数/计划完成数无名数分子分母不可互换 2

第五章平均指标和变异指标公式名称数学公式说明字母含义

算术平均数 nxx 简单 x：算术平均数

x：单位变量值 n：总体单位数 f：权数 

fxfx 加权

调和平均数 xnH1 简单

H：调和平均数

x：单位变量值 n：总体单位数 m：权数 

xmmH 加权

几何平均数 nxG

简单

G：几何平均数

n：变量值的个数 f：变量值的次数 ：连乘

ffxG 加权

中位数 dfsfLMmme12 下限公式

eM：中位数

L：中位数所在的下限

U：中位数所在的上限

1ms

：以下累计至中位数所在组

以下一组的次数 1ms

：以上累计至中位数所在组

以上一组的次数

mf：中位数所在组的次数

d：中位数所在组的组距

dfsfUMmme12 上限公式

众数 dLMo211

下限公式

oM：众数

L：众数所在的下限

U：众数所在的上限

1：众数所在组的次数与前一组

次数之差

2：众数所在组的次数与后一组

统计学公式

2.峰态系数（ K ）： K
3
xi x 4 n(n 1) 3(n 1) 2 ( ) . s (n 1)(n 2)(n 3) (n 2)(n 3)
2
统计学公式
二、概率分布
一、度量事件发生的可能性：
1.事件 A 发生的概率： P ( A) 二、随机变量的概率分布：
统计学公式
一、用统计量描述数据
一、水平的度量：
x x2 x3 1.简单平均数: x 1 n
xn

X
i 1
n
i
n
.
k
M f M 2 f2 M k fk 2.加权平均数： x 1 1 f1 f 2 f k
M
i 1
i i
f
n
.（如果原始数据被分成 k 组，各
2
E2
.
四、假设检验
一、一个总体参数的检验
1.大样本的检验
(1)在大样本的情况下，样本均值的抽样分布近似服从正态分布，其抽样标准差为 /
2
n.
采用正态分布的检验统计量.设假设的总体均值为 0 ,当总体方差已知时,总体均值检验的统计量为： z
x 0
/ n
.
(2)当总体方差未知时,可以采用样本方差 s 来代替,此时总体均值检验的统计量为：
组的组中值分别用 M1，M 2，，M k 表示，各组的频数分别用 f1，f 2，，f k 表示，则得到样本平均数计算公式）
x n 1 2 3.中位数（ M e ）： Me 1 x n x n 1 2 2 2

n
p ；
(1 )

统计学常用公式汇总

《统计学原理》常用公式汇总组距＝上限－下限组中值＝（上限+下限）÷2 缺下限开口组组中值＝上限－1/2邻组组距缺上限开口组组中值＝下限+1/2邻组组距111平均指标 1.简单算术平均数：2.加权算术平均数或iii.变异指标1.全距＝最大标志值－最小标志值2.标准差: 简单σ=；加权σ= 3.标准差系数:第五章抽样估计1.平均误差：重复抽样：不重复抽样：2.抽样极限误差3.重复抽样条件下：平均数抽样时必要的样本数目成数抽样时必要的样本数目4.不重复抽样条件下：平均数抽样时必要的样本数目第七章相关分析 1.相关系数2.配合回归方程ｙ＝ａ＋ｂｘ3.估计标准误：第八章指数分数一、综合指数的计算与分析(1)数量指标指数此公式的计算结果说明复杂现象总体数量指标综合变动的方向和程度。

(-)此差额说明由于数量指标的变动对价值量指标影响的绝对额。

(2)质量指标指数此公式的计算结果说明复杂现象总体质量指标综合变动的方向和程度。

（-）此差额说明由于质量指标的变动对价值量指标影响的绝对额。

加权算术平均数指数=加权调和平均数指数=(3)复杂现象总体总量指标变动的因素分析相对数变动分析：=×绝对值变动分析：-= (-)×（-）第九章动态数列分析一、平均发展水平的计算方法：(1)由总量指标动态数列计算序时平均数①由时期数列计算②由时点数列计算在间断时点数列的条件下计算：a.若间断的间隔相等，则采用“首末折半法”计算。

公式为：b.若间断的间隔不等，则应以间隔数为权数进行加权平均计算。

公式为：(2)由相对指标或平均指标动态数列计算序时平均数基本公式为：式中：代表相对指标或平均指标动态数列的序时平均数；代表分子数列的序时平均数；代表分母数列的序时平均数；逐期增长量之和累积增长量二. 平均增长量＝─────────＝─────────逐期增长量的个数逐期增长量的个数(1)计算平均发展速度的公式为：(2)平均增长速度的计算平均增长速度＝平均发展速度-１（100%）。

统计学公式大全

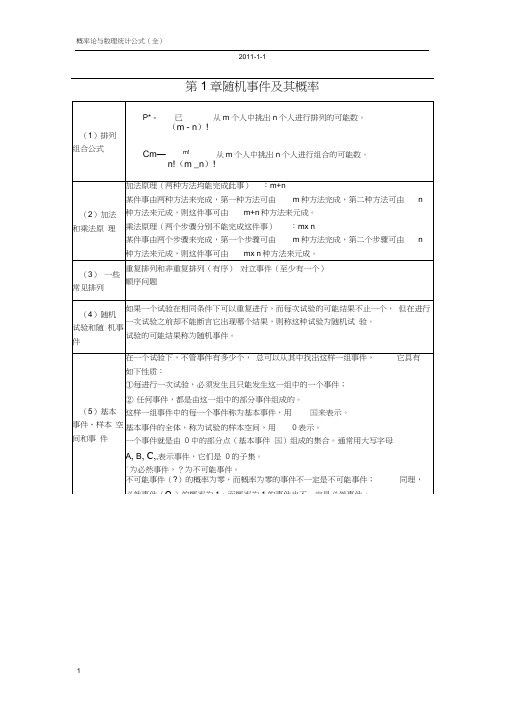
第1章随机事件及其概率第二章随机变量及其分布指数分布正态分布f (x)二0,x :: 0其中’0，则称随机变量X服从参数为’的指数分布。

X的分布函数为F(x)二1-e—'x0, x<0。

记住积分公式:■box n e」dx = n!设随机变量X的密度函数为1 . .2 --------------------------------- --------------------f（x）=^^^e 2口，—旳C X W+P,J2兀◎其中"、二0为常数，则称随机变量X服从参数为2 的正态分布或高斯（Gauss）分布，记为X〜N（.L,；-）。

f（x）具有如下性质:f（x）的图形是关于x i对称的；2°当x八I时，f（J —为最大值;^'2ncr的分布函数为dt1°若X〜N（1，JF（x）l2=x ?-e参数"、二=1时的正态分布称为标准正态分布，记为X ~ N（0,1）1其密度函数记为（【2二°",八::::，分布函数为1 x t2:：J（x）e. 2心:,J（x）是不可求积函数，其函数值，已编制成表可供查用。

口1①（-x）= 1-①（x）且①（0）=—2X A如果X 〜N （丄，二），贝V ~ N （0,1）。

F x 耳、（2dt。

第三章二维随机变量及其分布如果二维随机向量'(X ，Y )的所有可能取值为至多可列个有序对(x,y )，则称匕为离散型随机量。

设.=(X ，Y )的所有可能取值为(x ,y j )(i, j =1,2，…)，且事件｛ =(x i , y j )｝的概率为p j,,称P ｛(X,Y)=&,y j )｝二P j (i,j =1,2,)为.=(X ，Y )的分布律或称为 X 和Y 的联合分布律。

联合分布有时也用下面的概率分布表来表示：这里p j 具有下面两个性质:(1) p j > 0 (i,j=1,2,,); (2) 二二 p ij =1.i j(1 )联合离散型分布概率论与数理统计公式（全）2011-1-1若X1,X2, , X m X m+1, , %相互独立，h,g为连续函数，则: h（X1，X2, , X m）和g （X m+1, , X n）相互独立。

高等统计学常用公式汇总

高等统计学常用公式汇总描述统计均值（Mean）均值是指一组数据的算术平均数，用于描述数据的集中趋势。

计算公式如下：\[\overline{X} = \frac{{\sum_{i=1}^n X_i}}{n}\]其中，\(\overline{X}\)代表均值，\(X_i\)代表第i个观测值，\(n\)代表总观测数。

方差（Variance）方差是用来衡量数据分散程度的指标，计算公式如下：\[Var(X) = \frac{{\sum_{i=1}^n (X_i - \overline{X})^2}}{n-1}\]其中，\(Var(X)\)代表方差，\(X_i\)代表第i个观测值，\(\overline{X}\)代表均值，\(n\)代表总观测数。

标准差（Standard Deviation）标准差是方差的平方根，用于衡量数据的波动性。

计算公式如下：\[SD(X) = \sqrt{Var(X)}\]其中，\(SD(X)\)代表标准差，\(Var(X)\)代表方差。

相关系数（Correlation Coefficient）相关系数用于衡量两个变量之间的线性相关程度。

计算公式如下：\[r = \frac{{\sum_{i=1}^n (X_i - \overline{X})(Y_i -\overline{Y})}}{\sqrt{\sum_{i=1}^n (X_i - \overline{X})^2\sum_{i=1}^n (Y_i - \overline{Y})^2}}\]其中，\(r\)代表相关系数，\(X_i\)代表第i个X变量观测值，\(Y_i\)代表第i个Y变量观测值，\(\overline{X}\)和\(\overline{Y}\)分别代表X变量和Y变量的均值。

推断统计总体均值的置信区间（Confidence Interval for Population Mean）总体均值的置信区间用于估计总体均值的范围。

统计学常用公式总结

心理统计常用公式总结1 、组数 K（总体分布为正态）（ N 为数据个数， K 取近似整数）2 、算术平均数3 、中数4 、众数5 、加权平均数，其中 W i 为权数，其中为各小组的平均数， n i 为各小组人数6 、几何平均数，其中 n 为数据个数， X i 为数据的值7 、调和平均数8 、方差与标准差，其中9 、变异系数，其中 S 为标准差， M 为平均数10 、标准分数，其中 X 为原始数据，为平均数， S 为标准差11 、全距R＝最大数－最小数12 、平均差13 、四分差，其中 L b 为该四分点所在组的精确下限， F b 为该四分点所在组以下的累加次数，和为该四分点所在组的次数， i 为组距， N 为数据个数14 、积差相关基本公式：，其中N 为成对数据的数目， S x 、 S y 分别为 X 和 Y 的标准差变形：差法公式：用估计平均数计算：用相关表计算：15 、斯皮尔曼等级相关，其中 D 为各对偶等级之差直接用等级序数计算：，其中 R X 、 R Y 分别为二变量各等级数有相同等级时：16 、肯德尔等级相关有相同等级：17 、点二列相关，其中是两个二分变量对偶的连续变量的平均数， p 、 q 是二分变量各自所占的比率， p+q=1 ， S t 是连续变量的标准差18 、二列相关，其中 S T 与是连续变量的标准差与平均数， y 为 P 的正态曲线的高度19 、多系列相关，其中 P i 为每系列的次数比率， y 1 为每一名义变量下限的正态曲线高度，y h 为每一名义变量上线的正态曲线高度，为每一名义变量对偶的连续变量的平均数， S t 为连续变量的标准差20 、总体为正态，σ 2 已知：21 、总体为正态，σ 2 未知：22 、23 、24 、。

(完整word版)统计学常用公式

公式一1. 众数【MODE 】（1）未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。

（2）组距分组数据众数的计算对于组距分组数据，先找出出现次数最多的变量值所在组，即为众数所在组，再根据下面的公式计算计算众数的近似值。

下限公式： 1012M =L++i ∆⨯∆∆ 式中：0M 表示众数；L 表示众数的下线；1∆表示众数组次数与上一组次数之差；2∆表示众数组次数与下一组次数之差；i 表示众数组的组距。

上限公式：2012M =U-+i ∆⨯∆∆ 式中：U 表示众数组的上限。

2．中位数【MEDIAN 】（1）未分组数据中中位数的计算根据未分组数据计算中位数时，要先对数据进行排序，然后确定中位数的位置。

设一组数据按从小到大排序后为12N X X X ，，…，，中位数e M ，为则有：e N+M =X1（）2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭ 当N 为偶数（2）分组数据中位数的计算分组数据中位数的计算时，要先根据公式N / 2 确定中位数的位置，并确定中位数所在的组，然后采用下面的公式计算中位数的近似值：N=1m-1e m-S 2M =L+ii fd f ⨯∑式中：e M 表示中位数；L 表示中位数所在组的下限；m-1S 表示中位数所在组以下各组的累计次数；m f 表示中位数所在组的次数；d 表示中位数所在组的组距。

3．均值的计算【A VERAGE 】（1）未经分组均值的计算未经分组数据均值的计算公式为： 112n ++==nii x x x x x n n=∑…（2）分组数据均值计算分组数据均值的计算公式为： 11221121+++==+ki ik k i k kii x f x f x f x f x f f f f==+∑∑+4．几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根，计算公式为：式中：G 表示几何平均数；∏表示连乘符号。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

统计学公式汇总文档编制序号：[KKIDT-LLE0828-LLETD298-POI08] 统计学公式汇总（1） αβδμσνπρυt u F X s

2

（2）均数（mean）：nXn

XXXXn21 式中X表示样本均数，X1，X2，

Xn为各观察值。（3）几何均数（geometric mean, G）：

)lg(lg)lglglg(lg121121nXnXXXXXXGnnn•式中G表示

几何均数，X1，X2，Xn为各观察值。

（4）中位数（median, M） n为奇数时，)21(nXM

n为偶数时，2/][)12()2(nnXXM 式中n为观察值的总个数。（5）百分位数 )%(LxxfxnfiLP 式中Ｌ为Ｐx所在组段的下限，fx为其频

数，i为其组距，Lf为小于Ｌ各组段的累计频数。

（6）四分位数(quartile, Q) 第25百分位数P25，表示全部观察值中有25%（四分之

一）的观察值比它小，为下四分位数，记作QL；第75百分位数P75，表示全部观

察值中有25%（四分之一）的观察值比它大，为上四分位数，记作QU。（7）四分位数间距等于上、下四分位数之差。

（8）总体方差 N

X22)(

（9）总体标准差 N

X2)( （10）样本标准差 1/)(1)(222nnXXn

XXs

（11）变异系数(coefficient of variation, CV) %100

sCV

（12）样本均数的标准误理论值nX 估计值n

ssX 式中σ为总体标准差，s为

样本标准差，n为样本含量。（13）样本率的标准误理论值np)1( 估计值n

ppsp)1( 式中π为总体率，

p为样本率，n为样本含量。（14）总体率的估计：正态分布法，（nppupnppup/)1(,/)1(）式中p为样本均数，s为样本标准差，n为样本含量。

（15）总体均数的估计t分布法：（nstXn

stX,,,）式中X为样本均数，s

为样本标准差，n为样本含量，ν为自由度。（16）总体均数的估计u分布法：

总体标准差σ未知但较大时，（nsuXn

suX,）式中X为样本均

数，s为样本标准差，n为样本含量。总体标准差σ已知时，（nuXnuX,）式中X为样本均数，σ为总

体标准差，n为样本含量。（17）样本均数与总体均数比较的t检验：nsXt/0



 1n 式中X为样本均数，

0为欲比较的总体均数，s为样本标准差，n为样本含量，ν为自由度。（18）样本均数与总体均数比较的u检验： nsXu/0



 式中X为样本均数，0为欲比

较的总体均数，s为样本标准差，n为样本含量。（19）样本均数与总体均数比较的u检验：nXu/0





 式中X为样本均数，0为欲比

较的总体均数，σ为总体标准差，n为样本含量。（20）配对设计差值的符号秩和检验正态近似法公式：48)(24)12)(1(4/)1(3jjttnnn

nnTu

式中T为秩和，求秩和方法：差值d=（X-μ0）；依差值的绝对值从小到大编秩；

差值为0者，舍去不计；如果差值相等，取平均秩次；分别求出正、负秩次之和T（+）、T（-）；T为二者绝对值较小者；n为样本含量，但不包括差值等于0者；tj（=1，2，···）为第j个相同差值的个数。

（21）配对设计两样本均数比较的t检验：nsdtd/

0 1n

 式中d为差值d的均

数，sd为差值d的标准差，n为样本含量(即样本对子数)，差值d=各对子数据之

差（含正负号！），ν为自由度。（22）成组设计两样本均数比较的t检验：

)11(2/)(/)(21212222212121212211nnnnnXXnXXXXsXXtXX







221nn 式中1X和2X分别为两个样本均数， n1和n2为两个样本含量，ν

为自由度。（23）样本率与总体率的比较：未校正的正态近似法)1(000n

nXu 或

npu/)1(000式中X为样本阳性数，π0为欲比较的总体率，p为样本率， n

为样本含量。（24）样本率与总体率的比较：校正的正态近似法)1(5.0||000n

nXu 或

nnpu/)1(2/1||000式中X为样本阳性数，π0为欲比较的总体率，p为样本率， n

为样本含量。（25）样本率与总体率的比较：直接计算概率法：首先按照二项分布的原理计算从0到

n各个X的概率值P（X）=XXnXnXn00)1()!(!!。左单侧：PL表示从0到Xs

的累计概率；右单侧：PR 表示从Xs到n的累计概率；单侧概率P=MIN（PL,

PR）；双侧概率P的计算方法有三种：A，单侧概率乘2；B，当X大于nπ0时，双侧概率=P（≥X）+P（≤(2 nπ0-X)）；当X小于nπ0时，双侧概率=P（≤X）

+P（≥(2 nπ0-X)）；C，将P（X）≤P（Xs）的各个概率值相加，即得双侧累计概率，即P=∑P（X），X满足条件P（X）≤P（Xs）。式中X为样本阳性数，π

0为欲比较的总体率，Xs为样本阳性数， n为样本含量。（26）两个样本率的比较：正态近似法222111212221

)1()1(21nppnppppssppupp

 式中p

和p2分别为两个样本率， n1和n2为两个样本含量。

（27）两个样本率的比较：正态近似法213211

2121

,)11)(1(nnpnpnpnnppppuccc 式中

p1和p2分别为两个样本率， n1和n2为两个样本含量。（28）四格表2检验：TTA22)( ν＝（行数－１）（列数－１）式中A为实际

频数（actual frequency），T为理论频数（theoretical frequency），n

nnTCRRC 式

中TRC表示R行（row）C列（column）的理论频数，nR为相应行的合计值，nC

为相应列的合计值，n为总例数，ν为自由度。

（29）四格表2检验专用公式：))()()(()(22dbcadcbanbcad ν＝（行数－１）（列

数－１）式中a，b，c，d为四格表的四个实际频数，n为总例数，ν为自由度。（30）四格表2值的校正公式：))()()(()2/|(|22dbcadcbannbcad ν＝（行数－１）（列

数－１）式中a，b，c，d为四格表的四个实际频数，n为总例数，ν为自由度。（31）行×列表2检验公式：)1(22CRnnAn ν＝（R－１）（C－１）式中A为实

际频数（actual frequency），nR为相应行的合计值，nC为相应列的合计值，n为

总例数，，R为行数，C为列数，ν为自由度。（32）行×列表2检验公式：)1(112RiCjjiijmnAn ν＝（R－１）（C－１）式中Aij为

实际频数（actual frequency），ni为相应行的合计值，mj为相应列的合计值，n为

总例数，R为行数，C为列数，ν为自由度。（33）四格表的确切概率法：!!!!!)!()!()!()!(ndcba

dbcadcbaP 式中a，b，c，d为四格

表的四个实际频数，n为总例数。取表原则可分为“差数极端法”和“概率极端法”。多数情况下，二者所得结果一致，但个别情况下，所得结果不同。一般认为，“概率极端法”最准确。