全等三角形与勾股定理练习题(一)

合集下载

八下数学勾股定理与全等三角形综合大题

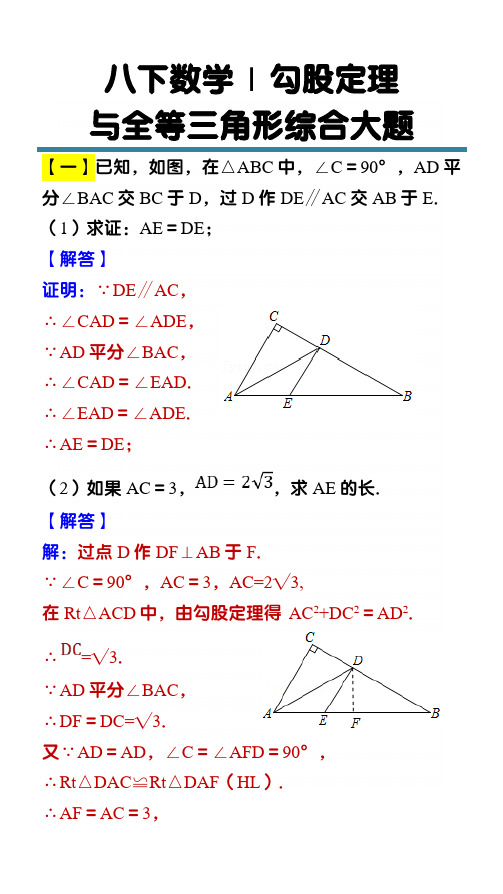
八下数学| 勾股定理与全等三角形综合大题【一】已知，如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于D，过D作DE∥AC交AB于E．（1）求证：AE＝DE；【解答】证明：∵DE∥AC，∴∠CAD＝∠ADE，∵AD平分∠BAC，∴∠CAD＝∠EAD．∴∠EAD＝∠ADE．∴AE＝DE；（2）如果AC＝3，，求AE的长．【解答】解：过点D作DF⊥AB于F．∵∠C＝90°，AC＝3，AC=2√3,在Rt△ACD中，由勾股定理得AC2+DC2＝AD2．∴=√3．∵AD平分∠BAC，∴DF＝DC=√3．又∵AD＝AD，∠C＝∠AFD＝90°，∴Rt△DAC≌Rt△DAF（HL）．∴AF＝AC＝3，∴Rt△DEF中，由勾股定理得EF2+DF2＝DE2．设AE＝x，则DE＝x，EF＝3﹣x，∴（3-x）²+（√3）²＝x²，∴x＝2．∴AE＝2．【二】如图，在Rt△ACB中，∠ACB＝90°，AB＝10，AC＝6．AD平分∠CAB交BC于点D．（1）求BC的长；【解答】解：在Rt△ACB中，∠ACB＝90°，由勾股定理得：=∠AB²-BC²∠10²-6²=．（2）求CD的长．【解答】解：过点D作DE⊥AB于点E，如图．∴∠DEA＝90°＝∠C（垂直定义）．∵AD平分∠CAB（已知），∴∠1＝∠2（角平分线定义）．在△AED和△ACD中，∠DEA=∠C，∠2=∠1，AD=AD△AED≌△ACD（AAS）．∴AE＝AC＝6，DE＝DC（全等三角形的对应边相等）．∴BE＝AB﹣AE＝4．设CD＝x，则DE＝x，DB＝8﹣x．在Rt△DEB中，∠DEB＝90°，由勾股定理，得（8﹣x）2＝x2+42．解得x＝3．即CD＝3．【三】如图，在△ABC中，∠ACB＝90°，AB＝10，BC＝6，点P从点A出发，以每秒2个单位长度的速度沿折线A﹣B﹣C运动．设点P的运动时间为t秒（t＞0）．（1）求AC的长．【解答】解：∵在△ABC中，∠ACB＝90°，AB＝10，BC＝6，∴AC=√AB2-BC2=√102-62=8;（2）求斜边AB上的高．【解答】解：设边AB上的高为h则S△ABC=1/2×BC=1/2AB•h,∴1/2×6×8=1/2×10×h，∴h=24/5，答：斜边AB上的高为24/5；（3）①当点P在BC上时，PC的长为16﹣2t ．（用含t的代数式表示）【解答】解：当点P在BC上时，点P运动的长度为AB+BP＝2t，则PC＝BC﹣BP＝6﹣（2t﹣10）＝6﹣2t+10＝16﹣2t；②若点P在∠BAC的角平分线上，则t的值为20/3 ．【解答】解：当点P'在∠BAC的角平分线上时，过点P作PD⊥AB，如图：∵AP平分∠BAC，PC⊥AC，PD⊥AB，∴PD＝PC，有①知，PC＝16﹣2t，BP＝2t﹣10，∴PD＝16﹣2t，在Rt△ACP和Rt△ADP中，AP=AP，PD=PC，∴Rt△ACP≌Rt△ADP（HL），∴AD＝AC＝8，又∵AB＝10，∴BD＝2，在Rt△BDP中，由勾股定理得：22+（16﹣2t）2＝（2t﹣10）2，解得：t=20/3．（4）在整个运动过程中，直接写出△PBC是等腰三角形时t的值．由图可知，当△BCP是等腰三角形时，点P必在线段AB上，①当点P在线段AB上时，若BC＝BP，则点P运动的长度为AP＝2t，∵AP＝AB﹣BP＝10﹣6＝4，∴2t＝4，∴t＝2；②若PC＝BC，如图，过点C作CH⊥AB于点H，则BP＝2BH，在△ABC中，∠ACB＝90°，AB＝10，BC＝6，AC ＝8，∴AB•CH＝AC•BC，∴10CH＝8×6，∴CH=24/5，在Rt△BCH中，由勾股定理得：BH=√BC2-CH2=√62-（24/5）2=18/5=3.6，∴BP＝2BH＝7.2，∴点P运动的长度为：AP＝AB﹣BP＝10﹣7.2＝2.8，∴2t＝2.8，∴t＝1.4；③若PC＝PB，如图所示，过点P作PQ⊥BC于点Q，则BQ＝CQ=1/2×BC＝3，∠PQB＝90°，∴∠ACB＝∠PQB＝90°，∴PQ∥AC，∴PQ为△ABC的中位线，∴PQ=1/2×AC=1/2×8＝4，在Rt△BPQ中，由勾股定理得：BP=√BQ2+PQ2=√32-42=5，点P运动的长度为AP＝2t，AP＝AB﹣BP＝10﹣5＝5，∴2t＝5，∴t＝2.5．综上，t的值为1.4或2或2.5．。

勾股定理练习题及答案(共6套)

勾股定理课时练（1）1。

在直角三角形ABC 中，斜边AB=1，则AB 222AC BC ++的值是( ）A 。

2 B.4 C 。

6 D 。

82.有一个形状为直角梯形的零件ABCD ，AD ∥BC ，斜腰DC 的长为10 cm ，∠D=120°，则该零件另一腰AB 的长是______ cm （结果不取近似值）.3。

直角三角形两直角边长分别为5和12,则它斜边上的高为_______．4.一根旗杆于离地面12m 处断裂，犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16m ，旗杆在断裂之前高多少m ?5.如图，如下图，今年的冰雪灾害中，一棵大树在离地面3米处折断，树的顶端落在离树杆底部4米处，那么这棵树折断之前的高度是米.6。

飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒，飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米?7。

如图所示，无盖玻璃容器，高18cm ，底面周长为60cm ，在外侧距下底1cm 的点C 处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口1cm 的F 处有一苍蝇，试求急于扑货苍蝇充饥的蜘蛛，所走的最短路线的长度。

8。

一个零件的形状如图所示，已知AC=3cm ，AB=4cm ，BD=12cm 。

求CD 的长。

第5题图第7题图第8题图9。

如图，在四边形ABCD 中，∠A=60°,∠B=∠D=90°,BC=2，CD=3，求AB 的长.10. 如图，一个牧童在小河的南4km 的A 处牧马，而他正位于他的小屋B 的西8km 北7km 处，他想把他的马牵到小河边去饮水，然后回家。

他要完成这件事情所走的最短路程是多少？11如图,某会展中心在会展期间准备将高5m ,长13m ，宽2m 的楼道上铺地毯，已知地毯平方米18元,请你帮助计算一下，铺完这个楼道至少需要多少元钱？12. 甲、乙两位探险者到沙漠进行探险，没有了水，需要寻找水源．为了不致于走散，他们用两部对话机联系，已知对话机的有效距离为15千米．早晨8:00甲先出发，他以6千米/时的速度向东行走，1小时后乙出发，他以5千米/时的速度向北行进，上午10：00,甲、乙二人相距多远？还能保持联系吗？第9题图5m 13m 第11题勾股定理的逆定理（2）一、选择题1.下列各组数据中,不能作为直角三角形三边长的是( ）A.9，12，15 B 。

2020年中考数学精选考点试卷13 三角形和勾股定理(解析版)

中考数学专题13.1三角形和勾股定理精选考点专项突破卷（一）考试范围：三角形和勾股定理；考试时间：90分钟；总分：120分一、单选题（每小题3分，共30分)1．（2017·江苏中考真题）三角形的重心是（）A ．三角形三条边上中线的交点B ．三角形三条边上高线的交点C ．三角形三条边垂直平分线的交点D ．三角形三条内角平行线的交点2．（2019·江苏中考真题）下列长度的三条线段，能组成三角形的是（）A ．2，2，4B ．5，6，12C ．5，7，2D ．6，8，103．（2019·山东中考真题）如图，D 是AB 上一点，DF 交AC 于点E ，DE FE =，//FC AB ，若4AB =，3CF =，则BD 的长是（）A ．0.5B ．1C ．1.5D ．24．（2019·吉林中考真题）如图，在ABC ∆中，ACB ∠为钝角．用直尺和圆规在边AB 上确定一点D ．使ADC 2B ∠=∠，则符合要求的作图痕迹是（）A ．B ．C ．D ．5．（2019·湖南中考真题）如图，在ABC ∆中，90︒∠=C ，8AC =，13DC AD =，BD 平分ABC ∠，则点D 到AB 的距离等于（）A ．4B ．3C ．2D ．16．（2018·浙江中考真题）如图，AD ，CE 分别是△ABC 的中线和角平分线．若AB=AC ，△CAD=20°，则△ACE 的度数是（）A ．20°B ．35°C ．40°D ．70°7．（2015·贵州中考真题）下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是（）A B ．C ．6,7,8 D ．2,3,48．（2019·湖南中考真题）如图，Rt△ABC 中，△C ＝90°，△B ＝30°，分别以点A 和点B 为圆心，大于12AB 的长为半径作弧，两弧相交于M 、N 两点，作直线MN ，交BC 于点D ，连接AD ，则△CAD 的度数是（）A ．20°B ．30°C ．45°D ．60°9．（2012·黑龙江中考真题）如图，△ABC 中，AB=AC=10，BC=8，AD 平分△BAC 交BC 于点D ，点E 为AC 的中点，连接DE ，则△CDE 的周长为（）A ．20B ．12C ．14D ．1310．（2019·广西中考真题）如图，ABC ∆为等边三角形，点P 从A 出发，沿A B C A →→→作匀速运动，则线段AP 的长度y 与运动时间x 之间的函数关系大致是（）A．B．C．D．二、填空题（每小题4分，共28分)11．（2019·沭阳县修远中学中考模拟）如图，A、B、C分别是线段A1B、B1C、C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积为____.12．（2019·山东中考模拟）如图，在线段AD，AE，AF中，△ABC的高是线段________.13．（2019·北京中考模拟）如图，在△ABC中，射线AD交BC于点D，BE△AD于E，CF△AD于F，请补充一个条件，使△BED△△CFD，你补充的条件是______（填出一个即可）．14．（2019·北京中考模拟）当三角形中的一个内角α是另一个内角β的一半时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为直角三角形，则这个“特征角”的度数为______．15．（2019·辽宁中考模拟）如图，已知AB△CF，E为DF的中点，若AB=8，CF=5，则BD=_______．16．（2018·安徽中考模拟）如图,在矩形ABCD中,AB=5,BC=7,点E是AD上的一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在△BCD的平分线上时,CA1的长为__.17．（2019·双柏县雨龙中学中考模拟）已知三角形的两边长分别是7和10，则第三边长a的取值范围是_____．三、解答题一（每小题6分，共30分)18．（2014·江苏中考真题）如图，已知：△ABC中，AB=AC，M是BC的中点，D、E分别是AB、AC边上的点，且BD=CE．求证：MD=ME．19．（2015·浙江中考真题）如图，已知△ABC，△C=90°，AC<BC，D为BC上一点，且到A，B两点的距离相等．（1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；（2）连结AD，若△B=37°，求△CAD的度数．20．（2013·浙江中考真题）如图，在△ABC中，△C=90°，AD平分△CAB，交CB于点D，过点D作DE△AB，于点E（1）求证：△ACD△△AED；（2）若△B=30°，CD=1，求BD的长．21．（2019·重庆中考真题）如图，在△ABC中，AB=AC，D是BC边上的中点，连结AD，BE平分△ABC交AC 于点E，过点E作EF△BC交AB于点F．（1）若△C=36°，求△BAD的度数．（2）若点E在边AB上，EF//AC叫AD的延长线于点F．求证：FB=FE．22．（2019·四川中考真题）如图，等腰直角三角板如图放置．直角顶点C在直线m上，分别过点A、B作AE△直线m于点E，BD△直线m于点D．；①求证：EC BD②若设△AEC三边分别为a、b、c，利用此图证明勾股定理．四、解答题二（每小题8分，共32分)23．（2017·江苏中考真题）如图，已知在四边形ABCD中，点E在AD上，△BCE=△ACD=90°，△BAC=△D，BC=CE．（1）求证：AC=CD；（2）若AC=AE，求△DEC的度数．24．（2018·山东中考真题）已知，在△ABC 中，△A=90°，AB=AC ，点D 为BC 的中点．（1）如图①，若点E 、F 分别为AB 、AC 上的点，且DE△DF ，求证：BE=AF ；（2）若点E 、F 分别为AB 、CA 延长线上的点，且DE△DF ，那么BE=AF 吗？请利用图②说明理由．25．（2015·广西中考真题）如图，在△ABC 中，△ACB=90°，AC=BC=AD ．（1）作△A 的平分线交CD 于E ；（2）过B 作CD 的垂线，垂足为F ；（3）请写出图中两对全等三角形（不添加任何字母），并选择其中一对加以证明．26．（2019·山东中考真题）在ABC ∆中，90BAC ∠=︒，AB AC =，AD BC ⊥于点D ．（1）如图1，点M ，N 分别在AD ，AB 上，且90BMN ∠=︒，当30AMN =︒∠，2AB =时，求线段AM 的长；（2）如图2，点E ，F 分别在AB ，AC 上，且90EDF ∠=︒，求证：BE AF =；（3）如图3，点M 在AD 的延长线上，点N 在AC 上，且90BMN ∠=︒，求证：AB AN +=．13.1三角形和勾股定理精选考点专项突破卷（一）参考答案1．A【解析】三角形的重心是三条中线的交点，故选A ．2．D【解析】根据三角形三边关系，看其中较小两边的和是否大于最长边即可判断各个选项中的三条线段是否能组成三角形．【详解】224+=Q ，2∴，2，4不能组成三角形，故选项A 错误，5612+<Q ，5∴，6，12不能组成三角形，故选项B 错误，527+=Q ，5∴，7，2不能组成三角形，故选项C 错误，6810+>Q ， 6∴，8，10能组成三角形，故选项D 正确，故选D ．【点睛】本题考查了三角形三边关系，解答本题的关键是明确三角形两边之和大于第三边．3．B【解析】根据平行线的性质，得出A FCE ∠=∠，ADE F ∠=∠，根据全等三角形的判定，得出ADE CFE ∆≅∆，根据全等三角形的性质，得出AD CF =，根据4AB =，3CF =，即可求线段DB 的长．【详解】△//CF AB ，△A FCE ∠=∠，ADE F ∠=∠，在ADE ∆和FCE ∆中A FCE ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，△()ADE CFE AAS ∆≅∆，△3AD CF ==，△4AB =，△431DB AB AD =-=-=.故选：B ．【点睛】本题考查了全等三角形的性质和判定，平行线的性质的应用，能判定ADE FCE ∆≅∆是解此题的关键．4．B【解析】由ADC 2B ∠=∠且ADC B BCD ∠=∠+∠知B BCD ∠=∠，据此得DB DC =，由线段的中垂线的性质可得答案．【详解】解：△ADC 2B ∠=∠且ADC B BCD ∠=∠+∠，△B BCD ∠=∠，△DB DC =，△点D 是线段BC 中垂线与AB 的交点，故选B【点睛】考核知识点：线段垂直平分线.理解线段垂直平分线性质是关键.5．C【解析】如图，过点D 作DE AB ⊥于E ，根据已知求出CD 的长，再根据角平分线的性质进行求解即可.【详解】如图，过点D 作DE AB ⊥于E ，AC 8=Q ，1DC AD 3=， 1CD 8213∴=⨯=+， C 90∠︒=Q ，BD 平分ABC ∠，DE CD 2∴==，即点D到AB的距离为2，故选C．【点睛】本题考查了角平分线的性质，熟练掌握角平分线上的点到角两边的距离相等是解题的关键. 6．B【解析】先根据等腰三角形的性质以及三角形内角和定理求出△CAB=2△CAD=40°，△B=△ACB=12（180°-△CAB）=70°．再利用角平分线定义即可得出△ACE=12△ACB=35°．【详解】△AD是△ABC的中线，AB=AC，△CAD=20°，△△CAB=2△CAD=40°，△B=△ACB=12（180°-△CAB）=70°．△CE是△ABC的角平分线，△△ACE=12△ACB=35°．故选B．【点睛】本题考查了等腰三角形的两个底角相等的性质，等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合的性质，三角形内角和定理以及角平分线定义，求出△ACB=70°是解题的关键．7．B【解析】试题解析：A．）2+）2≠2，故该选项错误；B．12+）2=2,故该选项正确；C．62+72≠82，故该选项错误；D．22+32≠42，故该选项错误.故选B.考点：勾股定理.8．B【解析】根据内角和定理求得△BAC=60°，由中垂线性质知DA=DB，即△DAB=△B=30°，从而得出答案．【详解】在△ABC中，△△B=30°，△C=90°，△△BAC=180°-△B-△C=60°，由作图可知MN为AB的中垂线，△DA=DB，△△DAB=△B=30°，△△CAD=△BAC-△DAB=30°，故选B．【点睛】本题主要考查作图-基本作图，熟练掌握中垂线的作图和性质是解题的关键．9．C【解析】解：△AB=AC，AD平分△BAC，BC=8，△AD△BC，CD=BD=12BC=4，△点E为AC的中点，△DE=CE=12AC=5，△△CDE的周长=CD+DE+CE=4+5+5=14．故选C．【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形三线合一的性质，熟记性质并准确识图是解题的关键．10．B【解析】根据题意可知点P从点A运动到点B时以及从点C运动到点A时是一条线段，故可排除选项C与D；点P从点B运动到点C时，y是x的二次函数，并且有最小值，故选项B符合题意，选项A不合题意．【详解】根据题意得，点P从点A运动到点B时以及从点C运动到点A时是一条线段，故选项C与选项D 不合题意；点P从点B运动到点C时，y是x的二次函数，并且有最小值，△选项B符合题意，选项A不合题意．故选B．【点睛】本题考查了动点问题的函数图象：通过分类讨论，利用三角形面积公式得到y与x的函数关系，然后根据二次函数和一次函数图象与性质解决问题．11．7【解析】如下图，连接A 1C ，B 1A ，C 1B ，，因B 是线段B 1C 的中点，所以B 1B=BC.△A 1B 1A 和△AB 1B 等底同高，根据等底同高的两个三角形面积相等可得S △B1AB =S △ABC =1；同理可得S △A1B1A =S △AB1B =1；所以=S △A1B1A +S △AB1B =1+1=2；同理可得S △C1CB1=2， S △C1AA1=2.S △A1B1C1= S △A1BB1+ S △C1CB1+ S △C1AA1+S △ABC =2+2+2+1=7.考点：等底同高的两个三角形面积相等.12．AF【解析】从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高．【详解】△AF△BC 于F ，△AF 是△ABC 的高线，故答案为：AF ．【点睛】本题主要考查了三角形的高线，锐角三角形的三条高在三角形内部，相交于三角形内一点，直角三角形有两条高与直角边重合，另一条高在三角形内部，它们的交点是直角顶点；钝角三角形有两条高在三角形外部，一条高在三角形内部，三条高所在直线相交于三角形外一点．13．答案不唯一，如BD=DC【解析】根据全等三角形的判定定理AAS 判定△BED△△CFD ．【详解】解：可以添加条件：BD=DC ．理由：△BD=CD ；又△BE△AD ，CF△AD ，△△E=△CFD=90°；△在△BED 和△CFD 中，90BDE CDF E CFD BD CD ∠∠⎧⎪∠∠︒⎨⎪⎩＝＝＝＝，△△BED△△CFD（AAS）．故答案是：答案不唯一，如BD=DC．【点睛】本题考查了全等三角形的判定．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．14．45°或30°【解析】分①“特征角”的2倍是直角时，根据“特征角”的定义列式计算即可得解；②“特征角”的2倍与“特征角”都不是直角，根据直角三角形两锐角互余列方程求解即可．【详解】解：①“特征角”的2倍是直角时，“特征角”=12×90°=45°；②“特征角”的2倍与“特征角”都不是直角时，设“特征角是x”，由题意得，x+2x=90°，解得x=30°，所以，“特征角”是30°，综上所述，这个“特征角”的度数为45°或30°．故答案为：45°或30°．【点睛】本题考查了直角三角形的性质，主要利用了直角三角形两锐角互余的性质，读懂题目信息，理解“特征角”的定义是解题的关键．15．3【解析】△AB//CF，△△A=△FCE，△ADE=△F，又△DE=FE，△△ADE△△CFE，△AD=CF=5，△AB=8，△BD=AB-AD=8-5=3，故答案为3.16．【解析】过点A1作A1M△BC于点M.由A1C是角平分线可知△A1CM=45°，可证明A1M=CM，可知△AMC是等腰直角三角形，设CM=A1M=x，在Rt△A1MB中利用勾股定理列方程求出x的值，根据△AMC是等腰直角三角形即可求出答案.【详解】过点A1作A1M△BC于点M.△点A的对应点A1恰落在△BCD的平分线上，△BCD=90°，△△A1CM=45°，即△AMC是等腰直角三角形，△设CM=A 1M=x,则BM=7-x.又由折叠的性质知AB=A 1B=5，△在直角△A 1MB 中，由勾股定理得A 1M 2=A 1B 2-BM 2=25-(7-x)2，△25-(7-x)2=x 2,解得x 1=3，x 2=4，△在等腰Rt△A 1CM 中,CA 1A 1M ，△CA 1或.【点睛】本题考查折叠性质及解直角三角形，图形折叠后对应边相等，对应角相等，熟练掌握折叠的性质是解题关键.17．3＜a ＜17．【解析】根据三角形的第三边大于两边之差，小于两边之和，即可解决问题．【详解】解：△三角形的两边长分别是10和7，△第三边长a 的取值范围是3＜a ＜17．故答案为3＜a ＜17．【点睛】本题考查三角形三边关系的运用，熟记三角形的第三边大于两边之差，小于两边之和是解题的关键．18．证明见解析.【解析】试题分析：根据等腰三角形的性质可证△DBM=△ECM ，可证△BDM△△CEM ，可得MD=ME ，即可解题．试题解析：证明：△ABC 中，△AB=AC ，△△DBM=△ECM.△M 是BC 的中点，△BM=CM.在△BDM 和△CEM 中，△，△△BDM△△CEM （SAS ）.△MD=ME ．BD CE DBM ECM BM CM =⎧⎪∠=∠⎨⎪=⎩考点：1.等腰三角形的性质；2.全等三角形的判定与性质.19．（1）点D的位置如图所示（D为AB中垂线与BC的交点）．（2）16°．【解析】（1）根据到线段两个端点的距离相等的点在这条线段的垂直平分线上，作出AB的中垂线．（2）要求△CAD的度数，只需求出△CAD，而由（1）可知：△CAD=2△B【详解】解：（1）点D的位置如图所示（D为AB中垂线与BC的交点）．（2）△在Rt△ABC中，△B=37°，△△CAB=53°．又△AD=BD，△△BAD=△B=37°．△△CAD=53°—37°=16°．考点：尺规作图，直角三角形两锐角互余、垂直平分线的性质．20．（1）见解析（2）BD=2【解析】解：（1）证明：△AD平分△CAB，DE△AB，△C=90°，△CD=ED，△DEA=△C=90°．△在Rt△ACD和Rt△AED中，AD AD {CD DE==，△Rt△ACD△Rt△AED（HL）．（2）△Rt△ACD△Rt△AED ，CD=1，△DC=DE=1．△DE△AB，△△DEB=90°．△△B=30°，△BD=2DE=2．（1）根据角平分线性质求出CD=DE，根据HL定理求出另三角形全等即可．（2）求出△DEB=90°，DE=1，根据含30度角的直角三角形性质求出即可．21．（1）54BAD︒∠=；（2）见解析.【解析】（1）利用等腰三角形的三线合一的性质证明△ADB=90°，再利用等腰三角形的性质求出△ABC即可解决问题.（2）只要证明△FBE=△FEB即可解决问题.【详解】解：（1）AB AC =QC ABC ∴∠=∠36C ︒∠=Q36ABC ︒∴∠=Q D 为BC 的中点，AD BC ∴⊥90903654BAD ABC ︒︒︒︒∴∠=-∠=-=（2）Q BE 平分ABC ∠ABE EBC ∴∠=∠又//EF BC QEBC BEF ∴∠=∠EBF FEB ∴∠=∠BF EF ∴=【点睛】本题考查等腰三角形的性质，平行线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型.22．①证明见解析；②见解析.【解析】①通过AAS 证得CAE BCD ∆≅∆，根据全等三角形的对应边相等证得结论；②利用等面积法证得勾股定理．【详解】①证明：△90ACB ︒∠=，△90ACE BCD ︒∠+∠=．△90ACE CAE ︒∠+∠=，△CAE BCD ∠=∠．在△AEC 与△BCD 中，CEA BDC CAE BCD AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩△()CAE BCD AAS ∆∆≌．△EC BD =；②解：由①知：BD CE a ==CD AE b == △1()()2AEDB S a b a b =++梯形 221122a ab b =++．又△AEC BCD ABC AEDB S S S S =++V V V 梯形2111222ab ab c =++ 212ab c =+． △222111222a ab b ab c ++=+．整理，得222+=a b c ．【点睛】主要考查了同角的余角相等，全等三角形的判定和性质，勾股定理的证明，解本题的关键是判断两三角形全等．23．（1）证明见解析；（2）112.5°．【解析】()1根据同角的余角相等可得到24∠=∠，结合条件BAC D ∠=∠，再加上BC CE =，可证得结论； ()2根据90ACD AC CD ∠=︒=，，得到145D ∠=∠=︒，根据等腰三角形的性质得到3567.5∠=∠=︒，由平角的定义得到1805112.5DEC ∠=︒-∠=︒．【详解】() 1证明：90BCE ACD ∠=∠=︒Q ，2334，∴∠+∠=∠+∠ 24∴∠=∠，在△ABC 和△DEC 中，24BAC D BC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AAS ABC DEC ∴V V ≌，AC CD ∴=；（2）△△ACD ＝90°，AC ＝CD ，△△1＝△D ＝45°，△AE ＝AC ，△△3＝△5＝67.5°，△△DEC ＝180°－△5＝112.5°．24．（1）证明见解析；（2）BE=AF ，证明见解析.【解析】分析：（1）连接AD ，根据等腰三角形的性质可得出AD=BD 、△EBD=△FAD ，根据同角的余角相等可得出△BDE=△ADF ，由此即可证出△BDE△△ADF （ASA ），再根据全等三角形的性质即可证出BE=AF ；（2）连接AD ，根据等腰三角形的性质及等角的补角相等可得出△EBD=△FAD 、BD=AD ，根据同角的余角相等可得出△BDE=△ADF ，由此即可证出△EDB△△FDA （ASA ），再根据全等三角形的性质即可得出BE=AF ．详（1）证明：连接AD ，如图①所示．△△A=90°，AB=AC ，△△ABC 为等腰直角三角形，△EBD=45°．△点D 为BC 的中点， △AD=12BC=BD ，△FAD=45°． △△BDE+△EDA=90°，△EDA+△ADF=90°，△△BDE=△ADF ．在△BDE 和△ADF 中，EBD FAD BD ADBDE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩，△△BDE△△ADF （ASA ），△BE=AF ；（2）BE=AF ，证明如下：连接AD ，如图②所示．△△ABD=△BAD=45°，△△EBD=△FAD=135°．△△EDB+△BDF=90°，△BDF+△FDA=90°，△△EDB=△FDA ．在△EDB 和△FDA 中，EBD FAD BD ADEDB FDA ∠=∠⎧⎪=⎨⎪∠=∠⎩， △△EDB△△FDA （ASA ），△BE=AF ．点睛：本题考查了全等三角形的判定与性质、等腰直角三角形、补角及余角，解题的关键是：（1）根据全等三角形的判定定理ASA 证出△BDE△△ADF ；（2）根据全等三角形的判定定理ASA 证出△EDB△△FDA ． 25．（1）作图见试题解析；（2）作图见试题解析；（3）△ACE△△ADE ，△ACE△△CFB ．【解析】试题分析：（1）利用角平分线的作法得出△A 的平分线；（2）利用钝角三角形高线的作法得出BF ；（3）利用等腰三角形的性质及全等三角形的判定得出答案．试题解析：（1）如图所示：AE 即为所求；（2）如图所示：BF 即为所求；（3）如图所示：△ACE△△ADE ，△ACE△△CFB ，△AC=AD ，AE 平分△CAD ，△AE△CD ，EC=DE ，在△ACE 和△ADE 中，△AE=AE ，△AEC=△AED ，EC=ED ，△△ACE△△ADE （SAS ）．考点：1．作图—复杂作图；2．全等三角形的判定．26．(1) AM =(2)见解析；(3)见解析.【解析】（1）根据等腰三角形的性质、直角三角形的性质得到 AD ＝BD ＝DC ＝，求出 △MBD ＝30°，根据勾股定理计算即可；（2）证明△BDE △△ADF ，根据全等三角形的性质证明；（3）过点 M 作 ME △BC 交 AB 的延长线于 E ，证明△BME △△AMN ，根据全等三角形的性质得到 BE ＝AN ，根据等腰直角三角形的性质、勾股定理证明结论．【详解】（1）解：90BAC ∠=︒Q ，AB AC =，AD BC ⊥，AD BD DC ∴==，45ABC ACB ∠=∠=︒，45BAD CAD ∠=∠=︒，2AB =Q ，AD BD DC ∴===，30AMN ∠=︒Q ，180903060BMD ∴∠=︒-︒-︒=︒，30BMD ∴∠=︒，2BM DM ∴=，由勾股定理得，222BM DM BD -=，即222(2)DM DM -=，解得，DM =AM AD DM∴=-=（2）证明：AD BC⊥Q，90EDF∠=︒，BDE ADF∴∠=∠，在BDE∆和ADF∆中，{B DAFDB DABDE ADF∠=∠=∠=∠，()BDE ADF ASA∴∆∆≌BE AF∴=；（3）证明：过点M作//ME BC交AB的延长线于E，90AME∴∠=︒，则AE=，45E∠=︒，ME MA∴=，90AME∠=︒∵，90BMN∠=︒，BME AMN∴∠=∠，在BME∆和AMN∆中，{E MANME MABME AMN∠=∠=∠=∠，()BME AMN ASA∴∆∆≌，BE AN∴=，AB AN AB BE AE∴+=+==．【点睛】本题考查的是等腰直角三角形的性质、全等三角形的判定和性质、直角三角形的性质，掌握全等三角形的判定定理和性质定理是解题的关键。

勾股定理基础练习题(含答案与解析)

勾股定理基础练习题(含答案与解析)勾股定理勾股定理基础练习题(含答案与解析)第Ⅰ卷（选择题）请点击修改第I卷的文字说明一．选择题（共15小题）1．在直角三角形中，有两边分别为3和4，则第三边是（）A．1 B．5 C．D．5或2．直角三角形有一条直角边为6，另两条边长是连续偶数，则该三角形周长为（）A．20 B．22 C．24 D．263．如图，两个较大正方形的面积分别为225，289，则字母A所代表的正方形的面积为（）A．4 B．8 C．16 D．644．Rt△ABC中，斜边BC=2，则AB2+AC2+BC2的值为（）A．8 B．4 C．6 D．无法计算5．如图，在△ABC中，AD⊥BC于D，AB=17，BD=15，DC=6，则AC的长为（）A．11 B．10 C．9 D．86．若等腰三角形的腰长为10，底边长为12，则底边上的高为（）A．6 B．7 C．8 D．97．一直角三角形的一直角边长为6，斜边长比另一直角边长大2，则斜边的长为（）A．4 B．6 C．8 D．108．如图所示：是一段楼梯，高BC是3m，斜边AC是5m，如果在楼梯上铺地毯，那么至少需要地毯（）勾股定理基础练习题(含答案与解析)A．5m B．6m C．7m D．8m9．如图，已知，CD是Rt△ABC斜边上的高，∠ACB=90°，AC=4m，BC=3m，则线段CD的长为（）A．5m B．C．D．10．若等边△ABC的边长为2cm，那么△ABC的面积为（）A．cm2B．2cm2 C．3cm2 D．4cm211．直角三角形的一直角边长是12，斜边长是15，则另一直角边是（）A．8 B．9 C．10 D．1112．如图，2×2的方格中，小正方形的边长是1，点A、B、C都在格点上，则AB边上的高长为（）A．B．C．D．13．用下列各组线段为边，能构成直角三角形的是（）A．1cm，2cm，3cm B．cm，cm，cm C．1cm，2cm，cm D．2cm，3cm，4cm14．将一个直角三角形的三边扩大3倍，得到的三角形是（）A．直角三角形 B．锐角三角形 C．钝角三角形 D．不能确定15．下列条件中，不能判断△ABC为直角三角形的是（）A．a=1.5，b=2，c=2.5 B．a：b：c=3：4：5C．∠A+∠B=∠C D．∠A：∠B：∠C=3：4：5勾股定理基础练习题(含答案与解析)第Ⅱ卷（非选择题）请点击修改第Ⅱ卷的文字说明评卷人得分二．填空题（共13小题）16．如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A，B，C，D的面积和是49cm2，则其中最大的正方形S 的边长为cm．17．如图，矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为．18．如图：5米长的滑梯AB开始在B点距墙面水平距离3米，当向后移动1米，A点也随着向下滑一段距离，则下滑的距离（大于，小于或等于）1米．19．如图，长方体长、宽、高分别为4cm，3cm，12cm，则BD′=．勾股定理基础练习题(含答案与解析)20．如图，由4个相同的直角三角形与中间的小正方形拼成一个大正方形，若大正方形面积是9，小正方形面积是1，直角三角形较长直角边为a，较短直角边为b，则ab的值是．21．2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图），如果大正方形的面积是25，小正方形的面积是1，直角三角形较短的直角边为a，较长的直角边为b，那么（a+b）2的值为．22．把两个全等的直角三角形拼成如图图形，那么图中三角形面积之和与梯形面积之间的关系用式子可表示为，整理后即为．23．如图，正方形网格中的△ABC，若小方格边长都为1，则△ABC是：三角形．勾股定理基础练习题(含答案与解析)24．如图，四边形ABCD中，∠B=90°，AB=4cm，BC=3cm，AD=13cm，CD=12cm，则四边形ABCD的面积cm2．25．如图，AD=8，CD=6，∠ADC=90°，AB=26，BC=24，该图形的面积等于．26．已知：如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止当t=时，△PBQ是直角三角形．27．如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm 的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到达内壁B处的最短距离为cm．勾股定理基础练习题(含答案与解析)28．一个圆桶儿，底面直径为16cm，高为18cm，有一只小虫从底部点A处爬到上底B处，则小虫所爬的最短路径长是（π取3）．评卷人得分三．解答题（共5小题）29．如图，已知一架竹梯AB斜靠在墙角MON处，竹梯AB=13m，梯子底端离墙角的距离BO=5m．（1）求这个梯子顶端A距地面有多高；（2）如果梯子的顶端A下滑4m到点C，那么梯子的底部B在水平方向上滑动的距离BD=4m吗？为什么？30．如图，一个直径为10cm的杯子，在它的正中间竖直放一根筷子，筷子露出杯子外1cm，当筷子倒向杯壁时（筷子底端不动），筷子顶端刚好触到杯口，求筷子长度和杯子的高度．勾股定理基础练习题(含答案与解析)31．在甲村至乙村的公路有一块山地正在开发，现有一C处需要爆破．已知点C与公路上的停靠站A的距离为300米，与公路上的另一停靠站B的距离为400米，且CA⊥CB，如图所示．为了安全起见，爆破点C周围半径250米范围内不得进入，问在进行爆破时，公路AB段是否有危险而需要暂时封锁？请通过计算进行说明．32．如图，一只蜘蛛在一块长方体木块的一个顶点A处，一只苍蝇在这个长方体的对角顶点G处，若AB=3cm，BC=5cm，BF=6cm，问蜘蛛要沿着怎样的路线爬行，才能最快抓到苍蝇？这时蜘蛛走过的路程是多少厘米？33．有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多什么米？勾股定理基础练习题(含答案与解析)本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

勾股定理与全等三角形

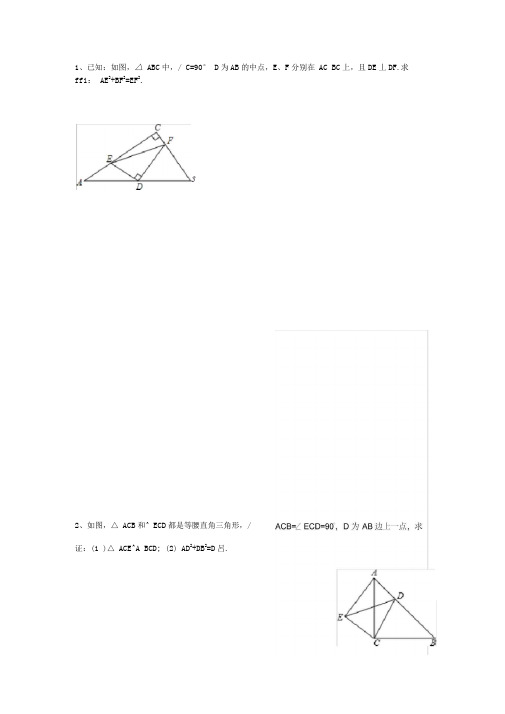
1、已知:如图,△ABC中,△C=90°,D为ＡB得中点,E、Ｆ分别在AC、BC上,且ＤＥ△DF.求证:AE2+BF2=EF２。

２、如图,△ACＢ与△ECＤ都就是等腰直角三角形,∠AＣB=∠ECＤ=90°,Ｄ为AB边上一点,求证:(1)△ＡＣE≌△BＣD;(2)AD２+DB2=DＥ２.3、如图,△ABC中,AB=BC,BＥ⊥ＡC于点E,AＤ⊥BＣ于点Ｄ,∠BAD=４5°,AD与ＢE交于点Ｆ,连接ＣＦ.(１)求证:BF=2AE;ﻫ(２)若CD＝2,求AD得长、4、如图①,已知点Ｄ在ＡＢ上,△ABC与△AＤE都就是等腰直角三角形,∠ABC=∠ADE=９0°,且M为ＥC得中点。

ﻫ)1)求证:△BMD为等腰直角三角形、(思路点拨:考虑M为EＣ得中点得作用,可以延长DM交BC于N,构造△ＣMＮ≌△EMD,于就是EＤ=ＣN=DA,即可以证明△BND也就是等腰直角三角形,且BM就是等腰三角形底边得中线就可以了。

)请您完成证明过程:(2)将△AＤE绕点Ａ再逆时针旋转90°时(如图②所示位置),△ＢＭD为等腰直角三角形得结论就是否仍成立?若成立,请证明:若不成立,请说明理由。

1、证明:延长EＤ到G,使DG=DE,连接ＥF、FG、CG,如图所示:△△DＦ=ＤF,△EDF=△FDG＝90°,DG=ＤＥ△△△EDＦ△△GDＦ(SAS),△△EF=FG△又△Ｄ为斜边BC中点△BD=ＤC又△△BDE=△CＤG,ＤＥ=ＤＧ△△BDE△△CDG(SＡS)△BE=ＣG,△B=△BCG △△AB△CG△△△GCA＝１80°－△A=１80°－9０°=90°在Rt△FCG中,由勾股定理得:FＧ2=ＣF2+CG2=CF2+BE2ﻫ△EF2＝ＦG２=BE2+CF２.证明:过点Ａ作AM△BC,交ＦD延长线于点M,连接ＥＭ、△AM△ＢC,△△MAE=△ACB=90°,△MAD=△B.△△AD=BD,△ADM=△BDF,△△ＡＤM△△BDF.△AM=ＢF,MD＝ＤF、又DE△DF,△EF=EM、△AE2+BＦ2=AＥ2+AM2＝EＭ2=ＥF２、２、证明:(1)∵∠ACB＝∠ECD,ﻫ∴∠ACＤ+∠ＢＣＤ=∠AＣD+∠ＡCE,ﻫ即∠BCD=∠AＣE.ﻫ∵BC=AC,DC=EＣ,∴△ACE≌△ＢCD。

勾股定理与全等三角形

1、已知：如图，△ ABC中，/ C=90° D为AB的中点，E、F分别在AC BC上，且DE丄DF.求ffi： AE2+BF2=EF2.32、如图，△ ACB和^ ECD都是等腰直角三角形，/证：(1 )△ ACE^A BCD; (2) AD2+DB2=D呂.3、如图，△ ABC 中，AB=BC BE丄AC于点E, AD丄BC 于点D,Z BAD=45°, AD 与BE交于点F,连接CF.(1)求证：BF=2AE(2)若CD= 2,求AD 的长.4、如图①，已知点D在AB上, △ ABC和^ ADE都是等腰直角三角形，/ ABC=/ ADE=90°,c1、证明：延长ED到G,使DG=DE,连接EF、FG、CG,如图所示:•/ DF=DE / EDF=Z FDG=90 ,° DG=DE:.△ EDF^A GDF ( SAS ,•••EF=FG又••• D为斜边BC中点•••BD=DC又•/ / BDE=/ CDG, DE=DG•••△ BDE^A CDG (SAS••• BE=CG / B=/ BCG ••• AB// CG ••• / GCA=180-° A=180 -90 =90 在RtA FCG中，由勾股定理得:FG2=CF+CG=CF+BE ••• EF2=FG=Be+CF.3证明：过点A作AM // BC,交FD延长线于点M，连接EM.•/ AM // BC,••• / MAE=/ ACB=90 ,° / MAD= / B.•/ AD=BD, / ADM= / BDF, •••△ ADM^A BDF.••• AM=BF, MD=DF.又DE丄DF, ••• EF=EM.••• AE2+BF2=AE2+AM2=EM2=E^.2、证明：（1）v/ ACB=^ ECD •••/ ACD+Z BCDK ACD+Z ACE 即/ BCD=^ ACE ••• BC=AC DC=EC(2)v^ ACB是等腰直角三角形,• / B=/ BAC=45度.•••/ B=/ CAE=45 •••/ DAE=^ CAE+Z BAC=45+45°90°, • AD2+AE2=DE2由（1）知AE=DB• AD2+DB2=DE23、解答：(1)证明：T AD丄BC,Z BAD=45,:.△ ABD是等腰直角三角形, /. AD=BD, •/ BE丄AC, AD 丄BC, ：•/ CAD+Z ACD=90 ,/ CBE+/ ACD=90 , ：•/ CAD=/ CBE在^ ADC和^ BDF中,/ CAD=Z CBEAD= BD/ ADC=Z BDF= 90°•: △ ADC^^ BDF (ASA),•: BF=AC •/ AB=BC BE丄AC, •: AC=2AE •: BF=2AE(2)解：•••△ ADC^^ BDF, •: DF=CD=在RtA CDF中，CF=DF+CD22=2,•/ BE丄AC,AE=EC•••AF=CF=2/. AD=AF+DF=2+團①4、解答：（1）证明：延长DM交BC于N,:EDA=Z ABC=90 ,/. DE//BC,•••/ DEM=Z MCB,在^ EMD和^ CMN中/ DEM=Z NCMEM = CM/EMD=Z NMC,.•.△ EMD" CMN, •••CN=DE=DA MN=MD ,•/ BA=BC /. BD=BN, •: △ DBN是等腰直角三角形，且BM是底边的中线, ••• BM 丄DM，/ DBM=/ DBN=45=/ BDM ,:.△ BMD为等腰直角三角形.(2)解：△ BMD为等腰直角三角形的结论仍成立, 证明：作CN// DE交DM的延长线于N,连接BN, ：•/ E=Z MCN=4° , vZ DME=Z NMC, EM=CM,：.△ EMDW CMN (ASA),：.CN=DE=DA MN=MD , 在^ DBA和^ NBC中DA= CNZ DAB=Z BCN,BA= BC•••/ DBA=Z NBC, DB=BN, /•Z DBN=Z ABC=90 , •/△ DBN是等腰直角三角形，且BM是底边的中线, ••• BM 丄DM , Z DBM=Z DBN=45=Z BDM ,:.△ BMD为等腰直角三角形.。

全等三角形与勾股定理练习题

全等三角形与勾股定理练习题（一）一．填空题1．一个矩形的抽斗长为24cm ，宽为7cm ,在里面放一根铁条，那么铁条最长可以是．2．在Rt △ABC 中，∠C ＝90°，BC ＝12cm ，S △ABC ＝30cm 2，则AB ＝ .3．在一棵树的10米高处有两只猴子，一只猴子爬下树走到离树20米处的池塘的A 处。

另一只爬到树顶D 后直接跃到A 处，距离以直线计算，如果两只猴子所经过的距离相等，则这棵树高_________________________米。

4．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm ,则正方形A ，B ，C ，D 的面积之和为___________cm 2。

5．直角三角形两直角边长分别为5和12，则它斜边上的高为__________。

6．在平静的湖面上，有一支红莲，高出水面1米，阵风吹来，红莲被吹到一边，花朵齐及水面，已知红莲移动的水平距离为2米，问这里水深是________m 。

7．已知两条线段的长为5c m 和12c m,当第三条线段的长为 c m 时,这三条线段能组成一个直角三角形.8．一个三角形三边之比为2:5:3,则这个三角形的形状是 . 9．将一根长为24㎝的筷子置于底面直径为5㎝，高为12㎝的圆柱形水杯中，设筷子露在杯子外面的长为h ㎝，则h 的取值范围是________________. 10．一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A 点沿纸箱爬到B 点，那么它所行的最短路线的长是____________.11.如图，在△ABC 中，AD 平分∠BAC ，AB ＝AC －BD ，则∠B ∶∠C 的值是___________。

12.如图，ABE △和ACD △是ABC △分别沿着AB AC ，边翻折180o 形成的，若150BAC ∠=o ，则θ∠的度数是．二．选择题1、若Rt ABC V 中，90C ︒∠=且c=37,a=12，则b=（）A 、50B 、35C 、34D 、262、如图，平行四边形ABCD 对角线AC,BD 交于O ，过O 画直线EF 交AD 于E ，交BC 于F,，则图中全等三角形共有（） (A)7对 (B)6对 (C)5对 (D)4对3.如图，△DAC 和△EBC 均是等边三角形，AE 、BD 分别与CD 、CE 交于点M 、N ，有如下结论：① △ACE ≌△DCB ； ② CM ＝CN ；③ AC ＝DN 。

八年级数学下册勾股定理习题(附答案)(含答案)

C勾股定理评估试卷（1）一、选择题（每小题3分，共30分）1. 直角三角形一直角边长为12，另两条边长均为自然数，则其周长为( ). （A ）30 （B ）28 （C ）56 （D ）不能确定2. 直角三角形的斜边比一直角边长2 cm ，另一直角边长为6 cm ，则它的斜边长（A ）4 cm（B ）8 cm （C ）10 cm（D ）12 cm3. 已知一个Rt △的两边长分别为3和4，则第三边长的平方是（）（A ）25（B ）14（C ）7（D ）7或254. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) （A ）13 （B ）8 （C ）25 （D ）645. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）715242520715202425157252024257202415(A)(B)(C)(D)6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )（A ）钝角三角形（B ）锐角三角形（C ）直角三角形（D ）等腰三角形. 7. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( ) （A ） 25 （B ） 12.5 （C ） 9 （D ） 8.5 8. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( ) （A ）等边三角形（B ）钝角三角形（C ）直角三角形（D ）锐角三角形.9.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°，AC=30米，AB=50米，如果要在这块空地上种植草皮，按每平方米草皮a 元计算，那么共需要资金（）. （A ）50a 元（B ）600a 元（C ）1200a 元（D ）1500a 元 10.如图，A B ⊥CD 于B ，△ABD 和△BCE 都是等腰直角三角形，如果CD=17，BE=5，那么AC 的长为（）.（A ）12 （B ）7 （C ）5 （D ）135米3米（第10题）（第11题）（第14题）二、填空题（每小题3分，24分）11. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.12. 在直角三角形ABC 中，斜边AB =2，则222AB AC BC ++=______. 13. 直角三角形的三边长为连续偶数，则其周长为 .14. 如图，在△ABC 中，∠C=90°，BC=3，AC=4.以斜边AB 为直径作半圆，则这个半圆的面积是____________.（第15题）（第16题）（第17题） 15. 如图，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞___________米. 16. 如图，△ABC 中，∠C =90°，AB 垂直平分线交BC 于D若BC =8，AD =5，则AC 等于______________. 17. 如图，四边形ABCD 是正方形，AE 垂直于BE ，且AE =3，BE =4，阴影部分的面积是______.18. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm,则正方形A ，B ，C ，D 的面积之和为___________cm 2.EABCDBDE ABCD第18题图7cm三、解答题（每小题8分，共40分）19. 11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题：“小溪边长着两棵棕榈树，恰好隔岸相望.一棵树高是30肘尺（肘尺是古代的长度单位），另外一棵高20肘尺；两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然，两只鸟同时看见棕榈树间的水面上游出一条鱼，它们立刻飞去抓鱼，并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多远？20. 如图，已知一等腰三角形的周长是16，底边上的高是4.求这个三角形各边的长.21. 如图，A 、B 两个小集镇在河流CD 的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A 、B 两镇供水，铺设水管的费用为每千米3万，请你在河流CD 上选择水厂的位置M ，使铺设水管的费用最节省，并求出总费用是多少？22. 如图所示的一块地，∠ADC=90°，AD=12m ，CD=9m ，AB=39m ，BC=36m ，求这块地的面积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

全等三角形与勾股定理练习题（一）
一．填空题
1.一个矩形的抽斗长为2４cm ,宽为7c ｍ,在里面放一根铁条,那么铁条最长可以是 .
２．在Rt △A ＢC 中，∠C ＝９0°，BC ＝12cm ,Ｓ△ABC ＝3０cm 2
,则AB ＝．
3．在一棵树的10米高处有两只猴子，一只猴子爬下树走到离树2０米处的池塘的Ａ处。

另一只爬到树顶D 后直接跃到A 处，距离以直线计算，如果两只猴子所经过的距离相等,则这棵树高＿_＿__＿_______＿＿__＿____＿__米。

4．如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm ,则正方
形A ，B,C ，D 的面积之和为__＿___＿_＿__cm ２。

5．直角三角形两直角边长分别为5和１2，则它斜边上的高为_＿_＿_＿_＿__。

６.在平静的湖面上，有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面，已知红莲移动的水平距离为２米，问这里水深是________m 。

7.已知两条线段的长为5c m 和12c m ，当第三条线段的长为 c m 时,这三条线段能组成一个直角三角形.
8.一个三角形三边之比为2:5:3,则这个三角形的形状是． 9．将一根长为2４㎝的筷子置于底面直径为５㎝，高为１2㎝的圆柱形水杯中, 设筷子露在杯子外面的长为h ㎝，则h 的取值范围是＿_____＿__＿＿＿_＿__. 10.一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A 点沿纸箱爬到Ｂ点,那么它所行的最短路线的长是__＿__＿_＿____.
11.如图,在△ABC 中，ＡD 平分∠BA Ｃ,A Ｂ＝AC -BD ，则∠B ∶∠C 的值是___________。

12.如图,ABE △和ACD △是ABC △分别沿着AB AC ，边翻折180形成的,若
150BAC ∠=，则θ∠的度数是 .
二．选择题
１、若Rt ABC 中，90C ︒
∠=且c=３7,a ＝12,则b=（ )
A 、50
B 、35 Ｃ、34 D 、26
2、如图，平行四边形AB ＣD 对角线AC,BD 交于O,过O 画直线EF 交ＡD 于E ，交BC 于F ，，则图中全等三角形共有( ） (A ）7对 (B ）6对 (C)5对（Ｄ)4对
3.如图，△DAC 和△ＥＢＣ均是等边三角形,ＡＥ、B Ｄ分别与C Ｄ、CE 交于点M 、N,有如下结论：① △ACE ≌△D ＣB ； ② CM ＝ＣＮ；③ ＡC=DN 。

正确结论的个数是( )．（Ａ) 3个 (B ）2个 (Ｃ)1个(Ｄ）0个
４.如图，在等腰Rt △ABC 中，∠C ＝９０°，AC ＝BC ,ＡD 平分∠ＢＡＣ交ＢＣ于D ,DE ⊥A Ｂ于D ,若A Ｂ=1
A B C D
7cm D B
C
A 第3题
A
B
A
C
D
A
E
B θ
D
C
B
A
０,则△ＢDE 的周长等于＿___.
5如图,直线l 过正方形ＡB ＣＤ的顶点B ，点C A 、到直线l 的距离分别是1和2，则正方形的边长为 .
６．等腰三角形底边上的高为８,周长为32，则三角形的面积为（）
A 、56ﻩﻩ Ｂ、４8ﻩ C 、4０ﻩﻩﻩＤ、32
7．已知等腰三角形的腰长为1０,一腰上的高为６，则以底边为边长的正方形的面积为( ) A 、40ﻩ Ｂ、８0ﻩﻩ C 、40或3６０ﻩ D 、８0或36０８.下列各组数中，能构成直角三角形的是( ）
Ａ、4,5,6 B 、１，1，2 Ｃ、6，８，11 D 、5，1２，23 ９．已知ａ、ｂ、c 是三角形的三边长，如果满足2
(6)810
0a b c -+-+-=,则三角形的形状是
（） A 、底与边不相等的等腰三角形B 、等边三角形 C 、钝角三角形 D 、直角三角形 10.正方形的面积是2，它的对角线长为( ) A 、1 B 、２ C 、2 Ｄ、
2
2
11一艘轮船以16海里∕小时的速度从港口A 出发向东北方向航行,另一轮船１2海里∕小时从港口A 出发向东南方向航行，离开港口3小时后,则两船相距( ） A 、３6 海里 B 、4８海里C 、60海里Ｄ、8４海里三．简答题
１、如图，在四边形ABCD 中,BC ＞BA ，ＡD=CD,BD 平分ABC ∠,
求证: 0
180=∠+∠C A
2.小明的叔叔家承包了一个矩形鱼池,已知其面积为４8m 2
，其对角线长为10m,为建栅栏,要计算这个矩形鱼池的周长,你能帮助小明算一算吗?
3、如图、,CD 是AB 上的高,A Ｃ＝4,ＢC=3, 95
DB =
E
D C B
A D
C
B
A
2.6m
4m
(1）求ＡD 的长
(2)ABC 是直角三角形吗？请说明理由
4、如图、四边形ＡBCD 中，6AB AD ==, 60A ︒
∠=, 150ADC ︒
∠=,已知四边形的周长为30,求ABCD S 四边形
５.如图所示,某住宅社区在相邻两楼之间修建一个上方是一个半圆，下方是长方形的仿古通道，现有一辆卡车装满家具后,高4米,宽2.8米，请问这辆送家具的卡车能否通过这个通道.
6．如图，△ＡCB 和△ECD 都是等腰直角三角形，A,C ，D 三点在同一直线上，连结BD ，A Ｅ，并延长AE 交BD 于Ｆ．
（１）求证:△ACE ≌△BC Ｄ．ﻩ
(2）直线A Ｅ与B Ｄ互相垂直吗？请证明你的结论．
7．已知:如图,△ＡBC 中，∠A ＢC ＝４5°,C Ｄ⊥ＡB 于Ｄ，ＢE 平分∠ABC ，
且B Ｅ⊥AC 于Ｅ,与ＣD 相交于点Ｆ,Ｈ是ＢC 边的中点,连结DH 与BE 相交于点G 。

(!)求证:BF =AC ; (2)求证:CE =
1
2
ＢF ； (３)CE 与BG 的大小关系如何?试证明你的结论。

A
B C D
E
F D
C
B
A
8、如图，△AＢＣ中，AD平分∠BAC,DG⊥ＢC且平分BＣ，ＤＥ⊥AB于E,ＤF⊥AC于F. （1)说明BE=CF 的理由；(２)如果AB=a，ＡC=b，求AE、BＥ的长.
11. 如图,已知:点C是∠FＡE的平分线ＡC上一点，ＣE⊥AＥ，CF
E
D
G
F
C B
A
⊥ＡＦ，E、Ｆ为垂足。

点Ｂ在AE的延长线上,点Ｄ在AF上。

若AB=21，AD＝９，BC＝DＣ＝10。

求AC的长。