2019北京市中学数学竞赛试题
北京市中学生数学竞赛高一级复赛参考解答

2020年北京市中学生数学竞赛高一年级复赛参考解答一、选择题(总分值40分,每题8分,将答案写在下面相应的空格中)1.二次三项式x 2+ax +b 的根是实数,其中a 、b 是自然数,且ab =22020,那么如此的二次三项式共有 个.答:1341.咱们发觉,事实上,数a 和b 是2的非负整数指数的幂,即,a =2k ,b =22020–k ,那么判别式Δ=a 2– 4b =22k – 422020–k =22k – 22021–k ≥0,得2k ≥2021–k ,因此k ≥32013=671,但k ≤2020,因此k 能够取2020–671+1=1341个不同的整数值.每一个k 恰对应一个所求的二次三项式,因此如此的二次三项式共有1341个.2.如右图,在半径为1的圆O 中内接有锐角三角形ABC ,H 是△ABC 的垂心,角平分线AL 垂直于OH ,那么BC = .解:易知,圆心O 及垂心H 都在锐角三角形ABC 的内部,延长AO 交圆于N ,连接AH 并延长至H 1与BC 相交,连接CN ,在Rt △CAN 和Rt △AH 1B 中,∠ANC =∠ABC ,于是有∠CAN =∠BAH 1,再由AL 是△ABC 的角平分线,得∠1=∠2.由条件AP ⊥OH ,得AH=AO=1.连接BO 交圆于M ,连接AM 、CM 、CH ,可知AMCH 为平行四边形,因此CM=AH=AO =1,BM =2,因为△MBC 是直角三角形,由勾股定理得BC ==3.已知概念在R 上的函数f (x )=x 2和g (x )=2x +2m ,假设F (x )=f (g (x )) – g (f (x ))的最小值为14,那么m = .答:14-.解:由f (x )=x 2和g (x )=2x +2m ,得F (x )= f (g (x )) – g (f (x ))=(2x +2m )2–(2x 2+2m )=2x 2+8mx +4m 2–2m ,F (x )=2x 2+8mx +4m 2–2m 的最小值为其图像极点的纵坐标()2222242(42)84284242m m m m m m m m ⨯⨯--=--=--⨯.由已知,21424m m --=,得21202m ⎛⎫+= ⎪⎝⎭,因此1.4m =-4.tan 37.5= . 答:6232-+-.解1:作Rt △ADB ,使得∠ADB =90º,AD =1,AB =2,那么∠B =30º,BD =3.延长BD 到C ,使BC =2,那么DC =23-.连接AC ,那么∠ACB =(180º–30º)÷2=75º.作∠ACD 的平分线交AD 于E ,那么∠ECD =º. 由于AC 2=AD 2+DC 2=1+(2–3)2=8–43,因此 ()2843621226262AC =-=-+=-=-.由三角形的角平分线定理,得AE AC ED DC=,于是AE ED AC DCED DC ++=,即()()()()322162233221ED AD DC AC CD ====-++-+-+-,因此()()tan 37.53221EDDC==-+6232=-+-.解2:作等腰直角三角形ABC ,使∠C =90º,AC =BC =1,那么AB =2. 作∠CAD =30º,那么CD =33,AD =233,那么∠DAB =15º. 作∠BAD 的平分线AE ,记CE =x ,那么BE =1–x ,DE =x –3. 因此33232x -=,整理得 ()()213221623 2.3232x +-+===-+--+tan 37.562321CE xAC ===-+-. 5.设f (x ) =113xx+-,概念f 1(x ) = f (f (x )),f n (x )=f (f n –1(x )) (n =2, 3,…),f 2020(2020)= . 答:10053017.A21 30º解:记01()()13x f x f x x +==-,那么()111113()()1131313xx x f x f f x x x x++--===--+-⋅-; ()211113()()11313xx f x f f x x x x--+===-+⋅+;()3201()()()()13x f x f f x f x f x x +====-; 接下来有41()()f x f x =,52()()f x f x =,63()()f x f x =,…,f n (x )的表达式是循环重复的,以3项为一周期.因此,20113670111()()()13x f x f x f x x ⨯+-===+,20112011120101005(2011)13201160343017f -===+⨯.二、(总分值15分)D 是正△ABC 的边BC 上一点,设△ABD 与△ACD 的内心别离为I 1,I 2,外心别离为O 1,O 2,求证:(I 1O 1)2+(I 2O 2)2=(I 1I 2)2. 证明:作以A 为中心、逆时针旋转60的变换(,60)R A ,使△ABD 到△ACD 1,由于∠ADC +∠AD 1C =∠ADC +∠ADB =180º,因此A 、D 、C 、D 1共圆,因此2O 是△AD 1C 的外心,也确实是(,60)12R A O O −−−−→,因此AO 1=DO 1=AO 2=DO 2=O 1O 2,因此∠O 1AO 2=∠O 1DO 2=60º.由∠AO 1O 2+∠ACB =120º+60º=180º,O 1在△ACD 的外接圆⊙O 2上.由于111(180)6012012022AI D ABD ABD ∠=∠+-∠=+⨯=,因此I 1在⊙O 2上,因此11118018030150O I D O AD ∠=-∠=-=,111118015030I O D I DO ∠+∠=-=.同理可证,I 2在△ABD 的外接圆⊙O 1上,因此22150DI O ∠=.由于12118090,2I DI ∠=⨯=而22111212906030I DO I DO I DI O DO ∠+∠=∠-=-=,比较可得1122I O D I DO ∠=∠.在△O 1I 1D 与△DI 2O 2中,因为已证O 1D=DO 2,1122150,O I D DI O ∠=∠=又1122.I O D I DO ∠=∠因此 △O 1I 1D ≌△DI 2O 2.因此,I 1O 1=DI 2,DI 1= I 2O 2.由于1290,I DI ∠=△I 1DI 2是直角三角形.依照勾股定理,有()()()2221212,DI DI I I +=而I 1O 1=DI 2,DI 1=I 2O 2. 因此()()()222112212.I O I O I I +=三、(总分值15分)n 是正整数,记n !=1×2×3×…×n ,如1!=1,2!=1×2=2,3!= 1×2×3=6,又记[a ]表示不超过a 的最大整数,求方程120111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的所有正整数解.解1:由于当x 是正整数时,[]1!x x ⎡⎤=⎢⎥⎣⎦,2!2x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦≥12x -,3!6x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦>6x –1,因此1126x x x -++-<2020即53x <120122,得方程的正整数解x 知足0<x <. 由于6!=720,7!=5040,因此方程的正整数解x <7!,即07!8!9!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦. 因此,方程20111!2!3!4!5!6!x x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的解与原方程的解是一样的.设小于7!的正整数x 为上述方程的解,咱们写出(1,2,3,4,5,6)!xk k =的带余除法表达式:设16!6!r x a =+,0≤r 1<6!,(0≤a ≤6,a ∈N );因此.6!x a ⎡⎤=⎢⎥⎣⎦① 12665!5!5!r r x a a b =+=++,0≤r 2<5!,(0≤b ≤5,b ∈N ),因此65!x a b ⎡⎤=+⎢⎥⎣⎦. ② 323053054!4!4!r r xa b a b c =++=+++,0≤r 3<4!,(0≤c ≤4,c ∈N ), 因此3054!x a b c ⎡⎤=++⎢⎥⎣⎦. ③341202*********!3!3!r r xa b c a b c d =+++=++++,0≤r 4<3!,(0≤d ≤3,d ∈N ); 因此1202043!x a b c d ⎡⎤=+++⎢⎥⎣⎦. ④5436060123360601232!2!2!r r xa b c d a b c d e =++++=+++++,0≤r 5<2, (e =0,1,2);因此360601232!x a b c d e ⎡⎤=++++⎢⎥⎣⎦. ⑤5720120246272012024621!1!r xa b c d e a b c d e f =+++++=+++++,(f =0,1); 因此72012024621!x a b c d e f ⎡⎤=+++++⎢⎥⎣⎦. ⑥①~⑥相加得1237a +206b +41c +10d +3e +f =2020. 显然a =1,因此206b +41c +10d +3e +f =2020–1237=774; 易知b =3,因此41c +10d +3e +f =774–206×3=156; 易知c =3,于是10d +3e +f =156–41×3=33;类似求得d =3,e =1,f =0.所求的x =1×720+3×120+3×24+3×6+1×2+0×1=1172.x =1172是方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的唯一正整数解. 解2:设f (x )=1!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,因为关于所有的正整数k ,!x k ⎡⎤⎢⎥⎣⎦都是单调增的,其和f (x )确实是增函数;又因为关于正整数x ,11!x +⎡⎤⎢⎥⎣⎦=1!x ⎡⎤⎢⎥⎣⎦+1,因此f (x )是严格单调的.经估数,将x =1172带入,求f (1172)的值,得f (1172)=2020,因此,x =1172是方程20111!2!3!10!11!x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的唯一正整数解.四、(总分值15分)平面上的n 个点,假设其中任3个点中必有2个点的距离不大于1,那么称如此的n 个点为“标准n 点组”.要使一个半径为1的圆纸片,对任意“标准n 点组”都能至少盖住其中的25个点,试求n 的最小值. 答案:49.解:第一证明,n min >48.在平面上画长为5的线段AB ,别离以A 、B 为圆心,画半径为的两个圆,在每一个圆内,取24个点,那么平面上有48个点满足题设条件(其中任意3点中必有2点的距离不大于1),显然,不可能画出一个半径为1的圆,其包括有25个所选的点,因此n >48.下面证明n min =49.若49=n ,设A 是其中的一点,作以A 为圆心半径为1的⊙A ,假设所有的点都在圆A 中,那么就知足题设条件.假设不是所有的点都在圆A 中,那么至少有一点B 不在圆A 中,再作以B 为圆心、半径为1的⊙B ,那么A 、B 的距离大于1(如右图),除A ,B 外,余下的47个点中每一点P 都与A 、B 组成3点组,必有两个点的距离不大于1,因此要么P A ≤1,要么PB ≤1,即点P 要么在⊙A 中,要么在⊙B 中,依照抽屉原理,必有一个圆至少包括了这47个点中的24个点,不妨设那个圆确实是⊙A ,再加上圆心A 点,就有很多于25个点在那个半径为1的⊙A 中(圆内或圆周上).因此n 的最小值是49.五、(总分值15分)已知函数f :R →R ,使得对任意实数x y z ,,都有11()()()()22f xy f xz f x f yz +-≥14, 求[1×f (1)]+[2×f (2)]+[3×f (3)]+…+[2020×f (2020)]的值.其中关于实数a ,[a ]表示不超过a 的最大整数.解:由于已知函数f R R →:,使得对任意实数x y z ,,都知足11()()()()22f xy f xz f x f yz +-≥14,可令0x y z ===,有 ()211(0)(0)(0)22f f f +-≥14,即21(0)2f ⎛⎫- ⎪⎝⎭≤0, 由于f (0)是一个实数,因此1(0).2f =再令1x y z ===,有()211(1)(1)(1)22f f f +-≥14,即21(1)2f ⎛⎫- ⎪⎝⎭≤0, 由于f (1)是一个实数,因此1(1).2f =又令0y z ==,有11(0)(0)()(0)22f f f x f +-≥14,代入1(0)2f =得对任意实数x ,都有()f x ≤12. ①又令1y z ==,有11()()()(1)22f x f x f x f +-≥14,代入1(1)2f =得对任意实数x ,都有()f x ≥12. ②综合①、②可得,对任意实数x ,都有1()2f x =.验证:函数1()2f x =知足题设条件,取的是等号,因此知足题设条件的函数的唯一解为1()2f x =.于是[][][][]1(1)2(2)3(3)2011(2011)f f f f ⨯+⨯+⨯++⨯1234201122222⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦011223310051005=+++++++++()21231005=⨯++++(11005)1005=+⨯.1011030。
北京一零一中学2019届九年级12月月考数学试题

北京101中学2019届上学期初中九年级12月月考数学试卷(满分:100分 考试时间:120分钟)一、选择题:(本大题共10小题,共20分)1. 如图,将一张矩形纸片沿对角线剪开得到两个直角三角形纸片,将这两个直角三角形纸片通过图形变换构成以下四个图形,这四个图形中是中心对称.....图形的是矩形纸片 A B C D 2. 抛物线1)2(2+-=x y 的顶点坐标是A. (2,1)B. (2,-1) C . (-2,1) D. (-2,-1)3. 老师将10份奖品分别放在10个完全相同的不透明礼盒中,奖品中有5份是文具,3份是读物,2份是科技馆通票。
小明从中随机取一份奖品,恰好取到读物的概率是A.21B.53C.51D.103 4. 若点A (a ,b )在双曲线xy 3=上,则代数式4-ab 的值为 A. -12 B. -7 C. -l D. 15. 若⊙O 的半径为3,圆心O 到直线l 的距离为2,则直线l 与⊙O 的位置关系是 A. 相交 B. 相切 C. 相离 D. 无法确定6. 两个相似三角形的相似比为1:2,较小三角形的面积为1,则较大三角形的面积为 A. 8B. 4C. 2D.27. 如图,⊙O 的半径为3,点P 是弦AB 延长线上的一点,连接OP ,若OP=4,∠P=30°,则弦AB 的长为A. 25B. 23C.5D. 28. 已知点),(11y x 、),(22y x 、),(33y x 在双曲线xy 1=上,当3210x x x <<<时,1y 、2y 、3y 的大小关系是A. 321y y y <<B. 231y y y <<C. 213y y y <<D. 132y y y <<9. 如图,在平面直角坐标系xOy 中,抛物线c bx x y ++=2与x 轴只有一个交点M ,与平行于x 轴的直线l 交于A 、B 两点。
2018-2019年高中数学北京高一竞赛测试检测试卷【1】含答案考点及解析
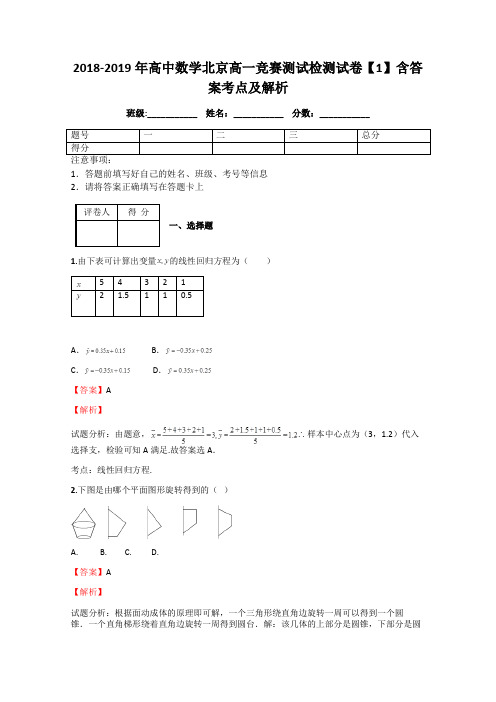
2018-2019年高中数学北京高一竞赛测试检测试卷【1】含答案考点及解析班级:___________ 姓名:___________ 分数:___________1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.由下表可计算出变量的线性回归方程为()543212A. B.C. D.【答案】A【解析】试题分析:由题意,∴样本中心点为(3,1.2)代入选择支,检验可知A满足.故答案选A.考点:线性回归方程.2.下图是由哪个平面图形旋转得到的()A. B. C. D.【答案】A【解析】试题分析:根据面动成体的原理即可解,一个三角形绕直角边旋转一周可以得到一个圆锥.一个直角梯形绕着直角边旋转一周得到圆台.解:该几体的上部分是圆锥,下部分是圆台,圆锥的轴截面是直角三角形,圆台的轴截面是直角梯形,∴这个几何图形是由直角三角形和直角梯形围绕直角边所在的直线为轴旋转一周得到.故选A考点:旋转体点评:本题主要考查空间感知能力,难度不大,学生应注意培养空间想象能力.3.cos300°= ()A.-B.-C.D.【答案】C【解析】试题分析:利用诱导公式把要求的式子化为 cos(360°-60°)=cos60°,由此求得结果.解:cos300°=cos(360°-60°)=cos60°=,故选C考点:诱导公式和特殊角的三角函数值点评:本题主要考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点.4.下列函数中,在区间上是增函数的是()A.B.C.D.【答案】C【解析】试题分析:根据基本初等函数的单调性知,在上单调递减;在上单调递减;在上单调递增;在上单调递减.考点:本小题主要考查基本初等函数的单调性.点评:考查函数的单调性,要记住基本初等函数的单调性,结合图象解决问题.5.若角和角的终边关于轴对称,则()A.,B.,C.,D.,【答案】A【解析】试题分析:因为α,β角的终边关于y轴对称,所以,即α+β=π+2kπ,(k∈z),考点:终边相同的角。
2020年北京市中学生数学竞赛高一年级试题(含答案)

2020年北京市中学生数学竞赛高一年级试题2020年6月 27日8:30~10:30一、填空题(满分40分,每小题8分)1.已知实函数f (x )满足f (x +y )=f (x )+f (y )+4xy ,且f (−1)·f (1)≥4.则293f ⎛⎫-= ⎪⎝⎭______. 2.等腰梯形ABCD (AB =CD )的内切圆与腰CD 的切点为M ,与AM 、BM 的交点分别为K 和L .则AM BM AK BL+的值等于______. 3.四位数abcd 比它的各位数字的平方和大2020,在所有这样的四位数中最大的一个是______.4.已知点O 在△ABC 内部,且2021202020193AB BC CA AO ++=,记△ABC 的面积为S 1,△OBC 的面积为S 2,则12S S =______. 5.有4个不同的质数a , b , c , d ,满足a +b +c +d 是质数,且a 2+bc 、a 2+bd 都是完全平方数,那么a +b +c +d = ______.二、(满分15分)面积为S 1,S 2,S 3,S 4,S 5,S 6的正方形位置如右图所示.求证:S 4+S 5+S 6=3(S 1+S 2+S 3).三、(满分15分)存在2020个不是整数的有理数,它们中任意两个的乘积都是整数四、(满分15分)如右图,已知D 为等腰△ABC BC 上任一点,⊙I 1、⊙I 2分别为△ABD 、△ACD 内切圆,M 为BC 的中点.求证:I 1M ⊥I 2M .五、(满分15分)将集合I ={1, 2, 3, 4, 5, 6, 7, 8, 9}B ={w , x , y , z },使得A ∪B =I ,A ∩B =Ø,且A 与B 的元素至少有一种排列组成的正整数满足2wxyz abcde ,则称A 与B 为集合I 的一个“两倍型2分划”.(1)写出集合I 的所有“两倍型2分划”,并给出理由;(2)写出集合I 的每个“两倍型2分划”对应的所有可能的2wxyz abcde .2020年北京市中学生数学竞赛(邀请)高一年级试题及参考解答2020年6月 27日8:30~10:30一、填空题(满分40分,每小题8分)1.已知实函数f (x )满足f (x +y )=f (x )+f (y )+4xy ,且f (−1)·f (1)≥4.则29()3f -=______. 解:令x =y =0得f (0)=0,令x =−1,y =1,得f (1)+f (−1)=4.平方得f 2(1)+2f (1)·f (−1)+f 2(−1)=16,又因为f (−1)·f (1)≥4,所以f 2(1)+2f (1)·f (−1)+f 2(−1)≤4f (1)·f (−1).即(f (1)−f (−1))2≤0.所以f (1)=f (−1)=2. 因为)32)(31(4)32()31()32(31)1(--⋅+-+-=⎪⎭⎫ ⎝⎛-+-=-f f f f 1118=3()4()()3339f , 所以 .234)31(3=+-f 因此.92)31(=-f 所以.9894)31(2)32(=+-=-f f 于是29()3f -=8.2.等腰梯形ABCD (AB =CD )的内切圆与腰CD 的切点为M ,与AM 、BM 的交点分别为K 和L .则AM BM AK BL+的值等于______. 解:设N 是边AD 的中点,a =AN ,x =AK ,y =AM ,α=∠ADM ,(如图).则ND=DM=a ,且根据余弦定理,对于△ADM ,有y 2=4a 2+a 2−4a 2cos α=a 2(5−4cos α). 另一方面,根据切割线定理,有xy=a 2,所以 2AM y y AK x xy ===5−4cos α. 类似地对于△BCM ,得到54cos .BM BLα=+ 因此,10.AM BM AK BL+= C BD A LK a y αMx3.四位数abcd 比它的各位数字的平方和大2020,在所有这样的四位数中最大的一个是______.解: 设abcd 为所求的自然数,则根据条件1000a +100b +10c +d =a 2+b 2+c 2+d 2+2020.考虑到 2000<a 2+b 2+c 2+d 2+2020≤92+92+92+92+2020=2344,可以断定a =2,于是100b +10c +d =b 2+c 2+d 2+24.即 b (100−b )+c (10−c )=d (d −1)+24 (*)由于c (10−c )>0,当b ≥1时,b (100−b )≥99,所以(*)式左边大于99,而(*)式右边小于9×8+24=96,因此要(*)式成立,必须b =0.当b =0时,(*)式变为 d 2−d =10c −c 2−24. 由于四位数abcd 中a =2,b =0,要使20cd 最大,必需数字c 最大.若c =9,c 2−c −24=90−92−24<0,而d 2−d ≥0故(*)式不能成立.同理,c =8和c =7时,(*)式均不能成立.当c =6时,c 2−c −24=60−62−24=0,这时,d =0及d =1,均有d 2−d =0,即(*)式均成立. 于是abcd =2060或2061.所以满足题设条件的四位数中最大的一个是2061.4.已知点O 在△ABC 内部,且2021202020193AB BC CA AO ++=,记△ABC的面积为S 1,△OBC 的面积为S 2,则12S S =______. 解:由2021202020193AB BC CA AO ++=,得22019()3AB BC AB BC CA AO ++++=,因为0AB BC CA ++=,所以23AB BC AO +=,故23AB AC AB AO +-=. 所以3AB AC AO +=,取BC 的中点D ,则23AD AO =.于是A 、D 、O 三点共线,且3AD OD =.所以123S AD S OD==.5.有4个不同的质数a , b , c , d ,满足a +b +c +d 是质数,且a 2+bc 、a 2+bd 都是完全平方数,那么a +b +c +d = ______.解:由a +b +c +d 是质数,可知a , b , c , d 中有2.如果a ≠2,那么b , c , d 中有2,从而a 2+bc 、a 2+bd 中有一个模4余3,不是完全平方数.故a =2.假设22+bc =m 2,那么bc =(m −2)(m +2).如果m −2=1,那么m =3,bc =5,与已知矛盾.故不妨设b =m −2,c =m +2,则c =b +4.同理d =b −4,所以{a , b , c , d }={a , b , b +4, b −4}.而b −4, b , b +4中有一个是3的倍数,又是质数,所以只能是b −4=3,此时a +b +c +d =2+3+7+11=23.二、(满分15分)面积为S 1,S 2,S 3,S 4,S 5,S 6的正方形位置如图所示.求证:S 4+S 5+S 6=3(S 1+S 2+S 3).证明:见右图:AKLB ,BMNC ,ACPQ 都是正方形,对应的面积为S 1、S 2和S 3.设,,βα=∠=∠ABC BAC .γ=∠ACB 因为,,,321S AC S BC S AB === 则根据余弦定理,有αcos 232321S S S S S -+=βcos 231312S S S S S -+=γcos 221213S S S S S -+= 由此,.cos 2cos 2cos 2321213132S S S S S S S S S ++=++γβα ①又因为 ,180,180,180γβα-=∠-=∠-=∠ NCP LBM QAK 以及,,,465S NP S LM S QK === 则有αcos 231315S S S S S ++= ②βcos 221216S S S S S ++= ③ γcos 232324S S S S S ++= ④由等式①~④得 S 4+S 5+S 6=3(S 1+S 2+S 3).三、(满分15分)存在2020个不是整数的有理数,它们中任意两个的乘积都是整数吗?如果存在,请给出例证,如果不存在,请说明理由.解:存在. 例证如下:因为质数有无限多个,所以任选2020个两两不同的质数122020,,,p p p ,构造2020个两两不同的数: 1220202ii p p p x p ,i =1, 2, 3, …, 2020. 易知,因为122020,,,x x x 的分子不被分母整除,皆为不是整数的有理数.而任意两个数的乘积 12202012202022i i i j p p p p p p x x p p 2222222222122020121111202022ii j j i j p p p p p p p p p p p p . 这2018个质数平方的乘积是整数,满足题意要求.A B C I 1 I 2 • • F 四、(满分15分)如图,已知D 为等腰△ABC 底边BC 上任一点,⊙I 1、⊙I 2分别为△ABD 、△ACD 的内切圆,M 为BC 的中点.求证:I 1M ⊥I 2M .证明: (1)当D 与M 重合时,显然有∠I 1MI 2=90°,即I 1M ⊥I 2M .(2)当D 不与M 重合时,不妨设BD >DC , 过I 1作I 1E ⊥BC 于点E ,过I 2作I 2F ⊥BC 于点F ,连结I 1D ,I 2D ,I 1I 2.因为⊙I 1为△ABD 的内切圆,⊙I 2为△ACD 的内切圆,所以 2AB BD AD BE +-=,2DC AD AC DF +-= 所以,EM =BM −BE=22BC AB BD AD +--()2BC BD AD AB -+-=.2DF AC AD DC =-+= 进而有 ED=MF .因为I 1、I 2分别为△ABD 、△ACD 的内心,易知∠I 1DI 2=90°. 由勾股定理得I 1D 2+I 2D 2=I 1I 22.(*)在Rt △I 1DE 与Rt △DI 2F 中,由勾 股定理得I 1E 2+ED 2=I 1D 2,I 2F 2+DF 2=I 2D 2,代入(*)式,得(I 1E 2+ED 2)+(I 2F 2+DF 2)= I 1I 22.注意EM=DF ,ED=MF 代换得(I 1E 2+MF 2)+(I 2F 2+EM 2)= I 1I 22.即 (I 1E 2+EM 2)+(I 2F 2+MF 2)= I 1I 22.所以 I 1M 2+I 2M 2=I 1I 22.根据勾股定理的逆定理,有△I 1MI 2为直角三角形,∠I 1MI 2=90°,即I 1M ⊥I 2M .五、(满分15分)将集合I ={1, 2, 3, 4, 5, 6, 7, 8, 9}划分为两个子集A ={a , b , c , d , e }和B ={w , x , y , z },使得A ∪B =I ,A ∩B =Ø,且A 与B 的元素至少有一种排列组成的正整数满足2wxyz abcde ,则称A 与B 为集合I 的一个“两倍型2分划”.(1)写出集合I 的所有“两倍型2分划”,并给出理由;(2)写出集合I 的每个“两倍型2分划”对应的所有可能的2wxyz abcde . 解:(1)集合I 共有2个“两倍型2分划”:A ={1, 3, 4, 5, 8},B ={2, 6, 7, 9}及A ={1, 4, 5, 6, 8},B ={2, 3, 7, 9}.理由简述如下:1° 由易知,a =1,所以a ∈A . A B C I 1 I 2 • •2° 由0∉ I ={1, 2, 3, 4, 5, 6, 7, 8, 9}=A ∪B ,而5×2=10,所以5∈A .3° 试验知,a , b , c , d , e 均不能等于9,所以9∈B ,进而有8∈A .4° 因为数wxyz abcde 和的9个数字和恰为1+2+3+4+5+6+7+8+9=45是9的倍数,可判知+abcde wxyz 是9的倍数,即+abcde wxyz ≡0(mod9). 又2wxyz abcde ,所以3wxyz ≡0(mod9).于是wxyz ≡0(mod3).所以)(wxyz S 是3的倍数,进而推得)(abcde S 也是3的倍数.5° 同样试验可判定7∈B .此时分配剩下的4个元素:2, 3, 4, 6.由于A 中的1+5+8=14,被3除余2,所以从2, 3, 4, 6中选出的两个数之和被3除余1.于是只能选3, 4或4, 6属于A ,对应剩下的2, 6或2, 3归属于B .因此,找到集合I 的两个“两倍型2分划”:A ={1, 3, 4, 5, 8},B ={2, 6, 7, 9}及A ={1, 4, 5, 6, 8},B ={2, 3, 7, 9}.(2)集合I 的“两倍型2分划”满足的不同的2wxyz abcde 共12个.1° 当B={2, 6, 7, 9}时,得到6个不同的式子:6729×2=13458, 6792×2=13584, 6927×2=13854,7269×2=14538, 7692×2=15384, 9267×2=18534.2° 当B={2, 3, 7, 9}时,得到6个不同的式子:7293×2=14586, 7329×2=14658, 7923×2=15846,7932×2=15864, 9273×2=18546, 9327×2=18654.。
2019年北京中考数学真题模拟题汇编专题5:方程与不等式之填空题(含解析)

2019年北京中考数学真题模拟题汇编专题05 方程与不等式之填空题一.填空题(共22小题)1.(2019•房山区二模)某校进行篮球联赛,每场比赛都要分出胜负,每胜1场得2分,负1场得1分.如果某队在10场比赛中得到16分,那么这个队胜负场数可以是胜6场,负4场.(写出一种情况即可)【答案】解:设这个队胜x场,负y场,根据题意,得.解得.故答案是:胜6场,负4场.【点睛】本题考查了二元一次方程组的应用和一元一次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.2.(2019•昌平区二模)某学校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元,至少买一个排球,在购买资金恰好用尽的情况下,购买方案有3种.【答案】解:设可以购买x个篮球,y个排球,依题意,得:120x+90y=1200,∴x=10y.∵y为正整数,x为非负整数,∴,,.∴共有3种购买方案.故答案为:3.【点睛】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.3.(2019•西城区二模)有大小两种货车,1辆大货车与3辆小货车额定载重量的总和为23吨,2辆大货车与5辆小货车额定载重量的总和为41吨.1辆大货车、1辆小货车的额定载重量分别为多少吨?设1辆大货车的额定载重量为x吨,1辆小货车的额定载重量为y吨,依题意,可以列方程组为.【答案】解:由题意可得,,故答案为:.【点睛】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.4.(2019•怀柔区二模)为打造世界级原始创新战略高地的综合性国家科学中心,经过延伸扩建的怀柔科学城,已经从怀柔区延伸到密云区,两区占地面积共100.9平方公里,其中怀柔区占地面积比密云占地面积的2倍还多3.4平方公里,如果设科学城怀柔占地面积为x平方公里,密云占地面积是y平方公里,则计算科学城在怀柔和密云的占地面积各是多少平方公里,依题意可列方程组为.【答案】解:设科学城怀柔占地面积为x平方公里,密云占地面积是y平方公里,依题意有.故答案为:.【点睛】此题考查了根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.5.(2019•丰台区二模)学校向同学们征集校园便道地砖铺设的图形设计,琳琳用学校提供的完全相同的小长方形模具(如图1)拼出一个大长方形和一个正方形(如图2、图3),其中所拼正方形中间留下一个小正方形的空白,如果所拼图形中空白的小正方形边长等于3cm,依据题意,列出关于a、b的方程组为:.【答案】解:由分析知方程组为.故答案是:.【点睛】本题考查了由实际问题抽象出二元一次方程组,此题的关键在于找到等量关系,仔细观察图形,根据矩形的边的性质,不难找到相应的等量关系.6.(2019•大兴区一模)鸡兔同笼问题是我国古代著名的数学趣题,出自《孙子算经》.原文为:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?小雪自己解决完此题后,又饶有兴趣地为同学编制了四道题目:①今有雉兔同笼,上有三十头,下有五十二足,问雉兔各几何?②今有雉兔同笼,上有三十头,下有八十一足,问雉兔各几何?③今有雉兔同笼,上有三十四头,下有九十足,问雉兔各几何?④今有雉兔同笼,上有三十四头,下有九十二足,问雉兔各几何?根据小雪编制的四道题目的数据,可以求得鸡兔只数的题目是③④(填题目前的序号).【答案】解:设笼中有x只雉,y只兔,根据题得,① ,解得,不符合题;② ,此方程组无整数解,不符合题意;③ ,解得,符合题意;④ ,解得,符合题意;故答案为:③④.【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.一般步骤:(1)审题:找出问题中的已知条件和未知量及它们之间的关系.(2)设元:找出题中的两个关键的未知量,并用字母表示出来.(3)列方程组:挖掘题目中的关系,找出两个等量关系,列出方程组.(4)求解.(5)检验作答:检验所求解是否符合实际意义,并作答.7.(2019•朝阳区一模)某班对思想品德,历史,地理三门课程的选考情况进行调研,数据如下:其中思想品德、历史两门课程都选了的有3人,历史、地理两门课程都选了的有4人,则该班选了思想品德而没有选历史的有16人;该班至少有学生29人.【答案】解:思想品德、历史两门课程都选了的有3人,∴选了思想品德而没有选历史的有19﹣3=16人,设三门课都选的有x人,同时选择地理和政治的有y人,则有总人数为19+18+13﹣3﹣4﹣2x﹣y=43﹣2x﹣y,∵选择历史没有选择政治的有6人,∴2x<6,∴x<3,∴x=1,2,∵只选政治的现在有19﹣3﹣4﹣1﹣y=11﹣y,∴y最大是10,该班至少有学生43﹣4﹣10=29,故答案为16;29;【点睛】本题考查统计的应用;能够将问题转化为二元一次方程,借助实际问题的取值情况,求至少的人数;8.(2019•大兴区一模)分式方程的解是x=3.【答案】解:去分母,得2x=3(x﹣1),去括号,得2x=3x﹣3,解得x=3,检验:将x=3代入原分式方程,左边右边,故原分式方程的解为x=3.故答案为x=3.【点睛】本题考查了分式方程的解,熟练解解分式方程是解题的关键.9.(2019•丰台区一模)京张高铁是2022年北京冬奥会的重要交通保障设施.京张高铁设计时速350公里,建成后,乘高铁从北京到张家口的时间将缩短至1小时.如图,京张高铁起自北京北站,途经昌平、八达岭长城、怀来等站,终点站为河北张家口南,全长174公里.如果按此设计时速运行,设每站(不计起始站和终点站)停靠的平均时间是x分钟,那么依题意,可列方程为.【答案】解:设每站(不计起始站和终点站)停靠的平均时间是x分钟,依题意得:.故答案是:.【点睛】考查了由实际问题抽象出一元一次方程,解题的关键是找准等量关系,列出方程.注意:将x分钟转化为小时.10.(2019•顺义区一模)已知|x﹣y+3|0,则x•y的值为﹣2.【答案】解:根据题意得:,方程可整理得:①,②①+②得:3x=﹣3,解得:x=﹣1,把x=﹣1代入①得:﹣1﹣y=﹣3,解得:y=2,原方程组的解为:,x•y=(﹣1)×2=﹣2,故答案为:﹣2.【点睛】本题考查了解二元一次方程组,非负数的性质:绝对值,非负数的性质:算术平方根,正确掌握绝对值,算术平方根的定义和加减消元法解二元一次方程组是解题的关键.11.(2019•西城区一模)高速公路某收费站出城方向有编号为A,B,C,D,E的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:在A,B,C,D,E五个收费出口中,每20分钟通过小客车数量最多的一个收费出口的编号是B.【答案】解:∵330﹣260=70,330﹣300=30,360﹣300=60,360﹣240=120,260﹣240=20,∴C>A,B>D,E>C,D>A,B>E,由B>D和D>A得B>A,由E>C和B>E得B>C,∴每20分钟通过小客车数量最多的一个收费出口的编号是B,故答案为:B.【点睛】本题考查了不等式的性质,正确的理解题意是解题的关键.12.(2019•海淀区一模)2019年2月,全球首个5G火车站在上海虹桥火车站启动,虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输8千兆数据,5G网络快720秒,求这两种网络的峰值速率,设4G网络的峰值速率为每秒传输x千兆,依题意,可列方程为720.【答案】解:设4G网络的峰值速率为每秒传输x千兆,则5G网络的峰值速率为每秒传输10x千兆,根据题意,得720.故答案为720.【点睛】本题考查了由实际问题抽象出分式方程,理解题意,找到等量关系列出方程是解题的关键.13.(2019•东城区一模)《九章算术》中记载:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?”其大意是:今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,总容量为2斛.问大容器、小容器的容积各是多少斛?设大容器的容积为x斛,小容器的容积为y斛,根据题意,可列方程组为(斛:古量器名,容量单位).【答案】解:设大容器的容积为x斛,小容器的容积为y斛,根据题意得:,故答案为:.【点睛】本题考查了由实际问题抽象出二元一次方程组,根据数量关系列出关于x、y的二元一次方程组是解题的关键.14.(2019•石景山区一模)我国古代数学著作《算法统宗》中记载了“绳索量竿”问题,其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.求绳索和竿的长度.设绳索长x尺,竿长y尺,可列方程组为.【答案】解:设绳索长x尺,竿长y尺,根据题意得:.故答案为:.【点睛】本题考查了由实际问题抽象出二元一次方程组以及数学常识,找准等量关系,正确列出二元一次方程组是解题的关键.15.(2019•北京一模)2019年1月1日起,新个税法全面施行,将个税起征额从每月3500元调整至5000元,首次增加子女教育、大病医疗、赡养老人等6项专项附加扣除.新的税率表(摘要)如下:(注:应纳税额=纳税所得额﹣起征额﹣专项附加扣除)小吴2019年1月纳税所得额是7800元,专项附加扣除2000元,则小吴本月应缴税款 24 元;与此次个税调整前相比,他少缴税款 301 元.【答案】解:根据调整后应纳税额=纳税所得额﹣起征额﹣专项附加扣除,设小吴2019年1月应纳税额为x 元:x =7800﹣5000﹣2000 ∴x =800,∴小吴本月应缴税款:800×3%=24元;按调整前来计算应纳税额为:7800﹣3500=4300元, 应纳税款为:1500×3%+(4300﹣1500)×10%=325元, 故与此次个税调整前相比,他少缴税款301元. 故答案为24;301.【点睛】本题是新税法变动后的税率计算应用题,紧密联系生活实际,属于中等难度题目.16.(2019•房山区一模)某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:则租车一天的最低费用为 1450 元. 【答案】解:依题意得:租车费用最低的前题条件是将68名师生同时送到目的地,其方案如下: ①全部一种车型:小巴车26座最少3辆,其费用为:3×550=1650元, 中巴车39座最少2辆,其费用为:2×800=1600元,大巴车55座最少2辆,其费用为:2×900=1800元∵1600<1650<1800,∴同种车型应选取中巴车2辆费用最少.②搭配车型:2辆26座小巴车和1辆39座中巴车,其费用为:550×2+800=1900元,1辆26座小巴车和1辆55座大巴车,其费用为:550+900=1450元,1辆39座中巴车和1辆55座大巴车,其费用为:800+900=1700元,∵1450<1700<1900,∴搭配车型中1辆26座小巴车和1辆55座大巴车最少.综合①、②两种情况,费用最少为1450元.故答案为1450.【点睛】本题考查了不等式的应用,主要考虑方案的可行性,正确分类并通过计算比较大小求解.17.(2019•平谷区一模)甲乙二人分别从相距20km的A,B两地出发,相向而行.如图是小华绘制的甲乙二人运动两次的情形,设甲的速度是xkm/h,乙的速度是ykm/h,根据题意所列的方程组是.【答案】解:设甲的速度是xkm/h,乙的速度是ykm/h,依题意,得:.故答案为:.【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.18.(2019•通州区一模)甲、乙两运动员在长为100m的直道AB(A,B为直道两端点)上进行匀速往返跑训练,两人同时从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点…,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后100s内,两人相遇的次数为4.【答案】解:设两人起跑后100s内,两人相遇的次数为x次,依题意得;每次相遇间隔时间t,A、B两地相距为S,V甲、V乙分别表示甲、乙两人的速度,则有:(V甲+V乙)t=2S∴t∴,解得:x=4.5又∵x是正整数,且只能取整,∴x=4故答案为4.【点睛】本题考查了一元一次方程解决行程中的相遇问题,突破口就是相遇时间等于每个人走的时间;结合实际问题中x的取值只能取整数,此题与方程的解既有区别又有联系.19.(2019•延庆区一模)某校要组织体育活动,体育委员小明带x元去买体育用品,若全买羽毛球拍刚好可以买20副,若全买乒乓球拍刚好可以买30个,已知每个乒乓球拍比每副羽毛球拍便宜5元,依题意,可列方程为5.【答案】解:依题意,得:5.故答案为:5.【点睛】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.20.(2019•崇文区校级一模)已知x1,x2是关于x的一元二次方程x2﹣(2m+3)x+m2=0的两个不相等的实数根,且满足x1+x2=m2,则m的值是3.【答案】解:∵关于x的一元二次方程x2﹣(2m+3)x+m2=0的两个不相等的实数根,∴△=(2m+3)2﹣4m2=12m+9>0,∴m>,∵x1+x2=2m+3,x1•x2=m2,又∵x1+x2=m2,∴2m+3=m2,解得:m=﹣1或m=3,∵m>,∴m=3,故答案为:3.【点睛】此题主要考查了根与系数的关系.一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系为:x1+x2,x1•x2.21.(2019•房山区一模)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中方程术是重要的数学成就.书中有一个方程问题:今有醇酒一斗,直钱五十;行酒一斗,直钱一十,今将钱三十,得酒二斗,问醇、行酒各得几何?意思是:今有美酒一斗的价格是50钱,普通酒一斗的价格是10钱,现在买两种酒2斗共付30钱,问买美酒各多少?设买美酒x斗,买普通酒y斗,则可列方程组为.【答案】解:依题意得:.故答案是:.【点睛】考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.22.(2019•门头沟区二模)《算法统宗》是中国古代数学名著,作者是明代著名数学家程大位.在其中有这样的记载“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”译文:有100名和尚分100个馒头,正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?设有大和尚x 人,小和尚y人,可列方程组为.【答案】解:设大和尚有x人,则小和尚有y人,根据题意得,故答案为:.【点睛】本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程组.。
【全国百强校】北京一零一中学2019届九年级12月月考数学试题

北京101中学2019届上学期初中九年级12月月考数学试卷(满分:100分考试时间:120分钟)一、选择题:(本大题共10小题,共20分)1.如图,将一张矩形纸片沿对角线剪开得到两个直角三角形纸片,将这两个直角三角形纸片通过图形变换构成以下四个图形,这四个图形中是中心对称.....图形的是矩形纸片A B C D2.抛物线1)2(2+-=x y 的顶点坐标是A.(2,1)B.(2,-1)C.(-2,1)D.(-2,-1)3.老师将10份奖品分别放在10个完全相同的不透明礼盒中,奖品中有5份是文具,3份是读物,2份是科技馆通票。
小明从中随机取一份奖品,恰好取到读物的概率是A.21 B.53 C.51 D.1034.若点A (a ,b )在双曲线xy 3=上,则代数式4-ab 的值为A.-12 B.-7 C.-l D.15.若⊙O 的半径为3,圆心O 到直线l 的距离为2,则直线l 与⊙O 的位置关系是A.相交 B.相切 C.相离 D.无法确定6.两个相似三角形的相似比为1:2,较小三角形的面积为1,则较大三角形的面积为A.8B.4C.2D.27.如图,⊙O 的半径为3,点P 是弦AB 延长线上的一点,连接OP ,若OP=4,∠P=30°,则弦AB 的长为A.25B.23C.5D.28.已知点),(11y x 、),(22y x 、),(33y x 在双曲线xy 1=上,当3210x x x <<<时,1y 、2y 、3y 的大小关系是A.321y y y <<B.231y y y <<C.213y y y << D.132y y y <<9.如图,在平面直角坐标系xOy 中,抛物线c bx x y ++=2与x 轴只有一个交点M ,与平行于x 轴的直线l 交于A 、B 两点。
若AB=3,则点M 到直线l 的距离为A.25 B.49 C.2 D.4710.罚球是篮球比赛中得分的一个组成部分,罚球命中率的高低对篮球比赛的结果影响很大。
北京市2019年中考数学试题(解析版)

北京市2019年中考数学试题(解析版)2019年北京市⾼级中等学校招⽣考试数学试卷⼀、选择题(本题共30分,每⼩题3分)第1-10题均有四个选项,符合题意的选项只.有.⼀个。
1. 如图所⽰,⽤量⾓器度量∠AOB,可以读出∠AOB的度数为(A) 45°(B) 55°(C) 125°(D) 135°答案:B考点:⽤量⾓器度量⾓。
解析:由⽣活知识可知这个⾓⼩于90度,排除C、D,⼜OB边在50与60之间,所以,度数应为55°。
2. 神⾈⼗号飞船是我国“神⾈”系列飞船之⼀,每⼩时飞⾏约28 000公⾥。
将28 000⽤科学计数法表⽰应为(A)(B) 28(C)(D)答案:C考点:本题考查科学记数法。
解析:科学记数的表⽰形式为10na?形式,其中1||10≤<,n为整数,28000=。
故选C。
a3. 实数a,b在数轴上的对应点的位置如图所⽰,则正确的结论是(A)a(B)(C)(D)答案:D考点:数轴,由数轴⽐较数的⼤⼩。
解析:由数轴可知,-3<a<-2,故A、B错误;1<b<2,-2<-b<-1,即-b在-2与-1之间,所以,。
4. 内⾓和为540的多边形是答案:c考点:多边形的内⾓和。
n-??,当n=5时,内⾓和为540°,所以,选C。
解析:多边形的内⾓和为(2)1805. 右图是某个⼏何体的三视图,该⼏何体是(A)圆锥(B)三棱锥(C)圆柱(D)三棱柱答案:D考点:三视图,由三视图还原⼏何体。
解析:该三视图的俯视为三⾓形,正视图和侧视图都是矩形,所以,这个⼏何体是三棱柱。
6. 如果,那么代数2()b aaa a b--g的值是(A) 2 (B)-2 (C)(D)答案:A考点:分式的运算,平⽅差公式。
解析:2()b aaa a b--g=22a b aa a b--g=()()a b a b aa a b-+-+=2。
7. 甲⾻⽂是我国的⼀种古代⽂字,是汉字的早期形式,下列甲⾻⽂中,不是轴对称的是答案:D考点:轴对称图形的辨别。
考点08 实际问题与一元一次方程——比赛积分问题(解析版)

考点08 实际问题与一元一次方程比赛积分问题1.(河南省南阳市卧龙区2019–2020学年九年级期末数学试题)学校要组织足球比赛.赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x 个球队参赛.根据题意,下面所列方程正确的是( ) A .221x = B .1(1)212x x -= C .21212x = D .(1)21x x -=【答案】B【解析】设有x 个队,每个队都要赛(x –1)场,但两队之间只有一场比赛,由题意得:1(1)212x x -=,故选B .2.(山西省(太原临汾地区)2019–2020学年七年级上学期阶段三质量评估数学试题)在开展校园足球对抗赛中,规定每队胜一场得3分,平一场得1分,负一场得0分,七年级(2)班一共比赛10场,且保持了不败战绩,一共得了24分,求七年级(2)班一共胜了几场,若设七年级(2)班一共胜了x 场,可列方程为( )A .31024x x +-=B .()31024x x -+=C .31024x x ++=D .()31024x x ++=【答案】A【解析】【分析】根据分数可得等量关系为:胜场的得分+平场的得分=24分,把相关数值代入求解即可. 【详解】解:设设七年级(2)班一共胜了x 场,则平了(10–x )场, 列方程得,3x +(10–x )=24, 故选:A .【点睛】此题考查了一元一次方程的应用,读懂题意,得到总得分的等量关系是解决本题的关键. 3.(安徽省蚌埠市局属初中2019–2020学年八年级下学期期末数学试题)有x 支球队参加篮球比赛,每两队之间都比赛一场,共比赛了21场,则下列方程中符合题意的是( ) A .x (x –1)=21 B .x (x –1)=42 C .x (x +1)=21D .x (x +1)=42【答案】B【解析】【分析】设这次有x队参加比赛,由于赛制为单循环形式(每两队之间都赛一场),则此次比赛的总场数为:12x(x–1)场.根据题意可知:此次比赛的总场数=21场,依此等量关系列出方程即可.【详解】设这次有x队参加比赛,则此次比赛的总场数为12x(x−1)场,根据题意列出方程得:12x(x−1)=21,整理,得:x(x−1)=42,故答案为x(x−1)=42.故选B.【点睛】本题考查由实际问题抽象出一元二次方程,准确找到等量关系是解题的关键.4.在2019年女排世界杯比赛中,中国队以11场全胜积32分的成绩成为女排世界杯五冠王、女排世界杯比赛积分规则如表所示,若中国队以大比分3:2取胜的场次有x场,则根据以上信息所列方程正确的是()A.3x+2x=32B.3(11–x)+3(11–x)+2x=32C.3(11–x)+2x=32D.3x+2(11–x)=32【答案】C【解析】【分析】设中国队以大比分3:2取胜的场次有x场,则中国队以小比分3:1或3:0取胜的场次有(11–x)场,根据总积分=3×小比分获胜的场次数+2×大比分获胜场次数,即可得出关于x的一元一次方程.【详解】解:设中国队以大比分3:2取胜的场次有x场,则中国队以小比分3:1或3:0取胜的场次有(11–x)场,依题意,得:2x+3(11–x)=32.故选C.【点睛】本题考查了一元一次方程的应用,正确理解题意、找准相等关系是解题的关键.5.(江苏省海安市八校2019–2020学年七年级下学期6月阶段性测试数学试题)篮球比赛规定:胜一场得3分,负一场得1分.某篮球队进行了6场比赛,得了14分,该队获胜的场数是()A .2B .3C .4D .5【答案】C【解析】【分析】可设该队获胜x 场,则负了(6–x )场,根据总分=3×获胜场数+1×负了的场数,即可得出关于x 的一元一次方程,解之即可得出结论.【详解】设该队获胜x 场,则负了(6–x )场,根据题意,得: 3x +(6–x )=14, 解得x =4.经检验x =4符合题意. 故该队获胜4场. 故选C .【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键. 6.(黑龙江省哈尔滨市德强中学2020–2021学年七年级上学期9月月考数学试题)某球队参加比赛,开局11场保持不败,积23分,按比赛规则,胜一场得3分,平一场得1分,则该队获胜的场数为( ) A .4 B .5C .6D .7【答案】C【解析】【分析】设该队获胜的场数为x 场,则平局了()11x -场,根据总得分=获胜场数⨯3+平局场数⨯1,即可列出关于x 的一元一次方程,求解即可得出答案. 【详解】解:设该队获胜的场数为x 场,则根据比赛规则可得,()31123x x +-=,解得6x = 故选C .【点睛】本题考查了一元一次方程的应用,读懂题意,找到等量关系式是解题的关键.7.(河北省定州市宝塔初级中学2019–2020学年七年级下学期期末数学试题)篮球比赛规定:胜一场得3分,负一场得1分,某篮球队共进行了6场比赛,得了12分,该队获胜的场数是( ) A .2 B .3C .4D .5【答案】B【解析】【分析】解答此题可设该队获胜x 场,则负了(6–x )场,根据总分=3×获胜场数+1×负了的场数,即可得出关于x 的一元一次方程,解之即可得出结论. 【详解】设该队获胜x 场,则负了(6-x )场. 根据题意得3x +(6-x )=12,解得x =3.经检验x =3符合题意. 故该队获胜3场. 故选B .【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键8.(湖北省黄石市新建中学2019–2020学年七年级下学期期中数学试题)一张试卷有25道选择题,做对一题得4分,做错一题得–1分,某同学做完了25道题,共得70分,那么他做对的题数是( ) A .17道 B .18道C .19道D .20道【答案】C【解析】【分析】设作对了x 道,则错了(25–x )道,根据题意列出方程进行求解. 【详解】设作对了x 道,则错了(25–x )道,依题意得4x –(25–x )=70, 解得x =19 故选C .【点睛】此题主要考查一元一次方程的应用,解题的关键是根据题意找到等量关系.9.(黑龙江省哈尔滨市松雷中学2020–2021学年七年级上学期9月月考数学试题)足球比赛的记分办法为:胜一场得3分,平一场得1分,负一场得0分.一个队打了14场比赛,负5场,共得19分,那么这个队胜了 A .3场 B .4场C .5场D .6场【答案】C【解析】【分析】设共胜了x 场,本题的等量关系为:胜的场数×3+平的场数×1+负的场数×0=总得分,解方程即可得出答案.【详解】设共胜了x 场,则平了(14–5–x )场, 由题意得:3x +(14–5–x )=19, 解得:x =5,即这个队胜了5场. 故选C .【点睛】此题考查了一元一次方程的应用,属于基础题,解答本题的关键是要掌握胜的场数×3+平的场数×1+负的场数×0=总得分,难度一般.10.(湖南省湘西州古丈县2019–2020学年七年级下学期期末数学试题)在某足球比赛的前9场比赛中,A 队保持连续不败,共积25分,按比赛规则,胜一场得3分,平一场得1分,设A 队胜了x 场,由题意可列方程为_____. 【答案】3925x x +-=【解析】【分析】设A 队胜了x 场,从而可得A 队平了(9)x -场,再根据“胜一场得3分,平一场得1分”和“共积25分”即可列出方程.【详解】设A 队胜了x 场,则A 队平了(9)x -场, 由题意得:3925x x +-=, 故答案为:3925x x +-=.【点睛】本题考查了列一元一次方程,理解题意,正确求出A 队平了(9)x -场是解题关键.11.某学校8个班级进行足球友谊赛,比赛采用单循环赛制(参加比赛的队,每两队之间进行一场比赛),胜一场得3分,平一场得1分,负一场得0分,某班共得15分,并以不败成绩获得冠军,那么该班共胜______场比赛. 【答案】4【解析】8个班进行友谊赛,也就是说每个班级要和其余7个班级比赛,根据总比赛场数为7,设赢了x 场,则3x +(7-x )=15,解得x =4,故答案为:4.12.(河北省张家口市怀安县2020–2021学年七年级入学调研室考试数学试题)王亮参加了一场知识竞赛,共得了82分.这次竞赛一共50道题,答对一道记2分,答错一道或不答均扣1分.王亮答对了_______道题. 【答案】44【解析】【分析】设王亮答对了x 道题,则不答或答错(50–x )道题,根据总分=2×答对题目数–1×答错或不答题目数,即可得出关于x 的一元一次方程,解之即可得出结论; 【详解】解:设王亮答对了x 道题,则不答或答错(50–x )道题, 根据题意得:2x –(50–x )=82, 解得:x =44.答:王亮在竞赛中答对了44道题 故答案为:44【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键. 13.(湖北省天门、仙桃、潜江、江汉油田2020年中考数学试题)篮球联赛中,每玚比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了_________场. 【答案】9【解析】【分析】设该对胜x 场,则负14–x 场,然后根据题意列一元一次方程解答即可. 【详解】解:设该对胜x 场由题意得:2x +(14–x )=23,解得x =9.故答案为9.【点睛】本题考查了一元一次方程的应用,弄清题意、设出未知数、找准等量关系、列出方程是解答本题的关键.14.(内蒙古巴彦淖尔市杭锦后旗2019–2020学年七年级上学期期末数学试题)足球比赛的记分规则为:胜一场得3分,平一场得1分,负一场记0分,一个队比赛了20场,平了5场,共得32分,那么该队胜___________场.【答案】9【解析】【分析】设该队胜x场,根据记分规则和得分总数,可列方程3x+5=32求解.【详解】解:设该队胜x场,依题意得:3x+5=32解得:x=9故答案为:9.【点睛】根据题目给出的条件,找出合适的等量关系列出方程,再求解.15.一名篮球运动员在一次比赛中20投12中得24分,投中的两分球的个数是投中三分球个数的4倍,则投中的三分球、两分球、罚球分别是几个?【答案】三分球2个,两分球8个,罚球2个【解析】【分析】设运动员三分球投中x球,则两分球投中4x球,罚球投中(12–x–4x)球,根据24分列出方程,求出方程的解即可得到结果.【详解】解:设运动员三分球投中x球,则两分球投中4x球,罚球投中(12–x–4x)球,,根据题意得:3x+2×4x+14–x–4x=24,整理得:2x+8x+14–5x=24,移项合并得:x=2,所以4x=8,12–x–4x=2,则该运动员三分球投中2球,两分球投中8球;罚球投中2球.【点睛】此题考查了一元一次方程的应用,弄清题意是解本题的关键.16.(新疆维吾尔自治区昌吉回族自治州教育共同体2019–2020学年七年级上学期期末数学试题)一次足球比赛共赛15场,胜一场积2分,平一场积1分,负一场积0分,某中学足球队所胜场数是所负场数的2倍,结果共得19分,则这个足球队共平几场?【答案】3【解析】【分析】设这个足球负了x场,则胜了2x场,平了(15–x–2x)场,根据胜的场数的得分+平的场数的得分=19,列方程求出其解即可.【详解】解:设这个足球队负了x场,则胜了2x场,平了(15–x–2x)场,根据题意得:2×2x+1×(15–x–2x)=19,解得,x=4,15–x–2x=15–4–8=3,答:这个足球队共平3场.【点睛】本题考查了一元一次方程的应用.根据题目给出的条件,找出合适的等量关系是解决问题的关键. 17.(湖北省咸宁市嘉鱼县2019–2020学年七年级上学期期末数学试题)下表是某年篮球世界杯小组赛C 组积分表:排名国家比赛场数胜场负场总积分1美国550102土耳其53283乌克兰52374多米尼加52375新西兰52376芬兰51m n(1)由表中信息可知,胜一场积几分?你是怎样判断的?(2)m=;n=;(3)若删掉美国队那一行,你还能求出胜一场、负一场的积分吗?怎样求?(4)能否出现某队的胜场积分与负场积分相同的情况,为什么?【答案】(1)胜一场积2分,理由见解析;(2)m=4,n=6;(3)胜一场积2分,负一场积1分;(4)不可能,理由见解析【解析】【分析】(1)由美国5场全胜积10分,即可得到答案;(2)由比赛场数减去胜场,然后计算m、n的值;(3)由题意,设胜一场积x分,然后列出方程组,即可求出胜一场、负一场的积分;(4)由题意,列出方程,解方程即可得到答案.【详解】解:(1)根据题意,则因为美国5场全胜积10分,所以1052÷=,所以胜一场积2分;(2)由题意,514m=-=;设负一场得x分,则3228x⨯+=;所以1x=;所以12416n=⨯+⨯=;故答案为:6;4;(3)设胜一场积x分,由土耳其队积分可知负一场积分832x-,根据乌克兰队积分可列方程:8323()72xx-+=,解得:2x=,此时831 2x-=;即胜一场积2分,负一场积1分;(4)设某球队胜y场,则21(5)y y=⨯-,解得:53y=;所以不可能出现某队的胜场积分与负场积分相同的情况.【点睛】本题考查了一元一次方程的应用,根据数量关系列出一元一次方程是解题的关键.18.(湖北省武汉市汉阳区2019–2020学年七年级上学期期末数学试题)下面表格是某次篮球联赛部分球队不完整的积分表:请根据表格提供的信息:(1)求出a 的值;(2)请直接写出m =______,n =______. 【答案】(1)18a =;(2)8m =,6n =.【解析】【分析】(1)由钢铁队的负场数及积分可得负一场的分值,由前进队的胜负场数及积分可得胜一场的分值,由此可求出卫星队的积分;(2)由远大队的总场数可得14m n =-,结合(1)中所求的胜一场及负一场的分值和远大队的积分可列出关于n 的一元一次方程,求解即可.【详解】解:(1)由钢铁队的负场数及积分可得负一场的分值为14141÷=(分),由前进队的胜负场数及积分可得胜一场的分值为(2441)102-⨯÷=(分),4210118a =⨯+⨯=, 所以a 的值为18;(2)由远大队的总场数可得14m n =-,根据题意得:2(14)122n n -+⨯= 解得6n =1468m =-=所以8m =,6n =.【点睛】本题考查了一元一次方程的实际应用,正确理解题意,从表格中获取信息是解题的关键. 19.(北京市海淀区2019–2020学年七年级上学期期末数学试题)2019年9月29日,中国女排以十一连胜的战绩夺得女排世界杯冠军,成为世界三大赛的“十冠王”2019年女排世界杯的参赛队伍为12支,比赛采取单循环方式,五局三胜,积分规则如下:比赛中以30-或者31-取胜的球队积3分,负队积0分;而在比赛中以32-取胜的球队积2分,负队积1分.前四名队伍积分榜部分信息如下表所示,(1)中国队11场胜场中只有一场以32-取胜,请将中国队的总积分填在表格中.(2)巴西队积3分取胜的场次比积2分取胜的场次多5场,且负场积分为1分,总积分见下表,求巴西队胜场的场数.【答案】(1)32;(2)7【解析】【分析】(1)根据比赛中以30-或者31-取胜的球队积3分,在比赛中以32-取胜的球队积2分,结合表格和已知条件即可得出(2)设巴西队积3分取胜的场数为x 场,则积2分取胜的场数为()5x -场,根据巴西队的总积分为21分,列出方程解方程即可得出答案【详解】解:(1)解:因为比赛中以30-或者31-取胜的球队积3分,在比赛中以32-取胜的球队积2分,中国队11场胜场中只有一场以32-取胜, 所以中国队的总积分=1031232⨯+⨯= 故答案为:32(2)设巴西队积3分取胜的场数为x 场,则积2分取胜的场数为()5x -场 依题意可列方程()325121x x +-+= 3210121x x +-+=530x =6x =则积2分取胜的场数为51x -=,所以取胜的场数为617+= 答:巴西队取胜的场数为7场.【点睛】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.20.(青海省西宁市2019–2020学年七年级上学期期末数学试题)某次篮球联赛中,两队的积分如下表所示:请回答下列问题:(1)负一场_________积分; (2)求胜一场积多少分?(3)某队的胜场总积分比负场总积分的3倍多3分,求该队胜了多少场? 【答案】(1)1;(2)胜1场得2分;(3)该队胜了9场. 【解析】【分析】(1)根据“钢铁”队的负场场次和积分即可得;(2)设胜一场积x 分,根据“前进”队的胜场场次、负场场次与积分建立方程求解即可;(3)设该队胜了a 场,则该队负了(14)a -场,再结合(1)、(2)的结论建立方程求解即可.【详解】(1)由“钢铁”队得:14141÷=故答案为:1;(2)设胜一场积x 分由题意得:104124x +⨯=解得:2x =答:胜一场积2分;(3)设该队胜a 场,则该队负(14)a -场由题意得:23(14)3a a =-+解得:9a =答:该队胜了9场.【点睛】本题考查了一元一次方程的实际应用,依据题意正确建立方程是解题关键.21.(四川省成都市金牛区2019–2020学年七年级上学期期末数学试题)2019年11月,我区组织了一次职工篮球联赛,比赛分初赛阶段和决赛阶段,在初赛阶段中,每队有10场比赛,每场比赛都要分出胜负,每队胜一场得2分,输一场得1分,积分超过15分才能获得决赛资格.(1)若乙队初赛获得4场胜利,问乙队是否有资格参加决赛?请说明理由.(2)已知甲队在初赛阶段的积分为18分,求甲队初赛阶段胜、负各多少场;【答案】(1)没有,理由见解析;(2)胜8场,负2场【解析】【分析】(1)根据得分标准进行计算,再比较大小即可;(2)设甲队胜了x 场,则负了(10-x )场,根据每队胜一场得2分,负一场得1分,利用甲队在初赛阶段的积分为18分,进而得出方程求出答案.【详解】解:(1)没有资格参加决赛,理由如下:乙队积分为:4×2+(10-4)×1=14<15,所以没有资格参加决赛;(2)设甲队初赛阶段胜x 场,则负了(10-x )场,由题意得:2x +1×(10-x )=18,解得:x =8,所以10-x =10-8=2,答:甲队初赛阶段胜8场,负2场.【点睛】本题考查一元一次方程的应用,明确得分标准,正确找出等量关系是解题的关键.22.(天津市河东区2019–2020学年七年级上学期期末数学试题)某校七年级组织知识竞赛,共设20道选择题,各题分值相同,每题必答,如表记录了5个参赛学生的得分情况,问:(1)答对一题得分,若错一题得分;(2)有一同学说:同学甲得了70分,同学乙得了50分,你认为谁的成绩是准确的?为什么?【答案】(1)5,–1;(2)同学甲的成绩是准确的,同学乙的成绩不准确,理由见解析【解析】【分析】(1)根据A参赛者答对20道题,答错0道题,得分100分,即可求得答对一题得5分,再;根据B参赛者答对19道题,答错1道题,得分94分,即可求得答案;(2)设同学甲答对了x道,则答错了(20–x)道,由题意建立方程求解即可.【详解】(1)因为答对20道题,答错0道题,得分100分,所以答对一题得5分,因为答对19道题,答错1道题,得分94分,所以答错一题得–1分;故答案为:5,–1;(2)同学甲的成绩是准确的,同学乙的成绩不准确.设同学甲答对了x道,则答错了(20–x)道,由题意得:5x–(20–x)=70,解得:x=15,设同学乙答对了y道,则答错了(20–y)道,由题意得:5y–(20–y)=50,解得:y=70 6因为x,y是做对题目个数,所以x,y是自然数.因此,同学甲的成绩是准确的,同学乙的成绩不准确.【点睛】本题考查了一元一次方程解实际应用题的运用,解答时关键是:答对的得分+加上答错的得分=总得分.。
