基本的RC电路计算
rc电路的全响应

rc电路的全响应RC电路指的是由电阻(R)和电容(C)组成的电路。
在RC电路中,电容器充电或放电的过程会产生响应,这种响应被称为RC电路的全响应。
在这篇文章中,我将介绍RC电路的全响应的相关概念和公式,以及一些应用和实例。
首先,我们需要了解RC电路的基本原理。
在一个简单的RC电路中,电容器通过电阻与电源相连接。
当电源打开时,电容器开始充电,并且在这个过程中产生电压的变化。
这个过程可以用以下方程来描述:V(t) = V0 * (1 - e^(-t/RC))其中,V(t)表示电容器上的电压随时间的变化,V0表示电容器的初始电压,t表示时间,R表示电阻的电阻值,C表示电容器的电容值。
根据这个方程,我们可以得到RC电路在不同时间的电压响应。
在开始时刻,电压会根据初始电压和时间常数RC的比例来变化。
随着时间的推移,电压逐渐趋于平稳,最终达到稳态。
在RC电路中,时间常数RC非常重要,它表示了电容器充电或放电的速度。
时间常数越大,电容器充电或放电的速度越慢。
在RC电路中,电容器充电或放电大约需要5个时间常数的时间才能完成90%的过渡过程。
因此,在分析和设计RC电路时,时间常数是一个重要的参考值。
除了基本的RC电路,RC电路的全响应在许多实际应用中也具有重要意义。
例如,RC电路可以用作低通滤波器。
当交流信号通过RC电路时,高频部分会被滤除,只有低频部分通过。
这对于信号处理和通信系统中的滤波功能非常有用。
另一个应用是RC电路在时间延迟电路中的使用。
通过调整电阻和电容的值,可以控制信号的延迟时间。
这在音频处理和电子仪器中具有重要意义。
此外,RC电路还用于数字电路和模拟电路的时间控制。
通过控制RC电路的充电和放电过程,可以实现精确的时间控制和时间延迟。
总结起来,RC电路的全响应是指电容器充电或放电过程中的电压变化。
通过使用RC电路的基本原理和相关方程,可以计算和预测电压随时间的变化。
在许多实际应用中,RC电路的全响应具有重要的意义,例如滤波、时间延迟和时间控制等。
RC电路充放电时间的计算(含计算公式)
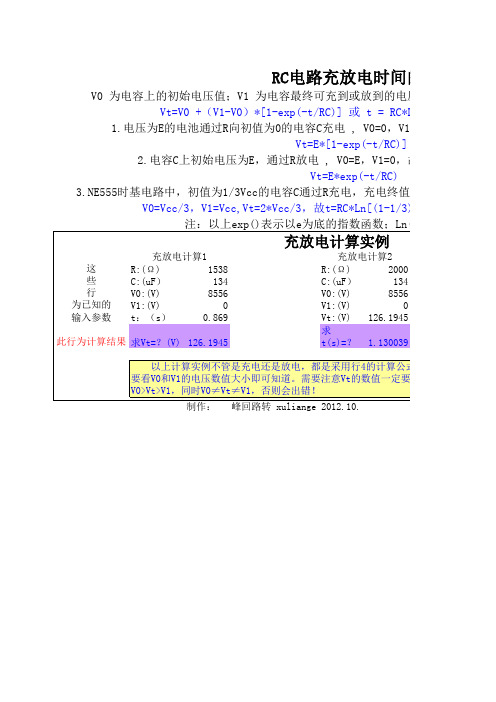
V0 为电容上的初始电压值;V1 为电容最终可充到或放到的电压值;Vt 为t时刻 Vt=V0 +(V1-V0)*[1-exp(-t/RC)] 或 t = RC*Ln[(V1 - V0)/(V1 1.电压为E的电池通过R向初值为0的电容C充电 , V0=0,V1=E,故充到t时刻 Vt=E*[1-exp(-t/RC)] 2.电容C上初始电压为E,通过R放电 , V0=E,V1=0,故放到t时刻电容上 Vt=E*exp(-t/RC) 3.NE555时基电路中,初值为1/3Vcc的电容C通过R充电,充电终值为Vcc,问充到2/ V0=Vcc/3,V1=Vcc,Vt=2*Vcc/3,故t=RC*Ln[(1-1/3)/(1-2/3)]=RC*Ln 注:以上exp()表示以e为底的指数函数;Ln()是e为底的对数函
充放电计算实例
这 些 行 为已知的 输入参数 此行为计算结果 充放电计算1 R:(Ω ) 1538 C:(uF) 134 V0:(V) 8556 V1:(V) 0 t:(s) 0.869 求Vt=?(V) 126.1945 充放电计算2 R:(Ω ) 2000 C:(uF) 134 V0:(V) 8556 V1:(V) 0 Vt:(V) 126.1945 求t(s)=? 1.130039
以上计算实例不管是充电还是放电,都是采用行4的计算公式,至于是计算的是 要看V0和V1的电压数值大小即可知道。需要注意Vt的数值一定要介于V0和V1之间方可 V0>Vt>V1,同时V0≠Vt≠V1,否则会出错! 制作: 峰回路转 xuliange 2012.10.
电时间的计算
放到的电压值;Vt 为t时刻电容上的电压值。则: t = RC*Ln[(V1 - V0)/(V1 - Vt)] V0=0,V1=E,故充到t时刻电容上的电压为: (-t/RC)] ,V1=0,故放到t时刻电容上的电压为: -t/RC) 充电终值为Vcc,问充到2/3Vcc需要的时间是多少? n[(1-1/3)/(1-2/3)]=RC*Ln2 =0.693RC 函数;Ln()是e为底的对数函数
rc移相电路计算公式

rc移相电路计算公式以RC移相电路计算公式为标题的文章一、引言RC移相电路是一种常见的电路,它能够实现信号的相位移动。
在电子工程领域中,我们经常需要对信号进行相位移动,以满足特定的应用需求。
本文将介绍RC移相电路的计算公式及其应用。
二、RC移相电路的基本原理RC移相电路是由电阻(R)和电容(C)组成的,它的基本原理是利用电容的特性来实现信号的相位移动。
当输入信号通过电容时,会产生一个滞后的输出信号。
通过调整电阻和电容的数值,可以实现不同程度的相位移动。
三、RC移相电路的计算公式RC移相电路的计算公式主要包括两个方面:相位移角度的计算和相位延迟时间的计算。
1. 相位移角度的计算相位移角度可以通过计算电路的角频率和电路的时间常数来得到。
电路的时间常数(τ)可以通过电阻和电容的数值计算得到。
公式如下:τ = R * C其中,τ为电路的时间常数,R为电阻的阻值,C为电容的电容值。
电路的相位移角度(θ)可以通过相位移角度和2π的比例来计算。
公式如下:θ = φ / 360° * 2π其中,θ为电路的相位移角度,φ为电路的相位移动。
2. 相位延迟时间的计算相位延迟时间是指信号通过RC移相电路后所产生的延迟时间。
它可以通过计算电路的时间常数和信号的周期来得到。
公式如下:t = τ / T其中,t为相位延迟时间,τ为电路的时间常数,T为信号的周期。
四、RC移相电路的应用RC移相电路在实际应用中有着广泛的应用。
下面将介绍几个常见的应用场景。
1. 信号延迟通过调整RC移相电路的参数,可以实现信号的延迟效果。
这在一些音频处理中常见,比如延迟效果的添加。
2. 相位校准在一些通信系统中,需要对信号进行相位校准,以确保信号的准确传输。
RC移相电路可以实现对信号相位的微调,从而达到相位校准的目的。
3. 滤波器设计RC移相电路也可以用于滤波器的设计。
通过调整电阻和电容的数值,可以实现滤波器的频率响应和相位响应的调节。
rc电路计算

计算RC电路的参数涉及电阻(R)和电容(C)。
以下是一些常见的RC电路计算问题和相应的计算公式:
1. RC电路的时间常数(τ)计算:
τ = R * C
2. RC电路的充电时间(t)计算:
t = 5 * τ (充电时间为RC电路达到63.2%的稳定电压所需的时间) 3. RC电路的放电时间(t)计算:
t = 5 * τ (放电时间为RC电路达到36.8%的稳定电压所需的时间) 4. RC电路的充电过程的电压(V)计算:
V = V0 * (1 - e^(-t/τ)) (V0为初始电压,t为充电时间,τ为时间常数) 5. RC电路的放电过程的电压(V)计算:
V = V0 * e^(-t/τ) (V0为初始电压,t为放电时间,τ为时间常数)
这些公式适用于理想的RC电路,其中没有考虑额外的电阻、电感或其他复杂的影响因素。
在实际应用中,可能需要考虑更多的因素来精确计算RC电路的行为。
请注意,以上公式仅提供了一些基本的计算方法,具体应用中可能会有不同的情况和计算要求。
在实际使用中,建议参考相关的电路理论和手册,并结合具体的电路参数和条件进行计算。
rc电路的电压公式

rc电路的电压公式
RC电路是一种常见的电路,由电阻R和电容C串联或并联而成。
在RC电路中,电压的变化是基于电容器的充电和放电过程。
当电容器充电时,电流从电源流入电容器,电容器内的电荷随之增加。
电容器两端的电压逐渐升高,直到达到与电源电压相等的值。
反之,当电容器放电时,电容器内的电荷流回电源,电压逐渐降低,直到等于0为止。
根据欧姆定律,电阻R上的电压V与电流I成正比,即V=IR。
因此,在RC电路中,电容器电压Vc和电阻电压VR之和等于电源电压VS,即Vc+VR=VS。
根据电容器的充放电特性,可以得到RC电路中电容器电压的变化公式:
Vc=VS(1-e^(-t/RC))
其中,t为时间,R为电阻,C为电容,e为自然常数
2.71828。
该公式说明了RC电路中电容器电压随时间的变化规律,也为电路分析和设计提供了理论依据。
- 1 -。
rc并联电路电流计算公式

rc并联电路电流计算公式在我们的电学世界里,RC 并联电路可是个有趣的家伙!今天咱们就来好好聊聊 RC 并联电路电流的计算公式。
咱们先从最基础的说起哈。
RC 并联电路呢,就是由电阻(R)和电容(C)并联在一起组成的电路。
在这个电路中,电流可不是简单地走直线,而是会有一些有趣的分配和变化。
电流计算公式的核心是要分别考虑电阻支路和电容支路的电流。
对于电阻支路,电流(IR)的计算很简单,就是电压(U)除以电阻(R),也就是 IR = U / R 。
这就好比你在平路上跑步,速度取决于你遇到的阻力大小。
而电容支路的电流(IC)就有点特别啦。
它跟电压的变化率有关,计算公式是 IC = C × dU/dt 。
这就像是在一个有弹性的跑道上跑步,速度不仅取决于当前的位置,还跟位置变化的快慢有关。
咱们来举个实际的例子感受一下。
比如说,你有一个电路,电阻是10 欧姆,电容是 10 微法,加在电路上的电压是 10 伏特,而且电压是匀速上升的,上升的速度是每秒 1 伏特。
那电阻支路的电流 IR 就是 10 伏特除以 10 欧姆,等于 1 安培。
而电容支路的电流 IC 呢,因为电压变化率是每秒 1 伏特,所以 IC 就是 10 微法乘以 1 伏特每秒,等于 10 微安。
在实际应用中,RC 并联电路电流的计算可是非常重要的。
就像我之前帮一个小朋友做电子小制作的时候,就是因为搞清楚了这个电流计算,才让他的小灯能按照预期的效果闪烁起来。
那时候,小朋友着急得不行,觉得自己的小制作要失败了。
我就静下心来,一步步给他分析这个 RC 并联电路,算出电流,调整了元件参数,最后成功啦!小朋友那高兴的样子,我现在都还记得。
再比如说,在一些通信设备里,RC 并联电路也经常出现。
准确计算电流能保证信号的稳定传输,不会出现混乱或者丢失的情况。
总之,RC 并联电路电流的计算公式虽然看起来有点复杂,但只要我们多琢磨琢磨,多结合实际例子来理解,就一定能掌握它,让它为我们的电学世界服务!就像我们在生活中解决各种难题一样,只要有耐心,有方法,都能迎刃而解。
RC吸收电路参数计算
RC吸收电路参数计算RC吸收电路是一种常见的电路配置,用于实现信号的滤波。
它由一个电阻(R)和一个电容(C)组成。
电阻用于限制信号流过电路的电流,而电容则负责在不同时间尺度上储存和释放电荷。
在RC吸收电路中,我们通常关心的是电阻值、电容值和截止频率。
下面将详细介绍如何计算这些参数。
1.电阻值(R)的计算:电阻值的选择主要取决于应用需求和电路中的其他元件。
你可以选择一个标准电阻值或使用数字电阻进行精确控制。
确保电阻值足够大,以限制电流流过电路,同时不要太大,否则会影响电路的动态响应。
选择电阻值的一种常用方法是根据截止频率进行估算,然后根据市场可用的电阻值进行调整。
2.电容值(C)的计算:电容值的选择取决于滤波器需要通过的频率范围。
根据需求,您可以选择陶瓷电容或电解电容。
陶瓷电容通常适用于低频范围,而电解电容则适用于高频范围。
计算电容值的一种常用方法是根据截止频率和电阻值进行估算。
截止频率可以根据信号需要通过的频率范围和滤波器类型进行选择。
3. 截止频率(f_cutoff)的计算:截止频率是滤波器的重要参数,它决定了滤波器的频率响应。
通过截止频率,我们可以了解信号在滤波器中的通过情况。
截止频率的计算公式为:f_cutoff = 1 / (2 * π * R * C)4.频率响应曲线的绘制:根据计算得到的截止频率和选定的电阻和电容值,我们可以绘制出滤波器的频率响应曲线。
在低于截止频率时,滤波器会较好地通过信号;而在高于截止频率时,滤波器会对信号进行衰减。
频率响应曲线可用于验证滤波器设计是否符合要求。
需要注意的是,以上计算和估算方法是理论值,实际使用过程中可能会存在误差。
由于电阻和电容元件的工艺制造和偏差等原因,实际结果可能与理论值有所不同。
因此,在实际应用中,可能需要对电路进行调整和调试。
总结起来,RC吸收电路参数的计算主要涉及电阻值、电容值和截止频率的确定。
通过选择合适的参数,可以实现对信号的滤波和调整。
rc电路延时时间计算
rc电路延时时间计算RC电路延时时间计算是在电子电路设计中常见的应用场景。
RC电路,即电阻电容电路,由电阻器和电容器组成。
当通过RC电路的电流发生变化时,电容器会储存电能,电阻器则会消耗电能。
这个过程会导致电流变化的速度受到限制,从而产生延时效果。
下面将详细介绍RC电路延时时间的计算方法及其影响因素。
RC电路延时时间的基本概念:在RC电路中,延时时间是指电流变化从一个稳态值到达另一个稳态值所需要的时间。
通常用τ(希腊字母tau)表示延时时间,单位为秒。
延时时间与电阻R和电容C的数值有关。
RC电路延时时间的计算方法:1.计算公式:RC电路延时时间τ的计算公式为:τ= RC其中,R为电阻器的电阻值,单位为欧姆(Ω);C为电容器的电容值,单位为法拉(F)。
2.影响因素:(1)电阻R和电容C的数值:电阻值越大,延时时间越长;电容值越大,延时时间越长。
(2)电源电压和电流:电源电压和电流的大小会影响电容器充电和放电的速度,从而影响延时时间。
在实际应用中,根据需要调整RC电路的延时时间,可以采取以下方法:1.调整电阻R的值:增大或减小电阻值,以达到所需的延时时间。
2.调整电容C的值:增大或减小电容值,以达到所需的延时时间。
3.并联电阻或电容:通过并联电阻或电容,可以缩短或延长延时时间。
总结与建议:RC电路延时时间计算是电子电路设计中的基础内容。
了解RC电路的基本原理和计算方法,可以帮助设计师快速准确地实现延时功能。
在实际应用中,根据需求调整电阻和电容的数值,可以获得理想的延时效果。
同时,注意电源电压和电流的影响,以确保电路稳定运行。
rc阻抗计算公式
rc阻抗计算公式好的,以下是为您生成的关于“rc 阻抗计算公式”的文章:在咱们的电学世界里,rc 阻抗计算公式就像是一把神奇的钥匙,能帮助我们打开理解电路特性的大门。
先来说说啥是 RC 电路吧。
想象一下,有一个电阻 R 和一个电容 C串联在一起,这就构成了一个简单的 RC 电路。
那 RC 阻抗又是啥呢?简单说,就是这个电路对电流的阻碍作用。
rc 阻抗计算公式是:Z = R + 1 / (jωC) 。
这里面的 Z 就是阻抗啦,R 是电阻值,ω 是角频率,C 是电容值,而 j 呢,就是那个让很多同学头疼的虚数单位。
记得我刚开始接触这个公式的时候,那叫一个懵。
有一次在实验室做实验,老师让我们通过改变电阻和电容的值,来计算 RC 阻抗并观察电路中的电流变化。
我当时拿着那些电阻和电容,手忙脚乱地接线路,心里紧张得不行,就怕出错。
好不容易接好了,开始计算的时候,却发现总是算不对。
看着周围的同学一个个都得出了结果,我急得满头大汗。
后来,我静下心来,仔细回想老师讲的知识点,一步一步地推导公式,才发现自己把角频率的计算给弄错了。
经过一番努力,终于算出了正确的 RC 阻抗,那一刻,心里别提多有成就感了。
咱们再深入聊聊这个公式里的每个部分。
电阻 R 很好理解,就是对电流的直接阻碍。
而电容 C 就有点“调皮”了,它的阻碍作用和频率有关。
频率越高,电容的阻碍就越小;频率越低,阻碍就越大。
在实际应用中,RC 阻抗计算公式可太有用了。
比如说在滤波电路里,我们可以通过选择合适的电阻和电容值,来让特定频率的信号通过或者被阻挡。
这在音响设备、通信系统里都经常能见到。
还有在电源电路中,为了稳定电压,也会用到 RC 电路来滤波。
如果阻抗计算不准确,那电源输出可能就会不稳定,影响整个设备的工作。
总之,rc 阻抗计算公式虽然看起来有点复杂,但只要咱们多琢磨,多实践,就能熟练掌握它,让它成为我们解决电路问题的得力工具。
就像我那次在实验室里,经历了挫折最终成功,只要不放弃,就能搞定这看似难缠的公式!希望通过我的这番讲解,能让您对 rc 阻抗计算公式有更清楚的认识和理解。
rc充电电路电阻功率计算
rc充电电路电阻功率计算RC充电电路电阻功率计算引言:在电子电路中,充电电路是一种常见的电路配置,用于将电能存储在电容器中。
在RC充电电路中,电阻器扮演着关键的角色,通过电阻器的电阻来控制电流的流动和电容器的充电速度。
本文将介绍如何计算RC充电电路中电阻器的功率。
一、RC充电电路简介RC充电电路是由电源、电阻器和电容器组成的电路。
当电路闭合时,电源通过电阻器向电容器充电,电容器的电压逐渐增加,直到达到电源电压。
在这个过程中,电阻器的功率是需要考虑的因素之一。
二、电阻器功率计算公式电阻器的功率可以通过以下公式计算:功率(P)= 电流(I)^2 × 电阻(R)其中,电流可以通过欧姆定律计算:电流(I)= 电压(V)/ 电阻(R)综合以上两个公式,可以得到电阻器功率的计算公式:功率(P)= 电压(V)^2 / 电阻(R)三、实例分析以一个具体的RC充电电路为例,假设电容器的电压为12V,电阻器的阻值为100Ω。
我们将计算电阻器的功率。
根据欧姆定律,可以计算电流:电流(I)= 12V / 100Ω = 0.12A然后,根据功率计算公式,可以计算功率:功率(P)= 12V^2 / 100Ω = 1.44W因此,在这个RC充电电路中,电阻器的功率为1.44瓦特。
四、功率和电阻的关系从计算公式可以看出,功率和电阻是成反比的关系。
当电阻增大时,功率会减小;当电阻减小时,功率会增大。
这是因为功率是由电流的平方和电阻的乘积决定的。
五、电阻器功率的影响因素电阻器的功率除了与电阻大小有关外,还受到其他因素的影响,比如电压和工作温度。
当电压增大时,功率也会增大;当工作温度升高时,电阻器的功率也会随之增大。
因此,在选择电阻器时,需要考虑电压和工作温度的要求,以确保电阻器能够正常工作而不超过额定功率。
六、电阻器功率的选择和优化在实际应用中,选择合适的电阻器功率是很重要的。
如果功率选择过小,电阻器可能会因为过热而损坏;如果功率选择过大,不仅增加了成本,还浪费了电能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
那么这个复杂的精确公式和工程估算之间,有怎样的联系呢?
三、精确计算的估算化简
指数函数可以展开成泰勒级数,公式如下:
exp(x)
=
ex
=
1
+
x
+
x2 2!
+
x3 3!
+
⋯+
xn n!
+
⋯
这里,因为t1或者t2都远远小于 1,所以,可以忽略掉级数的高次项,这里取:
τ1
τ2
exp(x) ≅ 1 + x 整理,代入前面的精确计算公式有:
R2) �
∗
D∗T C1
对于放电来说:
−t2 V放 = �VOUT + ∆V充� ∗ exp � τ2 �
这里忽略∆V充,有:
−t2 V放 = VOUT ∗ exp � τ2 � 同样,利用泰勒公式替换,整理一下,可以得到:
−t2
t2 VOUT T ∗ (1 − D)
∆V放 = VOUT ∗ [1 − exp � τ2 �] = VOUT ∗ τ2 = R2 ∗ C1
������������1 ∗ ������������2 ������������������������������������ = ������������1 + ������������2 令τ1 = Req ∗ C,t1 = T ∗ D假设输出稳定时,输出电压为 VOUT,那么,可以得到:
2.009
2.007 -2.014
4.52 50 50 100 50 90% 45 5 2500 5000
2.141
2.140 -1.074
4.52 50 50 100 50 100% 50 0 2500 5000
2.260
2.260
0.000
表 1 估算和精确计算不同的占空比下的输出电压 可以看到估算和精确计算的误差并不大:
2/5
图四 诺顿等效 采用诺顿等效,将电阻转化成并联的形式:
VIN Ieq =
R1
图五 戴维南等效
再使用戴维南等效,转换成经典的 RC 结构:
������������2 ������������������������������������ = ������������������������ ∗ ������������1 + ������������2
R2
t1 ∗ τ2
VOUT = VIN ∗ R1 + R2 ∗ t2 ∗ τ1 + t1 ∗ τ2
将各参数全部代入,最终得到:
������������
=
������������������������
∗
������������ ∗ ������������2 ������������1 + ������������2 ∗
∗
R2 R1 + R2
∗
1 − exp �−τt11� exp �τt22� − exp �−τt11�
这个公式稍微有点复杂,计算起来略微麻烦一点,我们可以用电子表格进行计算。
我们列一个电子表格,来计算一下,顺便对比一下精确计算的结果和估算的结果相差多少。计
算结果如下:
3/5
VIN R1 R2 C1 T D
0.750 -3.011
4.52 50 50 100 50 30% 15 35 2500 5000
1.043
1.039 -3.650
4.52 50 50 100 50 40% 20 30 2500 5000
1.291
1.288 -3.876
4.52 50 50 100 50 50% 25 25 2500 5000
������������ ∗ ∆������������ ∆ = ������������ 利用该公式计算充电和放电电压变化量为:
������������充 ∗ ∗ ������������ ������������������������ ������������ ∗ (������������1 + ������������2) ∗ ������������
������������充 =
������������1
− ������������2 = ������������1 −
������������1 ∗ ������������2
������������ ������������放 = ������������2
又由于电容上的充电和放电的变化量为:
这个是不是和工程计算的充电公式一样了?这个就是工程计算要求t ≪ τ的原因。
工程计算往往需要 10 倍的差距,就是因为 10 倍的差距的时候,某些数据项可以忽略掉,不如
计算的时候是利用电容的充电电压和放电电压变换量一致,但是计算时,输出电压又忽略掉了这个
变化量,工程计算更多的是一种估算,忽略对最终结果影响不大的细节部分,通过简化计算,得到
一、采用工程计算
T=50uS,而 R2C1=5mS,(R1//R2)C1=2.5mS,可以看出电路中的时间常数是远大于充放电的周 期的(在工程计算上,一般 10 倍以上的差距就可以加“远”字了),所以可以认为充放电的电流是 线性的。
电容的充电和放电流为:
������������������������ − ������������ ������������ ������������������������ ������������ ∗ (������������1 + ������������2)
1.507
1.503 -3.770
4.52 50 50 100 50 60% 30 20 2500 5000
1.695
1.692 -3.395
4.52 50 50 100 50 70% 35 15 2500 5000
1.861
1.858 -2.797
4.52 50 50 100 50 80% 40 10 2500 5000
假设占空比 D=10%时,VOUT=10%*(5-0.48)*(R2/(R1+R2))V=0.226V。
图一 仿真电路 但实际仿真结果如下(仿真结果与实际的电路结果是一致的):
图二 仿真结果
1/5
可以看到 VOUT 的稳定电压大约 0.408V,而直接使用占空比计算结果为 0.226V,误差太大了, 需要仔细的计算一下。当 VOUT 稳定时,电容 C1 上的充电电压变化量是与放电电压的变化量是相 等的。我们基于这一点进行计算。
5/5
−t1 V充 = VOUT + (Veq − VOUT) ∗ [1 − exp � τ1 �] 令τ2 = R2 ∗ C,t2 = T ∗ (1 − D),则可以得到放电后的电压为:
−t2 V放 = V充 ∗ exp � τ2 � = VOUT 把充电后的电压代入放电电压公式,可以得到:
VOUT
=
VIN
简单的 RC 计算
最近以前同事遇到一点小问题,设计好了一个电路,但是客户在使用时,发现测量结果与他给 的估算公式不相符。这个问题简化一下,就是下面这个简单的 RC 电路的计算。
电路如图一所示,他提供的简单的计算公式如下: V������������������������������������ = D ∗ VIN VIN = VI − VF
若电容上的初始电压为������������初,那么放电公式为:
−������������ ������������������������ (������������) = ������������初 ∗ exp �������������� 充电时,利诺顿等效和戴维南等效,可以化简电路。
图三 简化充电等效电路
������������1
= ������������2 ∗ ������������1
将充电和放电的电流代入,可以得到:
������������ ∗ ������������2 ������������ = ������������������������ ∗ ������������1 + ������������2 ∗ ������������ 我们尝试代入 T=50uS,D=10%,VIN=4.52V,R1=50K,R2=50K,得到 VOUT=0.411V,与仿真的 0.408V 相比,这个误差很小。
t1 t2 τ1 τ2 估算 VOUT 精确 VOUT 误差
单位 KΩ KΩ nF uS
uS uS uS uS
V
V
mV
4.52 50 50 100 50 10% 5 45 2500 5000
0.411
0.409 -1.847
4.52 50 50 100 50 20% 10 40 2500 5000
0.753
一个相对准确的结果,这样可以快速的判断设计的。
五、关于误差 注意观察,可以看到估算的结果是高于精确计算的结果的,实际的误差并没有这么大,这里通 过图示来说明一下。
图六 计算示意 估算时,VOUT 是取平均值;而精确计算时,VOUT 是取最小值。占空比 100%的时候,因为变 化量为 0,是直流,所以两者一样。但是不为零的时候,两者就会有充放电产生的纹波误差。 精确计算的结果如果加上∆V充/2,得到的结果与估算结果的误差就会变得很小。这里不再计算 了。另外,采用泰勒公式进行化简时,截断的尾数部分是可以用拉格朗日型余项进行估算的。 这些估算或者计算没有用到什么高深的知识,只是需要综合考虑一些细节。很多时候,你要忽 略一些细节的时候,要先确定一下,它对你的影响有多大,是否可以忽略。
τ
2.5mS
因为远小于 1,所以,才可以忽略 x 的高次项。
V充
=
VOUT
+
