联合载荷作用下高速角接触球轴承快速计算方法及接触角分析
高速角接触球轴承接触角计算与影响因素分析

触角为
sinAij =
d Rr dr
+
Rr r
RH+
X2 r Q=
0
( 1)
几何方程为
Er =
du dr
EH=
u r
( 2)
其应力- 应变方程为
Rr =
E 1-
M(
Er
+
MEH)
( 3)
RH=
E 1-
M(
EH+
MEr )
式中 Rr ) ) ) 径向正
X ) ) ) 轴承的角速度
u ) ) ) 径向位移分量 Q) ) ) 滚动体密度
的基础[ 1~ 5] 。 在角接触球轴承的工作过程中, 接触角受轴承
的安装、预 紧、转速、载荷 形式 等因 素的 影响[ 1, 6] 。 然而角接触球轴承高速旋转时离心力对接触角的影 响不容忽视, 一方面轴承内圈和轴在离心力作用下 产生的径向位移, 会引起轴承径向游隙的变化, 导致 接触角发生变化; 另一方面, 在离心力和陀螺力的作
ucr = u| r = d/ 2=
1 E
( 1-
M) C3
d 2
-
1
8
M2
QX2
d 2
3
( 10)
Rcr |
r=
d/ 2=
C3-
3+ 8
MQX2
d 2
3
= -P
( 11)
式中 C1、C 2、C3 为任意常数, 由边界条件确定。
轴和轴承内圈配合处的位移连续条件是[ 9]
$r = ucr +
$1 2
( 12)
由式( 5) 得轴承内圈内径的径向位移为
$r = u | r= d/2=
角接触轴承

角接触轴承角接触轴承是一种常见的轴承形式,被广泛应用于机械设备中。
它是一种可承受径向和推力荷载的轴承,具有较高的刚性和承载能力。
在角接触轴承的设计和使用中,需要考虑到多个因素,包括角接触角度、接触角接触面、负荷分布等。
本文将对角接触轴承的原理、设计、安装和维护等方面进行详细介绍。
首先,我们来了解一下角接触轴承的原理。
角接触轴承由内圈、外圈、钢球以及球保持器等部分组成。
内圈和外圈的接触面是以角度形式设计的,这个角度被称为角接触角。
角接触轴承能够同时承受径向和推力荷载,是因为在负荷作用下,内圈和外圈之间的接触角度会发生变化,从而改变轴承的接触点位置,使其能够承受推力荷载。
角接触轴承的设计过程需要考虑到多个因素。
首先是选择适当的角接触角度。
角接触角度的选择要根据实际应用情况来确定,一般常见的角接触角度有15度、25度和30度等。
较小的角接触角度可以提高轴承的刚性和承载能力,但也会增加摩擦和磨损。
较大的角接触角度可以减小轴承的刚性和承载能力,但摩擦和磨损较小。
其次是设计角接触轴承的接触面。
接触面的设计要考虑到轴承的刚性和承载能力。
接触面的设计形式有两种,一种是面对面设计,一种是背对背设计。
面对面设计可以提高轴承的刚性,适用于承受较大推力荷载的情况。
背对背设计可以提高轴承的承载能力,适用于承受较大径向荷载的情况。
角接触轴承在安装和维护过程中需要注意一些问题。
首先是在安装轴承时,要保证内圈和外圈之间的相对位置准确,避免因安装不当导致轴承失效。
其次是在使用过程中,要定期检查轴承的运行状态,及时发现并处理异常情况,以避免轴承损坏。
此外,在润滑方面,要根据实际工况选择适当的润滑方式和润滑剂,保证轴承的正常工作。
综上所述,角接触轴承是一种常见的轴承形式,具有较高的刚性和承载能力,能够同时承受径向和推力荷载。
在角接触轴承的设计、安装和维护过程中,需要考虑到多个因素,包括角接触角度、接触面设计、负荷分布等。
只有在合理的设计和科学的使用中,才能充分发挥角接触轴承的优势,提高设备的工作效率和可靠性。
联合外载荷作用下角接触球轴承内部载荷分布和变形的数值迭代计算

该方法 的正确性 。
关 键词 :角接触球轴承 ;联合外载荷 ;载荷 分布 ;变形 ;数值迭代 ;H r 接触 理论 ;接触角 et z
中图分类号 :T 1 3 H 2 文献标识码 :A 文章编号 :10 —38 【0 2 0 1 8 1 2 1 )3一 O 4 O l-
摘 要 :为了研究联合外载荷作用下球轴 承的 内部载荷分布 和变形特 性 ,提出一种基 于赫兹接 触理论 的数值迭代计算 方
法 。以角接 触球轴承为对象 ,考虑在预 紧力 、轴 向力 、径 向力等联合外载荷 工况条件 下 内外 圈滚道接触 角的变化 ,以及滚
珠 载荷 分布 、载荷大小随接触角 的变化 , 用滚道接触角与滚珠载荷之 间的关 系式 进行数值 迭代求解 ,来 寻找轴承受 载后 利 内部 的平衡 状态 。 通过 与典 型有限元分析结果 的比较 可以看出 :所提方 法不仅详 细计算 出了轴承 内部 的载荷情 况 ,而且更
联合外载荷作用下 角接触球轴承 内部载荷分布和变形的数值迭代计算
刘 显 军 ,洪 军 ,王 军。 ,刘 志 刚
( .中国工程 物理 研 究 院总体 工程研 究所 ,四 川绵 阳 6 10 ; 1 290 2 .西安 交通 大学机械 制 造 系统 工程 国 家重点 实验 室 ,陕 西西安 70 4 ) 109
Ab t a t I r e or s a c h tr a o d d sr u in a d d fr t n o al e r g u d rt e c n i o f o i e x s r c : n o d rt e e r h t e i e n l a i t b t n eo mai f l b ai n e o d t n o mb n d e - n l i o o b n h i c t r a o d,a n me c e aie c mp t t n me o a e n He t c na tt e r s r s n e .He e c n i e n s a o t c e n la l u r a i r t o ua i t d b s d o r o tc o y Wa p e e t d i l t v o h z h r o sd r g a u r c n a t i n l b l b a i g u d r t e c n i o r l a , rd a d a i o d,t e ma n t d n it b t n o o d o ol r lo g w t e ale rn n e h o d t n o p e o i f d a il a x a la n l h g i e a d d sr ui fl a r l ,a n i t u i o f e h h c a g f o tc ge o ol yb t n ie a d o ti e e e a ay e a d t eri tr c v ea in hp r s d t b an t ei — h n eo n a t c n a l frl wa 0l i sd u s ,w r l z d, I n d n n i n e a t e r lt s i swe u e o ti n h i o e o h tr a aa c tt f a ig . ̄ o s o aio t e I 协 o p c ii l me ta ay i .a c n l so s d a n t a y t i e n l l e sa e o r s b n e b n u h c mp rs n l r s l f y i a f t ee n n ss o c u i n i r w tb h s l l t l ne l h
角接触球轴承轴向力计算公式

角接触球轴承轴向力计算公式角接触球轴承是一种常用的滚动轴承,广泛应用于机械设备中。
在设计和使用角接触球轴承时,了解和计算轴向力是非常重要的。
轴向力是指作用在轴承轴向方向的力,它对轴承的运行和寿命有着直接的影响。
在本文中,我将介绍角接触球轴承轴向力的计算公式及其相关要点。
轴向力的计算公式是通过考虑轴承的负载、速度和角接触球轴承的特性来确定的。
以下是角接触球轴承轴向力的计算公式:Fa = (XFr + YFa) / (eP)其中,Fa是轴向力(单位为牛顿,N);X是轴承的动载荷系数;Fr是轴承的径向力(单位为牛顿,N);Y是轴承的静载荷系数;Fa是轴承的轴向力(单位为牛顿,N);e是轴承的接触角系数;P是轴承的当量动载荷(单位为牛顿,N)。
在计算轴向力时,需要明确轴承的负载(Fr)、速度和特性系数(X、Y、e、P)。
下面对这些要点进行详细的解释:1. 轴承的动载荷系数(X):动载荷系数(X)是考虑到轴承在动载荷作用下的变形和变位情况的。
X的取值范围通常为0.56-0.98,具体取值需要根据轴承的类型、尺寸和应用情况进行确定。
2. 轴承的静载荷系数(Y):静载荷系数(Y)是考虑到轴承在静载荷作用下的变形和变位情况的。
Y的取值范围通常为0.56-0.98,具体取值需要根据轴承的类型、尺寸和应用情况进行确定。
3. 轴承的接触角系数(e):接触角系数(e)是轴承接触角的函数,接触角是指球和滚道的接触角度。
e的取值范围通常为0.6-0.8,具体取值需要根据轴承的类型和设计要求进行确定。
4. 轴承的当量动载荷(P):当量动载荷(P)是指在轴承承受的径向力和轴向力同时作用下,所能承受的相当于纯径向载荷的动载荷。
P的计算公式通常为P = Fr + 1.2Fa,其中Fr为径向力,Fa为轴向力。
轴向力的计算公式的目的是为了确定角接触球轴承在实际工作中所承受的轴向力,以便进行轴承的选择和设计。
通过合理的计算和选择,可以保证轴承在工作过程中的可靠性和寿命。
角接触球轴承接触角的简易测量法

角接触球轴承接触角的简易测量法
范允英
【期刊名称】《轴承》
【年(卷),期】2009(000)003
【摘要】接触角的简易测量法是角接触球轴承生产过程中使用的一种测量方法.它是通过观测外圈转角来确定轴承的接触角.此法操作简便、成本低,很适合于生产车间使用.
【总页数】4页(P48-50,65)
【作者】范允英
【作者单位】湖州铧星轴承有限公司,浙江,湖州,313009
【正文语种】中文
【中图分类】TH133.33;TG806
【相关文献】
1.联合载荷作用下高速角接触球轴承快速计算方法及接触角分析 [J], 方斌;张进华;洪军;朱永生
2.角接触球轴承接触角的精确控制 [J], 王东峰;杨浩亮;张振强
3.基于虚拟仪器的角接触球轴承接触角测量仪 [J], 张中益; 方伟; 沈雪瑾; 顾家铭; 蒋武强
4.角接触球轴承接触角误差控制 [J], 孙东;方凯旋
5.X092型游隙检测仪在薄壁角接触球轴承接触角测量中的应用 [J], 张旭;焦叶凡;师歌;崔静伟;马磊
因版权原因,仅展示原文概要,查看原文内容请购买。
角接触球轴承计算方法
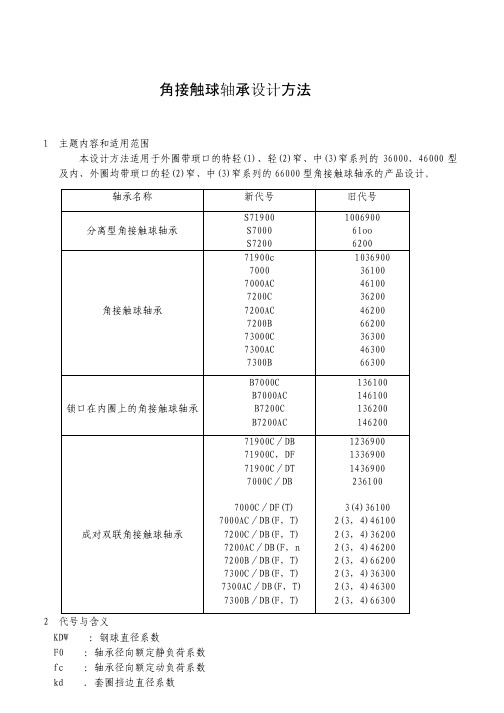
角接触球轴承设计方法1 主题内容和适用范围本设计方法适用于外圈带琐口的特轻(1)、轻(2)窄、中(3)窄系列的36000、46000型及内、外圈均带琐口的轻(2)窄、中(3)窄系列的66000型角接触球轴承的产品设计。
轴承名称 新代号 旧代号分离型角接触球轴承 S71900S7000S720010069006loo6200角接触球轴承 71900c70007000AC7200C7200AC7200B73000C7300AC7300B103690036l0046100362004620066200363004630066300锁口在内圈上的角接触球轴承B7000CB7000ACB7200CB7200AC136100146100136200146200成对双联角接触球轴承71900C/DB71900C,DF71900C/DT7000C/DB7000C/DF(T)7000AC/DB(F,T)7200C/DB(F,T)7200AC/DB(F,n7200B/DB(F,T)7300C/DB(F,T)7300AC/DB(F,T)7300B/DB(F,T)1236900133690014369002361003(4)361002(3,4)461002(3,4)362002(3,4)462002(3,4)662002(3,4)363002(3,4)463002(3,4)663002 代号与含义KDW :钢球直径系数F0 :轴承径向额定静负荷系数 fc :轴承径向额定动负荷系数 kd .套圈挡边直径系数kt、δt :装配锁口高度系数Kpi、kpe:内、外圈滚道直径系数εi、ε e:实体保持架内、外径引导间隙kc :实体保持架内、外径系数3 设计要点整篇文章把dn≥0.6×10^6的称为高速,dn≥1.8×10^6的称为超高速。
结构形式 优 点 缺 点 采用公司外圈单挡边、内圈双挡边.保持架外引导单挡边外圈有利于外圈沟道多余润滑剂流出,不仅减小润滑剂搅动摩擦.而且有利于降低接触SKF-7000FAG-B7000NSK-7000GMN-S6000外圈单挡边、内圈双挡边,保持架内引导 与上面相比,由于采刚内圈烈挡边引导保持架,运动平稳。
高速精密角接触球轴承刚度计算

高速精密角接触球轴承刚度计算洛阳轴承研究所(河南洛阳 471039) 杜迎辉洛阳工学院(河南洛阳 471039) 邱 明昆山恩斯克有限公司(江苏昆山 215335) 蒋兴奇浙江大学(浙江杭州 310027) 马家驹ABSTRACT On the base of analyzing forces and deformations of the bearing,the ne w method for calculating radial,axial and angle rigidities is put for ward in accordance with c ontact loads and contac tangles between balls and race ways of the spindle bearing.And the effect of speed,preload and race way curvatures of inner and outer race on bearing rigidity is analyzed and calculated. 滚动轴承中接触载荷和接触变形之间的关系是非线性的,因此,轴承刚度并非恒定。
但过去许多人对刚度特性的计算过于简化[1],一般都是把轴承简化成等效弹簧,忽略了刚度随载荷的非线性变化、角刚度以及刚度随旋转速度变化等。
即使考虑到上述因素,刚度计算误差也较大。
本文在计算两种预紧方式即定位预紧和定压预紧、球与内外圈沟道接触载荷和接触角的基础上,计算了每个球与内外圈沟道接触点的接触刚度,根据轴承内部变形的几何关系,提出了一种新的轴承径向刚度、轴向刚度和角刚度的计算方法,并通过实例计算分析了轴承旋转速度、预紧载荷和内外圈沟道曲率系数对刚度的影响。
所提出的机床主轴轴承刚度计算方法也适用于其他滚动轴承应用场合。
1 赫兹接触刚度由赫兹接触理论,两接触物体的接触载荷和接触变形之间的关系为[2]=F92RQkE21/3(1)式中两接触物体的接触变形F 第一类椭圆积分 第二类椭圆积分R 两接触物体接触点在主平面内的曲率和Q 两接触物体的接触载荷k 椭圆率参数,为接触椭圆长半轴与短半轴之比E两接触物体等效弹性模量求赫兹经典解,需要求解k 、F 、 和接触物体几何尺寸之间关系的超越方程或通过图表计算。
角接触球轴承轴向载荷计算方法

角接触球轴承(Angular Contact Ball Bearings )可同时承受径向负荷和轴向负荷。
能在较高的转速下工作。
接触角越大,轴向承载能力越高。
接触角为径 向平面内球和滚道的接触点连线与轴承轴线的垂直线间的角度。
高精度和高速轴承通常取15度接触角。
在轴向力作用下,接触角会增大。
角接触球轴承轴向载荷计算是怎样的?今天小编就来具体介绍一下吧。
(1)根据安装方式判明内部轴向力 FS1、FS2的方向;(2)判明轴向合力指向及轴可能移动的方向,分析哪端轴承被“压紧”,哪端轴承被“放松”;(3)“放松”端的轴向载荷等于自身的内部轴向力, “压紧”端的轴向载荷等于除去自身内部轴向力外其它轴向力的代数和。
滚动轴承的静强度计算:目的:防止在载荷作用下产生过大的塑性变形。
基本额定静载荷C0 :滚动轴承受载后,在承载区内受力最大的滚动体与滚道接触处的接触应力达到一定值时的静载荷。
当轴承同时承受径向力和轴向力时,需折算成当量静载荷P0,应满足000r 0a C S P X F Y F =+≤例1、已知:S1=1175 N,S2=3290 N,FA=1020 N求:Fa1、Fa2。
解:S2+FA = 3290+1020= 4310 >S1,轴承Ⅰ被“压紧”,轴承Ⅱ被“放松”例2:某轴系部件采用一对7208AC滚动轴承支承,如图。
R1=5000N,R2=8000N,FA=2000N,e=0.68,求Fa1、Fa2。
解:①由安装简图,轴承正装,S1 、S2 如图所示。
S1=0.68R1=0.68×5000=3400NS2=0.68R2=0.68×8000=5440N②求Fa1 , Fa2∵ S1+FA =3400+2000=5400N< S2=5440N∴轴承1被压紧轴承2被放松Fa1 =S2-FA =5440-2000=3440NFa2=S2=5440N例3 某工程机械传动中轴承配置形式如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
联 合 载 荷 作 用 下 高速 角 接 触 球 轴 承 快 速 计 算 方 法 及 接 触 角 分 析
方斌 ,张进华 ,洪 军 ,朱永 生
( 1 . 西 安 交 通 大学 机 械 制 造 系 统 工 程 国 家 重 点 实 验 室 ,7 1 0 0 4 9 ,西 安 ;
2 . 西 安 交 通 大 学 现 代 设 计 与转 子 轴 承 系 统 教 育 部 重 点 实 验 室 ,7 1 0 0 4 9 ,西 安 )
c h o s e n a s t h e i t e r a t i v e v a r i a b l e s ,a n d t h e p a r t i a l e q u i l i b r i u m e q u a t i o n s o f b a l l s a r e f u r t h e r d e d u c e d
Qu i c k Ca l c u l a t i o n Me t h o d a n d C o n t a c t An g l e A n a l y s i s f o r
Hi g h — S pe e d An g u l a r Co n t a c t Ba l l Be a r i ng u n d e r Co mb i ne d Lo a La r g e n u mb e r o f n o n l i n e a r e q u a t i o n s i n t h e e x i s t i n g b a l l b e a r i n g mo d e l s l e a d t O a l o we r
的求解效率 , 通过 施加适 当的力矩载荷 可消除 由于径 向载荷所 带来的接触 角分布 不均 匀的 负面影响。
关 键 词 : 角 接 触球 轴 承 ; 快速计 算 ; 接触角; 联 合 载 荷 中 图 分 类 号 :TH1 6 1 文 献 标 志 码 :A 文 章 编 号 :0 2 5 3 - 9 8 7 X( 2 0 1 7 ) 0 6 — 0 1 1 5 一 O 7
摘 要 :针 对 现有球 轴 承模 型的 所含 非线 性 方程 组 数 目较 多 、 模 型 计 算 效率 较低 的 问题 。在 J o n e s -
Ha r r i s 模 型的 基础 上 , 选 用 轴 承 内部 接 触 角 为 迭 代 变 量 , 并 对 轴 承 内部 局 部 平 衡 方 程 进 行 推 导 及
a nd s i mpl i f i e d, wh i c h f a c i l i t a t e s d e c r e a s i ng t he nu m be r of n o nl i n e a r e q ua t i o ns t o s i g ni f i c a n t l y r e du c e t he c ompu t i n g t a s k. Th e c o nt a c t a n gl e i s t a k e n a s t h e mo s t i mpo r t a n t d y na mi c p a r a me t e r
FANG Bi n , ZHANG J i n h u a , H ONG J u n , ZH U Yo n g s h e n g 。
( 1 .St a t e Ke y La bo r a t o r y f o r Ma n u f a c t u r i n g S y s t e ms En g i n e e r i n g,Xi ’ a n J i a o t o n g Un i v e r s i t y,Xi ’ a n 7 1 00 49 ,Ch i n a;2.Ke y La b o r a t o r y o f Ed u c a t i o n Mi n i s t r y f o r Mo d e r n De s i g n a n d Rot o r - Be a r i n g S y s t e m ,Xi ’ a n J i a o t o n g Un i v e r s i t y ,Xi ’ a n 7 1 0 0 4 9 ,Ch i n a )
化简, 有 效地 减 少 了轴 承模 型 中非 线性 方程组 的 个数 ( 减少了2 Z个非 线性 方程 , Z为 滚珠 个数 ) , 从 而大 幅减 少 了模 型 的计 算量 。此外 , 接 触 角作 为高速 角接 触球 轴承 最 为重要 的动 态参 数 , 在 上述 模 型的基 础上 , 分析 了多种 因素对轴承 内部接 触 角的影响规 律 。研 究结果表 明 , 改进后 的模 型具有更 高
第5 1 卷
第 6 期
西 安 交 通 大 学 学 报
J OURNAL OF XI ’ AN J I AOTONG UNI VERS I TY
Vo l _ 51 NO .6
2 0 1 7年 6月
J u n .2 0 1 7
D OI :1 0 . 7 6 5 2 / x j t u x b 2 0 1 7 0 6 0 1 9
c a l c u l a t i o n e f f i c i e n c y .F o l l o wi n g J o n e s — Ha r r i s mo d e l ,t h e c o n t a c t a n g e l s o f b a l l b e a r i n g a r e
