分式混合运算练习题(30题)
初二分式混合运算练习题

初二分式混合运算练习题混合运算是数学基础中的重要内容之一,它涉及到各种运算符号的组合和运用。
而分式是数学中常见的一种形式,也是混合运算中常常出现的类型。
在初二的学习中,我们需要掌握分式的基本概念和运算规则,并能灵活应用于混合运算中。
为了帮助同学们巩固这方面的知识,下面给出一些初二分式混合运算的练习题,希望能够帮助大家更好地理解和掌握。
1. 简化以下分式:a) $\frac{6x^2}{3x}$b) $\frac{8xy}{4y}$c) $\frac{15a^2}{5ab}$d) $\frac{12m^2}{4mn}$2. 将以下分式化简为整数或带分数:a) $\frac{9}{3}$b) $\frac{18}{6}$c) $\frac{15}{5}$d) $\frac{28}{7}$3. 计算以下混合运算:a) $2 + \frac{5}{2} \times 3$b) $4 \div \frac{1}{5} + 3$c) $(2 + \frac{1}{2}) \times 3$d) $6 \div (2 + \frac{1}{3})$4. 计算下列分式的和:a) $\frac{1}{4} + \frac{1}{8}$b) $\frac{5}{6} + \frac{1}{2}$c) $\frac{2}{3} + \frac{4}{9}$d) $\frac{3}{5} + \frac{2}{10}$5. 计算下列分式的积:a) $\frac{2}{3} \times \frac{4}{5}$b) $\frac{1}{6} \times \frac{6}{7}$c) $(\frac{1}{2})^2$d) $\frac{3}{4} \times (\frac{1}{2})^3$6. 计算下列混合运算:a) $2 \div \frac{1}{3} - 4$b) $\frac{4}{9} \times (\frac{3}{4} - \frac{1}{2})$c) $5 + \frac{2}{3} \div \frac{1}{6}$d) $\frac{12}{5} - \frac{2}{3} \times \frac{15}{4}$7. 用分数表示下列混合数:a) $3\frac{2}{5}$b) $7\frac{3}{4}$c) $5\frac{1}{3}$d) $1\frac{7}{8}$8. 按照指定的运算关系,计算下列混合运算:a) $3 \times (2 + 1)$b) $4 + (3 - 2)$c) $(7 + 4) \times 2$d) $(5 - 2) \times 6$以上就是一些初二分式混合运算的练习题,可以帮助大家巩固和提高分式和混合运算的能力。
分式混合运算练习题及答案

分式混合运算练习题及答案1. 小明需要将墙上的一段长方体装饰条剪成相等的三段,已知该长方体装饰条的长度为5/6米。
请问每段装饰条的长度是多少?解答:将装饰条剪成三段,每段长度为x。
根据题意,有以下等式:x + x + x = 5/63x = 5/6x = (5/6) ÷ 3x = 5/6 × 1/3x = 5/18答案:每段装饰条的长度为5/18米。
2. 小华将两个相同的大理石板用副伪币P贴在一起,已知每个大理石板的面积为3/5平方米。
请问贴在一起的两个大理石板的总面积是多少平方米?解答:将两个大理石板贴在一起,总面积为x。
根据题意,有以下等式:2 × (3/5) = x6/5 = x答案:贴在一起的两个大理石板的总面积为6/5平方米。
3. 假设一个圆形花坛的半径为2/3米,已知小明想在花坛中种上一圈半径为1/6米的小花。
请问小明一共需要准备多少米的小花?解答:花坛的半径为2/3米,小花的半径为1/6米。
需要计算一圈小花的周长,即2πr,其中r表示小花的半径。
周长= 2 × (π × 1/6)周长= π/3答案:小明一共需要准备π/3米的小花。
4. 小红前一天用2/5的时间完成了数学作业,剩下的时间用来做英语作业。
如果她共用了1小时做完这两门科目的作业,请问她用多长时间做完了英语作业?解答:小红前一天用2/5的时间完成了数学作业,剩下的时间用来做英语作业。
总时间为1小时。
假设小红用x小时完成了英语作业。
根据题意,有以下等式:2/5 + x = 1x = 1 - 2/5x = 3/5答案:小红用3/5小时完成了英语作业。
5. 小明将一条长绳剪成了3段,已知第一段长1/2米,第二段比第一段长1/3米,第三段比第二段长1/4米。
请问原始的长绳一共有多长?解答:将原始的长绳的长度设为x。
根据题意,有以下等式:x = 1/2 + (1/2 + 1/3) + (1/2 + 1/3 + 1/4)x = 1/2 + 3/6 + 4/12x = 6/12 + 6/12 + 4/12x = 16/12x = 4/3答案:原始的长绳一共有4/3米长。
六年级分式混合运算练习题

六年级分式混合运算练习题1. 小明买了3/4千克的苹果,他吃了1/8千克,还剩下多少千克?解答:首先,我们知道小明买了3/4千克的苹果,然后他吃了1/8千克。
我们可以使用分式减法来解决这个问题。
3/4 - 1/8 = ?求两个分式的最小公倍数作为分母,然后进行减法运算。
首先,找到两个分母2的最小公倍数,即2的一次方,也就是2本身。
接下来,我们需要将两个分数的分母都变为2。
3/4 = 6/8现在,我们可以进行减法运算:6/8 - 1/8 = 5/8小明剩下了5/8千克的苹果。
答案:小明剩下了5/8千克的苹果。
2. 小红有2/5千克的面粉,她想按照1/10千克的份量做饼干。
小红最多能做几份饼干?解答:小红有2/5千克的面粉,她想按照1/10千克的份量做饼干。
我们可以用分式除法来解决这个问题。
首先,我们需要将被除数和除数都转化为相同的分母,以便进行除法运算。
2/5 ÷ 1/10 = ?求两个分数的最小公倍数作为分母,然后进行除法运算。
首先,找到两个分母10的最小公倍数,即10本身。
接下来,我们需要将两个分数的分母都变为10。
2/5 = 4/10现在,我们可以进行除法运算:4/10 ÷ 1/10 = 4小红最多能做4份饼干。
答案:小红最多能做4份饼干。
3. 班级有32名学生,其中3/4的学生选择了足球作为课余活动,剩下的学生选择了篮球。
班级有多少名学生选择了篮球?解答:班级有32名学生,其中3/4的学生选择了足球作为课余活动。
我们可以用分式乘法和减法来解决这个问题。
首先,我们需要计算选择足球的学生人数:32 × 3/4 = ?将乘法转化为分数乘法:32/1 × 3/4 = ?计算分数乘法:(32 × 3)/(1 × 4) = 96/4 = 24选择足球的学生人数为24人。
接下来,我们可以计算选择篮球的学生人数:32 - 24 = ?班级有32名学生,减去选择足球的学生人数24人,剩下的学生选择了篮球。
四年级数学分式混合运算练习题

四年级数学分式混合运算练习题在数学学习中,分式混合运算是一个重要的知识点,它是将整数、分数以及四则运算相结合的运算方式。
通过练习分式混合运算题,可以提高我们的计算能力和解决问题的能力。
下面,我将为你提供一些适合四年级学生的分式混合运算练习题。
练习题一:1. 将3和1/4与2/3相加。
2. 将5/8减去1/4。
3. 将2和3/5乘以2/7。
4. 将4/9除以1/3。
5. 将1/2与2/3相加再减去3/4。
练习题二:1. 将2和1/3与3/4相加。
2. 将7/8减去3/5。
3. 将1和3/4乘以2/3。
4. 将2/5除以1/2。
5. 将3/4与2/3相加再减去1/2。
练习题三:1. 将3和2/5与1/2相加。
2. 将9/10减去2/5。
3. 将4和3/8乘以3/7。
4. 将3/7除以1/4。
5. 将2/3与3/4相加再减去1/5。
练习题四:1. 将2和3/4与1/3相加。
2. 将3/5减去1/4。
3. 将3和1/2乘以4/7。
4. 将5/6除以2/3。
5. 将1/2与5/6相加再减去2/3。
练习题五:1. 将4和1/3与2/5相加。
2. 将7/8减去2/5。
3. 将2和1/2乘以3/4。
4. 将3/7除以1/3。
5. 将2/3与1/2相加再减去1/4。
以上是一些适合四年级学生的数学分式混合运算练习题。
希望通过这些练习题,能够让你更好地掌握分式混合运算的方法和技巧。
同时也希望你能够在解题过程中注意计算的准确性和步骤的清晰性。
加油!。
分式混合运算专题目练习(经典集合)

合用标准文案分式的乘除乘方运算一、基础知识点:1.约分把一个分式的分子与分母的公因式约去,叫做约分.约分的依照是分式的根本性质 .假设分式的分子、分母是多项式,必定先把分子、分母分解因式,尔后才能约去公因式.分子与分母没有公因式的分式,叫做最简分式,又叫做既约分式.分式的运算结果必然要化为最简分式.2.分式的乘法乘法法测:a·c=ac.b d bd3.分式的除法除法法那么:a÷c=a · d = adb d bc bc4.分式的乘方求 n 个相同分式的积的运算就是分式的乘方,用式子表示就是a n () . b分式的乘方,是把分子、分母各自乘方.用式子表示为:(a n a n) =n (n 为正整数 ) b b二、典型例题例 1、以下分式15bc,3( a b) 2 a 2 b 2a2b2). 12a b,2(a,a中最简分式的个数是 (a b)b例 2. 计算:(1)4xy(2)a212a(3)3xy 26y2 3y 2x3 a 2a2x(4)a 2a 1 a 21例3、假设x y zxy yz zx的值 . 4a 4 a24 2 34,求x 2y 2z2例 4、计算〔 1〕〔2a2b 3x2)2(y23(y4 c3〕〔2〕())y x x〔 3〕( 2a2bc)3(3a3b2x 2y 2)2( x2xy)3(xy2 )〔4〕()例5计算:11248x 1 x 1 x2 1 x4 1 x81112x 4 x38x7练习: 1.计算:2x 2 a 4x 4a8x8a x a x a例 6.计算:11111324351719182011111练习 1、x 2 x 3x 3 x 4x 100 x 101 x 1 x 2例 7、2x 1A B( x 1)( x 2)x 1x 2,求 A. B 的值。
针对性练习: 1. 计算以下各题 :〔 1〕x 3yx 2 y 2x 3 y〔2〕 a23a11. x2y 2x 2y2y 2x2 a 2 1a1(3)16(4)x2- x- 1(5)a-a6+3 ,a 3 9 a2x 1 a 3 a23a a(6)2xy x y2b2⑻313 2⑺ a b211x 2 y 2 ⑽x 2x 1〕 ( a aa 24⑼xy2-2 〔 11).x y x yx 2x x 4 x 4a 2 a 2a2. x 为整数,且2 22 x 18为整数,求所有的吻合条件的 x 的值的和.x 3 3 x x 293、混杂运算:⑴ (2x 3 x 293x x 2x a 1a11)⑵x 2 x 2x 24⑶a 2 2a 1axxa 1⑷ ( a 25a 2 1)a 24 ⑸x 2 2x 1(1 x 3)a 2a 24a 4x 2 1x 1⑹x3 (x 2 5 ) ⑺1 1 x 1x 2x 2x 1 x 2 1 x 2 2x 1x 2 4x 4 x 22x 11⑼xy 1 1⑻24x 2x 2 y 2x y x yxx⑽ (a 2b 2a 2b 2x x 3 x 2 2x 1+2) ÷⑾x 21x 3ab a bx 1⑿ ( x2 x 1 ) x 2 16(13)、 (x 2)2 ( y 2 )3 ( y ) 4 x 22x x 2 4x 4 x 24xy x x〔 14 〕、3 m(m 25 ) 〔 15〕、2x 6 ( x 3)x 2x 6 2m 4m 24 4x x 23 x1 a 1b 2213b 2 c〔 16〕、22b 3〔 17〕、2x 2 18 3 x2a4 4xx22 x4. 算:( x 2x 1)4 x,并求当 x3 原式的 .x 2 2x x 2 4x 4 x5、先化 ,3xxx 21再取一个你喜 的数代入求 :x 1 x 1 xx 22x 1÷x 1 6、有 一道 : “ 算21x 2 x x-x 的 ,其中 x=2 004 〞甲同学把“ x=2 004 〞 抄成“ x=2 040 〞,但他的 算 果也正确,你 是怎么回事?11+117、 算、++⋯+。
分式混合运算专题练习(经典集合)
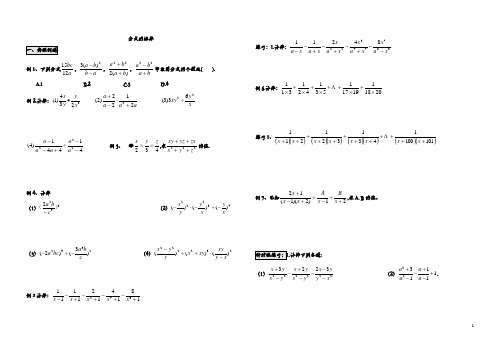
分式的运算一、典型例题例1、下列分式a bc 1215,a b b a --2)(3,)(222b a b a ++,b a b a +-22中最简分式的个数是( ).A.1B.2C.3D.4例2.计算:3234)1(x y y x ∙ a a a a 2122)2(2+⋅-+ x y xy 2263)3(÷41441)4(222--÷+--a a a a a 例3、 若432z y x ==,求222zy x zxyz xy ++++的值.例4、计算(1)3322)(c b a - (2)43222)()()(xy x y y x -÷-⋅-(3)2332)3()2(c b a bc a -÷- (4)232222)()()(xy xy xy x y y x -⋅+÷-例5计算:1814121111842+-+-+-+--x x x x x练习:1.计算:8874432284211x a x x a x x a x x a x a --+-+-+--例6.计算:2018119171531421311⨯+⨯++⨯+⨯+⨯练习1、()()()()()()()()1011001431321211++++++++++++x x x x x x x x例7、已知21)2)(1(12++-=+-+x Bx A x x x ,求A. B 的值。
针对性练习:1.计算下列各题:(1)2222223223xy yx y x y x y x y x ----+--+ (2)1111322+-+--+a a a a .(3)29631a a --+ (4) 21x x --x -1 (5)3a a --263a a a +-+3a ,(6)xy yy x x y x xy --++-222 ⑺b a b b a ++-22 ⑻293261623x x x -+--+⑼xy y x y x y x 2211-⋅⎪⎪⎭⎫ ⎝⎛+-- ⑽ 222x x x +--2144x x x --+(11)a a a a a a 4)22(2-⋅+--.2.已知x 为整数,且918232322-++-++x x x x 为整数,求所有的符合条件的x 的值的和.3、混合运算:⑴2239(1)x x x x ---÷ ⑵232224xx x x x x ⎛⎫-÷ ⎪+--⎝⎭⑶ a a a a a a 112112÷+---+⑷ 444)1225(222++-÷+++-a a a a a a ⑸ )1x 3x 1(1x 1x 2x 22+-+÷-+-⑹ )252(23--+÷--x x x x ⑺ 221111121x x x x x +-÷+--+⑻2224421142x x x x x x x -+-÷-+-+ ⑼2211xy x y x y x y ⎛⎫÷- ⎪--+⎝⎭⑽ (ab b a 22++2)÷ba b a --22 ⑾22321113x x x x x x x +++-⨯--+⑿ x x x x x x x x x 416)44122(2222+-÷+----+ (13)、22234()()()x y y y x x-⋅-÷-(14)、)252(423--+÷--m m m m (15)、x x x x xx x --+⋅+÷+--36)3(446222(16)、 ()3212221221------⎪⎭⎫ ⎝⎛ba cb b a (17)、⎪⎭⎫ ⎝⎛---÷⎪⎪⎭⎫ ⎝⎛+--x x x x x 23441823224.计算:x xx x x x x x -÷+----+4)44122(22,并求当3-=x 时原式的值.5、先化简,x x x x x x11132-⋅⎪⎭⎫ ⎝⎛+--再取一个你喜欢的数代入求值:6、有这样一道题:“计算22211x x x -+-÷21x x x -+-x 的值,其中x=2 004”甲同学把“x=2 004”错抄成“x=2 040”,但他的计算结果也正确,你说这是怎么回事?7、计算、)1(1+a a +)2)(1(1++a a +)3)(2(1++a a +…+)2006)(2005(1++a a 。
最新分式混合运算练习题(中考题汇编)

精品文档
精品文档
分式练习题
1.计算:
(1) (2)
2. 3..
4. 5. .
6. •(x2﹣9) 7. .
8. +. 9. ;
精品文档
精品文档
10. . 11.
12. ﹣a﹣1.
13.(1) (2)
14. a﹣2+ 15. .
16.化简:,并指出x的取值范围.
精品文档
精品文档
17.已知ab=1,试求分式:的值. 18.计算:﹣
19.计算: 20.
21. . 22.
23. . 24.
精品文档
精品文档
25. . 26.
27. 28. )÷.
29. . 30. ﹣x﹣2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.解答题1 .计算:(1) 分式精华练习题
(2) (﹣2m2n ﹣2 ) 2 • (3m ﹣1n3 ) ﹣3
15.计算:.
16.化简:,并指出x 的取值范围.
17. 17.已知 ab=1,试求分式:的值. 18.计算:﹣
2.计算: 3.化简:.19 .计算:20.化简4.化简: 5.计算:.21 .计算:
6.化简• (x2 ﹣ 9)7.计算:.22 .化简:
8 .计算:(2) 11.计算:
13 .计算:(1) + .9.计算: (1)
10.
12 .计算:
(2)
;23.计算: (1)
24 .化简:
.
25 .化简:
﹣a﹣1.
27 .计算:
; (2) .
. 26 化简:
28.计算:( ) ÷ .
29.化简. 30.计算:﹣ x ﹣ 2)
1
14.计算: a ﹣ 2+
.
2
1.在下列方程中,关于 x 的分式方程的个数(a 为常数)有( )
① 1 x 2 一 2 x + 4 = 0 ② . x = 4 ③ . a = 4; ④ .
x 2 一 9 = 1; ⑤ 1
= 6; 2 3 a x x + 3 x + 2
x 一 1 x 一 1
2. 关于 x 的分式方程 = 1,下列说法正确的是( ) x 一 5
A .方程的解是 x = m + 5
B . m > 一5 时,方程的解是正数
C . m
一5 时,方程的解为负数 D .无法确定
1 5 3
3.方程 + = 的根是( )
1 一 x
2 x + 1 1 一 x
3
A. x =1
B. x =-1
C. x =
D. x =2
8
4 4 2
4.1 一 + = 0, 那么 的值是( ) A.2 B.1 C.-2 D.-1 x x 2 x
5.下列分式方程去分母后所得结果正确的是( )
A.
1 = x + 2
一 1 去分母得, x +1 = (x 一 1)(x + 2) 一 1; x 一 1 x +1
x 5
6. .赵强同学借了一本书,共 280 页,要在两周借期内读完 .当他读了一半书时,发现平均每天要多 读 21 页才能在借期内读完 .他读前一半时,平均每天读多少页?如果设读前一半时,平均每天读 x
页,则下面所列方程中,正确的是 ( )
140 140 280 280 140 140 10 10
A. + =14
B. + =14
C. + =14
D. + =1
x x 一 21 x x + 21 x x + 21 x x + 21
7.若关于 x 的方程 一 = 0 ,有增根,则 m 的值是( )
8.若方程 + = 那么 A 、B 的值为( )
A.2, 1
B.1, 2
C.1, 1
D.-1, - 1
9.如果x = 士 1, b 士 0, 那么
= ( ) b a + b
1 x 一 1 1 1
A. 1-
B. C . x 一 D. x 一
x x + 1 x x + 1
10.使分式
4
x 2一4
与
+
的值相等的 x 等于( )
A.-4
B.-3
C.1
D.10
二、填空题(每小题 3 分,共 30 分)
11. 满足方程 1 = 2 的 x 的值是___ 12. 当 x=____ 时, 分式
1 + x
的值等于
1
x 一 1 x 一 2 5 + x 2 .
13.分式方程
x 2 一 2x
x 一2
= 0 的增根是.
14. 一汽车从甲地开往乙地,每小时行驶 v 1 千米, t 小时可到达,如果每小时多行驶 v 2 千米, 那么 可提前到达________小时.
15. 农机厂职工到距工厂 15 千米的某地检修农机,一部分人骑自行车先走 40 分钟后,其余人乘汽 车出发,结果他们同时到达,已知汽车速度为自行车速度的 3 倍,若设自行车的速度为 x 千米/时, 则所列方程为 .
16.已知
= , 则 =
.
y 5 x 2
一 y
2
17. a =
时, 关于 x 的方程
=
的解为零.
x 一 2 a + 5
18.飞机从 A 飞到 B 的路程 S ’、速度是v 1, ,返回的速度是 v 2 ,往返一次的平均速度是 .
19.当m =
时,关于 x 的方程
m
x 2一9
+
=
1x 一3
有增根.
20. 某市在旧城改造过程中, 需要整修一段全长 2400m 的道路. 为了尽量减少施工对城市交通所造 成的影响,实际工作效率比原计划提高了 20%,结果提前 8 小时完成任务.求原计划每小时修路 的长度.若设原计划每小时修路 x m ,则根据题意可得方程. 三、解答题(共 5 大题, 共 60 分) 21. .解下列方程 (1)
1
x 一3
+ 2 = 4 一 x
3一x
(2)
4
x 2一4
+ = (3) x
x 一2
一 1 = 1x 2一4
.
22. 有一项工程,若甲队单独做,恰好在规定日期完成,若乙队单独做要超过规定日期 3 天完成; 现在先由甲、乙两队合做 2 天后,剩下的工程再由乙队单独做,也刚好在规定日期完成,问规定日 期多少天?
24.小兰的妈妈在供销大厦用 12.50 元买了若干瓶酸奶, 但她在百货商场食品自选室内发现, 同样的 酸奶,这里要比供销大厦每瓶便宜 0.2 元钱,因此,当第二次买酸奶时,便到百货商场去买,结果 3
用去 18.40 元钱,买的瓶数比第一次买的瓶数多 倍,问她第一次在供销大厦买了几瓶酸奶?
5
B. + = 1 ,去分母得, x + 5 = 2x 一 5; 2x 一 5 5 一 2x
C. x 一 2 一 x + 2 = x
,去分母得, (x 一 2)2 一 x + 2 = x(x + 2); x + 2 x 2 一 4 x 一 2 D. 2 = 1
, 去分母得, 2 (x 一 1) = x + 3; x + 3 x 一 1
m 一 1 x
x 一 1 x 一 1 A.3 B.2 C.1 D.-1
A B 2x +1
x 一 3 x + 4 (x 一 3)(x + 4) , ⑥ + = 2 . A.2 个 B.3 个 C.4 个 D.5 个
a a
m
x 4 x 2 + y 2 a a 一 b x + 1 2a 一 3。
