数学强化班(武忠祥)-高数第五章二重积分
2010海天冲刺班讲义-武忠祥-

.co
αxα 8 = 则α = 1 + x tan x − cos x 3
.
m
考研休闲屋社区 友情提供:更多精品,尽请关注!
解 由
lim
x →0
1 0
f ( x) = A 知 lim f ( x ) = 0 知 x →0 x
x
0
lim ∫
x →0
∫ f ( xt )dt xt = u lim
x →0
f (u )du x
= lim f ( x) = 0
x →0
则原极限为“ 1∞ ”型. 又
lim
x →0
∫
1 0
f (tx)dt
sin x
x
= lim
x →0
∫
x
0
f (t )dt
= lim
x→0
∫
x
0
f (t )dt x
2
x sin x
=e .
A 2
= lim
x →0
f ( x) A = . 2x 2
考研休闲屋社区 友情提供:更多精品,尽请关注!
2010 年考研冲刺班讲义(高等数学) 主讲:武忠祥
一、函数、极限、连续 例 1 设有数列 xn 与 yn ,以下结论正确的是 (A)若 lim xn yn = 0 ,则必有 lim xn = 0 或 lim yn = 0 ;
f (0 + 0) = 0.
1 1 + a2 = (1 + a ) lim 1 = (1 + a ) lim =− 1 x →1 x →1 e 1 x x e −e − 2e x
2
lim f ( x) = lim
x →1 x →1
大一高数第五章知识点笔记

大一高数第五章知识点笔记在大一高数课程中,第五章是一个非常重要且充满挑战的章节。
本章主要讲解了一元函数的微分学和积分学,涵盖了导数和积分的基本概念、性质和应用。
在这篇文章中,我将为大家总结并梳理第五章的知识点,希望能够帮助大家更好地理解和掌握这一章节的内容。
一、导数的定义和性质导数是微分学的基本概念之一,它描述了函数在某一点的变化率。
在第五章中,我们学习了导数的定义和性质,并学会了如何计算函数的导数。
导数的定义如下:设函数$f(x)$在点$x_0$的某一邻域内有定义,当极限$$\lim_{{\Delta x}\to{0}}\frac{{f(x_0+\Delta x)-f(x_0)}}{{\Delta x}}$$存在时,称此极限为函数$f(x)$在点$x_0$处的导数,记作$f'(x_0)$。
导数具有以下性质:1. 可加性:$(f+g)'(x)=f'(x)+g'(x)$2. 可乘性:$(cf)'(x)=cf'(x)$,其中c为常数3. 乘法法则:$(fg)'(x)=f'(x)g(x)+f(x)g'(x)$4. 商法法则:$\left(\frac{f}{g}\right)'(x)=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}$ (其中$g(x)\neq0$)二、常用函数的导数公式在计算具体函数的导数时,我们需要掌握一些常用函数的导数公式。
以下是一些常见函数的导数:1. 常数函数:$f(x)=C$,导数为$f'(x)=0$,其中C为常数。
2. 幂函数:$f(x)=x^n$,导数为$f'(x)=nx^{n-1}$,其中n为正整数。
3. 指数函数:$f(x)=e^x$,导数为$f'(x)=e^x$。
4. 对数函数:$f(x)=\log_a{x}$,导数为$f'(x)=\frac{1}{x\ln{a}}$,其中$a>0$,且$a\neq1$。
高等数学第5章知识点总结

高等数学第5章知识点总结第5章二重积分(一)概念1. 二重积分的概念设二元函数f(x,y)在闭区域D上有界,把闭区域D分成n个小区域,记作ΔDi ,ΔSi为第i 个小区域的面积,ξi (i=1,2,3,…,n) 取在Di上的任一点,则二重积分的极限∬f(x,y)dA=lim n->∞ Σf(ξi)ΔSi(i=1,2,3,…,n)当这极限存在时,称其为在D上的二重积分,记作∬f(x,y)dA2. 二重积分的几何意义二重积分∬f(x,y)dA 表示把函数f(x,y)在闭区域D上的值与ΔS之积相加,其中ΔS是D上的微小面积。
即表示在闭区域D上f(x,y)在ΔS上的平均值与ΔS的面积之积的和。
3. 二重积分的计算法(1)累次积分法先对y积分,再对x积分。
(2)二次积分法先对x,y积分都在一起进行。
(3)极坐标法根据二重积分的边界条件,将直角坐标系转换为极坐标系。
(二)性质1. 线性性质若函数f(x,y)和g(x,y)在区域D上有界,则∬[f(x,y)+g(x,y)]dA = ∬f(x,y)dA + ∬g(x,y)dA2. 积分域的可加性若函数f(x,y)在区域D1和区域D2上有界,则∬f(x,y)dA = ∬f(x,y)dA1 + ∬f(x,y)dA23. 面积性质若函数f(x,y)在区域D上恒为1,则∬f(x,y)dA = S(D)(三)二重积分的应用1. 计算面积当f(x,y)=1时,二重积分∬1dA表示在闭区域D上的面积。
2. 计算质量、重心、转动惯量在力学中,可以利用二重积分计算平面薄片的质量、重心和转动惯量。
3. 计算电荷、电场在电磁学中,可以利用二重积分来计算平面薄片上的电荷、电荷分布和电场分布。
(四)二重积分的换元法1. 极坐标换元2. 线性换元3. 一般换元注:该知识点总结仅包括了高等数学第5章的基本内容,如需更多详细知识,请查阅相关资料。
大学高等数学第五章 定积分及其应用答案
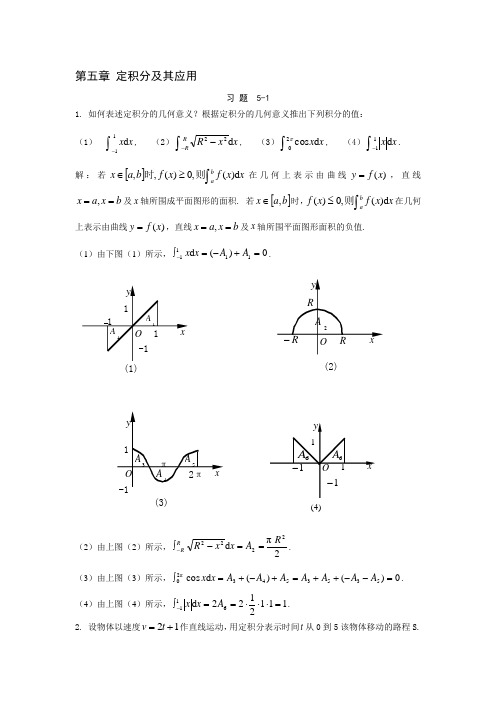
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义?根据定积分的几何意义推出下列积分的值: (1)⎰-x x d 11, (2)⎰--x x R R R d 22, (3)⎰x x d cos 02π, (4)⎰-x x d 11.解:若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时,⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围平面图形面积的负值. (1)由下图(1)所示,0)(d 1111=+-=⎰-A A x x .(2)由上图(2)所示,2πd 2222R A x x R R R==-⎰-.(3)由上图(3)所示,0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . (4)由上图(4)所示,1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动,用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解:=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解:任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =,小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式:∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解:上在]1,0[)(2x x f =连续函数,故可积,因此为方便计算,我们可以对[]0,1 n 等分,分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点,故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ(即时∞→n ),由定积分的定义得: 120d x x ⎰=31.5. 利用定积分的估值公式,估计定积分⎰-+-1134)524(x x x d 的值.解:先求524)(34+-=x x x f 在[]1,1-上的最值,由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小,知min max 5093,111024f f ==,由定积分的估值公式,得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ,哪个积分值较大?解:在[]0,1区间内:22xx x x e e ≥⇒≥ 由性质定理知道:⎰1d xe x≥⎰1d 2x e x7. 证明:⎰---<<2121212d 22x e ex 。
重积分运算的常用解法

重积分运算的常⽤解法积分运算的常⽤⽅法Warren K引⾔:本学期课程的⼀⼤重点在于重积分的运算、利⽤重积分解决实际问题的微元法以及线⾯积分及其应⽤。
这⾥根据⾃⼰学习的⼀些⼼得以及课本和参考书籍上的知识,归纳总结⼀些积分运算的常⽤⽅法。
⼀、⼆重积分(1)、化为累次积分公式==bax y x y dcy x y x s dxdy y x f dxdy y x f ds y x f )(2)(1)(2)(1)(),(),(),(例1:计算??)(s xyds ,其中S 为抛物线x y =2与直线2-=x y 所围成的区域.解将S 视为y 型区域,先对x 后对y 积分,得855])2[(5.02142212)(2=-+==--+dy y y y xydx dyxyds y s y 如果⽤直线把此区域(S )分成两部分,那么(S )可以看作是两个x 型区域的并。
先对y 后对x 积分得--+=412)(xx x xs xydy dx xydy dx xyds由上式可以得出同样的结果,但这种⽅法显然要⿇烦⼀些。
从这也可以看到,计算⼆重积分时,选取适当的积分顺序是⼀个值得注意的问题。
如果积分顺序选择不当,不仅可能引起计算上的⿇烦,⽽且可能导致积分⽆法算出。
(2)、化为极坐标若积分域(S )与被积函数f(x,y)⽤极坐标表⽰更为简便,则应考虑将其化为极坐标的⼆重积分来计算。
为此,建⽴极坐标系,令极点与xOy 直⾓坐标系的原点重合,x 轴取为极轴。
利⽤直⾓坐标与极坐标的转换公式),20,0(sin ,cos π?ρ?ρ?ρ≤≤+∞≤≤==y x将(S )的边界曲线化为极坐标,并把被积函数变换为).sin ,cos (),(?ρ?ρf y x f =接下来就是把⾯积微元由极坐标表⽰出来,.?ρρ??≈?s从⽽==βα?ρ?ρρρ?ρ?ρ??ρρ?ρ?ρ)()(21)sin ,cos (.)sin ,cos (),(d f d d d f ds y x f ss=??ba d f d )()(21)sin ,cos (ρ?ρ??ρ?ρ?ρρ例2:)0()(41022222>+-=??-+--a dy y x a dx I ax a a x解:将原积分化为极坐标下的累次积分计算.a d a d I a 224sin 2022-=-=??--πρρρθπθ(3)、曲线坐标下⼆重积分的计算法 1.正则变换⼆重积分??)(),(s ds y x f作变换.)(),()(),(),,(),,(22R s v u R s y x y x v v y x u u ?'∈?∈==若以下三个条件满⾜,则称上变换为⼀正则变换. a 、函数));((,)1(σC v u ∈b 、Jacobi ⾏列式);(),(,0),(),(σ∈?≠=??y x v u v u y x v u yyx x c 、此变换将域)(σ⼀⼀对应地映射为).(σ'2.x0y 坐标系下的⼆重积分与uOv 坐标系下⼆重积分之间的关系为σσσσ'??='d v u y x v u y v u x f d y x f ),(),()],(),,([),()( 例3:求-=σσd x y I )(,其中)(σ是由直线53,973,3,1+-=+-y x y x y x y 所围成的区域。
【精品推荐】2021考研高数二重积分计算

二重积分的计算
主讲 武忠祥 教授
一、利用直角坐标计算二重积分
(1) X 型区域:
称为累次积分,或称二次积分
(2) Y 型区域:
例1 计算
其中
直线
,及抛
例3 计算 区域.
,其中 是由
围成的
例4 计算
,其中
所围成的区域.
为直线
二、利用极坐标计算二重积分
例5 计算
其中 为不等式 所确定的区域.
例6 计算 轴所围成的区域.
其中 是由曲线
例7 计算
,其中 为圆域
内容小结
1.利用直角坐标计算 1)先 后 2)先 后
2.利用极坐标计算 1)先 后
【注】适合用极坐标计算的二重积分的特征 (1)适合用极坐标计算的被积函数:
(2)适合用极坐标的积分域: 如
作业
P156 1 (2), (4); 2 (3), (4); 5; 6 (2), (4); 11(2), (4); 13 (3), (4); 14 (2), (3); 15 (1), (4);
第五章 积分 5-2 原函数与微积分基本定理

如果 F (x) 是 f (x) 在区间 I 上的一个原函数, 则不定积分 积分变量
积分号 f (x) d x F (x) C
积分常数
被积函数 被积表达式 f (x) 的一个原函数
《高等数学》课件 (第五章第二节)
例 5 求 x d x ( 1).
解 由 1 x 1 是 x 的一个原函数,
《高等数学》课件 (第五章第二节)
若 F (x) 是 f (x) 在 I 上的一个原函数, 则对任意常数 C, F (x) + C 也是 f (x) 在 I 上的一个原函数.
若 G (x) 是 f (x) 在 I 上的另一原函数, 则在 I 上 (F (x) G (x))' 0,
从而 G (x) F (x) C (C 为常数), 即 f (x) 在 I 上的任何一个原函 数都可以表示成 F (x) C 的形式.
y =F (x) + C
x
《高等数学》课件 (第五章第二节)
性质 1 若 f (x) 在区间 I 上存在原函数, 则
( f ( x) d x) f ( x)
或
d ( f (x) d x) f (x) d x.
性质 2 若 f (x) 的导函数在区间 I 上可积, 则
f ( x) d x f ( x) C
得到积分中值定理.
又当积分中值定理成立时, 存在 [a, b] 使得
b
F (b) F (a) a f ( x) d x
f ( ) (b a) F ( ) (b a).
得到微分中值定理.
《高等数学》课件 (第五章第二节)
例 cos x 是 sin x 的一个原函数, 所以
0 sin x d x cos cos 0 2.
高等数学第五章课后习题答案

班级姓名学号1 第五章定积分1.证明定积分性质:òò=b abadxx f kdx x kf )()((k 是常数). 证:òåòå=D =D ==®=®banii ban ii x kf x kf x f k x f k)()(lim )(lim )(1010x x l l 2.估计下列积分值:(1)dxx )sin 1(4542ò+p p解:令x x f 2sin 1)(+=,则02sin cos sin 2)(===x x x x f ‘得驻点:,,221p p==x x 由23)4(,23)4(,1)(,2)2(====p p p pf f f f ,得2)(max ,1)(min ==x f x f 由性质,得pp p p2)(454££òdx x f (2)ò333arctan xdxx 解:令x x x f arctan )(=,01arctan )(2>++=xxx x f ‘,所以)(x f 在]333[,上单调增加,p p33)(max ,36)(min ==\x f x f ,)()(33333arctan 33336333-££-\òp pxdx x ,即pp32a r c t a n 9333££òx d x x班级班级 姓名姓名 学号学号3.比较下列积分值的大小:.比较下列积分值的大小: (1)dx x ò12与dxx ò13解:当10££x 时,有23x x £,且23x x -不恒等于0,0312>-\òdx x x )(,即,即 dxx dxx òò>1212。
(2)ò6pxdx 与ò6sin pxdx解:当60p££x 时,有x x £sin ,且x x sin -不恒等于0,0sin 10>-\òdx x x )(,即,即 dx x dx x òò>1010sin 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 二 重 积 分1.定义:∑⎰⎰=→∆=nk k k k Df y x f 10d ),(lim d ),(σηξσ2.几何意义:3.性质:1) 比较定理: 若),(),(y x g y x f ≤,则⎰⎰⎰⎰≤DDy x g y x f .d ),(d ),(σσ2) 估值定理: 若),(y x f 在D 上连续,则.d ),(MS y x f mS D⎰⎰≤≤σ3) 中值定理: 若),(y x f 在D 上连续,则S f y x f D),(d ),(ηξσ⎰⎰=.4.计算1) 直角坐标: 2) 极坐标:i) 适合用极坐标计算的被积函数:);(),(),(22yxf x y f y x f +ii)适合用极坐标的积分域:3) 利用奇偶性.①若积分域D 关于y 轴对称,则:⎰⎰⎰⎰⎪⎩⎪⎨⎧=≥DD x x y x f y x f y x f d y x f x .),(0.),(d ),(2),(0为奇函数关于为偶函数关于σσ②若积分域关于x 轴对称,则⎰⎰⎰⎰⎪⎩⎪⎨⎧=≥DD y y y x f y x f y x f d y x f y .),(0.),(d ),(2),(0为奇函数关于为偶函数关于σσ4) 利用对称性:若D 关于x y =对称,则`.d ),(d ),(⎰⎰⎰⎰=DDx y f y x f σσ特别的: ⎰⎰⎰⎰=DDd y f d x f σσ)()(题型一 计算二重积分例5.1计算⎰⎰+Dx ye x σd )|(|2,其中D 由曲线1||||=+y x 所围成.解 由奇偶性知原式=⎰⎰⎰⎰=14D Dxd d x σσ (其中1D 为D 在第一象限的部分).3241010==⎰⎰-x xdy dx例5.2设区域D 为222R y x ≤+,则⎰⎰+D b y a x σd )(2222=.解法1)11(4)sin cos ()(224320022222222b a R d b a d d b y a x R D+=+=+⎰⎰⎰⎰πρρθθθσπ. 解法2 由于积分域222:R y x D ≤+关于直线x y =对称,则σσd b x ay d b y a x D D ⎰⎰⎰⎰+=+)()(22222222. 从而有 21)(2222=+⎰⎰σd b y ax D [左端 + 右端] σd y x b a D ⎰⎰++=)()11(212222)11(4)11(21222004322ba R d db a R +=+=⎰⎰ππρρθ 例 5.3设区域{}0,0,4|),(22≥≥≤+y x y x y x D ,)(x f 为D 上正值连续函数,b a ,为常数,则⎰⎰=++Dy f x f y f b x f a σd )()()()(.A)πab , B)π2ab , C)π)(b a +, D)π2b a +. 解法1直接法 由于积分域D 关于直线x y =对称,则⎰⎰⎰⎰++=++DDd x f y f x f b y f a d y f x f y f b x f a σσ)()()()()()()()(.原式])()()()()()()()([21⎰⎰⎰⎰+++++=D Dd x f y f x f b y f a d y f y f y f b x f a σσ πσ2)(21ba db a D+=+=⎰⎰.故应选(D ). 解法2 排除法取,1)(≡x f 显然符合题设条件,而⎰⎰++Dy f x f y f b x f a σd )()()()(πσ2)(21ba db a D+=+=⎰⎰. 显然(A ),(B ),(C )均不正确,故应选(D )。
例 5.4 计算⎰⎰++Dy x yf x σd )](1[22,其中D 是由1,1,3-===x y x y 围成的区域,)(u f 为连续函数. 解d x d y y x xyf xdxdy dxdy y x yf x DDD⎰⎰⎰⎰⎰⎰++=++)()](1[2222. 而0)(22=+⎰⎰dxdy y x xyf D, (利用奇偶性) ⎰⎰⎰⎰--==Dx xdy dx xdxdy 111352, 则 原式.52-=例5.5 计算⎰⎰Dyyσd sin ,其中D 由x y =和x y =围成. 解⎰⎰⎰⎰⎰-=-==Dy y dy y y y dx y y dy dxdy y y101021sin 1]sin [sin sin sin 例5.6计算d x d y y x D⎰⎰+22,其中D 由曲线)0(222>=+a ay y x 所围成.解 ⎰⎰⎰⎰⎰==+ππθθρρθ03sin 203222sin 38d a d d dxdy y x a D3033932)cos 3cos (38a a =-=πθθ. 例5.7计算⎰⎰+Dy x σd )(,其中D 由y x y x +≤+22所确定.解法1 圆y x y x +=+22在极坐标下方程为θθρs i n c o s +=,则 ⎰⎰⎰⎰-++=+4342sin cos 0)sin (cos )(ππθθρρθθθσd d d y x D⎰-+=4344)sin (cos 31ππθθθd⎰-+=4344)4(sin 34ππθπθd⎰=+ππθ04sin 344tdt t22214338sin 38204πππ=⋅⋅⋅==⎰tdt .解法2 令⎪⎪⎩⎪⎪⎨⎧=-=-,sin 21,cos 21θρθρy x 此时θρρσd d d =,则⎰⎰⎰⎰⎰⎰=⋅==++=+ππππρρθρρθρθρθσ20202102102412)1sin cos ()(d d d d d y x D.注意:⎰⎰==ππθθθθ20200sin cos d d .解法3 由于⎰⎰⎰⎰+-+-=+D Dd y x d y x σσ]1)21()21[()(而⎰⎰⎰⎰=-=-D Dd y d x 0)21()21(σσ (利用奇偶性) 则⎰⎰⎰⎰==+DDd d y x 2)(πσσ (积分域面积).解法4 由对称性知S x xd d y x DD⎰⎰⎰⎰==+22)(σσ,其中x 为积分域D 的形心的x 坐标,应为21=x ,S 为积分域D 的面积,应为2π=S ,则2)(πσ=+⎰⎰d y x D.例 5.8计算⎰⎰Dy x y d d ,其中D 是由2,0,2==-=y y x ,以及曲线22y y x --=所围成.解法1 在直角坐标下化为累次积分计算dy y y y ydy dy y y y ydx dy ydxdy Dy y ⎰⎰⎰⎰⎰⎰⎰-----=--==222220222222]22[dy y y ⎰---=22)1(14 (令t y s i n1=-) ⎰--=+-=22224c o s )s i n 1(4πππt d t t .于是⎰⎰-=Dyd 24πσ.事实上,计算dy y y ⎰--22)1(1还有一种巧妙的方法:dy y dy y y dy y y ⎰⎰⎰--+---=--222222)1(1)1(1)1()1(1,0)1(1)1(22=---⎰dy y y .而dy y ⎰--22)1(1应等于半圆的面积2π,故 2)1(1202π=--⎰dy y .解法2⎰⎰⎰⎰⎰⎰-=-θππρθρθσsin 2022202sin d d ydy dx yd D⎰⎰-=-=πππθθθθ22044sin 384sin 384d d2422143384ππ-=⋅⋅⋅-=.解法3 由于积分域D 关于直线1=y 上下对称,则⎰⎰=-Dd y 0)1(σ.故⎰⎰⎰⎰⎰⎰-==+-=DDDd d y yd 24]1)1[(πσσσ.解法4 由形心计算公式知S y yd D⎰⎰=σ. 由于积分域D 关于1=y 对称,则1=y ,而24π-=S ,故 ⎰⎰-=Dyd 24πσ.例5.9设二元函数⎪⎩⎪⎨⎧≤+<+≤+=,2|||x | 1 ,1, 1|||x | , ),(222y y x y x y x f 计算二重积分⎰⎰Dy x f σd ),(,其中}.2|||||),{(≤+=y x y x D解 原式=⎰⎰⎰⎰++-+θθθθπρθcos sin 2cos sin 1201021044d d dy x dx x⎰++=20cos sin 431πθθθd=++=⎰2)4sin(2431ππθθd )12ln(2431++ 例5.10 计算⎰⎰D y σd 2,其中D 由)20()cos 1()sin (π≤≤⎩⎨⎧-=-=t t a y t t a x 与0=y 围成.解 ⎰⎰⎰⎰⎰==Dax y a dx x y dy y dx d y ππσ20)(020322)(31 ⎰--=π2033)cos 1()cos 1(31dt t a t a ⎰⎰==ππ0842084sin 33222sin 316udu a ut dtt a 令4420841235221436587364sin 364a a udu a πππ=⋅⋅⋅⋅⋅==⎰.例5.11 设D 是全,⎩⎨⎧≤≤-=,x x x f 其它,021,)(计算⎰⎰-Dy x f x f σd )()(2.解 原式=49)(1222122=-⎰⎰+--dy y x x dx x x例5.12计算⎰⎰-+Dy y x σd 222,其中D 由422≤+y x 所确定.解 ⎰⎰-+Dd y y x σ222σσd y y x d y x y D D ⎰⎰⎰⎰-++--=21)2()2(2222])2()2([)2(11222222σσσd y y x d y y x d y x y D DD ⎰⎰⎰⎰⎰⎰-+--++--=σσd y x y d y y x D D⎰⎰⎰⎰--+-+=1)2(2)2(2222⎰⎰⎰⎰=-+=ππθπρρρθρθρρθ2020sin 20239)sin 2(2d d d d .例5.13计算⎰⎰+-Dy xe y x σd },min{)(22,其中D 为全平面.解⎰⎰⎰⎰⎰⎰+-+-+-+=12222222)()()(},min{D D y xy xy xDd ye d xe d e y x σσσ⎰⎰∞+∞-∞---⋅=yy x dx e xe dy 222dy e y ⎰+∞∞---=222212122ππ-=-=-=⎰∞+∞--dt e ty t .注:⎰∞+∞--=πdt e t 2,这是概率论中一个常用结论.例5.14设)(x f 在区间]1,0[上连续,且⎰=1d )(A x x f ,求⎰⎰11.d )()(d xy y f x f x 解 由对称性知⎰⎰11d )()(d xy y f x f x ⎰⎰≤≤≤≤=1010)()(21y x dxdy y f x f .2)()(2121010A dy y f dx x f ==⎰⎰ 题型二 累次积分交换次序及计算例5.16 交换下列累次积分次序1) ⎰⎰-=2210;d ),(d y y x y x f y I2) ⎰⎰⎰⎰--+=x x x y y x f x y y x f x I 2021201;d ),(d d ),(d 23) ⎰⎰=202;d ),(d xxy y x f x I解 (1) ⎰⎰⎰⎰-+=1212022),(),(x x dy y x f dx dy y x f dx I .(2) ⎰⎰---=102112),(yy dx y x f dy I .(3) ⎰⎰⎰⎰⎰⎰--=1021422),(),(),(y yy yydx y x f dy dx y x f dy dx y x f dy I .例5.17 交换累次积分⎰⎰-=24cos 20d )sin ,cos (d ππθρρθρθρθa f I 的次序)0(>a .解 θρc o s 2a =是圆ax y x 222=+,则θρθρθρρθρθρθρρρπρρd f d d f d I aaa aaa⎰⎰⎰⎰--+=202arccos 4222arccos2arccos)sin ,cos ()sin ,cos (例5.18累次积分⎰⎰2cos 0d )sin ,cos (d πθρρθρθρθf 可写成A) ⎰⎰-201,),(d y y dx y x f y B) ⎰⎰-21010,),(d y dx y x f y C) ⎰⎰110,d ),(d y y x f x D) ⎰⎰-210.d ),(d x x y y x f x例5.19计算下列累次积分1);d d 222y e x xy ⎰⎰-2);d 2sind d 2sind 24221⎰⎰⎰⎰+xxxy yxx y yxy ππ3))0(;d )(41d 22222>+-⎰⎰-+--a y y x a x x a a xa;解 1)交换积分次序得⎰⎰⎰⎰⎰---==22022222xyy y y dy ye dx e dy dy e dx)1(21214202---=-=e e y. 2)交换积分次序得⎰⎰⎰⎰+=-=-==213212221842sin42cos22sin2πππππππyyd dy yy dx yxdy y y原式.3)将原累次积分化为极坐标下先ρ后θ的累次积分得a d a d a 222404sin 2022-=-=⎰⎰--πρρρθπθ原式例5.20设)(x f 为连续. 证明: ⎰⎰⎰--=-DA Adt t A t f dxdy y x f |)|)(()(2|| ,2|| :A y A x D ≤≤证 ⎰⎰⎰⎰---=-DAA A A dy y x f dx dxdy y x f 2222)()(⎰⎰+--=-2222)()(A x A x A A du u f dy y x f (令u y x =-)⎰⎰⎰⎰-+-=-DA A A x A x du u f dx dxdy y x f 2222)()( (交换积分次序)⎰⎰⎰⎰-+--+=22220)()(A A u AA u A Adx u f du dx u f dudu u A u f A A))((⎰--=题型三 与二重积分有关的综合题:例5.21设)(x f 为连续函数,⎰⎰=tytdx x f dy t F )()(1,则)2(F '等于A ))2(2fB ))2(fC ))2(f -D )0 解法1 交换积分次序得⎰⎰⎰-==t x tdx x f x dy x f dx t F 111)()1()()(.则 )()1()(t f t t F -=',则)2()2(f F =' 故应选(B ).解法2 排除法 1)(=t f例5.22设区域D 由y y x ≤+22和0≥x 所确定,),(y x f 为D 上的连续函数,且⎰⎰---=Dv u v u f y x y x f .d d ),(81),(22π求),(y x f .解法1 令A dudv v u f D=⎰⎰),(, ①则 A y x y x f π81),(22---=.将A y x y x f π81),(22---=代入①式得⎰⎰=---DA dxdy A y x ]81[22π,即⎰⎰=---DA A dxdy y x 221,于是 )322(61121121s i n 022022-=-=--=⎰⎰⎰⎰πρρρθθπd d dxdy y x A D .故 )322(341),(22----=ππy x y x f . 解法2 等式dudv v u f y x y x f D⎰⎰---=),(81),(22π两端在区域D 上作二重积分得dudv v u f dxdy y x dxdy y x f DDD⎰⎰⎰⎰⎰⎰---=),(1),(22.则)322(61121),(22-=--=⎰⎰⎰⎰πdxdy y x dxdy y x f DD. (解法一中已算过) 故 )322(341),(22----=ππy x y x f . 例5.23设)(t f 在),0[+∞上连续,且满足⎰⎰≤+++=22224224d d )21()(t y x t y x y x f e t f π,求)(t f . 解 显然1)0(=f ,且⎰⎰⎰⎰⎰≤+==+222420202022)21(2)21()21(t y x t t d f d f d dxdy y x f πρρρπρρρθ,则 ρρρππd f e t f t t ⎰+=204)21(2)(2.)(88)(24t tf te t f t πππ+='2242848)4(]8[)(t tdt t tdt e C t C dt e te e t f ππππππ+=+=⎰⎰-⎰.由1)0(=f 得1=C ,因此242)14()(t e t t f ππ+=.例5.24设),(y x f 是定义在10,10≤≤≤≤y x 上的连续函数,1)0,0(-=f ,求极限321d ),(d lim0x x t xx euu t f t -→-⎰⎰+.解法1 交换积分次序得)~1(),(lim 1),(lim3303232x e x dtu t f du e duu t f dt x xu x xx t xx -→-→--=-⎰⎰⎰⎰++203),(lim2xdt x t f x x ⎰+→-= (应用罗必达法则)2203),(lim x x c f x x +→-= (20x c ≤≤,这里应用了积分中值定理) 31)0,0(31=-=f . 解法2 由以上分析知⎰⎰⎰⎰-=-=2),(),(),(x Dt xS f dtdu u t f du u t f dt ηξ,其中S D ,),(∈ηξ为D 的面积.而 ⎰⎰⎰=-==2203031)(x x xt x dt t x du dt S ,故 313)0,0(31),(l i m 1),(l i m 3300032=-=⋅-=-++→-→⎰⎰f x x f e du u t f dt x xx t x x ηξ 例5.25 设),(y x f 在单位圆122≤+y x 上有连续一阶偏导数,且在边界上取值为零,证明:=)0,0(f y x yx yf xf D y x d d 21lim 220⎰⎰++-+→πε其中D 为圆环域≤+≤222y x ε 1. 证 从积分域和被积函数不难看出,应在极坐标下将本题中的重积分化为累次积分.⎰⎰⎰⎰+=++περθρθρθθρθρθθ20122)]sin ,cos (sin )sin ,cos ([cos d f f d dxdy y x yf xf y x Dy xθθεθεθθρθρππεd f d f ⎰⎰-==20201)sin ,cos (])sin ,cos ([]2,0[),sin ,cos (2πθθεθεπ∈-=f 则 )0,0()s i n ,c o s (lim 22lim 0220f f dxdy y x yf xf Dyx ==++-++→→⎰⎰θεθεπεε 题型四 与二重积分有关的积分不等式问题例5.26设,d )(,d ||2,d )(1||||2231||||2122122⎰⎰⎰⎰⎰⎰≤+≤+≤++==+=y x y x y x y x I xy I y x I σσσ则 A) 321I I I <<; B) 132I I I <<; D) 213I I I <<; D) ;123I I I <<解 先比较1I 和3I 的大小,由于1I 和3I 被积函数相同且非负,而1I 的积分域包含了3I 的积分域,则1I >3I .再比较2I 和3I ,2I 和3I 积分域相同,但xy y x 222≥+,则3I >2I . 从而有 1I >3I >2I . 故应选(B ). 例5.27设⎰⎰≤++=1322)(y x d y x M σ,⎰⎰≤++=1222)(y x d y x N σ, σd eP y x y x ⎰⎰≤+---=12222)1(,则必有( ).(A )P N M >> (B )P M N >> (C )N P M >> (D )M P N >> 解 选(B )例5.28设)(x f 在],[b a 上连续,且0)(>x f ,证明:⎰⎰-≥b ab aa b x x f x x f 2)(d )(1d )(. 证明 若记},),{(b y a b x a y x D ≤≤≤≤=,则⎰⎰⎰⎰⎰⎰=⋅=⋅b ab ab a b a Ddxdy y f x f dy y f dx x f dx x f dx x f )()()(1)()(1)(由于积分域D 关于x y =对称,则])()()()([21)(1)(⎰⎰⎰⎰⎰⎰+=⋅b ab aDD dxdy x f y f dxdy y f x f dx x f dx x f ⎰⎰⎰⎰⎰⎰≥+=+=D D D dxdy dxdy y f x f y f x f dxdy y f x f y f x f 1)()(2)()()()()()(2122222)(a b -=.例5.29设)(x f 在]1,0[上单调减的正值函数,证明:⎰⎰⎰⎰≤112112d )(d )(d )(d )(xx f x x f xx xf xx xf证 若记}10,10),{(≤≤≤≤=y x y x D ,则⎰⎰⎰⎰-=101010122)()()()(dx x f dx x xf dx x xf dx x f I⎰⎰⎰⎰⋅-⋅=1101122)()()()(dy y f dx x xf dy y yf dx x f⎰⎰⎰⎰⎰⎰-=-=DDDdxdy x y y f x f dxdy y f x xf dxdy y f x yf ))(()()()()()(222.由于D 关于x y =对称,则⎰⎰⎰⎰-=-=DDdxdy y x x f y f dxdy x y y f x f I ))(()())(()(22,]))(()())(()([2122⎰⎰⎰⎰-+-=DDdxdy y x x f y f dxdy x y y f x f Idxdy y f x f x y y f x f D⎰⎰--=)]()()[)(()(21. 由于)(x f 单调减且大于零,则0)]()()[)(()(≥--y f x f x y y f x f ,故0≥I . 原题得证.。
