完整版)小学奥数几何专题
(完整版)五年级奥数平面几何(一)

五年级奥数平面几何(一)【例 1】 如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积为.【巩固】如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?【例 2】 长方形ABCD 的面积为362cm ,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?E【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.【例 3】 如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 ._H_G_ F_E_D_C_B_ A _A_B_C_D_E_ F_ G_H_ A _ B_ G_ C _ E _ F_ D_ A _ B_ G_ C_ E_ F_ DB【巩固】如图,长方形ABCD 的面积是36,E 是AD 的三等分点,2AE ED =,则阴影部分的面积为 .BB【例 4】 已知ABC 为等边三角形,面积为400,D 、E 、F 分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)B【例 5】 如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .GFE DC BAABC DE FG【例 6】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBA ABCDE【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAA BCDE甲乙【例 7】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBAEDCB A【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGAB CD EF【例 9】 如图所示的四边形的面积等于多少?DB13131212【例 10】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【例 11】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.D【例 12】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FEABDCGFEABDC【例 13】 如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FED CBA33321F E DC BAABCDEF【巩固】如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?y B CD EGE D CBAEDB A【例 14】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABCDOH GA BCD O【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC 的面积;⑵:AG GC =?B【例 15】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE△的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGFEDCBA【例 16】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EF GABCD EF G【例 17】 如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.CBA【巩固】在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.A BCDEF【例 18】 已知ABCD 是平行四边形,:3:2BC CE ,三角形ODE 的面积为6平方厘米.则阴影部分的面积是 平方厘米.BB【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【例 19】 如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A B CDEF?852O A BC DEF【例 20】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?BB【例 21】 下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,()m n +的值等于 .BEE【例 22】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADEDEGF FGCB S S S =△四边形四边形 .EGF A D CB【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形.【例 23】 如图,已知正方形ABCD 的边长为4,F 是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △GFAEDCB【例 24】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点, BF交EC 于M ,求BMG ∆的面积.Q E GNM F PADCBMHGF E DCBA。
小学奥数几何图形大全

⼩学奥数⼏何图形⼤全⼏何图形综合1.如图,四边形ABCD 是直⾓梯形.其中AD=12(厘⽶),AB=8(厘⽶),BC=15(厘⽶),且△ADE ,四边形DEBF ,△CDF 的⾯积相等.阴影△DEF 的⾯积是多少平⽅厘⽶?2.如图,长⽅形ABCD 的⾯积是96平⽅厘⽶,E 是AD 边上靠近D 点的三等分点,F 是CD 边上靠近C 点的四等分点.阴影部分的⾯积是多少平⽅厘⽶?3.如图,把⼀个正⽅形的两边分别增加3和5厘⽶,⽶(阴影部分).原正⽅形的⾯积为多少平⽅厘⽶?4.如图,把⼀个正⽅形的相邻两边分别减少2厘⽶和446平⽅厘⽶(阴影部分).原正⽅形的⾯积为多少平⽅厘⽶?5.如图,在△ABC 中,AD 的长度是AB 的四分之三,AE 的长度是 AC 的三分之⼆.请问:△ADE 的⾯积是△ABC ⾯积的⼏分之⼏?6.如图,在△ABC 中,BC=3CD ,AC=3AE ,那么△ABC 的⾯积是△CDE 的多少倍?7.如图,某公园的外轮廓是四边形ABCD ,被对⾓线AC 、BD 分成四个部分.△AOB 的⾯积是3平⽅千⽶,△BOC 的⾯积是2平⽅千⽶,△COD 的⾯积是1平⽅千⽶,如果公园由⼤⼩为6.9平⽅千⽶的陆地和⼀块⼈⼯湖组成,那么⼈⼯湖的⾯积是多少平⽅千⽶?E DF B CA D E AB CE A D8.如图,在梯形ABCD 中,AD 长9厘⽶,BC 长15厘⽶, BD 长12厘⽶,那么OD 长多少厘⽶? 9.如图,有8个半径为1厘⽶的⼩圆,⽤它们圆周的⼀部分连成⼀个花瓣图形,图中的⿊点是这些圆的圆⼼.如果圆周率π取3.14,那么花瓣图形的周长和⾯积分别是多少? 10.图中甲区域⽐⼄区域的⾯积⼤57其中直⾓三⾓形竖直的直⾓边的长度是多少?(π取3.14) 11.如图,在3×3的⽅格表中,分别以A 、E 为圆⼼,3、2为半径,画出圆⼼⾓都是90o的两段圆弧.图中阴影部分的⾯积是多少? (π取3.14).(π取13.下图是⼀个直⾓边长为3厘⽶、4厘⽶的直⾓三⾓形.将该三⾓形⼀任意⼀条边所在直线为轴进⾏旋转,求所得⽴体图形的表⾯积和体积.14.如图,已知正⽅形ABCD 的边长为4厘⽶,求阴影部分的⾯积.A D OB C●●●●●●●●●●●●●●●a bc d e f hg15.斜边长为10厘⽶的等腰直⾓三⾓形的⾯积是多少?16.右图中两个完全相同的三⾓形重叠在⼀起,则阴影部分的⾯积是多少?17.求图中四边形的⾯积.18.图中⼋条边的长度正好分别是1,2,3,4,5,6,7,8厘⽶. 已知a =2厘⽶,b=4厘⽶,c =5厘⽶,求图形的⾯积.19.如图所⽰,∠1+∠2+∠3+∠4+∠5+∠6等于多少度?20.如图,⼀个边长为1⽶的正⽅形被分成4个⼩长⽅形,它们的⾯积分别是0.3平⽅⽶、0.4平⽅⽶、0.2平⽅⽶、0.1平⽅⽶. 已知图中的阴影部分是正⽅形,那么它的⾯积是多少平⽅⽶?21.如图所⽰,三⾓形ABC 中,DE 与BC 平⾏,且AD :DB=5求AE :EC 及DE :BC .22.如图,间相互重叠.已知露在外⾯的部分中,红⾊的⾯积是20,黄⾊的⾯积是14,绿⾊的⾯积是10.那么,B A D 1 2 3 4 5 6 绿23.如图所⽰,已知△ABC 的⾯积为1平⽅厘⽶,D 、E是AB 、AC 边的中点.求三⾓形OBC 的⾯积.24.在如图所⽰的正⽅形中,A 、B 、C 分别是ED 、EG 、GF的中点.请问:△CDO 的⾯积是△ABO ⾯积的⼏倍?25.如图,四边形ABCD 是平⾏四边形,⾯积为72平⽅厘⽶,E 、F 分别为边AB 、BC 的中点,请问:阴影部分的⾯积为多少平⽅厘⽶?26.如图,△ABC 中,CE=2AE ,F 是AD的中点,△ABC 为1,那么阴影部分的⾯积多少?27.如图,△ABC 中,AD 、BE 相交于点O ,△OAE 、△OAB△OBD 的⾯积分别为1、2、3,那么四边形ODCE28.图中有半径分别为5厘⽶、4厘⽶、3厘⽶的三个圆,A 部分(即两⼩圆重叠部分)的⾯积与阴影部分的⾯积相⽐,哪个⼤?⼤多少?29.如图,图中最⼤的长⽅形⾯积是27,最⼩的长⽅形⾯积是5⾯积.30.阅读理解:(1)阅读:勾股定理是⼏何学中⼀颗光彩夺⽬的明珠,被称为“⼏何学的基⽯”,中国是发现和研究勾股定理最古⽼的国家之⼀。
小学奥数几何专地题目
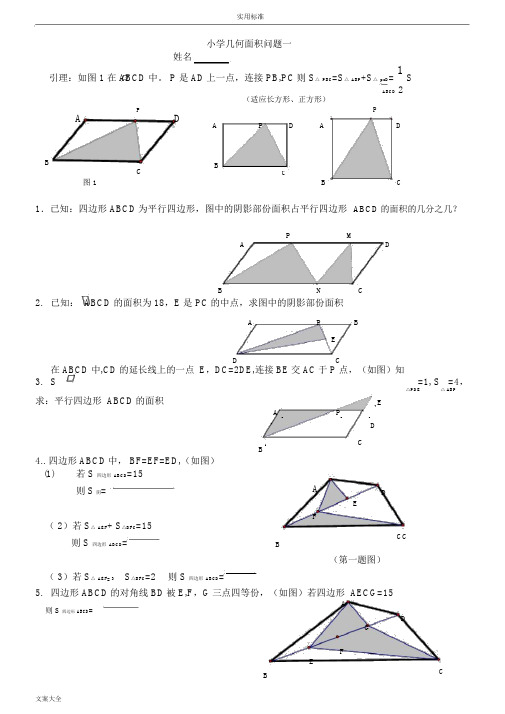
实用标准小学几何面积问题一姓名引理:如图 1 在 ABCD 中。
P 是 AD上一点,连接 PB,PC则 S△PBC=S△ABP+S△pcD= 1 SABCD 2(适应长方形、正方形)P PA DA P D A DB BC CC图 1B1.已知:四边形 ABCD为平行四边形,图中的阴影部份面积占平行四边形ABCD的面积的几分之几?P MA DB N C2.已知: ABCD 的面积为 18,E 是 PC的中点,求图中的阴影部份面积A P BED C3.在 ABCD 中,CD 的延长线上的一点 E,DC=2DE,连接 BE交 AC于 P 点,(如图)知S=1, S =4,△PDE△ ABP求:平行四边形 ABCD的面积AEA PD B CDE CB4.. 四边形 ABCD中, BF=EF=ED,(如图)(1)若 S 四边形ABCD=15则S阴=A DE ( 2)若 S△AEF+ S△BFC=15FCC 则 S 四边形ABCD=B(第一题图)( 3)若 S△AEF= 3 S△BFC=2则 S 四边形ABCD=5.四边形 ABCD的对角线 BD被 E,F,G三点四等份,(如图)若四边形 AECG=15A则 S 四边形ABCD=DGFEB C实用标准6. 四边形 ABCD 的对角线 BD 被 E,F , G 三点四等份,(如图)若阴影部份面积为 15则 S 四边形 ABCD =DAFEBC7. 若 ABCD 为正方形, F 是 DC 的中点,已知: S △BFC = 1AD E( 1)则 S 四边形 ADFB =F(2) S△DFE=(3) S △AEB =CB8. 直角梯形 ABCD 中.AE=ED,BC=18,AD=8,CD=6,且 BF=2FC,S △ GED =S △ GFC . 求 S 阴 =AEDGBF C小学几何面积问题二 姓名1. 如图 S △AEF= 2, AB=3AE CF=3EFCD则 S △ABC=2. 如图 S △BDE=30 ,AB=2AE , DC=4ACFC则 S △ABC=AE BE第1题BA第2题AD3. 正方形 ABCD 中, E,F,G 为 BC 边上四等份点,M,N,P 为对角线 AC 上的四等份点(如图) M若 S 正方形 ABCD=32 则 S △NGP=NP4. 已知: S △ABC=30 D 是 BC 的中点 BCEFGAE=2ED 则 S △BDE=BDE实用标准5.已知 :AD=DB DE=3EC AF=3FE若S△ABC=160求S△EFC=ACEFDB6.已知:在△ ABC中, FC=3AF EC=2BE BD=DF若 S△DFE=3 则 S△ABC=AFDBE C7.ABCD为平行四边形, AG=GC,BE=EF=FC,若 S△GEF=2,则 S ABCD=ADGA DD8.ABCD 是梯形, AD // BC( 如图 )则 S△ AOB=S△AOD=9.ABCD 是梯形, AD // BC( 如图 )则S△ DOC=S△BOC=B E F C6O12B C(第 8题)AD48OB C10.ABCD 是梯形, AD // BC( 如图 ), 且 BO=3OD, S △AOB=15则S 梯 ABCD=(第 9题)A DOBC(第 10 题)实用标准11. 如图 BD=DE, EC=3EF AF=2FD若△ DFE的面积等于 1则△ ABC的面积为AF EDB C(第 11 题)小学几何面积问题三姓名1. 在梯形 ABCD中, AD//BC, 图中阴影部分的面积为 4,OC=2AO,求 S 梯ABCD=ADO2 在梯形 ABCD中, AD//BC,S△BOC=14OC=2AO求 S 梯ABCD=3.在梯形 ABCD中, AD//BC,S△AOB=14OC=3AO求 S 梯ABCD=B CA DOBCBDAOB C4.在梯形 ABCD中, AD//BC, 图中阴影部分的面积为 30, OC=3AO,S△AOB=6 求 S空=A DO空BC 5. 读一读:A 若直线 L //L2( 如图一)L11一.当高不变,底扩大(或缩小)K 倍。
小学奥数几何题100道及答案(完整版)

小学奥数几何题100道及答案(完整版)题目1:一个正方形的边长是5 厘米,它的面积是多少平方厘米?解题方法:正方形面积= 边长×边长,即5×5 = 25(平方厘米)答案:25 平方厘米题目2:一个长方形的长是8 分米,宽是6 分米,它的周长是多少分米?解题方法:长方形周长= (长+ 宽)×2,即(8 + 6)×2 = 28(分米)答案:28 分米题目3:一个三角形的底是10 厘米,高是6 厘米,它的面积是多少平方厘米?解题方法:三角形面积= 底×高÷2,即10×6÷2 = 30(平方厘米)答案:30 平方厘米题目4:一个平行四边形的底是12 米,高是8 米,它的面积是多少平方米?解题方法:平行四边形面积= 底×高,即12×8 = 96(平方米)答案:96 平方米题目5:一个梯形的上底是 4 厘米,下底是6 厘米,高是5 厘米,它的面积是多少平方厘米?解题方法:梯形面积= (上底+ 下底)×高÷2,即(4 + 6)×5÷2 = 25(平方厘米)答案:25 平方厘米题目6:一个圆的半径是3 厘米,它的面积是多少平方厘米?解题方法:圆的面积= π×半径²,即3.14×3²= 28.26(平方厘米)答案:28.26 平方厘米题目7:一个半圆的半径是 4 分米,它的周长是多少分米?解题方法:半圆的周长= 圆周长的一半+ 直径,即3.14×4×2÷2 + 4×2 = 20.56(分米)答案:20.56 分米题目8:一个长方体的长、宽、高分别是5 厘米、4 厘米、3 厘米,它的表面积是多少平方厘米?解题方法:长方体表面积= (长×宽+ 长×高+ 宽×高)×2,即(5×4 + 5×3 + 4×3)×2 = 94(平方厘米)答案:94 平方厘米题目9:一个正方体的棱长是6 分米,它的体积是多少立方分米?解题方法:正方体体积= 棱长³,即6³= 216(立方分米)答案:216 立方分米题目10:一个圆柱的底面半径是2 厘米,高是5 厘米,它的侧面积是多少平方厘米?解题方法:圆柱侧面积= 底面周长×高,底面周长= 2×3.14×2,即2×3.14×2×5 = 62.8(平方厘米)答案:62.8 平方厘米题目11:一个圆锥的底面半径是3 厘米,高是4 厘米,它的体积是多少立方厘米?解题方法:圆锥体积= 1/3×底面积×高,底面积= 3.14×3²,即1/3×3.14×3²×4 = 37.68(立方厘米)答案:37.68 立方厘米题目12:两个边长为4 厘米的正方形拼成一个长方形,长方形的长和宽分别是多少?面积是多少?解题方法:长方形的长为8 厘米,宽为4 厘米,面积= 8×4 = 32(平方厘米)答案:长8 厘米,宽4 厘米,面积32 平方厘米题目13:一个三角形的面积是18 平方厘米,底是6 厘米,高是多少厘米?解题方法:高= 面积×2÷底,即18×2÷6 = 6(厘米)答案:6 厘米题目14:一个平行四边形的面积是24 平方米,底是 4 米,高是多少米?解题方法:高= 面积÷底,即24÷4 = 6(米)答案:6 米题目15:一个梯形的面积是30 平方分米,上底是5 分米,下底是7 分米,高是多少分米?解题方法:高= 面积×2÷(上底+ 下底),即30×2÷(5 + 7)= 5(分米)答案:5 分米题目16:一个圆环,外圆半径是5 厘米,内圆半径是 3 厘米,圆环的面积是多少平方厘米?解题方法:圆环面积= 外圆面积-内圆面积,即 3.14×(5²- 3²)= 50.24(平方厘米)答案:50.24 平方厘米题目17:一个长方体的棱长总和是48 厘米,长、宽、高的比是3:2:1,长方体的体积是多少立方厘米?解题方法:一条长、宽、高的和为48÷4 = 12 厘米,长为6 厘米,宽为4 厘米,高为2 厘米,体积= 6×4×2 = 48(立方厘米)答案:48 立方厘米题目18:一个正方体的表面积是54 平方分米,它的一个面的面积是多少平方分米?解题方法:一个面的面积= 表面积÷6,即54÷6 = 9(平方分米)答案:9 平方分米题目19:一个圆柱的底面直径是4 分米,高是3 分米,它的表面积是多少平方分米?解题方法:底面积= 3.14×(4÷2)²= 12.56 平方分米,侧面积= 3.14×4×3 = 37.68 平方分米,表面积= 2×12.56 + 37.68 = 62.8(平方分米)答案:62.8 平方分米题目20:一个圆锥的底面周长是18.84 分米,高是5 分米,它的体积是多少立方分米?解题方法:底面半径= 18.84÷3.14÷2 = 3 分米,体积= 1/3×3.14×3²×5 = 47.1(立方分米)答案:47.1 立方分米题目21:一个长方体的水箱,长 5 分米,宽4 分米,高 3 分米,里面装满水,把水倒入一个棱长为5 分米的正方体水箱,水深多少分米?解题方法:水的体积= 5×4×3 = 60 立方分米,正方体水箱底面积= 5×5 = 25 平方分米,水深= 60÷25 = 2.4 分米答案:2.4 分米题目22:一块长方形的铁皮,长8 分米,宽6 分米,从四个角各切掉一个边长为1 分米的正方形,然后做成一个无盖的盒子,这个盒子的容积是多少立方分米?解题方法:盒子长6 分米,宽4 分米,高1 分米,容积= 6×4×1 = 24(立方分米)答案:24 立方分米题目23:一个圆柱的体积是60 立方厘米,底面积是12 平方厘米,高是多少厘米?解题方法:高= 体积÷底面积,即60÷12 = 5(厘米)答案:5 厘米题目24:一个圆锥和一个圆柱等底等高,圆柱的体积是27 立方分米,圆锥的体积是多少立方分米?解题方法:等底等高的圆锥体积是圆柱体积的1/3,即27×1/3 = 9(立方分米)答案:9 立方分米题目25:把一个棱长为 6 厘米的正方体铁块熔铸成一个底面积为36 平方厘米的圆柱体,这个圆柱体的高是多少厘米?解题方法:正方体体积= 6³= 216 立方厘米,圆柱体的高= 体积÷底面积,即216÷36 = 6(厘米)答案:6 厘米题目26:一个直角三角形的两条直角边分别是3 厘米和4 厘米,斜边是5 厘米,这个三角形的面积是多少平方厘米?解题方法:直角三角形面积= 两条直角边乘积的一半,即3×4÷2 = 6(平方厘米)答案:6 平方厘米题目27:一个等腰三角形的周长是20 厘米,其中一条腰长8 厘米,底边长多少厘米?解题方法:等腰三角形两腰相等,所以底边长= 周长-腰长×2,即20 - 8×2 = 4(厘米)答案:4 厘米题目28:一个扇形的圆心角是90°,半径是6 厘米,这个扇形的面积是多少平方厘米?解题方法:扇形面积= 圆心角÷360°×圆的面积,即90÷360×3.14×6²= 28.26(平方厘米)答案:28.26 平方厘米题目29:一个长方体的底面是边长为5 厘米的正方形,高是8 厘米,这个长方体的体积是多少立方厘米?解题方法:长方体体积= 底面积×高,底面积= 5×5 = 25 平方厘米,体积= 25×8 = 200(立方厘米)答案:200 立方厘米题目30:一个圆柱的底面周长是18.84 厘米,高是10 厘米,它的体积是多少立方厘米?解题方法:底面半径= 18.84÷3.14÷2 = 3 厘米,体积= 3.14×3²×10 = 282.6(立方厘米)答案:282.6 立方厘米题目31:一个圆锥的底面直径是8 厘米,高是6 厘米,它的体积是多少立方厘米?解题方法:底面半径= 8÷2 = 4 厘米,体积= 1/3×3.14×4²×6 = 100.48(立方厘米)答案:100.48 立方厘米题目32:把一个棱长为8 厘米的正方体木块削成一个最大的圆柱,这个圆柱的体积是多少立方厘米?解题方法:圆柱的底面直径和高都是8 厘米,体积= 3.14×(8÷2)²×8 = 401.92(立方厘米)答案:401.92 立方厘米题目33:一个长方体玻璃缸,从里面量长4 分米,宽 3 分米,高5 分米,缸内水深2.5 分米。
小学奥数几何图练习及答案【三篇】

小学奥数几何图练习及答案【三篇】【第一篇】习题:一个长方形,如果宽不变,长增加8米,面积增加72平方米,如果长不变,宽减少4米,面积减少48平方米,原长方形的面积是( )。
考点:长方形、正方形的面积分析:用增加的面积除以增加的长,就是原来的宽,即72÷8=9米;用减少的面积除以减少的宽,就是原来的长,即48÷4=12米,从而利用长方形的面积公式即可求解。
解答:解:72÷8=9(米)48÷4=12(米)12×9=108(平方米);答:长方形的面积是108平方米。
故答案为:108平方米【第二篇】鸟头定理即共角定理。
燕尾定理即共边定理的一种。
共角定理:若两三角形有一组对应角相等或互补,则它们的面积比等于对应角两边乘积的比。
共边定理:有一条公共边的三角形叫做共边三角形。
共边定理:设直线AB与PQ交与M则S△PAB/S△QAB=PM/QM 这几个定理大都利用了相似图形的方法,但小学阶段没有学过相似图形,而小学奥数中,常常要引入这些,实在有点难为孩子。
为了避开相似,我们用相应的底,高的比来推出三角形面积的比。
例如燕尾定理,一个三角形ABC中,D是BC上三等分点,靠近B点。
连接AD,E是AD上一点,连接EB和EC,就能得到四个三角形。
很显然,三角形ABD和ACD面积之比是1:2因为共边,所以两个对应高之比是1:2而四个小三角形也会存在类似关系三角形ABE和三角形ACE的面积比是1:2三角形BED和三角形CED的面积比也是1:2所以三角形ABE和三角形ACE的面积比等于三角形BED和三角形CED的面积比,这就是传说中的燕尾定理。
以上是根据共边后,高之比等于三角形面积之比证明所得。
必须要强记,只要理解,到时候如何变形,你都能会做。
至于鸟头定理,也不要死记硬背,掌握原理,用起来就会得心应手。
【第三篇】习题:两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”。
(完整版)四年级几何奥数题

1、四个相同的长方形,拼成一个面积为100 cm2的大正方形。
每个长方形的周长是多少厘米?
2、将一个正方形分为9个小长方形,而这些小正方形周长总和位96cm,那么这个大正方形的面积是多少?
3、在长方体A、B、C、D中,AB等于120cm,截去一种正方形EBCF后,剩下的长方形AEFD的周长是多少?
A E B
D F C
4、两个长方形的边长相差8cm,面积相差100 cm2,求两个正方形的面积。
5、一个长方形的长增加3m,长方形的面积就增加12 m2,如果宽减少2m,面积减少14 m2,求原长方形面积。
6、大小两个正方形,周长相差4厘米,面积相差20 cm2。
求大、小两个正方形的面积。
7、一个长方形的长、宽各增加3cm,面积增加171 cm2。
如果长宽相差4cm,求正方形周长及面积。
8、如图A、B、C、D、E的面积分别是1、2、3、4、5,求大长方形的面积。
9、将一个长方形的长增加1Cm,宽增加3cm,就变长一个正方形,面积增加33 cm2。
求原长方形的面积。
10、将一个长方形的长增加2Cm,宽增加5cm,就变长一个正方形,面积增加60cm2。
求原长方形的面积。
小学奥数系列训练题-几何计数|通用版

2015年小学奥数计数专题——几何计数1.用3根等长的火柴可以摆成一个等边三角形.如图,用这样的等边三角形拼合成一个更大的等边三角形.如果这个大等边三角形昀每边由20根火柴组成,那么一共要用多少根火柴?2.如图,用长短相同的火柴棍摆成3×1996的方格网,其中每个小方格的边都由一根火柴棍组成,那么一共需用多少根火柴棍?3.图是一个跳棋棋盘,请你计算出棋盘上共有多少个棋孔?4.如图,在桌面上,用6个边长为l的正三角形可以拼成一个边长为1的正六边形.如果在桌面上要拼出一个边长为6的正六边形,那么,需要边长为1的正三角形多少个?5.如图,其中的每条线段都是水平的或竖直的,边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4厘米、6厘米、5厘米、1厘米.求图中长方形的个数,以及所有长方形面积的和.6.如图,18个边长相等的正方形组成了一个3×6的方格表,其中包含“*”的长方形及正方形共有多少个?7.图是由若干个相同的小正方形组成的.那么,其中共有各种大小的正方形多少个?8.图中共有多少个三角形?9.图是由18个大小相同的小正三角形拼成的四边形,其中某些相邻的小正三角形可以拼成较大的正三角形.那么,图中包含“*”的各种大小的正三角形一共有多少个?10.如图,AB,CD,EF,MN互相平行,则图中梯形个数与三角形个数的差是多少?11.在图中,共有多少个不同的三角形?12.如图,一块木板上有13枚钉子.用橡皮筋套住其中的几枚钉子,可以构成三角形、正方形、梯形等等,如图.那么,一共可以构成多少个不同的正方形?13.如图,用9枚钉子钉成水平和竖直间隔都为1厘米的正方阵.用一根橡皮筋将3枚不共线的钉子连结起来就形成一个三角形.在这样得到的三角形中,面积等于1平方厘米的三角形共有多少个?14.如图,木板上钉着12枚钉子,排成三行四列的长方阵.那么用橡皮筋共可套出多少个不同的三角形?15.如图,正方形ACEG的边界上有A,B,C,D,E,F,G这7个点,其中B,D,F分别在边AC,CE,EG上.以这7个点中的4个点为顶点组成的不同四边形的个数等于多少?16.数一数下列图形中各有多少条线段.17.数出下图中总共有多少个角.18.数一数下图中总共有多少个角?19.如下图中,各个图形内各有多少个三角形?20.如下图中,数一数共有多少条线段?共有多少个三角形?21.如右图中,共有多少个角?22.在图中(单位:厘米):①一共有几个长方形?②所有这些长方形面积的和是多少? 37421812523.由20个边长为1的小正方形拼成一个45 长方形中有一格有“☆”图中含有“☆”的所有长方形(含正方形)共有 个,它们的面积总和是 。
小学奥数专题之几何专题

小学奥数几何专题1、(★★)如图,已知四边形ABCD 中,AB=13,BC=3,CD=4,DA=12,并且BD 与AD 垂直,则四边形的面积等于多少?[思 路]:显然四边形ABCD 的面积将由三角形ABD 与三角形BCD 的面积求和得到.三角形ABD 是直角三角形,底AD 已知,高BD 是未知的,但可以通过勾股定理求出,进而可以判定三角形BCD 的形状,然后求其面积.这样看来,BD 的长度是求解本题的关键.解:由于BD 垂直于AD ,所以三角形ABD 是直角三角形.而AB=13,DA=12,由勾股定理,BD 2=AB 2-AD 2=132—122=25=52,所以BD=5.三角形BCD 中BD=5,BC=3,CD=4,又32十42=52,故三角形BCD 是以BD 为斜边的直角三角形,BC 与CD 垂直.那么:ABCD S 四边形=ABD S ∆+BCD S∆=12×5÷2+4×3÷2=36.. 即四边形ABCD 的面积是36. 2、(★★)如图四边形土地的总面积是48平方米,三条线把它分成了4个小三角形,其中2个小三角形的面积分别是7平方米和9平方米.那么最大的一个三角形的面积是________平方米;[分析]:剩下两个三角形的面积和是 48-7-9=32 ,是右侧两个三角形面积和的2 倍,故左侧三角形面积是右侧对应三角形面积的2倍,最大三角形面积是 9×2=18。
3.(★★)将下图中的三角形纸片沿虚线折叠得到右图,其中的粗实线图形面积与原三角形面积之比为2:3。
已知右图中3个阴影的三角形面积之和为1,那么重叠部分的面积为多少?[思 路]:小升初中常把分数,百分数,比例问题处理成份数问题,这个思想一定要养成。
解:粗线面积:黄面积=2:3绿色面积是折叠后的重叠部分,减少的部分就是因为重叠才变少的,这样可以设总共3份,后来粗线变2份,减少的绿色部分为1份,所以阴影部分为2-1=1份,7 94、(★★)求下图中阴影部分的面积:【解】如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完整版)小学奥数几何专题小学几何面积问题一引理:如图1在ABCD中,P是AD上一点,连接PB、PC,则S△PBC=S△ABP+S△pcD= P/AD(适应长方形、正方形)。
1.已知:四边形ABCD为平行四边形,求阴影部分面积占平行四边形ABCD的面积的几分之几?无需删除)2.已知:ABCD的面积为18,E是PC的中点,求阴影部分面积。
无需删除)3.在ABCD中,CD的延长线上的一点E,DC=2DE,连接BE交AC于P点,(如图)知S△PDE=1,S△ABP=4,求平行四边形ABCD的面积。
无需删除)4.四边形ABCD中,BF=EF=ED,(如图)1) 若S四边形ABCD=15,则S阴=(无需删除)2) 若S△AEF+S△BFC=15,则S四边形ABCD=(无需删除)3) 若S△AEF=3S△BFC,则S四边形ABCD=(无需删除)5.四边形ABCD的对角线BD被E、F、G三点四等分,(如图)若四边形AECG=15,则S四边形ABCD=(无需删除)6.四边形ABCD的对角线BD被E、F、G三点四等分,(如图)若阴影部分面积为15,则S四边形ABCD=(无需删除)7.若ABCD为正方形,F是DC的中点,已知:S△BFC=1。
1) 则S四边形ADFB=(无需删除)2) S△DFE=(无需删除)3) S△AEB=(无需删除)8.直角梯形ABCD中,AE=ED,BC=18,AD=8,CD=6,且BF=2FC,S△GED=S△GFC,求阴影部分面积。
无需删除)小学几何面积问题二1.如图S△AEF=2,AB=3AE,CF=3EF,则S△ABC=(无需删除)2.如图S△BDE=30,AB=2AE,DC=4AC,则S△ABC=(无需删除)3.正方形ABCD中,E、F、G为BC边上四等份点,M、N、P为对角线AC上的四等份点(如图),若S正方形ABCD=32,则S△NGP=(无需删除)4.已知:S△ABC=30,D是BC的中点,AE=2ED,则S△BDE=(无需删除)1.在梯形ABCD中,AD//BC,OC=2AO,阴影部分的面积为4,求梯形ABCD的面积。
解:由梯形的性质可知,阴影部分的面积等于平行四边形ABEF的面积减去三角形AOC的面积,即4=S平行四边形ABEF-S△AOC。
又因为OC=2AO,所以平行四边形ABEF的面积为2S△AOC。
代入得4=S△AOC,所以△AOC的面积为4.因为AD//BC,所以△AOC与△BOD全等,所以△BOD的面积也为4.梯形ABCD的面积为S梯形ABCD=S平行四边形ABEF+S△AOC+S△BOD=2S△AOC+4+4=2×4+4+4=12.2.在梯形ABCD中,AD//BC,S△BOC=14,OC=2AO,求梯形ABCD的面积。
解:由梯形的性质可知,S△BOC=S梯形ABCD-S△AOD。
又因为OC=2AO,所以S△AOD=2S△BOC=28.代入得S梯形ABCD=14+28=42.3.在梯形ABCD中,AD//BC,S△AOB=14,OC=3AO,求梯形ABCD的面积。
解:由梯形的性质可知,S△AOB=S梯形ABCD-S△DOC。
又因为OC=3AO,所以S△DOC=3S△AOB=42.代入得S梯形ABCD=14+42=56.4.在梯形ABCD中,AD//BC,OC=3AO,阴影部分的面积为30,求梯形ABCD的面积。
解:同第1题,阴影部分的面积等于平行四边形ABEF的面积减去三角形AOC的面积,即30=S平行四边形ABEF-S△AOC。
又因为OC=3AO,所以平行四边形ABEF的面积为3S△AOC。
代入得30=2S△AOC,所以△AOC的面积为15.因为AD//BC,所以△AOC与△BOD全等,所以△BOD的面积也为15.梯形ABCD的面积为S梯形ABCD=S平行四边形ABEF+S△AOC+S△BOD=3S△AOC+15+15=3×15+30=75.5.若直线L1//L2,当高不变,底扩大(或缩小)K倍,其面积也同时扩大(或缩小)K倍;当底不变,高扩大(或缩小)K倍,其面积也同时扩大(或缩小)K倍。
练题:1.如图(一):L1//L2,AB=10,BC=5,若S△HAB=6,求S△ABC。
解:因为S△HAB=6,所以△HAB的高为2,底为10.所以△ABC的高为4,底为20.所以S△ABC=1/2×4×20=40.2.在梯形ABCD中,AD//BC,S△BOC=14,OC=2AO,求S梯形ABCD。
解:同第2题,S梯形ABCD=42.3.在梯形ABCD中,AD//BC,S△AOB=14,OC=3AO,求S梯形ABCD。
解:同第3题,S梯形ABCD=56.4.在梯形ABCD中,AD//BC,OC=3AO,阴影部分的面积为30,求S梯形ABCD。
解:同第4题,S梯形ABCD=75.5.如图(二):L1//L2,AC=BC,H1=2H2,S△MAC=10,求S△NBC。
解:因为AC=BC,所以△ABC为等腰三角形,所以BN=NC。
因为L1//L2,所以S△NBC=2S△MAC=20.1.如图(二),在△NCB中,CB边上的高为H1,ACM 中,AC边上的高为H2,且H2=0.5H1,AC=CB。
已知△XXX的面积为100,求△ACM的面积。
2.将一个三角形分成三个小三角形,使它们的面积比为1:2:3.3.△ABC为等边三角形,AD为BC边上的高,已知△ABC的面积为2,求△ADC的面积。
4.△ABC为等边三角形,D为AB的中点,DH垂直于BC,H为垂足,已知△BDH的面积为2,求△ABC的面积。
5.在△ABC中,AE=BE,BD=2DC,FC=3AF,已知△ABC的面积为1,求△EFD的面积。
6.△ABC中,BC=3CD,AB=2BE,AC=4AF,已知△ABC的面积为240平方厘米,求△DEF的面积。
7.如图,BD=DE,EC=3EF,AF=2FD,已知△DFE的面积为1,求△XXX的面积。
8.如图,两个正方形拼成一个图形,求阴影部分的面积。
9.如图,三个正方形拼成一个图形,求阴影部分的面积。
10.如图,ABCD是矩形,EF∥AB,已知矩形ABCD的面积为24,求阴影部分的面积。
11.如图,平行四边形ABCD中,EF∥AC,已知△AED 的面积为72平方厘米,求△DCF的面积。
12.如图,ABCD为平行四边形,直线CF与AB交于E,与DA的延长线交于F,连BF,已知△BEF的面积为4平方厘米,求△EDA的面积。
13.如图,将正方形内接于等腰直角三角形,已知按左图放法时正方形的面积为441,求按右图放法时正方形的面积。
14.如图,一个长方形草地中间有两条宽2米的路,一条是长方形,另一条是平行四边形,已知长方形的长为18米,宽为10米,求草地的面积。
15.如图,大正方形的边长为20厘米,E、F、G、H分别是各边中点,求中间小正方形的面积。
4.给定一个由五个边长相等的正方形拼成的“十字架”,已知AB=20厘米,求该“十字架”的面积(单位:平方厘米)。
5.一个边长为21厘米的正方形被分成了四个长方形,它们的面积分别为原正方形面积的若干倍。
在其中一个长方形中,有一个小正方形位于阴影部分。
求该小正方形的面积(单位:平方厘米)。
6.在一个面积小于100的长方形内部,有三个小正方形,它们的边长都是整数。
已知正方形(二)的边长是长方形长的2/5,正方形(一)的边长是长方形宽的1/8.求图中阴影部分的面积(单位:平方单位)。
7.如图所示,ABCD为正方形,且AB//EF,BF=1厘米。
求阴影部分的面积(单位:平方厘米)。
8.在长方形ABCD中,长是宽的4倍,对角线BD=17厘米,求该长方形的面积(单位:平方厘米)。
1.给定长方形ABCD,向它的外部分别作正方形,已知四边形的周长之和为264厘米,面积之和为1378平方厘米。
求原长方形的面积(单位:平方厘米)。
2.如图,两个长方形叠放,其中小长方形宽为2厘米,A 是大长方形一边的中点,△ABC是等腰直角三角形。
求阴影部分的面积(单位:平方厘米)。
3.在边长为10的正方形ABCD的四边上分别取点E、F、G、H,已知E与G的水平距离为5厘米,H与F的水平距离为4厘米。
求四边形EFGH的面积(单位:平方厘米)。
4.长方形ABCD的长DC为8厘米,宽AD为4厘米。
EFCA也是长方形,求其面积(单位:平方厘米)。
5.如图,在直角梯形ABCD中,AB=10厘米,阴影部分的面积是该直角梯形面积的一半。
求该直角梯形的面积(单位:平方厘米)。
6.已知平行四边形ABCD中,P在AD上,BP⊥CP,且BP=8厘米,CP=6厘米。
求图中阴影部分的面积(单位:平方厘米)。
7.如图所示,梯形ABCD与梯形A'B'C'D'大小相同,重合。
已知EC=4厘米,DC=24厘米,EF=5厘米。
求阴影部分的面积(单位:平方厘米)。
CFD8.在一个梯形内,有两个三角形的面积分别是6平方厘米和8平方厘米,梯形的下底长是上底长的2倍,求阴影部分的面积。
小学几何面积问题七1.求图中阴影部分的面积。
2.求图中阴影部分的面积。
4.求梯形的面积。
5.求下图四边形的面积。
AD = 4 cm。
BC = 8平方厘米EF是梯形ABCD的中位线,求梯形ABCD的面积。
AD = 8 cm。
DC = 7 cm。
AB = 21 cm6.在下图中,长方形内有一个钝角三角形,按照图示的数,求这个三角形的面积。
角A = 6.角B = 4.角C = 8.边AC = 137.三个边长为10厘米、12厘米、8厘米的正方形拼放在一起,直线BC将整个图形面积平分,求线段AB的长。
AB = 88.如图有两个边长都是10厘米的正方形ABCD和A/B/C/D/,且正方形A/B/C/D/的顶点A/恰好是正方形ABCD 的中心,那么:阴影部分的面积是平方厘米。
小学几何面积问题八1.平行四边形ABCD的面积是32平方厘米,AD = 8 cm,∠B = 45度,求阴影部分的面积是平方厘米。
2.如图所示平行四边形ABCD中,CH = DE = FB = GC,如果阴影部分的面积为7平方厘米,那么,这个平行四边形的面积是平方厘米。
3.平行四边形ABCD已知:三角形AHB的面积是8平方厘米,三角形DFC的面积是6平方厘米。
求阴影部分的面积是平方厘米。
4.平行四边形ABCD中有一点E,已知,三角形ABE的面积是73平方厘米,三角形BEC的面积是10平方厘米。
求阴影部分三角形BED的面积是平方厘米。
5.一个45度的直角三角板,最长边为12厘米,那么,它的面积为72平方厘米。
6.如图长方形内画了一些直线,已知边上有三块面积分别为13平方厘米、35平方厘米、49平方厘米,那么图中的阴影部分面积是48平方厘米。
