高中数学基础能力训练(8)

合集下载

人教A版高中数学必修一1.2 集合间的基本关系专练(含解析)(8)

1.2 集合间的基本关系一、单选题 1．设集合{|,}24k M x x k ππ==+∈Z ，{|,}42k N x x k ππ==+∈Z ，则（） A ．MNB ．M N ⊆C ．M N ⊇D ．M N ⋂=∅2．已知集合A ＝x|x ＜－1，或x ＞2}，集合B ＝x|a －1≤x≤a＋1}，且A∩B＝B ，则实数a 的取值范围是( ) A ．a ＞3B ．a ＜－2C ．－2＜a ＜3D ．a ＜－2或a ＞33．设非空集合{}S x m x l =≤≤满足：当x S ∈时，有2x S ∈，给出如下四个命题：①若1m =，则{}1S =；②若12m =-，则114l ≤≤；③若12l =，则02m -≤≤；④若1l =，则10m -≤≤或1m =；其中正确的命题个数是（） A ．1B ．2C ．3D ．44．若集合|24M x x k k Z ππ⎧⎫==⋅-∈⎨⎬⎩⎭，，|42N x x k k Z ππ⎧⎫==⋅+∈⎨⎬⎩⎭，，则（）A ．M=NB ．M ⊆NC ．N ⊆MD ．没有包含关系 5．设A ＝1,4,2x}，若B ＝1，x 2}，若B ⊆A ，则x 的值为 A ．0 B ．－2 C ．0或－2 D ．0或±2 6．集合3{|40}M x x x =-=,则M 的子集个数为A ．2B ．3C ．4D ．8 7．已知集合{|64A x x m n ==+其中,}m n Z ∈，{|108B x x a b ==+，其中,}a b Z ∈则A 与B 的关系为 A ．A B =B ．B A ⊃≠C ．A B ⊃≠D ．A B =∅8．已知{}|3782A x x x =-≥-，{}|12B x a x =≥-，若A B ⊆，则实数a 的取值范围为（） A ．2a ≥B ．2a ≤C ．2a >D ．2a <9．已知集合{}|,A x x a a R =≤∈，{}|216xB x =<，若A B ，则实数a 的取值范围是（）A ．∅B ．RC ．(],4-∞D ．(),4-∞10．已知集合{}0,1A =, {}0,1,2B =，则,A B 的关系是（） A ．A B ∈ B ．A B ⊆ C ．A B = D ．A B B =二、填空题1．集合{}1,0,1-共有 ______ 个子集.2．已知集合{}2220A x mx x =-+>，({}20B x x =-，若A B =∅，则实数m 的取值范围3．集合{},,A a b c =有_______个子集.4．在①1⊆｛0,1,2｝；②｛1｝∈｛0,1,2｝；③｛0,1,2｝⊆｛0,1,2｝；④∅⊆｛0｝上述四个关系中，错误的是_________.5．已知[]R 1,2,,,4pB A A B ⎛⎫=-=-∞-⊆ ⎪⎝⎭,则实数p 取值范围是_________．三、解答题 1．已知命题P ：函数且|f （a ）|＜2，命题Q ：集合A=x|x 2+（a+2）x+1=0，x∈R}，B=x|x ＞0}且A∩B=∅，（1）分别求命题P 、Q 为真命题时的实数a 的取值范围；（2）当实数a 取何范围时，命题P 、Q 中有且仅有一个为真命题；（3）设P 、Q 皆为真时a 的取值范围为集合S ，，若∁R T ⊆S ，求m 的取值范围.2．已知集合{}27A x x =-≤≤，{}121B x m x m =+<<-，若B A ⊆，求实数m 的取值范围．3．已知集合{}2|40A x x x =+=,{}2|0B x x ax a =++=,若B A ⊆,求实数a 满足的条件.4．已知集合112168x A x +⎧⎫=≤≤⎨⎬⎩⎭，{}131B x m x m =+≤≤-.（1）求集合A ；（2）若B A ⊆，求实数m 的取值范围.5．已知集合A ＝x|x 2－3x －10≤0}，集合B ＝x|p ＋1≤x≤2p－1}．若B ⊆A ，求实数p 的取值参考答案一、单选题 1．C解析：从元素满足的公共属性的结构入手，对集合M 中的k 分奇数和偶数讨论，从而可得两集合的关系．详解：对于集合M ，当2()k m m =∈Z 时，,4222k m x m Z ππππ=+=+∈当21()k m m Z =-∈时，,4224k m x m Z ππππ=+=+∈∴{|,}{|,}2224m m M x x m Z x x m Z ππππ==+∈⋃=+∈ {|24k N x x ππ==+，}k Z ∈，M N ∴⊇,故选：C ．点睛：本题的考点是集合的包含关系判断及应用，解题的关键是对集合M 中的k 分奇数和偶数讨论，属于基础题. 2．D解析：根据A 与B 的交集为B ，得到B 为A 的子集，即可确定出a 的范围．详解：解：A B B =，B A ∴⊆，{|1A x x =<-或2}x >，{|11}B x a x a =-≤≤+，11a ∴+<-或12a ->，解得2a <-或3a >，故选：D ．点睛：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．解析：根据集合的定义，由m S ∈，l S ∈，得到2m S ∈，2l S ∈，即2m m ≥，21l ≤，然后利用一元二次不等式的解法化简后逐项判断. 详解：∵非空集合{}S x m x l =≤≤满足：当x S ∈时，有2x S ∈ ∴m S ∈，l S ∈，则2m S ∈，2l S ∈，且2m m ≥，21l ≤ 即0m ≤或1m ≥，01l ≤≤且1m①当1m =时，有1l =，所以{}1s =，故正确； ②当12m =时，214m S =∈，所以114l ≤≤，故正确；③当12l =时，2m S ∈，所以212m ≤，所以02m -≤≤，故正确； ④当1l =时，可知10m -≤≤或1m =，故正确；故选：D 点睛：本题主要考查集合的新定义，元素与集合的关系以及一元二次不等式的解法，还考查了逻辑推理、求解问题的能力，属于中档题. 4．B解析：通过分析两个集合的元素来确定正确选项. 详解：()()|21,,|2,44M x x k k Z N x x k k Z ππ⎧⎫⎧⎫==⋅-∈==⋅+∈⎨⎬⎨⎬⎩⎭⎩⎭，21k -为奇数，2k +为整数，所以M N ⊆.故选：B 5．C 详解：试题分析：∵{}1,4,2x A =，{}21,x B =，若B ⊆A ，则24x =或22x x =，解得2x =或2x =-或0x =．当2x =时，集合{}1,4,4A =不成立．当2x =-时，{}1,4,4A =-，{}1,4B =，满足条件B ⊆A ．当0x =时，{}1,4,0A =，{}1,0B =，满足条件B ⊆A ．故0x =或2x =-．故选C ．考点：集合的包含关系判断及应用．详解：本题考查的是集合的子集个数问题．由条件可知，，所以M 的子集个数为．应选D ．7．A解析：先任取11,64,,∈=+∈x A x m n m n Z ，分,m n 同为奇数或同为偶数和,m n 一奇一偶两种情况向集合B 进行变形，得到1108,,=+∈x a b a b Z 形式，说明1,∈x B 同理任取2,∈x B 2108,,=+∈x a b a b Z ，变形为()2642=++x a a b 说明2,∈x A 得到A B =.详解：任取11,64,,∈=+∈x A x m n m n Z当,m n 同为奇数或同为偶数时， 1108()2-=+n mx m 当,m n 一奇一偶时，1510(2)8()2-+=-+n m x m 因为,m n Z ∈所以2-∈n m Z ，52-+∈n m Z 所以1108,,=+∈x a b a b Z 所以1,∈x B任取2,∈x B 2108,,=+∈x a b a b Z ，()2642=++x a a b,∈a b Z ，2∴+∈a b Z所以2,∈x A 所以A B = 故选：A 点睛：本题主要考查了集合的包含关系的判断和应用，还考查了转化化归分类的思想，属于难题. 8．B解析：分别求出集合A 、B ，利用数轴即可得到答案. 详解：由已知，{}|3A x x =≥，{}|21B x x a =≥-，若A B ⊆，则213a -≤，解得2a ≤. 故选：B. 点睛：本题考查集合间的基本关系的应用，考查学生数形结合的思想，是一道基础题. 9．D解析：先化简{}{}|216|4xB x x x =<=<，再根据{}|,A x x a a R =≤∈，且A B 求解.详解：因为{}{}|216|4xB x x x =<=<，又因为{}|,A x x a a R =≤∈，且A B ，所以4a <. 故选：D 点睛：本题主要考查集合的基本运算，还考查了运算求解的能力，属于基础题. 10．B解析：通过分析集合中的元素,结合子集的概念可知选B. 详解：因为集合A 中的所有元素都是集合B 中的元素,所以集合A 是集合B 的子集,即A B ⊆, 又{0,1}A B B ⋂=≠. 故选:B. 点睛：本题考查了子集的概念,属于基础题.二、填空题 1．8 详解：集合-1,0,1}的子集有-1,0,1},-1,0},-1,1},0,1},-1},0},1},∅共8个.2．0m ≤解析：先求出集合B 中元素的范围，由A B =∅可得集合A 中的不等式2220mx x -+>在12x ≤≤时不成立，进而可得当12x ≤≤时，不等式2220mx x -+≤ 恒成立，转化为不等式恒成立可求实数m 的取值范围。

2022高中数学立体几何初步-简单几何体的表面积与体积第2课时球的表面积和体积课后提能训练新人教A版

第八章 8.3 第2课时A级——基础过关练1．(2021年长春月考)高为1的圆锥内接于半径为1的球，则该圆锥的体积为( ) A． B．C． D．π【答案】B　【解析】根据题意，高为1的圆锥内接于半径为1的球，则圆锥底面圆的半径r＝1，则该圆锥的体积为×πr2×h＝，故选B.2．已知球的表面积为16π，则它的内接正方体的表面积S的值是( )A．4π　B．32C．24 D．12π【答案】B　【解析】设球的内接正方体的棱长为a，由题意知球的半径为2，则3a2＝16，所以a2＝，正方体的表面积S＝6a2＝6×＝32.故选B.3．用与球心距离为1的平面去截球，所得截面圆的面积为π，则球的表面积为( ) A． B．C．8π D．【答案】C　【解析】设球的半径为R，则截面圆的半径为，∴截面圆的面积为S＝π＝(R2－1)π＝π.∴R2＝2.∴球的表面积S＝4πR2＝8π.4．把一个铁制的底面半径为r，高为h的实心圆锥熔化后铸成一个铁球，则这个铁球的半径为( )A． B．C． D．【答案】C　【解析】设铁球的半径为R，因为πr2h＝πR3，所以R＝.故选C.5．(2021年成都模拟)将直径为2的半圆绕直径所在的直线旋转半周而形成的曲面所围成的几何体的表面积为( )A．2π B．3πC．4π D．6π【答案】B　【解析】由题意知，该几何体为半球，表面积为大圆面积加上半个球面积，S＝π×12＋×4×π×12＝3π.6．若一个球的表面积与其体积在数值上相等，则此球的半径为________．【答案】3　【解析】设此球的半径为R，则4πR2＝πR3，R＝3.7．已知各顶点都在一个球面上的正四棱锥的高为3，体积为6，则这个球的表面积为________．【答案】16π　【解析】设正四棱锥的高为h，底面边长为a.由V＝a2h＝a2＝6，得a＝.由题意知球心在正四棱锥的高上，设球的半径为r，则(3－r)2＋()2＝r2，解得r＝2，则S球＝4πr2＝16π.8．已知两个正四棱锥有公共底面，且底面边长为4，两棱锥的所有顶点都在同一个球面上，若这两个正四棱锥的体积之比为1∶2，则该球的表面积为________．【答案】36π　【解析】∵两正四棱锥有公共底，且体积比为1∶2，∴它们的高之比为1∶2，设高分别为h，2h，球的半径为R，则h＋2h＝3h＝2R，∴R＝h.又∵底面边长为4，∴R2＝＝＋(2)2，解得h＝2，∴R＝3，∴S球＝4πR2＝36π.9．某组合体的直观图如图所示，它的中间为圆柱形，左右两端均为半球形，若图中r ＝1，l＝3，试求该组合体的表面积和体积．解：该组合体的表面积S＝4πr2＋2πrl＝4π×12＋2π×1×3＝10π.该组合体的体积V＝πr3＋πr2l＝π×13＋π×12×3＝.10．已知过球面上A，B，C三点的截面到球心的距离等于球半径的一半，且AB＝18，BC＝24，AC＝30，求球的表面积和体积．解：因为AB∶BC∶AC＝18∶24∶30＝3∶4∶5，所以△ABC是直角三角形，∠B＝90°.又球心O到截面△ABC的投影O′为截面圆的圆心，也即是Rt△ABC的外接圆的圆心，所以斜边AC为截面圆O′的直径(如图所示)．设O′C＝r，OC＝R，则球半径为R，截面圆半径为r.在Rt△O′CO中，由题设知sin ∠O′CO＝＝，所以∠O′CO＝30°，所以＝cos 30°＝，即R＝r，(*)又2r＝AC＝30⇒r＝15，代入(*)得R＝10.所以球的表面积为S＝4πR2＝4π×(10)2＝1 200π.球的体积为V＝πR3＝π×(10)3＝4 000π.B级——能力提升练11．已知长方体共顶点的三条棱长分别是3，4，x，且它的8个顶点都在同一个球面上．若这个球的表面积为125π，则x的值为( )A．5 B．6 C．8　D．10【答案】D　【解析】设球的半径为r，则4πr2＝125π，∴r2＝.又32＋42＋x2＝(2r)2，∴9＋16＋x2＝125，∴x2＝100，即x＝10.故选D.12．已知直三棱柱ABC－A1B1C1的6个顶点都在球O的球面上，若AB＝3，AC＝4，AB⊥AC，AA1＝12，则球O的表面积为( )A．153π B．160πC．169π D．360π【答案】C　【解析】由于直三棱柱的底面是直角三角形，所以可以把此三棱柱补成长方体，其体对角线就是外接球的直径，所以球O的半径R＝＝，所以球O的表面积S＝4π×＝169π，故选C.13．如果一个球的外切圆锥的高是这个球的半径的3倍，则圆锥的侧面积S1和球的表面积S2之比为( )A．4∶3 B．3∶1C．3∶2 D．9∶4【答案】C　【解析】画出轴截面如图所示，设球的半径为r，则OD＝r，PO＝2r，∠PDO＝90°，∴∠CPB＝30°.又∠PCB＝90°，∴CB＝PC＝r，PB＝2r，∴圆锥的侧面积S1＝π×r×2r＝6πr2，球的表面积S2＝4πr2，∴S1∶S2＝3∶2.14．若等边圆柱(轴截面是正方形)、球、正方体的体积相等，则它们的表面积的大小关系是( )A．S球＜S圆柱＜S正方体 B．S正方体＜S球＜S圆柱C．S圆柱＜S球＜S正方体 D．S球＜S正方体＜S圆柱【答案】A　【解析】设等边圆柱底面圆半径为r，球半径为R，正方体棱长为a，则πr2·2r＝πR3＝a3，＝，＝2π.S圆柱＝6πr2，S球＝4πR2，S正方体＝6a2，＝＝·＝＜1，＝＝·＝＞1.故选A.15．在封闭的直三棱柱ABC－A1B1C1内有一个体积为V的球．若AB⊥BC，AB＝6，BC＝8，AA1＝3，则V的最大值是________．【答案】　【解析】当球的半径最大时，球的体积最大．在直三棱柱内，当球和三个侧面都相切时，因为AB⊥BC，AB＝6，BC＝8，所以AC＝10，底面的内切圆的半径即为此时球的半径r ＝＝2，直径为4>侧棱．所以球的最大直径为3，半径为，此时体积V＝.16．(2021年沈阳月考)已知体积为的正三棱锥V－ABC的外接球的球心为O，满足OA＋OB＋OC＝0，则该三棱锥外接球的体积为________．【答案】π　【解析】由题意知，OA＋OB＝CO，说明正三角形ABC的顶点在球O的大圆上．设球的半径为R，则该三棱锥的底面正三角形ABC的高为，△ABC的边长为R，所以正三棱锥V－ABC的体积为××(R)2×R＝，解得R3＝4，则该三棱锥外接球的体积为πR3＝π.17．已知盛有水的圆柱形容器的内壁底面半径为5 cm，两个直径为5 cm的玻璃小球都浸没于水中．若取出这两个小球，则水面将下降多少厘米？解：设取出小球后，容器中的水面下降了h cm，两个小球的体积为V球＝2＝(cm3)．该体积等于它们在容器中排开水的体积V＝52×π·h，所以＝π×52×h，解得h＝.故取出这两个小球，水面将下降 cm.18．已知一倒置圆锥的母线长为10 cm，底面半径为6 cm.(1)求该圆锥的高；(2)若有一球刚好放进该圆锥(球与圆锥的底面相切)中，求这个球的半径以及此时圆锥剩余空间的体积．解：(1)设圆锥的高为h cm，底面半径为R cm，母线长为l cm，则h＝＝＝8，所以圆锥的高为8 cm.(2)球放入圆锥后的轴截面如图所示，设球的半径为r cm.易得△OCD∽△ACO1，则＝，即＝，解得r＝3.圆锥剩余空间的体积为圆锥的体积减去球的体积，即V圆锥－V球＝×π×62×8－π×33＝96π－36π＝60π(cm3)，故此时圆锥剩余空间的体积为60π cm3.C级——探索创新练19．有三个球，第一个球可内切于正方体，第二个球可与这个正方体的各条棱相切，第三个球可过这个正方体的各个顶点，这三个球的表面积之比为( )A．1∶∶ B．1∶4∶9C．1∶1∶1　D．1∶2∶3【答案】D　【解析】设正方体的棱长为2，则内切球的半径为1，与棱相切的球的半径就是正方体中相对棱的距离的一半，也就是面对角线长的一半为＝，外接球的半径为＝.∵球的表面积S＝4πR2，∴这三个球的表面积之比为4π×1∶4π×2∶4π×3＝1∶2∶3.故选D.。

高中数学人教A版2019必修第二册 8 6 2 直线与平面垂直的性质同步练习(解析版)

8.6.2 直线与平面垂直第2课时直线与平面垂直的性质基础巩固1．已知直线l ⊥平面α，直线m α⊂，则（）A ．l m ⊥B ．l ∥mC ．,l m 异面D ．,l m 相交而不垂直2．如图，点A α∈，点B α∈，点P α∉，PB α⊥，C 是α内异于A 和B 的动点，且PC AC ⊥，则动点C 在平面α内所组成的集合是（）A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．半圆D ．半圆，但要去掉两个点3．在长方体1111ABCD A B C D -中，M ，N 分别为11C D ，AB 的中点，4AB =，则MN 与平面11BCC B 的距离为（）A ．4B ．C ．2D 4．如图，l αβ=，点,A C α∈，点B β∈，且BA α⊥，BC β⊥，那么直线l 与直线AC 的关系是（）A ．异面B ．平行C ．垂直D ．不确定5．如图所示，如果MC ⊥菱形ABCD 所在的平面，那么MA 与BD 的位置关系是( )A ．平行B ．垂直相交C ．垂直但不相交D ．相交但不垂直6．在长方体1111ABCD A B C D -中，E ，F ，G ，H 分别为1AA ，1BB ，1CC ，1DD 的中点，14AA =，则平面ABCD 与平面EFGH 的距离为________.7．已知矩形ABCD 的边,3AB a BC ==，PA ⊥平面ABCD .若BC 边上有且只有一点M ，使PM DM ⊥，则a 的值为______.8．如图，PA ⊥平面ABD ，PC ⊥平面BCD ，E ，F 分别为BC ，CD 上的点，且EF AC ⊥.求证：CF CE DC BC=.能力提升9．如图所示，直线P A 垂直于⊙O 所在的平面，△ABC 内接于⊙O ，且AB 为⊙O 的直径，点M 为线段PB 的中点．现有结论：①BC ⊥PC ；②OM ∥平面APC ；③点B 到平面P AC 的距离等于线段BC 的长．其中正确的是( )A ．①②B ．①②③C ．①D ．②③10．如图，在直角梯形ABCD 中，BC DC ⊥，AE DC ⊥，M 、N 分别是AD 、BE 的中点，将三角形ADE 沿AE 折起，则下列说法正确的是______________.（1）不论D 折至何位置（不在平面ABC 内），都有//MN 平面DEC ；（2）不论D 折至何位置，都有MN AE ⊥；（3）不论D 折至何位置（不在平面ABC 内），都有//MN AB ；（4）在折起过程中，一定存在某个位置，使EC AD ⊥.11．如图所示，已知AF ⊥平面ABCD ，四边形ABEF 为矩形，四边形ABCD 为直角梯形，90DAB ∠=︒，AB //CD ，==2AD AF CD =，4AB =.（1）求证：AC ⊥平面BCE ；（2）求证：AD AE ⊥.素养达成12．如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且2MC MB =，求点C 到平面POM 的距离．8.6.2 直线与平面垂直第2课时直线与平面垂直的性质答案基础巩固1．已知直线l ⊥平面α，直线m α⊂，则（）A ．l m ⊥B ．C ．,l m 异面D ．,l m 相交而不垂直【答案】A【解析】根据线面垂直的定义，若直线与平面垂直，则直线垂直与该平面内的任意一条直线，因此 l m ⊥，故选A2．如图，点A α∈，点B α∈，点P α∉，PB α⊥，C 是α内异于A 和B 的动点，且PC AC ⊥，则动点C 在平面α内所组成的集合是（）A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．半圆D ．半圆，但要去掉两个点【答案】B 【解析】连接BC ，AB ，由于PC AC ⊥，PB AC ⊥，所以AC ⊥平面PBC ，BC ⊂平面PBC所以AC BC ⊥，说明动点C 在以AB 为直径的圆上，但不与点A B ，重合.所以B 正确故选：B3．在长方体1111ABCD A B C D -中，M ，N 分别为11C D ，AB 的中点，4AB =，则MN 与平面11BCC B 的距离为（）A ．4B ．C ．2 D【答案】C【解析】如图，MN ∥BC 1,又1BC ⊂平面11BCC B ，MN ∥平面11BCC B .∴MN 与平面11BCC B 的距离为N 到面11BCC B 的距离.又N 到平面11BCC B 的距离为122NB AB ==. ∴MN 与平面11BCC B 的距离为2.故选：C4．如图，l αβ=，点,A C α∈，点B β∈，且BA α⊥，BC β⊥，那么直线l 与直线AC 的关系是（）A ．异面B ．平行C ．垂直D ．不确定【答案】C【解析】BA α⊥，l αβ=，l α∴⊂，BA l ∴⊥；同理BC l ⊥；又BA BC B ⋂=，l ∴⊥平面ABC .AC ⊂平面ABC ，l AC ∴⊥.故选：C.5．如图所示，如果MC ⊥菱形ABCD 所在的平面，那么MA 与BD 的位置关系是( )A ．平行B ．垂直相交C ．垂直但不相交D ．相交但不垂直【答案】C 【解析】∵BD 是菱形ABCD 的一条对角线，菱形对角线互相垂直，∴AC ⊥BD .∵MC ⊥平面ABCD ，∴MC ⊥BD ，∵MC 和AC 相交于点C ，∴BD ⊥平面ACM ，∵MA ⊂平面AMC ，∴MA ⊥BD .又∵MA 与BD 是异面直线，∴MA 与BD 的位置关系是垂直但不相交.故选C.6．在长方体1111ABCD A B C D -中，E ，F ，G ，H 分别为1AA ，1BB ，1CC ，1DD 的中点，14AA =，则平面ABCD 与平面EFGH 的距离为________.【答案】2【解析】如图平面A BCD //平面EFGH又1AA ⊥平面ABCD .平面ABCD 与平面EFGH 的距离为1114222AA =⨯=. 故答案为：27．已知矩形ABCD 的边,3AB a BC ==，PA ⊥平面ABCD .若BC 边上有且只有一点M ，使PM DM ⊥，则a 的值为______. 【答案】32 【解析】PA ⊥平面ABCD ，DM ⊂平面ABCD ，PA DM ∴⊥.BC 边上存在点M ，使PM DM ⊥，且PM PA P ⋂=，DM ∴⊥平面PAM .AM ⊂平面,PAM DM AM ∴⊥，∴以AD 为直径的圆和BC 有公共点.3AD BC ==，∴圆的半径为32. ∴点M 是唯一的，BC ∴和半径为32的圆相切，32AB ∴=，即32a =. 故答案为：32． 8．如图，PA ⊥平面ABD ，PC ⊥平面BCD ，E ，F 分别为BC ，CD 上的点，且EF AC ⊥.求证：CF CE DC BC=.【答案】证明见解析【解析】∵PA ⊥平面ABD ，PC ⊥平面BCD ，又BD ⊂平面ABD ，,BD EF ⊂平面BCD∴PA BD ⊥，PC BD ⊥，PC EF ⊥.又PA PC P =，,PA PC ⊂平面PAC∴BD ⊥平面PAC .又EF AC ⊥，PC AC C =，,PC AC ⊂平面PAC ∴EF ⊥平面PAC ，∴EF //BD ，∴CF CE DC BC=. 能力提升9．如图所示，直线P A 垂直于⊙O 所在的平面，△ABC 内接于⊙O ，且AB 为⊙O 的直径，点M 为线段PB 的中点．现有结论：①BC ⊥PC ；②OM ∥平面APC ；③点B 到平面P AC 的距离等于线段BC 的长．其中正确的是( )A ．①②B ．①②③C ．①D ．②③【答案】B 【解析】对于①，∵P A ⊥平面ABC ，∴P A ⊥BC .∵AB 为⊙O 的直径，∴BC ⊥AC ，又∵P A ∩AC ＝A ，∴BC ⊥平面P AC ，又PC ⊂平面P AC ，∴BC ⊥PC ，对于②，∵点M 为线段PB 的中点，∴OM ∥P A ，∵P A ⊂平面P AC ，OM ⊄平面P AC ，∴OM ∥平面P AC ，对于③，由①知BC ⊥平面P AC ，∴线段BC 的长即是点B 到平面P AC 的距离，故①②③都正确．10．如图，在直角梯形ABCD 中，BC DC ⊥，AE DC ⊥，M 、N 分别是AD 、BE 的中点，将三角形ADE 沿AE 折起，则下列说法正确的是______________.（1）不论D 折至何位置（不在平面ABC 内），都有//MN 平面DEC ；（2）不论D 折至何位置，都有MN AE ⊥；（3）不论D 折至何位置（不在平面ABC 内），都有//MN AB ；（4）在折起过程中，一定存在某个位置，使EC AD ⊥.【答案】（1）（2）（4）【解析】折叠后如图，分别取,EC ED 中点,P Q ，连接,,NP PQ QM ，易知N 是,AC BE 的交点，因此N 也是AC 中点，而M 别是AD 的中点，∴////NP AE MQ ，12NP AE MQ ==，∴MNPQ 是平行四边形，∴//MN PQ ， MN ⊄平面DEC ，PQ ⊂平面DEC ，∴//MN 平面DEC ．（1）正确；折叠过程中,AE ED AE EC ⊥⊥保持不变，又EDEC E =，所以AE ⊥平面DEC ，从而AE PQ ⊥，所以AE MN ⊥，（2）正确；若//MN AB ，则,MN AB 共面，即,,,M N P Q 共面，从而直线,AM BN 共面，这样MN 在平面ABN 也即在平面ABC 内，矛盾，（3）错误；当ED EC ⊥时，又EC EA ⊥，而EDEA E =，∴EC ⊥平面ADE ，AD ⊂平面ADE ，所以EC AD ⊥．（4）正确．故答案为：（1）（2）（4）．11．如图所示，已知AF ⊥平面ABCD ，四边形ABEF 为矩形，四边形ABCD 为直角梯形，90DAB ∠=︒，AB //CD ，==2AD AF CD =，4AB =.（1）求证：AC ⊥平面BCE ；（2）求证：AD AE ⊥.【答案】（1）证明见解析；（2）证明见解析【解析】（1）在直角梯形ABCD 中，2AD CD ==，4AB =，则AC BC == 所以222AC BC AB +=，故AC BC ⊥.因为AF ⊥平面ABCD ，AF //BE ，所以BE ⊥平面ABCD ，所以BE AC ⊥. 又,BE BC ⊂平面BCE ，BEBC B =，所以AC ⊥平面BCE .（2）因为AF ⊥平面ABCD ，AD ⊂平面ABCD ，所以AF AD ⊥，又90DAB ∠=︒，所以AB AD ⊥. 又,AF AB ⊂平面ABEF ， AF AB A ⋂=，所以AD ⊥平面ABEF .又AE ⊂平面ABEF ，所以AD AE ⊥.素养达成12．如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且2MC MB =，求点C 到平面POM 的距离．【答案】（1）详见解析（2）5．【解析】（1）因为AP =CP =AC =4，O 为AC 的中点，所以OP ⊥AC ，且OP =连结OB ．因为AB =BC AC ，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB =12AC =2．由222OP OB PB +=知，OP ⊥OB ．由OP ⊥OB ，OP ⊥AC 知PO ⊥平面ABC ．（2）作CH ⊥OM ，垂足为H ．又由（1）可得OP ⊥CH ，所以CH ⊥平面POM ．故CH 的长为点C 到平面POM 的距离．由题设可知OC =12AC =2，CM =23BC ，∠ACB =45°．所以OM =3，CH =sin OC MC ACB OM ⋅⋅∠=5．所以点C 到平面POM。

高中数学人教A版选择性必修一精品专题讲练学生卷专题08 直线与圆综合大题归类

专题8 直线与圆综合大题归类目录【题型一】圆大题基础：轨迹 -圆 .......................................................................................................................... 1 【题型二】圆大题基础：轨迹 -直线 ...................................................................................................................... 2 【题型三】直线与圆：韦达定理型 .......................................................................................................................... 3 【题型四】直线与圆：定点 ...................................................................................................................................... 4 【题型五】直线与圆：定值 ...................................................................................................................................... 4 【题型六】直线与圆：定直线 .................................................................................................................................. 5 【题型七】探索性、存在性题型 .............................................................................................................................. 5 【题型八】面积与最值 .............................................................................................................................................. 6 【题型九】直线与圆的应用题 .................................................................................................................................. 7 培优第一阶——基础过关练 ...................................................................................................................................... 8 培优第二阶——能力提升练 ...................................................................................................................................... 9 培优第三阶——培优拔尖练 (11)【题型一】圆大题基础：轨迹 -圆【典例分析】（2021·全国·高二课时练习）已知A （3，3），点B 是圆x 2+y 2＝1上的动点，点M 是线段AB 上靠近A 的三等分点，则点M 的轨迹方程是（）A ．221(2)(2)9x y -+-=B ．221(2)(2)9x y -++=C ．221(3)(3)3x y -+-=D ．221(3)(3)3x y -++=1.（2022·全国·高二课时练习）已知直线1:310l mx y m --+=与2:310l x my m +--=相交于点P ，线段AB 是圆22:(1)(1)4C x y +++=的一条动弦，且||2AB =，则||PA PB +的最小值是（）A．B ．C．1 D ．22.（2017·北京海淀·高二期中）若动点P 在直线1:20l x y --=上，动点Q 在直线2:60l x y --=上，设线段PQ 的中点为00(,)M x y ，且2200(2)(2)8x y -++≤，则2200x y +的取值范围是__________．3.（2020·全国·高三专题练习）在平面直角坐标系xOy 中，已知,B C 为圆224x y +=上两点，点()1,1A ，且0AB AC ⋅=，()12AM AB AC =+，则OAM ∆面积的最大值为______.【题型二】圆大题基础：轨迹 -直线【典例分析】.（2022·全国·高二课时练习）已知点(),m n 在过()2,0-点且与直线20x y -=垂直的直线上，则圆C ：(()2214x y -++=上的点到点(),M m n 的轨迹的距离的最小值为（）A ．1B ．2C ．5D ．1.（2021·江苏·高二专题练习）已知圆221:4C x y +=与圆222:(1)(3)4C x y -+-=，过动点(,)P a b 分别作圆1C 、圆2C 的切线PM ，PN ，（,M N 分别为切点），若||||PM PN =，则226413a b a b +--+的最小值是A ．5B ．13C D ．852.（2020·全国·高二）已知圆1C ：221x y +=与圆2C ：22(2)(4)1x y -+-=，过动点()P a b ，分别作圆1C 、圆2C 的切线PM 、PN (M 、N 分别为切点），若PM PN =，的最小值是（）A B C D【题型三】直线与圆：韦达定理型【典例分析】（2021·广东·西樵高中高二阶段练习）已知过点(0,2)A 且斜率为k 的直线l 与圆22:(2)(3)1C x y -+-=交于M ，N 两点． (1)求k 的取值范围；(2)若12OM ON ⋅=，其中O 为坐标原点，求||MN ．（2021·江苏省镇江中学高二阶段练习）如图，已知图22:9C x y +=与x 轴的左右交点分别为A ，B ，与y 轴正半轴的交点为D ．（1）若直线l 过点(3,4)并且与圆C 相切，求直线l 的方程；（2）若点M ，N 是圆C 上第一象限内的点，直线AM ，AN 分别与y 轴交于点P ，Q ，点P 是线段OQ 中点，直线//MN BD ，求直线AM 的斜率．【题型四】直线与圆：定点【典例分析】（2022·四川省德阳中学校高二开学考试）已知两个定点()0,4A 、()0,1B ，动点P 满足2PA PB =，设动点P 的轨迹为曲线E ，直线:4l y kx =-．(1)求曲线E 的方程；(2)若1k =，Q 是直线l 上的动点，过Q 作曲线E 的两条切线QM 、QN ，切点为M 、N ，探究：直线MN 是否过定点？若过定点，求出定点的坐标；若不过定点，请说明理由．（2021·江苏·高二专题练习）在平面直角坐标系xOy 中，圆C ：22()()4x a y b -+-=与圆1C ：2268160x y x y +--+=相切于点6855A ⎛⎫⎪⎝⎭，，且直线l ：10x y +-=与圆C 有公共点．(1)求圆C 的方程；(2)设点P 为圆C 上的动点，直线l 分别与x 轴和y 轴交于点M ，N ． ①求证：存在定点B ，使得2PB PM =；①求当12PM PN +取得最小值时，直线PN 的方程．【题型五】直线与圆：定值【典例分析】（2022·江苏省如皋中学高二开学考试）已知直线:(2)(12)630l m x m y m ++-+-=与圆22:40C x y x +-=.(1)求证：直线l 过定点，并求出此定点坐标；(2)设O 为坐标原点，若直线l 与圆C 交于M ，N 两点，且直线OM ，ON 的斜率分别为1k ，2k ，则12k k +是否为定值？若是，求出该定值：若不是，请说明理由．【变式训练】（2021·湖南·怀化五中高二期中）已知圆C 的圆心坐标为(3,0)C ，且该圆经过点(0,4)A .(1)求圆C 的标准方程；(2)直线n 交圆C 于M ，N 两点，若直线AM ，AN 的斜率之积为2，求证：直线n 过一个定点，并求出该定点坐标.(3)直线m 交圆C 于M ，N 两点，若直线AM ，AN 的斜率之和为0，求证：直线m 的斜率是定值，并求出该定值.【题型六】直线与圆：定直线【典例分析】（2022·四川·遂宁中学高二开学考试（文））已知直线:1l x my =-，圆22:40C x y x ++=. (1)证明：直线l 与圆C 相交；(2)设l 与C 的两个交点分别为A 、B ，弦AB 的中点为M ，求点M 的轨迹方程；(3)在（2）的条件下，设圆C 在点A 处的切线为1l ，在点B 处的切线为2l ，1l 与2l 的交点为Q .试探究：当m 变化时，点Q 是否恒在一条定直线上？若是，请求出这条直线的方程；若不是，说明理由.【变式训练】（2021·江西·高二阶段练习（理））已知圆C 经过()(0,2,P Q 两点，圆心在直线0x y -=上.(1)求圆C 的标准方程；(2)若圆C 与y 轴相交于A ，B 两点（A 在B 上方）.直线:1l y kx =+与圆C 交于M ，N 两点，直线AM ，BN 相交于点T .请问点T 是否在定直线上？若是，求出该直线方程；若不是，说明理由.【题型七】探索性、存在性题型【典例分析】（2022·江苏·南京二十七中高二开学考试）已知圆C 过点()2,6A ，且与直线1:100l x y +-=相切于点()6,4B ． (1)求圆C 的方程；(2)过点()6,24P 的直线2l 与圆C 交于,M N 两点，若CMN △为直角三角形，求直线2l 的方程； (3)在直线3:2l y x =-上是否存在一点Q ，过点Q 向圆C 引两切线，切点为,E F ，使QEF △为正三角形，若存在，求出点Q 的坐标，若不存在，说明理由．【变式训练】（2021·江苏·高二专题练习）已知圆22:1O x y +=和点(1,4)M . (1)过M 作圆O 的切线，求切线的方程；(2)过M 作直线l 交圆O 于点C ，D 两个不同的点，且CD 不过圆心，再过点C ，D 分别作圆O 的切线，两条切线交于点E ，求证：点E 在同一直线上，并求出该直线的方程；(3)已知(2,8)A ，设P 为满足方程22106PA PO +=的任意一点，过点P 向圆O 引切线，切点为B ，试探究：平面内是否存在一定点N ，使得22PB PN 为定值？若存在，请求出定点N 的坐标，并指出相应的定值；若不存在，请说明理由.【题型八】面积与最值【典例分析】（2021·四川省遂宁市第二中学校高二期中（理））已知圆C ：222210x y x y +--+=，直线l 分别交x 轴，y 轴于A ，B 两点，O 为坐标原点，,OA a OB b ==(2,2)a b >>，且圆心C 到直线l 的距离为1.(1)求证：2)22()(a b --=；(2)设(3,1)N ，直线m 过线段CN 的中点M 且分别交x 轴与y 轴的正半轴于点P 、Q ，O 为坐标原点，求①POQ 面积最小时直线m 的方程； (3)求①ABC 面积的最小值.（2022·全国·高二课时练习）已知圆()()22:4C x a y b -+-=，圆心C 在直线y x =上，且被直线:2m x y +=截得弦长为（1）求圆C 的方程；（2）若0a ≤，点()0,1A ，过A 作两条直线l ，1l ，且满足1l l ⊥，直线l 交圆C 于M ，N 两点，直线1l 交圆C 于P ，Q 两点，求四边形PMQN 面积的最大值.【题型九】直线与圆的应用题【典例分析】（2022·江苏·高二）在①直线l 与B 、C 均相切，①直线l 截A 、B 、C 所得的弦长均相等，这两个条件中任选一个，补充在下面问题中，并求解该问题.问题：2020年是中国传统的农历“鼠年”，现用3个圆构成“卡通鼠”的头像.如图，()0,2A -是A 的圆心，且A 过原点；点B 、C 在x 轴上，B 、C 的半径均为1，B 、C 均与A 外切.直线l 过原点.若___________，求直线l 截A 所得的弦长.【变式训练】1（2022·全国·高二课时练习）赵州桥位于我国河北省，是我国现存最早､保存最好的巨大石拱桥.如图所示，它是一座空腹式的圆弧形石拱桥.(1)利用解析几何的方法，用赵州桥的跨度a 和圆拱高b 表示出赵州桥圆弧所在圆的半径r ； (2)已知37.02a =米，7.23b =米，计算半径r 的值.（结果保留2位小数）2.（2022·福建省永春第一中学高二期末）“跳台滑雪”是冬奥会中的一个比赛项目，俗称“勇敢者的游戏”，观赏性和挑战性极强．如图：一个运动员从起滑门点A 出发，沿着助滑道曲线())0f x b x =-≤≤滑到台端点B 起跳，然后在空中沿抛物线()()2200g x ax ax b x =-->飞行一段时间后在点C 着陆，线段BC 的长度称作运动员的飞行距离，计入最终成绩．已知()220g x ax ax b =--在区间[]0,30上的最大值为30-，最小值为70-．(1)求实数a ，b 的值及助滑道曲线AB 的长度．(2)若运动员某次比赛中着陆点C 与起滑门点A 的高度差为120米，求他的飞行距离（精确到米，5 2.236≈）．培优第一阶——基础过关练1.（2020·黑龙江·双鸭山一中高二阶段练习（理））由动点P 向圆221x y +=引两条切线PA 、PB 切点分别为A 、B ，若120APB ∠=︒，则动点P 的轨迹方程为__________．2.（2021·全国·高二期末）在平面直角坐标系xOy 中，点Q 为圆M ：22(1)(1)1x y -+-=上一动点，过圆M 外一点P 向圆M 引-条切线，切点为A ，若|P A |=|PO |，则||PQ 的最小值为（）A ．21-B ．21+C ．3214-D ．3214+3.（2021·江苏省响水中学高二阶段练习）已知圆C 过点P (1，1)，且与圆M ：2(2)x +＋22(y )+＝2r (r ＞0)关于直线x ＋y ＋2＝0对称．（1）求圆C 的方程；（2）设Q 为圆C 上的一个动点，求PQ MQ ⋅取得最小值时点Q 的坐标；（3）过点P 作两条相异直线分别与圆C 相交于A ，B ，且直线P A 和直线PB 的倾斜角互补，O 为坐标原点，试判断直线OP 和AB 是否平行？请说明理由．4.（2022·全国·高二课时练习）如图，在平面直角坐标系xOy 中，已知圆221:(1)1C x y ++=，圆222:(3)(4) 1.C x y -+-=设动圆C 同时平分圆1C ､圆2C 的周长.(1)求证：动圆圆心C 在一条定直线上运动.分阶培优练(2)动圆C 是否经过定点⋅若经过，求出定点的坐标;若不经过，请说明理由.5.（2021·广东·广州四十七中高二期中）在平面直角坐标系xOy 中，已知直线:20l x y ++=和圆22:1O x y +=，P 是直线l 上一点，过点P 作圆C 的两条切线，切点分别为A ，B ． (1)若PA PB ⊥，求点P 的坐标；(2)设线段AB 的中点为Q ，是否存在点T ，使得线段TQ 长为定值？若有在，求出点T ；若不存在，请说明理由．6.（2013·湖南长沙·一模（理））已知1,04A ⎛⎫⎪⎝⎭，点B 是y 轴上的动点，过B 作AB 的垂线l 交x 轴于点Q ，若()2,4,0AP AQ AB M +=.(1)求点P 的轨迹方程；(2)是否存在定直线x a =，以PM 为直径的圆与直线x a =的相交弦长为定值，若存在，求出定直线方程；若不存在，请说明理由．7.（2022·全国·高二单元测试）已知圆C 过坐标原点O 和点(6,A ，且圆心C 在x 轴上.(1)求圆C 的方程： (2)设点()10,0M -.①过点M 的直线l 与圆C 相交于P ，Q 两点，求当PCQ △的面积最大时直线l 的方程；①若点T 是圆C 上任意一点，试问：在平面上是否存在点N ，使得32TM TN =.若存在，求出点N 的坐标，若不存在，请说明理由.8.（2021·江苏·高二专题练习）圆C ：22(3)1x y +-=，点(,0)P t 为x 轴上一动点，过点P 引圆C 的两条切线，切点分别为M ，N . （1）若1t =，求切线方程；（2）若两条切线PM ，PN 与直线1y =分别交于A ，B 两点，求ABC 面积的最小值.9.（2021·江苏·扬州市江都区大桥高级中学高二阶段练习）如图，已知一艘海监船O 上配有雷达，其监测范围是半径为25 km 的圆形区域，一艘外籍轮船从位于海监船正东40 km 的A 处出发，径直驶向位于海监船正北30 km 的B 处岛屿，速度为28 km/h.问：这艘外籍轮船能否被海监船监测到？若能，持续时间多长？(要求用坐标法)培优第二阶——能力提升练1.（2021·山东·薛城区教育局教学研究室高二期中）已知圆()()22:254C x y -+-=，T 为圆C 外的动点，过点T 作圆C 的两条切线，切点分别为M 、N ，使TM TN ⋅取得最小值的点T 称为圆C 的萌点，则圆C 的萌点的轨迹方程为_______.2.（2017·重庆一中一模（理））过x 轴下方的一动点P 作抛物线2:2C x y =的两切线，切点分别为,A B ，若直线AB 到圆221x y +=相切，则点P 的轨迹方程为 A ．221(0)y x y -=< B ．22(2)1y x ++=C ．221(0)4y x y +=< D ．21x y =--3.（2021·新疆维吾尔自治区喀什第六中学高二阶段练习）已知直线l ：x +y +3＝0及圆C ：()()2239x a y -++=，令圆C 在x 轴同侧移动且与x 轴相切，（1）圆心在何处时，圆在直线l 上截得的弦最长；（2）C 在何处时，l 与y 轴的交点把弦分成1：3；（3）当圆C 移动过程中与直线l 交于A ，B 两点时，求OA ·OB 的取值范围.4.（2022·全国·高二课时练习）已知两个定点A （-4，0），B （-1，0），动点P 满足|P A |=2|PB |.设动点P 的轨迹为曲线E ，直线l ：y =kx -4. （1）求曲线E 的方程；（2）若直线l 与曲线E 交于不同的C ，D 两点，且①COD =90°（O 为坐标原点），求直线l 的斜率；（3）若k =12，Q 是直线l 上的动点，过Q 作曲线E 的两条切线QM ，QN ，切点为M ，N ，探究：直线MN 是否过定点.5.（2022·四川·盐亭中学高二开学考试）①圆心C 在直线:2780l x y -+=上，圆C 过点B (1，5)；①圆C 过直线:3580l x y +-=和圆226160x y y ++-=的交点；在①①这两个条件中任选一个，补充在下面的问题中进行求解．已知圆C 经过点A (6，0)，且 . (1)求圆C 的标准方程；(2)过点P (0，1)的直线l 与圆C 交于M ，N 两点 ①求弦M N 中点Q 的轨迹方程； ①求证PM PN ⋅为定值.注：若选择多个条件分别解答，按第一个解答计分. 6.（2021·安徽·高二阶段练习）已知圆C 过原点，圆心C 是直线2y x =+与直线22y x =-+的交点.(1)求圆C 的标准方程；(2)若圆C 与y 轴交于A ､B 两点（A 在B 上方），直线:1l y kx =+与圆C 交于M ､N 两点，直线AM ，BN 相交于T .请问点T 是否在定直线上？若是，求出该直线方程；若不是，说明理由.7.（2021·江西省铜鼓中学高二期中（文））已知点(2,0)P 及圆C ：226490x y x y +-++=. （1）若直线l 过点P 且与圆C 相切，求直线l 的方程；（2）设过P 直线1l 与圆C 交于M 、N 两点，当MN =求以MN 为直径的圆的方程；（3）设直线10ax y -+=与圆C 交于A ，B 两点，是否存在实数a ，使得过点(2,0)P 的直线2l 垂直平分弦AB ？若存在，求出实数a 的值.8.（2021·江苏·高二专题练习）如图，已知圆O ①224x y +=，过点E (1，0)的直线l 与圆相交于A ，B 两点.（1）当|AB l 的方程；（2）已知D 在圆O 上，C (2，0)，且AB ①CD ，求四边形ACBD 面积的最大值.9.（2022·全国·高二课时练习）河北省赵县的赵州桥是世界上著名的单孔石拱桥，它的跨度是37.02m ，圆拱高约为7.2m ，自建坐标系，求这座圆拱桥的拱所在圆的标准方程.（精确到0.01m ）培优第三阶——培优拔尖练1.（2021·江苏·高二专题练习）已知圆:O 229x y +=与x 轴交于点A 、B ，过圆上动点M (M 不与A 、B 重合)作圆O 的切线l ，过点A 、B 分别作x 轴的垂线，与切线l 分别交于点,C D ，直线CB 与AD 交于点Q ，Q 关于M 的对称点为P ，则点P 的轨迹方程为_______2.（2021·广东·湛江市第四中学高二期中）过点(,)P x y 作圆221:1C x y +=与圆222:(2)(2)1C x y -+-=的切线，切点分别为A ､B ，若PA PB =，则22x y +的最小值为（）AB ．2C ．D ．83.（2021·北京铁路二中高二期中）已知圆C 的圆心坐标为(3,0)C ，且该圆经过点(0,4)A .(1)求圆C 的标准方程；(2)若点B 也在圆C 上，且弦AB 长为8，求直线AB 的方程；(3)直线l 交圆C 于M ，N 两点，若直线,AM AN 的斜率之和为0，求直线l 的斜率.4.（2022·全国·高二课时练习）知圆22:4O x y +=，点P 是直线:4l x =上的动点．（1）若从点P 到圆O 的切线长为P 的坐标以及两条切线所夹的劣弧长；（2）若点()2,0A -，()2,0B ，直线PA ，PB 与圆O 的另一交点分别为M ，N ，求证：直线MN 经过定点()1,0Q ．5.（2021·全国·高二专题练习）已知点(4,0)A 和(4,4)B ，圆C 与圆22(1)(2)4x y -++=关于直线2450x y --=对称．(1)求圆C 的方程；(2)点P 是圆C 上任意一点，在x 轴上求出一点M （异于点)A 使得点P 到点A 与M 的距离之比PA PM 为定值，并求12PB PA +的最小值．6.（2021·四川省绵阳南山中学高二阶段练习）已知圆O ：224x y +=与x 轴的负半轴交于点P ，过点()1,0Q 且不与坐标轴重合的直线与圆O 交于A ，B 两点.（1）设直线PA ，PB 的斜率分别是1k ，2k ，试问12k k ⋅是否为定值？若是定值，求出该定值，若不是定值，请说明理由.（2）延长PA ，与直线4x =相交于点R ，证明：PBR △的外接圆必过除P 点之外的另一个定点，并求出该点坐标.7.（2020·江苏·苏州大学附属中学高二开学考试）已知圆22:1O x y +=，圆()()221:231O x y -+-=过1O 作圆O 的切线，切点为T （T 在第二象限）.（1）求1OO T ∠的正弦值；（2）已知点(),P a b ，过P 点分别作两圆切线，若切线长相等，求,a b 关系；（3）是否存在定点(),M m n ，使过点M 有无数对相互垂直的直线12,l l 满足12l l ⊥，且它们分别被圆O 、圆1O 所截得的弦长相等？若存在，求出所有的点M ；若不存在，请说明理由.8.（2020·安徽省太和第一中学高二期中）已知圆M 的圆心M 在x 轴上，半径为1，直线l ：4132y x =-被圆M M 在直线l 的下方. （1）求圆M 的方程；（2）设(0,),(0,6)(52)A t B t t +-≤≤-，若圆M 是△ABC 的内切圆，求△ABC 的面积S 的范围.9.（2022·全国·高二课时练习）如图，某海面上有O ，A ，B 三个小岛（面积大小忽略不计），A岛在O 岛的北偏东45°方向距O 岛B 岛在O 岛的正东方向距O 岛20千米处．以O 为坐标原点，O 的正东方向为x 轴的正方向，1千米为一个单位长度，建立平面直角坐标系．圆C 经过O ，A ，B 三点．(1)求圆C 的方程；(2)若圆C 区域内有未知暗礁，现有一船D 在O 岛的南偏西30°方向距O 岛40千米处，正沿着北偏东45°方向行驶，若不改变方向，试问该船有没有触礁的危险?。

高中数学第八章立体几何初步基本立体图形第1课时棱柱棱锥棱台的结构特征课后提能训练新人教A版必修第二册

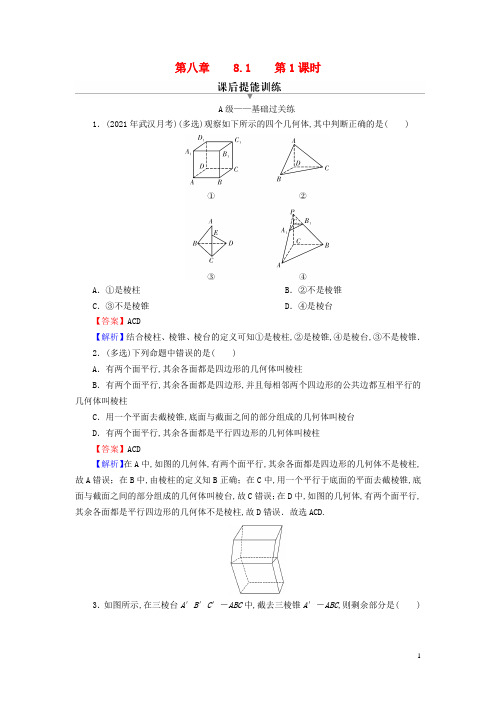
第八章 8.1 第1课时A级——基础过关练1．(2021年武汉月考)(多选)观察如下所示的四个几何体,其中判断正确的是( )A．①是棱柱B．②不是棱锥C．③不是棱锥D．④是棱台【答案】ACD【解析】结合棱柱、棱锥、棱台的定义可知①是棱柱,②是棱锥,④是棱台,③不是棱锥．2．(多选)下列命题中错误的是( )A．有两个面平行,其余各面都是四边形的几何体叫棱柱B．有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱C．用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台D．有两个面平行,其余各面都是平行四边形的几何体叫棱柱【答案】ACD【解析】在A中,如图的几何体,有两个面平行,其余各面都是四边形的几何体不是棱柱,故A错误；在B中,由棱柱的定义知B正确；在C中,用一个平行于底面的平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台,故C错误；在D中,如图的几何体,有两个面平行,其余各面都是平行四边形的几何体不是棱柱,故D错误．故选ACD.3．如图所示,在三棱台A′B′C′－ABC中,截去三棱锥A′－ABC,则剩余部分是( )A．三棱锥B．四棱锥C．三棱柱D．组合体【答案】B【解析】余下部分是四棱锥A′－BCC′B′.4．下列三种叙述,正确的有( )①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台；②两个底面平行且相似,其余各面都是梯形的多面体是棱台；③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台．A．0个B．1个C．2个D．3个【答案】A【解析】①中的平面不一定平行于底面,故①错；②③可用如图的反例检验,故②③错．故选A.5．下列图形中,不能折成三棱柱的是( )【答案】C【解析】C中,两个底面均在上面,因此不能折成三棱柱,其余均能折成三棱柱．6．四棱柱有________条侧棱,________个顶点．【答案】4 8【解析】四棱柱有4条侧棱,8个顶点(可以结合正方体观察求得)．7．对如图所示的几何体描述正确的是________(写出正确结论的序号)．①这是一个六面体；②这是一个四棱台；③这是一个四棱柱；④此几何体可由三棱柱截去一个小三棱柱而得到；⑤此几何体可由四棱柱截去一个小三棱柱而得到．【答案】①③④⑤【解析】在①中,∵这个几何体有六个面,∴这是个六面体,故①正确；在②中,∵这个几何体的侧棱延长后不能交于同一点,所以这不是个四棱台,故②错误；在③中,如果把这个几何体的正面或背面作为底面就会发现这是一个四棱柱,故③正确；在④中,如图1所示,此几何体可由三棱柱截去一个小三棱柱而得到,故④正确；在⑤中,如图2所示,此几何体可由四棱柱截去一个小三棱柱而得到,故⑤正确．故选①③④⑤.图1 图28．如图,M是棱长为2 cm的正方体ABCD－A1B1C1D1的棱CC1的中点,沿正方体表面从点A 到点M的最短路程是________cm.【答案】13【解析】由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2 cm,3 cm,故两点之间的距离是13 cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间的距离是17 cm.故沿正方体表面从点A到点M的最短路程是13 cm.9．如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.(1)折起后形成的几何体是什么几何体？(2)这个几何体共有几个面,每个面的三角形有何特点？(3)每个面的三角形面积为多少？解：(1)如图,折起后的几何体是三棱锥．(2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE和△DPF 均为直角三角形．(3)S △PEF ＝12a 2,S △DPF ＝S △DPE ＝12×2a ·a ＝a 2,S △DEF ＝S 正方形ABCD －S △PEF －S △DPF －S △DPE ＝(2a )2－12a 2－a 2－a 2＝32a 2. 10．如图所示,长方体ABCD －A 1B 1C 1D 1.(1)这个长方体是棱柱吗？如果是,则该图形是几棱柱？为什么？(2)用平面BCNM 把这个长方体分成两部分,各部分形成的几何体还是棱柱吗？如果是,则该图形是几棱柱,并用符号表示；如果不是,请说明理由．解：(1)是棱柱,并且是四棱柱,因为长方体相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义．(2)截面BCNM 的上方部分是三棱柱BB 1M －CC 1N ,下方部分是四棱柱ABMA 1－DCND 1.B 级——能力提升练11．下列命题中,真命题是( )A ．顶点在底面上的投影到底面各顶点的距离相等的三棱锥是正三棱锥B ．底面是正三角形,各侧面是等腰三角形的三棱锥是正三棱锥C ．顶点在底面上的投影为底面三角形的垂心的三棱锥是正三棱锥D ．底面是正三角形,并且侧棱都相等的三棱锥是正三棱锥【答案】D【解析】对于选项A,到三角形各顶点距离相等的点为三角形外心,该三角形不一定为正三角形,故该命题是假命题；对于选项B,如图所示,△ABC 为正三角形,若PA ＝PB ＝AB ＝BC ＝AC ≠PC ,△PAB ,△PBC ,△PAC 都是等腰三角形,但它不是正三棱锥,故该命题是假命题；对于选项C,顶点在底面上的投影为底面三角形的垂心,底面为任意三角形皆可,故该命题是假命题；对于选项D,顶点在底面上的投影是底面三角形的外心,又因为底面三角形为正三角形,所以外心即为中心,故该命题是真命题．故选D.12．(2021年焦作模拟)如图所示都是正方体的表面展开图,还原成正方体后,其中两个完全一样的是( )A ．①②B ．②③C ．③④D ．①④【答案】B 【解析】在图②③中,5不动,把图形折起,则2,5为对面,1,4为对面,3,6为对面,故图②③完全一样,而图①④则不同．13．五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱的对角线共有________条．【答案】10【解析】在上底面选一个顶点,同时在下底面选一个顶点,且这两个顶点不在同一侧面上,这样上底面每个顶点对应两条对角线,所以共有10条．14．给出两块正三角形纸片(如图所示),要求将其中一块剪拼成一个底面为正三角形的三棱锥模型,另一块剪拼成一个底面是正三角形的三棱柱模型,请设计一种剪拼方案,分别用虚线标示在图中,并作简要说明．解：如图1所示,沿正三角形三边中点连线折起,可拼得一个底面为正三角形的三棱锥．图1 图2如图2所示,在正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的14,有一组对角为直角,余下部分按虚线折成,可成为一个缺上底的底面为正三角形的三棱柱,而剪出的三个相同的四边形恰好拼成这个底面为正三角形的棱柱的上底．C 级——探索创新练15．(2021年哈尔滨月考)如图,在长方体ABCD －A 1B 1C 1D 1中,AB ＝3,BC ＝4,A 1A ＝5,现有一只甲壳虫从点A 出发沿长方体表面爬行到点C 1来获取食物,试画出它的最短爬行路线,并求其路程的最小值．解：把长方体的部分面展开,如图,有三种情况．对甲、乙、丙三种展开图利用勾股定理可得AC1的长分别为90,74,80,由此可见乙是最短线路,所以甲壳虫可以先在长方形ABB1A1内由A到E,再在长方形BCC1B1内由E到C1,也可以先在长方形AA1D1D内由A到F,再在长方形DCC1D1内由F到C1,其最短路程为74.。

高中数学必修二第八章立体几何初步必练题总结(带答案)

高中数学必修二第八章立体几何初步必练题总结单选题1、已知圆锥的底面半径为R ，高为3R ，在它的所有内接圆柱中，全面积的最大值是（） A ．2πR 2B ．94πR 2C ．83πR 2D ．πR 2 答案：B分析：根据圆柱的表面积公式以及二次函数的性质即可解出．设圆柱的底面半径为r ，圆柱的高为ℎ，所以在轴截面三角形中，如图所示：由相似可得，rR =3R−ℎ3R，所以，ℎ=3R −3r ，即圆柱的全面积为S =2πr 2+2πrℎ=2πr 2+2πr (3R −3r )=2π(−2r 2+3rR )=2π[−2(r −34R)2+98R 2]≤9π4R 2，当且仅当r =34R 时取等号．故选：B ．2、已知球O 的体积为36π，则该球的表面积为（） A ．6πB ．9πC ．12πD ．36π 答案：D分析：根据球的体积公式求出半径，即可求出表面积. 设球的体积为R ，则由题可得43πR 3=36π，解得R =3，则该球的表面积为4π×32=36π. 故选：D.3、在△ABC 中，AB =1，AC =2，∠BAC =60°，P 是△ABC 的外接圆上的一点，若AP ⃑⃑⃑⃑⃑ =mAB ⃑⃑⃑⃑⃑ + nAC ⃑⃑⃑⃑⃑ ，则m +n 的最小值是（）A ．−1B ．−12C ．−13D ．−16答案：B分析：先解三角形得到△ABC 为直角三角形，建立直角坐标系，通过AP ⃑⃑⃑⃑⃑ =mAB ⃑⃑⃑⃑⃑ + nAC ⃑⃑⃑⃑⃑ 表示出m +n ，借助三角函数求出最小值.由余弦定理得BC 2=AB 2+AC 2−2AB ⋅AC ⋅cos∠BAC = 1+4−2×1×2×cos 60∘=3，所以BC =√3，所以AB 2+BC 2=AC 2，所以AB ⊥BC ．以AC 的中点为原点，建立如图所示的平面直角坐标系，易得A （－1，0），C （1，0），B （－12，√32），设P 的坐标为(cosθ,sinθ)，所以AB⃑⃑⃑⃑⃑ =(12,√32)，AC ⃑⃑⃑⃑⃑ =(2,0)，AP ⃑⃑⃑⃑⃑ = (cosθ+1,sinθ)，又AP ⃑⃑⃑⃑⃑ =mAB ⃑⃑⃑⃑⃑ +nAC ⃑⃑⃑⃑⃑ ，所以(cosθ+1,sinθ)=m (12,√32)+ n (2,0)=(m2+2n ,√32m)，所以m =2√33sin θ，n =cos θ2+12−√36sin θ，所以m +n =2√33sin θ+cos θ2+12−√36sin θ =√32sin θ+cos θ2+12=sin (θ+π6)+12≥−1+12=−12，当且仅当sin (θ+π6)=−1时，等号成立．故选：B ．4、如图，矩形BDEF 所在平面与正方形ABCD 所在平面互相垂直，BD =2，DE =1，点P 在线段EF 上.给出下列命题：①存在点P ，使得直线DP//平面ACF ；②存在点P，使得直线DP⊥平面ACF；③直线DP与平面ABCD所成角的正弦值的取值范围是[√55,1]；④三棱锥A−CDE的外接球被平面ACF所截得的截面面积是9π8.其中所有真命题的序号（）A．①③B．①④C．①②④D．①③④答案：D分析：当点P是线段EF中点时判断①；假定存在点P，使得直线DP⊥平面ACF，推理导出矛盾判断②；利用线面角的定义转化列式计算判断③；求出△ACF外接圆面积判断④作答.取EF中点G，连DG，令AC∩BD=O，连FO，如图，在正方形ABCD中，O为BD中点，而BDEF是矩形，则DO//GF且DO=GF，即四边形DGFO是平行四边形，即有DG//FO，而FO⊂平面ACF，DG⊄平面ACF，于是得DG//平面ACF，当点P与G重合时，直线DP//平面ACF，①正确；假定存在点P，使得直线DP⊥平面ACF，而FO⊂平面ACF，则DP⊥FO，又DG//FO，从而有DP⊥DG，在Rt△DEF中，∠DEF=90∘，DG是直角边EF上的中线，显然在线段EF上不存在点与D连线垂直于DG，因此，假设是错的，即②不正确；因平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD=BD，则线段EF上的动点P在平面ABCD上的射影在直线BD上，于是得∠PDB是直线DP与平面ABCD所成角的，在矩形BDEF中，当P与E不重合时，∠PDB=∠DPE，sin∠PDB=sin∠DPE=DEDP =√DE2+EP2=√1+EP2，而0<EP≤2，则√55≤sin∠PDB<1，当P与E重合时，∠PDB=π2，sin∠PDB=1，因此，√55≤sin∠PDB≤1，③正确；因平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD=BD，BF⊥BD，BF⊂平面BDEF，则BF⊥平面ABCD，BC=√2，在△ACF中，AF=CF=√BC2+BF2=√3，显然有FO⊥AC，sin∠FAC=FOAF =√BO2+BF2AF=√2√3，由正弦定理得△ACF外接圆直径2R=CFsin∠FAC =√2，R=2√2，三棱锥A−CDE的外接球被平面ACF所截得的截面是△ACF的外接圆，其面积为πR2=9π8，④正确，所以所给命题中正确命题的序号是①③④.故选：D小提示：名师点评两个平面互相垂直，则一个平面内任意一点在另一个平面上的射影都在这两个平面的交线上.5、正方体中，点P，O，R，S是其所在棱的中点，则PQ与RS是异面直线的图形是（）A．B．C．D．答案：C分析：对于A，B，D，利用两平行线确定一个平面可以证明直线PQ与RS共面，对于C，利用异面直线的定义推理判断作答．对于A，在正方体ABCD−A1B1C1D1中，连接AC，A1C1，则AC//A1C1，如图，因为点P，Q，R，S是其所在棱的中点，则有PQ//AC，RS//A1C1，因此PQ//RS，则直线PQ与RS共面，A错误；对于B，在正方体ABCD−A1B1C1D1中，连接AC，QS，PR，如图，因为点P，Q，R，S是其所在棱的中点，有AP//CR且AP=CR，则四边形APRC为平行四边形，即有AC//PR，又QS//AC，因此QS//PR，直线PQ与RS共面，B错误；对于C，在正方体ABCD−A1B1C1D1中，如图，因为点P，Q，R，S是其所在棱的中点，有RS//BB1，而BB1⊂平面ABB1A1，RS⊄平面ABB1A1，则RS//平面ABB1A1，PQ⊂平面ABB1A1，则直线PQ与RS无公共点，又直线PQ与直线BB1相交，于是得直线PQ与RS不平行，则直线PQ与RS是异面直线，C正确；对于D，在正方体ABCD−A1B1C1D1中，连接A1B，D1C，PS，QR，如图，因为A1D1//BC且A1D1=BC，则四边形A1D1CB为平行四边形，有A1B//D1C，因为点P，Q，R，S是其所在棱的中点，有PS//A1B，QR//D1C，则PS//QR，直线PQ与RS共面，D错误.故选：C6、下面四个选项中一定能得出平面α/⁄平面β的是（）A．存在一条直线a，a//α，a//βB．存在一条直线a，a⊂α，a//βC．存在两条平行直线a，b，a⊂α，b⊂β，a//β，b//αD．存在两条异面直线a，b，a⊂α，b⊂β，a//β，b//α答案：D分析：对于A，B，C，举出符合条件的特例即可判断；对于D，过直线a作平面γ∩β=c，再证c//α即可. 如图，ABCD−A1B1C1D1是长方体，平面ABCD为平面α，平面ABB1A1为平面β，对于A，直线C1D1为直线a，显然a//α，a//β，而α与β相交，A不正确；对于B，直线CD为直线a，显然a⊂α，a//β，而α与β相交，B不正确；对于C，直线CD为直线a，直线A1B1为直线b，显然a⊂α，b⊂β，a//β，b//α，而α与β相交，C不正确；对于D，因a，b是异面直线，且a⊂α，b⊂β，过直线a作平面γ∩β=c，如图，则c//a，并且直线c与b必相交，而c⊄α，于是得c//α，又b//α，即β内有两条相交直线都平行于平面α，⁄平面β.因此，平面α/故选：D7、已知直线l⊥平面α，有以下几个判断：①若m⊥l，则m//α；②若m⊥α，则m//l；③若m//α，则m⊥l；④若m//l，则m⊥α；上述判断中正确的是（）A．①②③B．②③④C．①③④D．①②④答案：B分析：根据线面的位置关系，线面垂直的性质定理，线面平行的性质定理及线面垂直的性质逐项分析即得. 对于①，当m⊂平面α也可以有m⊥l，但m不平行于平面α，故①错；对于②，根据线面垂直的性质定理可知②正确；对于③，根据线面平行的性质定理可得存在n⊂α且m∥n．而直线l⊥平面α，故可根据线面垂直的性质得出l⊥n，故l⊥m正确；对于④，根据直线l⊥平面α，可在平面α内找到两条相交直线p，n，且l⊥p，l⊥n，又m∥l，所以m⊥p，m⊥n，故根据线面垂直的判定定理可知，m⊥α正确．即②③④正确．故选：B．8、圆柱的底面直径与高都等于球的直径，则球的表面积与圆柱的侧面积的比值为（）A．1∶1B．1∶2C．2∶1D．2∶3答案：A分析：按圆柱侧面积和球的表面积公式计算即可.设球的半径的r，依题意圆柱的底面半径也是r，高是2r，圆柱的侧面积=2πr·2r=4πr2，球的表面积为4πr2，其比例为1:1，故选：A.多选题9、如图，在棱长为2的正方体ABCD−A1B1C1D1中，M，N，P分别是C1D1，C1C，A1A的中点，则（）A．M，N，B，D1四点共面B．异面直线PD1与MN所成角的余弦值为√1010C．平面BMN截正方体所得截面为等腰梯形D．三棱锥P−MNB的体积为13答案：BCD分析：根据直线与直线的位置关系判定A；由异面直线所成角求解判定B；作出截面判定C；由体积公式判定D对于A，易知MN与BD1为异面直线，所以M，N，B，D1不可能四点共面，故A错误；对于B，连接CD1，CP，易得MN//CD1，所以∠PD1C为异面直线PD1与MN所成角，设AB=2，则CD1=2√2，D1P=√5，PC=3，所以cos∠PD1C=√2)2√5)222×2√2×√5=√1010，所以异面直线PD1与MN所成角的余弦值为√1010，故B正确；对于C，连接A1B，A1M，易得A1B//MN，所以平面BMN截正方体所得截面为梯形MNBA1，故C正确；对于D，易得D1P//BN，因为D1P⊄平面MNB，MN⊂平面MNB，所以D1P//平面MNB，所以V P−MNB=V D1−MNB =V B−MND1=13×12×1×1×2=13，故D正确.故选：BCD10、已知两条不重合的直线a和b两个不重合的平面α和β，则下列说法不正确的为（）A．若a∥α，b∥α，则a∥bB．若a⊂α，b⊂β，则a，b为异面直线C．若a∥b，a⊂α，则b∥α或b⊂αD．若a⊂α，b⊂α，a∥β，b∥β，则α∥β答案：ABD分析：根据线线，线面，面面的位置关系的概念想象，构造，即可做出判定.解：对于A，若a∥α，b∥α，则a∥b或a与b相交或a与b异面，故A错误；对于B，若a⊂α，b⊂β，则a，b的位置关系是平行、相交或异面，故B错误；对于C，若a∥b，a⊂α，则b∥α或b⊂α，故C正确；对于D，若a⊂α，b⊂α，a∥β，b∥β，则α∥β或α与β相交，添加条件a与b相交时，可得α∥β，故D错误．故选：ABD．小提示：本题考查空间中直线与直线、直线与平面位置关系的判定，考查空间想象能力与思维能力，是基础题．关键是空间想象,构造，不必严格使用相关定理论证.11、（多选）圆柱的侧面展开图是边长分别为2a，a的矩形，则圆柱的体积为（）A．a3πB．a32πC．a33πD．a34π答案：AB分析：按圆的高分类讨论，求出底面半径后由体积公式计算．设圆柱底面半径为r，若高是a，则2πr=2a，r=aπ，V=πr2a=π×(aπ)2×a=a3π，若高是2a，则2πr=a，r=a2π，V=πr2⋅2a=π×(a2π)2×2a=a32π．故选：AB．填空题12、已知一三角形ABC用斜二测画法画出的直观图是面积为√3的正三角形A′B′C′(如图)，则三角形ABC中边长与正三角形A′B′C′的边长相等的边上的高为______．答案：2√6分析：根据面积公式求出三角形的边长，以及高，利用斜二测画法的原理还原出原三角形的高，并求出答案. 设正三角形A′B′C′的边长为a，∵S△A′B′C′=√34a2=√3∴a=2，DC′=√3O′C′=√6∴O′C=2√6所以答案是：2√6.13、如图，已知棱长为2的正方体ABCD−A1B1C1D1中，点P在线段B1C上运动，给出下列结论：①异面直线AP与DD1所成的角范围为[π3,π2 ]；②平面PBD1⊥平面A1C1D；③点P到平面A1C1D的距离为定值2√33；④存在一点P，使得直线AP与平面BCC1B1所成的角为π3. 其中正确的结论是___________.答案：②③解析：数形结合说明异面直线AP 与DD 1所成的角的范围为[π4,π2]，故①错误；证明BD 1⊥平面A 1C 1D ，所以平面PBD 1⊥平面A 1C 1D ，故②正确；点P 到平面A 1C 1D 的距离为定值，且等于BD 1的13，即2√33，故③正确；AP与平面BCC 1B 1所成的角为∠APB ,tan ∠APB 最大值为√2<tan π3，故④不正确.对于①，当P 在C 点时，DD 1⊥AC ，异面直线AC 与DD 1所成的角最大为π2，当P 在B 1点时，异面直线AB 1与DD 1所成的角最小为∠D 1DC =π4，所以异面直线AP 与DD 1所成的角的范围为[π4,π2]，故①错误；对于②，如图，因为A 1C 1⊥B 1D 1,A 1C 1⊥B 1B,B 1D 1∩B 1B,B 1D 1,B 1B ⊂平面BB 1D ,所以A 1C 1⊥BD 1,同理DC 1⊥BD 1,又因为A 1C 1∩DC 1=C 1,A 1C 1,DC 1⊂平面DA 1C 1,所以BD 1⊥平面A 1C 1D ，所以平面PBD 1⊥平面A 1C 1D ，故②正确；对于③，因为B 1C //A 1D, B 1C ⊄平面A 1C 1D ,A 1D ⊂平面A 1C 1D ,所以B 1C //平面A 1C 1D ，所以点P 到平面A 1C 1D 的距离为定值，且等于BD 1的13，即2√33，故③正确；对于④，直线AP 与平面BCC 1B 1所成的角为∠APB ，tan∠APB =ABBP ，当BP ⊥B 1C 时，BP 最小，tan∠APB 最大，最大值为√2<tan π3，故④不正确，所以答案是：②③.小提示：关键点睛：解答本题的关键是判断命题①④的真假，它们都是求空间的角，它们都是利用数形结合的方法求空间角的最值，对于数形结合的这种数学思想要注意灵活运用.14、如图，在三棱锥P −ABC 中，平面EFMN 平行于对棱AC,PB,AC =PB =2,AC ⊥PB ，截面EFMN 面积的最大值是______.答案：1分析：由线面平行的性质可得AC//EN 、AC//MF 且PB//EF 、PB//MN ，易得EFMN 为平行四边形，结合AC ⊥PB 有EFMN 为矩形，进而设PE PA=EN AC=λ (0<λ<1)，由已知求EN 、EF 关于λ的表达式，即可得EFMN面积关于λ的函数，利用二次函数性质求最值即可.由题设，AC//面EFMN ，又AC,EN ⊂面PAC ，面PAC ∩面EFMN =EN ，所以AC//EN ，同理可证AC//MF ，故EN//MF ，又PB//面EFMN ，又PB,EF ⊂面PAB ，面PAB ∩面EFMN =EF ，所以PB//EF ，同理可证PB//MN ，故EF//MN ，故EFMN 为平行四边形，又AC ⊥PB ，即EN ⊥EF ，则EFMN 为矩形，若PE PA=EN AC=λ (0<λ<1)，则EA PA=EF PB=1−λ，又AC =PB =2，所以EN =2λ，EF =2(1−λ)，又EFMN 面积为S =EN ⋅EF =4λ(1−λ)，所以S =−4(λ−12)2+1，故当λ=12时S max =1.所以答案是：1. 解答题15、如图，在三棱锥A −BCD 中，平面ABD ⊥平面BCD ，AB =AD ，O 为BD 的中点.（1）证明：OA⊥CD；（2）若△OCD是边长为1的等边三角形，点E在棱AD上，DE=2EA，且二面角E−BC−D的大小为45°，求三棱锥A−BCD的体积.答案：(1)证明见解析；(2)√36.分析：(1)由题意首先证得线面垂直，然后利用线面垂直的定义证明线线垂直即可；(2)方法二：利用几何关系找到二面角的平面角，然后结合相关的几何特征计算三棱锥的体积即可.（1）因为AB=AD，O是BD中点，所以OA⊥BD，因为OA⊂平面ABD，平面ABD⊥平面BCD，且平面ABD∩平面BCD=BD，所以OA⊥平面BCD．因为CD⊂平面BCD，所以OA⊥CD.（2）[方法一]：通性通法—坐标法如图所示，以O为坐标原点，OA为z轴，OD为y轴，垂直OD且过O的直线为x轴，建立空间直角坐标系O−xyz，则C(√32,12,0),D(0,1,0),B(0,−1,0)，设A(0,0,m),E(0,13,23m),所以EB⃑⃑⃑⃑⃑ =(0,−43,−23m),BC ⃑⃑⃑⃑⃑ =(√32,32,0)，设n ⃑ =(x,y,z )为平面EBC 的法向量，则由{EB ⃑⃑⃑⃑⃑ ⋅n ⃑ =0EC ⃑⃑⃑⃑⃑ ⋅n ⃑ =0 可求得平面EBC 的一个法向量为n ⃑ =(−√3,1,−2m )．又平面BCD 的一个法向量为OA ⃑⃑⃑⃑⃑ =(0,0,m )，所以cos⟨n ⃑ ,OA⃑⃑⃑⃑⃑ ⟩=|m⋅√4+m 2|=√22，解得m =1．又点C 到平面ABD 的距离为√32，所以V A−BCD =V C−ABD =13×12×2×1×√32=√36，所以三棱锥A −BCD 的体积为√36． [方法二]【最优解】：作出二面角的平面角如图所示，作EG ⊥BD ，垂足为点G ．作GF ⊥BC ，垂足为点F ，连结EF ，则OA ∥EG ．因为OA ⊥平面BCD ，所以EG ⊥平面BCD ， ∠EFG 为二面角E −BC −D 的平面角．因为∠EFG =45°，所以EG =FG ．由已知得OB =OD =1，故OB =OC =1．又∠OBC =∠OCB =30°，所以BC =√3．因为GD=23,GB=43,FG=23CD=23,EG=23,OA=1，V A−BCD=13S△BCD×OA=13×2S△BOC×OA=13×2×(12×√32×1×1)×1=√36．[方法三]：三面角公式考虑三面角B−EDC，记∠EBD为α，∠EBC为β，∠DBC=30°，记二面角E−BC−D为θ．据题意，得θ=45°．对β使用三面角的余弦公式，可得cosβ=cosα⋅cos30°，化简可得cosβ=√32cosα．①使用三面角的正弦公式，可得sinβ=sinαsinθ，化简可得sinβ=√2sinα．②将①②两式平方后相加，可得34cos2α+2sin2α=1，由此得sin2α=14cos2α，从而可得tanα=±12．如图可知α∈(0,π2)，即有tanα=12，根据三角形相似知，点G为OD的三等分点，即可得BG=43，结合α的正切值，可得EG=23,OA=1从而可得三棱锥A−BCD的体积为√36．【整体点评】(2)方法一：建立空间直角坐标系是解析几何中常用的方法，是此类题的通性通法，其好处在于将几何问题代数化，适合于复杂图形的处理；方法二：找到二面角的平面角是立体几何的基本功，在找出二面角的同时可以对几何体的几何特征有更加深刻的认识，该法为本题的最优解.方法三：三面角公式是一个优美的公式，在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速.。

高中生计算能力提升专练及答案

高中数学运算能力训练题(1)（请在15分钟内完成）1.计算下列各式的值(每小题10分共40分) (1)125212.5602552⨯+⨯+⨯⨯=___________;（2）2﹣2﹣4×68+|﹣12|+（3.14﹣π）0=___________; （3）()2211210.5323⎡⎤⎛⎫⎡⎤----⨯⨯-- ⎪⎢⎥⎣⎦⎝⎭⎣⎦=___________; （4） 112234267314⎛⎫⎛⎫-÷-+- ⎪ ⎪⎝⎭⎝⎭=__________. 2.不等式组123122x x -<⎧⎪⎨+≤⎪⎩的正整数解的个数是．(10分)3．化简：(每小题10分共20分) （1）﹣÷==__________.（2）（﹣）÷=__________.4、已知：x=，y=．那么+= ．(10分)5、解方程: (每小题5分共10分)（1）方程x 2﹣2x ﹣8=0的解为__________；（2）方程22740x x -+=的解为__________.6、已知a ，b ，c 为正实数，2a 4+2b 4+c 4=2a 2c 2+2b 2c 2，则a:b:c =__________. (10分)高中数学运算能力训练题(2)（请在15分钟内完成）一、填空题（共10题，每题10分，满分100分） 1．计算4000(1683213)÷+÷= __________2．计算：3215537⎛⎫-⨯= ⎪⎝⎭__________ 3．111x x+>- 的解集是__________ 4．242x x -<+ 的解集是__________5．已知直角三角形的两条边长分别是方程214480x x -+= 的两根，则此三角形的周长是__________6．计算：362.4054.08.1362.4362.4854.2⨯-⨯-⨯=__________7．计算：个1999999 个1999999⨯+1个1999999=__________ 8．化简：()⎥⎦⎤⎢⎣⎡--+---+--4328438421432820220202022020x x x x x x x x =__________ 9．计算：111111111___1112319962341997231997111123_4_____96_19⎛⎫⎛⎫⎛⎫----⨯++++-----⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫++++= ⎪⎝⎭10．设实数x ，y 满足()()()()⎪⎩⎪⎨⎧=-+--=-+-1120151112015133y y x x ，则y x +=__________高中数学运算能力训练题(3)（请在15分钟内完成）一、填空题（共10题，每题10分，满分100分） 1．计算)37.125.8(63.975.4-+-=__________ 2．计算：7.21111.07.09999.0⨯+⨯= __________3．不等式12x< 的解集是__________ 4．化简：2211[(1)(1)1](1)22n n n n +-++--+=__________5．计算：186548362361548362-⨯⨯+= __________6．计算：2372×109 =__________7．已知方程3x 2-2x-1=0的两根是1x ，2x ，则2212x x +=________8⎛- ⎝=__________ 9．化简：(-2.5a 3)2·(-4a)3=__________10．将x ＝my ＋2代入x 26＋y 22＝1得到关于y 的一元二次方程，该方程的解为1y ，2y ，则212214)(y y y y -+=__________（用含有m 的式子表示）高中数学运算能力训练题(4)（请在15分钟内完成）一、填空题（共10题，每题10分，满分100分） 1.计算：10.4=2⎛⎫÷- ⎪⎝⎭（） A. 15-B. 15C. 45- D. 45 2.用提公因式法分解因式5()10()a x y b x y ---，提出的公因式应当为（） A ．510a b - B ．510a b + C ．5()x y - D ．y x + 3.若296(3)1a k a +-+是完全平方式，则 k 的值是（）A ．±4B ．±2C ．3D ．4或24.关于x 的不等式210ax bx +-< 的解集是 {}12x x -<< ，则 a 、b 的值分别是（） A .11,22- B. 10,2 C. 11,22- D. 1,125.在)5(log 2a b a -=-中，实数a 的范围是（）A 、 a >5或a <2B 、 25<<aC 、 23<<a 或 35<<aD 、 34<<a6. 关于x 的不等式11(1)1x x x+>>-其中的解集是 ( ) A .()1,2 B. ()1,+∞ C. (),1-∞ D. ()1,2-7.化简()43325⎥⎦⎤⎢⎣⎡-的结果为（） A ．5B ．5C ．5-D ．-58.化简xx 3-的结果是( ）A ．x --B ．xC ．x -D ．x -9.下列各式中，不正确的是（）A ．21521log 5=B ．311013lg =⎪⎭⎫ ⎝⎛ C ．55564log 214=D ．24log 2x x =10. 集合⎭⎬⎫⎩⎨⎧∈-<≤-N x x x ,2110log 1|1的真子集的个数是（）A. 1289- B. 1290- C. 1291- D. 1292-高中数学运算能力训练题(5)（请在15分钟内完成）1．计算：（﹣12）+65 +（﹣8）+（﹣710 ）+（﹣12）= __________。

高中数学第八章立体几何初步立体图形的直观图课后提能训练新人教A版必修第二册

第八章 8.2A级——基础过关练1．根据斜二测画法的规则画直观图时,把Ox,Oy,Oz轴画成对应的O′x′,O′y′,O′z′,则∠x′O′y′与∠x′O′z′的度数分别为( )A．90°,90°B．45°,90°C．135°,90°D．45°或135°,90°【答案】D【解析】根据斜二测画法的规则,∠x′O′y′的度数应为45°或135°,∠x′O′z′指的是画立体图形时的横轴与纵轴的夹角,所以度数为90°.2.(2021年绵阳模拟)(多选)如图,已知等腰三角形ABC,则如下所示的四个图中,可能是△ABC的直观图的是( )A B C D【答案】CD【解析】等腰三角形画成直观图后,原来的腰长不相等,CD两图分别为在∠x′O′y′成135°和45°的坐标系中的直观图．3．把△ABC按斜二测画法得到△A′B′C′(如图所示),其中B′O′＝C′O′＝1,A′O′＝32,那么△ABC是一个( )A．等边三角形B．直角三角形C．等腰三角形D．三边互不相等的三角形【答案】A【解析】根据斜二测画法还原三角形在直角坐标系中的图形,如图所示,由图易得AB＝BC＝AC＝2,故△ABC为等边三角形,故选A.4．(2021年南宁模拟)如果一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A ．2＋ 2B ．1＋22C ．2＋22D ．1＋ 2【答案】A【解析】画出其相应平面图易求S ＝12(1＋1＋2)×2＝2＋2,故选A.5．水平放置的△ABC ,有一边在水平线上,用斜二测画法作出的直观图是正三角形A ′B ′C ′,则△ABC 是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．任意三角形【答案】C【解析】将△A ′B ′C ′还原,由斜二测画法知,△ABC 为钝角三角形．故选C. 6．有一个长为4 cm,宽为3 cm 的矩形,则其直观图的面积为________cm 2. 【答案】3 2【解析】该矩形的面积为S ＝4×3＝12(cm 2),由平面图形的面积与直观图的面积间的关系,可得直观图的面积为S ′＝24S ＝32(cm 2)． 7．如图,矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图,其中O ′A ′＝6,O ′C ′＝3,B ′C ′∥x ′轴,则原平面图形的面积为________．【答案】36 2【解析】在直观图中,设B ′C ′与y ′轴的交点为D ′,则易得O ′D ′＝32,所以原平面图形为一边长为6,高为62的平行四边形,所以其面积为6×62＝36 2.8．在直观图中,四边形O′A′B′C′为菱形且边长为2 cm,则在坐标系xOy中原四边形OABC为________(填形状),面积为________cm2.【答案】矩形8【解析】由题意,结合斜二测画法可知,四边形OABC为矩形,其中OA＝2 cm,OC＝4 cm,所以四边形OABC的面积S＝2×4＝8(cm2)．9．画出一个上、下底面边长分别为1,2,高为2的正三棱台的直观图．解：(1)画轴．如图,画x轴、y轴、z轴相交于点O,使∠xOy＝45°,∠xOz＝90°.(2)画下底面．以O为线段中点,在x轴上取线段AB,使AB＝2,在y轴上取线段OC,使OC＝32.连接BC,CA,则△ABC为正三棱台的下底面的直观图．(3)画上底面．在z轴上取OO′,使OO′＝2,过点O′作O′x′∥Ox,O′y′∥Oy,建立坐标系x′O′y′.在x′O′y′中,类似步骤(2)的画法得上底面的直观图△A′B′C′.(4)连线成图．连接AA′,BB′,CC′,去掉辅助线,将被遮住的部分画成虚线,则三棱台ABC－A′B′C′即为要求画的正三棱台的直观图．10．如图,正方形O′A′B′C′的边长为1 cm,它是水平放置的一个平面图形OABC的直观图．请画出原来的平面图形的形状,并求原图形的周长与面积．解：如图,建立直角坐标系xOy,在x轴上取OA＝O′A′＝1 cm；在y 轴上取OB ＝2O ′B ′＝2 2 cm ；在过点B 的x 轴的平行线上取BC ＝B ′C ′＝1 cm.连接O ,A ,B ,C 各点,即得到了原图形．由作法可知OABC 为平行四边形,OC ＝OB 2＋BC 2＝8＋1＝3(cm),∴平行四边形OABC 的周长为(3＋1)×2＝8(cm),面积为S ＝1×22＝22(cm 2)．B 级——能力提升练11．下列选项中的△ABC 均是水平放置的边长为1的正三角形,在斜二测画法下,其直观图不是全等三角形的一组是( )A BC D【答案】C【解析】C 中,前者在斜二测画法下所得的直观图中,底边AB 不变,高变为原来的12,后者在斜二测画法下所得的直观图中,高OC 不变,底边AB 变为原来的12,故C 中两个图形在斜二测画法下所得直观图不全等．12．水平放置的△ABC 的直观图如图所示,已知B ′C ′＝4,A ′C ′＝3,B ′C ′∥y ′轴,则△ABC 中AB 边上的中线的长度为( )A ．732B ．73C ．5D ．52【答案】A【解析】由斜二测画法规则知AC ⊥BC ,即△ABC 为直角三角形,其中AC ＝3,BC ＝8,所以AB ＝73,AB 边上的中线长度为732.故选A. 13．已知两个圆锥,底面重合在一起,其中一个圆锥顶点到底面的距离为2 cm,另一个圆锥顶点到底面的距离为3 cm,则其直观图中这两个顶点之间的距离为( )A ．2 cmB ．3 cmC ．2.5 cmD ．5 cm【答案】D【解析】由题意可知其直观图如图,由图可知两个顶点之间的距离为5 cm.故选D.14．(2021年河南模拟)已知用斜二测画法,画得的正方形的直观图面积为182,则原正方形的面积为______．【答案】72【解析】如图,作出正方形OABC 的直观图O ′A ′B ′C ′,作C ′D ′⊥x ′轴于点D ′.S 直观图＝O ′A ′×C ′D ′.又S 正方形＝OC ×OA .所以S 正方形S 直观图＝OC ×OAO ′A ′×C ′D ′, 又在Rt △O ′D ′C ′中,O ′C ′＝2C ′D ′, 即C ′D ′＝22O ′C ′,结合平面图与直观图的关系可知OA ＝O ′A ′,OC ＝2O ′C ′, 所以S 正方形S 直观图＝OC ×OAOA ×22O ′C ′＝2O ′C ′22O ′C ′＝2 2.又S 直观图＝182,所以S 正方形＝22×182＝72.15．如图所示,△A ′O ′B ′表示水平放置的△AOB 的直观图,点B ′在x ′轴上,A ′O ′与x ′轴垂直,且A ′O ′＝2,则△AOB 的边OB 上的高为________．【答案】4 2【解析】设△AOB 的边OB 上的高为h ,由直观图中边O ′B ′与原图形中边OB 的长度相等,及S原图＝22S直观图,得12OB ×h ＝22×12×A ′O ′×O ′B ′,则h ＝4 2.故△AOB 的边OB 上的高为4 2.16．如图是一个边长为1的正方形A ′B ′C ′D ′,已知该正方形是某个水平放置的四边形用斜二测画法画出的直观图,试画出该四边形的原图形并求出其面积．解：四边形ABCD 的真实图形如图所示,因为A ′C ′在水平位置,四边形A ′B ′C ′D ′为正方形,所以∠D ′A ′C ′＝∠A ′C ′B ′＝45°,所以在原四边形ABCD 中,AD ⊥AC ,AC ⊥BC .因为AD ＝2D ′A ′＝2,AC ＝A ′C ′＝2, 所以S 四边形ABCD ＝AC ·AD ＝2 2.C 级——探索创新练17．如图所示的是水平放置的正方形ABCO ,在平面直角坐标系xOy 中,点B 的坐标为(4,4),则由斜二测画法画出该正方形的直观图中,顶点B ′到x ′轴的距离为________．【答案】 2【解析】水平放置的正方形ABCO ,在平面直角坐标系xOy 中,点B 的坐标为(4,4),由斜二测画法画出的该正方形的直观图如下：由斜二测画法的规则,得O ′A ′＝12OA ＝2,O ′C ′＝OC ＝4,∠A ′O ′C ′＝45°,四边形A ′B ′C ′O ′是平行四边形,∴顶点B ′到x ′轴的距离与A ′到x 轴的距离相等．∴顶点B ′到x ′轴的距离d ＝|O ′A ′|sin 45°＝2×22＝ 2.18．一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面尺寸一样,已知长方体的长、宽、高分别为20 m,5 m,10 m,四棱锥的高为8 m,若按1∶500的比例画出它的直观图,那么直观图中,长方体的长、宽、高和棱锥的高应分别为____________________．【答案】4 cm,0.5 cm,2 cm,1.6 cm【解析】由20 m ＝2 000 cm,2 000500＝4 cm,同理可得宽、高分别为1 cm 、2 cm,四棱锥的高为1.6 cm.在直观图中,宽变为一半,长、高不变．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数学能力训练（8）
1.如图所示，在三棱锥P ABC
-中，2
PA BC
==，
3
PB PC AB AC
====，则直线PA与平面
PBC所成角的余弦值为_______________.
2．已知,
,
2
1
x
x…，
6
x的方差为2，则
1
23
x+,
2
23
x+，… ,
6
23
x+的标准差是__________.
3. 某数学老师身高176cm，他爷爷、父亲和儿子的身高分别是173cm、170cm和
182cm.因儿子的身高与父亲的身高线性相关，该老师用线性回归分析的方法预测他孙子的身高为________cm.
【附】（1）y bx a
=+（2）11
2
22
11
n n
i i i i
i i
n n
i i
i i
x x y y x y nx y
b
x x x nx
==
==
(-)(-)-
==
(-)-
∑∑
∑∑
，a y bx
=-
4. 已知函数3()2f x x ax =+-在区间[1,)+∞上是增函数，则a 的取值范围是__________.
5. 已知函数321()213f x x ax x =
-++无极值点，则a 的取值范围是_________________. 6. 已知曲线31433
y x =+，则过点(2,4)P 的切线方程为____________________________. 7. 已知原命题为：相似三角形是全等三角形，则下列说法中正确的是________________． ① 原命题的否定为：存在相似三角形不是全等三角形；
② 原命题的否定为：不相似的三角形不全是全等三角形；
答案
2． 3. 185cm （提示：由条件可求得样本中心点(,)x y 为(173,176)，把相关数据代入线性回归方程得，1,3b a ==，即回归方程为：3y x =+，所以当182x =时，185y =）
4. [3,)-+∞
5. [
6. 20x y -+=或440x y --=
7.① ④。