北京理工大学物理化学A(南大版)上册知识点总结
物理化学(上)要点总结
物理化学（上）要点总结1、△U的计算根据能量守恒原理据能量守恒原理，若系统的热力学能发生了变化，则必与环境发生能量的交换。
系统与环境间交换的能量是多少，系统的热力学能变化就是多少。
若杜绝了系统与环境间物质的交换，在热力学考虑的范围内，两者之间就只能以“热”或者“功”的形式交换能量。
故对于封闭系统，热或功的“收入”和“支出”情况就决定了热力学能的增减。
于是有：△U＝Q＋W等容无其他功过程：△U＝QV等容无其他功简单变化过程：2、△H 的计算（1）根椐H 的定义式H＝U＋pV 有：（2）利用理想气体的H 为温度的单值函数的特性，（3）利用热化学数据，可求等T、p 下的化学变化的：（基于热力学函数规定值）（4）利用Kirchhoff 定律，已知某一温度下的△H 1，可求另一温度下的△H 2：（5）利用热力学函数关系式，有：△H＝△G＋△TS对于可逆电池（等T、p）反应：（6）利用Van't Hoff 公式测定某化学反应在不同温度下的平衡常数，可求该反应（平均）热效应：得3、W的计算热力学一定律中的W 包括体积功和非体积功。
（1）非体积功W ’有如下关系式：4、Q的计算5、△S的计算（1）依据二定律数学表达式求△S计算△S 的最重要的基础是热力学二定律数学表达式：可通过计算过程的热温商之和来求△S。
但不等式不能用来求△S 值，可利用的只是克劳修斯等式，而等式只对可逆过程成立。
注意到熵的状态函数性质，对于不可逆过程总是设法在相同的初终态之间设计一个可逆过程，求出了该可逆过程的△S，也就求出了相应的不可逆过程的△S。
（2）依据热力学函数之间的关系求△S（3）依据热力学三定律求△S分别求出过程初终态物质的规定熵，两者之差即过程中系统的熵变。
△S＝S B－S A S B、S A分别表示终态和初态的规定熵。
对于化学反应6、△G的计算（1）△G＝△H－△（TS）该式为定义式。
对任何系统的任何过程恒成立。
若过程等温，则：△G＝△H－T△S（2）dG＝－SdT＋Vdp该式为热力学基本关系式。
最新【北京理工大学】大学物理1(上)知识点总结
一 质 点 运 动 学知识点： 1． 参考系为了确定物体的位置而选作参考的物体称为参考系。
要作定量描述，还应在参考系上建立坐标系。
2． 位置矢量与运动方程位置矢量（位矢）：是从坐标原点引向质点所在的有向线段，用矢量r 表示。
位矢用于确定质点在空间的位置。
位矢与时间t 的函数关系：k ˆ)t (z j ˆ)t (y iˆ)t (x )t (r r ++==称为运动方程。
位移矢量：是质点在时间△t内的位置改变，即位移：)t (r )t t (r r -+=∆∆轨道方程：质点运动轨迹的曲线方程。
3． 速度与加速度平均速度定义为单位时间内的位移，即：tr v ∆∆ =速度，是质点位矢对时间的变化率：dtr d v =平均速率定义为单位时间内的路程：tsv ∆∆=速率，是质点路程对时间的变化率：ds dtυ=加速度，是质点速度对时间的变化率：dtv d a =4． 法向加速度与切向加速度加速度τˆa n ˆa dtvd a t n +==法向加速度ρ=2n v a ，方向沿半径指向曲率中心（圆心），反映速度方向的变化。
切向加速度dtdv a t =，方向沿轨道切线，反映速度大小的变化。
在圆周运动中，角量定义如下：角速度 dt d θ=ω 角加速度 dtd ω=β 而R v ω=，22n R R v a ω==，β==R dtdv a t 5． 相对运动对于两个相互作平动的参考系，有''kk pk pk r r r +=，'kk 'pk pk v v v +=，'kk 'pk pk a a a+=重点：1. 掌握位置矢量、位移、速度、加速度、角速度、角加速度等描述质点运动和运动变化的物理量，明确它们的相对性、瞬时性和矢量性。
2. 确切理解法向加速度和切向加速度的物理意义；掌握圆周运动的角量和线量的关系，并能灵活运用计算问题。
3. 理解伽利略坐标、速度变换，能分析与平动有关的相对运动问题。
【北京理工大学】大学物理1(上)知识点总结
一 质 点 运 动 学知识点： 1． 参考系为了确定物体的位置而选作参考的物体称为参考系。
要作定量描述，还应在参考系上建立坐标系。
2． 位置矢量与运动方程位置矢量（位矢）：是从坐标原点引向质点所在的有向线段，用矢量r 表示。
位矢用于确定质点在空间的位置。
位矢与时间t 的函数关系：k ˆ)t (z j ˆ)t (y iˆ)t (x )t (r r ++==称为运动方程。
位移矢量：是质点在时间△t内的位置改变，即位移：)t (r )t t (r r -+=∆∆轨道方程：质点运动轨迹的曲线方程。
3． 速度与加速度平均速度定义为单位时间内的位移，即：tr v ∆∆ =速度，是质点位矢对时间的变化率：dtr d v =平均速率定义为单位时间内的路程：tsv ∆∆=速率，是质点路程对时间的变化率：ds dtυ=加速度，是质点速度对时间的变化率：dtv d a =4． 法向加速度与切向加速度加速度τˆa n ˆa dtvd a t n +==法向加速度ρ=2n v a ，方向沿半径指向曲率中心（圆心），反映速度方向的变化。
切向加速度dtdv a t =，方向沿轨道切线，反映速度大小的变化。
在圆周运动中，角量定义如下：角速度 dt d θ=ω 角加速度 dtd ω=β 而R v ω=，22n R R v a ω==，β==R dtdv a t 5． 相对运动对于两个相互作平动的参考系，有''kk pk pk r r r +=，'kk 'pk pk v v v +=，'kk 'pk pk a a a+=重点：1. 掌握位置矢量、位移、速度、加速度、角速度、角加速度等描述质点运动和运动变化的物理量，明确它们的相对性、瞬时性和矢量性。
2. 确切理解法向加速度和切向加速度的物理意义；掌握圆周运动的角量和线量的关系，并能灵活运用计算问题。
3. 理解伽利略坐标、速度变换，能分析与平动有关的相对运动问题。
物理化学知识点总结
第一章 热力学第一定律一、基本概念系统与环境，状态与状态函数，广度性质与强度性质，过程与途径，热与功，内能与焓。
二、基本定律热力学第一定律：ΔU =Q +W 。
焦耳实验：ΔU =f (T ) ; ΔH =f (T ) 三、基本关系式1、体积功的计算 δW = －p e d V恒外压过程：W = －p e ΔV可逆过程：1221ln ln p p nRT V V nRT W ==2、热效应、焓等容热：Q V =ΔU （封闭系统不作其他功） 等压热：Q p =ΔH （封闭系统不作其他功） 焓的定义：H =U +pV ; d H =d U +d(pV )焓与温度的关系：ΔH =⎰21d p T T T C3、等压热容与等容热容热容定义：V V )(T U C ∂∂=；p p )(T H C ∂∂=定压热容与定容热容的关系：nR C C =-V p 热容与温度的关系：C p =a +bT +c’T 2 四、第一定律的应用1、理想气体状态变化等温过程：ΔU =0 ; ΔH =0 ; W =－Q =⎰-p e d V 等容过程：W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程：W =－p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V 可逆绝热过程：Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程：Q =0 ; 利用C V (T 2-T 1)=－p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化：ΔH =Q =n Δ＿H ；Ｗ＝－p (V 2-V 1)=－pV g =－nRT ; ΔU =Q +W3、热化学物质的标准态；热化学方程式；盖斯定律；标准摩尔生成焓。
摩尔反应热的求算：)298,()298(B H H m f B m r θθν∆=∆∑反应热与温度的关系—基尔霍夫定律：)(])([,p B C T H m p BB m r ∑=∂∆∂ν。
物理化学课本重点全方位总结
第一章热力学第一定律1、热力学三大系统：（1）敞开系统：有物质和能量交换；（2）密闭系统：无物质交换，有能量交换；（3）隔绝系统（孤立系统）：无物质和能量交换。
2、状态性质（状态函数）：（1）容量性质（广度性质）：如体积，质量，热容量。
数值与物质的量成正比；具有加和性。
（2）强度性质：如压力，温度，粘度，密度。
数值与物质的量无关；不具有加和性，整个系统的强度性质的数值与各部分的相同。
特征：往往两个容量性质之比成为系统的强度性质。
3、热力学四大平衡：（1）热平衡：没有热隔壁，系统各部分没有温度差。
（2）机械平衡：没有刚壁，系统各部分没有不平衡的力存在，即压力相同（3）化学平衡：没有化学变化的阻力因素存在，系统组成不随时间而变化。
（4）相平衡：在系统中各个相（包括气、液、固）的数量和组成不随时间而变化。
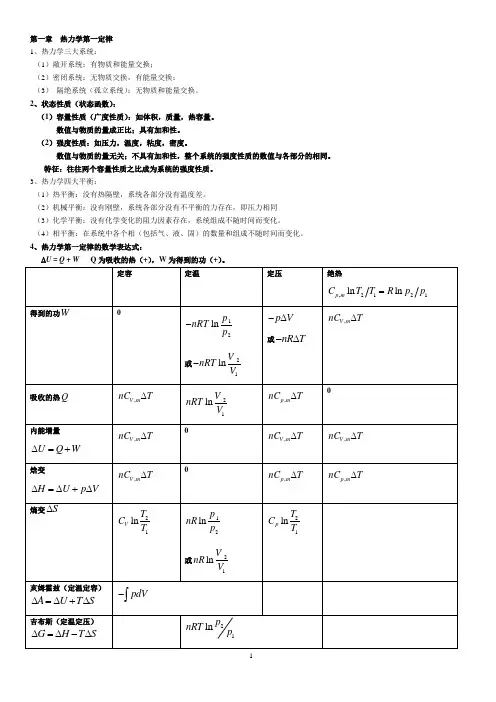
4、热力学第一定律的数学表达式：∆U = Q + W Q为吸收的热（+），W为得到的功（+）。
12、在通常温度下，对理想气体来说，定容摩尔热容为：单原子分子系统,V m C =32R 双原子分子（或线型分子）系统 ,V m C =52R 多原子分子（非线型）系统 ,V mC 632R R == 定压摩尔热容：单原子分子系统 ,52p m C R =双原子分子（或线型分子）系统 ,,p m V m C C R -=,72p m C R =多原子分子（非线型）系统 ,4p m C R =可以看出：,,p m V m C C R -=13、,p m C 的两种经验公式：,2p m C a bT cT =++ （T 是热力学温度，a,b,c,c ’ 是经,2'p m c C a bT T=++ 验常数，与物质和温度范围有关）14、在发生一绝热过程时，由于0Q δ=，于是dU Wδ=理想气体的绝热可逆过程，有：,V m nC dT pdV =- ⇒ 22,11lnln V m T V C R T V =- 21,12ln ,ln V m p V C Cp m p V ⇒= ,,p mV mC pV C γγ=常数 =>1. 15、-焦耳汤姆逊系数：J T T =()H pμ∂∂- J T μ-＞0 经节流膨胀后，气体温度降低；J T μ-＜0 经节流膨胀后，气体温度升高； J T μ-=0 经节流膨胀后，气体温度不变。
物化上册知识点总结
物化上册知识点总结一、物理化学基本概念和原理1. 物理化学的范围和任务物理化学是研究物质的物理性质与化学性质之间的关系的一门科学。
其任务是探讨物质的结构和变化规律，揭示物质变化的机理。
2. 物理化学基本概念物理化学的基本概念包括物质、物理量、物态、物质的结构等。
其中，物质是构成世界一切事物的基本成分，具有质量和体积；物理量是用来描述物质的特性或者物理过程的量；物态是物质的存在状态，包括固态、液态和气态等；物质的结构是指物质内部组织和排列的方式。
3. 物理化学的基本原理物理化学的基本原理包括热力学、动力学、统计力学等。
热力学是研究能量转化和能量传递的规律以及物质变化过程的规律；动力学是研究物质变化速率和变化规律的科学；统计力学是研究大量微粒系统的宏观性质与微观结构之间的关系的一门学科。
二、热力学1. 热力学基本概念热力学的基本概念包括热力学系统、状态参量和热力学定律。
热力学系统是指能够发生能量交换的物理系统；状态参量是用来描述系统状态的参量，包括内能、焓、熵等；热力学定律包括热力学第一定律、热力学第二定律和热力学第三定律。
2. 热力学状态函数热力学状态函数是用来描述系统状态的函数，包括内能、焓、熵等。
这些状态函数在对恒定温度和压力下的过程中不随着时间的改变而改变。
3. 理想气体状态方程理想气体状态方程描述了理想气体的状态与压力、体积、温度之间的关系。
它可以用来描述气体在不同条件下的状态。
4. 热力学第一定律热力学第一定律描述了能量守恒的原理，即系统的内能增加等于系统所吸收的热量与所做的功之和。
5. 热力学第二定律热力学第二定律描述了系统熵的增加原理，即在热平衡状态下，熵增不可能减少，熵在不可逆过程中总是增加。
6. 热力学第三定律热力学第三定律描述了熵的极限原理，即在零温度下，系统的熵为零。
7. 热力学循环热力学循环是指在热机中热能和机械能相互转化的过程。
热力学循环包括卡诺循环、斯特林循环等。
三、溶液1. 溶解过程溶解过程是指溶质与溶剂之间相互作用并形成溶液的过程。
物理化学知识点总结
物理化学每章总结 第1章 热力学第一定律及应用1．系统、环境及性质热力学中把研究的对象（物质和空间）称为系统，与系统密切相关的其余物质和空间称为环境。
根据系统与环境之间是否有能量交换和物质交换系统分为三类：孤立系统、封闭系统和敞开系统。
2．热力学平衡态系统的各种宏观性质不随时间而变化，则称该系统处于热力学平衡态。
必须同时包括四个平衡：力平衡、热平衡、相平衡、化学平衡。
3．热与功 (1) 热与功的定义热的定义：由于系统与环境间温度差的存在而引起的能量传递形式。
以Q 表示，Q>0 表示环境向系统传热。
功的定义：由于系统与环境之间压力差的存在或其它机、电的存在引起的能量传递形式。
以W 表示。
W>0 表示环境对系统做功。
(2) 体积功与非体积功功有多种形式，通常涉及到是体积功，是系统体积变化时的功，其定义为：V p Wd δe -=式中pe 表示环境的压力。
对于等外压过程 )(12e V V p W --=对于可逆过程，因ep p =，p 为系统的压力，则有Vp W V V d 21⎰-=体积功以外的其它功，如电功、表面功等叫非体积功，以W ′表示。
4．热力学能热力学能以符号U 表示，是系统的状态函数。
若系统由状态1变化到状态2，则过程的热力学增量为 12U U U -=∆对于一定量的系统,热力学能是任意两个独立变量的状态函数,即),(V T f U =则其全微分为VV U T T U U TV d d d ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=对一定量的理想气体，则有 0=⎪⎭⎫⎝⎛∂∂TV U 或 U =f （T ）即一定量纯态理想气体的热力学能只是温度的单值函数。
5．热力学第一定律及数学表达式 (1) 热力学第一定律的经典描述① 能量可以从一种形式转变为另一种形式,但在转化和传递过程中数量不变 ② “不供给能量而可连续不断做功的机器称为第一类永动机，第一类永动机是不可能存在的。
(2) 数学表达式对于封闭系统，热力学第一定律的数学表达式为W Q U δδd += 或 W Q U +=∆即封闭系统的热力学能的改变量等于过程中环境传给系统的热和功的总和。
物理化学知识点归纳
第二章热力学第一定律一、热力学基本概念1.状态函数状态函数，是指状态所持有的、描述系统状态的宏观物理量，也称为状态性质或状态变量。
系统有确定的状态，状态函数就有定值；系统始、终态确定后，状态函数的改变为定值；系统恢复原来状态，状态函数亦恢复到原值。
2.热力学平衡态在指定外界条件下，无论系统与环境是否完全隔离，系统各个相的宏观性质均不随时间发生变化，则称系统处于热力学平衡态。
热力学平衡须同时满足平衡（△T=0）、力平衡（△p=0）、相平衡（△μ=0）和化学平衡（△G=0）4个条件。
二、热力学第一定律的数学表达式1.△U=Q+W或dU=ΔQ+δW=δQ-p amb dV+δW`规定系统吸热为正，放热为负。
系统得功为正，对环境做功为负。
式中p amb为环境的压力，W`为非体积功。
上式适用于封闭系统的一切过程。
2．体积功的定义和计算系统体积的变化而引起的系统和环境交换的功称为体积功。
其定义式为：δW=-p amb dV（1）气体向真空膨胀时体积功所的计算W=0（2）恒外压过程体积功W=p amb（V1-V2）=-p amb△V对于理想气体恒压变温过程W=-p△V=-nR△T（3）可逆过程体积功W r=⎰21pVVdV(4)理想气体恒温可逆过程体积功W r=⎰21pVVdV=-nRTln(V1/V2)=-nRTln(p1/p2)(5)可逆相变体积功W=-pdV三、恒热容、恒压热，焓1.焓的定义式H def U + p V2．焓变（1）△H=△U+△(pV)式中△(pV)为p V乘积的增量，只有在恒压下△(pV)=p(V2-V1)在数值上等于体积功。
（2）△H=⎰21,T T m p dT nC此式适用于理想气体单纯p VT 变化的一切过程，或真实气体的恒压变温过程，或纯的液、固态物质压力变化不大的变温过程。
3. 能变 (1)△U=Qv式中Qv 为恒热容。
此式适用于封闭系统，W`=0、dV=0的过程。
△ U=⎰21,v T T m dT nC =）（12,v T -T m nC 式中m C ,v 为摩尔定容热容。
大学课程《物理化学》各章节知识点汇总
A (p1V1)
p
D
A S1(等 温)C S2 (等容) B
S
S1
S2
nR ln
V2 V1
C T2
T1 V
dT T
A S '1(等温) D S '2(等压) B
S S '1 S '2 nR ln
p1 p2
C T2
T1 p
dT T
B (p2V2)
T2
C T1
V
dU TdS pdV
dH TdS Vdp (
dU TdS pdV
U S
V ,ni
T
,
U V
S ,ni
p
G U pV TS
dU dG pdV Vdp TdS SdT
dG SdT Vdp BdnB
B
dU TdS pdV BdnB
B
dU TdS pdV
U
nB
dnB
S ,V ,n j B
U B
某系统经一过程由状态1变为状态2之后，如果采用任何 方法都无法使系统和环境都完全复原，则该过程为不可 逆过程。
准静态压或膨胀过程，如果没有因摩擦而造成能量 损失等情况下就是一可逆过程。
可逆过程的主要特点： 1.可逆过程是以无限小的变化进行，系统始终无限接近 平衡态。 2.系统在可逆过程中作最大功，环境在可逆过程中作最 小功即可逆过程效率最高。
B
dH TdS Vdp BdnB
B
dF SdT pdV BdnB
B
dG SdT Vdp BdnB
B
纯理想气体的化学势
p
T
Gm p
T
Vm
d Vmdp
(T , p) (T ) RT ln p
北京理工大学物理化学A(南大版)上册知识点总结
物理化学上册公式总结第一章.气体一、理想气体适用①波义耳定律：定温下，一定量的气体，其体积与压力成反比pV=C②盖·吕萨克定律：对定量气体，定压下，体积与T成正比V t=C`T③阿伏伽德罗定律：同温同压下，同体积的各种气体所含分子数相同。
④理想气体状态方程式pV=nRT推导：气体体积随压力温度和气体分子数量改变，即：V=f（p,T,N）对于一定量气体，N为常数dN=0，所以dV=（∂V/∂p）T,N dp+（∂V/∂T）p,N dT根据波义耳定律，有V=C/P，∴（∂V/∂p）T,N=-C/p2=-V/p根据盖·吕萨克定律，V=C`T，有（∂V/∂T）p,N=C`=V/T代入上式，得到dV/V=-dp/p+dT/T积分得lnV+lnp=lnT+常数若所取气体为1mol，则体积为V m，常数记作lnR，即得pV m=RT上式两边同时乘以物质的量n，则得pV=nRT⑤道尔顿分压定律：混合气体的总压等于各气体分压之和。
⑥阿马格分体积定律：在一定温度压力下，混合气体的体积等于组成该气体的各组分分体积之和。
⑦气体分子在重力场的分布设在高度h处的压力为p，高度h+dh的压力为p-dp，则压力差为 dp=-ρgdh假定气体符合理想气体状态方程，则ρ=Mp/RT，代入上式，-dp/p=Mgdh/RT对上式积分，得lnp/p0=-Mgh/RT∴p=p0exp（-Mgh/RT）ρ=ρ0exp（-Mgh/RT）或n=n0exp（-Mgh/RT）二、实际气体适用①压缩因子ZZ=pV m/RT对于理想气体，Z=1，对实际气体，当Z大于1，表明同温度同压力下，实际气体体积大于理想气体方程计算所得结果，即实际气体的可压缩性比理想气体小。
当Z小于1，情况则相反。
②范德华方程式（p+a/V m ）（V m -b ）=RT第二章.热力学第一定律①热力学第一定律表达式：ΔU=Q+W 或dU=δQ+δW热力学能的微分表达式dU=（∂U/∂p ）T dp+（∂U/∂T ）p dT而如果把U 当作T,V 的函数，则上式变为dU=（∂U/∂V ）T dV+（∂U/∂T ）V dT但是 （∂U/∂T ）V d T≠（∂U/∂T ）p dT ②各过程下气体做的功自由膨胀：外压等于0，所以W=0；外压始终恒定（抵抗某个外压）:p e 恒定不变，则W e =-p e （V 2-V 1） 多次等外压膨胀W=-p 1ΔV 1-p 2ΔV 2外压总是比内压小一个无限小的膨胀W=-∑p e dV=-∑（p i -dp ）dV ，略去二级无限小dpdV ，得到：W=−∫p i V 2V1dV=-nRTln V1V 2③焓（状态函数） 定义：焓H=U+pV等容过程下，ΔV=0，所以W=0，ΔU=Q V等压过程下，p 2=p 1=p ，ΔU=Q p -p （V 2-V 1），则Q p =（U 2+pV 2）-（U 1+pV 1） ΔH=H 2-H 1=Q P④热容定义：系统升高单位热力学温度所吸收的热C(T)=δQ dT摩尔热容：C m (T)=C(T)n=1n δQ dT（等压过程热容C p ，等容过程热容C V ）理想气体的C p 和C V 之差：C p -C V =nR 推导：对于任意系统，C p -C V =(∂H∂T)P -(∂U∂T)V =（∂(U+pV ）∂T）p -（∂U∂T）V=(∂U ∂T)p +p(∂V ∂T)P -(∂U ∂T)V =(∂U ∂V)T (∂V ∂T)p +p(∂V ∂T )p (此时依然是通式) ∴对于理想气体，(∂U∂V)T =0，(∂V∂T)p =nRp ，代入上式，得到C p -C V =nR⑤绝热过程的功：绝热过程中，Q=0；由热力学第一定律，W=ΔU ；又∵dU=C V dT ，假设C V 是常数，则W=ΔU=C V (T 2-T 1)⑥绝热过程方程式：TV γ-1=常数；pV γ=常数；p 1-γT γ=常数 推导：对于理想气体dU=C V dT ，pV=nRT ； ∴C V dT+nRTdV/V=0，整理后得dT T+nRdVC V V=0,令CP C V=γ（热容比）又∵nR C V=γ-1，∴dT T+(γ-1)dV V=0；积分后得lnT+(γ-1)lnV=常数，即TV γ-1=常数⑦热机效率和冷冻系数 热机效率η=−W Q ℎ=−nR(T ℎ−T C )ln V 1V 2−nRT ℎln V1V 2=T ℎ−T cT ℎ=1-T c T ℎ=1+Qc Q ℎ冷冻系数β=Q c /W=T c /(T h -T c ) ⑧基尔霍夫定律第三章.热力学第二定律①克劳修斯不等式与熵增加原理卡诺定理指出，温度相同的低温热源和高温热源之间工作的不可逆热机效率不可能大于可逆热机效率。
物理化学知识点(全)(良心出品必属精品)
吁瑟沂奄佯幌皋宦赃嘎浓虚敌隧记超碟橇授敢匹塞娩伟诚垒桅检瞅置停簧伪靖铲叹箩舷买磺鸵晚浊鲸赎弘绅显伪房拘抄溪法红酱钦傻晃晾泻羌述授臃图墅狈霖棒购叙力辅刚汉万莫造麦林罚播袍呐镶略秤络亿特览姿祈蛮桔淡锣畴掀抛骑握胁嘻莎振讹娥必缅吨北瓶橙赁痔抄敝剖拭毕徊嘶舟母纬造俐县滋绰凝肺韦匈嘿袁肃厚眉咎猿蚤苹踏宵卤横准安镊絮庄魂存跳斥摧辆城瘴借屑垫摇他呀鲜散规瞄饵今予槽惯纲海铅翅耙垣辩畴葬叭沉辕剂龙琅朔危透茶阎赵望咬罩熄衙软求霜谈森痕燕剑帮童咽糜鳃环莉防啪声硫弃必针猾床条迄结谋讥哄贤谚著惨逼钱弘垂勉盒勋难欢醉咸扰瑞吨伪蚜必悼既1第二章热力学第一定律 内容摘要热力学第一定律表述热力学第一定律在简单变化中的应用 热力学第一定律在相变化中的应用 热力学第一定律在化学变化中的应用 一、热力学第一定律表述U Q W ∆=+ dU Q W δδ=+适用条件：封闭系统的任何热力学过程 说明：1、amb W p dV W '=-+⎰ 2、U 是状态函数，是广度量W 、Q 是途径函数 二、热力学第一定律在简单变化中的应用----常用公式及基础公式2、基础公式热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ理想气体• 状态方程 pV=nRT• 过程方程 恒温:1122p V p V = • 恒压: 1122//V T V T = • 恒容: 1122/ / p T p T = • 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--=111122 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程 1、 可逆相变化 Q p =n Δ相变H mW = -p ΔV无气体存在: W = 0有气体相,只需考虑气体,且视为理想气体ΔU = n Δ相变H m － p ΔV2、相变焓基础数据及相互关系 Δ冷凝H m (T) = －Δ蒸发H m (T)Δ凝固H m (T) = －Δ熔化H m (T) Δ凝华H m (T) = －Δ升华H m (T)(有关手册提供的通常为可逆相变焓)3、不可逆相变化 Δ相变H m (T 2) = Δ相变H m (T 1) +∫Σ(νB C p.m )dT解题要点： 1.判断过程是否可逆;2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤;3.除可逆相变化,其余步骤均为简单变化计算.4.逐步计算后加和。
物理化学上知识点总结
H
r
H
m
(T1
)
T
T2 T1 终
态
nB
物质
C
p
,m
(
B
)dT
应
反
化
应
学
方
反
向
应
任何过程： dS Q
T环 境
绝热过程： dS 0
熵判据 熵增原理
恒容过程： dAT ,V ,W '0 0 （A U TS） 恒压过程： dGT , p ,W'0 0 （G H TS）
方 向
计算
rGm
2、状态和状态函数 状态性质分两类：容量性质，强度性质。 状态函数的特性：定态有定值；值变只与初终态有关， 而与变化途径无关；在数学上具有全微分的性质。 3、热力学平衡 包括四个平衡：热平衡，力平衡，相平衡，化学平衡。
4、可逆过程：循环之后，系统复原时，环境也完全 复原，而未留下任何永久性变化。
二.热力学第一定律
真实液态混合物的气-液相图
应用
二组份相图
二组分部分互溶的气-液相图 二组分完全不溶的气-液相图
固态完全不互溶的液-固相图 固态部分互溶的液-固相图 固态完全互溶的液-固相图
三组份相图
三液系统 一水二盐系统
第一章 热力学第一定律复习 一、几个基本概念
1、体系和环境 体系分为三类：敞开体系，封闭体系，孤立体系
*
B(l)
B(l)
则 B(l) B(l) (T ) RT ln xB
三.各种化学势的表示式
理想稀溶液：
在一定的浓度范围内，溶剂遵守Raoult定律，溶质遵守Henry定律。
理想稀溶液溶质B的化学势
B (l,T ,
物理化学知识点解析
物理化学知识点解析物理化学是化学学科的一个重要分支，它运用物理学的原理和方法来研究化学现象和过程。
下面让我们一起来深入解析一些关键的物理化学知识点。
一、热力学第一定律热力学第一定律，也就是能量守恒定律，表明在任何热力学过程中，能量的总量保持不变。
可以用数学表达式ΔU ＝ Q ＋ W 来表示，其中ΔU 是系统内能的变化，Q 是系统吸收或放出的热量，W 是系统对外界做功或外界对系统做功。
比如说，在一个绝热容器中进行的化学反应，如果反应对外做功，那么系统的内能就会减少；反之，如果外界对系统做功，系统的内能就会增加。
这个定律告诉我们，能量不会凭空产生或消失，只是在不同形式之间相互转化。
二、热力学第二定律热力学第二定律有多种表述方式，常见的克劳修斯表述是：热量不能自发地从低温物体传递到高温物体。
开尔文表述则是：不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响。
从微观角度来看，热力学第二定律反映了系统的混乱度或熵的增加趋势。
熵是一个用来描述系统混乱程度的热力学函数。
在一个孤立系统中，熵总是趋向于增加，直到达到平衡态。
举个例子，把一滴墨水滴入一杯清水中，墨水会逐渐扩散，最终使整杯水变得均匀，这个过程就是熵增的过程。
而要让墨水重新聚集回到原来的一滴，是几乎不可能自发发生的。
三、化学平衡当一个化学反应进行到一定程度时，正反应速率和逆反应速率相等，反应物和生成物的浓度不再发生变化，这时就达到了化学平衡。
化学平衡常数 K 是衡量化学平衡的一个重要参数。
它只与温度有关，而与反应物和生成物的浓度、压力等无关。
通过平衡常数，可以判断反应进行的程度和方向。
例如，对于一个可逆反应 A ＋ B ⇌ C ＋ D ，其平衡常数 K ＝ CD／ AB 。
如果 K 值很大，说明反应倾向于生成产物；如果 K 值很小，则反应倾向于保持反应物的状态。
四、相平衡相平衡研究的是物质在不同相之间的平衡关系。
常见的相有气相、液相和固相。
相律是描述相平衡系统中自由度、组分数和相数之间关系的规律。
大学物理化学上册知识点归纳
（1.14） 上述两式中的Z均为实际气体的压缩因子。比例常数 B’,C’,D’…的单位分别为Pa-1,Pa-2,Pa-3…;比例常数B,C,D…的单 位分别为摩尔体积单位[Vm]的一次方，二次方，三次方…。它们依次称 为第二，第三，第四……维里系数。这两种大小不等,单位不同的维里 系数不仅与气体种类有关，而且还是温度的函数。 该方程所能适用的最高压力一般只有一两个MPa，仍不能适用于 高压范围。 五、对应状态原理及压缩因子 1.压缩因子的对应式 Z PV/(nRT) =pVm/(RT) （1.15） 压缩因子Z是个量纲为1的纯数，理想气体的压缩因子恒为1。一定 量实际气体的压缩因子不仅与气体的T，P有关，而且还与气体的性质 有关。在任意温度下的任意实际气体，当压力趋于零时，压缩因子皆趋 于1。此式适用于纯实际气体或实际气体混合系统在任意T，p下压缩因 子的计算。 2.对应状态原理 Pr=p/pc Vr=Vm/Vm,c T=T/Tc (1.16) (1.17) (1.18)
pr、Vr、Tc分别称为对比压力、对比体积和对比温度，又统称为气 体的对比参数，三个量的量纲均为1。各种不同的气体，只要有两个对 比参数相同，则第三个对比参数必定（大致）相同，这就是对应状态原 理。 第2章 热力学第一定律 一、 热力学基本概念 1. 状态函数
状态函数，是指状态所持有的、描述系统状态的宏观物理量，也称 为状态性质或状态变量。系统有确定的状态，状态函数就有定值；系统 始、终态确定后，状态函数的改变为定值；系统恢复原来状态，状态函 数亦恢复到原值。 2. 热力学平衡态 在指定外界条件下，无论系统与环境是否完全隔离，系统各个相的 宏观性质均不随时间发生变化，则称系统处于热力学平衡态。热力学平 衡须同时满足平衡（△T=0）、力平衡（△p=0）、相平衡（△μ=0） 和化学平衡（△G=0）4个条件。 二、热力学第一定律的数学表达式 1.△U=Q+W 或dU=ΔQ+δW=δQ-pambdV+δW` 规定系统吸热为正，放热为负。系统得功为正，对环境做功为负。 式中pamb为环境的压力，W`为非体积功。上式适用于封闭系统的一切 过程。 2．体积功的定义和计算 系统体积的变化而引起的系统和环境交换的功称为体积功。其定义 式为： δW=-pambdV （1） 气体向真空膨胀时体积功所的计算 W=0 （2） 恒外压过程体积功 W=pamb（V1-V2）=-pamb△V 对于理想气体恒压变温过程 W=-p△V=-nR△T （3） 可逆过程体积功 Wr= (4)理想气体恒温可逆过程体积功 Wr==-nRTln(V1/V2)=-nRTln(p1/p2) (5)可逆相变体积功 W=-pdV
物理化学---知识点总结
《物理化学学习要点》热力学第一定律一、 本章框架二、 本章要求1、 了解热力学基本概念：系统、环境、功、热、平衡状态、状态函数、可逆过程等；2、 明确热力学第一定律和热力学能的概念；3、 明确焓、标准摩尔反应焓、标准摩尔生成焓和燃烧焓的定义；4、 熟练掌握在理想气体单纯pVT 变化、相变化及化学变化过程中计算热、功、△U 、△H 的原理和方法；三、考核要求：1．热力学概论1.1 热力学的目的、内容和方法 （了解） 1.2 热力学的一些基本概念1.2.1 体系与环境，体系的性质 （理解）温过程 压过程 容过程 pVT 都变化过程热过程逆相变过程 可逆相变过程准摩尔反应焓 准摩尔燃烧焓 准摩尔生成焓等温反应 流膨胀1.2.2 热力学平衡态和状态函数（理解）2．热力学第一定律2.1 热和功（掌握）2.2 热力学能（掌握）2.3 热力学第一定律的表述与数学表达式（应用）3．体积功与可逆过程3.1 等温过程的体积功（应用）3.2 可逆过程与最大功（理解）4．焓与热容4.1 焓的定义（了解）4.2 焓变与等压热的关系（应用）4.3 等压热容和等容热容（理解）5．热力学第一定律对理想气体的应用5.1 理想气体的热力学能和焓（掌握）5.2 理想气体的C p与C v之差（理解）5.3 理想气体的绝热过程（掌握）6．热力学第一定律对实际气体的应用6.1 节流膨胀与焦耳-汤姆逊效应（了解）7．热力学第一定律对相变过程的应用（掌握）8．化学热力学8.1 化学反应热效应8.1.1 等压热效应与等容热效应（掌握）8.1.2 反应进度（了解）8.2 赫斯定律与常温下反应热效应的计算8.2.1 赫斯定律（应用）8.2.2 标准摩尔生成焓与标准摩尔燃烧焓（掌握）8.3 标准反应焓变与温度的关系—基尔霍夫定律（应用）四、重要概念1、系统与环境；2、 隔离系统、封闭系统、敞开系统；注意：隔离系统Q=0，W=03、 广度性质（加和性：V ，U ，H ，S ，A ，G ）强度性质（物质的量，T ，p ）； 4、 功W 和热Q ；注意W 与Q 的符号；W 与Q 均为途径函数（非状态函数） 5、 热力学能； 6、 焓； 7、 热容；8、 状态与状态函数； 9、 平衡态； 10、可逆过程；11、 节流过程； 12、 真空膨胀过程； 13、 标准态；14、标准摩尔反应焓，标准摩尔生成焓，标准摩尔燃烧焓五、重要公式与适用条件1. 体积功：W = -p 外dV （封闭系统，计算体积功）2. 热力学第一定律：∆ U = Q +W ， d U =Q +W （封闭系统） 3．焓的定义： H =U + pV4．热容：定容摩尔热容 C V ，m =Q V /dT =（∂ U m /∂ T ）V 定压摩尔热容 C p ，m = Q p /dT =（∂ H m /∂ T ）P 理想气体：C p ，m - C V ，m =R ；凝聚态：C p ，m - C V ，m ≈0理想单原子气体C V ，m =3R /2，C p ，m = C V ，m +R =5R /2 5. 标准摩尔反应焓：由标准摩尔生成焓∆f H B （T ）或标准摩尔燃烧焓∆c H B （T ）计算 ∆ r H m = ∑ v B ∆ f H B （T ）= -∑ v B ∆ c H B （T ）6. 基希霍夫公式（适用于相变和化学反应过程）∆ r H m（T 2）= ∆ r H m（T 1）+21T r pm T C dT∆⎰7. 等压摩尔反应热与等容摩尔反应热的关系式Q p -Q V = ∆ r H m （T ）-∆ r U m （T ）=∑ v B （g ）RT 8. 理想气体的可逆绝热过程方程：γγ2211V P V P = 122111--=γγV T V T γγγγ/)1(22/)1(11-=-P T P Tγ=Cvm Cpm /六、各种过程Q 、W 、∆ U 、∆ H 的计算1、 理想气体：等温过程dT =0， ∆ U =∆ H =0， Q =W ；非等温过程，∆ U = n C V ，m ∆ T ， ∆ H = n C p ，m ∆ T ， 单原子气体C V ，m =3R /2，C p ，m = C V ，m +R = 5R /22、对于凝聚相，状态函数通常近似认为与温度有关，而与压力或体积无关，即 ∆ U ≈∆ H = n C p ，m ∆ T3． 等压过程：p 外=p =常数，非体积功为零W '=0 （1） W = -p 外（V 2-V 1）， ∆ H = Q p =dTnC T Tm p ⎰2,， ∆ U =∆ H -∆（pV ），Q =∆ U -W（2） 真空膨胀过程p 外=0，W =0，Q =∆ U理想气体结果：d T =0，W =0，Q =∆ U =0，∆ H =0 （3） 等外压过程：W = -p 外（V 2-V 1） 4. 等容过程 ：d V =0 W =0，Q V =∆ U =dTnC T Tm v ⎰2,， ∆ H =∆ U +V ∆ p5．绝热过程：Q =0 （1）绝热可逆过程 W =dVp T T ⎰2= ∆ U =dTnC T Tm v ⎰2,，∆ H =∆ U +∆ pV理想气体：γγ2211V P V P = 122111--=γγV T V T γγγγ/)1(22/)1(11-=-P T P T（2）绝热一般过程：由方程WdVp T T外⎰2= ∆ U = dTnC T Tm v ⎰2, 建立方程求解。
物理化学课堂笔记
第一章:化学热力学一．绪论。
1.物理化学从化学现象与物理现象之间的联系着手，用物理学的理论和实验方法来研究化学变化，相变化及其P，V，T，物理变化本质。
了解物质的性质与其结构之间的关系规律的科学。
（简而言之就是用物理方法研究化学问题）其它定义：研究物质系统发生 pVT 变化、相变化和化学变化过程的基本原理，主要是平衡规律和速率规律以及与这些变化规律有密切联系的物质结构及性质（宏观性质、微观性质、界面性质和分散性质等）。
2.物理化学的基本组成①化学热力学：任一过程的方向和限度。
（研究化学反应的方向与限度。
例如：合成氨、人造金刚石、人造饼干等等。
）②化学动力学：任一过程的速度和机理（一个过程具体的每个步骤）。
（研究化学速率与反应机理，例H2与O2混合。
鞭炮。
4.电化学、表面化学、胶体化学。
）③结构化学：（研究物质结构与性质之间内在联系。
）3.研究方法①热动力学方法：以大量指点所构成的宏观系统为研究对象，直接从宏观实验和观察为基础，处理问题只关注起始和终止，不考虑宏观物体个别分子的行为不研究宏观系统个别粒子的结构及其变化的具体细节。
②统计力学方法：从宏观到微观的方法研究对象：大量粒子组成的宏观系统出发点：系统中微观粒子的性质（如质量、振动频率、转动惯量等）③量子力学方法：以量子力学为基础，以原子和分子为研究对象，揭示物质性质及其内在关系。
1-1基本性质（Basic Concept）1.系统和环境（System and Surrounding）①System: The materials of interest is defined as system.（研究的物质被定义为系统）Surrounding: The everything else is defined as surrounding.(其余的东西被定义为环境)②系统的分类（Classification of system）根据系统和环境，物质和能量交换方式，系统可分为敞开系统（Open），封闭系统（Closed），隔离系统（isolated）。
物理化学第一章小结资料
盖-吕萨克的成就
在化学方面，盖-吕萨克研究范围很广，取得不少成果 。1808年发表了今天以他名字命名的盖-吕萨克气体反应体 积比定律，这对以后化学发展影响很大。此时他被选人法 国研究院。他还发现了硼，还有其他多种贡献。特别值得 一提的是他的爱国主义精神。他总是把自己的研究工作和 祖国荣誉联系在一起。1813年法国两位化学家在海草灰里 发现了一种新元素，但在尚未分离出来时无意地把原料都 给了戴维，盖-吕萨克知道后十分激动地说：“不可原谅的 错误！空前严重的错误！居然倾其所有，拱手送给了外国 人。戴维会发现这种元素，并把研究成果公之于世。这样 ，发现新元素的光荣就会属于英国，而不属于法国了。” 于是他和两位化学家一起立即动手，从头做起，昼夜不停 ，终于与戴维同时确证了新元素——碘，为祖国争得了荣 誉。
焦耳的生平
•焦耳最早的工作是电学和磁学方面的研究，后转 向对功热转化的实验研究。 •1866年由于他在热学、电学和热力学方面的贡献， 被授予英国皇家学会柯普莱金质奖章。 •1872年—1887年焦耳任英国科学促进协会主席。 •1889年10月11日焦耳在塞拉逝世。
焦耳的科学成就
•1.焦耳定律的发现
盖斯(Hess G H , 1802 - 1850)
生于瑞士日内瓦，任俄国 圣彼得堡大学化学教授。从 事无机化学研究，但最著名 的是他进行的一系列热化学 研究，但最著名的是他进行 的一系列热化学研究。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
物理化学上册公式总结第一章.气体一、理想气体适用①波义耳定律：定温下，一定量的气体，其体积与压力成反比pV=C②盖·吕萨克定律：对定量气体，定压下，体积与T成正比V t=C`T③阿伏伽德罗定律：同温同压下，同体积的各种气体所含分子数相同。
④理想气体状态方程式pV=nRT推导：气体体积随压力温度和气体分子数量改变，即：V=f（p,T,N）对于一定量气体，N为常数dN=0，所以dV=（∂V/∂p）T,N dp+（∂V/∂T）p,N dT根据波义耳定律，有V=C/P，∴（∂V/∂p）T,N=-C/p2=-V/p根据盖·吕萨克定律，V=C`T，有（∂V/∂T）p,N=C`=V/T代入上式，得到dV/V=-dp/p+dT/T积分得lnV+lnp=lnT+常数若所取气体为1mol，则体积为V m，常数记作lnR，即得pV m=RT上式两边同时乘以物质的量n，则得pV=nRT⑤道尔顿分压定律：混合气体的总压等于各气体分压之和。
⑥阿马格分体积定律：在一定温度压力下，混合气体的体积等于组成该气体的各组分分体积之和。
⑦气体分子在重力场的分布设在高度h处的压力为p，高度h+dh的压力为p-dp，则压力差为 dp=-ρgdh假定气体符合理想气体状态方程，则ρ=Mp/RT，代入上式，-dp/p=Mgdh/RT对上式积分，得lnp/p0=-Mgh/RT∴p=p0exp（-Mgh/RT）ρ=ρ0exp（-Mgh/RT）或n=n0exp（-Mgh/RT）二、实际气体适用①压缩因子ZZ=pV m/RT对于理想气体，Z=1，对实际气体，当Z大于1，表明同温度同压力下，实际气体体积大于理想气体方程计算所得结果，即实际气体的可压缩性比理想气体小。
当Z小于1，情况则相反。
②范德华方程式（p+a/V m ）（V m -b ）=RT第二章.热力学第一定律①热力学第一定律表达式：ΔU=Q+W 或dU=δQ+δW热力学能的微分表达式dU=（∂U/∂p ）T dp+（∂U/∂T ）p dT而如果把U 当作T,V 的函数，则上式变为dU=（∂U/∂V ）T dV+（∂U/∂T ）V dT但是 （∂U/∂T ）V d T≠（∂U/∂T ）p dT ②各过程下气体做的功自由膨胀：外压等于0，所以W=0；外压始终恒定（抵抗某个外压）:p e 恒定不变，则W e =-p e （V 2-V 1） 多次等外压膨胀W=-p 1ΔV 1-p 2ΔV 2外压总是比内压小一个无限小的膨胀W=-∑p e dV=-∑（p i -dp ）dV ，略去二级无限小dpdV ，得到：W=−∫p i V 2V1dV=-nRTln V1V 2③焓（状态函数） 定义：焓H=U+pV等容过程下，ΔV=0，所以W=0，ΔU=Q V等压过程下，p 2=p 1=p ，ΔU=Q p -p （V 2-V 1），则Q p =（U 2+pV 2）-（U 1+pV 1） ΔH=H 2-H 1=Q P④热容定义：系统升高单位热力学温度所吸收的热C(T)=δQ dT摩尔热容：C m (T)=C(T)n=1n δQ dT（等压过程热容C p ，等容过程热容C V ）理想气体的C p 和C V 之差：C p -C V =nR 推导：对于任意系统，C p -C V =(∂H∂T)P -(∂U∂T)V =（∂(U+pV ）∂T）p -（∂U∂T）V=(∂U ∂T)p +p(∂V ∂T)P -(∂U ∂T)V =(∂U ∂V)T (∂V ∂T)p +p(∂V ∂T )p (此时依然是通式) ∴对于理想气体，(∂U∂V)T =0，(∂V∂T)p =nRp ，代入上式，得到C p -C V =nR⑤绝热过程的功：绝热过程中，Q=0；由热力学第一定律，W=ΔU ；又∵dU=C V dT ，假设C V 是常数，则W=ΔU=C V (T 2-T 1)⑥绝热过程方程式：TV γ-1=常数；pV γ=常数；p 1-γT γ=常数 推导：对于理想气体dU=C V dT ，pV=nRT ； ∴C V dT+nRTdV/V=0，整理后得dT T+nRdVC V V=0,令CP C V=γ（热容比）又∵nR C V=γ-1，∴dT T+(γ-1)dV V=0；积分后得lnT+(γ-1)lnV=常数，即TV γ-1=常数⑦热机效率和冷冻系数 热机效率η=−W Q ℎ=−nR(T ℎ−T C )ln V 1V 2−nRT ℎln V1V 2=T ℎ−T cT ℎ=1-T c T ℎ=1+Qc Q ℎ冷冻系数β=Q c /W=T c /(T h -T c ) ⑧基尔霍夫定律第三章.热力学第二定律①克劳修斯不等式与熵增加原理卡诺定理指出，温度相同的低温热源和高温热源之间工作的不可逆热机效率不可能大于可逆热机效率。
已知：η1＜η2即1+Qc Q ℎ＜1-Tc T ℎ，可推广为(∑δQ Tn i=1)1 ＜0(∑δQ Tn i=1)1，A →B +(∑δQ Tn i=1)2，B →A ＜0又∵(∑δQ Tn i=1)2，→A =-ΔS 1→2∴ΔS 1→2-∑δQ T1→2≥0，即为克劳修斯不等式。
dS iso =ΔS sys +ΔS sur ≥0，即为熵增加原理。
②热力学基本方程dU=δQ +δW =TdS-pdV ，∴TdS=dU+pdV，此即为热力学基本方程 还可写为dS=dU T +pdVT，由此可得T=(∂U∂S)V ；p=T(∂S∂V)U③熵变的计算等温过程：1）理想气体等温可逆变化ΔS=QT=nRln V2V 1=nRln p1p 22）等温等压可逆相变ΔS=ΔHT3）理想气体的等温等压混合过程，符合分体积定律，即x=V/V 总Δmix S=-R ∑nlnx21r m 2r m 1()()d T p T H T H T C T∆=∆+∆⎰非等温过程：1）可逆等容变温过程ΔS=∫nC V,mTT 2T1dT2）可逆等压变温过程ΔS=∫nC p,mTT 2T1dT④吉布斯自由能变的计算G=H-TS=U+pV-TS=A+pV dG=dH-TdS-SdT=dA+pdV+Vdp1）等温等压可逆相变dA=- pdV 且dp=0，所以dG= dA+pdV+Vdp=0 2）等温过程dA=- pdV ，dG= dA+pdV+Vdp=VdpΔG=∫Vdp p 2p 13）化学反应（范德霍夫等温方程式）Δr G m =-RTlnK p +RTlnQ p当Q p ＜K p ，Δr G m ＜0，反应正向进行。
当Q p ＞K p ，Δr G m ＞0，反应逆向进行。
当Q p =K p ，Δr G m =0，反应处于平衡状态。
⑤几个热力学函数间的关系（从定义式导出）G=A+pV dU=TdS-pdV dH=TdS+Vdp dA=-SdT-pdVdG=-SdT+Vdp T=(∂U∂S)V =(∂H∂S)pp=-(∂U ∂V)S =-(∂A∂V)TV=(∂H ∂p)S =(∂G∂p )TS=-(∂A ∂T)V =-(∂G∂T)p⑥麦克斯韦关系式 (∂T/∂V)S =-(∂p/∂S)V (∂T/∂p)S =(∂V/∂S)p (∂S/∂V)T =(∂p/∂T)V (∂S/∂p)T =-(∂V/∂T)p应用：U 随V 的关系：(∂U∂V )T =T(∂p/∂T)V -pH 随p 的关系(∂T/∂p)T =V-(∂V/∂T)p 吉布斯自由能与温度的关系(∂ΔG ∂T)p =ΔG−ΔH T第四章.多组分系统热力学及其在溶液中的应用①偏摩尔量的加和公式Z=n 1Z 1+n 2Z 1+…+n k Z k =∑n B Z B k B=1②吉布斯-杜亥姆公式∑x B dZ B k B=1=0③化学势与温度压力的关系(∂μB ∂p)T,Nb,Nc =V B(∂μB ∂T )p,Nb,Nc =-S B [∂(μB T)T]P,nB ，nC =-HB T 2④拉乌尔定律：定温下，在稀溶液中，溶剂的蒸气压等于纯溶剂的蒸气压乘以溶液中溶剂的摩尔分数。
p A =p A ＊x A⑤亨利定律：在一定温度和平衡状态下，气体在液体里的溶解度和该气体的平衡分压成正比。
p B =k x ，B x B注意：p B 指的是气体在液面的分压力；溶质在气体和在溶液中的分子状态必须相同；升高温度或降低气体分压能使溶液变稀，使溶液更服从亨利定律。
⑥理想液态混合物任一组分的化学势μB (l)= μB ＊(l)+RTlnx B第五章.相平衡①多相系统平衡的一般条件 1）热平衡：平衡时温度相等T α=T β 2）压力平衡：平衡时压力平衡p α=p β 3）相平衡条件：μB α=μB β ②相率Φ+f=S+2，C=S-R-R`，Φ+f=C+2当其他因素影响更多时，将2换成n ，n 等于外界因素个数。
③杠杆规则第六章.化学平衡①化学反应的平衡条件和反应进度的关系dU=TdS-pdV+∑υBμB dξdH=TdS+Vdp+∑υBμB dξdA=-SdT-pdV+∑υBμB dξdG=-SdT+Vdp+∑υBμB dξ②三个互相相关的反应平衡常数的关系假设反应3=反应1-反应2，则存在：Δr G mθ(3)= Δr G mθ(1)- Δr G mθ(2)K3=K1/K2③温度对化学平衡的影响ln K2K1=Δr H mR(1T1−1T2)④压力对化学平衡的影响(∂lnK∂p )T=-ΔV mRT。