定积分的应用(面积)(参考研究)
(完整版)定积分的应用--平面图形的面积

C3x
跨度为6米, 高为3米,此抛物
线形拱桥的横截面积为多少?
解:如图建立平面直角坐标系,
A
-3
B
可设抛物线方程为
y ax2 (a 0)
于是抛物线形拱桥的横截面积
S= S长方形 - S曲边梯形
点 (3,3)代入方程,得
a 1
所以抛物线方程
3 y
1
x2
3
= 18 -
3 1 x2dx 3 3
=12 - 3 1 x2dx
3 3
计算
问题情境
b
a f ( x)dx 的几何意义是什么?
几何意义
y
当 f (x) ≥ 0,定积分
b
a f (x)dx
0
a
表示曲线 y = f (x),直线 x = a,
x = b和 x 轴所围成的曲边梯形
的面积
y f (x)
bx
几何意义
ya
b
当函数 f (x) 0 , 定积分 x
b
a f (x)dx
1 2
y2)d
y
所围图形
y y2 2x (8, 4)
o
yx4 x
(2, 2)
18
定积分在几何上的应用
y
y y 2 (x)
y 1(x)
oa x b
x
X —型:
a x b
d
y
cx 1( y) o
x 2 ( y)
x
Y —型:
c yd
h 2 (x) 1(x) h 2 ( y) 1( y)
y f (x)
就是位于x轴下方的曲边梯形
面积的相反数. 即
b
a f (x)dx S
定积分求平面图形面积在实际生活中的应用

定积分求平面图形面积在实际生活中的应用定积分是数学中重要的概念,定积分可以用来计算函数在一定范围(定义域)内的积分值。
它是一种可以用来计算面积或计算曲线积分问题的一种技术。
在实际生活中,定积分用于求解平面图形面积的问题,广泛应用于水利、建筑、航空航天等各个领域。
首先,定积分可以用于求解椭圆面积的问题。
椭圆面积可以用定积分来计算,其计算公式为:S=[π/2*(a2-b2)],其中a是椭圆的长轴,b是椭圆的短轴。
这个公式能够准确地计算出椭圆的面积,在水利等领域中,椭圆管道的运用非常广泛,可以用定积分计算出椭圆管道的面积,从而帮助水利设计者准确地计算水利结构的尺寸。
其次,定积分可以用于求解三角形面积的问题。
三角形的面积也可以通过定积分进行计算,其计算公式为:S=*a*b*sin(C),其中a 和b是三角形的底边,C是三角形的内角。
这个公式可以准确的计算出三角形的面积,在建筑设计等领域中,三角形结构的运用非常广泛,可以用定积分计算出三角形结构的面积,从而帮助设计者准确地计算建筑结构的尺寸。
此外,定积分还可以用于求解复杂图形的面积。
复杂图形的面积可以用定积分来计算,例如可以用定积分计算圆柱体的表面积、圆柱管的表面积以及球的表面积等。
在航空航天等领域中,复杂图形的运用也非常广泛,例如飞机机身的设计、航天器的设计等,可以用定积分计算出复杂图形的面积,从而帮助设计者准确地计算机构的尺寸。
综上所述,定积分在实际生活中极具价值,它可以用于求解椭圆
面积、三角形面积以及复杂图形的面积等问题,在水利、建筑、航空航天等各个领域都有很广泛的应用,其准确的计算方法可以为实际生活中的设计者提供帮助。
定积分在几何上的应用(面积)

r()
d
面积元素 dA1[()2]d
2
曲边扇形的面积为:
o
x
A 1[()2]d. 2
圆 扇 形 的 面 A积1r为 2
2
例 6求 双 纽 线 2 a 2c2 o所 s围 平 面 图 形
的 面 积 .
解 由对称性知总面积=4倍第
一象限部分面积
yx
A4A1
A404
1a2co2sd
2
a2.
A1 2a2co2s
ax
x bx
x+dx
b
b
Aa f(x)d xaydx
例 1计 算 由 两 条 抛 物 线 y2x和 yx 2所 围 成 的
图 形 的 面 积 .
解 两曲线的交点 (0,0) (1,1) 选 x为积分变量 x[0,1]
x y2 y x2
面积微元 dA ( xx2)dx
1
A0(
xx2)dx 32
1根据问题的具体情况选取一个变量例如分成n个小区间取其中任一小区间并记为与dx的乘积就把dx称为量f的微元且记作df上曲线下曲线xdxdx面积微元dx可直接由公式得到xdx求面积的一般步骤
第五章 定积分及其应用
§6 定积分在几何上的应用
§5.6 定积分在几何上的应用
若能把某个量表示 成定积分,我们就可以 计算了.
n
小窄曲边梯形的面积为Ai ,则AAi .
i1
( 2 ) 计 算 A i 的 近 似 值 A if(i) x i i xi
n
(3) 求和,得A的近似值 A f(i)xi.
(4) 求极限,得A的精确值 i1
n
Al i0m i1f(i)xi abf(x)dx
定积分的应用(面积)

x y
(t (t
) )
(a t b) 给出,
曲边梯形的面积为
n
n
b
A m y dx m (t) d[ (t)] a (t) (t)dt
Note: (1) 带绝对值; (2) 变量代换.
(3) 极坐标系下
①(3极) 点极在坐区标域系内下部 A 2 1 r 2 ( )d
设 rr()
(以 y 为积分变量还是以 x 为积分变量)
法 1 “横分”(以 y 为积分变量)
A
2 4
4
2
y
(
y
2
4)
dy
36 .
法 2 区间分割,用“竖分”(以 x 为积分变量)
竖分:没有代表区间,左半部 抛—抛 例 2 求由曲线 y2 4 x右与半x部 2 y直线4 所—围抛图形的面积.
法 2 区间分割,用“竖分”(以 x 为积分变量)
积分 [xi , §x5i1]定 [x积i , 分xi 的x应i ] ,用Q : f (i )xi ,
微元
[x, x dx] , dQ : f (x)dx .
b
a
n
f ( x)dx lim d 0 i1
f (i )xi Q
小区间上部分量的积累
“分割、取近似、求和、取极限”
“微元法”思想: 在[a, b] 上取代表小区间[x, x dx] 若 f (x)dx 为 Q 的线性主部(即 f ( x)dx dQ ).则称
f (x)
则 Alim
f ( x)dx
o
b f ( x)dx .
a x xdx b x
a
推广到一般
(1) 直角坐标系下
y y f (x)
定积分法求面积探究毕业论文

定积分法求面积的探究教学系:_____________专业:_________________年级:______________________姓名:_____________________学号:__________导师及职称:定积分是数学中十分重要的工具,其中求图形的面积正是它的运用之一,它的思想就是切割求和,在不同的坐标系下可采用特定的方法求解面积。
本文介绍了几种运用定积分来求面积的方法,其中列举了特殊的例题以及重要的问题解决方法。
如果实际问题中的所求量与某一区间有关且在该区间上具有可加性,我们就可以用函数的定积分来表示这个所求的量,因此我们就可以运用定积分来解决一些实际问题。
同时利用定积分求不规则平面图形的面积,是定积分在几何中的重要应用之一。
如何灵活地运用定积分的定义及有关公式,巧妙地将求不规则图形的面积问题等价转化为求定积分的数值问题就是一大关键,本文结合实例,介绍几种常用的转化方法与求解策略。
从而充分的体现数形结合的数学思想方法。
关键词:定积分;封闭图形;曲面域;对称性Research of square in defi nite in tegralABSTRACTA definite integral is very important mathematical tools, for which the graphics area is one of its applicati on, its thought is to cut and, un der differe nt coordi nate systems can use specific method to find the area. This paper introduces several methods of using the integral area to seek the. Which lists the specific examples and an important method to solve the problem. If practical problems for quantity with a certain interval and in the interval is additive, we can use the definite integral of a function to represent the desired amount. Therefore, we can use the defi nite in tegral to solve some practical problems.At the same time, the use of definite integrals for the irregular plane graphics area, is one of the important applications of integral in geometry. How to flexibly use definite integral is defi ned and the related formulae and skillfully will seek irregular graphic area equivale nt transformation to calculate the numerical integral is one of key, the paper with examples, in troduces several common ly used tran sformati on method and soluti on strategy. I n order to fully reflect the comb in ati on of the mathematical thought and method.Keywords: defi nite in tegral; closed graph; surface area; symmetry目录一、引言 (5)二、相关概念 (5)1.1 定积分的定义 (5)1.2定积分的常用计算方法 (5)1.2.1直接利用公式及性质计算 (5)1.2.2利用定积分的区间可加性计算 (2)三、定积分在面积问题中的应用 (2)3.1直角坐标系下求面积 (2)3.1.1 平面面积 (2)3.1.2 曲面面积 (5)3.2 极坐标 (6)3.3求旋转曲面的面积 (7)四、常见方法 (10)4.1 巧选积分变量 (10)4.2巧用对称性 (11)4.3巧用分割计算 (11)五、结束语 (12)参考文献 (13)致谢 (13)、引言积分在自然科学、工程技术、经济管理中有着广泛的应用,比如利用积分求平面图 形的面积、变力做功等都是微积分中定积分的应用问题, 在数学分析中占据了重要地位。
用定积分求面积的两个重要公式
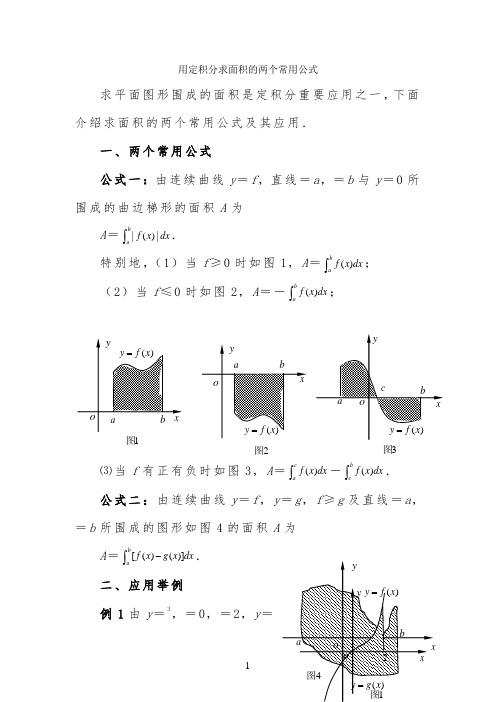
用定积分求面积的两个常用公式求平面图形围成的面积是定积分重要应用之一,下面介绍求面积的两个常用公式及其应用.一、两个常用公式公式一:由连续曲线y =f ,直线=a ,=b 与y =0所围成的曲边梯形的面积A 为A =|()|ba f x dx ⎰.特别地,(1)当f ≥0时如图1,A =()ba f x dx ⎰;(2)当f ≤0时如图2,A =-()baf x dx ⎰;⑶当f 有正有负时如图3,A =()caf x dx ⎰-()bcf x dx ⎰.公式二:由连续曲线y =f ,y =g ,f ≥g 及直线=a ,=b 所围成的图形如图4的面积A 为A =[()()]ba f x g x dx -⎰.二、应用举例例1由y =3,=0,=2,y =1图2图3图0围成的图形面积.分析:先画出图象,利用公式1转化为定积分问题即可解决.解:(1)如图1,由公式1,得S =230x dx ⎰=42440111|204444x =⨯-⨯=.评注:注意定积分与利用定积分计算曲线围成图形的面积区别.定积分是一种积分和的极限,可为正,也可为负或零,而平面图形的面积在一般意义上总为正.一般情况下,借助定积分分别求出每一部分曲边梯形的面积,然后将它们加在一起.例2(1)由曲线y =2,y 2=所围成图形的面积. (2)由y =142-1,y =12,y =34x 在第一象限所围成图形的面积.分析:先画图象找出范围,利用公式2,用积分表示,再求积分.解:(1)如图2,所求面积为阴影部分. 解方程组22y xy x⎧=⎪⎨=⎪⎩,得交点0,0,1,1,由公式2,得S =120)x dx ⎰=331202211()|33333x x -=-=.(2)如图3,解方程组211412y x y x ⎧=-⎪⎪⎨⎪=⎪⎩和211434y x y x ⎧=-⎪⎪⎨⎪=⎪⎩,得=0,=1+的舍去,=4.由公式2,得图形面积S=1031()42x dx -⎰+42111[(1)]42x x dx --⎰216-=.3图。
考研数学第六讲定积分的应用

第六讲 定积分的应用一、基础知识几何应用(一)平面图形的面积 1.直角坐标情形由曲线)0)(()(≥=x f x f y 及直线 x a =与 x b = ( a b < ) 与 x 轴所围成的曲边梯形面积A 。
()baA f x dx =⎰ 其中:f x dx ()为面积元素。
由曲线y f x =()与y g x =()及直线x a =,x b =(a b <)且f x g x ()()≥所围成的图形面积A 。
()()[()()]=-=-⎰⎰⎰b b baaaA f x dx g x dx f x g x dx2.极坐标情形设平面图形是由曲线 )(θϕ=r 及射线αθ=,βθ=所围成的曲边扇形。
取极角θ为积分变量,则 βθα≤≤,在平面图形中任意截取一典型的面积元素A ∆,它是极角变化区间为],[θθθd +的窄曲边扇形。
曲边梯形的面积元素 θθϕd dA 2])([21= ⎰=βαθθϕd A )(212(二)旋转体的体积计算由曲线y f x =()直线x a =,x b =及x 轴所围成的曲边梯形,绕x 轴旋转一周而生成的立体的体积。
取x 为积分变量,则],[b a x ∈,对于区间],[b a 上的任一区间],[dx x x +,它所对应的窄曲边梯形绕x 轴旋转而生成的薄片似的立体的体积近似等于以)(x f 为底半径,dx 为高的圆柱体体积。
即:体积元素为 []dx x f dV 2)(π=所求的旋转体的体积为 []dx x f V ba⎰=2)(π(三)平面曲线的弧长 1.直角坐标情形设函数)(x f 在区间],[b a 上具有一阶连续的导数,计算曲线)(x f y =的长度s 。
取x 为积分变量,则],[b a x ∈,在],[b a 上任取一小区间],[dx x x +,弧长元素为[]dx x f ds 2)(1'+= 弧长为 []⎰'+=badx x f s 2)(12.参数方程的情形若曲线由参数方程)()()(βαφϕ≤≤⎩⎨⎧==t t y t x 给出,弧微分[][]dt t t dy dx ds 2222)()()()(φϕ'+'=+=则 [][]⎰'+'=βαφϕdt t t s 22)()(3.极坐标情形若曲线由极坐标方程)()(βθαθ≤≤=r r 给出,将极坐标方程化成参数方程,曲线的参数方程为x r y r ==⎧⎨⎩≤≤()cos ()sin ()θθθθαθβ,弧长元素为θθθθθθθd r r d r r d r r dy dx ds 22222222)()cos sin ()()sin cos ()()('+=+'+-'=+= 从而有 ⎰'+=βαθd r r s 22(四).曲率与曲率半径 曲率记作,k 0lims d k s dsαα∆→∆==∆, 222''''tan '''sec sec 1'd d y y y y dx dx y ααααα=⇒=⋅⇒==+, 2''1'y d dx y α=+,又,ds =故322''(1')y d k dsy α==+.曲率半径 3221(1')''y k y ρ+==. 曲率圆二、例题1.平面图形的面积与旋转体的体积例 1. 已知抛物线2,y px qx =+(其中0,0p q <>)在第一象限内与直线5x y +=相切,且抛物线与x 轴所围成的平面图形的面积为s .问: (1)p q 和为何值时,s 达到最大值? (2)求出此最大值.【答案】,3p q =4=-5,22532s =例2.设⎪⎩⎪⎨⎧>≤=-0,0,)(22x ex e x F x x ,S 表示夹在x 轴与曲线()y F x =之间的面积. 对任何)(x f0t >,)(1t S 表示矩形t x t -≤≤,0()y F t ≤≤的面积. 求(I) 1()()S t S S t =-的表达式; (II) ()S t 的最小值.【答案】(I) t te t S 221)(--=,t ∈ (0 , +∞).(II) eS 11)21(-=. 例3.设曲线的极坐标方程为(0)a e a θρ=>,则该曲线上相应于θ从0到2π的一段弧与极轴所围成的图形的面积为41(1)4a e aπ-. 例 4.设1D 是由抛物线22y x =和直线x a =, 2x =及0y =所围成的平面区域; 2D 是由抛物线22y x =和直线x a =,0y =所围成的平面区域,其中02a <<.(1)试求1D 绕x 轴旋转而成的旋转体体积1V ;2D 绕y 轴旋转而成的旋转体体积2V . (2)问当a 为何值时,12V V +取得最大值?试求此最大值. 【答案】54(32)5a π- 4a π 1295π 例5.设曲线2(0,0)y ax a x =>≥与21y x =-交于点A ,过坐标原点O 和点A 的直线与曲线2y ax =围成一平面图形.问a 为何值时,该图形绕x 轴旋转一周所得的旋转体体积最大?最大体积是多少?【答案】4a =是体积最大,其最大体积为:522161518755V π=⋅= 例6.过坐标原点作曲线ln y x =的切线,该切线与曲线ln y x =及x 轴围成平面图形D . (1).求D 的面积A ;(2).求D 绕直线x e =旋转一周所得旋转体的体积V . 【答案】(1)112A e =- (2)2(5123)6V e e π=-+ 例7.(15-2) 设A>0,D 是由曲线段sin (0)2y A x x π=≤≤及直线0y =,2x π=所围成的平面区域,1V ,2V 分别表示D 绕x 轴与绕y 轴旋转成旋转体的体积,若12V V =,求A 的值.【答案】8π例8.(09-3-10 分)设曲线()y f x =,其中()y f x =是可导函数,且()0f x >,已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形,绕x 轴旋转一周所得的立体体积值是曲边梯形面积值的t π倍,求该曲线方程。
定积分的应用

定积分的应用定积分是微积分中的重要概念,它在数学和实际问题的解决中扮演着关键的角色。
本文将探讨定积分的应用,并结合实例详细说明其在解决各类问题中的重要作用。
一、定积分的概念定积分是微积分中的一种运算符号,表示在一定区间上的函数曲线与坐标轴所围成的面积。
通常用符号∫ 表示,即∫f(x)dx,其中f(x)为被积函数,dx表示积分变量。
定积分的结果是一个数值。
二、定积分的几何意义定积分的几何意义是曲线与坐标轴所围成的面积。
例如,我们可以通过计算函数曲线与x轴之间的面积来求取定积分。
这种面积计算方法可以应用于各种形状的曲线,包括折线、曲线、圆弧等。
三、定积分的物理应用定积分在物理学中有广泛的应用。
例如,当我们需要计算物体的质量、体积、位移、功等物理量时,可以通过定积分来进行计算。
定积分可以将一个连续变化的物理量表示为无限个微小变化的和,从而得到准确的结果。
四、定积分的经济学应用定积分在经济学领域也被广泛应用。
例如,当我们需要计算市场供求曲线下的固定区间所代表的消费者剩余或生产者剩余时,可以通过定积分来计算。
定积分可以将变化的价格和数量转化为面积,以方便计算。
五、定积分的工程应用在工程学中,定积分也具有重要的应用价值。
例如,在力学领域,当需要计算曲线所代表的力的作用效果时,可以通过定积分来计算。
定积分可以将一个连续变化的力量表示为无限个微小作用力的和,从而得到准确的结果。
六、定积分的统计学应用再一个例子的统计学领域中,定积分同样发挥着重要作用。
例如,在概率密度函数下计算所得的面积可以表示某一事件发生的概率。
定积分可以将一个连续变化的概率密度函数表示为无限个微小概率的和,从而得到准确的概率结果。
七、定积分的计算方法定积分的计算方法有多种,例如,常用的有牛顿-莱布尼茨公式、变量替换法、分部积分法等。
根据不同的问题和函数形式,选择合适的计算方法对于准确求解定积分非常关键。
八、结语定积分作为微积分中的重要概念,在各个领域中均得到了广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t
2
) dx
1
0
t
y = x2
[t 2 x
x3
]t
x3 [
t2x]1
t2
S2
30 3
t
S1
4t 3 t 2 1 ,0 t 1
3
3
x t1
S' 4t 2 2t 2t(2t 1) 令 0 ,得驻点: t 0, t 1 ,
当t 1 时两面积和最小.
2
2
资料部分
18
练习写出下列给定曲线所围成的图形面积的定积分表达式。
此题选y为积分变量比较好,
2 y4
A 4 ( y 4 y2 )dy
2
2
y2
y3 4
( 4y )
2
6
2
18 .
选择积分变量的原则: (1)尽量少分块;
yxx y4 4 y2
yx2 2x 2
(2资)料积部分分容易。
15
例3
求曲线 y
x2 2
,
y
1
1 x2
与直线x
3所
围成的平面图形的面积.
解 将 y0 3 带入抛物线方程,得横坐标 x0 2
( y 2)2 x 1两边关于x求导,得 2( y 2) y 1
代 入x0 2,y0 3, 得
y(2) 1 2
因此切线方程为
y
yx 3 212y( x 42)
3
y 3 1 ( x 2) 2
(xy12)2( y x2)21
A
f
( x)
g( x)]dx
c[g(x)
f ( x)]dx
c
a
f ( x) g( x) dx f ( x) g( x) dx
ab
c
a f ( x) g( x) dx资料部分
6
3. 由连续曲线 y=f(x), y=g(x), 直线 x=a, x=b (a<b)所围成的平面
图形的面积
y
ao
y f (x)
面积元素: dA f ( x)dx,
x x x
b
面积 A f ( x)dx a
bx
资料部分
9
由连续曲线 y=f(x), y=g(x), 直线 x=a, x=b (a<b)所围成 的平面图形的面积
y
y f (x)
y g(x)
a o x x x c
b
x
面积元素: dA f ( x) g( x) dx,
y
解 交点 x 1 ,
由对称性,
x2 y
2
1 y 1 x2
3 1 o
1 3x
A
2
11
( 0 1
x2
x2 )dx 2
2
1
3 x2 (
2
1
1 x
2
)
dx
2
3 .
3
3
资料部分
16
例4 求由抛物线 ( y 2)2 x 1 和与抛物线相切于纵坐
标 y0 3 处的切线及x轴所围成的平面图形的面积
资料部分 c
11
例1 计算由两条抛物线 y2 x 和 y x2 所围成的
图形的面积.
解 先求两曲线的交点
xy yx2
y x2
(0,0)
x
y2
(1,1)
y x2
选x为积分变量, x [0,1]
A
1
(
x
x2 )dx
(2
3
x2
x3
)1
1
.
0
3
30 3
能否选y为积分变量?
资料部分
12
例1 计算由两条抛物线 y2 x 和 y x2 所围成的
(1)y x, y x
1
A
x x dx 1
0
6
(2)y e, y ex , x 0 A 1 e ex dx 1 0
(3)
轴 A 1 3 2x x2 dx 32
3
3
资料部分
19
练习写出下列给定曲线所围成的图形面积的定积分表达式。
y2 2x
(2,2), (8,4).
y x4
y x4
选x为积分变量, x [0,8]
yy2 2x 2 x
2
8
A 0 [ 2x ( 2x )]dx 2 [ 2 x ( x 4)]dx
18 .
资料部分
14
2
8
A 0 [ 2x ( 2x )]dx 2 [ 2 x ( x 4)]dx
3
[1
(
y
2)2
(2
4
y
4)]dy
0
0
5
x
3
(
0
y2
6y
9)dy
y3 资料部(分3
3 y2
9 y)
3
9
17
0
例5 设y x2定义在0 x 1上, t是区间[0,1]上的任
一点, 当t为何值时,图中两阴影部分的面积和最小?
解 S S1 S2
y
t (t 2 x2 )dx
1
(
x2
b
A a f ( x) g( x) dx
资料部分
10
由曲线 x ( y) 、 x ( y) 直线 y c, y d(c d)
围成的平面图形的面积为
d
A ( y) ( y) dy
y
cy
d
x ( y) d
x ( y)
x ( y) x ( y)
c
xc
x
o
o
d
特别,若( y) ( y)时, A [ ( y) ( y)]dy .
第七节 定积分的应用
一.求平面图形的面积 二.求几何体的体积 三.在经济问题中的应用
资料部分
1
一.求平面图形的面积
复习:定积分的几何意义
曲边梯形面积 曲边梯形面积的负值
A1
A3
A2
A4
b
a f ( x)dx A1
A A 资料部分
2
3
A4
2
1.以x轴为底边的曲边梯形的面积
y
f (x)
y
a
y
y f (x)
y g(x)
ao
c
b
x
b
A a f ( x) g( x) dx
资料部分
7
特别,f ( x) g( x) 时,
y
y f (x)
y g(x)
ao
b
b
A a [ f ( x) g( x)]dx
资料部分
x
8
由连续曲线 y = f (x) ( f (x) 0), 直线 x=a, x=b (a<b)及x轴所围成的平面图形的面积
A a ( y) dy .
a• x 资料部分
x
5
3. 由连续曲线 y=f(x), y=g(x), 直线 x=a, x=b (a<b)所围成的平面
图形的面积
y
y f (x)
y g(x)
ao
c
b
x
c
c
b
b
A
a
f ( x)dx
g( x)dx
a
c
g( x)dx c
f ( x)dx
c
a
[
a
0
b
x
f (x)
0a
bx
资料部分
b
A a f ( x) dx .
3
若f (x)有正有负,则曲边梯形面积为
b
A a f ( x) dx . y y f (x)
y f (x)
ao
b
x
资料部分
4
2.以y轴为底边的曲边梯形的面积
ห้องสมุดไป่ตู้
y
b
x (y)
y
b
x (y)
a
a
0
x
0
y
b • x ( y)
b
图形的面积.
解 先求两曲线的交点
x y2
y x2
(0,0)
x
y2
(1,1)
yx xy2
选y为积分变量, y [0,1]
A
1
(
y
y2 )dy
(2
3
y2
y3
)1
1
.
0
3
30 3
资料部分
13
例2 计算由曲线 y2 2x 和直线 y x 4所围成
的图形的面积.
解 两曲线的交点
y 2x
