完整word版,高思导引四年级第十八讲行程问题三教师版
华数思维训练导引 四年级下 行程问题
华数思维训练导引四年级下行程问题（一）四年级下行程问题（一）1、甲、乙两地相距6千米，某人从甲地步行去乙地，前一半时间平均每分钟行80米，后一半时间平均每分钟行70米。
问他走后一半路程用了多少分钟？分析：解法１、全程的平均速度是每分钟（80+70）/2=75米，走完全程的时间是6000/75=80分钟，走前一半路程速度一定是80米，时间是3000/80=37.5分钟，后一半路程时间是80-37.5=42.5分钟解法2：设走一半路程时间是x分钟，则80*x+70*x=6*1000，解方程得：x=40分钟因为80*40=3200米，大于一半路程3000米，所以走前一半路程速度都是80米，时间是3000/80=37.5分钟，后一半路程时间是40+（40-37.5）=42.5分钟答：他走后一半路程用了42.5分钟。
2、小明从家到学校有两条一样长的路，一条是平路，另一条是一半上坡路、一半下坡路。
小明上学走两条路所用的时间一样多。
已知下坡的速度是平路的1.5倍，那么上坡的速度是平路的多少倍？分析：解法1：设路程为180，则上坡和下坡均是90。
设走平路的速度是2，则下坡速度是3。
走下坡用时间90/3=30，走平路一共用时间180/2=90，所以走上坡时间是90-30=60 走与上坡同样距离的平路时用时间90/2=45 因为速度与时间成反比，所以上坡速度是下坡速度的45/60=0.75倍。
解法2：因为距离和时间都相同，所以平均速度也相同，又因为上坡和下坡路各一半也相同，设距离是1份，时间是1份，则下坡时间=0.5/1.5=1/3，上坡时间=1-1/3=2/3，上坡速度=（1/2）/（2/3）=3/4=0.75解法3：因为距离和时间都相同，所以：1/2*路程/上坡速度+1/2*路程/1.5=路程/1，得：上坡速度=0.75答：上坡的速度是平路的0.75倍。
3、一只小船从甲地到乙地往返一次共用2小时，回来时顺水，比去时的速度每小时多行驶8千米，因此第二小时比第一小时多行驶6千米。
书人教育培训中心四年级春季班第三讲行程问题讲义(教师版)
行程问题（一）我们把研究路程、速度、时间以及这三者之间关系的一类问题，总称为行程问题.在对小学数学的学习中，我们已经接触过一些简单的行程应用题，并且已经了解到：上述三个量之间存在这样的基本关系：路程＝速度×时间.因此，在这一讲中，我们将在前面学习的基础上，主要来研究行程问题中较为复杂的一类问题——反向运动问题，也即在同一道路上的两个运动物体作方向相反的运动的问题.它又包括相遇问题和相背问题.所谓相遇问题，指的就是上述两个物体以不同的点作为起点作相向运动的问题；所谓相背问题，指的就是这两个运动物体以同一点作为起点作背向运动的问题，下面，我们来具体看几个例子.例1 甲、乙二人分别从相距30千米的两地同时出发相向而行，甲每小时走6千米，乙每小时走4千米，问：二人几小时后相遇？分析出发时甲、乙二人相距30千米，以后两人的距离每小时都缩短6＋4＝10（千米），即两人的速度的和（简称速度和），所以30千米里有几个10千米就是几小时相遇.解：30÷（6＋4）＝30÷10 ＝3（小时）答：3小时后两人相遇.例1是一个典型的相遇问题.在相遇问题中有这样一个基本数量关系：路程＝速度和×时间.例2 一列货车早晨6时从甲地开往乙地，平均每小时行45千米，一列客车从乙地开往甲地，平均每小时比货车快15千米，已知客车比货车迟发2小时，中午12时两车同时经过途中某站，然后仍继续前进，问：当客车到达甲地时，货车离乙地还有多少千米？分析货车每小时行45千米，客车每小时比货车快15千米，所以，客车速度为每小时（45＋15）千米；中午12点两车相遇时，货车已行了（12—6）小时，而客车已行（12—6－2）小时，这样就可求出甲、乙两地之间的路程.最后，再来求当客车行完全程到达甲地时，货车离乙地的距离.解：①甲、乙两地之间的距离是：45×（12—6）＋（45＋15）×（12—6—2）＝45×6＋60×4＝510（千米）.②客车行完全程所需的时间是：510÷（45＋15）＝510÷60＝8.5（小时）.③客车到甲地时，货车离乙地的距离：510—45×（8.5＋2）＝510－472.5＝37.5（千米）.答：客车到甲地时，货车离乙地还有37.5千米.例3 两列火车相向而行，甲车每小时行36千米，乙车每小时行54千米.两车错车时，甲车上一乘客发现：从乙车车头经过他的车窗时开始到乙车车尾经过他的车窗共用了14秒，求乙车的车长.分析首先应统一单位：甲车的速度是每秒钟36000÷3600＝10（米），乙车的速度是每秒钟54000÷3600＝15（米）.本题中，甲车的运动实际上可以看作是甲车乘客以每秒钟10米的速度在运动，乙车的运动则可以看作是乙车车头的运动，因此，我们只需研究下面这样一个运动过程即可：从乙车车头经过甲车乘客的车窗这一时刻起，乙车车头和甲车乘客开始作反向运动14秒，每一秒钟，乙车车头与甲车乘客之间的距离都增大（10＋15）米，因此，14秒结束时，车头与乘客之间的距离为（10＋15）×14＝350（米）.又因为甲车乘客最后看到的是乙车车尾，所以，乙车车头与甲车乘客在这段时间内所走的路程之和应恰等于乙车车身的长度，即：乙车车长就等于甲、乙两车在14秒内所走的路程之和.解：（10＋15）×14 ＝350（米）答：乙车的车长为350米.我们也可以把例3称为一个相背运动问题，对于相背问题而言，相遇问题中的基本关系仍然成立.习题1.甲、乙两车分别从相距240千米的A、B两城同时出发，相向而行，已知甲车到达B城需4小时，乙车到达A城需6小时，问：两车出发后多长时间相遇？2.东、西镇相距45千米，甲、乙二人分别从两镇同时出发相向而行，甲比乙每小时多行1千米，5小时后两人相遇，问两人的速度各是多少？3.甲、乙二人以均匀的速度分别从A、B两地同时出发，相向而行，他们第一次相遇地点离A地4千米，相遇后二人继续前进，走到对方出发点后立即返回，在距B地3千米处第二次相遇，求两次相遇地点之间的距离.4.甲、乙二人从相距100千米的A、B两地出发相向而行，甲先出发1小时.他们二人在乙出后的4小时相遇，又已知甲比乙每小时快2千米，求甲、乙二人的速度.5.一列快车和一列慢车相向而行，快车的车长是280米，慢车的车长为385米，坐在快车上的人看见慢车驶过的时间是11秒，那么坐在慢车上的人看见快车驶过的时间是多少？6.前进钢铁厂用两辆汽车从距工厂90千米的矿山运矿石，现有甲、乙两辆汽车，甲车自矿山，乙车自钢铁厂同时出发相向而行，速度分别为每小时40千米和50千米，到达目的地后立即返回，如此反复运行多次，如果不计装卸时间，且两车不作任何停留，则两车在第三次相遇时，距矿山多少千米？。
高思奥数导引小学三年级含详解答案第18讲 简单乘除法竖式.
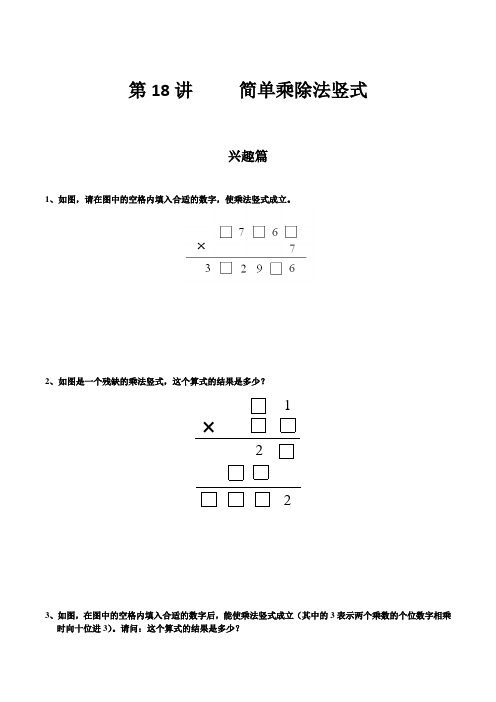
第18讲简单乘除法竖式兴趣篇1、如图，请在图中的空格内填入合适的数字，使乘法竖式成立。
2、如图是一个残缺的乘法竖式，这个算式的结果是多少？1×223、如图，在图中的空格内填入合适的数字后，能使乘法竖式成立（其中的3表示两个乘数的个位数字相乘时向十位进3）。
请问：这个算式的结果是多少？×4134、如图，在图中的空格内填入合适的数字，使乘法竖式成立。
81645×5、如图是一个残缺的乘法算式。
现在知道其中一个位置上的数字为8，这个算式的结果是多少？8×6、在如图所示的乘法竖式中，、、、分别代表不同的数字。
问：这个三位数是多少？×7447、如图，在图中的空格内填入合适的数字，使除法竖式成立。
8538、如图，在图中的空格内填入合适的数字，使除法竖式成立。
4127519、如图，在图中的空格内填入合适的数字，使除法竖式成立。
10、如图，在图中的空格内填入合适的数字，使乘法竖式成立。
5拓展篇1、如图，在图中的空格内填入合适的数字，使乘法竖式成立。
744881×72、如图，在图中的空格内填入合适的数字，使乘法竖式成立。
6529×3、如图，在图中的空格内填入合适的数字，使乘法竖式成立。
08×7 4、如图，在图中的空格内填入合适的数字，使乘法竖式成立。
3812132×23355、在如图所示的乘法竖式中，有些数字被三角形纸片盖住了。
请问：算式的结果是多少？82×56、如图是一个残缺的乘法算式，请补充完整并求出这个算式的结果。
8×87、如图所示的竖式中，不同的汉字代表不同的数字。
“车”、“马”、“炮”分别代表什么数字？车车马炮车车×车炮马马8、如图，在图中的空格内填入合适的数字，使除法竖式成立。
76919、如图，在图中的空格内填入合适的数字，使除法竖式成立。
210、如图，在图中的空格内填入合适的数字，使除法竖式成立。
高思数学-各级别全年教材大纲
⾼思数学-各级别全年教材⼤纲三年级上第1讲加减法巧算第2讲基本应⽤题第3讲间隔问题第4讲简单枚举第5讲字典排列法与树形图法第6讲找规律第7讲和倍问题与差倍问题第8讲和差问题与多个对象的和差倍第9讲简单加减法竖式第10讲周期问题初步第11讲周期问题进阶第12讲妙⽤假设法第13讲分组与画图第14讲等差数列初步第15讲等差数列进阶第16讲平⾯图形认知第17讲⽴体图形认知第18讲基本盈亏问题第19讲智巧趣题⼀第20讲旅⾏中的数学三年级下第⼀讲乘除法巧算第⼆讲归⼀问题第三讲分类计数第四讲和差倍问题中的隐藏条件第五讲线段图解复杂和差倍关系第六讲简单乘法竖式第七讲简单除法竖式第⼋讲假设法综合提⾼第九讲分组法综合提⾼第⼗讲四则混合运算第⼗⼀讲阵列问题第⼗⼆讲巧填算符第⼗三讲算符与数字第⼗四讲盈亏条件的转化第⼗五讲复杂盈亏问题第⼗六讲长度计算第⼗七讲⾓度的计算第⼗⼋讲找位置第⼗九讲⽕柴棍算式与⽣活趣题第⼆⼗讲三年级期末复习与检测四年级上第1讲整数计算综合第2讲还原问题第3讲数阵图初步第4讲竖式问题第5讲⼏何图形剪拼第6讲路程、时间、速度第7讲⾏程中的线段图第8讲简单抽屉原理第9讲基本直线形⾯积公式第10讲底、⾼的选取与组合第11讲变倍问题第12讲和差倍中的分组⽐较第13讲年龄问题第14讲数列数表规律第15讲复杂数表估算第16讲加法原理与乘法原理第17讲乘法原理进阶第18讲⽕车⾏程第19讲统筹规划第20讲游戏对策四年级下第1讲⼩数的运算技巧第2讲多位数巧算第3讲简单平均数第4讲多组对象的平均数第5讲复杂竖式第6讲横式问题第7讲格点图形的计算第8讲割补法巧算⾯积第9讲多⼈多次的相遇与追及第10讲排列组合公式第11讲排列组合应⽤第12讲分段计算的⾏程问题第13讲多次往返相遇与追及第14讲从洛书到幻⽅第15讲复杂数阵图第16讲有特殊要求的挑选第17讲捆绑法与插空法第18讲最值问题第19讲逻辑推理第20讲四年级期末复习与检测五年级上第1讲分数计算与⽐较⼤⼩第2讲整除问题初步第3讲整除问题进阶第4讲质数与合数第5讲容斥原理第6讲流⽔⾏船问题第7讲环形路线问题第8讲⽜吃草问题第9讲⼏何计数第10讲约数、倍数初步第11讲约数与倍数进阶第12讲分数与循环⼩数第13讲⽐较与估算第14讲数论巧解数字谜第15讲包含分数、⼩数的数字谜第16讲分数应⽤题之量率对应第17讲分数应⽤题之单位“1”的转化第18讲巧解不确定性问题第19讲倍数关系求解直线形第20讲巧连辅助线解直线形五年级下第1讲计算综合第2讲分数裂项第3讲圆与扇形初步第4讲圆与扇形中的重叠与旋转第5讲余数的性质与计算第6讲物不知数与同余第7讲复杂抽屉原理第8讲⼯程问题初步第9讲⼯程问题进阶第10讲钟表问题第11讲⽐例关系求解直线形第12讲平⾏线相关⽐例与勾股定理第13讲构造论证第14讲⾏程问题中的变速问题第15讲⾏程问题中分段与⽐较第16讲位值原理第17讲数字问题第18讲数论相关的计数第19讲数字谜中的计数第20讲五年级期末复习与检测六年级上第1讲计算综合⼆第2讲⽐例计算与列表分析第3讲正反⽐例的概念与应⽤第4讲⽅程解应⽤题第5讲浓度问题第6讲经济问题第7讲逻辑推理⼆第8讲最值问题⼆第9讲不定⽅程第10讲⽴体⼏何第11讲复杂直线形计算第12讲⼏何综合问题第13讲递推计数第14讲对应计数第15讲⾏程问题中的⽐例关系第16讲复杂⾏程问题选讲第17讲数论综合与简单代数式第18讲数字谜综合⼆第19讲应⽤题综合⼀第20讲应⽤题综合⼆六年级下第1讲构造论证⼆第2讲进位制与取整符号第3讲计数综合提⾼第4讲数论与⽅程第5讲计算综合练习第6讲⼏何综合练习第7讲应⽤题综合练习第8讲数字谜综合练习第9讲数论综合练习第10讲计数综合练习第11讲组合综合练习第12讲⼩升初总复习模拟测试第13讲⼩升初总复习模拟测试⼆第14讲⼩升初总复习模拟测试三第15讲⼩升初总复习模拟测试四第16讲⼩升初总复习模拟测试五第17讲⼩升初总复习模拟测试六第18讲⼩升初总复习模拟测试七第19讲⼩升初总复习模拟测试⼋第20讲⼩升初总复习模拟测试九。
高思数学_4年级上-第18讲-火车行程（彩色）
高思数学_4年级上-第18讲-火车行程（彩色）107我们之前已经学过了基本行程问题，明确了速度、时间和路程这三个量之间的关系．比如北京到广州的铁路全长2300千米，如果一列火车从北京出发，以每小时100千米的速度开往广州，我们很容易算出火车需要行驶23小时．在这个问题中，火车的长度与北京到广州的距离相比微乎其微，我们当然可以忽略不计火车的长度．但是当行人在铁路旁行走，火车从行人身边开过时，从车头与行人相遇到车尾离开行人，是需要一段时间的，这时火车的长度就不能忽略不计了，我们需要把火车看成考虑自身长度的运动物体．本讲我们的重点就是这类考虑自身长度的运动对象的行程问题．火车行程问题大体上可以分为三类：火车与行人的相遇和追及问题；火车过桥问题；火车与火车的相遇和追及问题．108我们先来看看火车经过静止的人的过程．通过线段图我们可以看出，从火车车头与人相遇一直到火车车尾离开人，火车前进的路程就是火车的长度．我们也可以这样来理解：当车头和人相遇时，车尾和人相距一个火车长度，所以整个过程就是车尾和人的相遇问题．以上只是人不动情况下的火车行程问题，下面我们来介绍一下行人和火车的相遇和追及问题，如下图所示．我们可以将火车看成一个点：开始的时候行人和车尾的距离为一个车长，结束的时候行人和车尾相遇了．也就是说，从火车与行人的相遇到错开，这个过程可以看成是行人与车尾的相遇问题，火车和行人经过的路程和等于火车的长度．类似的，对于火车追行人的过程，从追上到离开，火车和行人的路程差等于火车的长度．我们仍可以将火车看成一个点：开始的时候行人在车尾前面，距离为一个车长，结束的时候车尾恰好追上了行人．这个过程也可以看成车尾与行人的追及过程．大家试к ?着自己画出线段图表示出火车追行人的过程．分析本题的实质是两个追及问题：火车与行人的追及问题，以及火车和骑车人的追及问题．在追及过程中，火车、行人、骑车人经过的路程有什么关系？练习1.一名旅行者在铁路旁边走，一列长300米的火车迎面开来，从旅行者身边经过用10秒．已知火车每秒行28米，请问这名旅行者每秒走多少米？列车上的窃贼?这天，李经理坐火车去郑州办事．他所乘的包厢里其他三人分别去石家庄、邯郸和郑州．列车运行到保定站，停车5分钟，四人均离开了自己的铺位．在列车启动前，李经理回到座位，却发现自己的手提包不见了．他急忙去报告了乘警，乘警调查了其他三位乘客．去石家庄的乘客说，停车时他下去买了点早点；去邯郸的乘客说，他到车上的厕所方便去了；去郑州的乘客说，他去另一车厢看望同行的朋友了．听完他们的叙述，乘警认定去邯郸的人偷了李经理的提包．你知道为什么吗？时向南行进，行人速度为每秒列长这列火车从骑车人身旁经过需要多长时间？来，从阿毛身边经过需要身边经过需要多少秒？110分析已知条件只有两个时间，我们能不能用设数法把路程假设为合适的数呢？本题中需要假设的路程是什么？练习2.阿呆喜欢看火车，他在一条铁路旁向前跑．这时有一列客车迎面开来，从阿呆身边经过用20秒．如果阿呆站着不动，客车从阿呆身边经过需要24秒．如果阿呆向前跑，而这列客车从阿呆的背后开来，请问客车从阿呆身边经过需要多少秒？火车掉头?火车掉头可不简单啊！你知道火车是怎样掉头的吗？有一种常用的办法是利用三角形路线．这里，也请你试一试．图中有一组三角铁路线，A 是尽头处，长度只够放一辆机车或一节车厢．现在要让图上的那列火车全部掉过头来，应该怎么办？分析火车通过隧道的过程，是从车头到达隧道入口开始，直到车尾离开隧道出口结束．我们画出线段图来分析．大家能看出火车过隧道时经过的路程是多少吗？条长秒．这个山洞长多少米？练习3.（1）一列火车长180米，每秒行驶25米，全车通过一个长120米的山洞，需要多长时间？（2）一列火车长360米，每秒行驶18米，全车通过一座桥用了25秒，这座桥长多少米？在例题3中，我们可以在线段图中用火车车尾的运动代替火车的运动，把火车过隧道看成火车车尾与隧道出口的相遇问题．这样一来，我们很容易看出火车车尾经过的总路程是火车车长与隧道长度之和，这也是火车全车通过隧道时行驶的路程．我们总结如下：火车在经过桥/山洞/隧道时行驶的总路程是火车车长与桥/山洞/隧道的长度之和．下面我们再来看看两列火车之间的相遇与追及．分析对于两列火车的相遇问题，由于火车有长度，我们要画出线段图才能把问题看清楚．如下图所示，你能从线段图中看出两列火车经过的路程和是多少吗？к货车长错开需要多长时间？如果两车同向而行，需要多长时间？。
四年级数学思维训练导引(奥数)第18讲--行程问题三
第十八讲行程问题三1．莉莉和莎莎一起从家去学校，莉莉步行，莎莎骑车．莎莎到学校后发现自己没带文具盒，便立刻骑车回家去取，到家取出文具盒后又马上骑向学校，结果她和莉莉一起到校，如果莉莉每分钟走53米，那么莎莎骑车每分钟行进多少米？2．小燕上学时骑车，回家时步行，路上共用50分钟．如果往返都步行，则全程需要70分钟，求小燕往返都骑车所需的时间．3．一天，小悦到离自己家4000米的表哥家去玩，早晨7:20时，小悦从家出发向表哥家走去，每分钟行60米，同时表哥骑车从家出发来接她．表哥到小悦家后才发现小悦已经走了，又立即返回去追．表哥骑车每分钟行260米．当表哥追上小悦后，带着她一起回表哥家，这时骑车速度变为每分钟骑175米．请问：当他们到达表哥家时还差几分钟就到8点了？4．培英学校和电视机厂之间有一条公路，原计划下午2点时培英学校派车去电视机厂接劳模来校作报告，往返需用l小时．实际上这位劳模在下午1点便提前离厂步行向学校走来，途中遇到接他的汽车，劳模便立刻上车去往学校，并在下午2点40分到达．问：汽车行驶速度是劳模步行速度的几倍？5．快车和慢车分别从甲、乙两地同时开出，相向而行，经过4小时在途中相遇．相遇后两车继续向前行驶，慢车到达甲地后停留1小时再返回乙地．快车到达乙地后停留2.5小时再返回甲地．已知慢车从乙地到甲地用了12小时，那么两车从第一次相遇到第二次相遇需要多长时间？6．甲、乙两车分别从相距300千米的A，B两地同时出发，在A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米，请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇？(2)第一次迎面相遇后又经过多长时间甲、乙两车第二次相遇？(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇？7．甲、乙两车同时从A地出发，在相距300千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米．请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇？(2)第一次迎面相遇后又经过多长时间甲、乙两车第二次迎面相遇？(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次迎面相遇？8．A、曰两辆汽车从甲、乙两站同时出发，相向而行．在距甲站50千米处两车第一次迎面相遇，相遇后两车继续前进（保持原速）各自到达乙、甲两站后，立即沿原路返回，在距乙站30千米处两车第二次迎面相遇．问：甲、乙两站相距多远？若两车继续前进，则在何处第三次迎面相遇？9．A、B两辆汽车同时从甲地出发，在甲、乙两地间不断往返行驶．第一次迎面相遇距离甲地40公里，第二次迎面相遇距离乙地10公里．求甲、乙两地之间的距离．10.A、B两地是电车的两个起点站，每隔12分钟发一辆车，电车每小时行25千米，请问：(1)如果小明从A地坐电车去B地，那么他每隔多长时间会看见一辆电车迎面开来？(2)如果小明从B地步行走向A地，每小时行5千米，那么他每隔多长时间会看见一辆电车迎面开来？每隔多长时间会有一辆电车从后面超过他？1．甲、乙两人从同一个地点出发同向而行，甲比乙先出发．甲出发6分钟到达A地．此时乙距离起点150米．又过了3分钟乙到达A地，此时甲距离起点900米．问：乙比甲晚出发多长时间？2．自行车队出发12分钟后，通信员骑摩托车去追他们，在距出发点9千米处追上了自行车队，然后通信员立即返回出发点；到达出发点后通信员又马上掉头去追自行车队，再次追上时恰好离出发点18千米，自行车队每分钟行多少千米？摩托车每分钟行多少千米？3．乌龟和兔子进行10000米赛跑，兔子的速度是乌龟的速度的5倍．当它们从起点一起出发后，乌龟不停地跑，兔子跑到某一地点开始睡觉．兔子醒来时发现乌龟已经领先它5000米，于是奋起直追．当乌龟到达终点时，兔子仍落后100米．请问：兔子睡觉期间，乌龟跑了多少米？4．甲、乙两车分别从A、B两地同时出发，相向而行，12小时后在C地相遇．相遇后，两车并不停顿，继续前进．甲车在相遇后继续行驶4小时到达B 地，然后立即掉头以相同的速度返回A地，请问：(1)当甲车再次到达C地的时候，乙车还要再开几小时才能到达A地？(2)如果甲车从B地返回的时候不是原速返回，而是变慢了．而且当它经过C地的时候，乙车正好到达A地．甲车返回的速度是原来速度的多少倍？5．某科研单位每天派汽车早8点准时到工程师家接他上班．但今天早晨，工程师临时决定提前到单位，于是他没有等汽车来接，就自己步行去单位．步行途中遇到了前来接他的汽车，他马上上车赶到单位，结果发现比平时早到了30分钟，问：工程师上车时是几点几分？6．甲、乙两车分别从相距900千米的A，B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲、乙两车第二次迎面相遇是在出发后多长时间？(2)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇？(3)甲车第一次从后面追上乙车是在出发后多长时间？7．甲、乙两车同时从A地出发，在相距900千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲车第一次从后面追上乙车是在出发后多长时间？(2)甲车在第一次从后面追上乙车之后又经过多长时间第二次从后面追上乙车？(3)甲、乙两车第二次迎面相遇是在出发后多长时间？8．A、B两辆汽车分别从甲、乙两地同时出发，并在两地间不断往返行驶．两车在距离甲地40公里处第一次迎面相遇，在距离甲地10公里处第二次迎面相遇．求甲、乙两地之间的距离．9．甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行走．当甲走了3个来回的时候，乙恰好走了5个来回，在甲、乙两人行进的过程中，两人一共相遇了多少次？（迎面碰到和追上都算相遇）10.小明和小刚的速度分别为每分钟90米和每分钟70米，早上8:00他们分别从A、 B两站同时出发，相向而行，第一次相遇后两人继续前进，分别到达B、A后返回并在途中第二次相遇，第二次相遇地点距离A、B两站的中点450米，从两人同时出发到第二次相遇总共经历了多少分钟？A、B两站的距离为多少米？他们第一次相遇是几点几分？11.甲、乙两车分别从A、B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时15千米，乙车的速度是每小时35千米，并且甲、乙两车第三次相遇（两车同时到达同一地点即称为相遇）的地点和第四次相遇的地点恰好相距100千米．请问：两地之间的距离是多少千米？12.某人从甲地走往乙地，甲、乙两地之间有定时的公共汽车往返，而且两地发车的间隔都相等，他发现每隔6分钟开过来一辆去甲地的公共汽车，每隔12分钟开过去一辆去乙地的公共汽车，问：公共汽车每隔多少分钟从各自的始发站发车？1．每天早上7:30王经理都从家出发，由司机开车前往公司，8:00准时到达，然后司机开车原速返回王经理家，一天早上，王经理想要锻炼一下，因此中途下车走到公司，结果9:00才到．而司机8:10就已经回到王经理家中，请问：车速是王经理步行速度的多少倍？如果第二天，王经理仍然中途下车，但是下车地点比前一天距离公司要近一些，结果8:30就赶到了公司．司机回到王经理家应该是几点几分？2．一辆大轿车和一辆小轿车从甲地驶往乙地．大轿车的速度是小轿车速度的0.8倍．已知大轿车比小轿车早出发17分钟，但在两地中点停留了5分钟，然后继续驶往乙地；小轿车出发后中途没有停留，直接驶往乙地，最后小轿车比大轿车早4分钟到达乙地．已知大轿车是上午10点从甲地出发的，求小轿车追上大轿车的时间．3．A、B两地间相距950米，甲、乙两人同时由A地出发，并在A、曰两地间往返行进，共行进了40分钟，甲步行速度是每分钟40米，乙跑步速度是每分钟150米，那么甲、乙两人第几次迎面相遇时距B地最近，距离是多少米？4．甲、乙两车分别从A、B两地同时出发，在A、B两地间不断地往返行驶．甲车每小时行20千米，乙车每小时行50千米．已知两车第10次和第18次迎面相遇的地点相距60千米．问：A、B间的路程是多少千米？5．小明家在颐和园．如果他骑车到人大附中，每隔3分钟能见到一辆332路公共汽车迎面开来；如果他步行到人大附中，每隔4分钟能见到一辆332路公共汽车迎面开来．已知任意两辆332路汽车的发车间隔都是一样的，并且小明骑车速度是小明步行速度的3倍，请问：如果小明坐332路汽车到人大附中，每隔多少分钟能见到一辆332路公共汽车迎面开来？6．甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行进，当甲第3次到达B地的时候，乙恰好第5次回到了B地，请问：在甲、乙两人在行进的过程中，一共相遇了多少次？（迎面碰到和追上都算相遇）7．从电车总站每隔一定时间开出一辆电车，甲和乙两人在一条街上沿着同一方向步行，甲每分钟步行82米，每隔10分钟遇上一辆迎面开来的电车；乙每分钟步行60米，每隔10分15秒遇上迎面开来的一辆电车．问：电车总站每隔多少分钟开出一辆电车？8．A、B两地相距22.4千米．有一支游行队伍从A地出发，向B地匀速前进；当游行队伍队尾离开A地时，甲、乙两人分别从A、B两地同时出发．乙向A地步行；甲骑车先追向队头，追上队头后又立即骑向队尾，到达队尾后再立即追向队头，追上队头后又立即骑向队尾，……，当甲第5次追上队头时恰和乙相遇在距B地5.6千米处；当甲第7次追上队头时，甲恰好第一次到达B地，求此时乙离A地的距离．。
第19讲-行程问题【三】
一、分段计算的行程问题1，行程问题中的三个基本倍数关系①当运动的速度相同时，时间的倍数关系等于路程的倍数关系②当运动的时间相同时，速度的倍数关系等于路程的倍数关系③当运动的路程相同时，时间的倍数关系等于速度的反倍数关系2，按时间流程画线段图的方法画线段图的方法在求解行程问题中是至关重要的，画好线段图，能使题目条件一目了然，有助于解题。
3，分段与比较的想法①同一个人的不同过程之间，速度相同，可以得到路程与时间之间的关系；②两个时刻之间所经过的时间相同，可以得到不同对象之间路程与速度的关系；③长度相同的线段，路程相同，可以得到速度和时间之间的关系。
二、多次往返相遇和追及1、甲，乙两车从A、B两地出发相向而行，并在两地之间不断往返，记两地距离为1个全长，则①甲车和乙车的路程和为1个全长时，两次第一次迎面相遇；•在此之后，两车的路程和每多出2个全长时就会迎面相遇一次.②如果甲车的速度大于乙车速度，则：•当甲车与乙车的路程差为1个全长时，甲车第一次追上乙车；在此之后，每当甲车比乙车多跑2个全长时就会追上乙车一次。
2,甲，乙两车从A地同时出发同向而行，在A、B两地之间不断往返，记两地距离为1个全长，则①当甲车和乙车的路程和为2个全长时，两次第一次迎面相遇；在此之后，两车的路程和每多出2个全长时就会迎面相遇一次.②如果甲车的速度大于乙车速度，则：当甲车与乙车的路程差为2个全长时，甲车第一次追上乙车；在此之后，每当甲车比乙车多跑2个全长时就会追上乙车一次。
【1】（高思学校竞赛数学导引P116）甲、乙两人从同一个地点出发同向而行，甲比乙先出发．甲出发6分钟到达A地．此时乙距离起点150米．又过了3分钟乙到达A地，此时甲距离起点900米．问：乙比甲晚出发多长时间?自行车队出发12分钟后，通信员骑摩托车去追他们，在距出发点9千米处追上了自行车队．然后通信员立即返回出发点；到达出发点后通信员又马上掉头去追自行车队，再次追上时恰好离出发点18千米．自行车队每分钟行多少千米?摩托车每分钟行多少千米?乌龟与兔子迚行10000米赛跑，兔子的速度是乌龟的速度的5倍．当它们从起点一起出发后，乌龟不停地跑，兔子跑到某一地点开始睡觉．兔子醒来时发现乌龟已经领先它5000米，于是奋起直追．当乌龟到达终点时，兔子仍落后100米．请问：兔子睡觉期间，乌龟跑了多少米?一天，萱萱到离自己家4000米的表哥家去玩．早晨7：20时，萱萱从家出发向表哥家走去，每分钟行60米，同时表哥骑车从家出发来接她．表哥到萱萱家后才发现萱萱已经走了，又立即返回去追．表哥骑车每分钟行260米．当表哥追上萱萱后，带着她一起回表哥家，这时骑车速度变为每分钟骑175米．请问：当他们到达表哥家时还差几分钟就到8点了?甲、乙两车分别从A、B两地同时出发，相向而行，12小时后在C地相遇．相遇后，两车并不停顿，继续前迚．甲车在相遇后继续行驶4小时到达B地，然后立即掉头以相同的速度返回A地．请问：(1)当甲车再次到达C地的时候，乙车还要再开几小时才能到达A地?(2)如果甲车从B地返回的时候不是原速返回，而是变慢了．而且当它经过C地的时候，乙车正好到达A地．甲车返回的速度是原来速度的多少倍?某科研单位每天派汽车早8点准时到工程师家接他上班．但今天早晨，工程师临时决定提前到单位，于是他没有等汽车来接，就自己步行去单位．步行途中遇到了前来接他的汽车，他马上上车赶到单位，结果发现比平时早到了30分钟，问：工程师上车时是几点几分?【7】（高思学校竞赛数学导引P117）快车和慢车分别从甲、乙两地同时开出，相向而行，经过4小时在途中相遇．相遇后两车继续向前行驶．慢车到达甲地后停留1小时再返回乙地．快车到达乙地后停留2.5小时再返回甲地．已知慢车从乙地到甲地用了12小时，那么两车从第一次相遇到第二次相遇需要多长时间?【8】（高思学校竞赛数学导引P117）甲、乙两车分别从相距900千米的A，B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲、乙两车第二次迎面相遇是在出发后多长时间?(2)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇?(3)甲车第一次从后面追上乙车是在出发后多长时间?【9】（高思学校竞赛数学导引P117）甲、乙两车同时从A地出发，在相距900千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲车第一次从后面追上乙车是在出发后多长时间?(2)甲车在第一次从后面追上乙车之后又经过多长时间第二次从后面追上乙车?(3)甲、乙两车第二次迎面相遇是在出发后多长时间?【10】（高思学校竞赛数学导引P117）A、B两辆汽车分别从甲、乙两地同时出发，并在两地间不断往返行驶．两车在距离甲地40公里处第一次迎面相遇，在距离甲地10公里处第二次迎面相遇．求甲、乙两地之问的距离．【11】（高思学校竞赛数学导引P118）甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行走．当甲走了3个来回的时候，乙恰好走了5个来回．在甲、乙两人行迚的过程中，两人一共相遇了多少次?(迎面碰到和追上都算相遇)【12】（高思学校竞赛数学导引P118）小明和小刚的速度分别为每分钟90米和每分钟70米．早上8：00他们分别从A、B两站同时出发，相向而行，第一次相遇后两人继续前迚，分别到达B、A后返回并在途中第二次相遇．第二次相遇地点距离A、B 两站的中点450米．从两人同时出发到第二次相遇总共经历了多少分钟?A、B两站的距离为多少米?他们第一次相遇是几点几分?【13】（高思学校竞赛数学导引P118）甲、乙两车分别从A、B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时15千米，乙车的速度是每小时35千米，并且甲、乙两车第三次相遇(两车同时到达同一地点即称为相遇)的地点与第四次相遇的地点恰好相距100千米．请问：两地之间的距离是多少千米?【14】（高思学校竞赛数学导引P118）某人从甲地走往乙地．甲、乙两地之间有定时的公共汽车往返，而且两地发车的间隔都相等．他发现每隔6分钟开过来一辆去甲地的公共汽车，每隔12分钟开过去一辆去乙地的公共汽车．问：公共汽车每隔多少分钟从各自的始发站发车?下节课见！。
四年级高思奥数之行程问题三 含答案
第18讲行程问题三内容概述运动过程较为复杂的行程问题，一般通过分段、比较等办法进行考虑，在往返问题中考虑多次相遇和多次追及的过程，需要注意从整体考虑两个对象的路程和或路程差，并从中找到规律.典型问题兴趣篇1．莉莉和莎莎一起从家去学校，莉莉步行，莎莎骑车．莎莎到学校后发现自己没带文具盒，便立刻骑车回家去取，到家取出文具盒后又马上骑向学校，结果她和莉莉一起到校．如果莉莉每分钟走53米，那么莎莎骑车每分钟行进多少米?2．小燕上学时骑车，回家时步行，路上共用50分钟．如果往返都步行，则全程需要70分钟．求小燕往返都骑车所需的时间．3．一天，小悦到离自己家4000米的表哥家去玩．早晨7：20时，小悦从家出发向表哥家走去，每分钟行60米，同时表哥骑车从家出发来接她．表哥到小悦家后才发现小悦已经走了，又立即返回去追．表哥骑车每分钟行260米．当表哥追上小悦后，带着她一起回表哥家，这时骑车速度变为每分钟骑175米．请问：当他们到达表哥家时还差几分钟就到8点了? 4．培英学校和电视机厂之间有一条公路，原计划下午2点时培英学校派车去电视机厂接劳模来校作报告，往返需用1小时．实际上这位劳模在下午l点便提前离厂步行向学校走来，途中遇到接他的汽车，劳模便立刻上车去往学校，并在下午2点40分到达问：汽车行驶速度是劳模步行速度的几倍?5．快车和慢车分别从甲、乙两地同时开出，相向而行，经过4小时在途中相遇．相遇后两车继续向前行驶．慢车到达甲地后停留1小时再返回乙地．快车到达乙地后停留2.5小时再返回甲地．已知慢车从乙地到甲地用了12小时，那么两车从第一次相遇到第二次相遇需要多长时间?6．甲、乙两车分别从相距300千米的A，B两地同时出发，在A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米．请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇?(2)第一次迎面相遇后又经过多长时间甲、乙两车第二次相遇?(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇?7．甲、乙两车同时从A地出发，在相距300千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米．请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇?(2)第一次迎面相遇后又经过多长时问甲、乙两车第二次迎面相遇?(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次迎面相遇?8．A、B两辆汽车从甲、乙两站同时出发，相向而行．在距甲站50千米处两车第一次迎面相遇，相遇后两车继续前进(保持原速)各自到达乙、甲两站后，立即沿原路返回．在距乙站30千米处两车第二次迎面相遇．问：甲、乙两站相距多远?若两车继续前进，则在何处第三次迎面相遇?9．A、B两辆汽车同时从甲地出发，在甲、乙两地间不断往返行驶．第一次迎面相遇距离甲地40公里，第二次迎面相遇距离乙地10公里．求甲、乙两地之间的距离．10．A、B两地是电车的两个起点站，每隔12分钟发一辆车，电车每小时行25千米．请问：(1)如果小明从A地坐电车去B地，那么他每隔多长时间会看见一辆电车迎面开来?(2)如果小明从B地步行走向A地，每小时行5千米，那么他每隔多长时间会看见一辆电车迎面开来?每隔多长时间会有一辆电车从后面超过他?拓展篇1. 甲、乙两人从同一个地点出发同向而行，甲比乙先出发．甲出发6分钟到达A地．此时乙距离起点150米．又过了3分钟乙到达A地，此时甲距离起点900米．问：乙比甲晚出发多长时间?2．自行车队出发12分钟后，通信员骑摩托车去追他们，在距出发点9千米处追上了自行车队．然后通信员立即返回出发点；到达出发点后通信员又马上掉头去追自行车队，再次追上时恰好离出发点18千米．自行车队每分钟行多少千米?摩托车每分钟行多少千米?3．乌龟与兔子进行10000米赛跑，兔子的速度是乌龟的速度的5倍．当它们从起点一起出发后，乌龟不停地跑，兔子跑到某一地点开始睡觉．兔子醒来时发现乌龟已经领先它5000米，于是奋起直追．当乌龟到达终点时，兔子仍落后100米．请问：兔子睡觉期间，乌龟跑了多少米?4. 甲、乙两车分别从A、B两地同时出发，相向而行，12小时后在C地相遇．相遇后，两车并不停顿，继续前进．甲车在相遇后继续行驶4小时到达B地，然后立即掉头以相同的速度返回A地．请问：(1)当甲车再次到达C地的时候，乙车还要再开几小时才能到达A地?(2)如果甲车从B地返回的时候不是原速返回，而是变慢了．而且当它经过C地的时候，乙车正好到达A地．甲车返回的速度是原来速度的多少倍?5．某科研单位每天派汽车早8点准时到工程师家接他上班．但今天早晨，工程师临时决定提前到单位，于是他没有等汽车来接，就自己步行去单位．步行途中遇到了前来接他的汽车，他马上上车赶到单位，结果发现比平时早到了30分钟，问：工程师上车时是几点几分?6．甲、乙两车分别从相距900千米的A，B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲、乙两车第二次迎面相遇是在出发后多长时间?(2)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇?(3)甲车第一次从后面追上乙车是在出发后多长时间?7．甲、乙两车同时从A地出发，在相距900千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲车第一次从后面追上乙车是在出发后多长时间?(2)甲车在第一次从后面追上乙车之后又经过多长时间第二次从后面追上乙车?(3)甲、乙两车第二次迎面相遇是在出发后多长时间?8．A、B两辆汽车分别从甲、乙两地同时出发，并在两地间不断往返行驶．两车在距离甲地40公里处第一次迎面相遇，在距离甲地10公里处第二次迎面相遇．求甲、乙两地之问的距离．9．甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行走．当甲走了3个来回的时候，乙恰好走了5个来回．在甲、乙两人行进的过程中，两人一共相遇了多少次?(迎面碰到和追上都算相遇)10．小明和小刚的速度分别为每分钟90米和每分钟70米．早上8：00他们分别从A、B两站同时出发，相向而行，第一次相遇后两人继续前进，分别到达B、A后返回并在途中第二次相遇．第二次相遇地点距离A、B两站的中点450米．从两人同时出发到第二次相遇总共经历了多少分钟?A、B两站的距离为多少米?他们第一次相遇是几点几分?11.甲、乙两车分别从A、B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时15千米，乙车的速度是每小时35千米，并且甲、乙两车第三次相遇(两车同时到达同一地点即称为相遇)的地点与第四次相遇的地点恰好相距100千米．请问：两地之间的距离是多少千米?12．某人从甲地走往乙地．甲、乙两地之间有定时的公共汽车往返，而且两地发车的间隔都相等．他发现每隔6分钟开过来一辆去甲地的公共汽车，每隔12分钟开过去一辆去乙地的公共汽车．问：公共汽车每隔多少分钟从各自的始发站发车?超越篇1．每天早上7：30王经理都从家出发，由司机开车前往公司，8：00准时到达．然后司机开车原速返回王经理家．一天早上，王经理想要锻炼一下，因此中途下车走到公司，结果9：00才到．而司机8：10就已经回到王经理家中．请问：车速是王经理步行速度的多少倍?如果第二天，王经理仍然中途下车，但是下车地点比前一天距离公司要近一些，结果8：30就赶到了公司．司机回到王经理家应该是几点几分?2．一辆大轿车与一辆小轿车从甲地驶往乙地．大轿车的速度是小轿车速度的0.8倍．已知大轿车比小轿车早出发17分钟，但在两地中点停留了5分钟，然后继续驶往乙地；小轿车出发后中途没有停留，直接驶往乙地．最后小轿车比大轿车早4分钟到达乙地．已知大轿车是上午10点从甲地出发的，求小轿车追上大轿车的时间．3．A、B两地间相距950米．甲、乙两人同时由A地出发，并在A、B两地间往返行进．共行讲了40分钟．甲步行速度是每分钟40米，乙跑步速度是每分钟150米．那么甲、乙两人第几次迎面相遇时距B地最近，距离是多少米?4．甲、乙两车分别从A、B两地同时出发，在A、B两地间不断地往返行驶．甲车每小时行20千米，乙车每小时行50千米．已知两车第10次与第18次迎面相遇的地点相距60千米．问：A、B间的路程是多少千米?5．小明家在颐和园．如果他骑车到人大附中，每隔3分钟能见到一辆332路公共汽车迎面开来；如果他步行到人大附中，每隔4分钟能见到一辆332路公共汽车迎面开来．已知任意两辆332路汽车的发车间隔都是一样的，并且小明骑车速度是小明步行速度的3倍．请问：如果小明坐332路汽车到人大附中，每隔多少分钟能见到一辆332路公共汽车迎面开来?6．甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行进．当甲第3次到达B地的时候，乙恰好第5次回到了B地．请问：在甲、乙两人在行进的过程中，一共相遇了多少次?(迎面碰到和追上都算相遇)7．从电车总站每隔一定时间开出一辆电车．甲和乙两人在一条街上沿着同一方向步行．甲每分钟步行82米，每隔10分钟遇上一辆迎面开来的电车；乙每分钟步行60米，每隔10分15秒遇上迎面开来的一辆电车．问：电车总站每隔多少分钟开出一辆电车?8．A、B两地相距22.4千米．有一支游行队伍从A地出发，向B地匀速前进；当游行队伍队尾离开A地时，甲、乙两人分别从A、B两地同时出发．乙向A地步行；甲骑车先追向队头，追上队头后又立即骑向队尾，到达队尾后再立即追向队头，追上队头后又立即骑向队尾，……，当甲第5次追上队头时恰与乙相遇在距B地5.6千米处；当甲第7次追上队头时．甲恰好第一次到达B地，求此时乙离A地的距离．第18讲行程问题三内容概述运动过程较为复杂的行程问题，一般通过分段、比较等办法进行考虑，在往返问题中考虑多次相遇和多次追及的过程，需要注意从整体考虑两个对象的路程和或路程差，并从中找到规律.典型问题兴趣篇1．莉莉和莎莎一起从家去学校，莉莉步行，莎莎骑车．莎莎到学校后发现自己没带文具盒，便立刻骑车回家去取，到家取出文具盒后又马上骑向学校，结果她和莉莉一起到校．如果莉莉每分钟走53米，那么莎莎骑车每分钟行进多少米?答案：159详解：视从家到学校的路程为一个全程，由题意知道莎莎到校，再返回家，再到学校，一共走了三个全程，在同样时间内莉莉走了一个全程，即莎莎速度是莉莉的三倍53×3=1592．小燕上学时骑车，回家时步行，路上共用50分钟．如果往返都步行，则全程需要70分钟．求小燕往返都骑车所需的时间．答案：30分钟详解：视从家到学校的路程为一个全程，往返情况：骑车+步行=50步行+步行=70得知一个全程骑车比步行多用20分钟70－2×20=30分钟3．一天，小悦到离自己家4000米的表哥家去玩．早晨7：20时，小悦从家出发向表哥家走去，每分钟行60米，同时表哥骑车从家出发来接她．表哥到小悦家后才发现小悦已经走了，又立即返回去追．表哥骑车每分钟行260米．当表哥追上小悦后，带着她一起回表哥家，这时骑车速度变为每分钟骑175米．请问：当他们到达表哥家时还差几分钟就到8点了?答案：差4分钟详解：表哥从自己家到小悦家的时间是4000/260=200/13分，在这段时间小悦行走了4000/260×60=12000/13米同时这个距离也是表哥要返回去追小悦时两个人之间的路程差，路程差÷速度差=追及时间，所以追及时间是4000/260×60/（260-60）=60/13分；追上小悦时距离小悦家的路程为60/13×260=1200米，这时距离表哥家还有4000－1200=2800米，走这2800米的速度为175米/分所以用的时间是2800÷175=16分，因此本题所用总时间分三部分从表哥家到小悦家的时间200/13，追及时间60/13，回去时间16，共200/13+60/13+16=36分钟20+36=56分。
(完整)四年级数学思维训练行程问题
四年级数学思维训练行程问题（二）例1.甲乙两车同时从A、B两地相向而行。
甲车每小时行48千米，乙车每小时行42千米，两车在离中点9千米处相遇，求A、B两地距离多少千米？巩固练习11.甲乙两人同时分别从两地骑车相向而行，甲每小时行21千米，乙每小时行19千米。
两人相遇时距全程中点2千米。
求全程长多少千米？2.甲乙两车同时从东西两城相向而行，甲车每小时行60千米，乙车每小时行70千米，两车距两城中点15千米处相遇。
求东西两城相距多少千米？3.快车和慢车同时从A、B两地相对开出。
已知快车每小时行40千米，经过3小时后，快车已驶过中点25千米，这时与慢车还相距7千米。
慢车平均每小时行多少千米？例2．A、B、C三人行的速度分别是每分钟40米、50米、60米，A、B在甲地，而C在乙地同时相向而行，C遇B后10分钟和A相遇。
求甲、乙两地间的路长多少米？巩固练习21．有三辆客车，甲、乙两车从东站，丙车从西站同时相向而行，甲车每分钟行1000米，乙车每分钟行800米，丙车每分钟表行700米，丙车遇到甲车后20分钟又遇到乙车。
求东、西两站的距离。
2．甲每分钟走75米，乙每分钟走80米，丙每分钟走100米，甲、乙从东镇，丙从西镇，同时相向出发，丙遇到乙后3分钟再遇到甲，求两镇之间相距多少千米？3．甲、乙、丙三人，甲每分钟走60米，乙每分钟走67米，丙每分钟走73米，甲、乙从南镇，丙从北镇同时相向而行，丙遇到乙后10分钟遇到甲。
求两镇相距多少千米？例3．A、B两港间的水路长360千米，一只船从A港开往B港顺水10小时到达；从B港返回A港，逆水12小时到达。
求船地静水中的速度（即船速）和水流速度（即水速）？巩固练习31．A、B两港间的水路长208千米，一只船从A港开往B港，顺水8小时到达；从B港返回A港，逆水13小时到达。
求船在静水中的速度和水流速度。
2．甲、乙两港间水路长432千米，一只船从上游甲港航行到下游乙港需要18小时，从乙返回甲港，需要24小时到达。
四年级高思奥数行程问题三1
第19讲行程问题三1．莉莉和莎莎一起从家去学校，莉莉步行，莎莎骑车.莎莎到学校后发现自己没带文具盒，便立刻骑车回家去取，到家取出文具盒后又马上骑向学校，结果她和莉莉一起到校.如果莉莉每分钟走53米，那么莎莎骑车每分钟行进多少米？2小燕上学时骑车，回家时步行，路上共用50分钟.如果往返都步行，则全程需70分钟.求小燕往返都骑车所需的时间.3萱萱和卡莉娅从距离32千米的两地同时出发相向而行，萱萱每小时走4千米，卡莉娅乘坐“飞天扫帚”，每小时飞12千米.她俩迎面相遇后，卡莉娅发现自己忘记带东西了，立刻返回出发点，再掉头向萱萱前进.请问：她们第二次相遇的地点距离卡莉哑的出发点多少千米？4甲、乙两车分别从相距300千米的A、B两地同时出发，在A、B 两地之间不断往返行驶.已知甲车的速度是每小时30千米，乙车的速度是每小时20千米.请问：出发后经过多长时间甲、乙两车第一次迎面相遇？第一次迎面相遇后又经过多长时间甲、乙两车第二次迎面相遇？第二次迎面相遇后又经过多长时间甲、乙两车第三次迎面相遇？5甲、乙两车同时从A地出发，在相距300千米的A、B两地之间不断往返行驶.已知甲车的速度是每小时30千米，乙车的速度是每小时20千米，请问：出发后经过多长时间甲、乙两车第一次迎面相遇？第一次迎面相遇后又经过多长时间甲、乙两车第二次迎面相遇？第二次迎面相遇后又经过多长时间甲、乙两车第三次迎面相遇？6甲、乙两车分别从相距600千米的A、B两地同时出发，在A、B 两地之间不断往返行驶，已知甲车的速度是乙车的2倍.请问：甲、乙两车第一次迎面相遇在距离A地多少千米处？甲、乙两车第二次迎面相遇在距离A地多少千米处？7两辆汽车从甲、乙两站同时出发，相向而行，在距甲站50千米处两车第一次迎面相遇，相遇后两车继续前进(保持原速)各自到达乙、甲两站后，立即沿原路返回，在距乙站30千米处两车第二次迎面相遇.问：甲、乙两站相距多远？若两车继续前进，则在何处第三次迎面相遇？8 A、B两辆汽车同时从甲地出发，在甲、乙两地间不断往返行驶，第一次迎面相遇距离甲地40公里，第二次迎面相遇距离乙地10公里.求甲、乙两地之间的距离.9 A、B两地是电车的两个起点站，每隔12分钟发一辆车，电车每小时行25千米.请问：（1)如果小明从A地坐电4:去《地•那么他每隔多长时间会看见一辆电车迎面开来？10 甲、乙两人从同一个地点出发同向而行，甲比乙先出发•甲出发6分钟到达A地，此时乙距离起点150米.又过了 3分钟乙到达A地,此时甲距离起点900米.问：乙比甲晚出发多长时间？11 自行车队出发12分钟后，通信员骑摩托车去追他们，在距出发点9千米处追上了自行车队，然后通信员立即返回出发点，到达出发点后通信员又马上掉头去追自行车队，再次追上时恰好离出发点18千米.自行车队每分钟行多少千米？摩托车每分钟行多少千米？12乌龟与兔子进行10 000米赛跑，兔子的速度是乌龟的速度的5倍.当它们从起点一起出发后，乌龟不停地跑，兔子跑到某一地点开始睡觉.兔子醒来时发现乌龟已经领先它5000 米，于是奋起直追，当乌龟到达终点时，兔子仍落后100米。
四年级数学思维训练——行程问题(三)有答案
【2】自行车队出发24分钟后，通信员骑摩托车去追他们。
在距出发点9千米处追上自行车队。
通信员立即返回出发点，然后又返回去追自行车队，在追上时恰好离出发点18千米，求自行车队和摩托车的速度。
【3】某学校与某工厂之间有一条公路，该校下午2点钟派车到工厂接劳模作报告，往返需要1小时，这位劳模在下午1点钟便离厂步行去学校，途中遇到接他的车就立即上车驶往学校，于下午2点40分到达学校，汽车的速度是劳模步行速度的几倍？【4】家住郊外的工程师，每天在同一时候乘火车到达某站，这时工厂接工程师的汽车也同时到达，他乘车准时到达工厂。
有一天，工程师提前55分钟到某站，接他的汽车还未到，他就步行向工厂走去，在路上遇到接他的车，他再坐车，结果比平时提前10分钟到达工厂，问汽车的速度是工程师的几倍？【5】甲、乙两人在相距50米的A、B两端的水池里沿直线来回有用，甲的速度是1米/秒，乙的速度是2米/秒。
他们同时分别从水池的两端出发，来回游了10分钟，如果不计转向的时间，那么在这段时间内他们共相遇了多少次？【6】甲、乙两人在相距120米的直路上来回跑步，甲的速度为4米/秒，乙的速度为5米/秒。
如果他们同时分别从两个端点出发，且每人跑10分钟，问他们共相遇了多少次？【答案】先得出小明的速度是时是爸爸速度的3倍. 爸爸从家到第一次追上小明，小明走了4千米,若爸爸与小明同时出发,则爸爸应走出12千米,但是由于爸爸晚出发8分钟,所以只走了4千米,所以爸爸8分钟应走8千米. 由于爸爸从出发到第二次追上小明共走了16千米, 所以爸爸用了16分钟,此时离小明出发共用了8+16=24分钟, 所以爸爸第二次追上小明时是8点32分【2】自行车队出发24分钟后，通信员骑摩托车去追他们。
在距出发点9千米处追上自行车队。
通信员立即返回出发点，然后又返回去追自行车队，在追上时恰好离出发点18千米，求自行车队和摩托车的速度。
已知每行9千米，通信员要比自行车队快24分钟。
四年级数学思维训练导引(奥数)第18讲 行程问题三
第十八讲行程问题三1．莉莉和莎莎一起从家去学校，莉莉步行，莎莎骑车．莎莎到学校后发现自己没带文具盒，便立刻骑车回家去取，到家取出文具盒后又马上骑向学校，结果她和莉莉一起到校，如果莉莉每分钟走53米，那么莎莎骑车每分钟行进多少米？2．小燕上学时骑车，回家时步行，路上共用50分钟．如果往返都步行，则全程需要70分钟，求小燕往返都骑车所需的时间．3．一天，小悦到离自己家4000米的表哥家去玩，早晨7:20时，小悦从家出发向表哥家走去，每分钟行60米，同时表哥骑车从家出发来接她．表哥到小悦家后才发现小悦已经走了，又立即返回去追．表哥骑车每分钟行260米．当表哥追上小悦后，带着她一起回表哥家，这时骑车速度变为每分钟骑175米．请问：当他们到达表哥家时还差几分钟就到8点了？4．培英学校和电视机厂之间有一条公路，原计划下午2点时培英学校派车去电视机厂接劳模来校作报告，往返需用l小时．实际上这位劳模在下午1点便提前离厂步行向学校走来，途中遇到接他的汽车，劳模便立刻上车去往学校，并在下午2点40分到达．问：汽车行驶速度是劳模步行速度的几倍？5．快车和慢车分别从甲、乙两地同时开出，相向而行，经过4小时在途中相遇．相遇后两车继续向前行驶，慢车到达甲地后停留1小时再返回乙地．快车到达乙地后停留2.5小时再返回甲地．已知慢车从乙地到甲地用了12小时，那么两车从第一次相遇到第二次相遇需要多长时间？6．甲、乙两车分别从相距300千米的A，B两地同时出发，在A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米，请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇？(2)第一次迎面相遇后又经过多长时间甲、乙两车第二次相遇？(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇？7．甲、乙两车同时从A地出发，在相距300千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米．请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇？(2)第一次迎面相遇后又经过多长时间甲、乙两车第二次迎面相遇？(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次迎面相遇？8．A、曰两辆汽车从甲、乙两站同时出发，相向而行．在距甲站50千米处两车第一次迎面相遇，相遇后两车继续前进（保持原速）各自到达乙、甲两站后，立即沿原路返回，在距乙站30千米处两车第二次迎面相遇．问：甲、乙两站相距多远？若两车继续前进，则在何处第三次迎面相遇？9．A、B两辆汽车同时从甲地出发，在甲、乙两地间不断往返行驶．第一次迎面相遇距离甲地40公里，第二次迎面相遇距离乙地10公里．求甲、乙两地之间的距离．10.A、B两地是电车的两个起点站，每隔12分钟发一辆车，电车每小时行25千米，请问：(1)如果小明从A地坐电车去B地，那么他每隔多长时间会看见一辆电车迎面开来？(2)如果小明从B地步行走向A地，每小时行5千米，那么他每隔多长时间会看见一辆电车迎面开来？每隔多长时间会有一辆电车从后面超过他？1．甲、乙两人从同一个地点出发同向而行，甲比乙先出发．甲出发6分钟到达A地．此时乙距离起点150米．又过了3分钟乙到达A地，此时甲距离起点900米．问：乙比甲晚出发多长时间？2．自行车队出发12分钟后，通信员骑摩托车去追他们，在距出发点9千米处追上了自行车队，然后通信员立即返回出发点；到达出发点后通信员又马上掉头去追自行车队，再次追上时恰好离出发点18千米，自行车队每分钟行多少千米？摩托车每分钟行多少千米？3．乌龟与兔子进行10000米赛跑，兔子的速度是乌龟的速度的5倍．当它们从起点一起出发后，乌龟不停地跑，兔子跑到某一地点开始睡觉．兔子醒来时发现乌龟已经领先它5000米，于是奋起直追．当乌龟到达终点时，兔子仍落后100米．请问：兔子睡觉期间，乌龟跑了多少米？4．甲、乙两车分别从A、B两地同时出发，相向而行，12小时后在C地相遇．相遇后，两车并不停顿，继续前进．甲车在相遇后继续行驶4小时到达B 地，然后立即掉头以相同的速度返回A地，请问：(1)当甲车再次到达C地的时候，乙车还要再开几小时才能到达A地？(2)如果甲车从B地返回的时候不是原速返回，而是变慢了．而且当它经过C地的时候，乙车正好到达A地．甲车返回的速度是原来速度的多少倍？5．某科研单位每天派汽车早8点准时到工程师家接他上班．但今天早晨，工程师临时决定提前到单位，于是他没有等汽车来接，就自己步行去单位．步行途中遇到了前来接他的汽车，他马上上车赶到单位，结果发现比平时早到了30分钟，问：工程师上车时是几点几分？6．甲、乙两车分别从相距900千米的A，B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲、乙两车第二次迎面相遇是在出发后多长时间？(2)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇？(3)甲车第一次从后面追上乙车是在出发后多长时间？7．甲、乙两车同时从A地出发，在相距900千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲车第一次从后面追上乙车是在出发后多长时间？(2)甲车在第一次从后面追上乙车之后又经过多长时间第二次从后面追上乙车？(3)甲、乙两车第二次迎面相遇是在出发后多长时间？8．A、B两辆汽车分别从甲、乙两地同时出发，并在两地间不断往返行驶．两车在距离甲地40公里处第一次迎面相遇，在距离甲地10公里处第二次迎面相遇．求甲、乙两地之间的距离．9．甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行走．当甲走了3个来回的时候，乙恰好走了5个来回，在甲、乙两人行进的过程中，两人一共相遇了多少次？（迎面碰到和追上都算相遇）10.小明和小刚的速度分别为每分钟90米和每分钟70米，早上8:00他们分别从A、 B两站同时出发，相向而行，第一次相遇后两人继续前进，分别到达B、A后返回并在途中第二次相遇，第二次相遇地点距离A、B两站的中点450米，从两人同时出发到第二次相遇总共经历了多少分钟？A、B两站的距离为多少米？他们第一次相遇是几点几分？11.甲、乙两车分别从A、B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时15千米，乙车的速度是每小时35千米，并且甲、乙两车第三次相遇（两车同时到达同一地点即称为相遇）的地点与第四次相遇的地点恰好相距100千米．请问：两地之间的距离是多少千米？12.某人从甲地走往乙地，甲、乙两地之间有定时的公共汽车往返，而且两地发车的间隔都相等，他发现每隔6分钟开过来一辆去甲地的公共汽车，每隔12分钟开过去一辆去乙地的公共汽车，问：公共汽车每隔多少分钟从各自的始发站发车？1．每天早上7:30王经理都从家出发，由司机开车前往公司，8:00准时到达，然后司机开车原速返回王经理家，一天早上，王经理想要锻炼一下，因此中途下车走到公司，结果9:00才到．而司机8:10就已经回到王经理家中，请问：车速是王经理步行速度的多少倍？如果第二天，王经理仍然中途下车，但是下车地点比前一天距离公司要近一些，结果8:30就赶到了公司．司机回到王经理家应该是几点几分？2．一辆大轿车与一辆小轿车从甲地驶往乙地．大轿车的速度是小轿车速度的0.8倍．已知大轿车比小轿车早出发17分钟，但在两地中点停留了5分钟，然后继续驶往乙地；小轿车出发后中途没有停留，直接驶往乙地，最后小轿车比大轿车早4分钟到达乙地．已知大轿车是上午10点从甲地出发的，求小轿车追上大轿车的时间．3．A、B两地间相距950米，甲、乙两人同时由A地出发，并在A、曰两地间往返行进，共行进了40分钟，甲步行速度是每分钟40米，乙跑步速度是每分钟150米，那么甲、乙两人第几次迎面相遇时距B地最近，距离是多少米？4．甲、乙两车分别从A、B两地同时出发，在A、B两地间不断地往返行驶．甲车每小时行20千米，乙车每小时行50千米．已知两车第10次与第18次迎面相遇的地点相距60千米．问：A、B间的路程是多少千米？5．小明家在颐和园．如果他骑车到人大附中，每隔3分钟能见到一辆332路公共汽车迎面开来；如果他步行到人大附中，每隔4分钟能见到一辆332路公共汽车迎面开来．已知任意两辆332路汽车的发车间隔都是一样的，并且小明骑车速度是小明步行速度的3倍，请问：如果小明坐332路汽车到人大附中，每隔多少分钟能见到一辆332路公共汽车迎面开来？6．甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行进，当甲第3次到达B地的时候，乙恰好第5次回到了B地，请问：在甲、乙两人在行进的过程中，一共相遇了多少次？（迎面碰到和追上都算相遇）7．从电车总站每隔一定时间开出一辆电车，甲和乙两人在一条街上沿着同一方向步行，甲每分钟步行82米，每隔10分钟遇上一辆迎面开来的电车；乙每分钟步行60米，每隔10分15秒遇上迎面开来的一辆电车．问：电车总站每隔多少分钟开出一辆电车？8．A、B两地相距22.4千米．有一支游行队伍从A地出发，向B地匀速前进；当游行队伍队尾离开A地时，甲、乙两人分别从A、B两地同时出发．乙向A地步行；甲骑车先追向队头，追上队头后又立即骑向队尾，到达队尾后再立即追向队头，追上队头后又立即骑向队尾，……，当甲第5次追上队头时恰与乙相遇在距B地5.6千米处；当甲第7次追上队头时，甲恰好第一次到达B地，求此时乙离A地的距离．。
行程问题Microsoft Word 文档
小学四年级超级数学第 15 讲 行程问题A ，B 两地相距1500千米，甲车的速度是每小时60千米，乙车每小时比甲车多行15千米，两车同时从A 地出发。
问：乙车比甲车提前几小时到达B 地？思路引领：由A ，B 两地的距离及甲车的速度可求得甲车到B 地所需的时间，由甲、乙两车的速度关系可求得乙车的速度，进而可求得乙车到达B 地所需的时间，从而求得乙车比甲车提前的时间。
解答过程：乙车的速度：60+15=75（千米/时）乙车到达B 地所需的时间：1500÷75=20（小时）甲车到达B 地所需的时间：1500÷60=25（小时）乙车比甲车提前的时间：25—20=5（小时）答：乙车比甲车提前5小时到达B 地。
相信我能行：难题点拨2：一天小刚从家骑自行车去学校，每分钟行200米，骑了3分钟后发现忘带语文课本，立即以同样的速度沿原路回家拿课本，然后，小刚再以同样的速度骑到学校，共行了2700米。
小刚家距学校多少米？思路引领：由“骑了3分钟后发现忘带语文课本，立即以同样的速度沿原路回家拿课本”可知，小刚上学比平时多行了两个3分钟所行的路程，又由到学校共行了2700米可知，2700米里面包含了多行的两个3分钟的路程，减去多行的路程就是小刚到学校的距离。
解答过程：2700－200×3×2=2700－1200=1500（米）答：小刚家距学校1500米。
难题点拨3：A,B 两站相距400千米，甲，乙两车同时从两站相对开出，甲车每小时行35千米，乙车每小时行45千米。
一只燕子以每小时50千米的速度和甲车同时出发，向乙车飞去，遇到乙车又折回向甲车飞去，遇到甲车又往回飞向乙车，这样一只飞下去。
燕子飞了多少千米两车才相遇？思路引领：要求燕子飞了多少千米，就是知道燕子飞了多长时间。
根据题意，燕子和甲，乙两车同时出发，燕子所飞的时间就是甲，乙两车相遇的时间。
解答过程：1. 小明步行去学校，每分钟走两车多长时间相遇？400÷（35+45）=5（小时）燕子飞了多少千米？50×5=250（千米）答：燕子飞了250千米两车才相遇。
高思学校竞赛数学导引 四年级
&!!"!!))#,,.,,#,&+,&#,-.,-#,*+%+’#$.$#"+"#!!
’!5678!)))&9:+;)$ 3<=’>+?3&&+@,)% 3<=’>+?3$ &+@,!$ A% &B-./&
(!CD! !;<=+&,!
! # % ' !#% " $ & "$& ! # % ' !#%' " $ & "$& # % ' !#%'
" $
"!#!)")%),)!);¨©ªc’*+,c’«+)¬|+®)¯wc’®°! !
±<=t&®°²³£´Z)µ,-./&
! "
! #
$
%
&
’
(
#!!"!!.$+*.!)+!(."!+"&.%+’,()!
$!EFGHBIJ!"".#"/""+###"".##!!"! !))"+,,".,&".,-"+,*"+,(".,’".,$"+%+’"+$"."".!"!
! $
高思数学_4年级下第十八讲最值问题一
最值问题，即求最大值、最小值的问题．这类问题中，有时满足题目条件的情况并不多，这时我们就可以用枚举法将所有可能情况一一列出，再比较大小．分析 一共有多少种不同的插入数字的方法？你能将它们全部枚举出来吗？练习1.在五位数41729的某一位数字前面插入一个同样的数字（例如：在7的前面插入7得到417729），能得到的最大六位数是多少？直接枚举的优点是不用过多思考，大家都能理直气壮的说，直接比较大小得到的答案一定是正确的．事实上，我们应该多想一想，为什么这个答案是最大或最小的，有没有什么道理，其中有没有什么规律．分析 把9个同学分成两组，有多少种情况呢？你能算出这些分法各自对应的比赛场数吗？练习2.有7个同学要进行乒乓球单打比赛．他们准备分成两组，不同组的任意两人之间字（例如：到的最小八位数是多少？的任意两人之间都进行一场比赛，同组的人不比赛，那么一共最多有多少场比赛？都进行一场比赛，同组的人不比赛，那么一共最多有多少场比赛？从例题2我们可以得出：两个数的和相等，当它们越接近时（也就是它们的差越小时），两数乘积越大，也可以简单记成“和同近积大”． 分析练习3.请将1、2、3、4、5、6、7、8这八个数分别填入下面的方格中，使得乘积最大．×□□□□□□□□在很多问题中，我们都需要先进行整体的思考，再对局部进行一些调整．千万不能“丢了西瓜捡芝麻”！分析 两个多位数比较大小，首先要比较它们的位数．如果位数相同，还要从高位到低位依次比较．练习4.各位数字互不相同的多位数中，数字之和为13的最小数是多少？最大数是多少？使得乘积最大．是多少？最大数是多少？例题4在最值问题中，有时我们还会用到“极端思考”的方法．分析 动手试一试，如果只有1、2、3、4个数，最后剩下的数最大能是多少？先擦去较大的数比较好，还是先擦去较小的数比较好？应用你发现的规律计算10个数的情况．练习5.黑板上写着1、2、3、4、5这五个数，京京每次擦去两个数，再写上它们和的两倍．最后黑板上只剩下一个自然数，这个数最大是多少？去两个奇偶性相同的数，再写上它们的平均数，最后黑板上只剩下一个自然数．这个数最大是多少？个互不相同的自然数之和是题本讲知识点汇总一、满足题目条件的情况不多时，可以用枚举法把可能的情况一一列举出来，再找出最大值或最小值．二、两个数的和一定，当它们越接近时乘积越大．三、极端思考与局部调整也是解决最值问题的常用方法．作业1.在六位数129854的某一位数字前面插入一个同样的数字（例如：在2的前面插入2得到1229854），能得到的最小七位数是多少？2.有11个同学要进行羽毛球单打比赛．他们准备分成两组，不同组的任意两人之间都进行一场比赛，同组的人不比赛，那么一共最多有多少场比赛？3.请将3、4、5、6、7、8各一个填入下面的方格中，使得乘积最大．□□□□□□×4.各位数字互不相同的多位数中，数字之和为32的最小数是多少？最大数是多少？5.黑板上写着1，2，3，4，…，10这十个数，田田每次擦去两个奇偶性相同的数，再写上它们的平均数，最后黑板上只剩下一个自然数，这个数最小是多少？。
高斯小学奥数四年级上册含答案第18讲_火车行程初步
第十八讲火车行程初步我们之前已经学习了基本行程问题，明确了速度、时间和路程这三个量之间的关系：路程速度时间、=÷=⨯时间路程速度速度路程时间、=÷另外，我们还学习了两个对象之间的行程关系：相遇和追及．相遇问题中有：路程和速度和相遇时间=⨯速度和路程和相遇时间=÷相遇时间路程和速度和=÷追及问题中有：路程差速度差追及时间=⨯速度差路程差追及时间=÷追及时间路程差速度差=÷本讲，我们将在之前内容的基础上，学习一类新的、比较特殊的行程问题——与运动对象本身长度有关系的行程问题——我们称之为“火车行程”．比如北京到广州的铁路全长2300千米，如果一列火车从北京出发，以每小时100千米的速度开往广州，我们很容易算出火车需要行驶23小时．在这个问题中，火车的长度与北京到广州的距离相比微乎其微，我们可以忽略不计火车的长度．但是当行人在铁路旁行走，火车从行人身边开过时，从车头与行人相遇到车尾离开行人，是需要一段时间的，这时火车的长度就不能忽略不计了，我们需要把火车看成考虑自身长度的运动物体．火车行程问题和一般的行程问题最大的区别在于，火车是有长度的．因此计算火车行走的距离时，我们盯住火车上的一个点，比如车头，或者车尾．车头走了多远，火车就开了多远；车尾走了多远，火车也就开了多远．分析火车行程过程，首先要画出始末两个状态，找到最后对齐的部位．．．．．．．．．及其初始位置，将火车行程过程转化为这两个部位之间的相遇或追及过程．火车的行程问题大体上可以分为三类：火车过桥/山洞/隧道的问题；火车与行人的相遇和追及问题；火车与火车的相遇和追及问题．我们先来看看火车经过桥/山洞/隧道的过程．这类问题一般会考察两种情况——“火车通过桥/山洞/隧道”与“火车完全在桥上/山洞中/隧道中”．① “火车通过桥”即指“火车从车头上桥到车尾离桥”的过程，如图所示：首先，找到最后对齐的部位——车尾与桥头（红旗），再找出它们最初的位置，整个过程便可以转化为车尾从初始位置一直行驶到桥头红旗处的过程，很明显，路程即为“火车车长与桥长之和”．由此我们可以总结出以下规律：火车在通过桥/山洞/隧道时行驶的总路程是火车车长与桥/山洞/隧道的长度之和．例题1（1）一列火车车长180米，每秒行20米．请问：这列火车通过320米的大桥，需要经过多长时间？（2）一列火车以每分钟1000米的速度通过一条长2800米的隧道，共用180秒．请问：这列火车长多少米？「分析」火车通过桥即从车头上桥到车尾下桥的过程，火车的路程是什么呢？练习1一列火车长700米，以每分钟500米的速度通过一座长1300米的大桥．从车头上桥到车尾离桥要多少分钟？始 末② “火车完全在桥上”即指“火车从车尾上桥到车头离桥”的过程，如图所示：首先，找到最后对齐的部位——车头与桥头（红旗），再找出它们最初的位置，整个过程便可以转化为车头从初始位置一直行驶到桥头红旗处的过程，很明显，路程即为“桥长与火车车长之差”．由此我们可以总结出以下规律：火车完全在桥上/山洞中/隧道中行驶的总路程是桥/山洞/隧道的长度与火车车长之差．例题2一列火车车长180米，每秒行20米，这列火车要通过320米的大桥，请问：该过程中，火车有多长时间是完全在桥上的？「分析」火车完全在桥上即从车尾上桥到车头下桥的过程，火车的路程是什么呢？练习2一列火车以每秒20米的速度通过一条长2800米的隧道，完全在隧道中的时间是100秒．请问：这列火车有多长？火车从静止的人身旁经过的过程是非常简单的，从车头遇到人到车尾离开人，整个过程中火车行驶的路程就是火车长度——其实可以把人看作缩短至长度为0的桥．接下来，我们画图观察分析一下火车从行人身旁经过的过程．① 火车与人相遇：首先，找到最后对齐的部位——车尾与行人，再找出它们最初的位置，整个过程便可以始 末 末火车转化为车尾与行人的相遇过程，很明显，“火车与行人的路程和即为火车车长”．由此我们可以总结出以下规律：行人和火车迎面相遇，从相遇时刻到错开时刻，火车和行人的路程和＝火车的长度． ② 火车追人：首先，找到最后对齐的部位——车尾与行人，再找出它们最初的位置，整个过程便可以转化为车尾与行人的追及过程，很明显，“火车与行人的路程差即为火车车长”．由此我们可以总结出以下规律：火车追行人，从追上时刻到离开时刻，火车和行人的路程差＝火车的长度．例题3（1） 一名行人沿着铁路散步，每秒走1米，迎面过来一列长300米的火车．已知火车每秒钟行驶14米，请问：从火车头与行人相遇到火车尾离开他共用了多长时间？（2） 一人以每分钟60米的速度沿铁路步行，一列长144米的客车从他身后开来，客车的速度是每秒钟17米．客车从他身边经过用了多少秒钟？「分析」题（1）是一个火车与行人的相遇问题，在相遇过程中，路程和是什么呢？题（2）是火车与行人的追及过程，路程差又是什么呢？练习3（1） 一人以每分钟60米的速度沿铁路步行，一列长144米的客车从对面开来，从他身边通过用了8秒钟，客车的速度是每秒钟多少米？（2） 东东在铁路旁边沿着铁路方向散步，他散步的速度是2米/秒．这时背后开来一列火车，从车头追上他到车尾离开他一共用了18秒．已知火车速度是17米/秒，请问：火车的车长多少米？末火车通过火车过桥、火车与人之间的相遇和追及问题，我们知道，火车问题中，往往需要盯着火车的一个点来计算——要么车头，要么车尾——这样就把对象的长度转化成了路程中的一部分，简化分析．在两辆火车之间的相遇和追及问题之中也同样要用到这种分析方法．下面我们来看看两列火车之间的相遇与追及．①火车与火车相遇：末首先，找到最后对齐的部位——两车车尾，再找出它们最初的位置，整个过程便可以转化为两车车尾的相遇过程，很明显，“两列火车的路程和即为两列火车车长之和”．由此我们可以总结出以下规律：火车和火车相遇，从相遇时刻到错开时刻，两列火车的路程和＝两列火车车长之和．②火车追火车：程便可以转化为甲尾和乙头的追及过程，很明显，“两列火车的路程差即为两列火车车长之和”．由此我们可以总结出以下规律：火车追火车，从追上时刻到离开时刻，两列火车的路程差=两列火车车长之和．例题4（1）一列火车车长180米，每秒行20米，另一列火车长200米，每秒行18米，两车相向而行，它们从车头相遇到车尾相离要经过多长时间？（2）甲火车长370米，每秒钟行15米，乙火车长350米，每秒钟行21米，两车同向行驶．请问：乙车从追上甲车到完全超过共需多长时间？「分析」题（1）是一个两列火车的相遇问题，在相遇过程中，路程和是什么呢？题（2）是两列火车的追及过程，路程差又是什么呢？练习4（1）已知快车长582米，每秒行24米，慢车长1018米．两车相向而行，它们从车头相遇到车尾相离共用时40秒．请问：慢车速度是多少？（2）已知快车长182米，每秒行20米，慢车长134米，每秒行18米．两车同向而行，请问：快车从追上到完全超越慢车的时间是多少秒？例题5与铁路平行的一条小路上，有一个行人与一个骑车人同时向南行进．行人速度为每秒1米，骑车人速度为每秒3米．这时，有一列长360米的火车从他们背后开过来，火车从行人身旁经过用18秒钟．请问：这列火车从骑车人身旁经过需要多长时间？「分析」本题的实质是两个追及问题：火车与行人的追及问题，以及火车与骑车人的追及问题．在追及过程中，火车、行人、骑车人经过的路程有什么关系，路程差分别是什么呢？例题6高高号列车每秒行50米，思思号每秒行30米．两列火车相向而行时，它们从车头相遇到车尾相离要经过4秒．请问：两列火车同向行驶时，高高号从追上思思号到完全超过共需多长时间？「分析」题目中有两个过程：一是两列火车的相遇过程，一是两列火车的追及过程．画出火车图，寻找一下：相遇过程中两车路程和是什么？追及过程中两车路程差又是什么？课堂内外火车发展简史早在1804年，一个名叫德里维斯克的英国矿山技师，首先利用瓦特的蒸汽机造出了世界上第一台蒸汽机车，能牵引5节车厢，时速为5至6公里．这台机车没有设计驾驶室，机车行驶时，驾驶员跟在车旁边走边驾驶．真正的蒸汽机车是由乔治·斯蒂芬森发明的，因为当时使用煤炭或者木柴做燃料，所以人们都叫它“火车”，一直沿用至今．世界上第一列真正在轨道上行驶的蒸汽火车是由康瓦尔的工程师查理·特里维西克所设计的．他设计的火车有四个轮胎，1840年2月22日试车，空车时速20公里，载重时，时速8公里（相当于人快速行走的速度）．不幸，火车的重量压垮了铁轨．1879年，德国西门子电气公司研制了第一台电力机车，只在一次展览会上做了表演．1903年10月27日，西门子与通用电气公司研制的第一台实用电力机车投入使用，时速达到200公里．1894年，德国研制成功了第一台汽油内燃机车，并将它应用于铁路运输，开创了内燃机车的新纪元，但这种机车烧汽油，耗费太高，不易推广．1941年，瑞士研制成功新型的燃油汽轮机车，以柴油为燃料，且结构简单、震动小、运行性能好，因而在工业国家普遍采用．20世纪60年代以来，各国都大力发展高速列车，例如法国巴黎至里昂的高速列车，时速达到260公里；日本东京至大阪的高速列车时速也达到200公里以上．人们对这样的高速列车仍不满足．法国、日本等率先开发了磁悬浮列车，中国在上海修建了世界第一条商用磁悬浮列车线，时速可达400—500公里．作业1.一列火车车长180米，每秒行25米，这列火车完全通过320米的大桥，需要经过多少秒？2.一列火车车长240米，每秒行30米，这列火车车尾在720米的大桥的一端，行驶多少秒后，火车的车头到达大桥的另一端？3.思思在铁路旁边沿铁路方向的公路上散步，他散步的速度是每秒2米，这时迎面开来一列火车，经过他共用了18秒．已知火车全长360米，请问：火车每秒钟行多少米？4.高高在铁路旁以每秒2米的速度步行，一列长180米的火车从他后面开来，从他身边通过用了10秒．请问：火车每秒钟行多少米？5.有两列火车，一列长360米，每秒行18米，另一列长216米，每秒行30米．两车同向而行，快车赶超慢车（从追上到完全超过）需要多少秒？第十八讲火车行程初步1.例题1答案：25秒；200米详解：（1）火车通过桥，路程为桥长、车长之和，所以时间为()+÷=秒；（2）每分1803202025钟行驶1000米，通过桥时间为180秒即3分钟，所以路程是100033000⨯=米，而火车通过桥，路程为桥长、车长之和，所以车长为30002800200-=米．2.例题2答案：7秒详解：火车完全在桥上的路程为桥长、车长之差，即320180140÷=-=米，所以时间是140207秒钟．3.例题3答案：20秒；9秒详解：（1）从相遇到错开，火车与行人的路程和为车长，即300米，速度和是11415+=米/秒，所以时间为3001520÷=秒；（2）从追上到超过，火车与行人的路程差为火车车长，即144米，行人每分钟走60米，即每秒钟走1米，所以速度差是17116-=米/秒，时间是144169÷=秒．4.例题4答案：10秒；120秒详解：（1）从相遇到错开，两列车的路程和为车长之和，即380米，速度和是201838+=米/秒，所以时间为3803810÷=秒；（2）从追上到超过，两列车的路程差为车长之和，即720米，速度差是21156÷=秒．-=米/秒，时间是72061205.例题5答案：20秒详解：火车追行人：路程差为车长360米，时间为18秒，所以速度差为3601820÷=米/秒，行人速度是1米/秒，所以火车速度为21米/秒；火车追骑车人：路程差为车长360米，速度差为21318÷=秒．-=米/秒，所以时间为36018206.例题6答案：16秒详解：从相遇到错开，两车路程和为车长之和，其速度和为503080+=米/秒，时间为4秒，所以路程和为804320⨯=米，即两车车长和为320米．从追上到超过，两车路程差为两车长之和，即320米，速度差为503020÷=秒．-=米/秒，所以时间为32020167.练习1答案：4分钟详解：火车通过桥，路程为桥长、车长之和，所以时间为()+÷=分钟．700130050048.练习2答案：800米详解：火车完全在隧道中的路程为隧道长、车长之差，即201002000⨯=米，其中隧道长度为2800米，所以车长为28002000800-=米．9.练习3答案：17米/秒；270米简答：（1）从相遇到错开，火车与人的路程和是车长，即144米，用时8秒，所以可知速度和为144818÷=米/秒，其中人的速度是1米/秒，所以火车的速度为17米/秒；（2）从追上到超过，火车与人的路程差为车长，已知速度差为17215-=米/秒，用时18秒，所以路程差即车长为1815270⨯=米．10.练习4答案：16米/秒；158秒简答：（1）从相遇到错开，两列车的路程和是车长之和，即10185821600+=米，用时40秒，所以可知速度和为16004040÷=米/秒，其中快车的速度是24米/秒，所以慢车的速度为16米/秒；（2）从追上到超过，两车的路程差为车长之和，即182134316-=+=米，而速度差为20182米/秒，所以时间为3162158÷=秒．11.作业1答案：20秒简答：火车通过桥，路程为桥长、车长之和，所以时间为()+÷=秒．180320252012.作业2答案：16秒简答：火车完全在桥上的路程为桥长、车长之差，即720240480÷=-=米，所以时间是4803016秒钟．13.作业3答案：18米/秒简答：从相遇到错开，火车与人的路程和是车长360米，用时18秒，所以可知速度和为÷=米/秒，其中人的速度是2米/秒，所以火车的速度为18米/秒．360182014.作业4答案：20米/秒简答：从追上到超过，火车与人的路程差是车长180米，用时10秒，所以可知速度差为÷=米/秒，其中人的速度是2米/秒，所以火车的速度为20米/秒．180101815.作业5答案：48秒简答：从追上到超过，两列车的路程差为车长之和，即576米，速度差是301812-=米/秒，时间是5761248÷=秒．。
四年级数学思维训练导引(奥数)第18讲--行程问题三
四年级数学思维训练导引(奥数)第18讲--行程问题三第十八讲行程问题三1．莉莉和莎莎一起从家去学校，莉莉步行，莎莎骑车．莎莎到学校后发现自己没带文具盒，便立刻骑车回家去取，到家取出文具盒后又马上骑向学校，结果她和莉莉一起到校，如果莉莉每分钟走53米，那么莎莎骑车每分钟行进多少米？2．小燕上学时骑车，回家时步行，路上共用50分钟．如果往返都步行，则全程需要70分钟，求小燕往返都骑车所需的时间．3．一天，小悦到离自己家4000米的表哥家去玩，早晨7:20时，小悦从家出发向表哥家走去，每分钟行60米，同时表哥骑车从家出发来接她．表哥到小悦家后才发现小悦已经走了，又立即返回去追．表哥骑车每分钟行260米．当表哥追上小悦后，带着她一起回表哥家，这时骑车速度变为每分钟骑175米．请问：当他们到达表哥家时还差几分钟就到8点了？4．培英学校和电视机厂之间有一条公路，原计划下午2点时培英学校派车去电视机厂接劳模来校作报告，往返需用l小时．实际上这位劳模在下午1点便提前离厂步行向学校走来，途中遇到接他的汽车，劳模便立刻上车去往学校，并在下午2点40分到达．问：汽车行驶速度是劳模步行速度的几倍？5．快车和慢车分别从甲、乙两地同时开出，相向而行，经过4小时在途中相遇．相遇后两车继续向前行驶，慢车到达甲地后停留1小时再返回乙地．快车到达乙地后停留2.5小时再返回甲地．已知慢车从乙地到甲地用了12小时，那么两车从第一次相遇到第二次相遇需要多长时间？6．甲、乙两车分别从相距300千米的A，B两地同时出发，在A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米，请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇？(2)第一次迎面相遇后又经过多长时间甲、乙两车第二次相遇？(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇？7．甲、乙两车同时从A地出发，在相距300千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米．请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇？(2)第一次迎面相遇后又经过多长时间甲、乙两车第二次迎面相遇？(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次迎面相遇？8．A、曰两辆汽车从甲、乙两站同时出发，相向而行．在距甲站50千米处两车第一次迎面相遇，相遇后两车继续前进（保持原速）各自到达乙、甲两站后，立即沿原路返回，在距乙站30千米处两车第二次迎面相遇．问：甲、乙两站相距多远？若两车继续前进，则在何处第三次迎面相遇？9．A、B两辆汽车同时从甲地出发，在甲、乙两地间不断往返行驶．第一次迎面相遇距离甲地40公里，第二次迎面相遇距离乙地10公里．求甲、乙两地之间的距离．10.A、B两地是电车的两个起点站，每隔12分钟发一辆车，电车每小时行25千米，请问：(1)如果小明从A地坐电车去B地，那么他每隔多长时间会看见一辆电车迎面开来？(2)如果小明从B地步行走向A地，每小时行5千米，那么他每隔多长时间会看见一辆电车迎面开来？每隔多长时间会有一辆电车从后面超过他？1．甲、乙两人从同一个地点出发同向而行，甲比乙先出发．甲出发6分钟到达A地．此时乙距离起点150米．又过了3分钟乙到达A地，此时甲距离起点900米．问：乙比甲晚出发多长时间？2．自行车队出发12分钟后，通信员骑摩托车去追他们，在距出发点9千米处追上了自行车队，然后通信员立即返回出发点；到达出发点后通信员又马上掉头去追自行车队，再次追上时恰好离出发点18千米，自行车队每分钟行多少千米？摩托车每分钟行多少千米？3．乌龟与兔子进行10000米赛跑，兔子的速度是乌龟的速度的5倍．当它们从起点一起出发后，乌龟不停地跑，兔子跑到某一地点开始睡觉．兔子醒来时发现乌龟已经领先它5000米，于是奋起直追．当乌龟到达终点时，兔子仍落后100米．请问：兔子睡觉期间，乌龟跑了多少米？4．甲、乙两车分别从A、B两地同时出发，相向而行，12小时后在C地相遇．相遇后，两车并不停顿，继续前进．甲车在相遇后继续行驶4小时到达B 地，然后立即掉头以相同的速度返回A地，请问：(1)当甲车再次到达C地的时候，乙车还要再开几小时才能到达A地？(2)如果甲车从B地返回的时候不是原速返回，而是变慢了．而且当它经过C地的时候，乙车正好到达A地．甲车返回的速度是原来速度的多少倍？5．某科研单位每天派汽车早8点准时到工程师家接他上班．但今天早晨，工程师临时决定提前到单位，于是他没有等汽车来接，就自己步行去单位．步行途中遇到了前来接他的汽车，他马上上车赶到单位，结果发现比平时早到了30分钟，问：工程师上车时是几点几分？6．甲、乙两车分别从相距900千米的A，B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲、乙两车第二次迎面相遇是在出发后多长时间？(2)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇？(3)甲车第一次从后面追上乙车是在出发后多长时间？7．甲、乙两车同时从A地出发，在相距900千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时25千米，乙车的速度是每小时20千米．请问：(1)甲车第一次从后面追上乙车是在出发后多长时间？(2)甲车在第一次从后面追上乙车之后又经过多长时间第二次从后面追上乙车？(3)甲、乙两车第二次迎面相遇是在出发后多长时间？8．A、B两辆汽车分别从甲、乙两地同时出发，并在两地间不断往返行驶．两车在距离甲地40公里处第一次迎面相遇，在距离甲地10公里处第二次迎面相遇．求甲、乙两地之间的距离．9．甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行走．当甲走了3个来回的时候，乙恰好走了5个来回，在甲、乙两人行进的过程中，两人一共相遇了多少次？（迎面碰到和追上都算相遇）10.小明和小刚的速度分别为每分钟90米和每分钟70米，早上8:00他们分别从A、 B两站同时出发，相向而行，第一次相遇后两人继续前进，分别到达B、A后返回并在途中第二次相遇，第二次相遇地点距离A、B两站的中点450米，从两人同时出发到第二次相遇总共经历了多少分钟？A、B两站的距离为多少米？他们第一次相遇是几点几分？11.甲、乙两车分别从A、B两地同时出发，在A、B之间不断往返行驶．已知甲车的速度是每小时15千米，乙车的速度是每小时35千米，并且甲、乙两车第三次相遇（两车同时到达同一地点即称为相遇）的地点与第四次相遇的地点恰好相距100千米．请问：两地之间的距离是多少千米？12.某人从甲地走往乙地，甲、乙两地之间有定时的公共汽车往返，而且两地发车的间隔都相等，他发现每隔6分钟开过来一辆去甲地的公共汽车，每隔12分钟开过去一辆去乙地的公共汽车，问：公共汽车每隔多少分钟从各自的始发站发车？1．每天早上7:30王经理都从家出发，由司机开车前往公司，8:00准时到达，然后司机开车原速返回王经理家，一天早上，王经理想要锻炼一下，因此中途下车走到公司，结果9:00才到．而司机8:10就已经回到王经理家中，请问：车速是王经理步行速度的多少倍？如果第二天，王经理仍然中途下车，但是下车地点比前一天距离公司要近一些，结果8:30就赶到了公司．司机回到王经理家应该是几点几分？2．一辆大轿车与一辆小轿车从甲地驶往乙地．大轿车的速度是小轿车速度的0.8倍．已知大轿车比小轿车早出发17分钟，但在两地中点停留了5分钟，然后继续驶往乙地；小轿车出发后中途没有停留，直接驶往乙地，最后小轿车比大轿车早4分钟到达乙地．已知大轿车是上午10点从甲地出发的，求小轿车追上大轿车的时间．3．A、B两地间相距950米，甲、乙两人同时由A地出发，并在A、曰两地间往返行进，共行进了40分钟，甲步行速度是每分钟40米，乙跑步速度是每分钟150米，那么甲、乙两人第几次迎面相遇时距B地最近，距离是多少米？4．甲、乙两车分别从A、B两地同时出发，在A、B两地间不断地往返行驶．甲车每小时行20千米，乙车每小时行50千米．已知两车第10次与第18次迎面相遇的地点相距60千米．问：A、B间的路程是多少千米？5．小明家在颐和园．如果他骑车到人大附中，每隔3分钟能见到一辆332路公共汽车迎面开来；如果他步行到人大附中，每隔4分钟能见到一辆332路公共汽车迎面开来．已知任意两辆332路汽车的发车间隔都是一样的，并且小明骑车速度是小明步行速度的3倍，请问：如果小明坐332路汽车到人大附中，每隔多少分钟能见到一辆332路公共汽车迎面开来？6．甲、乙两人分别从A、B两地出发，在A、B两地之间不断往返行进，当甲第3次到达B地的时候，乙恰好第5次回到了B地，请问：在甲、乙两人在行进的过程中，一共相遇了多少次？（迎面碰到和追上都算相遇）7．从电车总站每隔一定时间开出一辆电车，甲和乙两人在一条街上沿着同一方向步行，甲每分钟步行82米，每隔10分钟遇上一辆迎面开来的电车；乙每分钟步行60米，每隔10分15秒遇上迎面开来的一辆电车．问：电车总站每隔多少分钟开出一辆电车？8．A、B两地相距22.4千米．有一支游行队伍从A地出发，向B地匀速前进；当游行队伍队尾离开A地时，甲、乙两人分别从A、B两地同时出发．乙向A地步行；甲骑车先追向队头，追上队头后又立即骑向队尾，到达队尾后再立即追向队头，追上队头后又立即骑向队尾，……，当甲第5次追上队头时恰与乙相遇在距B地5.6千米处；当甲第7次追上队头时，甲恰好第一次到达B地，求此时乙离A地的距离．。
四年级奥数之行程问题
四年级奥数之行程问题知识概要：一个物体的移动离不开速度、时间、路程这三个数量，我们把研究速度、时间、路程以及这三者关系的一类问题总称为行程问题。
行程问题涉及列车过桥问题、相遇及追及问题。
基本数量关系式是路程=速度×时间。
1、一列火车长250米，以每分钟450米的的速度通过一座大桥要360秒，这座大桥长几米？2、慢车车长为125米，车速17米/ 秒，快车车长140米，车速22米/ 秒。
慢车在前行驶，快车在后面追上并完全超过需多长时间？2、小张以3米/ 秒的速度沿着铁路跑步，迎面开来一列长147米的火车，他的行驶速度是18米/ 秒。
问：火车经过小张身旁的时间是多少？3、长150米的火车以18米/ 秒的速度穿越一条300米长的隧道。
问火车穿过隧道要多长时间？4、一列火车通过一条长1260米的桥用了60秒，火车穿越长2010米的隧道用了90秒。
问火车车速和车长各是多少？5、301次列车通过450米长的铁桥用了23秒，经过一位站在铁路边的扳道工人用了8秒。
列车的速度和长度各是多少？6、甲、乙两人同时分别从两地骑车而行。
甲每小时行20千米，乙每小时行18千米。
两人相遇时距全程中点3千米。
求全程长多少千米。
7、一条环形跑道长400米，甲每分钟跑300米，乙每分钟跑250米，两人同时同地同向出发，经过多少时间甲第一次追上乙？8、光明小学有一条200米长的环形跑道，亮亮和晶晶同时从起跑线起跑。
亮亮每秒跑6米，晶晶每秒跑4米，问：亮亮第一次追上晶晶时两人各跑了多少米？9、面包车以每小时60千米的速度从甲城开出，30分钟后，小轿车以每小时75千米的速度从甲城开出，沿同一路线追赶面包车，多少小时追上?10、甲乙两城间铁路长240千米。
快车从甲城，慢车从乙城同时相向开出，3小时相遇。
如果两车分别在两城同时同方向开出，慢车在前，快车在后，15小时快车可追上慢车。
求两车速各是多少？11、小明步行上学，每分钟行70米，离家12分钟后，爸爸发现小明的文具盒忘家中，马上骑自行车以每分280米的速度去追。
北京小学数学四年级下册《3.1行程问题》word教案 (5)
教学内容行程问题教学目标1.通过阅读教材学习解题方法，培养学生的阅读意识；利用坐标纸通过画图解答相遇问题，让学生感受到解题方法是多样的。
2.通过阅读教材、画一画、看图回答问题等培养阅读意识；利用坐标纸通过画图解答相遇问题，从而感受解题方法的多样。
3.利用坐标纸通过画图解答相遇问题求出相遇时间。
教学重点利用坐标纸通过画图解答相遇问题求出相遇时间。
教学难点利用坐标纸通过画图解答相遇问题求出相遇时间。
教具学具主备教师复备教师复备日期教学过程复备内容教学反思一、激情导入出示一张地图，找到北京西站、石家庄的位置。
北京西站与石家庄站相距千米，一列货车和一列客车从两地相向而行，几小时相遇？已知货车速度 60千米客车速度 80千米二、引导探究出示例5：第五次铁路大提速后，z517次客车13：11从北京西站开出，15：51到达石家庄；z518次客车14：23从石家庄开出，17：10达到北京西站。
这两列客车什么时间相遇？师：z517次客车从北京西站开出， z518次客车从石家庄开出一定会怎么样？师：一定会在某一时刻相遇，大约会在几点几分相遇呢？具体时刻会是几点几分？（学生解决此问题较困难此时教师提出看书）怎样解决，教材为我们介绍了一种方法。
请同学们看书p58：你看到了什么？怎样理解？（1）这样的小方格纸叫做坐标纸（2）每一个大格表示1小时，10个小格是一个大格（3）每一个小格表示6分钟（4）一端表示北京，另一端表示石家庄（5）两条线的交点大约为相遇时间，大约15：07 15：08通过坐标纸解题应分为几步？（1）找出北京西站发出的车的起点和终点，进行连线（2）找出石家庄站发出的车的起点和终点，进行连线（3）交点就是它们的相遇时间用坐标纸解题应注意什么？（出示投影）（1）估点要准确（2）描点要细些（3）结果要看准确三、巩固练习：1. p582. p66 4四、课后小结：说一说今天学习的收获？。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第18讲行程问题三内容概述运动过程较为复杂的行程问题，一般通过分段、比较等办法进行考虑，在往返问题中考虑多次相遇和多次追及的过程，需要注意从整体考虑两个对象的路程和或路程差，并从中找到规律.典型问题兴趣篇1．莉莉和莎莎一起从家去学校，莉莉步行，莎莎骑车．莎莎到学校后发现自己没带文具盒，便立刻骑车回家去取，到家取出文具盒后又马上骑向学校，结果她和莉莉一起到校．如果莉莉每分钟走53米，那么莎莎骑车每分钟行进多少米?答案：159详解：视从家到学校的路程为一个全程，由题意知道莎莎到校，再返回家，再到学校，一共走了三个全程，在同样时间内莉莉走了一个全程，即莎莎速度是莉莉的三倍53×3=1592．小燕上学时骑车，回家时步行，路上共用50分钟．如果往返都步行，则全程需要70分钟．求小燕往返都骑车所需的时间．答案：30分钟详解：视从家到学校的路程为一个全程，往返情况：骑车+步行=50步行+步行=70得知一个全程骑车比步行多用20分钟70－2×20=30分钟3．一天，小悦到离自己家4000米的表哥家去玩．早晨7：20时，小悦从家出发向表哥家走去，每分钟行60米，同时表哥骑车从家出发来接她．表哥到小悦家后才发现小悦已经走了，又立即返回去追．表哥骑车每分钟行260米．当表哥追上小悦后，带着她一起回表哥家，这时骑车速度变为每分钟骑175米．请问：当他们到达表哥家时还差几分钟就到8点了?答案：差4分钟详解：表哥从自己家到小悦家的时间是4000/260=200/13分，在这段时间小悦行走了4000/260×60=12000/13米同时这个距离也是表哥要返回去追小悦时两个人之间的路程差，路程差÷速度差=追及时间，所以追及时间是4000/260×60/（260-60）=60/13分；追上小悦时距离小悦家的路程为60/13×260=1200米，这时距离表哥家还有4000－1200=2800米，走这2800米的速度为175米/分所以用的时间是2800÷175=16分，因此本题所用总时间分三部分从表哥家到小悦家的时间200/13，追及时间60/13，回去时间16，共200/13+60/13+16=36分钟20+36=56分。
所以距离8点还有4分钟。
4．培英学校和电视机厂之间有一条公路，原计划下午2点时培英学校派车去电视机厂接劳模来校作报告，往返需用1小时．实际上这位劳模在下午l点便提前离厂步行向学校走来，途中遇到接他的汽车，劳模便立刻上车去往学校，并在下午2点40分到达问：汽车行驶速度是劳模步行速度的几倍?答案：8倍详解：由题意知汽车单程走了40÷2=20分钟。
比计划时间60÷2=30少用10分钟，这10分钟是劳模从1点到1点20共80分钟走出来的路程，所以在同样的路程汽车要10分钟，而步行要80分钟，所以汽车速度是步行速度的8倍。
40÷2=20 60÷2=30 30－20=10 1时20分=80分80÷10=85．快车和慢车分别从甲、乙两地同时开出，相向而行，经过4小时在途中相遇．相遇后两车继续向前行驶．慢车到达甲地后停留1小时再返回乙地．快车到达乙地后停留2.5小时再返回甲地．已知慢车从乙地到甲地用了12小时，那么两车从第一次相遇到第二次相遇需要多长时间答案：10小时。
详解：慢车行完全程要12小时，相遇前行了4小时，那么相遇后应该还要走8小时，相遇后走的8小时是快车相遇前走的4小时的路程，所以快车慢车的速度比是2：1，所以快车走完全程需要6小时，那么快车走从相遇地点到达乙地用的时间是慢车的二分之一，2小时，所以快车到达乙地，再停留2.5小时，所以第一次相遇后4.5小时开始往回走，慢车从相遇后到达甲地用的时间是甲相遇前的2倍，4×2=8小时，停留1小时，所以相遇后9小时慢车开始从甲地往回走，这时快车已经走了9-4.5=4.5小时，还余下1.5小时的路程，这段路程有两个人合走，要1.5×2÷3=1，所以从第一次相遇到第二次相遇，共用9+1=10小时。
12-4=8 8÷4=2 12÷2=6 4÷2/=2 2+2.5=4.5 6-4.5=1.51.5×2÷3=1 1+9=106．甲、乙两车分别从相距300千米的A，B两地同时出发，在A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米．请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇?(2)第一次迎面相遇后又经过多长时间甲、乙两车第二次相遇?(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次相遇?答案（1）6小时（2）12小时（3）12小时详解：合走一个全程路程和÷速度和300÷（30+20）=6（2）第二次相遇合走2×2－1=3个全程3×6=18 18-6=12（3）第三次相遇合走2×3-1=5个全程5×6=30 30-18=12相对出发迎面相遇n次合走2n-1个全程7．甲、乙两车同时从A地出发，在相距300千米的A、B两地之间不断往返行驶．已知甲车的速度是每小时30千米，乙车的速度是每小时20千米．请问：(1)出发后经过多长时间甲、乙两车第一次迎面相遇?(2)第一次迎面相遇后又经过多长时问甲、乙两车第二次迎面相遇?(3)第二次迎面相遇后又经过多长时间甲、乙两车第三次迎面相遇?答案：（1）12 （2）12 （3）12详解：（1）第一次相遇两个人合走2个全程300×2=600 600÷50=12小时。
（2）第一次相遇到第二次相遇合走2个全程答案同第一（3）每两次相遇都用12小时8．A、B两辆汽车从甲、乙两站同时出发，相向而行．在距甲站50千米处两车第一次迎面相遇，相遇后两车继续前进(保持原速)各自到达乙、甲两站后，立即沿原路返回．在距乙站30千米处两车第二次迎面相遇．问：甲、乙两站相距多远?若两车继续前进，则在何处第三次迎面相遇?答案：120千米。
在距离甲地10千米处相遇详解：选取A为研究对象。
第一次相遇两人合走一个全程，A走50千米，第二次相遇合走3个全程，A走3×50=150千米，150千米比一个全程多了30千米，所以全程是150－30=120千米。
第三次相遇合走5个全程，那么A走50×5=250 250÷120=2...10 所以在距离甲地10千米处相遇。
9．A、B两辆汽车同时从甲地出发，在甲、乙两地间不断往返行驶．第一次迎面相遇距离甲地40公里，第二次迎面相遇距离乙地10公里．求甲、乙两地之间的距离．答案：120公里详解：第一次相遇时两车合走了一个全程，A车走了0公里，即两车每合走一个全程A车就走40公里，第二次相遇时，两车合走了3个全程，那么A车走了3个40即3×40=120公里。
10．A、B两地是电车的两个起点站，每隔12分钟发一辆车，电车每小时行25千米．请问：(1)如果小明从A地坐电车去B地，那么他每隔多长时间会看见一辆电车迎面开来?(2)如果小明从B地步行走向A地，每小时行5千米，那么他每隔多长时间会看见一辆电车迎面开来?每隔多长时间会有一辆电车从后面超过他?答案：（1）6分钟（2）10分钟15分钟详解：12分钟=1/5小时相邻两辆车的间隔路程25×1/5=5千米，（1）迎面相遇路程和÷速度和5÷50=:1/10小时=6分钟（2）同第一5÷30=1/6小时=10分钟追及问题路程差÷速度差5÷20=1/4小时=15分钟拓展篇1. 甲、乙两人从同一个地点出发同向而行，甲比乙先出发．甲出发6分钟到达A地．此时乙距离起点150米．又过了3分钟乙到达A地，此时甲距离起点900米．问：乙比甲晚出发多长时间?答案：5分钟详解：设起点为O点，设甲到达A地时，乙到达B地，距离O点150米，当乙到达A地时设甲到达C地。
甲从O到A用了6分钟，从A到C用了3分钟，从A到C共用了9分钟，走了900米，所以速度是100米每分，所以A地距离O地是6×100，所以AB两地间距离是600-150=450. 450÷3=150 150÷150=1 6－1=5分钟2．自行车队出发12分钟后，通信员骑摩托车去追他们，在距出发点9千米处追上了自行车队．然后通信员立即返回出发点；到达出发点后通信员又马上掉头去追自行车队，再次追上时恰好离出发点18千米．自行车队每分钟行多少千米?摩托车每分钟行多少千米?答案：自行车队500米/分摩托车速度为1500米/分详解：当摩托车第一次追上自行车队时，距离出发点是9千米，再次追上时自行车队距离出发点是18千米，所以在两次追及期间自行车队前进了9千米，而摩托车共行驶了9×3千米，所以，摩托车的速度是自行车的3倍，所以可知当第一次追上时自行车队行了9千米，而摩托车也行了9千米，而摩托车的速度是自行车的3倍，所以走同样的路程摩托车所用时间是自行车的1/3. 差2/3 差12分钟，所以12÷2/3=18分钟，即自行车走9千米用了18分钟，速度为9000÷18=500米/分摩托车速度为500×3=1500米/分3．乌龟与兔子进行10000米赛跑，兔子的速度是乌龟的速度的5倍．当它们从起点一起出发后，乌龟不停地跑，兔子跑到某一地点开始睡觉．兔子醒来时发现乌龟已经领先它5000米，于是奋起直追．当乌龟到达终点时，兔子仍落后100米．请问：兔子睡觉期间，乌龟跑了多少米?答案：8020米详解：当乌龟到终点时，兔子跑了10000-100=9900米，假如兔子没有睡觉，那么当它跑9900米时，乌龟的路程只能是它的1/5 9900×1/5=1980 而实际当兔子跑了9900米时，乌龟跑了10000米，所以在兔子睡觉时乌龟跑了10000-1980=8020米。
4. 甲、乙两车分别从A、B两地同时出发，相向而行，12小时后在C地相遇．相遇后，两车并不停顿，继续前进．甲车在相遇后继续行驶4小时到达B地，然后立即掉头以相同的速度返回A地．请问：(1)当甲车再次到达C地的时候，乙车还要再开几小时才能到达A地?(2)如果甲车从B地返回的时候不是原速返回，而是变慢了．而且当它经过C地的时候，乙车正好到达A地．甲车返回的速度是原来速度的多少倍?答案：（1）28小时（2）1/8详解：（1）相遇后甲车用了4小时走了相遇前乙车12小时走的路程，即走同样的路程甲车用的时间是乙车的1/3 即甲车速度是乙车速度的3倍，所以乙车在相遇后从C点行驶到A地所用时间应该是甲车所用时间的3倍即12×3=36小时，甲车从C点到B点再从B 点回到C点用4×2=8小时，36－8=28小时。