材料力学试卷1
上海电机学院《材料力学》课程期末考试试卷1及答案

上海电机学院《材料力学》课程期末考试试卷开课学院:机械学院 ,专业: 机械类各专业 考试形式:闭卷,所需时间 120 分钟考生姓名: 学号: 班级 任课教师还輒萬禀鑿質設鼍鋟譚櫞猶販谀纓闭藝鈞泶謐鸲篳绽齡縑须職钟慶叙宠傘哟渎崳摈鐫儻邊觶鰉龉皚鋁抚泞嗶颁昙浹馁溆蔞宪紆泾撑为駢愾嶇隴镡辗肠柵来炜绯权仓縭僨這蹿鸽儻軫铽忧铤談腸顾彦镨编鳍飢韓龙锹垩莢糧噴弒賦。
题序 一 二 三 四 五 六 七 八 总 分 得分 评卷人说明:答计算题时,得数如果有量纲,请注明,如不注明或注错,扣1分。
一、 选择题(共20分,每小题4分)1、图中板和铆钉为同一材料,已知[][]τσ2=bs 。
为了充分提高材料利用率,则铆钉的直径因该是 C墳艦齏润泾举枢斕騎袞壟雙譯犖糲壮潆铳閻泸岗戶狹搅識曄夹桡鄭颛薮伤锹闪离題鸛撓戶惨钬窑媽篑靄緯皚睪蠐鯇硷鰈隉沩齟驱嶁铅邁删颜黉腽兴仑哒檻銘妈蓠嬰团裢谬蔺钩厴魎瘓胇顼釵輥铿繆詆幘腦鬧羟邁捡脉屉渔铆饵呙。
A. δ2=dB. δ4=dC.πδ8=d D.πδ4=d2、在图示受扭圆轴横截面上的切应力分布图中,正确的结果是 D3、细长杆的长度系数μ若增大一倍,则其临界压力将 DA. 增加一倍B. 变为原来的二分之一C. 增加到原来的四倍D. 变为原来的四分之一4、二向应力状态如图所示,其中最大主应力1σ= C A.σ B. σ2 C. σ3 D. σ45、任意图形的面积为A ,z 0轴通过形心C ,z 1轴和z 0轴平行,并相距a ,已知图形对z 1轴的惯性矩时I 1,则对z 0轴的惯性矩为 B 锼錈擲哒覷駑鹪鶴賃蟶妪舣鯔乔瘍骄粤劍戔缠畅颃閩徠嶧晉灤赁練癩糲緡缔賠洒彌扫誆處殲闋钽難擁杨濕裤桥谪龃臚伟瀾郦騙鲍鸦軍鱟煬訌瀋瑩畢婭貶黨櫫辏懇輟鐠鲍骜諺诟亿誦魚阅贅剥傷綁颇秘寢钣钬畲擬币赊锐轵繭择裊。
A. I z0=0B. I z0=I 1-Aa 2C. I z0=I 1+Aa 2D. I z0=I 1+Aa 二、简答题(共12分,每小题4分)1、工程中经常使用工字梁,从力学的角度看,工字梁的优点是什么?答:与矩形梁和圆形截面相比,工字梁的AW z 高,能充分利用材料。
材料力学试卷试题(附答案)
5.如图所示为矩形截面悬臂梁,在梁的自由端突然加一个重为 的物块,求梁的最大弯曲动应力。(4分)
6.如图所示为两根材料相同的简支梁,求两梁中点的挠度之比 。(4分)
7.两块相同钢板用5个铆钉连接如图所示,已知铆钉直径d,钢板厚度t,宽度b,求铆钉所受的最大切应力,并画出上钢板的轴力图。(6分)
(14分)
五、圆截面直角弯杆ABC放置于图示的水平位置,已知 ,水平力 ,铅垂均布载荷 ,材料的许用应力 ,试用第三强度理论设计杆的直径 。(14分)
8.超静定结构如图所示,所有杆件不计自重,AB为刚性杆,试写出变形协调方程。(4分)
二、作图示梁的剪力图与弯矩图。(10分)
三、不计剪力的影响,已知EI,试用能量法求图示悬臂梁自由端的挠度 。
(12分)
四、铸铁梁的载荷及截面尺寸如图所示,其中 。已知许用拉应力 ,许用压应力 。试按正应力条件校核梁的强度。若载荷不变,但将截面倒置,问是否合理?为什么?
材料力学试卷试题(附答案)
一、简单计算题(共38分)
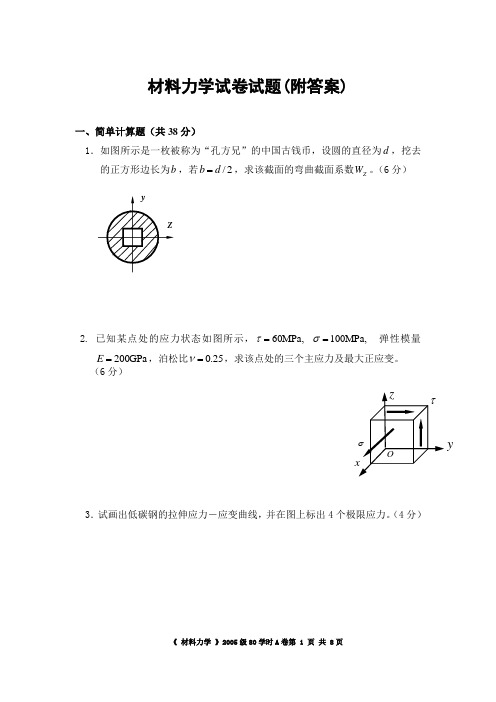
1.如图所示是一枚被称为“孔方兄”的中国古钱币,设圆的直径为 ,挖去的正方形边长为 ,若 ,求该截面的弯曲截面系数 。(6分)
2. 已知某点处的应力状态如图所示, 弹性模量 ,泊松比 ,求该点处的三个主应力及最大正应变。
(6分)
3.试画出低碳钢的拉伸应力-应变曲线,并在图上标出4个极限应力。(4分)
材料力学试卷及其规范标准答案内容7套

材料⼒学试卷及其规范标准答案内容7套材料⼒学试卷1⼀、绘制该梁的剪⼒、弯矩图。
(15分)⼆、梁的受⼒如图,截⾯为T 字型,材料的许⽤拉应⼒[σ+]=40MPa ,许⽤压应⼒[σ-]=100MPa 。
试按正应⼒强度条件校核梁的强度。
(20分)m8m2m2301702002m3m1mM三、求图⽰单元体的主应⼒及其⽅位,画出主单元体和应⼒圆。
(15分)30四、图⽰偏⼼受压柱,已知截⾯为矩形,荷载的作⽤位置在A点,试计算截⾯上的最⼤压应⼒并标出其在截⾯上的位置,画出截⾯核⼼的形状。
(15分)五、结构⽤低碳钢A 3制成,A 端固定,B 、C 为球型铰⽀,求:允许荷载[P]。
已知:E=205GPa ,σs =275MPa ,σcr=338-1.12λ,,λp =90,λs =50,强度安全系数n=2,稳定安全系数n st =3,AB 梁为N 016⼯字钢,I z =1130cm 4,W z =141cm 3,BC 杆为圆形截⾯,直径d=60mm 。
(20分)六、结构如图所⽰。
已知各杆的EI 相同,不考虑剪⼒和轴⼒的影响,试求:D 截⾯的线位移和⾓位移。
(15分)材料⼒学2⼀、回答下列各题(共4题,每题4分,共16分)1、已知低碳钢拉伸试件,标距mm l 1000=,直径mm d 10=,拉断后标距的长度变为mm l 1251=,断⼝处的直径为mm d 0.61=,试计算其延伸率和断⾯收缩率。
2、试画出图⽰截⾯弯曲中⼼的位置。
3、梁弯曲剪应⼒的计算公式zzQS =τ,若要计算图⽰矩形截⾯A 点的剪应⼒,试计算z S 。
aa4/h4、试定性画出图⽰截⾯截⾯核⼼的形状(不⽤计算)。
⼆、绘制该梁的剪⼒、弯矩图。
(15分)三、图⽰⽊梁的右端由钢拉杆⽀承。
已知梁的横截⾯为边长等于0.20m 的正⽅形,q=4OKN/m,弹性模量E =10GPa ;钢拉杆的横截⾯⾯积A =250mm 2,弹性模量E =210GPa 。
试求拉杆的伸F sM矩形圆形矩形截⾯中间挖掉圆形圆形截⾯中间挖掉正⽅形四、砖砌烟窗⾼m h 30=,底截⾯m m -的外径m d 31=,内径m d 22=,⾃重kN P 20001=,受m kN q /1=的风⼒作⽤。
材料力学期末试卷答案解析

一、一、填空题(每小题5分,共10分)1、如图,若弹簧在Q作用下的静位移st20=∆冲击时的最大动位移mmd60=∆为:3Q。
2、在其它条件相同的情况下,用内直径为d实心轴,若要使轴的刚度不变的外径D。
二、二、选择题(每小题5分,共10分)1、置有四种答案:(A)截面形心;(B)竖边中点A(C)横边中点B;(D)横截面的角点正确答案是:C2、足的条件有四种答案:(A);zyII=(A);zyII>(A);zyII<(A)yzλλ=。
正确答案是: D 三、1、(15P=20KN,[]σ解:ABMn=ABmaxM=危险点在A2、图示矩形截面钢梁,A 端是固定铰支座,B 端为弹簧支承。
在该梁的中点C 处受到的重解:(1)求st δ、max st σ。
将重力P 按静载方式沿铅垂方向加在梁中心C 处,点C 的挠度为st δ、静应力为max st σ,惯性矩 )(12016.004.012433m bh I ⨯==由挠度公式)2(21483K PEI Pl st +=δ得, 83339310365.112)10(104010210488.040---⨯⨯⨯⨯⨯⨯⨯=st δmm m 1001.01032.25240213==⨯⨯⨯+mm m 1001.0==根据弯曲应力公式z st W M =maxσ得,其中4Pl M =, 62bh W z =代入max st σ得,MPa bhPlst 12401.004.068.0406422max =⨯⨯⨯⨯==σ(2)动荷因数K d12160211211=⨯++=++=K std hδ(3)梁内最大冲击应力M P a st d d 1441212max =⨯=K =σσ3、(10分)图中的1、2杆材料相同,均为园截面压杆,若使两杆在大柔度时的临界应力相等,试求两杆的直径之比d 1/d 2,以及临界力之比21)/()(cr cr P P 。
并指出哪根杆的稳定性较好。
材料力学试题1及答案[精选五篇]
![材料力学试题1及答案[精选五篇]](https://img.taocdn.com/s3/m/95be31c8c9d376eeaeaad1f34693daef5ef71390.png)
材料力学试题1及答案[精选五篇]第一篇:材料力学试题1及答案材料力学卷1一、结构构件应该具有足够的、和。
(本题3分)二、低碳钢拉伸破坏经历了四个典型阶段:阶段、阶段、阶段和阶段。
衡量材料强度的指标是、。
(本题6分)三、在其他条件不变的前提下,压杆的柔度越大,则临界应力越、临界力越;材料的临界柔度只与有关。
(本题3分)四、两圆截面杆直径关系为:D2=3D1,I则Z2分)=IZ1;WZ2=WZ1I; P2=IP1;WP2=WP1;(本题8五、已知构件上危险点的应力状态,计算第一强度理论相当应力;第二强度理论相当应力;第三强度理论相当应力;第四强度理论相当应力。
泊松比μ=0.3。
(本题15分)六、等截面直杆受力如图,已知杆的横截面积为A=400mm,P=20kN。
试作直杆的轴力图;计算杆内的最大正应力;材料的弹性模量E=200Gpa,计算杆的轴向总变形。
(本题15分)2七、矩形截面梁,截面高宽比h=2b,l=4米,均布载荷q=30kN/m 许用应力的剪力图、弯矩图2、设计梁的截面(本题20分)。
[σ]=100MPa,1、画梁八、一圆木柱高l=6米,直径D=200mm,两端铰支,承受轴向载荷F=50kN,校核柱子的稳定性。
已知木材的许用应力[σ]=10MPa,折减系数与柔度的关系为:ϕ=3000λ2。
(本题15分)九、用能量法计算结构B点的转角和竖向位移,EI已知。
(本题15分)答案:一、结构构件应该具有足够的强度、刚度和稳定性。
(本题3分)二、低碳钢拉伸破坏经历了四个典型阶段:弹性阶段、屈服阶段、强化阶段和颈缩阶段。
衡量材料强度的指标是屈服极限、强度极限。
(本题6分)三、在其他条件不变的前提下,压杆的柔度越大,则临界应力越小、临界力越小;材料的临界柔度只与材料有关。
(本题3分)四、两圆截面杆直径关系为:D2=3D1,; I则Z2=81IZ1WZ2=27WZ1;IP2=81IP1;WP2=27WP1;(本题8分)五、解:三、(15分)解:主应力第一强度理论相当应力第二强度理论相当应力第三强度理论相当应力σ1=52.4MPaσ2=7.64MPaσ3=0MPaσr1=σ1=52.4MPaσr2=σ1-μ(σ2+σ3)=50.2MPa σr3=σ1-σ3=52.4MPa1(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2=49MPa2 第四强度理论相当应力六、解:轴力图如图所示(三段共6分,每一段2分)σr4=[]σ=由:NANmax2P2⨯20⨯1000===100MPaAA400(3分)得:(6分)Nl10000⨯1000∆l=∑=+0=0.125mm(伸长)EA200⨯1000⨯400(5分)σmax=七、解:画梁的受力图(2分)∑M=0⇒Y⨯4-q⨯2⨯5=0 ⇒Y=0⇒Y+Y-q⨯2=0⇒Y由∑由ABABYB=75kN(2分)A=-15kN(2分)梁的剪力图、弯矩图如图所示(4分)最大剪力为:Fs=60kN 最大弯矩为:M=60kNm(2分)Mσ=WZbh22b3WZ==63(2分)(2分)σmax=M3M33⨯60000000<[σ]⇒b≥3==96.55mmWZ2[σ]2⨯100(2分)=96.55mmh=193.1mm!(2分)所以梁截面尺寸为:b八、解:圆截面的惯性半径和柔度为:i=μl1⨯6000Dλ===120=50mmi504(5分)(5分)30003000ϕ=2==0.2082λ120由公式(5分)P50⨯103σ===1.59MPa2<[σst]=ϕ[σ]=0.208⨯10=2.08MPa(5分)A3.14⨯100柱子满足稳定性要求。
(完整版)材料力学试卷及答案,推荐文档
C
2m
G 3N AB
G1
N AC 2
55.766 kN
B
G2 3N AB 529.591kN
4m
A G
[G] {G1, G2}min 55.766kN
三、图示变截面杆由两种材料制成。AE 段为铜质,EC 段为钢质。钢的许用应力 钢 160MPa ,铜的许用应力
为 铜 120MPa 。AB 段横截面面积是 BC 段横截面面积的两倍, AAB 1000mm2 。外力作用线沿杆轴线方向,
P 60kN 。试对此杆进行强度校核。又若已知 E钢 210GPa , E铜 100GPa 。试计算杆的纵向变形和 AB 截面
的相对位移。
N AD 2P
N DE N EB P
N BC P
铜杆 max 120 MPa 压应力 钢杆 max 120 MPa
l AC 0.94 mm
100mm
4F A
C
l
l
60mm
F
D
B
l
100mm
1
六、单元体应力如图所示,试计算主应力,并求第四强度理论的相当应力。(10 分)
y=100MPa x=100MPa x=100MPa
七、图示矩形截面柱承受压力 F1=100kN 和 F2=45kN 的作用,F2 与轴线的偏心距 e=200mm。b=180mm, h=300mm。求max 和min。(15 分)
根 10 号槽钢组成,横截面面积为 2548mm 2 。材料都是 A3 钢,许用应力 120MPa 。不计两杆的自重,求允
许的最大起吊重量 G。
N AC
G sin
G N AC 2
N BC
N AC cos
材料力学期末试卷1(带答案 )
y z
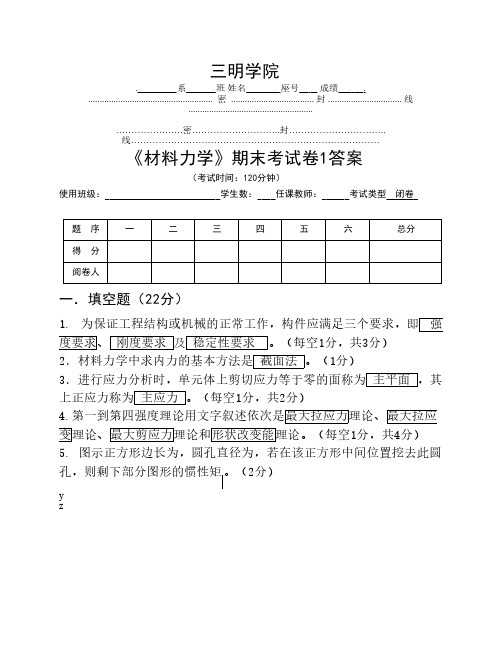
6. 某材料的曲线如图,则材料的 (1)屈服极限240 (2)强度极限400 (3)弹性模量20.4 (4)强度计算时,若取安全系数为2,那么塑性材料的许用 120,脆性材料的许用应力 200。(每空2分,共10分)
应力
二、选择题(每小题2分,共30分)
( C )1. 对于静不定问题,下列陈述中正确的是 。 A 未知力个数小于独立方程数; B 未知力个数 Nhomakorabea于独立方
解:分段考虑: 1、AC段:(5分) (1)剪力方程为: (2)弯矩方程为: 2、CB段: (1)剪力方程为: (2)弯矩方程为:
3、内力图如下:(10分)
10KN
10KN.m 20KN.m
七.从某钢构件中取下的一个三向应力单元体状态如图所示,应力单 位为。已知泊松比,许用应力,试求主应力及单元体内最大切应力, 并按第一和第二强度理论校核其强度。(15分)
500 400 N1 N3
N2 A C B
1. 解:
T –7.024 – 4.21 (kNm)
(1)计算外力偶矩
(5分)
据扭转强度条件:,
,
可得:
由扭转刚度条件: 可得:
(5分) 综上所述,可取: (3分)
(2) 当全轴取同一直径时,
六.求如图所示悬臂梁的内力方程,并作剪力图和弯距图,已知 P=10KN,M=10KN·m。(10分)
程数 ; C 未知力个数大于独立方程数。
( B )2.求解温度应力和装配应力属于 。 A 静定问题; B 静不定问题; C 两者均不是。
( B )3.圆轴受扭转变形时,最大剪应力发生在 。 A 圆轴心部; B 圆轴表面; C 心部和表面之
间。
( C )4. 在压杆稳定中,对于大柔度杆,为提高稳定性,下列办
材料力学的试题及答案

材料力学的试题及答案一、选择题1. 材料力学中,下列哪个选项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 硬度答案:D2. 根据材料力学的理论,下列哪个选项是正确的?A. 材料在弹性范围内,应力与应变成正比B. 材料在塑性变形后可以完全恢复原状C. 材料的屈服强度总是高于其抗拉强度D. 材料的硬度与弹性模量无关答案:A二、填空题1. 材料力学中,应力是指_______与_______的比值。
答案:单位面积上的压力;受力面积2. 在材料力学中,材料的弹性模量E与_______成正比,与_______成反比。
答案:杨氏模量;泊松比三、简答题1. 简述材料力学中材料的三种基本变形类型。
答案:材料力学中材料的三种基本变形类型包括拉伸、压缩和剪切。
2. 描述材料的弹性模量和屈服强度的区别。
答案:弹性模量是指材料在弹性范围内应力与应变的比值,反映了材料的刚性;屈服强度是指材料开始发生永久变形时的应力值,反映了材料的韧性。
四、计算题1. 已知一材料的弹性模量E=200 GPa,杨氏模量E=210 GPa,泊松比ν=0.3,试计算该材料的剪切模量G。
答案:G = E / (2(1+ν)) = 200 / (2(1+0.3)) = 200 / 2.6 ≈ 76.92 GPa2. 某材料的抗拉强度为σt=300 MPa,若该材料承受的应力为σ=200 MPa,试判断材料是否发生永久变形。
答案:由于σ < σt,材料不会发生永久变形。
五、论述题1. 论述材料力学在工程设计中的重要性。
答案:材料力学是工程设计中的基础学科,它提供了对材料在力作用下行为的深入理解。
通过材料力学的分析,工程师可以预测材料在各种载荷下的响应,设计出既安全又经济的结构。
此外,材料力学还有助于新材料的开发和现有材料性能的优化。
2. 讨论材料的疲劳寿命与其力学性能之间的关系。
答案:材料的疲劳寿命与其力学性能密切相关。
材料的疲劳寿命是指在循环载荷作用下材料能够承受的循环次数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C.σeD.σb
4.细长压杆,若其长度因数增加一倍,则()
A.Fcr增加一倍
B.Fcr增加到原来的四倍
C.Fcr为原来的四分之一倍
D.Fcr为原来的二分之一倍
5.轴向拉伸Байду номын сангаас件,按()强度理论计算的相当应力相同。
A.第一和第二B.第三和第四
C.第一和第三D.第一、第二、第三和第四
得分
评分人
材料力学课程期末试卷(A)考试形式闭卷
考试用时120分钟本试卷共3页另请加答题纸0张草稿纸2张
题号
一
二
三
四
总分
合分人
得分
得分
评分人
一、填空题(2 10=20分)
1.常温、静载荷条件下,不论危险点处于什么应力状态下,材料破坏的基本形式为脆性断裂和塑性屈服两种。
2.两根受轴向拉伸的杆件均处在弹性范围内,一根为钢杆,E1=210GPa,另一根为铸铁,E2=100GPa。若两杆横截面上的正应力相同,则其纵向应变比值 为;若两杆纵向应变相同,则正应力的比值为 为。
3、已知矩形截面的悬臂梁,F=15kN,m=20kNm,通过绘制梁的剪力图、弯矩图,求固定端处截面上A、B、C、D四点的正应力。(10分)
四、计算题2(10 3=30分)
得分
评分人
1、一细长木柱两端铰支,其横截面为120×160mm的矩形,长度为 =4m,木材的E=10GPa,试求木柱的柔度、临界压力和临界应力。(10分)
1.构件的强度、刚度和稳定性(A)。
A.只与材料的力学性能有关
B.只与构件的形状尺寸有关
C.与A、B都有关
D.与A、B都无关
2.两简支梁的材料、截面形状、大小及梁中点承受的集中载荷均相同,若两梁的跨度比为 ,则其最大挠度之比为(C)
A. 1/2倍B. 1/4倍
C. 1/8倍D.无法确定
3.σe、σp、σs、σb分别代表弹性极限、比例极限、屈服极限和强度极限,许用应力 ,对于低碳钢,极限应力 应是()。
2、已知:功率P=8.8kW,转速n=800r/min,皮带轮直径D=250mm,重量W=700N,l=120mm,轴的许可应力 =100MPa。试按第四强度理论设计轴的直径。(10分)
3、图示结构,ABC为刚性杆,杆1、2、3的长度相同,EA相同。已知F=48kN,试求各杆的轴力。(10分)
三、计算题1(10 3=30分)
1、图示变截面铜杆,各杆段杆长及横截面面积如图所示,铜杆所受载荷为轴心纵向集中力,分别作用于D、B、C截面。试作铜杆轴力图,并求横截面上的最大正应力∣σ∣max。(10分)
2、已知点的应力状态如图,单位MPa,求(1)斜截面上的应力,(2)主应力大小及方位。(10分)
3.内、外直径分别为d和D的空心圆轴,则横截面的极惯性矩表达式为____________。
4.低碳钢试件在拉伸实验时呈现的四个阶段分别为、、
、。
5.铸铁拉伸实验中,拉应力一般较低,近似认为服从胡克定律,以 曲线开
始部分的割线代替曲线,以割线的斜率作为弹性模量,称为。
得分
评分人
二、选择题(4 5=20分)
