大学物理(第四版)课后习题及答案 电流备课讲稿
大学物理第四版下册课后题答案

大学物理第四版下册课后题答案习题1111-1.直角三角形ABC 的A 点上,有电荷C 108.191-⨯=q ,B 点上有电荷C 108.492-⨯-=q ,试求C 点的电场强度(设0.04m BC =,0.03m AC =)。
解:1q 在C 点产生的场强:11204ACq E irπε=, 2q 在C 点产生的场强:22204BCq E j r πε=,∴C 点的电场强度:4412 2.710 1.810E E E i j =+=⨯+⨯;C 点的合场强:22412 3.2410VE E E m =+=⨯,方向如图: 1.8arctan33.73342'2.7α===。
11-2.用细的塑料棒弯成半径为cm 50的圆环,两端间空隙为cm 2,电量为C 1012.39-⨯的正电荷均匀分布在棒上,求圆心处电场强度的大小和方向。
解:∵棒长为2 3.12l r d m π=-=, ∴电荷线密度:911.010q C m l λ--==⨯⋅可利用补偿法,若有一均匀带电闭合线圈,则圆心处的合场强为0,有一段空隙,则圆心处场强等于闭合线圈产生电场再减去m d 02.0=长的带电棒在该点产生的场强,即所求问题转化为求缺口处带负电荷的塑料棒在O 点产生的场强。
解法1:利用微元积分:21cos 4O x Rd dE Rλθθπε=⋅,∴2000cos 2sin 2444O dE d R R R ααλλλθθααπεπεπε-==⋅≈⋅=⎰10.72V m -=⋅;解法2:直接利用点电荷场强公式:由于d r <<,该小段可看成点电荷:112.010q d C λ-'==⨯, 则圆心处场强:1191220 2.0109.0100.724(0.5)O q E V m R πε--'⨯==⨯⨯=⋅。
方向由圆心指向缝隙处。
11-3.将一“无限长”带电细线弯成图示形状,设电荷均匀分布,电荷线密度为λ,四分之一圆弧AB 的半径为R ,试求圆αi2cm O R x αα心O 点的场强。
大学物理(第四版)课后习题及答案 静电场

题7.1:1964年,盖尔曼等人提出基本粒子是由更基本的夸克构成,中子就是由一个带e 32的上夸克和两个带e 31-下夸克构成,若将夸克作为经典粒子处理(夸克线度约为10-20 m ),中子内的两个下夸克之间相距2.60⨯10-15 m 。
求它们之间的斥力。
题7.1解:由于夸克可视为经典点电荷,由库仑定律r r 220r 2210N 78.394141e e e F ===r e r q q πεπεF 与r e 方向相同表明它们之间为斥力。
题7.2:质量为m ,电荷为-e 的电子以圆轨道绕氢核旋转,其动能为E k 。
证明电子的旋转频率满足42k20232me E εν=其中是0ε真空电容率,电子的运动可视为遵守经典力学规律。
题7.2分析:根据题意将电子作为经典粒子处理。
电子、氢核的大小约为10-15 m ,轨道半径约为10-10 m ,故电子、氢核都可视作点电荷。
点电荷间的库仑引力是维持电子沿圆轨道运动的向心力,故有220241r e r v m πε= 由此出发命题可证。
证:由上述分析可得电子的动能为re mv E 202k 8121πε==电子旋转角速度为30224mr e πεω=由上述两式消去r ,得43k 20222324me E επων== 题7.3:在氯化铯晶体中,一价氯离于Cl -与其最邻近的八个一价格离子Cs +构成如图所示的立方晶格结构。
(1)求氯离子所受的库仑力;(2)假设图中箭头所指处缺少一个铯离子(称作品格缺陷),求此时氯离子所受的库仑力。
题7.3分析:铯离子和氯离子均可视作点电荷,可直接将晶格顶角铯离子与氯离子之间的库仑力进行矢量叠加。
为方便计算可以利用晶格的对称性求氯离子所受的合力。
解:(l )由对称性,每条对角线上的一对铯离子与氯离子间的作用合力为零,故01=F (2)除了有缺陷的那条对角线外,其它铯离子与氯离子的作用合力为零,所以氯离子所受的合力2F 的值为N 1092.134920220212-⨯===ae rq q F πεπε2F 方向如图所示。
大学物理(第四版)课后习题及答案_相对论

第十六章相对论题16.1:设'S 系以速率v = 0.60c 相对于S 系沿'xx 轴运动,且在t ='t = 0时,0'==x x 。
(1)若有一事件,在 S 系中发生于t = 2.0×10-7 s ,x = 50 m 处,该事件在 'S 系中发生于何时刻?(2)如有另一事件发生于 S 系中 t = 3.0×10-7 s ,x = 10 m 处,在 S ′系中测得这两个事件的时间间隔为多少?题16.1解:(1)由洛伦兹变换可得S ′系的观察者测得第一事件发生的时刻为s 1025.1/1'7221211-⨯=--=c v x c v t t(2)同理,第二个事件发生的时刻为s 105.3/1'7222222-⨯=--=c v x c v t t所以,在S ′系中两事件的时间间隔为s 1025.2'''721-⨯=-=∆t t t题16.2:设有两个参考系S 和S ′,它们的原点在t = 0和t ′ = 0时重合在一起。
有一事件,在 S ′系中发生在 t ′ = 8.0×10-8 s ,x ′ = 60 m ,y ′ = 0,z ′ = 0处,若S ′系相对于S 系以速率v = 0.6c 沿xx ′轴运动,问该事件在S 系中的时空坐标各为多少?题16.2解:由洛伦兹逆变换得该事件在S 系的时空坐标分别为m 93/1''22=-+=c v vt x x 0'==y y0'==z zs 105.2/1''7222-⨯=-+=c v x c v t t题16.3:一列火车长 0.30 km (火车上观察者测得),以 100 km/h 的速度行驶,地面上观察者发现有两个闪电同时击中火车的前后两端。
问火车上的观察者测得两闪电击中火车前后两端的时间间隔为多少?题16.3解:设地面为S 系,火车为S ′系,把闪电击中火车前后端视为两个事件(即两组不同的时空坐标)。
大学物理(第四版)课后习题及答案_电介质

电解质题8.1:一真空二极管,其主要构件是一个半径R 1 = 5.0⨯10-4 m 的圆柱形阴极和一个套在阴极外,半径m 105.432-⨯=R 的同轴圆筒形阳极。
阳极电势比阴极电势高300 V ,阴极与阳极的长度均为L = 2.5⨯10-2 m 。
假设电子从阴极射出时的速度为零。
求:(1)该电子到达阳极时所具有的动能和速率;(2)电子刚从阳极射出时所受的力。
题8.1分析:(1)由于半径L R <<1,因此可将电极视作无限长圆柱面,阴极和阳极之间的电场具有轴对称性。
从阴极射出的电子在电场力作用下从静止开始加速,电于所获得的动能等于电场力所作的功,也即等于电子势能的减少。
由此,可求得电子到达阳极时的动能和速率。
(2)计算阳极表面附近的电场强度,由E F q =求出电子在阴极表面所受的电场力。
解:(1)电子到达阳极时,势能的减少量为J 108.417ep -⨯-=-=∆eV E由于电子的初始速度为零,故 J 108.417ep ek ek -⨯=∆-=∆-E E E因此电子到达阳极的速率为17eks m 1003.122-⋅⨯===meVmE v (2)两极间的电场强度为r 02e E r πελ-=两极间的电势差1200ln 2d 2d 2121R R r r V R R R R πελπελ-=-=⋅=⎰⎰r E 负号表示阳极电势高于阴极电势。
阴极表面电场强度r 121r 10ln 2e e E R R R V R =-=πελ电子在阴极表面受力N e E F r 141037.4-⨯=-=e这个力尽管很小,但作用在质量为9.11⨯10-31 kg 的电子上,电子获得的加速度可达重力加速度的5⨯1015倍。
题8.2:一导体球半径为R 1,外罩一半径为R 2的同心薄导体球壳,外球壳所带总电荷为Q ,而内球的电势为V 0。
求此系统的电势和电场的分布。
题8.2分析:不失一般情况,假设内导体球带电q ,导体达到静电平衡时电荷的分布如图所示,依照电荷的这一分布,利用高斯定理可求得电场分布。
大学物理(第四版)课后习题及答案_电介质

电解质题8.1:一真空二极管,其主要构件是一个半径R 1 = 5.0⨯10-4 m 的圆柱形阴极和一个套在阴极外,半径m 105.432-⨯=R 的同轴圆筒形阳极。
阳极电势比阴极电势高300 V ,阴极与阳极的长度均为L = 2.5⨯10-2 m 。
假设电子从阴极射出时的速度为零。
求:(1)该电子到达阳极时所具有的动能和速率;(2)电子刚从阳极射出时所受的力。
题8.1分析:(1)由于半径L R <<1,因此可将电极视作无限长圆柱面,阴极和阳极之间的电场具有轴对称性。
从阴极射出的电子在电场力作用下从静止开始加速,电于所获得的动能等于电场力所作的功,也即等于电子势能的减少。
由此,可求得电子到达阳极时的动能和速率。
(2)计算阳极表面附近的电场强度,由E F q =求出电子在阴极表面所受的电场力。
解:(1)电子到达阳极时,势能的减少量为J 108.417ep -⨯-=-=∆eV E由于电子的初始速度为零,故 J 108.417ep ek ek -⨯=∆-=∆-E E E因此电子到达阳极的速率为17eks m 1003.122-⋅⨯===meVmE v (2)两极间的电场强度为r 02e E r πελ-=两极间的电势差1200ln 2d 2d 2121R R r r V R R R R πελπελ-=-=⋅=⎰⎰r E 负号表示阳极电势高于阴极电势。
阴极表面电场强度r 121r 10ln 2e e E R R R V R =-=πελ电子在阴极表面受力N e E F r 141037.4-⨯=-=e这个力尽管很小,但作用在质量为9.11⨯10-31 kg 的电子上,电子获得的加速度可达重力加速度的5⨯1015倍。
题8.2:一导体球半径为R 1,外罩一半径为R 2的同心薄导体球壳,外球壳所带总电荷为Q ,而内球的电势为V 0。
求此系统的电势和电场的分布。
题8.2分析:不失一般情况,假设内导体球带电q ,导体达到静电平衡时电荷的分布如图所示,依照电荷的这一分布,利用高斯定理可求得电场分布。
大学物理(第四版)课后习题及答案 电流

题:已知铜的摩尔质量1mol g 75.63-⋅=M ,密度3cm g 9.8-⋅=ρ,在铜导线里,假设每一个铜原子贡献出一个自由电子,(1)为了技术上的安全,铜线内最大电流密度2m mm A 0.6-⋅=j ,求此时铜线内电子的漂移速率d v ;(2)在室温下电子热运动的平均速率是电子漂移速率d v 的多少倍题分析:一个铜原子的质量A /N M m =,其中A N 为阿伏伽德罗常数,由铜的密度ρ可以推算出铜的原子数密度m n /ρ=根据假设,每个铜原子贡献出一个自由电子,其电荷为e ,电流密度d m nev j =。
从而可解得电子的漂移速率d v 。
将电子气视为理想气体,根据气体动理论,电子热运动的平均速率 e8m kTv π=其中k 为玻耳兹曼常量,e m 为电子质量。
从而可解得电子的平均速率与漂移速率的关系。
解:(1)铜导线单位体积的原子数为M N n /A ρ=电流密度为m j 时铜线内电子的漂移速率14A m m d s m 1046.4//--⋅⨯===e N M j ne j v ρ(2)室温下(K 300=T )电子热运动的平均速率与电子漂移速率之比为8edd 1042.281⨯≈=m kTv v v π 室温下电子热运动的平均速率远大于电子在稳恒电场中的定向漂移速率。
电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加。
考虑到电子的漂移速率很小,电信号的信息载体显然不会是定向漂移的电子。
实验证明电信号是通过电磁波以光速传递的。
题:有两个同轴导体圆柱面,它们的长度均为m 20,内圆柱面的半径为mm 0.3,外圆柱面的半径为mm 0.9。
若两圆柱面之间有μA 10电流沿径向流过,求通过半径为mm 0.6的圆柱面上的电流密度。
题分析:如图所示,是同轴柱面的横截面。
电流密度j 对中心轴对称分布。
根据稳恒电流的连续性,在两个同轴导体之间的任意一个半径为r 的同轴圆柱面上流过的电流I 都相等,因此可得rL I j π2/=解:由分析可知,在半径mm 0.6=r 的圆柱面上的电流密度25m A 1033.12/--⋅⨯==rL I j π题:有两个半径分别为1R 和2R 的同心球壳。
大学物理第四版下册课后题答案教学提纲

习题1111-1.直角三角形ABC 的A 点上,有电荷C 108.191-⨯=q ,B 点上有电荷C 108.492-⨯-=q ,试求C 点的电场强度(设0.04m BC =,0.03m AC =)。
解:1q 在C 点产生的场强:11204ACq E ir πε=vv ,2q 在C 点产生的场强:22204BC q E j r πε=v v ,∴C 点的电场强度:4412 2.710 1.810E E E i j =+=⨯+⨯v v v v v ; C 点的合场强:22412 3.2410VE E E m =+=⨯,方向如图: 1.8arctan33.73342'2.7α===o o 。
11-2.用细的塑料棒弯成半径为cm 50的圆环,两端间空隙为cm 2,电量为C 1012.39-⨯的正电荷均匀分布在棒上,求圆心处电场强度的大小和方向。
解:∵棒长为2 3.12l r d m π=-=, ∴电荷线密度:911.010q C m l λ--==⨯⋅可利用补偿法,若有一均匀带电闭合线圈,则圆心处的合场强为0,有一段空隙,则圆心处场强等于闭合线圈产生电场再减去m d 02.0=长的带电棒在该点产生的场强,即所求问题转化为求缺口处带负电荷的塑料棒在O 点产生的场强。
解法1:利用微元积分:21cos 4O x Rd dE R λθθπε=⋅,∴2000cos 2sin 2444O dE d R R R ααλλλθθααπεπεπε-==⋅≈⋅=⎰10.72V m -=⋅;解法2:直接利用点电荷场强公式:由于d r <<,该小段可看成点电荷:112.010q d C λ-'==⨯,则圆心处场强:1191220 2.0109.0100.724(0.5)O q E V mR πε--'⨯==⨯⨯=⋅。
方向由圆心指向缝隙处。
11-3.将一“无限长”带电细线弯成图示形状,设电荷均匀分布,电荷线密度为λ,四分之一圆弧AB 的半径为R ,试求圆αj v iv2cm O R x αα心O 点的场强。
大学物理(第四版)课后知识题及答案解析磁场
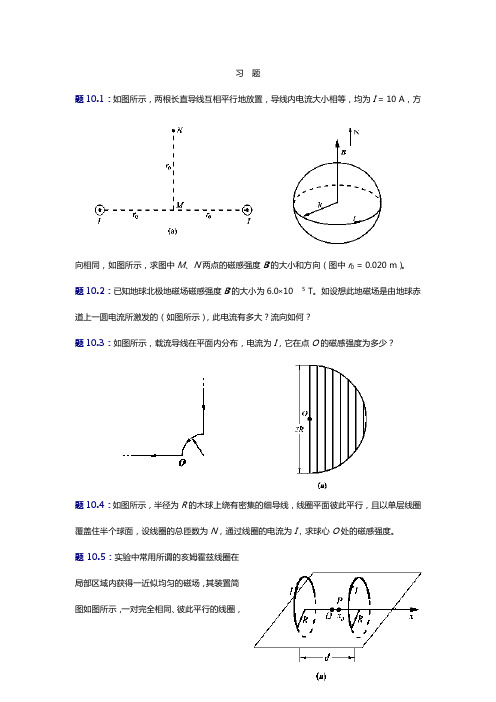
习题题10.1:如图所示,两根长直导线互相平行地放置,导线内电流大小相等,均为I = 10 A,方向相同,如图所示,求图中M、N两点的磁感强度B的大小和方向(图中r0 = 0.020 m)。
题10.2:已知地球北极地磁场磁感强度B的大小为6.0 105 T。
如设想此地磁场是由地球赤道上一圆电流所激发的(如图所示),此电流有多大?流向如何?题10.3:如图所示,载流导线在平面内分布,电流为I,它在点O的磁感强度为多少?题10.4:如图所示,半径为R的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈覆盖住半个球面,设线圈的总匝数为N,通过线圈的电流为I,求球心O处的磁感强度。
题10.5:实验中常用所谓的亥姆霍兹线圈在局部区域内获得一近似均匀的磁场,其装置简图如图所示,一对完全相同、彼此平行的线圈,它们的半径均为R ,通过的电流均为I ,且两线圈中电流的流向相同,试证:当两线圈中心之间的距离d 等于线圈的半径R 时,在两线圈中心连线的中点附近区域,磁场可看成是均匀磁场。
(提示:如以两线圈中心为坐标原点O ,两线圈中心连线为x 轴,则中点附近的磁场可看成是均匀磁场的条件为x B d d = 0;0d d 22=xB ) 题10.6:如图所示,载流长直导线的电流为I ,试求通过矩形面积的磁通量。
题10.7:如图所示,在磁感强度为B 的均匀磁场中,有一半径为R 的半球面,B 与半球面轴线的夹角为α,求通过该半球面的磁通量。
题10.8:已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热。
电流在导线横截面上均匀分布。
求:(1)导线内、外磁感强度的分布;(2)导线表面的磁感强度。
题10.9:有一同轴电缆,其尺寸如图所示,两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑。
试计算以下各处的磁感强度:(1)r <R 1;(2)R 1<r <R 2;(3)R 2<r <R 3;(4)r >R 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理(第四版)课后习题及答案电流题9.1:已知铜的摩尔质量1mol g 75.63-⋅=M ,密度3cm g 9.8-⋅=ρ,在铜导线里,假设每一个铜原子贡献出一个自由电子,(1)为了技术上的安全,铜线内最大电流密度2m mm A 0.6-⋅=j ,求此时铜线内电子的漂移速率d v ;(2)在室温下电子热运动的平均速率是电子漂移速率d v 的多少倍?题9.1分析:一个铜原子的质量A /N M m =,其中A N 为阿伏伽德罗常数,由铜的密度ρ可以推算出铜的原子数密度m n /ρ=根据假设,每个铜原子贡献出一个自由电子,其电荷为e ,电流密度d m nev j =。
从而可解得电子的漂移速率d v 。
将电子气视为理想气体,根据气体动理论,电子热运动的平均速率 e8m kT v π=其中k 为玻耳兹曼常量,e m 为电子质量。
从而可解得电子的平均速率与漂移速率的关系。
解:(1)铜导线单位体积的原子数为M N n /A ρ=电流密度为m j 时铜线内电子的漂移速率 14A m m d s m 1046.4//--⋅⨯===e N M j ne j v ρ(2)室温下(K 300=T )电子热运动的平均速率与电子漂移速率之比为8edd 1042.281⨯≈=m kTv v v π 室温下电子热运动的平均速率远大于电子在稳恒电场中的定向漂移速率。
电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加。
考虑到电子的漂移速率很小,电信号的信息载体显然不会是定向漂移的电子。
实验证明电信号是通过电磁波以光速传递的。
题9.2:有两个同轴导体圆柱面,它们的长度均为m 20,内圆柱面的半径为mm 0.3,外圆柱面的半径为mm 0.9。
若两圆柱面之间有μA 10电流沿径向流过,求通过半径为mm 0.6的圆柱面上的电流密度。
题9.2分析:如图所示,是同轴柱面的横截面。
电流密度j 对中心轴对称分布。
根据稳恒电流的连续性,在两个同轴导体之间的任意一个半径为r 的同轴圆柱面上流过的电流I 都相等,因此可得rL I j π2/=解:由分析可知,在半径mm 0.6=r 的圆柱面上的电流密度25m A 1033.12/--⋅⨯==rL I j π题9.3:有两个半径分别为1R 和2R 的同心球壳。
其间充满了电导率为γ(γ为常量)的介质,若在两球壳间维持恒定的电势差U 。
求两球壳间的电流。
题9.3分析:可采用两种方法求解,(1)根据欧姆定律的微分形式E j γ=和电流S j d ⋅=⎰I 。
球壳间的电场分布应为球对称。
假设内、外球壳分别均匀带电荷Q ±,则球壳间的电场强度r 2r 04e E r Q επε=,两球壳的电势差⎰⋅=21d R R U r E另外球壳间的电流密度j 沿径向且在球面上均匀分布,因此,两球壳间的电流24d r j I π⋅=⋅=⎰S j由上述关系可解得两球壳间的径向电流。
(2)在求得球壳间径向电阻的基础上,由欧姆定律求球壳间的径向电流。
在介质中任取一同心球壳作微元,球壳面积为24r π,厚度为r d ,依照电阻的定义,该微元内、外表面间的电阻24d 1d r rR πγ=导体球壳间的总电阻⎰=21d R R R R 。
再由欧姆定律求出径向电流。
解1:假设内、外球壳分别带电Q ±,两球壳间的电势差)11(4d 21r021R R Q U R R -=⋅=⎰επεr E 球壳间的电流强度1221244d R R R R U r I -=⋅=⋅=⎰γππγE S j解2:导体球壳间的总电阻)11(414d 121221R R r r R R R -==⎰πγπγ 由欧姆定律,径向电流强度12214R R R R U R U I -==γπ题9.4:同样粗细的碳棒和铁棒串联,能使两棒的总电阻不随温度而变化。
问此时两棒的长度比应为多少?解:设室温下两棒的电阻分别为C R 和Fe R ,温度改变T ∆后电阻分别为)1()1(Fe Fe FeC C CT R R T R R ∆+='∆+='αα式中C α和Fe α分别为室温时碳和铁的电阻温度系数,查表得碳和铁的电阻率和电阻温度系数分别为13C 17Fe 14C 15C K100.5m 100.1K 105m 105.3-------⨯=⋅Ω⨯=⨯-=⋅Ω⨯=αραρ;;依照题意,串联后的总电阻不随温度改变,故有0Fe Fe C C =+ααR R又根据电阻的定义SlR ρ=,在两导线截面相同的条件下,则有 2C C Fe Fe Fe C 1086.2//-⨯=-=ραραl l题9.5:如图所示,截圆锥体的电阻率为ρ,长为l,两端面的半径分别为1R和2R。
试计算此锥体两端面之间的电阻。
题9.5分析:对于粗细不均匀导体的电阻,不能直接用SlRρ=计算。
垂直于锥体轴线截取一半径为r、厚为x d的微元,此微元电阻2ddrxRπρ=,沿轴线对元电阻R d积分,即得总电阻⎰=RR d。
解:由分析可得锥体两端面间的电阻⎰=2drxRπρ(1)由几何关系可得)/()(/212RRRrlx--=则rRRlx dd21-=(2)将式(2)代人式(1)得21221d)(12RRlrrRRlR RRπρπρ=-=⎰题9.6:一同轴电缆,其长m105.13⨯=L,内导体外径mm0.11=R,外导体内径mm0.52=R,中间填充绝缘介质。
由于电缆受潮,测得绝缘介质的电阻率降低到m104.65⋅Ω⨯。
若信号源是电动势V24=ε,内阻Ω0.3i=R的直流电源,求在电缆末端的负载电阻kΩ0.1=R上的信号电压为多大?题9.6分析:由于电缆受潮,同轴电缆内、外导体间存在径向漏电电阻R ,它与负载电阻0R 构成并联电路,其等效电路图如图所示。
根据全电路欧姆定律可求出负载上的信号电压。
解:同轴电缆的径向漏电电阻12ln 2R R L R πρ=它与负载电阻并联后的总电阻为Ω=+='5.9800RR RR R 由全电路的欧姆定律∑+'=)(r R I ε,可得负载上的信号电压V 3.23=+''='=rR R I R U ε比较电缆受潮前后负载的端电压,可知电压下降了V 7.0。
题9.7:有一平板电容器,其电容μF 0.1=C ,极板间介质的电阻率m Ω100.213⋅⨯=ρ,相对电容率0.5r =ε,求该电容器两极间的电阻值。
题9.7解:根据电阻的定义,两极板间的电阻Sd R ρ= 而充满均匀介质的平板电容器,其电容d S C /r 0εε=,由上述两式可得Ω1085.88r0⨯==CR εερ题9.8:如图所示,在两块薄铜板之间,放置内、外半径分别为1r 和2r 的环形硅,cm 0.5cm,0.3,cm 80.021===h r r ,如在两极间加V 200的电势差,求电路中的电流。
题9.8解:根据电阻的定义,环形硅的电阻)(2122r r hR -=πρ查表知硅的电阻率m Ω104.62⋅⨯=ρ,在恒定电压U 的作用下,硅中的电流为mA 4.16A 1064.1)(22122=⨯=-==-U lr r R U I ρπ题9.9:在相距km 0.15的A 、B 两地之间地下,铺设有一条双股电缆,其中一根导线因某处绝缘层破损触地而发生故障。
检修人员用图所示装置可找出故障点位置。
该装置中R R ,Ω1000.230⨯=为可变电钮。
现通知A 地工作人员将该对电缆短接,测得检流计G 没有电流时电阻Ω1086.13⨯=R 。
求电缆损坏处到B 的距离x 。
(电缆每千米直流阻抗为Ω150 )题9.9分析:以接地点P 为分割点,将电缆分成AP 、 PB 两段,它们的电阻分别1R 、2R ,并与测试装置构成如图所示的电桥电路。
当电桥平衡时(即检流计G 内没有电流流过),有0201::)(R R R R R =+由于1R 、2R 均与电缆长度成正比。
参照单位长度电缆的直流电阻,可求得故障处到B 的距离x 。
解:设η为单位长度电缆线的直流电阻,L 是A 、B 两地间的电缆长度,由电桥平衡条件ηη)2(x L R x -=+解得km 8.82=-=ηRL x 题9.10:如图所示,V 0.221==εε,内阻Ω8.4,Ω0.5,Ω1.021i2i1====R R R R 。
试求:(1)电路中的电流;(2)电路中消耗的功率;(3)两电源的端电压。
题9.10解:(1)由闭合电路的欧姆定律可得电路中的电流A 4.0i2i12121=++++=R R R R I εε(2)电路中消耗的功率为W 6.1)(i2i1212=+++=R R R R I N(3)电源的端电压分别为V96.1V 96.1i222i111=-==-=IR U IR U εε题9.11:在如图所示的电路中,V 0.2,V 0.621==εε,,Ω0.4,Ω0.3,Ω0.2,Ω0.14321====R R R R求:(1)流过各电阻的电流;(2)A 、B 两点的电势差AB U ?题9.11解:(1)取电流和回路绕行方问如图所示,由闭合电路欧姆定律,得A 85.0)/(43432121=+++-=R R R R R R I εε流过各电阻的电流分别为A 85.021===I I IA 49.04343=+=I R R R IA 36.043334=+=-=I R R R I I I (2)由一段含源电路的欧姆定律得V 2.511AB -=-=εIR U。
