arcgis空间内插值教程
ArcGIS中几种空间插值方法
ArcGIS 中几种空间插值方法1. 反距离加权法(IDW)ArcGIS 中最常用的空间内插方法之一，反距离加权法是以插值点与样本点之间的距离为权重的插值方法，插值点越近的样本点赋予的权重越大，其权重贡献与距离成反比。
可表示为：1111()()n nip p i i i i Z Z D D ===∑∑ 其中Z 是插值点估计值，Z i (i=1Λn)是实测样本值，n 为参与计算的实测样本数，D i 为插值点与第i 个站点间的距离，p 是距离的幂，它显著影响内插的结果，它的选择标准是最小平均绝对误差。
2.多项式法多项式内插法(Polynomial Interpolation)是根据全部或局部已知值，按研究区域预测数据的某种特定趋势来进行内插的方法,属统计方法的范畴。
在GA 模块中，有二种类型的多项式内插方法，即全局多项式内插和局部多项式内插。
前者多用于分析数据的全局趋势；后者则是使用多个平面来拟合整个研究区域，能表现出区域内局部变异的情况。
3.样条函数内插法样条函数是一个分段函数，进行一次拟合只有少数点拟合，同时保证曲线段连接处连续，这就意味着样条函数可以修改少数数据点配准而不必重新计算整条曲线。
样条函数的一些缺点是：样条内插的误差不能直接估算，同时在实践中要解决的问题是样条块的定义以及如何在三维空间中将这些“块”拼成复杂曲面,又不引入原始曲面中所没有的异常现象等问题。
4.克里格插值法克里格法是GIS 软件地理统计插值的重要组成部分。
这种方法充分吸收了地理统计的思想，认为任何在空间连续性变化的属性是非常不规则的，不能用简单的平滑数学函数进行模拟，可以用随机表面给予较恰当的描述。
这种连续性变化的空间属性称为“区域性变量”，可以描述象气压、高程及其它连续性变化的描述指标变量。
地理统计方法为空间插值提供了一种优化策略，即在插值过程中根据某种优化准则函数动态的决定变量的数值。
Kriging 插值方法着重于权重系数的确定，从而使内插函数处于最佳状态，即对给定点上的变量值提供最好的线性无偏估计。
gis基于点空间插值操作步骤
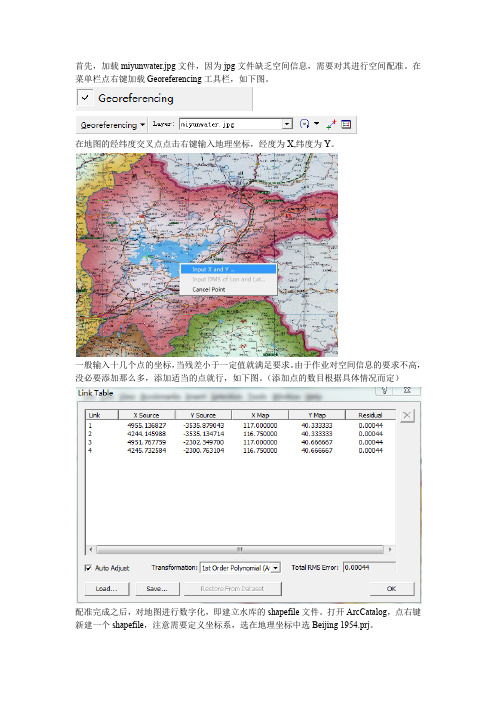
首先，加载miyunwater.jpg文件，因为jpg文件缺乏空间信息，需要对其进行空间配准。
在菜单栏点右键加载Georeferencing工具栏，如下图。
在地图的经纬度交叉点点击右键输入地理坐标，经度为X,纬度为Y。
一般输入十几个点的坐标，当残差小于一定值就满足要求。
由于作业对空间信息的要求不高，没必要添加那么多，添加适当的点就行，如下图。
（添加点的数目根据具体情况而定）配准完成之后，对地图进行数字化，即建立水库的shapefile文件。
打开ArcCatalog，点右键新建一个shapefile，注意需要定义坐标系，选在地理坐标中选Beijing 1954.prj。
Shp文件建立之后，添加到数据层中，打开editor工具，开始编辑。
选取草图工具，勾勒出密云水库的边界，最后画完后，切记要保存编辑，如下图。
然后再加载sampledata.xls，操作如下图，同样注意经度为X，纬度为Y，定义坐标系为beijing1954.prj，如下下图。
稍后将加载的点导成shp文件，如下图。
前一步的结果如下图，然后对两个shp文件定义投影坐标（这步可有可无，对插值结果无影响，具体方法是用project命令，选取投影坐标系高斯克里格，如果选用6度带，就是20带）。
定义好投影坐标之后即可对数据进行空间插值，首先需要加载Spatial Analyst工具栏如下图。
完成这步需要之前在tools-extension选项里勾选上Spatial Analyst。
进行插值之前，需要设置空间分析的范围。
点options选项，在extent里设置，因为是基于水库插值，所以设置same as layer “密云水库_project”。
范围设置之后进行插值，在Z value field中选N，也就是说是基于N这个字段进行插值。
效果如下图。
现在需要用水库的shp文件来裁剪插值的结果，命令为extract by mask，设置如下图。
效果如下图，设置不同颜色即可。
arcgis克里金插值等值线标注
arcgis克里金插值等值线标注摘要：1.ArcGIS克里金插值介绍2.克里金插值原理与应用3.等值线标注方法与步骤4.插值结果的可视化与分析正文：ArcGIS是一款强大的地理信息系统软件，其中克里金插值（Kriging Interpolation）是一种常用的空间数据插值方法。
本文将详细介绍ArcGIS克里金插值的原理、应用，以及如何进行等值线标注，最后对插值结果进行可视化和分析。
一、ArcGIS克里金插值介绍克里金插值是一种基于统计学的空间插值方法，它通过利用已知的样本点数据，估算未知的空间位置值。
ArcGIS中的克里金插值工具可以根据不同的数据类型和需求，生成不同类型的插值结果，如栅格数据、点数据等。
二、克里金插值原理与应用克里金插值原理主要基于变异函数理论和最小二乘法。
变异函数描述了空间数据在不同距离上的变化规律，而最小二乘法则用于求解最佳拟合参数。
在ArcGIS中，克里金插值应用于各种领域，如土壤侵蚀、矿产资源预测、气象数据重建等。
三、等值线标注方法与步骤1.准备数据：首先，需要准备好克里金插值所需的样本点数据和相应的属性值。
这些数据可以是栅格数据、点数据或线数据等。
2.创建表面：在ArcGIS中，利用克里金插值工具生成插值表面。
可以根据需求选择不同的插值类型，如普通克里金插值、简单克里金插值等。
3.提取等值线：利用ArcGIS的等值线提取工具，根据插值表面的数值范围和间隔，提取等值线。
4.标注等值线：在提取的等值线上添加标注，如数值、图例等。
可以通过ArcGIS的标注工具或Python脚本实现。
四、插值结果的可视化与分析1.插值结果可视化：利用ArcGIS的图层功能，将插值表面、等值线和标注等数据进行可视化展示。
2.插值结果分析：通过ArcGIS的属性查询、统计分析等功能，对插值结果进行进一步分析，如空间分布特征、趋势分析等。
总之，ArcGIS克里金插值是一种实用且广泛应用于地理信息系统领域的空间插值方法。
arcgis空间分布反距离插值
arcgis空间分布反距离插值
空间分布反距离插值（IDW）是一种基于离散空间点的插值方法，根据点之间的距离和权重，计算未知位置的值。
在ArcGIS中，可以通过使用IDW工具进行空间分布反距离插值。
以下是在ArcGIS中进行空间分布反距离插值的步骤：
1. 打开ArcMap或ArcGIS Pro，并加载包含点数据的图层。
2. 确定您要插值的字段。
在图层属性表中选择一个具有您想要插值的值的字段。
3. 在ArcToolbox中的Spatial Analyst Tools工具中，找到“Interpolation”工具集，然后选择“IDW”工具。
4. 在弹出的IDW工具对话框中，选择要进行插值的输入点图层。
5. 选择要插值的字段。
6. 选择输出栅格图层的位置和名称。
7. 可选：设置其他参数，如邻近点数、最大距离和幂。
8. 单击“OK”开始插值过程。
ArcGIS将根据所选的参数执行反距离插值，并将结果生成为栅格图层。
您可以使用栅格图层进行数据分析和空间分布分析。
请注意，插值结果的准确性和效果取决于所选参数和输入数据的分布。
在使用插值方法之前，建议对您的输入数据进行预处理和分析，以确保得到准确和可靠的插值结果。
arcgis插值步骤
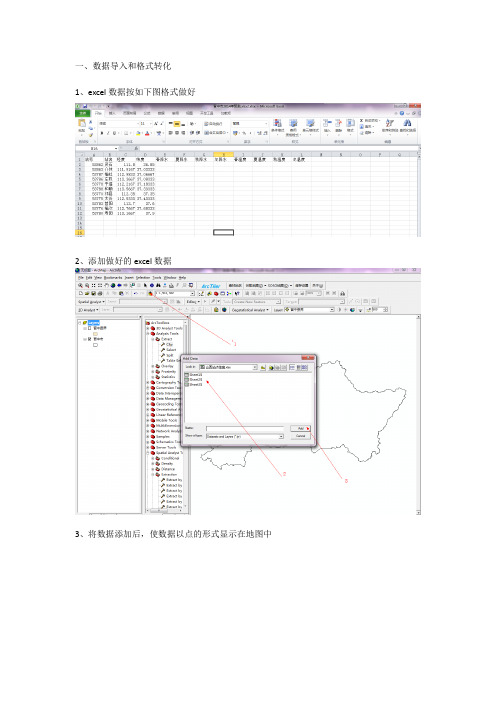
一、数据导入和格式转化
1、excel数据按如下图格式做好
2、添加做好的excel数据
3、将数据添加后，使数据以点的形式显示在地图中
在表上右键选Display XY
Data
4、X Fleld、Y Fleld按如下图选填好，点“确定”和“OK”
2
3
4
5、如图，在Sheet2$ Events文件上右键选Data---Export Data，并命名保存。
在弹出的对话框选“是”，将得到的点矢量数据
导入结果图
二、数据的插值
1、在工具箱中如图选择
2、批量插值：如图，在IDW上右键选择batch
3、点“加号”按钮增加处理行数，并如图填入要处理的数据，输入完成后点击“√”按钮，检查是否输入错误。
4、输入无错后，如下图步骤在General Settings和Raster Analysis Settings中点选作图范围“晋中市”，填完后点“OK”开始插值运行。
arcgis插值运算
arcgis插值运算【实用版】目录1.插值运算概述2.ArcGIS 插值运算方法2.1 空间插值2.2 统计插值2.3 样条插值2.4 普通插值2.5 三维插值3.插值运算的应用4.常见问题与解决方案正文一、插值运算概述插值运算是一种通过已知数据点来预测或估计未知数据点的方法，广泛应用于地理信息系统（GIS）和遥感领域。
其目的是在空间上或时间上对数据进行平滑或预测，以填充数据空白或扩展数据范围。
二、ArcGIS 插值运算方法1.空间插值空间插值是根据已知数据点的空间关系来预测未知数据点的方法，主要包括以下几种：- 线性插值：通过计算已知点之间的线性关系，预测未知点的值。
- 反距离权重法：根据已知点与预测点的距离，赋予已知点不同的权重，然后计算预测点的值。
- 样条插值：通过计算已知点之间的曲线关系，预测未知点的值。
2.统计插值统计插值是根据已知数据点的统计特征来预测未知数据点的方法，主要包括以下几种：- 普通插值：根据已知数据点的平均值、最大值、最小值等统计特征，预测未知点的值。
- 三维插值：在三维空间中，根据已知数据点的三维坐标和统计特征，预测未知点的值。
3.样条插值样条插值是一种通过计算已知数据点之间的样条函数来预测未知数据点的方法，可以很好地处理数据点的非线性关系。
4.普通插值普通插值是根据已知数据点的平均值、最大值、最小值等统计特征，预测未知点的值，适用于数据点分布较为均匀的情况。
5.三维插值三维插值是在三维空间中，根据已知数据点的三维坐标和统计特征，预测未知点的值，适用于处理立体空间数据的情况。
三、插值运算的应用插值运算在 GIS 领域有着广泛的应用，例如：- 地形分析：通过插值运算，可以生成连续的地形模型，用于地形分析和制图。
- 气象预测：通过插值运算，可以预测未来一段时间内的气象数据，用于气象预报和防灾减灾。
- 生态环境评价：通过插值运算，可以预测生态系统的变化趋势，用于生态环境评价和保护。
arcgis 克里金插值 实验步骤
arcgis 克里金插值实验步骤克里金插值是地理信息系统（GIS）中常用的一种插值方法，用于根据已知点的空间分布和属性值来推断未知点的属性值。
在ArcGIS软件中，克里金插值是一个强大的空间分析工具，可以帮助用户更好地理解空间数据的分布规律。
在进行克里金插值实验之前，首先需要准备一些必要的数据和工具。
下面是在ArcGIS中进行克里金插值实验的具体步骤：1. 打开ArcGIS软件，并加载要进行插值的数据。
这些数据可以是点数据、线数据或面数据，其中点数据最为常用。
确保数据的属性字段中包含有用于插值的数值字段。
2. 确定插值的参数设置。
在ArcGIS中，克里金插值的参数包括插值方法、搜索半径、插值权重等。
根据实际情况，选择合适的参数值进行插值。
3. 打开“空间分析”工具箱，在“插值”工具集中选择“克里金插值”工具。
在弹出的参数设置对话框中，选择要插值的数据图层、插值字段和输出栅格数据的保存位置。
4. 设置克里金插值的参数。
根据实际情况，设置插值方法（如简单克里金、普通克里金、泛克里金等）、搜索半径、插值权重等参数值。
5. 运行插值分析。
点击“运行”按钮，ArcGIS将根据所设置的参数值进行克里金插值分析，并生成插值结果。
在插值结果中，可以看到未知点的预测值和插值的插值误差。
6. 分析插值结果。
查看插值结果的插值图和插值误差图，分析插值的精度和可靠性。
根据需要，可以对插值结果进行进一步的处理和分析。
通过以上步骤，您可以在ArcGIS中进行克里金插值实验，并得到插值结果。
克里金插值是一种常用的空间插值方法，可以帮助您更好地理解地理数据的分布规律，为地理分析和决策提供有力的支持。
希望以上步骤对您有所帮助，祝您实验顺利！。
arcgis插值运算
arcgis插值运算摘要：一、ArcGIS插值运算概述1.插值运算定义2.ArcGIS中插值运算的重要性二、ArcGIS插值运算方法1.距离权重插值2.样条插值3.克里金插值4.插值结果的优化与调整三、插值运算在GIS应用案例1.地形分析2.气象数据预测3.环境监测与评估4.城市规划与管理四、ArcGIS插值运算实践技巧与注意事项1.数据准备与处理2.插值参数设置与优化3.结果输出与分析4.插值运算在实际应用中的困境与解决方法正文：ArcGIS插值运算是一种在地理信息系统（GIS）领域广泛应用的技术。
它通过对空间数据进行插值，从而实现对未知区域数据的估计和预测。
本文将从插值运算的定义、ArcGIS中插值运算的方法、实际应用案例以及实践技巧等方面进行详细阐述。
一、ArcGIS插值运算概述1.插值运算定义插值运算是一种通过已知数据点来估计未知数据点的方法。
在GIS领域，插值运算主要用于将离散的空间数据转换为连续的表面数据，以便进行进一步的分析与应用。
2.ArcGIS中插值运算的重要性ArcGIS作为一款强大的GIS软件，为用户提供了丰富的插值运算功能。
通过插值运算，用户可以方便地生成连续的地理表面，从而在地形分析、气象预测、环境监测等领域发挥重要作用。
二、ArcGIS插值运算方法1.距离权重插值距离权重插值是一种基于距离的插值方法。
它根据已知数据点与未知数据点之间的距离，对未知数据点进行估计。
在ArcGIS中，距离权重插值可通过Interpolation工具实现。
2.样条插值样条插值是一种基于分段多项式的插值方法。
它具有良好的局部性和光滑性，适用于规则或不规则的数据点分布。
在ArcGIS中，样条插值可通过Spline Interpolation工具实现。
3.克里金插值克里金插值是一种基于协方差矩阵的插值方法。
它考虑了数据点之间的空间相关性，适用于具有较强空间相关性的数据。
在ArcGIS中，克里金插值可通过Kriging Interpolation工具实现。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
GIS空间插值（局部插值方法）实习记录一、空间插值的概念和原理当我们需要做一幅某个区域的专题地图，或是对该区域进行详细研究的时候，必须具备研究区任一点的属性值，也就是连续的属性值。
但是，由于各种属性数据（如降水量、气温等）很难实施地面无缝观测，所以，我们能获取的往往是离散的属性数据。
例如本例，我们现有一幅山东省等降雨量图，但是最终目标是得到山东省降水量专题图（覆盖全省，统计完成后，各地均具有自己的降雨量属性）。
空间插值是指利用研究区已知数据来估算未知数据的过程，即将离散点的测量数据转换为连续的数据曲面。
利用空间插值，我们就可以通过离散的等降雨量线，来推算出山东省各地的降雨量了。
二、空间插值的几种方法及本次实习采用的原理和方法–整体插值方法»边界内插方法»趋势面分析»变换函数插值–局部分块插值方法»自然邻域法»移动平均插值方法：反距离权重插值»样条函数插值法（薄板样条和张力样条法）»空间自协方差最佳插值方法：克里金插值■局部插值方法的控制点个数与控制点选择问题局部插值方法用一组已知数据点（我们将其称为控制点）样本来估算待插值点（未知点）的值，因此控制点对该方法十分重要。
为此，第一要注意的是控制点的个数。
控制点的个数与估算结果精确程度的关系取决于控制点的分布与待插值点的关系以及控制点的空间自相关程度。
为了获取更精确的插值结果，我们需要着重考虑上述两点因素（横线所示）。
第二需要注意的是怎样选择控制点。
一种方法是用离估算点最近的点作为控制点；另一种方法是通过半径来选择控制点，半径的大小必须根据控制点的分布来调整。
S6、按照不同方法进行空间插值，并比较各自优劣打开ArcToolbox——Spatial Analyst 工具——插值，打开插值方法列表，如下图：A、采用反距离权重法（IDW）对降水量数据进行插值：反距离权重法的特点是按照距离待插值点的远近核定已知数据点的权重，从而对待插值点进行插值的过程。
一个已知数据点距离待插值点越远，权重就越低，它的值对待插值点的影响就越小。
影响的程度用点之间距离乘方的倒数表示，通过“power”设置乘方。
乘方为1意味着点之间数值变化率为恒定，称为线性插值法；乘方为2或更高则意味着越靠近已知点，数值的变化率越大。
这种插值方法的优点是对于数据分布均匀的区域，插值效果好；缺点是在数据分布不均地区插值容易出现小的封闭等值线（“球状突起”）和因数据缺乏而产生的不规则等值线。
双击ArcToolbox里面的“反距离权重法”，输入点要素选择“prec”，Z值字段选择“prec”，输出像元大小选择1000。
点击确定，效果如下图：由图像可以看出，山东省内陆地区由于布点均匀，插值效果比较好；但是沿海地区出现两条“球状弧线”，如下图：B、采用克里金法对降水量数据进行插值：克里金插值与IDW插值的区别在于权重的选择。
IDW仅仅是将距离的倒数作为权重，而克里金考虑了空间相关性的问题。
克里金法首先将每两个点进行配对，这样就能产生一个以两点之间距离为自变量的函数。
对于这种方法，原始的输入点可能会发生变化。
在数据点多时，内插的结果可信度较高。
1、双击ArcToolbox里面的“克里金法”，输入点要素选择“prec”，Z值字段选择“prec”，半变异函数属性中，设置克里金方法为普通克里金（Ordinary Krigging，OK），半变异模型选择球面（Sphere）；输出栅格命名为“ok_sphere”，输出像元大小选择1000。
点击确定，效果如下图：发现，局部存在比较明显的“锯齿现象”，如图：2、同样是克里金插值方法，本次采用线形普通克里金插值，效果如图：效果比较理想。
对于各种方法，依次展示如下：高斯：指数：圆：泛克里金——与一次漂移函数成线性关系：泛克里金——与二次漂移函数成线性关系：3、依次尝试各种克里金插值法，对比得出：克里金方法半变异模型插值效果普通克里金球面在数据点分布稀疏地区，锯齿现象和撕裂现象明显线性结合了球面方法和指数方法的优点，插值效果比较理想高斯数据范围被剧烈拉伸，不能很好地反映降水量分布指数斑块状撕裂现象基本避免了，但是锯齿现象仍旧明显圆插值效果和线性类似，比较理想泛克里金与一次漂移函数成线性关系中部插值效果比较理想，但边缘地带出现严重的数据误差与二次漂移函数呈线性关系数据拉伸剧烈；区分度小C、采用薄板样条函数法对降水量数据进行插值：薄板样条函数法使用样条函数来对空间点进行插值，它有两个基本条件：a.表面必须完全通过控制点（样本点）b.使所有点的坡度变化最小，换句话说，表面的二阶曲率是最小的。
该方法适用于高程面、水位面、气候数据（如平均降水量）的插值。
有一个缺点是，在数据贫乏的地区坡度较大，经常涉及如同过伸的情况。
样条函数插值分为两种，规则样条函数和张力样条函数。
下面分别进行操作：1、双击ArcToolbox里面的“样条函数法”，输入点要素选择“prec”，Z值字段选择“prec”，样条函数类型选择：REGULARIZED（规则样条函数），输出像元大小选择1000。
点击确定，效果如下图：观察发现，规则样条函数也是对数据进行了一定程度的拉伸，但是拉伸幅度不大，拉伸后的像元值介于99—1108之间（相比之下，普通克里金的高斯方法和泛克里金的与二次漂移函数呈线性关系方法拉伸幅度分别达到了-597—4903、-5347—4292），可以说是拉伸范围适宜；在山东省内部区域插值分布比上述所有方法都要更加均匀一些；虽然在边缘地带出现一定的数据突兀（如下图，色调偏白的区域年平均降雨量只有200mm以下），但总体效果基本上能令人满意。
2、双击ArcToolbox里面的“样条函数法”，输入点要素选择“prec”，Z值字段选择“prec”，样条函数类型选择：TENSION（张力样条函数），输出像元大小选择1000。
点击确定，效果如下图：可见得，张力样条插值不存在数据过拉伸现象，插值平滑且无突兀地带，插值效果非常好。
D、采用自然邻域法对降水量数据进行插值：这种方法的原理是构建voronoi多边形，也就是泰森多边形。
首先将所有的已知数据点构建一组voronoi多边形，然后将待插值点也构建一组voronoi多边形，这样后一组多边形与原多边形有很多相交的地方。
接下来，根据每一块的面积按比例设置权重，这样就能求得待插值点的值了。
双击ArcToolbox里面的“自然邻域法”，输入点要素选择“prec”，Z值字段选择“prec”，输出像元大小选择1000。
点击确定，效果如下图：可见，该方法在有数据的区域，插值效果非常好，优于上述各种方法；但是由于自然邻域法是基于邻近点的算法，所以图上山东省轮廓边缘（如鲁西北、威海荣成成山头附近）出现数据空白区，不符合最后成图要求。
S7、对插值效果最好的一种方法，调整插值参数经过上述比较，得出插值效果最理想的是薄板张力样条插值方法，接下来调整搜索半径，比较在不同的插值半径下不同的效果。
1、双击ArcToolbox里面的“样条函数法”，输入点要素选择“prec”，Z值字段选择“prec”，样条函数类型选择：TENSION（张力样条函数），输出像元大小选择1000，权重值填0.1，点数填12。
文件名设为ten_A_12。
点击确定，效果如下图：只改变权重值，不改变其他参数，重新尝试。
权重值填2，点数12。
确定，效果如下图：再次改变权重值，不改变其他参数。
权重值填12，点数填12。
点击确定，效果如下图：通过对比，可得：对薄板张力样条插值方法来说，在选取同样多的控制点的前提下，权重越小，生成的表面越光滑。
例如，权重0.1的效果＞权重2的效果＞优于权重12的效果。
2、同理，对比在同一权重值下，控制点数目不同所产生的效果差异：在权重为0.1的前提下，我们设置控制点数量为5个、30个，跟控制点12个的作比较：■5个控制点：■30个控制点：可见得，控制点5个和30个的情况均不如12个的时候效果好，也就是说，控制点不一定要太多，也不一定要少，要结合已知数据点的个数和分布来判定最佳方案。
因此我们最终选择权重0.1、12个控制点的图像进行插值。
S8、制作山东省县域年平均降水量地图1、首先制作一个山东省轮廓图。
保存一份山东省县界图的副本，命名为sd.shp，鼠标点击编辑器——开始编辑，将所有要素选中，点击编辑器下拉菜单中的“合并”，生成的文件就是山东省轮廓范围了；2、利用山东省轮廓范围矢量图对ten_A_12栅格图进行裁剪。
打开数据管理工具——栅格——栅格处理——裁剪，弹出“裁剪”对话框。
输入栅格选择ten_A_12，输出范围选择sd，在“将输入要素用于裁剪几何”处打对勾，目的是为了按照山东省的边界来裁剪降水量图（否则，默认是按照矢量多变性的最小外接矩形来裁剪栅格图像）。
如下图：3、现在生成了一幅灰度图像。
我们还是按照颜色对其进行分类：鼠标右键点击sd_prec，选择属性——符号系统——已分类，弹出计算直方图对话框，询问是否计算直方图，选择“是”。
目前最大值是835，最小值是490，数据跨度为345，因此我们按照每25mm为一个降水量带，对图像进行分类制图。
345÷25+1≈15，因此我们将分类设为15档，色带选择蓝色调，如图：4、鼠标右键点击sd_county——属性——标注，勾选“标注此图层中的要素”，使县市的名称显示在地图中；5、按照地图符号及视觉特征实现的要求，对地图进行设计和整饰，最终成图如下：（注：可编辑下载，若有不当之处，请指正，谢谢!）。