新人教七年级下第5章自主学习达标检测(§5.3~§5.4)
人教版七年级数学下册第五章测试题(含答案)

农村管理创新探讨随着城市化的推进和农村经济的快速发展,农村管理面临着新的挑战和需求。
如何利用现代科技和管理理念,提升农村管理水平,助力农村发展,成为亟待解决的问题。
本文将从不同角度出发,探讨农村管理的创新。
一、数字农村建设随着信息技术的迅猛发展,数字化已经成为农村管理的关键词之一。
数字农村建设将现代化技术引入到农村,实现农村基础设施的信息化和智能化。
通过建设农村信息化平台,实现数据的互通共享,可以提高资源的配置效率,并为农村发展提供积极支持。
二、贫困农村的创新案例在农村管理创新的过程中,贫困地区的农村发展是重点和难点。
为了解决贫困问题,一些地方政府和社会组织提出了一些创新案例。
例如,通过发展特色农业和乡村旅游,传统贫困地区的农民可以增加收入。
此外,推动农民参与农产品加工和电商平台的建设,也为贫困地区农民创造了更多就业机会。
三、农村土地管理农村土地管理一直是一个复杂而重要的问题。
传统的土地占有权和承包权制度已经无法满足现代农村管理的需求。
一些地方已经开始尝试土地流转和农地集体经营的改革,以适应现代产业发展的需求。
改革可以通过确保农民权益和保护农村环境等方面,推动农村土地资源的更加合理利用。
四、农村金融服务创新传统金融服务往往难以满足农村的需求,例如小额贷款和农民保险等。
现代金融服务的创新可以提供更多种类的金融产品和服务,满足农村发展的多样化需求。
例如,一些地方政府和金融机构合作,成立农村金融合作社,为农民提供方便快捷的金融服务。
五、农村社会组织建设农村社会组织是促进农村管理创新的重要力量。
传统的村民自治组织在一些地方存在效率低下和权力滥用等问题。
为了解决这些问题,一些地方政府开始鼓励和支持农村社会组织的建设。
通过培育和引导有效的农村社会组织,可以提高村民的自治能力,推动农村管理的创新。
六、农村教育创新农村教育是农村人才培养和农村社会发展的重要基础。
农村教育普及和教师素质提升一直是农村管理创新的重要方向。
新人教版七年级下第五章测试题

西溪中学七年级数学第五章测试题班级:_____________ 姓名:_____________ 成绩:_____________一、选择题(每小题3分,共30分)1.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )A.0 B.1 C.2 D.3121212122.下列说法不正确的是( )A.同位角相等,两直线平行 B.两直线平行,内错角相等C.内错角相等,两直线平行 D.同旁内角互佘,两直线平行3.如果两条平行线被第三条直线所截,那么同位角的平分线( )A.互相平行 B.互相垂直 C.交角是锐角 D.交角是钝角4.同一平面内的四条不重合的直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( ) A.a∥b B.b⊥d C.a⊥d D.b∥c5.经过直线外一点,有几条直线和已知直线平行 ( )A.0条B.1条C.2条D.3条6.如图,若m∥n,∠1 = 105°,则∠2 =( )A.55° B.60° C.65° D.75°1 2m n7.下列说法中正确的是( )A.有且只有一条直线垂直于已知直线。
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
C.互相垂直的两条直线一定相交。
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短线段的长是3cm,则点A 到直线c的距离是3cm。
8.如图,a∥b,∠2是∠1的3倍,则∠2等于( )A.45°B.90°C.135°D.150°(第8题图) (第9题图)9.如图所示,已知∠1=∠2,要使∠3=∠4,则需( )A.∠1=∠3 B. ∠2=∠4 C. ∠1=∠3 D.AB∥CD10. 三条直线两两相交于同一点时,对顶角有m对,交于不同三点时,对顶角有n对,则m与n的关系是( )A.m = n B.m>n C.m<n D.m + n = 10二、填空题(每小题3分,共30分)11.两个角的两边两两互相平行,且一个角的12等于另一个角的13,则这两个角的度数分别为。
人教版七年级初一数学下学期第五章 相交线与平行线单元自检题学能测试试题
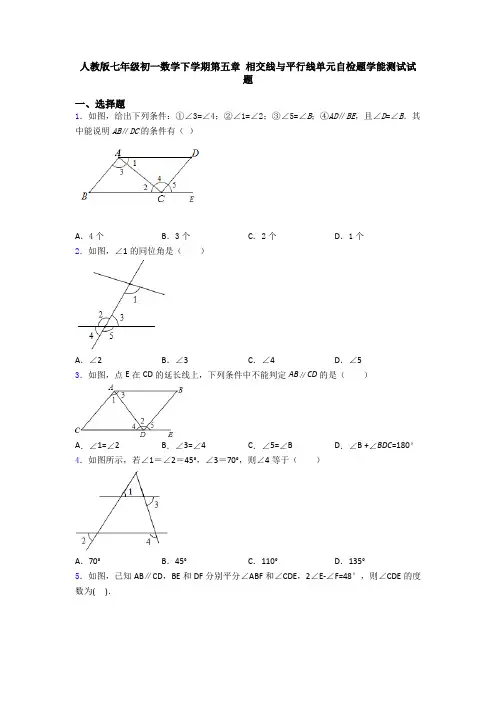
人教版七年级初一数学下学期第五章相交线与平行线单元自检题学能测试试题一、选择题1.如图,给出下列条件:①∠3=∠4;②∠1=∠2;③∠5=∠B;④AD∥BE,且∠D=∠B.其中能说明AB∥DC的条件有()A.4个B.3个C.2个D.1个2.如图,∠1的同位角是()A.∠2 B.∠3 C.∠4 D.∠53.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是()A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B +∠BDC=180°4.如图所示,若∠1=∠2=45°,∠3=70°,则∠4等于()A.70°B.45°C.110°D.135°5.如图,已知AB∥CD,BE和DF分别平分∠ABF和∠CDE,2∠E-∠F=48°,则∠CDE的度数为( ).A .16°B .32°C .48°D .64°6.两条平行线被第三条直线所截,则下列说法错误的是( )A .一对邻补角的平分线互相垂直B .一对同位角的平分线互相平行C .一对内错角的平分线互相平行D .一对同旁内角的平分线互相平行7.下列命题是假命题的有( )①邻补角相等;②对顶角相等;③同位角相等;④内错角相等.A .1个B .2个C .3个D .4个8.给出下列说法:(1)两条直线被第三条直线所截,同位角相等;(2)不相等的两个角不是同位角;(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(4)从直线外一点到这条直线的垂线段,叫做该点到直线的距离;(5)过一点作已知直线的平行线,有且只有一条.其中真命题的有( )A .0个B .1个C .2个D .3个9.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( ) A .∠1=50°,∠2=40°B .∠1=50°,∠2=50°C .∠1=∠2=45°D .∠1=40°,∠2=40° 10.已知,//AB CD ,且2CD AB ,ABE △和CDE △的面积分别为2和8,则ACE △的面积是( )A .3B .4C .5D .6二、填空题11.如图,现给出下列条件:①∠1=∠2,②∠B =∠5,③∠3=∠4,④∠5=∠D ,⑤∠B+∠BCD =180°,其中能够得到AD ∥BC 的条件是______(填序号);能够得到AB ∥CD 的条件是_______.(填序号)12.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为_______.13.平面内不过同一点的n 条直线两两相交,它们交点个数记作n a ,并且规定10a =,则2a =__________,1n n a a --=____________.14.如图,在△ABC 中,6BC cm =,将△ABC 以每秒2cm 的速度沿BC 所在直线向右平移,所得图形对应为△DEF ,设平移时间为t 秒,若要使2AD CE =成立,则t 的值为_____秒.15.如图,已知AB ∥CD,∠EAF =14∠EAB,∠ECF=14∠ECD ,则∠AFC 与∠AEC 之间的数量关系是_____________________________16.如图①:MA 1∥NA 2,图②:MA11NA 3,图③:MA 1∥NA 4,图④:MA 1∥NA 5,……,则第n 个图中的∠A 1+∠A 2+∠A 3+…+∠A n+1______.(用含n 的代数式表示)17.如图,直线a ∥b ,且∠1=28°,∠2=50°,则∠ABC =_______.18.若∠A 与∠B 的两边分别平行,且∠A 比∠B 的3倍少40°,则∠B =_____度.19.一副直角三角尺叠放如图 1 所示,现将 45°的三角尺ADE 固定不动,将含 30°的三角尺 ABC 绕顶点 A 顺时针转动(旋转角不超过 180 度),使两块三角尺至少有一组边互相平行.如图 2:当∠BAD=15°时,BC ∥DE .则∠BAD (0°<∠BAD <180°)其它所有可能符合条件的度数为________.20.如图,AB ∥CD ,∠B =75°,∠E =27°,则∠D 的度数为_____.三、解答题21.已知:直线//AB CD ,点E ,F 分别在直线AB ,CD 上,点M 为两平行线内部一点. (1)如图1,∠AEM ,∠M ,∠CFM 的数量关系为________;(直接写出答案)(2)如图2,∠MEB 和∠MFD 的角平分线交于点N ,若∠EMF 等于130°,求∠ENF 的度数;(3)如图3,点G 为直线CD 上一点,延长GM 交直线AB 于点Q ,点P 为MG 上一点,射线PF 、EH 相交于点H ,满足13PFG MFG ∠=∠,13BEH BEM ∠=∠,设∠EMF =α,求∠H 的度数(用含α的代数式表示).22.如图 1,直线GH 分别交,AB CD 于点 ,E F (点F 在点E 的右侧),若12180︒∠+∠= (1)求证://AB CD ;(2)如图2所示,点M N 、在,AB CD 之间,且位于,E F 的异侧,连MN , 若23M N ∠=∠,则,,AEM NFD N ∠∠∠三个角之间存在何种数量关系,并说明理由.(3)如图 3 所示,点M 在线段EF 上,点N 在直线CD 的下方,点P 是直线AB 上一点(在E 的左侧),连接,,MP PN NF ,若2,2MPN MPB NFH HFD ∠=∠∠=∠,则请直接写出PMH ∠与N ∠之间的数量23.已知,90AOB ︒∠=,点C 在射线OA 上,//CD OE .(1)如图 1,若120OCD ︒∠=,求∠BOE 的度数;(2)把“90AOB ︒∠=°”改为“120AOB ︒∠=”,射线OE 沿射线OB 平移,得到O E ',其它条件不变(如 图 2 所示),探究,OCD BO E '∠∠ 的数量关系;(3)在(2)的条件下,作PO OB '⊥,垂足为O ' ,与OCD ∠ 的角平分线CP 交于点P ,若BO E α'∠= , 用含 α 的式子表示CPO '∠(直接写出答案).24.问题情境:我们知道,“两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补”,所以在某些探究性问题中通过“构造平行线”可以起到转化的作用.已知三角板ABC 中,60,30,90BAC B C ∠=∠=︒∠=︒︒,长方形DEFG 中,DE GF .问题初探:(1)如图(1),若将三角板ABC 的顶点A 放在长方形的边GF 上,BC 与DE 相交于点M ,AB DE ⊥于点N ,求EMC ∠的度数.分析:过点C 作CH GF ∥,则有CH DE ∥,从而得,CAF HCA EMC MCH ∠=∠∠=∠,从而可以求得EMC ∠的度数.由分析得,请你直接写出:CAF ∠的度数为____________,EMC ∠的度数为___________.类比再探:(2)若将三角板ABC 按图(2)所示方式摆放(AB 与DE 不垂直),请你猜想写出CAF ∠与EMC ∠的数量关系,并说明理由.25.问题情境(1)如图①,已知360B E D ∠+∠+∠=︒,试探究直线AB 与CD 有怎样的位置关系?并说明理由.小明给出下面正确的解法:直线AB 与CD 的位置关系是//AB CD .理由如下:过点E 作//EF AB (如图②所示)所以180B BEF ∠+∠=︒(依据1)因为360B BED D ∠+∠+∠=︒(已知)所以360B BEF FED D ∠+∠+∠+∠=︒所以180FED D ∠+∠=︒所以//EF CD (依据2)因为//EF AB所以//AB CD (依据3)交流反思上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?“依据1”:________________________________;“依据2”:________________________________;“依据3”:________________________________.类比探究(2)如图,当B 、E ∠、F ∠、D ∠满足条件________时,有//AB CD .拓展延伸(3)如图,当B 、E ∠、F ∠、D ∠满足条件_________时,有//AB CD .26.直线AB ∥CD ,点M ,N 分别在直线AB ,CD 上,点E 为平面内一点.(1)如图①,探究∠AME ,∠MEN ,∠ENC 的数量关系,并说明理由;(2)如图②,∠AME =30°,EF 平分∠MEN ,NP 平分∠ENC ,EQ ∥NP ,求∠FEQ 的度数; (3)如图③,点G 为CD 上一点,∠AMN =m ∠EMN ,∠GEK =m ∠GEM ,EH ∥MN 交AB 于点H ,直接写出∠GEK ,∠BMN ,∠GEH 之间的数量关系(用含m 的式子表示).【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【详解】解:34∠∠=//AB CD ∴,①正确;12∠=∠//AD BC ∴,②不正确;5B∠=∠AB CD∴,③正确;//AD BE//∴∠=∠5D∠=∠B D∴∠=∠B5AB CD∴,④正确;//综上所述,①、③、④正确,故选B.2.D解析:D【分析】根据同位角定义可得答案.【详解】解:解:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角,根据定义,结合图形,∠1的同位角是∠5.故选:D.【点睛】本题考查同位角的定义,解题关键是熟练理解同位角的定义,本题属于基础题型.3.A解析:A【分析】运用平行线的判定方法进行判定即可.【详解】解:选项A中,∠1=∠2,只可以判定AC//BD(内错角相等,两直线平行),所以A错误;选项B中,∠3=∠4,可以判定AB//CD(内错角相等,两直线平行),所以正确;选项C中,∠5=∠B,AB//CD(内错角相等,两直线平行),所以正确;选项D中,∠B +∠BDC=180°,可以判定AB//CD(同旁内角互补,两直线平行),所以正确;故答案为A.【点睛】本题考查平行的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.4.C解析:C【分析】根据对顶角的性质可得∠1=∠5,再由等量代换得∠2=∠5,即可得到到a∥b,利用两直线平行同旁内角互补可得∠3+∠4=180°,最后根据∠3的度数即可求出∠4的度数.【详解】解:∵∠1与∠5是对顶角,∴∠1=∠2=∠5=45°,∴a∥b,∴∠3+∠6=180°,∵∠3=70°,∴∠4=∠6=110°.故答案为C.【点睛】本题考查了对顶角的性质、平行线的性质及判定,其中掌握平行线的性质和判定是解答本题的关键.5.B解析:B【解析】【分析】已知BE和DF分别平分∠ABF和∠CDE,根据角平分线分定义可得∠ABE=12∠ABF,∠CDF=12∠CDE;过点E作EM//AB,点F作FN//AB,即可得////AB CD EM//FN,由平行线的性质可得∠ABE=∠BEM,∠MED=∠EDC,∠ABF=∠BFN,∠CDF=∠DFN,由此可得∠BED=∠BEM+∠DEM=∠ABE+∠CDE=12∠ABF+∠CDE,∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +12∠CDE,又因2∠BED-∠BFD=48°,即可得2(12∠ABF+∠CDE)-(∠ABF +12∠CDE)=48°,由此即可求得∠CDE=32°.【详解】∵BE和DF分别平分∠ABF和∠CDE,∴∠ABE=12∠ABF,∠CDF=12∠CDE,过点E作EM//AB,点F作FN//AB,∵//AB CD,∴////AB CD EM//FN,∴∠ABE=∠BEM,∠MED=∠EDC,∠ABF=∠BFN,∠CDF=∠DFN,∴∠BED=∠BEM+∠DEM=∠ABE+∠CDE=12∠ABF+∠CDE,∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +12∠CDE,∵2∠BED-∠BFD=48°,∴2(12∠ABF+∠CDE)-(∠ABF +12∠CDE)=48°,∴∠CDE=32°.故选B.【点睛】本题考查了平行线的性质,根据平行线的性质确定有关角之间的关系是解决问题的关键. 6.D解析:D【解析】试题分析:A、两条平行线被第三条直线所截,一对邻补角的平分线互相垂直,故本选项正确;B、两条平行线被第三条直线所截,同位角的平分线互相平行,故本选项正确;C、两条平行线被第三条直线所截,内错角的平分线互相平行,故本选项正确;D、两条平行线被第三条直线所截,同旁内角的平分线互相垂直,故本选项错误;故选:D.7.C解析:C【解析】试题分析:根据命题的正确与否,直接可知:邻补角相加和为180°,不一定相等,故①是假命题;根据对顶角相等的性质,可知②是真命题;根据平行线的性质,两直线平行,同位角相等,可知③是假命题;根据平行线的性质,两直线平行,内错角相等,可知④是假命题.故选C.8.B解析:B【解析】试题分析:根据两平行线被第三条直线所截,同位角相等,故(1)不正确;同位角不一定相等,只有在两直线平行时,同位角相等,故(2)不正确;平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交,故(3)正确; 从直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离,故(4)不正确; 过直线外一点作已知直线的平行线,有且只有一条,故(5)不正确.故选B.9.C解析:C【分析】能说明是假命题的反例就是能满足已知条件,但不满足结论的例子.【详解】A 、满足条件∠1+∠2=90°,也满足结论∠1≠∠2,故A 选项错误;B 、不满足条件,故B 选项错误;C 、满足条件,不满足结论,故C 选项正确;D 、不满足条件,也不满足结论,故D 选项错误.故选:C .【点睛】此题考查了命题与定理的知识,理解能说明它是假命题的反例的含义是解决本题的关键. 10.B解析:B【分析】利用平行线间的距离相等可知ABC 与ACD △的高相等,底边之比等于面积之比,设ACE △的面积为x ,建立方程即可求解.【详解】∵//AB CD∴ABC 与ACD △的高相等∵2CD AB =∴=2ACD ABC S S设ACE △的面积为x ,则=8+=+ACD CDE ACE SS S x ,=2+=+ABC ABE ACE S S S x ∴()822+=+x x解得4x =∴=4ACE S故选B .【点睛】本题考查平行线间的距离问题,由平行线间的距离相等得到两三角形的高相等,从而建立方程是解题的关键.二、填空题11.①④ ②③⑤【分析】同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断即可.【详解】解:∵①∠1=∠2,∴AD∥BC;②∵∠B=∠5,解析:①④ ②③⑤【分析】同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断即可.【详解】解:∵①∠1=∠2,∴AD∥BC;②∵∠B=∠5,∴AB∥DC;③∵∠3=∠4,∴AB∥CD;④∵∠5=∠D,∴AD∥BC;⑤∵∠B+∠BCD=180°,∴AB∥CD,∴能够得到AD∥BC的条件是①④,能够得到AB∥CD的条件是②③⑤,故答案为①④,②③⑤.【点睛】本题考查的是平行线的判定,熟知同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解答此题的关键.12.或【分析】由两角的两边互相平行可得出两角相等或互补,再由题意,其中一个角比另一个角的3倍少,可得出答案.【详解】解:设为x,则为,若两角互补,则,解得,;若两角相等,则,解得,.故答案解析:125︒或20︒【分析】由两角的两边互相平行可得出两角相等或互补,再由题意,其中一个角比另一个角的3倍少40︒,可得出答案.【详解】解:设β∠为x ,则α∠为340x -︒,若两角互补,则340180x x +-︒=︒,解得55x =︒,125α∠=︒;若两角相等,则340x x =-︒,解得20x =︒,20α∠=︒.故答案为:125︒或20︒.【点睛】本题考查了平行线的性质,解题的关键是注意若∠α与∠β的两边分别平行,即可得∠α与∠β相等或互补,注意方程思想与分类讨论思想的应用.13.【分析】条直线相交只有一个交点,条直线相交,交点数是,条直线相交,交点数是,即,可写出, 的解.【详解】解:求平面内不过同一点的条直线两两相交的交点个数,可由简入繁, 当2条直线相交时,交点解析:1n -【分析】2条直线相交只有一个交点,3条直线相交,交点数是12+,n 条直线相交,交点数是123(1)n ++++-,即1123(1)(1)2n a n n n =++++-=-,可写出2a , 1n n a a --的解.【详解】解:求平面内不过同一点的n 条直线两两相交的交点个数,可由简入繁,当2条直线相交时,交点数只有一个;当3条直线相交时,交点数为两条时的数量+第3条直线与前两条的交点2个,即交点数是12+;同理,可以推导当n 条直线相交时,交点数是123(1)n ++++-,即1123(1)(1)2n a n n n =++++-=-, 212(21)12a ∴=⨯⨯-=, 111(1)(1)(2)122n n a a n n n n n -∴-=----=-,n .本题的答案为:1,1【点睛】本题考查了平面内直线两两相交交点数的计算,涉及到一种很重要的数学方法数学归纳法的初步应用接触,此方法在推导证明中比较常用.14.2或6.【解析】【分析】分两种情况:(1)当点E在C的左边时;(2)当点E在C的右边时.画出相应的图形,根据平移的性质,可得AD=BE,再根据AD=2CE,可得方程,解方程即可求解.【详解】解析:2或6.【解析】【分析】分两种情况:(1)当点E在C的左边时;(2)当点E在C的右边时.画出相应的图形,根据平移的性质,可得AD=BE,再根据AD=2CE,可得方程,解方程即可求解.【详解】解:分两种情况:(1)当点E在C的左边时,如图根据图形可得:线段BE和AD的长度即是平移的距离,则AD=BE,设AD=2tcm,则CE=tcm,依题意有2t+t=6,解得t=2.(2)当点E在C的右边时,如图根据图形可得:线段BE和AD的长度即是平移的距离,则AD=BE,设AD=2tcm,则CE=tcm,依题意有2t-t=6,解得t=6.故答案为2或6.【点睛】本题考查了平移的性质,解题的关键是理解平移的方向,由图形判断平移的方向和距离.注意分类讨论.15.4∠AFC=3∠AEC【解析】【分析】连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=18解析:4∠AFC=3∠AEC【解析】【分析】连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=180°-(4x°+4y°),求出∠AEC=4(x°+y°),∠AFC═3(x°+y°),即可得出答案.【详解】连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,∵AB∥CD,∴∠BAC+∠ACD=180°,∴∠CAE+4x°+∠ACE+4y°=180°,∴∠CAE+∠ACE=180°-(4x°+4y°),∠FAC+∠FCA=180°-(3x°+3y°),∴∠AEC=180°-(∠CAE+∠ACE)=180°-[180°-(4x°+4y°)]=4x°+4y°=4(x°+y°),∠AFC=180°-(∠FAC+∠FCA)=180°-[180°-(3x°+3y°)]=3x°+3y°=3(x°+y°),∴∠AFC=34∠AEC,即:4∠AFC=3∠AEC,故正确答案为:4∠AFC=3∠AEC.【点睛】本题考查了平行线性质和三角形内角和定理的应用,注意:两直线平行,同旁内角互补.16.【解析】分析:分别求出图①、图②、图③中,这些角的和,探究规律后,理由规律解决问题即可.详解:如图①中,∠A1+∠A2=180∘=1×180∘,如图②中,∠A1+∠A2+∠A3=360∘=2解析:n180︒【解析】分析:分别求出图①、图②、图③中,这些角的和,探究规律后,理由规律解决问题即可.详解:如图①中,∠A1+∠A2=180∘=1×180∘,如图②中,∠A1+∠A2+∠A3=360∘=2×180∘,如图③中,∠A1+∠A2+∠A3+∠A4=540∘=3×180∘,…,第n个图,∠A1+∠A2+∠A3+…+∠A n+1学会从=n180︒,故答案为180n︒.点睛:平行线的性质.17.78°【解析】解:过点B作BE∥a,∵a∥b,∴a∥b∥BE,∴∠1=∠3=28°,∠2=∠4=50°,∴∠ABC=∠3+∠4=78°.故答案为:78°.点睛:此题考查了平行线的性质:两直线解析:78°【解析】解:过点B作BE∥a,∵a∥b,∴a∥b∥BE,∴∠1=∠3=28°,∠2=∠4=50°,∴∠ABC=∠3+∠4=78°.故答案为:78°.点睛:此题考查了平行线的性质:两直线平行,内错角相等.解此题的关键是辅助线的作法.18.55或20【分析】根据平行线性质得出∠A+∠B=180°①,∠A=∠B②,求出∠A=3∠B﹣40°③,把③分别代入①②求出即可.【详解】解:∵∠A与∠B的两边分别平行,∴∠A+∠B=180解析:55或20【分析】根据平行线性质得出∠A+∠B=180°①,∠A=∠B②,求出∠A=3∠B﹣40°③,把③分别代入①②求出即可.【详解】解:∵∠A与∠B的两边分别平行,∴∠A+∠B=180°①,∠A=∠B②,∵∠A比∠B的3倍少40°,∴∠A=3∠B﹣40°③,把③代入①得:3∠B﹣40°+∠B=180°,∠B=55°,把③代入②得:3∠B﹣40°=∠B,∠B=20°,故答案为:55或20.【点睛】本题考查平行线的性质,解题的关键是掌握由∠A和∠B的两边分别平行,即可得∠A =∠B或∠A+∠B=180°,注意分类讨论思想的应用.19.45°,60°,105°,135°.【解析】分析:根据题意画出图形,再由平行线的判定定理即可得出结论.详解:如图,当AC∥DE时,∠BAD=∠DAE=45°;当BC∥AD时,∠DAE=∠解析:45°,60°,105°,135°.【解析】分析:根据题意画出图形,再由平行线的判定定理即可得出结论.详解:如图,当AC∥DE时,∠BAD=∠DAE=45°;当BC ∥AD 时,∠DAE =∠B =60°;当BC ∥AE 时,∵∠EAB =∠B =60°,∴∠BAD =∠DAE +∠EAB =45°+60°=105°;当AB ∥DE 时,∵∠E =∠EAB =90°,∴∠BAD =∠DAE +∠EAB =45°+90°=135°.故答案为45°,60°,105°,135°.点睛:本题考查了平行线的判定与性质.要证明两直线平行,需使其所构成的同位角、内错角相等(或同旁内角是否互补).20.48°【分析】将BE 与CD 交点记为点F ,由两直线平行同位角相等得出∠EFC 度数,再利用三角形外角的性质可得答案.【详解】解:如图所示,将BE 与CD 交点记为点F ,∵AB ∥CD ,∠B =75°解析:48°【分析】将BE 与CD 交点记为点F ,由两直线平行同位角相等得出∠EFC 度数,再利用三角形外角的性质可得答案.【详解】解:如图所示,将BE 与CD 交点记为点F ,∵AB ∥CD ,∠B =75°,∴∠EFC =∠B =75°,又∵∠EFC =∠D +∠E ,且∠E =27°,∴∠D =∠EFC ﹣∠E =75°﹣27°=48°,故答案为:48°.【点睛】本题考查平行线的性质和三角形外角性质,解题的关键是掌握两直线平行,同位角相等这一性质.三、解答题21.(1)M AEM CFM ∠=∠+∠;(2)115ENF ∠=︒;(3)1603H α∠=︒-.【分析】(1)过点M 作//ML AB ,利用平行线的性质可得1AEM ∠=∠,2CFM ∠=∠,由12EMF ∠=∠+∠,经过等量代换可得结论;(2)过M 作//ME AB ,利用平行线的性质以及角平分线的定义计算即可.(3)如图②中设BEH x ∠=,PFG y ∠=,则3BEM x ∠=,3MFG y ∠=,设EH 交CD 于K .证明H x y ∠=-,求出x y -即可解决问题.【详解】(1)如图1,过点M 作//ML AB ,//AB CD ,////ML AB CD ∴,1AEM ∴∠=∠,2CFM ∠=∠,12EMF ∠=∠+∠,M AEM CFM ∴∠=∠+∠;(2)过M 作//ME AB ,//AB CD ,//ME CD ∴,24180BEM DFM ∴∠+∠=∠+∠=︒,1802BEM ∴∠=︒-∠,1804DFM ∠=︒-∠, EN ,FN 分别平分MEB ∠和DFM ∠,112BEM ∴∠=∠,132DFM ∠=∠, 111113(1802)(1804)180(24)1801301152222∴∠+∠=︒-∠+︒-∠=︒-∠+∠=︒-⨯︒=︒, 36013360115130115ENF EMF ∴∠=︒-∠-∠-∠=︒-︒-︒=︒;(3)如图②中设BEH x ∠=,PFG y ∠=,则3BEM x ∠=,3MFG y ∠=,设EH 交CD 于K .//AB CD ,BEH DKH x ∴∠=∠=,PFG HFK y ∠=∠=,DKH H HFK ∠=∠+∠,H x y ∴∠=-,EMF MGF α∠=∠=,180BQG MGF ∠+∠=︒,180BQG α∴∠=︒-,QMF QMF EMF MGF MFG ∠=∠+∠=∠+∠,3QME MFG y ∴∠=∠=,BEM QME MQE ∠=∠+∠,33180x y α∴-=︒-,1603x y α∴-=︒-, 1603H α∴∠=︒-. 【点睛】本题考查平行线的性质和判定,三角形的外角的性质,三角形的内角和定理等知识,作出平行线,利用参数解决问题是解题的关键.22.(1)证明过程见解析;(2)12N AEM NFD ∠=∠-∠,理由见解析;(3)13∠N+∠PMH=180°. 【分析】(1)根据同旁内角互补,两直线平行即可判定AB ∥CD ;(2)设∠N=2α,∠M=3α,∠AEM=x ,∠NFD=y ,过M 作MP ∥AB ,过N 作NQ ∥AB 可得∠PMN=3α-x ,∠QNM=2α-y ,根据平行线性质得到3α-x =2α-y ,化简即可得到12N AEM NFD ∠=∠-∠; (3)过点M 作MI ∥AB 交PN 于O ,过点N 作NQ ∥CD 交PN 于R ,根据平行线的性质可得∠BPM=∠PMI ,由已知得到∠MON=∠MPN+∠PMI=3∠PMI 及∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD ,根据对顶角相等得到∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM ,化简得到∠FNP+2∠PMI-2∠RFM=180°-∠PMH ,根据平行线的性质得到3∠PMI+∠FNP+∠FNH=180°及3∠RFM+∠FNH=180°,两个等式相减即可得到∠RFM-∠PMI=13∠FNP,将该等式代入∠FNP+2∠PMI-2∠RFM=180°-∠PMH,即得到1 3∠FNP=180°-∠PMH,即13∠N+∠PMH=180°.【详解】(1)证明:∵∠1=∠BEF,12180︒∠+∠=∴∠BEF+∠2=180°∴AB∥CD.(2)解:12N AEM NFD ∠=∠-∠设∠N=2α,∠M=3α,∠AEM=x,∠NFD=y 过M作MP∥AB,过N作NQ∥AB∵//AB CD,MP∥AB,NQ∥AB∴MP∥NQ∥AB∥CD∴∠EMP=x,∠FNQ=y∴∠PMN=3α-x,∠QNM=2α-y∴3α-x=2α-y即α=x-y∴12N AEM NFD ∠=∠-∠故答案为12N AEM NFD ∠=∠-∠(3)解:13∠N+∠PMH=180°过点M作MI∥AB交PN于O,过点N作NQ∥CD交PN于R.∵//AB CD,MI∥AB,NQ∥CD∴AB∥MI∥NQ∥CD∴∠BPM=∠PMI∵∠MPN=2∠MPB∴∠MPN=2∠PMI∴∠MON=∠MPN+∠PMI=3∠PMI∵∠NFH=2∠HFD∴∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD∵∠RFN=∠HFD∴∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM∴∠MON+∠PRF+∠RFM=360°-∠OMF即3∠PMI+∠FNP+180°-3∠RFM+∠RFM=360°-∠OMF ∴∠FNP+2∠PMI-2∠RFM=180°-∠PMH∵3∠PMI+∠PNH=180°∴3∠PMI+∠FNP+∠FNH=180°∵3∠RFM+∠FNH=180°∴3∠PMI-3∠RFM+∠FNP=0°即∠RFM-∠PMI=13∠FNP∴∠FNP+2∠PMI-2∠RFM=∠FNP-2(∠RFM-∠PMI)=180°-∠PMH∠FNP-2×13∠FNP=180°-∠PMH13∠FNP=180°-∠PMH即13∠N+∠PMH=180°故答案为13∠N+∠PMH=180°【点睛】本题主要考查了平行线的判定与性质.解题的关键是正确作出辅助线,通过运用平行线性质得到角之间的关系.23.(1) 150°;(2) ∠OCD+∠BO'E=240°;(3) 30°+12α.【分析】(1)先求出到∠AOE的度数,再根据直角、周角的定义即可求解;(2)过O点作OF//CD,根据平行线的判定和性质可得∠OCD、∠BO'E的数量关系;(3)根据四边形内角和为360°,再结合(2)的结论以及角平分线的定义即可解答.【详解】解:(1)∵CD//OE,∴∠AOE=∠OCD=120°,∴∠BOE=360°-90°-120°=150°;(2)如图2,过O点作OF//CD,∴CD//OE,∴OF∥OE,∴∠AOF=180°-∠OCD,∠BOF=∠EO'O=180°-∠BO'E,∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO'E=360°-(∠OCD+∠BO'E)=120°,∴∠OCD+∠BO'E=240°;(3)∵CP是∠OCD的平分线,∴∠OCP=12∠OCD,∴∠CPO'=360°-90°-120°-∠OCP=150°-12∠OCD=150°-12(240°-∠BO'E)=30°+1 2α【点睛】本题考查了平行线的判定和性质、周角的定义、角平分线的定义,确定∠OCD、∠B0'E的数量关系是解答本题的关键.24.(1)30°,60°;(2)∠CAF+∠EMC=90°,理由见解析【分析】(1)利用∠CAF=∠BAF-∠BAC求出∠CAF度数,求∠EMC度数转化到∠MCH度数;(2)过点C作CH∥GF,得到CH∥DE,∠CAF与∠EMC转化到∠ACH和∠MCH中,从而发现∠CAF、∠EMC与∠ACB的数量关系.【详解】(1)过点C作CH∥GF,则有CH∥DE,所以∠CAF=∠HCA,∠EMC=∠MCH,∵∠BAF=90°,∴∠CAF=90°-60°=30°.∠MCH=90°-∠HCA=60°,∴∠EMC=60°.故答案为30°,60°.(2)∠CAF+∠EMC=90°,理由如下:过点C作CH∥GF,则∠CAF=∠ACH.∵DE∥GF,CH∥GF,∴CH∥DE.∴∠EMC=∠HCM.∴∠EMC+∠CAF=∠MCH+∠ACH=∠ACB=90°.【点睛】考查了平行线的判定和性质,解题关键是熟记并灵活运用其性质和判定.25.(1)两直线平行,同旁内角互补;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;(2)∠B+∠E+∠F+∠D=540°;(3)∠B +∠E+∠D-∠F=180°.【分析】(1)根据平行线的性质和判定,平行公理的推论回答即可;(2)过点E、F分别作GE∥HF∥CD,根据两直线平行,同旁内角互补及已知条件求得同旁内角∠ABE+∠BEG=180°,得到AB∥GE,再根据平行线的传递性来证得AB∥CD;(3)过点E、F分别作ME∥FN∥CD,根据两直线平行,内错角相等及已知条件求得同旁内角∠B+∠BEM=180°,得到AB∥ME,再根据平行线的传递性来证得AB∥CD.【详解】解:(1)由题意可知:“依据1”:两直线平行,同旁内角互补;“依据2”:同旁内角互补,两直线平行;“依据3”:如果两条直线都与第三条直线平行,那么这两条直线也互相平行;(2)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.理由:如图,过点E、F分别作GE∥HF∥CD,则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,∴∠GEF+∠EFD+∠FDC=360°;又∵∠B+∠BEF+∠EFD+∠D=540°,∴∠ABE+∠BEG=180°,∴AB∥GE,∴AB∥CD;(3)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠D-∠F=180°时,有AB∥CD.如图,过点E、F分别作ME∥FN∥CD,则∠MEF=EFN,∠D=∠DFN,∵∠B+∠BEF+∠D-∠EFD=180°,∴∠B+∠BEM+∠MEF+∠D-∠EFN-∠DFN=180°,∴∠B+∠BEM=180°,∴AB∥ME,∴AB∥CD.【点睛】本题考查平行线的判定和性质的综合应用,作出合适的辅助线,灵活运用平行线的性质定理和判定定理是解题的关键.26.(1)∠MEN=∠AME+∠ENC,见解析;(2)∠FEQ=15°;(3)∠BMN+∠GEK-m∠GEH=180°.【分析】(1)过点E作l∥AB,利用平行线的性质可得∠1=∠BME,∠2=∠DNE,由∠MEN=∠1+∠2,等量代换可得结论;(2)利用角平分线的性质可得∠NEF=12∠MEN,∠ENP=12∠END,由EQ∥NP,可得∠QEN=∠ENP=12∠ENC,由(1)的结论可得∠MEN=∠AME+∠ENC,等量代换得出结论;(3)由已知可得∠EMN=1m∠BMN,∠GEN=1m∠GEK,由EH∥MN,可得∠HEM=∠ENM=1m∠AMN,因为∠GEH=∠GEM-∠HEM,等量代换得出结论.【详解】解:(1)过点E作l∥AB,∵AB∥CD,∴l∥AB∥CD∴∠1=∠AME,∠2=∠CNE.∵∠MEN=∠1+∠2,∴∠MEN=∠AME+∠ENC;(2)∵EF平分∠MEN,NP平分∠ENC,∴∠NEF=12∠MEN,∠ENP=12∠ENC.∵EQ∥NP,∴∠QEN=∠ENP=12∠ENC.由(1)可得∠MEN=∠AME+∠ENC,∴∠MEN-∠ENC=∠AME=30°.∴∠FEQ=∠NEF-∠NEQ=12(∠MEN-∠ENC)=12×30°=15°;(3)∠BMN+∠GEK-m∠GEH=180°.理由如下:∵∠AMN=m∠EMN,∠GEK=m∠GEM,∴∠EMN=1m∠AMN,∠GEM=1m∠GEK.∵EH∥MN,∴∠HEM=∠EMN=1m∠AMN.∵∠GEH=∠GEM-∠HEM=1m∠GEK-1m∠AMN,∴m∠GEH=∠GEK-∠AMN.∵∠BMN+∠AMN=180°,∴∠BMN+∠GEK-m∠GEH=180°.【点睛】本题主要考查了平行线的性质,平行公理以及角平分线的定义等知识点,作出适当的辅助线,结合图形等量代换是解答此题的关键.。
2021七年级下册语文第五单元自主学习综合检测试卷(解析版)

七年级下册语文第五单元自主学习综合检测卷(解析版)(时量120分钟,总分150分)班级姓名学号计分一、语言文字积累与运用(共34分)(一)单项选择题(共15分,每小题3分)1.下列词语中加点字的注音完全正确的一项是( )(3分)A.猥.琐(wěi)笼罩.(zhào) 褪.尽(tuì) 枯槐.(huái) 迸.溅(bìng)B.莅.临(lì)伫.立(chù) 瀑.布(pù) 侍.弄(shì) 赤裸.(luǒ)C.梦寐.(mèi)颤.抖(zhàn) 孱.头(càn) 瞬.息(shùn) 幼稚.(zhì)D.萋.萋(qī)沉淀.(diàn) 灼.灼(zhuó) 忏.悔(chàn) 矜.持(jīn)【答案】D【解析】A项“迸”应读bèng,B项“伫”应读zhù,C项“颤”应读chàn。
2.下列词语中没有错别字的一项是( )(3分)A.褪尽挑逗忍俊不禁仙露琼桨B.幽寂凝望垂垂幕老祸不单行C.渺小魂魄血气方刚轰轰烈烈D.笼罩猥琐盘虬卧龙荒草凄凄【答案】C【解析】A项“仙露琼桨”应为“仙露琼浆”;B项“垂垂幕老”应为“垂垂暮老”;D项“荒草凄凄”应为“荒草萋萋”。
3.依次填入下面一段文字横线处的语句,衔接最恰当的一组是()有人说:山穷水尽,走投无路,陷入绝境,等死而已,不能创造。
但是遭遇;;。
绝望是懦夫的幻想。
歌德说,没有勇气一切都完。
是的,生路是要勇气探出来,走出来,造出来的。
①粮水断绝、众叛亲离之哥伦布,毕竟发现了美洲②八十一难之玄奘,毕竟取得佛经③冻饿病三重压迫下之莫扎特,毕竟写出了《安魂曲》A.②③①B.①③②C.①②③D.②①③【答案】D【解析】本题考查排序。
根据人物所处的年代,从早到晚排序即可。
玄奘生活在7世纪,哥伦布,毕竟发现了美洲是在15世纪末期,莫扎特,写出了《安魂曲》是在18世纪末期。
(完整word版)人教版七年级数学下册第五章测试题(含答案)

.
14.如图,直线 AB,CD,EF 相交于点 O,且 AB⊥CD,∠1 与∠2 的关
系是
.
第 5 页,共 16 页
第 17 题图
第 18 题
图
18.( 2012• 郴 州 ) 如 图 , 已 知 AB∥ CD, ∠ 1=60° , 则 ∠ 2=
度.
三、解答题(共 6 小题,满分 46 分) 第
19.(7 分)读句画图:如图,直线 CD 与直线 AB
两直线平行),故正确;
∠2=180°。
而选项 A 中,∠1 与∠2 是直线 AC、BD 被直线 AD 所截形成 又∵∠1=36°,∴ ∠2=180°36°=144°.
的内错角,∵ ∠1=∠2,∴ AC∥BD,故 A 错误.选 A.
12。 50 解析:∵∠BAC=80°,∴∠EAC=100°.
8. D 解析 :如题图所示,∵ DC∥EF,∴ ∠DCB=∠EFB。
尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我 和我的同事精心编辑整理后发布的,发布之前 我们对文中内容进行仔细校对,但是难免会有 疏漏的地方,但是任然希望((完整 word 版) 人 教 版 七 年 级 数 学 下 册 第 五 章 测 试 题 (含 答 案)(word 版可编辑修改))的内容能够给您的 工作和学习带来便利。同时也真诚的希望收到 您的建议和反馈,这将是我们进步的源泉,前 进的动力。 本文可编辑可修改,如果觉得对您有帮助请收 藏以便随时查阅,最后祝您生活愉快 业绩进
第 9 页,共 16 页
第 10 页,共 16 页
平行),故正确;
(完整 word 版)人教版七年级数学下册第五章测试题(含答案)(word 版可编辑修改)
故选 B.
七年级数学下册《第5章 综合测试》导学案 (新版)新人教版

课后3题、4题
7、学习反思:
学法指导
复习提问,巩固所学知识
学生归纳总结本 章知识,利用所学知识解决实际问题
学生独立完成再和同伴交流,互相完善认识,得出结论:
小组交流、讨论、共同完成,实现生生互助的教学模式
学生总结,相补充,培养分析归纳能力
【教学反思】
名人名言或名人 故事:精诚所至,金石为开。
14、如图7,AB∥DE,BC∥FE,则∠E+∠B=。
15、把命题“对顶角相等”写成“如果……,那么……。”的形式为
。
16.如图,直线AB,CD相交于点O若∠1=28º则∠2=___________ _
28.( 8分)如图所示,直线AB∥CD,∠1=75°,求∠2的度数.
五、课堂小结:(2分钟)
学会分析问题,解决问题的能力,注意解题的规范性
《5章综合测试》导学案
课题
课时
2
审核
班级
授课节次
【学习目标】
1.了解相交和平行的三线八角,以及平行线的判定和性质
2.自主、合作、交流
3.进一步发展空间观念,增强审美意识
【重点】
垂线、平行线的作图
【难点】
利用平行线性质和判定解 决实际问题
【学习过程】
一复习 导入:(2分钟)
利用本章所学知识,解决实际问题
A. 40°B. 45°C. 30°D. 35°
4、如图2,AD‖BC,点E在BD的延长线上,若∠ADE=155°,
则∠DBC的度数为( ).
A.155°B.25°C.45° D.35°
5、在 同一平面内,两条直线的位置关系()。
A、相交或平行B、相交或垂直C、平行或垂直D、不能确定
七年级下册第五单元预习检测及达标测评.doc
课标链接:1、能用普通话正确、流利、有感情地朗读。
2、养成默读习惯,有一定速度,阅读一般的现代文,每分钟不少于500字。
能较熟练地运用略读和浏览的方法,扩大阅读范围。
3、在通读课文的基础上,理清思路,理解、分析主要内容,体味和推敲重要词句在语言环境中的意义和作用。
4、对课文的内容和表达有自己的心得,能提出自己的看法,并能运用合作的方式,共同探讨、分析、解决疑难问题。
预习目标:1.快速默读课文,把握内容,体会作者感情。
2.理清故事情节,体味关键语句。
3.激起探索未知世界的兴趣,培养团结合作,勇于牺牲的精神。
预习重点:通过默读、朗读,体味关键语句,认识人类挑战自身,实现生命价值的伟大。
预习难点:体会作者的写作意旨。
一、预习任务:1、查字典,正确识记理解生字词。
2、朗读课文,概括课文内容。
二、预习检测1、给加点的字注音:茨威格()拉拽()毛骨悚然()怏怏不乐()吞噬()羸弱()告罄()毋宁()2、本文作者,作家,他的主要成就体现在和方面。
3、故事发生的地点在,主人公是,在这一个英雄的集体里还有等共名探险队员。
4、同样一句话,重音不同,所强调的意思也不同。
请根据以下重音提示,分别写出相应的提问。
他叫你明天去。
_____________________________他叫你明天去。
_____________________________7、下列各句中,加点的词语使用恰当的一项是()A、许静的朗诵字正腔圆,令李老师喜从天降,他立即同意让许静参加诗歌朗诵会。
B、这部著作是他长期工作经验的总结,是他经过反复修改后处心积虑写出来的。
C、2001年教育部放宽高校招生报考条件,各高校对大龄考生和应届生等量齐观。
D、愚公之所以能感动上天,搬走太行、王屋二山,靠的就是持之以恒的精神。
9、本文题为"伟大的悲剧”该如何理解?预习质疑:《伟大的悲剧》达标检测一、给下列加点字注音或根据拼音写汉字。
无垠()遗孀()夜不成眠()毛骨悚()然凛冽()()zhuai ()出来dian()狂步1击()鲁ma ng ()忧心chong chong ()()二、找出并修改下列词语中的错别字。
2022-2023学年新人教版初中七年级数学下册第五单元学习质量检测卷(附参考答案)
2022-2023学年新人教版初中七年级数学下册第五单元学习质量检测卷时间:90分钟满分:120分班级__________姓名__________得分__________一.选择题(共10小题,满分30分,每小题3分)1.(3分)将含30︒角的直角三角尺如图摆放,直线//∠的度数为(∠=︒,则2a b,若165)A.45︒B.50︒C.55︒D.60︒2.(3分)如图,下列条件:①12∠=∠,②34180∠+∠=︒,④∠+∠=︒,③56180a b的有()∠=∠中能判断直线//∠=∠+∠,⑥23741180∠+∠-∠=︒,⑤723A.3个B.4个C.5个D.6个3.(3分)如图,在长方形ABCD纸片中,//AB CD,把纸片沿EF折叠后,点AD BC,//∠等于()∠=︒,则AED'C、D分别落在C'、D'的位置.若65EFBA .70︒B .65︒C .50︒D .25︒4.(3分)如图,点B ,C ,E 在一条直线上,下列条件能判定//AB CD 的是( )A .23∠=∠B .14∠=∠C .5D ∠=∠ D .180D BCD ∠+∠=︒5.(3分)如图,ABCD 为一长条形纸带,//AB CD ,将ABCD 沿EF 折叠,A 、D 两点分别与A '、D '对应,若122∠=∠,则AEF ∠的度数为( )A .60︒B .65︒C .72︒D .75︒6.(3分)如图,12∠=∠,AC 平分DAB ∠,且:2:1D DAB ∠∠=,则D ∠的度数是( )A .120︒B .130︒C .140︒D .150︒7.(3分)如图,将三角形ABE 向右平移1cm 得到三角形DCF ,如果三角形ABE 的周长是10cm ,那么四边形ABFD 的周长是( )A .12cmB .16cmC .18cmD .20cm8.(3分)如图,170∠=︒,直线a 平移后得到直线b ,则23(∠-∠= )A .70︒B .180︒C .110︒D .80︒9.(3分)如图,如果把ABC ∆的顶点A 先向右平移2格,再向下平移6格到达D 点,连接DB ,那么线段DB 与线段AC 的关系是( )A .互相垂直B .相等C .互相平分D .互相平分且垂直10.(3分)如图,//AB CD ,ABK ∠的角平分线BE 的反向延长线和DCK ∠的角平分线CF 的反向延长线交于点H ,27K H ∠-∠=︒,则(K ∠= )A .76︒B .78︒C .80︒D .82︒二.填空题(共5小题,满分15分,每小题3分)11.(3分)如图,直线AB 与直线CD 相交于点O ,且2BOD BOC ∠=∠,若以点O 为端点的射线OE CD ⊥,则BOE ∠的度数为 .12.(3分)如图,点E 在AC 的延长线上,对于下列给出的四个条件:①34∠=∠;②12∠=∠;③A DCE ∠=∠;④180D ABD ∠+∠=︒.能判断//AB CD 的有 (填正确结论的序号)13.(3分)如图,//AE CF ,ACF ∠的平分线交AE 于点B ,G 是CF 上的一点,GBE ∠的平分线交CF 于点D ,且BD BC ⊥,下列结论:①BC 平分ABG ∠;②//AC BG ;③与DBE ∠互余的角有2个;④若A α∠=,则1808BDF α∠=︒-.其中正确的是 .(请把正确结论的序号都填上)14.(3分)如图,直线AB ,CD 相交于点O ,OE AB ⊥,34DOB ∠=︒,则COE ∠= ︒.15.(3分)如图,直角三角形DEF 是直角三角形ABC 沿BC 平移得到的,如果8AB =,3BE =,2DH =,则图中阴影部分的面积是 .三.解答题(共8小题,满分75分)16.(9分)完成下面的证明.如图,AB 和CD 相交于点O ,//EF AB ,C COA ∠=∠,D BOD ∠=∠,求证:A F ∠=∠. 证明:C COA ∠=∠,D BOD ∠=∠又COA BOD ∠=∠( )C ∴∠= ( )//AC BD ∴( )A ∴∠= ( )//EF ABF ∴∠= ( )A F ∴∠=∠( )17.(9分)阅读并填充理由(不完整的补充完整):如图所示,已知://DE BC ,DF 、BE 分别平分ADE ∠和ABC ∠,试说明FDE DEB ∠=∠. 解://DE BC ,ADE ∴∠= , DF 、BE 分别平分ADE ∠和ABC ∠(已知), 12ADF ∴∠= ,12ABE ∠= , ADF ABE ∴∠=∠,∴ // ,FDE ∴∠= .18.(9分)如图,直线AB 、CD 相交于点O ,OE 平分BOD ∠,OE OF ⊥,70DOF ∠=︒,求AOC ∠的度数.19.(9分)如图,直线12//l l ,125BAE ∠=︒,85ABF ∠=︒,则12∠+∠等于多少度?20.(9分)如图,在ABC ∆中,//EF AB ,1B ∠=∠.(1)证明://DE BC .(2)若66A ∠=︒,145∠=︒,求C ∠的度数.21.(10分)在平面直角坐标系中,三角形ABC 的三个顶点的位置如图所示,且点A '的坐标为(2,2)-,现将三角形ABC 平移,使点A 变换为A ',点B '、C '分别是点B 、C 的对应点.(1)请画出平移后的三角形A B C ''',并直接写出点B '、C '的坐标;(2)若三角形ABC 内有一点P 的坐标为(,)a b ,则点P 的对应点P '的坐标为 .(3)求四边形A BCC ''的面积.22.(10分)(1)(问题)如图1,若//AB CD ,40AEP ∠=︒,130PFD ∠=︒.求EPF ∠的度数;(2)(问题迁移)如图2,//AB CD ,点P 在AB 的上方,问PEA ∠,PFC ∠,EPF ∠之间有何数量关系?请说明理由;(3)(联想拓展)如图3所示,在(2)的条件下,已知EPF α∠=,PEA ∠的平分线和PFC ∠的平分线交于点G ,用含有α的式子表示G ∠的度数.23.(10分)已知一个角的两边与另一个角的两边分别垂直,结合图形,试探索这两个角之间的数量关系.(1)如图1,AB DE ⊥,BC EF ⊥.1∠与2∠的数量关系是: .(2)如图2,AB DE ⊥,BC EF ⊥.1∠与2∠的数量关系是: .说明理由.(3)由(1)(2)你得出的结论是:如果 ,那么 .(4)若两个角的两边互相垂直,且一个角比另一个角的3倍少40 ,则求这两个角度数.参考答案1.C ; 2.C ; 3.C ; 4.B ; 5.C ; 6.A ; 7.A ; 8.C ; 9.A ; 10.B ; 11.30°或150°;12.②③④;13.①②;14.56;15.21;16.C COA ∠=∠,D BOD ∠=∠又COA BOD ∠=∠ (对顶角相等)C D ∴∠=∠(等量代换)//AC BD ∴ (内错角相等,两直线平行)A ABD ∴∠=∠(两直线平行,内错角相等)//EF ABF ABD ∴∠=∠(两直线平行,同位角相等)A F ∴∠=∠ (等量代换)故答案是:对顶角相等;D ∠;等量代换; 内错角相等,两直线平行;ABD ∠;两直线平行,内错角相等;ABD ∠; 两直线平行,同位角相等; 等量代换.17.//DE BC (已知),ADE ABC ∴∠=∠(两直线平行,同位角相等). DF 、BE 分别平分ADE ∠和ABC ∠,12ADF ADE ∴∠=∠,12ABE ABC ∠=∠,ADF ABE ∠=∠ (等量代换),//DF BE ∴(同位角相等,两直线平行),FDE DEB ∴∠=∠(两直线平行,内错角相等).故答案为:(已知),ABC ∠,ADE ∠,ABC ∠,DF ,BE ,DEB ∠.18.OE 平分BOD ∠,2BOD DOE ∴∠=∠,OE OF ⊥,90FOE ∴∠=︒,20DOE ∴∠=︒,40BOD ∴∠=︒,40AOC ∴∠=︒.19.如图,延长AB 交1l 于点M ,交2l 于点N .12//l l ,180EMA ANB ∴∠+∠=︒.又1EAB EMA ∠=∠+∠,2FBA FNB ∠=∠+∠, 12EAB FBA EMA FNB ∴∠+∠=∠+∠+∠+∠. 12()12585210EMA FNB ∴∠+∠+∠+∠=︒+︒=︒. 12180210∴∠+∠+︒=︒.1230∴∠+∠=︒.20.(1)证明://EF AB ,B EFC ∴∠=∠,1B ∠=∠,1EFC ∴∠=∠,//DE BC ∴;(2)解:145∠=︒,1B ∠=∠,45B ∴∠=︒,66A ∠=︒,18069C A B ∴∠=︒-∠-∠=︒.21.(1)如图,△A B C '''即为所求;(4,1)B '∴-、(1,1)C '--;(2)P '的坐标为(5,2)a b --.故答案为:(5,2)a b --.(3)四边形A BCC ''的面积为:11116452231331132222⨯-⨯⨯-⨯⨯-⨯⨯-⨯⨯=. 22.(1)如图1,过点P 作//PM AB ,140AEP ∴∠=∠=︒.(两直线平行,内错角相等) //AB CD ,(已知) //PM CD ∴,(平行于同一条直线的两直线平行) 2180PFD ∴∠+∠=︒. (两直线平行,同旁内角互补)130PFD ∠=︒,218013050∴∠=︒-︒=︒.12405090∴∠+∠=︒+︒=︒.即90EPF ∠=︒.(2)PFC PEA P ∠=∠+∠.理由:如图2,过P 点作//PN AB ,则//PN CD ,PEA NPE ∴∠=∠,FPN NPE FPE ∠=∠+∠,FPN PEA FPE ∴∠=∠+∠,//PN CD ,FPN PFC ∴∠=∠,PFC PEA FPE ∴∠=∠+∠,即PFC PEA P ∠=∠+∠;(3)如图,过点G 作AB 的平行线GH .//GH AB ,//AB CD ,////GH AB CD ∴,HGE AEG ∴∠=∠,HGF CFG ∠=∠,又PEA ∠的平分线和PFC ∠的平分线交于点G ,12HGE AEG AEP ∴∠=∠=∠,12HGF CFG CFP ∠=∠=∠, 由(1)可知,CFP P AEP ∠=∠+∠,11()()22HGF P AEP AEP α∴∠=∠+∠=+∠, 1111()2222EGF HGF HGE AEP AEP HGE ααα∴∠=∠-∠=+∠=+∠-∠=. 23.(1)如图1,AB DE ⊥,BC EF ⊥,90EGB ∴∠=︒,90EHB ∠=︒,2490∴∠+∠=︒,1390∠+∠=︒,34∠=∠,12∴∠=∠.故答案为:相等.(2)如图2,AB DE ⊥,BC EF ⊥,90EGB ∴∠=︒,90EHB ∠=︒,12360EGB EHB ∴∠+∠+∠+∠=︒,12180∴∠+∠=︒.故答案为:互补.(3)由(1)(2)的分析可得结论:如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等或互补;故答案为:一个角的两边与另一个角的两边分别垂直,这两个角相等或互补;(4)设另一个角的度数为α,则一个角的度数为340α-︒,根据题意可得,340αα=-︒或340180αα+-︒=︒,解得20α=︒或55︒,当20α=︒时,34020α-︒=︒,当55α=︒时,340125α-︒=︒,∴这两个角的度数为20︒,20︒或55︒,125︒.。
人教版英语七年级下册第五章测试卷(含答案)
人教版英语七年级下册第五章测试卷(含答案)一、单项选择(15分)1. What ____ you do yesterday?A. didB. doesC. doD. will答案:A2. He usually _____ his bike to school.A. rideB. rodeC. ridesD. riding答案:C3. What _____ he _____?A. does, doesB. is, doingC. does, doingD. is, do答案:B4. Would you like _____ juice?A. someB. anyC. aD. many答案:A5. There are _____ concerts on the weekend.A. a lot ofB. a fewC. a littleD. a little bit答案:A6. I like _____ TV.A. watchB. watchesC. watchingD. watched 答案:C7. What are you going to do _____ the weekend?A. onB. atC. inD. for答案:A8. She is good _____ English.A. forB. toC. atD. in答案:C9. Where _____ you _____ lunch every day?A. do, haveB. are, haveC. do, hasD. are, had 答案:A10. What’s _____ name?A. himB. herC. theirD. its答案:B11. Could you _____ me your pen?A. borrowB. lendC. takeD. get答案:B12. What time do you _____ up on the weekend?A. wakeB. wokeC. wakingD. wakes答案:A13. My father is a _____.A. farmerB. docterC. dancerD. teacher答案:D14. We like to eat _____ for breakfast.A. bread and coffeeB. cereal and milkC. soup and fishD. rice and noodles答案:B15. _____ does your brother live?A. WhoB. WhatC. WhenD. Where答案:D二、完形填空(10分)Linda is my __1__. She is sixteen years old. She is __2__ student. She __3__ school at seven in the morning. She has French, English, Chinese, math and history classes. She has __4__ for lunch. She __5__ apples and bananas. She goes home at four in the afternoon. She __6__ to go swimming. After that, she does her homework __7__ six. She watches TV at nine and goes to bed at ten.1. A. brotherB. fatherC. sisterD. mother答案:C2. A. an AmericanB. a JapaneseC. a ChineseD. an English答案:C3. A. hasB. getsC. wantsD. likes答案:B4. A. noodlesB. breadC. riceD. pizza答案:C5. A. eatsB. likesC. drinksD. has答案:A6. A. wantsB. likeC. likesD. to like答案:A7. A. atB. inC. onD. for答案:D三、阅读理解(10分)This is Mary. She is a good student. She gets up at six every morning. She has breakfast at seven. She goes to school at eight. She has English, math, Chinese, history and science classes. She has lunch at twelve. After lunch, she has music and art classes. She goes back home at four in the afternoon. She likes to swim and paint. She usually goes swimming with her father on Sundays. She likes to paint pictures of flowers.1. What time does Mary have breakfast?A. At six.B. At seven.C. At eight.D. At twelve.答案:B2. What classes does Mary have?B. English, math, Chinese, history, science.C. English, math, Chinese, geography, history.D. English, math, Chinese, art, music.答案:B3. What does Mary usually do on Sundays?A. Goes swimming with her mother.B. Goes to the park.C. Watches TV.D. Goes swimming with her father.答案:D4. What does Mary like to paint?A. Pictures of people.B. Pictures of buildings.C. Pictures of animals.D. Pictures of flowers.答案:D四、书面表达(20分)你喜欢运动吗?请根据下面的要求写一篇短文。
七年级数学下册第五章自我测试题试题
智才艺州攀枝花市创界学校集备时间是20测试时间是_______案型施行案成绩________一、选择题〔每一小题4分,一共计24分〕: 1、下面四个图形中,∠1与∠2是对顶角的图形有〔〕 〔A 〕0个〔B 〕1个〔C 〕2个〔D 〕3个2、一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是〔〕 〔A 〕第一次右拐50º,第二次左拐130º〔B 〕第一次左拐50º,第二次右拐50º〔C 〕第一次左拐50º,第二次左拐130º〔D 〕第一次右拐50º,第二次右拐50º 3、同一平面内的四条直线假设满足a ⊥b ,b ⊥c ,c ⊥d ,那么以下式子成立的是〔〕 〔A 〕a ∥d 〔B 〕b ⊥d 〔C 〕a ⊥d 〔D 〕b ∥c4、三条直线两两相交于同一点时,对顶角有m 对;交于不同三点时对顶角有n 对,那么m 与 n 的关系是〔〕〔A 〕m =n 〔B 〕m >n 〔C 〕m <n 〔D 〕m +n =10 5、假设m ∥n ,∠1=105º,那么∠2=〔〕 〔A 〕55º〔B 〕60º〔C 〕65º〔D 〕75º 6、以下说法中正确的选项是〔〕 〔A 〕有且只有一条直线垂直于直线。
〔B 〕从直线外一点到这条直线的垂线段, 叫做这点到这条直线的间隔。
【1题图】【5题图】21 mn〔C 〕互相垂直的两条线段一定相交。
〔D 〕直线c 外一点A 与直线c 上各点连结而成的所有线段中最短线段的长是3cm ,那么点A 到直线c 的间隔是3cm 。
二、填空题〔每一小题4分,一共20分〕: 7、两个角的两边两两互相平行,且一个角的12等于另一个角的13,那么这两个角的度数分别是_______________________。
8、猜谜语〔打本章两个几何名称〕。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新人教七年级下第5章自主学习达标检测 (§5.3~§5.4)
(时间45分钟 满分100分)
班级 学号 姓名 得分
一、填空题(每小题3分,共30分)
1.如图1所示,如果DC ∥AB ,那么∠A+______=180°,或∠B+_____=180°,根据是______; 2.如图2所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、•后的两条路平行,若
第一次拐角是150°,则第二次拐角为________.
C
B
A
(1) (2 (3) (4)
3.如图3所示,AB ∥CD ,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=____,∠ACD=•____. 4.在平移过程中,平移后的图形与原来的图形______和______都相同,•因此对应线段和对应角都________.
5.如图4,AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,ED 平分∠BEF .若∠1=68°,则∠2的度数是 .
6.如图5所示,长方体中,平移后能得到棱AA 1的棱有____. 7.小明的一本书一共有104页,在这104页的页码中有两个数码的,并且这两个数码经过平移其中一个能得到另一个,则这样的页共有________页.
8.一手扶电梯向上的传送速度为每分钟20m ,小红以每分钟16m 的速度通过电梯上楼,如果小红用了15秒到达楼上,那么这部电梯的长为_____m . 二、选择题(每小题3分,共24分)
11.如图6所示,AB ∥CD ,则与∠1相等的角(∠1除外)共有( )
A .5个
B .4个
C .3个
D .2个
D 1C 1B 1A 1C
B
A
D
F
E D
C
B
A 21(5)
(6) (7)
12.如图7所示,已知DE ∥BC ,CD 是∠ACB 的平分线,∠B=72°,∠ACB=40°,•那么∠BDC
等于( )
A .78°
B .90°
C .88°
D .92°
13.下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行; ③内错角相等,
两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( ) A .① B .②和③ C .④ D .①和④
14.若两条平行线被第三条直线所截,则一组同位角的平分线互相( ) A .垂直 B .平行 C .重合 D .相交
15.在俄罗斯方块游戏中,已拼成的图案如图所示,现又出现一小方块拼图向下运动,为了
使所有图案消失,你必须进行以下哪项操作,才能拼成一个完整的图案,才能拼成一个完整的图案,使其自动消失.( ) A.向右平移1格 B.向左平移1格 C.向右平移2格
D.向右平移3格
16.将图形A 向右平移3个单位得到图形B ,再将图形B 向左平移5个单位得到图形C 。
如果直接将图形A 平移到图形C ,则平移方向和距离为( )
A 、向右2个单位
B 、向右8个单位
C 、向左8个单位
D 、向左2个单位 17.如图8所示,右边的两个图形中,经过平移能得到左边的图形的是( )
18.在5×5方格纸中将图9(1)中的图形N 平移后的位置如图5(2)中所示,那么正确的
平移方法是( ).
D
C
B
A 1
E
D
C
B
A
_D
_C
_B
_A
图
8
(A)先向下移动1格,再向左移动1格 (B)先向下移动1格,再向左移动2格 (C)先向下移动2格,再向左移动1格 (D)先向下移动2格,再向左移动2格 三、解答题(每小题3分,共24分)
19.(本题6分)如图所示,AD ∥BC ,∠1=78°,∠2=40°,求∠ADC 的度数.
20.(本题6分)如图所示,AB ∥CD ,AD ∥BC ,∠A 的2倍与∠C 的3倍互补,求∠A 和∠D
的度数.•
21.(本题8分)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
a
341
2
22.(本题8分)如图所示,已知AB ∥CD ,分别探索下列四个图形中∠P 与∠A ,∠C 的关系,
•请你从所得的四个关系中任选一个加以说明.
P
D
C
B
A P D
B
A
P D
C
B A P
D
C
B A
(1) (2) (3) (4)
D
C
B
A
1
2
D C
B
A
图9(1) 图9(2)
23.(本题8分)如图所示,
平移得到
,写出图中所有相等的线段、角,以
及平行的线段.
24.(本题10分)图形的操作过程(本题中四个矩形的水平方向的边长为a ,竖直方向的边长
b)
∙在图甲中,将线段
向右平移1个单位得到
,得到封闭图形
21B B (即阴影部分);
∙在图乙中, 将折线
向右平移1个单位得到
,得到封闭图形
321B B B (即阴影部分);
(1)在图丙中,请你类似的画一条有两个折点的折线,同样向右平移一个单位,从而得到一个封闭图形,并用斜线画出阴影;
(2)请你分别写出上述三个图形中阴影部分的面积:
=1S _________;=2S __________;=3S ___________.
(3)联想与探索:如图丁,在一个矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少?并说明你猜想的正确性.
2
1 A
A 2
1 B B 2
1 A A 3
2 1 A A A 3
2 1 B B B 3
2 1 A
A A ABC
△ DEF △
A 1 A 2
B 1
B
2
甲 A 1 A 2
B 1
B 2
乙
A 3
B 3
丙
丁
(§5.3~§5.4)参考答案
一、填空题 1.∠AED ∠BDE 两直线平行,同旁内角互补 DF AC 内错角相等,两直线平行 2.150° 3.60° 40° 4.形状 大小 相等 5.44 6.BB 1,CC 1,DD 1 7.9 8.9 二、选择题
11.C 12.C 13.A 14.B 15.C;16.D ;17.C ;18.C 三、解答题 19.∠ADC=118° 20.∠A=36°,∠D=144° 21.∠BED=78° 22.(1)∠P=360°-∠A-∠C ,
(2)∠P=∠A+∠C , (3)∠P=∠C -∠A , (4)∠ P=∠ A -∠ C(说明略).
23.相等的线段:AB DE =,BC EF =,AC DF =;
相等的角:BAC EDF =∠∠,ABC DEF =∠∠,BCA EFD =∠∠; 平行的线段:AB DE ∥,BC EF ∥,AC DF ∥ 24.540平方米.
2.略解:(1)略.(2) =1S ab-b ;=2S ab-b ;=3S ab-b .
(3)猜想类似面积仍是ab-b .方案:①将“路”沿左右两边界剪去;②把左右两侧草地合拼一个新矩形(如图4),则新矩形长为(a-1),宽为b ,面积为(a-1)b=ab-b .
图
4。
