二手房降价蔓延:4月份北京87%房源挂牌价下调
男女衣服裤子体重身高对照表(全)

体重(斤)80 ------ 90-----100--110---120--130-----140---150---160---170码数(裤子)25- --- 26- ----27- --28- - -29----30- ----31 ---32 ---33 ----34腰围(尺寸)1尺8-- --1尺9---2尺--2尺1--2尺2--2尺3--2尺4--2尺5--2尺6--2尺7腰围(厘米)64------- 67------70---72-----74-----77-----79-----82----87-----90腰围(尺寸)2尺5-- - 2尺6---2尺7--2尺8--2尺9--3尺--3尺1--3尺2--3尺3--3尺4臀围(厘米)83------- 86------89--- 92-----96-----100--103---107---110----113男上装S号165适合身高165CM左右,体重100斤以内M号170适合身高170CM左右,体重120斤以内L号175适合身高175CM左右,体重120-140斤以内XL号180适合身高180CM左右,体重140-160斤以内XXL号185适合身高185CM左右,体重160斤以上男裤XS号165A 28码腰围2尺1S号165B 29码腰围2尺2M号170A 30码腰围2尺3L号170B 32码腰围2尺4XL号175A 34码腰围2尺5XXL号175B 36码腰围2尺6XXXL号180 38码腰围2尺7希望可以帮都你------------------------------------------------------------------------------------------女装上衣尺码服装尺码中国号型胸围CM 腰围CM 肩宽CMS 38 153/157A 78-81 62-66 36M 40 158/162A 82-85 67-70 38L 42 163/167A 86-89 71-74 40XL 44 168/172A 90-93 75-79 42XXL 46 173/177A 94-97 80-84 44XXXL 48 177/180A 98-102 85-89 46服装尺码-国标尺码:XXS XS S M L XL XXL XXXL 加大XXXL 均码对应身高等尺寸解释! MEN 男装尺码1/XXS 2/XS 3/S 4/M 5/L 6/XL身高(cm) 155 160 165 170 175 180胸围(cm) 76 80 84 88 92 96腰围(cm) 64 68 72 76 80 84WOMEN 女装尺码1/XXS 2/XS 3/S 4/M 5/L 6/XL 7/XXL身高(cm) 150 155 160 165 170 175 180胸围(cm) 76 80 84 88 92 96 100腰围(cm) 60 64 68 72 76 80 84S SMALL 小的意思M MIDDLE 中的意思L LAGER 大的意思XL EXTRA LARGE 特大号XXL EXTRA EXTRA LARGE 超特大号女装----号型:前者表示身高/后者表示胸围针织号型(如T恤等):155/80---S160/85---M165/90---L170/95---XL梭织号型(如衬衫等):155/80B---S160/84B---M165/88B---L170/92B---XL------------------------------------------------------------------------------------------衣服型号与适合身体体型对应表S号:适合身高为1.55小玉米M号:长70cm,胸围51cm*2,适合身高为1.55~1.65人士,以女士和灵巧男士为主L号:长70cm,胸围54cm*2,适合身高为1.65~1.73人士,以挺拔女士和精干男士为主XL号:长73cm,胸围57cm*2,适合身高为1.73~1.80人士,以普通魁梧男士为主XXL号:长74cm,胸围60cm*2,适合身高为1.80~1.90人士,以威猛男士和发福者为主是英文缩写S=SMALL;M=MEDIUM;L=LARGE;XL=EXTRA LARGE;XXL=EXTR EXTRA LARGE1、上装尺码为:01码表示代码为:“XXS”02码表示代码为:“XS”03码表示代码为:“S”04码表示代码为:“M”05码表示代码为:“L”06码表示代码为:“XL”07码表示代码为:“XXL”2、茄克装尺码为:70表示代码为:“48”(M)71表示代码为:“50”(L)72表示代码为:“52”(XL)73表示代码为:“54”(XXL)3、裤装尺码为:26代表腰围为:“1.9尺”27代表腰围为:“2.0尺”28代表腰围为:“2.1尺”29代表腰围为:“2.2尺”30代表腰围为:“2.3尺”31代表腰围为:“2.4尺”32代表腰围为:“2.5尺”33代表腰围为:“2.6尺”34代表腰围为:“2.7尺”36代表腰围为:“2.8尺”38代表腰围为:“2.9尺”40代表腰围为:“3.0尺”42代表腰围为:“3.1尺”44代表腰围为:“3.2尺”50代表腰围为:“3.4尺”52代表腰围为:“3.5尺”54代表腰围为:“3.6尺”4、西服装尺码为:80表示代码为:“145”81表示代码为:“150”82表示代码为:“155”83表示代码为:“160”84表示代码为:“165”85表示代码为:“170”86表示代码为:“175”87表示代码为:“180”88表示代码为:“185”5、衬衣装尺码为:60表示代码为:“38”61表示代码为:“39”62表示代码为:“40”63表示代码为:“41”64表示代码为:“42”65表示代码为:“43”66表示代码为:“44”67表示代码为:“45”68表示代码为:“46”------------------------------------------------------------------------------------------男装尺寸尺码号型肩宽胸围后衣长袖长领宽前领深袖口袖肥袖笼(直量)袖底长S 165/88A 44 100 66 21 18 10.5 1`6.5 19 22.5 9.5M 170/92A 45 104 68 22 18.5 10.5 17 19.5 22.5 10L 175/96A 46 108 70 22.5 19.5 11.5 17.7 20 23 10XL 180/100A 47 112 72 23 20 12 18 20.5 23.5 10XXL 185/104A 48 116 74 23.5 21 12 18.5 21 24.5 10.5XXXL 190/108B 49 120 76 24 21.5 12.5 19 21.5 25.5 11女装尺码尺码号型肩宽胸围后衣长袖长领宽前领深袖口袖肥袖笼袖底长XS 155/76A 35 75 56 11.5 18.5 11.5 14 16.5 20 3.5S 160/80A 36 79 58 12 19 11.5 14.5 17 20.5 4M 165/84A 37 83 60 12.5 19.5 12 15 17.5 21 4.5L 170/88A 38 87 62 13 20 12.5 15.5 1`8 21.5 4.5XL 175/92A 39 91 64 13.5 20.5 12.5 16 18.5 22 5备注:后衣长从后领窝向下量体重(斤)80 ------ 90-----100--110---120--130-----140---150---160---170码数(裤子) 25- --- 26- ----27- --28- - -29----30- ----31 ---32 ---33 ----34腰围(尺寸) 1尺8-- --1尺9---2尺--2尺1--2尺2--2尺3--2尺4--2尺5--2尺6--2尺7腰围(厘米)64------- 67------70---72-----74-----77-----79-----82----87-----90腰围(尺寸) 2尺5-- - 2尺6---2尺7--2尺8--2尺9--3尺--3尺1--3尺2--3尺3--3尺4臀围(厘米)83------- 86------89--- 92-----96-----100--103---107---110----113男上装S号165适合身高165CM左右,体重100斤以内M号170适合身高170CM左右,体重120斤以内L号175适合身高175CM左右,体重120-140斤以内XL号180适合身高180CM左右,体重140-160斤以内XXL号185适合身高185CM左右,体重160斤以上男裤XS号 165A 28码腰围2尺1S号 165B 29码腰围2尺2M号 170A 30码腰围2尺3L号 170B 32码腰围2尺4XL号 175A 34码腰围2尺5XXL号 175B 36码腰围2尺6XXXL号 180 38码腰围2尺7体重(斤)80 ------ 90-----100--110---120--130-----140---150---160---170码数(裤子) 25- --- 26- ----27- --28- - -29----30- ----31 ---32 ---33 ----34腰围(尺寸) 1尺8-- --1尺9---2尺--2尺1--2尺2--2尺3--2尺4--2尺5--2尺6--2尺7腰围(厘米)64------- 67------70---72-----74-----77-----79-----82----87-----90腰围(尺寸) 2尺5-- - 2尺6---2尺7--2尺8--2尺9--3尺--3尺1--3尺2--3尺3--3尺4臀围(厘米)83------- 86------89---92-----96-----100--103---107---110----113 男上装S号165适合身高165CM左右,体重100斤以内M号170适合身高170CM左右,体重120斤以内L号175适合身高175CM左右,体重120-140斤以内XL号180适合身高180CM左右,体重140-160斤以内XXL号185适合身高185CM左右,体重160斤以上男裤XS号 165A 28码腰围2尺1S号 165B 29码腰围2尺2M号 170A 30码腰围2尺3L号 170B 32码腰围2尺4XL号 175A 34码腰围2尺5XXL号 175B 36码腰围2尺6XXXL号 180 38码腰围2尺7。
国际标准单位

国际标准单位我公司常用计量单位:g 、kg 、t、lb、klb、N、kN1法定计量单位的构成我国的法定计量单位包括:国际标准单位(见表4-1);国际单位制的辅助单位(见表 4-2);国际单位制中具有专门名称的导出单位(见表4-3);国家选定的非国际单位制单位(见表4-4);由以上单位构成的组合形式的单位;由词头(见表4-5)和以上单位所构成的十进倍数和分数单位。
国际标准单位(表4-1)量的名称长度面积体积质量密度时间电流热力学温度物质的量发光强度国际单位制的辅助单位(表4-2)量的名称平面角立体角国际单位制中具有专门名称的导出单位(表4-3)量的名称频率力;重力压力,压强能量;功;热功率;辐射通量电荷量电位;电压;电动势电容电阻电导磁通量磁通量密度、磁感应强度电感摄氏温度光通量光照度放射性活度吸收剂量单位名称米米2米3千克(公斤)千克/米3秒安[培] 开[尔文] 摩[尔] 坎[德拉]单位名称弧度球面度单位名称赫[兹] 牛[顿] 帕[斯卡] 焦[耳] 瓦[特] 库[仑] 伏[特] 法[拉] 电阻西[门子] 韦[伯] 特[斯拉] 亨[利] 摄氏度流[明] 勒[克斯] 贝可[勒尔] 戈[瑞]单位符号mm2m3kgkg/m3s A K mol cd单位符号rad sr单位符号Hz N Pa J W C V F Ω S Wb T H ℃ lm lx Bq Gy剂量当量国家选定的非国际单位制单位(表4-4)希[沃特] 单位名称分 [小]时天(日) [角]秒Sv 单位符号min h d (″) (′) (°) r/min n mile kn t u L,(1) eV tex量的名称时间平面角旋转速度长度速度质量体积能级差用于构成十进倍数和分数单位的词头(表4-5)[角]分度转每分海里节吨原子质量单位升电子伏特[克斯]所表示的因数10 10 10 10 10 10 10 10 10 10-3-2-11236182124词头名称尧[它] 泽[它] 艾[可萨]兆千百十分厘毫词头符号Y Z E M k h da d c m所表示的因数10 10 10 10 10 10 10 10 10 10-24-21-18-15-12-9-691215词头名称拍[它] 太[拉] 吉[咖] 微纳[诺] 皮[可] 飞[母拖] 阿[托] 仄[普托] 么[科托]词头符号P T G μ n p f a z y(1)周、月、年(年的符号为a)为一般常用时间单位。
人教版九年级上第21章《一元二次方程》实际应用题练习含答案

《一元二次方程》实际应用题专项练习(一)1.今年国庆中秋双节同庆,某店推出了莲蓉蛋黄月饼和流心芝士月饼两种月饼,其中莲蓉蛋黄月饼每盒成本15.5元售价40元,流心芝士月饼每盒成本18元售价48元.两种月饼均为整盒出售,不售散装.中秋节前,莲蓉蛋黄月饼和流心芝士月饼共销售了400盒,销售总额为17440元.(1)中秋节前,莲蓉蛋黄月饼卖了多少盒?(2)为迎接双节,中秋当日该店大促销,莲蓉蛋黄月饼“买一送一”(买一盒送一盒)但销售单价不变,其当日销量(不算赠品)达到中秋前售卖的莲蓉蛋黄月饼总销量的;流心芝士月饼每盒销售单价减少,其当日销量比中秋节前流心芝士月饼总销量增加了5a%.中秋当日两种月饼的销售利润为2736元,求a的值.2.某商场销售一批衬衫,平均每天可售出30件,每件盈利50元.为了扩大销售,增加盈利,商场采取了降价措施.经调查发现,衬衫的单价每降1元,商场平均每天可多售出2件.(1)若某天该衬衫每件降价5元,则当天该衬衫的销量为件,当天可获利元;(2)设每件衬衫降价x元,则商场日销售量增加件,每件衬衫盈利元(用含x的代数式表示);(3)如果商场销售这批衬衫要保证每天盈利200元,同时尽快减少库存,那么衬衫的单价应降多少元?3.随着现代互联网技术的广泛应用和快递行业的高速发展,网上购物的人越来越多,“双十一”当天更是成为了全民狂欢的网购节.据统计,某天猫官方旗舰店在2017年和2019年“双十一”当天的订单量分别为20万件和45万件,现假设该旗舰店每年“双十一”当天的订单量增长率相同.(1)求该旗舰店“双十一”当天订单量的年平均增长率;(2)如果该旗舰店的客服平均每人每天最多可以处理0.2万件订单,那么该旗舰店现有的250名客服能否当天完成2020年“双十一”网购节的所有订单?如果不能,请问至少还需要增加多少名客服?4.“新冠”疫情蔓延全球,口罩成了人们的生活必需品.某药店销售普通口罩和N95口罩,今年3月份的进价如表:普通口罩N95口罩进价(元/包)8 20(1)计划N95口罩每包售价比普通口罩售价贵16元,7包普通口罩和3包N95口罩总售价相同,求普通口罩和N95口罩每包售价;(2)按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包.该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天的利润为320元,求此时普通口罩每包售价.5.“疫情”期间,某小区准备搭建一个面积为12平方米的矩形临时隔离点ABCD,如图所示,矩形一边利用一段已有的围墙(可利用的围墙长度仅有5米),另外三边用9米长的建筑材料围成,为方便进出,在与围墙平行的一边要开一扇宽度为1米的小门EF,求AB的长度为多少米?6.今年某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件.为了促进疫情期间的市民消费,从而扩大销售,商场决定采取适当降价的方式促销.经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?7.如图,在Rt△ABC中,∠B=90°,AB=8cm,BC=10cm,点P由点A出发,沿AB边以1cm/s的速度向点B移动;点Q由点B出发,沿BC边以2cm/s的速度向点C移动.如果点P,Q分别从点A,B同时出发,问:(1)经过几秒后,AP=CQ?(2)经过几秒后,△PBQ的面积等于15cm2?8.10月份,是柚子上市的季节,柚子味酸甜,略带苦味,含有丰富的维生素c和大量的营养元素.有健胃补血,降血糖等功效,百果园大型水果超市的红心柚与沙田柚这两种水果很受欢迎,红心柚售价12元/千克,沙田柚售价9元/千克.(1)若第一周红心柚的销量比沙田柚的销量多200千克,要使这两种水果的总销售额不低于6600元,则第一周至少销售红心柚多少千克?(2)若该水果超市第一周按照(1)中红心柚和沙田柚的最低销量销售这两种水果,并决定第二周继续销售这两种水果,第二周红心柚售价降低了a%,销量比第一周增加了a%,沙田柚的售价保持不变,销量比第一周增加了a%,结果这两种水果第二周的总销售额比第一周增加了%,求a的值.9.2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.世界卫生组织提出:如果1人传播10人以上而且被传染的人已经确定为新冠肺炎,那么这个传播者就可以称为”超级传播者”.如果某地区有1人不幸成为新冠肺炎病毒的携带者,假设一个病毒携带者每轮传染的人数相同,经过两轮传染后共有81人成为新冠肺炎病毒的携带者.(1)请判断最初的这名病毒携带者是”超级传播者”吗?求他每轮传染的人数;(2)若不加以控制传染渠道,经过3轮传染,新冠肺炎病毒的携带者共有多少人?10.如图,有一道长为10m的墙,计划用总长为54m的篱笆,靠墙围成由六个小长方形组成的矩形花圃ABCD.若花圃ABCD面积为72m2,求AB的长.参考答案1.解:(1)设中秋节前,莲蓉蛋黄月饼卖了x盒,则流心芝士月饼卖了(400﹣x)盒,依题意得:40x+48(400﹣x)=17440,解得:x=220.答:中秋节前,莲蓉蛋黄月饼卖了220盒.(2)依题意得:(40﹣2×15.5)×220×+[48(1﹣)﹣18]×(400﹣220)(1+5a%)=2736,整理得:3a2+25a﹣148=0,解得:a1=4,a2=﹣(不合题意,舍去).答:a的值为4.2.解:(1)30+2×5=40(件),(50﹣5)×40=1800(元).故答案为:40;1800.(2)设每件衬衫降价x元,则商场日销售量增加2x件,每件衬衫盈利(50﹣x)元.故答案为:2x;(50﹣x).(3)设衬衫的单价应降m元,则每件衬衫盈利(50﹣m)元,商场日销售量为(30+2m)件,依题意得:(50﹣m)(30+2m)=2000,整理得:m2﹣35m+250=0,解得:m1=10,m2=25,又∵要尽快减少库存,∴m=25.答:衬衫的单价应降25元.3.解:(1)设该旗舰店“双十一”当天订单量的年平均增长率为x,依题意得:20(1+x)2=45,解得:x1=0.5=50%,x2=﹣2.5(不合题意,舍去).答:该旗舰店“双十一”当天订单量的年平均增长率为50%.(2)45×(1+50%)=67.5(万件).∵0.2×250=50(万件),50<67.5,∴该旗舰店现有的250名客服不能当天完成2020年“双十一”网购节的所有订单. 设需要增加m 名客服,依题意得:0.2×(250+m )≥67.5,解得:m ≥87,又∵m 为正整数,∴m 的最小值为88.答:该旗舰店现有的250名客服不能当天完成2020年“双十一”网购节的所有订单,至少还需要增加88名客服.4.解:(1)设普通口罩每包的售价为x 元,N 95口罩每包的售价为y 元.依题意得:,解得:. 答:普通口罩每包的售价为12元,N 95口罩每包的售价为28元.(2)设普通口罩每包的售价降低m 元,则此时普通口罩每包的售价为(12﹣m )元,日均销售量为(120+20m )包.依题意得:(12﹣m ﹣8)(120+20m )=320,整理得:m 2+2m ﹣8=0,解得:m 1=2,m 2=﹣4(不合题意,舍去),∴12﹣m =10.答:此时普通口罩每包的售价为10元.5.解:设AB =x 米,则BC =(9+1﹣2x )米,根据题意可得,x (10﹣2x )=12,解得x 1=3,x 2=2,当x =3时,AD =4<5,当x =2时,AD =6>5,∵可利用的围墙长度仅有5米,∴AB 的长为3米.答:AB 的长度为3米.6.解:设要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价x 元,由题意,得(360﹣x﹣280)(5x+60)=7200,解得:x1=8,x2=60.∵有利于减少库存,∴x=60.答:要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价60元.7.解:(1)设经过x秒后,AP=CQ,则AP=xcm,CQ=(10﹣2x)cm,依题意,得:x=10﹣2x,解得:x=.答:经过秒后,AP=CQ.(2)设经过y秒后,△PBQ的面积等于15cm2,则BP=(8﹣y)cm,BQ=2ycm,依题意,得:(8﹣y)×2y=15,化简,得:y2﹣8y+15=0,解得:y1=3,y2=5.答:经过3秒或5秒后,△PBQ的面积等于15cm2.8.解:(1)设第一周销售红心柚x千克.则沙田柚(x﹣200)千克,根据题意得:12x+9(x﹣200)≥6600,解得:x≥400.答:第一周至少销售红心柚400千克;(2)根据题意得:12(1﹣a%)×400(1+a%)+9×200(1+a%)=6600(1+%),∴a1=45,a2=0(舍去).答:a的值为45.9.解:(1)设每人每轮传染x人,依题意,得:1+x+(1+x)•x=81,解得:x1=8,x2=﹣10(不合题意,舍去),∵8<10,∴最初的这名病毒携带者不是“超级传播者”;(2)81×(1+8)=729(人),答:若不加以控制传染渠道,经过3轮传染,共有729人成为新冠肺炎病毒的携带者.10.解:设AB的长是xm,则BC的长是(18﹣x)m.根据题意,得x(18﹣x)=72,解这个方程,得x1=6,x2=12,当x=6时,18﹣x=12>10(不合题意,舍去).当x=12时,18﹣x=6符合题意.答:AB的长是12m.《一元二次方程》实际应用题专项练习(二)1.某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.(1)请直接写出y与x的函数关系式;(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?2.全球疫情爆发时,医疗物资极度匮乏,中国许多企业都积极的宣布生产医疗物资以应对疫情,某工厂及时引进了一条口罩生产线生产口罩,开工第一天生产500万个,第三天生产720万个,若每天增长的百分率相同.试回答下列问题:(1)求每天增长的百分率;(2)经调查发现,1条生产线最大产能是1500万个/天,若每增加1条生产线,每条生产线的最大产能将减少50万个/天.①现该厂要保证每天生产口罩6500万件,在增加产能同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?②是否能增加生产线,使得每天生产口罩15000万件,若能,应该增加几条生产线?若不能,请说明理由.3.万州区某民营企业生产的甲、乙两种产品,已知2件甲商品的出厂总价与3件乙商品的出厂总价相同,3件甲商品的出厂总价比2件乙商品的出厂总价多150元.(1)求甲、乙商品的出厂单价分别是多少元?(2)为促进万州经济持续健康发展,为商家搭建展示平台,为行业创造交流机会,2019年万州区举办了多场商品展销会.外地一经销商计划购进甲商品200件,购进乙商品的数量是甲的4倍,恰逢展销会期间该企业正在对甲商品进行降价促销活动,甲商品的出厂单价降低了a%,该经销商购进甲的数量比原计划增加了2a%,乙的出厂单价没有改变,该经销商购进乙的数量比原计划减少了,结果该经销商付出的总货款与原计划的总货款恰好相同,求a的值(a>0).4.某村计划建造如图所示的矩形蔬菜温室,要求长为24m,宽为12m,在温室内,沿前侧内墙保留2m宽的空地,其它三侧内墙各保留等宽的通道.当通道的宽为多少时,蔬菜种植区域的面积是210m2?5.现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,长沙某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递总件数分别为10万件和14.4万件,现假定该公司每月投递总件数的增长率相同.(1)求该快递公司投递总件数的月平均增长率;(2)如果平均每人每月最多可投0.5万件,那么该公司现有的29名快递投递员能否完成今年6月份的快递投递任务?如果不能,请问需要至少增加几名业务员?6.温润有度,为爱加温.近年来设计精巧、物美价廉的暖风机逐渐成为人们冬天必备的“取暖神器”,今年11月下旬某商场计划购进A、B两种型号的暖风机共900台,每台A型号暖风机售价为600元,每台B型号暖风机售价为900元.(1)若要使得A、B两种型号暖风机的销售额不低于69万元,则至多购进多少台A型号暖风机?(2)由于质量超群、品质卓越,11月下旬购进的A、B两种型号的暖风机全部售完.该商场在12上旬又购进了A、B两种型号的暖风机若干台,并且进行“双12”促销活动,每台A型号暖风机的售价比其11月下旬的售价优惠a%,A型号暖风机12月上旬的销售量比其在(1)问条件下的最高购进量增加a%,每台B型号暖风机的售价比其11月下旬的售价优惠a%,B型号暖风机12月上旬的销售量比其在(1)问条件下的最低购进量增加a%,A、B两种型号的暖风机在12月上旬的销售额比(1)问中最低销售额增加了a%,求a的值.7.柚子糖度高、酸味低,有益身体健康,深受大家喜爱.某水果店在去年8月份购进福建蜜柚和泰国青柚共900个,福建蜜柚进价为6元/个,泰国青柚进价为20元个,两种柚子的总进价不超过12400元.(1)该水果店去年8月份购进福建蜜柚最少多少个?(2)今年8月份,该水果店用和去年8月份相同的进价购进两种柚子,福建蜜柚购进数量为去年8月份购进数量的最小值,售价为16元/个.泰国青柚购进数量为去年8月份购进数量的最大值,售价为30元/个,两种柚子全部卖出.今年9月份,该水果店购进与上个月数量相同,进货单价相同的福建蜜柚.为了进一步占领市场份额,水果店对福建蜜柚进行了降价促销,它的售价在上个月的基础上先降价a%,再“买三送一”(每买3个就免费赠送1个,即4个装成一袋,一袋以3个的价格出售,但消费者只能整袋购买).受各种因素的影响,与上个月相比,泰国青柚的进价下降40%,进货量下降a%,售价上涨2a%.两种柚子卖完后,该水果店今年9月份销售两种柚子的总利润比上个月上涨,求a的值.8.为实现“先富带动后富,从而达到共同富裕”,某县为做好“精准扶贫”,2017年投入资金1000万元用于教育扶贫,以后投入资金逐年增加,2019年投入资金达到1440万元.(1)从2017年到2019年,该县投入用于教育扶贫资金的年平均增长率是多少?(2)假设保持这个年平均增长率不变,请预测一下2020年该县将投入多少资金用于教育扶贫?9.草根学堂院内有一块长30m,宽20m的矩形空地,准备将其建成一个矩形花坛,要求在花坛中修建三条长方形的矩形小道(如图),剩余的地方种植花草,要使种植花草的面积为532m2,那么小道的宽度应为多少米?(注:所有小道宽度相等)10.今年8月双福国际农贸市场某水果批发商用2.2万元购得“象牙芒”和“红富士苹果”共400箱,其中,“象牙芒”、“红富士”的数量比为5:3.已知每箱“象牙芒”的售价是每箱“红富士”的售价的2倍少10元,预计3月可全部销售完.(1)该批发商想通过本次销售至少盈利8000元,则每箱“象牙芒”至少卖多少元?(总利润=总销售额﹣总成本)(2)实际销售时,受中央“厉行节约”号召的影响,在保持(1)中最低售价的基础上,“象牙芒”的销售下降了%,售价下降了a%;“红富士”的销售量下降了a%,但售价不变.结果导致“象牙芒”、“红富士”的销售总额相等.求a的值.参考答案1.解:(1)设y与x的函数关系式为y=kx+b(k≠0),将(22,36),(24,32)代入y=kx+b,得:,解得:,∴y与x的函数关系式为y=﹣2x+80(20≤x≤28).故答案为:y=﹣2x+80(20≤x≤28).(2)依题意,得:(x﹣20)(﹣2x+80)=150,整理,得:x2﹣60x+875=0,解得:x1=25,x2=35(不合题意,舍去).答:每本纪念册的销售单价是25元.2.解:(1)设每天增长的百分率为x,依题意,得:500(1+x)2=720,解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).答:每天增长的百分率为20%;(2)①设应该增加m条生产线,则每条生产线的最大产能为(1500﹣50m)万件/天,依题意,得:(1+m)(1500﹣50m)=6500,解得:m1=4,m2=25,又∵在增加产能同时又要节省投入,∴m=4.答:应该增加4条生产线;②设增加a条生产线,则每条生产线的最大产能为(1500﹣50a)万件/天,依题意,得:(1+a)(1500﹣50a)=15000,化简得:a2﹣29a+270=0,∵△=(﹣29)2﹣4×1×270=﹣239<0,方程无解.∴不能增加生产线,使得每天生产口罩15000万件.3.解:(1)设甲商品的出厂单价是x元/件,则乙商品的出厂单价是x元/件,根据题意得:3x﹣2×x=150,解得:x=90,∴x =60.答:甲、乙商品的出厂单价分别是90、60元.(2)由题意得:, 解得:a 1=0(舍去),a 2=15.答:a 的值为15.4.解:设通道的宽为xm ,则蔬菜种植区域为长(24﹣2﹣x )m ,宽(12﹣2x )m 的矩形, 依题意,得:(24﹣2﹣x )(12﹣2x )=210,整理,得:x 2﹣28x +27=0,解得:x 1=1,x 2=27(不合题意,舍去).答:当通道的宽为1m 时,蔬菜种植区域的面积是210m 2.5.解:(1)设该快递公司投递总件数的月平均增长率为x ,根据题意,得10(1+x )2=14.4解得x 1=0.2,x 2=﹣2.2(不符合题意,舍去),答:该快递公司投递总件数的月平均增长率为20%.(2)由(1)得,14.4×1.2=17.28(万件),29×0.5=14.5,14.5<17.28,故不能完成任务.因为(17.28﹣14.5)÷0.5=5.56,所以还需要至少增加6名业务员.答:需要至少增加6名业务员.6.解:(1)设购进x 台A 型号暖风机,则购进(900﹣x )台B 型号暖风机, 依题意,得:600x +900(900﹣x )≥690000,解得:x ≤400.答:至多购进400台A 型号暖风机.(2)依题意,得:600(1﹣a %)×400(1+a %)+900(1﹣a %)×(900﹣400)(1+a %)=690000(1+a%),整理,得:150a﹣12a2=0,解得:a1=12.5,a2=0(不合题意,舍去).答:a的值为12.5.7.解:(1)设该水果店去年8月份购进福建蜜柚x个,则购进泰国青柚(900﹣x)个,依题意,得:6x+20(900﹣x)≤12400,解得:x≥400.答:水果店去年8月份购进福建蜜柚最少400个.(2)由(1)可知:今年8月份,该水果店购进福建蜜柚400个、泰国青柚500个.依题意,得:[16(1﹣a%)×﹣6]×400+[30(1+2a%)﹣20×(1﹣40%)]×500(1﹣a%)=[(16﹣6)×400+(30﹣20)×500]×(1+),整理,得:90a﹣3.6a2=0,解得:a1=25,a2=0(不合题意,舍去).答:a的值为25.8.解:(1)设该地投入教育扶贫资金的年平均增长率为x,根据题意,得:1000(1+x)2=1440,解得:x=0.2或x=﹣2.2(舍),答:从2017年到2019年,该地投入教育扶贫资金的年平均增长率为20%;(2)2020年投入的教育扶贫资金为1440×(1+20%)=1728万元.9.解:设小道进出口的宽度为x米,依题意得(30﹣2x)(20﹣x)=532.整理,得x2﹣35x+34=0.解得,x1=1,x2=34.∵34>20(不合题意,舍去),∴x=1.答:小道进出口的宽度应为1米.10.(1)设象牙芒有5x箱,则红富士有3x箱,根据题意得:5x+3x=400,解得x=50,则象牙芒有250箱,红富士有150箱.设每箱象牙芒y元,则250(2y﹣10)+150y﹣22000≥8000.解得:y≥50,∴2y﹣10≥90答:每箱“象牙芒”至少卖90元;(2)根据题意得:250(1﹣a%)•90(1﹣a%)=150(1﹣a%)•50,令t=a%,整理,得:4t2﹣5t+1=0,……(7分)解得:t=1(不合题意,舍去)或t=0.25,∴a=25.答:a的值为25.。
字母汉字

w山b白日夕黑风光p尸户八一乙丿巳二十己已幺厶夂m门門丑行内j皮毛发骨血手齿q车舟爻片邑x火贝革y艹n鸟飞羽z辶之赱`身母比匕两艮生長辰走足北s石r页夂止仑又叉文齐开习方zi卜[金钅l刀刂力勺七至弓戈d土癶鬼隶t疒病歹辛隶鬼g马牛羊犬豕k虫h禾米谷韭黄非4罒田皿丙酉而冗里首西]广厂小玄高贤v豸犭虎廘龙龍龟赤鼠5心血矢臼瓦7术殳矛予耒瓦9鱼c木f亠穴宀⺳⺈a幺丝糸纟o口e月_冫氵u礻衣衤.忄/食舌餐饣6雨水气卤⺮麻黍青2竹瓜麦豆麻黍0耳目鼻面见見8扌3王 玉1人亻子父,女母i言讠ㄗ阝ba巴bo孛be 备b-比b,不b.白b?包b6必b2般b0 邦b8本b3布b1卑bia\霸bia友bio皮bie 边bi,阜bi.百bi/表bi6辟bi2 扁bi0半bi8宾bi3并bi1北pa辟po 叵pe匹p-丕p, 普p/暴p6业p2番p0旁p8彭p3朋p1币pia否pio发pie片pi,卜pi.派pi/票pi6 樊pi2扁pi0 向pi8平pi3频pi1酉p.牌1ba爸oba吧8ba把yba芭hba粑tba疤xba靶ba8扒ba\八bao叭ba[钯2ba笆8bia拔9ba鲅;bia跋wba岜tba魃bia-灞biad坝biad壩bia3玐biac朳lbo勃_lbo渤ebo脖bo1伯bo-泊boq舶boc柏bo[铂bo2箔1bo侼/bo饽_bo浡biop博bio-y薄bio8搏bio2簙bioe膊_bio波bios礡2bio簸;bio跛3bio玻obio啵ybio菠bio.愽obo哱bo3碧tb-毙ob-吡]b-庇,b-妣yb-芘b-\毕b-o哔b-y荜b-n鸨5be惫1be俻1b1偹bex 贬bes砭bef 窆bet疺bie边2bie笾bie5 憋bie9鳖bie;蹩biel彆biev虌biek蟞bieu襒biet瘪cb.柏abi.絔b.1伯b.8拝b.+拜1bi.佰cbi.栢hbi.粨bi.8摆bi.\罢bi.u襬xbe韛8b/抱9b/鲍/b/饱yb/苞1b/孢6b/雹lb/\佨lb/刨jb/龅b/\保b/d堡b/x煲b/y葆b/u褒b/,媬b/d堢ubi/裱,bi/婊1bi/俵bi/e膘bi/[镖bi/g骠bi/1僄bi/d墂bi/p幖bi/c標bi/8摽bi/8c檦bi/t瘭bi.x熛bi/s磦bi/2篻[b6铋yb6 苾bb6毖_b6泌ob6咇1b6佖b61俾b6.婢b6j髀b6u裨b6w崥dbi6壁zbi6避3bi6璧ebi6臂bi6薜,bi6嬖]bi6廦bi64鼻bi6-濞bi6t痹bi62箅bi6\畀bi6,嬶b6]庳.b6怭8b2搬b28扳b2q版b2c板b2'阪b2d坂b2[钣b2h 粄b2b昄b2q\舨tb2瘢jn2搫b2w岅b27瓪zbi2遍abi2编mbi2匾xbi2煸kbi2蝙9bi2鳊1bi2徧.bi2惼8bi2揙7bi2牑bi2-汴bi2\卞bi2y苄bi28抃bi2.忭vbi2猵7\bi2甂hbi2稨sbi2碥bi2x炞b2-汳bi23玣hbi2\糄ybi2萹yhbi2藊ubi2褊lb0帮ab0绑cb0梆8b0挷pb0幚db0垹b0c榜b0s磅b01傍b0e膀b0i谤b0[镑b0y蒡b0d塝b08搒b07牓b07艕b0j髈1bi0伴8bi0拌.bi0怑abi0绊dbi0坢;bi0跘,bi0姅cbi0柈hbi0秚ub2褩kb2螌bi0\敝bi0t弊bi0y蔽bi0p幣b-;跸2b8笨[b8钵yb8苯b8\奔b8[锛b8o喯b88捹b8-渀b8z逩b3w崩b3;蹦b3a绷b3o嘣b31傰傰b0w嵭b0o嗙b3d堋b3dw塴b3f奟b3t痭;bi3跰1bi3倂zbi3迸/bi3饼8bi3摒pbi3屏1bi3併dbi3垪]bi3庰cbi3栟9bi3鮩.b3怖ob3咘1b3佈[b3钸8b3抪cb3柨bi3q辈bi35悲bi33琲bi3c棑`bi8兵tbi8殡_bi8滨jbi8鬓abi8缤[bi8镔cbi8槟j\bi8髌ebi8膑8bi8摈1bi8傧3bi8瑸c+bi8梹jibi8鬂bi8c柄bi8t病bi8\丙bi8x炳bi81邴bi88抦bi8y苪bi8.怲bi8b昞bi8b\昺bi8f窉bi81\陃bi80眪sb1碑bio陂]b1庳cb1椑xb1鞞b1\贝b1[钡b1o呗b1v狈ubi1褙ybi1苝bi1邶ebi1背8bi1揹bi11倍bi1x焙bi1y蓓1bi1偝bi1s碚bi1.悖bi1c棓cb,杯4b,罘b,8捕bi,u补bi,埠dbi,逋b,d埔bi,\卜b,o哺bi,o卟ob,吥b,b晡[b,钚b,u補b,w峬b,.悑b,f尃b,h秿b.]庯lpa劈1pa僻tpa癖6pa霹ipa譬opa噼npa䴙paj爬pa7耙pay葩pa33琶pac杷pa,妑pap帊pa[钯paq舥pa-潖pa2筢pab皅ba-汃pa;跁tpia痞pia.怕piap帕piao啪piay苩piau袙po叵fpo尀poz廹poz迫po3珀po-泊pios破piod坡pio-泼piot魄pio'陂piow岥[pi,钋pioy蔢piow岥pior颇[pio䥽pow岶pe匹pe\盘pes磐pe4盤pec槃pep幋pe,媻pie片9pie魸pie8撇pie0瞥piej撆pie,嫳pie[鐅pie-潎p-丕dp-坯op-呸ep-胚cp-柸,p-妚p-邳xp-噽xp-o嚭p-8批p-p屁p-4毗p-33琵p-o吡p-y芘p-4毘bi.x罴p,普ip,谱p,[铺p,-浦p,-y蒲8pi,扑cpi,朴1pi,仆p,e脯p,d埔p,ly葡p,m圃p,-f溥p,l 匍p,y莆pi,o噗pi,3璞pi,;蹼pi,-濮pi,1僕[p,镨pi,d墣p.牌2p.簰ep.簲4p.箄p.11俳p.8排b.-湃p.11徘pi.派p.v猅opi.哌pi.y苩pi.8拍pi/迫.z廹pi..怕ypi.蒎[pi.鎃p.c棑p.q輫p/暴xp/爆bp/曝1p/儤_p/瀑p/;跑p/-泡p/x炮p/l刨p/u袍p/t疱p.o咆p/]庖op/嚗p/v狍p/s砲p/-y萢p/2匏p/d垉p/x炰p/j皰p/j\爮pi/票bpi/ 飘 _pi/漂,pi/嫖0pi/瞟2pi/瓢opi/嘌api/缥gpi/骠tpi/瘭api/缥bpi/\飄lpi/剽1pi/僄.pi/慓api/\彯11pi/徱lpi/\勡2pi/\篻npi/翲pi/\皮pi/'陂pi/8披pi/t疲pi/[铍p6业p6邺cp6業wp6嶫dp6壶p6\匕p6o叱p6]庀pi6樊jpi6攀upi6襻pi6y蓖pi62篦pi6v貔pi6,媲pi6.嫓p2番_p2潘kp2蟠8p2播1p2僠sp2磻_pie沜p20盼2p2籓ep2膰p2x贫p28扮p2r颁p2r\攽pi2y扁gpi2骗2pi2篇1pi2偏npi2翩,pi2媥ipi2谝cpi2楄pi2c楩pi2\便pi2g犏pi2a緶pi2x鞭pi22箯p0旁sp0磅ep0膀kp0螃_p0滂7p0耪op0嗙yp0蒡1p0徬,p0嫎p0e脾p0o啤p0'郫p00睥p0d埤p0w崥pi0向opi0响/pi0饷,pi0姠bpi0 晌pi0r叛pi0u袢pi0-泮pi0e胖pi0l判pi04畔pi0;跘pi0p牉pi00眫p8彭_p8澎op8嘭ep8膨p8\盆p8-湓p8y葐pi8平_ypi8萍ipi8评dpi8坪ypi8苹cpi8枰opi8呯spi8砰.pi8怦8pi8抨3pi8玶pi88拼pi8,姘p2s砏pi87瓶pi8dp塀pi8p屏pi8p\帡pi8pp幈pi8]庰pi8s硑pi80聠pi8-洴pi82p箳p3朋np3鹏cp3棚sp3硼1p3倗swp3磞p3o喷p3-濆p3r歕p3=賁ypi3蘋pi8频4pi3颦pi32篷pi2y蓬p3a纄p1币1p1佩p1-沛p11伂ppi1配pi1酉_pi1酒pi1'陪pi1x赔pi1d培p.u裴pi1l剖pi1\咅8bu抔pi18掊pi1,婄3p1珮,p1姵pi1[锫pi14醅ypi1蓜pi13琣ma马oma吗sma码,ma妈ooma骂3ma玛kma蚂mia麻omia嘛,mia嫲maw密mak蜜mah秘ma-泌maf宓mao嘧mial弥miau祢miav猕mia-沵mo莫8mo摸emo膜cmo模/mo馍fmo寞_mo漠1mo摹imo谟vmo貘,mo嫫moj摩mos磨mot魔mol劘mom麽ymio茉mio末8mio抹_mio沫miot殁mio-没gmo蓦mosy蘑hmo秣,mo妺omo嗼dmo塻bmo暯m1么]m1庅pmio帓m-米zm-迷om-咪izm-谜0m-眯4zm-醚4im-谧hm-糜em-脒yzm-蒾_m-洣moh靡rm-敉vm-麋mou縻cme棉me 帛ame绵mec枚me3玫med坆mie灭_mie沔0mie眄,me婂mie丏miey蔑mie.懱mie2篾miek蠛mie-瀎miep幭mies礣meg牧m,母,m,姆m,p幕m,5慕m,b暮m,l募m,d墓m1仫.mo慔8m,拇dm,坶pmo幙mi,木ymi,莯_mi,沐6mi,霂vmi,狇mi,[钼mi,6睦mi,\目mi,y苜gm,牳m.y买pm.卖ym.荬m.d埋m.6霾mi.矛ymi.茅ccmi.懋umi.袤mi.e霡mie5衇m.y薶epi.脈6pi.霢kmi.蟊drmi.堥m/毛jm/\耄jm/ 髦gm/牦ym/芼fm/旄m/p帽m/\冒m/3瑁m/,媢0m/眊5rmi.愗cm/枆wrmi.嵍cmi.柕0rmi.瞀mi/苗0mi/瞄vmi/猫[mi/锚_mi/渵omi/喵8mi/描,mi/媌]mi/庿nmi/鹋mi/h秒mi/,妙mi/0眇mi/-0渺mi/a缈mi/c杪mi/20篎m6牟0m6眸om6哞km6蛑1m6侔cm6桙.m6恈_m6洠m6d墨m6v默m6x黙m6,嫼mi6某xmi6煤imi6谋,mi6媒mi6a缪mi6i谬m2曼.m2慢_m2漫ym2蔓am2缦/m2馒9m2鳗pm2幔im2谩xm2熳dm2墁[m2镘1m2僈jm2鬘cm2槾8m2摱vm2獌m2-满m20瞞m20瞒m2k螨m2c樠mi2免lmi2勉,mi2娩bmi2冕mi2.愐mi2\面mi2a缅mi21偭mi2麺mi2o喕mi2-湎mi2e腼mi2l勔1mi2俛mi2,媔,me嬵m0莽km0蟒_m0漭m00盳mo.忙m00盳m00盲m0'邙m0y芒m0-y茫m01氓m0g牤m0o吂m0-汒mi0\尨mi0,娏mi0o哤mi0g牻m0c杗mi0]庬m0.y恾m8门1m8们5m8闷xm8焖8m8扪[m8钔m8門m25懑m2b暪m8=冥m8-溟m80瞑m8b暝m8k螟m8y蓂m8,嫇m8.慏m8c榠mi8民0mi8眠8mi8抿_mi8泯3mi8珉wmi8岷omi8呡ymi8苠5mi8愍lmi8刡,mi8姄mi8[铭mi8\名mi8y茗mi8-洺mi81佲mi84酩mi8i詺mi80眳mi8,姳m3=蒙em3朦cm3檬_m3濛m3v猛m3\孟m3[锰m3l勐勐m3k蜢bm3曚vm3獴m38掹mi3明ymi3萌4mi3盟mi3b梦mi3b夢mi3.懵mi3z夣mi31儚mi37甍mi3t薨mi3.b懜.m3懞cmi3橗8mi3擝m1每cm1梅6m1霉4m1酶ym1莓,m1媚mi1眉cmi1楣_mi1湄wmi1嵋m1.妹m1t魅m1f寐m1b昧m10眛[mi1镅mi1\美mi1[镁mi1,媄mi1-渼dmi1堳m1-沬oli8命omi8鸣4mi8皿;u/]庙wa瓦8wa挖wao哇wa,娃hmio袜1wa佤wa-洼wak蛙owa咓wa-f漥wia巫iwia诬owia噬2wia筮wia\亏wiad圬wia-污wam街wo我swo硪wiae肟wo\呙wof窝wok蜗woy莴wo-涡wo-z濄owio喔8wio握_wio渥wio屋jwio龌1wio偓pwio幄cwio楃wio-沃ewio腛w-为1w-伪w-\卫1w-\僞w,乌dw,坞w.\邬w,呜wio[鋈wi,午1wi,仵.wi,忤1wi,伍wi,五wi,\戊wi,h戌wi,d戍[w,钨_w6潕4w6舞w6无yw6芜1w6儛w6\武iw6譕,w6妩dw6墲w6n鹉wi6吾owi6唔.wi6悟8wi6捂cwi6梧bwi6晤xwi6焐_wi6浯fwi6寤.w6怃1wi6俉]w6庑wi6,婺wi6n鹜w.\外w.\歪;w.处wi.威wwi.崴wi.\兀ow/喂w/畏xw/煨vw/猥1w/偎w/隈w/y蔚w/5慰ww/嵔w/x熨owi/味wi/未w/\尉wi/\微wi/y薇wi/a徽ywi.葳yi/w嶶_w-沩w2万zw2迈w2a纨w2\丸,wi2婉ewi2腕wi2宛ywi2菀wi2\弯wi2-湾hwi2豌3wi2琬lwi2剜dwi2塆_wi2涴.wi2惋4wi2畹kwi2蜿1wi2倇dwi2埦w0王_w0汪0w0望1w0往bw0旺cw0枉1\w0仼w0\完w0y莞w0x烷w0b皖w0e脘a9i2绾w2y芄w03琓5wi0忘wi0亡,wi0妄ywi0莣1w0彺wi0a网wi0\罔wi0a網wi0t魍wi0.惘wi0q辋hw0尪zw0迋ow8吻w8勿yw8芴w8-温w88搵w8t瘟w8p韫wi8文awi8纹6wi8雯kwi8蚊_wi8汶wi80闻wi8o问3wi8玟xwi8炆uwi8紊,wi8妏lw8刎w8ay藴w83瑥w3翁ow3嗡_w3滃7w3瓮yw3蓊lw3勜dw3塕ww3嵡bw3暡w30齆w3]廱w3-灉w3\邕w3o嗈wi3务6wi3雾wi3i误wi3\吴wi3k蜈w1委awi1纬tw1痿7w1矮wi1韦xwi1炜3wi1玮1wi1伟mwi1围w1o唯yw1萎w1.惟w1a维w1p帷pwi1帏wi1c桅,we娓we尾wex贿w1-潍zwi1违ywi1苇wie'隗wie\魏_w-沩wiew巍wie胃iwie谓vwie猬_wie渭qwie艉ywi1菋we-洧cwe梶swi1韪iw1诿,wie媦h..斡wo8挝1w1倭ja加cja架1ja伽zja迦yja茄tja痂gja驾3ja珈cja枷uja袈4ja嘉jaw岬ja\甲ja[钾jae胛pjua幏,jua嫁hjua稼jua家[jua鎵1jua傢[jua镓jua1假juay葭jua9嘏jua,婽2ja笳lja乫jo节cjo栉je介‘je阶4je界yje芥je-洁jel劼jea结jeh桔8juo掘juo屈1juo倔juo8捷juo,婕juo0睫the疥tjo疖jei诘jeh秸hje蚧jer颉oje吤juoo啑,je妎8juee撅jue厥yjue蕨wjuo崛ojue噘jue-决jue3玦juei诀jue8抉jue7缺juex炔jueu袂jo8揭jof竭jog羯j-几cj-机/j-饥ej-肌oj-叽sj-矶3j-玑ij-讥j-8挤j-l剂j--济j-;跻j-6霁j-y荠j-o哜lj.剧8j,据j,居[j,锯3j,琚;j,踞1j,倨uj,裾j,\局j,x焗cj,椐j,[锔j,1侷oj,啹j.-减j.兼j.2箴j.s碱ju.建[ju.键eju.腱1ju.健jju.毽j.a缄ju.;践ju./钱ju.2笺ju.a线ju.\戋y9i2菅yci3茧ju./饯gju.犍cju.楗1j.傔8ju.揵j/交qj/较ej/胶j/郊,j/姣kj/蛟/j/饺bj/皎aj/绞vj/狡[j/铰;j/跤1j/佼yj/茭cj/校9j/鲛nj/䴔j/,娇j/q轿j/7矫j/w峤j/g骄1ju/僬ju/焦僬yju/蕉sju/礁4ju/醮cju/櫵ju/a缴ju/c檄ju/1徼ju/11儌ju/-激ju/z邀ju/o噭j6久3j6玖tj6疚xj6灸cj6柩_j6汣j6\就j6]厩j6n鹫j61僦j6t殧ju6九fju6究nji6鸠_ju6氿lju6勼1ju6仇ju6\臼ju6i旧ju61舅ju6y舊j2间[j2简_j2涧[j2锏uj2裥j2l剑j2c检j21俭j2s硷ju2卷lju2劵0ju2眷1ju2倦mju2圈.ju2惓8ju2捲[ju2锩lju2勌ju2,娟ju28捐ju2a绢ju2n鹃ju2-涓ju2v狷ju2d埍ju2.悁ju24罥ju2c梋ju20睊ju27瓹.ju2慻ju2x焆eju2腃j0将fj0奖yj0蒋4j0酱6j0浆cj0桨ju0夅ju0年ju0降aju0绛8j0摪[j0锵j01僵j0a缰j0ld疆juo-江ju0h豇juoy茳ju0c匞j0d壃j0t殭j0c橿j0ld彊j0s礓[j8镜j8竟dj8境1j8傹\j8竞2j8竸j8a经j81径j8l劲j8r颈j8-泾j8y茎j8e胫j8z迳j8t痉ju8君ju8郡3ju8珺yju8莙fju8窘ju8g骏ju81俊ju8f竣ju8w峻ju8-浚ju8x焌ju84畯ju8b晙8ju8捃cju8桾ju8y葰ju8d埈zju3近ju3斤xju3靳cju3匠1ju3伒j3\晋j3a缙j33瑨ju3禁uju3襟oju3噤ju3x炯ju3b囧ju3z迥ju3x烱1ju8侰ju3d坰ju3bd埛ju3-泂ju3-b浻2j1笕j1见]j1觅fj1觉8j1搅3j1现qj1舰8j1挸j1[鑑j1\监j1h尴j1[鉴j3l戬lju1剪ju1前2ju1箭xju1煎nju1翦ju1\柬ju1i谏j2l捡ve8拣yqa荚rqa颊qa夹qa郏_qa浃8qa挟[qa铗oqa唊qa.恰qa-洽qau袷qac匼qap帢ce8揢cej髂qua启oqua啓qua8掐qua/馅qua'陷quao啗qo欠rqo软wqo嵌yqo芡1que儙qo-渐qod堑quo泉_quo湶cquo楾equo腺aquo缐quom圈quoa绻quok蜷quoj拳quoo啳quo,婘quol弮quo8捲quo8棬3quo瑔quo.惓quoc椦qe切fqe窃sqe砌qe\且_qe沏qe,姐qe;趄.qa悏.mqa惬2qa箧mqa匧qe2笡1que儙que遣ique谴aque缱que\雀ques确quec榷que1傕quen鹤que8搉quew崅q-其cq-棋3q-琪fq-旗eq-期_q-淇uq-祺rq-欺gq-骐uq-綦vq-麒yq-萁q-;起uq-\褀q-w岂q-c杞rquq啟sq-碁sze碛q-3玘q,去uq,祛qek蛆oq,呿qe1伹q,m衢q,\瞿q,1忂8q,抾.q,怯q.妾pq.帹8q.接cq.椄_q.淁6q.霎q.g骞q.c寨q.j搴vwi8虔qu.肩;q.踥8qu.掮qu.2签qu.\佥qu.g验qu.'险q/巧fq/窍q/1俏q/.悄q.x鞘q.w峭r3d壳qu/l劁qu/0瞧cqu/桥1qu/侨qu/乔yqu/荞squ/硚wqu/峤qu/c樵qu/.憔qu/i谯q/i诮qu/,嫶ju/8撽3q6球q6求zq6逑1q6俅uq6裘jqi6毬_Q6浗q6\丘q6'邱q6d坵q6k蚯tq6殏qu6秋_qu6湫cqu6楸9qu6鳅yqu6萩,qu6媝8qu6揪qu6z遒qu6\酋qu6k䲡qu6w崷qu6x煪q2千1q2仟zq2迁[q2钎aq2纤.q2忏yq2芊q2阡8q2扦ju.-浅q2[钤q2b黔q2x贪yqu2荃[qu2铨iqu2诠4yqu2醛qu2全squ2硂2qu2筌1qu2佺tqu2痊,qu2姾.qu2恮wqu2峑qu2r颧qu2c權qu2c权qu2l劝qu2,孉qu2w巏qu2l勸q0强[q0镪uq0襁lq0勥gq0犟8q0摾wq0嵹q08抢q0o呛q0x炝q0c枪ek3腔qol戗q0;跄oqu0嗴qu0羌i[8讲qu0姜ju0y姜_qu0溬qu0d墙qu0c樯qu0y蔷qu0,嫱qu0]廧q8青_q8清iq8请.q8情bq8晴2q8箐6q8氰kq8蜻9q8鲭xq8䞍mq8圊oq8啨q81侵q8f寝q8-f寖q8-浸q8g骎q8[锓q81f寑1qu8倾qu8顷]qu8庼qu8g群qu8u裙qu8g羣qu8p帬qu8u裠q3穷4q3寡lq3穹yq3䓖llq3宆q3c桏q33琼q3\邛q32筇q3k蛩xq3焪qu33琴qu3y芩qu3禽8qu3擒qu3u衾_]3沁[q1锲vq1猰cq1楔q1契q1-漆q1e膝qu1犬oqu1吠ooqu1哭4qu1畎4oqu1器qu1i谦qu1r歉qu1.慊8qi/撬cqi/橇ge7乾[g2钳q'祁zak虬]da庆xa下oxa吓kxa虾xab暇xa3瑕xaz遐xa\叚xa6霞xuaq辖xua0瞎xa0睱xa1徦xua夏]xua厦fxua廈xo写_xo泻fxo冩xoc榭xoi谢xod塮xuo鲜yxuo藓txuo廯xuo1仙xuoh籼xuow佡.xe懈xe解kxe蟹zxe邂xe8撷xe\颉xue雪9xue鳕cxue樰xfia靴xue6泶xue1学exue膤xuer敩xued壆xuew峃_xe澥vxe獬]xe廨xea缬xxo寫x-希hx-稀xx-烯bx-晞x-郗ox-唏_x-浠1x-俙x-=息x-,媳x-x熄x-.悕x-k螅x-[鎴vx-豨x,虚ox,嘘dx,墟rx,歔x.\胥x,,婿x,i谞x,1偦x,d壻x,8揟px.协x.办ex.胁x.\显x.-湿xuoy苮xu.穴dxu.坹wxu.岤_xu.泬xu.8掀xuo6氙xu.[锨rx.顕xx/小x/肖_x/消[x/销lx/削fx/宵6x/霄zx/逍tx/魈sx/硝ax/绡x/l効x/c校x/r效x/1傚x/,姣oxu/哮bxu/晓xu/孝xu/o啸xu/2箫xu/y萧xu/-潇xu/l彇1xu/侾rxu/教fxu/宯xu/c橚txu/痚x6休ox6咻vx6貅jx6髹xx6烌]x6庥x6w岫x6u袖3xu6璓xu6秀axu6绣[xu6锈3xu6琇xu6\臭zxu6透xu6-溴xu6o嗅xu6k螑xu64齅9x6鮴ix6诱yxu6莠x2先fx2宪_x2冼[x2铣4x2酰;x2跣2x2筅x2n鹇x2,娴,j.嫌x2t痫x2\闲x21僩,x2姺_x2-洗xu2宣zx2选yxu2萱txuo癣oxu2喧xxu2煊3xu2瑄bxu2暄cxu2楦_xu2渲,xu2媗sxu2碹xu2\玄xu2x炫xu20眩xu2[铉xu2-泫xu23玹xu2,妶xu21伭xu2.怰x0相5x0想2x0箱_x0湘]x0厢yx0葙ax0缃fx0廂x0u祥x0i详x0]庠x0n翔x0a絴axu0像xu0象cxu0橡lxu0勨wxu0嶑xu0\乡xu0/飨xu0y芗xu09鲞xu0j郷_xu0潒xu0e膷x8星4x8醒vx8猩ex8腥.x8惺xx8煋ix8謃3x8瑆0x0睲2x8篂9x8鯹x8ld型x8a形x8ld刑x8y荇x81邢x8-洐x8s硎x81l侀x8-y葕xu8旬ixu8询yxu8荀_xu8洵3xu8珣1xu8徇txu8殉.xu8恂xu8郇wxu8峋11xu8侚oxu8咰,xu8姰xu8i训xu8z巡xu8g驯xu8c杊xu8a紃x3凶elx3胸lx3匈_x3汹1x3兇.x3忷olx3哅.lx3恟_lx3洶ix3訩ix3讻ilx3詾ex3胷x3\幸x3.悻x3a緈x3,婞x31倖x3-涬xu3兄_xu3况oxu3咒uxu3祝xu3,姓xu3.性xu3v狌xu39鮏ox1啣x1卸x1\县x15悬xu1旋3xu1璇axu1縼_xu1漩axu8绚[xu1镟,xu1嫙xu1i谐xu11偕h0香yh0萫li/'隙f/i项d9ed鞋ya邪77io斜d,a续ya牙oya呀yya芽4ya雅1ya伢nya鸦iya讶[ya䥺kya蚜3ya琊y4ya蕥_ya冴]ya厊yaw崖ya-涯ya\厓oyua啞yua亚oyua哑,yua娅6yua氩dyua垭cyua桠1yua俹yad堐yuad压。
江苏省百校大联考2024届高三上学期第二次考试数学含答案解析

江苏省百校联考高三年级第二次考试数学试卷注意事项:1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
选择题部分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z满足z(1+i)=1-3i,则复数z的共轭复数z−的模长为()A.√2B.√3C.2D.√52.已知集合M={x|1xx-1<-1},N={x|ln x<1},则M∪N=()A.(0,1]B.(1,e)C.(0,e)D.(-∞,e)3.已知平面向量a=(-2,1),c=(2,t),则“t>4”是“向量a与c的夹角为锐角”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.若函数f(x)=sin(ωx+φ)(ω>0,|φ|<π2)的部分图象如图所示,A(π3,0),B(7π12,-1),则f(x)的解析式是()A.f(x)=sin(x+π6)B.f(x)=sin(x-π6)C.f(x)=sin(2x+π3)D.f(x)=sin(2x-π6)5.将一枚均匀的骰子独立投掷两次,所得的点数依次记为x,y,记A事件为“C8xx>C8yy”,则P(A)=()A.1136B.13C.1336D.5126.若直线y=ax+b是曲线y=ln x(x>0)的一条切线,则2a+b的最小值为()A.2ln 2B.ln 2C.12ln 2D.1+ln 27.已知抛物线C:y2=2px(p>0)的焦点为F,且抛物线C过点P(1,-2),过点F的直线与抛物线C交于两点,A1,B1分别为A,B两点在抛物线C准线上的投影,M为线段AB的中点,O为坐标原点,则下列结论正确的是()A.线段AB长度的最小值为2B.△A1FB1的形状为锐角三角形C.A,O,B1三点共线D.M的坐标不可能为(3,-2)8.设数列{a n}的前n项和为S n,且S n+a n=1,记b m为数列{a n}中能使a n≥12mm+1(m∈N*)成立的最小项,则数列{b m}的前2023项和为()A.2023×2024B.22024-1C.6-327D.112-328二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知定义在R上的奇函数f(x)满足f(x-1)=f(x+1),则以下说法正确的是()A.f(0)=0B.f(x)的一个周期为2C.f(2023)=1D.f(5)=f(4)+f(3)10.双曲线C:xx2aa2-yy2bb2=1(a>0,b>0),左、右顶点分别为A,B,O为坐标原点,如图,已知动直线l与双曲线C左、右两支分别交于P,Q两点,与其两条渐近线分别交于R,S两点,则下列命题正确的是()A.存在直线l,使得AP∥ORB.l在运动的过程中,始终有|PR|=|SQ|C.若直线l的方程为y=kx+2,存在k,使得S△ORB取到最大值D.若直线l的方程为y=-√22(x-a),RRRR�����⃗=2RRSS�����⃗,则双曲线C的离心率为√311.在平行六面体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,∠BAD=∠BAA1=∠DAA1=60°,动点P在直线CD1上运动,以下四个命题正确的是()A.BD⊥APB.四棱锥P-ABB1A1的体积是定值C.若M为BC的中点,则AA1B�������⃗=2AAAA������⃗-AACC1�������⃗�����⃗·PPCC�����⃗的最小值为-14D.PPAA12.已知函数f(x)=a(e x+a)-x,则下列结论正确的有()A.当a=1时,方程f(x)=0存在实数根B.当a≤0时,函数f(x)在R上单调递减C.当a>0时,函数f(x)有最小值,且最小值在x=ln a处取得D.当a>0时,不等式f(x)>2ln a+32恒成立非选择题部分三、填空题:本题共4小题,每小题5分,共20分.13.若关于x的不等式ax2-2x+a≤0在区间[0,2]上有解,则实数a的取值范围是▲.14.已知{a n}是递增的等比数列,且满足a3=1,a1+a3+a5=919,则a4+a6+a8=▲.15.如图,若圆台的上、下底面半径分别为r1,r2,且r1r2=3,则此圆台的内切球(与圆台的上、下底面及侧面都相切的球叫圆台的内切球)的表面积为▲.16.设a>0,已知函数f(x)=e x-a ln(ax+b)-b,若f(x)≥0恒成立,则ab的最大值为▲.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)锐角△ABC的内角A,B,C的对边分别为a,b,c,已知1-cos AA sin AA=sin2SS1+cos2SS.(1)证明:cos B=aa2bb.(2)求aa bb的取值范围.18.(12分)受环境和气候影响,近阶段在相邻的甲、乙、丙三个市爆发了支原体肺炎,经初步统计,这三个市分别有8%,6%,4%的人感染了支原体肺炎病毒,已知这三个市的人口数之比为4∶6∶10,现从这三个市中任意选取一个人. (1)求这个人感染支原体肺炎病毒的概率;(2)若此人感染支原体肺炎病毒,求他来自甲市的概率. 19.(12分)设数列{a n }的前n 项和为S n ,已知a 1=3,2S n =3a n -3. (1)证明数列{a n }为等比数列;(2)设数列{a n }的前n 项积为T n ,若1log )232)(21(13+•>+−−∑=n a T a S k n nk k k k λ对任意n ∈N *恒成立,求整数λ的最大值. 20.(12分)设椭圆xx 2aa 2+yy2bb2=1(a>b>0)的左、右顶点分别为A 1,A 2,右焦点为F ,已知AA 1F �������⃗=3FFAA 2�������⃗.(1)求椭圆的离心率.(2)已知椭圆右焦点F 的坐标为(1,0),P 是椭圆在第一象限的任意一点,且直线A 2P 交y 轴于点Q.若△A 1PQ 的面积与△A 2FP 的面积相等,求直线A 2P 的斜率. 21.(12分)如图所示,在四棱锥P-ABCD 中,底面ABCD 是正方形,平面PAD ⊥平面ABCD ,平面PCD ⊥平面ABCD. (1)证明:PD ⊥平面ABCD.(2)若PD=AD , M 是PD 的中点,N 在线段PC 上,求平面BMN 与平面ABCD 夹角的余弦值的取值范围.22.(12分)已知函数f (x )=x ln x-12ax 2(a>0).(1)若函数f (x )在定义域内为减函数,求实数a 的取值范围; (2)若函数f (x )有两个极值点x 1,x 2 (x 1<x 2),证明:x 1x 2>1aa .江苏省百校联考高三年级第二次考试数学试卷参考答案1.D【解析】法一:因为z(1+i)=1-3i,所以z=1-3i1+i=(1-3i)(1-i)(1+i)(1-i)=1-3-4i2=-1-2i,所以|z−|=|z|=√5,故选D.法二:两边取模|z(1+i)|=|1-3i|,得|z|·|1+i|=|1-3i|,所以|z−|=|z|=√5,故选D.2.C【解析】解不等式1xx-1<-1,即xx xx-1<0,所以0<x<1,即M=(0,1),由ln x<1,得0<x<e,所以N=(0,e),所以M∪N=(0,e),故选C.3.C【解析】a=(-2,1),c=(2,t).若a∥c,t×(-2)=2×1,得t=-1,此时a与c互为相反向量;若a·c=(-2)×2+t=t-4>0,得t>4,此时向量a与c的夹角为锐角.故“t>4”是“向量a与c的夹角为锐角”的充要条件,故选C.4.C【解析】由图象知T=4×(7π12-π3)=π,故ω=2.将(7π12,-1)代入解析式,得sin(7π6+φ)=-1,所以7π6+φ=-π2+2kπ,k∈Z,又|φ|<π2,即φ=π3,所以f(x)=sin(2x+π3).故选C.5.C【解析】抛掷两次总的基本事件有36个.当x=1时,没有满足条件的基本事件;当x=2时,y=1满足;当x=3时,y=1,2,6满足;当x=4时,y=1,2,3,5,6满足;当x=5时,y=1,2,6满足;当x=6时,y=1满足.总共有13种满足题意,所以P(A)=1336,故选C.6.B【解析】设切点为(x0,ln x0),y'=1xx,则�aa=1xx0,aaxx0+b=ln xx0,得b=ln x0-1,∴2a+b=2xx0+ln x0-1.设f(x)=2xx+ln x-1(x>0),f'(x)=-2xx2+1xx=xx-2xx2,当x∈(0,2)时,f'(x)<0,当x∈(2,+∞)时,f'(x)>0,∴f(x)min=f(2)=ln 2,∴2a+b的最小值为ln 2.7.C【解析】因为抛物线C过点P(1,-2),所以抛物线C的方程为y2=4x,线段AB长度的最小值为通径2p=4,所以A错误;由定义知AA1=AF,AA1∥x轴,所以∠AFA1=∠AA1F=∠A1FO,同理∠BFB1=∠B1FO,所以∠A1FB1=90°,所以B错误;设直线与抛物线C交于AB:x=my+1,联立抛物线,得y2-4my-4=0,设A(x1,y1),B(x2,y2),则y1·y2=-4,k OA=yy1xx1=4yy1=-y2,因为B1(-1,y2),所以kk OOBB1=-y2=k OA,A,O,B1三点共线,所以C正确;设AB的中点为M(x0,y0),则y0=yy1+yy22=2m,x0=my0+1=2m2+1,取m=-1,M(3,-2),所以D错误.故选C. 8.D【解析】当n=1时,a1=12,由S n+1+a n+1=1,得2a n+1-a n=0,∴a n=12nn,显然{a n}递减,要使得a n最小,即要使得n最大,令12nn≥12mm+1,得2n≤2m+1.若m=1,则n≤1,b1=a1=12;若2≤m≤3,则n≤2,b m=a2=14;若4≤m≤7,则n≤3,b m=a3=18;若8≤m≤15,则n≤4,b m=a4=116;…;若1024≤m≤2047,则n≤11,b m=a11=1211.∴T1=b1=12,T3=b1+(b2+b3)=12+12=1,T7=b1+(b2+b3)+(b4+b5+b6+b7)=12+12+12=32,…,∴T204 7=11×12=112,∴T2023=112-24211=112-328,故选D.9.ABD【解析】f(x)是R上的奇函数,因此f(0)=0,A正确;由f(x-1)=f(x+1)得f(x)=f(x+2),所以2是它的一个周期,B正确;f(2023)=f(2×1011+1)=f(1),而f(1)=0,C错误;f(4)=f(0)=0,f(5)=f(3),因此f(5)=f(4)+f(3),D正确.故选ABD.10.BD【解析】A选项,与渐近线平行的直线不可能与双曲线有两个交点,故A错误;B选项,易证明线段PQ与线段RS的中点重合,故B正确;C选项,当k,S△ORB会趋向于无穷,不可能有最大值,故C错误;D选项,联立直线l与渐近线y=bb aa x,解得S(aa2√2b+a,aabb√2b+a),联立直线l与渐近线y=-bb aa x,解得R(aa2-√2b+a,aabb√2b-a),由题可知,RRRR�����⃗=2RRSS�����⃗,所以y S-y R=2(y B-y S),即3y S=y R+2y B,3aabb√2b+a=aabb√2b-a,解得b=√2a,所以e=√3,故D正确.故选BD.11.BCD【解析】对于A,假设BD⊥AP,则BD⊥平面ACD1,因为AC⊂平面ACD1,所以BD⊥AC,则四边形ABCD是菱形,AB=AD,A不正确;对于B,由平行六面体ABCD-A1B1C1D1得CD1∥平面ABB1A1,所以四棱锥P-ABB1A1的底面积和高都是定值,所以体积是定值,B正确;对于C,AACC1�������⃗=AASS�����⃗+AAAA�����⃗+AAAA1�������⃗,AAAA������⃗=AASS�����⃗+12AAAA�����⃗,故2AAAA������⃗-AACC1�������⃗=AASS�����⃗-AAAA1�������⃗=AA1B�������⃗,故C正确;对于D,设PPCC�����⃗=λAA1C�������⃗,PPAA�����⃗·PPCC�����⃗=(PPCC�����⃗+CCSS�����⃗+SSAA�����⃗)·PPCC�����⃗=(λAA1C�������⃗-AAAA�����⃗-AASS�����⃗)·λAA1C�������⃗=(λAA1B�������⃗-AAAA�����⃗-AASS�����⃗)·λAA1B�������⃗=(λAASS�����⃗-λAAAA1�������⃗-AAAA�����⃗-AASS�����⃗)·(λAASS�����⃗-λAAAA1�������⃗)=λ(λ-1)|AASS�����⃗|2-λ2AAAA1�������⃗·AASS�����⃗-λAAAA�����⃗·AASS�����⃗-λ(λ-1)AASS�����⃗·AAAA1�������⃗+λ2|AAAA1�������⃗|2+λAAAA�����⃗·AAAA1�������⃗=λ(λ-1)|AASS�����⃗|2-(2λ2-λ)AAAA1�������⃗·AASS�����⃗-λAAAA�����⃗·AASS�����⃗+λ2|AAAA1�������⃗|2+λAAAA�����⃗·AAAA1�������⃗=λ(λ-1)×4-(2λ2-λ)×4cos 60°-λ×2cos 60°+4λ2+λ·2cos 60°=4λ2-2λ=(2λ-12)2-14≥-14,当且仅当λ=14时,等号成立,所以PPAA�����⃗·PPCC�����⃗的最小值为-14,故D正确.故选BCD.12.BD【解析】对于A,因为a=1,所以方程f(x)=0即e x+1-x=0,又e x≥x+1>x-1,所以e x+1-x>0恒成立,所以方程f(x)=0不存在实数根,所以A错误.对于B,因为f(x)=a(e x+a)-x,定义域为R,所以f'(x)=a e x-1,当a≤0时,由于e x>0,则a e x≤0,故f'(x)=a e x-1<0恒成立,所以f(x)在R上单调递减,所以B正确.对于C,由上知,当a>0时,令f'(x)=a e x-1=0,解得x=-ln a.当x<-ln a时,f'(x)<0,则f(x)在(-∞,-ln a)上单调递减;当x>-ln a时,f'(x)>0,则f(x)在(-,+∞)上单调递增.当a>0时,f(x)在(-∞,-ln a)上单调递减,在(-ln a,+∞)上单调递增.所以函数f(x)有最小值,即最小值在x=-ln a处取得,所以C错误.对于D,由上知f(x)min=f(-ln a)=a(e-ln a+a)+ln a=1+a2+ln a,要证f(x)>2ln a+32,即证1+a2+ln a>2ln a+32,即证a2-12-ln a>0恒成立,令g(a)=a2-12-ln a(a>0),则g'(a)=2a-1aa=2aa2-1aa.令g'(a)<0,则0<a<√22;令g'(a)>0,则a>√22.所以g(a)在(0,√22)上单调递减,在(√22,+∞)上单调递增,所以g(a)min=g(√22)=(√22)2-12-ln√22=ln√2>0,则g(a)>0恒成立,所以当a>0时,f (x )>2ln a+32恒成立,D 正确.综上,故选BD . 13.(-∞,1] 【解析】因为x ∈[0,2],所以由ax 2-2x+a ≤0,得a ≤2xxxx 2+1, 因为关于x 的不等式ax 2-2x+a ≤0在区间[0,2]上有解,所以只需a 小于或等于2xxxx 2+1的最大值,当x=0时,2xxxx 2+1=0,当x ≠0时,2xx xx 2+1=2xx +1xx≤1,当且仅当x=1时,等号成立,所以2xxxx 2+1的最大值为1,故a ≤1,即实数a 的取值范围是(-∞,1].故答案为(-∞,1].14.273 【解析】设公比为q ,a 1+a 3+a 5=aa3qq 2+a 3+a 3q 2=919,解得q 2=9或19,因为{a n }递增,所以q=3,则a 4+a 6+a 8=(a 1+a 3+a 5)q 3=919×33=273.故答案为273.15.12π 【解析】设圆台上、下底面圆心分别为O 1,O 2,则圆台内切球的球心O 一定在O 1O 2的中点处,设球O 与母线AB 切于M 点,∴OM ⊥AB ,∴OM=OO 1=OO 2=R (R 为球O 的半径),∴△AOO 1与△AOM 全等,∴AM=r 1,同理BM=r 2,∴AB=r 1+r 2,∴O 1OO 22=(r 1+r 2)2-(r 1-r 2)2=4r 1r 2=12,∴O 1O 2=2√3,∴圆台的内切球半径R=√3,∴内切球的表面积为4πR 2=12π.故答案为12π.16.e2【解析】f (x )≥0⇔ax+e x ≥a ln(ax+b )+(ax+b ),设g (x )=a ln x+x ,易知g (x )在(0,+∞)上递增,且g (e x )=a ln e x +e x =ax+e x ,故f (x )≥0⇔g (e x )≥g (ax+b )⇔e x ≥ax+b.法一:设y=e x 在点P (x 0,e xx 0)处的切线斜率为a ,e xx 0=a ,即x 0=ln a ,切线l :y=ax+a (1-ln a ),由e x ≥ax+b 恒成立,可得b ≤a (1-ln a ),∴ab ≤a 2(1-ln a ),设h (a )=a 2(1-ln a ),a>0,h'(a )=2a (12-ln a ),当a ∈(0,e 12)时,h'(a )>0,当a ∈(e 12,+∞)时,h'(a )<0,∴h (a )max =h (e 12)=e 2,∴ab 的最大值为e2.故答案为e 2.法二:设h (x )=e x -ax-b ,h'(x )=e x -a ,当x ∈(-∞,ln a )时,h'(x )<0,当x ∈(ln a ,+∞)时,h'(x )>0,∴h (x )min =h (ln a )=a (1-ln a )-b ≥0,即有b ≤a (1-ln a ),∴ab ≤a 2(1-ln a ),下同法一.17.【解析】(1)证法一:因为1-cos AA sin AA =sin2SS 1+cos2SS =2sin SS cos SS 2cos 2B=sin SScos SS ,所以(1-cos A )·cos B=sin A ·sin B , ............................................................................................................................... 2分 所以cos B=cos A cos B+sin A sin B ,即cos(A-B )=cos B ,而-π2<A-B<π2,0<B<π2,所以A-B=B ,即A=2B , .............................................................................................................. 4分 所以sin A=sin 2B=2sin B cos B.由正弦定理得 a=2b cos B ,即cos B=aa2bb ....................................................................................................................... 5分 证法二:由1-cos AA sin AA =2sin 2AA22sin AA 2cos AA 2=sin AA2cos AA 2=sin2SS 1+cos2SS ,所以sin AA2cos AA 2=sin2SS1+cos2SS , 即sin AA2·(1+cos 2B )=cos AA 2·sin 2B ,所以sin AA2=sin 2B ·cos AA 2-cos 2B ·sin AA 2=sin(2B-AA 2), 又0<A<π2,0<B<π2且A+B>π2,所以AA 2=2B-AA 2或AA 2+(2B-AA 2)=2B=π,所以A=2B 或B=π2(与锐角△ABC 不合,舍去).综上知,A=2B.所以sin A=sin 2B=2sin B cos B ,由正弦定理得 a=2b cos B ,即cos B=aa2bb . (2)由上知A=2B ,则C=π-A-B=π-3B ,在锐角△ABC 中,π6<B<π4, .............................................................................. 7分由正弦定理,得aa bb =sin AA sin SS =sin2SS sin SS =2sin SS cos SSsin SS=2cos B ∈(√2,√3), ......................................................................................... 9分所以aabb 的取值范围是(√2,√3). ........................................................................................................................................ 10分 18.【解析】(1)记事件D :选取的这个人感染了支原体肺炎病毒,记事件E :此人来自甲市,记事件F :此人来自乙市,记事件G :此人来自丙市. ............................................................................................................................................ 1分Ω=E ∪F ∪G ,且E ,F ,G 彼此互斥,由题意可得P (E )=420=0.2,P (F )=620=0.3,P (G )=1020=0.5, P (D|E )=0.08,P (D|F )=0.06,P (D|G )=0.04, ................................................................................................................... 3分由全概率公式可得P (D )=P (E ).P (D|E )+P (F ).P (D|F )+P (G ).P (D|G )=0.2×0.08+0.3×0.06+0.5×0.04=0.054, (5)分所以从三市中任取一人,这个人感染支原体肺炎病毒的概率为0.054. ................................................................... 6分 (2)由条件概率公式可得P (E|D )=PP (AADD )PP (AA )=PP (DD )·PP (AA |DD )PP (AA )=0.2×0.080.054=827. ........................................................................... 11分所以当此人感染支原体肺炎病毒时,他来自甲市的概率为827.................................................................................. 12分19.【解析】(1)因为2S n -3a n +3=0,①当n ≥2时,2S n-1-3a n-1+3=0,② ..................................................................................................................................... 2分①-②得 a n =3a n-1(n ≥2),即aann aa nn -1=3(n ≥2),所以数列{a n }是首项为3,公比为3的等比数列. .......................................................................................................... 4分 (2)由(1)知a n=3n ,所以S n =3(1-3nn )1-3=3nn +1-32,T n =a 1a 2a 3…a n =3×32×33×…×3n =31+2+3+…+n =3nn (nn +1)2, ........................................................................................... 6分所以�kk=1nn (1-2kk )(RR kk -2aa kk +32)log 3TT kk =�kk=1nn (1-2kk )(3kk +1-32-2·3kk +32)log 33kk (kk +1)2 =�kk=1nn (2kk -1)3kkkk (kk +1)=�kk=1nn(3kk +1kk +1-3kk kk )=3nn +1nn +1-3>λλ·3nnnn +1对任意n ∈N *恒成立, .................................................................................. 8分 故λ<3-nn +13nn -1恒成立, ........................................................................................................................................................... 9分令f (n )=3-nn +13nn -1,则f (n+1)-f (n )=3-nn +23nn -(3-nn +13nn -1)=2nn +13nn >0, ........................................................................................ 11分所以数列{f (n )}单调递增,所以f (n )min =f (1)=1,所以λ<1,故整数λ的最大值为0. ............................................ 12分20.【解析】(1)由题可知,|A 1A 2|=2a ,由AA 1F �������⃗=3FFAA 2�������⃗,所以|AA 1F �������⃗|=3|FFAA 2�������⃗|,所以|AA 1F �������⃗|=34|A 1A 2|=32a ,即a+c=32a ,所以椭圆的离心率e=cc aa =12. ......................................................................................................................... 3分 (2)法一:由题意知,c=1,a=2,所以椭圆方程为xx 24+yy 23=1,直线A 2P 的斜率存在,设直线A 2P 的斜率为k , 则直线方程为kx-y-2k=0且k<0,设A 1到直线A 2P 的距离为h 1,F 到直线A 2P 的距离为h 2, 则h 1=|-4kk |�kk 2+1,h 2=|-kk |�kk 2+1, .................................................................................................................................................... 5分又RR △AA 1PQ =12h 1·|PQ|,RR △AA 2FP =12h 2·|A 2P|,RR △AA 1PQ =RR △AA 2FP ,所以|PPPP||AA2P|=ℎ2ℎ1=14, ................................................................................................................................................................. 8分由图可得AA2P�������⃗=45AA2Q��������⃗,又因为A2(2,0),Q(0,-2k),所以P(25,-85k), ............................................................................... 10分又P在椭圆上,代入椭圆方程解得k2=98,因为k<0,所以k=-3√24. .......................................................................... 12分法二:由题意知,直线A2P的斜率存在,设直线A2P的斜率为k,则直线方程为kx-y-2k=0且k<0,联立�kkxx-yy-2kk=0,xx24+yy23=1,消去y得到方程(3+4k2)x2-16k2x+16k2-12=0,所以xx AA2·x P=16kk2-123+4kk2,所以x P=8kk2-63+4kk2, ................................................................................................................................ 5分代入直线方程得P(8kk2-63+4kk2,-12kk3+4kk2),Q(0,-2k), .................................................................................................................... 7分RR△AA2FP=12|A2F|·y P=yy PP2,RR△AA1PQ=RR△QQAA1AA2-RR△PPAA1AA2=12·4·(-2k)-12·4·y P,又因为RR△AA1PQ=RR△AA2FP,所以52y P=-4k, ......................................................................................................................... 10分所以52·-12kk3+4kk2=-4k,解得k2=98,因为k<0,所以k=-3√24................................................................................................ 12分21.【解析】(1)∵四边形ABCD是正方形,∴AD⊥CD.∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,AD⊂平面ABCD,∴AD⊥平面PCD,∵PD⊂平面PCD,∴AD⊥PD,........................................................................................................................................... 2分同理CD⊥PD.∵AD∩CD=D,AD⊂平面ABCD,CD⊂平面ABCD,∴PD⊥平面ABCD. .......................................................................................................................................................... 4分(2)由(1)知AD⊥PD,CD⊥PD,AD⊥CD,∴DA,DC,DP两两垂直,如图,以D为原点,DA,DC,DP所在直线分别为x,y,z轴,建立空间直角坐标系.设PD=AD=2,则D(0,0,0),P(0,0,2),B(2,2,0),C(0,2,0),M(0,0,1).∵PD⊥平面ABCD,∴平面ABCD的一个法向量为m=(0,0,1), .................................................................................................................. 5分CCCC�����⃗=λCCPP�����⃗(0≤λ≤1),∴SSAA������⃗=(-2,-2,1),CCPP�����⃗=(0,-2,2),∴SSCC������⃗=SSCC�����⃗+CCCC�����⃗=SSCC�����⃗+λCCPP�����⃗=(-2,0,0)+λ(0,-2,2)=(-2,-2λ,2λ),设平面BMN的法向量为n=(x,y,z),则�SSAA������⃗·nn=-2xx-2yy+zz=0,SSCC������⃗·nn=-2xx-2λλyy+2λλzz=0,取x=λ,则y=1-2λ,z=2-2λ,∴平面BMN的一个法向量为n=(λ,1-2λ,2-2λ)......................................................................................................... 7分设平面BMN与平面ABCD的夹角为θ,则cos θ=|cos<n,m>|=|nn·mm|nn||mm||=|2-2λλ|�λλ2+(1-2λ)2+(2-2λ)2=|2-2λλ|�9λλ2-12λ+5, .............................................................................. 8分设t=1-λ,则0≤t≤1.①当t=0时,cos θ=0. ..................................................................................................................................................... 9分②当t≠0时,cos θ=2|tt|�9tt2-6t+2=2�tt29tt2-6t+2=2�12(1tt)2-6×1tt+9=2�12[(1tt-32)2+92],当t=23时,cos θ=2√23,∴0<cos θ≤2√23.......................................................................................................................... 11分综上,0≤cos θ≤2√23.∴平面BMN与平面ABCD夹角的余弦值的取值范围为[0,2√23]........................................ 12分22.【解析】(1)f(x)的定义域为(0,+∞),f'(x)=ln x-ax+1, .......................................................................................... 1分由题意,f'(x)≤0恒成立,即a≥ln xx+1xx恒成立,.................................................................................................................... 2分设h(x)=ln xx+1xx,h'(x)=-ln xx xx2,当x∈(0,1)时,h'(x)>0,h(x)递增,当x∈(1,+∞)时,h'(x)<0,h(x)递减, ...................................................................... 3分∴h(x)max=h(1)=1,∴a≥1................................................................................................................................................. 4分(2)证法一:∵函数f(x)有两个极值点,由(1)可知0<a<1,设g(x)=f'(x)=ln x-ax+1,则x1,x2是g(x)的两个零点,∵g'(x)=1xx-a,当x∈(0,1aa)时,g'(x)>0,当x∈(1aa,+∞)时,g'(x)<0,∴g(x)在(0,1aa)上递增,在(1aa,+∞)上递减,∴0<x1<1aa<x2,又∵g(1)=1-a>0,∴0<x1<1<1aa<x2, ............................................................................................................................................................... 6分要证x1x2>1aa,只需证x2>1aaxx1(>1aa),只需证g(x2)<g(1aaxx1),即证g(1aaxx1)=-ln(ax1)-1xx1+1>0,即证ln(ax1)+1xx1-1<0,(*) ........................................................................................... 8分由g(x1)=ln x1-ax1+1=0,设ax1=t∈(0,1),则ln x1=t-1,x1=e t-1,则(*)⇔ln t+e1-t-1<0, ................................. 10分设G(t)=ln t+e1-t-1(0<t<1),G'(t)=1tt-1e tt-1=e tt-1-t tt e tt-1,由(1)知ln x≤x-1,∴e x-1≥x,∴e t-1-t≥0,即G'(t)≥0,G(t)在(0,1)上递增,G(t)<G(1)=0,故(*)成立,即x1x2>1aa.................................................................................................................... 12分证法二:先证明引理:当0<t<1时,ln t<2(tt-1)tt+1,当t>1时,ln t>2(tt-1)tt+1.设G(t)=ln t-2(tt-1)tt+1(t>0),G'(t)=1tt-4(tt+1)2=(tt-1)2tt(tt+1)2≥0,∴G(t)在(0,+∞)上递增,又G(1)=0,当0<t<1时,G(t)<G(1)=0,当t>1时,G(t)>G(1)=0,∴引理得证............................................................................................... 5分∵函数f(x)有两个极值点,由(1)可知0<a<1,设g(x)=f'(x)=ln x-ax+1,则x1,x2是g(x)的两个零点,∵g'(x)=1xx-a,当x∈(0,1aa)时,g'(x)>0,当x∈(1aa,+∞)时,g'(x)<0,∴g(x)在(0,1aa)上递增,在(1aa,+∞)上递减,∴0<x1<1aa<x2,即0<ax1<1<ax2................................................................... 6分要证x1x2>1aa,只需证ln x1+ln x2>-ln a,即证a(x2+x1)>2-ln a,(*) .......................................................................... 7分由引理可得ax2+ln a-1=ln(ax2)>2(aaxx2-1)aaxx2+1,化简可得a2xx22+a(ln a-2)x2+ln a+1>0,①....................................... 9分同理ax1+ln a-1=ln(ax1)<2(aaxx1-1)aaxx1+1,即有a2xx12+a(ln a-2)x1+ln a+1<0.②......................................................... 10分由①-②可得,a2(x2+x1)(x2-x1)+a(ln a-2)(x2-x1)>0,即a2(x2+x1)+a(ln a-2)>0,即a(x2+x1)>2-ln a,故(*)得证,从而x1x2>1aa. ................................................................................................................................................................... 12分。
螺纹标准
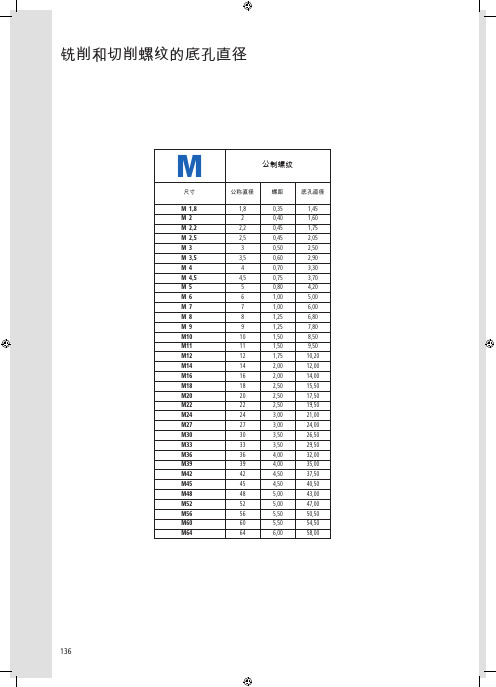
W
尺寸 1/8“ 3/16“ 1/4“ 5/16“ 3/8“ 7/16“ 1/2“ 5/8“ 3/4“ 7/8“ 1“ 1 1/8“ 1 1/4“ 1 3/8“ 1 1/2“ 1 5/8“ 1 3/4“ 1 7/8“ 2 公称直径 3,175 4,762 6,350 7,938 9,525 11,113 12,700 15,876 19,051 22,226 25,401 28,576 31,751 34,926 38,101 41,277 44,452 47,627 50,802
惠氏螺纹
螺距������� t.p.i. 40 24 20 18 16 14 12 11 10 9 8 7 7 6 6 5 5 41/2 41/2 底孔直径 2,60 3,60 5,10 6,50 7,90 9,25 10,50 13,50 16,50 19,25 22,00 24,75 27,75 30,50 33,50 35,50 39,00 41,50 44,50
4-甲基-2-戊酮_核磁氢谱_概述及解释说明

4-甲基-2-戊酮核磁氢谱概述及解释说明1. 引言1.1 概述核磁共振(Nuclear Magnetic Resonance,简称NMR)技术在现代化学分析中扮演着重要的角色。
作为一种非常有效的结构表征手段,核磁共振可以提供有机物、生物分子以及无机物的高分辨率谱图,并通过对谱线位置、形状和强度的解读,帮助我们了解它们的结构和性质。
其中,核磁氢谱是最为常见和广泛应用的一种。
本文将重点介绍4-甲基-2-戊酮(4-Methyl-2-pentanone)这种有机化合物的核磁氢谱。
首先,我们将概述核磁氢谱的基本原理,包括其背后的物理原理和仪器设备。
接着,我们将详细解释如何分析核磁氢谱谱图,并讲解常见峰位、峰面积等概念的意义。
1.2 文章结构本文主要分为五个部分。
除了本引言外,第二部分将介绍核磁氢谱的基本原理,包括什么是核磁共振以及如何通过核磁共振技术获取氢谱。
第三部分将详细探讨4-甲基-2-戊酮的核磁氢谱分析,包括其化学结构和特性介绍、核磁氢谱图的解读以及结果与讨论部分。
第四部分将阐述核磁氢谱在有机化学中的应用,包括定量分析和定性识别、反应动力学研究和机理探索以及结构表征和异构体确认。
最后,第五部分为总结与展望。
1.3 目的本文的目的在于通过对4-甲基-2-戊酮核磁氢谱的深入研究,阐述核磁共振技术在有机化学领域中应用的重要性和价值。
我们希望读者可以通过本文对核磁氢谱原理及其解读方法的全面了解,为实际应用中不仅能准确判断化合物结构,还可以从数据中获得更多有益信息提供帮助。
另外,我们也将对未来核磁共振技术发展方向进行展望,并提出建议以促进该领域的进一步发展。
2. 核磁氢谱的基本原理2.1 基本概念核磁氢谱是一种常用的分析技术,用于确定有机化合物中氢原子的化学位移和环境。
该技术基于核磁共振现象,通过对样品中的氢原子进行辐射,观察其与外加磁场相互作用后产生的能级跃迁。
在核磁共振过程中,当样品置于强大而恒定的磁场中时,氢原子核将分裂成不同的能级。
YE4系列(IE4)高效率三相异步电动机样本

额定 功率 kW
额定 转速 r/min
0.75 2910 1.1 2888 1.5 2910 2.2 2910 3 2905 4 2915 5.5 2925 7.5 2925 11 2945 15 2945 18.5 2950 22 2955 30
2965 37 45 2970 55 2970 75 90 110
3 产品系列型谱
电动机产品系列型谱(见表 2)。
机座号
80M1 80M2 90S 90L 100L1 100L2 112M 132S1 132S2 132M1 132M2 160M1 160M2 160L 180M 180L 200L1 200L2 225S 225M 250M 280S
表2
3000
万元/吨,50WH470硅钢板0.68万元/吨),有效材料费用增加360元。与YE3系列电动机相比,采用YE4
电动机所增加的费用可从节约的电费中回收,在回收期以后节约的运行费用为净收入,每年节约的电能
(见图2),回收期(见图3)。
6000
5500 5000 4500
4000 3500
3000 2500 2000
3
4 5.5
7.5
11 15 18.5 22 30 37 45
3
280M 315S 315M 315L1 315L2 355M 355L 3551 3552
90
90
55
110
110
75
132
132
90
160
160
110
200
200
132
250
250
200
315
315
250
355
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二手房降价蔓延:4月份北京87%房源挂牌价下调
宏观经济21世纪经济报道[微博]2014-05-08 03:19
我要分享
1003
历时5个月,李静(化名)终于将她的房子卖出去,但最终成交价比她最初挂牌价整整降低了32万。
而与李静同期挂牌的同楼栋另一业主,由于市场低迷,已经决定“不卖了”。
在楼市降价预期不断强化的背景下,观望情绪抬头,一些购房者选择延迟入市,以期房价有所下跌,楼市向买方市场转变。
中原监测数据显示,4月份6个重点城市二手住宅成交总量较3月缩减约1成,市场活跃度的降低使得价格压力加剧。
北京中原地产数据统计显示,5月第一周,北京二手房成交价格也延续了前4月调整迹象,二手房价格调整逐渐加速。
中原地产分析师张大伟称,“成交量已经连跌3个月,自然就该价格松动。
二手房因为受到信贷等收紧的影响更大,所以在本轮市场调整的反应最早。
”
87%二手房业主降价
李静的房子位于北五环外北苑一带,面积为48平米的开间。
最近这5个月,李静感觉到了市场的明显变化。
春节前,李静将房子挂出。
“最初挂牌时,心理预期底价是240万,但挂牌价挂了260万,想能卖高就卖高。
我楼上的业主挂了265万呢。
”李静说,春节前到清明节期间,她感觉市场状态还可以,当时有买家想以240万买,她没同意。
但没想到,清明节后,市场越来越低迷。
来看房的买家要么是“漫无边际地看看”,要么就是“不靠谱地讲价。
”直至5月6日,她终于碰到一对“靠谱”的买家,谈定的价格为228万。
“心理多少有些后悔,清明节240万就能卖出去。
”李静称。
李静的房源由于地段尚好,又属于学区房,出售相对容易。
而另一位近期挂出通州两套房的二手房业主赵洁(化名)更加感受到市场的寒意。
半个月内,仅一套房有一个客户看过一次,并且没有购买意向。
通州一位二手房中介告诉21世纪经济报道记者,目前大部分购房者都在观望,如果想在1至1个半月内卖出去,必须降到市场最低价。
记者在链家在线查阅数据发现,赵洁所在的小区二手房自从2月12日以后就再也没有成交一套房产。
链家地产分析师张旭介绍,“总体来讲,近郊区域二手房成交价在小幅下降,而中心城区二手房业主的挂牌价也不再像以往那样,动辄挂高价,而是开始逐渐下调。
”
市场的寒意在五一期间表现更为明显。
据链家地产市场研究部统计,2014年五一假期(5.1-5.3),北京市二手住宅网签量仅为31套,与去年同期下降了82%,为近6年来最低。
此外,4月北京市二手住宅总成交量仅为7616套,为近11个月(除去春节月)以来最低水平。
从链家地产所监测到的房价指数看,自1月以来,北京二手房挂牌价持续下调。
其中,4月下调幅度最大,为2.2%,降价房源占比逐渐扩大。
4月份,87%的房源都对挂牌价进行了下调。
据21世纪不动产提供的数据,在北京朝青区域,目前挂牌房源基本都有35万-50万的降价幅度,即使业主已主动让价,也少有成交,购房者仍表示要等等看。
从全市来看,挂牌价与实际成交价出现10%的下降,是较为普遍的现象。
市场下调将持续
楼市购房心理向来是“买涨不买跌”。
在二手房市场降价逐渐蔓延的背景下,购房者越发犹豫起来。
据21世纪不动产门店走访调查发现,不少刚需客户表现出了较浓的观望态度,新房和二手房成交量的冷淡,让他们更加不敢入市了。
消费者的观望,反过来又加重了楼市交易的僵局。
过去几年的情况表明,如果楼市持续上涨,购房者会毫无顾忌地“抢购”,唯恐房价不停上涨,迟了就更吃亏;而当楼市陷入观望,价格稍微有所下调,购房者会错过最佳购买时期,以为房价还会继续下降。
链家地产也观察到,从新增房客源变化情况来看,五一期间日均新增房源量与节前三天水平相比基本持平,客源量也并未出现明显回升,部分区域客源量还出现了一定程度的下降,市场冷清的状态依然持续。
链家地产市场研究部张旭认为,从五一假期期间的二手房市场情况来看,购房者深度观望的情绪仍未有任何改善。
目前多数购房者认为房价未来还有进一步下降的可能,这正是导致楼市需求深度观望的主要原因。
此外,自住型商品房陆续入市也对二手房客源的入市心理产生了不小的影响,部分刚需也因此被分流。
在当前无论是从政策层面还是市场层面都尚未出现任何利好信号的背景下,5月楼市出现明显回温的可能性很小,预计此轮市场的自发性调整还将持续一段时间。
21世纪不动产市场发展中心总监桑豫峰分析,从全国情况看,一线城市楼市比二三线城市要相对坚挺,尚未出现大的降价现象,但购房者期待降价的心情比较强烈,市场情绪一触即发。
某全国知名房企副总裁对未来房地产市场趋势的悲观看法,经网络传播开来,影响非常大。
极少数城市小心翼翼的放松限购措施,未能扭转整个楼市继续向下调整的形势。
中原经理指数和中原报价指数也显示,二手房成交价已经连续两个月下滑,分别反映出门店经理和业主对后市的不乐观,目前这两个先行指数均以进入临界区间,从历史数据来看,房价下跌已是大概率事件,预计5月,六城市二手住宅价格下跌的或将增多,跌幅也会有所扩大。
桑豫峰表示,宏观经济仍未走出低谷,房地产信贷持续偏紧,部分城市楼盘降价,观望情绪蔓延,这几个综合因素是导致今年以来商品房成交不振的原因。
二季度的走势将在很大程度决定全年的楼市表现,目前来看,5月份表现仍不乐观。
(21世纪经济报道)。
