2020年冀教版九年级数学上学期第28章单元检测卷(含答案)
冀教版九年级数学上册 第28章章末检测(含答案)

第28章章末检测一、选择题(本题共10小题,每小题3分,共30分)1. 若四边形ABCD是⊙O的内接四边形,且∠A:∠B:∠C=1:3:8,则∠D的度数是()A. 10°B. 30°C. 80°D. 120°2. 如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为()(第2题图)A. 3B. 4C. 5D. 63. 如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为()(第3题图)A. π-2B. π-1C. π-4D. π-24. 边长为6的正三角形的外接圆的面积为()A. 36πB. 4πC. 12πD. 16π5. 如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于()(第5题图)A. 60°B. 70°C. 120°D. 140°6. 已知圆锥底面圆的半径为2,母线长是4,则它的全面积为()A. 4πB. 8πC. 12πD. 16π7. 如图,当半径为30 cm的转动轮转过120°圆心角时,传送带上的物体A平移的距离为()(第7题图)A. 900π cmB. 300π cmC. 60π cmD. 20π cm8. 现有一圆心角为90°,半径为12 cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为()A. cmB. 2cmC. 3cmD. 6cm9. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为()(第9题图)A. rB. 2rC. rD. 3r10. 已知弦AB把圆周分成1:5的两部分,则弦AB所对应的圆心角的度数为()(第10题图)A. 60°B. 30°或150°C. 30°D. 60°或300°二、填空题(本题共8小题,每小题3分,共24分)11. 圆的一条弦分圆成4:5的两部分,则此弦所对的圆心角等于________.12. 如图,已知圆锥的底面半径OA=3 cm,高SO=4 cm,则该圆锥的侧面积为________ cm2.(第12题图)13. 用等分圆周的方法,在半径为1的图中画出如图的图形,则图中阴影部分的面积为________.(第13题图)14. 如图,⊙O是正三角形ABC的外接圆,点P在劣弧AB上,∠ABP=22°,则∠BCP的度数为________°.(第14题图)15. 如图,CD是圆O的直径,∠DOE=78°,AE交圆O于点B,AB=OC,则∠A= ________.(第15题图)16. ________确定圆的位置,________确定圆的大小.17. 在圆内接四边形ABCD中,∠A:∠B:∠C=2:4:7,则四边形ABCD的最大内角是________°.18. 已知圆锥底面圆的半径为6 cm,它的侧面积为60π cm2,则这个圆锥的高是________ cm.三、解答题(本题共6小题,共46分)19.(6分)如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E,F.(1)四边形ABCD是什么特殊的四边形?请说明理由.(2)求证:BE=CF.(第19题图)20.(6分)赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦)长为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,请求出赵州桥的主桥拱半径.(结果保留小数点后一位)(第20题图)21.(6分)如图,⊙O的直径EF为10 cm,弦AB,CD分别为6 cm,8 cm,且AB∥EF∥CD.求图中阴影部分的面积之和.(第21题图)22.(8分)(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图①,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近.(2)如果甲、乙走的路程图改成图②,两人走的路程远近相同吗?①②(第22题图)23.(10分)如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24 cm,CD=8 cm.(1)求作此残片所在的圆(不写作法,保留作图痕迹);(2)求(1)中所作圆的半径.(第23题图)24.(10分)O为等腰三角形ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.求证:(1)∠AOE=∠BOD;(2)(第24题图)答案一、1. D 2. D 3. A 4. C 5. D 6. C 7. D 8. C 9. B 10. A二、11. 160°12. 15π13. π-14. 38 15. 26°16. 圆心;半径17. 140 18. 8三、19. (1)解:四边形ABCD是矩形.理由如下:∵AC与BD是圆的直径,∴∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,∴四边形ABCD是矩形.(2)证明:∵BO=CO,BE⊥AC于点E,CF⊥BD于点F,∴∠BEO=∠CFO=90°.在△BOE和△COF中,∴△BOE≌△COF(AAS),∴BE=CF.20. 解:如答图,设O为圆心,作OD⊥AB于点D,交弧AB于点C.∵拱桥的跨度AB=37.4 m,拱高CD=7.2 m,∴AD=AB=18.7(m),∴AD 2 = OA 2 -(OC -CD)2,即18.7 2 = AO 2 -(AO-7.2)2,解得AO≈27.9.答:赵州桥的主桥拱半径为27.9 m.(第20题答图)21. 解:如答图,作直径MN,使MN⊥EF于点O,交AB于点G,交CD于点H,连接OA,OB,OC,OD.在Rt△OBG中,BG=3 cm,OB=5 cm,∴由勾股定理,得OG=4(cm).在Rt△OCH中,CH=4 cm,OC=5 cm,∴由勾股定理,得OH=3(cm).∴sin∠DOF=,sin∠BOF=,sin∠COE=,sin∠AOE=,即∠DOF=∠AOM=∠COE=∠BOM,∠CON=∠DON=∠AOE=∠BOF,∴S扇形OAE = S扇形OBF= S扇形CON= S扇形ODN,∴S阴影= S△ABE+ S弓形AMB + S△CDF + S弓形CND = S△OAB + S弓形AMB + S△OCD + S弓形CND = S扇形OAB + S扇形OCN + S扇形ODN = S扇形OAB + S扇形OAE + S扇形OBF =S⊙O =12.5π(cm2).故图中阴影部分的面积之和为12.5π cm2.(第21题答图)22. 解:(1)BC=AB-AC=10,甲所走的路径长为×2π×=×2π×=20π(m),乙所走的路径长为×2π×+×2π×=×2π×+×π×=20π(m),所以两人所走路程的相等.(2)两人走的路程远近相同.理由如下:甲所走的路径长为×2π×=π•AB,乙所走的路径长为×2π×+×2π ×+×π×=π(AC+CD+DB)=π•AB,所以两人走的路程远近相同.23. 解:(1)如答图,M就是所求的圆的圆心.(2)设圆的半径是r.在直角△ADM中,AM=r,AD=24,DM=r-8.根据勾股定理,得r2 =242+(r-8)2,解得r=13.即圆的半径为13 cm.(第23题答图)24.证明:(1)∵CA=CB,∴∠A=∠B.∵OA=OD,OB=OE,∴∠A=∠ODA,∠B=∠OEB,∴∠AOD=∠BOE,∴∠AOD+∠DOE=∠BOE+∠DOE,∴∠AOE=∠BOD.(2)∵∠AOD=∠BOE,∴.。
冀教版数学九年级上第28章《圆》测试(含答案及解析)
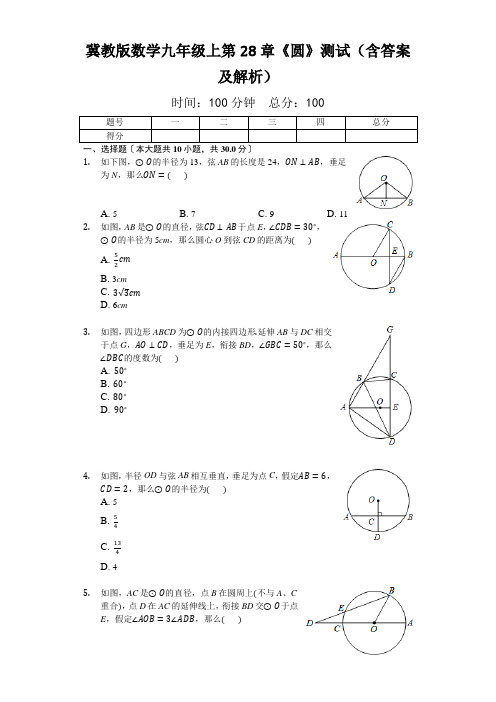
冀教版数学九年级上第28章《圆》测试(含答案及解析)时间:100分钟总分:100题号一二三四总分得分1.如下图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,那么ON=()A. 5B. 7C. 9D. 112.如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30∘,⊙O的半径为5cm,那么圆心O到弦CD的距离为()cmA. 52B. 3cmC. 3√3cmD. 6cm3.如图,四边形ABCD为⊙O的内接四边形.延伸AB与DC相交于点G,AO⊥CD,垂足为E,衔接BD,∠GBC=50∘,那么∠DBC的度数为()A. 50∘B. 60∘C. 80∘D. 90∘4.如图,半径OD与弦AB相互垂直,垂足为点C,假定AB=6,CD=2,那么⊙O的半径为()A. 5B. 54C. 134D. 45.如图,AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延伸线上,衔接BD交⊙O于点E,假定∠AOB=3∠ADB,那么()A. DE=EBB. √2DE=EBC. √3DE=DOD. DE=OB6.如图,在Rt△ABC中,∠A=90∘,BC=2√2,以BC的中点O为圆心⊙O区分与AB,AC相切于D,E两点,那么DE⏜的长为()A. π4B. π2C. πD. 2π7.如图,将半径为2,圆心角为120∘的扇形OAB绕点A逆时针旋转60∘,点O,B的对应点区分为O′,B′,衔接BB′,那么图中阴影局部的面积是()A. 2π3B. 2√3−π3C. 2√3−2π3D. 4√3−2π38.如图,AB是⊙O的直径,点C在⊙O上,衔接AC、BC,点D是BA延伸线上一点,且AC=AD,假定∠B=30∘,AB=2,那么CD的长是()A. √5B. 2C. 1D. √39.如图,四边形ABCD内接于⊙O,假定四边形ABCO是平行四边形,那么∠ADC的大小为()A. 45∘B. 50∘C. 60∘D. 75∘10.如图,圆内接四边形ABCD的两组对边的延伸线区分相交于点E,F,假定∠A=55∘,∠E=30∘,那么∠F=()A. 25∘B. 30∘C. 40∘D. 55∘二、填空题〔本大题共10小题,共30.0分〕11.如图,AB是⊙O的直径,C、D是⊙O上的两点,假定∠ABD=62∘,那么∠BCD=______.12.如图,⊙O的半径为1,PA,PB是⊙O的两条切线,切点区分为A,B.衔接OA,OB,AB,PO,假定∠APB=60∘,那么△PAB的周长为______.13.圆锥底面圆的半径为2,母线长为5,它的正面积等于______(结果保管π).14.如图,圆周角∠ACB=130∘,那么圆心角∠AOB=______.15.如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.假定∠CAD=30∘,那么∠BOD=______ ∘.16.如图,等边△ABC的边长为6,以AB为直径的⊙O与边AC、BC区分交于D、E两点,那么劣弧DE⏜的长为______.17.如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45∘,假定点M、N区分是AB、AC的中点,那么MN长的最大值是______.18.如图,OA,OB是⊙O的半径,点C在⊙O上,衔接AC,BC,假定∠AOB=120∘,那么∠ACB=______度.19.如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160∘,那么∠BCD的度数为______.20.如图,半圆O的直径AB=2,弦CD//AB,∠COD=90∘,那么图中阴影局部的面积为______ .三、计算题〔本大题共4小题,共24.0分〕21.如图,在△ABC中,以AB为直径的⊙O区分与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.(1)求证:DF是⊙O的切线;(2)假定AD=5√3,∠CDF=30∘,求⊙O的半径.22.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,衔接BD、CD,过点D作BC的平行线,与AB的延伸线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△PBD∽△DCA;(3)当AB=6,AC=8时,求线段PB的长.23.如图,CD是⊙O的直径,AC⊥BC,垂足为C,点E为圆上一点,直线BE、CD相交于点A,且∠A+2∠AED=90∘.(Ⅰ)证明:直线AB是⊙O的切线;(Ⅱ)当BC=1,AE=2,求tan∠OBC的值.24.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,衔接AC、BC,假定∠BAC=30∘,CD=6cm.(1)求∠BCD的度数;(2)求⊙O的直径.四、解答题〔本大题共2小题,共16.0分〕25.如图,在△ABC中,∠C=90∘,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.(1)求证:AC是⊙O的切线;(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;(3)假定CD=1,EH=3,求BF及AF长.26.如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延伸线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.(1)求证:DE是⊙O的切线;(2)假定AE=6,∠D=30∘,求图中阴影局部的面积.答案和解析【答案】1. A2. A3. C4. C5. D6. B7. C8. D9. C10. C11. 28∘12. 3√313. 10π14. 100∘15. 12016. π17. 5√2218. 6019. 100∘20. π421. 解:(1)衔接OD,∵BD=CD,OB=OA,∴OD为△ABC的中位线,∴OD//AC,∵DF⊥AC,∴OD⊥DF,那么DF为圆O的切线;(2)∵DF⊥AC,∠CDF=30∘,∴∠C=60∘,∵OD//AC,∴∠ODB=∠C=60∘,∵OB=OD,∴∠B=∠ODB=60∘,∵AB为圆的直径,∴∠ADB=90∘,∴∠BAD=30∘,设BD=x,那么有AB=2x,依据勾股定理得:x2+75=4x2,解得:x=5,∴AB=2x=10,那么圆的半径为5.22. (1)证明:∵圆心O在BC上,∴BC是圆O的直径,∴∠BAC=90∘,衔接OD,∵AD平分∠BAC,∴∠BAC=2∠DAC,∵∠DOC=2∠DAC,∴∠DOC=∠BAC=90∘,即OD⊥BC,∵PD//BC,∴OD⊥PD,∵OD为圆O的半径,∴PD是圆O的切线;(2)证明:∵PD//BC,∴∠P=∠ABC,∵∠ABC=∠ADC,∴∠P=∠ADC,∵∠PBD+∠ABD=180∘,∠ACD+∠ABD=180∘,∴∠PBD=∠ACD,∴△PBD∽△DCA;(3)解:∵△ABC为直角三角形,∴BC2=AB2+AC2=62+82=100,∴BC=10,∵OD垂直平分BC,∴DB=DC,∵BC为圆O的直径,∴∠BDC=90∘,在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=100,∴DC=DB=5√2,∵△PBD∽△DCA,∴PBDC =BDAC,那么PB=DC⋅BDAC =5√2×5√28=254.23. (Ⅰ)证明:衔接OE,CE,OB,∵DC为圆O的直径,∴∠DEC=90∘,即∠CEB+∠AED=90∘,∴2∠AED+∠2∠CEB=180∘,∵AC⊥BC,∴∠ACB=90∘,∴∠A+∠ABC=90∘,∵∠A+2∠AED=90∘,∴∠ABC=2∠AED,∴∠ABC+2∠CEB=180∘,∵∠ABC+∠CEB+∠ECB=180∘,∴∠CEB=∠ECB,∴BC=BE,在△OEB和△OCB中{BE=BC OE=OC OB=OB,∴△OEB≌△OCB,∴∠OEB=∠ACB=90∘,即OE⊥AB,∴AB是⊙O切线.(Ⅱ)解:∵BE=BC=1,AB=2+1=3,在Rt△ACB中,由勾股定理得:AC=√32−12=2√2,∵∠A=∠A,∠AEO=∠ACB=90∘,∴△AEO∽△ACB,∴OEBC =AEAC,∴OEBC =2√2=√22,∴tan∠OBC=OCBC =OEBC=√22.24. 解:(1)∵直径AB⊥CD,∴B^C=B^D,∴∠DCB=∠CAB=30度;(2)∵直径AB⊥CD,CD=6cm,∴CE=3cm,在Rt△ACE中,∠A=30∘,∴AC=6cm,∵AB是直径,∴∠ACB=90∘,在Rt△ACB中,AB=ACcos∠A =6cos30∘=4√3(cm).25. 证明:(1)如图,衔接OE.∵BE⊥EF,∴∠BEF=90∘,∴BF是圆O的直径.∵BE平分∠ABC,∴∠CBE=∠OBE,∵OB=OE,∴∠OBE=∠OEB,∴∠OEB=∠CBE,∴OE//BC,∴∠AEO=∠C=90∘,∴AC是⊙O的切线;(2)如图,连结DE.∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,∴EC=EH.∵∠CDE+∠BDE=180∘,∠HFE+∠BDE=180∘,∴∠CDE=∠HFE.在△CDE与△HFE中,{∠CDE=∠HFE∠C=∠EHF=90∘EC=EH,∴△CDE≌△HFE(AAS),∴CD=HF.(3)由(2)得CD=HF,又CD=1,∴HF=1,在Rt△HFE中,EF=√32+12=√10,∵EF⊥BE,∴∠BEF=90∘,∴∠EHF=∠BEF=90∘,∵∠EFH=∠BFE,∴△EHF∽△BEF,∴EFBF =HFEF,即√10BF=1√10,∴BF=10,∴OE=12BF=5,OH=5−1=4,∴Rt△OHE中,cos∠EOA=45,∴Rt△EOA中,cos∠EOA=OEOA =45,∴5OA =45,∴OA=254,∴AF=254−5=54.26. (1)证明:衔接OC,∵OA=OC,∴∠OAC=∠OCA,∵AC平分∠BAE,∴∠OAC=∠CAE,∴∠OCA=∠CAE,∴OC//AE,∴∠OCD=∠E,∵AE⊥DE,∴∠E=90∘,∴∠OCD=90∘,∴OC⊥CD,∵点C在圆O上,OC为圆O的半径,∴CD是圆O的切线;(2)解:在Rt△AED中,∵∠D=30∘,AE=6,∴AD=2AE=12,在Rt△OCD中,∵∠D=30∘,∴DO=2OC=DB+OB=DB+OC,∴DB=OB=OC=13AD=4,DO=8,∴CD=√DO2−OC2=√82−42=4√3,∴S△OCD=CD⋅OC2=4√3×42=8√3,∵∠D=30∘,∠OCD=90∘,∴∠DOC=60∘,∴S扇形OBC =16×π×OC2=83π,∵S阴影=S△COD−S扇形OBC∴S阴影=8√3−8π3,∴阴影局部的面积为8√3−8π3.【解析】1. 解:由题意可得,OA=13,∠ONA=90∘,AB=24,∴AN =12,∴ON =√OA 2−AN 2=√132−122=5, 应选A .依据⊙O 的半径为13,弦AB 的长度是24,ON ⊥AB ,可以求得AN 的长,从而可以求得ON 的长.此题考察垂径定理,解题的关键是明白垂径定理的内容,应用垂径定了解答效果. 2. 解:衔接CB .∵AB 是⊙O 的直径,弦CD ⊥AB 于点E , ∴圆心O 到弦CD 的距离为OE ;∵∠COB =2∠CDB(同弧所对的圆周角是所对的圆心角的一半),∠CDB =30∘, ∴∠COB =60∘; 在Rt △OCE 中,OC =5cm ,OE =OC ⋅cos∠COB , ∴OE =52cm .应选A .依据垂径定理知圆心O 到弦CD 的距离为OE ;由圆周角定理知∠COB =2∠CDB =60∘,半径OC 的长,即可在Rt △OCE 中求OE 的长度.此题考察了垂径定理、圆周角定理及解直角三角形的综合运用.解答这类题一些先生不会综合运用所学知识解答效果,不知从何处入手形成错解. 3. 解:如图,∵A 、B 、D 、C 四点共圆, ∴∠GBC =∠ADC =50∘, ∵AE ⊥CD , ∴∠AED =90∘,∴∠EAD =90∘−50∘=40∘, 延伸AE 交⊙O 于点M , ∵AO ⊥CD ,∴CM ⏜=DM⏜, ∴∠DBC =2∠EAD =80∘. 应选:C .依据四点共圆的性质得:∠GBC =∠ADC =50∘,由垂径定理得:CM ⏜=DM⏜,那么∠DBC =2∠EAD =80∘.此题考察了四点共圆的性质:圆内接四边形的恣意一个外角等于它的内对角,还考察了垂径定理的运用,属于基础题.4. 解:连结OA ,如图,设⊙O 的半径为r , ∵OD ⊥AB ,∴AC =BC =12AB =8,在Rt △OAC 中,∵OA =r ,OC =OD −CD =r −2,AC =3, ∴(r −2)2+32=r 2,解得r =134.应选C .连结OA ,如图,设⊙O 的半径为r ,依据垂径定理失掉AC =BC =12AB =3,再在Rt △OAC 中应用勾股定理失掉(r −2)2+32=r 2,然后解方程求出r 即可.此题考察了的是垂径定理,依据题意作出辅佐线,结构出直角三角形,应用勾股定理求解是解答此题的关键.5. 解:衔接EO.∵OB=OE,∴∠B=∠OEB,∵∠OEB=∠D+∠DOE,∠AOB=3∠D,∴∠B+∠D=3∠D,∴∠D+∠DOE+∠D=3∠D,∴∠DOE=∠D,∴ED=EO=OB,应选D.衔接EO,只需证明∠D=∠EOD即可处置效果.此题考察圆的有关知识、三角形的外角等知识,解题的关键是添加除以辅佐线,应用等腰三角形的判定方法处置效果,属于中考常考题型.6. 解:衔接OE、OD,设半径为r,∵⊙O区分与AB,AC相切于D,E两点,∴OE⊥AC,OD⊥AB,∵O是BC的中点,∴OD是中位线,∴OD=AE=12AC,∴AC=2r,同理可知:AB=2r,∴AB=AC,∴∠B=45∘,∵BC=2√2∴由勾股定理可知AB=2,∴r=1,∴DE⏜=90π×1 180=π2应选:B.衔接OE、OD,由切线的性质可知OE⊥AC,OD⊥AB,由于O是BC的中点,从而可知OD是中位线,所以可知∠B=45∘,从而可知半径r的值,最后应用弧长公式即可求出答案.此题考察切线的性质,解题的关键是衔接OE、OD后应用中位线的性质求出半径r的值,此题属于中等题型.7. 解:衔接OO′,BO′,∵将半径为2,圆心角为120∘的扇形OAB绕点A逆时针旋转60∘,∴∠OAO′=60∘,∴△OAO′是等边三角形,∴∠AOO′=60∘,OO′=OA,∴点O′中⊙O上,∵∠AOB=120∘,∴∠O′OB=60∘,∴△OO′B是等边三角形,∴∠AO′B=120∘,∵∠AO′B′=120∘,∴∠B′O′B=120∘,∴∠O′B′B=∠O′BB′=30∘,∴图中阴影局部的面积=S△B′O′B−(S扇形O′OB −S△OO′B)=12×1×2√3−(60⋅π×22360−1 2×2×√3)=2√3−2π3.应选:C.衔接OO′,BO′,依据旋转的性质失掉∠OAO′=60∘,推出△OAO′是等边三角形,失掉∠AOO′=60∘,推出△OO′B是等边三角形,失掉∠AO′B=120∘,失掉∠O′B′B=∠O′BB′= 30∘,依据图形的面积公式即可失掉结论.此题考察了扇形面积的计算,等边三角形的判定和性质,旋转的性质,正确的作出辅佐线是解题的关键.8. 解:衔接OC,∵AB是⊙O的直径,∴∠ACB=90∘.∵∠B=30∘,∴∠BAC=60∘.∵AC=AD,∴∠D=∠ACD=30∘.∵OC=OB,∠B=30∘,∴∠DOC=60∘,∴∠OCD=90∘.∵AB=2,∴OC=1,∴CD=OCtan30∘=√33=√3.应选D.衔接OC,先依据AB是⊙O的直径得出∠ACB=90∘,再由∠B=30∘得出∠BAC=60∘,依据AC=AD可知∠D=∠ACD,由三角形外角的性质得出∠D=∠ACD=30∘,再由OC= OB,∠B=30∘得出∠DOC=60∘,故可得出∠OCD=90∘,再由AB=2可知OC=1,依据锐角三角函数的定义即可得出结论.此题考察的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.9. 解:设∠ADC的度数=α,∠ABC的度数=β;∵四边形ABCO是平行四边形,∴∠ABC=∠AOC;∵∠ADC=12β,∠ADC=α;而α+β=180∘,∴{α+β=180∘α=12β,解得:β=120∘,α=60∘,∠ADC=60∘,应选:C.设∠ADC的度数=α,∠ABC的度数=β,由题意可得{α+β=180∘α=12β,求出β即可处置效果.该题主要考察了圆周角定理及其运用效果;应结实掌握该定理并能灵敏运用.10. 解:∵四边形ABCD是圆内接四边形,∴∠BCF=∠A=55∘,∵∠CBF是△ABE的一个外角,∴∠CBF=∠A+∠E=85∘,∴∠F=180∘−∠BCF−∠CBF=40∘,应选:C.依据圆内接四边形的性质求出∠BCF,依据三角形的外角的性质求出∠CBF,依据三角形内角和定理计算即可.此题考察的是圆内接四边形的性质和三角形的外角的性质,掌握圆内接四边形的恣意一个外角等于它的内对角是解题的关键.11. 解:∵AB是⊙O的直径,∴∠ADB=90∘,∵∠ABD=62∘,∴∠A=90∘−∠ABD=28∘,∴∠BCD=∠A=28∘.故答案为28∘.依据圆周角定理的推论由AB是⊙O的直径得∠ADB=90∘,再应用互余计算出∠A= 90∘−∠ABD=28∘,然后再依据圆周角定理求∠BCD的度数.此题考察了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90∘的圆周角所对的弦是直径.12. 解:∵PA、PB是半径为1的⊙O的两条切线,∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,而∠APB=60∘,∴∠APO=30∘,△PAB是等边三角形,∴PA=√3AO=√3,∴△PAB的周长=3√3.故答案为:3√3.依据切线的性质失掉OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,推出△PAB是等边三角形,依据直角三角形的性质失掉PA=√3AO=√3,于是失掉结论.此题考察了切线的性质,直角三角形的性质,三角形的周长的计算,熟练掌握切线的性质是解题的关键.13. 解:依据圆锥的正面积公式:πrl=π×2×5=10π,故答案为:10π.依据圆锥的底面半径为4,母线长为5,直接应用圆锥的正面积公式求出它的正面积.此题主要考察了圆锥正面积公式.掌握圆锥正面积公式:S侧=πrl是处置效果的关键.14. 解:∵2∠ACB=260∘,∴∠AOB=360∘−260∘=100∘.故答案为100∘.依据圆周角定理即可得出结论.此题考察了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.15. 解:∵AC与⊙O相切,∴∠BAC=90∘,∵∠CAD=30∘,∴∠OAD=60∘,∴∠BOD=2∠BAD=120∘,故答案为:120.依据切线的性质求出∠BAC=90∘,求出∠OAD=60∘,依据圆周角定理得出∠BOD=2∠BAD,代入求出即可.此题考察了切线的性质和圆周角定理,能依据定理得出∠BAC=90∘和∠BOD=2∠BAD 是解此题的关键.16. 解:衔接OD、OE,如下图:∵△ABC是等边三角形,∴∠A=∠B=∠C=60∘,∵OA=OD,OB=OE,∴△AOD、△BOE是等边三角形,∴∠AOD=∠BOE=60∘,∴∠DOE=60∘,∵OA=12AB=3,∴DE⏜的长=60π×3180=π;故答案为:π.衔接OD、OE,先证明△AOD、△BOE是等边三角形,得出∠AOD=∠BOE=60∘,求出∠DOE=60∘,再由弧长公式即可得出答案.此题考察了等边三角形的性质与判定、弧长公式;熟练掌握弧长公式,证明三角形是等边三角形是处置效果的关键.17. 解:如图,∵点M,N区分是AB,AC的中点,∴MN=12BC,∴当BC取得最大值时,MN就取得最大值,当BC是直径时,BC最大,衔接BO并延伸交⊙O于点C′,衔接AC′,∵BC′是⊙O的直径,∴∠BAC′=90∘.∵∠ACB=45∘,AB=5,∴∠AC′B=45∘,∴BC′=ABsin45∘=√22=5√2,∴MN最大=5√22.故答案为:5√22.依据中位线定理失掉MN的长最大时,BC最大,当BC最大时是直径,从而求得直径后就可以求得最大值.此题考察了三角形的中位线定理、等腰直角三角形的性质及圆周角定理,解题的关键是了解当什么时分MN的值最大,难度不大.18. 解:∵∠AOB=120∘,∴∠ACB=120∘×12=60∘,故答案为:60.依据圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半可得答案.此题主要考察了圆周角定理,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.19. 解:∵∠BOD=160∘,∴∠BAD=12∠BOD=80∘,∵A、B、C、D四点共圆,∴∠BCD+∠BAD=180∘,∴∠BCD=100∘,故答案为:100∘.依据圆周角定理求出∠BAD,依据圆内接四边形性质得出∠BCD+∠BAD=180∘,即可求出答案.此题考察了圆内接四边形的性质,处置此题的关键是求出∠BAD的度数和得出∠BCD+∠BAD=180∘.20. 解:∵弦CD//AB,∴S△ACD=S△OCD,∴S阴影=S扇形COD=∠COD360⋅π⋅(AB2)2=90∘360×π×(22)2=π4.故答案为:π4.由CD//AB可知,点A、O到直线CD的距离相等,结合同底等高的三角形面积相等即可得出S△ACD=S△OCD,进而得出S阴影=S扇形COD,依据扇形的面积公式即可得出结论.此题考察了扇形面积的计算以及平行线的性质,解题的关键是找出S阴影=S扇形COD.此题属于基础题,难度不大,处置该题型标题时,经过火割图形找出面积之间的关系是关键.21. (1)衔接OD,由BD=CD,OB=OA,失掉OD为三角形ABC的中位线,失掉OD 与AC平行,依据DF垂直于AC,失掉DF垂直于OD,即可得证;(2)由直角三角形两锐角互余求出∠C的度数,应用两直线平行同位角相等求出∠ODB的度数,再由OB=OD,应用等边对等角求出∠B的度数,设BD=x,应用勾股定理列出关于x的方程,求出方程的解失掉x的值,即可确定出圆的半径.此题考察了切线的判定,圆周角定理,三角形中位线定理,勾股定理,以及含30度直角三角形的性质,熟练掌握切线的判定方法是解此题的关键.22. (1)由直径所对的圆周角为直角失掉∠BAC为直角,再由AD为角平分线,失掉一对角相等,依据同弧所对的圆心角等于圆周角的2倍及等量代换确定出∠DOC为直角,与平行线中的一条垂直,与另一条也垂直失掉OD与PD垂直,即可得证;(2)由PD与BC平行,失掉一对同位角相等,再由同弧所对的圆周角相等及等量代换失掉∠P=∠ACD,依据同角的补角相等失掉一对角相等,应用两对角相等的三角形相似即可得证;(3)由三角形ABC为直角三角形,应用勾股定理求出BC的长,再由OD垂直平分BC,失掉DB=DC,依据(2)的相似,得比例,求出所求即可.此题考察了相似三角形的判定与性质,切线的判定与性质,熟练掌握各自的判定与性质是解此题的关键.23. (I)衔接OE,CE,OB,求出BC=BE,证出△OEB≌△OCB,推出∠OEB=∠ACB=90∘,依据切线的判定推出即可;(II)证△AEO∽△ACB,推出OEBC =AEAC,求出OEBC=√22,解直角三角形求出即可.此题考察了全等三角形的性质和判定,切线的判定和性质,相似三角形的性质和判定,解直角三角形的运用,主要考察先生综合运用性质停止推理和计算的才干.24. (1)由垂径定理知,B^C=B^D,∴∠DCB=∠CAB=30∘;CD=3,AB是直径,∴∠ACB=90∘,(2)由垂径定理知,点E是CD的中点,有CE=12再求出AC的长,应用∠A的余弦即可求解.此题应用了垂径定理和圆周角定理及锐角三角函数的概念求解.25. (1)衔接OE,由于BE是角平分线,那么有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么应用内错角相等,两直线平行,可得OE//BC;又∠C=90∘,所以∠AEO=90∘,即AC是⊙O的切线;(2)连结DE,先依据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF.(3)先证得△EHF∽△BEF,依据相似三角形的性质求得BF=10,进而依据直角三角形斜边中线的性质求得OE=5,进一步求得OH,然后解直角三角形即可求得OA,得出AF.此题主要考察了切线的判定,全等三角形的判定与性质,三角形相似的判定和性质以及解直角三角形等.要证某线是圆的切线,此线过圆上某点,衔接圆心与这点(即为半径),再证垂直即可.26. (1)衔接OC,先证明∠OAC=∠OCA,进而失掉OC//AE,于是失掉OC⊥CD,进而证明DE是⊙O的切线;(2)区分求出△OCD的面积和扇形OBC的面积,应用S阴影=S△COD−S扇形OBC即可失掉答案.此题主要考察了切线的判定以及扇形的面积计算,解(1)的关键是证明OC⊥DE,解(2)的关键是求出扇形OBC的面积,此题难度普通.。
冀教版九年级数学上册 第28章 圆 单元评估检测试卷(有答案)
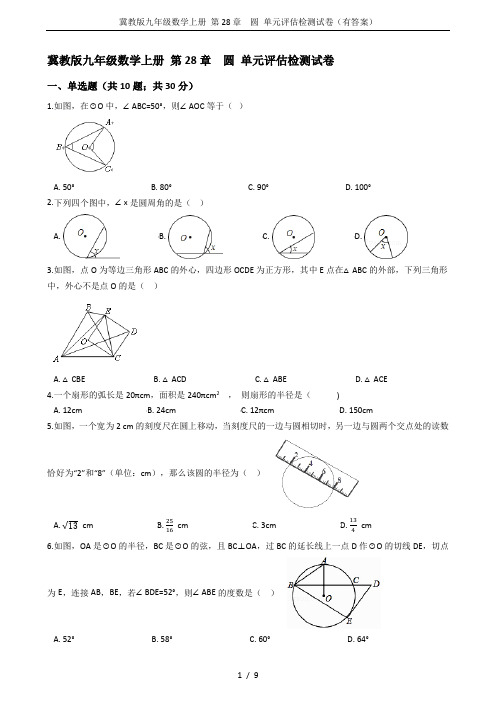
冀教版九年级数学上册第28章圆单元评估检测试卷一、单选题(共10题;共30分)1.如图,在⊙O中,∠ABC=50°,则∠AOC等于()A. 50°B. 80°C. 90°D. 100°2.下列四个图中,∠x是圆周角的是()A. B. C. D.3.如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是()A. △CBEB. △ACDC. △ABED. △ACE4.一个扇形的弧长是20πcm,面积是240πcm2,则扇形的半径是()A. 12cmB. 24cmC. 12πcmD. 150cm5.如图,一个宽为2 cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),那么该圆的半径为()A. cmB. cmC. 3cmD. cm6.如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是()A. 52°B. 58°C. 60°D. 64°7.下列语句中,不正确的个数是()①直径是弦;②弧是半圆;③长度相等的弧是等弧;④经过圆内一定点可以作无数条直径.A. 1个B. 2个C. 3个D. 4个8.某花园内有一块五边形的空地如图所示,为了美化环境,现计划在五边形各顶点为圆心,2 m长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是( )A. 6πm2B. 5πm2C. 4πm2D. 3πm29.如图,在半径为5的⊙O中,如果弦AB的长为8,那么它的弦心距OC等于()A. 2B. 3C. 4D. 610.(2017•天水)如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ,则S阴影=()A. 2πB. πC. πD. π二、填空题(共10题;共30分)11.已知圆锥的底面直径是8cm,母线长是5cm,其侧面积是________cm2(结果保留π).12.若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是________.13.如图,A,B,C,D是⊙O上的四个点, = ,若∠AOB=58°,则∠BDC=________度.14.已知扇形的弧长为π,半径为1,则该扇形的面积为________15.如图,AB为△ADC的外接圆⊙O的直径,若∠BAD=50°,则∠ACD=________°.16.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上,那么△ ABC的外接圆半径是________.17.如图,AB为半圆O的直径,C、D是半圆上的三等分点,若⊙O的半径为1,E为线段AB上任意一点,则图中阴影部分的面积为________.18.如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为________(度).19.边长为4cm的正方形ABCD绕它的顶点A旋转180°,顶点B所经过的路线长为 ________cm.20.四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).若四边形OBCD是平行四边形时,那么∠OBA和∠ODA的数量关系是________.三、解答题(共8题;共60分)21.如图,已知AB,CB为⊙O的两条弦,请写出图中所有的弧.22.已知排水管的截面为如图所示的⊙O,半径为10,圆心O到水面的距离是6,求水面宽AB.23.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.(1)求∠E的度数;(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值24.如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BC=2,连接CD,求BD的长.25.如图,已知⊙O中,弦AB与CD相交于点P.求证:PA•PB=PC•PD.26.如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P.求证:(1)D是BC的中点;(2)△BEC∽△ADC.27.如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小28.如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.(1)求证:AC=AE;(2)求△ACD外接圆的直径.答案解析部分一、单选题1.【答案】D2.【答案】C3.【答案】B4.【答案】B5.【答案】D6.【答案】D7.【答案】C8.【答案】A9.【答案】B10.【答案】B二、填空题11.【答案】20π12.【答案】12013.【答案】2914.【答案】15.【答案】4016.【答案】17.【答案】18.【答案】55.19.【答案】4π20.【答案】∠OBA﹣∠ODA=60°或∠OBA+∠ODA=60°或∠ODA﹣∠OBA=60°或∠OBA+∠ODA=120°三、解答题21.【答案】解:图中的弧为22.【答案】解:如图,过O点作OC⊥AB,连接OB,根据垂径定理得出AB=2BC,再根据勾股定理求出BC===8,从而求得AB=2BC=2×8=16.23.【答案】解:(1)连接BD,∵四边形ABCD是⊙O的内接四边形,∴∠BAD+∠C=180°,∵∠C=120°,∴∠BAD=60°,∵AB=AD,∴△ABD是等边三角形,∴∠ABD=60°,∵四边形ABDE是⊙O的内接四边形,∴∠AED+∠ABD=180°,∴∠AED=120°;(2)连接OA,∵∠ABD=60°,∴∠AOD=2∠ABD=120°,∵∠DOE=90°,∴∠AOE=∠AOD﹣∠DOE=30°,=12.∴n=°°24.【答案】解:∵∠A和∠D所对的弧都是弧BC,∴∠D=∠A=45°,∵BD是直径,∴∠DCB=90°,∴∠D=∠DBC=45°,∴CB=CD=2,由勾股定理得:BD= =225.【答案】证明:连接AC、BD.∵∠A=∠D,∠C=∠B,∴△ACP∽△DBP,∴= ,∴PA•PB=PC•PD.26.【答案】证明:(1)∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴D是BC的中点;(2)∵AB是⊙O的直径,∴∠AEB=∠ADB=90°,即∠CEB=∠CDA=90°,∵∠C是公共角,∴△BEC∽△ADC.27.【答案】解:如图:作点C关于AB的对称点M,点E关于AB的对称点N,连结CM、FM,设CM交AB于点Q,依题可得AB⊥CM,CQ=MQ,∴∠CFA=∠AFM,又∵∠CFA=∠DFB,∴∠AFM=∠DFB,∴D、F、M三点共线,同理可得D、G、N三点共线,又∵弧AC=60°,弧BE=20°,∴弧AM=弧AC=60°,弧BN=弧BE=20°,∴弧MN=180°-60°-20°=100°,∴∠FDG=×100°=50°.28.【答案】(1)证明:∵∠ACB=90°,且∠ACB为⊙O的圆周角,∴AD为⊙O的直径,∴∠AED=90°,∴∠ACB=∠AED.∵AD是△ABC中∠BAC的平分线,∴∠CAD=∠EAD,∴CD=DE,在Rt△ACD与Rt△AED中,,∴△ACD≌△AED(HL),∴AC=AE;(2)∵△ABC是直角三角形,且AC=6,BC=8,∴AB===10,∵由(1)得,∠AED=90°,∴∠BED=90°.设CD=DE=x,则DB=BC﹣CD=8﹣x,EB=AB﹣AE=10﹣6=4,在Rt△BED中,根据勾股定理得,BE2=BE2+ED2,即(8﹣x)2=x2+42,解得x=3,∴CD=3,∵AC=6,△ACD是直角三角形,∴AD2=AC2+CD2=62+32=45,∴AD=.。
冀教版九年级数学上册第28章达标测试卷附答案

冀教版九年级数学上册第二十八章达标测试卷一、选择题(1~10题每题3分,11~16题每题2分,共42分)1.下列说法不正确...的是()A.圆是中心对称图形B.三点确定一个圆C.半径相等的两个圆是等圆D.每个圆都有无数条对称轴2.如图,⊙O中,∠B=50°,则∠AEC的度数为()A.65°B.75°C.50°D.55°(第2题)(第3题)3.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是() A.1 B. 2 C. 3 D.24.如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO=() A.10°B.20°C.30°D.40°(第4题)(第5题)5.如图,在⊙O中,弦AB=8,OC⊥AB,垂足为点C,且OC=3,则⊙O的半径为()A.5B.10C.8D.66.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠A 等于()A.128°B.100°C.64°D.32°(第6题)(第7题)7.如图,A,B,C,D是圆上的点,∠1=68°,∠A=40°,则∠D的度数为() A.68°B.40°C.28°D.22°8.如图,在平面直角坐标系中,以原点为圆心,半径为5的圆内有一点P(0,-3),那么经过点P的所有弦中,最短的弦的长为()A.4 B.5 C.8 D.10(第8题)(第9题)(第10题)9.如图,点A,B,C,D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O 的直径的长是()A. 5 B.4 C.11 D.1310.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD =6,则BC的长为()A.5 B.6 C.7 D.811.在△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的全面积是()A.25 π B.65 π C.90 π D.130 π12.已知扇形的面积为4π,扇形的弧长为π,则该扇形的半径为() A.4 B.6 C.8 D.8π13.如图,在⊙O中,弦BC=1,点A是⊙O上一点,且∠BAC=30°,则⊙O 的半径是()A.1 B.2 C. 3 D. 5(第13题)(第14题)(第15题)14.如图,已知⊙O 的半径为5,P 是⊙O 内一点,且OP =3,过点P 作⊙O 的一条弦AB ,则AB 的长不可以是( ) A .7B .8C .9D .1015.如图,已知⊙O 是等腰直角三角形ABC 的外接圆,点D 是AC ︵上一点,BD交AC 于点E ,若BC =4,AD =45,则AE 的长是( ) A .3B .2C .1D .1.2(第16题)16.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径为60 cm ,则这块扇形铁皮的半径是( ) A .40 cm B .50 cm C .60 cmD .80 cm二、填空题(17、18题每题3分,19题每空2分,共12分) 17.如图,在⊙O 中,AB ︵=AC ︵,∠A =40°,则∠B =________.(第17题) (第18题)18.如图,△ABC 内接于⊙O ,AH ⊥BC 于点H ,若AC =24,AH =18,⊙O 的半径OC =13,则AB =________. 19.已知△ABP 的外接圆⊙O 的半径为1.(1)当A ,O ,B 三点共线时,∠APB =__________; (2)当∠APB =60°时,AB =________;(3)当1≤AB ≤2时,∠APB 的范围是____________________.三、解答题(20、21题每题8分,22、23题每题9分,24、25题每题10分,26题12分,共66分)20.如图,AB是半圆O的直径,C,D是半圆O上的两点,OD∥BC,OD与AC交于点E.(第20题)(1)若∠D=70°,求∠CAD的度数;(2)若AC=8,DE=2,求AB的长.21.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.(1)求证:CB∥PD;(2)若BC=3,sin P=35,求⊙O的直径.(第21题)22.如图,已知一个圆锥的轴截面ABC是等边三角形,它的全面积为75πcm2.求这个圆锥的底面半径和母线长.(第22题)23.如图,在平面直角坐标系中,已知⊙M经过坐标原点,与x轴,y轴分别交于A,B两点,点B的坐标为(0,2 3),OC与⊙M相交于点C,且∠OCA =30°,求图中阴影部分的面积.(第23题)24.如图,已知P为反比例函数y=4x(x>0)图像上一点,以点P为圆心,OP长为半径画圆,⊙P与x轴相交于点A,连接P A,且点A的坐标为(4,0).求:(第24题)(1)⊙P的半径;(2)图中阴影部分的面积.25.感受文化生态,体验运动休闲,6月28日—29日,第六届石家庄市旅游产业发展大会在元氏召开.如图①是元氏乡村一角的草坪,草坪是由一块弓形草地和一块三角形草地组成的.现需要给草坪装上自动喷灌装置,并且用喷灌龙头浇水时,既要保证草坪的每个角落都能浇上水,又能最大化地节约水,于是选择了一种转角在0°~180°内(含180°)可以自由设定(按设定的转角可以往复转动喷灌)、射程长短也可以自由设定的喷灌龙头.如图②,已知弓形高DE=6 3米,弓形宽AB=24米.△ABC的边BC=12米,AC=12 3米.若经测算,将喷灌龙头安装在△ABC的顶点C时为最优方案.(第25题)(1)喷灌龙头的最小转角应设置为多少度?(2)求喷灌龙头的最短射程.26.如图①,在矩形ABCD中,AB=9,BC=12,点P是线段AD上的一个动点.以点P为圆心,PD长为半径作⊙P,连接CP.(1)当⊙P经过PC的中点时,PC的长为________;(2)如图②,当⊙P与AC交于E,F两点,且EF=9.6时,求点P到AC的距离.(第26题)答案一、1.B 2.C 3.D 4.B 5.A 6.C 7.C 8.C 9.D 10.B 11.C 12.C 13.A 14.A15.C 【点拨】∵⊙O 是等腰直角三角形ABC 的外接圆,BC =4,∴AB 为⊙O 的直径,AC =4,AB =4 2. ∴∠D =90°.在Rt △ABD 中,AD =45,AB =4 2, ∴BD =285.∵∠D =∠C ,∠DAE =∠CBE , ∴△ADE ∽△BCE .∴AD ∶BC =AE ∶BE =DE ∶CE =45∶4=1∶5.∴相似比为1∶5. 设AE =x ,则BE =5x .∴DE =285-5x . ∴CE =5DE =28-25x . 又∵AC =4,∴x +28-25x =4. 解得x =1.∴AE =1. 16.A二、17.70° 18.392 19.(1)90° (2) 3(3)30°≤∠APB ≤45°或135°≤∠APB ≤150° 【点拨】(3)如图,连接OA ,OB . 在△AOB 中,当AB =1时, ∵OA =OB =1,∴∠AOB =60°.当点P 在优弧APB ︵上时,∠APB =12∠AOB =30°; 当点P 在劣弧AB ︵上时,∠AP ′B =12(360°-∠AOB )=150°.当AB =2时,∵OA =OB =1,AB =2, ∴OA 2+OB 2=AB 2.∴∠AOB =90°. 当点P 在优弧APB ︵上时, ∠APB =12∠AOB =45°;当点P 在劣弧AB ︵上时,∠AP ′B =12(360°-∠AOB )=135°. ∴当1≤AB ≤2时, 30°≤∠APB ≤45°或135°≤∠APB ≤150°.(第19题)三、20.解:(1)∵OA =OD ,∠D =70°,∴∠OAD =∠D =70°.∴∠AOD =180°-∠OAD -∠D =40°. ∵AB 是半圆O 的直径, ∴∠C =90°.∵OD ∥BC , ∴∠AEO =∠C =90°, 即OD ⊥AC .∴AD ︵=CD ︵. ∴∠CAD =12∠AOD =20°.(2)由(1)可知OD ⊥AC , ∴AE =12AC =12×8=4.设OA =x ,则OE =OD -DE =x -2. 在Rt △OAE 中,OE 2+AE 2=OA 2, 即(x -2)2+42=x 2,解得x =5. ∴AB =2OA =10.21.(1)证明:∵∠BCD =∠P ,∠1=∠BCD ,∴∠1=∠P .∴CB ∥PD .(2)解:连接AC .∵AB 为⊙O 的直径,∴∠ACB =90°. 又∵CD ⊥AB ,∴BD ︵=BC ︵, ∴∠P =∠CAB .∵sin P =35,∴sin ∠CAB =BC AB =35. 又∵BC =3,∴AB =5, 即⊙O 的直径为5.22.解:设这个圆锥的底面半径为r cm ,则母线长为2r cm.依题意,得12×2πr ×2r +πr 2=75π,解得r =5(负值舍去),∴2r =10. 故这个圆锥的底面半径为5 cm ,母线长为10 cm. 23.解:连接AB ,∵∠AOB =90°,∴AB 是直径.根据同弧所对的圆周角相等,得∠OBA =∠OCA =30°. 由题意知OB =2 3,∴OA =OB ·tan ∠OBA =OB ·tan 30°= 2 3×33=2,AB =AO sin ∠OBA =AO sin 30°=4,∴圆的半径为2.∴阴影部分的面积等于圆的面积的一半减去△ABO 的面积, 即22π2-12×2×2 3=2π-2 3. 24.解:(1)过点P 作PD ⊥x 轴于点D .∵点A 的坐标为(4,0),∴OA =4. ∴OD =2,即点P 的横坐标为2. 将x =2代入y =4x ,可得y =2, 即PD =2.在Rt △OPD 中,根据勾股定理可得OP =2 2,即⊙P 的半径为2 2. (2)由(1)可得PD =OD =OA , 且∠ODP =∠ADP =90°,∴∠POD =∠P AD =45°,∴∠OP A =90°.∴S 阴影=S 扇形OP A -S △OP A =90×(2 2)2×π360-4×22=2π-4.25.解:(1)∵AB =24米,BC =12米,AC =12 3 米,∴BC 2+AC 2=AB 2,∴∠ACB =90°,∴喷灌龙头的最小转角应设置为90°. (2)如图,作射线ED 交AC 于点M , ∵AD =DB ,ED ⊥AB ,AB ︵是劣弧, ∴AB ︵所在圆的圆心在射线ED 上.假设圆心为O ,半径为r 米,连接OA ,则OA =r 米,OD =(r -6 3) 米, ∵AD =12AB =12 米,∴在Rt △AOD 中,r 2=122+(r -6 3)2,解得r =7 3,∴OD = 3 米. 过点C 作CN ⊥AB ,垂足为N ,∵∠ACB =90°,AB =24 米,BC =12 米, ∴sin ∠BAC =12,∴∠BAC =30°,∴CN =AC ·sin 30°=6 3 米,DM =AD ·tan 30°=4 3 米,AN =AC ·cos 30°=18 米,∴BN =6 米.∵OD <MD ,∴点O 在△ACB 内部.连接CO 并延长交AB ︵于点F ,在AB ︵上任取异于点F 的一点G ,连接GO ,GC ,则CF =OC +OF =OC +OG >CG ,∴CF >CG ,即CF 为草坪上的点到C 点的最大距离.过点O 作OH ⊥CN ,垂足为H ,易得OH =DN =6 米,CH =6 3-3=5 3 (米),∴OC =CH 2+OH 2= (5 3)2+62=111(米), ∴CF =OC +r =(111+7 3)米,答:喷灌龙头的最短射程为(7 3+111)米.(第25题) 26.解:(1) 6 3(2)如图,过点P 作PH ⊥AC 于H ,连接PF .∵四边形ABCD 为矩形,AD =BC =12,AB =DC =9,∴AC =15. ∴sin ∠P AH =PH AP =CD AC =35. 设⊙P 的半径为x ,则PF =PD =x ,∴AP =12-x . ∴PH =35(12-x ).在⊙P 中,∵PH ⊥EF ,EF =9.6, ∴HF =245.在Rt △PHF 中,PH 2+HF 2=PF 2, 即⎣⎢⎡⎦⎥⎤35(12-x )2+⎝ ⎛⎭⎪⎫2452=x 2, 解得x 1=6,x 2=-392(舍去).∴PD =6.∴PH =35(12-x )=185,即点P 到AC 的距离为185.(第26题)九年级数学上册期末达标检测卷一、选择题(每题4分,共40分)1.已知a,d,c,b是成比例线段,其中a=3 cm,b=2 cm,c=6 cm,则d的长度为()A.4 cm B.1 cm C.9 cm D.5 cm2.在反比例函数y=k-1x图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是()A.k<0 B.k>0 C.k<1 D.k>13.对于抛物线y=-12(x+2)2+3,有下列结论:①抛物线的开口向下;②对称轴为直线x=2;③顶点坐标为(-2,3);④当x>2时,y随x的增大而减小.其中正确结论的个数为()A.1 B.2 C.3 D.44.如图,在▱ABCD中,E是AD边的中点,连接BE并延长交CD的延长线于点F,则△EDF与△BCF的周长之比是()A.1:2 B.1:3 C.1:4 D.1:55.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=5,BC =2,则sin∠ACD的值为()A.52 B.2 55 C.53 D.236.如图,P为线段AB上一点,AD与BC相交于点E,∠CPD=∠A=∠B,BC 交PD于点F,AD交PC于点G,则图中相似三角形有()A.1对B.2对C.3对D.4对7.如图,在直角平面坐标系中,△OAB 的顶点为O (0,0),A (4,3),B (3,0).以点O 为位似中心,在第三象限内作与△OAB 的相似比为13的位似图形△OCD ,则点C 的坐标为( )A .(-1,-1) B.⎝ ⎛⎭⎪⎫-43,-1 C.⎝ ⎛⎭⎪⎫-1,-43 D .(-2,-1) 8.如图,在笔直的海岸线l 上有A ,B 两个观测站,且AB =2 km.从A 站测得船C 在北偏东45°方向,从B 站测得船C 在北偏东22.5°方向,且tan 22.5°=2-1,则船C 离海岸线l 的距离(即CD 的长)为( ) A .4 kmB .(2+2)kmC .2 2 kmD .(4-2)km9.如图,已知边长为4的正方形EFCD 截去一角成为五边形ABCDE ,其中AF=2,BF =1.在AB 上找一点P ,使得矩形PNDM 有最大面积,则矩形PNDM 面积的最大值为( ) A .8B .12C.252D .1410.如图,在平面直角坐标系中,抛物线y =-x 2+2 3x 的顶点为A ,且与x轴的正半轴交于点B ,点P 为该抛物线对称轴上一点,则OP +12AP 的最小值为( ) A.3+2214B.3+232C .3D .2 3二、填空题(每题5分,共20分)11.如图,在由边长相同的小正方形组成的网格中,点A ,B ,C ,D 都在这些小正方形的顶点上,AB ,CD 相交于点P ,则tan ∠APD 的值是________.12.如图,点P 是反比例函数y =43x (x >0)图象上一动点,在y 轴上取点Q ,使得以P ,Q ,O 为顶点的三角形是含有30°角的直角三角形,则符合条件的点Q 的坐标是________________.13.如图是二次函数y =ax 2+bx +c (a ≠0)的图象,其与x 轴的交点的横坐标分别为x 1,x 2,其中-2<x 1<-1,0<x 2<1,下列结论:①abc >0;②4a -2b +c <0;③2a -b <0.其中正确的有____________(填序号).14.如图,在矩形纸片ABCD 中,AB =6,BC =10,点E 在CD 上,将△BCE沿BE 折叠,使点C 恰好落在边AD 上的点F 处;点G 在AF 上,将△ABG 沿BG 折叠,使点A 恰好落在线段BF 上的点H 处,有下列结论:①∠EBG =45°;②△DEF ∽△ABG ;③S △ABG =32S △FGH ;④AG +DF =FG .其中正确的有____________(填序号).三、解答题(15~18题每题8分;19,20题每题10分;21,22题每题12分;23题14分,共90分)15.计算:(-1)2 022-6tan30°+⎝ ⎛⎭⎪⎫12-2+|1-3|.16.已知抛物线y =12x 2-4x +7与直线y =12x 交于A ,B 两点(点A 在点B 左侧).(1)求A ,B 两点的坐标;(2)求抛物线顶点C 的坐标,并求△ABC 的面积.17.如图,在△ABC中,AB=43,AC=10,∠B=60°,求△ABC的面积.18.如图,△ABC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O 为位似中心,将△ABC放大为原来的2倍得到△A′B′C′.(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法);(2)计算△A′B′C′的面积.19.如图,已知在正方形ABCD中,BE平分∠DBC,交CD边于点E,将△BCE 绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.(1)求证:△BDG∽△DEG;(2)若EG·BG=4,求BE的长.20.设P(x,0)是x轴上的一个动点,它与原点的距离为y1.(1)求y1关于x的函数表达式,并画出这个函数的图象;(2)若反比例函数y2=kx的图象与函数y1的图象相交于点A,且点A的纵坐标为2.①求k的值;②结合图象,当y1>y2时,写出x的取值范围.21.如图,某大楼DE的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:3,AB=8米,AE=12米.(1)求点B距水平面AE的高度BH;(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:2≈1.414,3≈1.732)22.某公司经销一种绿茶,每千克成本为50元.经市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体表达式为w =-2x+240.设这种绿茶在这段时间内的销售利润为y元,解答下列问题:(1)求y与x的函数表达式;(2)当x取何值时,y的值最大?(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2 250元的销售利润,销售单价应定为多少?23.矩形ABCD 的一条边AD =8,将矩形ABCD 折叠,使得点B 落在CD 边上的点P 处.(1)如图①,已知折痕与边BC 交于点O .① 求证:△OCP ∽△PDA ;② 若△OCP 与△PDA 的面积比为1:4,求边AB 的长;(2)如图②,在(1)的条件下,擦去AO 和OP ,连接BP .动点M 在线段AP 上(不与点P ,A 重合),动点N 在线段AB 的延长线上,且BN =PM ,连接MN 交PB 于点F ,作ME ⊥BP 于点E .试问动点M ,N 在移动的过程中,线段EF 的长度是否发生变化?若不变,求出线段EF 的长度;若变化,说明理由.答案一、1.B 2.D3.C 【点拨】∵a <0,∴抛物线的开口向下,①正确;抛物线y =-12(x +2)2+3的对称轴为直线x =-2,②错误;顶点坐标为(-2,3),③正确;④抛物线开口向下,当x >2时,图象是下降趋势,y 随x 的增大而减小,④正确.故选C.4.A 【点拨】在▱ABCD 中,AD =BC ,AD ∥BC ,∵E 是AD 的中点,∴DE =12AD =12BC .由AD ∥BC 可得,△EDF ∽△BCF .它们的周长比等于相似比,∴周长比等于ED BC =12BC :BC =1:2.故选A.5.C 【点拨】∵在Rt △ABC 中,∠ACB =90°,AC =5,BC =2,∴AB =AC 2+BC 2=(5)2+22=3. ∵∠ACB =90°,CD ⊥AB , ∴∠ACD +∠BCD =90°,∠B +∠BCD =90°,∴∠ACD =∠B , ∴sin ∠ACD =sin B =AC AB =53. 故选C.6.C 【点拨】∵∠CPD =∠A ,∠D =∠D ,∴△ADP ∽△PDG ,∴∠APD =∠PGD ,∴∠FPB =∠AGP .∵∠CPF =∠B ,∠C =∠C ,∴△CPF ∽△CBP ,∴∠CFP =∠CPB ,∴∠PFB =∠APG ;在△AGP 和△BPF 中,∠AGP =∠BPF ,∠APG =∠BFP ,∴△AGP ∽△BPF .故选C. 7.B 8.B9.B 【点拨】延长NP 交EF 于点G ,设PG =x ,则PN =4-x . ∵PG ∥BF ,∴△APG ∽△ABF , ∴AG AF =PG BF ,即AG 2=x 1, 解得AG =2x ,∴PM =EG =EA +AG =2+2x ,∴S 矩形PNDM =PM ·PN =(2+2x )(4-x )=-2x 2+6x +8=-2⎝ ⎛⎭⎪⎫x -322+252(0≤x ≤1),当x =1时,矩形PNDM 的面积最大,最大值为12.故选B .10.C 【点拨】连接AB ,过点P 作PC ⊥AB 于点C .设抛物线的对称轴与x 轴的交点为点D .易求出抛物线的对称轴为直线x =3,顶点A (3,3),故BD =OD =3,AD =3,在Rt △ABD 中,tan ∠BAD =BD AD =33,∴∠BAD =30°,∴PC =12AP .当O ,P ,C 三点共线时,OP +PC 的长最短,最短距离为sin ∠OBC ·OB =sin 60°×2 3=3.∴OP +12AP 的最小值为3.故选C.二、11.212.(0,23)或(0,2)或⎝ ⎛⎭⎪⎫0,833或(0,8) 13.①②③ 【点拨】①∵图象开口向下, ∴a <0,∵图象的对称轴在y 轴左侧, ∴-b2a <0,而a <0,∴b <0, ∵图象与y 轴的交点在正半轴上, ∴c >0,∴abc >0,故结论正确. ②∵-2<x 1<-1,∴当x =-2时,y =4a -2b +c <0,故结论正确. ③∵-2<x 1<-1,0<x 2<1, ∴-b2a >-1,∵a <0, ∴2a -b <0,故结论正确. 故正确的结论有①②③.14.①③④ 【点拨】∵△BCE 沿BE 折叠,点C 恰好落在边AD 上的点F 处, ∴∠1=∠2,CE =FE ,BF =BC =10.在Rt △ABF 中,∵AB =6,BF =10, ∴AF =102-62=8,∴DF =AD -AF =10-8=2.设EF =x ,则CE =x ,DE =CD -CE =6-x .在Rt △DEF 中,∵DE 2+DF 2=EF 2,∴(6-x )2+22=x 2,解得x =103,∴DE =83.∵△ABG 沿BG 折叠,点A 恰好落在线段BF 上的点H 处,∴∠3=∠4,BH =BA =6,AG =HG ,∴∠EBG =∠2+∠3=12∠ABC =45°,∴①正确.HF =BF -BH =10-6=4,设AG =y ,则GH =y ,GF =8-y .在Rt △HGF 中,∵GH 2+HF 2=GF 2,∴y 2+42=(8-y )2,解得y =3,∴AG =GH =3,GF =5.∵∠A =∠D ,AB DE =94,AG DF =32,∴AB DE ≠AGDF ,∴△ABG 与△DEF 不相似,∴②错误.∵S △ABG =12AB ·AG =12×6×3=9,S △FGH =12GH ·HF =12×3×4=6,∴S △ABG =32S △FGH ,∴③正确.∵AG +DF =3+2=5,而FG =5,∴AG +DF =FG ,∴④正确.三、15.解:原式=1-6×33+4+3-1=4- 3.16.解:(1)联立⎩⎪⎨⎪⎧y =12x 2-4x +7,y =12x ,解得⎩⎨⎧x =2,y =1或⎩⎪⎨⎪⎧x =7,y =72.∴A (2,1),B ⎝ ⎛⎭⎪⎫7,72.(2)∵y =12x 2-4x +7=12(x -4)2-1, ∴顶点C 的坐标为(4,-1).过顶点C 作CD ∥x 轴交直线y =12x 于点D ,如图.在y =12x 中,令y =-1,得12x =-1,解得x =-2,∴CD =6,∴S △ABC =S △BCD -S △ACD =12×6×⎝ ⎛⎭⎪⎫72+1-12×6×(1+1)=7.5.17.解:过点A 作AD ⊥BC 于点D .在Rt △ABD 中,AD =AB ·sin B =4 3×32=6,BD =AB ·cos B =4 3×12=2 3.在Rt △ACD 中,CD =AC 2-AD 2=102-62=8, ∴BC =BD +CD =2 3+8.∴S △ABC =12BC ·AD =12×(23+8)×6=63+24. 18.解:(1)如图.(2)S △A ′B ′C ′=4×4-12×2×2-12×2×4-12×2×4=6.19.(1)证明:∵BE 平分∠DBC , ∴∠DBG =∠CBE ,根据旋转的性质,得∠EDG =∠CBE , ∴∠DBG =∠EDG , 又∵∠DGB =∠EGD , ∴△BDG ∽△DEG .(2)解:由(1)知△BDG ∽△DEG , ∴BG DG =DGEG ,∴DG 2=EG ·BG . ∵EG ·BG =4,∴DG 2=4, ∴DG =2(负值舍去).∵∠EDG =∠CBE ,∠DEG =∠BEC , ∴∠BGD =∠BCE =90°. ∴∠BGF =∠BGD =90°.又∵BG =BG ,∠DBG =∠FBG , ∴△DBG ≌△FBG .∴DG =FG ,∴DF =2DG =4, 由题意可知,BE =DF , ∴BE =4.20.解:(1)由题意得,y 1=||x ,即y 1=||x =⎩⎨⎧x ,x ≥0,-x ,x <0.函数图象如图所示.(2)①∵点A 的纵坐标为2,点A 在函数y 1的图象上,∴||x =2,即x =±2.∴点A 的坐标为(2,2)或(-2,2).∴k =±4.②当k =4时,图象如图①,当y 1>y 2时,x 的取值范围为x <0或x >2; 当k =-4时,图象如图②,当y 1>y 2时,x 的取值范围为x <-2或x >0. 21.解:(1)过点B 作BG ⊥DE 于点G ,如图. 在Rt △ABH 中,tan ∠BAH =13=33,∴∠BAH =30°, ∴BH =12AB =4(米).∴点B距水平面AE的高度BH为4米.(2)由(1)知BH=4(米),∴GE=BH=4(米),AH=4 3(米).∴BG=HE=AH+AE=(4 3+12)米.在Rt△BGC中,∠CBG=45°,∴CG=BG=(4 3+12)米.在Rt△ADE中,∠DAE=60°,AE=12米,∴DE=AE·tan ∠DAE=12·tan 60°=12 3(米).∴CD=CG+GE-DE=4 3+12+4-12 3=16-8 3≈16-8×1.732≈2.1(米).∴广告牌CD的高度约为2.1米.22.解:(1)由题意得y=(x-50)·w=(x-50)·(-2x+240)=-2x2+340x-12 000,∴y与x的函数表达式为y=-2x2+340x-12 000.(2)y=-2x2+340x-12 000=-2(x-85)2+2 450,∴当x=85时,y的值最大.(3)当y=2 250时,可得-2(x-85)2+2 450=2 250,解这个方程,得x1=75,x2=95,根据题意知,x=95不合题意,故舍去,∴销售单价应定为75元/千克.23.(1)①证明:如图,∵四边形ABCD 是矩形, ∴∠C =∠D =∠B =90°, ∴∠1+∠3=90°.由折叠可得∠APO =∠B =90°, ∴∠1+∠2=90°. ∴∠3=∠2. 又∵∠C =∠D , ∴△OCP ∽△PDA .②解:∵△OCP 与△PDA 的面积比为1:4,且△OCP ∽△PDA , ∴OP P A =CP DA =12.∴CP =12AD =4,AP =2OP . 设OP =x ,则易得CO =8-x . 在Rt △PCO 中,∠C =90°, 由勾股定理得 x 2=(8-x )2+42. 解得x =5.∴AB =AP =2OP =10.(2)解:线段EF 的长度不变.作MQ ∥AN ,交PB 于点Q ,如图.∵AP =AB ,MQ ∥AN ,∴∠APB =∠ABP =∠MQP . ∴MP =MQ . 又∵BN =PM , ∴BN =QM . ∵MQ ∥AN ,∴∠QMF =∠BNF ,∠MQF =∠FBN , ∴△MFQ ≌△NFB . ∴QF =FB . ∴QF =12QB .∵MP =MQ ,ME ⊥PQ , ∴EQ =12PQ .∴EF =EQ +QF =12PQ +12QB =12PB . ∵PC =4,BC =8,∠C =90°. ∴PB =82+42=4 5, ∴EF =12PB =2 5.∴动点M ,N 在移动的过程中,线段EF 的长度不变,恒为2 5.。
第28章 圆 数学九年级上册-单元测试卷-冀教版(含答案)

第28章圆数学九年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、下列命题中,错误的是()A.三角形三边的垂直平分线的交点到三个顶点的距离相等B.两组对角分别相等的四边形是平行四边形C.对角线相等且互相平分的四边形是矩形 D.顺次连接菱形各边中点所得的四边形是正方形2、如图所示方格纸上一圆经过(2,6)、(﹣2,2);(2,﹣2)、(6,2)四点,则该圆圆心的坐标为()A.(2,﹣1)B.(2,2)C.(2,1)D.(3,1)3、下列各命题正确的是 : ()A.若两弧相等,则两弧所对圆周角相等B.有一组对边平行的四边形是梯形.C.垂直于弦的直线必过圆心D.有一边上的中线等于这边一半的三角形是直角三角形.4、如图,在正方形ABCD中,AB=1,将正方形ABCD绕点A顺时针旋转60°,得正方形AB′C′D′,则线段AC扫过的面积为()A. πB. πC. πD. π5、如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为()A.2mB.2.5mC.4mD.5m6、下列五个命题:(1 )直径是弦;(2 )经过三个点一定可以作圆;(3 )三角形的外心到三角形三条边的距离相等;(4 )半径相等的两个半圆是等弧;(5 )矩形的四个顶点在同一个圆上.其中正确的有()A.4个B.3个C.2个D.1个7、如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是()A.10B.6C.5D.38、如图,在⊙O中,点B是弧AC上的一点,∠AOC=140°,则∠ABC的度数为()A.70°B.110°C.120°D.140°9、在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是()A.30°B.30°或150°C.60°D.60°或120°10、如图,三个小正方形的边长都为1,则图中阴影部分面积的和是()A. B. C. D.11、下列说法错误的是().A.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线B.到点距离等于的点的轨迹是以点为圆心,半径长为的圆C.到直线距离等于的点的轨迹是两条平行于且与的距离等于的直线D.等腰三角形的底边固定,顶点的轨迹是线段的垂直平分线12、如图,AB是⊙o直径,M,N是上两点,C是上任一点,∠ACB角平分线交⊙o于点D,∠BAC的平分线交CD于点E,当点C从M运动到N时,C、E两点的运动路径长之比为( )A. B. C. D.13、如图,为⊙的直径,点在⊙上.若,则等于()A.75°B.95°C.100°D.105°14、如图,是的弦,半径于点,下列判断中错误的是()A. B. C. D.15、已知扇形的圆心角为60°,半径为1,则扇形的弧长为()A. B.π C. D.二、填空题(共10题,共计30分)16、如图,点D为∠BAC边AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作半圆,交AC于另一点E,交AB于点F、G,连接EF.若∠BAC=22°,则∠EFG=________°.17、如图,O为△ABC的外心,△OCP为正三角形,OP与AC相交于D点,连接OA.若∠BAC=69°14′,AB=AC,则∠ADP的度数________.18、如图,圆内接四边形ABCD中,圆心角∠1=100°,则圆周角∠ABC等于________.19、一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD水平,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为________cm.20、如图,在半径为2cm的扇形纸片AOB中,∠AOB=90°,将其折叠使点B落在点O 处,折痕为DE,则图中阴影部分的面积为________cm221、如图,⊙A与x轴相切于点O,点A的坐标为(0,1),点P在⊙A上,且在第一象限,∠PAO=60°,⊙A沿x轴正方向滚动,当点P第n次落在x轴上时,点P的横坐标为________22、如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是________(结果保留π).23、如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于________.24、如图,的直径⊥弦,垂足为点,连接,若CD=2 ,,则的长为________.25、已知圆锥的底面半径为4cm,高为3cm,则这个圆锥的侧面积为________ cm2.三、解答题(共5题,共计25分)26、现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计)求该圆锥底面圆的半径.27、如图,已知A、B、C、D是⊙O上的四点,延长DC,AB相交于点E,若DA=DE,求证:△BCE是等腰三角形.28、如图,在⊙O中,弦AB与DC相交于E,且BE=DE,求证:.29、如图,在⊙O中,= ,OD= AO,OE= OB,求证:CD=CE.30、如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:(1)∠CAD的度数;(2)设AD、BC相交于E,AB、CD的延长线相交于F,求∠AEC、∠AFC的度数;(3)若AD=6,求图中阴影部分的面积.参考答案一、单选题(共15题,共计45分)1、D2、B3、D4、C5、B6、B7、C8、B9、B10、B11、D12、A13、D14、A15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
第28章 圆 数学九年级上册-单元测试卷-冀教版(含答案)

第28章圆数学九年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是()A.AC=BC+CDB. AC=BC+CDC. AC=BC+CDD.2AC=BC+CD2、已知圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则∠D的大小是()A.45°B.60°C.90°D.135°3、三角形的外心是三角形中()A.三条高的交点B.三条中线的交点C.三条角平分线的交点D.三边垂直平分线的交点4、如图,四边形内接于圆,过点作于点,若,,则的长度为( )A. B.6 C. D.不能确定5、如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为()A.28°B.56°C.60°D.62°6、如图,等边的边长为,以O为圆心,为直径的半圆经过点A,连接,相交于点P,将等边从与重合的位置开始,绕着点O顺时针旋转,交点P运动的路径长是( )A. B. C. D.7、如图,在扇形中,为弦,,,,则的长为()A. B. C. D.8、如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为()A.4πB.5πC.8πD.10π9、如图,CD是圆O的直径,AB是圆O的弦,且CD=10,AB=8,若于点E,则OE的长为()A.3B.4C.5D.610、如果两条弦相等,那么( )A.这两条弦所对的圆心角相等B.这两条弦所对的弧相等C.这两条弦所对的弦心距相等D.以上说法都不对11、如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为()A.65°B.130°C.50°D.100°12、圆锥的底面半径为4cm,高为5cm,则它的表面积为()A.12πcm 2B.26πcm 2C. πcm 2D.(4 +16)πcm 213、一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O 到水面的距离OC是()A.4B.5C.6D.814、如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a ,EF=b ,NH= c ,则下列各式中正确的是()A.a > b > cB.a =b =cC.c > a > bD.b > c > a15、下列命题正确的是()A.三点确定一个圆B.平分弦的直径垂直于弦C.等圆中相等的圆心角所对的弧相等D.圆周角的度数等于圆心角度数的一半二、填空题(共10题,共计30分)16、如图,在平面直角坐标系中,与轴相切于原点,平行于轴的直线交于、两点,若点的坐标是,则弦M 的长为________ .17、如图,是一个圆心人工湖的平面图,弦AB是湖上的一座桥,已知桥长100m,测得圆周角∠ACB=30°,则这个人工湖的直径为________m.18、如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=18°,则∠AOC的度数为________度.19、如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD 于点E,则图中阴影部分的面积是________(结果保留π)20、已知,如图,A,B,C,D是反比例函数y=图象上四个整数点(横、纵坐标均为整数),分别过这些点向横轴、纵轴作垂线段,以短垂线段为边作正方形(如图),分别以正方形的边长为半径作两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的周长总和是________(用含π的代数式表示)21、如图,△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若OD=2,则BC=________.22、如图,PA、PB是⊙0的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC=________.23、正六边形的中心角等于________ 度.24、如图,等腰△AOB中,∠AOB=120°,AO=BO=2,点C为平面内一点,满足∠ACB=60°,且OC的长度为整数,则所有满足题意的OC长度的可能值为________ .25、如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=________.三、解答题(共5题,共计25分)26、如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O 的半径为1,求图中阴影部分的面积(结果保留π).27、如图,折扇完全打开后,OA,OB的夹角为120°,OA的长为18cm,AC的长为9cm,求图中阴影部分的面积S.28、如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,∠ADB=45°. 求⊙O半径的长.29、如图,在半径为6的⊙O中,弦AB长为6.求弦AB与所围成的阴影部分的面积.30、如图,在⊙O中,,∠ACB=60°,求证∠AOB=∠BOC=∠COA.参考答案一、单选题(共15题,共计45分)2、C3、D4、B5、D6、B7、B8、A9、A10、D11、C12、D13、C14、B15、C二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、29、30、。
九年级上册数学单元测试卷-第28章 圆 -冀教版(含答案)

九年级上册数学单元测试卷-第28章圆 -冀教版(含答案)一、单选题(共15题,共计45分)1、在圆内接四边形ABCD中,若,则()A.40B.50C.130D.1502、下列说法,正确的是( )A.半径相等的两个圆大小相等B.长度相等的两条弧是等弧C.直径不一定是圆中最长的弦D.圆上两点之间的部分叫做弦3、如图,AB是⊙O的直径,CD是弦,且AB∥CD,若AB=8,∠ABC=30°,则弦AD的长为()A. B. C. D.84、一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为()A. cmB. cmC.3cmD. cm5、如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是()A.8≤AB≤10B.8<AB≤10C.4≤AB≤5D.4<AB≤56、已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是()A.40πB.24πC.20 πD.12π7、如图,在⊙O中,若∠AOB=120°,则∠C的度数是()A.70°B.65°C.60°D.50°8、△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则AE的长为( )A. B. C. D.9、下列四个结论,不正确的是()①过三点可以作一个圆;②圆内接四边形对角相等③平分弦的直径垂直于弦;④相等的圆周角所对的弧也相等A.②③B.①③④C.①②④D.①②③④10、如图,AB,CD分别是⊙O的弦和直径,AB⊥CD于点E,若CD=10,AB=8,则sin∠ACD 的值为()A.30°B.C.D.211、如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为,则图中阴影部分的面积为()A. B. C. D.12、在半径为1的⊙O中,120°的圆心角所对的弧长是()A. B. C. D.13、如图,在⊙O中,∠AOB=120°,P为弧AB上的一点,则∠APB的度数是()A.100°B.110°C.120°D.130°14、如图,AB、AC是圆的两条弦,AD是圆的一条直径,且AD平分∠BAC,下列结论中不一定正确的是()A. B. C.BC⊥AD D.∠B=∠C15、如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是()A.30°B.45°C.55°D.60°二、填空题(共10题,共计30分)16、如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA 的延长线于点E,若AE=2,则弦BD的长为________.17、如图,在△ABC中,AC上的点D关于AB的对称点D'在△ABC的外接圆⊙O上,若⊙O 的半径为3,∠C=80°,D'为的中点,则的长是________。
新2020年秋期冀教版数学初三(九年级)上册第二十八章达标测试卷

第二十八章达标测试卷一、选择题(1~10题每题3分,11~16题每题2分,共42分)1.下列说法不正确...的是()A.圆是中心对称图形B.三点确定一个圆C.半径相等的两个圆是等圆D.每个圆都有无数条对称轴2.如图,⊙O中,∠B=50°,则∠AEC的度数为()A.65°B.75°C.50°D.55°3.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是() A.1 B. 2 C. 3 D.24.如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO=() A.10°B.20°C.30°D.40°5.如图,在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径为()A.5B.10C.8D.66.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠A 等于()A.128°B.100°C.64°D.32°7.如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则tan∠BAC的值是()A. 3 B.1 C.32 D.338.如图,在平面直角坐标系中,以原点为圆心,半径为5的圆内有一点P (0,-3),那么经过点P 的所有弦中,最短的弦的长为( )A .4B .5C .8D .109.如图,点A ,B ,C ,D 都在⊙O 上,∠ABC =90°,AD =3,CD =2,则⊙O的直径的长是( ) A. 5 B .4 C.11 D.1310.如图,△ABC 内接于⊙O ,∠BAC =120°,AB =AC ,BD 为⊙O 的直径,AD=6,则BC 的长为( )A .5B .6C .7D .811.在△ABC 中,∠C =90°,AC =12,BC =5,将△ABC 绕边AC 所在直线旋转一周得到圆锥,则该圆锥的全面积是( )A .25 πB .65 πC .90 πD .130 π12.已知扇形的面积为4π,扇形的弧长为π,则该扇形的半径为( )A .4B .6C .8D .8π13.如图,在⊙O 中,弦BC =1,点A 是圆上一点,且∠BAC =30°,则⊙O 的半径是( )A .1B .2 C. 3 D. 514.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,CD ⊥AB 于点E ,则下列结论中不成立的是( )A .∠A =∠D B.CB ︵=BD ︵C .∠ACB =90°D .∠COB =3∠D15.如图,已知⊙O 是等腰直角三角形ABC 的外接圆,点D 是AC ︵上一点,BD交AC 于点E ,若BC =4,AD =45,则AE 的长是( )A .3B .2C .1D .1.2(第16题)16.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径为60 cm ,则这块扇形铁皮的半径是( )A .40 cmB .50 cmC .60 cmD .80 cm二、填空题(17题3分,其余每空2分,共11分)17.如图,在⊙O 中,AB ︵=AC ︵,∠A =40°,则∠B =________.18.如图,△ABC 内接于⊙O ,AH ⊥BC 于点H ,若AC =24,AH =18,⊙O 的半径OC =13,则sin B =________,AB =________.19.如图,在Rt △ABC 中,∠ACB =90°,AC =2 3,以点C 为圆心,CB 的长为半径画弧,与AB 边交于点D ,将BD ︵绕点D 旋转180°后点B 与点A 恰好重合,则图中阴影部分的面积为__________,周长为______________.三、解答题(20题8分,21~23题每题9分,24~25题每题10分,26题12分,共67分)20.如图,AB是半圆O的直径,C,D是半圆O上的两点,OD∥BC,OD与AC交于点E.(1)若∠D=70°,求∠CAD的度数;(2)若AC=8,DE=2,求AB的长.21.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.(1)若CD=16,BE=4,求⊙O的直径;(2)若∠M=∠D,求∠D的度数.22.如图,已知一个圆锥的轴截面ABC是等边三角形,它的全面积为75π cm2.求这个圆锥的底面半径和母线长.23.如图,在平面直角坐标系中,已知⊙M经过坐标原点,与x轴,y轴分别交于A,B两点,点B的坐标为(0,2 3),OC与⊙M相交于点C,且∠OCA =30°,求图中阴影部分的面积.24.如图,已知P为反比例函数y=4x(x>0)图像上一点,以点P为圆心,OP长为半径画圆,⊙P与x轴相交于点A,连接P A,且点A的坐标为(4,0).求:(1)⊙P的半径;(2)图中阴影部分的面积.25.如图,四边形ABCD内接于⊙O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连接AF,CF.(1)求证:∠BAC=2∠CAD;(2)若AF=10,BC=4 5,求tan∠BAD的值.26.【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα=35,求sin 2α的值.小娟是这样给小芸讲解的:如图①,在⊙O 中,AB 是直径,点C 在⊙O 上,所以∠ACB =90°.设∠BAC=α,则sin α=BC AB =35.易得∠BOC =2α.设BC =3x ,则AB =5x ……【问题解决】(1)请按照小娟的思路,利用图①求出sin 2α的值;(写出完整的解答过程)(2)如图②,点M ,N ,P 为⊙O 上的三点,且∠P =β,sin β=14,求sin 2β的值.答案一、1.B 2.C 3.D 4.B 5.A 6.C 7.D 8.C 9.D 10.B11.C 12.C 13.A 14.D15.C :∵⊙O 是等腰直角三角形ABC 的外接圆,BC =4,∴AB 为⊙O 的直径,AC =4,AB =4 2.∴∠D =90°.在Rt △ABD 中,AD =45,AB =4 2,∴BD =285.∵∠D =∠C ,∠DAE =∠CBE ,∴△ADE ∽△BCE .∴AD ∶BC =AE ∶BE =DE ∶CE =45∶4=1∶5.∴相似比为1∶5.设AE =x ,则BE =5x .∴DE =285-5x .∴CE =5DE =28-25x .又∵AC =4,∴x +28-25x =4.解得x =1.16.A二、17.70°18.1213;392 :延长CO 与圆交于点D ,连接AD ,可得∠B =∠D ,故sin B =sinD .∴AH AB =AC CD ,即18AB =2426,可得AB =392. 19.2 3-2π3;2+2 3+23π :依题意,有AD =BD ,又∠ACB =90°,所以CB =CD =BD ,即△BCD 为等边三角形,所以∠BCD =∠ABC =60°,∠BAC =∠ACD =30°.由AC =2 3,得BC =2,AB =4.阴影部分面积为S △ACD -S 弓形AD =S △ACD -S 弓形BD =S △ACD -(S 扇形BCD -S △BCD )=S △ABC -S 扇形BCD ,根据面积公式计算即可.三、20.解:(1)∵OA =OD ,∠D =70°,∴∠OAD =∠D =70°.∴∠AOD =180°-∠OAD -∠D =40°.∵AB 是半圆O 的直径,∴∠C =90°.∵OD ∥BC ,∴∠AEO =∠C =90°,即OD ⊥AC . ∴AD ︵=CD ︵.∴∠CAD =12∠AOD =20°.(2)由(1)可知OD ⊥AC ,∴AE =12AC =12×8=4.设OA =x ,则OE =OD -DE =x -2.在Rt △OAE 中,OE 2+AE 2=OA 2,即(x -2)2+42=x 2,解得x =5.∴AB =2OA =10.21.解:(1)∵AB ⊥CD ,CD =16,∴CE =DE =8.设OB =x ,则OD =x ,OE =x -4.在Rt △DOE 中,DO 2=OE 2+DE 2,即x 2=(x -4)2+82,解得x =10.∴AB =2OB =20,即⊙O 的直径是20.(2)由圆周角定理可得∠M =12∠BOD .∵∠M =∠D ,∴∠D =12∠BOD .∵AB ⊥CD ,∴∠BOD +∠D =90°.∴∠D =30°.22.解:设这个圆锥的底面半径为r cm ,则母线长为2r cm.依题意,得12×2πr ×2r +πr 2=75π,解得r =5,∴2r =10.故这个圆锥的底面半径为5 cm ,母线长为10 cm.23.解:连接AB ,∵∠AOB =90°,∴AB 是直径.根据同弧所对的圆周角相等得∠OBA =∠OCA =30°,由题意知OB =2 3, ∴OA =OB ·tan ∠ABO =OB ·tan 30°=2 3×33=2,AB =AO ÷sin 30°=4,即圆的半径为2.∴阴影部分的面积等于半圆的面积减去△ABO 的面积,即22π2-12×2×2 3=2π-2 3.24.解:(1)过点P 作PD ⊥x 轴于点D .∵A 点的坐标为(4,0),∴OA =4.∴OD =2,即点P 的横坐标为2.将x =2代入y =4x ,可得y =2,即PD =2.在Rt △OPD 中,根据勾股定理可得OP =2 2,即⊙P 的半径为2 2.(2)由(1)可得PD =OD ,且∠ODP =90°,∴∠OPD =45°.又∵OP =P A ,∴∠APD =∠OPD =45°.∴∠OP A =90°. ∴S 阴影=S 扇形OP A -S △OP A =90×(2 2)2×π360-4×22=2π-4.25.(1)证明:∵AB =AC ,∴AB ︵=AC ︵,∠ABC =∠ACB .∴∠ABC=∠ADB,∠ABC=12(180°-∠BAC)=90°-12∠BAC.∵BD⊥AC,∴∠ADB=90°-∠CAD.∴90°-12∠BAC=90°-∠CAD.∴12∠BAC=∠CAD.∴∠BAC=2∠CAD.(2)解:∵DF=DC,∴∠DFC=∠DCF.∴∠BDC=2∠DFC.∴∠BFC=12∠BDC=12∠BAC=∠CAD=∠FBC.∴CB=CF.又BD⊥AC,∴AC是线段BF的垂直平分线,∴AB=AF=10,∴AC=10. 设AE=x,则CE=10-x,由BE2=AB2-AE2=BC2-CE2,得102-x2=(4 5)2-(10-x)2,解得x=6. ∴AE=6,BE=8,CE=4.∵∠DCE=∠ABE,∠CED=∠BEA,∴△CED∽△BEA.∴DEAE=CEBE.∴DE=AE·CEBE=6×48=3.∴BD=BE+DE=8+3=11.作DH⊥AB,垂足为H,∵12AB·DH=12BD·AE,∴DH=BD·AEAB=11×610=335.∴BH=BD2-DH2=445.∴AH=AB-BH=10-445=65.∴tan∠BAD=DHAH=112.26.解:(1)设∠BAC=α,则∠COB=2α,∵AB为直径,点C在⊙O上,∴∠ACB=90°.在Rt△ACB中,∵sin α=BCAB=35,∴设BC=3x,AB=5x,∴AC=4x.作CD⊥AB于D,∵12CD·AB=12AC·BC,∴CD=4x·3x5x=125x.在Rt△COD中,sin∠COD=CDOC=125x52x=2425,即sin 2α=2425.(2)如图,作直径NQ,连接QM,OM,作MH⊥NQ于H,∵NQ为直径,∴∠NMQ=90°.∵∠Q=∠P=β,∴sin Q=sin β=MNNQ=14.设MN=t,则NQ=4t,∴MQ=(4t)2-t2=15t.精品文档 用心整理资料来源于网络 仅供免费交流使 ∵12MH ·NQ =12MN ·MQ ,∴MH =t ·15t 4t =154t .在Rt △OMH 中,sin ∠HOM =MH OM =15t42t =158,∵∠MON =2∠P ,∴sin 2β=158.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十八章检测卷(120分,90分钟)一、选择题(每题3分,共30分)1.下列命题为真命题的是()A.两点确定一个圆B.度数相等的弧相等C.垂直于弦的直径平分弦D.相等的圆周角所对的弧相等,所对的弦也相等2.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是() A.点P在⊙O外B.点P在⊙O内C.点P在⊙O上D.无法确定3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是()A.70°B.60°C.50°D.30°(第3题)(第4题) (第5题) (第6题)4.如图,⊙O 的弦AB =8,M 是AB 的中点,且OM =3,则⊙O 的半径等于( )A .8B .4C .10D .55.(中考·兰州)如图,CD 是⊙O 的直径,弦AB ⊥CD 于E ,连接BC ,BD.下列结论中不一定正确的是( )A .AE =BEB .AD ︵=BD ︵C .OE =DED .∠DBC =90°6.如图,A ,B ,P 是半径为2的⊙O 上的三点,∠APB =45°,则弦AB 的长为( )A .2B .4C . 2D .2 27.如图,在△ABC 中,∠ACB =90°,∠ABC =30°,AB =2.将△ABC 绕直角顶点C 逆时针旋转60°得△A′B′C ,则点B 转过的路径长为( )A .π3B .3π3C .2π3D .π (第7题)(第8题) (第9题) (第10题)8.如图,如果从半径为9 cm 的圆形纸片剪去13圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )A .6 cmB .3 5 cmC .8 cmD .5 3 cm9.如图,将半径为2 cm 的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB 的长为( )A .2 cmB . 3 cmC .2 3 cmD .2 5 cm10.如图,半径为5的⊙A 中,弦BC ,ED 所对的圆心角分别是∠BAC ,∠EAD.已知DE =6,∠BAC +∠EAD =180°,则弦BC 的弦心距等于( )A .412B .342C .4D .3 二、填空题(每题3分,共30分)11.如图,点A ,B ,C 在⊙O 上,∠AOC =60°,则∠ABC 的度数是________.12.如图,⊙O 的直径为10,弦AB 的长为6,M 是弦AB 上的一动点,则线段OM 的长的取值范围是________.13.如图,AD 为⊙O 的直径,AD =6 cm ,∠DAC =∠ABC ,则AC =________.(第11题)(第12题) (第13题) (第14题)(第16题) 14.如图,在四边形ABCD中,若AB=AC=AD,则下列等式不一定成立的是________.①∠1=2∠4 ②∠2=2∠7 ③∠3+∠4=∠5 ④∠6=∠1+∠815.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是________.16.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.17.如图,水平放置的圆柱形油槽的截面直径是52 cm,装入油后,油深CD为16 cm,那么油面宽度AB=________cm.(第17题)(第18题)(第20题)18.如图,半径为5的⊙P 与y 轴交于点M(0,-4),N(0,-10),函数y =k x(x<0)的图像过点P ,则k =________.19.已知在半径为4的⊙O 中,弦AB =43,点P 在⊙O 上,则∠APB =________.20.如图,在扇形AOB 中,∠AOB =90°,点C 为OA 的中点,CE ⊥OA 交AB ︵于点E ,以点O为圆心,OC 的长为半径作CD ︵交OB 于点D.若OA =2,则阴影部分的面积为________.三、解答题(21、22题每题8分,23、24题每题10分,其余每题12分,共60分)21.如图,AB 是⊙O 的一条弦,OD ⊥AB ,垂足为点C ,交⊙O 于点D ,点E 在⊙O 上.(1)若∠AOD =52°,求∠DEB 的度数;(2)若OC=3,OA=5,求AB的长.(第21题)22.“不在同一条直线上的三个点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.23.如图,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径.求证:∠BAM =∠CAP.(第23题)24.如图,在△ABC 中,AB =AC =45,cos C =55. (1)动手操作:利用尺规作以AC 为直径的⊙O ,并标出⊙O 与AB 的交点D ,与BC 的交点E(保留作图痕迹,不写作法);(2)综合应用:在你所作的图中,①求证:DE ︵=CE ︵;②求点D 到BC 的距离.(第24题)25.如图,一拱形公路桥,圆弧形桥拱的水面跨度AB =80米,桥拱到水面的最大高度为20米.(1)求桥拱的半径.(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.(第25题)26.如图,在Rt△ABC中,∠ACB=90°,半径长为1的圆A与边AB相交于点D,与边AC 相交于点E,连接DE并延长,与线段BC的延长线交于点P,连接AP.(1)当∠B=30°时,若△AEP与△BDP相似,求CE的长;(2)若CE=2,BD=BC,求∠BPD的正切值;(3)若tan ∠BPD =13,设CE =x ,△ABC 的周长为y ,求y 关于x 的函数表达式.(第26题)答案一、1.C 2.A 3.B 4.D 5.C 6.D 7.B8.B 点拨:∵留下的扇形的弧长为23×2π×9=12π(cm ).∴围成圆锥的底面圆半径r =12π2π=6(cm ).又∵圆锥母线长l =9 cm ,∴圆锥的高h =l 2-r 2=92-62=35(cm ).9.C10.D 点拨:∵∠BAC +∠EAD =180°,(第10题)∴可将△ABC旋转,让AC和AD重合,则AB和AE在一条直线上,如图所示.∵BE为直径,∴∠BDE=90°.作AF⊥DE,垂足为F,AG⊥BD,垂足为G,则四边形AFDG为矩形,∴AG=DF=12DE=3.∴弦BC的弦心距等于3.二、11.150°12.4≤OM≤513.3 2 cm14.④15.8或1016.215点拨:∵A,B,C,D四点共圆,∴∠B+∠ADC=180°.又∵A,C,D,E四点共圆,∴∠E+∠ACD=180°.∴∠ACD+∠ADC+∠B+∠E=360°.∵∠ACD+∠ADC=180°-35°=145°,∴∠B+∠E=360°-145°=215°.17.4818.28(第19题)19.60°或120° 点拨:如图,当点P(P 1)在弦AB 所对的优弧上时,过点O 作OC ⊥AB 于点C ,连接OA ,OB.在等腰三角形OAB 中易得AC =2 3.在Rt △OAC 中,OC =OA 2-AC 2=2=12OA ,所以∠OAC =30°,所以弦AB 所对的圆心角∠AOB =120°,所以∠AP 1B =60°.同理当点P(P 2)在弦AB 所对的劣弧上时,∠AP 2B =120°. 20.32+π12 点拨:连接OE.∵点C 是OA 的中点,∴OC =12OA =1,∵OE =OA =2,∴OC =12OE =1.∵CE ⊥OA ,∴∠OEC =30°,∴∠COE =60°.在Rt △OCE 中,CE =OE 2-OC 2=3,∴S △OCE =12OC·CE =32.∵∠AOB =90°,∴∠BOE =∠AOB -∠COE =30°,∴S 扇形OBE =30π×22360=π3.又S 扇形OCD =90π×12360=π4.因此S 阴影=S 扇形OBE +S △OCE -S 扇形OCD =π3+32-π4=π12+32. 三、21.解:(1)∵OD ⊥AB ,∴AD ︵=DB ︵.∴∠DEB =12∠AOD =26°. (2)在Rt △AOC 中,OC =3,OA =5,由勾股定理得AC =4.∴AB =2AC =8.22.解:设经过A ,B 两点的直线的解析式为y =kx +b.∵A(2,3),B(-3,-7),∴⎩⎪⎨⎪⎧2k +b =3,-3k +b =-7.解得⎩⎪⎨⎪⎧k =2,b =-1. ∴经过A ,B 两点的直线的解析式为y =2x -1.当x =5时,y =2×5-1=9≠11,∴点C(5,11)不在直线AB 上,即A ,B ,C 三点不在同一条直线上.∴平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)可以确定一个圆.(第23题)23.证明:如图,连接BM.∵AP ⊥BC 于P ,∴∠CAP =90°-∠C.∵AM 为⊙O 的直径,∴∠ABM =90°,∴∠BAM =90°-∠M ,又∵∠M =∠C ,∴∠BAM =∠CAP.24.(1)解:如图(1)所示.(2)①证明:如图(2),连接AE.∵AC 为直径,∴∠AEC =90°.又AB =AC ,∴∠BAE =∠CAE ,∴DE ︵=CE ︵.(第24题)②解:如图(2),连接CD ,过点D 作DF ⊥BC 于点F.∵AB =AC =45,cos ∠ACB =55,∴EC =AC·cos ∠ACB =4.∵AB =AC ,AE ⊥BC ,∴BC =2CE =8,∴AE =AC 2-CE 2=(45)2-42=8.∵AC 为直径,∴∠ADC =90°,∴S △ABC =12AB·CD.又∠AEC =90°,∴S △ABC =12AE·BC ,∴12AB·CD =12AE·BC.可得CD =1655,∴AD =AC 2-CD 2=1255,∴BD =AB -AD =855.∵S △DBC =12BD·CD ,S △DBC =12DF·BC ,∴BD·CD =DF·BC ,可得DF =165, ∴点D 到BC 的距离为165. 25.解:(1)如图,点E 是桥拱所在圆的圆心.过点E 作EF ⊥AB 于点F ,延长EF 交⊙E 于点C ,连接AE ,则CF =20米.由垂径定理知,F 是AB 的中点,∴AF =FB =12AB =40米.设圆的半径是r 米,由勾股定理,得AE 2=AF 2+EF 2=AF 2+(CE -CF)2,即r 2=402+(r -20)2.解得r =50.∴桥拱的半径为50米.(第25题)(2)这艘轮船能顺利通过.理由如下:宽60米的轮船可通过拱桥的最大高度为图中MN 所示. 连接EM ,设EC 与MN 的交点为D ,MD =30米.∵DE ⊥MN ,∴DE =EM 2-DM 2=502-302=40(米).∵EF =EC -CF =50-20=30(米),∴DF =DE -EF =40-30=10(米).∵10米>9米,∴这艘轮船能顺利通过.26.解:(1)∵∠B =30°,∠ACB =90°,∴∠BAC =60°.又AD =AE ,∴∠AED =60°=∠PEC ,∴∠EPC =30°=∠B ,∴△BPD 为等腰三角形.又∵△AEP 与△BDP 相似,∴∠B =∠BPD =∠EAP =∠APE =30°,∴EP =AE =1,∴CE =12PE =12×1=12.(第26题)(2)过A 作AF ⊥DE 交BC 于F ,过F 作FM ⊥AB 于M(如图所示).易知∠FAC =∠BPD ,∵AF ⊥DE ,AD =AE ,∴∠FAC =∠FAM ,∵FM ⊥AB ,FC ⊥AC ,∴FM =FC ,∴Rt △AFM ≌Rt △AFC ,∴AC =AM.在Rt △ABC 中,设BC =m ,则AB =m +1,AC =CE +AE =2+1=3,由AC 2+BC 2=AB 2,解得m =4.∴AB =5.又AM =3,∴BM =2.又tan B =AC BC =34,tan B =MF BM =MF 2,∴MF 2=34,∴MF =FC =32, ∴tan ∠FAC =FC AC =323=12, 即tan ∠BPD =12. (3)∵CE =x ,AE =1,∴AC =x +1.易知,∠FAC =∠FAB =∠BPD ,又tan ∠BPD =13, ∴tan ∠CAF =13=CF AC =CF x +1, ∴CF =13(x +1)=FM , ∵∠B =∠B ,∠FMB =∠ACB =90°,∴△BFM ∽△BAC ,∴MF AC =BM BC =13(x +1)x +1=13, ∴BM =13BC ,设BM =a ,则BC =3a ,在Rt △BMF 中,由BM 2+MF 2=BF 2,有a 2+19(x +1)2=⎣⎡⎦⎤3a -13(x +1)2, 即a 2+19(x +1)2=9a 2-2a(x +1)+19(x +1)2,∴a =14(x +1),∴BC =3a =34(x +1). ∴AB =AM +BM =x +1+14(x +1)=54(x +1), ∴y =AB +AC +BC =54(x +1)+(x +1)+34(x +1)=3(x +1),即y =3x +3,其中x >0.1、只要朝着一个方向努力,一切都会变得得心应手。
