冀教版九年级下册数学 《直线与圆的位置关系》PPT课件 (3)
合集下载
新冀教版九年级下册数学课件(第29章 直线与圆的位置关系)

思考: 足球运动员踢出的足球在球场上滚动,在足球
穿越中圈区(中间圆形区域)的过程中,可将足球 看成一个点,这个点与圆具有怎样的位置关系?
在同一个平面内,点与圆有三种位置关系: 点在圆外、点在圆上和点在圆内. 点P与☉O的位置关系如图所示.
知1-导
知1-导
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
知2-练
1 已知一个圆的直径为10. 如果这个圆的圆心到一条 直线的距离分别等于3,5,6,那么这条直线与这个圆 的位置关系分别是怎样的?
解:因为圆的直径为10,所以圆的半径为5.当直线与圆 心的距离等于3时,因为3<5,所以直线与圆相交; 当直线与圆心的距离等于5时,因为5=5,所以直 线与圆相切; 当直线与圆心的距离等于6时,因为6>5,所以直 线与圆相离.
B.点P法确定
知1-练
4 【中考·宜昌】在公园的O处附近有E,F,G,H 四棵树,位置如图所示(图中小正方形的边长均相 等).现计划修建一座以O为圆心,OA为半径的圆 形水池,要求池中不留树木,则E,F,G,H四棵 树中需要被移除的为( A ) A.E,F,G B.F,G,H C.G,H,E D.H,E,F
解:如图,过点A作AC⊥ON于C, 以点A为圆心,200米为半径作 圆,与MN交于点B,D,连接 AB,AD,则AB=AD=200米,
知2-讲
∵∠QON=30°,OA=240米, ∴AC=120米. 当火车到B点时对A处产生噪音影响, ∵AB=200米,AC=120米, ∴由勾股定理得BC=160米,同理可得CD=160米, ∴BD=320米. ∵72千米/时=20米/秒, ∴A处受到噪音影响的时间应是320÷20=16(秒).
的公共点个数有____三____种情况.
精品九年级数学下册29直线与圆的位置关系小结与复习课件新版冀教版精品ppt课件
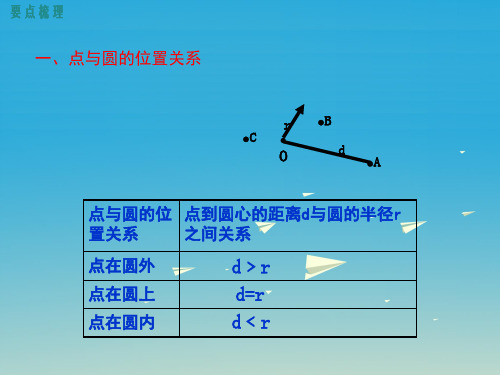
图2
方法总结
本题之类的题目中,常因混淆了“直线与圆只有一个交点 ”和“线段与圆只有一个交点”或“射线与圆只有一个交点”的区 别.实际上,当直线与圆只有一个交点时,直线与圆一定相切 ,而线段与圆只有一个交点或射线与圆只有一个交点时,它 们与圆的位置关系可能相切,也可能是相交.
针对训练
1.如图,直线l:y=x+1M为圆心,2个单位长度为
针对训练
4. 如图,正六边形ABCDEF内接于半径为 5的⊙O,四边形EFGH是正方形.
⑴求正方形EFGH的面积;
⑵连接OF、OG,求∠OGF的度数.
解:⑴∵正六边形的边长与其半径相等,∴EF=OF=5.
∵四边形EFGH是正方形,∴FG=EF=5,∴正方形EFGH
的面积是25.
⑵∵正六边形的边长与其半径相等,∴∠OFE=600.
点和圆的位置关系
与圆有关的位置关系
直线和圆的位置关系 切线的判定与性质
三角形的内切圆
圆
正多边形和圆
等分圆
中心角及内角和的计算
课后作业
见《学练优》河北中考热点专练
半径作⊙M,当⊙M与直线l相切时,则m的值为_2__5___2_.
考点二 切线的性质与判定
例2 如图,以△ABC的边AB为直径的⊙O交边AC于点D, 且过点D的切线DE平分边BC. 问:BC与⊙O是否相切?
解:BC与⊙O相切. 理由:连接OD,BD, ∵DE切⊙O于D,AB为直径, ∴∠EDO=∠ADB=90°. 又DE平分CB,∴DE=2(1)BC=BE. ∴∠EDB=∠EBD. 又∠ODB=∠OBD,∠ODB+ ∠EDB=90°,∴∠OBD+∠DBE=90°, 即∠ABC=90°. ∴BC与⊙O相切.
公共点,求r的值或取值范围. 解:当射线OM与⊙P相切时,射线OM与⊙P只有 一个公共点. 过点P作PA⊥OM于A,如图1所示. 在Rt△AOP中,r=PA=OP·sin∠POA=2.5(㎝).
方法总结
本题之类的题目中,常因混淆了“直线与圆只有一个交点 ”和“线段与圆只有一个交点”或“射线与圆只有一个交点”的区 别.实际上,当直线与圆只有一个交点时,直线与圆一定相切 ,而线段与圆只有一个交点或射线与圆只有一个交点时,它 们与圆的位置关系可能相切,也可能是相交.
针对训练
1.如图,直线l:y=x+1M为圆心,2个单位长度为
针对训练
4. 如图,正六边形ABCDEF内接于半径为 5的⊙O,四边形EFGH是正方形.
⑴求正方形EFGH的面积;
⑵连接OF、OG,求∠OGF的度数.
解:⑴∵正六边形的边长与其半径相等,∴EF=OF=5.
∵四边形EFGH是正方形,∴FG=EF=5,∴正方形EFGH
的面积是25.
⑵∵正六边形的边长与其半径相等,∴∠OFE=600.
点和圆的位置关系
与圆有关的位置关系
直线和圆的位置关系 切线的判定与性质
三角形的内切圆
圆
正多边形和圆
等分圆
中心角及内角和的计算
课后作业
见《学练优》河北中考热点专练
半径作⊙M,当⊙M与直线l相切时,则m的值为_2__5___2_.
考点二 切线的性质与判定
例2 如图,以△ABC的边AB为直径的⊙O交边AC于点D, 且过点D的切线DE平分边BC. 问:BC与⊙O是否相切?
解:BC与⊙O相切. 理由:连接OD,BD, ∵DE切⊙O于D,AB为直径, ∴∠EDO=∠ADB=90°. 又DE平分CB,∴DE=2(1)BC=BE. ∴∠EDB=∠EBD. 又∠ODB=∠OBD,∠ODB+ ∠EDB=90°,∴∠OBD+∠DBE=90°, 即∠ABC=90°. ∴BC与⊙O相切.
公共点,求r的值或取值范围. 解:当射线OM与⊙P相切时,射线OM与⊙P只有 一个公共点. 过点P作PA⊥OM于A,如图1所示. 在Rt△AOP中,r=PA=OP·sin∠POA=2.5(㎝).
九年级数学直线与圆的位置关系PPT课件

-2
例题5
如图:在射线OB上取一点M,OM=10cm,以 M为圆心作一直径为10cm的⊙M,试问:过O的射线 OA与OB所夹的锐角β取什么值时射线OA与⊙M : (1)相交, (2)相切 (3)相离
分析:这道题是上面题目的逆反应用,⊙M为一定圆,射线 OA为一动线,我们可以从特殊到一般,看当β为多少时 ⊙M与OA相切,即点M到OA的距离MN=5=r时,OM=10, 则β为30°. A 解(1)当β<30°时,⊙M与OA相交 (2)当β=30°时,MN=d=r=5cm, N ⊙M与OA相切 (3)当β>30°时,⊙M与OA相离
活动一、复习提问:
1、点与圆有几种位置关系?
C.
.B
.A
2、怎样判定点和圆的位置关系?
大于半径时,点在圆外。 (1)点到圆心的距离____ (2)点到圆心的距离等于 ____半径时,点在圆上。 (3)点到圆心的距离小于 ____半径时,点在圆内。
3.直线与圆的位置关系
图形 直线与圆的 位置关系
.O r d ┐ l .o d r ┐ l .
C
3
A
(2)当r=2.4cm时,∵d=r, ∴⊙C与AB相切。 (3)当r=3cm时, ∵d<r, ∴⊙C与AB相交。
例题4.若⊙O与直线m的距离为d,⊙O 的半径为r,若d,
r是方程 (a 1) x 2 ax 1 0 的两个根, 且直线m与⊙O相切, 求a 的值。
分析:直线m与⊙O相切,则d=r,即方程有两相等的 实数根即∆=0 解:据题意可得:方程中的∆=0 即 a 2 4a 4 0 解得a =
O
10
M
B
动动脑筋
活动三:大家动手,做一做
冀教版数学九下2直线与圆的位置关系教学课件

在Rt△ABC中,∠C=90°,AC=3cm, BC=4cm,以C为圆心,r为半径作圆.
1、当r满足_0__c_m_<__r_<__2_._4_c_m__时,
⊙C与直线AB相离.
B
d=2.4c m
2、当r满足_r_=__2_.4__c_m____ 时,
⊙C与直线AB相切.
5
3、当r满足__r_>___2_.4__c_m__时,
系?若把 A向左平移呢? ⊙
[z x x k 学科网]
(2)若要使⊙A与x轴、y轴都相切,则圆心A应当移到
什么位置?请写出点A所有可能位置的坐标. [zxxk学科网]
是方程X2-4x+m=0的两根,且直线m与⊙O相
切,则m的值为__4_____。
4、选择题:
(1)已知∠OAB = 30°,OA = 10,则以O为圆心,6为半径 的圆与射线AB的位置关系是(A )
A.相交 B.相切 C.相离 D.不能确定
(2)设圆的直径长为a,一条直线和圆有公共点,直线和圆心 的距离为d,则(B )
解:过点M作MC⊥OA于C ,
∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm ⑴ ∵ d=MC=2.5, r=2 即r=4 即d < r
O
∴ ⊙O与OA相交;
A C
.
MB
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙O与OA相切.
随堂检测
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( A):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( C ):
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)根据定义,由_直__线___与__圆___的__公__共_ 点 的个数来判断;
(2)由_圆__心__到__直__线__的__距__离__d与半径r 的大小关系来判断.
在实际应用中,常采用第二种方法判定.
当堂检测
1、已知⊙O的半径为6cm,圆心O与直线AB的距离为d, 根据 条件填写d的范围:
O 30°
2.5
MC= 1 OM= 1 x5=2.5
2
25Mຫໍສະໝຸດ B即圆心 M 到OA的距离 d = 2.5 cm.
(1) 当 r = 2 cm 时,有 d > r, 因此⊙M 和 直线OA 相离. (2) 当 r = 4 cm 时,有 d < r, 因此⊙M 和直线O A 相交.
(3) 当 r = 2.5cm 时,有 d = r ,因此⊙M 和直线 OA 相切.
(2)
(3)
l
·O
·O
l
·O
l
相离 (4)
相交
相切
·O
相交
l
思考讨论
O
l
相交
O
Al
相切
O
l
相离
上述变化过程中,除了公共点的个数发生了变化, 还有什么量在改变?你能否用数量关系来判别直线 与圆的位置关系?
温馨提示
过直线外一点作这条直线的垂线段, 垂线段的长度叫点到直线 的距离.
.A
D
l
二、直线与圆的位置关系量化
D
d
知识小结 直线与圆的位置关系:
图形
.O r d┐ l
直线与圆的 位置关系
相离
公共点的个数 0
圆心到直线的距离
d 与半径 r 的关系 d>r
公共点的名称
直线名称
.o
.O
d .┐r l
A
. r ┐d .
B
lC
相切 相交
1
2
d=r 切点 切线
d<r 交点 割线
拓展练习
如图:AB=8是大圆⊙O的弦,大圆半径为R=5, 则以O为圆心,半径为3的小圆与A B的位置关系 是( B )
D
d
1 CD AB 1 AC BC
2
2
∴ CD AC BC 3 4 2.4(cm)
AB
5
即圆心C到AB的距离d=2.4cm
所以 (1)当r=2cm时,有d>r,因此⊙C和AB相离.
(2)当r=2.4cm时,有d=r, 因此⊙C和AB相切.
D
d
(3)当r=3cm时,有d<r, 因此,⊙C和AB相交.
试卷下载:
PPT论坛:
PPT素材: PPT图表: PPT教程: 范文下载:
教案下载:
PPT课件:
语文课件: 数学课件:
英语课件: 美术课件:
科学课件: 物理课件:
化学课件: 生物课件:
地理课件:
历史课件:
直线叫做圆的割线
直线和圆只有一个公共点,这时我们就说这条直线和圆相切, 这条直线叫做圆的切线,这个点叫做切点.
A相离 B相切 C相交 D都有可能
O
5
3
A
4B
D
8
课后作业
必做题:A组1题 B组1题
选做题:B组2题
你能根据d与r的大小关系确定直线与圆的位置关系吗?
d:圆心O到直线的距离为d 过圆心作直线的垂线段
r ●O ┐d
相交
(1)直线和圆相交 (2)直线和圆相切 (3)直线和圆相离
r ●O
d ┐ 相切
d < r;
d = r;
d > r;
r ●O
d
┐ 相离
尝试归纳
判定直线 与圆的位置关系的方法有__两__种:
种情况
探究活动二
• 请同学们在练习本上画一个圆,把直尺边缘看成 一条直线,平移直尺,
直线和圆分别有几个公共点?
没有公共点
两个公共点
●O
一个公共点
●O 直线与圆的交
●O
点个数可判定
它们关系
相交
相切
相离
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条 PPT模板: PPT背景: PPT下载: 资料下载:
1)若AB和⊙O相离,则 d > 6cm ; 2)若AB和⊙O相切,则 d = 6cm ; 3)若AB和⊙O相交,则 0cm≤ d < 6cm .
2.直线和圆有2个交点,则直线和圆__相__交_____; 直线和圆有1个交点,则直线和圆__相__切_____; 直线和圆有没有交点,则直线和圆__相__离_____;
2.在Rt△ABC中,∠C=90°,AC=3cm, BC=4cm,以C为圆心,r为半径的圆与AB 有怎样的位置关系?为什么? (1)r=2cm;(2)r=2.4cm (3)r=3cm.
B
4
D
d
C
A
3
解:过C作CD⊥AB,垂足为D
在△ABC中,
AB= AC2 BC2 32 42 5 根据三角形的面积公式有
直线和圆没有公共点,这时我们就说这条直线和圆相离.
一、直线与圆的位置关系(公共点的个数)
1.直线和圆的位置关系有三种(从直线与圆
公共点的个数) 2.用图形表示如下:
有两个公共点
有一个公共点
没有公共点
.o
l
相交
.o
.
.o
l
l
相切
相离
交 点
割 线
切 点
切 线
请你判断
看图判断直线l与⊙O的位置关系.
(1)
灵活应用
1. 如图:∠AOB = 30°M是OB上的一点,且OM =5 cm 以M为 圆心,以r 为半径的圆与 直线OA 有怎样的关系?为什么?A (1)r = 2 cm ; (2) r = 4 cm ; (3) r = 2.5 cm .
解: 过 M 作 MC⊥OA 于 C,在 Rt C
△OMC 中, ∠AOB = 30°
直线与圆的位置关系
复习回顾 点和圆的位置关系有哪几种?
A
d
B
C
O
点到圆心距离为d
⊙O半径为r
(1)d<r (2)d=r (3)d>r
点A在圆内
点B在圆上 点C 在圆外
三种位置关系
观察探究一
把太阳看成一个圆,地平线看成一条直线,注 意观察直线与圆的公共点的个数
a(地平线)
●
●
●
●
a(地平线)
•你发现这个自然现象反映出直线和圆的公共点个数有 三
(2)由_圆__心__到__直__线__的__距__离__d与半径r 的大小关系来判断.
在实际应用中,常采用第二种方法判定.
当堂检测
1、已知⊙O的半径为6cm,圆心O与直线AB的距离为d, 根据 条件填写d的范围:
O 30°
2.5
MC= 1 OM= 1 x5=2.5
2
25Mຫໍສະໝຸດ B即圆心 M 到OA的距离 d = 2.5 cm.
(1) 当 r = 2 cm 时,有 d > r, 因此⊙M 和 直线OA 相离. (2) 当 r = 4 cm 时,有 d < r, 因此⊙M 和直线O A 相交.
(3) 当 r = 2.5cm 时,有 d = r ,因此⊙M 和直线 OA 相切.
(2)
(3)
l
·O
·O
l
·O
l
相离 (4)
相交
相切
·O
相交
l
思考讨论
O
l
相交
O
Al
相切
O
l
相离
上述变化过程中,除了公共点的个数发生了变化, 还有什么量在改变?你能否用数量关系来判别直线 与圆的位置关系?
温馨提示
过直线外一点作这条直线的垂线段, 垂线段的长度叫点到直线 的距离.
.A
D
l
二、直线与圆的位置关系量化
D
d
知识小结 直线与圆的位置关系:
图形
.O r d┐ l
直线与圆的 位置关系
相离
公共点的个数 0
圆心到直线的距离
d 与半径 r 的关系 d>r
公共点的名称
直线名称
.o
.O
d .┐r l
A
. r ┐d .
B
lC
相切 相交
1
2
d=r 切点 切线
d<r 交点 割线
拓展练习
如图:AB=8是大圆⊙O的弦,大圆半径为R=5, 则以O为圆心,半径为3的小圆与A B的位置关系 是( B )
D
d
1 CD AB 1 AC BC
2
2
∴ CD AC BC 3 4 2.4(cm)
AB
5
即圆心C到AB的距离d=2.4cm
所以 (1)当r=2cm时,有d>r,因此⊙C和AB相离.
(2)当r=2.4cm时,有d=r, 因此⊙C和AB相切.
D
d
(3)当r=3cm时,有d<r, 因此,⊙C和AB相交.
试卷下载:
PPT论坛:
PPT素材: PPT图表: PPT教程: 范文下载:
教案下载:
PPT课件:
语文课件: 数学课件:
英语课件: 美术课件:
科学课件: 物理课件:
化学课件: 生物课件:
地理课件:
历史课件:
直线叫做圆的割线
直线和圆只有一个公共点,这时我们就说这条直线和圆相切, 这条直线叫做圆的切线,这个点叫做切点.
A相离 B相切 C相交 D都有可能
O
5
3
A
4B
D
8
课后作业
必做题:A组1题 B组1题
选做题:B组2题
你能根据d与r的大小关系确定直线与圆的位置关系吗?
d:圆心O到直线的距离为d 过圆心作直线的垂线段
r ●O ┐d
相交
(1)直线和圆相交 (2)直线和圆相切 (3)直线和圆相离
r ●O
d ┐ 相切
d < r;
d = r;
d > r;
r ●O
d
┐ 相离
尝试归纳
判定直线 与圆的位置关系的方法有__两__种:
种情况
探究活动二
• 请同学们在练习本上画一个圆,把直尺边缘看成 一条直线,平移直尺,
直线和圆分别有几个公共点?
没有公共点
两个公共点
●O
一个公共点
●O 直线与圆的交
●O
点个数可判定
它们关系
相交
相切
相离
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条 PPT模板: PPT背景: PPT下载: 资料下载:
1)若AB和⊙O相离,则 d > 6cm ; 2)若AB和⊙O相切,则 d = 6cm ; 3)若AB和⊙O相交,则 0cm≤ d < 6cm .
2.直线和圆有2个交点,则直线和圆__相__交_____; 直线和圆有1个交点,则直线和圆__相__切_____; 直线和圆有没有交点,则直线和圆__相__离_____;
2.在Rt△ABC中,∠C=90°,AC=3cm, BC=4cm,以C为圆心,r为半径的圆与AB 有怎样的位置关系?为什么? (1)r=2cm;(2)r=2.4cm (3)r=3cm.
B
4
D
d
C
A
3
解:过C作CD⊥AB,垂足为D
在△ABC中,
AB= AC2 BC2 32 42 5 根据三角形的面积公式有
直线和圆没有公共点,这时我们就说这条直线和圆相离.
一、直线与圆的位置关系(公共点的个数)
1.直线和圆的位置关系有三种(从直线与圆
公共点的个数) 2.用图形表示如下:
有两个公共点
有一个公共点
没有公共点
.o
l
相交
.o
.
.o
l
l
相切
相离
交 点
割 线
切 点
切 线
请你判断
看图判断直线l与⊙O的位置关系.
(1)
灵活应用
1. 如图:∠AOB = 30°M是OB上的一点,且OM =5 cm 以M为 圆心,以r 为半径的圆与 直线OA 有怎样的关系?为什么?A (1)r = 2 cm ; (2) r = 4 cm ; (3) r = 2.5 cm .
解: 过 M 作 MC⊥OA 于 C,在 Rt C
△OMC 中, ∠AOB = 30°
直线与圆的位置关系
复习回顾 点和圆的位置关系有哪几种?
A
d
B
C
O
点到圆心距离为d
⊙O半径为r
(1)d<r (2)d=r (3)d>r
点A在圆内
点B在圆上 点C 在圆外
三种位置关系
观察探究一
把太阳看成一个圆,地平线看成一条直线,注 意观察直线与圆的公共点的个数
a(地平线)
●
●
●
●
a(地平线)
•你发现这个自然现象反映出直线和圆的公共点个数有 三
