11.1.3函数的图像(1)vb
VB常用函数介绍

VB常用函数介绍一、常用内部函数在VB内部提供了大量函数。
在这些函数中,有些是通用的。
有些则与某种操作有关的。
大体分成五类,分别是:转换函数、数学函数、日期函数、时间函数和随机函数。
(1)转换函数函数名功能Int(x) 返回不大于自变量的最大整数。
Fix(x) 去掉一个浮点数的小数部分,保留其整数部分。
Hex(x) 把一个十进制数转换成为十六进制数。
Oct(x) 把一个十进制数转换成为八进制数。
Asc(x) 返回字符串中第一个字符的ASCII码。
Chr(x) 把值转换为相应的ASCII字符。
Str(x) 把值转换为一个字符串Cint(x) 把小数部分四舍五入,转换为整数。
Ccur(x) 把值转换为货币类型,小数部分最多保留4位。
CDbl(x) 把值转换为双精度数值。
CLng(x) 把值小数部分四舍五入转换为长整型数值。
CSng(x) 把值转换为单精度数值。
CVar(x) 把值转换为变体类型值。
(2)数学函数函数名功能Sin(x) 返回正弦值。
Cos(x) 返回余弦值。
Tan(x) 返回正切值。
Atn(x) 返回反正切值。
Abs(x) 返回绝对值。
Sgn(x) 返回自变量的符号。
即:值为负数时,函数返回-1值为0时,函数返回0值为正数时,函数返回1Sqr(x) 返回自变量x的平方根,自变量必须大于或等于0。
Exp(x) 返回以e为底数,以x为指数的值,即求e的x 次方。
(3)日期函数函数名功能Day(Now) 返回当前的日期。
WeekDay(Now) 返回当前的星期。
Month(Now) 返回当前的月份。
Year(Now) 返回当前的年份。
(4)时间函数函数名功能Hour(Now) 返回小时(0~23)。
Minute(Now) 返回分钟(0~59)。
Second(Now) 返回秒(0~59)。
(5)随机函数Rnd(x) 产生一个0~1之间的单精度随机数Rnd函数可以产生随机数,当一个应用程序不断地重复使用随机数时,同一序列的随机数会反复出现,用Randomize语句可以消除这种情况。
VB函数的综合应用课件

Dim x As Integer
For i = 1 To 10 Picture1.Print
Int(Rnd() * 6 + 1)
Next i
End Sub
4
5 6
我来试一试:
5
6 4
1、扔硬币
Int(Rnd()*2)
2、随机产生双色球红球的号码(1-33)
Int(Rnd()*33+1)
3、为小学生出任意两位整数加法题
Int(x)取整函数
Sqr(x)开平方函数
Len(x)求字符长度函数
Rnd(x)随机函数
Int(x)取整函数 Rnd()随机函数
Exp(x)指数函数 Mid(x)字符串截取函数
Abs(x)绝对值函数 Str(x)数值转字符函数
Hour(x)小时函数
1
2 3
随机 产生骰子六个面的整数
随机函数Rnd( )
2
3 1
取整函得数到In一t个(x()0,1)之间的随机小数 随机函数Rnd( 不)与包取含整0和函1数Int(x),
一起使用时,用来表示得到一定
范得围到之一内个的不随大于机x整的数最。大整数
3 例如:Int(3.5)= ?
- 4 Int(-3.5)= ?
随机产生骰子六个面的整数
3
1 2
的函数表达式
Int(Rnd()*90+10)
①骰子的6个面数字是[1,6]
五 ②把范围写成[1,7)
步 ③Rnd()*(7-1)
Rnd()*(上界-下界)
法 ④Rnd()*6+1 ⑤Int(Rnd()*6+1)
…… +下界 ……取整Βιβλιοθήκη 掷10次骰子,观察产生的整数
vb中三角函数

vb中三角函数三角函数是数学中的重要概念,它们是描述角度与边长之间关系的函数。
在VB中,我们可以通过调用相应的函数来计算三角函数的值。
下面让我们来了解一下VB中常用的三角函数及其应用。
一、正弦函数(Sin)正弦函数是三角函数中最基本的函数之一,它描述了一个角的对边与斜边之间的比值。
在VB中,我们可以通过调用Sin函数来计算一个角度的正弦值。
在三角形中,角的正弦值等于该角的对边与斜边之比。
因此,正弦函数在解决三角形中的问题时非常有用。
例如,在给定一个角度和斜边长度的情况下,我们可以使用正弦函数来计算该角对应的对边长度。
二、余弦函数(Cos)余弦函数是三角函数中另一个重要的函数,它描述了一个角的邻边与斜边之间的比值。
在VB中,我们可以通过调用Cos函数来计算一个角度的余弦值。
在三角形中,角的余弦值等于该角的邻边与斜边之比。
因此,余弦函数在解决三角形中的问题时非常有用。
例如,在给定一个角度和斜边长度的情况下,我们可以使用余弦函数来计算该角对应的邻边长度。
三、正切函数(Tan)正切函数是三角函数中另一个常用的函数,它描述了一个角的对边与邻边之间的比值。
在VB中,我们可以通过调用Tan函数来计算一个角度的正切值。
在三角形中,角的正切值等于该角的对边与邻边之比。
因此,正切函数在解决三角形中的问题时非常有用。
例如,在给定一个角度和邻边长度的情况下,我们可以使用正切函数来计算该角对应的对边长度。
四、反正弦函数(Asin)反正弦函数是三角函数中的逆函数,它描述了一个角的正弦值对应的角度。
在VB中,我们可以通过调用Asin函数来计算一个正弦值对应的角度。
反正弦函数在解决三角形中的问题时非常有用。
例如,在给定一个正弦值和斜边长度的情况下,我们可以使用反正弦函数来计算该正弦值对应的角度。
五、反余弦函数(Acos)反余弦函数是三角函数中的逆函数,它描述了一个角的余弦值对应的角度。
在VB中,我们可以通过调用Acos函数来计算一个余弦值对应的角度。
经典数学函数图像大全-数学函数图像-函数图像 全
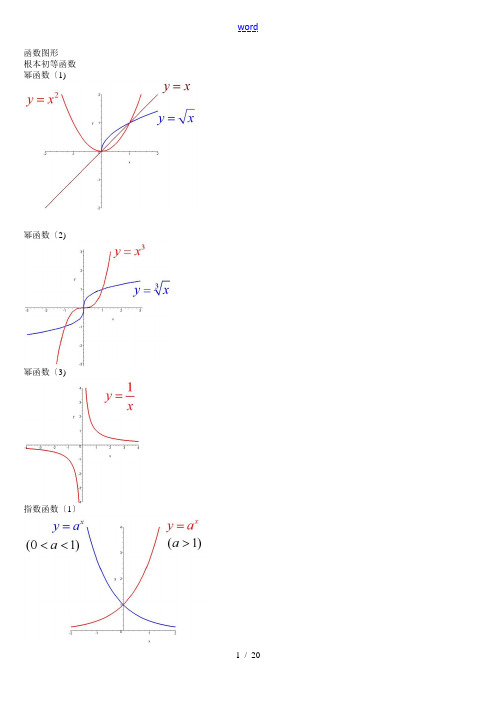
函数图形根本初等函数幂函数〔1)幂函数〔2)幂函数〔3)指数函数〔1〕指数函数〔2〕指数函数〔3〕对数函数〔1〕对数函数〔2〕三角函数〔1〕三角函数〔2〕三角函数〔3〕三角函数〔4〕三角函数〔5〕反三角函数〔1〕反三角函数〔2〕反三角函数〔3〕反三角函数〔4〕反三角函数〔5〕反三角函数〔6〕反三角函数〔7〕反三角函数〔8〕双曲函数〔1〕双曲函数〔2〕双曲函数〔3〕双曲函数〔4〕双曲函数〔5〕双曲函数〔6〕双曲函数〔7〕反双曲函数〔4〕反双曲函数〔1〕反双曲函数〔2〕反双曲函数〔3〕反双曲函数〔5〕反双曲函数〔6〕y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1) y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
vb常用函数一览表

v b常用函数一览表(总3页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除常用内部函数数学函数函数功能示例结果说明Abs(x)绝对值Abs(-50.3)50.3Exp(x) 自然指数Exp(2) e*e e(自然对数的底)的某次方Fix(x) 取整(取参数的整数部分)Fix(-99.8) -99Int(x)取整(取小于或等于参数的最大整数)Int(-99.8)Int(99.8)-10099Log(x) 常用对数Log(1) 0 求自然对数值Rnd 随机产生0~1的单精度值Int(6*Rnd)+11~6要产生一个从Min到Max的整数,应使用公式Int((Max-Min+1)*Rnd+Min)Round(x,n)按小数位数四舍五入Round(3.14159,3) 3.142第2个参数为小数位数Sgn(x) 取参数的符号值Sgn(8.8)Sgn(-8.8)Sgn(0) 1-10 参数大于0,返回1参数小于0,返回-1参数等于0,返回0Sin(x) 正弦 1三角函数以“弧度”为单位Cos(x) 余弦/180*180) -1Atn(x) 计算反正切Atn(1) 0.7854Tan(x) 计算正切 1Sqr(x) 算术平方根Sqr(9) 3 相当于字符串函数函数功能示例结果说明Len(x)求字符串的长度(字符个数)Len("Vb技术")4LenB(x) 求字符串的字节个数LenB("Vb技术") 8 VB中采用Unicode(ISO 字符标准)来存储字符,所有字符都占2个字节Mid(x,n1,n2)从x字符串左边第n1个位置开始向右取n2个字符Mid("Vb技术",2,2)"b技"。
11.1.3函数的图象(3)vb

X (小时)
如图表示一艘轮船和一艘快艇沿相 同路线从甲港出发到乙港行驶过程中路 程随时间变化的图像(分别是正比例函 数图象和一次函数图象).根据图像解答 S(千米) 下列问题:
160
0
2
6
x 8 (时)
从图中可以获得哪些信息呢?
小结
作业
一水库的水位在最近5小时内持续 上涨,下表记录了这5小时的水位高度.
t/时 y/米 0 10.00 1 10.05 2 10.10 3 10.15 4 10.20 5 10.25
(1)由记录表推出这5小时中水位高度y(米) 随时间t(时)变化的函数解析式,并画出函数图 象; (2)据估计这种上涨的情况还会持续2小时,预 测通过2小时水位高度将达到多少米?
11.1.3函数的图象(3)
y
o
x
已知大米的单价是2元/千克,试 用尽可能多的方法表示大米的总价y(元) 与所买数量x(千克)之间的函数关系.
x y
… …
0
0
1
2
2
4
y
3
6
…
…
y=2x
0
x
已知大米的单价是2元/千克,试 用尽可能多的方法表示大米的总价y(元) 与所买数量x(千克)之间的函数关系.
C
120
120 80 40
(A)
2 4
s(千米)
80
40
(B)
2 4
s(千米)
O
120 80 40
6 t(时)
O
120
6 t(时)
(C)
2 4 6 t(时)
80
40
(D)
2 4 6 t(时)
O
O
函数图像大全

函数图像大全函数图像是数学中的重要概念之一,它可以直观地展现出函数的性质和特点。
在数学教学中,函数图像也是一个重要的教学内容,通过观察函数的图像,可以更好地理解函数的变化规律和特点。
本文将对常见的函数图像进行详细介绍,希望能够帮助读者更好地理解和掌握函数图像的相关知识。
一、线性函数图像。
线性函数是最简单的一类函数,它的图像通常是一条直线。
线性函数的一般形式为y=kx+b,其中k和b为常数,k表示直线的斜率,b表示直线与y轴的交点。
当k大于0时,直线向上倾斜;当k小于0时,直线向下倾斜;当k等于0时,直线平行于x轴。
b的取值决定了直线与y轴的交点的位置。
线性函数的图像特点明显,通过观察直线的斜率和截距,可以快速了解函数的性质。
二、二次函数图像。
二次函数的一般形式为y=ax^2+bx+c,其中a、b、c为常数且a不等于0。
二次函数的图像通常是一个抛物线,其开口方向由a的正负决定。
当a大于0时,抛物线开口向上;当a小于0时,抛物线开口向下。
二次函数的图像特点较为复杂,需要通过求导、配方法等手段来确定抛物线的顶点、焦点等重要特征点。
三、指数函数图像。
指数函数的一般形式为y=a^x,其中a为常数且a大于0且不等于1。
指数函数的图像通常是一条曲线,其特点是随着自变量x的增大,函数值呈指数增长或指数衰减。
指数函数的图像在x轴的左侧逐渐逼近y轴,而在x轴的右侧则迅速增长。
指数函数是一种常见的增长模型,在经济、生物、物理等领域有着广泛的应用。
四、对数函数图像。
对数函数的一般形式为y=loga(x),其中a为常数且a大于0且不等于1。
对数函数的图像通常是一条曲线,其特点是随着自变量x的增大,函数值呈对数增长。
对数函数的图像在x轴的右侧逐渐逼近y轴,而在x轴的左侧则迅速减小。
对数函数是一种常见的减小模型,在金融、生物、信息论等领域有着广泛的应用。
五、三角函数图像。
三角函数包括正弦函数、余弦函数、正切函数等,它们的图像都具有周期性。
VB教程 全套课件 vb-11

姓名
专业 物理 物理 。。 。 建筑
课程 数学 外语 。。 。 建筑学
成绩 85 90 。。 。 90
MoveLast MoveNext
990001 990002
万林 庄前
。。 。 黎明
MovePrevious
。。 。 990010
Nomarch =False
Data1.Recordset. FindFirst "姓名=' 黎明' "
11.3.4 记录集的属性与方法 1 属性
Bof
学号 990001
姓名
专业 物理 物理 。。 。 建筑
课程 数学 外语 。。 。 建筑学
成绩 85 90 。。 。 90
RecordCount
万林 庄前
。。 。 黎明
BookMark
990002 。。 。 990010
Eof
2 记录集的方法
学号
MoveFirst
11.5.2 使用SELECT语句查询
1.使用SELECT语句
从数据库中的获取数据称为查询数据库,查询数据库通过使用SELECT 语句。常见的SELECT语句形式为: Select 字段表 From 表名 Where 查询条件 Group By 分组字段 Order By 字段[Asc|Desc] 可以在设计或代码中对数据控件的RecordSource属性设置SQL语句,也 可将SQL语句赋予对象变量。 在建立SQL语句时,如果需要通过变量构造条件,则需要在应用程序 中将变量连接到SELECT语句。例如: "Select * From 基本情况 Where 专业 =' " & Text1 & " ' " 例11.7 将例11.4中的查找功能改用SQL语句处理。 例11.8 用SQL语句从两个数据表中选择数据构成记录集。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x y
画出函数 y=x+0.5的图象。 自变量怎样取值比较合理? … -2.5 -1.5 -0.5 0 0.5 1.5 2.5 … … -2 -1 0 0.5 1 2 3 … y 3 2 1
画出函数 y= 6 的图象. x
(4)(0,0.5) ;
1 (6)( 2 ,12)
(5)(1,6);
6 画出函数 y=x+0.5和y= 的图象. x
再观察图象Байду номын сангаас看看还能获取哪些 信息.
谈谈你的收获
作业:
11.1.3函数的图象(1)
y
o
x
根据图象你能获得哪些信息?
1.最大、最小值2.哪一段下降哪一段上升 3.哪一段温度不变4.每个时刻的温度
正方形的面积s与边长x的函数关 s=x2 ,其中自变量x的取 系为 值范围是 x>0 .
为了直观、清晰的看出两个变量s、x之间 的关系,我们如何画出函数s=x2的图象呢?
两个变量
有序实数对
图象
. (x,s)
s、x
(x,s)
2的图象呢? 如何画出函数s=x
计算并填写下表:
x s 0
0
0.5
0.25
1
1
1.5
2.25
2
4
2.5
6.25
3
9
3.5
12.25
4
16
这个点如何表示呢?
s 5 4 3
●
2 1
●
●
●
○
o
1 2
3 4
5 6
x
1.列表.列表给出自变量与函数的一些对应值.
x y
6 画出函数 y= x 的图象. … -3 -2 -1.5 1 1.5 2
…
3
…
…
-2
-3 -4 y 3 2 1
6
4
3
2
-4 -3 -2 -1 o 1 2 3 4 -1 -2 -3
x
想一想,下列各有序实数对所对 应的点,分别在哪个函数图象上?为 什么?
(1) ( -4,-3.5 ); (2)(-2,-3) (3)(10,10.5)
● ● ● ●
-1 o 1 2 -1 -2
3 4
x
想一想,下列各有序实数对所对应的 点,哪些在函数y=x+0.5的图象上? 哪些不在这个函数的图象上?
(1) ( -4,-3.5 ); (2)(-5,-5.5) (3)(10,10.5) (4)(99,88.5) ; (6)(2001,2000.5) (5)(1000,1000.5)
