轴系的扭转振动
毕业论文-船舶轴系扭转振动的研究

毕业论文-船舶轴系扭转振动的研究
摘要
轴系在工作过程中,承受着不断变化的扭矩、推力及弯曲力矩作用,因而船舶轴系在运动过程中可能产生以下三种形式的振动:扭转振动,回旋振动和纵向振动。
本文主要针对扭转振动的计算进行软件系统的开发。
船舶轴系在发动机、螺旋桨等周期性扭矩激励下所产生的周向交变运动及其相应变形即为船舶轴系的扭转振动。
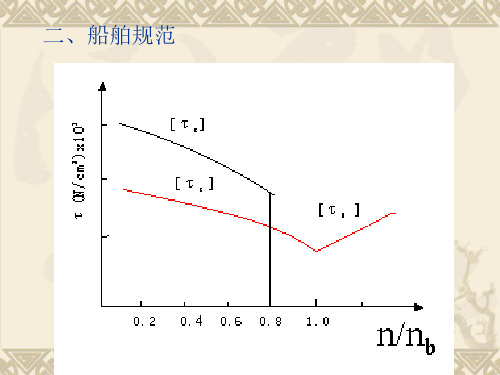
在世界各国的船舶规范中,
都列有共同的条款,凡是船用柴油机(主机或辅机)和气轮机动力装置,均必须通过扭转振动的计算,测试的检验,合格之后方可投入运营。
这是因为船舶轴系的扭转振动常常
是造成严重事故的主要原因之一,而且扭转振动还常常会诱发船体、动力装置的强烈振动和噪声,传动轴系的断裂,发动机零件磨损的加剧等等问题。
随着柴油机功率、转速的不断提高,与其配套的动力装置样式也越来越多,出现严重的扭转振动现象也就逐步增加了,同时,对船舶轴系扭转振动的研究也得到了进一步的发展。
本文分析了我国轴系扭转振动研究的情况及与世界先进水平相比较的差距;简单介绍了扭
转振动的一些理论和计算方法。
并以163000DWT油轮为例编写了扭转振动计算的软件。
用计算数据做校核计算,得出结论。
关键词: 船舶轴系;计算程序;扭转振动校核
I。
船舶推进轴系的扭转振动与控制
当量轴段长 6)轴系中有弹性联轴器或气胎离合器时,应把它们的主、从动
部分分为两集中质量 7)轴系中有液力偶合器时为界,分成两个独立的扭振系统 8)被发动机拖动的机械,转动惯量大的也要作一集中质量
二、多质量系统无阻尼简谐振动计算
等,振幅不同,惯量大的振幅小,惯量小 的振幅大,且振动方向永远相反。
振型图
A1
e12 O
A1
单结 A2
e12
e23
单结
A1
A2
双结
取A1=1,A2=-I1/I2, O为结点,振幅为0, 应力最大,双质量 只有一个结点。
A2
三质量系统有两个
自振频率,单结或
双结,即两个结点。
A3 A3
n个质量就有n-1个 振型,n-1个自振 频率。
(
2 n
2)2
4n 2 2
2 n
2
Asin(t )
A
h
h
1
(
2 n
2)2
4n 2
2
2 n
[1 ( n
)2 ]2
n2
4
2 n
(
n
)2
h
பைடு நூலகம்
2 n
M I
Ie
Me
Ast
静振幅
放大系数
m A Ast
1
f ( , )
[1 ( )2 ]2 ( )2
n
n
n
讨论:
1)
0
n
m 1
有因
IK
次
eK,K+1
AK
n2
Uk,,k+1=(AK+1-AK)/ eK,K+1
轴系扭振

电信号扰动下的轴系扭振摘要本文用一种改进的Riccati扭转传递矩阵结合Newmark-β方法研究非线性轴系的扭转振动响应。
首先,该系统被模化成一系列由弹簧和集中质量点组成的系统,从而建立一个由多段集中质量组成的模型。
第二,通过这种新发展起来的程序可以从系统的固有频率和扭振响应中消除累计误差。
这种增量矩阵法,联合结合了Newmark-β法改进的Riccati扭转传递矩阵法,进一步应用于解决非线性轴系扭转振动的动力学方程。
最后,将一种汽轮发电机组作为一个阐述的例子,另外仿真分析已被应用于分析典型电网扰动下的轴系扭振瞬时响应,比如三相短路,两相短路和异步并置。
实验结果验证了本方法的正确性并用于指导涡轮发电机轴的设计。
关键词:传递矩阵法;Newmark-β法;汽轮发电机轴;电学干扰;扭转振动1.引言转子动力学在很多工程领域起着很重要的作用,例如燃气轮机,蒸汽轮机,往复离心式压气机,机床主轴等。
由于对高功率转子系统需求的持续增长,计算临界转速和动态响应对于系统设计,识别,诊断和控制变得必不可少。
由于1970年和1971年发生于南加州Edison’sMohave电站的透平转子事故,业界的注意力集中在由传动行为导致的透平发电机组内的轴的扭转振动。
当代的大型透平发电机组单元轴系系统是一种高速共轴回转体。
它是由弹性联轴器连接,由透平转子,发电机和励磁机组成。
电力系统故障或操作条件的变化引起的机电暂态过程可能导致轴的扭转振动,而轴的扭转振动对于设计来说是非常重要的。
对于透平发电机轴系扭振的研究,如发生次同步谐振和高速重合,基本的是对固有频率和振动响应的计算的研究。
当前,有限元法和传递矩阵法是最流行的两种分析轴系扭振的方法。
有限元法(FEM)通过二阶微分方程构造出转子系统直接用于控制设计和评估,而传递矩阵法(TMM)解决频域内的动态问题。
TMM使用了一种匹配过程,即从系统一侧的边界条件开始沿着结构体连续的匹配到系统的另一端。
大型汽轮发电机组轴系扭振

☆可控硅控制的给水泵电动机反馈作用 联邦德国Wilbel Shave火电站的1台770MW机组曾由于可控硅控制的16.8MVA给水 泵电动反馈作用,造成频率为15.75Hz的次同步谐振。 ☆电液调节系统 加拿大安大略省电力公司的1台665MW核电汽轮机组在试运期间因快速电液涡轮 调速系统存在与轴系低阶扭振频率合拍的频率分量,引起调节阀强烈振动,并因此 激发了轴系的扭转振动。 ☆直流输电系统 1972年,美国试验投入第一条可控硅控制的直流输电系统,在送端电厂切除交 流输电线而通过直流输电系统送电时,发生了次同步谐振。其原因是当在直流输电 系统控制其变化时,引起发电机转速及其交流电压相位的变化,结果导致直流系统 中可控硅阀触发角的变化,又改变了直流输电的功率,从而构成了一个闭合系统而 引起次同步谐振。
二、机电系统扰动类型 一方面单机容量不断增大,功率密度亦相应增加,轴系长度加长和轴系截面积相 对下降,整个轴系不可再视为转动刚体,而是由多跨转子组成的弹性质量扭振系统; 另一方面输电网络的大容量化、长距离化、系统结构复杂化、电力负荷多样化以及 新型输电技术的采用,对轴系的影响因素也日趋增多。由于这两方面的原因,易导 致机网耦合,诱发轴系扭振,并造成扭转疲劳损耗;损伤程度取决于轴系本身的扭 振特性、机电扰动性质等因素,轻者可忽略不计,重者可使轴系损坏甚至酿成灾难 性事故。 从汽轮发电机组轴系的外施激励看,引起轴系扭振的原因有两方面:由同步发电 机引入的电气扰动和汽轮机引入的机械扰动。电气扰动包括电气短路故障、自动重 合闸、非同期并网、甩负荷及串联电容补偿、高压直流输电的调节环节和电力系统 稳定器的不适当配置等;机械扰动相对较少,主要包括不适当的进汽方式、调速系 统晃动、快控汽门等。
曲轴轴系的扭转振动计算

文献标志码 :A
To so a b a in Cac lt n o a k h f y tm r i n lVi r t lu a i fCr n s a tS se o o
DENG Jn Z NG e ,V B n 2 ig , HO W PL ig ( .h nd o pesrPa tC C J hi o e q imetC mpn , hn d 1 10, hn ;.ra l D ln nier gC mpn ii d 1C e gu C m rso ln, NP i a P w rE up n o ay C eg u6 0 0 C ia2G erWa rl gE gne n o oyLm t e l ii i e
4e+ 2e= .5 - rdN・ + 3e+ 591 x O7( / m) l a
()装有齿轮的轴段 1 ,= (d z :+ ) 39 x 0 ( g m2 f4 = . k . ) 11 + 51
4
轴段3 的柔 度
()装有平衡重的轴段 2
I2 p '= 4
文章 编号 :0 6 2 7 ( 0 2 0 — 0 6 0 10 — 9 1 2 1 )4 0 2 — 5
曲轴轴系的扭转振动计算
邓 晶’ ,钟 蔚 吕 冰z ,
(. 1 中国石油集 团济柴 动力 总厂成都压缩 机厂 , 四川 成都 600 ;. 城钻探工程有 限公 司苏里格气 田项 目 , 1102 长 部 内蒙古 苏里格 14 1) 200
() 对 于 曲 轴 的 曲拐 部 分 , 由于 几 何 形 状 极 3
为复杂 ,且在整个 曲拐扭转 时各部 分发生不 同形 式 的变形 ,因此很 难用纯理论公式 进行计算 ,目 前 一 般 采 用 实 验 数 据 修 正 过 的半 经 验 公 式 进 行 计
第七章船舶推进轴系的扭转振动与控制

e12
2 n
I
1
A1
2
e23
2 n
I i Ai
i 1
Ak
k 1
Ak 1 ek 1,k
2 n
I i Ai
i 1
0
n
m 1
A Ast
2)
m0
n
3) 1
n
n
m 1
此时阻尼对放大系数的影响最大
4) 2 m 1
n
2 n
1 Ie
增大I或e可使n 下降
时共振
n
tg 1 2n
2 n
2
2
小结: 1)系统自振频率仅与结构有关 n 1/(I e)
1 2 n1
A(1) 1
A(2) 1
A(n1) 1
高速机一般只考虑
1, 2, 3
k
A(1) k
sin(1t
1
)
A(2) k
sin(
2t
2
)
A(n1) k
s
in(
n1t
n1 )
取第一质量作为分离体
S1 U12 0
A
h
h
1
(
2 n
2)2
4n 2
2
2 n
[1 ( n
)2 ]2
n2
4
2 n
(
动车车轴的扭转振动特性分析

动车车轴的扭转振动特性分析为了确保动车的安全运行和乘客的舒适性,对动车车轴的振动特性进行分析和研究非常重要。
动车车轴的扭转振动特性直接影响着列车的平稳性和牵引力输出效率。
本篇文章将重点讨论动车车轴的扭转振动特性,并探讨其对动车运行的影响。
一、动车车轴的扭转振动现象在动车行驶过程中,车轴会受到许多外部和内部力的作用,导致车轴产生扭转振动。
这些力包括车轮压力、牵引和制动力、轴承摩擦力、轮胎非线性特性等。
这些力的作用下,车轴会发生扭矩变化,导致车轮出现扭转变形和轴向动态位移,进而引起车轮-轨道系统的振动。
车轮-轨道系统的振动会进一步影响车辆的运行稳定性和乘坐舒适度。
二、动车车轴振动的分析方法为了分析动车车轴的扭转振动特性,需要采用一系列先进的研究方法和工具,包括数学建模、仿真计算和试验验证。
1. 数学建模数学建模是分析动车车轴振动的基础。
通过建立适当的数学模型,可以描述车轴的结构特性、边界条件和扭转振动响应。
常用的数学建模方法包括有限元法、多体动力学方法和计算流体力学方法等。
这些方法可以用来模拟车轴的扭转动力学行为和振动响应,对车轴的设计和优化起到重要作用。
2. 仿真计算仿真计算是研究动车车轴振动特性的重要手段。
通过利用数学模型进行计算,可以预测车轴的扭转振动情况。
仿真计算可以提供车轴的振动频率、模态形式、振动幅值等重要参数,对车辆的振动控制和优化设计提供指导。
3. 试验验证为了验证数学模型的准确性和可靠性,需要进行实际试验。
试验可以通过安装传感器在动车车轴上进行数据采集,获取车轴的振动信号。
试验还可以通过加载不同的力和扭矩,模拟实际工况下车轴的振动情况。
通过与数学模型的对比分析,可以评估数学模型的准确性,并为动车车轴的设计和控制提供实验依据。
三、动车车轴振动对运行的影响动车车轴的振动特性直接影响列车的平稳性、行驶速度和能源消耗等方面。
1. 平稳性车轴振动会导致列车的不稳定性,影响乘客的舒适度。
当车轴受到扭矩变化时,会产生横向力和不对称的摩擦力,进而引起车辆的不稳定横向振动。
轴系的扭转振动

2) 两种自振频率, ωe1<ωe2。 12 9 数值取决于转动惯量和轴段柔度。 3) 在不同圆频率下振动的振型是不同的。 在低圆频率ωe1下的振动是单节振动。 在高圆频率ωe2下的振动是双节振动,它有两个节点, 质量愈大离节点愈近,振幅愈小。
I1 + I 2 I 2 + I3 2 1) = ω 由两种简谐振动相加而成; ω 23 = e12 I1 I 2 e23 I 2 I 3
17 15
2
2
16
2. 轴系阻尼
1)柴油机阻尼 2)轴段阻尼 3)螺旋桨阻尼
Байду номын сангаас15
3.轴系的强制扭转振动特性 1) 轴系的共振 激振力矩频率f=νn 当某次简谐力矩的变化频率等于轴系的某个自振频率 时,轴系便会产生这个自振频率及振动形式下的共振 产生共振转速称临界转速 2)主临界转速与副临界转速
2 12
11
3. n 质量系统的无阻尼自由扭转振动特性
ϕ1=A1(1)sin(ωe1t+ε1)+A1(2)sin(ωe2t+ε2)+… …+A1(n-1)sin(ωe(n-1)t+εn-1) ϕ2=A2(1)sin(ωe1t+ε1)+A2(2)sin(ωe2t+ε2)+… …+A2(n-1)sin(ωe(n-1)t+εn-1) … … … … ϕn=An(1)sin(ωe1t+ε1)+An(2)sin(ωe2t+ε2)+… …+An(n-1)sin(ωe(n-1)t+εn-1)
1) 每个质量扭振均为(n-1)种简谐振动相加而成; 2) 有(n-1)个自振频率, ωe1<ωe2<ωe3<…<ωe(n-1)。单节点振动振幅 最大,多节点振动的振幅递减; 3) 有(n-1)个振型 即单节点、双节点、三节点……(n-1)节点自由 14 9 扭转振动振型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2) 两种自振频率, ωe1<ωe2。 12 9 数值取决于转动惯量和轴段柔度。 3) 在不同圆频率下振动的振型是不同的。 在低圆频率ωe1下的振动是单节振动。 在高圆频率ωe2下的振动是双节振动,它有两个节点, 质量愈大离节点愈近,振幅愈小。
I1 + I 2 I 2 + I3 2 1) = ω 由两种简谐振动相加而成; ω 23 = e12 I1 I 2 e23 I 2 I 3
17 15
2
2
16
2. 轴系阻尼
1)柴油机阻尼 2)轴段阻尼 3)螺旋桨阻尼
15
3.轴系的强制扭转振动特性 1) 轴系的共振 激振力矩频率f=νn 当某次简谐力矩的变化频率等于轴系的某个自振频率 时,轴系便会产生这个自振频率及振动形式下的共振 产生共振转速称临界转速 2)主临界转型
通常把轴系转化为只有柔度而无转动惯量的轴段和 只有转动惯量而无柔度的集中质量组成的扭振系统。 当量扭振系统。 二质量系统;三质量系统;……;n质量系统系统
2
三、轴系的自由扭转振动特性
1.双质量系统无阻尼自由振动 双质量系统无阻尼自由振动 2.三质量系统的自由扭转振动特性
10
11
3. n质量系统的无阻尼自由扭转振动特 质量系统的无阻尼自由扭转振动特 性
13
2
1.双质量系统无阻尼自由振动
ϕ1 = A1 sin( ω et + ε ) ϕ 2 = A2 sin( ω e + ε ) ω e = (I1 + I 2 ) / e12 I1 I 2 A2 I1 ϕ2 = =− ϕ1 A1 I2
2 12
11
3. n 质量系统的无阻尼自由扭转振动特性
ϕ1=A1(1)sin(ωe1t+ε1)+A1(2)sin(ωe2t+ε2)+… …+A1(n-1)sin(ωe(n-1)t+εn-1) ϕ2=A2(1)sin(ωe1t+ε1)+A2(2)sin(ωe2t+ε2)+… …+A2(n-1)sin(ωe(n-1)t+εn-1) … … … … ϕn=An(1)sin(ωe1t+ε1)+An(2)sin(ωe2t+ε2)+… …+An(n-1)sin(ωe(n-1)t+εn-1)
特征: (1)是一种简谐振动 (2)频率fe≈9.55ωe 只取决于(I、e) (3)振幅A大小取决于 外力矩大小
3
2扭摆的有阻尼自由扭转振动
φ = e − nt A sin( ω e2 − n 2 t + ε )
n——阻尼比 特征: (1)是简谐振动。振幅是衰减的。一定时间后其振 幅e-nt·A→0,即扭振终止。阻尼比n越大,衰 减愈快。 (2)自振圆频率ωe2-n2小于无阻尼自由振动圆频 率ωe,大小也与外力矩无关。 3
主临界转速为主共振的相应转速 主共振是由简谐次数ν等于曲轴 每转发火气缸数整数倍的激振力 矩(称主谐量)所引起的共振。 二冲程机主谐量νk=mi, 四冲程机主谐量νk=mi/2 副临界转速为主临界转速以外的所有临界转速
15
4.现代船用大型柴油机的扭振特点 •现代船用大型柴油机发展的显著特点是: –长行程或超长行程; –单缸功率大、缸数少 •现代船用大型柴油机的扭振特点 – 使得柴油机输出扭矩更加不均匀,使激振力矩增加; – 轴系的自振频率降低,易出现由低次简谐力矩激起 的扭振共振; – 柴油机回转不均匀引起螺旋桨推力不均匀,易激 发轴系的纵振和船体振动。 15
3
8
9
15
一、扭摆扭转振动的特性
1扭摆的无阻尼自由扭转振动 2扭摆的有阻尼自由扭转振动 3扭摆的有阻尼强制扭转振动
4 5
6
2
一、扭摆扭转振动的特性
1扭摆的无阻尼自由扭转振动 扭摆:圆轴只有弹性而无转动惯量, 圆盘只有转动惯量而无弹性 φ=A·sin(ω t+ε)
e
ωe =
K = I
1 Ie
1) 每个质量扭振均为(n-1)种简谐振动相加而成; 2) 有(n-1)个自振频率, ωe1<ωe2<ωe3<…<ωe(n-1)。单节点振动振幅 最大,多节点振动的振幅递减; 3) 有(n-1)个振型 即单节点、双节点、三节点……(n-1)节点自由 14 9 扭转振动振型。
13
四、轴系的强制扭转振动
特点: (1)两质量都进行简谐振动 频率、初相位相同;方向相反 (2)两质量振幅与转动惯量成反比 (3)自振圆频率取决于转动惯量和轴的柔度
9
节(结)点 节点处的扭矩最大 两质量扭振只有一个节点,且节点靠近转动惯量较大处
2三质量系统的自由扭转振动特性
ϕ1=A1(1)sin(ωe1t+ε1)+A1(2)sin(ωe2t+ε2) ϕ2=A2(1)sin(ωe1t+ε1)+A2(2)sin(ωe2t+ε2) ϕ3=A3(1)sin(ωe1t+ε1)+A3(2)sin(ωe2t+ε2) ω e1 1 2 1 2 1 2 2 (ω12 + ω 23 ) ∓ 4 (ω12 − ω 23 ) + = 2 ω e2 2 e12 e23 I 2
1.激振力矩 2.轴系阻尼 3.轴系的强制扭转振动特性
16
18
19
4.现代船用大型柴油机的扭振特点
20
2
1.激振力矩
πD 2 sin( α + β ) M = p R 4 cos β
M = Mm +
∑ M γ sin( γωt + ψ γ )
γ =1or
1 2
∞
γ-简谐次数(曲轴一转中激振力矩的作用次数) 二冲程机γ=1、2、3、… 1、1、1 1 、2、… 四冲程机γ= ω-曲轴回转角速度,ω=2лn/60 简谐次数γ越高,简谐力矩的振幅Mν越小, 对扭振影响越小。一般只考虑γ≤12的激振力矩。
3扭摆的有阻尼强制扭转振动
激励力矩:Mt=Msinωt
φ=A1sin(ωt-ψ)+ e
特征:
− nt
A sin( ω e2 − n 2 t + ε ) =φ1+φ2
(1)由强制振动φ1与有阻尼自由扭振φ2两种简谐振动合成的。 (2)强制振动φ1是由激振力矩Mt激起的,其圆频率与激振力 矩圆频率相同。 (3)强制振动φ1与激振力矩Mt在相位上不同步。 φ1比Mt在相位上落后ψ角,而且其振幅A1也不同于 由M使轴产生的扭转角。 (4)A1大小主要取决于扭摆的自振圆频率ωe与阻尼比n。 系统共振(ωe=ω)
第三节 轴系的扭转振动
扭转振动: 轴系在柴油机、螺旋桨等周期性的激振力矩作 用下所产生的周向交变运动及相应变形称为轴 系的扭转振动。 扭振的危害: 轴系裂纹和断裂 损坏传动齿轮、联轴器 等等
第四节 轴系的扭转振动 一、扭摆扭转振动的特性 二、轴系扭转振动的力学简化模型 三、轴系的自由扭转振动特性 四、轴系的强制扭转振动
