弹塑性动力时程分析若干问题的分析与探讨_张剑
动力弹塑性时程分析技术在建筑结构抗震设计中的实践研究

动力弹塑性时程分析技术在建筑结构抗震设计中的实践研究作者:张崑来源:《建筑工程技术与设计》2014年第34期【摘要】在社会经济的推动下,我国建筑行业有了进一步发展,加上城市化进程加快,工程项目增多,建筑企业也越来越多,竞争日益加剧。
现代化建筑对质量、经济、环保、外型等方面都非常重视,为实现多功能化,新技术、新材料相继被应用其中。
尤其是新技术,在提高工程质量、保证施工安全、达到减震设计上起着关键性作用。
就目前而言,我国建筑业在技术上并未发生质的变化,其中,动力弹塑性时程分析技术虽然已经达到国际水准,但整体水平与国外相比尚有差距,需继续努力。
本文通过对动力弹塑性时程分析技术的阐述,重点对动力弹塑性时程分析技术在建筑结构减震设计中的实践应用进行了研究。
【关键词】动力弹塑性时程分析技术;建筑结构;抗震设计;实践研究高层建筑是当前建筑的主要形式,新材料、新技术的应用使得建筑质量提高,功能越来越齐全。
但其结构设计也更复杂,施工难度加大,因此对其抗震施工技术提出了更高的要求。
高层建筑的投资数额较大,周期也相对较长,而动力弹性时程分析技术是一项综合性较强的技术工作,涉及每一个环节,一旦出现问题,必将影响到施工质量。
从而延误工期,甚至引发安全事故,带来严重的损失。
所以,在施工过程中,必须加强建筑结构抗震设计中对动力弹塑性时程分析技术的应用,进而保证及时解决潜在的隐患。
1.动力弹塑性时程分析技术概述弹塑性时程分析方法可以有效的将结构作为弹塑性振动体系进行相应的分析,并通过对地震波数据在地面运动中的输入应用,可以有效的进行下一步的积分运算,进而可以得出地面加速度随着时间的变化而发生的变化,同时,还可以得出结构的内力与变形随着时间的变化而变化的整个过程。
动力弹塑性时程分析技术的应用通常有以下几个步骤:第一,通过对几何模型的建立,进而实现网格的划分工作;第二,对材料的本构关系进行确定,并根据各个构件自身的单元类型及材料类型的确定,进而对结构的质量、刚度及阻尼矩阵进行确定;第三,根据本场地的地震波,并对模型的边界条件进行定义,进而得出相应的计算结果;第四,根据计算所得出的结果进行进一步的处理工作,并根据处理的结果进行结构整体性可靠度的评估。
某超高层建筑结构弹塑性动力时程分析

某超高层建筑结构弹塑性动力时程分析
张琳;李晶
【期刊名称】《广东土木与建筑》
【年(卷),期】2010(000)012
【摘要】某工程是存在多项基本不规则项的复杂超高层建筑,文中采用弹塑性动力时程分析法,分析结构在罕遏地震作用下的变形特征、构件内力及剪力墙、连梁、框架柱及框架梁损伤等非线性动力响应;研究结构在罕遇地震作用下的整体抗震性能,找出薄弱部位和构件,为施工图设计中采取有针对性的加强措施来实现"大震不倒"的设防目标提供设计依据。
【总页数】3页(P11-13)
【作者】张琳;李晶
【作者单位】深圳市华阳国际工程设计有限公司,深圳518400
【正文语种】中文
【中图分类】TU973
【相关文献】
1.重庆某超高层住宅弹塑性动力时程分析 [J], 李松
2.基于绕轴矩阵算法的超高层弹塑性动力时程分析 [J], 张超;陶婷;王丹
3.某超限高层建筑结构弹塑性动力时程分析实例 [J], 李忻
4.弹塑性分析在超高层建筑结构设计中的应用 [J], 刘颖涛
5.弹塑性分析在超高层建筑结构设计中的应用 [J], 吴雨杨
因版权原因,仅展示原文概要,查看原文内容请购买。
YJK动力弹塑性时程分析详解
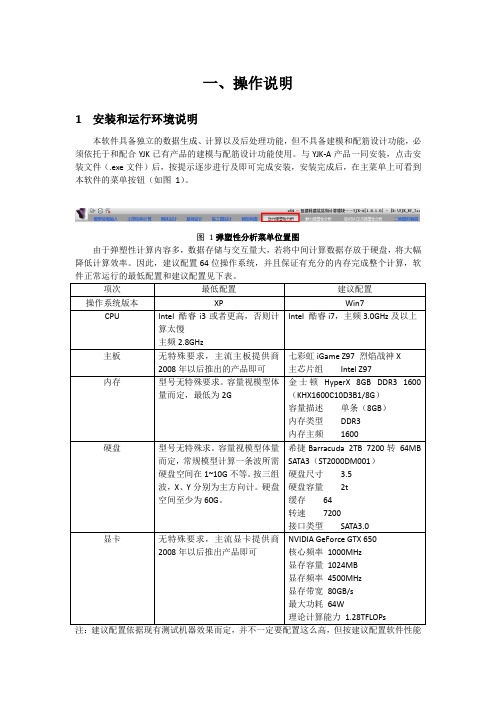
目标最佳。
2 弹塑性时程分析流程
完整的弹塑性时程分析过程如下图所示,程序提供下图所有功能模块,计算完成后以图 形和表格的方式输出超限结构弹塑性分析报告所用数据。
线弹性分析 与设计
分析与设计 施工图
选择地震波
3组或7组
弹塑性时程 分析
生成数据
含钢筋数据
动力方程求解
NewMark数 00200 -0.00200 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 0.00000 -0.00100 0.00000 -0.00000 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 0.00000 -0.00200 0.00200 0.00100 -0.00000 -0.00100 … 对话框中参数应按如下方式设置: 步长设置:0.02; 故数据起始行号:5,因前 5 行数据为说明行; 一行数据个数:5。
4.1.2 地震波选择
弹塑性动力时程分析结果,对地震波的依赖程度比较高。同一结构,采用不同的地震波, 计算结果可能有非常明显的差异。依据《高规》[4]5.5.1 条第 6 款:进行动力弹塑性计算时, 地面运动的加速度时程的选取、预估罕遇地震作用时的峰值加速度取值以及计算结果的选用 应符合该规程第 4.3.5 的规定。
弹塑性动力时程分析若干问题的分析与探讨

弹塑性 方 法 , 应 采 用 弹 塑性 动 力 时程 分 析 方 法 。 而
随着 建筑 功能 与师创 作水 平 的 日益 提 高 , 筑 结 构 的 形 态 日趋 建 复杂 。另 一方 面 , 人们 对 结 构 的安 全 性 与 经 济性 的 要求 也越 来越 高 , 导致结 构设 计难 度 越来 越大 , 传统 的一 些 简化分 析计 算手 段 已难 以满 足复 杂结 构 的设
第 3 3卷 第 5期
21 0 1年 1 O月
工 程 抗 震 与 加 固 改 造
Vo . 1 33. . NO 5 0c . 2 1 t OI
Ea t u k ssa gn e i g a d Rer ft n rhq a e Re itntEn i e rn n toit g i
计要 求 。此外 , 构 受 力 变形 过 程 本 来 就 是 一 个 非 结
[ 章 编 号 ] 10 —4 2 2 1 )50 7 —6 文 0 28 1 (0 0 — 40 1 0
弹 塑 性 动 力 时 程 分 析 若 干 问题 的 分 析 与 探 讨
5 剑( 长 深圳大学建筑设计研究院, 广东 深圳 580) 100
[ 摘 要 ] 分 析 并 探 讨 了弹 塑性 动力 时程 的 主 流 分 析 软 件 ( B Q S 关 于 混 凝 土 及 钢 管 混 凝 土 的 本 构 关 系 、 殊 情 况 下 单 A AU ) 特
弹塑性时程分析

弹塑性时程分析方法将结构作为弹塑性振动体系加以分析,直接按照地震波数据输入地面运动,通过积分运算,求得在地面加速度随时间变化期间内,结构的内力和变形随时间变化的全过程,也称为弹塑性直接动力法。
基本原理多自由度体系在地面运动作用下的振动方程为:式中、、分别为体系的水平位移、速度、加速度向量;为地面运动水平加速度,、、分别为体系的刚度矩阵、阻尼矩阵和质量矩阵。
将强震记录下来的某水平分量加速度-时间曲线划分为很小的时段,然后依次对各个时段通过振动方程进行直接积分,从而求出体系在各时刻的位移、速度和加速度,进而计算结构的内力。
式中结构整体的刚度矩阵、阻尼矩阵和质量矩阵通过每个构件所赋予的单元和材料类型组装形成。
动力弹塑性分析中对于材料需要考虑包括:在往复循环加载下,混凝土及钢材的滞回性能、混凝土从出现开裂直至完全压碎退出工作全过程中的刚度退化、混凝土拉压循环中强度恢复等大量非线性问题。
基本步骤弹塑性动力分析包括以下几个步骤:(1) 建立结构的几何模型并划分网格;(2) 定义材料的本构关系,通过对各个构件指定相应的单元类型和材料类型确定结构的质量、刚度和阻尼矩阵;(3) 输入适合本场地的地震波并定义模型的边界条件,开始计算;(4) 计算完成后,对结果数据进行处理,对结构整体的可靠度做出评估。
计算模型在常用的商业有限元软件中,ABAQUS、ADINA、ANSYS、MSC.MARC都内置了混凝土的本构模型,并提供了丰富的单元类型及相应的前后处理功能。
在这些程序中一般都有专用的钢筋模型,可以建立组合式或整体式钢筋。
以ABAQUS为例,它提供了混凝土弹塑性断裂和混凝土损伤模型以及钢筋单元。
其中弹塑性断裂和损伤的混凝土模型非常适合于钢筋混凝土结构的动力弹塑性分析。
它的主要优点有:(1) 应用范围广泛,可以使用在梁单元、壳单元和实体单元等各种单元类型中,并与钢筋单元共同工作;(2) 可以准确模拟混凝土结构在单调加载、循环加载和动力荷载下的响应,并且可以考虑应变速率的影响;(3) 引入了损伤指标的概念,可以对混凝土的弹性刚度矩阵进行折减,可以模拟混凝土的刚度随着损伤增加而降低的特点;(4) 将非关联硬化引入到了混凝土弹塑性本构模型中,可以更好的模拟混凝土的受压弹塑性行为,可以人为指定混凝土的拉伸强化曲线,从而更好的模拟开裂截面之间混凝土和钢筋共同作用的情况;(5) 可以人为的控制裂缝闭合前后的行为,更好的模拟反复荷载作用下混凝土的反应。
动力弹塑性时程分析的方法及其应用

型 , 目前 可 以进 行 P A的商用 计算软 件包 括 M D S 过 积 分 运 算 , 求 得 在 地 面 加 速 度 随 时 间 变 化 期 间 O IA / GN等 ,是将 剪力墙 简化 为两根 刚体梁 通过 非线性 弹 内 ,结构 的 内力和 变 形 随 时间 变化 的全 过程 ,也 称 E
大分地震也出现 了类似 的情况。相反,i 5 年墨西 标位移 或发 生破坏 ,将 此时 的结构 的变形和 承载 力与 97 大震不倒 ”的要 哥城地 震 中 i ~ 1 的许 多建筑 物遭 到破坏 ,而首 允许 值 比较 , 以此来 判断是否 满足 “ 6层 i
次采 用 了动力 弹塑 性分析 的一 座 4 4层 建筑 物 却安然 求 。 2. 算模 型 计 无 恙 ,1 8 9 5年该 建筑 又经 历 了一 次 8 i 地 震依然 . 级
( 深 圳 市 电予 院设 计 有 限 公 司 2 中 国石 油大 学 ) 1
【 摘要 】 本 文对现有 的弹塑性分析 方法进行 了概 述 ,重点介 绍 了动 力弹塑性时程分析 的理论 、优 点和 : 基本 方法 ,及 该 方法在 东莞一 实 际工程 中的成功 应用 ,对 于动 力弹塑性 时程分 析方 法在 高层 、特 别
形 。
裂或屈服 ;
历 史上 的多次 震 害也 证 明 了弹 塑性 分 析 的必 要
( 4 于开裂 或屈 服 的杆 件 ,对其 刚度进 行修 改 )对
性 :1 6 9 8年 日本 的十橱 冲 地震 中不 少按 等效 静 力方 后,再增加 一级荷载 ,又使得 一个或 一批杆件 开裂或
法进行抗震设 防 的多层钢 筋混凝 土结构遭到 了严重破 屈 服 ; ( 5 )不断 重复步骤 ( 、( ,直 至 结构达 到某一 目 3 4 ) ) 坏 ,1 7 年美 国 S n F r a d 9i a e n n o地 震 、 1 7 年 日本 95
高层建筑动力弹塑性时程分析方法研究

高层建筑动力弹塑性时程分析方法研究
张 小 方 ’
( 甘肃省建筑设计研究院 ,甘肃 兰 州 7 3 0 0 0 0)
【 摘 要】 近些年我 国高层建筑发展较快 ,怎样分析 高层 建筑
的抗震 性能成为 了重要 问题 ,时程分析可 以进一步判 断一栋建 筑物 的抗震 能力。本文介 绍 了动力弹塑性时程分析法 的作 用,指 出 了采
差。
( 4 ) 对工程技术人 员素质要求较高 从结构模型建立 , 地震波 选取 、材料 本构选 取、到参数 控制及庞 大计 算结果的整理及甄别都 要求技术人 员具有扎实 的专业素质 以及丰富的工程经验。 5 动力弹塑性时程分析方法计算 结果的处理 首先 要判断所 选多条地震波的计算结果是否基本一致 ,从而确 定所选地震 波的合理性。第二要查看各条地震波计算 的最大层间位 移角 能否满 足规 范的要求,这也是做弹塑性时程分析 的主要 目的 第三 , 在最大有害层间位移角 曲线中找到结构的薄弱层 ,出现开裂 、 塑性铰 的部位,帮助设计人员对这些部位采取加强措旌 ,提高其抗 拉和抗压承 载力,从而改善结构的抗震性能 。 ‘ 最后 ,结构最大层 问 位 移角出现 位置 并不一定表示该层就是薄弱层 ,结构薄弱层 的判断 宜以结构 最大有害位移 角出现 的位置为准 。
6 结 论
( 2 ) 选择使 用于本场地的地 震波 不同的 地震 波会对弹性 动力 对程分析的计算结果产生一定的影响,有时影响较大 嗣此合理的 选波 ,往往成为采用这计算方法的关键 本文 建议 ,首先通过 弹性 时程分析得到基底剪力,然后与振型分解反应谱法进行对比,筛选
出合适的地震波进行弹塑性动力时程 分析 ‘ ( 3 ) 确 定混凝土、钢材两种材料的滞回; 构关系 , 其中钢材的 本构关系常采用双线性本构关系。棍凝 土常采用三线性本梅关系0 ( 4 ) 定义计算过程各参数 。 ( 5 ) 计算完成后查看计算结果, 找 出结构 的最大层 间及有害层 间位移角 的数值 ,结构破坏情况 ,从而可 以评估结构的抗震能力 。
建筑工程结构动力弹塑性时程分析

建筑工程结构动力弹塑性时程分析摘要:本文主要对深圳某建筑工程结构动力弹塑性时程情况进行了分析,包括弹塑性分析方法、单元类型及有限元模型、抗震情况等,最后对该工程的总体抗震性能作出评价,并提出建议。
关键词:结构; 动力弹塑性; 时程分析; ABAQUSAbstract: this paper mainly to the shenzhen a building engineering structure dynamic elastic-plastic time history analysis, including elasto-plastic analysis method, the unit type and finite element model, such as seismic situation, and finally, the engineering of the overall seismic performance evaluation to make, and puts forward some Suggestions.Keywords: structure; Dynamic elastic-plastic; Time history analysis; ABAQUS 工程概况该项目位于深圳地铁3号线六约站原检修主厂房的上部,为12层的保障性住房。
原检修主厂房为纯框架结构水平向跨度为12m,竖向跨度为18m及21m。
层高12.3m,基础为人工挖孔桩。
本次设计是在原有已完工建筑基础上进行。
先设一层转换层,层高7.2m,然后是塔楼部分,均为12层,结构形式为剪力墙结构。
工程特点:一是转换结构,塔楼没有墙肢落地;二是大跨结构,混凝土转换梁最大跨度达21m;三是竖向刚度突变,首层层高12.3m,第二层层高7.2m。
结构动力弹塑性时程分析(一)弹塑性分析方法目前常用的弹塑性分析方法从分析理论上分有静力弹塑性(pushover)和动力弹塑性两类,从数值积分方法上分有隐式积分和显式积分两类。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的应力 - 应变关系曲线来把握混凝土塑性损伤模型 的主要概念 。 如图 1 所示, 曲线 OAC 代表单轴单向受拉的应 曲线 OLK 代表单轴单向受压的应力 力 - 应变曲线, - 应 变 曲 线, 曲 线 OABDEFHIJ 代 表 单 轴 特 征 荷 载 作用下的应力 - 应变曲线 。 直线 OA 段代表单轴受 拉的弹性阶段, 当应变增 大 并 超 过 A 点 所 对 应 的 应 混凝土受拉 屈 服, 并 进 入 受 拉 塑 性 区; 当 应 变 变时,
1
引言 随着建筑功能与美观等方面要求的不断增加及
标可在基本目 标 下 进 一 步 细 化 与 提 高 。 一 般 来 说, 在安全与经济双重目标要求下, 结构在小震状态下, 基本上处于弹性状态, 变形也较小, 此时采用线弹性 方法分析 内 力 与 变 形 是 可 行 的 。 结 构 在 中 震 状 态 下, 少部分构件已进入塑性状态且变形加大 。 此时, 若仍然采 用 线 弹 性 方 法 来 分 析, 则 存 在 较 大 误 差。 结构在大震状态下, 部分构件已进入塑性状态, 并产 生大变形, 其 P-Δ 效 应 加 剧, 几 何 非 线 性 程 度 加 大, 故计算分析不能采 用 线 弹 性 方 法, 也不宜采用静力 弹塑性方 法, 而 应 采 用 弹 塑 性 动 力 时 程 分 析 方 法。 所以说弹塑性动力时程分析方法是实现结构大震与 中震下结构性能目标的基本分析方法 。 3 弹塑性动力时程分析的基本原理与基本过程 结构 分 析 的 主 要 目 标 是 获 取 结 构 的 位 移 场 、 应 变场及应力场, 三者之间具有密切的关系, 故仅需获 得结构位移场即 可 。 通 过 离 散 化 的 方 法, 按粘性阻 尼理论, 可将结构的弹塑性动力学方程表达如下: ¨ + Cu + Ku = F ( t ) Mu ( 1) 式中: u 为节点位移向量, 结构连续体的 位 移 场 可 通
Abstract : In this paper ,several problems of elastic-plastic dynamic time-history about constitutive relation of concrete and steel tuberestrained concrete ,selection of element in special case ,influence of higher modes damping ratio ,selection of algorithm under the load of gravitity are analyzed , and the actual solution are given. Besides , some suggestions about using the software of elastic-plastic dynamic time-history analysis are put forward. Keywords : elastic-plastic dynamic time-history analysis ; concrete damaged plasticity ; damping ; explicit algorithm Email : sword1963@ 163. com
[收稿日期] 2010 0617
第 33 卷第 5 期
张
剑: 弹塑性动力时程分析若干问题的分析与探讨
· 75 ·
过节 点 位 移 向 量 求 得; M 为 质 量 矩 阵; C 为 阻 尼 矩 阵; K 为刚度 矩 阵; F 为 外 力 向 量 函 数; t 为 时 间 变 ¨ g, ¨ g 为地面运动 F ( t ) = - Mu 量, 地震作用时, 其中 u 即地震波 。 加速度, 由于 在 外 力 作 用 下, 结构可能具有几何非线性 与本构 非 线 性 ( 弹 塑 性 本 构 是 非 线 性 本 构 中 的 一 种) , 结构 的 形 态 、 刚 度 矩 阵 及 阻 尼 矩 阵 不 断 变 化, 使得上述方程 的 求 解 非 常 复 杂 。 就 刚 度 矩 阵 而 言, 它是由单元刚度 矩 阵 K e 组 装 而 成 。 根 据 弹 塑 性 力 学原理, 单元刚度矩阵可表示为: Ke =
| ) = u u|
( t + Δ t)
( t- 2 )
Δt
+
( t + Δ t)
( t)
)
¨ | u
( t)
= u ( t) + Δ t |
| u
( t+ 2 )
Δt
∫[B] [D][B]dv
T e
( 2)
第二步: 单元应力计算 ① 由节点位移, 可求单元位移场, 由此可求出应 变场及应变率场, 进一步可求出各处应变增量 dε 。 ② 根据本构关系计算应力 σ dε) σ | ( t + Δ t) = f ( σ | ( t) , ③ 由 I = C u + Ku 可求节点内力 I | ( t + Δ t) 第三步: 将时间 t 变为( t + Δ t ) , 返回第一步 。 由上 述 内 容 可 知, 地震作用下弹塑性动力时程 单元选用 、 分析的主要问题是材料本构关系的建构 、 大变形的描述 、 地震波选取 、 阻尼选取及算法选择 。 4 ABAQUS 弹塑性动力时程分析 ABAQUS 是目前国际上最先进的大型通用有 限 它的非线性功能达到世界领先水 元分析软件之一, 平, 从而使其具有力学系统仿真的功能, 它广泛应用 我国工程界将它 于工程和科研各 个 领 域 。 近 年 来, 成功应用于弹塑性 动 力 时 程 分 析, 其分析结果得到 业内专家们的广泛认可 。 4. 1 材料本构关系 ABAQUS 自带丰富的本构关系模型, 可描述混凝 土、 钢材 、 岩 土、 高分子材料等物质的应力与应变关 ABAQUS 还提供用户材料接口程序 UMAT 系 。 另外, 及 UVMAT , 因此, 可使用户自定义材料本构关系 。 对建 筑 结 构 来 说, 主要涉及混凝土与钢材两种 材料, 钢材本构关系 可 采 用 二 折 线 或 三 折 线 弹 塑 性 由于钢 材 质 地 均 匀 、 性 能 稳 定, 其动力滞 本构关系, 回模型也较为简单, 本文重点描述混凝土的本构关 系 。 ABAQUS 软件中, 混凝土本构关系模型有混凝 土弥散开裂模型 、 混凝土开裂模型及混凝土塑性损 伤 模 型 。 其 中 混 凝 土 塑 性 损 伤 模 型 ( Concrete Damaged Plasticity ) 可 描 述 混 凝 土 受 动 力 往 返 作 用
B] 式中: [ 为几 何 矩 阵, 通 过 几 何 矩 阵, 由位移可求 D]为 本 构 矩 阵, 得应变; [ 通 过 本 构 矩 阵, 由应变可 [B] 、 [D]矩 阵 是 不 断 求得应力 。 由于非线性效应, 变化的 。 对弹塑性 问 题 而 言, 一旦知道任何时刻的 本构矩 阵, 通 过 积 分 点 的 数 值 积 分, 即可 几何矩阵 、 得到单元刚度矩 阵 。 也 就 是 说, 各积分点无论是处 于弹性或塑性状态, 都可以得到对应时刻的单元刚 即可逐步求解得到节点 度矩阵 。 再通过边 界 条 件, 位移向量, 进一步可求得任意一处的位移 、 应变及应 实现分析的目标 。 在上述离散化过程中, 最一般 力, 其位移模式可以是线性的 的单元是三维实体 单 元, 或者是二次的, 视 精 度 与 效 率 的 要 求 而 定。 在 具 体 问题中, 由于受力与变形机制的特殊性, 导致位移场 与应力场具有一些特殊性, 合理利用这些特殊性, 并 作出相应的假定, 可 大 大 提 高 计 算 效 率 和 精 度。 如 采用直法线等假定 形 成 板 单 元, 采用平截面等假定 形成梁单元等 。 对弹 塑 性 动 力 方 程 的 求 解, 一般可分为两种求 解算法: 即隐 式 与 显 式 。 隐 式 算 法 常 采 用 Newmark 法, 但它需要求解 全 区 域 的 联 立 方 程, 因 此, 它不但 求解过程 复 杂, 而 且 容 易 导 致 结 果 不 收 敛 的 情 况。 显式算法采用中心 差 分 法, 对动力学方程进行时间 由一个时间增 量 步 的 动 力 学 条 件 求 解 下 一 时 积分, 间增量步的动力学条件, 当时间增量充分小时, 不会 可获得问题的解答, 因此显 产生结果不收敛的情况, 式算法特别适合弹 塑 性 动 力 时 程 分 析, 它的基本过 程如下 。 先将式( 1 ) 改写如下: ¨ = F ( t) - C u - Ku Mu + Ku I = Cu 令: P = F ( t ) ,
则式( 3 ) 变为: ¨ = P - I Mu 第一步: 节点变量求解 ① 动力平衡方程 ¨ | ( t) = ( M ) u ② 对时间显式积分 | u
( t+ 2 )
Δt
( 4)
-1
(P|
( t)
- I|
( t)
)
M 为对角矩阵, 式中, 易于求解 。 ( Δt | + Δt | 2
( t + Δ t)
第 33 卷第 5 期 2011 年 10 月
工程抗震与加固改造 Earthquake Resistant Engineering and Retrofitting
Vol. 33 , No. 5 Oct. 2011
[文章编号] 10028412 ( 2011 ) 05007406
弹塑性动力时程分析若干问题的分析与探讨
Research on Issues of Elasticplastic Dynamic Timehistory Analysis
Zhang Jian ( Shenzhen University Institute of Architectural Design & Research , Shenzhen 518000 , China )
