弹塑性时程分析实例
结构大震弹塑性时程分析中的能量反应分析
第47卷第5期2014年5月土木工程学报CHINA CIVIL ENGINEEＲING JOUＲNALVol．47May No．52014基金项目：北京市自然科学基金（8122040）作者简介：温凌燕，博士，高级工程师收稿日期：2012-02-14结构大震弹塑性时程分析中的能量反应分析温凌燕1娄宇1聂建国2（1．中国电子工程设计院，北京100142；2．清华大学，北京100084）摘要：采用ABAQUS 对23个钢管混凝土框架-钢筋混凝土核心筒结构分析模型进行了大震弹塑性时程分析，分析模型变量为楼层总高度、地震波及地震波峰值加速度。
通过对23个分析模型中得到的各种能量项数值的统计与分析，结合现行规范中结构损伤程度的评估标准，对输入能与地震加速度及结构损伤程度的关系、不同结构损伤程度下塑性耗能在构件中的分配、阻尼耗能比例和塑性耗能比例与结构损伤程度的关系进行了研究。
研究成果为能量法在结构地震反应中的应用及钢管混凝土框架-核心筒结构体系的设计提供参考。
关键词：大震；弹塑性时程；输入能；塑性耗能；阻尼耗能；结构损伤；钢管框架-核心筒中图分类号：TU375．4文献标识码：A文章编号：1000-131X （2014）05-0001-08Energy-based analysis in elastic-plastic time-history analysisof structure under large earthquakeWen Lingyan 1Lou Yu 1Nie Jianguo 2（1．China Electronics Engineering Design Institute ，Beijing100142，China ；2．Tsinghua University ，Beijing100084，China ）Abstract ：Elastic-plastic time history analyses of 23CFST frame-reinforced concrete core wall structure models under large earthquake have been conducted by using ABAQUS ，and the studied model variables include the total structural height ，earthquake wave and peak acceleration of wave．Based on the statistical analysis of the energy items from 23examples and combined with the evaluation standard on structural damage degree in the present specifications ，the relation between input energy and wave acceleration or structural damage degree ，distribution of plastic energy dissipation in structural members under different structural damages ，relations between the ratio of damping energy dissipation or plastic energy dissipation to input energy and the structural damage have been studied．Ｒesearch results may provide references for the application of energy analysis method in structural seismic analysis as well as the design of CFST frame-core wall structures．Keywords ：large earthquake ；elastic-plastic time-history ；input energy ；plastic energy dissipation ；damping energy dissipation ；structure damage ；CFST frame-core wall E-mail ：wenlingyan@ceedi．cn引言结构地震反应的能量分析方法是一种能较好地反映结构在强震作用下的全过程及其自身弹塑性性能的方法。
某稀柱筒体结构弹塑性时程分析
应用见 缝插针 的方式在人 行道 窄的路段 栽植植 株冠 幅小 的
【 ］ 孟欣慧 ． ３ 菏泽城 区道 路绿地 现状调查 及规划 设计研 究 ［ ］ Ｄ．
济南 ： 山东农业大学 ，： ６ ２０ ． ０
观 花或观干灌木 ； 行 道路 宽 的位置 交 叉种植 变 叶乔 木或 人 灌 木 ， 富的乔灌 木搭 配烘 托 老城 区历史 风格 ； 外 ， 以 丰 另 可 在 街区空间可 以容纳 的范 围 内添置与街 区风 格相宜 的悬挂
张萌 萌
（ 济 大 学 结构 工 程 与 防 灾 研 究 所 ， 上 海 同 ２ ０９ ０ ０ ２）
【 摘
要】 针对某稀柱筒体结构 ， 采用 Ｎ ｓ Ａ ｏａ Ｄ有限元软件建立整体结构分析模型。通过 ７ Ｃ 度多遇和 ７度
罕遇烈度下 的弹塑性 时程分 析 ， 究 了该结 构的变形 、 研 内力 、 破坏情况 的发展历 程 ， 算结果表 明 ， 构可 以满 足 计 结
“ 小震不 坏 ， 大震不倒 ” 的抗 震设防要求 ； 体构件破坏顺序较 为合理 ， 筒 能较好 的耗散地震能量 。
超高层连体结构弹塑性时程分析
（ Ｃ Ｉ Ｔ １ Ｃ Ｇ ｅ ｎ ｅ ｒ ａ ｌ Ｉ ｎ ｓ ｔ ｉ ｔ ｕ ｔ ｅ ｏ ｆＡ ｒ ｃ ｈ ｉ ｔ ｅ ｃ ｔ ｕ ｒ ａ ｌ Ｄ ｅ ｓ ｉ ｇ ｎ Ａ ｎ ｄ Ｒ ｅ ｓ ｅ ａ ｒ ｃ ｈ Ｃ ｏ ．Ｌ ｔ ｄ ，Ｗ ｕ ｈ ａ ｎ ４ ３ ０ ０ １ ４ ， Ｃ ｈ ｉ ｎ ａ ）
王红 军， 张达 生 ， 杨 竞 （ 中 信建筑设计研究总院有限公司， 湖 北 武汉 ４ ３ ０ ０ １ ４ ）
【 提 要］ 本文以一超高层连体结构实 际工程为 例 ， 采 用 Ｍｉ ｄ ａ ｓ Ｂ ｕ ｉ ｌ ｄ ｉ ｎ ｇ有 限 元 软 件 对 该 结 构 进 行 详 细 弹 塑 性 时 程 计 算 分
ａ ｎ ｇ ｌ ｅ ｏ ｆ ｍｏ ｎｏ ｍｅ ｒ ｍｏ ｄ ｅ ｌ ｉ ｓ １ ／１ ０ ２，ａ ｎ ｄ ｔ ｈｅ ｃ ｏ ｎ ｎ ｅ ｃ ｔ ｏ ｒ ｍｏ ｄ ｅ ｌ ｉ ｓ １ ／１ ３５，ｂ ｏ ｔ ｈ ｍｅ ｅ ｔ ｔ ｈ ｅ ｓ ｐ ｅ ｃ ｉ ｆ ｉ ｃ ａ ｔ ｉ ｏ ｎ ｒ ｅ ｑ ｕｉ ｒ ｅ ｄ ｍｉ ｎｉ ｍｕｍ ｓ ｔ ａ ｎ ｄ ａ ｒ ｄ １ ／１ ００．
［ 文章编号 】 １ ０ ０ ２ ． ８ ４ １ ２ （ ２ ０ １ ４ １ ０ １ — ０ ０ １ ０ ￣ ８
YJK动力弹塑性时程分析详解
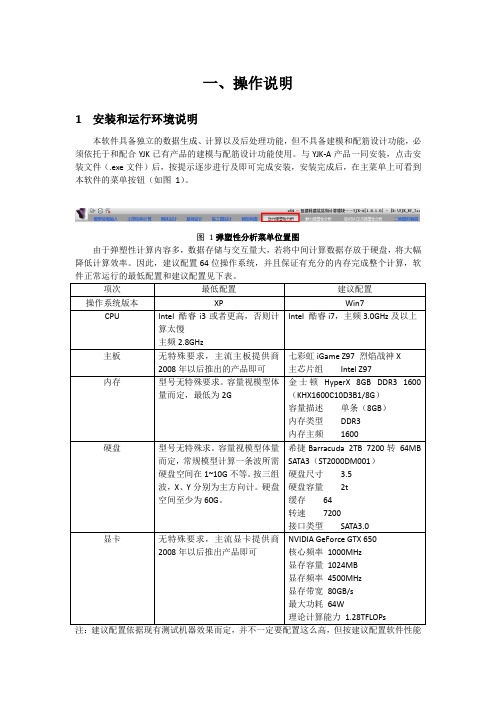
目标最佳。
2 弹塑性时程分析流程
完整的弹塑性时程分析过程如下图所示，程序提供下图所有功能模块，计算完成后以图 形和表格的方式输出超限结构弹塑性分析报告所用数据。
线弹性分析 与设计
分析与设计 施工图
选择地震波
3组或7组
弹塑性时程 分析
生成数据
含钢筋数据
动力方程求解
NewMark数 00200 -0.00200 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 0.00000 -0.00100 0.00000 -0.00000 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 0.00000 -0.00200 0.00200 0.00100 -0.00000 -0.00100 … 对话框中参数应按如下方式设置： 步长设置：0.02； 故数据起始行号：5，因前 5 行数据为说明行； 一行数据个数：5。
4.1.2 地震波选择
弹塑性动力时程分析结果，对地震波的依赖程度比较高。同一结构，采用不同的地震波， 计算结果可能有非常明显的差异。依据《高规》[4]5.5.1 条第 6 款：进行动力弹塑性计算时， 地面运动的加速度时程的选取、预估罕遇地震作用时的峰值加速度取值以及计算结果的选用 应符合该规程第 4.3.5 的规定。
MIDAS钢筋混凝土框架动力弹塑性分析
例题动力弹塑性分析2 例题. 钢筋混凝土框架动力弹塑性分析概要此例题将介绍利用MIDAS/Gen做动力弹塑性分析的整个过程，以及查看分析结果的方法。
此例题的步骤如下:1.简要2.设定操作环境及定义材料和截面3.用建模助手建立模型平面4.生成框架柱5.楼层复制及生成层数据文件6.定义边界条件7.输入楼面荷载8.定义结构类型9.定义质量10.定义配筋11.定义及分配铰特性值12.输入时程分析数据13.运行分析14.查看结果例题 动力弹塑性分析31.简要本例题介绍使用MIDAS/Gen 的动力弹塑性分析功能来进行抗震设计的方法。
例题模型为二层钢筋混凝土框架结构。
(该例题数据仅供参考) 基本数据如下：轴网尺寸：见平面图 柱: 300x300 主梁： 200x300 混凝土： C30 层高： 一～二层 ：3.0m 地震波： El Centro分析时间： 12 秒图1 分析模型例题动力弹塑性分析4 2.设定操作环境及定义材料和截面在建立模型之前先设定环境及定义材料和截面1.主菜单选择文件>新项目2.主菜单选择文件>保存:输入文件名并保存3.主菜单选择工具>单位体系:长度 m, 力 kN图2 定义单位体系4.主菜单选择模型>材料和截面特性>材料：添加：定义C30混凝土材料号：1 名称：C30 规范：GB(RC)混凝土：C30 材料类型：各向同性5.主菜单选择模型>材料和截面特性>截面：添加：定义梁、柱截面尺寸注：也可以通过程序右下角随时更改单位。
例题 动力弹塑性分析5图3 定义材料图4 定义梁、柱截面例题动力弹塑性分析6 3.用建模助手建立模型主菜单选择文件>新项目主菜单选择模型>结构建模助手>框架：输入：添加x坐标，距离3，重复2；添加z坐标，距离3，重复2；编辑： Beta角，90度；材料，C30；截面，200x300；生成框架；插入：插入点，0，0，0；Alpha，－90。
1王亚勇-弹塑性分析输出结果解读(贵阳2015)
30000
US052 US169 AS735-1 规范谱
X向
Y向
检验-底部剪力对比(满足规范要求)
规范谱 X向 Y向 US052 US169 S735-1 最大值/ 规范谱 87% 94% 最小值/ 规范谱 105% 72% 平均值/ 规范谱 98% 86%
30684.3 31527.5 32489.4 26742.6 28526.1 26916.6 26380.7 20581.3
40 US031 30 20
加速度（gal）
10 0
加速度（gal）
20 40 t (sec) 60
-10 -20 -30 40 -40 30 0
20
10 0 -10 -20 US032
80 -30
-40 0
100
20 40 t (sec) 60 80
加速度（gal）
10 0 -10 -20 -30 -40 0 20 40 60 80
L033-地震波输入外框架柱型钢M桁架Mises应力
XI’AN IFC ARCHITECTURAL DESIGN
L033-地震波输入外框架梁Mises应力
“超限汇报” XI’AN IFC ARCHITECTURAL DESIGN
错误的选波方法 - Tg
• • • • 挑选”小“的 不分场地类别 不分地震分组（近、远震） 由一条地震加速度记录的反应谱计算Tc： SA=ώPSV=（2π/TC）PSV TC= 2π（PSV/SA），是确定性的。 而规范反应谱是由统计平均得到，所以
Tg ≠ TC
小震弹性
输入地震波: 二组实际地震记录和一组人工模拟加速度时程（AS735、US052和 US169)
时间 （s）
MATLAB弹塑性时程分析法编程(参照类别)
MATLAB编程：format short g;F(21,14)=0;xg=[0 600 1100 1500 2100 2500 2900 350 2050 1500 1000 600 200 -700 -1300 -1700 -2000 -1800 -1500 -700 -250 200 -100 0 0 0];xg1=xg*2200/max(xg);xg2=diff(xg1);f(14)=0;f(4)=9000;t=0.05;m=250;c=240;for i =1:21f(3)=xg2(i);f(1)=0.05*i-0.05;f(2)=xg1(i);f(6)=-m*(f(3)-6*f(12)/t-3*f(11))+c*(3*f(12)+f(11)/2*t); f(5)=f(4)+6*m/t^2+3*c/t;f(7)=f(6)/f(5);f(9)=3/t*f(7)-3*f(12)-0.5*f(11)*t;f(8)=6/0.05^2*f(7)-6/0.05*f(12)-3*f(11);f(13)=f(2)+f(11);f(14)=f(13)*m;F(i,:)=f(1,:);f(10)=f(10)+f(7);f(12)=f(12)+f(9);f(11)=f(11)+f(8);if abs(f(10))>2&F(1,7)*f(7)>0f(4)=0;else f(4)=9000;endenda=max(abs(F(:,13)));b=max(abs(F(:,14)));Fabxlswrite('表格2.xls',F)计算书：课程设计计算书（题二）根据加速度调幅公式：m i a t a a a /)(max ,00*=)/(29002902s mm Gal a m ==得：29/)(222900/)(22000i i t a t a a =*= )(i t a =[0 600 1100 1500 2100 2500 2900 350 2050 1500 1000 600 200 -700 -1300 -1700 -2000 -1800 -1500 -700 -250 200 -100 0 0 0];所以经调幅后为0a =[0 455.2 834.9 1138.5 1593.9 1897.5 2201.1 265.7 1556.0 1138.5 759 455.4 151.8 -531.3 -986.7 -1290.3 -1518 -1366.2 -1138.5 -531.3 -189.8 151.8 -75.9 0 0 0 ]2.45502.455''1''2=-=-U U7.3792.4559.834''2''3=-=-U U依次类推可以求出地面运动加速度的差值。
精编弹塑性时程分析法资料
服点，后续反向加载时直线指向所经历过的最大位移点。 ④ 中途卸载时，卸载刚度取 k1。
《工程结构抗震与防灾》电子教案 东南大学 源自幼亮§4 弹塑性时程分析法
9
2. 双线型模型力学描述：
设 P(Ui ) 、U i 表示ti 时刻结构的恢复力与变形，则在ti1时刻刚度退化双线
P(Ui ) P(U7 )
刚度降低系数为
4
k4 k1
Py U yk1
故
P(U i1 )
P(U3)
P(U
7
)
Py Uy
(U i1
Py Uy
(U i1
U3) U7
)
（4.1.11）
《工程结构抗震与防灾》电子教案
东南大学
丁幼亮
§4 弹塑性时程分析法
U 0 ，U U6
初始条件为
U i U 6 ， P(U i ) P(U 6 ) 0
刚度降低系数为
P(U 2 )
(U 2 U 6 )k1
故
P(U i1 )
P(U 2 ) U2 U6
(U i1
U6 )
（4.1.7）
需要指出，式（4.1.2）～式（4.1.7）中，U 2 、 P(U 2 ) 、U 3 、U5 、 P(U5)
(1) 在弹性阶段,K 是定值,不随变形而变化. (2) 在弹塑性阶段,K 值随结构变形状态不同而改变。 (3) 由于地震下结构变形为一个循环往复的过程，因此 K 值随着变形也是
个循环往复的过程。
因此，弹塑性时程分析法必须首先确定刚度与变形之间的关系，
北京大兴国际机场南航基地1号机库大厅弹塑性时程分析
第51卷第3期2021年2月上建筑结构Building StructureVol．51No．3Feb．2021DOI ：10.19701/j．jzjg．2021.03.010作者简介：曾一，博士研究生，Email ：meishuzengyi@163．com ；通信作者：潘鹏，博士，教授，Email ：panpeng @tsinghua．edu．cn 。
北京大兴国际机场南航基地1号机库大厅弹塑性时程分析曾一1，胡妤2，张东彬1，赵伯友2，潘鹏1（1清华大学土木工程系，北京100084；2中国航空工业规划设计研究院，北京100120）［摘要］为充分考察北京大兴国际南航基地1号机库大厅结构抗震性能，采用ABAQUS6.11对结构进行弹性时程分析和弹塑性时程分析，分析中采用ABAQUS 提供的材料本构模型和用户自定义材料本构模型，计算了小震和大震作用下机库大厅的响应。
计算结果表明：小震和大震作用下，机库大厅的柱顶最大位移角均小于规范限值。
网架整体保持弹性，局部与柱顶相连部分有轻微屈曲；工字形双肢格构柱保持弹性，多肢格构式钢管混凝土柱的柱底有轻微屈服；格构柱柱间防屈曲支撑有轻微屈服，大门角柱普通支撑屈曲失稳。
多肢格构式钢管混凝土柱和大门中柱的混凝土历史最大压应变均小于峰值应变。
由于结构X 方向长度较长，在计算的过程中，考虑了行波效应对结构的影响。
大震作用下，考虑行波效应后，整体结构最大柱顶位移角有所增加，但依然满足规范限值。
［关键词］北京大兴国际机场；机库大厅；弹塑性时程分析；行波效应；大跨空间网架中图分类号：TU318文献标识码：A文章编号：1002-848X （2021）03-0056-06［引用本文］曾一，胡妤，张东彬，等．北京大兴国际机场南航基地1号机库大厅弹塑性时程分析［J ］．建筑结构，2021，51（3）：56-61．ZENG Yi ，HU Yu ，ZHANG Dongbin ，et al．Elasto-plastic time history analyses of No．1hangar hall of China Southern Airlines base in Beijing Daxing International Airport ［J ］．Building Structure ，2021，51（3）：56-61．Elasto-plastic time history analyses of No．1hangar hall of China Southern Airlines basein Beijing Daxing International AirportZENG Yi 1，HU Yu 2，ZHANG Dongbin 1，ZHAO Boyou 2，PAN Peng 1（1Department of Civil Engineering ，Tsinghua University ，Beijng 100084，China ；2China Aviation Planning and Construction Development Co．，Ltd．，Beijing 100120，China ）Abstract ：In order to fully investigate the seismic performance of the NO．1hangar hall of China Southern Airlines base in Beijing Daxing International Airport ，the elastic time-history analysis and elasto-plastic time-history analysis of the structure were carried out by ABAQUS 6.11，and the response of hangar hall under small earthquakes and rare earthquakes was calculated．The material constitutive model provided by ABAQUS and user-defined material constitutive model were used in the analysis．The results show that the maximum story drift angle of the column top of hangar hall is less than the limiting value given in the code under small earthquakes and rare earthquake．The space truss remains elastic as a whole ，and the part connected to the top of the column is slightly buckled ；the I-shaped double-leg lattice column remains elastic．The column bottom of the multi-leg lattice concrete-filled steel tube column yielded slightly ；the BＲB between the lattice column columns yielded slightly ，and the gate corner column ordinary support buckled instability．The maximum historical compressive strains of concrete in the multi-leg lattice concrete-filled steel tube column and the central column of the gate are less than the peak strain．Because the span in X direction of structure is so large ，the traveling wave effect on the structure is also considered in the calculation process．Under the action of a rare earthquake ，considering the traveling wave effect ，the maximum story drift angle of the overall structure increases ，but it still can meet the limiting value of code．Keywords ：Beijing Daxing International Airport ；hangar hall ；elasto-plastic time history analyses ；traveling wave effect ；long-span space truss1工程概况北京大兴国际机场南航基地1号机库大厅（简称机库大厅）是现有的世界上跨度最大的机库，其总跨度达到了404.5m 。
动力弹塑性时程分析技术在建筑结构抗震设计中的应用
动 力弹塑 性时程分 析技术在 建筑结 构抗 震设 计 中的应
参考文献
［ １ 】 闫澈 ，孙 东红．循环流 化床锅 炉 电厂燃料 系统设计．东北电
力 学 院 学报 ， １ ９ ９ ５ 年１ ２ 月
用》 的主要读者对象 为专业的建筑设计 师、施工人员及高校相 关专业 的师生。
虑 ，适应煤种变化的能 力较小 ，易存在 易堵、过破碎和不 能完全破碎情况 ，进而造成锅炉燃烧不稳定 ，煤耗偏高，
排 渣 困难 ，锅 炉 热效 率 下 降 ，除 尘 器 负荷 增加 ，排 灰量 及
飞灰含碳量增大 ，细灰综合利用难度加大等问题 。采用破 碎机前增加 筛分及破碎机 后增加检查筛措 施 ，能有效改 善破碎机使用工况 ，控制入炉煤粒径 ，最终改善锅炉燃烧 效果 ，对存在类似情况的电厂提供一条新的解决 问题的途
中 国科 技信 患 ２ ０ １ ４年笼 ０ ２期 ・ Ｃ Ｈ Ｉ Ｎ Ａ Ｓ Ｃ Ｉ Ｅ Ｎ Ｃ Ｅ ＡＮ Ｄ Ｔ Ｅ Ｃ Ｈ Ｎ ＯＬ ＯＧ Ｙ Ｉ Ｎ Ｆ ＯＲ ＭＡ Ｔ Ｉ ＯＮ Ｊ ａ ｎ 。 ２ ０ １ ４
推 广 技 术
仓 的有 效 容积 １ ５ ０ ｍ ，能 储 存８ 小 时运 行 时产 生 的矸 石 。矸
，
动力弹 塑性 时程分析技术在 建 筑结构抗震设计 中的应用
烟气中粉尘的浓度降低 ，从而实现节能、减排 、增效的 目
的。
６ 经验总结
６ ． １ 检查筛上物后返料需增加一级除铁器 ，主要是为 了防止破碎机中锤头等铁件脱落会返 回系统 ，进而造成破 碎机损坏。实际安装时 ，由于增加的返料系统转运环节较 多 ，易出现故障 ，返料系统并未安装 ，从检查筛上物进入 矸 石 仓 的物 料 来 看 ，也 多 是石 头 ，对 保 护破 碎 机 、运 营 方 便 、节省投资的角度来看也是很有益处的。 ６ ． ２ 增加筛分同时也增加了运行中堵煤环节，采用不 易堵煤的筛子 ，如 白清洁滚筒筛可有效减少这类情况的发
建筑结构爆破地震反应弹塑性精细时程分析
建筑结构爆破地震反应弹塑性精细时程分析[摘要]根据爆破的地震影响下的建筑的结构安全方面评价的分析，提出使用时程的分析方式进行整体的评价爆破方面的地震波安全程度，成立比较精确的结构弹塑性方面的动力研究结构的方式，制定了建筑结构中的爆破地震的反应中弹塑性的时程研究过程。
本文就建筑机构爆破地震反应弹塑性精细时程进行分析。
[关键词]建筑结构爆破地震弹塑性精细时程中图分类号：tu973.2 文献标识码：a 文章编号：1009-914x （2013）10-0129-01建筑的结构在爆破的地震波的影响中作出的安全评价长久以来都是人们非常重视的问题。
一些爆破的安全制度中也有很的明确规定，要将爆破的地震波动频率的峰值进行安全地振动的速度要求，但是地震波动的速度与主要频率的选择和采用都有着很大的困难。
现在所设计的结构都是根据抗震的规则来进行预防的设置的，但爆破的地震和自然的地震还是有着非常明显的不同。
必须采用时程的分析研究，才可以精准地断定爆破地震的状况下，结构产生动力的反应，从而进行全方位爆破震波的安全性的评估。
爆破的振动产生的破坏其实就是动态的随机的破坏情况。
从动力学的角度研究结构振动的动力反应，这个已经是分析振动对结构造成破坏的有效途径。
使用成熟一点的响应谱的理论方式来研究结构体处在不一样的动力环境中的爆破振动的反应，并且得到了一些成果。
但是，响应谱的理论是根据单个的自由程度系统的弹性的动力进行研究，不可以完全地表现出爆破时地震波对多个自由度的系统弹塑性的动力特点。
将实际测量的爆破的地震记录与爆破的震波模仿当作基础，通过时程的研究方式与有限元的原理研究结构将进行爆破震波与自然震波的环境中所出现的动力反应的不同。
但这样的方式都差分近似，并且对时间都特别地敏锐，并且精确度也不够高，在计算的时候会遇到一些问题。
1、结构的爆破地震响应中弹塑性的动力研究（一）结构中爆破地震响应中弹塑性的动力研究通过爆破的地震波的影响，结构体通常会从弹性的形态步入到弹塑性的形态，分析弹塑性的结构系统在爆破的地震环境里面的动力影响是非常有价值的，使用机制的质量方式或者是有限元的方式，获得n个自由方面结构体的动力计算方式。
超高层塔楼罕遇地震作用下动力弹塑性时程分析报告
目录1 工程概况 (64)1.1工程介绍 (64)1.2进行罕遇地震弹塑性时程分析的目的 (65)2分析方法及采用的计算软件 (65)2.1分析方法 (65)2.2分析软件 (65)2.3材料模型 (65)2.3.1 混凝土材料模型 (65)2.3.2 钢材本构模型 (66)2.4构件模型 (66)2.4.1 梁单元 (66)2.4.2 楼板模型 (67)2.5分析步骤 (67)2.6结构阻尼选取 (67)3 结构抗震性能评价指标 (68)3.1结构的总体变形 (68)3.2构件性能评估指标 (68)4 动力特性计算 (70)5 施工加载过程计算 (70)5.1施工阶段设置 (70)5.2施工阶段计算结果 (70)6 罕遇地震分析总体信息结果汇总 (71)6.1地震波选取 (71)6.2基底剪力 (73)6.3层间位移角 (75)6.3.1 左塔楼 (75)6.3.2 右塔楼 (80)6.4结构顶点水平位移 (85)6.5柱底反力 (88)6.8结构弹塑性整体计算指标评价 (89)7构件性能分析 (90)7.1钢管混凝土柱 (90)7.2斜撑 (90)7.3连梁 (92)7.3主要剪力墙 (92)7.4钢梁的塑性应变 (100)7.5楼板应力及损伤 (100)8 罕遇地震作用下结构性能评价 (103)1 工程概况1.1 工程介绍上海临港中心——结构总高度为180m；主体结构采用框架-核心筒体系，外框架为圆钢管混凝土柱、钢框架梁。
钢管混凝土柱截面为Φ1200x1140～Φ900x860。
核心筒采用钢筋混凝土剪力墙体系，外墙厚750mm～400mm，内墙厚500mm～300mm，部分墙体内配置10mm厚钢板。
在32层以下，结构由左右两个塔楼构成，中间通过钢梁及6-7层、17-20层两道“人”字形斜撑连接，斜撑截面为BOX 560x1060x80x80。
上部主体结构分析时，以地下室顶板为嵌固端。
主要构件信息：（1）框架柱均采用圆钢管混凝土柱，混凝土强度等级为C60。
103 天津某超高层项目ABAQUS软件大震弹塑性时程分析报告
[] = [] + []
α = 4ξπ/T
上式中，[]为结构阻尼矩阵，[]和[]分别为结构质量矩阵和刚度矩阵。实际工程计算时，
常忽略 β 阻尼，α 由阻尼比 ξ与周期 T 反算而得。
1.4.6
分析步骤
第一步：施工模拟加载。利用 ABAQUS 隐式计算模块 ABAQUS/STANDARD，通过单元的“生”
1.5.1
结构总体变形控制
（1）能够完成整个弹塑性时程分析过程而不发散；
（2）结构的最终状态仍然竖立不倒；
（3）结构主体的最大层间位移角小于规范限值，框架-核心筒结构为 1/100。
1.5.2
构件性能目标
《高层建筑混凝土结构技术规程》 （JCJ3-2010）第 3.11 节 结构抗震性能设计，将结
构的抗震性能分为 1～5 五个水准，对应的构件损坏程度则分为“无损坏、轻微损坏、轻度
损坏、中度损坏、比较严重损坏”五个级别。
《建筑抗震设计规范》
（GB5001-2010）附录 M
提供了实现构件性能水准评价的具体方法。
在 Abaqus 软件中构件的损坏主要以混凝土的受压损伤因子及钢材（钢筋）的塑性应变
程度作为评定标准，参照前述规范条文采用如下损伤程度与构件性能水准的对应关系：
1）钢材在屈服后其强度并不会下降，衡量其损坏程度的主要指标是塑性应变值。设钢
条相同。但对整个剪力墙构件而言，由于墙肢一般不满足平截面假定，在边缘混凝土单元出
现受压损伤后，构件承载力不会立即下降，其损坏判断标准应有所放宽。考虑到剪力墙的初
始轴压比通常为 0.5～0.6，当 50%的横截面受压损伤达到 0.5 时，构件整体抗压和抗剪承
载力剩余约 75%，仍可承担重力荷载，因此以剪力墙受压损伤横截面面积作为其严重损坏
浅谈弹塑性动力时程分析方法
浅谈弹塑性动力时程分析方法对于结构地震响应分析方法，发展到目前为止，可以归纳为以下三个发展阶段：静力法、拟静力法（即反应谱法）、动力法（主要为时程分析法）。
在结构进入弹塑性阶段后，结构的一些构件进入屈服状态、结构刚度发生变化、产生塑性区域。
而弹性静力法忽略了结构的动力特性和结构的非刚性等重要特性，此时已经不再适用，因此使用弹性静力法已经不能满足现代建筑结构的设计要求。
反应谱法能考虑结构的动力特性及其与地震作用之间的相互关系，但它不能给出结构地震反应的全过程，更无法给出各构件进入弹塑性变形阶段的内力和变形状态。
为了研究和计算高层建筑结构的弹塑性变形，有必要进行结构的弹塑性分析。
目前，结构的弹塑性分析主要分为弹塑性动力分析和弹塑性静力分析两大类[1] [2]。
1 现有弹塑性分析方法综述1.1 静力弹塑性分析方法静力弹塑性分析方法，即我们常说的Push-over法，主要用于进行变形验算，尤其是在大震下的抗倒塌验算。
它是结构地震相应分析的简化方法[3] [4] [5]。
Push-over法基本步骤大致如下[1]：（1）建立结构的计算模型、确定构件的相关参数以及要采用的恢复力模型。
（2）求出作用在结构上的竖向荷载并求出结构在竖向荷载作用下的内力，以便和水平荷载作用下的内力进行组合。
（3）根据结构的具体情况，确定对结构施加的水平荷载分布形式：倒三角或与第一振型等小的水平荷载模式。
水平荷载施加于各楼层的质心处，逐渐单调增加侧向力，以产生的那里跟善意不计算所得的内力叠加后，刚好使一个或者一批构件开列进入屈服状态为宜。
（4）对于上一步进入屈服的构件进行修改，形成一个“新”的结构，修改结构的刚度矩阵并求出“新”结构的自振周期，不断重复第3步直到结构的侧向位移达到预定的目标位移、或是结构变成为机构为止。
记录每一步的结构自振周期并累计每一步施加的荷载。
（5）将每一个不同的结构自振周期及其对应的水平力总量与结构自重（重力荷載代表值）的比值（地震影响系数）绘成曲线，也把相应场地的各条反应谱曲线绘在一起，以此来评估结构的抗震性能。
某超高办公楼罕遇地震作用下动力弹塑性时程分析要点
某超高办公楼罕遇地震作用下动力弹塑性时程分析要点发表时间：2019-10-17T14:56:38.940Z 来源：《建筑细部》2019年第8期作者：胡凯[导读] 本办公楼项目位于安徽省合肥市滨湖新区用地面积约1.6万平方米，容积率6.0，总建筑面积约12.6万平方米。
深圳市建筑设计研究总院有限公司广东深圳 518000摘要：某超高办公楼项目为超A类高度办公楼，地下3层，地上40层，主要屋面高度179.9米，采用框架-核心筒结构体系，由于建筑平面宽度及核心筒宽度均较窄，结合建筑避难层设置钢支撑，为避免X向与Y向刚度相差过大，仅在Y向边榀框架上设置钢支撑，本项目采用PKPM系列软件中的SATWE模块，MIDAS Building软件对结构进行整体对比分析，本文简要介绍了采用MIDAS Building软件对结构罕遇地震作用下动力弹塑性时程分析。
1、工程概况本办公楼项目位于安徽省合肥市滨湖新区用地面积约1.6万平方米，容积率6.0，总建筑面积约12.6万平方米。
地上包含一栋179.9米超高层办公塔楼及7层裙房，地下设三层地下室。
项目地块占地平面尺寸约70m～105.6 x102m，地下3层，地上塔楼建筑层数40层（不包括三层构架），塔楼房屋高度179.9m，裙房7层，裙房房屋高度31.7m，地上各层层高均为4.5m，塔楼避难层层高4.4m，地下一层层高5.4m，地下二层层高4.8m，地下三层层高3.7m，主要建筑功能为办公，建筑效果图详见图1，建筑标准层平面图详见图2。
图1 图2工程抗震设防烈度为7度，为避免平面严重不规则，在塔楼与裙楼交接部位设置抗震缝，使得塔楼与裙楼脱开，本文仅针对超高塔楼。
2、结构体系本塔楼结构采用框架-核心筒结构，核心筒尺寸为36.6米x10.1米，Y向宽度较窄，为保证结构侧向刚度，结合建筑避难层位置，在12层、23层及34层避难层Y向边榀框架设置Y向腰桁架，并且为有效控制结构扭转效应，钢支撑设置在边榀框架上，支撑相关的框架梁及框架柱均设置钢骨。
SAP2k第6章弹性及弹塑性时程分析
f r k d 1 r yield z
式中：k为弹性弹簧常数；yield为屈服力；r为指定的屈
服后刚度对弹性刚度的比值；z为一个内部的滞后变量，
此变量范围为|z|≤ 1，其屈服面由|z|= 1代表。。
其中exp 为等于或大于1 的指数。
此指数越大，屈服比率越陡。实际指
数限值大约是20。公式z‘ 等价于
Wen 模型A＝1 及α＝β＝0.5。
2.3 单元类型介绍——滞回（橡胶）隔震属性
双轴的滞后隔振器，对于两个剪切变形有耦合的塑性属性
，且对余下的4个变形有线性的有效刚度属性。 对 每 一 个
剪切变形自由度，用户可独立的指定线性或非线性的行为。
2.3 单元类型介绍——滞回（橡胶）隔震属性
●在每一曲线终点的斜率不能为负
2.3 单元类型介绍——多段线性塑性连接单元
用户定义多段线性曲线上的点时，对称的成对点将被
连接，即使是非对称的曲线。这样能够对滞回曲线的形状
进行一些控制。
2.3 单元类型介绍——多段线性塑性连接单元
Takeda模型
Takeda模型在卸载过程中，当通过水平轴时，卸载曲线
沿反向加载路径（Backbone Force Deformat ion ）
的切线方向。
2.3 单元类型介绍——多段线性塑性连接单元
枢纽点（Pivot）模型
这个模型与Takeda 塑性模型相似，但是具有一个附加
参数来控制退化滞回曲线。适用于钢筋混凝土单元，是基
于趋向于在力－变形（或弯矩－转动）平面内指定点、也
筏板基础等。
体单元
主要用于细部分析。
点单元
也称连接单元，可在两节点之间绘制，也可在一个节
弹塑性时程分析法
形关系式简述如下。
（1）正向或反向弹性阶段（01 段或 04 段）
此阶阶段有 U 0 ，U U y ；或U 0 ， U U y
初始条件为 U 0 0 ， P(U 0 ) 0 刚度降低系数为 1
故
P(Ui 1 )
k1Ui1 ，
k1
Py Uy
（4.1.2）
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
（4）正向硬化阶段卸载至零且第一次反向加载（34 段）
此阶段有U 0 ，U U 3
初始条件为U i U 3 ， P(U i ) P(U 3 ) 0
刚度降低系数为
(U 3
Py U
y
)k1
故P (U i 1 ) Nhomakorabea
U3
Py U
y
(U i 1
U3)
（4.1.5）
（5）反向硬化阶段加载（56 段）
p(x)
2
Qx
arctan
(2
x
)Qx
（3）正向硬化阶段卸载（23 段）
此阶段有U 0 ，U U 2
初始条件为U i U 2 ， P(U i ) P(U 2 ) 刚度降低系数为 1
故 P(U i1 ) P(U 2 ) k1 (U i1 U 2 )
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
11
§4 弹塑性时程分析法
刚度降低系数为
1
k2 k1
1
故 P(Ui1) Pc 1k1(Ui1 Uc )
（4.1.9）
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
16 （3）正向或反向硬化段（23 段或 67 段）
某8度区超高层结构弹塑性时程分析
， ２ ０ １ ｌ ， ２ ３ （ １ ） ：
［ ９ ３ Ｍ ｓ ｓ ｈ ｋ ｏ ｃ ｒ Ａ， Ｊ ａ ｃ ｑ ｕ ｏ ￣ Ｊ Ｐ ．Ｃ ￣ ｉ ｄ ｄ ｉ ｎ ｅ ｓ ． ｆ ｕ ｒ Ｆ ｉ ｍ ｍｌ Ｄ ｅ ｍ ａ Ｊ ｎＭ ｏ ｄ ｅ ｌ － ｉ ｎ ｇｉ ｎＥ ｖ ｅ ｎ ｔ —Ｂ［ Ｃ ］ ．ｈｏ ｃ ． ｔ ｈ ｅ２ ｍ ｌ硼 Ｅ Ｅｔ ３ ｔ ｈ】 ｌ ｌ ｉ ∞
［ ４ ］ 杨先桥 ， 傅学怡 ， 黄用军． 深圳平安金融中心塔楼 动力弹塑性
分析［ Ｊ ］ ． 建筑结构学报 ， ２ ０ １ Ｉ ， （ Ｏ ７ ） ． ［ ５ ］ 杨学林 ， 周平槐 ， 徐燕青． 兰州红楼时代 广场超 限高层性 能化 抗震设计ｔ Ｊ ］ ． 建 筑结构 ， ２ ｏ １ ２ ， （ Ｏ ＆
４ 结
论
本 文通 过对 ８度 区某 超 高 层 结 构 的 Ａ Ｂ Ａ Ｑ Ｕ Ｓ 动力 弹塑性 时程分 析 ， 可 以得到 如下 结论 ： （ Ｉ ）罕遇地 震作 用下 ， 结构 的层 间位移 角 满足 规范 １ ／ １ ０ ０的限值要求 ， 在完 成 弹塑性 时程分 析后 ，
［ ２ ］ 吴 晓涵 ． Ｎ ｏ ｓ ａ Ｃ Ａ Ｄ与 Ａ Ｂ Ａ Ｑ Ｕ Ｓ 和Ｐ ｅ ｒ ｏ ｆ ｒ ｍ ３ Ｄ弹塑性 模型转换
及分析应用 ［ Ｊ ］ ． 建筑结构 ， ２ ０ １ ２ ， （ １ １ ） ． ［ ３ ］ 庄茁 ， 张帆 ， 岑松 ． Ａ Ｂ Ａ Ｑ Ｕ Ｓ非线性有 限元分析 与实例 ［ Ｍ］ ．
北京 ： 科学 出版社 ， ２ ０ ０ ５ ．
结构仍保持直立， 满足“ 大震不倒” 的设防要求． （ ２ ）在动力时程分析过程 中， 连梁受压损伤明 显， 起到了很好的耗能作用 ， 结构进入弹塑性 阶段 ； 大部分墙肢未现受压损伤 ， 保证了结构 安全性．
浅谈超限高层建筑大震弹塑性分析方法及步骤
浅谈超限高层建筑大震弹塑性分析方法及步骤摘要：随着城市超高层建筑越来越多，超高层建筑结构的超限审查也越来越严格，因此结构超限计算和分析也显得尤为重要，超限计算包括弹性计算、弹性时程分析、等效弹性分析、静力弹塑性和动力弹塑性分析，本文仅针对过程和方法较为复杂的动力弹塑性分析方法和步骤作简单介绍。
关键词：超限性能目标罕遇地震地震波动力弹塑性分析结构损伤1概述本文以武汉某超高层住宅楼为例，简要介绍超限高层结构的动力弹塑性方法和步骤。
2工程概况武汉某超高层住宅楼，结构高度为166.6m，为B级高度，地上55层，地下3层。
结构标准层长约48m，等效宽度约18.7m，高宽比约9.1；采用混凝土剪力墙结构型式。
按《高层建筑混凝土结构技术规程》（以下简称《高规》）及武城建[2016]5号、[2016]154号文规定，本楼栋抗震设防类别为标准设防类。
剪力墙、框架梁及连梁抗震等级均为二级。
本楼栋建筑结构安全等级为二级，结构设计使用年限为50年。
根据《建筑抗震设计规范》（以下简称《抗规》），本地区设计抗震设防烈度为6度，场地类别为Ⅱ类，基本地震加速度为0.05g，设计地震分组为一组；按《中国地震动参数区划图》相关规定，多遇地震、设防地震、罕遇地震作用下的地震加速度的最大值分别为17cm/s2、50cm/s2、115cm/s2，水平地震影响系数最大值αmax分别为0.0417、0.125、0.2875，特征周期分别为0.35、0.35、0.4.3结构超限情况及解决方案3.1结构超限情况根据国家《超限高层建筑工程抗震设防管理规定》和《超限高层建筑工程抗震设防专项审查技术要点》中的相关规定，本项目为钢筋混凝土剪力墙，超限高度限值为140m，因此高度超限，无其他超限项；需要进行抗震超限审查。
3.2抗震性能目标根据《高规》第3.11节及条文说明，本项目可选用结构抗震性能目标为D级，具体如下：规范抗震概念：小震不坏、中震可修、大震不倒；性能水准为1、4、5；性能目标：关键构件（底部加强区、楼梯间及端山墙通高剪力墙）：在小震作用下无损坏、弹性；中震作用下轻度损坏、抗震承载力满足不屈服；大震作用下中度损坏、抗震承载力宜满足不屈服。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
80 第40卷 增刊 建 筑 结 构 2010年6月北京某超高层商住楼动力弹塑性时程分析徐晓龙，高德志，桂满树，姜毅荣，何四祥，王 侃（北京迈达斯技术有限公司，北京 100044）[摘要] 基于梁柱塑性铰和剪力墙纤维模型，利用MIDAS Building 软件实现了超高层建筑结构的弹塑性时程分析。
结合该结构研究了在大震作用下结构将出现的破坏模式、塑性发展特点等，并与弹性分析进行了对比，说明弹塑性分析更能反映实际情况，能对结构的抗震性能给出较为合理全面的评价，并对工程设计给出指导。
[关键词] 动力弹塑性时程分析；MIDAS Building ；纤维模型Elastic-plastic time-history analysis on the super-high business-living building in BeijingXu Xiaolong, Gao Dezhi, Gui Manshu, Jiang Yirong, He Sixiang, Wang Kan （Beijing MIDAS Technology Information Co.,Ltd,. Beijing 100044,China ）Abstract: Based on the theory of plastic hinges （beams and columns ） and fiber model （walls ）, elastic-plastic time-history analysis is performed on the super-high business-living building in Beijing by MIDAS Building software under the scarce earthquake load. Failure Modes and plastic zone development are researched according to the feature of the structure. Through the comparison with the elastic analysis, it is considered that evaluation on the structure can be deduced from the elastic-plastic analysis more reasonably and comprehensively, and there will be better instruction to the projects.Keywords: dynamic elastic-plastic analysis; MIDAS Building; fiber model1 结构特点某50层的超高层商住两用建筑，地上50层，结构高度达到236.3m ，采用钢骨混凝土柱框筒结构形式，平面尺寸64.8m ×43.8m （轴线尺寸）。
结构已经超过型钢混凝土框架-钢筋混凝土筒体结构8度（0.2g ）抗震设防下的最大适用高度（150m ），该结构为抗震超限结构，故有必要对结构进行动力弹塑性时程分析，以考察其在罕遇地震作用下的响应、薄弱环节、破坏模式等。
结构整体模型及首层平面见图1，2。
2 动力弹塑性时程分析图1 结构模型图 图2 首层平面图时程分析法[1]被认为是目前结构弹塑性分析的最可靠和最精确的方法，它不仅能对结构进行定性分析，同时又可给出结构在罕遇地震下的量化性能指标，并且得到结构在各个时刻的真实地震反应。
弹塑性时程分析方法将结构作为弹塑性振动体系加以分析，直接按照地震波数据输入地面运动，通过逐步积分运算，求得在地面加速度随时间变化期间内，结构的内力和变形随时间变化的全过程，也称为弹塑性直接积分法。
弹塑性动力时程分析有如下优点：1）输入的是罕遇地震波的整个过程，可以真实反映各个时刻地震作用引起的结构响应，包括变形、内力、损伤状态（开裂和破坏）等；2）有些程序通过定义材料的本构关系来考虑结构的弹塑性性能，故可以准确模拟任何结构，计算模型简化较少；3）该方法基于塑性区的概念，对带剪力墙的结构，结果更为准确可靠。
基于MIDAS Building 动力弹塑性分析平台，对北京某超高层商住楼进行了罕遇地震作用下的动力时程分析，研究其各个抗震性能指标以及破坏模式。
2.1 弹塑性动力分析的基本方法弹塑性动力分析包括以下几个步骤：1）建立结构81的几何模型；2）分析设计后更新配筋，定义材料的本构关系，通过对各个构件指定相应的单元类型和材料类型确定结构的质量、刚度和阻尼矩阵；3）输入适合本场地的地震波，开始计算；4）计算完成后，对结果数据进行处理，对结构整体的可靠度做出评估。
2.2 力学模型MIDAS Building 提供了混凝土弹塑性损伤模型以及钢筋单元。
而混凝土损伤模型适合钢筋混凝土结构的动力弹塑性分析。
为了减小计算工作量，对梁柱等一维构件采用塑性铰模型，对剪力墙采用纤维模型。
对梁柱和剪力墙构件，程序有两种考虑钢筋的方式：读入施工图的实配钢筋或采用考虑超配系数后的计算筋。
对于剪力墙构件，按照定义的网格尺寸，程序自动划分为若干墙元，每个墙元又按照定义的水平向和竖向纤维数量划分为相应的宏纤维，即所谓的“纤维单元”。
每个纤维有一个积分点，剪切变形则计算每个墙单元的4个高斯点位置的剪切变形。
考虑到墙单元产生裂缝后，水平向、竖向、剪切方向变形具有一定的独立性，故Building 的非线性墙单元假设水平向、竖向、剪切变形相互独立。
纤维模型见图3。
图3 墙元纤维模型程序提供了两种混凝土剪力墙纤维模型：文[2]附录C 的单轴应力-应变关系和日本混凝土规范的滞回模型。
本工程采用文[2]附录C 的滞回模型，钢筋采用双折线滞回模型。
见图4。
梁采用MM 塑性铰模型，柱采用PM 相关的塑性图4 墙纤维滞回模型和钢筋滞回模型铰模型，梁柱铰特性值均采用修正的武田三折线模型。
2.3 计算条件由于实际地震作用是在结构的恒载和活载的基础上施加的，在MIDAS Building 中勾选“使用初始荷载：1×DL+0.5×LL ”。
程序将以此状态作为弹塑性时程分析时的初始状态。
根据规范和安评报告，共选取了两组天然波和一组人工波。
由于结构平面较为规则，故仅对结构进行单向地震输入，以考察在罕遇地震作用下，结构的损伤程度。
另进行了一组弹性计算，作为弹塑性分析的参考补充。
弹塑性模型规模为：节点数18681，自由度数92322，梁铰数2125个FEMA 铰（RC ），柱铰数800个FEMA 铰（SRC+RC ），墙单元数1356个（纤维模型）。
微机配置：CPU1.73GHz ，2G 内存。
单次完成持时20s 的地震波计算需时17h 左右。
2.4 计算结果及评价对该结构采用Building 进行了常遇地震下的弹性计算，如表1所示。
各项指标均满足现行规范要求。
整体计算结果表 表1计算参数结果 计算振型数 30 T 1（X ）/s 5.04 T 2（Y ）/s 4.85 T 3（扭转）/s 4.18 T t /T 10.83 底部剪重比（X ）/% 2.71 底部剪重比（Y ）2.62 地震最大层间位移角（X ） 1/628 地震最大层间位移角（Y ） 1/584 底层剪力墙最大轴压比 0.43 底层框架柱最大轴压比 0.442.4.1 整体性能指标在罕遇地震作用下，结构X 向顶点最大位移为565mm 。
所有楼层中的最大层间位移角为1/316，满足规范不大于1/100的要求；结构未出现倒塌现象，实现了“大震不倒”的设防目标。
结构在10s 时的框架塑性铰出铰状况和剪力墙应力见图5，6。
2.4.2 结构楼层状况观察层间位移角曲线（图7），虽在层19和层44产生一定程度的突变现象，但仍小于层间位移角限值。
82图5 10s 时的框架铰状态 图6 10s 时剪力墙应变状态 图7 结构X 向最大层间位移角曲线02468101214161820-140000-120000-100000-80000-60000-40000-20000020000400006000080000100000120000140000160000180000200000层剪力(k N )时间(s)图8 层剪力曲线 图9 连梁滞回曲线 图10 SRC 柱滞回曲线图11 剪力墙滞回曲线 图12 弹性与弹塑性分析层剪力 图13 弹性与弹塑性分析层间位移角选取1F ，10F ，25F 和50F 输出层剪力，见图8。
2.4.3 构件状况以1F 为例，选取分别连梁、SRC 柱和一片剪力墙输出构件在弹塑性分析时的滞回特性，分别见图9～11。
可见其与定义的滞回特性基本一致。
2.4.4 弹性与弹塑性对比分析在同样地震波下做了弹性时程分析，结合反应谱分析、静力弹塑性分析（Pushover ）和动力弹塑性分析，见图12，13和表2。
在性能设计中，一般认为弹塑性分析的基底剪力为反应谱分析基底剪力的2.8倍左右，这样设计的结构是比较合理的设计。
3 结论（1）对重要的高层建筑和复杂结构进行动力弹塑性分析，可以弥补弹性分析方法的不足，帮助设计人员找到其薄弱部位；对结构在罕遇地震作用下的可靠度进行评估，减少了设计的盲目性，使结构设计更弹性与弹塑性分析层剪力和层间位移角 表3分析方法 基底剪力 µ 层间位移角 µ 反应谱 60965 1 0.00165 1 弹性时程68642 1.13 0.00165 1 小震51570 0.85 0.00091 0.55 中震 63910 1.04 0.00113 0.68 Pushover大震149285 2.45 0.00885 5.36 Pushover （极限状态）162435 2.66 0.00986 5.98 动力弹塑性2113333.470.003392.05加安全合理。
（2）结构直立不倒，最大层间位移角满足规范要求，整个地震过程中结构未出现不可恢复的整体变形。
（3）塑性铰首先出现在连梁中，墙肢中出现较晚，（下转第148页）正常设计、正常施工、正常使用的条件下，不同结构类型都应该能够完成预定功能（三水准设防目标等），因此可靠度基本相同。
但不同结构类型的抗震能力则不同，一般情况下是：框架-抗震墙结构优于框架结构，框架结构优于砌体结构。
因此在设计中把适用砌体结构的方案改用框架结构，适用框架结构的改用框架-抗震墙结构，适用框架-抗震墙结构的适当增加抗震墙量，会更有效地提高其抗震能力，尤其是遭遇大震和特大震时的抗倒塌能力。