大学物理自测题下(黄皮书)机械波动要点及详细答案
《大学物理学》机械波练习题
《大学物理学》机械波部分自主学习材料（解答）一、选择题10-1．图（a ）表示0t =时的简谐波的波形图，波沿x 轴正方向传播，图（b ）为一质点的振动曲线，则图（a ）中所表示的0x =处质点振动的初相位与图（b ）所表示的振动的初相位分别为（ C ） （A ）均为2π； （B ）均为π-； （C ）π与π-； （D ）2π-与2π。
【提示：图（b ）为振动曲线，用旋转矢量考虑初相角为2π-，图（a ）为波形图，可画出过一点时间的辅助波形，可见0x =处质点的振动为由平衡位置跑向负方向，则初相角为2π】10-2．机械波的表达式为0.05cos(60.06)y t x ππ=+，式中使用国际单位制，则（ C ） （A ）波长为5m ； （B ）波速为110m s -⋅；（C ）周期为13秒； （D ）波沿x 正方向传播。
【提示：利用2k πλ=知波长为1003λ=m ，利用u k ω=知波速为1100u m s -=⋅，利用2T πω=知周期为13T =秒，机械波的表达式中的“+”号知波沿x 负方向传播】10-3．一平面简谐波沿x 轴负方向传播，角频率为ω，波速为u ，设4Tt =时刻的波形如图所示，则该波的表达式为（ D ）（A ）cos[()]xy A t u ωπ=-+； （B ）cos[()]2x y A t u πω=--；（C ）cos[()]2x y A t u πω=+-；（D ）cos[()]xy A t uωπ=++。
【提示：可画出过一点时间的辅助波形，可见在4Tt =时刻，0x =处质点的振动为由平衡位置向正方向振动，相位为2π-，那么回溯在0t=的时刻，相位应为π】10-4．如图所示，波长为λ的两相干平面简谐波在P 点相遇，波在点1S 振动的初相是1ϕ，到P 点的距离是1r 。
波在点2S 振动的初相是2ϕ，到P 点的距离是2r 。
以k 代表零或正、负整数，则点P 是干涉极大的条件为（ D ）OO1S 2S r（A ）21r r k π-=； （B ）212k ϕϕπ-=； （C ）212122r r k ϕϕππλ--+=；（D ）122122r r k ϕϕππλ--+=。
大学物理(第四版)课后习题及答案 波动
第十四章波动14-1 一横波再沿绳子传播时得波动方程为。
（1）求波得振幅、波速、频率及波长；（2）求绳上质点振动时得最大速度；（3）分别画出t=1s 和t=2s时得波形，并指出波峰和波谷。
画出x=1.0m处质点得振动曲线并讨论其与波形图得不同。
14-1分析（1）已知波动方程（又称波函数）求波动的特征量（波速、频率、振幅A及彼长 等），通常采用比较法。
将已知的波动方程按波动方程的一般形式书写，然后通过比较确定各特征量（式中前“－”、“＋”的选取分别对应波沿x轴正向和负向传播）。
比较法思路清晰、求解简便，是一种常用的解题方法。
（2）讨论波动问题，要理解振动物理量与波动物理量之间的内在联系与区别。
例如区分质点的振动速度与波速的不同，振动速度是质点的运动速度，即；而波速是波线上质点运动状态的传播速度（也称相位的传播速度、波形的传播速度或能量的传播速度），其大小由介质的性质决定。
介质不变，彼速保持恒定。
（3）将不同时刻的t值代人已知波动方程，便可以得到不同时刻的波形方程，从而作出波形图。
而将确定的x值代入波动方程，便可以得到该位置处质点的运动方程，从而作出振动图。
解（1）将已知波动方程表示为与一般表达式比较，可得则（2）绳上质点的振动速度则（3） t=1s和 t＝2s时的波形方程分别为波形图如图14－1（a）所示。
x＝1.0m处质点的运动方程为振动图线如图14－1（b）所示。
波形图与振动图虽在图形上相似，但却有着本质的区别前者表示某确定时刻波线上所有质点的位移情况，而后者则表示某确定位置的时间变化的情况。
14-2 波源作简谐运动，其运动方程为，它所形成得波形以30m/s的速度沿一直线传播。
（1）求波的周期及波长；（2）写出波的方程。
14-2分析 已知彼源运动方程求波动物理量及波动方程，可先将运动方程与其一般形式进行比较，求出振幅地角频率及初相，而这三个物理量与波动方程的一般形式中相应的三个物理量是相同的。
大学物理自测题下(黄皮书)电磁感应要点及详细答案共51页
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ；权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
谢谢！
5、虽然权力是一头固执的熊，可是金 子可以 拉着它 的鼻子 走。——莎士 比
61、奢侈是舒适的，否则就不是奢侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
大学物理练习册习题及答案波动学基础
习题及参考答案第五章 波动学基础参考答案思考题5-1把一根十分长的绳子拉成水平，用手握其一端，维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则（A ）振动频率越高，波长越长； （B ）振动频率越低，波长越长； （C ）振动频率越高，波速越大； （D ）振动频率越低，波速越大。
5-2在下面几种说法中，正确的说法是（A ）波源不动时，波源的振动周期与波动的周期在数值上是不同的； （B ）波源振动的速度与波速相同；（C ）在波传播方向上的任二质点振动位相总是比波源的位相滞后； （D ）在波传播方向上的任一质点的振动位相总是比波源的位相超前 5-3一平面简谐波沿ox 正方向传播，波动方程为010cos 2242t x y ππ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦. (SI)该波在t =0.5s 时刻的波形图是（ ）5-4图示为一沿x 轴正向传播的平面简谐波在t =0时刻的波形，若振动以余弦 函数表示，且此题各点振动初相取-π到π之间的值，则（）（A ）1点的初位相为φ1=0（B ）0点的初位相为φ0=-π/2(m)(A )(m)(m)(B )(C )(D )思考题5-3图思考题5-4图（C ）2点的初位相为φ2=0 （D ）3点的初位相为φ3=05-5一平面简谐波沿x 轴负方向传播。
已知x=b 处质点的振动方程为[]0cos y A t ωφ=+，波速为u ，则振动方程为（ ）(A)()0cos y A t b x ωφ⎡⎤=+++⎣⎦(B)(){}0cos y A t b x ωφ⎡⎤=-++⎣⎦(C)(){}0cos y A t x b ωφ⎡⎤=+-+⎣⎦ (D)(){}0cos y A t b x u ωφ⎡⎤=+-+⎣⎦ 5-6一平面简谐波，波速u =5m·s -1，t =3s 时刻的波形曲线如图所示，则0x =处的振动方程为（ ）（A ）211210cos 22y t ππ-⎛⎫=⨯- ⎪⎝⎭ (SI) （B ）()2210cos y t ππ-=⨯+ (SI) （C ）211210cos 22y t ππ-⎛⎫=⨯+ ⎪⎝⎭ (SI) （D ）23210cos 2y t ππ-⎛⎫=⨯- ⎪⎝⎭ (SI) 5-7一平面简谐波沿x 轴正方向传播，t =0的波形曲线如图所示，则P 处质点的振动在t =0时刻的旋转矢量图是（ ）5-8当一平面简谐机械波在弹性媒质中传播时，下述各结论一哪个是正确的？ （A ）媒质质元的振动动能增大时，其弹性势能减少，总机械能守恒； （B ）媒质质元的振动动能和弹性势能都作周期变化，但两者的位相不相同；（C ）媒质质元的振动动能和弹性势能的位相在任一时刻都相同，但两者的数值不相等； （D ）媒质质元在其平衡位置处弹性势能最大。
大学物理自测题下(黄皮书)光学要点及详细答案共33页文档
i '0
tg 60 0 n2 n1
n2 n1tg600 3
DN
解： x D D D d N N
0.75
解：在介质中时： xDx3mm
dn n 4
3
1.33
解： r2r13 n 4 1.33
r1 r2
介质 n(r2r1)4
3
1 .2
解: 暗环条件为: 2e(2k1) k0,1,2暗环
明暗 b
纹纹
n
d
dk dk+1
牛顿环
2n2d/2
R
透镜的曲率半径
r
od
R m 1r k 2 m r k 2 m 1r k m r k r k m r k
迈克耳逊干涉仪
d N
2
光的衍射
暗 bsin 2k
k1,2
明 bsin(2k21) k0,1,2L
2
sinx/ f
3.6mm
x0
2f
b
20.66 0.60 1 10 0 3 0 91.21 0 3m
bsin3
x3
2f
3
b
3.6mm
解: 单缝衍射暗纹条件为: bsink
x2f sin 2 f k
b
b fk x 2 3 1 2 0 6 1 3 0 2 8 2 1 0 1 0 7 .6 1 0 2 m m
0
I I0co2s
强度为I0的自然光经过偏振片后的强度为：
I I0 / 2
自然光
i0
部分 偏振光
n 1 自然光
布儒斯特角
i0
tg
i0
n22 n1
i0
线偏振
光 n1
大学物理机械波习题附答案
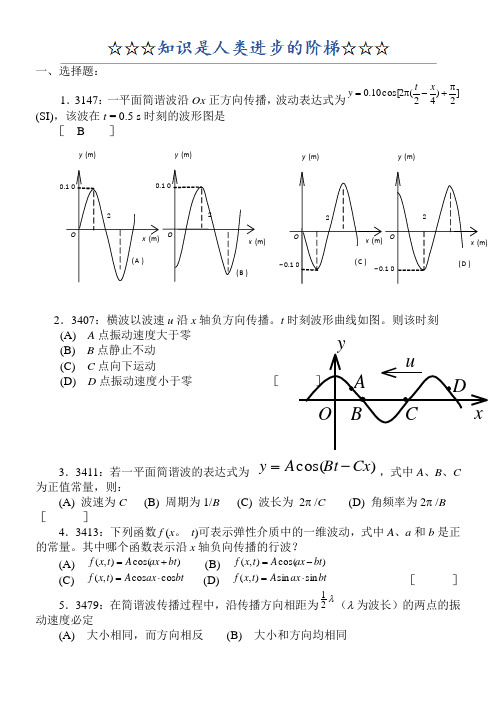
一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻 (A) A 点振动速度大于零 (B) B 点静止不动(C) C 点向下运动(D) D 点振动速度小于零 ［ ］3．3411：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B ［ ］4．3413：下列函数f (x 。
t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt ax A t x f sin sin ),(⋅= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定(A) 大小相同，而方向相反 (B) 大小和方向均相同xu A B C D Ox (m) O 2 0.1 0y (m) ( A ) xO 2 0.1 0 y (m) ( B ) x (m) O 2 - 0.1 0 y (m) ( C ) x (m)O 2 y (m) ( D )- 0.1 0(C) 大小不同，方向相同 (D) 大小不同，而方向相反 ［ ］6．3483：一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8（其中λ 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。
大学物理机械波习题附答案
一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 ［3．3411：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2? /C (D) 角频率为2? /B ［］4．3413：下列函数f (x 。
t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D)bt ax A t x f sin sin ),(⋅= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为λ21（??为波长）的两点的振动速度必定(A) 大小相同，而方向相反 (B) 大小和方向均相同(C)大小不同，方向相同 (D) 大小不同，而方向相反y (m) y (m) - y (m) y (m)［ ］6．3483：一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距? /8（其中? 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。
维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则 (A) 振动频率越高，波长越长 (B) 振动频率越低，波长越长(C) 振动频率越高，波速越大 (D) 振动频率越低，波速越大 ［ ］ 8．3847：图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
大学物理机械波习题附答案
一、选择题：一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0p+-p =x t y (SI)，该波在t = 0.5 s 时刻的波形图是时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻时刻波形曲线如图。
则该时刻 (A) A 点振动速度大于零点振动速度大于零 (B) B 点静止不动点静止不动(C) C 点向下运动点向下运动 (D) D 点振动速度小于零点振动速度小于零 ［ ］3．3411：若一平面简谐波的表达式为：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则：为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为波长为 2p /C C (D) 角频率为2p /B ［ ］4．3413：下列函数f (x 。
t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波？轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(×= (D) bt ax A t x f sin sin ),(×= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为l21（l 为波长）的两点的振动速度必定动速度必定(A) 大小相同，而方向相反大小相同，而方向相反 (B) 大小和方向均相同大小和方向均相同 (C) 大小不同，方向相同大小不同，方向相同 (D) 大小不同，而方向相反大小不同，而方向相反xu A y B C D Ox (m) O 2 0.1 0y (m)( A ) x (m)O 2 0.1 0y (m) ( B )x (m) O 2- 0.1 0 y (m) ( C ) x (m)O 2 y (m)( D )- 0.1 0［ ］6．3483：一简谐横波沿Ox 轴传播。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1）在波动的传播过程中，任意时刻的动能和势能不仅大小 相等而且相位相同，同时达到最大，同时等于零。 2）在波传动过程中，任意质元的能量不守恒，所以波动过
程实质上是能量的传递过程。
惠更斯原理：在波的传播过程中，波面（波前）上的各点，
都可以看作是发射子波的波源，在其后的任一时刻，这些子波 的包迹就成为新的波面。
v A sin( t 0 )
x A cos( t 0 )
1 1 2 2 E k mv E p kx 2 2 1 2 1 2 kA sin2 ( t 0 ) kA cos 2 ( t 0 ) 2 2
1 2 E E k E p kA 2
k 2 , T 2 m
m k
kT 2 200 0.04 2 m 2.0 (kg ) 2 2 4 4
解：由能量守恒定律可知：左右两侧所 处最高位置应该相等，即势能相等。
mg l 0.451 cos 1 mgl 1 cos 2
答案为（c)
1 1 1 弹簧串联： k k k'
T 2
k k' 2
m 2 k' 2m k
2
弹簧并联： k ' x kx kx mg
k ' 2k
m 2k
T
2
2
m 2 k'
５．一弹簧振子作简谐振动，总能量为E1,如果简谐振动振幅 增加为原来的两倍，重物的质量增为原来的四倍，则它的总能 量E1变为： (A)E1/4 (B)E1/2 (C)2E1 (D)4E1 谐振动系统的能量=系统的动能Ek+系统的势能Ep 某一时刻，谐振子速度为v，位移为x
两根并联时
k ' 3k
1 2 2
k '' m
k '' 2k ' 6k
所以振动系统的频率为：（Ｂ）
解：
mg k1 x1 k2 x2 x1 nx2 mg k1 x1 k2 x2 kx x x1 x2
k2 nk1
1 1 1 k1 k2 k
cos(t )
A1 1 A2 2 1.5 1.2 1.05
注意这相当于两个振动而不是两列波 A1 10 / 2 A 20 0
o
2
x
频率相等，所以相位差等于初相差：
2 1 20 10 0 / 2 / 2
在波动的传播过程中，某质元任意时刻的动能和势能不仅大小相等而且相 位相同，同时达到最大，同时等于零。在平衡位置动能和势能同时达到最 t o, , b, d ,大值， 在最大位移处动能和势能同时为零. f
1 2 E kA 2
m T 2 / 2 k
1 4 2 m 2 E 2 A 2 T
坡因廷矢量
1 2 1 电磁波的能量密度： w E H 2 2 2
电磁波的能流密度(坡因廷矢量)： S wu
S EH S EH
E
S
H
1. 一轻弹簧,上端固定,下端挂有质量为m的重物，其自由振动 的周期为Ｔ．今已知振子离开平衡位置为x时，其振动速度 为v，加速度为a，试判下列计算倔强系数的公式中那个是 错误的：
8. 一长为l 的均匀细棒悬于通过其一端的光滑水平 固定轴上，（如图所示），作成一复摆。已知 细棒绕通过其一端的轴的转动惯量 J ml 2 / 3， 此摆作微小振动的周期为:
O
l
d 2 l mgl 转动定理： J mg sin 2 dt 2 2 d 2 mgl 0 2 dt 2J
T
波动方程
2
2
1
T u
2
u
y 2 y u 2 2 t x
平面简谐波的波动式
x y A cos (t ) u xyt振动图
O
u
x
o
x
波动图
p
波中各质点的总机械能为：
x E Ek E p A sin (t ) V u Ek E p
1 1 m(k1 k2 ) m 答案：C T 2 2 m 2 k k1k2 k1 k2
1、将一个劲度系数为k的弹簧一截为二，则一半长的弹簧的劲度
系数为多少？
解：设弹簧截断后的劲度系数为k1， k1，平衡时分别伸长了x1， x2，则
kx mg k1 x1 mg
1 1 2 2 2 E k mv kA sin ( t / 2) 2 2
动能之比为（Ｄ）2:1
解：弹性力所做的功等于动能的变化量，所以半个 周期所做的功为零。
E kA2/2 o x t E
Ep
Ek
E p Ek
T
t
12.一列机械横波在t时刻的波形曲线如图所示，则该时刻能 量为最大值的媒质质元的位置是： (A) o, b, d , f (C) o, d (B) a, c, e, g (D) b, f
kx mg k1 x1 k2 x2 mg
k k1 k2 k3
x x1 x2
3、把一根弹簧在其一半处折叠成一根双股弹簧，其弹簧的劲度
系数为多少？
k ' 2k
k '' 2k ' 4k
解：截成三等份，设每等份的倔强系数为 k ' , 则
1 1 1 1 k' k' k' k
mgl 2J
2l 3g
周期为:
T
2
2
2J 2 mgl
９. 一质点作简谐振动，周期为T．当它由平衡位置向x轴正 方向运动时，从二分之一最大位移处到最大位移处这段 路程所需要的时间为
(A) T /12． (B) T /8． (C) T /6． (D) T /4．
解：采用旋转矢量法：
总能量变为（Ｄ）
6.一物体作简谐振动，振动方程 x A cos(t / 2)，则该物体 在t=0时刻的动能与t =T/8 (T为振动周期)时刻的动能之比为：
(A)1:4 解：动能为
(B)1:2
（C)1:1 (D)2:1
1 2 2 Ek kA sin t=0时刻， 2 2 1 2 2 T t=T/8时刻， Ek kA sin 2 8 2 1 2 2 2 1 2 2 3 kA sin kA sin 2 8 2 2 4
多普勒效应
u v0 ' u vs
v0 观察者向着波源运动 + ，远离 - ；
vs 波源向着观察者运动 - ，远离 + 。
电磁波的性质
x E E0 cos (t ) c
y
H
x H H0 cos (t ) c
平面电磁波
o
z
E
u x
u
c
r r
E H
1 cos 1 mgl 1.5 1 cos 2 mg l 0.45 1.05 2 1 1 2sin 2 1 / 2 1 1 cos 1 1.5 2 1 cos 2 1 1 2sin 2 / 2 2 1.05
x x1 x2 , x A cos(t )
A A A 2 A1 A2 cos(2 1 )
2 1 2 2
x x1 x2
A1 sin 1 A2 sin 2 tg A1 cos 1 A2 cos 2
波的周期 T 、频率 v 和波长 之间的关系
k 0,1, 2,3,...
称为波程差：
2
,
r2 r1
2k 1 , 2
k 0,1, 2,3,...
驻波方程
相邻波腹或相邻波节间的距离都为：
x 2
波节两侧的点振动相位相反，波节之间的点其振动相位相同。
半波损失
当波从波疏媒质入射到波密媒质界面上反射时，有半波损失； 当波从波密媒质入射到波疏媒质界面上反射时，无半波损失。
简谐振动微分方程
其通解为： x
d x 2 x 0 2 dt
简谐振动的运动学方程
2
A cos(t )
A, ,
v0
利用初始条件确定
A
x0 2 (
)2
v0 tan x0
T 2
2 2 T
1 T 2
简谐振动的旋转矢量表示法
3. 劲度系数分别为k1和k2的两个轻弹簧串联在 一起，下面挂着质量为m的物体，构成一个 竖挂的弹簧振子，则该系统的振动周期为：
解：设弹簧串联后弹簧的劲度系数为k， 平衡时伸长了x,则
k1 k2 m
kx mg k1 x1 mg
x x1 x2
k2 x2 mg
1 1 1 1 k k1 k2 k3
t=t A
t+0
0
A t=0
x X
o
x A cos(t 0 )
简谐振动系统机械能守恒
1 2 1 2 1 2 机械能 E E p Ek kx mv kA 2 2 2 同方向、同频率的两个简谐振动的合成 A A x1 (t ) A1 cos(t 1 ) 2 x2 (t ) A2 cos(t 2 ) A1 2 1 x1 x2 合振动 :
波的相干条件
1.具有相同的频率 2.振动方向相同 3.具有恒定的相位差