2009年湖南长沙市中考数学试题(含答案)

合集下载

长沙市中考数学压轴题(含答案)

7、（本题满分 10 分）【2006】
如图 1，已知直线 y 1 x 与抛物线 y 1 x2 6 交于 A，B 两点．
2
4
（1）求 A，B 两点的坐标；
（2）求线段 AB 的垂直平分线的解析式；（3）如图 2，取与线段 AB 等长的一根橡皮筋，端点分别固定在 A，B 两处．用铅笔拉着这根橡皮筋使笔尖 P 在直线 AB 上方的抛物线上移动，动点 P 将与 A，B 构成无数个三角形，这些三角形中是否存在一个面积最大的三角
（1）求实数 a，b，c 的值；
（2）若点 M、N 同时从 B 点出发，均以每秒 1 个单位长度的速度分别沿 BA、BC 边运动，其中一个点到达终点
时，另一点也随之停止运动．当运动时间为 t 秒时，连结 MN ，将 △BMN 沿 MN 翻折， B 点恰好落在 AC 边上的
P 处，求 t 的值及点 P 的坐标；
P、Q 分别从 O、C 同时出发，P 在线段 OA 上沿 OA 方向以每秒 2 cm 的速度匀速运动，Q 在线段 CO 上沿
CO 方向以每秒 1 cm 的速度匀速运动．设运动时间为 t 秒．（1）用 t 的式子表示△OPQ 的面积 S；（2）求证：四边形 OPBQ 的面积是一个定值，并求出这个定值；
APQ．当点 P 运动到原点 O 处时，记 Q 的位置为 B．
y A
.B
P
O
x
.
Q
（第 26 题）（1）求点 B 的坐标；（2）求证：当点 P 在 x 轴上运动（P 不与 O 重合）时，∠ABQ 为定值；（3）是否存在点 P，使得以 A、O、Q、B 为顶点的四边形是梯形？若存在，请求出 P 点的坐标；若不存在，
请说明理由．
5、（本题满分 10 分）【2012】

[学子教育]2009年全国中考数学压轴题5(修订版) (2)

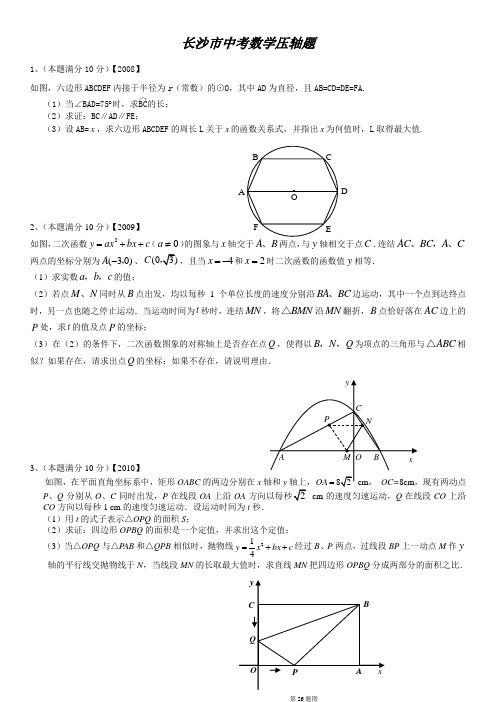
2009年全国中考数学分类试题---综合题压轴题汇编5教师答案版1（09湖南长沙）26．（本题满分10分）如图，二次函数2y ax bx c =++（0a ≠）的图象与x 轴交于A B 、两点，与y 轴相交于点C ．连结AC BC A C 、，、两点的坐标分别为(30)A -，、(0C ，且当4x =-和2x =时二次函数的函数值y 相等．（1）求实数a b c ，，的值；（2）若点M N 、同时从B 点出发，均以每秒1个单位长度的速度分别沿BA BC 、边运动，其中一个点到达终点时，另一点也随之停止运动．当运动时间为t 秒时，连结MN ，将B M N △沿MN 翻折，B 点恰好落在AC 边上的P 处，求t 的值及点P 的坐标；（3）在（2）的条件下，二次函数图象的对称轴上是否存在点Q ，使得以B N Q ，，为项点的三角形与ABC △相似？如果存在，请求出点Q 的坐标；如果不存在，请说明理由．2（09湖南衡阳）26、（本小题满分9如图12，直线4+-=x y AB 上任意一点（A 、B 两点除外），过M D ．（1）当点M 在AB 上运动时，你认为四边形OCMD 的周长是否发生变化？并说明理由；（2）当点M 运动到什么位置时，四边形OCMD 的面积有最大值？最大值是多少？（3）当四边形OCMD 为正方形时，将四边形OCMD 沿着x 轴的正方向移动，设平移的距离为)40<<a a （，正方形OCMD 与△AOB 重叠部分的面积为S ．试求S 与a 的函数关系式并画出该函数的图象．解：（1）设点M 的横坐标为x ，则点M 的纵坐标为－x+4（0<x<4，x>0，－x+4>0）；则：MC ＝∣－x+4∣＝－x+4，MD ＝∣x ∣＝x ； ∴C 四边形OCMD ＝2（MC+MD ）＝2（－x+4+x ）＝8∴当点M 在AB 上运动时，四边形OCMD 的周长不发生变化，总是等于8；（2）根据题意得：S 四边形OCMD ＝MC ·MD ＝（－x+4）· x ＝－x 2+4x ＝－(x-2)2+4 ∴四边形OCMD 的面积是关于点M 的横坐标x （0<x<4）的二次函数，并且当x ＝2，即当点M 运动到线段AB 的中点时，四边形OCMD 的面积最大且最大面积为4；（3）如图10（2），当20≤<a 时，42121422+-=-=a a S ；如图10（3），当42<≤a 时，22)4(21)4(21-=-=a a S ；∴S 与a 的函数的图象如下图所示：图12图12图123（09湖南娄底）25．（本小题12分）如图11，在△ABC 中，∠C =90°，BC =8，AC =6，另有一直角梯形DEFH（HF ∥DE ，∠HDE =90°）的底边DE 落在CB 上，腰DH 落在CA 上，且DE =4，∠DEF =∠CBA ，AH ∶AC =2∶3（1）延长HF 交AB 于G ，求△AHG 的面积. （2）操作：固定△ABC ，将直角梯形DEFH 以每秒1个单位的速度沿CB 方向向右移动，直到点D 与点B重合时停止，设运动的时间为t 秒，运动后的直角梯形为DEFH ′（如图12）.探究1：在运动中，四边形CDH ′H 能否为正方形？若能，请求出此时t 的值；若不能，请说明理由.探究2：在运动过程中，△ABC 与直角梯形DEFH ′重叠部分的面积为y ，求y 与t 的函数关系.25．（12分）解：（1）∵AH ∶AC =2∶3，AC=6∴AH =23AC =23×6=4又∵HF ∥DE ，∴HG ∥CB ，∴△AHG ∽△ACB (1)分∴AH AC=HG BC，即46=8HG ，∴HG =163 (2)分∴S △AHG =12AH ·HG =12×4×163=323 (3)分（2）①能为正方形…………………………………………………………………4分∵HH ′∥CD ，HC ∥H ′D ，∴四边形CDH ′H 为平行四边形又∠C =90°，∴四边形CDH ′H 为矩形…………………………………5分又CH =AC-AH =6-4=2∴当CD =CH =2时，四边形CDH ′H 为正方形此时可得t =2秒时，四边形CDH ′H 为正方形…………………………6分②（Ⅰ）∵∠DEF =∠ABC ，∴EF ∥AB∴当t =4秒时，直角梯形的腰EF 与BA 重合.当0≤t ≤4时，重叠部分的面积为直角梯形DEFH ′的面积.…………7分过F 作FM ⊥DE 于M ，FM ME=tan ∠DEF =tan ∠ABC =AC BC=68=34∴ME =43FM =43×2=83，HF=DM=DE-ME =4-83=43∴直角梯形DEFH ′的面积为12（4+43）×2=163∴y =163 (8)分（Ⅱ）∵当4＜t ≤513时，重叠部分的面积为四边形CBGH 的面积-矩形CDH ′H 的面积.…………………………………………………………9分而S 边形CBGH =S △ABC -S △AHG =12×8×6-323=403S 矩形CDH ′H=2t∴y =403-2t ……………………………………………… (10)分（Ⅲ）当513＜t ≤8时，如图，设H ′D 交AB于P .BD =8-t又PD DB=tan ∠ABC =34∴PD =34DB =34（8-t ）………………11分 ∴重叠部分的面积y =S△PDB =12PD ·DB=12·34（8-t ）（8-t ） =38（8-t ）2=38t 2-6t+24∴重叠部分面积y 与t的函数关系式： y=316（0≤t ≤4）403-2t （4＜t ……………………………………12分≤513）38t 2-6t +24（513＜t ≤8）（注：评分时，考生未作结论不扣分）4（09湖南益阳）六、解答题：本题满分14分． 20.阅读材料：如图12-1，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a )，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法：ah S ABC 21=∆，即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题：如图12-2，抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0)，交y轴于点B .(1)求抛物线和直线AB 的解析式；(2)点P 是抛物线(在第一象限内)上的一个动点，连结PA ，PB ，当P 点运动到顶点C 时，求△CAB 的铅垂高CD 及CAB S ∆；(3)是否存在一点P ，使S △PAB =89S △CAB ，若存在，求出P 点的坐标；若不存在，请说明理由.六、解答题：本题满分14分．20．解：(1)设抛物线的解析式为：4)1(21+-=x a y····· 1分把A （3,0）代入解析式求得1-=a所以324)1(221++-=+--=x x x y ······· 3分设直线AB 的解析式为：b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( ··· 4分把)0,3(A ，)3,0(B 代入b kx y +=2中图12-2 x C O y ABD1 1图12-1A解得：3,1=-=b k所以32+-=x y ·············· 6分 (2)因为C 点坐标为(１,4) 所以当x ＝１时，y 1＝4，y 2＝2所以CD ＝4-2＝2 ············· 8分32321=⨯⨯=∆CAB S (平方单位) ········10分 (3)假设存在符合条件的点P ，设P 点的横坐标为x ，△PAB 的铅垂高为h ，则x x x x x y y h 3)3()32(2221+-=+--++-=-= ·· 12分由S △PAB =89S △CAB得：389)3(3212⨯=+-⨯⨯x x 化简得：091242=+-x x 解得，23=x将23=x 代入3221++-=x x y 中，解得P 点坐标为)415,23( ··········· 14分 5（09湖南株洲）23．（本题满分12分）如图，已知ABC ∆为直角三角形，90ACB ∠=︒，AC BC =,点A 、C 在x 轴上，点B 坐标为（3，m ）（0m >），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B 、D ．（1）求点A 的坐标（用m 表示）；（2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点BE ，连结 BQ 并延长交AC 于点F 23．（1）由(3,)B m 可知3OC =，BC m =，又m =，3OA m =-，所以点A 的坐标是（3,0m -3分（2）∵45ODA OAD ∠=∠=︒ ∴3OD OA m ==-，则点D 的坐标是（0,3m -）. 又抛物线顶点为(1,0)P ，且过点B 、D ，所以可设抛物线的解析式为：2(1)y a x =-，得：22(31)(01)3a m a m ⎧-=⎪⎨-=-⎪⎩ 解得14a m =⎧⎨=⎩ ∴抛物线的解析式为221y x x =-+ ………7分（3）过点Q 作QM AC ⊥于点M ，过点Q 作QN BC ⊥于点N ，设点Q 的坐标是2(,21)x x x -+，则2(1)QM CN x ==-，3MC QN x ==-.∵//QM CE ∴PQM ∆∽PEC ∆ ∴QM PMEC PC =即2(1)12x x EC --=，得2(1)EC x =- ∵//QN FC ∴BQN ∆∽BFC ∆ ∴QN BN FC BC =即234(1)4x x FC ---=，得41FC x =+ 又∵4AC = ∴444()[42(1)](22)2(1)8111FC AC EC x x x x x x +=+-=+=⋅+=+++ 即()FC AC EC +为定值8. ……………………12分。

湖南长沙2009-2017年中考数学真题类编：第20课时相似三角形(Word版)

第四单元三角形第二十课时相似三角形长沙9年中考 (2009～2017)命题点1 相似三角形的性质与判定(必考)1．(2013长沙16题3分)如图，在△ABC 中，点D 、点E 分别是边AB 、AC 的中点，则△ADE 与△ABC 的周长之比等于________．第1题图第2题图2．(2015长沙17题3分)如图，在△ABC 中，DE ∥BC ，AD AB ＝13，DE ＝6，则BC 的长是________．3．(2014长沙16题3分)如图，在△ABC 中，DE ∥BC ，DE BC ＝23，△ADE 的面积是8，则△ABC 的面积为________．第3题图4．(2015株洲)如图，已知AB 、CD 、EF 都与BD 垂直，垂足分别是B 、D 、F ，且AB ＝1，CD ＝3，那么EF 的长是( )A 、 13B 、 23C 、 34D 、 45第4题图第5题图5．(2014娄底)如图，小明用长为3 m 的竹竿CD 做测量工具，测量学校旗杆AB 的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点O ，此时O 点与竹竿的距离OD ＝6 m ，竹竿与旗杆的距离DB ＝12 m ，则旗杆AB 的高为________m 、6．(2015邵阳)如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF 来测量操场旗杆AB 的高度，他们通过调整测量位置，使斜边DF 与地面保持平行，并使边DE 与旗杆顶点A 在同一直线上，延长DF 交AB 于点C ，已知DE ＝0、5米，EF ＝0、25米，目测点D 到地面的距离DG ＝1、5米，到旗杆的水平距离DC ＝20米，求旗杆的高度．第6题图答案1．1∶2 2、18 3、184、 C 【解析】∵AB ⊥BD ，EF ⊥BD ，∴△EFD ∽△ABD ，∴EF AB ＝FD BD，同理，EF CD ＝BF BD ，∴EF AB ＋EF CD ＝FD BD ＋BF BD ＝FD ＋BF BD＝1，∵AB ＝1，CD ＝3，∴EF 1＋EF 3＝1，解得EF ＝34、 5、 9 【解析】由题意得，CD ∥AB ，∴△OCD ∽△OAB ，∴CD AB ＝OD OB，即3AB ＝66＋12，解得AB ＝9 m 、 6、解：根据题意，得DC ⊥AC ，EF ⊥AD ，∴∠ACD＝∠FED＝90°，又∵∠ADC＝∠FDE，∴△ACD∽△FED，∴ACFE＝DCDE，即AC0.25＝200.5，∴AC＝10(米)．∵四边形BCDG是矩形，∴BC＝DG＝1、5(米)，∴旗杆高度为AB＝AC＋BC＝10＋1、5＝11、5(米)．答：旗杆的高度为11、5米．。

湖南长沙2009-2017年中考数学真题类编：第14课时二次函数的实际应用(Word版)

第三单元函数第十四课时二次函数的实质应用长沙 9 年中考(2009 ～2017)1、 (2009 长沙 25 题 10 分) 为了扶助大学生自主创业，市政府供给了 80 万元无息贷款，用于某大学生创办企业生产并销售自主研发的一种电子产品，并商定用该企业经营的收益逐渐偿还无息贷款．已知该产品的生产成本为每件40 元，职工每人每个月薪资为 2500元，企业每个月需支付其余花费 15 万元，该产品每个月销量y( 万件)与销售单价 x(元)之间的函数关系如下图．(1)求月销售量 y( 万件)与销售单价 x(元)之间的函数关系式；(2)当销售单价定为 50 元时，为保证企业月收益达到 5 万元 ( 收益＝销售额－生产成本－职工薪资－其余花费 ) ，该企业可安排职工多少人？(3)若该企业有 80 名职工，则该企业最早可在几个月后还清无息贷款？第 1 题图2、(2012长沙25 题10 分) 在长株潭建设两型社会的过程中，为推动节能减排，发展低碳经济，我市某企业以25 万元购得某项节能产品的生产技术后，再投入 100 万元购置生产设施，进行该产品的生产加工．已知生产这类产品的成本价为每件20 元，经过市场调研发现，该产品的销售单价定在25 元到 35 元之间较为合理，而且该产品的年销售量y(万件)与销售单价x(元)之间的函数关系式为： y＝40－x（25≤x≤30）、25－0.5x （30＜x≤35）( 年赢利＝年销售收入－生产成本－投资成本)(1)当销售单价定为 28 元时，该产品的年销售量为多少万件？(2)求该企业第一年的年赢利W(万元)与销售单价x(元)之间的函数关系式，并说明投资的第一年，该企业是盈余仍是损失？若盈余，最大收益是多少？若损失，最小损失是多少？(3)第二年，该企业决定给希望工程捐钱 Z 万元，该项捐钱由两部分构成：一部分为 10 万元的固定捐钱；另一部分则为每销售一件产品，就抽出一元钱作为捐钱．若除掉第一年的最大盈余( 或最小亏损) 以及第二年的捐钱后，到第二年年末，两年的总盈余不低于67、5万元，请你确立此时销售单价的范围．3．(2016 郴州 ) 某商铺本来均匀每日可销售某种水果200 千克，每千克可盈余 6 元．为减少库存，经市场检查，假如这类水果每千克降价1 元，则每日可多售出20 千克．(1)设每千克水果降价 x 元，均匀每日盈余 y 元，试写出 y 对于x的函数表达式；(2)若要均匀每日盈余 960 元，则每千克应降价多少元？4．(2015 邵阳 ) 为了响应政府提出的由中国制造向中国创建转型的呼吁，某企业自主设计了一款成本为40 元可控温杯，并投放市场进行试销售，经过检查发现该产品每日的销售量y( 件)与销售单价x(元)知足一次函数关系： y＝－10x＋1200、(1)求出收益 S(元)与销售单价 x(元)之间的关系式；(收益＝销售额－成本 )(2)当销售单价定为多少时，该企业每日获取的收益最大？最大收益是多少元？答案1、解：(1) 当 40≤x ≤60 时，设直线分析式为 y ＝kx ＋b ，40k ＋b ＝4k ＝－110，则，解得60k ＋b ＝2b ＝81∴ y ＝－ 10x ＋8，1同理，当 60＜x ≤80 时， y ＝－ 20x ＋5，1－ 10x ＋8（40≤x ≤60）∴ y ＝；(4 分)1－ 20x ＋5（60＜x ≤80）(2) 设该企业可安排职工 a 人，当销售单价 x ＝50 元时，1由题意得， 5＝( －10×50＋ 8)(50 －40) － 15－0、25a ，解得 a ＝40、答：该企业可安排职工 40 人； (7 分)(3) 设该企业每个月的收益为 w 万元，1当 40≤x ≤60 时，收益 w 1＝( －10x ＋8)( x －40) －15－0、25×8012＝－( x －60) ＋5，1∵－ 10＜ 0，∴ w 1 有最大值，∴当 x ＝60 时， w 最大＝5( 万元 ) ；(8 分)1当60＜x≤80 时，收益w2＝( －20x＋5)( x－40) －15－0、25×80 12＝－( x－70) ＋10，1∵－20＜ 0，∴ w2有最大值，∴当 x＝70时， w最大＝10(万元)，(9分)∴要尽早还清贷款，只有当单价x＝70元时，获取最大月收益10万元，设该企业 n 个月后还清贷款，则10n≥80，∴n≥8、答：该企业最早可在8 个月后还清无息贷款． (10 分)2、解：(1) 当x＝28 时，将x＝28 代入y＝40－x得y＝40－28＝12( 万件 ) ；(3 分)(2)分两种情况来议论：①当 25≤x≤30 时，W＝(40 －x)( x－20) －25－100＝－x2＋60x－925＝－(x－30) 2－25，∵－ 1＜0，∴ W有最大值，∴当 x＝30时， W最大为－25万元，即该企业最小损失是25 万元； (4 分)1 2②当 30＜x≤35 时，W＝(25 －0、5x)( x－20) －25－100＝－2x＋35x－625＝－12( x－35) －12、5，1∵－2＜0，∴ W有最大值，∴当 x＝35时，W最大为－12、5万元，即该企业最小损失是12、5 万元； (5 分)综合①②可知，投资的第一年，该企业是损失的，最小损失是 12、5 万元； (6 分)(3)分两种情况来议论：①当 25≤x≤30 时，W＝(40 －x)( x－20－1) －12、5－10＝－x2＋61x－862、5，由题意得， W≥67、5，即－ x2＋61x－862、5≥67、5，化简得 x2－61x＋930≤0，解得 30≤x≤31，∴ x＝30，此时当销售单价为30 元时两年的总盈余不低于67、5 万元； (8分)②当 30＜x≤35 时，W＝(25 －0、5x)( x－20－1) －12、5－10＝1 2－2x ＋35、5x－547、5，1 2由题意得， W≥67、5，即－2x ＋35、5x－547、5≥67、5，化简得x2－71x＋1230≤0，解得 30≤x≤41，∴30＜x≤35，综上所述，当两年的总盈余不低于67、5 万元时，销售单价的范围是 30≤x≤35、 (10 分)3、解：(1) 依据题意，得y＝(6－x)(200＋20x)＝－20x2－80x＋1200，∴y 对于 x 的函数表达式为 y＝－20x2－80x＋1200；(2)令 y＝960，得－20x2－80x＋1200＝960，解得 x1＝2，x2＝－6(舍去)．答：若要均匀每日盈余 960 元，则每千克应降价 2 元．4、解：(1) ∵每件成本 40 元，销售单价为x 元，∴每件收益为 ( x－40) 元，∴S＝( x －40) y＝( x －40)(－10x＋1200)＝－10x2＋1600x －48000，即S＝－10x2＋1600x－48000(x＞40)；b1600(2)∵a＝－10＜0，函数的对称轴 x＝－2a＝－2×（－10）＝80，∴当销售单价定为 80 元时，收益最大，当 x＝80时， S＝16000元、答：当销售单价定为 80 元时，该企业每日获取收益最大，最大收益为 16000 元．。

2009年至2017年长沙市中考分类汇编及答案：第23课时矩形、菱形、正方形(Word版)

第 4 题图
命题点 2 菱形的相关证明与计算 (9 年 7 考)
5. (2014 长沙 8 题 3 分)如图，已知菱形 ABCD 的边长为 2，∠ DAB＝ 60°，则对角线 BD 的长是 ( )
A．1 B. 3 C．2 D．2 3
第 5 题图
第 6 题图
6. (2012 长沙 8 题 3 分 )如图，菱形 ABCD 中，对角线 AC 与 BD 相交于点 O，
第 12 题图
命题点 3 正方形的相关证明与计算 (9 年 3 考)
第 13 题图
13. (2017 长沙 12 题 3 分 )如图，将正方形 ABCD 折叠，使顶点 A 与 CD 边上
的一点 H 重合 (H 不与端点 C， D 重合 )，折痕交 AD 于点 E，交 BC 于点 F，
边 AB 折叠后与边 BC 交于点 G，设正方形 ABCD 的周长为 m，△CHG 的周
n 长为 n，则 m的值为 ( )
2
1
A. 2
B. 2
5－ 1 C. 2
D. 随 H 点位置的变化而变化
14. (2011 长沙 22 题 8 分)在正方形 ABCD 中， AC 为对角线， E 为 AC 上一
点，连接 EB、ED. (1)求证：△ BEC≌△ DEC； (2)延长 BE 交 AD 于 F，当∠ BED＝120°时，求∠ EFD 的度数．
第 14 题图 15. (2012 长沙 24 题 9 分 )如图，已知在正方形 ABCD 中， BE 平分∠ DBC 且交 CD 边于点 E，将△ BCE 绕点 C 顺时针旋转到△ DCF 的位置，并延长 BE 交 DF 于点 G. (1)求证：△ BDG∽△ DEG； (2)若 EG·BG＝4，求 BE 的长．

长沙中考数学试题9年分类汇编 (2009～2017)- 函数

第三单元函数第十课时平面直角坐标系与函数长沙9年中考(2009～2017) 命题点1 点的平移(9年2考)1.(2016长沙8题3分)若将点A(1，3)向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为()A. (－2，－1)B. (－1，0)C. (－1，－1)D. (－2，0)2. (2011长沙4题3分)如图，在平面直角坐标系中，点P(－1，2)向右平移3个单位长度后的坐标是()第2题图A. (2，2)B. (－4，2)C. (－1，5)D. (－1，1)3．(2013邵阳)如图是我市几个旅游景点的大致位置示意图，如果用(0，0)表示新宁崀山的位置，用(1，5)表示隆回花瑶的位置，那么城步南山的位置可以表示为()A. (2，1)B. (0，1)C. (－2，－1)D. (－2，1)第3题图4．(2017邵阳)如图所示，三架飞机P ，Q ，R 保持编队飞行，某时刻在坐标系中的坐标分别为(－1，1)，(－3，1)，(－1，－1).30秒后，飞机P 飞到P ′(4，3)位置，则飞机Q ，R 的位置Q′，R′分别为( )A. Q ′(2，3)，R ′(4，1)B. Q ′(2，3)，R ′(2，1)C. Q ′(2，2)，R ′(4，1)D. Q ′(3，3)，R ′(3，1)命题点2 函数自变量的取值范围(9年2考)5. (2010长沙2题3分)函数y ＝1x ＋1的自变量x 的取值范围是( )A . x ＞－1B . x ＜－1C . x ≠－1D . x ≠16. (2012长沙11题3分)已知函数关系式y ＝x －1，则自变量x 的取值范围是________．命题点3 分析判断函数图像(仅2012年考查)7. (2012长沙7题3分)小明骑自行车上学，开始时以正常速度匀速行驶，但行至中途时，自行车出了故障，只好停下来修车，车修好后，因怕耽误上课，他比修车前加快了速度继续匀速行驶．下面是行驶路程s (m )关于时间t (min )的函数图象，那么符合小明行驶情况的大致图象是( )8．(2014衡阳)小明从家出发，外出散步，到一个公共阅报栏前看了一会报后，继续散步了一段时间，然后回家．如图描述了小明在散步过程中离家的距离s (米)与散步所用时间t(分)之间的函数关系．根据图象，下列信息错误．．的是( )A. 小明看报用时8分钟B. 公共阅报栏距小明家200米C. 小明离家最远的距离为400米D. 小明从出发到回家共用时16分钟9．(2016湘潭)如图，等腰直角△EFG 的直角边GE 与正方形ABCD 的边BC 在同一直线上，且点E 与点B 重合，△EFG 沿BC 方向匀速运动，当点G 与点C 重合时停止运动．设运动时间为t ，运动过程中△EFG 与正方形ABCD 的重叠部分面积为S ，则S 关于t 的函数图象大致为( )第9题图答案1. C2. A3. C4. A5. C6. x ≥17. C 【解析】由题意可知，小明开始匀速行驶，图象为倾斜直线；修车时路程不变，图象为平行于t 轴的线段；后来速度加快，图象为倾斜直线，且倾斜程度变大．8. A9. A 【解析】如解图①，由题意得BE ＝BM ＝t ，∴S ＝12·t ·t ＝12t 2, 其图象是第一象限内开口向上的一段图象；如解图②，线段GE 在线段BC 上移动时，重合部分的面积就是△GEF 的面积，其图象是第一象限内一条平行于x 轴的线段；如解图③，把△FGE 的面积当做“1”，设CE ＝CN ＝t′，则重合部分四边形FGCN 的面积＝1－12·t ′·t ′＝1－12t′2，即S ＝－12t ′2＋1，其图象是第一象限内开口向下的一段图象．故选A.第三单元函数第十一课时一次函数及其应用长沙9年中考(2009～2017) 命题点1 一次函数的图像与性质(9年5考)1. (2015长沙9题3分)一次函数y＝－2x＋1的图象不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2. (2012长沙14题3分)如果一次函数y＝mx＋3的图象经过第一、二、四象限，则m的取值范围是________．命题点2 一次函数与几何结合(9年2考)3.(2014长沙18题3分)如图，在平面直角坐标系中，已知点A(2，3)，点B(－2，1)，在x轴上存在点P到A，B两点的距离之和最小，则P点的坐标是________．第3题图4．(2014株洲)直线y＝k1x＋b1(k1＞0)与y＝k2x＋b2(k2＜0)相交于点(－2，0)，且两直线与y轴围成的三角形面积为4，那么b1－b2等于________．5．(2014永州)如图，已知直线l1：y＝k1x＋4与直线l2：y＝k2x－5交于点A，它们与y轴的交点分别为点B，C，点E，F分别为线段AB、AC的中点，则线段EF的长度为________．第5题图第6题图6．(2014株洲)如图，已知A、B、C、D是平面直角坐标系中坐标轴上的点，且△AOB≌△COD，设直线AB的表达式为y＝k1x＋b1，直线CD的表达式为y ＝k 2x ＋b 2，则k 1·k 2＝________．命题点3 一次函数的实际应用(9年2考)7. (2017长沙24题9分)连接湖南与欧洲的“湘欧快线”开通后，我省与欧洲各国经贸往来日益频繁，某欧洲客商准备在湖南采购一批特色商品，经调查，用16000元采购A 型商品的件数是用7500元采购B 型商品的件数的2倍，一件A 型商品的进价比一件B 型商品的进价多10元．(1)求一件A ，B 型商品的进价分别为多少元？(2)若该欧洲客商购进A ，B 型商品共250件进行试销，其中A 型商品的件数不大于B 型商品的件数，且不小于80件，已知A 型商品的售价为240元/件，B 型商品的售价为220元/件，且全部售出，设购进A 型商品m 件，求该客商销售这批商品的利润y 与m 之间的函数关系式，并写出m 的取值范围；(3)在(2)的条件下，欧洲客商决定在试销活动中每售出一件A 型商品，就从一件A 型商品的利润中捐献慈善资金a 元，求该客商售完所有商品并捐献慈善资金后获得的最大收益．答案1. C2. m ＜03. (－1，0) 【解析】如解图，作点B 关于x 轴的对称点C ，得到点C 的坐标是(－2，－1)，设直线AC 的解析式为y ＝kx ＋b ，代入点A 、C 的坐标，得⎩⎨⎧2k ＋b ＝3－2k ＋b ＝－1，解得⎩⎨⎧k ＝1b ＝1，∴直线AC 的解析式为y ＝x ＋1，直线AC 与x 轴交点P 的坐标是(－1，0)．第3题解图4. 4 【解析】如解图，直线y ＝k 1x ＋b 1(k 1＞0)与y 轴交于B 点，则OB ＝b 1，直线y ＝k 2x ＋b 2(k 2＜0)与y 轴交于C 点，则OC ＝－b 2，∵△ABC 的面积为4，∴12OA ·OB ＋12OA ·OC ＝4，∴12×2·b 1＋12×2·(－b 2)＝4，解得：b 1－b 2＝4.第4题解图5. 92 【解析】∵直线l 1：y ＝k 1x ＋4，直线l 2：y ＝k 2x －5，∴B (0，4)，C (0，－5)，则BC ＝9.又∵点E ，F 分别为线段AB 、AC 的中点，∴EF 是△ABC的中位线，∴EF ＝12BC ＝92.6. 1 【解析】直线AB 与x 轴的交点坐标为(－b 1k 1，0)，与y 轴的交点坐标为(0，b 1)，直线CD 与x 轴的交点坐标为(－b 2k 2，0)，与y 轴的交点坐标为(0，b 2)，∵△AOB ≌△COD ，∴OA ＝OC ，OB ＝OD ，∴－b 1k 1＝b 2，－b 2k 2＝ b 1，整理得，k 1k 2＝1.7. 解：(1)设B 型商品的进价为x 元，则A 型商品的进价为(x ＋10)元，根据题意得 16000x ＋10＝2×7500x ，解得x ＝150，经检验，x ＝150是原方程的解，且符合题意，∴x ＋10＝160(元)．答：A 型商品的进价为160元，B 型商品的进价为150元；(3分)(2)根据题意，A 型商品每件的利润为240－160＝80(元)，B 型商品每件的利润为220－150＝70(元)，则销售完这批商品的总利润为y ＝80m ＋70(250－m )＝10m ＋17500，∵A 型商品的件数不超过B 型商品的件数，且不小于80件，∴80≤m ≤250－m ，∴m 的取值范围是80≤m ≤125，∴y ＝10m ＋17500(80≤m≤125)；(6分)(3)设该客商售完所有商品并捐献慈善资金后获得的收益是w 元．根据题意，w ＝(80－a )m ＋70(250－m )＝(10－a )m ＋17500(80≤m ≤125)， ∴当0≤a ＜10时，w 随m 的增大而增大，即m ＝125时，w 最大＝125(10－a )＋17500＝－125a ＋18750(元)；当a ＝10时，w ＝17500(元)；当10＜a ≤80时，y 随m 的增大而减小，即m ＝80时，w 最大＝80(10－a )＋17500＝－80a ＋18300.综上所述，w 最大＝⎩⎨⎧－125a ＋18750 （0≤a ＜10）17500 （a ＝10）－80a ＋18300 （10＜a≤80）.(9分)第三单元函数第十二课时反比例函数及其应用长沙9年中考 (2009～2017)命题点1 反比例函数表达式的确定(9年3考)1. (2011长沙12题3分)反比例函数y ＝k x 的图象经过点A (－2，3)，则k 的值为________．2. (2012长沙9题3分)某闭合电路中，电源的电压为定值，电流强度I (A )与电阻R (Ω)成反比例函数关系．其函数图象如图所示，则电流I (A )与电阻R (Ω)的函数解析式为( )A . I ＝2RB . I ＝3RC . I ＝6RD . I ＝－6R第2题图命题点2 反比例函数的图象与性质(9年6考)3. (2010长沙13题3分)已知反比例函数y ＝1－m x 的图象如图，则m 的取值范围是________．第3题图第4题图 4. (2017长沙18题3分)如图，点M 是函数y ＝3x 与y ＝k x 的图象在第一象限内的交点，OM ＝4，则k 的值为________．5. (2009长沙22题6分)反比例函数y ＝2m －1x 的图象如图所示，A (－1，b 1)，B (－2，b 2)是该图象上的两点．(1)比较b 1与b 2的大小；(2)求m 的取值范围．第5题图答案1. －62. C3. m ＜1 【解析】由于反比例函数的图象在第一、三象限，结合反比例函数的图象性质可得1－m ＞0，解得m ＜1.4. 43 【解析】∵点M 在函数y ＝3x 的图象上，∴设点M 的坐标为(m ， 3m )，∵OM ＝4，∴m 2＋(3m )2＝42，解得m ＝±2，∵点M 在第一象限，∴m ＞0，即点M 的坐标为(2，23)，∵点M 在反比例函数y ＝k x 上，∴k＝xy ＝2×23＝4 3.5. 解：(1)由题图可知，在第三象限内，y 随x的增大而减小，∵－1＞－2，∴b 1＜b 2；(3分)(2)∵函数图象在第一、三象限，∴2m －1＞0，解得m ＞12.(6分) 第三单元函数第十三课时二次函数的图象与性质长沙9年中考 (2009～2017)命题点1 二次函数的顶点坐标、对称轴与增减性(9年4考)1. (2011长沙7题3分)如图，关于抛物线y ＝(x －1)2－2，下列说法错误的是( )A . 顶点坐标为(1，－2)B . 对称轴是直线x ＝1C . 开口方向向上D . 当x ＞1时，y 随x 的增大而减小命题点2 二次函数图象与a 、b 、c 的关系(9年3考)2. (2014长沙10题3分)函数y ＝a x 与y ＝ax 2(a≠0)在同一平面直角坐标系中的图象可能是( )3. (2013长沙10题3分)二次函数y ＝ax 2＋bx ＋c 的图象如图所示，则下列关系式错误．．的是( ) A . a ＞0B . c ＞0C . b 2－4ac ＞0D . a ＋b ＋c ＞04. (2016长沙12题3分)已知抛物线y ＝ax 2＋bx ＋c (b ＞a ＞0)与x 轴最多有一个交点．现有以下四个结论：①该抛物线的对称轴在y 轴左侧；②关于x 的方程ax 2＋bx ＋c ＋2＝0无实数根；③a －b ＋c ≥0；④a ＋b ＋c b －a 的最小值为3.其中，正确结论的个数为( )A . 1个B . 2个C . 3个D . 4个命题点3 二次函数与一元二次方程的关系(9年6考)5. (2010长沙25题10分)已知：二次函数y＝ax 2＋bx －2的图象经过点(1，0)，一次函数图象经过原点和点(1，－b )，其中a ＞b ＞0且a 、b 为实数．(1)求一次函数的表达式(用含b 的式子表示)；(2)试说明：这两个函数的图象交于不同的两点； (3)设(2)中的两个交点的横坐标分别为x 1、x 2，求|x 1－x 2|的取值范围．答案1. D2. D 【解析】反比例函数图象在第一、三象限，故a ＞0，二次函数图象开口向下，故a ＜0，故A 错误；反比例函数图象在第二、四象限，故a ＜0，二次函数图象开口向上，故a ＞0，故B 错误；二次函数图象开口向上，故a >0，当a ＞0时，反比例函数图象在第一、三象限，而图中反比例函数图象在第一、二象限，不符合反比例函数图象的性质，故C 错误；反比例函数图象在第二、四象限，故a ＜0，二次函数图象开口向下，故a ＜0，故D 正确．3. D4. D 【解析】∵b >a>0，∴抛物线的对称轴x ＝－b 2a <0，∴对称轴在y 轴左侧，故①正确；∵抛物线y ＝ax 2＋bx ＋c 与x 轴最多有一个交点，且抛物线的开口向上，∴y ＝ax 2＋bx ＋c ≥0，∴方程ax 2＋bx ＋c ＋2≥2，即ax 2＋bx ＋c ＋2＝0无实数根，故②正确；由②得，y ＝ax 2＋bx ＋c≥0，∴当x ＝－1时，y ＝a －b ＋c ≥0，故③正确；∵当x ＝－2时，y ＝4a －2b ＋c ≥0，∴a ＋b ＋c ≥3(b －a )，∵b >a >0，∴a ＋b ＋c b －a ≥3，即a ＋b ＋c b －a的最小值为3，故④正确．综上所述，正确结论的个数为4个．5. (1)解：∵一次函数图象经过原点，∴设一次函数的表达式为y ＝kx ，∵一次函数图象过点(1，－b )，∴k ＝－b ，∴一次函数的表达式为y ＝－bx ；(3分)(2)证明：∵y ＝ax 2＋bx －2的图象经过点(1，0)，∴a ＋b ＝2，即b ＝2－a ，联立⎩⎨⎧y ＝－bx y ＝ax 2＋bx －2，整理得ax 2＋2(2－a )x －2＝0①， ∵Δ＝4(2－a )2＋8a ＝4(a －1)2＋12＞0，∴方程①有两个不相等的实数根，即方程组有两组不同的解，∴这两个函数的图象交于不同的两点；(6分)(3)解：∵两交点的横坐标x 1、x 2分别是方程①的解，∴x 1＋x 2＝2（a －2）a ＝2a －4a ，x 1x 2＝－2a， ∴|x 1－x 2|＝（x 1＋x 2）2－4x 1x 2＝4a 2－8a ＋16a 2＝（4a －1）2＋3，(8分) ∵a ＞b ＞0，a ＋b ＝2，∴2＞a ＞1，令t ＝(4a －1)2＋3，∵当1＜a ＜2时，t 随a 的增大而减小，∴4＜(4a －1)2＋3＜12，(9分)∴2＜（4a －1）2＋3＜23， ∴2＜|x 1－x 2|＜2 3.(10分)第三单元函数第十四课时二次函数的实际应用长沙9年中考 (2009～2017)1. (2009长沙25题10分)为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月工资为2500元，公司每月需支付其他费用15万元，该产品每月销量y(万件)与销售单价x (元)之间的函数关系如图所示．(1)求月销售量y(万件)与销售单价x (元)之间的函数关系式；(2)当销售单价定为50元时，为保证公司月利润达到5万元(利润＝销售额－生产成本－员工工资－其他费用)，该公司可安排员工多少人？(3)若该公司有80名员工，则该公司最早可在几个月后还清无息贷款？第1题图2. (2012长沙25题10分)在长株潭建设两型社会的过程中，为推进节能减排，发展低碳经济，我市某公司以25万元购得某项节能产品的生产技术后，再投入100万元购买生产设备，进行该产品的生产加工．已知生产这种产品的成本价为每件20元，经过市场调研发现，该产品的销售单价定在25元到35元之间较为合理，并且该产品的年销售量y (万件)与销售单价x (元)之间的函数关系式为：y ＝⎩⎨⎧40－x （25≤x≤30）25－0.5x （30＜x≤35）. (年获利＝年销售收入－生产成本－投资成本)(1)当销售单价定为28元时，该产品的年销售量为多少万件？(2)求该公司第一年的年获利W (万元)与销售单价x (元)之间的函数关系式，并说明投资的第一年，该公司是盈利还是亏损？若盈利，最大利润是多少？若亏损，最小亏损是多少？(3)第二年，该公司决定给希望工程捐款Z 万元，该项捐款由两部分组成：一部分为10万元的固定捐款；另一部分则为每销售一件产品，就抽出一元钱作为捐款．若除去第一年的最大盈利(或最小亏损)以及第二年的捐款后，到第二年年底，两年的总盈利不低于67.5万元，请你确定此时销售单价的范围．3．(2016郴州)某商店原来平均每天可销售某种水果200千克，每千克可盈利6元．为减少库存，经市场调查，如果这种水果每千克降价1元，则每天可多售出20千克．(1)设每千克水果降价x 元，平均每天盈利y 元，试写出y 关于x 的函数表达式；(2)若要平均每天盈利960元，则每千克应降价多少元？4．(2015邵阳)为了响应政府提出的由中国制造向中国创造转型的号召，某公司自主设计了一款成本为40元可控温杯，并投放市场进行试销售，经过调查发现该产品每天的销售量y(件)与销售单价x (元)满足一次函数关系：y ＝－10x ＋1200.(1)求出利润S (元)与销售单价x (元)之间的关系式；(利润＝销售额－成本)(2)当销售单价定为多少时，该公司每天获取的利润最大？最大利润是多少元？答案1. 解：(1)当40≤x ≤60时，设直线解析式为y ＝kx ＋b ，则⎩⎨⎧40k ＋b ＝460k ＋b ＝2，解得⎩⎪⎨⎪⎧k ＝－110b ＝8， ∴y ＝－110x ＋8，同理，当60＜x ≤80时，y ＝－120x ＋5，∴y ＝⎩⎪⎨⎪⎧－110x ＋8（40≤x≤60）－120x ＋5（60＜x≤80）；(4分) (2)设该公司可安排员工a 人，当销售单价x ＝50元时，由题意得，5＝(－110×50＋8)(50－40)－15－0.25a ，解得a ＝40.答：该公司可安排员工40人；(7分)(3)设该公司每月的利润为w 万元，当40≤x ≤60时，利润w 1＝(－110x ＋8)(x －40)－15－0.25×80＝－110(x －60)2＋5，∵－110＜0，∴w 1有最大值，∴当x ＝60时，w 最大＝5(万元)；(8分)当60＜x ≤80时，利润w 2＝(－120x ＋5)(x －40)－15－0.25×80＝－120(x －70)2＋10，∵－120＜0，∴w2有最大值，∴当x＝70时，w最大＝10(万元)，(9分)∴要尽早还清贷款，只有当单价x＝70元时，获得最大月利润10万元，设该公司n个月后还清贷款，则10n≥80，∴n≥8.答：该公司最早可在8个月后还清无息贷款．(10分)2.解：(1)当x＝28时，将x＝28代入y＝40－x得y＝40－28＝12(万件)；(3分)(2)分两种情形来讨论：①当25≤x≤30时，W＝(40－x)(x－20)－25－100＝－x2＋60x－925＝－(x－30)2－25，∵－1＜0，∴W有最大值，∴当x＝30时，W最大为－25万元，即该公司最小亏损是25万元；(4分)②当30＜x≤35时，W＝(25－0.5x)(x－20)－25－100＝－12x2＋35x－625＝－12(x－35)2－12.5，∵－12＜0，∴W有最大值，∴当x＝35时，W最大为－12.5万元，即该公司最小亏损是12.5万元；(5分)综合①②可知，投资的第一年，该公司是亏损的，最小亏损是12.5万元；(6分)(3)分两种情形来讨论：①当25≤x≤30时，W＝(40－x)(x－20－1)－12.5－10＝－x2＋61x－862.5，由题意得，W≥67.5，即－x2＋61x－862.5≥67.5，化简得x2－61x＋930≤0，解得30≤x≤31，∴x＝30，此时当销售单价为30元时两年的总盈利不低于67.5万元；(8分)②当30＜x≤35时，W＝(25－0.5x)(x－20－1)－12.5－10＝－12x2＋35.5x－547.5，由题意得，W≥67.5，即－12x2＋35.5x－547.5≥67.5，化简得x2－71x＋1230≤0，解得30≤x≤41，∴30＜x≤35，综上所述，当两年的总盈利不低于67.5万元时，销售单价的范围是30≤x≤35.(10分)3. 解：(1)根据题意，得y＝(6－x)(200＋20x)＝－20x2－80x＋1200，∴y关于x的函数表达式为y＝－20x2－80x＋1200；(2)令y＝960，得－20x2－80x＋1200＝960，解得x1＝2，x2＝－6(舍去)．答：若要平均每天盈利960元，则每千克应降价2元．4. 解：(1)∵每件成本40元，销售单价为x元，∴每件利润为(x－40)元，∴S＝(x－40)y＝(x－40)(－10x＋1200)＝－10x2＋1600x－48000，即S＝－10x2＋1600x－48000(x＞40)；(2)∵a＝－10＜0，函数的对称轴x＝－b2a＝－16002×（－10）＝80，∴当销售单价定为80元时，利润最大，当x＝80时，S＝16000元.答：当销售单价定为80元时，该公司每天获得利润最大，最大利润为16000元．第三单元函数第十五课时二次函数的综合性问题长沙9年中考(2009～2017)命题点1 与函数有关的阅读理解(9年6考)1．(2016长沙25题10分)若抛物线L：y＝ax2＋bx＋c(a，b，c是常数，abc≠0)与直线l都经过y轴上的一点P，且抛物线L的顶点Q在直线l上，则称此直线l与该抛物线L具有“一带一路”关系．此时直线l叫做抛物线L的“带线”，抛物线L叫做直线l的“路线”．(1)若直线y＝mx＋1与抛物线y＝x2－2x＋n具有“一带一路”关系，求m，n 的值；(2)若某“路线”L的顶点在反比例函数y＝6x的图象上，它的“带线”l的解析式为y＝2x－4，求此“路线”L的解析式；(3)当常数k满足12≤k≤2时，求抛物线L：y＝ax2＋(3k2－2k＋1)x＋k的“带线”l与x轴，y轴所围成的三角形面积的取值范围．2．(2015长沙25题10分)在直角坐标系中，我们不妨将横坐标、纵坐标均．为整数的点．．．．．称之为“中国结”．(1)求函数y＝3x＋2的图象上所有“中国结”的坐标；(2)若函数y＝kx(k≠0，k为常数)的图象上有且只有两个“中国结”，试求出常数k的值与相应“中国结”的坐标；(3)若二次函数y＝(k2－3k＋2)x2＋(2k2－4k＋1)x＋k2－k(k为常数)的图象与x 轴相交得到两个不同的“中国结”，试问该函数的图象与x轴所围成的平面图形中(含边界)，一共包含有多少个“中国结”？3．(2014长沙25题10分)在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为“梦之点”．例如点(－1，－1)，(0，0)，(2，2)，…都是“梦之点”，显然，这样的“梦之点”有无数个．(1)若点P(2，m)是反比例函数y＝nx(n为常数，n≠0)的图象上的“梦之点”，求这个反比例函数的解析式；(2)函数y＝3kx＋s－1(k，s是常数)的图象上存在“梦之点”吗？若存在，请求出“梦之点”的坐标；若不存在，请说明理由；(3)若二次函数y＝ax2＋bx＋1(a，b是常数，a>0)的图象上存在两个不同的“梦之点”A(x1，x1)，B(x2，x2)，且满足－2<x1<2，|x1－x2|＝2，令t＝b2－2b＋157 48，试求t的取值范围．4．(2013长沙25题10分)设a，b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”．(1)反比例函数y＝2013x是闭区间[1，2013]上的“闭函数”吗？请判断并说明理由；(2)若一次函数y＝kx＋b(k≠0)是闭区间[m，n]上的“闭函数”，求此函数的解析式；(3)若二次函数y＝15x2－45x－75是闭区间[a，b]上的“闭函数”，求实数a，b的值．5. (2017长沙25题10分)若三个非零实数x，y，z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x，y，z构成“和谐三数组”．(1)实数1，2，3可以构成“和谐三数组”吗？请说明理由；(2)若M(t，y1)，N(t＋1，y2)，R(t＋3，y3)三点均在函数y＝kx(k为常数，k≠0)的图象上，且这三点的纵坐标y1，y2，y3构成“和谐三数组”，求实数t的值；(3)若直线y＝2bx＋2c(bc≠0)与x轴交于点A(x1，0)，与抛物线y＝ax2＋3bx ＋3c(a≠0)交于B(x2，y2)，C(x3，y3)两点．①求证：A，B，C三点的横坐标x1，x2，x3构成“和谐三数组”；②若a>2b>3c，x2＝1，求点P(ca，ba)与原点O的距离OP的取值范围．6．(2011长沙25题10分)使得函数值为零的自变量的值称为函数的零点．例如，对于函数y＝x－1，令y＝0，可得x＝1，我们就说1是函数y＝x－1的零点．已知函数y＝x2－2mx－2(m＋3)(m为常数)．(1)当m＝0时，求该函数的零点；(2)证明：无论m取何值，该函数总有两个零点；(3)设函数的两个零点分别为x 1和x 2，且1x 1＋1x 2＝－14，此时函数图象与x 轴的交点分别为A 、B (点A 在点B 左侧)，点M 在直线y ＝x －10上，当MA ＋MB 最小时，求直线AM 的函数解析式．命题点2 二次函数综合题(必考)7. (2016长沙26题10分)如图，直线l ：y ＝－x ＋1与x 轴，y 轴分别交于A ，B 两点，点P ，Q 是直线l 上的两个动点，且点P 在第二象限，点Q 在第四象限，∠POQ ＝135°.(1)求△AOB 的周长；(2)设AQ ＝t ＞0，试用含t 的代数式表示点P 的坐标；(3)当动点P ，Q 在直线l 上运动到使得△AOQ 与△BPO 的周长相等时，记tan ∠AOQ ＝m .若过点A 的二次函数y ＝ax 2＋bx ＋c 同时满足以下两个条件： ①6a ＋3b ＋2c ＝0；②当m ≤x ≤m ＋2时，函数y 的最大值等于2m .求二次项系数a 的值．第7题图8. (2017长沙26题10分)如图，抛物线y ＝mx 2－16mx ＋48m (m >0)与x 轴交于A ，B 两点(点B 在点A 左侧)，与y 轴交于点C ，点D 是抛物线上的一个动点，且位于第四象限，连接OD 、BD 、AC 、AD ，延长AD 交y 轴于点E.(1)若△OAC 为等腰直角三角形，求m 的值；(2)若对任意m >0，C ，E 两点总关于原点对称，求点D 的坐标(用含m 的式子表示)；(3)当点D 运动到某一位置时，恰好使得∠ODB ＝∠OAD ，且点D 为线段AE 的中点，此时对于该抛物线上任意一点P (x 0，y 0)总有n ＋16≥－43my 20－123y 0－50成立，求实数n 的最小值．第8题图9. (2010长沙26题10分)如图，在平面直角坐标系中，矩形OABC 的两边分别在x 轴和y 轴上，OA ＝8 2 cm ，OC ＝8 cm.现有两动点P 、Q 分别从O 、C 同时出发，P 在线段OA 上沿OA 方向以每秒 2 cm 的速度匀速运动，Q 在线段CO 上沿CO 方向以每秒1 cm 的速度匀速运动．设运动时间为t 秒．(1)用含t 的式子表示△OPQ 的面积S ；(2)求证：四边形OPBQ 的面积是一个定值，并求出这个定值；(3)当△OPQ 与△P AB 和△QPB 相似时，抛物线y ＝14x 2＋bx ＋c 经过B 、P 两点，过线段BP 上一动点M 作y 轴的平行线交抛物线于N ，当线段MN 的长取最大值时，求直线MN 把四边形OPBQ 分成两部分的面积之比．第9题图10. (2015长沙26题10分)若关于x 的二次函数y ＝ax 2＋bx ＋c (a ＞0，c ＞0，a ，b ，c 是常数)与x 轴交于两个不同的点A (x 1，0)，B (x 2，0)(0＜x 1＜x 2)，与y 轴交于点P ，其图象顶点为点M ，点O 为坐标原点．(1)当x 1＝c ＝2，a ＝13时，求x 2与b 的值；(2)当x 1＝2c 时，试问△ABM 能否为等边三角形？判断并证明你的结论；(3)当x 1＝mc(m ＞0)时，记△MAB 、△P AB 的面积分别为S 1、S 2，若△BPO ∽△P AO ，且S 1＝S 2，求m 的值．第10题图11. (2014长沙26题10分)如图，抛物线y＝ax2＋bx＋c(a，b，c是常数，a≠0)的对称轴为y轴，且经过(0，0)和(a，116)两点，点P在该抛物线上运动，以点P为圆心的⊙P总经过定点A(0，2)．(1)求a，b，c的值；(2)求证：在点P运动的过程中，⊙P始终与x轴相交；(3)设⊙P与x轴相交于M(x1，0)，N(x2，0)(x1＜x2)两点，当△AMN为等腰三角形时，求圆心P的纵坐标．第11题图12. (2009长沙26题10分)如图，二次函数y＝ax2＋bx＋c(a≠0)的图象与x 轴交于A、B两点，与y轴相交于点C，连接AC、BC，A、C两点的坐标分别为A(－3，0)，C(0，3)，且当x＝－4和x＝2时二次函数的函数值y相等．(1)求实数a，b，c的值；(2)若点M，N同时从B点出发，均以每秒1个单位长度的速度分别沿BA，BC边运动，其中一个点到达终点时，另一点也随之停止运动，当运动时间为t秒时，连接MN，将△BMN沿MN翻折，B点恰好落在AC边上的P处，求t的值及点P的坐标；(3)在(2)的条件下，二次函数图象的对称轴上是否存在点Q，使得以B，N，Q为顶点的三角形与△ABC相似？如果存在，请求出点Q的坐标；如果不存在，请说明理由．第12题图答案1．(1)解：由题意可知，直线y ＝mx ＋1与y 轴的交点P (0，1)在抛物线y ＝x 2－2x ＋n 上， ∴n ＝1，∴抛物线解析式为y ＝x 2－2x ＋1＝(x －1)2，则顶点Q 的坐标为(1，0)，将Q (1，0)代入y ＝mx ＋1得0＝m ＋1，∴m ＝－1， ∴m ＝－1，n ＝1；(2分)(2)设“路线”L 的解析式为y ＝a (x －h )2＋k ， ∵顶点(h ，k)在y ＝6x 和y ＝2x －4上，∴⎩⎪⎨⎪⎧k ＝6h k ＝2h －4，解得⎩⎨⎧h 1＝－1k 1＝－6或⎩⎨⎧h 2＝3k 2＝2， ∴顶点为(－1，－6)或(3，2)，(3分)∴“路线”L 的解析式为y ＝a (x ＋1)2－6或y ＝a(x －3)2＋2，(4分) ∵“路线”L 过(0，－4)，将(0，－4)代入“路线”L 的解析式，解得a ＝2或a ＝－23， ∴“路线”L 的解析式为y ＝2(x ＋1)2－6或y ＝－23(x －3)2＋2；(5分)(3)抛物线L 的顶点坐标为 Q (－3k 2－2k ＋12a，4ak－（3k2－2k＋1）24a)，与y轴的交点为P(0，k)，设“带线”l的解析式为y＝px＋k(p≠0)，代入顶点坐标得p＝3k2－2k＋12，∴y＝3k2－2k＋12x＋k，(6分)令y＝0，解得x＝－－2k3k2－2k＋1，∴“带线”l交x轴于(－－2k3k2－2k＋1，0)，∵12≤k≤2，3k2－2k＋1＝3(k－13)2＋23＞0，∴“带线”l与坐标轴围成的三角形面积为S＝12·2k3k2－2k＋1·k＝k23k2－2k＋1＝11k2－2·1k＋3，(8分)令t＝1 k，∵12≤k≤2，∴12≤t≤2，∴S＝1t2－2t＋3，∴1S＝t2－2t＋3＝(t－1)2＋2，∵12≤t≤2，1＞0，∴当t＝2，即k＝12时，S的最大值为3，此时1S的最小值为13；当t＝1时，即k＝1时，1S的最小值为2，此时S的最大值为12，∴13≤S≤12.故三角形面积的取值范围为13≤S≤12.(10分)2．解：(1)∵x的系数是无理数，∴只有当x＝0时，y才能取得整数，即当x＝0时，y＝2，此时坐标为(0，2)，∴函数y ＝3x ＋2的图象上所有“中国结”的坐标是(0，2)； (2分)(2)①当k ＝1时， xy ＝1，显然反比例函数的图象上有且只有两个“中国结”，其坐标分别为(1，1)、(－1，－1)；(3分)②当k ＝－1时， xy ＝－1，同理反比例函数的图象上有且只有两个“中国结”，其坐标分别为(－1，1)、(1，－1)；(3分)③当k ≠±1时，如k ＝2时，则图象上的“中国结”个数超过两个，有(2，1)、(－2，－1)、(1，2)、(－1，－2)，类似的当k ≠±1时，中国结个数必将多于两个．∴只有当k 值取±1时，反比例函数图象上有且只有两个“中国结”， ∴当k ＝1时，其相应“中国结”的坐标分别是(1，1)、(－1，－1)；当k ＝－1时，其相应“中国结”的坐标分别是(－1，1)、(1，－1)．(6分) (3)由题意得(k 2－3k ＋2)x 2＋(2k 2－4k ＋1)x ＋k 2－k ＝0，解得x 1＝－k k －1，x 2＝－k －1k －2， ∵交点都是“中国结”，∴当k ≠1且k ≠2时，关于x 的二次方程有两个不相等的整数根x 1、x 2，由x 1＝－k k －1，可得k ＝x 1x 1＋1，同理，由x 2＝－k －1k －2，可得k ＝ 2x 2＋1x 2＋1， ∴x 1x 1＋1＝2x 2＋1x 2＋1，化简得x 1x 2＋2x 2＝－1，即x 2(x 1＋2)＝－1， ∵x 1，x 2是整数，∴得到关于x 1，x 2的方程组： ⎩⎨⎧x 2＝1x 1＋2＝－1或⎩⎨⎧x 2＝－1x 1＋2＝1，解得⎩⎨⎧x 1＝－3x 2＝1或⎩⎨⎧x 1＝－1x 2＝－1(舍去)，(7分)当⎩⎨⎧x 1＝－3x 2＝1时，k ＝x 1x 1＋1＝32，此时二次函数解析式是y ＝－14x 2－12x ＋34＝－14(x ＋3)(x －1)＝1－14(x ＋1)2，(8分)∴由其图象可以得到，二次函数图象与x 轴所围成的平面图形中(含边界)，一共包含6个“中国结”，分别为(－3，0)，(－2，0)，(－1，0)，(－1，1)，(0，0)，(1，0)．(10分)3．(1)解：∵点P (2，m )是一个“梦之点”，且“梦之点”横、纵坐标相等， ∴m ＝2，即点P 坐标是(2，2)，又∵点P 在反比例函数y ＝nx 的图象上， ∴n ＝xy ＝4，∴反比例函数的解析式是y ＝4x ；(2分)(2)解：假设函数y ＝3kx ＋s －1图象上存在“梦之点”，则y ＝x ， ∴x ＝3kx ＋s －1，整理得(1－3k )x ＝s －1，分类讨论如下：①当k ＝13且s ＝1时，x 有无数个解，因此有无数个“梦之点”；(3分) ②当k ＝13且s ≠1时，方程无解，图象上所有的点都不是“梦之点”；(4分) ③当k ≠13时，图象上仅有一个“梦之点”(1－s 3k －1，1－s 3k －1)；(5分)(3)解：根据“梦之点”的定义得x ＝ax 2＋bx ＋1有两个不相等的实数根，即ax 2＋(b －1)x ＋1＝0(a ＞0，a 、b 都是常数)， ∴方程的根是－（b －1）±2a2a，∵|x 1－x 2|2＝(x 1＋x 2)2－4x 1x 2＝（b －1）2a 2－4a＝4，∴(b －1)2＝4a 2＋4a ，又∵Δ＝(b －1)2－4a ＝4a 2＞0，a ＞0， ∴(b －1)＝±2a 2＋a ，分类讨论如下：①当(b －1)＝2a 2＋a 时，方程的根是－2a 2＋a±2a 2a＝－a 2＋a±aa＝－1＋1a ±1，∵－2<x 1<2，且0<x 2<4，则－1＋1a －1不符合题意，取x ＝－1＋1a ＋1，显然x 1＝－1＋1a ＋1；(6分)②当(b －1)＝－2a 2＋a 时，方程的根是2a 2＋a±2a 2a ＝a 2＋a±aa ＝1＋1a±1，∵－2<x 1<2，且0<x 2<4， ∴x 1＝1＋1a －1， x 2＝1＋1a ＋1，根据题意，b 2－2b ＋15748＝t ，整理得(b －1)2＝t －10948， ∵(b －1)2＝4a 2＋4a ，∴4a 2＋4a ＋1＝(2a ＋1)2＝t －10948＋1＝t －6148，a ＞0，2a ＋1＞1＞0，(7分) ①的情况下：－2＜－1＋1a ＋1＜2，化简得－3＜－1＋1a ＜1，∴1＋1a ＜3，1＋1a ＜9，∴a ＋1＜9a ，则a ＞18，t －6148＝(2a ＋1)2＞(54)2，故t ＞176；(8分) ②的情况下：－2＜1＋1a －1＜2，－2＋1＜1＋1a －1＋1＜2＋1，－1＜1＋1a ＜3，∴1＋1a ＜3，1＋1a ＜9，∴a ＋1＜9a ，则a ＞18，t －6148＝(2a ＋1)2＞(54)2， ∴t ＞176，(9分)综上所述，t 的取值范围是t ＞176.(10分)4．解：(1)是．理由如下：根据“闭区间”和“闭函数”的规定， ∵反比例函数y ＝2013x 在第一象限，y 随x 的增大而减小，当x ＝1时，y ＝2013，当x ＝2013时，y ＝1，当1≤x ≤2013时，12013≤1x ≤1，1≤2013x ≤2013，即1≤y ≤2013，∴反比例函数y ＝2013x 是闭区间[1，2013]上的“闭函数”；(2分) (2)分两种情况讨论，k ＞0和k ＜0，①当k ＞0时，一次函数y 随x 的增大而增大，根据闭函数的定义有⎩⎨⎧km ＋b ＝m ①kn ＋b ＝n ②，①－②得k ＝1，代入①得b ＝0， ∴此时一次函数的解析式为y ＝x ；(4分)②当k ＜0时，此一次函数y 随x 的增大反而减小，根据闭函数的定义有⎩⎨⎧km ＋b ＝n ①kn ＋b ＝m ②，①－②得k ＝－1，代入①得b ＝m ＋n ，∴此时一次函数的解析式为y ＝－x ＋m ＋n ；(6分)(3)已知二次函数y ＝15(x －2)2－115，可知二次函数开口向上，对称轴是x ＝2，顶点坐标是(2，－115)，分三种情况讨论如下：①当a ＜b ≤2时，y 随x 增大而减小，当a ≤x≤b 时，15b 2－45b －75≤y ≤15a 2－45a －75，由闭函数的定义可得 ⎩⎪⎨⎪⎧15a 2－45a －75＝b ①15b 2－45b －75＝a ②，①－②得15(a ＋b )＝－15，由于a ≠b ，得a ＋b ＝－1，a ＝－b －1，代入方程②得b 2＋b －2＝0，解得b ＝－2(不符合题意，舍去)或b ＝1，由于a ＜b ，b ＝1，a ＝－2，故⎩⎨⎧a ＝－2b ＝1；(7分)②当a ＜2＜b 时，函数的最小值为－115，根据闭函数的定义，当a ≤x ≤b 时，－115≤y ≤15a 2－45a －75或－115≤y ≤15b 2－45b －75，于是⎩⎪⎨⎪⎧a ＝－11515a 2－45a －75＝b 或⎩⎪⎨⎪⎧a ＝－11515b 2－45b －75＝b，解得⎩⎪⎨⎪⎧a ＝－115b ＝166125＜2(舍去)或⎩⎪⎨⎪⎧a ＝－115b ＝9＋1092＞2或⎩⎪⎨⎪⎧a ＝－115b ＝9－1092＜2(舍去)；(8分)③当2≤a ＜b 时，y 随x 增大而增大，当a ≤x ≤b 时，15a 2－45a －75≤y ≤15b 2－45b －75，根据闭函数的定义有，15a 2－45a －75＝a ，15b 2－45b －75＝b ，即a 、b 是15s 2－95s －75＝0的两个根，s ＝9±1092，其中9－1092(不符合题意，舍去)，(9分)综上所述，a 、b 的值为⎩⎨⎧a ＝－2b ＝1或⎩⎪⎨⎪⎧a ＝－115b ＝9＋1092 .(10分)5. 解：(1)不能．理由如下：∵ 1的倒数为1，2的倒数为12，3的倒数为13， ∴1＞12＞13， ∵12＋13＝56≠1，∴1，2，3不能构成“和谐三数组”；(3分)(2)∵M (t ，y 1)，N(t ＋1，y 2)，R (t ＋3，y 3)三点均在反比例函数y ＝kx 的图象上， ∴y 1＝k t ，y 2＝k t ＋1，y 3＝k t ＋3，∴1y 1＝t k ，1y 2＝t ＋1k ，1y 3＝t ＋3k ， ∵y 1，y 2，y 3构成“和谐三数组”，∴(i )1y 1＋1y 2＝1y3，即t k ＋t ＋1k ＝t ＋3k ，解得t ＝2；(ii ) 1y 1＋1y 3＝1y 2，即t k ＋t ＋3k ＝t ＋1k ，解得t ＝－2；(iii )1y 2＋1y 3＝1y 1，即t ＋1k ＋t ＋3k ＝t k ，解得t ＝－4.综上所述，t 的值为－4或－2或2；(6分) (3)①直线y ＝2bx ＋2c ，令y ＝0，得x 1＝－c b ，联立抛物线与直线得⎩⎨⎧y ＝ax 2＋3bx ＋3c y ＝2bx ＋2c，整理得ax 2＋bx ＋c ＝0， ∵直线与抛物线交于B (x 2，y 2)，C (x 3，y 3)两点， ∴x 2＋x 3＝－b a ，x 2·x 3＝ca ， ∴ 1x 2＋ 1x 3＝x 2＋x 3x 2·x 3＝－bac a＝－b c ＝1x 1， ∴A ，B ，C 三点的横坐标x 1，x 2，x 3能构成“和谐三数组”；(8分)②∵x 2＝1，则B 点坐标为(1，2b ＋2c )，将点B 代入抛物线y ＝ax 2＋3bx ＋3c 中，得a ＋3b ＋3c ＝2b ＋2c ，即b ＝－a －c ，又∵a ＞2b ＞3c ，∴a ＞－2a －2c ＞3c ，即－32＜c a ＜－25， ∵bc ≠0，∴b ≠0， ∴－a －c ≠0，即ca ≠－1，∵P (c a ，ba )，且P 到原点O 的距离为非负数，∴OP＝b2＋c2a2＝（a＋c）2＋c2a2＝1＋2ca＋2（ca）2＝2（ca＋12）2＋12，∴当ca＝－12时，OP min＝22，当ca＝－32时，OP max＝102，当ca＝－1时，OP＝1，∴22≤OP＜102且OP≠1.(10分)6．(1)解：当m＝0时，y＝x2－6，(1分)令y＝0，x2－6＝0，解得x＝6或x＝－6，即当m＝0时，该函数的零点为6、－6；(2分)(2)证明：令y＝0，则x2－2mx－2(m＋3)＝0，∴Δ＝b2－4ac＝(－2m)2－4×1×[－2(m＋3)]＝4m2＋8m＋24＝4(m2＋2m＋1－1)＋24＝4(m＋1)2＋20，∵无论m为何值，4(m＋1)2≥0，即4(m＋1)2＋20>0，∴一元二次方程x2－2mx－2(m＋3)＝0一定有两个不相等的实数根，(3分) ∴无论m取何值，函数y＝x2－2mx－2(m＋3)(m为常数)总有两个零点；(4分)(3)解：设函数的两个零点分别为x1和x2，则x1和x2是一元二次方程x2－2mx －2(m＋3)＝0的两个根，∴x1＋x2＝2m, x1·x2＝－2(m＋3)，∴1x1＋1x2＝x1＋x2x1x2＝2m－2（m＋3）＝－mm＋3，(5分)又∵1x1＋1x2＝－14，∴mm＋3＝14，解得m＝1，经检验，m＝1是mm＋3＝14的解，。

湖南长沙2009-2017年中考数学真题类编：第24课时圆的基本性质(Word版)

第六单元圆第二十四课时圆的基本性质长沙9年中考(2009～2017)命题点1 圆周角定理及其推论(必考)1、(2014长沙13题3分)如图，A，B，C是⊙O上的三点，∠AOB ＝100°，则∠ACB＝________度．第1题图第2题图2、(2009长沙5题3分)如图，AB是⊙O的直径，C是⊙O上一点，∠BOC＝44°，则∠A的度数为________．命题点2 垂径定理及其推论(9年4考)3、(2017长沙15题3分)如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD＝6，EB＝1，则⊙O的半径为________．第3题图第4题图4、 (2015长沙18题3分)如图，AB是⊙O的直径，点C是⊙O 上的一点，若BC＝6，AB＝10，OD⊥BC于点D，则OD的长为________．5、(2011长沙22题8分)如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB＝40°，∠APD＝65°、(1)求∠B的大小；(2)已知圆心O 到BD 的距离为3，求AD 的长．第5题图6、 (2012长沙22题8分)如图，A ，P ，B ，C是半径为8的⊙O 上的四点，且满足∠BAC ＝∠APC＝60°、(1)求证：△ABC 是等边三角形；(2)求圆心O 到BC 的距离OD 、第6题图答案1、 502、 22°3、 5 【解析】如解图，连接OC ，∵AB 是⊙O 的直径，CD ⊥AB 于点E ，∴CE ＝ED ＝3，∠CEO ＝90°，∵OB ＝OC ，EB ＝1，∴OE ＝OB －EB ＝OC －1，则在Rt △OCE 中，根据勾股定理得OE 2＋CE 2＝OC 2，即(OC －1)2＋32＝OC 2，解得OC ＝5、第3题解图4、 4 【解析】∵OD ⊥BC ，∴BD ＝CD ＝12BC ＝3，∠ODB ＝90°，又∵AB ＝10，∴OB ＝5，∴在Rt △BOD 中，OD ＝OB 2－BD 2＝52－32＝4、5．解：(1)∵∠APD 是△APC 的外角，∴∠APD ＝∠CAP ＋∠C ，(1分)∴∠C ＝∠APD －∠CAP ＝65°－40°＝25°，第5题解图∴∠B ＝∠C ＝25°；(4分)(2)如解图，过点O 作OE ⊥BD ，垂足为点E ，则OE ＝3，(5分) 由垂径定理可知BE ＝DE ，∵OA ＝OB ，∴OE 是△ABD 的中位线，(7分)∴AD ＝2OE ＝6、(8分)6．(1)证明：∵∠B ＝∠APC ＝60°，∠BAC ＝60°，∴∠ACB ＝60°，(2分)∴∠BAC ＝∠B ＝∠ACB ，(3分)∴△ABC 是等边三角形；(4分)第6题解图(2)解：如解图，连接OB ，OC ，∵OB ＝OC ，∠BOC ＝2∠BAC ＝120°，(5分)由垂径定理知∠BOD ＝12∠BOC ＝60°，(6分) ∴在Rt △OBD 中，OD ＝OB·cos 60°＝8×12＝4、(8分)。

2009年全国 117个地区中考试卷及答案

2009年全国各地中考试题及答案112份下载地址（截止到7月11日）（7月7日前的为红色）2009年安徽省初中毕业学业考试数学试题及答案2009年安徽省芜湖市初中毕业学业考试题及答案2009年北京高级中学中等学校招生考试数学试题及答案2009年福建省福州市课改实验区中考试卷及参考答案2009年福建省龙岩市初中毕业、升学考试试题及答案2009年福建省宁德市初中毕业、升学考试试题及答案2009年福建省莆田市初中毕业、升学考试试卷及答案2009年福建省泉州市初中毕业、升学考试试题及答案2009年福建省漳州市初中毕业暨高中阶段招生题及答案2009年甘肃省定西市中考数学试卷及答案2009年甘肃省兰州市初中毕业生学业考试试卷及答案2009年甘肃省庆阳市高中阶段学校招生考试题及答案2009年广东省佛山市高中阶段学校招生考试题及答案2009年广东省茂名市高中阶段招生考试试题及答案2009年广东省梅州市初中毕业生学业考试试题及答案2009年广东省清远市初中毕业生学业考试试题及答案2009年广东省深圳市初中毕业生学业考试试卷及答案2009年广东省肇庆市初中毕业生学业考试试题及答案2009年广西省崇左市初中毕业升学考试数学试题及答案2009年广西省桂林市百色市初中毕业暨升学试卷及答案2009年广西省河池市初中毕业暨升学统一考试卷及答案2009年广西省贺州市初中毕业升学考试试卷及答案2009年广西省柳州市初中毕业升学考试数学试卷及答案2009年广西省南宁市中等学校招生考试题及答案2009年广西省钦州市初中毕业升学考试试题卷及答案2009年广西省梧州市初中毕业升学考试卷及答案2009年贵州省安顺市初中毕业、升学招生考试题及答案2009年贵州省黔东南州初中毕业升学统一考试题及答案2009年河北省初中毕业生升学文化课考试试卷及答案2009年河南省初中学业水平暨高级中等学校招生卷及答2009年黑龙江省哈尔滨市初中升学考试题及答案2009年黑龙江省牡丹江市初中毕业学业考试题及答案2009年黑龙江省齐齐哈尔市初中毕业学业考试题及答案2009年黑龙江省绥化市初中毕业学业考试卷及答案（答案为扫描版）2009年湖北省鄂州市初中毕业及高中阶段招生题及答案2009年湖北省恩施自治州初中毕业生学业考试题及答案2009年湖北省黄冈市初中毕业生升学考试试卷及答案2009年湖北省黄石市初中毕业生学业考试联考卷及答案2009年湖北省黄石市初中毕业生学业考试试题及答案2009年湖北省十堰市初中毕业生学业考试试题及答案2009年湖北省武汉市初中毕业生学业考试试题及答案2009年湖北省襄樊市初中毕业、升学统一考试题及答案2009年湖北省孝感市初中毕业生学业考试试题及答案2009年湖北省宜昌市初中毕业生学业考试试题及答案2009年湖南省长沙市初中毕业学业考试试卷及答案2009年湖南省常德市初中毕业学业考试试题及答案2009年湖南省郴州市初中毕业考试数学试题及答案2009年湖南省衡阳市初中毕业学业考试试卷及参考答案2009年湖南省怀化市初中毕业学业考试卷及答案2009年湖南省娄底市初中毕业学业考试试题及答案2009年湖南省邵阳市初中毕业学业水平考试卷及答案2009年湖南省湘西自治州初中毕业学业考试卷及答案2009年湖南省益阳市普通初中毕业学业考试试卷及答2009年湖南省株洲市初中毕业学业考试数学试题及答案2009年吉林省长春市初中毕业生学业考试试题及答案2009年吉林省初中毕业生学业考试数学试题及答案2009年江苏省苏州市中考数学试题及答案（答案为扫描版）2009年江苏省中考数学试卷及参考答案2009年江西省中等学校招生考试数学试题及参考答案2009年辽宁省本溪市初中毕业生学业考试试题及答案2009年辽宁省朝阳市初中升学考试数学试题及答案2009年辽宁省抚顺市初中毕业生学业考试试卷及答案2009年辽宁省锦州市中考数学试题及答案2009年辽宁省铁岭市初中毕业生学业考试试题及答案2009年内蒙古赤峰市初中毕业、升学统一考试题及答案（答案为扫描版）2009年内蒙古自治区包头市高中招生考试试卷及答案2009年宁夏回族自治区初中毕业暨高中阶段招生题及答案2009年山东省德州市中等学校招生考试数学试题及答案2009年山东省东营市中等学校招生考试试题及答案2009年山东省济南市高中阶段学校招生考试试题及答案2009年山东省济宁市高中阶段学校招生考试试题及答案2009年山东省临沂市中考数学试题及参考答案2009年山东省日照市中等学校招生考试试题及参考答案2009年山东省泰安市高中段学校招生考试试题及答案2009年山东省威海市初中升学考试数学试卷及参考答案2009年山东省潍坊市初中学业水平考试数学试题及答案2009年山东省烟台市初中学生学业考试试题及答案2009年山东省枣庄市中等学校招生考试数学试题及答案2009年山东省中等学校招生考试数学试题及参考答案2009年山东省淄博市中等学校招生考试试题及答案2009年山西省初中毕业学业考试数学试卷及答案2009年山西省太原市初中毕业学业考试试卷及答案2009年陕西省初中毕业学业考试数学试题及答案2009年上海市初中毕业统一学业考试数学试卷及答案2009年四川省成都市高中学校统一招生考试试卷及答案2009年四川省达州市高中招生统一考试题及答案2009年四川省高中阶段教育学校招生统一考试题及答案2009年四川省泸州市高中阶段学校招生统一考试题及答（答案为扫描版）2009年四川省眉山市高中阶段教育学校招生试题及答案2009年四川省南充市高中阶段学校招生统一考试卷及答2009年四川省遂宁市初中毕业生学业考试试题及答案2009年台湾第一次中考数学科试题及答案2009年天津市初中毕业生学业考试数学试题及答案2009年新疆维吾尔自治区初中毕业生学业考试题及答案2009年云南省高中（中专）招生统一考试试题及答案2009年浙江省杭州市各类高中招生文化考试试题与答案2009年浙江省湖州市初中毕业生学业考试试题及答案2009年浙江省嘉兴市初中毕业生学业考试试卷及答案2009年浙江省金华市初中毕业生学业考试试卷及答案2009年浙江省丽水市初中毕业生学业考试试卷及答案2009年浙江省丽水市初中毕业生学业考试试题及答案2009年浙江省宁波市初中毕业生学业考试试题及答案2009年浙江省衢州市初中毕业生学业考试数学卷及答案2009年浙江省台州市初中学业考试数学试题及参考答案2009年浙江省温州市初中毕业生学业考试试题及答案（答案为扫描版）2009年浙江省义乌市初中毕业生学业考试题及参考答案2009年浙江省舟山市初中毕业生学业考试数学卷及答案2009年重庆市初中毕业暨高中招生考试数学试题及答案2009年重庆市江津市初中毕业学业暨高中招生试题及答2009年重庆市綦江县初中毕业暨高中招生考试题及答案。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

www.HuiLanGe.com 回澜阁教育免费下载天天更新 2009年长沙市初中毕业学业考试试卷数学

考生注意：本试卷共26道小题，时量120分钟，满分120分．一、填空题（本题共8个小题，每小题3分，满分24分） 1．(6) ．

2．因式分解：224aa ． 3．据报道，今年“五·一”期间我市旅游总收入同比增长超过两成，达到563 000 000元，用科学记数法表示为元． 4．如图，ABCD⊥于点BBE，是ABD的平分线，则CBE的度数为．

5．如图，AB是O⊙的直径，C是O⊙上一点，44BOC°，则A的度数为． 6．如图，等腰ABC△中，ABAC，AD是底边上的高，若5cm6cmABBC，，则AD cm． 7．从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：种子粒数 100 400 800 1 000 2 000 5 000 发芽种子粒数 85 398 652 793 1 604 4 005 发芽频率 0.850 0.745 0.851 0.793 0.802 0.801 根据以上数据可以估计，该玉米种子发芽的概率约为（精确到0.1）．

8．已知关于x的不等式组0521xax≥，只有四个整数解，则实数a的取值范围是．二、选择题（本题共8个小题，每小题3分，满分24分） 9．下列各式中，运算正确的是（）

A．632aaa B．325()aa

C．223355 D．632 10．已知三角形的两边长分别为3cm和8cm，则此三角形的第三边的长可能是（） A．4cm B．5cm C．6cm D．13cm

11．已知关于x的方程260xkx的一个根为3x，则实数k的值为（） A．1 B．1 C．2 D．2

A E

D B C 第4题

C B A O

第5题

C D B 第6题 www.HuiLanGe.com 回澜阁教育免费下载天天更新 12．分式111(1)aaa的计算结果是（） A．11a B．1aa C．1a D．1aa 13．甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差分别为0.56s2甲，0.60s2乙，20.50s丙，20.45s丁，则成绩最稳定的是（） A．甲 B．乙 C．丙 D．丁 14．如图，矩形ABCD的两条对角线相交于点O，602AOBAB°，，则矩形的对角线AC的长是（）

A．2 B．4 C．23 D．43

15．如图，已知O⊙的半径6OA，90AOB°，则AOB所对的弧AB的长为（） A．2π B．3π C．6π D．12π

16．已知实数a在数轴上的位置如图所示，则化简2|1|aa的结果为（） A．1 B．1 C．12a D．21a 三、解答题（本题共6个小题，每小题6分，满分36分）

17．计算：121(2)2(3)3．

18．先化简，再求值： 22()()()2abababa，其中133ab，．

19．某校九年级数学兴趣小组的同学开展了测量湘江宽度的活动．如图，他们在河东岸边的A点测得河西岸边的标志物B在它的正西方向，然后从A点出发沿河岸向正北方向行进

550米到点C处，测得B在点C的南偏西60°方向上，他们测得的湘江宽度是多少米？（结

果保留整数，参考数据：21.414≈，31.732≈）

O D C A B 第14题

O B

第15题 1 1 0

第16题

北东西南 C

A B www.HuiLanGe.com 回澜阁教育免费下载天天更新 20．为了提高返乡农民工再就业能力，劳动和社会保障部门对400名返乡农民工进行了某项专业技能培训，为了解培训的效果，培训结束后随机抽取了部分参调人员进行技能测试，测试结果分成“不合格”、“合格”、“良好”、“优秀”四个等级，并绘制了如图所示的统计图，请根据统计图提供的信息，回答下列问题：（1）培训结束后共抽取了名参训人员进行技能测试；（2）从参加测试的人员中随机抽取一人进行技能展示，其测试结果为“优秀”的概率为．（3）估计这400名参加培训的人员中，获得“优秀”的总人数大约是多少？

21．如图，EF、是平行四边形ABCD对角线AC上两点，BEDF∥，求证：AFCE． 22．反比例函数21myx的图象如图所示，1(1)Ab，，2(2)Bb，是该图象上的两点．（1）比较1b与2b的大小；（2）求m的取值范围．

四、解答题（本题共2个小题，每小题8分，满分16分） 23．（本题满分8分）某中学拟组织九年级师生去韶山举行毕业联欢活动．下面是年级组长李老师和小芳、小明同学有关租车问题的对话：李老师：“平安客运公司有60座和45座两种型号的客车可供租用，60座客车每辆每天的租金比45座的贵200元．”

人数（人）不合格合格良好优秀等级

16 14 12 10 8 6 4 2 0

D C A

B E

y x O www.HuiLanGe.com 回澜阁教育免费下载天天更新小芳：“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观，一天的租金共计5000元．” 小明：“我们九年级师生租用5辆60座和1辆45座的客车正好坐满．” 根据以上对话，解答下列问题：（1）平安客运公司60座和45座的客车每辆每天的租金分别是多少元？（2）按小明提出的租车方案，九年级师生到该公司租车一天，共需租金多少元？

24．（本题满分8分）在RtABC△中，90ACB°，D是AB边上一点，以BD为直径的O⊙与边AC相切于点E，连结DE并延长，与BC的延长线交于点F．（1）求证：BDBF；（2）若64BCAD，，求O⊙的面积．

五、解答题（本题共2个小题，每小题10分，满分20分） 25．（本题满分10分）为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元．该产品每月销售量y（万件）与销售单价x（元）之间的函数关系如图所示．（1）求月销售量y（万件）与销售单价x（元）之间的函数关系式；（2）当销售单价定为50元时，为保证公司月利润达到5万元（利润＝销售额－生产成本－员工工资－其它费用），该公司可安排员工多少人？（3）若该公司有80名员工，则该公司最早可在几个月后还清无息贷款？

A E D

B C

4 2 1 40 60 80

x （元）

（万件） y O www.HuiLanGe.com 回澜阁教育免费下载天天更新 26．（本题满分10分）如图，二次函数2yaxbxc（0a）的图象与x轴交于AB、两点，与y轴相交于点

C．连结ACBCAC、，、两点的坐标分别为(30)A，、(03)C，，且当4x和2x时

二次函数的函数值y相等．（1）求实数abc，，的值；（2）若点MN、同时从B点出发，均以每秒1个单位长度的速度分别沿BABC、边运动，其中一个点到达终点时，另一点也随之停止运动．当运动时间为t秒时，连结MN，将BMN△沿MN翻折，B点恰好落在AC边上的P处，求t的值及点P的坐标；

（3）在（2）的条件下，二次函数图象的对称轴上是否存在点Q，使得以BNQ，，为项点

的三角形与ABC△相似？如果存在，请求出点Q的坐标；如果不存在，请说明理由． y

O x C N B P M A www.HuiLanGe.com 回澜阁教育免费下载天天更新 2009年长沙市初中毕业学业考试试卷数学参考答案及评分标准一、填空题（本题共8个小题，每小题3分，满分24分） 1．6 2．2(2)aa 3．85.6310 4．135° 5．22° 6．4 7．0.8 8．32a≤ 二、选择题（本题共8个小题，每小题3分，满分24分） 9．D 10．C 11．A 12．C 13．D 14．B 15．B 16．A 三、解答题（本题共6个小题，每小题6分，满分36分）

17．解：121(2)2(3)3 463 ················································································································· 3分

1． ·························································································································· 6分

18．解：22()()()2abababa

2222222abaabba

2ab ························································································································ 5分

当3a，13b时，12233ab 2 ·························································································· 6分

19．解：由题意得：ABC△中，9060550BACACBAC°，°，， tanABACACB

5503≈ ························································································································· 4分

952.6≈ 953≈（米）．

答：他们测得湘江宽度为953米． ························································································ 6分 20．解：（1）40； ·················································································································· 2分