中考数学一轮复习整式及运算

合集下载

初中数学中考总复习——整式(合并同类项整式加减乘法除法混合运算分解因式图文详解)

初中数学总复习整式
多项式的项数与次数
例3 下列多项式次数为3的是（ C）
A. 5x 2 6x 1
B.x 2 x 1
C .a 2b ab b2
D.x2 y2 2x3 1
注意（1）多项式的次数不是所有项的次数的和，而是它的最高次项次数；
（2）多项式的每一项都包含它前面的符号；（3）再强调一次， “π”当作数字，而不是字母
—
~~~——
~~~
一找
＝（4x2－3x2）+ (－8x＋6x)+ (5－4）二移
＝ x2 －2x ＋1
三并
初中数学总复习整式
合并同类项的步骤：
1、找出同类项用不同的线标记出各组同类项，注意每一项的符号。 2、把同类项移在一起
用括号将同类项结合，括号间用加号连接。
3、合并同类项系数相加,字母及字母的指数不变。
项式，最高次项是____x__23_y_2_，常数项是____13_____；
初中数学总复习整式
易错题
例5 下列各个式子中，书写格式正确的是（ F）
A.a b D.a3
B. 1 1 ab 2
C.a 3
E. 1ab
F. a2b 3
初中数学总复习整式
小结：
1、代数式中用到乘法时，若是数字与数字乘，要用“×” 若是数字与字母乘，乘号通常写成”.”或省略不写，如 3×y应写成3·y或3y，且数字与字母相乘时，字母与字母相乘，乘号通常写成“·”或省略不写。
初中数学总复习整式
多项式的项数与次数
例4 、请说出下列各多项式是几次几项式，并写出多项式的最高次
项和常数项；
(1)25 x2 y xy3是 __四___次 __三___ 项式，最高次项是_____x_y__3_，常数项是___2__5____；

2024年中考数学一轮复习提高讲义：整式的乘除

整式的乘除知识梳理1.同底数幂的运算(1) 乘法: aᵐ⋅aⁿ=aᵐ⁺ⁿ,(aᵐ)ⁿ=aᵐⁿ,(ab)ⁿ=aⁿbⁿ(其中m,n 都是正整数). 注意事项：①am⋅a′′=am+n区别加法aᵐ+aⁿ≠aᵐ⁺ⁿ(如2³+2²=12≠32=2⁵);②区分−aᵐ⋅aⁿ与((--a)" · a" ,-一个是积的符号，另一个是底数的符号；③推广(aᵐ)ⁿ=aᵐⁿ:[(aᵐ)ⁿ]ᵖ=aᵐⁿᵖ.(2)除法(将除法转化为乘法计算)：circle1a m÷a n=a m⋅1a n =a m−n=a m⋅a−n,由此我们还可以得到1a n=a−n;②a⁰=1,因为aᵐ÷a′′=1=a′m−m=a⁰.2.单项式相乘单项式与单项式相乘的法则：把它们的系数、同底数幂分别相乘，其余字母连同它的指数不变，作为积的因式.3.多项式相乘(1)多项式与单项式相乘：利用分配律，用单项式去乘以多项式的每一项，再把所得的积相加.m(a+b+c)=ma+mb+mc(2)多项式与多项式相乘：先用一个多项式中的每一项乘以另一个多项式中的每一项，再把所得的积相加.(a+b+c)(d+e)=ad+ae+bd+be+cd+ce多项式乘法结束后，一般按照各项的次数高低进行排列.4.重要公式(1)平方差公式:a²−b²=(a+b)(a−b)(2)完全平方公式：(a+b)²=(a+b)(a+b)=a²+2ab+b²(a−b)²=(a−b)(a−b)=a²−2ab+b²典型例题例 1计算：(1)(−2x²)⋅(−3x²y³z)(2)−6x2y⋅(a−b)3⋅13xy2⋅(b−a)2(3)(−4ab3)⋅(−18ab)−(12ab2)2分析本题主要考查单项式的乘法运算和混合运算，乘法运算可以根据单项式与单项式的乘法法则进行.特别是第(3)题注意运算顺序，先算乘方，再算乘法，最后算减法.解 (1)原式: =(−2)⋅(−3)⋅x²⋅x²y³z=6x⁴y³z(2) 原式=−6x2y⋅13xy2⋅(a−b)3⋅(b−a)2=−6x2y⋅13xy2⋅(a−b)3⋅(a−b)2=−6⋅13⋅x2y⋅xy2⋅[(a−b)3⋅(a−b)2]=−2⋅x3y3⋅(a−b)5(3) 原式=(−4ab3)⋅(−18ab)−14a2b4=12a2b4−14a2b4=14a2b4例 2计算：(1)(x+1)(x²−1)(2)(x−y)(x²+x+y)分析本题考查的是多项式的乘法运算，可以根据多项式与多项式的乘法法则进行. 解 (1)原式=x³−x+x²−1=x³+x²−x−1(2) 原式=x³+x²+xy−x²y−xy−y²=x³−x²y+x²−y=:例 3计算：(1)(−13x+34y3)(−34y3−13x)(2)(2a²+b)(−2a²+b)分析本题主要考查平方差公式的运用.解(1) 原式=−(34y3−13x)(34y3+13x)=−(34y3)2+(13x)2=−916y6+19x3(2) 原式: =(b+2a²)(b−2a²)=b²−4a⁴双基训练1.下面是某同学在一次作业中的计算摘录：⑬a+2b=5ab;②4m³n−5mn³=−m³n;③4x³⋅(−2x²)=−6x³;④4a³b÷(−2a²b)=−2a;⑤(a³)²=a⁵;⑥(−a)³÷(−a)== -a²其中正确的个数有( ).A. 1个B.2个C.3 个D. 4个2.计算(x²−3x+n)(x²+mx+8)的结果中不含x²和 x³的项，则 m，n 的值分别为( ).A. m=3,n=1B. m=0,n=0C. m=-3,n=-9D. m=-3,n=83.下列分解因式不正确的是( ).A.x³−x=x(x²−1)B.m²+m−6=(m+3)(m−2)C.(a+4)(a−4)=a²−16D.x²+y²=(x+y)(x−y)4.我们约定a⊗b=10“×10”,如: 2⊗3=10²×10³=10⁵,,那么 4⊗8 为 ( ).A.32B. 10³²C.10¹²D. 12¹⁰5.下列各式是完全平方式的是( ).A.x2−x+14B.1+4x²C.a²+ab+b²D.x²+2x−16.如图18-1所示,矩形花园ABCD 中,AB=a,AD=b,花园中建有一条矩形道路LMPQ 及一条平行四边形道路RST K.若 LM=RS=c，则花园中可绿化部分的面积为( ).A.bc−ab+ac+b²B.a²+ab+bc−acC.ab−bc−ac+c²D.b²−bc+a²−ab7.如图18-2(a)所示，从边长为a 的正方形中去掉一个边长为b 的小正方形，然后将剩余部分裁剪后拼成一个矩形(如图18-2(b)所示)，上述操作所能验证的等式是( ).A.a²−b²=(a +b )(a −b )B.(a −b )²=a²−2ab +b²C.(a +b )²=a²+2ab +b²D.a²+ab =a (a +b )8.下列多项式中能用平方差公式分解因式的是( )A.a²+(−b )²B.5m²−20mnC.−x²−y²D.−x²+99.若 9x²+mxy +16y²是一个完全平方式，那么 m 的值是 .10.(23)2007×(1.5)2008÷(−1)2009=¯.11.分解因式: a²−1+b²−2ab =.12.如果((2a+2b+1)(2a+2b-1)=63,那么a+b 的值为 .13.把20厘米长的一根铁丝分成两段，将每一段围成一个正方形，如果这两个正方形的面积之差是5平方厘米，则这两段铁丝分别长 .14. 多项式 9x²+1加上一个单项式后，能成为一个完全平方式，那么加上的单项式可能是 .15. 若 3x =12,3y =23,则 3ˣ⁻²ʸ等于 .16. 比较3⁵⁵⁵,4⁴⁴⁴,5³³³的大小: > > .17.计算.(1)(23a 2b)3÷(13ab 2)2×34a 3b 2(2)(x 4+3y)2−(x 4−3y)2(3)(2a-3b+1)²(4)(x²−2x −1)(x²+2x −1)18.化简求值: [(x +12y)2+(x −12y)2](2x 2−12y 2),其中 x =−3,y =4.19.已知实数x 满足x+1x =3,求x2+1x2的值.20.已知.A=2x+y,B=2x-y,计算A²−B².能力提升21.若x+y=2m+1, xy=1,且21x²−48xy+21y²=2010,则m= .22. 设(1+x)²(1−x)=a+bx+cx²+dx³,则。

中考数学一轮复习讲义2__整式

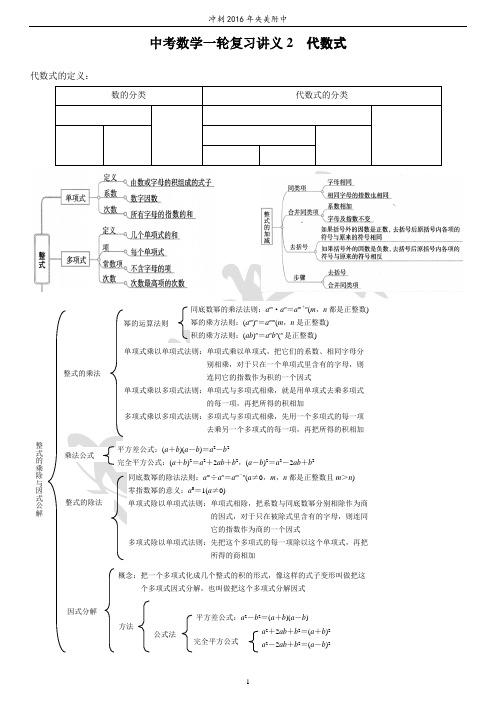
中考数学一轮复习讲义2 代数式代数式的定义：整式的乘法整式的乘除与因式公解幂的运算法则同底数幂的乘法法则：a m·a n＝a m＋n(m，n都是正整数)幂的乘方法则：(a m)n＝a mn(m，n是正整数)积的乘方法则：(ab)n＝a n b n(n是正整数)单项式乘以单项式法则：单项式乘以单项式，把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式单项式乘以多项式法则：单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加多项式乘以多项式法则：多项式与多项式相乘，先用一个多项式的每一项去乘另一个多项式的每一项，再把所得的积相加同底数幂的除法法则：a m÷a n＝a m－n(a≠0，m，n都是正整数且m＞n)零指数幂的意义：a0＝1(a≠0)单项式除以单项式法则：单项式相除，把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式多项式除以单项式法则：先把这个多项式的每一项除以这个单项式，再把所得的商相加乘法公式平方差公式：(a＋b)(a－b)＝a2－b2完全平方公式：(a＋b)2＝a2＋2ab＋b2，(a－b)2＝a2－2ab＋b2整式的除法因式分解概念：把一个多项式化成几个整式的积的形式，像这样的式子变形叫做把这个多项式因式分解，也叫做把这个多项式分解因式方法公式法平方差公式：a2－b2＝(a＋b)(a－b)完全平方公式a2＋2ab＋b2＝(a＋b)2a2－2ab＋b2＝(a－b)2题型一整式的加减运算例1 已知与是同类项，则a b 的值为. 例2 计算：（7x 2＋5x －3）－（5x 2－3x ＋2）．题型二整式的求值例3 已知（a ＋2）2＋|b ＋5|＝0，求3a 2b 一[2a 2b －（2ab －a 2b ）－4a 2]－ab 的值．例例5例例7例8例9A.解析：第二个图案中正三角形的个数为：第三个图案中正三角形的个数为：．．，；第n 个图案中正三角形的个数为：题型四：幂的运算法则及其逆运用例1 计算2x 3·(－3x )２＝．例2 计算[a 4(a 4－4a )－(－3a 5)2÷(a 2)3]÷(－2a 2)2．3313a x y --533b y x -85a +题型五：整式的混合运算与因式分解例3 计算[(a －2b )(2a －b )－(2a ＋b )2＋(a ＋b )(a －b )－(3a )2]÷(－2a )．例4 分解因式． (1)m 3－m ； (2)(x ＋2)(x ＋3)＋x 2－4．例5 分解因式a 2－2ab ＋b 2－c 2．例6 (1)已知x ＋y ＝7，xy ＝12，求(x －y )2； (2)已知a ＋b ＝8，a －b ＝2，求ab 的值．15.（2011•临沂，2，3分）下列运算中正确的是（） A 、（﹣ab ）2=2a 2b 2B 、（a+b ）2=a 2+1C 、a 6÷a 2=a 3D 、2a 3+a 3=3a 316.（2011泰安，2，3分）下列运算正确的是（） A ．3a 2＋4a 2＝7a 4B ．3a 2－4a 2＝－a 2C ．3a ×4a 2＝12a 2D ．2222434)3(a a a -=÷17.（2011四川眉山，2，3分）下列运箅正确的是（） A ．2a 2﹣a=aB ．（a+2）2=a 2+4C ．（a 2）3=a 6D ．3)3(2-=-19.（2011•南充，11，3分）计算（π﹣3）0=．20.（2011四川攀枝花，3，3分）下列运算中，正确的是（） A 、2+3=5 B 、a 2•a=a 3C 、（a 3）3=a 6D 、327=－3中考真题精选21.（2011泰安，5，3分）下列等式不成立的是（） A ．m 2－16＝（m －4）（m ＋4）B ．m 2＋4m ＝m （m ＋4）C ．m 2－8m ＋16＝（m －4）2D ．m 2＋3m ＋9＝（m ＋3）22.（2011•丹东，4，3分）将多项式x 3﹣xy 2分解因式，结果正确的是（） A 、x （x 2﹣y 2）B 、x （x ﹣y ）2C 、x （x+y ）2D 、x （x+y ）（x ﹣y ）4.（2011天水，4，4）多项式2a 2﹣4ab +2b 2分解因式的结果正确的是（） A 、2（a 2﹣2ab +b 2）B 、2a （a ﹣2b ）+2b 2C 、2（a ﹣b ）2D 、（2a ﹣2b ）25.（2011江苏无锡，3，3分）分解因式2x 2﹣4x+2的最终结果是（） A ．2x （x ﹣2）B ．2（x 2﹣2x+1） C ．2（x ﹣1）2D ．（2x ﹣2）26.（2011•台湾5，4分）下列四个多项式，哪一个是2x 2+5x ﹣3的因式（） A 、2x ﹣1B 、2x ﹣3C 、x ﹣1D 、x ﹣37.（2011台湾，24，4分）下列四个多项式，哪一个是33x ＋7的倍式（） A ．33x 2－49B ．332x 2＋49C ．33x 2＋7xD ．33x 2＋14x10.（2011梧州，6，3分）因式分解x 2y ﹣4y 的正确结果是（） A 、y （x+2）（x ﹣2）B 、y （x+4）（x ﹣4）C 、y （x 2﹣4）D 、y （x ﹣2）211.（2011河北，3，2分）下列分解因式正确的是（） A ．－a ＋a 3＝－a （1＋a 2） B ．2a －4b ＋2＝2（a －2b ）C ．a 2－4＝（a －2）2D ．a 2－2a ＋1＝（a －1）213.（2011，台湾省，25,5分）若多项式33x 2﹣17x ﹣26可因式分解成（ax+b ）（cx+d ），其中a 、b 、c 、d 均为整数，则|a+b+c+d|之值为何？（） A 、3B 、10C 、25D 、2914.（2011浙江金华，3，3分）下列各式能用完全平方式进行分解因式的是（） A ．x 2 +1 B.x 2+2x －1 C.x 2+x +1 D.x 2+4x +415.（2011浙江丽水，3，3分）下列各式能用完全平方公式进行分解因式的是（） A 、x 2+1 B 、x 2+2x ﹣1 C 、x 2+x +1D 、x 2+4x +4综合验收评估测试题1一、选择题l. 在代数式－2x 2，3xy ，，，0，mx －ny 中，整式的个数为（） A ．2 B ．3 C ．4 D. 5 2. 二下列语句正确的是（）A ．x 的次数是0B ．x 的系数是0 C. －1是一次单项式 D ．－1是单项式 3.4.5. 6. 7. 8. C ．m ≠－1，n 为大于3的整数 D ．m ≠－1，n ＝5二、填空题9. －mx n y 是关于x ，y 的一个单项式，且系数是3，次数是4，则m ＝，n ＝． 10. 多项式ab 3－3a 2b 2－a 3b －3按字母a 的降幂排列是．按字母b 的升幂排列是． 11. 当b ＝时，式子2a ＋ab －5的值与a 无关． 12. 若－7xy n ＋1 3x m y 4是同类项，则m ＋n ．13．多项式2ab －5a 2＋7b 2加上等于a 2－5ab ．b a 3xy -三、解答题14．先化简，再求值：，其中m ＝－l ，n ＝.综合验收评估测试题2一、选择题(每小题3分，共30分) 1．计算(a 3)2的结果是 ( ) A ．a 5 B ．a 6 C ．a 8 D ．a 9 2．下列运算正确的是 ( )A ．a 2·a 3＝a 4B ．(－a )4＝a 4C ．a 2＋a 3＝a 5D ．(a 2)3＝a 5 3．已知x －3y ＝－3，则5－x ＋3y 的值是 ( ) A ．0 B ．2 C ．5 D ．8 4．若m ＋n ＝3，则2m 2＋4mn ＋2n 2－6的值为 ( ) A ．12 B ．6 C ．3 D ．05．如图15－4所示，在边长为a 的正方形中挖去一个边长为b 的小正方形(a ＞b )，把余下的部分拼成一个矩形，根据两个图形中阴影部分的面积相等，可以验证 ( )A ．(a ＋b )2＝a 2＋2ab ＋b 2B ．(a －b )2＝a 2－2ab ＋b 2C ．a 2－b 2＝(a ＋b )(a －b )D ．(a ＋2b )(a －b )＝a 2＋ab －2b 2 6．下列各式中，与(a －b )2一定相等的是 ( )A ．a 2＋2ab ＋b 2B ．a 2－b 2C ．a 2＋b 2D ．a 2－2ab ＋b 0 7．已知x ＋y ＝－5，xy ＝6，则x 2＋y 2的值为 ( ) A ．1 B ．13 C ．17 D ．25 8．下列从左到右的变形是因式分解的是 ( )A ．ma ＋mb －c ＝m (a ＋b )－cB ．(a －b )(a 2＋ab ＋b 2)＝a 3－b 3C ．a 2－4ab ＋4b 2－1＝a (a －4b )＋(2b ＋1)(2b －1)D ．4x 2－25y 2＝(2x ＋5y )(2x －5y ) 9．下列各式中，能用平方差公式分解因式的是 ( ) A ．－a 2＋b 2 B ．－a 2－b 2 C ．a 2＋b 2 D ．a 3－b 3 10．如果(x －2)(x －3)＝x 2＋px ＋q ，那么p ，q 的值是 ( )A ．p ＝－5，q ＝6B ．p ＝1，q ＝－6C ．p ＝1，q ＝6D ．p ＝5，q ＝－622222212(52)3(2)2m n mn m n mn mn m n ⎛⎫+---- ⎪⎝⎭13二、填空题(每小题3分，共30分) 11．已知10m ＝2，10n ＝3，则103m＋2n＝．12．当x ＝3，y ＝1时，代数式(x ＋y )(x －y )＋y 2的值是． 13．若a －b ＝1，ab ＝－2，则(a ＋1)(b －1)＝． 14．分解因式：2m 3－8m ＝． 15．已知y ＝31x －1，那么31x 2－2xy ＋3y 2－2的值为． 16．计算：5752×12－4252×12＝．17 18192021 22(1)m 2n (m23．已知a ，b 是有理数，试说明a 2＋b 2－2a －4b ＋8的值是正数．24．先化简，再求值：(a ＋b )(a －b )＋(4ab 3－8a 2b 2)÷4ab ，其中a ＝2，b ＝1．25．(1)计算．①(a －1)(a ＋1)；②(a －1)(a 2＋a ＋1)；③(a －1)(a 3＋a 2＋a ＋1)；④(a －1)(a 4＋a 3＋a 2＋a ＋1)． (2)根据(1)中的计算，你发现了什么规律?用字母表示出来． (3)根据(2)中的结论，直接写出下题的结果． ①(a －1)(a 9＋a 8＋a 7＋a 6＋a 5＋a 4＋a 3＋a 2＋a ＋1)＝； ②若(a －1)·M ＝a 15－1，则M ＝； ③(a －b④(226(1) (2) (3) (4)(5)答案：1．D 解析：不是整式，故选D ． 2．D 解析：x 的次数是1，系数是1；－1是单项式．故选D ．3．C 解析：所含字母相同，并且相同字母的指数也相同的项叫做同类项．故选C ：4．D 解析：如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反．故选D ．5．6．B ． 7．2n ＋38．910 1112137b 2． 142×＝1．15 50πa 2＋100ab ．答：美化这块空地共需资金（50πa 2＋100ab ）元．点拨：根据题意，可以先求出建造花台及种花所需费用，再求出种草的费用，两者相加即为美化这块空地共需的资金．ba1314π4a ⨯参考答案1．B2．B[提示：选项A ：a 2·a 3＝a 5；选项C ：a 2和a 3不能合并；选项D ：(a 2)3＝a 6．] 3．D[提示：5－x ＋3y ＝5－(x －3y )＝5－(－3)＝8．]4．A ［提示：2m 2＋4mn ＋2n 2－6＝2(m ＋n )2－6＝2×32－6＝12．]5．6．7．8．9．10111213141531(x －3y )2－216] 17181920] 21＋1)(2x －1)－＝20002－(200022(x ＋y －8)2．232)2≥0，∴(a －1)＝a 2－b 2＋b 2－25n －2＋…＋a 3＋a 2＋a ＋1)＝a n ＋1－1． (3)①a 10－1 ②a 14＋a 13＋a 12＋a 11＋…＋a 3＋a 2＋a ＋1 ③a 6－b 6④32x 5－126．解：(1)各层对应的点数依次为：4，8．12，16，20，24；所有层的总点数依次为：4，12，24，40，60．84． (2)4n ． (3)2n (n ＋1)． (4)第24层． (5)有，第25层．。

2023年中考数学一轮复习满分突破专题04 整式的乘除-【题型方法解密】

专题04 整式的乘除【热考题型】【知识要点】知识点一幂的运算同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加。

n m n m a a a +=·（其中m 、n 为正整数）【注意事项】1）当底数为负数时,先用同底数幂乘法法则计算，再根据指数的奇偶来确定结果的正负，并且化简到底。

2）不能疏忽指数为1的情况。

例：a ·a 2＝a1＋2＝a 33）乘数a 可能是有理数、单项式或多项式。

4）如果底数互为相反数时可先变成同底后再运算。

5）逆用公式：n m n m a a a ·=+（m,n 都是正整数）【扩展】三个或三个以上同底数幂相乘时，也具有这一性质，即p n m p n m a a a a ++=··（m ，n ，p 都是正整数）考查题型一同底数幂的乘法典例1．（2022·浙江嘉兴·中考真题）计算a 2·a （） A ．aB ．3aC ．2a 2D ．a 3变式1-1．（2022·河南·中考真题）《孙子算经》中记载：“凡大数之法，万万曰亿，万万亿曰兆．”说明了大数之间的关系：1亿＝1万×1万，1兆＝1万×1万×1亿，则1兆等于（） A ．810B ．1210C ．1610D ．2410变式1-2．（2022·内蒙古包头·中考真题）若42222m ⨯=，则m 的值为（）A ．8B ．6C ．5D ．2变式1-3．（2022·湖南邵阳·中考真题）5月29日腾讯新闻报道，2022年第一季度，湖南全省地区生产总值约为11000亿元，11000亿用科学记数法可表示为1210a ⨯，则a 的值是（） A ．0.11 B ．1.1 C ．11 D ．11000易错点总结：幂的乘方法则：幂的乘方，底数不变，指数相乘.mnn m a a =)((其中m ，n 都是正整数).【注意事项】1）负号在括号内时,偶次方结果为正,奇次方为负,负号在括号外结果都为负。

人教版初中数学中考一轮复习---整式和整式的加减运算(含解析)

整式与整式的加减运算例1：因式分解：22mx my -．例2：已知：，2-=b ，．求代数式:24a b c +-的值．例3：先化简，再求值：（1+a ）（1﹣a ）+（a ﹣2）2，其中a=﹣3．例4：先化简，再求值：，其中x =A 组1、指出下列各单项式的系数和次数：23223,5,,37a x y ab a bc π- 2. 判断下列各式哪些是单项式： ①2ab x ②a ③25ab -④x y +⑤0.85-⑥12x +⑦2x⑧0 3. 对于多项式2221x yz xy xz -+-- （1）最高次数项的系数是；（2）是次项式；（3）常数项是。

3=a 21=c 2(2)(21)(21)4(1)x x x x x +++--+4.已知多项式221345xy x y --，试按下列要求将其重新排列。

（1）按字母x 作降幂排列；（2）按字母y 作升幂排列。

点拨：在按照定义的要求情况下，注意各项前的符号。

5. 把下列各式填在相应的大括号里7x -，13x ，4ab ，23a ，35x -，y ，st，13x +，77x y +，212x x ++，11m m -+，38a x ，1-。

单项式集合{ } 多项式集合{ } 整式集合 { }6、三个连续的奇数中，最小的一个是23n -,那么最大的一个是。

7、当2x =-时，代数式－221x x +-= ，221x x -+= 。

8、写出一个关于x 的二次三项式，使得它的二次项系数为-5，则这个二次三项式为。

9、如果3y -+2(24)x -=0，那么2x y -=___。

10、多项式221x x -+的各项分别是（） A 、22,,1x x B 、22,,1x x - C 、22,,1x x -- D 、22,,1x x --- 11、计算：35_____x x -=； 12、()22______326271x x x x +--=--+13、买一个足球需要m 元，买一个篮球需要n 元，则买4个足球、7个篮球共需要（）元。

精品中考数学一轮综合复习第02课整式(整式的加减乘除及因式分解)

8.若 m+n=3，则 2m 2 4mn 2n 2 6 的值为（ A.12 B.6
C.3
D.0
9.若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如 a b c 就是完．．．．．全对称式.下列三个代数式：① ( a b) ；② ab bc ca ；③ a 2b b 2 c c 2 a ．其中是完全对称式的是
例 3.当 x=1 时，代数式 ax 3 bx 2014 等于 2013，则当 x=-1 时，代数式 ax 3 bx 2014 值为多少？
例 4.若多项式 4 x 2 6 xy 2 x 3 y 与 ax 2 bxy 3ax 2by 的和不含二次项，求 a、b 的值。
5
7.若 2 x 3,4 y 5 ,则 2 x 2 y 的值为（ A.
3 5
9 3
B.-2
2
3 5 5
D.
6 5
8.已知 a=1.610 ，b=410 ，则 a 2b=(
7 A.210
)
5 C.3.210 14 D.3.210
B.410
14
9.把多项式 ax 2 ax 2a 分解因式，下列结果正确的是（ A. a ( x 2)( x 1) B. a ( x 2)( x 1) C. a( x 1) 2
第 4 页共 8 页
2 (5) 27 x 18 x 3
2 2 (6) 3a 6ab 3b
3 (7) 2 x 8 x
2 (8) x 5 x 6
(9) x 2 12 x 35
(10) ax 2 3ax 28a
(11) x 2 6 x 16

安徽数学中考一轮复习课件：2整式的运算及因式分解

2015年考查了填空题，其余都是以8分的解答题出现；
4
考纲解读
考
单元
代
数
式
试
内
容
知识条目
(1)用字母表示数的意义，代数式
(2)代数式的值
考试要求目标
A B C D
√
√
5
考纲解读
考
单元
整
式
与
分
式
试
内
容
考试要求目标
知识条目
(1)整式的概念
(2)整式的加、减运算
A B C D
(3)整数指数幂的意义和基本性质
单项式叫做同类项,常数项是 (填“是”或“不是”)同类项.
(2)合并同类项法则:几个同类项相加,把它们的系数相加,
所得的结果作为系数,字母和字母的次数都不变 .
(3)去括号法则:a+(b-c)=a+b-c ;a-(b-c)=a-b+c .(口诀:“+”
不变,“-”变号)
(4)整式加减运算可归纳为:先去括号,再合并同类项.
考点精讲
3.整式乘法运算
单项式乘
单项式
单项式乘
多项式
多项式乘
多项式
乘法公式
把系数、同底数幂分别相乘,对于只在一个单项式
里含有的字母,则连同它的指数作为积的一个因
式
m(a+b)=ma+mb
(m+n)(a+b)=m(a+b)+n(a+b)=ma+mb+na+nb
平方差公式:(a+b)(a-b)=a2-b2
√
(4)乘法公式
(5)整式的乘法运算(多项式相乘仅指一次式之间以及一次式与

备战九年级中考数学一轮复习第2课整式(含因式分解)(全国通用)

13.(202X·哈尔滨)把多项式m2n＋6mn＋9n分解因式的结果是_____n_(m__＋__3_)2_____.
14.(202X·重庆)已知a＋b＝4，则代数式1＋ a ＋b 的值 22
为( A )
A.3
B．1
C．0
D．－1
考点3 求代数式的值
15.【例3】(202X·广东)已知x＝5－y，xy＝2，计算代数式 3x＋3y－4xy＝____7____.
第2课整式(含因式分解)
1．(1)单项式：数与字母的积所表示的代数式叫做单项式，单独一个数或者一个字母也是单项式． (2)多项式：几个单项式的和叫做多项式． (3)整式：单项式与多项式统称为整式.
1．(1)单项式－3xy2的系数是__－__3____，次数是____3____； (2)多项式2x－5xy3－1是____4____次____三____项式，其中一次项为____2_x___，一次项系数为____2____．
23．(202X·天水)分解因式：m3n－mn＝ mn(m＋1)(m－1) .
24．(海南中考)某工厂去年的产值是a万元，今年比去年增加10%，今年的产值是__1_._1_a___万元．
25．(广东中考)下列计算正确的是( C )
A．b6＋b3＝b2
B．b3·b3＝b9
C．a2＋a2＝2a2
C．2kk
D．k2＋k
31.(202X·苏州)若单项式2xm－1y2与单项式1 x2yn＋1是同类项， 3
则m＋n＝___4_____.
32．(202X·枣庄)若a＋b＝3，a2＋b2＝7，则ab＝___1_____.
C组 33．(202X·聊城)因式分解：x(x－2)－x＋2＝ (x－1)(x－2) .

2020年中考数学第一轮复习第三节整式知识点+真题(后含答案)

2020年中考数学第一轮复习第一章数与式第三节整式【基础知识回顾】一、整式的有关概念：单项式：。

1、整式：多项式：。

单项式中的叫做单项式的系数，所有字母的叫做单项式的次数。

组成多项式的每一个单项式叫做多项式的，多项式的每一项都要带着前面的符号。

2、同类项：①定义：所含相同，并且相同字母的也相同的项叫做同类项，常数项都是同类项。

②合并同类项法则：把同类项的相加，所得的和作为合并后的，不变。

【注意：1、单独的一个数字或字母都是式。

2、判断同类项要抓住两个相同：一是相同，二是相同，与系数的大小和字母的顺序无关。

】二、整式的运算：1、整式的加减：①去括号法则：a+(b+c)=a+ ,a-(b+c)=a- .②添括号法则：a+b+c= a+( )，a-b-c= a-( )③整式加减的步骤是先，再。

【注意：在整式的加减过程中有括号时一般要先去括号，特别强调：括号前是负号去括号时括号内每一项都要。

】2、整式的乘法：①单项式乘以单项式：把它们的系数、相同字母分别，对于只在一个单项式里含有的字母，则连同它的作为积的一个因式。

②单项式乘以多项式：用单项式去乘多项式的每一项，再把所得的积，即m(a+b+c)= 。

③多项式乘以多项式：先用第一个多项式的每一项去乘另一个多项式的每一项，再把所得的积，即（m+n）(a+b)= 。

④乘法公式：Ⅰ、平方差公式：（a＋b）（a—b）＝，Ⅱ、完全平方公式：（a±b）2 = 。

【注意：1、在多项式的乘法中有三点注意：一是避免漏乘项，二是要避免符号的错误，三是展开式中有同类项的一定要。

2、两个乘法公式在代数中有着非常广泛的应用，要注意各自的形式特点，灵活进行运用。

】3、整式的除法：①单项式除以单项式，把、分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式。

②多项式除以单项式，先用这个多项式的每一项这个单项式，再把所得的商。

即（am+bm ）÷m= 。

中考数学复习第一章数与式数与式第2课整式及其运课件

解：(2)∵(x＋y)2＝x2＋y2＋2xy， ∴2xy＝(x＋y)2－(x2＋y2)＝72－25＝24， ∴x－y)2＝x2＋y2－2xy＝25－24＝1. ∵x>y，∴x－y＝ 1 ＝1.
探究提高 1.算式中的局部直接使用乘法公式、简化运算，
任何时候都要遵循先化简，再求值的原则. 2.在利用完全平方公式求值时，通常用到以下
探究提高整式的加减，实质上就是合并同类项，有括号的，先去括号．只要算式中没有同类项，就是最后的结果．
知能迁移1 (1)(2011·义乌)下列计算正确的是( D )
A．x2＋x4＝x6
B．2x＋3y＝5xy
C．x6÷x3＝x2
D．(x3)2＝x6
解析：(x3)2＝x3×2＝x6.
(2)(2011·台北)化简(－4x＋8)－3(4－5x)，
题型四整式的混合运算及求值
【例4】 (本题5分)先化简，再求值： 3x(x2－x－1)－(x＋1)(3x2－x)，其中x＝－1 . 2
解题示范——规范步骤，该得的分，一分不丢！
解：原式＝3x3－3x2－3x－(3x3－x2＋3x2－x)
[2分]
＝3x3－3x2－3x－3x3＋x2－3x2＋x
＝－5x2－2x.
3．整式：单项式和多项式统称为整式． 4．同类项：多项式中所含字母相同并且相同字母的指数也
相同的项，叫做同类项．
6．整式乘法：单项式与单项式相乘，把系数、同底数幂分别相乘作为积的因式，只在一个单项式里含有的字母，连同它的指数作为积的一个因式．单项式乘多项式：m(a＋b)＝ ma＋mb . 多项式乘多项式：(a＋b)(c＋d)＝ ac＋ad＋bc＋bd .
第2个图形所需的棋子数为11＝6×2－1. 第3个图形所需的棋子数为17＝6×3－1， …… 第n个图形所需的棋子数为6n－1.

中考数学复习课件第四节整式及其运算课件

平方差
整乘
公式
式法
的运乘法
运算公式
几何背景：公式：_(a_±__b_)_2_＝__a_2±__2_a_b_＋__b_2__
算
完全平
方公式几何背景：
整单项式除以单项式：把系数、同底数幂分别相除后，作为商的因式，对于只式除在被除式里含有的字母，则连同它的指数一起作为商的一个因式，如的法 6x4y÷2x3＝(6÷2)x4－3y＝3xy(x≠0) 运运
项：多项式中的每个单项式, 其中不含字母的项叫做_常__数__项___ 次数：多项式中次数最高的项的次数
念整式：单项式和多项式的统称
同类项：_所__含__字__母__相__同__，__并__且__相__同__字__母__的__指__数__也__相__同__的__项___，
所有的常数项都是同类项
整式加减运算的实质是合并同类项
B．(－3a2b)2＝6a4b2 D．2a2b÷b＝2a2
6．下列计算正确的是( B ) A．3mn－2mn＝1 C．(－m)3·m＝m4
B．(m 2n 3)2＝m 4n 6 D．(m ＋n )2＝m 2＋n 2
创新考法
7．(2021荆州)若等式2a2·a＋( 以是( C ) A．a C．a3
)＝3a3成立，则(
B．a2 D．a4
8．若k为正整数，则 (k k …… k)k ＝( A )
A．k2k
B．k2k＋1
k个k
C．2kk D．k2＋k
)中填写单项式可
B．(x－y)2＝x2－y2 D．(－x )2·x 3＝x 5
B．2x＋3x＝5x D．x 6÷x 3＝x 2
4．下列计算正确的是( C ) A．3a＋2b＝5ab C．(－a3b)2＝a6b2 5．下列计算正确的是( D ) A．5ab－3a＝2b C．(a－1)2＝a2－1

2025年广东省中考数学一轮复习：整式(附答案解析)

2025年广东省中考数学一轮复习：整式
一．选择题（共10小题）
1．下列运算正确的是（）
A．5a﹣4a＝1B．（a﹣b）（b﹣a）＝b2﹣a2
C．（﹣3a）2＝﹣9a2D．（﹣2a）3（﹣a）2＝﹣8a5
2．下列运算正确的是（）
A．（3a2）3＝9a6B．a3÷a3＝a
C．（a2）3＝a5D．a2•a3＝a5
3．下列运算中，正确的是（）
A．（m+n）2＝m2+n2
B．（a2x3）2＝a2x5
C．p2021÷p2＝p2019（p≠0）
D．（﹣a+b）（a﹣b）＝a2﹣b2
4．如图，在边长为a的正方形上剪去一个边长为b的小正方形（a＞b），把剩下的部分剪拼成一个梯形，分别计算这两个图形阴影部分的面积，由此可以验证的等式是（
）
A．（a﹣b）2＝a2﹣2ab+b2B．（a+b）2＝a2+2ab+b2
C．a2﹣b2＝（a+b）（a﹣b）D．a（a﹣b）＝a2﹣ab 5．（−12）2019•（﹣2）2020的计算结果是（）
A．2B．﹣2C．4D．﹣4
6．已知a3＝3，b5＝4，则a和b的大小关系为（）
A．a＞b B．a＜b C．a＝b D．无法判断7．如图，从边长为a的正方形中去掉一个边长为b的小正方形，然后用剩余的部分剪开后拼成一个长方形，上述操作能验证的等式是（）
第1页（共16页）。

备考2023年中考数学一轮复习-数与式_整式_整式的混合运算-填空题专训及答案

备考2023年中考数学一轮复习-数与式_整式_整式的混合运算-填空题专训及答案整式的混合运算填空题专训1、(2012泰州.中考真卷) 若代数式x2+3x+2可以表示为（x﹣1）2+a（x﹣1）+b的形式，则a+b的值是________．2、(2013南京.中考真卷) 计算（1﹣）（）﹣（1﹣﹣）（）的结果是________．3、(2015南通.中考真卷) 计算（x﹣y）2﹣x（x﹣2y）=________4、(2015镇江.中考真卷) 化简：（1﹣x）2+2x=________5、(2017东丽.中考模拟) 计算：0.5a×（﹣2a3b）2=________．6、(2018山西.中考模拟) 计算：3a2·a4－(－2a3)2＝________．7、(2018嘉定.中考模拟) 计算：=________．8、(2018嘉定.中考模拟) 计算：________．9、(2019绍兴.中考模拟) 如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立，根据图乙，利用面积的不同表示方法，仿照上边的式子写出一个等式________．10、(2019菏泽.中考真卷) 计算的结果是________．11、(2019梧州.中考模拟) 计算：（x+1）2﹣（x﹣1）（x+1）＝________.12、(2015崇左.中考真卷) 4个数a，b，c，d排列成，我们称之为二阶行列式．规定它的运算法则为：=ad﹣bc．若=12，则x= ________．13、(2016贵阳.中考模拟) 先化简，再求值：（x﹣1）2+x（x+2），其中x=________．14、(2017靖远.中考模拟) 化简：（1﹣x）2+2x=________．15、(2018天水.中考真卷) 观察下列运算过程：S=1+3+32+33+…+32017+32018①，①×3得3S=3+32+33+…+32018+32019②，②﹣①得2S=32019﹣1，S= ．运用上面计算方法计算：1+5+52+53+…+52018=________．16、(2016西宁.中考真卷) 已知x2+x﹣5=0，则代数式（x﹣1）2﹣x（x﹣3）+（x+2）（x﹣2）的值为________．17、(2019蒙城.中考模拟) 贾宪三角（如图1）最初于11世纪被发现，原图载于我国北宋时期数学家贾宪的《黄帝九章算法细草》一书中，原名“开方作法本源图”，用来作开方运算，在数学史上占有领先地位．我国南宋时期数学家杨辉对此有着记载之功，他于1261年写下的《详解九章算法》一书中记载着这一图表．因此，后人把这个图表称作贾宪三角或杨辉三角．与我们现在的学习练习最紧密的要算施蒂费尔的二项式乘方后展开式的系数规律（如图2）．在贾宪三角中，第三行的三个数恰好对应着两数和的平方公式（a+b）2＝a2+2ab+b2展开式的系数．再如，第四行的四个数恰好对应着两数和的立方公式（a+b）3＝a3+3a2b+3ab2+b3展开式的系数，第五行的五个数恰好对应着两数和的四次方公式（a+b）4＝a4+4a3b+6a2b2+4ab3+b4展开式的系数，等等．由此可见，贾宪三角可以看作是对我们现在学习的两数和的平方公式的指数推广而得到的．同学们，贾宪三角告诉了我们二项式乘方展开式的系数规律，你发现其中的字母及字母指数的排列规律了吗？如果发现了，请你试着写出（a+b）5、（a+b）6与（a+b）7的展开式．（a+b）5＝________ ,（a+b）6＝________,（a+b）7＝________18、(2020安顺.中考真卷) 化简的结果是________.19、(2020台州.中考模拟) 阅读材料：定义：如果一个数的平方等于﹣1，记为i2＝﹣1，这个数i叫做虚数单位，把形如a+bi（a，b为实数）的数叫做复数，其中a叫这个复数的实部，b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.例如计算：（4+i）+（6﹣2i）＝（4+6）+（1﹣2）i＝10﹣i；（2﹣i）（3+i）＝6﹣3i+2i﹣i2＝6﹣i﹣（﹣1）＝7﹣i；（4+i）（4﹣i）＝16﹣i2＝16﹣（﹣1）＝17；（2+i）2＝4+4i+i2＝4+4i﹣1＝3+4i根据以上信息，完成下面计算：（1+2i）（2﹣i）+（2﹣i）2＝________.20、(2021邵阳.中考模拟) 化简的结果是. 整式的混合运算填空题答案1.答案：2.答案：3.答案：4.答案：5.答案：6.答案：7.答案：8.答案：9.答案：10.答案：11.答案：12.答案：13.答案：14.答案：15.答案：16.答案：17.答案：18.答案：19.答案：20.答案：。

《中考大一轮数学复习》课件课时3 整式及其运算

中考大一轮复习讲义◆ 数学
中考大一轮复习讲义◆ 数学
2
夯实基本
中考大一轮复习讲义◆ 数学知识结构梳理
知已知彼
1 2
3
3
夯实基本
中考大一轮复习讲义◆ 数学
知已知彼
基础知识回顾 1. 代数式：用运算符号 ( 加、减、乘、除、乘方、开方 ) 把 ________ 或表示 ____________连接而成的式子叫做代数式. 2. 代数式的值：用__________代替代数式里的字母，按照代数式里的运算关系，计算后所得的__________叫做代数式的值． 3. 整式 (1) 单项式：由数与字母的 ________ 组成的代数式叫做单项式 ( 单独一个数或 ________ 也是单项式 ) ．单项式中的 __________ 叫做这个单项式的系数；单项式中的所有字母的____________叫做这个单项式的次数． (2)多项式：几个单项式的________叫做多项式．在多项式中，每个单项式叫做多项式的________，其中次数最高的项的________叫做这个多项式的次数．不含字母的项叫做__________． (3)整式：________与__________统称整式．
1 2
10
3
热点看台
中考大一轮复习讲义◆ 数学
快速提升
热点三整式的化简热点搜索在求整式的值时，应先将整式进行化简，即去括号、合并同类项，然后再把整式中字母的值代入计算，可化繁为简，使运算简便．
典例分析 3 (2013·湖南娄底 )先化简，再求值： (x＋y)(x－y)－ (4x3y－ 3 . 3
1 2
7
3
热点看台
中考大一轮复习讲义◆ 数学
快速提升
点对点训练 1. 某班共有x个学生，其中女生人数占45%，用代数式表示该班的男 0.55x ．生人数是________ 2. (2014·吉林)如图，矩形ABCD的面积为 ________(用含x的代数式表示)． (x＋3)(x＋2)(或写为x2＋5x＋6的形式)

中考数学一轮复习第2讲整式(一)

第2讲整式(一)【考查要求】1.代数式（1）借助现实情境了解代数式，进一步理解用字母表示数的意义．（2）能分析简单问题中的数量关系，并用代数式表示．（3）会求代数式的值．2.整式（1）了解整数指数幂的意义和基本性质；（2）理解整式的概念，掌握合并同类项和去括号的法则，能进行简单的整式加法和减法运算；能进行简单的整式乘法运算（其中多项式相乘仅指一次式之间以及一次式与二次式相乘）．（3）能推导乘法公式：(a ＋b )(a －b )＝a 2＋b 2；(a ±b )2＝ a 2±2ab ＋b 2．了解公式的几何背景，并能利用公式进行简单计算．（4）了解代数推理.【基础过关】1．（1）－13x 2y 的系数是，次数是；（2）多项式x 2－2x 2y 2＋3y 3的次数是，各项系数分别是．2．下列运算中，正确的是( )．A ．a 2a 3＝a 6B ．a 3÷a 2＝aC ．(a 3)2＝a 9D ．a 2＋a 2＝a 53．若2x 3y m 与－3x n y 2 是同类项，则m ＋n ＝_________．4．计算:（1）b －(－a ＋2b )＝；（2）(－2xy )2·x 2＝；（3）(2a －b )(b ＋2a )＝．5．先化简，再求值：(x ＋1)2－(x －1)(x+1)，其中x ＝1．【典型例题】例1 用代数式表示（1）原价为a 元的某种常用药降价40%，则降价后此药的价格是元；（2）一辆汽车以80千米/小时的速度行驶，从A 城到B 城需t 小时，如果该车行驶速度增加v 千米/小时，那么从A 城到B 城需小时．例2 计算:（1）3x 2－2(5x －2x 2)；（2）(1－a )2－(a ＋2)2；（3）(a －1)2－(1－a )(a ＋1)；（4）(x －2y ＋1)(x ＋2y －1)．例3 （1）若3a 2－a －2＝0，则5＋2a －6a 2＝；（2）计算：．【课后作业】1．用代数式表示：（1）买一个篮球需要m 元，买一个排球需要n 元，则买3个篮球和5个排球共需要元；（2）观察一列单项式:a ，－2a 2，4a 3，－8a 4，… 根据你发现的规律，第n 个单项式为；（3）从边长为a 的正方形内去掉一个边长为b 的小正方形(如图1)，然后将剩余部分剪去拼成一个矩形（如图2），根据两个图形的面积关系得到的数学公式．⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛------⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛----51413121615141312116151413121514131211图12．填空题:（1）多项式4x2＋Mxy＋9y2是一个完全平方式，则M等于；（2）计算(－a)3÷(－a2)的结果是；（3）“减去一个数，等于加上这个数的相反数”是实数的减法法则，请通过字母表示数，借助符号描述该法则：；（4）如果a－b－2＝0，那么代数式1－2a＋2b的值是．3．选择题:（1）(－a2)3的运算结果是( )．A．－a6B．a6C．－a5D．a5（2）计算(b＋2a)(2a－b)的结果( )．A．4a2－b2 B．b2－4a2C．2a2－b2D．b2－2a2（3）计算a8÷(－a3)2×a5的结果是( )．A．－a8B．－a7C．a7D．a84．计算:（1）5a2b•(－2ab3)2；（2）(2x2)3－3x4(x2－x)；（3）9×3n×3n－1；（4）[(x－y)2＋(x＋y)(x－y)]÷2x．5．先化简，再求值：2a(a＋b)－(a＋b)2，其中a＝3，b＝5．6．有若干张如图所示的正方形卡片A､B和长方形卡片C，如果要拼一个长为(2a＋b)､宽为(a＋b)的矩形，则需要A类卡片张，B类卡片张，C类卡片张．请你在右下方的大矩形中画出一种拼法．a+b2a+b【挑战中考】一、选择题1．（2022•泰州）下列计算正确的是（）A．3ab+2ab＝5ab B．5y2﹣2y2＝3C．7a+a＝7a2D．m2n﹣2mn2＝﹣mn2 2．（2022•宿迁）下列运算正确的是（）A．2m﹣m＝1B．m2•m3＝m6C．（mn）2＝m2n2D．（m3）2＝m5 3．（2022•淮安）计算a2•a3的结果是（）A．a2 B．a3C．a5D．a6 4．（2022•镇江）下列运算中，结果正确的是（）A．3a2+2a2＝5a4B．a3﹣2a3＝a3C．a2•a3＝a5D．（a2）3＝a5 5．（2022•徐州）下列计算正确的是（）A．a2•a6＝a8B．a8÷a4＝a2C．2a2+3a2＝6a4D．（﹣3a）2＝﹣9a2 6．（2022•盐城）下列计算，正确的是（）A．a+a2＝a3B．a2•a3＝a6C．a6÷a3＝a2D．（a2）3＝a6二、填空题7．（2022•连云港）计算：2a+3a＝．8．（2022•苏州）计算：a•a3＝．9．（2022•常州）计算：m4÷m2＝．10．（2022•宿迁）按规律排列的单项式：x，﹣x3，x5，﹣x7，x9，…，则第20个单项式是．三、解答题11．（2022•常州）（x+1）2﹣（x﹣1）（x+1）．12．（2022•无锡）a（a+2）﹣（a+b）（a﹣b）﹣b（b﹣3）．13．（2022•苏州）已知3x2﹣2x﹣3＝0，求（x﹣1）2+x（x+）的值．14．（2022•盐城）先化简，再求值：（x+4）（x﹣4）+（x﹣3）2，其中x2﹣3x+1＝0．。

【初中数学】中考数学知识考点：整式与分式运算

【初中数学】中考数学知识考点：整式与分式运算中考数学知识考场：积分与分数运算整式：①数与字母的乘积的代数式叫单项式，几个单项式的和叫多项式，单项式和多项式统称整式。

②一个单项式中，所有字母的指数和叫做这个单项式的次数。

③一个多项式中，次数最高的项的次数叫做这个多项式的次数。

整数运算：如果在加法和减法过程中遇到括号，请先删除括号，然后合并类似项。

幂的运算：am+an=a(m+n)（am）n=amn(a/b)n=an/bn除法一样。

他的字母的乘积，加上字母的系数，和他的字母的乘积是一样的。

② 用一个多项式乘以一个项，就是根据分布规律将多项式的每一项乘以一个项，然后将所得乘积相加。

③ 要将一个多项式乘以一个多项式，首先将一个多项式的每一项乘以另一个多项式的每一项，然后将结果相加。

公式两条：平方差公式/完全平方公式积分公式的划分：① 除以单项式，将系数除以基数的幂，然后将其作为商的因子；对于仅包含在除法公式中的字母，它与指数一起被视为商的一个因子。

② 将多项式除以单项式。

首先将多项式的每一项除以单项式，然后加上商。

分解因式：把一个多项式化成几个整式的积的形式，这种变化叫做把这个多项式分解因式。

方法：采用公因子法、公式法、分组分解法和交叉乘法。

分式：①整式a除以整式b，如果除式b中含有分母，那么这个就是分式，对于任何一个分式，分母不为0。

②分式的分子与分母同乘以或除以同一个不等于0的整式，分式的值不变。

分数运算：乘法：把分子相乘的积作为积的分子，把分母相乘的积作为积的分母。

除法：除以分数等于乘以分数的倒数。

加减法：①同分母分式相加减，分母不变，把分子相加减。

②异分母的分式先通分，化为同分母的分式，再加减。

分数方程式：① 分母未知的方程称为分数阶方程。

② 使方程分母为0的解称为原始方程的附加根。

备考2023年中考数学一轮复习-数与式_整式_整式的加减运算

备考2023年中考数学一轮复习-数与式_整式_整式的加减运算整式的加减运算专训单选题：1、(2017磴口.中考模拟) 已知实数a、b在数轴上的位置如图所示，化简的结果为（）A . 0B . ﹣2aC . 2bD . ﹣2a﹣2b2、(2022开鲁.中考模拟) 下列计算正确的是（）A . 2a＋3b＝5abB . (a－b)2＝a2－b2C . (2x2)3＝6x6D . x8÷x3＝x53、(2016义乌.中考模拟) 下列运算正确的是（）A . 2x+3y=5xyB . a3﹣a2=aC . a﹣（a﹣b）=﹣bD . （a﹣1）（a+2）=a2+a ﹣24、(2017巨野.中考模拟) 下列计算正确的是（）A . 2a3+a2=2a5B . （﹣2ab）3=﹣2ab3C . 2a3÷a2=2aD .5、(2020昌吉.中考模拟) 下列计算正确的是（）A . x2﹣3x2＝﹣2x4B . （﹣3x2）2＝6x2C . x2y•2x3＝2x6yD . 6x3y2÷（3x）＝2x2y26、(2019黄陂.中考模拟) 如图，两个面积分别为35，23的图形叠放在一起，两个阴影部分的面积分别为a，b(n>6)，则a-b的值为（）A . 6B . 8C . 9D . 127、(2018黄石.中考真卷) 下列计算中，结果是a7的是（）A . a3﹣a4B . a3•a4C . a3+a4D . a3÷a48、(2018张家界.中考真卷) 下列运算正确的是（）A . a2+a=2a3B . =aC . （a+1）2=a2+1D . （a3）2=a69、(2017陕西.中考模拟) 下列运算正确的是（）A . （﹣ab）2=﹣a2b2B . （a+b）（a﹣b）=a2﹣b2C . 3a2+2b=6a2bD . （a﹣b）2=a2+b210、(2022温州.中考模拟) 下列运算正确的是（）A .B .C .D .填空题：11、(2017淮安.中考真卷) 计算：2（x﹣y）+3y=________．12、(2012温州.中考真卷) 化简：2（a+1）﹣a=________．13、(2019柳州.中考模拟) 已知多项式6x2+(1﹣2m)x+7m的值与m的取值无关，则x ＝________.14、(2018来宾.中考模拟) 把四张形状大小完全相同的小长方形卡片（如图①），卡片长为x，宽为y，不重叠地放在一个底面为长方形（宽为a）的盒子底部（如图②），盒底面未被卡片覆盖的部分用阴影表示．则图②中两块阴影部分周长和是________（用只含b的代数式表示）．15、(2018来宾.中考模拟) 若△ABC三条边长为a，b，c，化简：|a﹣b﹣c|﹣|a+c ﹣b|=________．16、(2016内江.中考真卷) 二次函数y=ax2+bx+c的图象如图所示，且P=|2a+b|+|3b ﹣2c|，Q=|2a﹣b|﹣|3b+2c|，则P，Q的大小关系是________．17、(2021南开.中考模拟) 化简：.18、已知三角形第一边的长为，第二边比第一边长a-b，第三边比第二边短a，则这个三角形的周长是（用含字母的代数式表示）解答题：19、(2018宁晋.中考模拟) 已知a1， a2， a3，…，a2015都是正整数，设：M=（a1+a2+a3+…+a2014）（a2+a3+…+a2015），N=（a1+a2+a3+…+a2015）（a2+a3+…+a2014），试着比较M，N的大小．20、(2016定州.中考模拟) 一节地理课结束后，小明拿出地球仪，突发奇想：地球仪环形支架的长度比地球仪上画的赤道的长度长多少？活动一：如图1，求大圆与小圆的周长之差？活动二：如图2，以O为圆心，任意画出两个圆，两圆半径相差6cm，求大圆与小圆的周长之差？活动三：若地球仪与环形支架之间的间隙为k（cm），请直接写出地球仪环形支架的长度比地球仪上画的赤道的长度长多少？21、(2017嘉兴.中考模拟) 计算：22、(2018河北.中考真卷) 嘉淇准备完成题目：化简：(x2+6x+8)-(6x+5x2+2)，发现系数“”印刷不清楚．（1）他把“”猜成3，请你化简：（3x2+6x+8）﹣（6x+5x2+2）；（2）他妈妈说：“你猜错了，我看到该题标准答案的结果是常数．”通过计算说明原题中“”是几？23、(2019衡水.中考模拟) 自习课上小明在准备完成题目：化简：（x2+6x+8)-（6x+8x2+2）发现系数“ ”印刷不清楚、（1）他把“ ”猜成6，请你帮小明完成化简：（6x2+6x+8)-（6x+8x2+2)；（2）小明同桌看到他化简的结果说：“你猜错了，我看到该题标准答案的结果是常数。