江西省赣州市八年级上学期开学数学试卷
江西省赣州市八年级上学期数学期末考试试卷

江西省赣州市八年级上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)(2019·福田模拟) 下面是同学们利用图形变化的知识设计的一些美丽的图案,其中既是轴对称图形又是中心对称图形的是()A .B .C .D .2. (2分)(2016·来宾) 下列计算正确的是()A . (﹣x3)2=x5B . (﹣3x2)2=6x4C . (﹣x)﹣2=D . x8÷x4=x23. (2分)计算8x8÷(﹣2x2)的结果是()A . ﹣4x2B . ﹣4x4C . ﹣4x6D . 4x64. (2分)计算÷ 的结果是()A .B .C .D .5. (2分) (2019八下·温江期中) 下列各式由左边到右边的变形中,是因式分解的是A .B .C .D .6. (2分)若4x2+ax+1是一个完全平方式,则a的值为()A . ±1B . ±2C . ±4D . 47. (2分)(2018·通辽) 如图,▱ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD= AB,连接OE.下列结论:①S▱ABCD=AD•BD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE ,其中正确的个数有()A . 1个B . 2个C . 3个D . 4个8. (2分) (2019八上·椒江期中) 一个正多边形的内角和为900°,那么从一点引对角线的条数是()A . 3B . 4C . 5D . 69. (2分) (2019八上·秀洲月考) 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线。
江西省赣州市八年级数学上学期段考试卷(含解析) 新人教版-新人教版初中八年级全册数学试题

2016-2017学年某某省某某市兴国七中八年级(上)段考数学试卷一、选择题:(共6小题,每小题3分,共18分,每小题只有一个正确选项)1.下列图形中,△A′B′C′与△ABC成轴对称的是()A.B. C. D.2.下列计算错误的是()A.x2•x2=2x4B.(﹣2a)3=﹣8a3C.(﹣a3)2=a6D.(a3)2=a63.在△ABC中,已知∠A=∠B=∠C,则三角形是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形4.如图,A,B,C表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在()A.AC,BC两边高线的交点处B.AC,BC两边中线的交点处C.AC,BC两边垂直平分线的交点处D.∠A,∠B两内角平分线的交点处5.如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是()A.15° B.20° C.25° D.30°6.如图所示,l是四边形ABCD的对称轴,AD∥BC,现给出下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC.其中正确的结论有()A.1个B.2个C.3个D.4个二、填空题:(共6小题,每小题3分,共18分)7.一个多边形的每一个外角都等于36°,则该多边形的内角和等于度.8.若点P(m,m﹣1)在x轴上,点P关于y轴对称的点坐标为.9.已知:x m=2,x n=3,则x3m+2n=.10.等腰三角形一个角为50°,则此等腰三角形顶角为.11.如图,在△ABC中,D为三角形内一点,∠A=65°,∠ABD=20°,∠ACD=35°,BD∥CE,则∠DCE=.12.如图:AC=AD=DE=EA=BD,∠BDC=32°,∠ADB=38°,则∠BEC=.三、计算题:(共5小题,每小题6分,共30分)13.现有M和N两个村庄,欲在其旁两条公路OH、OF上建立A、B两个候车厅,使MA+AB+BN 距离最小,请你在OH、OF上确定A、B两点的位置(保留作图痕迹)14.化简:(﹣2a2b3)3+3a4b3×(﹣ab3)2.15.如图,已知AO=DO,∠OBC=∠OCB.求证:∠1=∠2.16.如图,AB=AC,∠A=100°,CE平分∠ACD,求∠ECD的度数.17.如图,在等腰三角形△ABC中,AB=AC,BD平分∠ABC,在BC的延长线上取一点E,使CE=CD,连接DE,求证:BD=DE.四、(共4小题,每小题8分,共32分)18.如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,(1)求∠F的度数;(2)若CD=5,求DF的长.19.如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于x轴对称的△A′B′C′;(2)写出A′、B′、C′三点的坐标(直接写答案);(3)在(1)(2)条件下,连接OAB′三点,求△OAB′的面积.20.如图,OE平分∠AOB,EF∥OB,EC⊥OB.(1)求证:OF=EF(2)若∠BOE=15°,EC=5求:OF的值.21.如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.(1)证明:∠CAE=∠CBF;(2)证明:AE=BF.五、(共2小题,第22小题10分,第23题12分,共22分)22.如图,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形.(1)求证:AB∥CQ;(2)AQ与CQ能否互相垂直?若能互相垂直,指出点P在BC上的位置,并给予证明;若AQ 与CQ不能互相垂直,请说明理由.23.如图,平面直角坐标系中,已知点A(a﹣b,2),B(a+b,0),AB=4,且+(a+b﹣4)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.(1)求证:AO=AB;(2)求证:∠AOC=∠ABD;(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?(提示:在直角三角形中,若两直角边分别为a、b,斜边为c,则有a2+b2=c2)2016-2017学年某某省某某市兴国七中八年级(上)段考数学试卷参考答案与试题解析一、选择题:(共6小题,每小题3分,共18分,每小题只有一个正确选项)1.下列图形中,△A′B′C′与△ABC成轴对称的是()A.B. C. D.【考点】轴对称的性质.【分析】根据中心对称,轴对称,平移变换的性质对各选项分析判断即可得解.【解答】解:A、是中心对称图形,故本选项错误;B、是轴对称图形,故本选项正确;C、是平移变换图形,故本选项错误;D、是旋转变换图形,故本选项错误.故选B.2.下列计算错误的是()A.x2•x2=2x4B.(﹣2a)3=﹣8a3C.(﹣a3)2=a6D.(a3)2=a6【考点】幂的乘方与积的乘方;同底数幂的乘法.【分析】结合同底数幂的乘法、幂的乘方与积的乘方的概念与运算法则进行求解即可.【解答】解:A、x2•x2=x4≠2x4,本选项错误;B、(﹣2a)3=﹣8a3,本选项正确;C、(﹣a3)2=a6,本选项正确;D、(a3)2=a6,本选项正确.故选A.3.在△ABC中,已知∠A=∠B=∠C,则三角形是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形【考点】三角形内角和定理.【分析】根据三角形内角和定理求出三个内角的度数即可判断.【解答】解:设∠A=α,∴∠B=α,∠C=2α,∵∠A+∠B+∠C=180°,∴α+α+2α=180°,∴α=45°,∴∠C=90°,∴该三角形是等腰直角三角形.故选(D)4.如图,A,B,C表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在()A.AC,BC两边高线的交点处B.AC,BC两边中线的交点处C.AC,BC两边垂直平分线的交点处D.∠A,∠B两内角平分线的交点处【考点】线段垂直平分线的性质.【分析】要求到三个小区的距离相等,首先思考到A小区、C小区距离相等,根据线段垂直平分线定理的逆定理知满足条件的点在线段AC的垂直平分线上,同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上,于是到三个小区的距离相等的点应是其交点,答案可得.【解答】解:A,B,C表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在AC,BC两边垂直平分线的交点处.故选C.5.如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是()A.15° B.20° C.25° D.30°【考点】等腰三角形的性质;线段垂直平分线的性质.【分析】根据等腰三角形两底角相等求出∠ABC的度数,再根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,根据等边对等角的性质可得∠ABD=∠A,然后求解即可.【解答】解:∵AB=AC,∠A=40°,∴∠ABC===65°,∵MN垂直平分线AB,∴AD=BD,∴∠ABD=∠A=50°,∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°.故选A.6.如图所示,l是四边形ABCD的对称轴,AD∥BC,现给出下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC.其中正确的结论有()A.1个B.2个C.3个D.4个【考点】轴对称的性质.【分析】根据轴对称图形的性质,四边形ABCD沿直线l对折能够完全重合,再根据两直线平行,内错角相等可得∠CAD=∠ACB=∠BAC=∠ACD,然后根据内错角相等,两直线平行即可判定AB∥CD,根据等角对等边可得AB=BC,然后判定出四边形ABCD是菱形,根据菱形的对角线互相垂直平分即可判定AO=OC;只有四边形ABCD是正方形时,AB⊥BC才成立.【解答】解:∵l是四边形ABCD的对称轴,∴∠CAD=∠BAC,∠ACD=∠ACB,∵AD∥BC,∴∠CAD=∠ACB,∴∠CAD=∠ACB=∠BAC=∠ACD,∴AB∥CD,AB=BC,故①②正确;又∵l是四边形ABCD的对称轴,∴AB=AD,BC=CD,∴AB=BC=CD=AD,∴四边形ABCD是菱形,∴AO=OC,故④正确,∵菱形ABCD不一定是正方形,∴AB⊥BC不成立,故③错误,综上所述,正确的结论有①②④共3个.故选C.二、填空题:(共6小题,每小题3分,共18分)7.一个多边形的每一个外角都等于36°,则该多边形的内角和等于1440 度.【考点】多边形内角与外角.【分析】任何多边形的外角和等于360°,可求得这个多边形的边数.再根据多边形的内角和等于(n﹣2)•180°即可求得内角和.【解答】解:∵任何多边形的外角和等于360°,∴多边形的边数为360°÷36°=10,∴多边形的内角和为(10﹣2)•180°=1440°.故答案为:1440.8.若点P(m,m﹣1)在x轴上,点P关于y轴对称的点坐标为(﹣1,0).【考点】关于x轴、y轴对称的点的坐标.【分析】直接利用x轴上点的坐标性质得出m的值,进而利用关于y轴对称的点坐标性质得出答案.【解答】解:∵点P(m,m﹣1)在x轴上,∴m﹣1=0,则m=1,故P(1,0),则点P关于y轴对称的点坐标为:(﹣1,0).故答案为:(﹣1,0).9.已知:x m=2,x n=3,则x3m+2n= 72 .【考点】幂的乘方与积的乘方;同底数幂的乘法.【分析】根据同底数幂的乘法与除法,幂的乘方与积的乘方的运算法则计算即可.【解答】解:∵x m=2,x n=3,∴x3m+2n=x3m•x2n=(x m)3•(x n)2=8×9=72.故答案为72.10.等腰三角形一个角为50°,则此等腰三角形顶角为50°或80°.【考点】等腰三角形的性质;三角形内角和定理.【分析】已知没有给出50°的角是顶角和是底角,所以要分两种情况进行讨论.【解答】解:分为两种情况:当50°是顶角时,顶角为50°当50°是底角时,其顶角是180°﹣50°×2=80°故填50°或80°.11.如图,在△ABC中,D为三角形内一点,∠A=65°,∠ABD=20°,∠ACD=35°,BD∥CE,则∠DCE= 60°.【考点】平行线的性质.【分析】先根据三角形内角和定理求出∠DBC+∠DCB的度数,再由平行线的性质得出∠DBC=∠ECB,由此可得出结论.【解答】解:∵△ABC中,∠A=65°,∠ABD=20°,∠ACD=35°,∴∠DBC+∠DCB=180°﹣65°﹣35°﹣20°=60°.∵BD∥CE,∴∠DBC=∠ECB,∴∠DCE=∠DBC+∠DCB=60°.故答案为:60°.12.如图:AC=AD=DE=EA=BD,∠BDC=32°,∠ADB=38°,则∠BEC= 21°.【考点】等腰三角形的性质.【分析】根据等腰三角形的性质和等边三角形的性质分别得出∠AEC,∠BED,∠AED的度数,由∠BEC=∠AEC+∠BED﹣∠AED即可求解.【解答】解:∵AC=AD=DE=EA=BD,∠BDC=32°,∠ADB=38°,∴∠ADC=38°+32°=70°,∠CAD=180°﹣2×70°=40°,∠DAE=∠ADE=∠AED=∠60°,在△ACE中,∠CAE=60°+40°=100°,∠AEC=÷2=40°.又∵在△BDE中,∠BDE=60°+38°=98°,∴∠BED=÷2=41°∴∠BEC=∠AEC+∠BED﹣∠AED=40°+41°﹣60°=21°.故答案为:21°.三、计算题:(共5小题,每小题6分,共30分)13.现有M和N两个村庄,欲在其旁两条公路OH、OF上建立A、B两个候车厅,使MA+AB+BN 距离最小,请你在OH、OF上确定A、B两点的位置(保留作图痕迹)【考点】作图—应用与设计作图;轴对称-最短路线问题.【分析】直接利用对称点的性质得出M,N分别关于OH,OF的对称点,进而连接得出答案.【解答】解:如图所示:A,B点即为所求.14.化简:(﹣2a2b3)3+3a4b3×(﹣ab3)2.【考点】单项式乘单项式;幂的乘方与积的乘方.【分析】先算积的乘方,再算单项式乘单项式,最后合并同类项即可求解.【解答】解:(﹣2a2b3)3+3a4b3×(﹣ab3)2=﹣8a6b9+3a4b3×a2b6=﹣8a6b9+3a6b9=﹣5a6b9.15.如图,已知AO=DO,∠OBC=∠OCB.求证:∠1=∠2.【考点】全等三角形的判定与性质.【分析】欲证明∠1=∠2,只要证明△AOD≌△DOC即可.【解答】证明:∵∠OBC=∠OCB,∴OB=OC,在△AOB和△DOC中,,∴△AOB≌△DOC,∴∠1=∠2.16.如图,AB=AC,∠A=100°,CE平分∠ACD,求∠ECD的度数.【考点】等腰三角形的性质.【分析】利用等腰三角形的性质得到∠B的度数,再根据三角形外角的性质得出∠ACD的度数,进而利用角平分线的性质得出答案.【解答】解:∵AB=AC,∠A=100°,∴∠B=÷2=40°,∴∠ACD=100°+40°=140°,∵CE平分∠ACD,则∠ECD=70°.17.如图,在等腰三角形△ABC中,AB=AC,BD平分∠ABC,在BC的延长线上取一点E,使CE=CD,连接DE,求证:BD=DE.【考点】等腰三角形的性质.【分析】求出∠ABC=∠ACB,求出∠DBC=∠ABC,根据等腰三角形性质和三角形外角性质求出∠E=∠ACB,推出∠E=∠DBC即可.【解答】证明:∵AB=AC∴∠ABC=∠ACB,∵BD平分∠ABC,∴∠DBC=∠ABC,∵CD=CE,∴∠E=∠CDE,∵∠ACB=∠E+∠CDE,∴∠E=∠ACB,∴∠E=∠DBE,∴BD=DE.四、(共4小题,每小题8分,共32分)18.如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,(1)求∠F的度数;(2)若CD=5,求DF的长.【考点】等边三角形的性质;平行线的性质.【分析】(1)根据平行线的性质可得∠EDC=∠B=60°,根据三角形内角和定理即可求解;(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.【解答】解:(1)∵△ABC是等边三角形,∴∠B=60°,∵DE∥AB,∴∠EDC=∠B=60°,∵EF⊥DE,∴∠DEF=90°,∴∠F=90°﹣∠EDC=30°;(2)∵∠ACB=60°,∠EDC=60°,∴△EDC是等边三角形.∴ED=DC=5,∵∠DEF=90°,∠F=30°,∴DF=2DE=10.19.如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于x轴对称的△A′B′C′;(2)写出A′、B′、C′三点的坐标(直接写答案);(3)在(1)(2)条件下,连接OAB′三点,求△OAB′的面积.【考点】作图-轴对称变换.【分析】(1)利用关于x轴对称的点的坐标特征写出A′、B′、C′三点的坐标,然后描点即可得到△A′B′C′;(2)由(1)得A′、B′、C′三点的坐标;(3)用一个矩形的面积减去三个三角形的面积可计算出△OAB′的面积.【解答】解:(1)如图,△A′B′C′为所作;(2)A′(1,﹣2)、B′(3,﹣1)、C′(﹣2,1);(3)△OAB′的面积=3×3﹣×3×1﹣×2×3﹣×2×1=3.5.20.如图,OE平分∠AOB,EF∥OB,EC⊥OB.(1)求证:OF=EF(2)若∠BOE=15°,EC=5求:OF的值.【考点】角平分线的性质;平行线的性质.【分析】(1)根据角平分线的定义得到∠BOE=∠AOE,由平行线的性质得到∠BOE=∠OEF,等量代换得到∠OEF=∠FOE,于是得到结论;(2)过E作ED⊥OA于D,根据三角形的外角的性质得到∠EFD=30°,根据直角三角形的性质即可得到结论.【解答】(1)证明:∵OE平分∠AOB,∴∠BOE=∠AOE,∵EF∥OB,∴∠BOE=∠OEF,∴∠OEF=∠FOE,∴OF=EF;(2)解:过E作ED⊥OA于D,∵∠BOE=15°,∴∠OEF=∠FOE=15°,∴∠EFD=30°,∵CE⊥OB,∴DE=CE=5,∴EF=2DE=10,∴OF=EF=10.21.如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.(1)证明:∠CAE=∠CBF;(2)证明:AE=BF.【考点】全等三角形的判定与性质;等腰三角形的性质.【分析】(1)根据等腰三角形三线合一的性质可得CH平分∠ACB,再证明△ACE和△BCF全等,然后根据全等三角形对应角相等可得结论;(2)证明△AEC≌△BFC,根据全等三角形对应边相等即可证明.【解答】(1)证明:在等腰△ABC中,∵CH是底边上的高线,∴∠ACH=∠BCH,在△ACP和△BCP中,,∴△ACP≌△BCP(SAS),∴∠CAE=∠CBF(全等三角形对应角相等);(2)在△AEC和△BFC中,∴△AEC≌△BFC(ASA),∴AE=BF(全等三角形对应边相等).五、(共2小题,第22小题10分,第23题12分,共22分)22.如图,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形.(1)求证:AB∥CQ;(2)AQ与CQ能否互相垂直?若能互相垂直,指出点P在BC上的位置,并给予证明;若AQ 与CQ不能互相垂直,请说明理由.【考点】全等三角形的判定与性质;等边三角形的性质.【分析】(1)根据等边三角形性质得出AB=AC,AP=AQ,∠BAC=∠B=∠PAQ=60°,求出∠BAP=∠CAQ,根据SAS证△ABP≌△ACQ,推出∠ACQ=∠B=60°=∠BAC,根据平行线的判定推出即可.(2)根据等腰三角形性质求出∠BAP=30°,求出∠B AQ=90°,根据平行线性质得出∠AQC=90°,即可得出答案.【解答】(1)证明:∵△ABC和△APQ是等边三角形,∴AB=AC,AP=AQ,∠BAC=∠B=∠PAQ=60°,∴∠BAP=∠CAQ=60°﹣∠PAC,在△ABP和△ACQ中∴△ABP≌△ACQ(SAS),∴∠ACQ=∠B=60°=∠BAC,∴AB∥CQ.(2)AQ与CQ能互相垂直,此时点P在BC的中点,证明:∵当P为BC边中点时,∠BAP=∠BAC=30°,∴∠BAQ=∠BAP+∠PAQ=30°+60°=90°,又∵AB∥CQ,∴∠AQC=90°,即AQ⊥CQ.23.如图,平面直角坐标系中,已知点A(a﹣b,2),B(a+b,0),AB=4,且+(a+b﹣4)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.(1)求证:AO=AB;(2)求证:∠AOC=∠ABD;(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?(提示:在直角三角形中,若两直角边分别为a、b,斜边为c,则有a2+b2=c2)【考点】三角形综合题;全等三角形的判定与性质;等腰三角形的性质;等边三角形的性质.【分析】(1)根据算术平方根和平方的非负性质即可求得a、b的值,进而求得A,B点坐标,求得OA,AB长度即可;(2)易证∠OAC=∠BAD,即可证明△OAC≌△BAD,根据全等三角形的性质,可得对应角相等;(3)点P在y轴上的位置不发生改变,先判定△AOB是等边三角形,易证∠OBP=60°,根据OB长度固定和∠OPB=30°,即可求得OP的长为定值.【解答】解:(1)∵+(a+b﹣4)2=0,∴,解得,∴A(2,2),B(4,0),∴AO==4,又∵AB=4,∴AO=AB;(2)∵∠CAD=∠OAB,∴∠CAD+∠BAC=∠OAB+∠BAC,即∠OAC=∠BAD,在△OAC和△BAD中,,∴△OAC≌△BAD(SAS),∴∠AOC=∠ABD;(3)点P在y轴上的位置不发生改变.证明:由(1)可得,AB=BO=AO=4,∴∠AOB=∠ABO=60°,由(2)知△AOC≌△ABD,∴∠ABD=∠AOB=60°,∴∠OBP=60°,∵∠POB=90°,∴∠OPB=30°,∴Rt△BOP中,BP=2OB=8,∴OP==4,即OP长度不变,∴点P在y轴上的位置不发生改变.。
赣州市八年级(上)期末数学试卷含答案
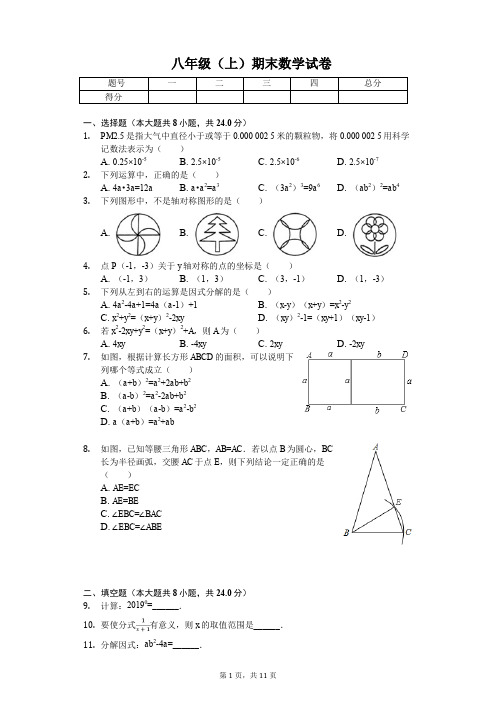
八年级(上)期末数学试卷一、选择题(本大题共8小题,共24.0分)1.PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为()A. 0.25×10-5B. 2.5×10-5C. 2.5×10-6D. 2.5×10-72.下列运算中,正确的是()A. 4a•3a=12aB. a•a2=a3C. (3a2)3=9a6D. (ab2)2=ab43.下列图形中,不是轴对称图形的是()A. B. C. D.4.点P(-1,-3)关于y轴对称的点的坐标是()A. (-1,3)B. (1,3)C. (3,-1)D. (1,-3)5.下列从左到右的运算是因式分解的是()A. 4a2-4a+1=4a(a-1)+1B. (x-y)(x+y)=x2-y2C. x2+y2=(x+y)2-2xyD. (xy)2-1=(xy+1)(xy-1)6.若x2-2xy+y2=(x+y)2+A,则A为()A. 4xyB. -4xyC. 2xyD. -2xy7.如图,根据计算长方形ABCD的面积,可以说明下列哪个等式成立()A. (a+b)2=a2+2ab+b2B. (a-b)2=a2-2ab+b2C. (a+b)(a-b)=a2-b2D. a(a+b)=a2+ab8.如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是()A. AE=ECB. AE=BEC. ∠EBC=∠BACD. ∠EBC=∠ABE二、填空题(本大题共8小题,共24.0分)9.计算:20190=______.10.要使分式有意义,则x的取值范围是______.11.分解因式:ab2-4a=______.12.如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件______使得△ABC≌△DEF.13.如图,某小区规划在边长为xm的正方形场地上,修建两条宽为ym的甬道(阴影部分),其余部分种草,则阴影部分的面积是______m2.14.如图,边长为a、b的矩形,它的周长为14,面积为10,则a2b+ab2的值为______.15.若(m+n)2=5,(m-n)2=36,则m2-mn+n2=______.16.已知△ABO关于x轴对称,点A的坐标为(1,﹣2),若在坐标轴上有一个点P,满足△BOP的面积等于2,则点P的坐标为____.三、计算题(本大题共1小题,共6.0分)17.解方程:=0四、解答题(本大题共7小题,共46.0分)18.化简:2ab•3b-12a3b2÷4a219.如图,AB=CD,DE⊥AC,BF⊥AC,点E,F是垂足,AE=CF,求证:(1)△ABF≌△CDE;(2)AB∥CD.20.如图,在正五边形ABCDE中,请仅用无刻度的直尺,分别按下列要求作,(1)在图1中,画出过点A的正五边形的对称轴;(2)在图2中,画出一个以点C为顶点的72°的角.21.先化简,后求值:,其中a=-.22.如图,已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点。
江西省赣州市章贡区第三中学2023-2024学年八年级上学期月考数学试题(解析版)

2023-2024学年八年级上学期第一次月考数学试卷班级___________姓名___________分数____________(考试时间:120分钟试卷满分:150分)注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分.答卷前,考生务必将自己的班级、姓名填写在试卷上.2.回答第I卷时,选出每小题答案后,将答案填在选择题上方的答题表中.3.回答第II卷时,将答案直接写在试卷上.4.考试范围:人教版八年级上册第11章——12章第Ⅰ卷(选择题共40分)一、选择题:本题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列长度的三条线段能组成三角形的是()A.1,2,3B.2,2,4C.3,4,5D.3,4,8【答案】C【解析】【详解】A、1+2=3,不能构成三角形,故A错误;B、2+2=4,不能构成三角形,故B错误;C、3+4>5,能构成三角形,故C正确;D、3+4<8,不能构成三角形,故D错误.故选C.的高的是()2.下列四个图形中,线段BE是ABCA. B.C. D.【答案】C【解析】【分析】线段BE 是ABC 的高指的是过点B 作对边的垂线,垂足为E ,由此即可求解.【详解】解:根据题意可得,线段BE 是ABC 的高,∴BE AC ⊥,故选:C .【点睛】本题主要考查三角形高的理解,掌握高的作图方法,三角形高的定义是解题的关键.3.如图,在△ABC 中,AB =AC ,D 为BC 中点,∠BAD =35°,则∠C 的度数为()A.35°B.45°C.55°D.60°【答案】C【解析】【分析】根据等腰三角形的三线合一的性质可直接得到AD 平分∠BAC ,AD ⊥BC ,结合图形,利用各角之间的关系及三角形内角和定理即可得.【详解】解:∵△ABC 为等腰三角形,∴AD 平分∠BAC ,AD ⊥BC ,∴35DAC BAD ∠=∠=︒,90ADC ∠=︒,∴18055C ADC DAC ∠=︒-∠-∠=︒,故选C .【点睛】题目主要考查等腰三角形三线合一的性质,三角形内角和定理,理解题意,找准各角之间的数量关系是解题关键.4.如图,已知AB AD =,那么添加下列一个条件后,仍无法判定ABC ADC △≌△的是()A.CB CD= B.BAC DAC ∠=∠C.BCA DAC∠=∠ D.90B D ∠=∠=︒【答案】C【解析】【分析】根据三角形全等的判定逐个判断即可得到答案;【详解】解:由题意可得,AB AD =,AC AC =,结合CB CD =得到SSS 判定,故A 不符合题意,结合BAC DAC ∠=∠得到SAS 判定,故B 不符合题意,结合BCA DAC ∠=∠不能判定三角形全等,故C 符合题意,结合90B D ∠=∠=︒得到HL 定理,故D 不符合题意,故选:C ;【点睛】本题考查三角形全等的判定,解题的关键是结合选项得到相应的判定.5.如图,ACE △≌DBF ,若11cm AD =,5cm =BC ,则AB 长为()A.6cmB.7cmC.4cmD.3cm【答案】D【解析】【分析】根据全等三角形的性质得到AC BD =,结合图形计算,得到答案.【详解】解:ACE Q V ≌DBF ,AC BD ∴=,AC BC BD BC ∴-=-,即AB CD =,11cm AD = ,5cm =BC ,()11523cm AB ∴=-÷=,故选D .【点睛】本题考查全等三角形的性质,线段的和与差.掌握全等三角形的对应边相等是解题的关键.6.如图是用直尺和圆规作已知角的平分线的示意图,则说明CAD DAB ∠=∠的依据是()A.SASB.ASAC.AASD.SSS【答案】D【解析】【分析】根据作图过程可得,两个三角形三条边对应相等,所以可得两个三角形全等.【详解】由作图过程可得:AE AF DE DF AD AD ===,,,所以ADF ADE ≌ (SSS ),∴CAD DAB ∠=∠,故选:D .【点睛】本题考查了作角平分线,三角形全等判定定理:三组对应边分别相等的两个三角形全等(简称SSS 或“边边边”),掌握以上知识是解题的关键.7.如图,点F ,B ,E ,C 在同一条直线上,ABC DEF ≌△△,若36A ∠=︒,24F ∠=︒,则DEC ∠的度数为()A.50°B.60°C.65°D.120°【答案】B【解析】【分析】根据ABC DEF ≌△△得到∠D =∠A =36°,运用三角形外角性质得到∠DEC =∠D +∠F =60°.【详解】∵ABC DEF ≌△△,∴∠D =∠A =36°,∴∠DEC =∠D +∠F =60°.故选B .【点睛】本题考查了全等三角形,三角形外角,熟练掌握全等三角形角的性质和三角形外角性质是解决此题的关键.8.多边形的内角和不可能为()A.180°B.540°C.1200°D.1800°【答案】C【解析】【分析】根据多边形的内角和计算公式及多边形边数为正整数,计算得结论.【详解】解:∵多边形的内角和()2180n -⨯︒=,多边形的边数n 为正整数,∴多边形的内角和是180°的倍数.180180154018031200180 6.7180018010︒÷︒︒÷︒︒÷︒≈︒÷︒=,=,,=,故选:C .【点睛】本题考查了多边形的内角和,掌握多边形的内角和公式是解决本题的关键.9.一副三角板如图所示放置,AB ∥DC ,∠CAE 的度数为()A.45°B.30°C.15°D.10°【答案】C【解析】【分析】由平行线的性质可得∠BAC =∠ACD =30°,由三角形外角的性质可求解.【详解】解:∵AB ∥CD ,∴∠BAC =∠ACD =30°,∵∠AED =45°,∴∠EAC =∠AED ﹣∠ACD =15°.故选:C .【点睛】本题考查了三角形外角的性质,平行线的性质,灵活运用这些性质解决问题是本题的关键.10.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作等边△ABC 和等边△ECD ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q 连接PQ .以下五个结论正确的是()①AD BE =;②PQ ∥AE ;③AP BQ =;④DE DP =;⑤60AOB ∠=A.①③⑤B.①③④⑤C.①②③⑤D.①②③④⑤【答案】C【解析】【分析】①由于△ABC 和△CDE 是等边三角形,可知AC =BC ,CD =CE ,∠ACB =∠DCE =60°,从而证出△ACD ≌△BCE ,可推知AD =BE ;②由△ACD ≌△BCE 得∠CBE =∠DAC ,加之∠ACB =∠DCE =60°,AC =BC ,得到△CQB ≌△CPA (ASA ),再根据∠PCQ =60°推出△PCQ 为等边三角形,又由∠PQC =∠DCE ,根据内错角相等,两直线平行,可知②正确;③根据②△CQB ≌△CPA (ASA ),可知③正确;④根据∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,∠CDE =60°,可知∠DQE ≠∠CDE ,可知④错误;⑤利用等边三角形的性质,BC ∥DE ,再根据平行线的性质得到∠CBE =∠DEO ,于是∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°,可知⑤正确.【详解】解:∵等边△ABC 和等边△CDE ,∴60AC BC CD CE ACB DCE ==∠=∠=︒,,,∴ACB BCD DCE BCD ∠+∠=∠+∠,即ACD BCE ∠=∠,∴ACD BCE SAS ≌(),∴AD =BE ,∴①正确,∵≌ACD BCE V V ,∴CBE DAC ∠=∠,又∵60ACB DCE ︒∠=∠=,∴60BCD ∠=︒,即ACP BCQ ∠=∠,又∵AC BC =,∴CQB CPA ASA ≌(),∴CP CQ =,又∵∠PCQ =60°可知△PCQ 为等边三角形,∴60PQC DCE ∠=∠=︒,∴PQ ∥AE ②正确,∵△CQB ≌△CPA ,∴AP =BQ ,③正确,∵AD =BE ,AP =BQ ,∴AD AP BE BQ -=-,即DP =QE ,∵6060DQE ECQ CEQ CEQ CDE ∠=∠+∠=︒+∠∠=︒,,∴∠DQE ≠∠CDE ,∴DE ≠DP ,故④错误;∵∠ACB =∠DCE =60°,∴∠BCD =60°,∵等边△DCE ,∠EDC =60°=∠BCD ,∴BC ∥DE ,∴∠CBE =∠DEO ,∴∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°,∴⑤正确.故选:C .【点睛】本题综合考查了等边三角形判定与性质、全等三角形的判定与性质、平行线的判定与性质等知识点的运用.要求学生具备运用这些定理进行推理的能力,此题的难度较大.第II 卷(非选择题共110分)二、填空题:共6小个题,每小题4分,共24分.请考生根据要求作答.11.已知三角形的两边长分别是2和5,则第三边长c 的取值范围是___________.【答案】37c <<【解析】【分析】根据三角形的第三边大于两边之差,小于两边之和,即可解决问题.【详解】解:∵三角形的两边长分别是2和5,∴第三边长c 的取值范围是5252c -<<+,即37c <<.故答案为:37c <<.【点睛】本题考查三角形三边关系的运用,熟记三角形的第三边大于两边之差,小于两边之和是解题的关键.12.若一扇窗户打开后,用窗钩将其固定,主要运用的几何原理是_________.【答案】三角形的稳定性【解析】【详解】解:一扇窗户打开后,用窗钩可将其固定,这里所运用的几何原理是三角形的稳定性.故答案为:三角形的稳定性.13.如图,AE AD =,要使ABE ACD ≌,应添加的条件是_______.(添加一个条件即可)【答案】AB AC =或C B ∠=∠或AEB ADC∠=∠【解析】【分析】根据三角形全等的判定(SSS ,SAS ,ASA ,AAS ,HL()直角三角形)即可求解.【详解】解:已知AE AD =,A ∠是公共角,∴要使ABE ACD ≌,可以添加的条件有:①SAS ,即AE AE A A AB AC =⎧⎪∠=∠⎨⎪=⎩;②AAS ,即A A C B AE AD ∠=∠⎧⎪∠=∠⎨⎪=⎩;③ASA ,即A A AE AD AEB ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩,故答案为:AB AC =或C B ∠=∠或AEB ADC ∠=∠.【点睛】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键.14.如图,OP 平分∠MON ,PA ⊥ON 于点A ,点Q 是射线OM 上一个动点,若PA =3,则PQ 的最小值为_____.【答案】3【解析】【分析】由垂线段最短可知,当PQ 与OM 垂直的时候,PQ 的值最小.【详解】解:由垂线段最短可知,当PQ 与OM 垂直的时候,PQ 的值最小,根据角平分线的性质可知,此时PA =PQ =3.故答案为:3.【点睛】本题考查了角平分线的性质,垂线段最短,解题的关键是掌握垂线段距离最短.15.如图,七边形ABCDEFG 中,AB ,ED 的延长线交于点O ,若l ∠,2∠,3∠,4∠的外角和等于210 ,则BOD ∠的度数为______.【答案】30【解析】【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和,由五边形内角和可求得五边形OAGFE 的内角和,则可求得∠BOD .【详解】1 ∠、2∠、3∠、4∠的外角的角度和为210 ,12342104180∠∠∠∠∴++++=⨯ ,1234510∠∠∠∠∴+++= ,五边形OAGFE 内角和()52180540=-⨯= ,1234BOD 540∠∠∠∠∠∴++++= ,BOD 54051030 ∠∴=-=.故答案为30【点睛】本题主要考查多边形的内角和,利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键.16.如图,在△ABC 中,∠C =90°,BC =8cm ,AC =6cm ,点E 是BC 的中点,动点P 从A 点出发,以每秒2cm 的速度沿A →C →E 运动.若设点P 运动的时间是t 秒,那么当t =____时,△APE 的面积等于8.【答案】2或113【解析】【分析】分点P 在线段AC 上和点P 在线段CE 上两种情况考虑,根据三角形的面积公式分别列出关于t 的一元一次方程,解之即可得出结论.【详解】解:∵BC =8cm ,点E 是BC 的中点,∴CE =12BC =4cm ,当点P 在线段AC 上,如图1所示,AP =2t ,∵∠C =90°,∴S △APE =12AP •CE =12×2t ×4=4t =8,解得:t =2;当点P 在线段CE 上,如图2所示,AC =6cm ,PE =10-2t ,∴S △APE =12PE •AC =12×(10-2t )×6=8,解得:t =113.故答案为∶2或113.【点睛】本题考查了直角三角形的性质的运用,三角形的面积公式的运用,以及解一元一次方程,和分类讨论的数学思想,解答时灵活运用三角形的面积公式求解是关键.三、解答题:共9小题,共86分.解答应写出文字说明、证明过程或演算步骤17.一个正多边形的所有内角与它的所有外角之和是1620°,求该正多边形的边数及一个外角的度数.【答案】边数为9,一个外角为40【解析】【分析】设这个多边形边数是n ,根据题意列出方程,解方程,即可求解.【详解】解:设这个多边形边数是n ,根据题意得,()21803601620n -⨯+=,解得:9n =,∴这个正多边形的边数为9,则一个外角的度数为360940︒÷=︒.【点睛】本题考查了多边形内角和与外角和问题,熟练掌握多边形的内角度公式()2180n -⨯︒是解题的关键.18.已知,ABC DCB ∠=∠,ACB DBC ∠=∠,求证:ABC DCB △≌△.【答案】证明见解析【解析】【分析】由条件∠ABC =∠DCB ,∠ACB =∠DBC ,根据ASA 证明△ABC ≌△DCB即可.【详解】证明:在△ABC 和△DCB 中,ABC DCB BC CB ACB DBC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC ≌△DCB (ASA );【点睛】此题主要考查了全等三角形的判定,解题关键是找到图中的公共边的条件证明全等.19.如图所示,在△ABC 中,AD 是BC 边上的高,点E 是AB 上一点,CE 交AD 于点M ,且∠DCM =∠MAE ,求证△ACE是直角三角形.【答案】见解析【解析】【分析】由于AD 是BC 边上的高,根据直角三角形的两个锐角互余可得∠DMC+∠DCM=90°;又根据∠DMC 和∠AME 为对顶角以及等角的余角相等,还可推出∠DCM=∠MAE ;接下来,通过角度之间的等量代换得到∠MEA=90°,至此即可解答题目.【详解】∵AD 是BC 边上的高,∴∠DMC+∠DCM=90°.∵∠DMC=∠AME ,∠DCM=∠MAE ,∴∠AME+∠MAE=90°,∴∠MEA=90°,即△ACE 是直角三角形.【点睛】此题考查直角三角形的性质,解题关键在于得到△ACE 中有一个角是直角.20.如图,在ABC 中,90C ∠=︒.(1)过点B 作ABC ∠的平分线交AC 于点D (尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);(2)若3CD =,16AB BC +=,求ABC 的面积.【答案】(1)见解析(2)24【解析】【分析】(1)根据角平分线的作法,画出图形即可;(2)作DH ⊥AB 于H .只要证明CD =DH ,根据三角形的面积公式即可解决问题.【小问1详解】∠ABC 的平分线如图所示.【小问2详解】作DH ⊥AB 于H .∵BD 平分∠ABC ,DC ⊥BC ,DH ⊥AB ,∴CD =DH =3,∴△ABC 的面积=S △BCD +S △ABD =12BC •CD +12AB •DH =12×3BC +12×3AB =12×3(BC +AB )=12×3×16=24.【点睛】本题考查了角平分线的性质,三角形的面积的计算,熟练掌握角平分线的性质是解题的关键.21.如图,△ABE 中,∠E =90°,AC 是∠BAE 的角平分线.(1)若∠B =40°,求∠BAC 的度数;(2)若D 是BC 的中点,△ADC 的面积为16,AE =8,求BC 的长.【答案】(1)25BAC ∠=︒;(2)8BC =【解析】【分析】(1)先利用互余计算出∠BAE =50°,再利用角平分线的定义得到∠BAC =12∠BAE =25°;(2)先根据三角形面积公式得出DC ,利用D 是BC 的中点得到BC 即可.【小问1详解】解:∵∠B =40°,∠E =90°,∴∠BAE =90°﹣40°=50°,∵AC 是∠BAE 的角平分线,∴∠BAC =12∠BAE =25°;【小问2详解】∵S △ADC =12DC •AE ,∴12×DC ×8=16,∴DC =4,∵D 是BC 的中点,∴BC =2CD =8.【点睛】本题考查了角平分线的定义,线段的中点,角平分线的定义的正确运用是解题的关键.22.如图,AB =AD ,BC =DC ,点E 在AC 上.求证:BE =DE .【答案】证明见解析【解析】【分析】本题可先根据SSS 判定△ABC ≌△ADC ,得出∠DAE=∠BAE ,再根据SAS 判定△ABE ≌△ADE ,从而得出BE=DE .【详解】证明:在△ABC 和△ADC 中,∵AB=AD ,BC=DC ,AC=AC ,∴△ABC ≌△ADC (SSS );∴∠DAE=∠BAE .在△ABE 和△ADE 中,AB AD DAE BAE AE AE ⎧⎪∠∠⎨⎪⎩===∴△ABE ≌△ADE (SAS ),∴BE=DE .【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、HL 等.注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.23.已知:如图,90B C ∠=∠=︒,M 是BC 的中点,DM 平分ADC ∠.(1)求证:AM 平分BAD ∠;(2)试说明线段DM 与AM 有怎样的位置关系?(3)线段CD 、AB 、AD 间有怎样的关系?直接写出结果.【答案】(1)见解析(2)DM AM ⊥(3)CD AB AD+=【解析】【分析】(1)首先要作辅助线,ME AD ⊥则利用角的平分线上的点到角的两边的距离相等可知ME MC =,再利用中点的条件可知ME MB =,再利用到角两边距离相等的点在角的平分线上的逆定理证明AM 平分DAB ∠;(2)根据平行线性质得出180CDA BAD ∠+∠=︒,求出1+3=90∠∠︒,根据三角形内角和定理求出即可;(3)证Rt Rt DCM DEM ≌,推出CD DE =,同理得出AE AB =,即可得出CD AB AD +=.【小问1详解】证明:如图,作ME AD ⊥于E ,MC DC ⊥ ,ME DA ⊥,MD 平分ADC ∠,ME MC ∴=,M 是BC 的中点,MB MC ∴=,又ME MC = ,ME MB =∴,又∵ME AD ⊥,MB AB ⊥,AM ∴平分DAB ∠;【小问2详解】DM AM ⊥,理由是:DM 平分CDA ∠,AM 平分DAB ∠,12∴∠=∠,3=4∠∠,DC AB ∥,180CDA BAD ∴∠+∠=︒,1390∴∠+∠=︒,()1801390DMA ∴∠=︒-∠+∠=︒,即DM AM ⊥;【小问3详解】CD AB AD +=,理由是:ME AD ⊥ ,MC CD ⊥,90C DEM ∴∠=∠=︒,CD DE ∴=,在Rt DCM 和Rt DEM 中,DM DM EM CM=⎧⎨=⎩,()Rt Rt HL DCM DEM ∴≌ ,ME MC∴=ME AD ⊥ ,MB AB ⊥,90B AEM ∴∠=∠=︒,BM EM ∴=,在Rt MBA 和Rt MEA △中,AM AM BM EM =⎧⎨=⎩,()Rt Rt HL MBA MEA ∴ ≌,AE AB ∴=,AE DE AD += ,CD AB AD ∴+=.【点睛】本题考查了角平分线的判定与性质,平行线的性质,三角形内角和,全等三角形的判定与性质,利用角平分线性质得到ME MC =是解答本题的关键.24.[尝试探究]如图1,在一张三角形纸片上,剪去ABC ,得到四边形BCHG ,1∠与2∠分别为ABC 的两个外角(1)请你试着说明:12180A∠+∠=︒+∠(2)如图2,如果沿着EF 再剪一刀,3∠与4∠分别为AEF △的两个外角,那么12∠+∠和34∠+∠的数量关系为(3)如图3,EP ,FP 分别平分外角FEG ∠、EFH ∠,求EPF ∠与A ∠的数量关系;[拓展提升](4)如图4,在四边形BCFE 中,EP 、FP 分别平分外分FEG ∠、EFH ∠,请写出EPF ∠,1∠、2∠这三个角的数量关系,并说明理由.【答案】(1)见解析(2)1234∠+∠=∠+∠(3)1902A ︒-∠(4)122360P ∠+∠+∠=︒,见解析【解析】【分析】(1)根据外角的性质得到1180ABC ∠=︒-∠,2180ACB ∠=︒-∠,求得()12360ABC ACB ∠+∠=︒-∠+∠,根据三角形的内角和即可得到结论;(2)由(1)得,12180A ∠+∠=︒-∠,同理得到34180A ∠+∠=︒-∠,于是得到结论;(3)由(1)得,180GEF HFE A ∠+∠=︒-∠,根据角平分线的定义即可得到结论;(4)由(3)得到2180A P ∠+∠=︒,由(1)得到12180A ∠+∠=︒+∠,于是得到结论.【小问1详解】解:∵1∠与2∠分别为ABC 的两个外角,∴1180ABC ∠=︒-∠,2180ACB ∠=︒-∠,∴()12360ABC ACB ∠+∠=︒-∠+∠,∵三角形的内角和为180︒,∴180ABC ACB A ∠+∠=︒-∠,∴()12360180180A A ∠+∠=︒-︒-∠=︒+∠;【小问2详解】由(1)得,12180A ∠+∠=︒+∠,同理,34180A ∠+∠=︒+∠,∴1234∠+∠=∠+∠,故答案为:1234∠+∠=∠+∠;【小问3详解】由(1)得,180GEF HFE A ∠+∠=︒+∠,∵EP ,FP 分别平分外角FEG ∠、EFH ∠,∴12PEF GEF ∠=∠,12PFE HFE ∠=∠,∴11()(180)22PEF PFE GEF HFE A ∠+∠=∠+︒∠=+∠,∴11180()180(180)9022P PEF PFE A A ∠=-∠+∠=-+∠=︒-︒︒∠︒;【小问4详解】数量关系:122360P ∠+∠+∠=︒,理由:如图,由(3)可知,2180A P ∠+∠=︒,由(1)可知,12180A ∠+∠=︒+∠,∴()121802180P ∠+∠-︒+∠=︒,∴122360P ∠+∠+∠=︒.【点睛】本题考查的是角平分线的定义、三角形内角和定理,掌握三角形内角和等于180︒是解题的关键.25.(1)如图1,在ABC 中,AD 平分BAC ∠交BC 于D ,DE AB ⊥于E ,DFAC ⊥于F ,则有相等关系DE DF =,AE AF =.(2)如图2,在(1)的情况下,如果MDN EDF ∠=∠,MDN ∠的两边分别与AB 、AC 相交于M 、N 两点,其它条件不变,那么又有相等关系AM +2AF =,请加以证明.(3)如图3,在Rt ABC △中,90C ∠=︒,60BAC ∠=︒,6AC =,AD 平分BAC ∠交BC 于D ,120MDN ∠=︒,ND AB ∥,求四边形AMDN 的周长.【答案】(1)证明见详解;(2)AN ,(3)20;【解析】【分析】(1)证明ADE ADF V V ≌即可得到答案;(2)证明MDE NDF △≌△即可得到答案;(3)过D 作DF AB ⊥,根据角平分线得到30BAD CAD ∠=∠=︒,即可得到30︒角三角形直角边与斜边的关系,结勾股定理求出相应线段的长度,证明ADF ADC ≌得到线段关系即可得到答案;【详解】(1)解:∵DE AB ⊥,DF AC ⊥,∴90AED AEM AFD CFD ∠=∠=∠=∠=︒,∵AD 平分BAC ∠,∴∠∠EAD FAD =,在ADE V 与ADF △中,AED AFD EAD FAD AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴(AAS)ADE ADF △≌△,∴DE DF =,AE AF =;(2)解:∵MDN EDF ∠=∠,+EDF NDF EDN ∠=∠∠,+MDN MDE EDN ∠=∠∠,∴=MDE NDF ∠∠,在MDE 与NDF 中,=MDE NDF DE DF MED NFD ∠∠⎧⎪=⎨⎪∠=∠⎩,∴(ASA)MDE NDF ≌,∴ME NF =,∵AE AF =,AN NF AF +=,∴2AM AN AF +=;(3)解:过D 作DF AB ⊥,∵90C ∠=︒,∴AC BC ⊥,∵AD 平分BAC ∠,DF AB ⊥,ACBC ⊥,∴30BAD CAD ∠=∠=︒,DF DC =,∵90C ∠=︒,60BAC ∠=︒,∴30ABC ∠=︒,∵6AC =,∴212AB AC ==,∵30CAD ∠=︒,∴2AD DC =,∴22246DC DC -=,∴DC =AD =∵ND AB ∥,∴30ADN BAD NAD ∠=∠=∠=︒,30B NDC ∠=∠=︒,∴BD AD ==,2DN AN CN ==,∴2224CN CN DC -=,∴233CN =,∴2CN =,4DN =,在ADF △与ADC △中,DF DC AD AD=⎧⎨=⎩∴(HL)ADF ADC ≌,∴2CN MF ==,4MD DN ==,6AF AC ==,∴6244(62)20AMDN C AM MD DN AN =+++=++++-=;【点睛】本题考查角平分线的性质,直角三角形30︒角所对直角边等于斜边一半,三角形全等的判定与性质,解题的关键是作出辅助线得到相应线段大小.。
江西省赣州市八年级上学期数学第一次月考试卷
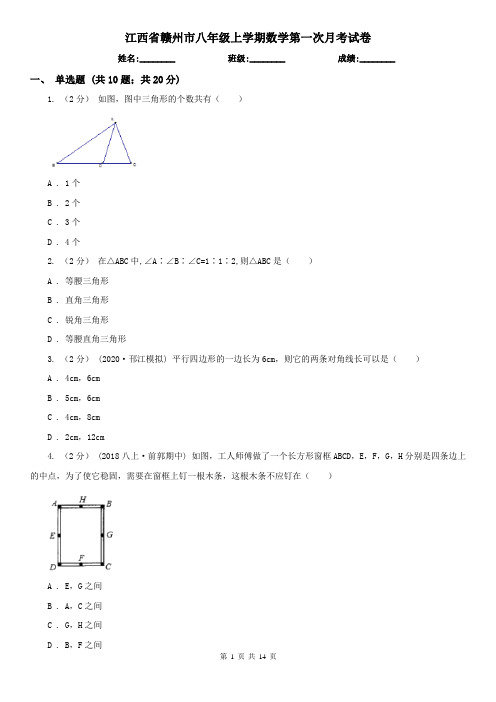
江西省赣州市八年级上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)如图,图中三角形的个数共有()A . 1个B . 2个C . 3个D . 4个2. (2分)在△ABC中,∠A∶∠B∶∠C=1∶1∶2,则△ABC是()A . 等腰三角形B . 直角三角形C . 锐角三角形D . 等腰直角三角形3. (2分)(2020·邗江模拟) 平行四边形的一边长为6cm,则它的两条对角线长可以是()A . 4cm,6cmB . 5cm,6cmC . 4cm,8cmD . 2cm,12cm4. (2分) (2018八上·前郭期中) 如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在()A . E,G之间B . A,C之间C . G,H之间D . B,F之间5. (2分)四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数为()A . 80°B . 90°C . 170°D . 20°6. (2分) (2018八上·天河期末) 若一个三角形三个内角度数的比为1:2:3,则其内角度数最大的是()A . 60°B . 90°C . 120°D . 无法判断7. (2分) (2017八下·潮阳期末) 若一个等腰直角三角形的面积为8,则这个等腰三角形的直角边长为()A . 2B . 4C . 4D . 88. (2分) (2020七下·高新期中) 如图,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的大小为()A . 14°B . 16°C . 90°-αD . α-44°9. (2分)如图,∠AOP=∠BOP=15°,PC∥OA,若PC=4,则PD等于()A . 1B . 3C . 4D . 210. (2分) (2020八下·丽水期中) 当多边形的边数增加1时,它的内角和会()A . 增加160°B . 增加180°C . 增加270°D . 增加360°二、填空题 (共5题;共5分)11. (1分) (2016八上·江宁期中) 已知等腰△ABC,AC=AB,∠A=70°,则∠B=________°.12. (1分)三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为________ 度.13. (1分) (2020八上·思茅期中) 如图,两个三角形全等,根据图中所给条件,可得∠α=________°.14. (1分) (2019七下·东台月考) 一个凸 n 边形,其每个外角都等于30°,则n =________.15. (1分)(2019·保定模拟) 一个正多边形每一个外角为36°,则这个多边形的内角和为________.三、解答题 (共6题;共30分)16. (5分) (2017九上·姜堰开学考) 如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,求∠A的度数.17. (5分) (2019九上·天河期末) 如图的反比例函数图象经过点A(2,5)(1)求该反比例函数的解析式;(2)过点A作AB⊥x轴,垂足为B,在直线AB右侧的反比例函数图象上取一点C,若△ABC的面积为20,求点C的坐标.18. (5分)如图,在△ABC中,∠C=90°,在BC上找一点P,使P到AB的距离等于PC.请在图中标出点P 的位置(不写作法,但保留作图痕迹).19. (5分) (2020八上·阳东月考) 如图,已知△ABC的高AD,角平分线AE,∠B=26°,∠ACD=56°,求∠AED 的度数.20. (5分)如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB 的度数.21. (5分)(2018·崇仁模拟) 在四边形OABC中,AB∥OC,∠OAB=90°,∠OCB=60°,AB=2,OA=2 .(1)如图①,连接OB,请直接写出OB的长度;(2)如图②,过点O作OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,设点P运动的时间为t秒,△OPQ的面积为S(平方单位).①求S与t之间的函数关系式;②设PQ与OB交于点M,当△OPM为等腰三角形时,试求出△OPQ的面积S的值.参考答案一、单选题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:二、填空题 (共5题;共5分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:三、解答题 (共6题;共30分)答案:16-1、考点:解析:答案:17-1、答案:17-2、考点:解析:答案:18-1、考点:解析:答案:19-1、考点:解析:答案:20-1、考点:解析:答案:21-1、考点:解析:。
江西省赣州市八年级上学期数学第一次月考试卷

江西省赣州市八年级上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、选择题(本题有10小题,每小题3分,共30分) (共10题;共26分)1. (2分) (2019九上·临沧期末) 下列图形中,既是轴对称图形又是中心对称图形的是()A .B .C .D .2. (3分)(2020·邯郸模拟) 下列命题是假命题的是()A . 三角形两边的和大于第三边B . 正六边形的每个中心角都等于C . 半径为的圆内接正方形的边长等于D . 只有正方形的外角和等于3. (3分) (2019八上·西湖期末) 对于命题若a2=b2 ,则a=b,下面四组关于a,b的值中,能说明这个命题属于假命题的是()A . a=3,b=3B . a=-3,b=-3C . a=3,b=-3D . a=-3,b=-24. (3分) (2018八上·沙洋期中) 如图,已知:MA∥NC,MB∥ND,MB=ND.则△MAB≌△NCD的理由是()D . 边边角5. (2分) (2020七下·江阴期中) 下列说法正确的是()A . 三角形的中线、角平分线和高都是线段;B . 若三条线段的长、、满足,则以、、为边一定能组成三角形;C . 三角形的外角大于它的任何一个内角;D . 三角形的外角和是 .6. (3分) (2018八上·黄石期中) 如图,△ABC中∠A=100°,BO,CO分别是∠ABC,∠ACB的角平分线且相交于O点,则∠BOC的度数为()A . 110°B . 120°C . 130 °D . 140°7. (2分)如图,DE为△ABC中AC边的中垂线,BC=8,AB=10,则△EBC的周长是()A . 16B . 18C . 26D . 288. (2分) (2020七下·重庆月考) 如图,直线a∥b ,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2=()D . 30°9. (3分) (2019八上·海珠期末) 已知图中的两个三角形全等,图中的字母表示三角形的边长,则∠1等于()A . 72°B . 60°C . 50°D . 58°10. (3分) (2019八上·成都月考) 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a ,较短直角边长为b.若,大正方形的面积为25,则小正方形的边长为()A . 9B . 6C . 4D . 3二、填空题(本题有10小题,每小题3分,共30分) (共10题;共30分)11. (3分) (2018八上·东台月考) 已知:△ABC≌△FED,若∠B=45°,∠C=40°,则∠F=________度.12. (3分)(2019七下·淮安月考) 如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=________°.13. (3分)三角形的两边长分别是3和9,第三边长是方程x2﹣13x+40=0的根,则该三角形的周长为________.,把线段绕着点逆时针旋转度后,如果点恰好落在的边上,那么 ________.15. (3分)如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是________.(只填一个即可)16. (3分)如图,l∥m,等边△ABC的顶点A、B分别在直线l、m上,∠1=25°,则∠2=________.17. (3分)在格点图中,横排或竖排相邻两格点间的距离都为1,若格点多边形边界上有12个格点,图形内有4个格点,则这个格点多边形的面积为________.18. (3分) (2019七下·宜兴期中) 如图,把沿线段折叠,使点落在点处,,若∠A+∠B=110°,则 =________.19. (3分)(2016·慈溪模拟) 如图,A点的坐标是(0,6),AB=BO,∠ABO=120°,C在x轴上运动,在坐标平面内作点D,使AD=DC,∠ADC=120°,连结OD,则OD的长的最小值为 ________.20. (3.0分) (2019八上·哈尔滨月考) 如图,已知△ABC和△ADE都是正三角形,连接CE、BD、AF,BF=4,CF=7,求AF的长________ .三、解答题(本题有6小题;共40分) (共6题;共40分)21. (6分)(2020·顺德模拟) 如图,在Rt△ABC中,∠C=90°,AB=8.(1)作△ABC的内角∠CAB的平分线,与边BC交于点D(用尺规作图,保留作图痕迹,不要求写作法);(2)若AD=BD,求CD的长度.22. (6分)(2020·建水模拟) 如图,E、F是线段BD上的两点,且,,,求证: .23. (6分) (2019九上·南岗期中) 概念理解:对角线互相垂直的四边形叫做垂美四边形(1)性质探究:如图1,四边形ABCD是垂美四边形,直接写出AB2、CD2、AD2、BC2的数量关系:________.(2)解决问题:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE ,连结CE、BG、GE .若AC=4,AB=5,求GE的长(可直接利用(1)中性质)24. (6分)如图,正方形AEFG的顶点E在正方形ABCD的边CD上,AD的延长线交EF于H点.若E为CD的中点,正方形ABCD的边长为4,求DH的长.25. (8分) (2019九上·防城期中) 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结BE.(1)求证:△ACD≌△BCE;(2)当∠1=25°时,求∠E的度数.26. (8.0分) (2020八下·长兴期中) 如图所示,已知正方形OEFG的顶点O为正方形ABCD对角线AC,BD 的交点,连接CE,DG。
2024-2025学年江西省赣州中学八年级(上)开学数学试卷(含答案)

2024-2025学年江西省赣州中学八年级(上)开学数学试卷一、选择题:本题共6小题,每小题3分,共18分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )A. (−3)2=−9B. (−5)2=−5C. 9=±3D. 3−64=−42.如果m<n,那么下列结论错误的是( )A. m+2<n+2B. −2m<−2nC. 2m<2nD. m−2<n−23.如图的两个三角形全等,则∠1的度数为( )A. 50°B. 58°C. 60°D. 62°4.如图,在△ABC中,∠C=70°,若沿图中的虚线截去∠C,则∠1+∠2=( )A. 360°B. 250°C. 180°D. 140°5.将一个含有45°的三角板按如图所示,摆放在一组平行线内,∠1=20°,则∠2的度数为( )A. 45°B. 60°C. 70°D. 80°6.已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )A. 1个B. 2个C. 3个D. 4个二、填空题:本题共6小题,每小题3分,共18分。
7.16的平方根是______,(−6)2的算术平方根是______.8.已知直线MN//x轴,且M(2,5),N(1−2m,m+3),则m的值为______.9.已知一个样本有40个数据,把它分成5组,第一组到第四组的频数分别是10、4、x、16,第五组的频率是0.1,则x的值为______.10.若x的不等式组{2x−a<02x+1≥−3有两个整数解,则a的取值范围是______.11.8个一样大小的长方形恰好可以拼成一个大的长方形,如图甲所示,若拼成如图乙所示的正方形,中间还留下一个洞,恰好是边长为2厘米的小正方形.设一个小长方形的长为x厘米,宽为y厘米,则所列二元一次方程组是______.12.如图,CA⊥BC,垂足为C,AC=2cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动。
赣州市八年级上学期开学数学试卷(五四学制)

赣州市八年级上学期开学数学试卷(五四学制)姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分) (2016九下·宁国开学考) 抛物线y=﹣(x﹣2)2+3的顶点坐标是()A . (﹣2,3)B . (2,3)C . (2,﹣3)D . (﹣2,﹣3)2. (2分) (2017九上·钦南开学考) 在同一坐标系中,二次函数y=ax2+bx+c(b>0)与一次函数y=ax+c 的大致图象可能是()A .B .C .D .3. (2分) (2016九上·北京期中) 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有()A . ①④B . ②③④C . ③④⑤D . ①③⑤4. (2分)二次函数y=x2+px+q中,由于二次项系数为1>0,所以在对称轴左侧,y随x增大而减小,从而得到y越大则x越小,在对称轴右侧,y随x增大而减大,从而得到y越大则x也越大,请根据你对这句话的理解,解决下面问题:若关于x的方程x2+px+q+1=0的两个实数根是m、n(m<n),关于x的方程x2+px+q﹣5=0的两个实数根是d、e(d<e),则m、n、d、e的大小关系是()A . m<d<e<nB . d<m<n<eC . d<m<e<nD . m<d<n<e5. (2分)将抛物线y=﹣2x2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为()A . y=﹣2(x+1)2﹣1B . y=﹣2(x+1)2+3C . y=﹣2(x﹣1)2﹣1D . y=﹣2(x﹣1)2+36. (2分) (2016八上·沂源开学考) 烟花厂为扬州烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣ +20t+1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为()A . 3sB . 4sC . 5sD . 6s7. (2分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是()A . ac>0B . 当x>1时,y随x的增大而减小C . b﹣2a=0D . x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根8. (2分)在一块底边长为12cm,高为6cm的锐角三角形铁板上,截出一块矩形铁板,使它的一边在底边上,另外两个顶点分别在三角形的另外两边上.若矩形垂直于三角形底边的那条边长为xcm,矩形的面积为Scm2 ,则S与x之间的函数关系式为()A . S=x2B . S=x2C . S=12x﹣2x2D . S=4x29. (2分)(2020·凉山模拟) 直线y1=x+1与抛物线y2=﹣x2+3的图象如图,当y1>y2时,x的取值范围为()A . x<﹣2B . x>1C . ﹣2<x<1D . x<﹣2或x>110. (2分)如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),二次函数图象对称轴为x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论是()A . ②④B . ①③C . ②③D . ①④二、填空题 (共5题;共5分)11. (1分)(2014·淮安) 将二次函数y=2x2﹣1的图象沿y轴向上平移2个单位,所得图象对应的函数表达式为________.12. (1分)已知点A(x1 , y1)、B(x2 , y2)在二次函数y=(x-1)2+1的图象上,若x1>x2>1,则y1________y2(填“>”、“<”或“=”).13. (1分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加利润,尽快减少库存,商场决定采取适当的降价措施.经调查发现:如果每件衬衫降价1元,商场平均每天可多售出2件.则商场降价后每天盈利y(元)与降价x(元)的函数关系式为________.14. (1分)二次函数y=2x2+3x﹣9的图象与x轴交点的横坐标是________.15. (1分)(2019·河南模拟) 二次函数的图象上有三个点,分别为A(﹣2,y1),B(﹣1,y2),C(1,y3),则y1 , y2 , y3的大小关系是________.三、解答题 (共4题;共52分)16. (12分) (2017九上·北京期中) 已知二次函数的解析式是y=x2﹣2x﹣3.(1)与x轴的交点坐标是________;顶点坐标是________;(2)在坐标系中利用描点法画出此抛物线.x…________________________________________…y…________________________________________…17. (15分) (2016九上·海盐期中) 某商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价每上涨1元,则每个月少卖10件.设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)求y与x的函数关系式;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)若每个月的利润不低于2160元,售价应在什么范围?18. (10分) (2019九上·宜昌期中) 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.(1)以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;(2)某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由19. (15分)如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于C点,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求D点的坐标;(2)求一次函数的表达式;(3)根据图象写出使一次函数值大于二次函数值的x的取值范围.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共5题;共5分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共4题;共52分)16-1、16-2、17-1、17-2、17-3、18-1、18-2、19-1、19-2、19-3、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江西省赣州市八年级上学期开学数学试卷
姓名:________ 班级:________ 成绩:________
一、选择题: (共20题;共40分)
1. (2分) (2016七下·南陵期中) 下列运动属于平移的是()
A . 冷水加热过程中小气泡上升成为大气泡
B . 急刹车时汽车在地面上的滑动
C . 投篮时的篮球运动
D . 随风飘动的树叶在空中的运动
2. (2分)(2017·内江) PM2.5是指大气中直径小于或等于2.5μm(1μm=0.000001m)的颗粒物,也称为可入肺颗粒物,它们还有一定量的有毒、有害物质,对人体健康和大气环境质量有很大影响.2.3μm用科学记数法可表示为()
A . 23×10﹣5m
B . 2.3×10﹣5m
C . 2.3×10﹣6m
D . 0.23×10﹣7m
3. (2分)如图所示,已知直线BF、CD相交于点O,∠D=40°,下面判定两条直线平行正确的是()
A . 当∠C=40°时,AB∥CD
B . 当∠A=40°时,AC∥DE
C . 当∠E=120°时,CD∥EF
D . 当∠BOC=140°时,BF∥DE
4. (2分)已知二元一次方程3x﹣y=1,当x=2时,y﹣8等于()
A . 5
B . -3
C . -7
D . 7
5. (2分)(2011·绵阳) 下列运算正确的是()
A . a+a2=a3
B . 2a+3b=5ab
C . (a3)2=a9
D . a3÷a2=a
6. (2分) (2018七上·临沭期末) 如图所示,数轴上点A,B对应的有理数分别为,,下列关系式:
①;② ;③ ;④ .正确的有()
A . ①②
B . ②③
C . ①③④
D . ①②③
7. (2分)不等式组的解集在数轴上表示为()
A .
B .
C .
D .
8. (2分) (4x2-5y)需乘以下列哪个式子,才能使用平方差公式进行计算() w
A . -4x2-5y
B . -4x2+5y
C . (4x2-5y)2
D . (4x+5y)2
9. (2分) (2019七下·灌阳期中) 下列各式从左边到右边的变形中,是因式分解的为()
A . 9(x+y)=9x+9y
B . 8x2-4x=4x(2x-1)
C . x2-4x+4=x(x-4)+4
D . x2-16x+3x=(x+4)(x-4)+3x
10. (2分) (2019七上·巴州期末) 4a-a的计算结果是()
A . 3
B . 3a
C . 4
D . 4a
11. (2分)下列长度的三条线段能组成一个三角形的是()
A . 1,2,4
B . 4,5,9
C . 6,8,10
D . 5,15,8
12. (2分) (2019七下·邢台期中) 已知方程组中的 x,y互为相反数,则m的值为()
A . 2
B . ﹣2
C . 0
D . 4
13. (2分) (2018八上·深圳期末) 下列命题中,假命题的是()
A . 三角形中至少有两个锐角
B . 如果三条线段的长度比是3:3:5,那么这三条线段能组成三角形
C . 直角三角形一定是轴对称图形
D . 三角形的一个外角一定大于和它不相邻的任何一个内角
14. (2分) (2016七下·五莲期末) 下列说法正确的是()
A . 两条直线被第三条直线所截,内错角相等
B . 直线外一点到这条直线的垂线段,叫做点到直线的距离
C . 若a⊥b,b⊥c,则a⊥c
D . 不相等的角不是对顶角
15. (2分) (2017七下·扬州期中) 803﹣80能被()整除.
A . 76
B . 78
C . 79
D . 82
16. (2分) (2019八上·历城期中) 已知方程组,的解满足,则的值为()
A .
B .
C .
D .
17. (2分) (2020八上·成都月考) 若有意义,则的取值范围是().
A .
B .
C .
D .
18. (2分)△ABC的两边长分别为2和3,第三边的长是方程x2﹣8x+15=0的根,则△ABC的周长是()
A . 8
B . 10
C . 8或10
D . 7
19. (2分)下列各式:①a0=1;②a2•a3=a5;③2﹣2=﹣;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 ,其中正确的是()
A . ①②③
B . ①③⑤
C . ②③④
D . ②④⑤
20. (2分) (2019八上·深圳期末) 如图,在△ABC中,CD是AB边上的高线,BE平分∠ABC ,交CD于点
E , BC=5,DE=,则△BCE的面积等于()
A . 3
B .
C . 4
D .
二、解答题: (共2题;共20分)
21. (10分) (2019八上·德惠期中) 已,求:
(1);
(2) .
22. (10分) (2018·合肥模拟) 目前节能灯在城市已基本普及,今年云南省面向县级及农村地区推广,为相应号召,某商场计划用3800元购进节能灯120只,这两种节能灯的进价、售价如下表:
类别/单价成本价销售价(元/箱)
甲2530
乙4560
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?
参考答案一、选择题: (共20题;共40分)
答案:1-1、
考点:
解析:
答案:2-1、
考点:
解析:
答案:3-1、
考点:
解析:
答案:4-1、考点:
解析:
答案:5-1、考点:
解析:
答案:6-1、考点:
解析:
答案:7-1、考点:
解析:
答案:8-1、考点:
解析:
答案:9-1、考点:
解析:
答案:10-1、考点:
解析:
答案:11-1、考点:
解析:
答案:12-1、考点:
解析:
答案:13-1、考点:
解析:
答案:14-1、考点:
解析:
答案:15-1、考点:
解析:
答案:16-1、考点:
解析:
答案:17-1、考点:
解析:
答案:18-1、考点:
解析:
答案:19-1、考点:
解析:
答案:20-1、考点:
解析:
二、解答题: (共2题;共20分)答案:21-1、
答案:21-2、
考点:
解析:
答案:22-1、
答案:22-2、
考点:
解析:。
