高考数学 第21题优美解 新课标
最值巧破解,技巧妙归纳——2021年高考数学全国乙卷(理)第21题的研究

2023年4月上半月㊀试题研究㊀㊀㊀㊀最值巧破解,技巧妙归纳 2021年高考数学全国乙卷(理)第21题的研究◉江苏省梅村高级中学㊀包正峰㊀㊀圆锥曲线中的取值范围(或最值)问题一直是历年高考数学试卷中的常见题型之一,常考常新,创新新颖,形式各样,主要在选择题或填空题㊁解答题中以压轴题形式出现.此类问题对考生的代数恒等变形能力㊁数学运算能力㊁推理论证能力等都有较高的要求,同时突出对数学知识㊁数学思想方法㊁数学核心素养的考查,具有较好的选拔性与区分度,备受命题者青睐.1真题呈现[2021年高考数学全国乙卷(理科)第21题]已知抛物线C:x2=2p y(p>0)的焦点为F,且F与圆M: x2+(y+4)2=1上点的距离的最小值为4.(1)求p;(2)若点P在M上,P A,P B为C的两条切线, A,B是切点,求әP A B面积的最大值.2真题剖析该题以抛物线为问题背景,巧妙融入圆的方程以及圆的切线等相关问题,确定三角形面积的最值,设置比较常见,场景比较熟悉,很好地实现了圆锥曲线与圆的融合与交汇,在一定程度上降低了试题的难度.这也是高考数学对圆锥曲线部分命题的大体变化趋势,适当降低难度.具体破解时,抓住切线这一关键点,或借助导数的视角,通过导数的几何意义,利用求导以及切线斜率的求解来确定对应的切线方程;或借助方程的视角,通过直线与抛物线方程的联立,对应的方程的判别式为0来解决.其中,不同的设点㊁设线等技巧与方法,都可以很好实现对相应位置关系的转化以及代数式的变形,最终转化为相应的函数问题,再结合函数的图象与性质以及相关参数的取值限定,来确定对应的最值问题.3真题破解对于第(1)问,由题可得圆心M(0,-4),半径r=1,则焦点F(0,p2)到圆M上点的距离的最小值为|F M|-r=p2+4-1=4,解得p=2.下面主要研究第(2)问的破解方法.方法一:导数的视角 设点与设线法.解法1:由(1)知,抛物线C的方程为x2=4y,即y=14x2,求导可得yᶄ=12x.设切点A(x1,14x12),B(x2,14x22).易得切线P A的方程为y-x214=x12(x-x1),即y=x12x-x214;切线P B的方程为y=x22x-x224.联立两直线方程可得交点P(x1+x22,x1x24).设直线A B的方程为y=k x+b,联立抛物线方程,消去参数y并整理,可得x2-4k x-4b=0.由Δ=16k2+16b>0,得k2+b>0.又x1+x2=4k,x1x2=-4b,则知P(2k,-b).所以|A B|=1+k2 |x1-x2|=1+k2 (x1+x2)2-4x1x2=1+k2 16k2+16b.又点P到直线A B的距离为d=|2k2+2b|k2+1,所以әP A B面积为㊀㊀㊀S=12|A B|d=4(k2+b)32.①又点P(2k,-b)在圆M:x2+(y+4)2=1上,则㊀㊀㊀㊀k2=14[1-(b-4)2].②将②式代入①式,可得S=4(-b2+12b-154)32=12(-b2+12b-15)32=12[-(b-6)2+21]32.由k2=14[1-(6-4)2]ȡ0,得bɪ[3,5],所以当b=5时,S m a x=205.故әP A B面积的最大值为205.点评:通过求导,结合切点的设置以及导数的几何意义,确定两条相应的切线方程,进而求得两切线交点P的坐标;同时设出两切点对应的直线A B的方36Copyright©博看网. All Rights Reserved.试题研究2023年4月上半月㊀㊀㊀程,与抛物线方程联立,结合韦达定理,确定弦A B 的长以及点P 到直线A B 的距离,进而建立әP A B 面积S 的关系式,结合参数的取值范围确定әP A B 面积的最大值.从导数的视角切入,设点与设线全面登场,结合方程思想的应用,利用函数思想来处理.方法二:导数的视角设点与直线系法.解法2:由(1)知,抛物线C 的方程为x 2=4y ,即y =14x 2,求导可得y ᶄ=12x .设A (x 1,y 1),B (x 2,y 2),P (x 0,y 0).易得切线P A 的方程为y -y 1=x 12(x -x 1),即y =x 12x -y 1,亦即x 1x -2y -2y 1=0.同理,可得切线P B 的方程为x 2x -2y -2y 2=0.由于点P 为两切线的公共点,则有x 1x 0-2y 0-2y 1=0,x 2x 0-2y 0-2y 2=0.{所以点A ,B 的坐标满足方程x 0x -2y 0-2y =0,即直线A B 的方程为x 0x -2y -2y 0=0.联立x 0x -2y -2y 0=0,y =14x 2,{可得x 2-2x 0x +4y 0=0.由韦达定理,得x 1+x 2=2x 0,x 1x 2=4y 0.所以|A B |=1+(x 02)2|x 1-x 2|=1+(x 02)2(x 1+x 2)2-4x 1x 2=1+(x 02)24x 20-16y 0=(x 20+4)(x 20-4y 0).易得点P 到直线A B 的距离为d =|x 20-4y 0|x 20+4.所以,可得әP A B 的面积S =12|A B |d =12(x 20+4)(x 20-4y 0) |x 20-4y 0|x 20+4=12(x 20-4y 0)32.而x 20-4y 0=1-(y 0+4)2-4y 0=-y 20-12y 0-15=-(y 0+6)2+21,由已知可得y 0ɪ[-5,-3],所以当y 0=-5时,S m a x =205.故әP A B 面积的最大值为205.点评:方法2与方法1的不同点在于,方法1是直接设出切点A ,B 所在的直线方程,而方法2是利用两切线的交点P 同时满足两条切线方程,确定直线系得到直线A B 的方程,避免了求交点P .方法三:导数的视角设点法.解法3:由(1)知,抛物线C 的方程为x 2=4y ,即y =14x 2,求导可得y ᶄ=12x .设A (x 1,y 1),B (x 2,y 2),P (x 0,y 0).易得切线P A 的方程为y -y 1=x 12(x -x 1),即y =x 12x -y 1;切线P B 的方程为y =x 22x -y 2.联立两直线方程可得交点P (x 1+x 22,x 1x 24).于是x 0=x 1+x 22,y 0=x 1x 24,又线段A B 的中点为Q (x 1+x 22,y 1+y 22).所以,әP A B 面积S =12|P Q | |x 1-x 2|=12|y 1+y 22-y 0| |x 1-x 2|=14|x 21+x 224-x 1x 22| |x 1-x 2|=116((x 1+x 2)2-4x 1x 2)3=116(4x 20-16y 0)3=12(x 20-4y 0)3.而x 20-4y 0=1-(y 0+4)2-4y 0=-y 20-12y 0-15=-(y 0+6)2+21,由已知可得y 0ɪ[-5,-3],所以当y 0=-5时,S m a x =205.故әP A B 面积的最大值为205.点评:通过求导,结合切点的设置以及导数几何意义的应用,确定两条相应的切线方程,进而求得两切线的交点P 的坐标;发现线段A B 的中点Q 的坐标与点P 坐标面积,则知直线P Q 垂直于x 轴,巧妙转化三角形的面积,引入线段P Q 的长度与点A ,B 两点横坐标的差的绝对值,进而建立әP A B 面积S 的关系式.从导数的视角切入,设点引入,转化三角形面积的求解方式,结合方程思想㊁函数思想来处理.4教学启示破解圆锥曲线中的最值问题的基本技巧策略一般有以下两种:①几何法.抓住平面图形的几何特征,巧妙利用圆锥曲线的定义㊁方程与几何性质,以及平面几何的有关结论加以数形结合,通过直观形象思维来确定相应的最值问题.此类问题往往经常出现在小题(选择题或填空题)中.②代数法.抓住平面图形的代数方程,巧妙利用圆锥曲线的方程㊁直线的方程等加以联立方程组㊁等量代换,通过消参等转化为相应的代数关系式,利用基本不等式㊁二次函数的图象与性质㊁三角函数的图象与性质等,综合参数的取值限制㊁圆锥曲线自身的几何性质等来解决相应的最值问题.Z46Copyright ©博看网. All Rights Reserved.。
2020年高考数学一卷21题解答赏析

2020年高考数学一卷21题解答赏析
21.(12分)
方法一:在《高考数学核心题型与解题技巧》一书中,有题型总结:利用两个课本中的不等式解答高考试题,通过例题,学习的重点是利用这两个不等式进行放缩,去解决证明求参问题。
利用解答这类不等式的经验和技巧,下面的解答思路水到渠成!
现已将该方法总结到书中;
方法二:在《高考数学核心题型与解题技巧》一书中,有题型总结:利用公切线确定参数范围。
掌握了该种题型的解答策略,由我们总结的模板,本题可以使用公切线法确定参数范围!
现已将该方法总结到书中;两种解法无论从思路还是运算量都可谓是简短容易。
方法三:在《高考数学核心题型与解题技巧》一书中,有题型总结:反函数问题,对课本中比较边角的知识点反函数性质的应用列举了比较深刻的三个例题,如果使用该题型模式解答本题,就更漂亮了:
现已将该方法总结到书中;我们看这三个方法无论哪一个都具有优势,都可以实现问题的快速解答。
方法四:在《高考数学核心题型与解题技巧》一书中,有题型总结:利用同构秒杀高考试题魅力无限,阐述了同构的解题思路,有函数题,有导数题,有解析几何题,是比较系统的一个专题,利用同构思想获得该题的秒解:
下面是资料的部分截图:
2020年,整个试卷可以说对于难点部分题型全部出现,小题中很多可以实现光速解法。
我们从来不去离开基础追求“秒杀”,我们的实力来自对学生的了解,对考试大纲的深度理解核和对高考命题规律的准确把握!
对于该四种解法都体现了方法上的优势,漂亮!。
2021年全国甲卷理科数学第21题

2021年全国甲卷理科数学第21题是一道备受关注的题目,涉及复合函数和导数的计算。
这是一道典型的高中数学题目,考察学生对于函数和导数的理解和运用能力。
在这篇文章中,我们将从深度和广度两个方面对这道题目进行全面评估,并据此撰写一篇有价值的文章。
让我们来简单回顾一下这道题目。
题目给出了一个函数y=f[g(x)],其中f(x)和g(x)均为可导函数,要求求出y=f[g(x)]的导数。
这道题目考察了学生对于复合函数和链式法则的理解和运用,是一个典型的高中数学题目。
接下来,我们将从简到繁,由浅入深地探讨这道题目。
我们将简要介绍复合函数和链式法则的概念和基本公式,以便读者能更好地理解这道题目。
我们将详细解析这道题目的解题方法和步骤,逐步推导出y=f[g(x)]的导数,并加以解释和验证。
在解析的过程中,我们将多次提及题目中的关键词和公式,以便读者能更深入地理解和记忆这道题目。
我们还将探讨这道题目的一般解法和相关的数学知识,以便读者能够在解类似题目时灵活运用所学的知识。
在文章的总结和回顾部分,我们将对整篇文章所涉及的内容进行梳理和总结,以便读者能全面、深刻和灵活地掌握这道题目和相关的数学知识。
我们还将共享个人对于这道题目和相关知识的观点和理解,以便读者能够与我们进行思想交流和讨论。
我们将以非Markdown格式的普通文本撰写这篇文章,遵循知识文章格式,并在文章内容中多次提及这道题目的关键词和公式。
文章的总字数将大于3000字,确保对这道题目进行了全面的评估和深入的探讨。
在本篇文章中,我们将通过对2021年全国甲卷理科数学第21题的深入解析和全面评估,帮助读者更好地理解和掌握这道题目,提高数学解题能力,拓展数学思维,让数学变得更加有趣和有意义。
复合函数和链式法则是高中数学中非常重要的概念和技巧。
复合函数是指一个函数中嵌套了另一个函数,即外函数的自变量是内函数。
在解题过程中,我们需要使用链式法则来求解复合函数的导数。
7新课标高考数学卷第21题函数解答题的解题策略探究.doc
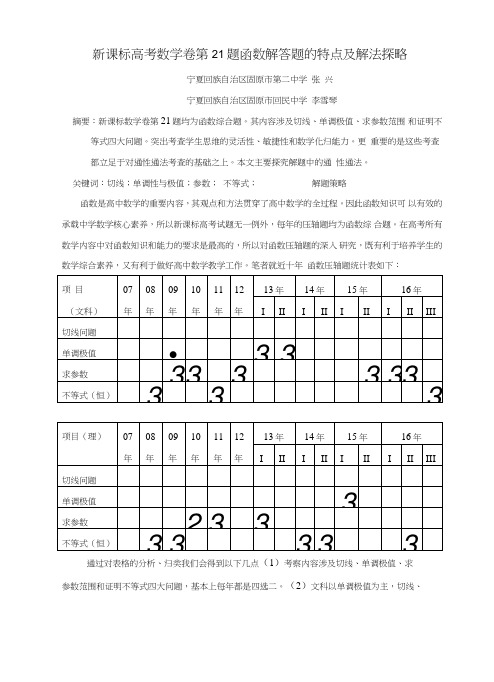
新课标高考数学卷第21题函数解答题的特点及解法探略宁夏回族自治区固原市第二中学张兴宁夏回族自治区固原市回民中学李雪琴摘要:新课标数学卷第21题均为函数综合题。
其内容涉及切线、单调极值、求参数范围和证明不等式四大问题。
突出考查学生思维的灵活性、敏捷性和数学化归能力。
更重要的是这些考查都立足于对通性通法考查的基础之上。
本文主要探究解题中的通性通法。
关键词:切线;单调性与极值;参数;不等式;解题策略函数是高中数学的重要内容,其观点和方法贯穿了高中数学的全过程。
因此函数知识可以有效的承载中学数学核心素养,所以新课标高考试题无一例外,每年的压轴题均为函数综合题。
在高考所有数学内容中对函数知识和能力的要求是最高的,所以对函数压轴题的深入研究,既有利于培养学生的数学综合素养,又有利于做好高中数学教学工作。
笔者就近十年函数压轴题统计表如下:通过对表格的分析、归类我们会得到以下几点(1)考察内容涉及切线、单调极值、求参数范围和证明不等式四大问题,基本上每年都是四选二。
(2)文科以单调极值为主,切线、求参数次之,涉及不等式的比较少。
理科以求参数范围为主,单调极值、不等式问题次之, 切线问题涉及比较少。
(3)通过对比、分析,就会发现通性通法与灵活化归是解题的主要策 略。
一、切线问题例【1】£2014理I (21)』设函数=+竺1,曲线y = /(x )在点(1, /(I))x处的切线为y = e(x-l) + 2. ( I )求彳/?;• a rT f (x) = ae x\nx + — e x又・・•切点(l,b)・・・斜率k= f\\) = ae•••切线方程:y-b=6?e (x-1) 又;•切线为y 二幺(兀一1) + 2例【2】K2015 理 I (21)3 己知函数 /'(%) =x 3 +6ZX + —,g(x) = -lnx. ( I )当 a 为何值时,4"轴为曲线j = f(x)的切线;【解析(2) ]( I )・・・f\x) = 3x 2+a 设曲线y = /(x)与兀轴相切于点(无),0),, j / a 2_兀:+ ax© H — — 0£ = /(兀)=3 兀 °则 /(x o ) = O, /(x o ) = O,即]4,3%0 +。
2020年新高考全国Ⅰ卷(山东卷)数学第21题解法研究——同构放缩携起手导数不等式难题不再有

2020年新高考全国Ⅰ卷(山东卷)数学第21题解法研究同构放缩携起手导数不等式难题不再有高振宁(山东省新泰市第一中学㊀271200)摘㊀要:本文通过对2020年高考数学山东卷第21题解法的探研ꎬ从命题人的角度来反思问题解决的方法ꎬ发现放缩法㊁隐零点法㊁同构法放缩法㊁分而治之法之间的联系与区别ꎬ得出导数解决高考数学中函数与导数压轴题的基本途径ꎬ旨在高中导数与函数复习中提高实效.关键词:导数与单调性ꎻ同构与放缩ꎻ分而治之ꎻ隐零点中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2020)28-0026-02收稿日期:2020-07-05作者简介:高振宁(1983.4-)ꎬ男ꎬ本科ꎬ中学一级教师ꎬ从事高中数学教学研究.㊀㊀原题再现㊀已知函数f(x)=aex-1-lnx+lna.(1)当a=e时ꎬ求曲线y=f(x)在点(1ꎬf(1))处的切线与两坐标轴围成的三角形的面积ꎻ(2)若f(x)ȡ1ꎬ求a的取值范围.解㊀(1)略.(2)方法一(隐零点法):由f(x)=aex-1-lnx+lnaꎬ则fᶄ(x)=aex-1-1xꎬ显然a>0.设g(x)=fᶄ(x)ꎬ则gᶄ(x)=aex-1+1x2>0ꎬ所以g(x)在0ꎬ+¥()上单调递增ꎬ即fᶄ(x)在0ꎬ+¥()上单调递增.当a=1时ꎬfᶄ(1)=0ꎬ当xɪ(0ꎬ1)ꎬfᶄ(x)<0ꎬf(x)在0ꎬ1()上是减函数ꎻxɪ(1ꎬ+¥)时ꎬfᶄ(x)>0ꎬf(x)在(1ꎬ+¥)上是增函数.ʑf(x)min=f(1)=1ꎬ故fx()ȡ1恒成立.当a>1时ꎬ1a<1ꎬ所以e-1<1ꎬfᶄ(1a)fᶄ(1)=a(e-1-1)(a-1)<0ꎬ故存在唯一x0>0ꎬ使得fᶄ(x0)=aex-1-1x0=0ꎬ且当xɪ(0ꎬx0)时fᶄ(x)<0ꎬ当xɪ(x0ꎬ+¥)时ꎬfᶄ(x)>0ꎬ所以aex-1=1x0ꎬ即lna+x0-1=-lnx0.因此f(x)min=f(x0)=aex-1-lnx0+lna=1x0+lna+x0-1+lnaȡ2lna-1+21x0x0=2lna+1>1ꎬ所以f(x)ȡ1恒成立.当0<a<1时ꎬf(1)=a+lna<a<1ꎬʑf(1)<1ꎬf(x)ȡ1不恒成立.综上所述ꎬ实数a的取值范围是[1ꎬ+ɕ).方法二(放缩法):当0<a<1时ꎬf(1)=a+lna<1.当a=1时ꎬf(x)=ex-1-lnxꎬfᶄ(x)=ex-1-1xꎬ显然fᶄ(x)在(0ꎬ+¥)上是增函数.当xɪ(0ꎬ1)时ꎬfᶄ(x)<0ꎬf(x)在(0ꎬ1)上是减函数ꎻxɪ(1ꎬ+¥)时ꎬfᶄ(x)>0ꎬf(x)在(1ꎬ+¥)上是增函数.所以f(x)最小值=f(1)=1ꎬ从而f(x)ȡ1恒成立ꎬ当a>1时ꎬf(x)=aex-1-lnx+lnaȡex-1-lnxꎬ由a=1的结论可知f(x)=ex-1-lnxȡ1恒成立.综上可知:a的取值范围是1ꎬ+¥[).方法三(同构函数y=ex+x):显然a>0ꎬa=elnaꎬ则f(x)=aex-1-lnx+lna=elna+x-1-lnx+lnaȡ1ꎬ等价于elna+x-1+lna+x-1ȡlnx+x=elnx+lnx.令gx()=ex+xꎬ上述不等式等价于g(lna+x-1)ȡg(lnx).显然g(x)为R上的单调增函数ꎬ故lna+x-1ȡlnxꎬ即lnaȡlnx-x+1.令h(x)=lnx-x+1ꎬ则hᶄ(x)=1x-1=1-xxꎬ在(0ꎬ1)上hᶄ(x)>0ꎬh(x)是增函数ꎻ在(1ꎬ+¥)上hᶄ(x)<0ꎬh(x)是减函数.ʑh(x)max=h(1)=0ꎬ则lnaȡ0ꎬ即aȡ1ꎬ即a的取值范围是[1ꎬ+ɕ).方法四(同构函数y=xex):因f(1)=a+lnaȡ1ꎬ设g(a)=a+lnaꎬ显然y=g(a)在区间0ꎬ+¥()上是增函数ꎬg(a)ȡg(1)=1ꎬ故aȡ1.f(x)=aex-1-lnx+lnaȡ1ꎬ得aex-1ȡlnexa⇔exȡealnexa⇔xexȡexalnexa.显然x>0ꎬexa=eln(e/a)ꎬ则原不等62式等价于xexȡlnexaeln(e/a).设g(x)=xexꎬ显然g(x)在0ꎬ+¥()上是增函数ꎬ则上述不等式等价于g(x)ȡg(lnexa).当lnexa<0时g(x)>0ꎬg(lnexa)<0ꎬ显然g(x)ȡg(lnexa)成立ꎻ当lnexa>0时ꎬ原不等式等价于xȡlnexaꎬ由于exȡ1+xꎬ且aȡ1则可得ex-1ȡxȡxaꎬ故a的取值范围是1ꎬ+¥[).方法五(同构函数y=xlnx):同方法四可得xexȡexalnexaꎬ即exlnexȡexalnexa.设g(x)=xlnxꎬ则上述不等式等价于g(ex)ȡg(exa).gᶄ(x)=lnx+1ꎬg(x)在0ꎬ1eæèçöø÷上是减函数ꎬ在(1eꎬ+¥)上是增函数.当exa<1时ꎬg(ex)>0ꎬ而g(exa)<0ꎬ显然有g(ex)ȡg(exa)成立ꎻ当exaȡ1>1e时ꎬ不等式g(ex)ȡg(exa)⇔exȡexa⇔ex-1ȡxa.以下同方法四.方法六(分而治之法):f(x)=aex-1-lnx+lnaȡ1⇔aex-1ȡlnexa⇔aexeȡlnexa⇔aeˑexxȡlnexaexaˑea.aeˑ(exx)minȡ(lnexaexa)maxˑea.设g(x)=exxꎬx>0ꎬgᶄ(x)=(x-1)exx2ꎬ易知g(x)=exx在0ꎬ1()上是减函数ꎬ在1ꎬ+¥()上是增函数ꎬ故g(x)min=g(1)=e.设h(x)=lnxx(x>0)ꎬhᶄ(x)=1-lnxx2ꎬ易知h(x)=lnxx在(0ꎬe)上是增函数ꎬ在(eꎬ+¥)上是减函数ꎬ故h(x)max=h(e)=1eꎬ则知(lnexaexa)max=1eꎬ则aȡ1aꎬ故a的取值范围是1ꎬ+¥[).从解决问题方法的角度看ꎬ隐零点法是解决问题的一般性通法ꎬ但是此种方法需要强大的计算能力作为基础ꎬ特别是在利用aex-1=1x0进行代换得到lna+x0-1=-lnx0的这种思路ꎬ应该作为一种基本的解决导数不等式压轴题的基本思路进行培养.放缩法是山东省教育招生考试院给出的官方答案ꎬ此种办法的优点是ꎬ计算量不是大ꎬ借助分类讨论思想ꎬ利用特殊点明确参数的范围进而证明此范围符合题意ꎬ但是在实际的教学中ꎬ新教材已经把分析法和综合法等不等式证明方法删除ꎬ学生证明不等式能力较弱的情况下掌握放缩法不易ꎬ这就需要教师在教学中渗透不等式的证明方法.为了突破这个教学难点ꎬ笔者认为可以利用具体的证明方法ꎬ而不用过多的纠缠这种方法的具体含义和要求ꎬ比方说把 执果索因 给学生讲解成 把结论等价变形成能解决问题的形式 ꎬ在教学的实践中怎么充实这一点ꎬ还需要不断的在实际中摸索与探究.方法三㊁四㊁五可以归结成同构法ꎬ同构法的本质是构造目标函数ꎬ借助目标函数单调性把复杂函数简单化递减ꎬ比方说若F(x)ȡ0能等价变形为F(f(x))ȡF(g(x))ꎬ若F(x)递增ꎬ则问题转化为f(x)ȡg(x)ꎬ若F(x)递减ꎬ则问题转化为f(x)ɤg(x).此类方法的关键是构造目标函数ꎬ高考压轴题中的构造常见形式可分为两类:(1)aeaɤblnb可以同构aeaɤlnbelnbꎬ借助函数f(x)=xex解决ꎬ也可以同构ealneaɤblnbꎬ借助f(x)=xlnx解决ꎬ更可以同构为lna+aɤlnb+ln(lnb)ꎬ借助f(x)=x+lnx解决.(2)eaaɤblnb可以同构eaaɤelnblnbꎬ借助函数f(x)=exx解决ꎬ也可以同构为ealneaɤblnbꎬ借助函数f(x)=xlnx解决ꎬ更可以同构a-lnaɤlnb-ln(lnb)ꎬ借助函数f(x)=x-lnx解决.当然ꎬ用同构法解题ꎬ除了要有同构法的思想意识外ꎬ对观察能力㊁对代数式的变形能力的要求也是比较高的.但是笔者认为ꎬ利用同构法可以最接近命题者的原始创作方向ꎬ此题目设计思路的开始点应该是exȡexa.正所谓ꎬ同构新天地ꎬ放缩大舞台!方法六属于解决问题的巧妙方法ꎬ不属于通性解法ꎬ一般情况下f(x)ȡg(x)不等价于f(x)minȡg(x)maxꎬ但是对于极个别的问题ꎬ利用上分而治之的方法ꎬ会极大地降低运算程度ꎬ但是构造不等式两侧的目标函数有一定的技巧性ꎬ学生不易掌握.㊀㊀参考文献:[1]陈永清.轻松快捷巧记高中数学知识与解题方法[M].长沙:湖南师范大学出版社ꎬ2020:42-47.[责任编辑:李㊀璟]72。
2019高考数学全国2卷第21题五种解法赏析

2
2
1 tan 1 t ,
2
2
则 tan
2
tan(
2
)
tan tan 2
1 tan tan
1t 2
1 1 t2
1 t 2
1 22
,等号成立
2
2
t
当且仅当 t
2 ,此时 2
2 sin( ) 最大值为 16 , 9
8
tan
1 tan
,
由 y x 1 单调性易得 S '
x
PQG
2
8 2
1
16 9
2
,
等号成立当且仅当 kPQ
1,
22
所以
S PQG
max
2 2
S' PQG
max
16 9
A. (0,1] [9, )
B. (0, 3] [9, )
C. (0,1] [4, )
D. (0, 3] [4, )
解析:(夹角公式+椭圆第三定义)很自然想到夹角公式 tan AMB k1 k2 ,由椭圆上 1 k1k2
的点到长轴端点连线斜率之积为
b2 a2
且 tan
kP' Q
k
' PG
1 kP' QkP' G
2kPQ 2kPG 1 2kPQkPG
2kPQ 2kPG 2 2kPQ (kPG ) 2 2 ,
S' PQG
1 2
PQ
PG
2022_年新高考全国Ⅰ卷第21_题的探究

2022年新高考全国Ⅰ卷第21题的探究林国红(广东省佛山市乐从中学ꎬ广东佛山528315)摘㊀要:文章对2022年新高考全国Ⅰ卷第21题进行探究ꎬ给出两种解法ꎬ并将试题推广ꎬ得到椭圆㊁双曲线和抛物线的一般性结论.关键词:高考试题ꎻ圆锥曲线ꎻ探究ꎻ推广中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)13-0018-04收稿日期:2023-02-05作者简介:林国红(1977-)ꎬ男ꎬ广东省佛山人ꎬ本科ꎬ中学高级教师ꎬ从事中学数学教学研究.1题目呈现与解答题目㊀(2022年新高考全国Ⅰ卷第21题)已知点A(2ꎬ1)在双曲线C:x2a2-y2a2-1=1(a>1)上ꎬ直线l交C于P㊁Q两点ꎬ直线APꎬAQ的斜率之和为0.(1)求l的斜率ꎻ(2)若tanøPAQ=22ꎬ求әPAQ的面积.本题的解法较多ꎬ下面给出其中的两种解法.解法1㊀(1)将点A(2ꎬ1)代入双曲线方程ꎬ得4a2-1a2-1=1.化简ꎬ得a4-4a2+4=0ꎬ解得a2=2.故双曲线C的方程为x22-y2=1.由题可知直线l的斜率存在ꎬ设直线l的方程为y=kx+mꎬ设P(x1ꎬy1)ꎬQ(x2ꎬy2).联立y=kx+mꎬx22-y2=1ꎬìîíïïï得(2k2-1)x2+4kmx+2m2+2=0.从而有x1+x2=-4km2k2-1ꎬx1x2=2m2+22k2-1.又因kAP+kAQ=y1-1x1-2+y2-1x2-2=kx1+m-1x1-2+kx2+m-1x2-2=0ꎬ化简ꎬ得2kx1x2+(m-1-2k)(x1+x2)-4(m-1)=0.所以2k(2m2+2)2k2-1+(m-1-2k)ˑ-4km2k2-1-4(m-1)=0.化简整理ꎬ得(k+1)(m+2k-1)=0.当m+2k-1=0ꎬ即m=1-2k时ꎬ直线l的方程为y=kx+1-2k=k(x-2)+1ꎬ此时直线l过点A(2ꎬ1)ꎬ不符合题意ꎬ故m+2k-1ʂ0.所以k+1=0ꎬ即k=-1.所以直线l的斜率为-1.(2)不妨设直线AP的倾斜角为锐角且为αꎬ由于直线APꎬAQ的斜率之和为0ꎬ故直线APꎬAQ的倾斜角互补ꎬ所以2α+øPAQ=πꎬ即øPAQ=π-2α.由tanøPAQ=tan(π-2α)=-tan2α=-2tanα1-tan2α=22ꎬ解得tanα=2.故kAP=tanα=2ꎬ即y1-1x1-2=2.联立y1-1x1-2=2ꎬx212-y21=1ꎬìîíïïïï解得x1=10-423ꎬy1=42-53.即P(10-423ꎬ42-53).代入直线l的方程y=-x+mꎬ得m=53ꎬx1+x2=203ꎬx1x2=689.由于|AP|=1+k2APˑ|x1-2|=3ˑ|x1-2|ꎬ|AQ|=1+k2AQˑ|x2-2|=3ˑ|x2-2|ꎬ故|AP| |AQ|=3ˑ|x1-2|ˑ3ˑ|x2-2|=3ˑ|x1x2-2(x1+x2)+4|=3ˑ|689-2ˑ203+4|=163.由tanα=sinαcosα=2ꎬsin2α+cos2α=1ꎬìîíïïï解得sinα=23ꎬcosα=13.故sinøPAQ=sin(π-2α)=sin2α=2sinαcosα=2ˑ23ˑ13=223.所以әPAQ的面积为S=12|AP| |AQ|sinøPAQ=12ˑ163ˑ223=1629.评注㊀解法1通过联立直线与双曲线方程ꎬ利用韦达定理及直线斜率的定义进行求解.运算量虽不小ꎬ但方法是解析几何中的常用方法ꎬ这种通性通法在数学解题中有重要作用.所以在平时的教学中要注重一般性的解题规律和方法(即通性通法)ꎬ要重视知识的生成过程ꎬ尽量创设问题情境引导学生探究知识ꎬ培养学生分析问题㊁解决问题的能力.解法2㊀(1)由解法1可知ꎬ双曲线C的方程为x22-y2=1.设直线AP的参数方程为x=2+tcosαꎬy=1+tsinα{(t为参数)ꎬ代入双曲线方程ꎬ化简并整理ꎬ得(cos2α-2sin2α)t2+4(cosα-sinα)t=0.解得t1=0或t1=4(cosα-sinα)cos2α-2sin2α.当t1=0时ꎬ此时是点A的坐标ꎬ舍去ꎬ故t1=4(cosα-sinα)cos2α-2sin2α.由于直线AP㊁AQ的斜率之和为0ꎬ所以直线APꎬAQ的倾斜角互补ꎬ故直线BP的参数方程为x=2+tcos(π-α)=2-tcosαꎬy=1+tsin(π-α)=1+tsinα{(t为参数).同理可得t2=-4(cosα+sinα)cos2α-2sin2α.于是t2-t1=-8cosαcos2α-2sin2αꎬt2+t1=-8sinαcos2α-2sin2α.故y2-y1x2-x1=1+t2sinα-(1+t1sinα)2-t2cosα-(2+t1cosα)=(t2-t1)sinα-(t2+t1)cosα=-8cosαcos2α-2sin2αˑsinα--8sinαcos2α-2sin2αˑcosα=-1.所以直线l的斜率为-1.(2)不妨设α为锐角ꎬ由于直线AP㊁AQ的斜率之和为0ꎬ故直线AP㊁AQ的倾斜角互补.所以2α+øPAQ=π.即øPAQ=π-2α.由tanøPAQ=tan(π-2α)=-tan2α=-2tanα1-tan2α=22ꎬ解得tanα=2.由tanα=sinαcosα=2ꎬsin2α+cos2α=1ꎬìîíïïï解得sinα=23ꎬcosα=13.从而t1=4(cosα-sinα)cos2α-2sin2α=-42+43ꎬt2=-4(cosα+sinα)cos2α-2sin2α=-42-43.又sinøPAQ=sin(π-2α)=sin2α=2sinαcosα=2ˑ23ˑ13=223ꎬ所以әPAQ的面积为S=12|t1t2|sinøPAQ=12ˑ|-42+43ˑ-42-43|ˑ223=1629.评注㊀一般情况下ꎬ圆锥曲线大题的解答过程往往涉及繁冗运算ꎬ要减少圆锥曲线的运算量ꎬ规避运算风险ꎬ算理就显得非常重要.解法2利用直线的参数方程ꎬ其代数变形较简单ꎬ运算量少ꎬ解题过程比解法1更简洁.2问题的提出问题1㊀在试题中ꎬ若将点A(2ꎬ1)改为其它值ꎬ则直线l的斜率为多少?问题2㊀在试题中ꎬ若将点A(2ꎬ1)改为A(x0ꎬy0)(y0ʂ0)ꎬ并将双曲线一般化ꎬ则直线l的斜率为多少?问题3㊀在试题的问题(1)中ꎬ若将试题改为:点A(2ꎬ1)在双曲线x22-y2=1上ꎬ直线l交C于PꎬQ两点ꎬ且直线l的斜率为-1ꎬ则直线AP㊁AQ的斜率之和为多少?问题4㊀在问题2或问题3中ꎬ若将双曲线改为椭圆或抛物线ꎬ又有什么结论?3试题问题(1)的推广与类比性质结合上述问题ꎬ经探究ꎬ可得到试题问题(1)的推广与类比性质:结论1㊀已知点P(x0ꎬy0)(y0ʂ0)在椭圆C:x2a2+y2b2=1(a>b>0)上ꎬM㊁N是椭圆C上的两个动点ꎬ若直线PM㊁PN的斜率分别为k1㊁k2ꎬ则k1+k2=0的充要条件是直线MN的斜率为b2x0a2y0.结论2㊀已知点P(x0ꎬy0)(y0ʂ0)在双曲线C:x2a2-y2b2=1(a>0ꎬb>0)上ꎬM㊁N是双曲线C上的两个动点ꎬ若直线PM㊁PN的斜率分别为k1ꎬk2ꎬ则k1+k2=0的充要条件是直线MN的斜率为-b2x0a2y0.结论3㊀已知点P(x0ꎬy0)(y0ʂ0)在抛物线C:y2=2px(p>0)上ꎬM㊁N是抛物线C上的两个动点ꎬ若直线PM㊁PN的斜率分别为k1ꎬk2ꎬ则k1+k2=0的充要条件是直线MN的斜率为-py0.评注㊀①结论1至结论3的证明ꎬ可以参照试题(1)的解答ꎬ限于篇幅ꎬ不再给出.②由结论2可知ꎬ当P(x0ꎬy0)=A(2ꎬ1)ꎬ双曲线方程为x22-y2=1ꎬkAP+kAQ=0时ꎬ则直线PQ(即直线l)的斜率为-b2x0a2y0=-12ˑ21=-1ꎬ这正是高考题的问题(1).4探究延伸结论1至结论3均是k1+k2=0与直线MN的斜率之间的关系.那么在一般的条件下ꎬ直线PM㊁PN㊁MN三者的斜率之间有什么联系?此时ꎬ能否求得әPMN的面积?经进一步探究ꎬ可得到如下结论:结论4㊀已知点P(x0ꎬy0)(y0ʂ0)在曲线C:Ax2+By2=1(ABʂ0)上ꎬM㊁N是曲线C上的两个动点ꎬ若直线PM㊁PN㊁MN的斜率分别为k1㊁k2㊁k3ꎬ则(1)k3=A[(A-Bk1k2)x0+B(k1+k2)y0]B[(A-Bk1k2)y0-A(k1+k2)x0]ꎻ(2)SәPMN=|2(k2-k1)(Ax0+Bk1y0)(Ax0+Bk2y0)(A+Bk21)(A+Bk22)|.证明㊀因为平移不改变直线的斜率及图形的面积ꎬ故平移坐标系ꎬ使得点P为坐标原点ꎬ则曲线C变为A(x+x0)2+B(y+y0)2=1ꎬ且Ax20+By20=1.此时直线PM的方程为y=k1xꎬ设M(xMꎬyM)ꎬN(xNꎬyN).联立y=k1xꎬA(x+x0)2+B(y+y0)2=1ꎬ{化简整理ꎬ得(A+Bk21)x2+(2Ax0+2Bk1y0)x=0.解得xM=-2(Ax0+Bk1y0)A+Bk21.同理ꎬxN=-2(Ax0+Bk2y0)A+Bk22.从而(1)k3=yM-yNxM-xN=k1xM-k2xNxM-xN=-2k1(Ax0+Bk1y0)A+Bk21--2k2(Ax0+Bk2y0)A+Bk22-2(Ax0+Bk1y0)A+Bk21--2(Ax0+Bk2y0)A+Bk22=A[(A-Bk1k2)x0+B(k1+k2)y0]B[(A-Bk1k2)y0-A(k1+k2)x0].(2)SәPMN=12|xMyN-xNyM|=12|(k2-k1)xMxN|=|2(k2-k1)(Ax0+Bk1y0)(Ax0+Bk2y0)(A+Bk21)(A+Bk22)|.结论5㊀已知点P(x0ꎬy0)(y0ʂ0)在抛物线C:y2=2px(p>0)上ꎬM㊁N是抛物线C上的两个动点ꎬ若直线PM㊁PN㊁MN的斜率分别为k1㊁k2㊁k3ꎬ则(1)k3=k1k2p(k1+k2)p-k1k2y0ꎻ(2)SәPMN=|2(k2-k1)(p-k1y0)(p-k2y0)k21k22|.证明㊀因为平移不改变直线的斜率及图形的面积ꎬ故平移坐标系ꎬ使得点P为坐标原点ꎬ则曲线C变为(y+y0)2=2p(x+x0)ꎬ且y20=2px0.此时直线PM的方程为y=k1xꎬ设M(xMꎬyM)ꎬN(xNꎬyN).联立y=k1xꎬ(y+y0)2=2p(x+x0)ꎬ{化简整理ꎬ得k21x2+(2k1y0-2p)x=0.解得xM=2(p-k1y0)k21.同理ꎬxN=2(p-k2y0)k22.从而(1)k3=yM-yNxM-xN=k1xM-k2xNxM-xN=2k1(p-k1y0)k21-2k2(p-k2y0)k222(p-k1y0)k21-2(p-k2y0)k22=k1k2p(k1+k2)p-k1k2y0.(2)SәPMN=12|xMyN-xNyM|=12|(k2-k1)xMxN|=12|(k2-k1)ˑ2(p-k1y0)k21ˑ2(p-k2y0)k22|=|2(k2-k1)(p-k1y0)(p-k2y0)k21k22|.评注㊀当P(x0ꎬy0)=A(2ꎬ1)ꎬ双曲线方程为x22-y2=1时ꎬ则A=12ꎬB=-1ꎬkAP+kAQ=0ꎬ且由解法1ꎬ可知kAP=2ꎬkAQ=-2.分别代入结论4ꎬ可得直线PQ的斜率为-1ꎬәPAQ的面积为1629ꎬ这正是高考题的情形.高考试题是精心之作ꎬ每年的高考题在命题角度㊁题型㊁难度等方面都进行了充分考量ꎬ是知识㊁能力和思想方法的载体ꎬ具有典型性㊁示范性和权威性.高考试题除了具有测试与选拔功能外ꎬ还具有良好的教学功能ꎬ要了解高考动向ꎬ把握高考脉搏.高考试题的研究是重要的路径ꎬ所以在复习中要加强高考题的渗透ꎬ通过高考真题的训练体会命题思想ꎬ善于作解后反思和方法的归类ꎬ并对试题进行挖掘㊁拓展㊁引申ꎬ扩大高考题的辐射面ꎬ从而实现高考试题功能的最大化㊁最优化.参考文献:[1]林国红.一道圆锥曲线竞赛试题的推广探究[J].数学通讯ꎬ2022(04):44-45ꎬ55.[2]林国红.圆锥曲线中两根不对称问题的处理方法[J].高中数学教与学ꎬ2018(19):12-14.[责任编辑:李㊀璟]。
2023_年高考数学全国甲卷理科第21_题的多解与变式探究

㊀㊀解题技巧与方法㊀㊀122㊀2023年高考数学全国甲卷理科第21题的多解与变式探究2023年高考数学全国甲卷理科第21题的多解与变式探究Һ张英杰㊀(白蒲高级中学,江苏㊀南通㊀226511)㊀㊀ʌ摘要ɔ2023年高考数学全国甲卷理科第21题是三角函数与导数的综合题,考查三角函数的导数㊁函数的单调性和恒成立问题.文章从必要性与充分性的讨论,利用常见不等式进行放缩和利用均值不等式,取点技巧等三个不同的角度给出解答,并给出试题的变式探究,以期为一线教育工作者提供更多的解题思路和参考.ʌ关键词ɔ2023年高考;全国甲卷;导数;三角函数;恒成立问题2023年高考数学全国甲卷第21题,试题以三角函数㊁多项式函数为背景,构造了所要研究的函数.通过对函数性质的研究,试题全面考查了导数及其应用,这也是中学教学的重点与难点.试题的第(1)问面向全体考生,体现试题的基础性,利用导数就能得到函数的单调性,考查考生通过导数解决实际问题的能力㊁计算与转化的能力,体现函数与方程的数学思想在中学教学的应用.试题的第(2)问体现了试题的选拔性,考查了考生化归与转化的思想㊁分类讨论的思想以及逻辑推理能力㊁数学运算能力.一㊁真题再现2023年高考数学全国甲卷理科第21题如下:已知f(x)=ax-sinxcos3x,xɪ0,π2æèçöø÷.(1)当a=8时,讨论f(x)的单调性;(2)若f(x)<sin2x,求a的取值范围.二㊁解法探究(1)当a=8时,fᶄ(x)=8-3-2cos2xcos4x=(2cos2x-1)(4cos2x+3)cos4x.当xɪ0,π4æèçöø÷时,fᶄ(x)>0,f(x)在区间0,π4æèçöø÷单调递增;当xɪπ4,π2æèçöø÷时,fᶄ(x)<0,f(x)在区间π4,π2æèçöø÷单调递减.综上,f(x)的单调增区间是0,π4æèçöø÷,单调减区间是π4,π2æèçöø÷.(2)解法1㊀若aɤ0,则f(x)<sin2x.下设a>0.当xɪ0,π2æèçöø÷时,f(x)<sin2x,当且仅当1cos3x+2cosx>axsinx.因为当xɪ0,π2æèçöø÷时,sinx<x,所以当1cos3x+2cosx>axsinx时,有1cos3x+2cosx>a.设g(t)=1t3+2t,则gᶄ(t)=2-3t4.当tɪ(0,1)时,gᶄ(t)<0,故g(t)在(0,1)单调递减.所以当tɪ(0,1)时,g(t)>g(1)=3.故xɪ0,π2æèçöø÷时,函数1cos3x+2cosx的取值范围为(3,+ɕ),所以aɤ3.当aɤ3时,f(x)-sin2xɤ3x-sinxcos3x-sin2x.设h(x)=3x-sinxcos3x-sin2x,则hᶄ(x)=3-3-2cos2xcos4x-2cos2x=-4cos6x+5cos4x+2cos2x-3cos4x.令F(t)=-4t3+5t2+2t-3,则Fᶄ(t)=-12t2+10t+2=2(1-t)(6t+1).当tɪ(0,1)时,Fᶄ(t)>0,故F(t)在(0,1)单调递㊀㊀㊀解题技巧与方法123㊀㊀增.所以当tɪ(0,1)时,F(t)<F(1)=0.故当xɪ0,π2æèçöø÷时,-4cos6x+5cos4x+2cos2x-3<0,从而hᶄ(x)<0,所以h(x)在0,π2æèçöø÷单调递减.故当xɪ0,π2æèçöø÷时,h(x)<h(0)=0,所以f(x)<sin2x.综上,a的取值范围是(-ɕ,3].点评先讨论必要性,得到要满足的必要条件:aɤ3.再讨论充分性,即证明当aɤ3时命题成立.解法2㊀令g(x)=3x-2sinx-tanx,xɪ0,π2æèçöø÷,则gᶄ(x)=3cos2x-2cos3x-1cos2x.令h(x)=-2cos3x+3cos2x-1,0<x<π2,则hᶄ(x)=6sinxcosx(cosx-1)<0.h(x)在区间0,π2æèçöø÷单调递减,所以h(x)<h(0)=0.从而gᶄ(x)<0,g(x)在区间0,π2æèçöø÷单调递减,故g(x)<g(0)=0.所以当xɪ0,π2æèçöø÷时,2sinx+tanx>3x.当aɤ3时,f(x)-sin2xɤ3x-sinxcos3x-sin2x<2sinx+tanx-sinxcos3x-2sinxcosx=sinx(1-cosx)2-1cos2x-1cos3xæèçöø÷<0.当a>3时,取x0ɪ0,π2æèçöø÷,满足cosx0>13a-2,又因为当xɪ0,π2æèçöø÷时,sinx<x,所以fx0()-sin2x0=ax0-sinx0cos3x0-2sinx0cosx0ȡsinx0a-1cos3x0-2cosx0æèçöø÷ȡsinx0a-2-1cos3x0æèçöø÷>0.综上,a的取值范围是(-ɕ,3].点评㊀三角函数中,常用的不等式有:当xɪ0,π2æèçöø÷时,sinx<x<tanx,tanx+2sinx>3x.这两个不等式需要在平时的学习过程中积累.利用这两个不等式,可以对问题进行放缩,使问题简化.解法3㊀设g(x)=sinxcos3x+sin2x-ax,xɪ0,π2æèçöø÷,则gᶄ(x)=cosxcos3x+sinx(3cos2xsinx)cos6x+2cos2x-a=cos2x+3sin2xcos4x+(2cos2x-1)+(1-2sin2x)-a=1+2sin2xcos4x+2cos2x-2sin2x-a=1cos2x+cos2x+cos2xæèçöø÷+2sin2x1cos4x-1æèçöø÷-a.由三元均值不等式知1cos2x+cos2x+cos2xȡ3;又2sin2x1cos4x-1æèçöø÷ȡ0.以上两个不等式当且仅当x=0时取到等号.由于xɪ0,π2æèçöø÷,故gᶄ(x)>3-a.①当aɤ3时,gᶄ(x)>3-aȡ0,即g(x)在0,π2æèçöø÷上单调递增,所以g(x)>g(0)=0,即f(x)<sin2x恒成立.②当a>3时,取cosx0=31a-2ɪ(0,1),由于∀xɪ0,π2æèçöø÷,sinx-x<0,所以此时g(x0)=(a-2)sinx0+2sinx0cosx0-ax0<(a-2)sinx0+2sinx0-ax0=a(sinx0-x0)<0.因此,存在x0=arccos31a-2ɪ0,π2æèçöø÷,使得g(x0)<0,即f(x0)>sin2x0,这与f(x)<sin2x矛盾.综上,a的取值范围是[3,+ɕ).点评㊀利用三元均值不等式进行放缩,使问题变得简单了.后面的关键是 取点 ,那如果不会 取点 ,那该如何处理呢?㊀㊀解题技巧与方法㊀㊀124㊀我们的目的是证明存在xɪ0,π2æèçöø÷,使得g(x)<0,故可以做如下处理.当a>3时,gᶄ(0)=3-a<0,而gᶄ(x)ң+ɕxңπ2æèçöø÷,故存在x0ɪ0,π2æèçöø÷,使得gᶄ(x0)=0.所以当xɪ(0,x0)时,gᶄ(x)<0,g(x)在(0,x0)上单调递减,因此当xɪ(0,x0)时g(x)<g(0)=0,此时f(x)<sin2x不成立.三㊁试题亮点试题巧妙地将三角函数与多项式函数结合,讨论函数之间的不等式问题.三角函数的导数是中学教学的重点与难点,具有一定的综合性.试题设计新颖,紧扣课程标准,考查利用导数讨论函数的单调性等与导数有关的问题,具有较好的选拔功能,对中学数学教学具有较好的引导作用.四㊁变式探究已知函数f(x)=ax-3sinxcos2x,xɪ0,π2æèçöø÷.(1)求证:2tanx+3sinx>5x;(2)若f(x)<sin2x,求a的取值范围.解㊀(1)令g(x)=2tanx+3sinx-5x,0<x<π2,则gᶄ(x)=2cos2x+3cosx-5=3cos3x-5cos2x+2cos2x.令h(x)=3cos3x-5cos2x+2,0<x<π2,则hᶄ(x)=9cos2x(-sinx)-5ˑ2cosx(-sinx)=sinxcosx(10-9cosx)>0,所以h(x)在0,π2æèçöø÷上单调递增,则h(x)>h(0)=0,即gᶄ(x)>0,所以g(x)在0,π2æèçöø÷上单调递增,故g(x)>g(0)=0,即2tanx+3sinx>5x.(2)由(1)知,5x<2tanx+3sinx,所以当aɤ5时,有f(x)-sin2xɤ5x-3sinxcos2x-sin2x<2tanx+3sinx-3sinxcos2x-sin2x=sinxcos2x(3+2cosx+3cos2x-2cos3x)=sinxcos2x(cos2x-1)(3-2cosx)<0.当a>5时,取x0ɪ0,π2æèçöø÷,满足cosx0>3a-2.又因为当xɪ0,π2æèçöø÷时,sinx<x,所以f(x0)-sin2x0=ax0-3sinx0cos2x0-2sinx0cosx0>sinx0a-3cos2x0-2cosx0æèçöø÷>sinx0a-2-3cos2x0æèçöø÷>0.综上,a的取值范围是(-ɕ,5].点评㊀这里给出的解法是利用第(1)问的不等式进行放缩,使问题变得简单,其实也可以参考真题的解法1,给出类似的解法.结㊀语三角函数与导数的综合题,是高考数学中导数综合题的一个难点,而且在最近几年的高考试题中也经常出现这类试题,这值得引起一线教师的重视.破解三角函数与导数的综合题的策略主要有:求导㊁利用单调性;根据泰勒公式得到的常用不等式;利用均值不等式进行放缩;转化为代数问题处理等.希望一线教师重视对这类试题的研究,并对题型与方法进行归纳,加强学生对这类试题的训练,从而达到做一道题,会一类的教学效果.ʌ参考文献ɔ[1]杨林军,韩静波,周当侠,.深化基础考查㊃强化关键能力㊃突出思维品质 2023年高考 函数与导数 专题命题分析[J].中国数学教育,2023(18):24-29.[2]李昭平,陈俊国.对2023年高考一道函数与导数压轴题的思考[J].中学数学杂志,2023,No.405(07):60-63.[3]李鸿昌.高考题的高数探源与初等解法[M].合肥:中国科学技术大学出版社,2022.4[4]李鸿昌,徐章韬.关于对数平均的一个不等式的推广[J].数学通报,2023,62(08):50-52.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年全国高考数学(新课标)第21题(理)试题优美解
试题(21)(本小题满分12分)
已知函数()f x 满足满足121()(1)(0)2
x f x f e f x x -'=-+
; (1)求()f x 的解析式及单调区间; (2)若21()2
f x x ax b ≥
++,求(1)a b +的最大值。
优美解:(1)1211()(1)(0)()(1)(0)2x x f x f e f x x f x f e f x --'''=-+⇒=-+ 令1x =得:(0)1f = 1211()(1)(0)(1)1(1)2x f x f e x x f f e f e --'''=-+
⇒==⇔= 得:21()()()12x x f x e x x g x f x e x '=-+
⇒==-+
()10()x g x e y g x '=+>⇒=在x R ∈上单调递增
()0(0)0,()0(0)0f x f x f x f x ''''>=⇔><=⇔<
得:()f x 的解析式为21()2
x f x e x x =-+ 且单调递增区间为(0,)+∞,单调递减区间为(,0)-∞
(2)21()()(1)02
x f x x ax b h x e a x b ≥++⇔=-+-≥得()(1)x h x e a '=-+ ①当10a +≤时,()0()h x y h x '>⇒=在x R ∈上单调递增,但 x →-∞时,()h x →-∞与条件()0h x ≥矛盾。
②当10a +>时,()0ln(1),()0ln(1)h x x a h x x a ''>⇔>+<⇔<+ 得:当ln(1)x a =+时,min ()(1)(1)ln(1)0h x a a a b =+-++-≥ 22
(1)(1)(1)ln(1)(10)a b a a a a +≤+-+++>
令22()ln (0)F x x x x x =->;则()(12ln )F x x x '=-
()00()0F x x F x x ''>⇔<<
<⇔>
当x =max ()2e F x =
当1,a b ==(1)a b +的最大值为
2e 赏析:函数与其导数,不等式的有机结合,给考查学生的综合应用能力和理解推理论证提供了很好的空间。
