物流管理定量分析
物流管理定量分析.2

授人以鱼不如授人以渔
2.2.2 特殊矩阵 P33 朱明工作室 zhubob@ 1.零矩阵:所有元素都为0的矩阵。 2.单位矩阵:对角线上的元素均是1,其余 元素均是0的方阵称为单位矩阵,记为I。 3.对角矩阵:主对角线以外的元素全为0的方 阵称为对角矩阵。 4.三角矩阵:主对角线下方的元素全为0的 方阵称为上三角矩阵;主对角线上方的元 素全为0的矩阵称为下三角矩阵。 5.对称矩阵:P34
授人以鱼不如授人以渔
2.5 解线性规划的单纯形法 2.5.1 线性规划的矩阵表示 1. 线性规划模型的标准形式: .目标函数求最大值 .除变量非负限制外的约束均为等式 .常数项非负 2.线性规划问题标准化的步骤 P78 3.线性规划模型的矩阵形式 P80
朱明工作室
zhubob@
授人以鱼不如授人以渔
2.用初等行变换法解线性方程组 P60 朱明工作室 zhubob@ 步骤: .写出增广矩阵A; .用初等行变换将A化成行简化阶梯形矩阵; .由行简化阶梯形矩阵,写出线性方程组的 解。
授人以鱼不如授人以渔
2.4.4 用MATLAB软件解线性方程组范例 朱明工作室 zhubob@ P67 1.输入系数矩阵 2 .输入常数矩阵 3.求增广阵 4.化增广矩阵为行简化阶梯矩阵 rref( )
授人以鱼不如授人以渔
2.5.3用MATLAB软件解线性规划范例 P102 朱明工作室 zhubob@ 要求:目标函数为最小值 格式: [X,fval,exitflag]=linprog(C,A,B,Aeq,Beq,LB) 要求: 目标函数为最小值 AX<=B时,Aeq,Beq为空 AX=B时,A,B为空 LB表示变量的下界
物流定量指标分析

物流定量指标分析物流定量指标分析是指对物流业务运作中的数据进行量化分析,以便更好地评估和改进物流管理绩效。
这些指标可以帮助物流管理者了解业务的运作情况、发现问题、制定改进策略,并评估改进的效果。
本文将从物流成本、物流效率和物流质量三个方面,对物流定量指标进行分析。
一、物流成本指标分析物流成本是衡量企业物流管理绩效的一个重要指标。
常用的物流成本指标包括:运输成本比率、仓储成本比率、物流总成本比率等。
1. 运输成本比率:指运输费用占销售总额的比例。
该指标反映了企业在物流过程中所投入的运输资源与销售业绩之间的关系。
较低的运输成本比率通常表示物流运作效率较高,成本控制较好。
物流管理者可以通过优化运输路线、合理配置运力和运输工具,降低运输成本比率。
2. 仓储成本比率:指仓储费用占销售总额的比例。
该指标反映了企业在仓储过程中所投入的资源与销售业绩之间的关系。
降低仓储成本比率的方法包括:提高仓库利用率、优化仓储布局、减少仓储设备损耗等。
3. 物流总成本比率:指物流总成本占销售总额的比例。
该指标反映了企业在物流过程中所投入的资源与销售业绩之间的关系。
减少物流总成本比率的关键在于优化物流管理,降低成本,提高物流效率。
二、物流效率指标分析物流效率是指企业在物流过程中所投入的资源和所取得的成果之间的关系。
常用的物流效率指标包括:订单处理周期、库存周转率、装卸效率等。
1. 订单处理周期:指订单从接受到交付的时间。
较短的订单处理周期通常表示企业的物流运作效率较高。
物流管理者可以通过优化订单处理流程、提高员工工作效率等措施,缩短订单处理周期。
2. 库存周转率:指单位时间内库存的周转次数。
较高的库存周转率通常表示物流运作效率较高。
物流管理者可以通过优化进货和销售的时间安排,减少库存积压,提高库存周转率。
3. 装卸效率:指单位时间内装卸货物的数量。
较高的装卸效率通常表示物流运作效率较高。
物流管理者可以通过提高装卸工人的技能水平、使用物流设备和工具等措施,提高装卸效率。
《物流管理定量分析方法》形成性考核册作业 参考答案
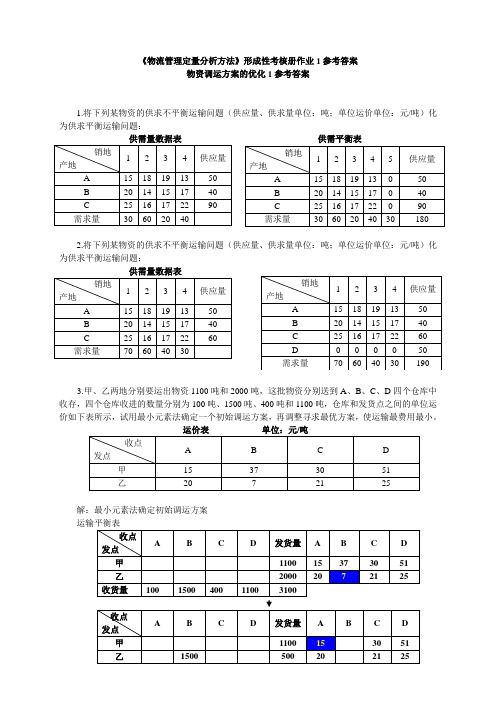
《物流管理定量分析方法》形成性考核册作业1参考答案物资调运方案的优化1参考答案1.将下列某物资的供求不平衡运输问题(供应量、供求量单位:吨;单位运价单位:元/吨)化为供求平衡运输问题:供需量数据表 供需平衡表2.将下列某物资的供求不平衡运输问题(供应量、供求量单位:吨;单位运价单位:元/吨)化为供求平衡运输问题:供需量数据表3.甲、乙两地分别要运出物资1100吨和2000吨,这批物资分别送到A 、B 、C 、D 四个仓库中收存,四个仓库收进的数量分别为100吨、1500吨、400吨和1100吨,仓库和发货点之间的单位运价如下表所示,试用最小元素法确定一个初始调运方案,再调整寻求最优方案,使运输最费用最小。
运价表 单位:元/吨解:最小元素法确定初始调运方案 运输平衡表应用闭回路方法计算检验数:λ12 = 37—51+25—7 = 4﹥0 λ= 30—51+25—21 = —17﹤013λ23 = 21—30+51—25 = 21 ﹥0这样,所有的检验数已全部非负,因此调整后的调运方案就是最优方案。
最小运输费用为:S = 100×15+400×30+600×51+1500×7+500×25 = 56300(元)4.某物资要从产地A、B、C调往销地一、二、三,运输平衡表(单位:吨)与运价(单位:元/吨)如下表所示,试用最小元素法编制初始调运方案,并求最调运方案。
解:用编制初始调运方案,过程如下:运输平衡表与运价表运输平衡表与运价表运输平衡表与运价表5.某物资要从产地A、B、C调往销地一、二、三、四,运输平衡表(单位:吨)与运价表(单位:百元/吨)如下表所示,试问应怎样调运才能使总运费最省?解:用最小元素法编制初始运输方案运输平衡表与运价表运输平衡表与运价表运输平衡表与运价表运输平衡表与运价表初始物资调运方案为:应用闭回路方法计算检验数λ11= 3 —3 + 2 —1 = 1 ﹥0λ12= 11 —3 + 2 —9 = 1 ﹥0λ24= 9 —2 + 3 —12 = -2﹤0λ31= 7 —1 + 2 —3 + 12 —5 = 12 ﹥0 λ32= 4 —9 + 2 —3 + 12 —5 = 1 ﹥0 λ33= 10 —3 + 12—5 = 15 ﹥0= 2 —3 + 12 —9 = 2 ﹥023故调整后的运输方案为最优方案,其运费为:6. 有一3个其始点A、B、C和4个目的点一、二、三、四的运输问题,3个起始的供应量分别为50吨、50吨、75吨,4个目的点的需求量分别为40吨、55吨、60吨、和20吨。
物流管理定量分析方法考试复习重点

物流管理定量分析方法期末考试复习重点考试的题型:一、单项选择题单项选择题有5小题,每小题4分,共20分。
其中第1章、第3章、第4章各1题,第2章2题。
二、计算题计算题有3小题,每小题7分,共21分。
其中第2章、第3章、第4章各1题。
三、编程题编程题有2小题,每小题6分,共12分。
其中第3章、第4章各1题。
四、应用题应用题共47分。
其中第1章、第2章、第3章各1题。
(说明:考试形式:闭卷笔试,试卷满分100分;答卷时限:90分钟;编程题要求会写出命令语句;本课程不能带计算器参加期末考试。
)重点的公式:1、导数基本公式: 常数的导数:0)(='c 幂函数的导数:1)(-αα⋅α='x x指数函数的导数:x x x x a a a e )e (,ln )(='=' 对数函数的导数:xx a x x a 1)(ln ,ln 1)(log ='=' (分数求导:11x x-=,因此211()x x '=-) 2、导数的四则运算法则:加减法:)()(])()([x v x u x v x u '±'='± 乘法:)()()()(])()([x v x u x v x u x v x u '+'='除法:2)]([)()()()(])()([x v x v x u x v x u x v x u '-'='有常数c 相乘时,)())((x u c x cu '=' (其中c 为常数)3、积分的公式:c x a x x a a ++=+⎰111d (a ≠-1) c x x +=⎰1d ,推广为:c kx x k +=⎰d (k 为任意常数)4、记住两个函数值:e 0=1,ln 1=05、MATLAB 常用函数表达式对编程问题,要记住函数e x ,ln x ,x ,,,a x x a x在MATLAB 软件中相应的命令函数exp(x),lo g(x),sqrt(x),(),,x a a x abs x ∧∧第1章考点【重难点分析】初始调运方案的编制,物资调运方案的优化【考点1】供需平衡问题(选择题1个)供需平衡问题:当总供应量等于总需求量时,供求平衡;当总供应量大于总需求量时,供过于求,增设虚销地;当总供应量小于总需求量时,供不应求,增设虚产地。
物流定量分析范文

物流定量分析范文物流定量分析是指通过数量化的手段,对物流活动进行系统化分析和评估的过程。
它主要侧重于利用一系列的数学模型和方法,对物流网络、物流成本、物流效率等进行定量测算和分析,以提高物流系统的效益和运作效率。
下面将从物流网络优化、物流成本控制和物流效率提升三个方面对物流定量分析展开讨论。
首先,物流网络优化是物流定量分析中的一个重要方面。
物流网络优化的目标是在满足客户需求的前提下,通过优化物流节点的布局和路径选择,以最小化总的物流成本。
在实际应用中,可以利用线性规划、整数规划、网络流等数学模型和方法,确定最优的物流节点位置和路径规划。
通过建立数学模型,可以优化物流网络的布局,减少物流节点之间的距离,提高货物的运输效率,降低货物的运输成本。
另外,物流网络优化还可以考虑供应链中的多种约束条件,比如仓储容量、运输能力等,以提高整个物流系统的效率和灵活性。
其次,物流成本控制是物流定量分析中的另一个重要方面。
物流成本控制的目标是通过对物流活动中各项成本进行准确计算和分析,找出成本的高低和分布的原因,以及改进的空间,从而降低物流成本。
在实际应用中,可以利用成本测算方法、成本分析方法、成本控制方法等,对物流活动中各个环节的成本进行定量分析。
通过建立成本核算模型,可以准确计算物流活动中的各个成本项目,找出成本高低的原因,明确影响成本的因素,进而采取相应的措施降低成本。
例如,在运输成本方面,可以通过优化运输路径、减少装载率等方式降低运输成本;在仓储成本方面,可以通过优化存货管理、减少库存周转时间等方式降低仓储成本。
最后,物流效率提升是物流定量分析中的另一个重要方面。
物流效率提升的目标是通过提高物流活动的运作效率,实现物流活动的快速、准确和低成本进行。
在实际应用中,可以利用运作效率评估方法、排队论等,对物流活动中的时间、速度、质量等指标进行定量测算和分析。
通过建立效率评估模型,可以评估物流活动中的损耗和浪费,找出效率低下的环节,提出改进措施。
物流管理定量分析.3

朱明工作室
zhubob@
授人以鱼不如授人以渔
3.2.4 经济函数 P122 1.总成本函数 2.利润函数 3.其他经济函数
朱明工作室
zhubob@
授人以鱼不如授人以渔
3.3 导数 P128 3.3.1 极限与连续概念 P128 1.极限概念与运算 P128 2.函数的连续性 P133
朱明工作室
zhubob@
授人以鱼不如授人以渔
3.3.8 用MATLAB软件求导数范例 P144 zhubob@ 1.写出对应的表达式 2.输入表达式 3. 求导数 diff()
朱明工作室
授人以鱼不如授人以渔
朱明工作室 3.4 求最值的导数方法 P148 zhubob@ 3.4.2 函数极值及其判定 P150 3.4.3 求最值的导数方法 P152 3.4.4用MATLAB求极值和最值范例 P153
朱明工作室
zhubob@
3.3.2 导数定义 P133 1.实例 2.导数的定义
授人以鱼不如授人以渔
3.3.3 导数公式 P136 3.3.4 导数的四则运算法则 P137 3.3.5 复合函数求导法则 3.3.6 高阶导数 P140 3.3.7 边际概念 P141 1.边际成本 2.边际收入 3.边际利润
朱明工作室
zhubob@
第三章 库存管理中优化的导数方法
授人以鱼不如授人以渔
3.1 经济批量问题 P112 zhubob@ 经济批量: 设某企业按年度计划需要某种物资D单位, 已知该物资每单位每年库存费为a元,每次 订货费为b元,订货批量为q单位,假定企 业对这种物资的使用是均匀的,则库存总 成本为 P113 经济批量就是使年库存总成本最小的订货 批量。
物流管理定量分析方法练习题
物流管理定量分析方法练习题物流管理定量分析方法是一种通过对物流相关数据进行统计分析,以评估和优化物流过程的方法。
这种方法可以帮助企业更好地理解物流活动的成本、效率和质量,从而制定出更加有效的物流策略。
本练习题将介绍几种常见的物流管理定量分析方法,并通过案例形式进行实际操作。
某电商企业计划对仓库布局进行调整,希望通过定量分析方法评估不同布局方案的优劣。
该企业提供了以下资料:仓库布局方案:现有两种布局方案,分别为直线型和L型。
库存数据:过去一年内,库存总量为100万件,其中畅销商品占60%,滞销商品占20%,一般商品占20%。
仓储成本数据:现有仓储成本为每月10万元,希望通过调整布局降低成本。
客户需求数据:客户对不同商品的订单数量有一定差异,平均每个订单需要10件商品。
线性回归分析:使用线性回归模型分析库存数据和仓储成本之间的关系,预测不同布局方案下的仓储成本。
聚类分析:根据商品销售量和仓储成本等指标,对商品进行聚类分析,确定不同类别的商品对仓储成本的影响程度。
模拟分析:根据客户需求数据和不同商品的订单数量,模拟不同布局方案下的库存周转情况,评估库存积压和缺货情况。
(1)收集和整理数据:收集过去一年的库存数据和仓储成本数据,整理成适合线性回归分析的格式。
(2)构建线性回归模型:以仓储成本为因变量,以库存量为自变量,构建线性回归模型。
(3)模型拟合和检验:使用统计软件进行模型拟合和检验,分析模型是否具有统计学意义和实际意义。
(4)预测未来成本:根据模型预测不同布局方案下的仓储成本。
(1)数据预处理:对商品销售量和仓储成本等指标进行数据清洗和标准化处理。
(2)聚类分析:使用K-means聚类算法将商品分为不同的类别,根据聚类结果分析不同类别商品对仓储成本的影响程度。
(1)建立模拟模型:根据客户需求数据和不同商品的订单数量,建立模拟模型。
(2)模拟不同布局方案:根据不同布局方案,模拟库存周转情况。
(3)评估库存积压和缺货情况:比较不同布局方案的库存积压和缺货情况,评估不同方案的优劣。
物流管理定量分析.4
授人以鱼不如授人以渔
4.3 原函数与不定积分概念 4.3.1 原函数 P201 4.3.2 不定积分概念 P201 1.不定积分的定义 P201 2.不定积分的性质 P202
朱明工作室
zhubob@
授人以鱼不如授人以渔
4.4 不定积分基本公式与直接积分法 朱明工作室 zhubob@ 4.4.1 不定积分基本公式 P202 4.4.2 直接积分法 P203 由不定积分基本公式及运算性质可以直接 求出一些简单函数的不定积分,这种方法一 般称为直接积分法.` 4.4.3 用MATLAB软件求积分范例 P206 int(y)
授人以鱼不如授人以渔
朱明工作室 4.5 积分在物流经济分析中应用的实例 zhubob@ 4.5.1 由边际物流量求该物流量和增量的实 例 P209 1.总成本函数及其增量 P210 2.收入函数及其增量 P210 3.利润函数及其增量 P211
授人以鱼不如授人以渔
朱明工作室
zhubob@
第四章 物流经济量的微元变化积累
授人以鱼不如授人以渔
4.1 由边际成本求成本的增量 定义4.1 微分:P193
朱明工作室
zhubob@
4.2 定积分的定义与性质 4.2.1 定积分的定义 P197 4.2.2 微积分基本定量 P199 4.2.3 定积分的基本性质 P199
物流管理定量分析方法试题答案
物流管理定量分析方法试题答案IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】《物流管理定量分析方法》期末复习题一、线性规划法 1. 设⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=011101,132031B A ,求:AB T . 解:⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡---=1121011011132031T AB 2.已知矩阵⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-=2101111412210101C B A ,,,求:AB +C. 解:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡-=+3702210116012101111412210101C AB 3.已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=131211203012011B A ,,求:AB. 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=531421131211203012011AB 4. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011B A ,,求:B T A. 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1723422011201110011653042001T A B 5.设110012212601A B ⎡⎤-⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,,求:(1) 2B T -A ;(2) AB . 解:12000122121126TB A -⎡⎤⎡⎤-=-⎢⎥⎢⎥-⎣⎦⎣⎦240001241242126164-⎡⎤⎡⎤⎡⎤=-=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦6. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011B A ,,求:AB. 解: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011AB 7. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=321212113101012111B A ,,求:AB .解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=434014646321212113101012111AB 二、导数方法1.设y =(x 2-3) ln x ,求:y '解:xx x x x x x x y 3ln 2)(ln )3(ln )3(22-+='⋅-+⋅'-=' 2.设y =(1+x 3) ln x ,求:y '解:22331ln 3)(ln )1(ln )1(x xx x x x x x y ++='⋅++⋅'+=' 3.设y =(1+x 2)ln x ,求:y '解:xx x x x x x x y 2221ln 2))(ln 1(ln )1(++='++'+='4. 设xx y e 4=,求:y '解:x x x x x x x y )e 4()e (e )(4344+='⋅+⋅'=' 5.设31ln xxy +=,求:y ' 解:23232333)1(ln 31)1()1()(ln )1()(ln x x x x x x x x x x y +-+=+'+⋅-+⋅'='6.设xy x+=1e ,求:y '解:22)1(e )1()1(e )1()e (x x x x x y xx x +=+'+-+'='7.设y =x 3ln x ,求:y '解:2233ln 3)(ln ln )(x x x x x x x y +='⋅+⋅'='三、微元变化累积 1.计算定积分:⎰+1d )e 3(x x x解:25e 3)e 321(d )e 3(|1021-=+=+⎰x x x x x 2.计算定积分:⎰+312d )2(x xx解:3ln 2326|)|ln 231(d )2(|313312+=+=+⎰x x x x x3.计算定积分:⎰+103d )e 24(x x x 解: 1e 2)e 2(d )e 24(|1413-=+=+⎰x x x x x4.计算定积分:⎰+13d )e 2(x x x解:47e 2)e 241(d )e 2(|1413-=+=+⎰x x x x x5.计算定积分:⎰+21d )12(x xx解:2ln 3|)|ln (d )12(|21221+=+=+⎰x x x xx6..计算定积分:⎰+21d )1e (x xx解:2ln e e |)|ln e (d )1e (22121|+-=+=+⎰x x xx x7.计算定积分:⎰+212d )1(x xx解:2ln 37|)|ln 31(d )1(|213212+=+=+⎰x x x x x 四、表上作业法1.某公司从三个产地A1,A2,A3运输某物资到三个销地B1,B2,B3,各产地的供应量(单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表所示:(1)在下表中写出用最小元素法编制的初始调运方案:(2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总费用。
物流管理定量分析方法
物流管理定量分析方法1 / 9物流管理定量分析方法复习资料A.、名词解释和选择题 1.“商流”:对象物所有权转移的活动称为商流。
2.“物流”:物流是物品从供应地向接收的地的实体流动过程。
根据实际需要,将运输、储存、装卸、搬运、包装、流通加工、配送、信息处理等基本功能进行有机结合。
3.商物分离论:指流通中的商业物流和实物物流两个部分从过去的同一概念和统一运动中分离出来,各自按照自己的规律和渠道独自运动的实现; 4.“黑大陆”:物流是一个尚未了结,尚未认识,尚未开发的领域,这个领域未知的东西还很多 5.“物流冰山”:物流是一座冰山,启辰在水面下的部分是我们所看不到的黑色区域,我们看到的只不过是一小部分,因而人们对物流费用的了解是一片空白; 6.“第三利润源” :物流发展的潜力巨大,被人们视为第三利润源; 7.“效益背反”:物流的若干要素之间存在着损益的矛盾,即一个功能的优化往往会导致另一个要素损失,的一种此消彼长,此赢彼亏的现象; 8.成本中心说、认为物流是企业营业成本产生的中心节点,会对企业成本产生影响; 9.利润中心说、物流可以提供大量直接和间接的利润,是企业利润的重要来源; 10.服务中心说:物流最重要的作用在于提高企业竞争力,服务水平,利于企业生存; 11.集装盘(托盘):是用于集装、堆放、搬运、运输和放置,是货物和制品的水平平台装置,有便于叉车从下部叉入并将台板托起的叉入口。
托盘最初是在装卸领域出现,与叉车同步发展起来的。
目前托盘已经是和集装箱一样重要的集装方式,它们形成了集装系统的两大支柱,在现代物流运输系统的建立过程中起到了重要作用。
托盘具有自重小、亦返空、易装盘的优点。
但装载量和保护性比较低,不易露天存放。
12.绿色包装:能够循环使用、再生利用或降解腐化,且在货物的生命周期中对环境不造成公害的适度包装。
13.流通加工:是物品在生产地到使用地的过程中,根据需要施加包装、分割、计量、分拣、刷标志、拴标签、组装等作业的总称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物流管理定量分析内部编号:(YUUT-TBBY-MMUT-URRUY-UOOY-DBUYI-0128)《物流管理定量分析》第一次作业(物资调运方案的优化的表上作业法)1.将下列某物资的供求不平衡运输问题(供应量、供求量单位:吨;单位运价单位:元/吨)化为供求平衡运输问题:供需量数据表解因为供大于求,所以增设一个虚销地,得供求平衡运输问题如下:2.将下列某物资的供求不平衡运输问题(供应量、供求量单位:吨;单位运价单位:元/吨)化为供求平衡运输问题:供需量数据表解 因为供小于求,所以增设一个虚产地,得供求平衡运输问题如下:3.甲、乙两产地分别要运出物资1100吨和2000吨,这批物资分别送到A,B,C,D 四个仓库中收存,四仓库收进的数量分别为100吨、1500吨、400吨和1100吨,仓库和发货点之间的单位运价如下表所示:运价表 单位:元/吨试用最小元素法确定一个初始调运方案,再调整寻求最优调运方案,使运输总费用最小。
解 用最小元素法编制初始调运方案如下:运输平衡表与运价表⑤ ④填有数字的格子数 = 2+4-1 = 5 用闭回路法计算检验数:4725513712=-+-=λ,0172125513013<-=-+-=λ因为有负检验数,所以此方案不是最优的,需进一步调整,调整量为: 调整后的调运方案是:运输平衡表与运价表求最新调运方案的检验数:4725513712=-+-=λ,312551152021=-+-=λ因为所有检验数均大于0,所以此方案最优,最小运输费用为:671002550071500516003040015100=⨯+⨯+⨯+⨯+⨯=S (元)4.设某物资要从产地321,,A A A 调往销地321,,B B B ,运输平衡表(单位:吨)与运价表(单位:元/吨)如下表所示:运输平衡表与运价表试用最小元素法编制初始调运方案,并求最优调运方案。
解 编制初始调运方案如下:运输平衡表与运价表⑤ ③ ②计算检验数:105030104012=-+-=λ,308050309023=-+-=λ702080506031=-+-=λ,6020805030103032=-+-+-=λ因为所有检验数均大于0,所以此方案是最优方案,最小运费为: 5.设某物资要从产地321,,A A A 调往销地4321,,,B B B B ,运输平衡表(单位:吨)与运价表(单位:百元/吨)如下表所示:运输平衡表与运价表试问应怎样调运才能使总运费最省 解 编制初始调运方案如下:运输平衡表与运价表计算检验数:1123311=-+-=λ,045121112=-+-=λ因为有负检验数,所以此方案不是最优的,需进一步调整,调整量为: 调整后的调运方案是:运输平衡表与运价表求最新调运方案的检验数:0194512312=-+-+-=λ,045121112=-+-=λ 1945123223=-+-+-=λ,01945924<-=-+-=λ因为有负检验数,所以此方案不是最优的,继续调整,调整量为: 调整后的调运方案是:运输平衡表与运价表求最新调运方案的检验数:因为有负检验数,所以此方案不是最优的,继续调整,调整量为: 调整后的调运方案是:运输平衡表与运价表求最新调运方案的检验数:1459131112=-+-+-=λ,13191214=-+-=λ 1459922=-+-=λ,1331223=-+-=λ10591731=-+-=λ,133********=-+-+-=λ因为所有检验数均大于0,所以此方案最优,最省运费为:88534693113532=⨯+⨯+⨯+⨯+⨯+⨯=S (百元)6.有一3个起始点321,,A A A 和4个目的点4321,,,B B B B 的运输问题,3个起始点的供应量分别为50吨、50吨、75吨,4个目的点的需求量分别为40吨、55吨、60吨、20吨。
它们之间的距离(单位:公里)如下表所示:相关情况表假设每次装车的额外费用不计,运输成本与所行驶的距离成正比,试求最优的调运方案。
解 按距离最短优先供应的最小元素法编制初始调运方案如下:运输平衡表与距离表① ⑤计算检验数:3231311=-+-=λ,03139413<-=-+-=λ因为有负检验数,所以此方案不是最优的,需进一步调整,调整量为: 调整后的调运方案是:运输平衡表与距离表求最新调运方案的检验数:3231311=-+-=λ,5132514=-+-=λ323148721=-+-+-=λ,02148322<-=-+-=λ因为有负检验数,所以此方案不是最优的,需进一步调整,调整量为: 调整后的调运方案是:运输平衡表与距离表求最新调运方案的检验数:523384311=-+-+-=λ,2384112=-+-=λ 748332514=-+-+-=λ,5233721=-+-=λ4332624=-+-=λ,1833933=-+-=λ因为所有检验数均大于0,所以此方案最优。
第二作业(资源合理配置的线性规划法)一、填空题 1.设A=⎥⎦⎤⎢⎣⎡-7321x ,B=⎥⎦⎤⎢⎣⎡721x ,并且A=B ,则=x (23) 2.设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-300010002,则1-A =(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-31000100021)3.设1-A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡200010101,则A=(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-21000102101) 4.设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡123,B=[]321,则TT A B =(⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡369246123) 5.设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-100112,B=[]321,则BA=([]40) 6.设A=⎥⎦⎤⎢⎣⎡4321,B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-101201,则T AB =(⎥⎦⎤⎢⎣⎡--4103241) 7.若A 为3⨯4矩阵,B 为2⨯5矩阵,其乘积T T B AC 有意义,则C 为(5⨯4)矩阵。
8.设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-430421,B=⎥⎦⎤⎢⎣⎡--413021,则B A T+=(⎥⎦⎤⎢⎣⎡--815360) 9.设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100110111⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡200714201,则A 中的元素23a =(9) 二、单项选择题1.设A 为43⨯矩阵,I 是单位矩阵,满足IA=A ,则I 为( A )阶矩阵. A .B AC T B .T T B AC C .T ACB D .ACB 2. 设B A ,为同阶方阵且满足O AB =,则(D ). A.O A =,O B ≠ B. O A ≠,O B = C. O A =,O B = D.A ,B 可能都不是03.设A ,B 为35⨯矩阵,则下列运算中( D )可以进行. A .AB B .BA C .T B A + D .T AB 5.设矩阵⎥⎦⎤⎢⎣⎡=5321A ,则1-A 为( C )。
(A) ⎥⎦⎤⎢⎣⎡--5321 (B) ⎥⎦⎤⎢⎣⎡-5321 (C) ⎥⎦⎤⎢⎣⎡--1325(D) ⎥⎦⎤⎢⎣⎡--1325三、计算题1.设矩阵,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321212113B ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=101012111B ,,计算 (1)3A-2B (2)B A T +3.(3)AB-BA解:(1) 3A-2B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡761652117(2)B A T +3=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡10646254710 (3)AB-BA=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--434402320 2.设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--131211,B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--203012011,计算 BA 解:BA=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--203012011⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--131211=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--531421 3.设矩阵A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---312143201,求1-A . 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=102710013740001201100312010143001201)(AI 1-A =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---3543513515151513583523513 4.设⎥⎦⎤⎢⎣⎡-=110021A ,求:T 1()AA - 解:⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡-=2225101201110021T AA T 1()AA -⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=65313131=⎥⎦⎤⎢⎣⎡5222615.解线性方程组:解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=344103441011111344100112311111A 线性方程组的解为:⎩⎨⎧+--=-+=344233432431x x x x x x (其中3x ,4x 是自由未知量)6.解线性方程组:解:线性方程组的解为:⎪⎩⎪⎨⎧=-=-=845321x x x7.解齐次线性方程组⎪⎩⎪⎨⎧=+-=+-=+-05830352023321321321x x x x x x x x x解: 因为系数矩阵A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---110110231583352231⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→0500110101λ 方程组一般解为⎩⎨⎧==3231x x x x (其中3x 是自由未知量) 8. 某物流公司下属企业生产甲、乙两种产品,要用A ,B ,C 三种不同的原料,从工艺资料知道:每生产一件产品甲,需用三种原料分别为1,1,0单位;生产一件产品乙,需用三种原料分别为1,2,1单位。
每天原料供应的能力分别为6,8,3单位。
又知销售一件产品甲,企业可得利润3万元;销售一件产品乙,企业可得利润4万元。
试写出能使利润最大的线性规划模型,并用单纯形法求解。
解:设生产甲、乙两种产品的产量分别为x 1件和x 2件。
显然,x 1,x 2≥0 分别销售一件甲、乙产品,企业可得利润3万元和4万元,故目标函数为:max S =3x 1+4x 2生产x 1件甲产品,需要A 原料x 1单位;同样,生产x 2件乙产品,需要A 原料x 2单位。
A 原料每天的供应能力为6单位,故x 1+x 2≤6同理,对原料B ,C ,有x 1+2x 2≤8 x 2≤3故,线性规划模型为: 线性规划模型的标准形式为:标准形式中的一组变量 (x3,x4,x5) 的系数构成单位矩阵,故本例可用基本单纯形法求解。
写出矩阵形式:选负检验数最大者“-4”所在第二列为主元列,用最小比值原则确定第三行为主元行,第三行第二列元素“1”为主元。
对主元作旋转变换,得: 还有一个负检验数“-3”,它所在的第一列为主元列,用最小比值原则确定第二行为主元行,第二行第一列元素“1”为主元。
