初二下册数学题精选八年级数学拔高专题训练
初二数学拔高练习题推荐
初二数学拔高练习题推荐数学作为一门基础学科，对于中学生的学习非常重要。
通过不断的练习和提高，可以帮助学生更好地理解和掌握数学知识。
在初二阶段，为了能够更好地拔高自己的数学水平，以下是一些数学拔高练习题的推荐。
1. 代数方程练习题1.1 解方程：求解2x + 5 = 17的解。
1.2 模型应用：某图书馆现有图书n本，已借出了8本，还剩下的图书比已借出的图书的3倍多5本，请问图书馆共有多少本图书？1.3 字母代数：如果ab = 12，且a + b = 7，求a和b的值。
2. 几何运算练习题2.1 曲线长度：计算抛物线y = x^2在区间[0, 2]上的弧长。
2.2 三角形相似：已知两个三角形的两角分别相等，另一角对应边的比为3:4，判断这两个三角形是否相似。
3. 概率与统计练习题3.1 概率计算：有5个白球和3个黑球放在一个盒子里，从中随机摸出2个球，求摸出的两个球颜色相同的概率。
3.2 统计分析：在班级的一次数学测验中，40名学生的得分情况如下：60分及以下10人，60-70分15人，70分以上15人，请根据这个数据回答以下问题：- 60分及以下的学生占总人数的百分之几？- 70分以上的学生占总人数的百分之几？- 平均分是多少？4. 数列与函数练习题4.1 等差数列：已知某数列的前四项分别是-5、-2、1、4，请写出该数列的通项公式。
4.2 函数应用：已知函数f(x) = 2x^2 + 3x - 2，请计算f(-1)的值。
5. 实际问题应用练习题5.1 比例问题：某地区有3000名中学生，其中男生占总数的35%，女生占其余的65%，计算男生和女生的人数各是多少。
5.2 利息问题：小明存入银行1000元，年利率为4%，存款时间为3年，请计算存款到期后的总金额。
通过解答以上的练习题，可以帮助初二学生更好地巩固和提高数学知识。
同时，还可以培养学生的思维能力、逻辑思维和问题解决能力。
建议学生在课余时间，结合教材和学校作业，进行这些拔高练习题的练习。
初二数学拔高试卷答案
一、选择题（每题5分，共25分）1. 已知函数f(x) = 2x - 3，则f(2)的值为（）A. 1B. 3C. 5D. 7答案：C2. 下列各式中，绝对值最小的是（）A. |x-1|B. |x+1|C. |x-2|D. |x+2|答案：B3. 若a、b、c为等差数列，且a+b+c=12，则a+c的值为（）A. 6B. 8C. 10D. 12答案：C4. 在直角坐标系中，点A（-3，2）关于原点的对称点为（）A.（-3，-2）B.（3，-2）C.（-3，2）D.（3，2）答案：B5. 下列函数中，y=2x-1是y=mx+b的一次函数，其中m和b的值分别为（）A. m=2，b=-1B. m=1，b=-1C. m=0，b=-1D. m=2，b=0答案：A二、填空题（每题5分，共25分）6. 若x=3是方程2x-5=0的解，则方程3x+7的解为______。
答案：27. 若a、b、c成等比数列，且a+b+c=27，则b的值为______。
答案：98. 在△AB C中，∠A=45°，∠B=90°，∠C=45°，则△ABC的周长为______。
答案：4√29. 若函数y=kx+b（k≠0）的图象经过点（1，-2），则k和b的值分别为______。
答案：k=-1，b=-110. 已知二次函数y=ax^2+bx+c（a≠0）的图象开口向上，且顶点坐标为（-1，3），则a、b、c的值分别为______。
答案：a=1，b=-2，c=2三、解答题（共50分）11. （15分）已知函数f(x) = x^2 - 4x + 3，求f(x)的最小值。
解答：f(x) = x^2 - 4x + 3可以写成f(x) = (x-2)^2 - 1的形式。
因为(x-2)^2总是非负的，所以f(x)的最小值为-1，当x=2时取得。
12. （15分）已知数列{an}的前三项分别为a1=2，a2=4，a3=8，且数列{an}为等比数列，求该数列的通项公式。
初二数学拔高题
**初二数学拔高题**1. **题目**：在三角形ABC中，AB = AC，D是BC的中点，DE⊥AB于点E，DF⊥AC于点F。
求证：DE = DF。
**分析**：由于AB = AC，所以∠B = ∠C。
因为D是BC的中点，所以BD = CD。
结合DE⊥AB和DF⊥AC的信息，可以通过三角形的全等来证明DE = DF。
2. **题目**：已知x^2 - 4x + 1 = 0，求x^2 + 1/x^2的值。
**分析**：从给定的方程x^2 - 4x + 1 = 0开始，我们可以将其转化为x - 4 + 1/x = 0，进而求得x + 1/x = 4。
然后平方两边，得到(x + 1/x)^2 = x^2 + 2 + 1/x^2 = 16。
最后求得x^2 + 1/x^2 = 14。
3. **题目**：对于任意的正整数n，求证：√(n+√n) < √(n+1)。
**分析**：为了证明上述不等式，我们可以首先平方两边，得到n + √n < n + 1。
然后简化得到√n < 1，这对所有的正整数n都是成立的。
因此，原不等式成立。
4. **题目**：在平行四边形ABCD中，E、F分别是BC、AD的中点，连接AE、CF交于点O。
求证：点O是BD的中点。
**分析**：由于ABCD是平行四边形，所以AD∥BC，进而得出AF = CE （因为中点的关系）。
再通过平行四边形的性质和平行线的性质证明△AFO与△CEO全等，从而得出FO = EO。
利用相似的方法证明BO = DO，最后证明O 是BD的中点。
5. **题目**：已知a、b、c是三角形的三边，且a^2 + b^2 + c^2 - ab - bc - ca = 0。
判断此三角形的形状并证明。
**分析**：首先将原式乘以2得到2a^2 + 2b^2 + 2c^2 - 2ab - 2bc - 2ca = 0。
这可以转化为(a-b)^2 + (b-c)^2 + (c-a)^2 = 0。
2022-2023学年北师大版八年级下册数学期末拔高试题
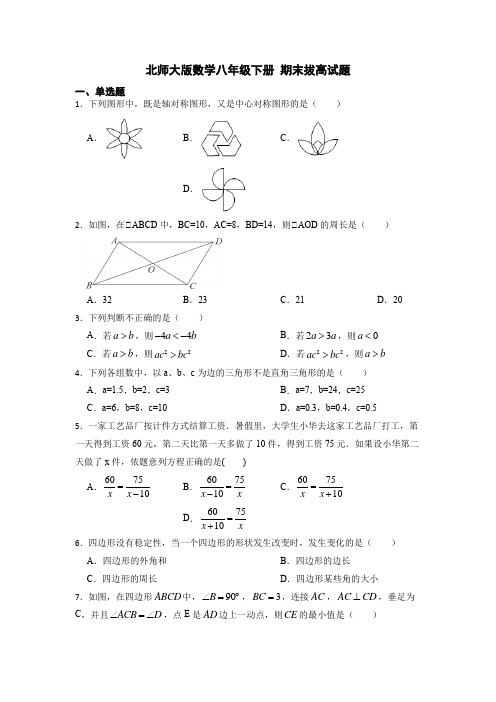
北师大版数学八年级下册 期末拔高试题一、单选题1．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A ．B ．C ．D ．2．如图，在▱ABCD 中，BC=10，AC=8，BD=14，则▱AOD 的周长是（ ）A ．32B ．23C ．21D ．203．下列判断不正确的是（ ）A ．若a b >，则44a b -<-B ．若23a a >，则0a <C ．若a b >，则22ac bc >D ．若22ac bc >，则a b >4．下列各组数中，以a 、b 、c 为边的三角形不是直角三角形的是（ ）A ．a=1.5，b=2，c=3B ．a=7，b=24，c=25C ．a=6，b=8，c=10D ．a=0.3，b=0.4，c=0.55．一家工艺品厂按计件方式结算工资．暑假里，大学生小华去这家工艺品厂打工，第一天得到工资60元，第二天比第一天多做了10件，得到工资75元．如果设小华第二天做了x 件，依题意列方程正确的是( ) A ．607510x x =- B ．607510x x=- C ．607510x x =+D ．607510x x=+ 6．四边形没有稳定性，当一个四边形的形状发生改变时，发生变化的是（ ）A ．四边形的外角和B ．四边形的边长C ．四边形的周长D ．四边形某些角的大小7．如图，在四边形ABCD 中，90B ∠=︒，3BC =，连接AC ，AC CD ⊥，垂足为C ，并且ACBD ∠=∠，点E 是AD 边上一动点，则CE 的最小值是（ ）A ．1.5B ．3C ．3.5D ．48．边长为a 、b 的长方形周长为12，面积为10，则 22a b ab + 的值为( )A ．120B ．60C ．80D ．409．若关于 x 的不等式组 0721x m x -<⎧⎨-≤⎩ 的整数解共有3个，则 m 的取值范围是（ ） A ．56m <<B ．56m <≤C ．56m ≤≤D ．67m <≤10．若数a 使关于x 的不等式组 2122274x x x a-⎧≤-+⎪⎨⎪+>-⎩ 有且仅有四个整数解，且使关于y 的分式方程2a y - + 22y- =2有非负数解，则所有满足条件的整数a 的值之和是（ ） A ．3B ．1C ．0D ．﹣311．如图，在数轴上，点A 表示1，现将点A 沿数轴做如下移动；第一次将点A 向左移动3个单位长度到达点 1A ，第二次将点A 向右移动6个单位长度到达点 2A ，第三次将点 2A 向左移动9个单位长度到达点 3A ，按照这种移动规律移动下去，第n 次移动到点 n A ，如果点 n A 与原点的距离不小于17，那么n 的最小值是（ ）A ．9B ．10C ．11D ．1212．如图，正方形ABCD 的边长为6，点E 、F 分别在AB ，AD 上，若CE=3 5，且▱ECF=45°，则CF 长为（ ）A ．210B ．3 5C ．5103D ．53二、填空题13．矩形ABCD 的两条对角线相交于点O ，▱AOB ＝60°，AC ＝4cm ，则AB＝ ，矩形ABCD 的面积＝ ．14．因式分解： 244b b -+= ． 15．当m +n ＝1时，代数式 231m m mn m n ⎛⎫+⎪--⎝⎭•（m 2﹣n 2）的值为 ． 16．如图，一副三角板的三个内角分别是90°，45°，45°和90°，60°，30°，按如图所示叠放在一起（点A ，D ，B 在同一直线上），若固定▱ABC ，将▱BDE 绕着公共顶点B 顺时针旋转α度（0＜α＜180），当边DE 与▱ABC 的某一边平行时，相应的旋转角α的值为 ．17．甲，乙，丙三人做一个抽牌游戏，三张纸牌上分别写有个数字0，x ，y （x ，y 均为正整数，且x ＜y ），每人抽一张纸牌，纸牌上的数字就是这一轮的得分.经过若干轮后（至少四轮），甲的总得分为20，乙的总得分为10，丙的总得分为9.则甲抽到x 的次数最多为 .三、解答题18．某工厂计划在规定时间内生产24000个零件.由于销售商突然急需供货，工厂实际工作效率比原计划提高了50%，并提前5天完成这批零件的生产任务.求该工厂原计划每天加工这种零件多少个？19．当x 满足条件 ()()133114423x x x x +<-⎧⎪⎨-<-⎪⎩ 时，求出方程x 2﹣2x ﹣4=0的根． 20．如图，把一副三角板如图甲放置，其中 90ACB DEC ∠=∠=︒ ， 45A ∠=︒ ，30D ∠=︒ ，斜边 6cm AB = ， 7cm DC = ，把三角板 DCE 绕点C 顺时针旋转15°得到D CE '' （如图乙）．这时 AB 与 CD ' 相交于点O ， D E '' 与 AB 相交于点F ．求线段 AD ' 的长．21．如图，▱ABC中，点A（﹣2，1）、B（﹣3，4）C（﹣5，2）均在格点上．在所给直角坐标系中解答下列问题：将▱ABC平移得▱A1B1C1使得点B的对应点B1与原点O重合，在所给直角坐标系中画出图形；在图中画出▱ABC关于y轴对称的▱A2B2C2，并写出A2、B2、C2的坐标；在x轴上找一点P，使得▱PAB2的周长最小，请直接写出点P的坐标．22．如图所示，在▱ABC中，AB=AC，AC边上的中线把三角形的周长分为24cm和30cm的两部分，求三角形各边的长．23．已知多项式2x-x+m有一个因式(2x+1),求m的值.24．已知四边形ABCD的对角线AC与BD交于点O，给出下列四个论断①OA＝OC ②AB＝CD ③▱BAD＝▱DCB ④AD▱BC请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：（1）构造一个真命题，画图并给出证明；（2）构造一个假命题，举反例加以说明.。
适合初二数学拔高的试卷
一、选择题（每题5分，共50分）1. 已知函数f(x) = 2x - 3，若f(a) = f(b)，则a与b的关系是：A. a > bB. a < bC. a = bD. a + b = 32. 在等腰三角形ABC中，AB = AC，若∠BAC = 40°，则∠ABC的度数是：A. 40°B. 50°C. 60°D. 70°3. 已知一元二次方程x² - 4x + 3 = 0，则该方程的解是：A. x₁ = 1, x₂ = 3B. x₁ = 2, x₂ = 2C. x₁ = -1, x₂ = -3D. x₁ = -2, x₂ = -24. 在直角坐标系中，点P(2, 3)关于y轴的对称点是：A. P'(-2, 3)B. P'(2, -3)C. P'(-2, -3)D. P'(2, 3)5. 若一个正方形的对角线长为10cm，则该正方形的周长是：A. 20cmB. 25cmC. 30cmD. 40cm6. 已知函数y = kx + b，若k > 0，b > 0，则函数图像在以下哪个象限：A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 在三角形ABC中，若AB = AC，且∠B = 50°，则∠A的度数是：A. 50°B. 60°C. 70°D. 80°8. 若一个数的平方根是-2，则这个数是：A. 4B. -4C. 16D. -169. 在直角坐标系中，直线y = 2x + 1与y轴的交点坐标是：A. (0, 1)B. (1, 0)C. (0, 2)D. (2, 0)10. 若a² + b² = c²，则a、b、c构成什么三角形？A. 等腰三角形B. 等边三角形C. 直角三角形D. 钝角三角形二、填空题（每题5分，共50分）11. 若x² - 5x + 6 = 0，则x的值为______。
初二数学拔高练习题推荐
初二数学拔高练习题推荐在初二学习阶段，数学是一个学科中至关重要的部分。
数学拔高练习题可以帮助学生巩固基础知识，提高解题能力和思维灵活度。
本文将推荐一些适合初二学生的数学拔高练习题，帮助他们在数学学习中取得更好的成绩。
一、整数类练习题1. 求出[-5, 5]范围内所有奇数的和。
2. 找出[-10, 10]范围内与13互质的正整数。
3. 若整数a和b满足a-b=13，且(a+17)(b-5)=164，求a和b的值。
二、分数类练习题1. 将 3/5 和 4/7两个分数相加，结果化简为最简形式。
2. 将 5 1/3 和 7 2/5两个带分数相加，结果转化为假分数的形式。
3. 若 4/x + 3/y = 7，其中 x 和 y 为正整数，求 x 和 y 的最小公倍数。
三、代数类练习题1. 解方程：2x - 3 = 7x + 5。
2. 已知 x + y = 5，2x - y = 9，求 x 和 y。
3. 现有一包含20个数的集合，其中除了一个数为7外，其余都是6，求这个数。
四、几何类练习题1. 设一个三角形的三条边分别为a, b, c，且满足a^2 + b^2 = 25，c = 3，请求三条边的长度。
2. 若已知一个长方形的周长为20cm，且长是宽的6倍，求长和宽的长度。
3. 一个圆形的半径为5cm，求其周长和面积。
五、概率与统计类练习题1. 一个有10个红球和10个蓝球的袋子，从中随机取出3个球，求其中至少两个是红球的概率。
2. 假设某种品牌手机的故障率为5%，求正常使用的概率。
3. 一次抛掷两枚骰子，其点数和为6的概率是多少？这些数学拔高练习题涵盖了初二数学的各个章节和知识点，对学生的数学素养提高非常有帮助。
希望同学们在完成这些练习题的过程中，能够逐渐提升自己的解题能力和思维灵活度，为将来更深入的数学学习打下坚实基础。
人教版八年级数学下《正方形》拔高练习
人教版八年级数学下《正方形》拔高练习《正方形》拔高练习一、选择题（本大题共5小题，共25.0分）1．（5分）如图，正方形ABCD中，点E、F、H分别是AB、BC、CD的中点，CE、DF交于G，连接AG、HG．下列结论：①CE⊥DF；②AG＝AD；③∠CHG＝∠DAG；④HG＝AD．其中正确的有（）A．1个B．2个C．3个D．4个2．（5分）如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的角平分线分别交AB、BD于M、N两点．若AM＝，则线段BN的长为（）A．B．C．2D．13．（5分）如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的平分线分别交AB、BD于点M、N，若AD＝4，则线段AM 的长为（）A．2B．2C．4﹣D．8﹣44．（5分）如图，有两个正方形A，B，现将B放置在A的内部得到图甲．将A，B并列放置，以正方形A与正方形B的边长之和为新的边长构造正方形得到图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的面积之和为（）A．13B．14C．15D．165．（5分）已知?ABCD，其对角线的交点为O，则下面说法正确的是（）A．当OA＝OB时?ABCD为矩形B．当AB＝AD时?ABCD为正方形C．当∠ABC＝90°时?ABCD为菱形D．当AC⊥BD时?ABCD为正方形二、填空题（本大题共5小题，共25.0分）6．（5分）如图，Rt△ABC中，∠C＝90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC＝3，OC＝6，则另一直角边BC的长为．7．（5分）如图，直线l上有三个正方形a，b，c，若a，c的面积分别为7和9，则b的面积为．8．（5分）已知正方形①、②在直线上，正方形③如图放置，若正方形①、②的面积分别27和54，则正方形③的边长为．9．（5分）如图，有两个正方形夹在AB与CD中，且AB∥CD，若∠FEC＝10°，两个正方形临边夹角为150°，则∠1的度数为度（正方形的每个内角为90°）10．（5分）一个正方形和两个等边三角形的位置如图所示，则∠1+∠2+∠3的度数为°．三、解答题（本大题共5小题，共50.0分）11．（10分）如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长，交BC边的延长线于E点，对角线BD交AG于F 点．已知FG＝2，求线段AE的长度．12．（10分）如图，在正方形ABCD中，E为边BC上一点，F 是AE的中点，过点F垂直于AE的直线与边CD的交点为M，与AD 的延长线的交点为N．若AB＝12，BE＝5，求DN的长．13．（10分）如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE、BF相交于点O，请判断AE和BF的关系，并说明理由．14．（10分）如图，已知E是正方形ABCD的边CD的中点，点F在BC上，且∠DAE＝∠F AE，求证：AF＝AD+CF．15．（10分）如图1，P为正方形ABCD内一点，且P A：PB：PC＝1：2：3，求∠APB的度数．小明同学的想法是：不妨设P A＝x，PB＝2x，PC＝3x，设法把P A、PB、PC相对集中，于是他将△BCP绕点B顺时针旋转90°得到△BAE（如图2），然后连结PE，问题得以解决．请你回答图2中∠APB＝度．请你参考小明同学的方法，解答下列问题．如图3，P是等边△ABC内一点，P A：PB：PC＝3：4：5，那么∠APB＝度．请写出推理过程．《正方形》拔高练习参考答案与试题解析一、选择题（本大题共5小题，共25.0分）1．（5分）如图，正方形ABCD中，点E、F、H分别是AB、BC、CD的中点，CE、DF交于G，连接AG、HG．下列结论：①CE⊥DF；②AG＝AD；③∠CHG＝∠DAG；④HG＝AD．其中正确的有（）A．1个B．2个C．3个D．4个【分析】连接AH，由四边形ABCD是正方形与点E、F、H分别是AB、BC、CD 的中点，易证得△BCE≌△CDF与△ADH≌△DCF，根据全等三角形的性质，易证得CE⊥DF与AH⊥DF，根据垂直平分线的性质，即可证得AG＝AD，由直角三角形斜边上的中线等于斜边的一半，即可证得HG＝AD，根据等腰三角形的性质，即可得∠CHG＝∠DAG．则问题得解．【解答】解：∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD，∠B＝∠BCD＝90°，∵点E、F、H分别是AB、BC、CD的中点，∴BE＝CF，在△BCE与△CDF中，∴△BCE≌△CDF，（SAS），∴∠ECB＝∠CDF，∵∠BCE+∠ECD＝90°，∴∠ECD+∠CDF＝90°，∴∠CGD＝90°，∴CE⊥DF，故①正确；在Rt△CGD中，H是CD边的中点，∴HG＝CD＝AD，故④正确；连接AH，同理可得：AH⊥DF，∵HG＝HD＝CD，∴DK＝GK，∴AH垂直平分DG，∴AG＝AD，故②正确；∴∠DAG＝2∠DAH，同理：△ADH≌△DCF，∴∠DAH＝∠CDF，∵GH＝DH，∴∠HDG＝∠HGD，∴∠GHC＝∠HDG+∠HGD＝2∠CDF，∴∠CHG＝∠DAG．故③正确．故选：D．【点评】此题考查了正方形的性质，全等三角形的判定与性质，等腰三角形的性质以及垂直平分线的性质等知识．此题综合性很强，难度较大，解题的关键是注意数形结合思想的应用．2．（5分）如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的角平分线分别交AB、BD于M、N两点．若AM＝，则线段BN的长为（）A．B．C．2D．1【分析】作MH⊥AC于H，如图，根据正方形的性质得∠MAH＝45°，则△AMH 为等腰直角三角形，再求出AH，MH，MB，然后证明∠BNM＝∠BMN，BN ＝BM＝1．【解答】解：作MH⊥AC于H，如图，∵四边形ABCD为正方形，∴∠MAH＝45°，∴△AMH为等腰直角三角形，∵AM＝，∴AH＝MH＝1，∵CM平分∠ACB，∠ACB＝45°，∠MBC＝90°∴∠ACM＝∠BCM＝22.5°，BM＝MH＝1，∵∠BAC＝45°，∴∠BMC＝45°+22.5°＝67.5°，∵∠BNM＝∠ONC＝90°﹣22.5°＝67.5°，∴∠BNM＝∠BMN，∴BN＝BM＝1，故选：D．【点评】本题考查了正方形的性质，角平分线的性质，根据角平分线的性质作辅助线是解决问题的关键．3．（5分）如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的平分线分别交AB、BD于点M、N，若AD＝4，则线段AM 的长为（）A．2B．2C．4﹣D．8﹣4【分析】过点M作MF⊥AC于点F，根据角平分线的性质可知FM＝BM，再由四边形ABCD为正方形，可得出∠F AM＝45°，在直角三角形中用∠F AM的正弦值即可求出FM与AM的关系，最后由AM+BM＝4列方程求解即可．．【解答】解：过点M作M F⊥AC于点F，如图所示．∵MC平分∠ACB，四边形ABCD为正方形，∴∠CAB＝45°，FM＝BM．在Rt△AFM中，∠AFM＝90°，∠F AM＝45°，AM＝2，∴BM＝FM＝AM?sin∠F AM＝AM．又∵AM+BM＝4，∴AM+AM＝4，解得：AM＝8﹣4．故选：D．【点评】本题考查了正方形的性质以及角平分线的性质，解题的关键是求出FM 的长度与AM的关系．本题属于基础题，难度不大，解决该题型题目时，根据角平分的性质及正方形的特点找出边角关系，再利用解直角三角形的方法即可得以解决．4．（5分）如图，有两个正方形A，B，现将B放置在A的内部得到图甲．将A，B并列放置，以正方形A与正方形B的边长之和为新的边长构造正方形得到图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的面积之和为（）A．13B．14C．15D．16【分析】设正方形A的边长为a，正方形B的边长为b，由图形得出关系式求解即可．【解答】解：设正方形A的边长为a，正方形B的边长为b，由图甲得a2﹣b2﹣2（a﹣b）b＝1即a2+b2﹣2ab＝1，由图乙得（a+b）2﹣a2﹣b2＝12，2ab＝12，所以a2+b2＝13，故选：A．【点评】本题主要考查了正方形的性质，完全平方公式的几何背景，解题的关键是根据图形得出数量关系．5．（5分）已知?ABCD，其对角线的交点为O，则下面说法正确的是（）A．当OA＝OB时?ABCD为矩形B．当AB＝AD时?ABCD为正方形C．当∠ABC＝90°时?ABCD为菱形D．当AC⊥BD时?ABCD为正方形【分析】直接利用矩形、菱形的判定方法分析得出答案．【解答】解：A、当OA＝OB时，可得到?ABCD为矩形，故此选项正确；B、当AB＝AD时?ABCD为菱形，故此选项错误；C、当∠ABC＝90°时?ABCD为矩形，故此选项错误；D、当AC⊥BD时?ABCD为菱形，故此选项．故选：A．【点评】此题主要考查了矩形、菱形的判定，正确掌握相关判定方法是解题关键．二、填空题（本大题共5小题，共25.0分）6．（5分）如图，Rt△ABC中，∠C＝90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC＝3，OC＝6，则另一直角边BC的长为9．【分析】过O作OF⊥BC，过A作AM⊥OF，根据正方形的性质得出∠A OB＝90°，OA＝OB，求出∠BOF＝∠OAM，根据AAS证△AOM≌△BOF，推出AM＝OF，OM＝FB，求出四边形ACFM为矩形，推出AM＝CF，AC＝MF＝3，得出等腰三角形三角形OCF，根据勾股定理求出CF＝OF＝6，求出BF，即可求出答案．【解答】解：过O作OF⊥BC于F，过A作AM⊥OF于M，∵∠ACB＝90°，∴∠AMO＝∠OFB＝90°，∠ACB＝∠CFM＝∠AMF＝90°，∴四边形ACFM是矩形，∴AM＝CF，AC＝MF＝3，∵四边形ABDE为正方形，∴∠AOB＝90°，OA＝OB，∴∠AOM+∠BOF＝90°，又∵∠AMO＝90°，∴∠AOM+∠OAM＝90°，∴∠BOF＝∠OAM，在△AOM和△OBF中，∴△AOM≌△OBF（AAS），∴AM＝OF，OM＝FB，∴OF＝CF，∵∠CFO＝90°，∴△CFO是等腰直角三角形，∵OC＝6，由勾股定理得：CF＝OF＝6，∴BF＝OM＝OF﹣FM＝6﹣3＝3，∴BC＝6+3＝9．故答案为：9．【点评】本题考查了等腰直角三角形，勾股定理，正方形的性质，全等三角形的性质和判定的应用，主要考查学生综合运用性质进行推理的能力，有一定的难度．7．（5分）如图，直线l上有三个正方形a，b，c，若a，c的面积分别为7和9，则b的面积为16．【分析】运用正方形边长相等，再根据同角的余角相等可得∠BAC ＝∠DCE，然后证明△ACB≌△DCE，再结合全等三角形的性质和勾股定理来求解即可．【解答】解：由于a、b、c都是正方形，所以AC＝CD，∠ACD＝90°；∵∠ACB+∠DCE＝∠ACB+∠BAC＝90°，即∠BAC＝∠DCE，在△ABC和△CED中，∴△ACB≌△CDE（AAS），∴AB＝CE，BC＝DE；在Rt△ABC中，由勾股定理得：AC2＝AB2+BC2＝AB2+DE2＝7+9＝16，即S b＝16，则b的面积为16，故答案为16【点评】本题主要考查对全等三角形和勾股定理的综合运用，关键是证明△ACB ≌△DCE．8．（5分）已知正方形①、②在直线上，正方形③如图放置，若正方形①、②的面积分别27和54，则正方形③的边长为9．【分析】根据正方形的性质就可以得出∠EAB＝∠EBD＝∠BCD＝90°，BE＝BD，∠AEB＝∠CBD，就可以得出△ABE≌△CDB，得出AE＝BC，AB＝CD，由勾股定理就可以得出BE的值，进而得出结论．【解答】解：∵四边形①、②、③都是正方形，∴∠EAB＝∠EBD＝∠BCD＝90°，BE＝BD，∴∠AEB+∠ABE＝90°，∠ABE+∠DBC＝90°，∴∠AEB＝∠CBD．在△ABE和△CDB中，，∴△ABE≌△CDB（AAS），∴AE＝BC，AB＝CD．∵正方形①、②的面积分别27cm2和54cm2，∴AE2＝27，CD2＝54．∴AB2＝27．在Rt△ABE中，由勾股定理，得BE2＝AE2+AB2＝27+54＝81，∴BE＝9．故答案为：9．【点评】本题考查的是勾股定理，正方形的性质的运用，正方形的面积公式的运用，三角形全等的判定及性质的运用，解答时证明△ABE≌△CDB是关键．9．（5分）如图，有两个正方形夹在AB与CD 中，且AB∥CD，若∠FEC＝10°，两个正方形临边夹角为150°，则∠1的度数为70度（正方形的每个内角为90°）【分析】如图，延长KH交EF的延长线于M，作MG⊥AB于G，交CD于H．利用四边形内角和36°，求出∠HMF，再根据∠KME＝∠MKG+∠MEH，求出∠MKG即可解决问题；【解答】解：如图，延长KH交EF的延长线于M，作MG⊥AB 于G，交CD于H．∵∠GHM＝∠GFM＝90°，∴∠HMF＝180°﹣150°＝30°，∵∠HMF＝∠MKG+∠MEH，∠MEH＝10°，∴∠MKG＝20°，∴∠1＝90°﹣20°＝70°，故答案为70．【点评】本题利用正方形的四个角都是直角，直角的邻补角也是直角，四边形的内角和定理和两直线平行，内错角相等的性质，延长正方形的边构造四边形是解题的关键．10．（5分）一个正方形和两个等边三角形的位置如图所示，则∠1+∠2+∠3的度数为150°．【分析】设围成的小三角形为△ABC，分别用∠1、∠2、∠3表示出△ABC的三个内角，再利用三角形的内角和等于180°列式整理即可得解．【解答】解：如图，∠BAC＝180°﹣60°﹣∠2＝120°﹣∠2，∠ABC＝180°﹣90°﹣∠1＝90°﹣∠1，∠ACB＝180°﹣60°﹣∠3＝120°﹣∠3，在△ABC中，∠BAC+∠ABC+∠ACB＝180°，∴90°﹣∠1+120°﹣∠3+120°﹣∠2＝180°，∴∠1+∠2+∠3＝150°．故答案为：150．【点评】本题考查了正方形的性质、等边三角形的性质、三角形的内角和定理，用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键，也是本题的难点．三、解答题（本大题共5小题，共50.0分）11．（10分）如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长，交BC边的延长线于E点，对角线BD交AG于F 点．已知FG＝2，求线段AE的长度．【分析】根据正方形的性质可得出AB∥CD，进而可得出△ABF∽△GDF，根据相似三角形的性质可得出＝2，结合FG＝2可求出AF、AG的长度，由AB∥CD，可得，即可得AE＝2AG＝12．【解答】解：∵G为CD边中点，∴CG＝DG＝CD∵四边形ABCD为正方形，∴AB＝CD，AB∥CD，∴∠ABF＝∠GDF，∠BAF＝∠DGF，∴△ABF∽△GDF，∴＝2，∴AF＝2GF＝4，∴AG＝6．∵AB∥DC∴∴AE＝2GE＝2（AE﹣AG）∴AE＝2AG＝12【点评】本题考查了相似三角形的判定与性质、正方形的性质以及三角形的中位线，利用相似三角形的性质求出AF的长度是解题的关键12．（10分）如图，在正方形ABCD中，E为边BC上一点，F 是AE的中点，过点F垂直于AE的直线与边CD的交点为M，与AD 的延长线的交点为N．若AB＝12，BE＝5，求DN的长．【分析】根据正方形的性质得到AB＝AD，∠B＝90°，AD∥BC，根据平行线的性质得到∠AEB＝∠F AN，根据新的数据线的性质和勾股定理得到AN＝16.9，根据线段的和差即可得到结论．【解答】解：∵四边形ABCD是正方形，∴AB＝AD，∠B＝90°，AD∥BC，∴∠AEB＝∠F AN，∵FN⊥AE，∴∠AFN＝90°，∴∠B＝∠AFN，∴△ABE∽△NF A，∴，在Rt△ABE中．AE＝＝＝13，∵F是AE的中点，∴AF＝AE＝6.5，∴＝，∴AN＝16.9，∵AB＝AD＝12，∴DN＝AN﹣AD＝4.9．【点评】本题考查了正方形的性质，相似三角形的判定和性质，勾股定理，熟练掌握相似三角形的判定和性质是解题的关键．13．（10分）如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE、BF相交于点O，请判断AE和BF的关系，并说明理由．【分析】根据正方形的性质得到AD＝CD＝AB＝BC，∠ADE＝∠BAF＝90°，证明△BAF≌△ADE，根据全等三角形的性质证明．【解答】解：AE＝BF，AE⊥BF，理由如下：∵四边形ABCD是正方形，∴AD＝CD＝AB＝BC，∠ADE＝∠BAF＝90°，∵CE＝DF，∴AF＝DE，在△BAF和△ADE中，，∴△BAF≌△ADE（SAS），∴AE＝BF，∠ABF＝∠DAE，∵∠DAE+∠BAE＝90°，∴∠ABF+∠BAE＝90°，即AE⊥BF．【点评】本题考查的是正方形的性质，全等三角形的判定和性质，掌握正方形的四条边相等，四个角都是90°是解题的关键．14．（10分）如图，已知E是正方形ABCD的边CD的中点，点F在BC上，且∠DAE＝∠F AE，求证：AF＝AD+CF．【分析】过E点作EG⊥AF，垂足为G，根据题干条件首先证明Rt△AEG≌Rt △AED，即可得AG＝AD，同理证明出CF＝GF，于是结论可以证明AF＝AD+CF．【解答】解：过E点作EG⊥AF，垂足为G，∵∠DAE＝∠EAF，∠B＝∠AGE＝90°，即AE为角平分线，ED⊥AD，EG⊥AG，∴DE＝EG，在Rt△AEG和Rt△AED中，，∴Rt△AEG≌Rt△AED（HL），∴AG＝AD，∵E是CD的中点∴DE＝EC＝EG同理可知CF＝GF，∴AF＝AG+FG＝AD+CF．【点评】本题主要考查正方形的性质和全等三角形的判定与性质的知识点，解答本题的关键是熟练掌握正方形的性质，此题难度不大．15．（10分）如图1，P为正方形ABCD内一点，且P A：PB：PC＝1：2：3，求∠APB的度数．小明同学的想法是：不妨设P A＝x，PB＝2x，PC＝3x，设法把P A、PB、PC相对集中，于是他将△BCP绕点B顺时针旋转90°得到△BAE（如图2），然后连结PE，问题得以解决．请你回答图2中∠APB＝135度．请你参考小明同学的方法，解答下列问题．如图3，P是等边△ABC内一点，P A：PB：PC＝3：4：5，那么∠APB＝150度．请写出推理过程．。
初二数学练习题拔高
初二数学练习题拔高在学习数学的过程中，练习题是非常重要的一部分。
通过做练习题可以巩固和加深对数学知识的理解，提高解题能力和思维灵活性。
初二数学是一个非常关键的阶段，对于学生来说掌握好基础知识尤为重要。
下面是一些初二数学拔高题目，希望能帮助同学们提高数学水平。
一、选择题1.若3(x - 1) = 4(2x - 3)，则x的值是多少？A. -1B. 1C. 2D. 32.下列四个分数中，哪一个是最小的？A. 5/6B. 6/7C. 7/8D. 8/93.已知a:b = 2:3，b:c = 3:4，求a:c的值。
A. 2:4B. 3:8C. 4:6D. 2:74.求下列多项式的值：3x² - 4x + 2，当x = 1时。
A. 1B. 2C. -1D. 35.已知△ABC中，AB = 3，AC = 4，BC = 5，求△ABC的面积。
A. 3B. 6C. 8D. 10二、填空题1.若a + 2b = 3，b - c = 4，则a - c的值为__。
2.根据图形的特点，填写括号中的数字：正方形的周长是( )，矩形的周长是( )。
3.若a:b = 4:5，b:c = 7:8，则a:c的值为( )。
4.若一本书正常价格为60元，打折后为原价的80%，则打折后的价格为( )元。
5.某种商品A的价格是商品B的2/3，商品B的价格是商品C的4/5，那么商品A的价格是商品C的( )。
三、解答题1.计算：12 + 31 - 8 + 172.用长方形的周长表示长和宽的关系，并表示出长和宽的关系式。
3.解方程：4x + 5 = 94.已知△ABC中，∠ABC = 90°，AB = 5，BC = 12，求AC的值。
5.某商品原价为120元，现在打8折出售，请计算打折后的价格。
以上就是一些初二数学拔高题目，希望能对同学们提高数学水平有所帮助。
请同学们尝试独立解答这些题目，并检查答案是否正确。
通过不断地练习和思考，相信你们的数学水平会有明显的提高！。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初二（下册）数学题精选分式：一：如果abc=1,求证11++a ab +11++b bc +11++c ac =1二：已知a 1+b 1=)(29b a +，则a b +b a等于多少？三：一个圆柱形容器的容积为V 立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管２倍的大水管注水。
向容器中注满水的全过程共用时间t 分。
求两根水管各自注水的速度。
四：联系实际编拟一道关于分式方程2288+=xx 的应用题。
要求表述完整，条件充分并写出解答过程。
五：已知M ＝222y x xy-、N ＝2222y x y x -+，用“+”或“－”连结M 、N,有三种不同的形式，M+N 、M-N 、N-M ，请你任取其中一种进行计算，化简求值，其中x ：y=5：2。
反比例函数：一：一张边长为16cm 正方形的纸片，剪去两个面积一定且一样的小矩形得到一个“E ”图案如图1所示．小矩形的长x （cm ）与宽y （cm ）之间的函数关系如图2所示：（1）求y 与x 之间的函数关系式； （2）“E ”图案的面积是多少？（3）如果小矩形的长是6≤x ≤12cm ，求小矩形宽的范围.二：是一个反比例函数图象的一部分，点(110)A ，，(101)B ，是它的两个端点．（1）求此函数的解析式，并写出自变量x 的取值范围； （2）请你举出一个能用本题的函数关系描述的生活实例．三：如图，⊙A 和⊙B 都与x 轴和y 轴相切，圆心A 和圆心B 都在反比例函数1y x 的图象上，则图中阴影部分的面积等于 .四：如图11，已知正比例函数和反比例函数的图像都经过点M （－2，1），且P （1，－2）为双曲线上的一点，Q 为坐标平面上一动点，PA 垂直于x 轴，QB 垂直于y 轴，垂足分别是A 、B ． （1）写出正比例函数和反比例函数的关系式；（2）当点Q 在直线MO 上运动时，直线MO 上是否存在这样的点Q ，使得△OBQ 与△OAP 面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图12，当点Q 在第一象限中的双曲线上运动时，作以OP 、OQ 为邻边的平行四边形OPCQ ，求平行四边形OPCQ 周长的最小值．五：如图，在平面直角坐标系中，直线AB 与Y 轴和X 轴分别交于点A 、点8，与反比例函数y 一罟在第一象限的图象交于点c(1，6)、点D(3，x)．过点C 作CE 上y 轴于E ，过点D 作DF 上X 轴于F ． (1)求m ，n 的值；(2)求直线AB 的函数解析式；A BO xy1 111 AB O xy图xyBAOMQP图xyBCAOMPQ勾股定理：一：清朝康熙皇帝是我国历史上对数学很有兴趣的帝王．近日，•西安发现了他的数学专著，其中有一文《积求勾股法》，它对“三边长为3、4、5的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：“若所设者为积数（面积），以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数”．用现在的数学语言表述是：“若直角三角形的三边长分别为3、4、5的整数倍，•设其面积为S ，则第一步：6S＝m ；第二步：m =k ；第三步：分别用3、4、5乘以k ，得三边长”． （1）当面积S 等于150时，请用康熙的“积求勾股法”求出这个直角三角形的三边长；（2）你能证明“积求勾股法”的正确性吗？请写出证明过程．（二题图） （三题图）二：一张等腰三角形纸片，底边长l5cm ，底边上的高长22．5cm ．现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是( )A ．第4张 B ．第5张 C ．第6张 D ．第7张 三：如图，甲、乙两楼相距20米，甲楼高20米，小明站在距甲楼10米的A 处目测得点A 与甲、乙楼顶B C 、刚好在同一直线上，且A 与B 相距350米，若小明的身高忽略不计，则乙楼的高度是 米．四：恩施州自然风光无限，特别是以“雄、奇、秀、幽、险”著称于世．著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧，50km AB A =，、B 到直线X 的距离分别为10km 和40km ，要在沪渝高速公路旁修建一服务区P ，向A 、B 两景区运送游客．小民设计了两种方案，图（1）是方案一的示意图（AP 与直线X 垂直，垂足为P ），P 到A 、B 的距离之和1S PA PB =+，图（2）是方案二的示意图（点A 关于直线X 的对称点是A '，连接BA '交直线X 于点P ），P 到A 、B 的距离之和2S PA PB =+． （1）求1S 、2S ，并比较它们的大小；（2）请你说明2S PA PB =+的值为最小；（3）拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直，建立如图（3）所示的直角坐标系，B 到直线Y 的距离为30km ，请你在X 旁和Y 旁各修建一服务区P 、Q ，使P 、A 、B 、Q 组成的四边形的周长最小．并求出这个最小值．五：已知：如图，在直角梯形ABCD 中，AD ∥BC ，∠ABC ＝90°，DE ⊥AC 于点F ，交BC 于点G ，交AB 的延长线于点E ，且AE AC =．（1）求证：BG FG =； （2）若2AD DC ==，求AB 的长．20米乙C B A甲10？米2BAPX图（1）YXBA QP O图（3）BAP X A ' 图（2）DCB GAF四边形：一：如图，△ACD 、△ABE 、△BCF 均为直线BC 同侧的等边三角形.(1) 当AB ≠AC 时，证明四边形ADFE 为平行四边形；(2) 当AB = AC 时，顺次连结A 、D 、F 、E 四点所构成的图形有哪几类？直接写出构成图形的类型和相应的条件.二：如图，已知△ABC 是等边三角形，D 、E 分别在边BC 、AC 上，且CD=CE ，连结DE 并延长至点F ，使EF=AE ，连结AF 、BE 和CF 。
（1）请在图中找出一对全等三角形，用符号“≌”表示，并加以证明。
（2）判断四边形ABDF 是怎样的四边形，并说明理由。
（3）若AB=6，BD=2DC ，求四边形ABEF 的面积。
三：如图，在△ABC 中，∠A 、∠B 的平分线交于点D ，DE ∥AC 交BC 于点E ，DF ∥BC 交AC 于点F ．（1）点D 是△ABC 的________心； （2）求证：四边形DECF 为菱形．四：在矩形ABCD 中，点E 是AD 边上一点，连接BE ，且∠ABE ＝30°，BE ＝DE ，连接BD ．点P 从点E 出发沿射线ED 运动，过点P 作PQ ∥BD 交直线BE 于点Q ．(1) 当点P 在线段ED 上时（如图1），求证：BE ＝PD ＋33PQ ；（2）若 BC ＝6，设PQ 长为x ，以P 、Q 、D 三点为顶点所构成的三角形面积为y ，求y 与 x 的函数关系式（不要求写出自变量x的取值范围）；（3）在②的条件下，当点P 运动到线段ED 的中点时，连接QC ，过点P 作PF ⊥QC ，垂足为F ，PF 交对角线BD 于点G （如图2），求线段PG 的长。
EFDABC五：如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图．．．,并写出它们的周长. 4222六：已知:如图,在矩形ABCD 中,E 、F 分别是边BC 、AB 上的点,且EF=ED,EF ⊥ED.求证:AE 平分∠七：如图,矩形纸片ABCD 中,AB =8,将纸片折叠,使顶点B 落在边AD 的E 点上,BG =10. (1)当折痕的另一端F 在AB 边上时,如图(1).求△EFG 的面积.(2)当折痕的另一端F 在AD 边上时,如图(2).证明四边形BGEF 为菱形,并求出折痕GF 的长.HA BCDEF G八：（1）请用两种不同的方法，用尺规在所给的两个矩形中各作一个不为正方形的菱形，且菱形的四个顶点都在矩形的边上．（保留作图痕迹） （2）写出你的作法．图（2）ABCDE FG H (A)(B)A BCDE F G图（1）（第23题）EDBAF九：如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在射线BC上，且PE=PB.（1）求证：①PE=PD；②PE⊥PD；（2）设AP=x, △PBE的面积为y.①求出y关于x的函数关系式，并写出x的取值范围；②当x取何值时，y取得最大值，并求出这个最大值..十：如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．（2）将原题中正方形改为矩形（如图4—6），且AB=a，BC=b，CE=ka， CG=kb (a≠b，k>0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．（3）在第(2)题图5中，连结DG、BE，且a=3，b=2，k=12，求22BE DG+的值．AB CPDE数据的分析：一：为了帮助贫困失学儿童，某团市委发起“爱心储蓄”活动，鼓励学生将自己的压岁钱和零花钱存入银行，定期一年，到期后可取回本金，而把利息．．捐给贫困失学儿童.某中学共有学生1200人，图1是该校各年级学生人数比例．．．．分布的扇形统计图，图2是该校学生人均存款．．．．情况的条形统计图. （1）九年级学生人均存款元；（2）该校学生人均存款多少元？（3）已知银行一年期定期存款的年利率是2.25%（“爱心储蓄”免收利息税），且每351元能提供 给一位失学儿童一学年的基本费用，那么该校一学年能帮助多少为贫困失学儿童。
二：如图是连续十周测试甲、乙两名运动员体能训练情况的折线统计图。
教练组规定：体能测试成绩70分以上（包括70分）为合格。
⑴请根据图11中所提供的信息填写下表：⑵请从下面两个不同的角度对运动员体能测试结果进行判断：①依据平均数与成绩合格的次数比较甲和乙， 的体能测试成绩较好； ②依据平均数与中位数比较甲和乙， 的体能测试成绩较好。
⑶依据折线统计图和成绩合格的次数，分析哪位运动员体能训练的效果较好。