八年级下册数学好题难题精选(1)
八年级下数学好题难题集锦含答案(317511805版权所有)
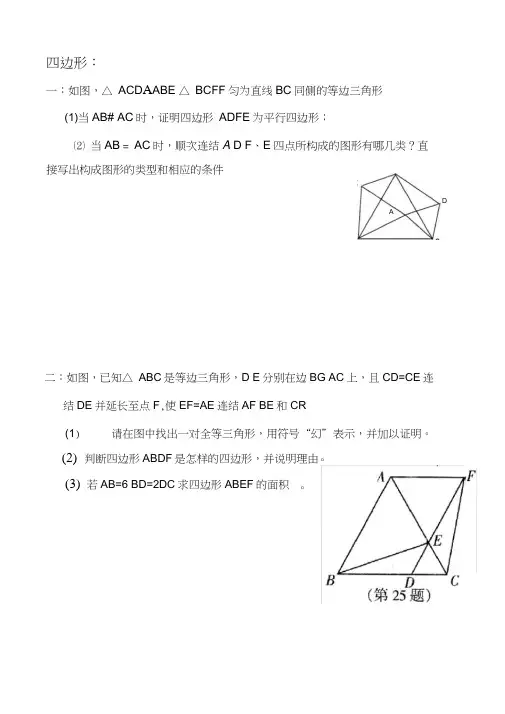
四边形:一:如图,△ ACD A ABE △ BCFF 匀为直线BC 同侧的等边三角形(1)当AB# AC 时,证明四边形 ADFE 为平行四边形;⑵ 当AB = AC 时,顺次连结A D F 、E 四点所构成的图形有哪几类?直二:如图,已知△ ABC 是等边三角形,D E 分别在边BG AC 上,且CD=CE 连结DE 并延长至点F ,使EF=AE 连结AF BE 和CR 请在图中找出一对全等三角形,用符号“幻”表示,并加以证明。
接写出构成图形的类型和相应的条件(2) 判断四边形ABDF 是怎样的四边形,并说明理由 (3) 若AB=6 BD=2DC 求四边形ABEF 的面积(1)ADO四:在矩形ABCD 中,点E 是AD 边上一点,连接 BE 且/ ABE= 30°, BE= DE 连接BD •点P 从点E 出发沿射线ED 运动,过点P 作PQ// BD 交直线BE 于点Q(1) 当点P 在线段ED 上时(如图1),求证:BE = PD^l l PQ3(2) 若BC = 6,设PQ 长为x ,以P 、Q D 三点为顶点所构成的三角形面积为 y ,求y 与x 的函数关系式(不要求写出自变量 x 的取值范围);(3) 在②的条件下,当点P 运动到线段ED 的中点时,连接QC 过点P 作PF 丄QC 垂足为F , PF 交对角线BD 于点G (如图2),求线段PG 的长恵<3 •••/ EPM=30 • PM= PE • PE= PQ23•/ BE=DE=PD+PE • BE=PD+ PQ3 1(2)解:由题意知 AE=—BE • DE=BE=2AE2•/ AD=BC=6 • AE=2 DE=BE=4当点P 在线段ED 上时(如图1)解:(1)证明:•••/ A=90° / ABE=30 / AEB=60•/ EB=ED •••/ EBD 玄 EDB=30 •/ PQ// BDEQP=/ EBD / EPQ 2 EDB•••/ EPQ=/ EQP=30 • EQ=EP过点E 作EM L OP 垂足为 M • PQ=2PM41 1 过点Q 做QH 丄AD 于点H QH= —PQ=_x2 2由(1)得 PD=BE-三 PQ=4-—3QC= . PQ 2 PC 2=2、7 •••/PGN=90 - / FPC / PCF=901 分 •••/ PNG2 QPC=90 PN&A QPC五:如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的 纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪 几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.• • •解:如图所示• y= 1 PD- QH= 2、、32x12当点P 在线段 ED 的延长线上时(如图 2)过点Q 作QHL DA 交DA 延长线于点 H' • QH =- x2过点E 作EM 丄PQ 于点M3. ;3 同理可得 EP=EQ 亠 PQ • BE= PQ-PD3• PD==^x-4 y= 1 PD- QH3 2」2 x12(3)解:连接 PC 交BD 于点 (如图3)v 点P 是线段ED 中点 • EP=PD=2 • PQ=2 .. 3 ■/ DC=AB=A E tan60 = 2.3 • PC= PD 2DC 2=4PD 1• cos / DPC= =—PC 2•••/ DPC=60•••/ QPC=180 - / EPQ-Z DPC=90•/ PQ// BDPND=/ QPC=90 • PN=1 PD=12•••/ PCN M PCFPG PN QC PQ• PG=213 2 7 遗②卿长対珂六:已知:如图,在矩形ABC[中,E、F分别是边BGAB上的点,且EF=ED,EFL ED.求证:AE平分/ BAD.证明:•••四边形ABGD是矩形•••/ B=/ G=/ BAD=90 AB=GD•••/ BEF+/ BFE=90°•/ EF L ED/. / BEF+/ GED=90•/ BEF=/ CED••/ BEF=/ GDE 又v EF=ED" EBF^A CDE• BE=CD• BE=AB\/ BAE=/ BEA=45•/ EAD=45•/ BAE=/ EAD• AE平分/ BAD七:如图,矩形纸片ABGD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BC=10.F在AD边上时,如图(2).证明四边形BGE为菱形,并求出折痕GF的长.(1)当折痕的另一端F在AB边上时,如图(1).求厶EFG勺面积.解:(1)过点G作GH L AD则四边形ABGH^矩形,二GHAB=8,AH=B(=10,由图形的折叠可知△ BFG^A EFG二EGBG10, / FE(=Z B=90 ° ;/• EH=6,AE=4, / AEF+Z HEG90°, v/ AEF+Z AFE=90°, A / HEG/ AFE 又(2)当折痕的另一端EF AE 1 1EHG/ A=90° ,•••△EAF^A EHG:, A EF=5,二S A EF(= EF- EG—x 5x 10=25.EG GH 2 2(2)由图形的折叠可知四边形ABG產四边形HEGF:BG=EGAB=EH/ BGF Z EGF:EF// BG BG=Z EFGEGF= / EFG•- EF=EG• BG=EF, •四边形BGEF为平行四边形,又EF=EG •平行四边形BGEF为菱形;连结BE BEFG互相垂直平分,在Rt△ EFH中,EF=BG=10, EH=AB=8,由勾股定理可得FH=AF=6 , ••AE=16 , ••BE= J AE2AB2=8 丘,A B(=4 y[5,FG2OG2 B O=4yf5。
(完整版)八年级数学经典难题

经典难题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥C O.求证:CD=GF.(初二)2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15度求证:△PBC是正三角形.(初二)3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA 1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初二)4、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二)经典难题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)2、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.(初二)3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.(初二)4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO 相交于B、D.求证:AB=DC,BC=AD.(初三)经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:√3≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=80度,D、E分别是AB、AC上的点,∠DCA =30度,∠EBA=20度,求∠BED的度数.答案经典难题(一)4.如下图连接AC并取其中点Q,连接QN和QM,所以可得∠QMF=∠F,∠QNM=∠D EN和∠QMN=∠QNM,从而得出∠DEN=∠F。
初二数学好题难题集锦含答案

八年级下册数学难题精选分式:一:如果abc=1,求证11++a ab +11++b bc +11++c ac =1二:已知a 1+b 1=)(29b a +,则a b +ba等于多少?三:一个圆柱形容器的容积为V 立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水。
向容器中注满水的全过程共用时间t 分。
求两根水管各自注水的速度。
四:联系实际编拟一道关于分式方程2288+=xx 的应用题。
要求表述完整,条件充分并写出解答过程。
五:已知M =222y x xy -、N =2222yx y x -+,用“+”或“-”连结M 、N,有三种不同的形式,M+N 、M-N 、N-M ,请你任取其中一种进行计算,并简求值,其中x :y=5:2。
反比例函数:一:一张边长为16cm 正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E ”图案如图1所示.小矩形的长x (cm )与宽y (cm )之间的函数关系如图2所示:(1)求y 与x 之间的函数关系式; (2)“E ”图案的面积是多少?(3)如果小矩形的长是6≤x ≤12cm ,求小矩形宽的范围.二:是一个反比例函数图象的一部分,点(110)A,,(101)B,是它的两个端点.(1)求此函数的解析式,并写出自变量x的取值范围;(2)请你举出一个能用本题的函数关系描述的生活实例.三:如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数1yx的图象上,则图中阴影部分的面积等于 .四:如图11,已知正比例函数和反比例函数的图像都经过点M(-2,1),且P(1,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图12,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的OPCQ周长的最小值.五:如图,在平面直角坐标系中,直线AB 与Y 轴和X 轴分别交于点A 、点8,与反比例函数y 一罟在第一象限的图象交于点c(1,6)、点D(3,x).过点C 作CE 上y 轴于E ,过点D 作DF 上X 轴于F . (1)求m ,n 的值;(2)求直线AB 的函数解析式;勾股定理:一:清朝康熙皇帝是我国历史上对数学很有兴趣的帝王.近日,•西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,•设其面积为S ,则第一步:6S=m ;第二步:m =k ;第三步:分别用3、4、5乘以k ,得三边长”.(1)当面积S 等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.二:一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )A.第4张 B.第5张 C.第6张 D.第7张三:如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A处目测得点A与甲、乙楼顶B C、刚好在同一直线上,且A与B相距350米,若小明的身高忽略不计,则乙楼的高度是米.20乙CBA甲1020四:恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧,50km AB A =,、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和1S PA PB =+,图(2)是方案二的示意图(点A 关于直线X 的对称点是A ',连接BA '交直线X 于点P ),P 到A 、B 的距离之和2S PA PB =+. (1)求1S 、2S ,并比较它们的大小; (2)请你说明2S PA PB =+的值为最小;(3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.P图(1)图(3)图(2)五:已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE AC =. (1)求证:BG FG =;(2)若2AD DC ==,求AB 的长. 四边形:一:如图,△ACD 、△ABE 、△BCF 均为直线BC 同侧的等边三角形. (1) 当AB ≠AC 时,证明四边形ADFE 为平行四边形;(2) 当AB = AC 时,顺次连结A 、D 、F 、E 四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.DCEB GAFEFDABC二:如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF。
初二数学难题30道

初二数学难题30道1. 解析几何:在直角坐标系中,点A(2, 3),点B(1, 2),求线段AB的中点坐标。
2. 代数方程:解方程 2x + 5 = 3x 4。
3. 函数问题:给定函数 f(x) = x^2 2x + 1,求 f(3) 的值。
4. 不等式求解:解不等式 5x 2 > 3。
5. 平行四边形:已知平行四边形ABCD,AB = 6cm,BC = 8cm,求对角线AC的长度。
6. 解析几何:在直角坐标系中,点A(1, 2),点B(3, 4),求线段AB的长度。
7. 代数方程:解方程 3x^2 4x + 1 = 0。
8. 函数问题:给定函数 g(x) = 2x + 3,求 g(2) 的值。
9. 不等式求解:解不等式 2x 5 < 1。
10. 平行四边形:已知平行四边形ABCD,AB = 7cm,BC = 9cm,求对角线BD的长度。
11. 解析几何:在直角坐标系中,点A(4, 5),点B(2, 1),求线段AB的长度。
12. 代数方程:解方程 4x^2 9x + 2 = 0。
13. 函数问题:给定函数 h(x) = x^3 3x^2 + 2x,求 h(1) 的值。
14. 不等式求解:解不等式3x + 4 ≤ 7。
15. 平行四边形:已知平行四边形ABCD,AB = 8cm,BC = 10cm,求对角线AC的长度。
16. 解析几何:在直角坐标系中,点A(3, 2),点B(1, 1),求线段AB的中点坐标。
17. 代数方程:解方程 5x 3 = 2x + 7。
18. 函数问题:给定函数 f(x) = x^2 + 4x + 4,求 f(0) 的值。
19. 不等式求解:解不等式4x 8 ≥ 2。
20. 平行四边形:已知平行四边形ABCD,AB = 9cm,BC = 11cm,求对角线BD的长度。
21. 解析几何:在直角坐标系中,点A(2, 3),点B(1, 4),求线段AB的长度。
22. 代数方程:解方程 6x^2 5x 1 = 0。
八下数学试题难题及答案

八下数学试题难题及答案一、选择题(每题3分,共30分)1. 若a、b、c是三角形的三边长,则下列不等式中正确的是()。
A. a + b > cB. a + b = cC. a + b < cD. a + b ≤ c答案:A2. 计算下列算式的结果:\(\sqrt{4} + \sqrt{9} - \sqrt{16}\) 的值是()。
A. 1B. 2C. 3D. 4答案:C3. 一个数的平方是9,这个数是()。
A. 3B. -3C. 3或-3D. 0答案:C4. 一个数的立方是-8,这个数是()。
A. 2B. -2C. 1D. -1答案:B5. 计算下列算式的值:\((-2)^3\) 的结果是()。
A. -8B. 8C. -2D. 2答案:A6. 一个等腰三角形的两边长分别为3和5,那么它的周长是()。
A. 8B. 11C. 13D. 16答案:C7. 一个数的绝对值是5,这个数是()。
A. 5B. -5C. 5或-5D. 0答案:C8. 计算下列算式的值:\((-3)^2\) 的结果是()。
A. 9B. -9C. 3D. -3答案:A9. 一个数的相反数是-7,那么这个数是()。
A. 7B. -7C. 0D. 14答案:A10. 计算下列算式的值:\(\frac{1}{2} + \frac{1}{3}\) 的结果是()。
A. \(\frac{1}{5}\)B. \(\frac{5}{6}\)C. \(\frac{3}{5}\)D. \(\frac{1}{6}\)答案:B二、填空题(每题4分,共20分)1. 一个数的平方根是4,那么这个数是______。
答案:162. 一个数的立方根是-2,那么这个数是______。
答案:-83. 一个数的绝对值是7,那么这个数可以是______。
答案:7或-74. 一个等腰三角形的两边长分别为4和6,那么它的周长是______。
答案:14或165. 计算下列算式的值:\(\frac{3}{4} - \frac{1}{2}\) 的结果是______。
初中八年级的下册的数学好题难题精选.doc

八年级下册数学好题难题精选分式:111一:如果 abc=1, 求证aba1 + bc b 1 + ac c 1 =11 19b a二:已知a + b=2( a b),则a +b 等于多少三:一个圆柱形容器的容积为 V 立方米,开始用一根小水管向容器内注水, 水面高度达到容器高度一半后, 改用一根口径为小水管2倍的大水管注水。
向容器中注满水的全过程共用时间 t 分。
求两根水管各自注水的速度。
四:联系实际编拟一道关于分式方程8 8 2的应用题。
要求表述完整,条件 x 2x充分并写出解答过程。
五:已知 M = 2xy 2 、N = x 2 y 2 ,用“ +”或“-”连结 M 、N, 有三种不同的2 y x 2 y 2 x形式, M+N 、 M-N 、N-M ,请你任取其中一种进行计算,并简求值,其中 x : y=5:2。
反比例函数:一:一张边长为16cm 正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“ E”图案如图 1 所示.小矩形的长x ()与宽y()之间的函cm cm数关系如图 2 所示:(1)求 y 与 x 之间的函数关系式;(2)“ E”图案的面积是多少(3)如果小矩形的长是 6≤ x≤ 12cm,求小矩形宽的范围 .二:是一个反比例函数图象的一部分,点A(110),, B(10,1) 是它的两个端点.(1)求此函数的解析式,并写出自变量x的取值范围;(2)请你举出一个能用本题的函数关系描述的生活实例.y10 AB1O110x三:如图,⊙ A 和⊙ B 都与x 轴和y 轴相切,圆心 A 和圆心 B 都在反比例函数y 1的图象上,则图中阴影部分的面积等于. xyAO x B五:如图,在平面直角坐标系中,直线 AB 与 Y 轴和 X 轴分别交于点 A 、点 8,与反比例函数 y 一罟在第一象限的图象交于点 c(1 ,6) 、点 D(3,x) .过点 C 作 CE上 y 轴于 E ,过点 D 作 DF 上 X 轴于 F . (1) 求 m ,n 的值;(2) 求直线 AB 的函数解析式;勾股定理:一:清朝康熙皇帝是我国历史上对数学很有兴趣的帝王. 近日, ? 西安发现了他的数学专著,其中有一文《积求勾股法》 ,它对“三边长为 3、4、5 的整数倍的直角三角形,已知面积求边长” 这一问题提出了解法:“若所设者为积数 (面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数” .用现在的数学语言表述是: “若直角三角形的三边长分别为 3、4、5 的整数倍, ? 设其面积为 S ,则第一步: S=m ;第二步: m =k ;第三步:分别用 3、4、5 乘6以 k ,得三边长”.( 1)当面积 S 等于 150 时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;( 2)你能证明“积求勾股法”的正确性吗请写出证明过程.二:一张等腰三角形纸片,底边长 l5cm ,底边上的高长 22.5cm .现沿底边依次从下往上裁剪宽度均为 3cm 的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是 ( )A .第 4 张B .第 5 张C .第 6 张D .第 7 张三:如图,甲、乙两楼相距20 米,甲楼高20 米,小明站在距甲楼10 米的A 处目测得点 A 与甲、乙楼顶B、 C 刚好在同一直线上,且 A 与B 相距50米,若小3明的身高忽略不计,则乙楼的高度是米.乙C米B甲20A1020四:恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷 ( A) 和世界级自然保护区星斗山 ( B) 位于笔直的沪渝高速公路 X 同侧,AB 50km,A 、B到直线X的距离分别为 10km 和 40km ,要在沪渝高速公路旁修建一服务区 P ,向 A 、 B 两景区运送游客.小民设计了两种方案,图( 1)是方案一的示意图( AP 与直线 X 垂直,垂足为 P ), P 到 A 、 B 的距离之和S1 PA PB ,图(2)是方案二的示意图(点A关于直线X的对称点是A,连接 BA 交直线 X 于点P ), P 到 A 、 B 的距离之和 S2 PA PB .(1)求S1、S2,并比较它们的大小;(2)请你说明S2PA PB的值为最小;(3)拟建的恩施到张家界高速公路 Y 与沪渝高速公路垂直,建立如图( 3)所示的直角坐标系, B 到直线 Y 的距离为 30km ,请你在 X 旁和 Y 旁各修建一服务区P 、Q,使 P 、 A 、 B 、Q组成的四边形的周长最小.并求出这个最小值.YB BB QA AAP X P A X O P X 图( 1)图( 2)图( 3)五:已知:如图,在直角梯形 ABCD 中, AD ∥BC ,∠ ABC = °, DE ⊥ AC 于点 90交 BC 于点 G ,交 AB 的延长线于点 E ,且 AE AC . A ( 1)求证: BG FG ;( )若2 ,求 AB 的长. F 2AD DCF ,DBCGE四边形:一:如图,△ ACD 、△ ABE 、△BCF 均为直线 BC 同侧的等边三角形 .(1) 当 AB ≠AC 时,证明四边形 ADFE 为平行四边形;(2) 当 AB= AC 时,顺次连结 A 、D 、F 、E 四点所构成的图形有哪几类直接写出构成图形的类型和相应的条件 .FEDAB C二:如图,已知△ ABC 是等边三角形, D 、E 分别在边 BC 、 AC 上,且 CD=CE ,连结 DE 并延长至点 F ,使 EF=AE ,连结 AF 、BE 和 CF 。
八年级数学经典难题(答案 解析)
初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.GM=BCADMG=BC3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.PQ=(PQ=PQ=5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.PE=2PE==2CF=EF=CE===即正方形的边长为6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.解之得:经检验得:∴小口径水管速度为立方米7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.Y=上的一点,所以,所以正比例函数解析式为x,|OB×m|所以有,)=))﹣OP=(=28.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值..BE PF=x﹣xx xx x=()<时,9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.y=的图象上,﹣=12=,即PE=CE10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.xx与双曲线在双曲线××=×)))。
初二数学八年级各种经典难题例题(含答案)非常经典
1 已知一个等腰三角形两内角的度数之比为 1 : 4 ,则这个等腰三角形顶角的度数为() A. 2 0 B. 1 2 0 C. 2 0 或 1 2 0 D. 3 61.一个凸多边形的每一个内角都等于 150°,则这个凸多边形所有对角线的条数总共有 ( ) A.42 条 B.54 条 C.66 条 D.78 条3、若直线 y k1x 1 与 y k2x 4 的交点在 x 轴上,那么k1 等于() k2A . 4 B. 4 C .1 1 D . 4 41 1 4 的最小值为:( 4 x 4y)(竞赛)1 正实数 x, y 满足 xy 1 ,那么(A)1 2(B)5 8(C)1(D) 2(竞赛)在△ABC 中,若∠A>∠B,则边长 a 与 c 的大小关系是( A、a>c B、c>a C、a>1/2c) D、c>1/2a16.如图,直线 y=kx+6 与 x 轴 y 轴分别交于点 E,F.点 E 的 坐标为(-8,0),点 A 的坐标为(-6,0). (1)求 k 的值; (2)若点 P(x,y)是第二象限内的直线上的一个动点,当 点 P 运动过程中,试写出△OPA 的面积 S 与 x 的函数 关系式,并写出自变量 x 的取值范围; (3)探究:当 P 运动到什么位置时,△OPA 的面积为27 ,并说明理由. 86 、已知,如图,△ ABC 中,∠ BAC=90 °, AB=AC,D 为 AC 上一点,且∠ BDC=124°,延长 BA 到点 E,使 AE=AD,BD 的延长线交 CE 于点 F,求∠E 的 度数。
7.正方形 ABCD 的边长为 4,将此正方形置于平面直角坐标系中,使 AB 边落在 X 轴的正半 轴上,且 A 点的坐标是(1,0) 。
4 8 ①直线 y= x- 经过点 C,且与 x 轴交与点 E,求四边形 AECD 的面积; 3 3 ②若直线 l 经过点 E 且将正方形 ABCD 分成面积相等的两部分求直线 l 的解析式, ③若直线 l1 经过点 F 2 3 .0 且与直线 y=3x 平行,将②中直线 l 沿着 y 轴向上平移 个单位 3 2 交 x 轴于点 M ,交直线 l1 于点 N ,求 NMF 的面积.(竞赛奥数)如图,在△ABC 中,已知∠C=60°,AC>BC,又△ABC′、△BCA′、△CAB′ 都是△ABC 形外的等边三角形,而点 D 在 AC 上,且 BC=DC (1)证明:△C′BD≌△B′DC; (2)证明:△AC′D≌△DB′A;9.已知如图,直线 y 3x 4 3 与 x 轴相交于点 A,与直线 y 3x 相交于点 P. ①求点 P 的坐标. ②请判断 OPA 的形状并说明理由. ③动点 E 从原点 O 出发,以每秒 1 个单位的速度沿着 O→P→A 的路线向点 A 匀速运动(E 不与点 O、 A 重合) , 过点 E 分别作 EF⊥x 轴于 F, EB⊥y 轴于 B. 设运动 t 秒时, 矩形 EBOF 与△OPA 重叠部分的面积为 S.求: S 与 t 之间的函数关系式.y PB OEFAx16 多边形内角和公式等于(n - 2)×180 根据题意即(n - 2)×180=150n,求得 n=12, 多边形的对角线的条数公式等于 n(n-3)/2 带入 n=12, 则这个多边形所有对角线 的条数共有 54 条因为两直线交点在 x 轴上,则 k1 和 k2 必然不为 0,且交点处 x=-1/k1=4/k2, 所以 k1:k2=-1:41/x^4+1/4y^4=(y^4+x^4)/x^4y^4 因为 xy=1 所以 x^4y^4=1 所以 原式=y^4+x^4 因为(x^2-y^2)^2>0 且(x^2-y^2)^2=y^4+x^4-x^2y^2 大于或等于 0 所以 y^4+x^4 大于或等于 x^2y^2 即 1 所以 y^4+x^4 的最小值为 1竞赛解:在△ABC 中, ∵∠A>∠B, ∴a>b, ∵a+b>c, ∴2a>a+b>c, ∴a>12c. 故选 C.1、y=kx+6 过点 E(-8,0)则 -8K+6=0 K=3/4 2、 因点 E(-8,0) 则 OE=8 直线解析式 Y=3X/4+6 当 X=0 时,Y=6,则点 F(0,6) 因点 A(0,6),则 A、F 重合 OA=6 设点 P(X,Y) 则点 P 对于 Y 轴的高为|X| 当 P 在第二象限时,|X|=-X S=OA×|X|/2=-6X/2=-3X 3、 S=3|X| 当 S=278 时 278=± 3X X1=278/3,X2=-278/3 Y1=3X1/4+6=3/4×278/3+6=151/2 Y2=3X2/4+6=-3/4×278/3+6=-127/2 点 P1(278/3,151/2),P2(-278/3,-127/2)6 解:在△ABD 和△ACE 中, ∵AB=AC,∠DAB=∠CAE=90° AD=AE, ∴△ABD≌△ACE(SAS) , ∴∠E=∠ADB. ∵∠ADB=180° -∠BDC=180° -124° =56° , ∴∠E=56° .7(1)由题意知边长已经告诉,易求四边形的面积; (2)由第一问求出 E 点的坐标,设出 F 点,根据直线 l 经过点 E 且将正方形 ABCD 分成面积相等的两部分,其实是两个直角梯形,根据梯形面积公式,可求 出 F 点坐标,从而解出直线 l 的解析式.解:(1)由已知条件正方形 ABCD 的 边长是 4, ∴四边形 ABCD 的面积为:4×4=16; (2)由第一问知直线 y=4/3x-8/3 与 x 轴交于点 E, ∴E(2,0), 设 F(m,4), 直线 l 经过点 E 且将正方形 ABCD 分成面积相等的两部分,由图知是两个直角 梯形, ∴S 梯形 AEFD=S 梯形 EBCF= 1/2(DF+AE)•AE= 1/2(FC+EB) ∴m=4, ∵F(4,4),E(2,0), ∴直线 l 的解析式为:y=2x-4竞赛奥数 (1) 先证△ABC≌△C1BD:∵AB=C1B, ∠ABC=∠C1BD (因为都是 60° +∠ ABD), BD=BC。
八年级下册数学期中好题必刷 专题01 三角形的证明(北师大版)(解析版)
专题01 三角形的证明一、单选题1.(广东韶关·八年级期中)若三角形内一点到三边的距离相等,则这个点是()A.三条边的垂直平分线的交点B.三条中线的交点C.三条高的交点D.三条角平分线的交点【答案】D【提示】根据角平分线的判定定理到角两边距离相等的点在角平分线上,得出到到三边的距离相等的点是三角形三个角的平分线交点即可.【解答】解:根据角平分线的判定定理:到角两边距离相等的点在角平分线上,∴到到三边的距离相等的点是三角形三个角的平分线交点.故选择D.【点睛】本题考查角平分线的判定,以及角平分线交点的性质,掌握角平分线的判定与性质是解题关键.2.(湖北省直辖县级单位·八年级期中)如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB =10,S△ABD=15,则CD的长为()A.3 B.4 C.5 D.6【答案】A【提示】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用△ABD的面积列式计算即可得解.【解答】解:如图,过点D作DE⊥AB于E,∵∠C=90°,AD平分∠BAC, ∴DE=CD,∴S△ABD=12AB×DE=12×10×DE=15,解得DE=3,∴CD=DE=3,故选:A.【点睛】本题考查了三角形的面积和角平分线的性质,能熟记角平分线上的点到角两边的距离相等是解此题的关键.3.(黑龙江·牡丹江四中八年级期中)等腰三角形底边长为5,一腰上的中线把周长分成两部分的差为3cm,则腰长为()A.8cm或2cm B.2cm C.8cm D.8cm或25cm【答案】C【提示】根据题意,画出图形,然后分两种情况讨论,即可求解.【解答】解:如图,CD为△ABC的中线,AB=AC,底边BC=5cm,∴AD=BD,根据题意得:当(AD+AC+CD)-(BD+BC+CD)=3cm时,则AC-BC=3cm,∴AB=AC=8cm;当(BD+BC+CD)-(AD+AC+CD)=3cm时,则BC -AC =3cm,∴AB=AC=2cm,∵4AB AC BC +=<,不合题意,舍去; 综上所述,腰长为8cm . 故选:C 【点睛】本题主要考查了等腰三角形的性质,熟练掌握等腰三角形的两腰相等是解题的关键. 4.(山东济宁·八年级期中)如图,已知ABC 是等边三角形,点B ,C ,D ,E 在同一直线上,且CG CD =,DF DE =,则E ∠=( )A .30°B .20°C .15°D .10°【答案】C 【提示】由于△ABC 是等边三角形,那么∠B =∠1=60°,而CD =CG ,那么∠CGD =∠2,而∠1是△CDG 的外角,可得∠1=2∠2,同理有∠2=2∠E ,等量代换有4∠E =60°,即可求得∠E . 【解答】 解:如图所示,∵△ABC 是等边三角形, ∴∠B =∠1=60°, ∵CD =CG , ∴∠CGD =∠2,∴∠1=∠CGD +∠2=2∠2, ∵DF =DE , ∴∠DFE =∠E ,∴∠2=∠DFE +∠E =2∠E , ∴4∠E =60°, ∴∠E =15°. 故选:C . 【点睛】本题考查了等边三角形的性质、等腰三角形的性质、三角形外角的性质,解题的关键是利用外角性质得出∠1=2∠2,∠2=2∠E .5.(辽宁·沈阳市第四十三中学八年级期中)如图,在△ABC 中,∠C =90°,∠B =15°,AB 的垂直平分线交BC 于D ,交AB 于E ,若DB =10cm,则CD 的长为( )A .5B .3C .55D .10【答案】B 【提示】利用线段垂直平分线的性质求得AD =BD =10 cm,及∠ADC =30°,再利用含30度角的直角三角形的性质以及勾股定理即可求解. 【解答】解:∵AB 的垂直平分线交BC 于D ,交AB 于E , ∴AD =BD =10 cm,∠DBA =∠BAD =15°, ∴∠ADC =30°, ∴AC =12AD =5(cm ),CD 222210553AD AC --=cm ). 故选:B 【点睛】本题考查了含30°角的直角三角形,勾股定理,解题的关键是:熟记含30°角的直角三角形的性质,线段垂直平分线的性质及三角形的外角性质.6.(重庆市凤鸣山中学八年级期中)如图,在ABC 中,AB AC =,36A ∠=︒,AB 的中垂线DE 交AC 于点D ,交AB 于点E ,下述结论中正确的是( )A .点D 是线段AC 的中点B .AD BD BC == C .BDC 的周长等于AB CD + D .BD 平分EDC ∠【答案】B 【提示】由在△ABC 中,AB =AC ,∠A =36°,根据等边对等角与三角形内角和定理,即可求得∠ABC 与∠C 的度数,又由AB 的垂直平分线是DE ,根据线段垂直平分线的性质,即可求得AD =BD ,继而求得∠ABD 的度数,则可知BD 平分∠ABC ;可得△BCD 的周长等于AB +BC ,又可求得∠BDC 的度数,求得AD =BD =BC ,则可求得答案;注意排除法在解选择题中的应用. 【解答】解:∵36A ∠=︒,AB AC =, ∴72ABC C ∠=∠=︒, ∵DE 垂直平分AB , ∴AD BD =, ∴36ABD A ∠=∠=︒, ∴36DBC ∠=︒, ∵C DBC ∠>∠, ∴BD >CD , ∴AD >CD ,∴点D 不是线段AC 的中点,故A 错误; ∵∠DBC =36°,∠C =72°,∴∠BDC =180°−∠DBC −∠C =72°, ∴∠BDC =∠C , ∴BD =BC ,∴AD =BD =BC ,故B 正确;∴△BCD 的周长为:BC +CD +BD =BC +CD +AD =BC +AC =BC +AB ,故C 错误; ∵在△ABC 中,AB =AC ,∠A =36°,∴∠ABC=∠C=180362︒-︒=72°,∵AB的垂直平分线是DE,∴AD=BD,∴∠ABD=∠A=36°,∴∠DBC=∠ABC−∠ABD=72°−36°=36°,∴72BCD BDC∠=∠=︒,∵9054EDB ABD∠=︒-∠=︒,∴EDB BDC∠≠∠,故D错误;故选:B.【点睛】此题考查了等腰三角形的性质,线段垂直平分线的性质以及三角形内角和定理等知识.此题综合性较强,但难度不大,解题的关键是注意数形结合思想的应用,注意等腰三角形的性质与等量代换.7.(江苏苏州·八年级期中)如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=4,BD=6,则CD的长为()A.25B.5 C.2 D.213【答案】A【提示】将△BCD绕点C顺时针旋转60°得到△ACE,连接CE,DE,由旋转的性质知DC=EC、∠DCE=∠ACB=60°、BD=AE=6,即可得△DCE为等边三角形,根据∠ADC=30°得到∠ADE=90°,根据勾股定理即可得到结论.【解答】解:如图所示,将△BCD绕点C顺时针旋转60°得到△ACE,连接CE,DE,由旋转的性质知DC =EC ,∠DCE =∠ACB =60°,BD =AE =6, 则△DCE 为等边三角形, ∵∠ADC =30°, ∴∠ADE =90°, ∴AD 2+DE 2=AE 2, ∴42+DE 2=62, ∴DE =CD =25. 故选:A . 【点睛】本题考查旋转变换,熟练掌握旋转变换的性质、等边三角形的判定与性质、勾股定理,正确的作出辅助线是解题的关键.8.(福建·龙岩二中八年级期中)如图,在Rt ACB 中,90BAC ∠=︒,AD BC ⊥垂足为D .ABD △与'ADB 关于直线AD 对称,点B 的对称点是点'B ,若'14B AC ∠=︒,则B 的度数为( )A .38︒B .48︒C .52︒D .54︒【答案】D 【提示】通过折叠角相等,∠BAD +∠B ´AD +∠B ´AC =90°计算得∠BAD ,进而用余角进行计算. 【解答】解:∵∠BAD +∠B ´AD +∠B ´AC =90°,且∠BAD =∠B ´AD ,∠B ´AC =14°, ∴∠BAD =38°, ∴∠B =90°−38°=52°. 故选:D . 【点睛】本题考查折叠以及直角三角形中角的转化与计算,属于中考常考题型.9.(福建师范大学附属中学初中部八年级期中)如图,直线m 是△ABC 中BC 边的垂直平分线,点P是直线m 上的一动点,若AB =5,AC =4,BC =6,则△APC 周长的最小值是( )A .9B .10C .11D .12.5【答案】A 【提示】根据垂直平分线的性质BP PC =,所以APC △周长9AC AP PC AC AP BP AC AB =++=++≥+=. 【解答】∵直线m 是ABC 中BC 边的垂直平分线, ∴BP PC =∴APC △周长AC AP PC AC AP BP =++=++ ∵两点之间线段最短 ∴AP BP AB +≥APC ∴的周长AC AP BP AC AB =++≥+ 4AC =,5AB =∴APC △周长最小为9AC AB += 故选:A 【点睛】本题主要考查线段垂直平分线的性质定理,以及两点之间线段最短.做本题的关键是能得出AP BP AB +≥,做此类题的关键在于能根据题设中的已知条件,联系相关定理得出结论,再根据结论进行推论.10.(2022·全国·八年级期中)如图,等腰ABC 中,AB AC =,120BAC ∠=︒,AD DC ⊥于D ,点O 是线段AD 上一点,点P 是BA 延长线上一点,若OP OC =,则下列结论:①30APO DCO ∠+∠=︒;②APO DCO ∠=∠;③POC △是等边三角形;④AB OA AP =+.其中正确的是( )A.①③④B.①②③C.②③④D.①②③④【答案】A【提示】①利用等边对等角得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;④证明△OP A≌△CPE,则AO =CE,得AC=AE+CE=AO+AP.【解答】解:①如图1,连接OB,∵AB=AC,AD⊥BC,∴BD=CD,∠BAD=12∠BAC=12×120°=60°,∴OB=OC,∠ABC=90°﹣∠BAD=30°∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°,故①正确;②由①知:∠APO=∠ABO,∠DCO=∠DBO,∵点O是线段AD上一点,∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确;③∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,∴∠POC=180°﹣(∠OPC+∠OCP)=60°, ∵OP=OC,∴△OPC是等边三角形,故③正确;④如图2,在AC上截取AE=P A,∵∠P AE=180°﹣∠BAC=60°,∴△APE是等边三角形,∴∠PEA=∠APE=60°,PE=P A,∴∠APO+∠OPE=60°,∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠CPE,∵OP=CP,在△OP A和△CPE中,PA PEAPO CPEOP CP=⎧⎪∠=∠⎨⎪=⎩,∴△OP A≌△CPE(SAS),∴AO=CE,∴AC=AE+CE=AO+AP,∴AB=AO+AP,故④正确;正确的结论有:①③④,故选:A.【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质等知识,正确作出辅助线是解决问题的关键.二、填空题11.(云南·弥勒市长君实验中学八年级期中)一个等腰三角形一腰上的高与另一腰的夹角为50°,则该等腰三角形的顶角度数为__________.【答案】40°或140°【提示】本题要分情况讨论.当等腰三角形的顶角是钝角或者等腰三角形的顶角是锐角两种情况.【解答】解:①当为锐角三角形时,如图1,∵∠ABD=50°,BD⊥AC,∴∠A=90°−50°=40°,∴三角形的顶角为40°;②当为钝角三角形时,如图2,∵∠ABD=50°,BD⊥AC,∴∠BAD=90°−50°=40°,∵∠BAD+∠BAC=180°,∴∠BAC=140°∴三角形的顶角为140°,故答案为40°或140°.【点睛】本题主要考查了等腰三角形的性质及三角形内角和定理,做题时,考虑问题要全面,必要的时候可以做出模型帮助解答,进行分类讨论是正确解答本题的关键,难度适中.12.(上海市西南位育中学八年级期中)如图在△ABC中,AB=AC,BF=CD,BD=CE,∠FDE=70°,那么∠A=_____.【答案】40°【提示】先证明△BDF≌△CED,得到∠BFD=∠CDE,根据三角形的内角和与平角的定义推出∠FDE与∠B相等,再利用三角内角和定理整理即可得出结论.【解答】解:∵AB=AC,∴∠B=∠C,在△BDF和△CED中,BF CDB CBD CE⎧⎪∠∠⎨⎪⎩===,∴△BDF≌△CED(SAS),∴∠BFD=∠CDE,∴∠FDE=180°-∠CDE-∠BDF=180°-∠BFD-∠BDF=∠B,∵∠FDE=70°,∴∠B=70°,∵∠B+∠C+∠A=180°,∴∠A=40°.故答案为:40°.【点睛】本题考查了三角形全等的性质与判定.解题的关键是通过三角形全等利用角的等量代换得到∠FDE =∠B .13.(山东济宁·八年级期中)如图,AD 是ABC 中BAC ∠的角平分线,DE AB ⊥于点E ,7ABC S =△,2DE =,4AB =,则AC 长是______.【答案】3 【提示】作DF ⊥AC 于点F ,由角平分线的性质可得DF =DE =2,然后根据三角形的面积公式求解. 【解答】解:作DF ⊥AC 于点F ,∵AD 是ABC 中BAC ∠的角平分线,DE AB ⊥, ∴DF =DE =2, ∵11722AB DE AC DF ⋅+⋅=, ∴11422722AC ⨯⨯+⨯=, ∴AC =3, 故答案为:3.【点睛】本题考查了角平分线的性质,熟练掌握角平分线上的点到角两边的距离相等是解答本题的关键. 14.(北京市师达中学八年级期中)如图,BD 是∠ABC 的平分线,点P 是射线BD 上一点,PE ⊥BA 于点E ,2PE =,点F 是射线BC 上一个动点,则线段PF 的最小值为_________.【答案】2【提示】过P作PH⊥BC,根据垂线段最短得出此时PH的长最小,根据角平分线的性质得出PE=PH,再求出答案即可.【解答】解:过P作PH⊥BC,此时PH的长最小,∵BD是∠ABC的平分线,PH⊥BC,PE⊥BA,∴PE=PH,∵PE=2,∴PH=2,即PF的最小值是2,故答案为:2.【点睛】本题考查了垂线段最短和角平分线的性质,能找出当PF最小时点F的位置是解此题的关键.∠+∠+∠=______°.15.(浙江杭州·八年级期中)如图是单位长度为1的正方形网格,则123【答案】135如图,证明ABC≌AEF可得1390∠+∠=︒,根据等腰直角三角形的性质可得245∠=︒,进而即可求得答案.【解答】解:如图,在ABC与AEF 中AB AEB EBC FE=⎧⎪∠=∠⎨⎪=⎩∴ABC≌AEF∴4=3∠∠1490∠+∠=︒1390∴∠+∠=︒245∴∠=︒123135∴∠+∠+∠=︒故答案为:135【点睛】本题考查了全等三角形的性质与判定,等腰直角三角形的性质,掌握全等三角形的性质与判定是解题的关键.16.(江苏·无锡市江南中学八年级期中)已知直角三角形△ABC的三条边长分别为3,4,5,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画___条.【答案】6【提示】根据等腰三角形的性质分别利用AB,AC为底以及为腰得出符合题意的图形即可.解:如图所示:当BC 2=CC 2,AC 1=AC ,BC =BC 3,BC =CC 4,BC =CC 5,C 6A =C 6B 都能得到符合题意的等腰三角形. 故答案为:6. 【点睛】此题主要考查了等腰三角形的判定以及应用设计与作图等知识,正确利用图形分类讨论得出是解题关键.17.(福建·厦门市湖里中学八年级期中)如图,ABC 中,6AB =,4AC =,AD 平分∠BAC ,DE ⊥AB 于点E ,BF ⊥AC 于点F ,2DE =,则BF 的长为______.【答案】5 【提示】过点D 作DG AC ⊥,根据角平分线的性质可得2DG DE ==,结合图形得出6ABDS=,4ACDS=,10ABCS=,利用等面积法计算即可得出结果.【解答】解:如图所示:过点D 作DG AC ⊥,∵AD 平分BAC ∠,DG AC ⊥,DE AB ⊥,∴2DG DE ==, ∵6AB =,4AC =, ∴1·62ABDS AB DE ==,1·42ACDS AC DG ==, ∴10ABCABDACDS S S=+=,∴1·102ABCSAC BF ==, 即14?102BF ⨯=, 解得:5BF =, 故答案为:5. 【点睛】题目主要考查角平分线的性质及三角形等面积法求三角形的高,理解题意,熟练掌握运用角平分线的性质是解题关键.18.(云南·云大附中八年级期中)如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点G ,过点G 作EF //BC 交AB 于E ,交AC 于F ,过点G 作GD AC ⊥于D ,下列五个结论:①EF BE CF =+;②BE CF =;③1902BGC A ∠=︒+∠;④点G 到△ABC 各边的距离相等;⑤设GD m =,AE AF n +=,则AEF S mn =△.其中正确的结论是______(请填写序号).【答案】①③④ 【提示】①根据BG 、CG 为角平分线,且EF ∥BC ,可得△BEG 和△CFG 为等腰三角形,从而得出结论; ②G 为角平分线交点,不能得到BE 和CF 相等;③先根据角平分线的性质得出∠GBC +∠GCB =12(∠ABC +∠ACB ),再由三角形内角和定理即可得出结论;④根据角平分线定理即可得出答案;⑤连接AG,根据三角形面积公式即可得出答案. 【解答】解:①∵∠ABC 和∠ACB 的平分线相交于点G ; ∴∠EBG =∠CBG ,∠FCG =∠BCG .∵EF ∥BC ,∴∠EGB =∠CBG ,∠FGC =∠BCG ; ∴∠EBG =∠EGB ,∠FGC =∠FCG , ∴EB =EG ,FG =FC ,∴EF =EG +FG =BE +CF ,故本小题正确;②G 点是角平分线的交点,G 不一定是EF 中点,故本小题错误; ③∵∠ABC 和∠ACB 的平分线相交于点G ; ∴∠GBC +∠GCB =12ABC ACB ∠+∠()=18012A ︒-∠(),∴∠BGC =180GBC GCB ︒-∠+∠()=11180802A ︒-︒-∠()=190+2A ︒∠,故本小题正确; ④∵CG 平分∠ACB ,∴G 到AC 、BC 的距离相等; ∵BG 平分∠ABC ,∴G 到AB 、BC 的距离相等; ∴G 到三边的距离都相等,故本小题正确;⑤连接AG ,∵点G 是角平分线的交点,GD m =,AE AF n +=, ∴1122AEF S AE GD AF GD =⋅+⋅△=()12AE AF GD +⋅=12nm ,故本小题错误. 答案为:①③④【点睛】本题主要考查的是等腰三角形的性质与判定、角平分线的性质、三角形内角和定理,熟练掌握相关内容是解题的关键. 三、解答题19.(广东·深圳市福田区第二实验学校八年级期中)如图,在△ABC 中,AB =4,BC 5点D 在AB 上,且BD =1,CD =2.(1)求证:CD ⊥AB ; (2)求AC 的长. 【答案】(1)见解析 13【提示】(1)根据勾股定理逆定理证明△BCD 是直角三角形,即可得证; (2)先求得AD =AB DB -3=,在Rt △ACD 中,勾股定理求解即可. (1)证明:∵在△BCD 中,BD =1,CD =2,BC 5∴BD 2+CD 2=12+2252=BC 2, ∴△BCD 是直角三角形,且∠CDB =90°, ∴CD ⊥AB ; (2)解:∵CD ⊥AB , ∴∠ADC =90°, ∵AB =4,DB =1, ∴AD =3,在Rt △ACD 中,∵CD =2,∴AC 22AD CD +2232+13∴AC 13 【点睛】本题考查了勾股定理以及勾股定理的逆定理,掌握勾股定理是解题的关键. 20.(天津·八年级期中)如图,AC BC ⊥,BD AD ⊥,AC 与BD 交于点O ,AC BD =.(1)求证:ΔΔADB BCA ≅; (2)求证:OAB ∆是等腰三角形. 【答案】(1)见解析 (2)见解析 【提示】根据AC BC ⊥,BD AD ⊥可证角相等并等于90度,进而可证Rt ABD Rt BAC ≌; 由(1)可知Rt ABD Rt BAC ≌,进而可证OA OB =,从而可证OAB 是等腰三角形. (1) 证明:AC BC ⊥,BD AD ⊥90D C ∴∠=∠=︒,在Rt ABD △和Rt BAC 中,AC BDAB BA =⎧⎨=⎩, ∴()Rt ABD Rt BAC HL ≌. (2)∵Rt ABD Rt BAC ≌DBA CAB ∴∠=∠,OA OB ∴=,即OAB 是等腰三角形. 【点睛】本题考查直角三角形的判定,全等三角形的性质,等腰三角形的证明,能够找到判定全等所需的条件进行全等判定是解决本题的关键.21.(重庆·八年级期中)点C 、D 都在线段AB 上,且AD BC =,AE BF =,A B ∠=∠,CE 与DF 相交于点G .(1)求证:ΔΔACE BDF ≅; (2)若10CE =,4DG =,求EG 的长. 【答案】(1)见解析 (2)6 【提示】( 1)由“SAS ”可证ΔΔACE BDF ≅;( 2)由全等三角形的性质可得ACE BDF ∠=∠,可得4CG DG ==,即可求解. (1) 证明:AD BC =,AD DC BC DC ∴+=+,AC BD ∴=,在ACE ∆与BDF ∆中, AC BD A B AE BF =⎧⎪∠=∠⎨⎪=⎩, ()ΔΔACE BDF SAS ∴≅;(2)由(1)得:ΔΔACE BDF ≅,ACE BDF ∴∠=∠, 4CG DG ∴==,1046EG CE CG ∴=-=-=.【点睛】本题考查了全等三角形的判定和性质,等腰三角形的判定与性质,证明三角形全等是解题的关键. 22.(广东·珠海市文园中学八年级期中)如图,已知:E 是∠AOB 的平分线上一点,EC ⊥OB ,ED ⊥OA ,C 、D 是垂足,连接CD ,且交OE 于点F .(1)求证:OE是CD的垂直平分线;(2)若∠AOB=60°,请直接写出OE与EF之间的数量关系.【答案】(1)见解析(2)OE=4EF【提示】(1)先根据E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA得出△ODE≌△OCE,可得出OD=OC,DE=CE,OE=OE,可得出△DOC是等腰三角形,由等腰三角形的性质即可得出OE是CD的垂直平分线;(2)先根据E是∠AOB的平分线,∠AOB=60°可得出∠AOE=∠BOE=30°,由直角三角形的性质可得出OE=2DE,同理可得出DE=2EF即可得出结论.(1)证明:∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,∴DE=CE,∵OE=OE,∴Rt△ODE≌Rt△OCE,∴OD=OC,∴△DOC是等腰三角形,∵OE是∠AOB的平分线,∴OE是CD的垂直平分线;(2)解:∵OE是∠AOB的平分线,∠AOB=60°,∴∠AOE=∠BOE=30°,∵EC⊥OB,ED⊥OA,∴OE=2DE,∠ODF=∠OED=60°,∴∠EDF=30°,∴OE=4EF.【点睛】本题考查的是角平分线的性质及直角三角形的性质、等腰三角形的判定与性质,熟知以上知识是解答此题的关键.23.(山东·昌乐县教学研究室八年级期中)△ABC中,AB=AC,BD平分∠ABC交AC于点D,从点A作AE∥BC交BD的延长线于点E.(1)若∠BAC=40°,求∠E的度数;(2)点F是BE上一点,且FE=BD.取DF的中点H,请问AH⊥BE吗?试说明理由.【答案】(1)∠E=35°;(2)AH⊥BE.理由见解析.【提示】(1)根据等腰三角形两底角相等,已知顶角,可以求出底角,再根据角平分线的定义求出∠CBD的度数,最后根据两直线平行,内错角相等求出;(2)由“SAS”可证△ABD≌△AEF,可得AD=AF,由等腰三角形的性质可求解.【解答】解:(1)∵AB=AC,∴∠ABC=∠ACB,∵∠BAC=40°,∴∠ABC=12(180°-∠BAC)=70°,∵BD平分∠ABC,∴∠CBD=12∠ABC=35°,∵AE∥BC,∴∠E=∠CBD=35°;(2)∵BD平分∠ABC,∠E=∠CBD, ∴∠CBD=∠ABD=∠E,在△ABD和△AEF中,AB AEE ABDBD EF=⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△AEF(SAS),∴AD=AF,∵点H是DF的中点,∴AH⊥BE.【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明三角形全等是解题的关键.24.(广西柳州·八年级期中)如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.(1)若∠B=70°,则∠NMA的度数是_________.(2)连接MB,若AB=8cm,BC=6cm.①求△MBC的周长;②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,直接写出△PBC的周长最小值;若不存在,说明理由.【答案】(1)50°;(2)①14cm;②存在,14cm.【提示】(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;(2)①根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;②根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.【解答】解:(1)∵∠B=70°,AB=AC,∴∠B=∠C=70°,∴∠A=180°-∠B-∠C=50°,∵MN⊥AB,∴∠ANM=90°,∴∠NMA=90°-∠A=50°,故答案为:50°;(2)如图:①∵MN垂直平分AB.∴MB=MA,又∵BC=6cm,AC=BC=8cm,∴△MBC的周长是MB+MC+BC= MA+MC+BC=AC+BC=14(cm);②当点P与M重合时,△PBC周长的值最小,理由:∵PB+PC=P A+PC,P A+PC≥AC,∴P与M重合时,P A+PC=AC,此时PB+PC最小,∴△PBC周长的最小值=AC+BC=8+6=14(cm).【点睛】本题主要考查了轴对称的性质,等腰三角形的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,熟记性质是解题的关键.25.(江苏盐城·八年级期中)如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高.(1)求证:AD垂直平分EF;(2)若AB+AC=10,S△ABC=15,求DE的长.【答案】(1)见解析;(2)3DE(1)由角平分线的性质得DE =DF ,再根据HL 证明Rt △AED ≌Rt △AFD ,得AE =AF ,从而证明结论; (2)根据DE =DF ,得111++()15222ABDACDS SAB ED AC DF DE AB AC ==+=,代入计算即可. 【解答】(1)证明:∵AD 是△ABC 的角平分线,DE 、DF 分别是△ABD 和△ACD 的高, ∴DE =DF ,在Rt △AED 与Rt △AFD 中,AD ADDE DF =⎧⎨=⎩, ∴Rt △AED ≌Rt △AFD (HL ), ∴AE =AF , ∵DE =DF ,∴AD 垂直平分EF ; (2)解:∵DE =DF , ∴111++()15222ABDACDSSAB ED AC DF DE AB AC ==+=, ∵AB +AC =10, ∴DE =3. 【点睛】本题考查了全等三角形的判定与性质,角平分线的性质,解题的关键是掌握这些知识点.26.(湖北武汉·八年级期中)如图,在△ABC 中,∠ACB =90°,∠A =30°,D 为AB 上一点,以CD 为边在CD 右侧作等边△CDE .(1)如图1,当点E 在边AC 上时,求证:DE =AE ;(2)如图2,当点E 在△ABC 内部时,猜想ED 和EA 数量关系;(3)当点E 在△ABC 外部时,过点E 作EH ⊥AB 点H ,EF ∥AB ,CF =2,AH =3.直接写出AB 的长为 .【答案】(1)见解析;(2)ED =EA ,理由见解析;(3)16(1)根据等边三角形的性质、三角形的外角的性质得到∠EDA=∠A,根据等腰三角形的判定定理证明;(2)取AB的中点O,连接CO、EO,分别证明△BCD≌△OCE和△COE≌△AOE,根据全等三角形的性质证明;(3)取AB的中点O,连接CO、EO、EA,根据(2)的结论得到△CEF≌△DCO,根据全等三角形的性质解答.【解答】(1)证明:∵△CDE是等边三角形,∴∠CED=∠DCE=60°,∴∠EDA=60°﹣∠A=30°,∵∠A=30°,∴∠EDA=30°,∴∠EDA=∠B,∴DE=EA;(2)结论:ED=EA,理由:如图2中,取AB的中点O、EO,∵∠ACB=90°,∠BAC=30°,∴∠B=60°,OC=OB,∴△BCO为等边三角形,∴CB=CO=BO=AO,∵△CDE是等边三角形,∴∠BCD=∠OCE,在△BCD和△OCE中,CB COBCD OCECD CE=⎧⎪∠=∠⎨⎪=⎩,∴∠COE=∠B=60°,∴∠AOE=60°,在△COE和△AOE中,OC OACOE AOEOE OE=⎧⎪∠=∠⎨⎪=⎩,∴△COE≌△AOE(SAS),∴EC=EA,∴ED=EA;(3)解:如图3中,取AB的中点O、连接EO,AE,由(2)得△BCD≌△OCE,∴∠COE=∠B=60°,∴∠AOE=60°,同法可得△COE≌△AOE,∴EC=EA,∴ED=EA,∵EH⊥AB,∴DH=AH=5,∵EF∥AB,∴∠F=180°﹣∠B=120°,∵∠FCD=∠FCE+60°=∠CDB+60°,∴∠FCE=∠CDB,在△CEF和△DCO中,F CODECF ODCCE CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴CF=OD=2,∴OA=OD+AD=2+6=8,∴AB=2OA=16.【点睛】本题主要考查了等边三角形判定和性质,全等三角形的判定和性质,熟练掌握等边三角形判定和性质定理,全等三角形的判定和性质定理是解题的关键.27.(四川·成都外国语学校八年级期中)如图1,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,∠ACE=45°.(1)求证:△AEF≌△CEB.(2)若G在BC的延长线上,连接GA,若GA=GB,求证:AC平分∠DAG.(3)如图2,在(2)的条件下,H为AG的中点,连接DH交AC于M,连接EM、ED,若S△EMC=4,∠BAD =15°,求AM的长.【答案】(1)见解析(2)见解析(3)6【提示】(1)先判断出AE=CE,再利用等角的余角相等判断出∠EAF=∠ECB,进而判断出AEF CEB△≌△,即可得出结论;(2)先利用三角形外角的性质得出∠AEF=45︒+∠CAD,进而得出∠B=45︒+∠CAD,而∠B=∠BAG,得出∠BAG=45︒+∠CAD,而∠BAG=45︒+∠CAG,即可得出结论;(3)先判断出ADH是等边三角形,进而利用含30度角的直角三角形的性质判断出AM=3CM,进而求出ACM的面积,即可求出AE,进而求出AC,即可得出结论.(1)证明:∵CE⊥AB,∴∠AEC =∠BEC =90°, ∵∠ACE =45°, ∴∠CAE =45°=∠ACE , ∴AE =CE , ∵AD ⊥BC , ∴∠ADC =90°, ∴∠ECB +∠CFD =90°, ∵∠CFD =∠AFE , ∴∠ECB +∠AFE =90°, ∵∠EAF +∠AFE =90°, ∴∠EAF =∠ECB , 在AEF 和CEB 中,90EAF ECB AE CE AEF CEB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴AEF CEB △≌△(ASA ); (2)∵AEF CEB △≌△, ∴∠AFE =∠B ,∵∠AFE =∠ACE +∠CAD =45°+∠CAD , ∴∠B =45°+∠CAD , ∵AG =BG , ∴∠B =∠BAG , ∴∠BAG =45°+∠CAD ,∵∠BAG =∠CAE +∠CAG =45°+∠CAG , ∴∠CAD =∠CAG , ∴AC 平分∠DAG ; (3)∵∠BAD =15°,∠CAE =45°, ∴∠CAD =∠CAE ﹣∠BAD =30°, ∵∠CAD =∠CAG ,∴∠DAG=2∠CAD=60°,在Rt△ADG中,点H是AG的中点,∴DH=AH,∴△ADH是等边三角形,∴∠ADH=60°,AD=AH,∵∠CAD=∠CAG,∴AC⊥DH,即:∠AMD=∠DMC=90°∵∠ADC=90°,∴∠CDM=30°,在Rt△DMC中,DM,在Rt△AMD中,AM=3CM, ∴S△AEM=3S△CEM=3×4=12,∴S△ACE=S△CEM+S△AEM=16,∵∠AEC=90°,AE=CE,∴S△ACE=12AE2=16,∴AE=∴AC=8,∴AM+CM=8,∵AM=3CM,∴3CM+CM=8,∴CM=2,∴AM=3CM=6.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等角的余角相等,等边三角形的判定和性质,三角形外角的性质,含30度角的直角三角形的性质,求出AE是解本题的关键.。
2020-2021学年人教版八年级数学下册第18章平行四边形解答题典型必练(一)
人教版八年级数学下册第18章《平行四边形》解答题典型必练(一)1.如图,点E在▱ABCD内部,AF∥BE,DF∥CE.(1)求证:△BCE≌△ADF;(2)设▱ABCD的面积为6,求四边形AEDF面积.2.如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足AE=CG,AH=CF.(1)求证:四边形EFGH是平行四边形;(2)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.3.如图,在正方形ABCD中,AC,BD相交于点O,E,F分别在OA,OD上,∠ABE =∠DCF.(1)求证:△ABE≌△DCF.(2)若BC=4,AE=3,求BE的长.4.如图,在正方形ABCD中,E是边AB上的一动点(不与点A,B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)直接写出GF与GC的数量关系:;(2)用等式表示线段BH与AE的数量关系,并证明.5.四边形ABCD是矩形,点P在边CD上,∠PAD=30°,点G与点D关于直线AP对称,连接BG.(1)如图,若四边形ABCD是正方形,求∠GBC的度数;(2)连接CG,设AB=a,AD=b,探究当∠CGB=120°时,a与b的数量关系.6.如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE 关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,(1)当∠ADE=15°时,求∠DGC的度数;(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;(3)如图2,当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论.7.如图,在正方形ABCD中,点E为线段BC上一动点(点E不与点B、C重合),点B关于直线AE的对称点为F,作射线EF交CD于H,连接AF.(1)求证:AF⊥EH;(2)连接AH,小王通过观察、实验,提出猜想:点E在运动过程中,∠EAH的度数始终保持不变.你帮助小王求出∠EAH的度数.8.如图,正方形ABCD中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接FC.(1)求证:∠FBC=∠CDF;(2)作点C关于直线DE的对称点G,连接CG,FG,猜想线段DF,BF,CG之间的数量关系,并证明你的结论.9.已知AP为正方形ABCD外的一条射线,B′为点B关于直线AP的对称点,连接B′D.如图1所示.(1)如果∠BAP=20°,求∠ADB′的度数的大小.(2)如图2所示,M为射线B′B上一点,且∠BMC=135°.①求证:BB′=CM.②求证:CM∥B′D.10.在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.(1)依题意补全图1;图2;(2)若∠PAB=25°,求∠ADF的度数;(3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间数量关系,并证明.11.如图,已知正方形ABCD边长为1,点P是射线AD的上的一个动点,点A关于直线BP的对称点是点Q,设AP=x.(1)求当D,Q,B三点在同一直线上时对应的x的值.(2)当△CDQ为等腰三角形时,求x的值.12.在正方形ABCD中,点P是射线CB上一个动点.连接PA,PD,点M,N分别为BC,AP的中点,连接MN交PD于点Q.(1)如图1,当点P在线段CB的延长线上时,请判断△QPM的形状,并说明理由.(2)如图2,正方形的边长为4,点P'与点P关于直线AB对称,且点P'在线段BC上.连接AP',若点Q恰好在直线AP'上,求P'M的长.13.如图,在边长为6的正方形ABCD中,G是边BC的中点,点C关于直线DG的对称点为F,连接GF并延长交AB于点E,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:△ADE≌△FDE;(2)求AE的长;(3)求BH的长;14.如图,经过正方形ABCD的顶点A在其外侧作直线AP,点B关于直线AP的对称点为E,连接BE、DE,其中DE交直线AP于点F.(1)依题意补全图1.(2)若∠PAB=30°,求∠ADF的度数.(3)如图,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.15.在小学,我们已经初步了解到,正方形的每个角都是90°,每个边都是相等.如图,在正方形ABCD外侧作直线AQ,点D关于直线AQ的对称点为E,连接DE、BE,BE交AD于点F,若∠QAD=15°.(1)求∠ABE的度数;(2)若AB=6,求AF的长.参考答案1.(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ABC+∠BAD=180°,∵AF∥BE,∴∠EBA+∠BAF=180°,∴∠CBE=∠DAF,同理得∠BCE=∠ADF,在△BCE和△ADF中,,∴△BCE≌△ADF(ASA);(2)解:∵点E在▱ABCD内部,,∴S△BEC+S△AED=S▱ABCD由(1)知:△BCE≌△ADF,∴S△BCE=S△ADF,∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=S,▱ABCD ∵▱ABCD的面积为6,∴四边形AEDF的面积为3.2.(1)证明:∵四边形ABCD是矩形,∴∠A=∠C.∴在△AEH与△CGF中,,∴△AEH≌△CGF(SAS),∴EH=GF,同理证得△EBF≌△GDH,则EF=GH,∴四边形EFGH是平行四边形;(2)解:四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.理由如下:作G关于BC的对称点G′,连接EG′,可得EG′的长度就是EF+FG的最小值.连接AC,∵CG′=CG=AE,AB∥CG′,∴四边形AEG′C为平行四边形,∴EG′=AC.在△EFG′中,∵EF+FG′>EG′=AC,∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.3.证明:(1)∵四边形ABCD是正方形,∴AB=CD,∠BAE=∠CDF=45°,∵∠ABE=∠DCF,在△ABE与△DCF中,,∴△ABE≌△DCF(ASA);(2)∵四边形ABCD是正方形,∴AB=BC,OA=OB=OC=OD,∠ABC=∠AOB=90°,∵BC=4,∴AB=4,∴AC=,∴OA=OB=4,∵AE=3,∴OE=OA﹣AE=4﹣3=1,在Rt△BOE中,BE=.4.证明:(1)如图1,连接DF,∵四边形ABCD是正方形,∴DA=DC,∠A=∠C=90°,∵点A关于直线DE的对称点为F,∴△ADE≌△FDE,∴DA=DF=DC,∠DFE=∠A=90°,∴∠DFG=90°,在Rt△DFG和Rt△DCG中,,∴Rt△DFG≌Rt△DCG(HL),∴GF=GC;(2)BH=AE,理由是:证法一:如图,在线段AD上截取AM,使AM=AE,∵AD=AB,∴DM=BE,由(1)知:∠ADE=∠EDF,∠FDG=∠GDC,∵∠ADC=90°,∴∠ADE+∠EDF+∠FDG+∠GDC=90°,∴2∠EDF+2∠FDG=90°,∴∠EDF+∠FDG=45°,即∠EDG=45°,∵EH⊥DE,∴∠DEH=90°,∴△DEH是等腰直角三角形,∴∠AED+∠BEH=∠AED+∠ADE=90°,DE=EH,∴∠ADE=∠BEH,在△DME和△EBH中,,∴△DME≌△EBH(SAS),∴EM=BH,Rt△AEM中,∠A=90°,AM=AE,∴EM=AE,∴BH=AE;证法二:如图,过点H作HN⊥AB于N,∴∠ENH=90°,由方法一可知:DE=EH,∠1=∠NEH,在△DAE和△ENH中,,∴△DAE≌△ENH(AAS),∴AE=HN,AD=EN,∵AD=AB,∴AB=EN=AE+BE=BE+BN,∴AE=BN=HN,∴△BNH是等腰直角三角形,∴BH=HN=AE.5.解:(1)连接DG,交AP于点E,连接AG,如图1,∵点G与点D关于直线AP对称,∴AP垂直平分DG,∴AD=AG.∵在△ADG中,AD=AG,AE⊥DG,∴∠PAG=∠PAD=30°,又∵在正方形ABCD中,AD=AB,∠DAB=∠ABC=90°,∴AG=AB,∠GAB=∠DAB﹣∠PAD﹣∠PAG=30°,∴在△GAB中,∠ABG=∠AGB==75°,∴∠GBC=∠ABC﹣∠ABG=15°;(2)连接DG,AG.由(1)可知,在△ADG中,AD=AG,∠DAG=∠PAD+∠PAG=60°,∴△ADG是等边三角形,∴DG=AG=AD,∠DAG=∠ADG=∠DGA=60°,又∵在矩形ABCD中,AB=DC,∠DAB=∠ADC=∠ABC=90°,∴∠DAB﹣∠DAG=∠ADC﹣∠ADG,即∠GAB=∠GDC=30°,∴△GAB≌△GDC(SAS),∴GB=GC.当∠CGB=120°时,点G可能在矩形ABCD的内部或外部.若点G在矩形ABCD的内部,∵在△BGC中,GB=GC,∠CGB=120°,∴∠GBC==30°,∴∠GBA=∠ABC﹣∠GBC=90°﹣30°=60°,在△ABG中,∠AGB=180°﹣∠GAB﹣∠GBA=90°,∴a=b,若点G在矩形ABCD的外部,在△BGC中,∠GBC=30°,∴∠ABG=120°,又∵∠GAB=30°,∴∠AGB=180°﹣30°﹣120°=30°.∴BA=BG,过点B作BH⊥AG,垂足为H,∴AH=AG=b.在Rt△ABH中,∠AHB=90°,∠HAB=30°,∴cos∠HAB==,∴a=b,在Rt△ADP中,∠ADP=90°,∠PAD=30°,∴tan∠PAD==,∴DP=b.所以无论点G在矩形ABCD内部还是点G在矩形ABCD外部,都有DP≤DC,均符合题意.综上,当∠CGB=120°时a与b的数量关系为a=b或a=b.6.解:(1)∵∠ADE=15°,∴∠FDE=15°,∠CDF=60°.∵DC=AD=DF,∴∠CFD=60°.又∠CFD=∠DGC+∠FDE=15°+∠DGC,∴∠DGC=45°;(2)不变,理由如下:∵△ADE与△FDE关于DE对称,∴∠AGD=∠DGF.设∠ADE=x,可得∠FDE=x,∠CDF=90°﹣2x,∵DC=AD=DF,∴∠CFD=45°+x.又∠CFD=∠DGC+∠FDE=x+∠DGC,∴∠DGC=45°;(3)四边形AGFM是正方形;理由:∵∠DAE=∠DFE=90°,点M为DE的中点,∴AM=FM=DM=DE,∴∠ADM=∠DAM,∠MDF=∠DFM,∴∠AME=∠EMF=2∠ADM=2∠MDF=45°,∴∠AMF=90°,∵∠MGF=45°,∴FM=FG,在△ADG与△FDG中,,∴△ADG≌△FDG(SAS),∴AG=FG,∴AM=MF=FG=AG,∵∠AMF=90°,∴四边形AGFM是正方形.7.解:(1)证明:∵点B关于直线AE的对称点为F,∴AB=AF,BE=EF,又∵AE=AE,∴△ABE≌△AFE(SSS),∴∠AFE=∠B=90°,∴AF⊥EH;(2)连接AH,如图:由(1)得AB=AF,AF⊥EH,∴AF=AD,∠D=∠AFH=90°,AH=AH,∴△AFH≌△ADH(HL),∴∠FAH=∠DAH,又∵∠BAE=∠FAE,在正方形ABCD中,∠BAD=90°,∴∠EAH=45°.8.解:(1)∵ABCD为正方形,∴∠DCE=90°.∴∠CDF+∠E=90°,又∵BF⊥DE,∴∠FBC+∠E=90°,∴∠FBC=∠CDF(2)如图所示:在线段FB上截取FM,使得FM=FD.∵∠BDC=∠MDF=45°,∴∠BDM=∠CDF,∴∠CFE=∠FCD+∠CDF=∠DBM+∠BDM=∠DMF=45°,∴∠EFG=∠EFC=45°,∴∠CFG=90°,∵CF=FG,∴CG=CF,∴BM=CG,∴BF=BM+FM=CG+DF.补充方法:连接GM,证明四边形BMGC是平行四边形即可.9.(1)解:连接AB',如图1,∵B′为点B关于直线AP的对称点,∴AB=AB',∴∠BAP=∠B'AP=20°,∵四边形ABCD是正方形,∴AB=AD,∴AB'=AD,∴∠AB'D=∠ADB',∵∠B'AD=∠B'AB+∠BAD=90°+40°=130°,∴∠ADB'=25°.(2)证明:①设B'D与AP的交点为N,连接AB',BN.由(1)得:∠1=∠2,∠3=∠4,∵∠1+∠2+∠3+∠4=90°,∴∠1+∠3=45°,∴∠B'NP=45°,∵∠B'NP=∠BNP,∴∠BNP=45°,则△BNB'为等腰直角三角形.∴BB'=BN,∠ANB=135°,∴∠BMC=∠ANB=135°,∵∠5+∠6=45°,∠4+∠5=45°,∴∠4=∠6.在△ANB和△BMC中,,∴△ANB≌△BNC(AAS),∴BN=CM,∴BB'=CM;②∵△BB'N为等腰直角三角形,∴∠NB'B=45°,∴∠NB'B=∠7=45°,∴B'D∥MC.10.解:(1)如图1、图2所示:(2)连接AE,如图3所示:则∠PAB=∠PAE=25°,AE=AB=AD,∴∠AED=∠ADF,∵四边形ABCD是正方形,∴∠BAD=90°,∴∠EAD=90°+25°+25°=140°,∴∠ADF=(180°﹣∠EAD)=20°;(3)连接AE、BF、BD,如图4所示:则EF=BF,AE=AB=AD,∴∠ABF=∠AEF=∠ADF,∴∠BFD=∠BAD=90°,∴BF2+FD2=BD2,∴EF2+FD2=AB2+AD2=2AB2,即EF2+FD2=2AB2.11.解:(1)连接DB,若Q点落在BD上,由AP=x,则PD=1﹣x,PQ=x.∵∠PDQ=45°,∴PD=PQ,即1﹣x=x.∴x=﹣1.(2)①如图2,连接BQ1、CQ1,作PQ1⊥BQ1交AD于P,过点Q1,作EF⊥AD于E,交BC于F.∵△BCQ1为等边三角形,正方形ABCD边长为1,∴Q1F=Q1E=.在四边形ABPQ1中,∵∠ABQ1=30°,∴∠APQ1=150°,∴△PEQ1为含30°的直角三角形,∴PE=Q1E=,∵AE=,∴x=AP=AE﹣PE=2﹣.②如图3,连接BQ2,AQ2,过点Q2作PG⊥BQ2,交AD于P,连接BP,过点Q2作EF⊥CD于E,交AB于F.∵EF垂直平分CD,∴EF垂直平分AB,∴AQ2=BQ2.∵AB=BQ2,∴△ABQ2为等边三角形.在四边形ABQP中,∵∠BAD=∠BQP=90°,∠ABQ2=60°,∴∠ABP=30°,∴x=AP=.③如图4,连接BQ1,CQ1,BQ3,CQ3,过点Q3作BQ3⊥PQ3,交AD的延长线于P,连接BP,过点Q1,作EF⊥AD于E,此时Q3在EF上,不妨记Q3与F重合.∵△BCQ1为等边三角形,△BCQ3为等边三角形,BC=1,∴Q1Q2=,Q1E=,∴EF=.在四边形ABQ3P中,∵∠ABF=∠ABC+∠CBQ3=150°,∴∠EPF=30°,∴EP=EF=.∵AE=,∴x=AP=AE+PE=+2.综上所述,△CDQ为等腰三角形时x的值为2﹣,,2+.12.解:(1)△QPM是等腰三角形,理由如下:延长BC至E,使CE=BP,连接AE,∵PB=CE,∴PB+BC=CE+BC,∴CP=BE,∵四边形ABCD是正方形,∴AB=CD,∠ABC=∠DCB=90°,在△DCP和△ABE中,∴△DCP≌△ABE(SAS)∴∠DPC=∠AEB,∵M是BC的中点,∴MB=MC,∴MB+BP=MC+CE,∴MP=ME,∴M是PE的中点,又∵N是AP的中点,∴MN∥AE,∴∠PMN=∠AEB,∴∠PMN=∠DPC,∴QP=QM,∴△QPM是等腰三角形;(2)延长BC至E,使CE=BP,连接AE,∵M是BC的中点,BC=4,∴BM=CM=2,又∵BP=CE,∴BM+BP=CM+CE,即PM=ME,∴M是PE的中点,且点N是AP中点,13.证明:(1)如图1,连接DF,∵四边形ABCD是正方形,∴DA=DC,∠A=∠C=90°,∵点C关于直线DG的对称点为F,∴△DCG≌△DFG,∴DC=DF=DA,∠DFG=∠C=90°,∴∠DFE=90°,在Rt△ADE和Rt△FDE中,∵,∴Rt△ADE≌Rt△FDE(HL);(2)∵G是边BC的中点,BC=6,∴CG=BG=FG=3,∵△ADE≌△FDE,∴AE=EF,设AE=x,则BE=6﹣x,EG=EF+FG=x+3,∵在Rt△EBG中,BE2+BG2=EG2,∴(6﹣x)2+32=(x+3)2,解得x=2,∴AE=2;(3)如图2,过点H作HN⊥AB于点N,∴∠ENH=90°,由(1)知∠ADE=∠EDF,∠FDG=∠CDG,∵∠ADC=90°,∴2∠EDF+2∠FDG=90°,∴∠EDF+∠FDG=45°,即∠EDG=45°,∵EH⊥DE,∴∠DEH=90°,△DEH是等腰直角三角形,∴DE=EH,∠ADE=∠NEH,在△DAE和△ENH中,∵,∴△DAE≌△ENH(AAS),∴AE=HN,AD=EN,∵AD=AB,∴AB=EN=AE+BE=BE+BN,∴AE=BN=HN,∴△BNH是等腰直角三角形,∴BH=.14.解:(1)如图1、图2所示:(2)连接AE,如图3所示:则∠PAB=∠PAE=30°,AE=AB=AD,∴∠AED=∠ADF,∵四边形ABCD是正方形,∴∠BAD=90°,∴∠EAD=90°+30°+30°=150°,∴∠ADF=(180°﹣∠EAD)=15°;(3)连接AE、BF、BD,如图4所示:则EF=BF,AE=AB=AD,∴∠ABF=∠AEF=∠ADF,∴∠BFD=∠BAD=90°,∴BF2+FD2=BD2,∴EF2+FD2=AB2+AD2=2AB2,即EF2+FD2=2AB2.15.解:(1)连接AE,如图1所示:∵点D关于直线AQ的对称点为E,∴AE=AD,AQ垂直平分DE,∴∠EAQ=∠QAD=15°,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠BAE=15°+15°+90°=120°,AE=AB,∴∠ABE=(180°﹣120°)=30°;(2)作A⊥BE于M,如图2所示:则∠AMB=∠AMF=90°,∴AM=AB=3,∵∠1=90°﹣30°=60°,∴∠2=90°﹣60°=30°,∴∠FAM=15°+30°=45°,∴△AMF是等腰直角三角形,∴AF=AM=3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级下册数学好题难题精选
分式:
一:如果abc=1,求证
11++a ab +11++b bc +11
++c ac =1
二:已知a 1+b 1=
)(29b a +,则a b +b a
等于多少?
三:一个圆柱形容器的容积为V 立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水。
向容器中注满水的全过程共用时间t 分。
求两根水管各自注水的速度。
四:联系实际编拟一道关于分式方程228
8+=x
x 的应用题。
要求表述完整,条件
充分并写出解答过程。
五:已知M =2
22y
x xy
-、N =22
22y x y x -+,用“+”或“-”连结M 、N,有三种不同的
形式,M+N 、M-N 、N-M ,请你任取其中一种进行计算,并简求值,其中x :y=5:
2。
反比例函数:
一:一张边长为16cm正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E”图案如图1所示.小矩形的长x(cm)与宽y(cm)之间的函数关系如图2所示:
(1)求y与x之间的函数关系式;
(2)“E”图案的面积是多少?
(3)如果小矩形的长是6≤x≤12cm,求小矩形宽的范围.
二:是一个反比例函数图象的一部分,点(110)
A,,(101)
B,是它的两个端点.(1)求此函数的解析式,并写出自变量x的取值范围;
(2)请你举出一个能用本题的函数关系描述的生活实例.
三:如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比
例函数
1
y
x
的图象上,则图中阴影部分的面积等于 .
A
B
O x
y
1
1 10
10 A
B
O x
y
五:如图,在平面直角坐标系中,直线AB 与Y 轴和X 轴分别交于点A 、点8,与反比例函数y 一罟在第一象限的图象交于点c(1,6)、点D(3,x).过点C 作CE 上y 轴于E ,过点D 作DF 上X 轴于F . (1)求m ,n 的值;
(2)求直线AB 的函数解析式;
勾股定理:
一:清朝康熙皇帝是我国历史上对数学很有兴趣的帝王.近日,•西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,•设其
面积为S ,则第一步:6
S
=m ;第二步:m =k ;第三步:分别用3、4、5乘以k ,
得三边长”.
(1)当面积S 等于150时,请用康熙的“积求勾股法”求出这个直角三角形
的三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
二:一张等腰三角形纸片,底边长l5cm ,底边上的高长22.5cm .现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A .第4张
B .第5张
C .第6张
D .第7张
三:如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A 处目测得点A 与甲、乙楼顶B C 、刚好在同一直线上,且A 与B 相距3
50
米,若小明的身高忽略不计,则乙楼的高度是 米.
四:恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧,50km AB A =,、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和1S PA PB =+,图(2)是方案二的示意图(点A 关于直线X 的对称点是A ',连接BA '交直线X 于点P ),P 到A 、B 的距离之和2S PA PB =+. (1)求1S 、2S ,并比较它们的大小; (2)请你说明2S PA PB =+的值为最小;
(3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.
P
图(1)
图(3)
图(2)
五:已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE AC =.
(1)求证:BG FG =;
(2)若2AD DC ==,求AB 的长.
四边形:
一:如图,△ACD 、△ABE 、△BCF 均为直线BC 同侧的等边三角形. (1) 当AB ≠AC 时,证明四边形ADFE 为平行四边形; (2) 当AB = AC 时,顺次连结A 、D 、F 、E 四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.
二:如图,已知△ABC 是等边三角形,D 、E 分别在边BC 、AC 上,且CD=CE ,连结DE 并延长至点F ,使EF=AE ,连结AF 、BE 和CF 。
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明。
(2)判断四边形ABDF 是怎样的四边形,并说明理由。
(3)若AB=6,BD=2DC ,求四边形ABEF 的面积。
三:如图,在△ABC 中,∠A 、∠B 的平分线交于点D ,DE ∥AC 交BC 于点E ,DF
∥BC 交AC 于点F .
(1)点D 是△ABC 的________心; (2)求证:四边形DECF 为菱形.
D
C
E
B G
A F
E
F D
A
B C
四:在矩形ABCD 中,点E 是AD 边上一点,连接BE ,且∠ABE =30°,BE =DE ,连接BD .点P 从点E 出发沿射线ED 运动,过点P 作PQ ∥BD 交直线BE 于点Q .
(1) 当点P 在线段ED 上时(如图1),求证:BE =PD +
3
3
PQ ; (2)若 BC =6,设PQ 长为x ,以P 、Q 、D 三点为顶点所构成的三角形面积为y ,求y 与 x 的函数关系式(不要求写出自变量x 的取值范围);
(3)在②的条件下,当点P 运动到线段ED 的中点时,连接QC ,过点P 作PF ⊥QC ,垂足为F ,PF 交对角线BD 于点G (如图2),求线段PG 的长。
五:如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的
纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图...
,并写出它们的周长.
2
2
2
六:已知:如图,在矩形ABCD 中,E 、F 分别是边BC 、AB 上的点,且EF=ED,EF ⊥ED.
求证:AE 平分∠BAD.
(第23题)
E D
B
A
F
七:如图,矩形纸片ABCD 中,AB =8,将纸片折叠,使顶点B 落在边AD 的E 点上,BG =10.
(1)当折痕的另一端F 在AB 边上时,如图(1).求△EFG 的面积.
(2)当折痕的另一端F 在AD 边上时,如图(2).证明四边形BGEF 为菱形,并求出折痕GF 的长.
H
A
B
C
D
E F G
八:(1)请用两种不同的方法,用尺规在所给的两个矩形中各作一个
不为正方形的菱形,且菱形的四个顶点都在矩形的边上.(保留作图痕迹) (2)写出你的作法.
九:如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C 不重合),
点E 在射线BC 上,且PE=PB .
(1)求证:① PE=PD ; ② PE ⊥PD ;
(2)设AP =x , △PBE 的面积为y .
① 求出y 关于x 的函数关系式,并写出x 的取值范围; ② 当x 取何值时,y 取得最大值,并求出这个最大值.
图(2)
A
B
C
D
E F
G H (A)
(B)A B
C
D E F G
图(1)
A
B C
P D
E
一:如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
(2)将原题中正方形改为矩形(如图4—6),且AB=a,BC=b,CE=ka, CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结DG、BE,且a=3,b=2,k=1
2
,求22
BE DG
+的值.。
