第12讲 相关样本(多样本)非参数检验
多配对样本的非参数检验

多配对样本的非参数检验
多配对样本的非参数检验室通过分析多组配对样本数据,推断样本来自的多个总体的中位数或分布是否存在显著差异。
例如手机乘客对多家航空公司是否满意的数据,分析航空公司的服务水平是否存在差异等等。
多配对样本的Friedman检验
多配对样本的Fiedman检验是利用秩实现对多个总体分布是否存在显著差异的非参数检验方法,其零假设是多个配对样本来自的总体的分布无显著差异。
(思想见参考书)
多配对样本的Cochran Q检验
多配对样本的Cochran Q检验通过对多个配对样本的分析,推断样本来自的多个总体的分布是否存在显著差异,其零假设是多个配对样本来自的多个总体的分布无显著差异。
(思想见参考书)
多配对样本的Kendall协同系数检验
多配对样本的Kendall协同系数检验也是一种多配对样本的非参数检验方法,与Friedman 检验方法相结合,可方便地实现对评判者的评判标准是否一致的分析。
其零假设是评判者的评判标准不一致。
(思想见参考书)。
非参检验PPT课件

Npar
两均值比较相 独关 立样 样本 本中符 符秩数号 号和检等检检验级验验法检法法(((验MSMieg法adnn(i)Wnani)lWcohxiotnne)y U ) 多均值比较随完机全区随组机::弗克里 瓦德氏曼方方差差分分析析((KFrruiesdkmalaann)d Wallis H )
非参数检验
1
非参数检验是与参数检验相对应的,参数 检验指的是在总体分布已知,满足某些 假定条件(独立性、方差齐性等),检验的 数据一般为连续数据的情况下进行的检 验。如果有些条件不能满足, 则采用非参 数检验,可以根据实际情况采用如下一 些方法进行检验, 这些检验都是在 Nonparametric tests菜单项里执行。
9
练习
• 输入以下数据并检验两组数据的差异性:
– 甲:12,14,15,12,21,31,26,21 – 乙:21,32,15,21,12,14,12,15
• 1.假设上述配对样本资料 • 2.假设上述资料不是配对样本资料
10
2020/1/1
11
3
两独立样本非参数检验例题
设有两种安眠药,考虑它们的治疗效果(失眠者服用之 后睡眠延长的小时数),现将20名患者分成两组,分别服用 一种药,收集的数据如下:
甲 1.9 0.8 1.1 0.1 0.1 4.4 5.5 1.6 4.6 3.4 乙 0.7 –1.6 –0.2 –1.2 –0.1 3.4 3.7 0.8 0.0 2.0 由于延长的时数的分布不明,我们考虑用非参数检验 ! Mann-Whitney U 类似于t检验。
由于脉博跳动的次数不服从正态分布,我们考虑用非 参数检验。
5
2020/1/1
6
多个独立样本非参数检验例1
非参数检验

非参数检验符号检验法符号检验法是通过对两个相关样本的每对数据之差的符号(正号或负号)进行检验,以比较这两个样本所代表的总体的差异显著性,对应于参数检验中两相关样本差异显著性的T检验。
其基本思想是:若两总体差异不显著,则两样本差值的正号与负号应大致各占一半,即中位数为0,可见符号检验是以中数作为统计量进行假设检验的。
1、符号检验法的假设是:H0:差值的总体中位数为0;H1:差值的总体中位数不为0。
2、符号检验法的步骤为:①标记出每对数据之差的符号,正号个数记为n+,负号的个数记n-,(显然差值为0的不计算在任何一个中),这两数中最小者记为r,两数之和记为N,即:N = n+ + n-;r = min(n+,n-)②分两种情况进行检验:在双侧检验,.05水平下,若Z值落在-1.96~1.96之间,则表明两总体差异不显著;在此之外则表明差异显著。
在单侧检验,.05水平下,若Z值落在-1.645~1.645之间,则表明两总体差异不显著;在此之外则表明差异显著。
上面第二种情况采用正态分布,是因为将N分成n+和n-两部分,服从二项分布,而当N很大时,二项分布近似于正态分布。
八、多个相关样本检验K related Samples Test•(一)检验方法•三种• 1. Friedman检验:利用秩实现多个配对总体分布的检验,数据要求为等距数据。
• 2.Kendall和谐系数检验:主要评价者的评判标准是否一致或是否公平。
•3Cochran Q检验:它所处理的变量为二分变量。
•(二)分析路径• 1. Analyze-> Nonparametric Tests-> k related Samples。
• 2.在弹出的对话框中,将要比较的变量添加到test variable中,根据不同的数据选择不同的比较方法。
• 3.单击statistics按钮,选择Descriptive.•例如(1)检验10个人服用减肥药后,三次所称体重有无显著性差异。
统计学中的非参数检验方法介绍

统计学中的非参数检验方法介绍统计学是一门研究收集、分析和解释数据的科学。
在统计学中,我们经常需要进行假设检验,以确定样本数据是否代表了总体特征。
非参数检验方法是一种不依赖于总体分布假设的统计方法,它在现实世界中的应用非常广泛。
本文将介绍一些常见的非参数检验方法。
一、Wilcoxon符号秩检验(Wilcoxon Signed-Rank Test)Wilcoxon符号秩检验是一种用于比较两个相关样本的非参数检验方法。
它的原理是将两个相关样本的差值按绝对值大小进行排序,并为每个差值分配一个秩次。
然后,通过比较秩次总和与期望总和的差异来判断两个样本是否具有统计学上的显著差异。
二、Mann-Whitney U检验(Mann-Whitney U Test)Mann-Whitney U检验是一种用于比较两个独立样本的非参数检验方法。
它的原理是将两个样本的所有观测值按大小进行排序,并为每个观测值分配一个秩次。
然后,通过比较两个样本的秩次总和来判断它们是否具有统计学上的显著差异。
三、Kruskal-Wallis检验(Kruskal-Wallis Test)Kruskal-Wallis检验是一种用于比较三个或更多独立样本的非参数检验方法。
它的原理是将所有样本的观测值按大小进行排序,并为每个观测值分配一个秩次。
然后,通过比较各组样本的秩次总和来判断它们是否具有统计学上的显著差异。
四、Friedman检验(Friedman Test)Friedman检验是一种用于比较三个或更多相关样本的非参数检验方法。
它的原理类似于Kruskal-Wallis检验,但是对于相关样本,它将每个样本的观测值按照相对大小进行排序,并为每个观测值分配一个秩次。
然后,通过比较各组样本的秩次总和来判断它们是否具有统计学上的显著差异。
五、秩相关系数检验(Rank Correlation Test)秩相关系数检验是一种用于检验两个变量之间相关性的非参数检验方法。
SPSS操作:多个相关样本的非参数检验(CochransQ检验)

SPSS操作:多个相关样本的⾮参数检验(CochransQ检验)点击Settings→Customize tests,勾选Cochran's Q (k samples)。
点击Define Success,在Cochran's Q: Define Success对话框中,点击Combine values into success category,在Success框中填⼊1(这⾥是“成功”对应的编码,本例中即为通过体能测试,“Passed”对应的是1,所以这⾥填“1”)。
点击OK→Run,输出结果。
3.4 不符合假设4的“精确”Cochran's Q检验当不符合假设4时,需要使⽤“精确”Cochran's Q检验。
在主界⾯点击Analyze→Nonparametric Tests→Legacy Dialogs→K Related Samples,出现Tests for Several Related Samples对话框。
将变量initial_fitness_test、month3_fitness_test和final_fitness_test选⼊Test Variables框中。
在Test Type 下⽅去掉Friedman,然后勾选Cochran's Q。
(如果数据符合假设4,则此时点击OK,结果与3.3部分的操作结果⼀致)点击Exact,在Exact Tests对话框中,点击Exact,点击Continue→OK。
3.5 “精确”Cochran's Q检验后的两两⽐较对于符合假设4的Cochran's Q检验(3.3部分),事后的两两⽐较将在结果解释部分展⽰(4.2部分)。
对于不符合假设4的“精确”Cochran's Q检验(3.4部分)事后的两两⽐较,可采⽤经Bonferroni法校正的多重McNemar检验。
在主界⾯点击Analyze→Nonparametric Tests→Legacy Dialogs→2 Related Samples。
第12讲 相关样本(多样本)非参数检验
Q
2 (k 1)[k C 2 ( C ) j ] j
k C j Ri2
~ 2 (k 1)
Q=0.529
在0.05显著性水平下,可用R软件求出临界值
ห้องสมุดไป่ตู้
2 0.95
(3) 7.81
Q小于临界值,接受原假设,认为评者间差异不显著。
2 d
• 1提出假设: • 2计算统计量: • 其中,
2 Sd
2.56
2 ( d d ) i
n 1
3.972
d 2.93
查T分布表,得临界值为2.3,所以,t的绝对值大于2.3,落入拒绝域,认为改 制前后的竞争力有显著差异。
2问解题过程:
由上表可知,S+ =1, S- =7,可以初步判断,正数的个数太少,前后差别显著。 准确判断可查符号检验临界值表,下页。 结论:接受原假设,认为没有显著差异。 若企业先后进行了两种改革,一是承包制(改制1),二是股份制(改制2), 还是判断前后竞争力有无显著差异,又该如何做?
对于K个相关样本,原假设是:
H0:这K个样本的所有位置参数都相同。 1、对每一行排序求秩,有结时用平均秩。 2、计算每一个样本的秩和。
R j rank ( xij ), j 1, 2,..., k
i 1
其中, n是每个样本的大小,因为是相关样本,所以n相同。
n
3、求每个样本的平均秩: j 4、(无结时)统计量为:
若企业先后进行了两种改革一是承包制改制1二是股份制改制2还是判断前后竞争力有无显著差异又该如何做
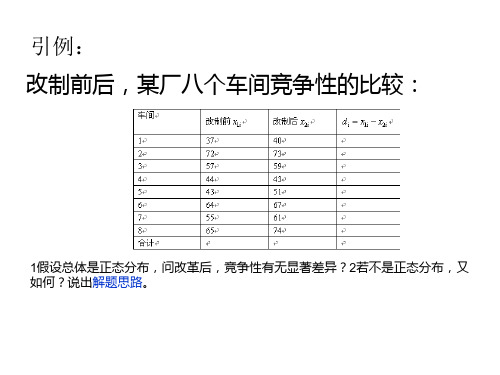
引例: 改制前后,某厂八个车间竞争性的比较:
1假设总体是正态分布,问改革后,竞争性有无显著差异?2若不是正态分布,又 如何?说出解题思路。
非参数检验

组别 95-99 90-94 85-89 80-84 75-79 70-74 65-69 60-64 55-59 50-54 45-49
fo 4 12 18 28 44 72 46 40 22 18 10 314
组上限 99.5 94.5 89.5 84.5 79.5 74.5 69.5 64.5 59.5 54.5 49.5
fe 行合计数 列合计数 总次数
, fb , fd
( a b )( b d ) abcd ( c d )( b d ) abcd
注意:2×2列联表的自由度df=(2-1)(2-1)=1
例 为比较某新药与传统药物治疗脑动脉硬化的疗效, 临床试验结果见表,问两种药物的疗效有无差异? 表 两种药物治疗脑动脉硬化的疗效 处理措施 新药组 有效 无效 合计 44 24 68
41(38.18) 3(5.82)
传统药物组 18(20.82) 6(3.18) 合计 59 9
• 4、关于2×2列联表在数据合并上应注意 的问题 • 2×2列联表只是 的一个特例,实际上, 在很多情况下,变量的分类不止两个,当 我们把各部分数据合并成2×2列联表来表 达时,可能会忽略其中一些重要的变量, 造成 检验的失真,即可能会出现这样的 情况:单独分析每一个2×2列联表所得的 结果与合并成一个2×2列联表所做的 分 析结果相矛盾。
2
( 69 74 . 4 ) 74 . 4
(16 11 . 6 ) 11 . 6
22 . 2748
• 3、推断:
取 0 . 05 , df 5 1 4 , 查表得: 22 . 2748
2 2 0 . 05 ( 4 ) 2 0 . 05 ( 4 )
参数检验和非参数检验

一.单因素方差分析(one-way ANOVA),用于完全随机设计的多个样本均数间的比较,其统计推断是推断各样本所代表的各总体均数是否相等。
完全随机设计(completely random design)不考虑个体差异的影响,仅涉及一个处理因素,但可以有两个或多个水平,所以亦称单因素实验设计。
在实验研究中按随机化原则将受试对象随机分配到一个处理因素的多个水平中去,然后观察各组的试验效应;在观察研究(调查)中按某个研究因素的不同水平分组,比较该因素的效应。
二.T检验,亦称student t检验(Student's t test),主要用于样本含量较小(例如n<30),总体标准差σ未知的正态分布资料。
t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。
它与Z检验、卡方检验并列。
t检验t检验分为单总体检验和双总体检验。
单总体t检验时检验一个样本平均数与一个已知的总体平均数的差异是否显著。
当总体分布是正态分布,如总体标准差未知且样本容量小于30,那么样本平均数与总体平均数的离差统计量呈t分布。
单总体t检验统计量为:双总体t检验是检验两个样本平均数与其各自所代表的总体的差异是否显著。
双总体t 检验又分为两种情况,一是独立样本t检验,一是配对样本t检验。
独立样本t检验统计量为:S1 和S2 为两样本方差;n1 和n2 为两样本容量。
(上面的公式是1/n1 + 1/n2 不是减!)配对样本t检验统计量为:t检验的适用条件(1) 已知一个总体均数;(2) 可得到一个样本均数及该样本标准差;(3) 样本来自正态或近似正态总体。
t检验步骤以单总体t检验为例说明:问题:难产儿出生体重n=35,X拔=3.42,S =0.40,一般婴儿出生体重μ0=3.30(大规模调查获得),问相同否?解:1.建立假设、确定检验水准αH0:μ = μ0 (无效假设,null hypothesis)H1:μ≠μ0(备择假设,alternative hypothesis,)双侧检验,检验水准:α=0.052.计算检验统计量3.查相应界值表,确定P值,下结论查附表1,t0.05 / 2.34 = 2.032,t < t0.05 / 2.34,P >0.05,按α=0.05水准,不拒绝H0,两者的差别无统计学意义例:某校二年级学生期中英语考试成绩,其平均分数为73分,标准差为17分,期末考试后,随机抽取20人的英语成绩,其平均分数为79.2分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Q
2 (k 1)[k C 2 ( C ) j ] j
k C j Ri2
~ 2 (k 1)
Q=0.529
在0.05显著性水平下,可用R软件求出临界值
2 0.95
(3) 7.81
Q小于临界值,接受原假设,认为评者间差在测试一个新产品4种不同配方的效果,数据表如下,表中 数据为去污能力值,1~10分之间。请判断配方之间有无显著差异。
基本工具:求秩和各配方的平均秩(大家做)
1哪一配方表现最好,哪一个最差? 2差别显著吗? 思路:构建一个包含平均秩的统计量,并能确定它的分布类型
第12讲 相关样本(多样本)非参数检验1: Friedman检验
Kendall’s W检验,也叫Kendall协和系数检验,对于K个相关样本,原假设 是:
H0:这K个样本分布相同。 协和系数(W)是
F W n(k 1)
其中,F是Friedman卡方统计量。 上一案例中,可计算出
W
8.593 8.593 0.477 6(4 1) 18
检验的统计量与Friedman统计量相同。
R
Rj n
k 12 2 2 2 R 3 n ( k 1) ~ (k 1) j nk (k 1) j 1
5、有结时用修正公式:
k 12 2 R j 3n( k 1) nk (k 1) l 1 2 3 ( ) 1 nk (k 2 1)
引例: 改制前后,某厂八个车间竞争性的比较:
1假设总体是正态分布,问改革后,竞争性有无显著差异?2若不是正态分布,又 如何?说出解题思路。
1问解题过程:
H0 : d 0; H1 : d 0
t d d S n
2 d
• 1提出假设: • 2计算统计量: • 其中,
2 Sd
2.56
传统的非参数统计
• 单样本非参数检验 • 两样本(独立和相关)非参数检
验 • 多样本(独立和相关)非参数检
验
相关样本(多样本)非参数检验主要方法 13.1 Friedman 检验
13.2 Kendall’s W检验 13.3 Cochran’Q(略)
13.1 Friedman 检验
Friedman检验也称Friedman卡方检验,是1937年Friedman提出的检验 方法,主要检验位置参数。
2 ( d d ) i
n 1
3.972
d 2.93
查T分布表,得临界值为2.3,所以,t的绝对值大于2.3,落入拒绝域,认为改 制前后的竞争力有显著差异。
2问解题过程:
由上表可知,S+ =1, S- =7,可以初步判断,正数的个数太少,前后差别显著。 准确判断可查符号检验临界值表,下页。 结论:接受原假设,认为没有显著差异。 若企业先后进行了两种改革,一是承包制(改制1),二是股份制(改制2), 还是判断前后竞争力有无显著差异,又该如何做?
R软件进行Friedman检验:
1、打开R软件
2、建立程序文件:
x1=c(2,9,4,9,6,9) x2=c(7,10,6,7,8,4) x3=c(3,7,1,4,4,2) x4=c(6,5,4,5,3,6) x=cbind(x1,x2,x3,x4) friedman.test(x)
第13讲 相关样本(多样本)非参数检验2: Kendall’s W检验
• W=0.117,三个影评家之间的一致性很低,
第13讲 相关样本(多样本)非参数检验3: Cochran Q检验
适用范围:二分类变量 原假设:K个样本分布相同
案例:一家厂家请四位消费者对该厂的6种产品给出评价,1为满意,0为 不满意,见下表,请判断评者间是否有显著差异。
操作:1、数出每一个纪录(商品)中1的个数Ri(大家算); 2、数出每个样本( 评者)给出的1的个数Cj 3、统计量为
对于K个相关样本,原假设是:
H0:这K个样本的所有位置参数都相同。 1、对每一行排序求秩,有结时用平均秩。 2、计算每一个样本的秩和。
R j rank ( xij ), j 1, 2,..., k
i 1
其中, n是每个样本的大小,因为是相关样本,所以n相同。
n
3、求每个样本的平均秩: j 4、(无结时)统计量为:
可见,Kendall W检验在本质上与Friedman检验相同,但它提供了进一步的信 息:一致性信息。
Kendall协和系数在0~1之间,系数越大,一致性就越高。
案例:
请三位电影评家对8部电影打分,评分结果如下:试问三个评家的评价结果是 否具有一致性,已知Friedman卡方值为1.867。
答案:
其中,τ表示结长 用上例计算。
2 1
(k 1)
2 10.05
(3)
2 0.95
(3) ?
程序:chisq.R
Easy!
2 0.95
(3) 7.81
不查表,你会求出上面的结果吗?
打开R,输入qchisq(0.95,3),回车! 最终结果: Friedman chi-squared = 8.5932, df = 3, p-value = 0.03522,P值小于 0.05,所以拒绝原假设,认为4种配方之间存在显著差异。 不用SPSS,你会用其它软件计算吗?
