圆形边界磁场
专题:圆形磁场问题

B v0
长,偏转角度越大。而弧小于半
aα r
O
b
个圆周时,弦越长则弧越长。
R
sin = r/R = 37º,
α
最大偏转角为 2 = 74º。
例题:如图所示,在真空中半径r=3.0×10-2 m的圆 形区域内,有磁感应强度B=0.2 T,方向如图的匀强 磁场,一批带正电的粒子以初速度v0=1.0×106 m/s, 从磁场边界上直径ab的一端a沿着各个方向射入磁场, 且初速度方向与磁场方向都垂直,该粒子的比荷为q/m
r
O
所以磁场区域的下边界也是半径为r,圆心为(0,r)的
圆弧应是磁场区域的下边界。
两边界之间图形的面积即为所求。图中的阴影区域面 积,即为磁场区域面积:
S
2( 1 4
r2
r2 2
)
(
2
1)
m2v02 e2B2
例题:(2009年浙江卷)如图,在xOy平面内与y轴平行的匀
强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。
T=2qπBm, 运动时间 tm=22πα×T=2qαB·m,
又 sinα=Rr =35,∴tm=6.4×10-8 s.
一点发散成平行
R r
R r
平行会聚于一点
结论4:如果在圆形匀强磁场区域的 边界上某点向磁场发射速率相同的 带电粒子,且粒子在磁场中运动的 轨道半径与磁场区域半径相同,那 么粒子射出磁场时运动方向一定相 同.反之,粒子以相同速度平行射 人这样的磁场,粒子就能会聚于磁 场边界上的某点。
为多大?(不考虑电子间的相互作用)
y
v0
O
O1
x
O2 O3
O5O4 On
解2: 磁场上边界如图线所示。
圆形边界磁场

圆形边界磁场
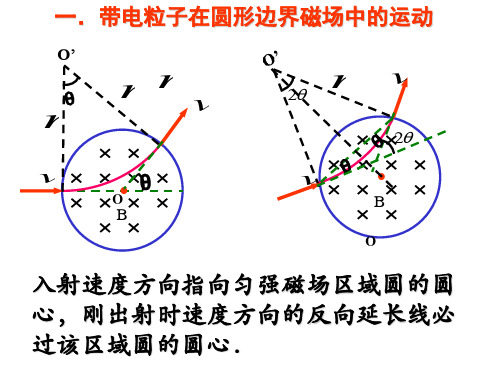
1.在圆形有界匀强磁场区域内,沿径向射入的粒子,一定沿径向射出。
2.磁场圆与轨迹圆公共弦最长时等于其中一个的直径。
3.轨迹圆半径等于(匀强)磁场圆半径的粒子会平行离开磁场。
圆形边界磁场运动的特点:
带电粒子在有界匀强磁场中做不完整的圆周运动,由于磁场区域边界可能是圆形的、三角形的、矩形的等各种几何形状及粒子射入的速度不同,造成它在磁场中运动的圆弧轨迹﹑偏转角度、运动时间等各不相同,这成为学生学习的一个难点。
带电粒子在圆形边界磁场

2
探讨带电粒子在复杂磁场和边界条件下的动力学 行为,例如磁场的不均匀性和边界的曲率变化。
3
将研究成果应用于实际问题,如粒子加速器、核 聚变反应堆、磁流体发电等,以提高相关设备的 性能和效率。
THANKS FOR WATCHING
感谢您的观看
带电粒子在圆形边界磁场
目录
• 引言 • 带电粒子在磁场中的基本性质 • 圆形边界磁场的特点 • 带电粒子在圆形边界磁场中的运动 • 带电粒子在圆形边界磁场中的应用 • 结论与展望
01 引言
主题介绍Βιβλιοθήκη 01带电粒子在圆形边界磁场中的运 动是物理学中的一个经典问题, 涉及到磁场对带电粒子的作用力 以及粒子在磁场中的轨迹变化。
02
该问题在理论研究和实际应用中 都具有重要意义,如粒子加速器 、核聚变反应等领域。
研究背景和意义
随着科技的发展,磁场对带电粒子的 作用力在许多领域中得到了广泛应用 ,如医学成像、核聚变能源等。
研究带电粒子在圆形边界磁场中的运 动有助于深入理解磁场对带电粒子的 作用机制,为相关领域的技术进步提 供理论支持。
偏转距离
带电粒子在磁场中的偏转距离与 粒子的速度和磁感应强度有关, 粒子速度越大,偏转距离越远。
带电粒子在磁场中的能量和动量变化
能量变化
带电粒子在磁场中的运动过程中,由于受到洛伦兹力作用, 其能量会发生变化。当带电粒子做旋转运动时,其动能和势 能不断转化;当带电粒子做偏转运动时,其动能和势能也会 发生变化。
约束力
由于圆形边界的限制,洛伦兹力将带 电粒子约束在磁场区域内,使其沿圆 形轨迹运动。
04 带电粒子在圆形边界磁场 中的运动
带电粒子在磁场中的旋转运动
旋转方向
圆形边界磁场知识讲解
B
·
O•1 R
x
r2R vqBr2qBR r
mm
qU 1 mv2 2
U 2qB2R2
600
r
O2
6.如图所示,一个质量为m、电量为q的正离子,在小 孔S处正对着圆心O以速度v射入半径为R的绝缘圆筒中。
圆筒内存在垂直纸面向里的匀强磁场,磁感应强度的大
小为B。要使带电粒子与圆筒内壁碰撞多次后仍从A点 射出,求正离子在磁场中运动的时间t.设粒子与圆筒内 壁碰撞时无能量和电量损失,不计粒子的重力。
此时速度方向与y轴的夹角为300,P到O的距离为L,如图
所示.不计重力的影响.求磁场的磁感强度B的大小和xy
平解:面上qv磁B场区m域v的2 半径LR. 3r
300 y
r
B mv 3mv qr qL
P Lr A
r
R2rco3s00 3L 3
0 vR
1. 如图所示,当滑动变阻器R3的滑片C向B方向移 动时,电路中各电表示数如何变化?(电表内阻对电 路的影响不计)
O’
y
v
y
P(x y)
v
oO• x
B
t 600 T12mm
3600 6 qB 3qB xRco6s00 1R 2
yRsin600 3R
x
2
P(1 R, 3 R)
22
2.在圆形区域内有垂直纸面向里的匀强磁场.从磁
场边缘A点沿半径方向射人一束速率不同的质子,对
这些质子在磁场中的运动情况的分析中,正确的是:
无损失)
B
解:粒子经过n=2,3,4……次与圆筒
碰撞从原孔射出,其运动轨迹具
有对称性.当发生最少碰撞次数
r
. R vO0
高考物理试题库 专题3.11 圆形边界磁场问题(基础篇)(解析版)

(选修3-1)第三部分磁场专题3.11 圆形边界磁场问题(基础篇)一.选择题1.(2019合肥三模)图示为一粒子速度选择器原理示意图。
半径为l0cm的圆柱形桶内有一匀强磁场,磁感应强度大小为1.0×10-4T,方向平行于轴线向外,圆桶的某直径两端开有小孔,粒子束以不同角度由小孔入射,将以不同速度从另一个孔射出。
有一粒子源发射出速度连续分布、比荷为2.0×1011C/kg的带正电粒子,若某粒子出射的速度大小为×106m/s,粒子间相互作用及重力均不计,则该粒子的入射角θ为()A. B. C. D.【参考答案】B【命题意图】本题以带电粒子射入圆形匀强磁场区域做匀速圆周运动为情景,考查洛伦兹力、牛顿运动定律及其相关知识点。
【解题思路】画出粒子在圆形匀强磁场区域运动轨迹,如图所示,由图中几何关系可得rcosθ=R,由洛伦兹力提供向心力,qvB=m2vr,q/m=2.0×1011C/kg,联立解得θ=45°,选项B正确。
【方法归纳】对于带电粒子在有界匀强磁场中的运动,首先根据题述情景画出带电粒子运动轨迹,根据几何关系得出轨迹半径r (或r 的表达式),然后利用洛伦兹力等于向心力列方程解答。
2.(多选)(2019·广东省惠州市模拟)如图所示,在半径为R 的圆形区域内充满磁感应强度为B 的匀强磁场,MN 是一竖直放置的感光板.从圆形磁场最高点P 以速度v 垂直磁场正对着圆心O 射入带正电的粒子,且粒子所带电荷量为q 、质量为m ,不考虑粒子重力,关于粒子的运动,以下说法正确的是( )A .粒子在磁场中通过的弧长越长,运动时间也越长B .射出磁场的粒子其出射方向的反向延长线也一定过圆心OC .射出磁场的粒子一定能垂直打在MN 上D .只要速度满足v =qBR m ,入射的粒子出射后一定垂直打在MN 上【参考答案】 BD【名师解析】 速度不同的同种带电粒子在磁场中做匀速圆周运动的周期相等,对着圆心入射的粒子,速度越大在磁场中轨道半径越大,弧长越长,轨迹对应的圆心角θ越小,由t =θ2πT 知,运动时间t 越小,故A 错误;带电粒子的运动轨迹是圆弧,根据几何知识可知,对着圆心入射的粒子,其出射方向的反向延长线一定过圆心,故B 正确;速度不同,半径不同,轨迹对应的圆心角不同,对着圆心入射的粒子,出射后不一定垂直打在MN 上,与粒子的速度有关,故C 错误;速度满足v =qBR m 时,粒子的轨迹半径为r =mvqB =R ,入射点、出射点、O 点与轨迹的圆心构成菱形,射出磁场时的轨迹半径与最高点的磁场半径垂直,粒子一定垂直打在MN 板上,故D 正确.3.(6分)(2019湖北武汉武昌5月调研)如图所示,真空中,垂直于纸面向里的匀强磁场只在两个同心圆所夹的环状区域存在(含边界),两圆的半径分别为R 、3R ,圆心为O .一重力不计的带正电粒子从大圆边缘的P 点沿PO 方向以速度v 1射入磁场,其运动轨迹如图,轨迹所对的圆心角为120°.若将该带电粒子从P 点射入的速度大小变为v 2时,不论其入射方向如何,都不可能进入小圆内部区域,则v 1:v 2至少为( )A.B.C.D.2【参考答案】B【命题意图】本题以带电粒子在圆环形磁场区域的运动为情景,意在考查洛伦兹力和牛顿运动定律及其相关知识点。
圆形磁场中的几个典型问题

圆形磁场中的几个典型问题许多同学对带电粒子在圆形有界磁场中的运动问题常常无从下手,一做就错.常见问题分别是“最值问题、汇聚发散问题、边界交点问题、周期性问题”.对于这些问题,针对具体类型,抓住关键要素,问题就能迎刃而解,下面举例说明.一、最值问题的解题关键——抓弦长1.求最长时间的问题例1 真空中半径为R=3×10-2m的圆形区域内,有一磁感应强度为B=0.2T的匀强磁场,方向如图1所示一带正电的粒子以初速度v0=106m / s 从磁场边界上直径ab 一端a 点处射入磁场,已知该粒子比荷为q/m=108C / kg ,不计粒子重力,若要使粒子飞离磁场时偏转角最大,其入射时粒子初速度的方向应如何?(以v0与Oa 的夹角 表示)最长运动时间多长?小结:本题涉及的是一个动态问题,即粒子虽然在磁场中均做同一半径的匀速圆周运动,但因其初速度方向变化,使粒子运动轨迹的长短和位置均发生变化,并且弦长的变化一定对应速度偏转角的变化,同时也一定对应粒子做圆周运动轨迹对应圆心角的变化,因而当弦长为圆形磁场直径时,偏转角最大.2 .求最小面积的问题例2 一带电质点的质量为m,电量为q,以平行于Ox 轴的速度v从y轴上的a点射人如图3 所示第一象限的区域.为了使该质点能从x轴上的b点以垂直于x轴的速度v 射出,可在适当的地方加一个垂直于xoy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,试求此圆形磁场区域的最小面积,重力忽略不计.小结:这是一个需要逆向思维的问题,而且同时考查了空间想象能力,即已知粒子运动轨迹求所加圆形磁场的位置.解决此类问题时,要抓住粒子运动的特点即该粒子只在所加磁场中做匀速圆周运动,所以粒子运动的1 / 4 圆弧必须包含在磁场区域中且圆运动起点、终点必须是磁场边界上的点,然后再考虑磁场的最小半径.上述两类“最值”问题,解题的关键是要找出带电粒子做圆周运动所对应的弦长.二、汇聚发散问题的解题关键——抓半径当圆形磁场的半径与圆轨迹半径相等时,存在两条特殊规律;规律一:带电粒子从圆形有界磁场边界上某点射入磁场,如果圆形磁场的半径与圆轨迹半径相等,则粒子的出射速度方向与圆形磁场上入射点的切线方向平行,如甲图所示。
圆形边界磁场知识点总结

圆形边界磁场知识点总结磁场是指在空间中出现的一种物理现象,是由电荷运动所产生的基本物理场。
在工程和科学应用中,圆形边界磁场是一种常见的磁场形式,它在许多领域中都有广泛的应用。
本文将对圆形边界磁场的相关知识进行总结,包括其定义、性质、计算方法等方面,以便对圆形边界磁场有更深入的了解。
一、圆形边界磁场的定义圆形边界磁场是指由一个或多个电流元在圆形环路内产生的磁场。
在平面上,若电流I在半径为r的圆形环路上均匀分布,则在圆心的磁场大小可以用以下公式表示:\[ B = \frac{\mu_0 I}{2r} \]其中,B代表磁场强度,μ0代表真空磁导率, I代表磁场环路上的电流,r代表圆形环路的半径。
二、圆形边界磁场的性质1. 磁场方向圆形边界磁场有明确的磁场方向。
根据安培定则,磁场环路内部的磁场方向为环路的法向,指向环路内部;环路外部的磁场方向为环路的法向,指向环路外部。
2. 磁场大小圆形边界磁场的大小与环路的半径成反比,与环路上的电流成正比。
当环路的半径越大,磁场强度越小;当环路上的电流越大,磁场强度越大。
3. 磁场分布圆形边界磁场的分布是均匀的,即在圆形环路的内部,磁场大小和方向是均匀分布的。
4. 磁场叠加在多个圆形环路产生的磁场可以叠加。
根据叠加原理,多个圆形环路产生的磁场可以通过矢量合成得到总的磁场。
5. 磁场方向的变化圆形边界磁场的方向与环路上的电流方向有关。
根据右手定则,当电流方向与环路的法向方向相同时,环路内部的磁场方向指向环路内部;当电流方向与环路的法向方向相反时,环路内部的磁场方向指向环路外部。
三、圆形边界磁场的计算方法1. 定义电流元在计算圆形边界磁场时,先需要定义一个电流元,然后再将电流元叠加起来以得到总的磁场。
2. 利用比奥-萨伐尔定律计算磁场比奥-萨伐尔定律是用来计算电流元产生的磁场的公式,可以用来计算圆形边界磁场。
该定律表明,一个长直导线在某一点产生的磁场与该点到导线的距离成反比,与导线上的电流成正比。
关于圆形有界磁场的几个结论

关于圆形有界磁场的几个结论
1.圆形有界磁场的磁感应是沿着圆形有界磁场的中心点放射且向偏离中心点的位置递减的。
2.圆形有界磁场的磁感应强度受圆形有界磁场的半径的影响,当半径变大时磁感应强度变小。
3.圆形有界磁场的磁场强度沿着圆形磁场的中心点向偏离中心点方向递减,但在距离磁场中心太远时磁场强度几乎不受影响。
4.由于圆形有界磁场的磁感应强度和磁场强度是沿着圆形磁场的中心点向偏离中心点方向递减的,因此圆形有界磁场可用两个独立的、以原点为中心的坐标系统来确定。
