朗肯土压力范例
土力学典型范例

典型范例【例7-1】如图所示一高5m的挡土墙,墙后填土由两层组成,填土表面有20kPa的均布荷载,计算作用在墙上的总的主动土压力和作用点的位置。
【解题思路】本题是典型的利用朗肯土压力理论计算土压力的实际应用,在填土表面有均布荷载作用,并且墙背后填土分层,在计算土压力时,应根据每一层的土压力系数分别进行计算。
由于上下两层都是粘土层,注意要判断是否存在负侧压力区,若存在负侧压力区,在计算土压力强度中应该不予考虑。
总的土压力合力是土压力强度分布图形的面积,相应作用点在强度分布图形的形心处。
【解答】(1)主动土压力系数计算第一层填土主动土压力系数为第二层填土主动土压力系数为(2)粘性土层中负侧压力区的判断对于粘性土,需判别填土中是否存在拉应力区。
计算第一层填土中的临界深度说明在第一层中存在负侧压力区,深度为地表范围内0.50m。
第二层填土中的临界深度说明在第二层土中不存在负侧压力区。
(3)墙后各点主动土压力强度计算B点的主动土压力为F点交界面以上的主动土压力为F点交界面以下的主动土压力为A点的主动土压力为(4)主动土压力合力计算第一层总的主动土压力为第二层总的主动土压力为整个墙上总的主动土压力为(5)合力作用点计算土压力合力作用点在分布图形的形心处。
合力Ea的作用点在A点以上的距离【例7-2】某折线型挡土墙如图所示,墙背为砂性填土,填土的内摩擦角ϕ=400,重度γ=19kN/m3,与墙背的外摩擦角δ=ϕ/2=200,墙顶填土面倾角β=29°45’(1∶1.75),上段墙背倾角α1=18°26’(3∶1)。
下段墙背倾角为α2=-14°02’(1∶0.25)。
试用延长墙背法计算该挡土墙背的土压力分布及其合力。
【解题思路】本题是库仑土压力理论在实际工程中具体应用的典型算例,墙背后填土不水平,墙背不光滑同时墙背倾斜而且分成两段,这种挡土墙的实用计算方法如下:将折线型挡土墙AB(上)段视为一俯斜型挡土墙,计算墙背土压力Ea1,延长BC(下)段墙背与填土面相交,得交点D,并以虚线相连,将DC视为仰斜型挡土墙墙背计算土压力Ea2(但不计虚线部分土压力),计算折线型挡土墙墙背土压力合力Ea(为Ea1和Ea2的矢量和)及其作用方向与水平面的夹角(Ea 的作用点为Ea1和Ea2作用线的交点,可通过几何关系求得)【解答】(1) AB墙段上的土压力计算AB(上)段墙背土压力分布可由库仑土压力理论求得主动土压力系数土压力分布情况A点:B点:合力大小:合力作用方向与水平面的夹角为:(2) BC墙段上的土压力计算BC(下)段墙背,计算时将其延长至与填土面相交,其交点可由填土面直线方程及BC段墙背直线方程求得,若设A点为坐标原点,则B点坐标为(0.667,-2)。
朗肯土压力计算

5.3朗肯土压力理论朗肯土压力理论是根据半空间的应力状态和土的极限平衡条件而得出的土压力计算方法。
图5-5(a)表示一表面为水平面的半空间,即土体向下和沿水平方向都伸展至无穷,在离地表z 处取一单位微体M ,当整个土体都处于静止状态时,各点都处于弹性平衡状态。
设土的重度为γ,显然M 单元水平截面上的法向应力等于该处土的自重应力,即:而竖直截面上的法向应力为:由于土体内每一竖直面都是对称面,因此竖直截面和水平截面上的剪应力都等于零,因而相应截面上的法向应力z σ和x σ都是主应力,此时的应力状态用莫尔圆表示为如图5-5(b)所示的圆Ⅰ,由于该点处于弹性平衡状态,故莫尔圆没有和抗剪强度包线相切。
图5-5半空间的极限平衡状态设想由于某种原因将使整个土体在水平方向均匀地伸展或压缩,使土体由弹性平衡状态转为塑性平衡状态。
如果土体在水平方向伸展,则M 单元在水平截面上的法向应力z σ不变而竖直截面上的法向应力却逐渐减少,直至满足极限平衡条件为止(称为主动朗肯状态),此时z σ达最低限值a σ,因此,a σ是小主应力,而z σ圆平方向压缩,那末x σ不断增加而z σ)时x σ达最大限值p σ,这时,p σ为⎪⎭⎫ ⎝⎛-︒245ϕ由土的强度理论可知,当土体中某点处于极限平衡状态时,大主应力1σ和小主应力3σ之间应满足以下关系式:粘性土:245tan(2)245(tan 231ϕϕσσ+︒++︒=c 或245tan(2245(tan 213ϕϕσσ-︒--︒=c 无粘性土:)245(tan 231ϕσσ+︒=或245(tan 213ϕσσ-︒= 对于如图5-6所示的挡土墙,设墙背光滑(为了满足剪应力为零的边界应力条件)、直立、填土面水平。
当挡土墙偏离土体时,由于墙后土体中离地表为任意深度z 处的竖向应力z z γσ不变,亦即大主应力不变,而水平应力x σ却逐渐减少直至产生主动朗肯状态,此时,z σ是小主应力a σ,也就是主动土压力强度,由极限平衡条件得: 无粘性土:)245(tan 2ϕγσ-︒=z a (5-3) 或 a a zk γσ= (5-4) 粘性土:)245tan(2)245(tan 2ϕϕγσ-︒--︒=c z a (5-5) 或a a a K c zK 2-=γσ (5-6)上列各式中a K —主动土压力系数,)245(tan 2ϕ-︒=a K ;γ —墙后填土的重度,kN/m3,地下水位以下用有效重度;c —填土的粘聚力,kPa ; ϕ —填土的内摩擦角,度;z —所计算的点离填土面的深度,m 。
朗肯土压力范例

基本假设:1、墙本身是刚性的,不考虑墙身 的变形;2、墙后填土延伸到无限远处,填土 表面水平(=0);3、墙背垂直光滑。
τ
主动状态
f c tg
A O
σx=K0σz σz
被动状态 σ
表面水平的均质弹性半空间体的极限平衡状 态图
二、朗肯主动土压力计算
用1,3作摩尔应力圆,如图中应力圆I所示。
当墙后填土中有水时,需考虑地下水位以下的 填土由于浮力作用使有效重量减轻引起的土压 力减小,水下填土部分采用浮容重进行计算。
在计算作用在墙背上的总压力中应包括水压力 的作用。
五、填土为成层土时的土压力计算
由于各层填土重度不同,使得填土竖向应力分布 在土层交界面上出现转折
由于各层填土粘聚力和内摩擦角不同,所以在计 算主动或被动土压力系数时,需采用计算点所在 土层的粘聚力和内摩擦角
的趋势,墙面的法向应力h增大 。h、 v为大 小主应力。当挡土墙的位移使得h增大到使土 体达到极限平衡状态时,则h达到最高限值pp ,即为所求的朗肯被动土压力强度。
(一)基本计算公式
朗肯理论的被动土压力系数
(二)无粘性土的被动土压力计算
(三)粘性土的被动土压力计算
四、填土中有地下水时的土压力计算
朗肯土压 力理论
ห้องสมุดไป่ตู้
英国科学家 土力学 热力学
William John Maquorn Rankine (1820 - 1872)
朗肯土压力理论
1857年英国学者朗肯(Rankine)从研究弹性半空 间体内的应力状态,根据土的极限平衡理论,得 出计算土压力的方法,又称极限应力法。
一、基本原理和基本假设 基本原理:认为墙后填土达到极限平衡状态时, 与墙背接触的任一土单元体都处于极限平衡状态, 然后根据土单元体处于极限平衡状态时应力所满 足的条件来建立土压力的计算公式。
用朗肯土压力理论计算图示挡土墙上
如图所示,某挡土墙高7m,填土表面作用均布荷载q=20kPa。填土分两层,第一层土: h1=3m,;第二层土:h2=4m,。按朗肯压力理论计算作用在挡土墙背上的主动土压力分 布及合力Ea的大小,并绘出主动土压力强度分布图。 (2011年10月)
.按朗肯土压力理论,确定图示挡土墙上的主动土压力沿墙高的分布,并计算其 合力。 (2011年1月)
•
201210:某地基中有一土层,其厚度为h=2m,其顶面的自重应力=92kPa,底面的自 重应力=108kPa,已知该土层在外荷载作用下顶面受到的附加应力=64kPa,底面受到 的附加应力=36kPa。求:该土层的最终压缩量大小。(注:计算时仅分一层即可)压 力和孔隙比e的填土由两层土组成,填土表面作用q=30kPa均布荷载,第 一层土为粉质粘土,厚度hl=2.0m,=15.68kN/m3,cl=9.8kPa,=10°。第二层土为粘土, 厚度h2=3.0m,=17.64kN/m3,c2=14.7kPa,=20°。试利用朗肯土压力理论,求作用在挡 土墙墙背上的主动土压力及其合力。 (2009年10月倒数第二题)
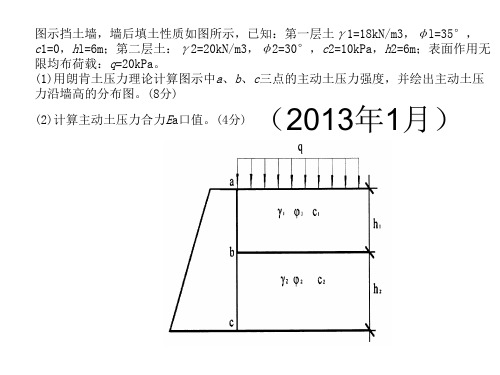
(2013年1月)
图示挡土墙,墙后填土的性质指标如图示,试用朗肯理论计算并画出图示挡土墙上的主 动土压力分布图,并计算其合力大小。(12分)(2012年10月)
如图所示,某挡土墙高6m,墙后填土由两层组成,地下水位距墙底2m。第一层土为细砂,其厚 度为2m,γ1=15.8kN/m3,φ 1=10°,c1=0;第二层土为粉质粘土,其厚度为4m, γ2=17.8kN/m3,γ2sat=19.8kN/m3,φ 2=16°,c2=10kPa。按朗肯土压力理论计算作用在 挡土墙背上的主动土压力Ea的大小,并绘出主动土压力强度的分布图。 (2012年1月)
第一课用朗肯土压力理论计算图示挡土墙上

某挡土墙,其高度为5.0m,墙后填土由两层土组成,填土表面作用q=30kPa均布荷载,第 一层土为粉质粘土,厚度hl=2.0m,=15.68kN/m3,cl=9.8kPa,=10°。第二层土为粘土, 厚度h2=3.0m,=17.64kN/m3,c2=14.7kPa,=20°。试利用朗肯土压力理论,求作用在挡
图示挡土墙,墙后填土性质如图所示,已知:第一层土γ 1=18kN/m3,φ l=35°, c1=0,hl=6m;第二层土:γ 2=20kN/m3,φ 2=30°,c2=10kPa,h2=6m;表面作用无 限均布荷载:q=20kPa。 (1)用朗肯土压力理论计算图示中a、b、c三点的主动土压力强度,并绘出主动土压 力沿墙高的分布图。(8分)
下图示为一高度为6.0m的拱桥桥台。桥台后第一层填土为粉质粘土,厚度为4.0m, 天然重度r=18kN/m3,内摩擦角,内聚力c=13kPa;第二层填土为粘土,厚度为 2.0m,天然重度r=17.5kN/m3,内摩擦角,内聚力c=15kPa。试用朗肯土压力理
论计算桥台墙背上的被动土压力,绘出其分布图。 (2010年1月)
布及合力Ea的大小,并绘出主动土压力强度分布图。 (2011年10月)
.按朗肯土压力理论,确定图示挡土墙上的主动土压力沿墙高的分布,并计算其 合力。 (2011年1月)
用朗肯土压力理论计算图示挡土墙上的主动土压力合力EA的大小。(10分)
已知:上层土hl=6m,γ 1=19.7kN/m3,=35°,c1=0; 下层土h2=6m,γ 2=18.0kN/m3,=30°,c2=10kPa; 表面作用无限均布荷载q=30kPa。 (2010年10月)
土墙墙背上的主动土压力及其合力。 (2009年10月倒数第二题)
按朗肯土压力理论计算下图所示挡土墙上的主动土压力合力Ea,绘出主动土压力强度分布 图。已知土的性质:第一层为粉质粘土,厚度3m,γ=18kN/m3,=30°,c=10kPa;第二
31朗肯土压力理论

1(
2
1
-
)=
3
1(
2
+
1
3)sin+
c
cos
填土为砂土 1.静止土压力
v
z
z
z
h h
h
HH
v
H/3
(a)
(b)
竖向应力为自重应力: z=z
水平向应力为原来土体内部应力 变成土对墙的应力,即为静止土 压力强度P0: P0=K0z
H
Ep
90+ 3=z
H/3
45-/2
HKp
1= p
Pp=1=tg2(45+f/2 )z,Kp= tg2(45+f/2 )
合力 Ep=Kp H2/2
SUCCESS
THANK YOU
2019/11/6
填土为粘性土 1.主动土压力
2c Ka
Z0(临界深度)
主
Ea
动
区
HKa
(H-Z0)/3 HKa-2c Ka
HK0 按经验公式确定:
K0 1 sin'
K0 0.95 sin'
填土为砂土 2.主动土压力
1=z
H
Ea
H/3
45+/2
HKa
Pa=3=tg2(45-f/2 )z, Ka= tg2(45-f/2 ) 合力 Ea=Ka H2/2
3= a
填土为砂土
3.被动土压力
Pa
3
ztg 2 (45o
) 2c tg(45o
2
)
2
zKa 2c Ka
33几种工程中常见的土压力计算

KagH1
H2
不透水层
KagH2
gwH2
g g /
/
a/z2 t(4 g o 5 2) 2 c t( g 4o 5 2)w z
墙基不透水
库仑理论
H1
d
H2
Ea
σw
不透水
土压力
Ea
水压力 σw
填土渗透系数比地基土小得多
垂直有效 应力=总应力
H1
gH1
H2
透水地基
gsatH2
(3) 整体绕点B逆时针旋转q 则 =+q, =+q H =Hcos(+q )/cos
(4) 用库仑理论(图)数解得到地震下动土 压力: Eae= (1-Kv)/2*H2Kae
式中:Kae = f (q, , , f, d
十、车辆载荷作用下的土压力计算:
• 《公路桥涵设计通用规范》(JTJ021-89): • 将破坏棱体范围内的车辆荷载∑G化为均布
三. 填土中有水
完工
完工 混凝土挡土墙及复合排水管
1. 挡土墙构造要求: 墙后设排水孔以及反滤层,一般用
砂性土,填土表面设沟、堤等截流 2. 水上、水下部分的应力状态
水上为正常状态的土压力σa 水下:土压力为有效应力σa
水压力
(静水压力、渗流压力、超静孔压)
墙基不透水
朗肯理论
土压力 水压力
H1
(2) 作用在真实墙面AC上的土压力
五. 墙背形状有变化(1)
DA
DA
d
Ea1
B
B
Ea2
C
C
E a1E a2E a
五. 存在卸荷平台(2)
六. 墙后填土受限制
用朗肯土压力理论计算图示挡土墙上共16页文档
201901:地基中某一土层,其厚度h1=1.6m,该土层顶面处土自重应力σc1=92kPa,附加 应力
σz1=64kPa,该层底面处的自重应力σc2=108kPa,附加应力σz2=36kPa,该土的压缩试 验成果如下表所示,试计算该土层的最ቤተ መጻሕፍቲ ባይዱ压缩量。(注:仅分一层计算即可)(8分)
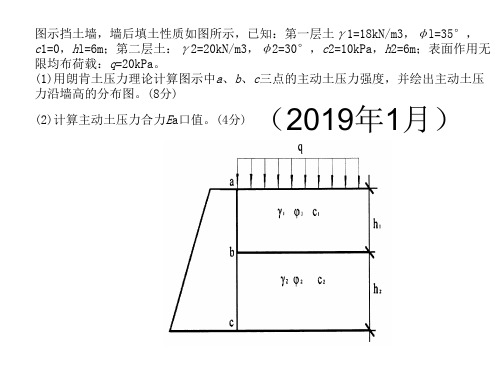
图示挡土墙,墙后填土性质如图所示,已知:第一层土γ1=18kN/m3,φl=35°, c1=0,hl=6m;第二层土:γ2=20kN/m3,φ2=30°,c2=10kPa,h2=6m;表面作用无 限均布荷载:q=20kPa。 (1)用朗肯土压力理论计算图示中a、b、c三点的主动土压力强度,并绘出主动土压 力沿墙高的分布图。(8分)
布及合力Ea的大小,并绘出主动土压力强度分布图。 (2019年10月)
.按朗肯土压力理论,确定图示挡土墙上的主动土压力沿墙高的分布,并计算其 合力。 (2019年1月)
用朗肯土压力理论计算图示挡土墙上的主动土压力合力EA的大小。(10分) 已知:上层土hl=6m,γ1=19.7kN/m3,=35°,c1=0; 下层土h2=6m,γ2=18.0kN/m3,=30°,c2=10kPa; 表面作用无限均布荷载q=30kPa。 (2019年10月)
γ2=17.8kN/m3,γ2sat=19.8kN/m3,φ2=16°,c2=10kPa。按朗肯土压力理论计算作用在
挡土墙背上的主动土压力Ea的大小,并绘出主动土压力强度的分布图。 (2019年1月)
如图所示,某挡土墙高7m,填土表面作用均布荷载q=20kPa。填土分两层,第一层土: h1=3m,;第二层土:h2=4m,。按朗肯压力理论计算作用在挡土墙背上的主动土压力分
(2019年1月) (2)计算主动土压力合力Ea口值。(4分)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
体达到极限平衡状态时,则 h 达到最高限值 pp
,即为所求的朗肯被动土压力强度。
(一)基本计算公式
朗肯理论的被动土压力系数
(二)无粘性土的被动土压力计算
(三)粘性土的被动土压力计算
四、填土中有地下水时的土压力计算
当墙后填土中有水时,需考虑地下水位以下的 填土由于浮力作用使有效重量减轻引起的土压 力减小,水下填土部分采用浮容重进行计算。 在计算作用在墙背上的总压力中应包括水压力 的作用。
(一)基本计算公式
朗肯理论的主动土压力系数
(二)无粘性土的主动土压力计算
(三)粘性土的主动土压力计算
ea=0Βιβλιοθήκη 有均布荷载时粘性土的主动土压力有荷载
出现拉力区
不出现拉力区
三、朗肯被动土压力计算
同计算主动土压力一样用 1 、 3 作摩尔应力圆,
如下图。
使挡土墙向右方移动,则右半部分土体有压缩 的趋势,墙面的法向应力h增大 。h、 v为大 小主应力。当挡土墙的位移使得 h 增大到使土
朗肯土压 力理论
英国科学家 土力学 热力学
William John Maquorn Rankine
(1820 - 1872)
朗肯土压力理论
1857年英国学者朗肯(Rankine)从研究弹性半空 间体内的应力状态,根据土的极限平衡理论,得 出计算土压力的方法,又称极限应力法。
一、基本原理和基本假设 基本原理:认为墙后填土达到极限平衡状态时, 与墙背接触的任一土单元体都处于极限平衡状态, 然后根据土单元体处于极限平衡状态时应力所满 足的条件来建立土压力的计算公式。
五、填土为成层土时的土压力计算
由于各层填土重度不同,使得填土竖向应力分布 在土层交界面上出现转折
由于各层填土粘聚力和内摩擦角不同,所以在计 算主动或被动土压力系数时,需采用计算点所在 土层的粘聚力和内摩擦角
习 题
THE END
基本假设:1、墙本身是刚性的,不考虑墙身 的变形;2、墙后填土延伸到无限远处,填土 表面水平(=0);3、墙背垂直光滑。
τ 主动状态
g t c f
被动状态
O
A σ σx=K0σz σz
表面水平的均质弹性半空间体的极限平衡状
态图
二、朗肯主动土压力计算
用1,3作摩尔应力圆,如图中应力圆I所示。
