采用朗肯土压力理论计算主动
朗肯土压力3个公式

朗肯土压力3个公式朗肯土压力公式是土压力理论中的一种计算公式,用于计算土体在受压状态下的水平和垂直方向上的土压力大小。
下面将介绍三个与朗肯土压力公式相关的公式。
一、朗肯土压力公式朗肯土压力公式是在假设土体为塑性流体的基础上推导出来的,其表达式为:P = KσH其中,P为土压力,K为土的压力系数,σ为土的有效应力,H为土的高度。
朗肯土压力公式是土力学中常用的一个公式,适用于均匀土层和水平地面。
二、朗肯土压力公式的推导朗肯土压力公式的推导基于土体的弹塑性特性,假设土体是塑性流体。
根据土体的应变关系,可以得到土体的应力关系。
在水平方向上,土体的应力是均匀的,即σh = σ。
在垂直方向上,土体的应力随深度变化,根据土压力平衡条件可以得到下面的公式:σv = Kσ其中,K为土的压力系数,表示土的抗压性能。
根据土体的单轴压缩试验可以确定土的压力系数K的值。
常见的土的压力系数K的取值范围为0.3-0.6。
三、朗肯土压力公式的应用朗肯土压力公式广泛应用于土木工程、地基工程和岩土工程中的土压力计算。
在设计土木结构时,需要考虑土体对结构的水平和垂直方向上的压力,以确定结构的稳定性和安全性。
在地基工程中,朗肯土压力公式可以用于计算土的侧压力,以确定地基的稳定性和抗震性能。
在岩土工程中,朗肯土压力公式可以用于计算土体对边坡、挡墙和隧道等结构的作用力,以确定结构的稳定性和安全性。
总结:朗肯土压力公式是土力学中常用的计算公式,用于计算土体在受压状态下的水平和垂直方向上的土压力大小。
通过推导和应用朗肯土压力公式,可以确定土的压力系数和计算土压力,从而为土木工程、地基工程和岩土工程的设计和施工提供依据。
土体主动、主动土压力概念及计算公式

[ 指南] 土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p可用图6-2 来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857 年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中, 首先作出以下基本假定。
(1) 挡土墙是刚性的墙背垂直;(2) 挡土墙的墙后填土表面水平;(3) 挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζ仍保持不变,但ζ将不断增大并超过Z 值,ZXZ当土墙挤压土体使Z增大到使土体达到被动极限平衡状态时,如图6-4的应力园O, Z x3z变为小主应力,Z变为大主应力,即为朗肯被动土压力(p) 。
土体中产生的两组破裂面与xp,45:, 水平面的夹角为。
2 朗肯主动土压力的计算根据土的极限平衡条件方程式,,2 Z =Z tg(45?+)+2c?tg(45?+) 1322,,2 Z =Z tg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,Z = Z = Y Z, Z = Z =p,代入上式得1z3xa1) 填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap= γztg(45?-)-2c?tg(45?-)= γzK-2c (6-3) aa22由公式(6-3) ,可知,主动土压力p 沿深度Z 呈直线分布,如图6-5 所示。
土主动被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p>P o>P a。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直;(2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式σ1=σ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ)σ3=σ1tg2(45°-ϕ)-2c·tg(45°-2ϕ)2土体处于主动极限平衡状态时,σ1=σz=γz,σ3=σx=p a,代入上式得1)填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为p a=γztg2(45°-ϕ)-2c·tg(45°2-ϕ)=γzK a-2c a K(6-3)2由公式(6-3),可知,主动土压力p a沿深度Z呈直线分布,如图6-5所示。
第三节朗肯压力理论(1857年提出)

第三节 朗肯土压力理论(1857年提出)一、基本原理朗肯研究自重应力作用下,半无限土体内各点的应力从弹性平衡状态发展为极限平很状态的条件,提出计算挡土墙土压力的理论。
(一)假设条件1.挡土墙背垂直、光滑; 2.墙后填土表面水平并无限延伸;3.挡墙背面光滑即不考虑墙与土之间的摩擦力。
(二)分析方法1.当土体静止不动时,深度z 处土单元体的应力为rz z =σ,rz k x 0=σ;2.当代表土墙墙背的竖直光滑面mn 面向外平移时,右侧土体的水平应力h σ逐渐减小,而z σ保持不变。
当mm 位移至''n m 时,应力园与土体的抗剪强度包线相交——土体达到主动极限平衡状态。
此时,作用在墙上的土压力x σ达到最小值,即为主动土压力,a p ; 3.当代表土墙墙背的竖直光滑面mn 面在外力作用下向填土方向移动,挤压土时,x σ将逐渐增大,直至剪应力增加到土的抗剪强度时,应力园又与强度包线相切,达到被动极限平衡状态。
此时作用在''''n m 面上的土压力达到最大值,即为被动土压力,p p 。
二、朗肯主动土压力当墙后填土达主动极限平衡状态时,作用于任意z 处土单元上的1σσ==rz z ,3σσ==a x p ,即x z σσ>。
1、无粘性土将rz r ==σσ1,a p =3σ代入无粘性土极限平衡条件:a rzK tg =-=)245(213ϕσσο式中:)245(2ϕ-=οtg K a ——朗肯主动土压力系数。
a p 的作用方向垂直于墙背,沿墙高呈三角形分布,当墙高为h (z=h ),则作用于单位墙高度上的总土压力Ka rh E a 22=,a E 垂直于墙背,作用点在距墙底3h处。
2、粘性土将a z p rz ===31,σσσ,代入粘性土极限平衡条件:)245(2)245(213ϕϕσσ-•--=οοtg c tg 得Kaa a crzK tg c tg p 2)245(2)245(21-=-•--=ϕϕσοο说明:粘性土得主动土压力由两部分组成,第一项:a rzK 为土重产生的,是正值,随深度呈三角形分布;第二项为粘结力c 引起的土压力a K c 2,是负值,起减少土压力的作用,其值是常量。
土主动、被动土压力概念及计算公式.

基本原理
库伦于1776年根据研究挡土墙墙后滑动土楔体的静力平衡条件,提出了计算土压力的理论。他假定挡土墙是刚性的,墙后填土是无粘性土。当墙背移离或移向填土,墙后土体达到极限平衡状态时,填后填土是以一个三角形滑动土楔体的形式,沿墙背和填土土体中某一滑裂平面通过墙踵同时向下发生滑动。根据三角形土楔的力系平衡条件,求出挡土墙对滑动土楔的支承反力,从而解出挡土墙墙背所受的总土压力。
墙背所受总主动土压力为P a ,其值为土压力分布图中的阴影部分面积,即
γ+-γ=--γ=
22c 2K cH 2K H 21z H (K c 2HK (2
1
P a a 0a a a (6-5
2填土为无粘性土(砂土时
根据极限平衡条件关系方程式,主动土压力为
a a zK 2
45(ztg p 2γ=ϕ
-︒γ= (6-6
p p p K c zK tg c ztg p 22
45(2245(2+=+︒⋅++︒=γϕ
ϕγ (6-8
填土为无粘性土时
p p zK ztg p γϕ
γ=+
︒=2
45(2 (6-9
式中: P p ——沿墙高分布的土压力强度,kPa ;
K p ——被动土压力系数,2
45(2
ϕ
+
=tg Kp ;
其余符号同前。
取土楔ABC为脱离体,作用于滑动土楔体上的力有:①是墙对土楔的反力P ,其作用方向与墙背面的法线成δ角(δ角为墙与土之间的外摩擦角,称墙摩擦角;②是滑动面PC上的反力R ,其方向与BC面的法线φ角(φ为土的内摩擦角;③是土楔ABC的重力W。根据静力平衡条件W、P、R三力可构成力的平衡三角形。利用正弦定理,得:
河海大学_土力学_课后习题答案

河海大学_土力学_课后习题答案思考题2 2-1土体的应力,按引起的原因分为自重应力和附加应力两种;按土体中土骨架和土中孔隙(水、气)的应力承担作用原理或应力传递方式可分为有效应力和孔隙应(压)力。
有效应力是指由土骨架传递(或承担)的应力。
孔隙应力是指由土中孔隙流体水和气体传递(或承担)的应力。
自重应力是指由土体自身重量所产生的应力。
附加应力是指由外荷(静的或动的)引起的土中应力。
2-2 自重应力是指由土体自身重量所产生的应力。
由静水位产生的孔隙水应力称为静孔隙水应力。
土体自重应力应由该点单位面积上土柱的有效重量来计算,如果存在地下水,且水位与地表齐平或高于地表,则自重应力计算时应采用浮重度,地下水位以下的土体中还存在静孔隙水应力。
2-3 附加应力是指由外荷(静的或动的)引起的土中应力。
空间问题有三个附加应力分量,平面问题有两个附加应力分量。
计算地基附加应力时,假定地基土是各向同性的、均匀的、线性变形体,而且在深度和水平方向上都是无限的。
2-4 实际工程中对于柔性较大(刚度较小)能适应地基变形的基础可以视为柔性基础。
对于一些刚度很大不能适应地基变形的基础可视为刚性基础。
柔性基础底面压力的分布和大小完全与其上的荷载分布于大小相同;刚性基础下的基底压力分布随上部荷载的大小、基础的埋深和土的性质而异。
2-5 基地中心下竖向附加应力最大,向边缘处附加应力将减小,在基底面积范围之外某点下依然有附加应力。
如果该基础相邻处有另外的荷载,也会对本基础下的地基产生附加应力。
2-6 在计算地基附加应力时,假定地基土是各向同性的、均质的、线性变形体,而且在深度的水平方向上都是无限的,这些条件不一定同时满足,因而会产生误差,所以计算结果会经常与地基中实际的附加应力不一致。
2-7 有效应力是指由土骨架传递(或承担)的应力。
孔隙应力是指由土中孔隙流体水和气体传递(或承担)的应力。
静孔隙水应力:习题22-1 解:根据图中所给资料,各土层交界面上的自重应力分别计算如下:cz0 0urhwwcz1 1h1 18.5'cz2 1h1 cz2 1h1 cz3 1h1 cz4 1h1 2-2解:23kPa7kPa55 (2 03h 37 1 8 122h 'h2' 55 222h 'h2 '2 'h3 221 0 )1kPa65 (1 946 5 10 )3kPa9 22kPa1 11h 'h2 '2 'h3 3'h 2249 2(1 9.5 10 )土的最大静孔隙水应力为:u0 rwhw 10 6 60kPa FV P G P GAd 2106基底压力:2 0 63 __ 3(1 62kN46 6pmpmaxinFvl b(16el)0.3178.k1Pa) 95.k9Pa6基底静压力:pn pmin r0d 95.9 17 1.0 78.9kPa pt pmaxpmin178.1 95. 98k2P.2 a只有前两章的,不过包括所有的思考题① 求O点处竖向附加应力由:m lzo12 n z 0 0 KS 0.250 0bb.5 4KSpn 4 0.25 78.9 78.9kPa b 1.5 0.5 n zb 0.5pt2由:m l0 Kt1 0 Kt2 0.2500 2 0.2582.2220.55kPazo2 2Kt1由:m lpt20 zo3 2Kt2bzo4 2KS4pt22 n z 2 0.25b82.22.50 KS4 0.250 020.55kPaz0 z01 z02 z03 z04 120kPa②求A点下4m处竖向附加应力由:m lzA16 4 n z 4 2.7 KS 0.103 6bb.52KSpn 2 0.1036 78.9 16.35kPa0.67 Kt 0.0695b662Ktpt 2 0.0695 82.2 11.4258kPa1.50.25 n z4由:m lzA2③zA zA1 zA2 16.35 11.4258 27.78kPa求B点下4m处竖向附加应力由:m l zB11.33 KS 0.1412b3b32KSpn 2 0.1412 78.9 22.28kPapt20.141282.225.80kPa3 1 n z 4zB2 KS由:m lzB3 Kt1pt2pt231 n z82.2282.221.33 Kt1 0.058 5Kt2 0.08260.0585 0.08262.39kPa3.39kPazB2 Kt2zB zB1 zB2 zB3 zB4 33.86kPa2-3 解:2-4 解:① 求自重应力zM 1h1 1'h2 19 4 (20 9.8) 1 86.19kPa zN zM 3'h3 86.19 (18.5 9.8) 3 112.26kPa 第三章思考题3 3-1水在土中的渗透速度与试样两端水平面间的水位差成正比,而与渗径长度成反比,即:v khLki 即为达西定律。
建筑基坑侧壁主动土压力计算原则分析探讨

建筑基坑侧壁主动土压力计算原则分析探讨发布时间:2022-03-10T06:58:25.632Z 来源:《新型城镇化》2022年1期作者:谢建勇[导读] 并通过项目案例的方式,就邻近建筑物低于基坑情况下,基坑侧壁土压力计算进行分析。
身份证号码:45222319880223xxxx 摘要:基坑壁土压力计算一般采用朗肯土压力理论,在面对荷载形式不同的情况下,土压力计算方式也各不相同,本文在各项规范对基坑侧壁主动土压力计算方式的基础上,归纳出五项不同的荷载力形式,并通过项目案例的方式,就邻近建筑物低于基坑情况下,基坑侧壁土压力计算进行分析。
关键词:建筑基坑;主动土压力;计算前言:在节约用地政策不断深入和建筑不断增多的背景下,为了满足需要工程建方向不断朝着地下发展,基坑工程开展通常与已有兼职距离较近,并且部分建筑物地下室面积远超过地面使用面积,面对这样的情况,基坑工程与相邻建筑基础之间的土体便会受到限制,在基坑支护结构上的土压力称之为有限土压力,基坑支护机构承受的荷载力不同,其计算方式也不同,一般根据《建筑基坑支护技术规程》规定进行土压力计算。
一、主动土压力形式在没有附荷的情况下,各规范提供主动土压力计算原则一般都是朗肯土压力理论,但是在有荷载的情况下,《建筑地基基础设计规范》给出了基本计算理论,并指定计算方式按照地区经验进行设计,在不同荷载下,主动土压力计算也无法进行比较分析,附加荷载主要有以下几种方式[1]。
(一)均匀荷载就均匀荷载而言,各项规范荷载计算是一致的,如图1所示是基坑壁顶均匀分布荷载示意图,当基坑壁顶存在均匀荷载q时,产生的竖向附加应力也为q,其产生的土压力为E,公式为:E=q·kai,其中,q表示为均匀荷载(kPa);kai表示为主动土压力系数。
图2:基坑壁顶集中荷载示意图图中P表示集中荷载;φ表示土体内摩擦角;Ka表示主动土压力系数;?Ea表示集中荷载竖向应力;d表示竖向应力分布范围。
excel计算大全-房建-主动土压力计算(库仑、朗肯理论)
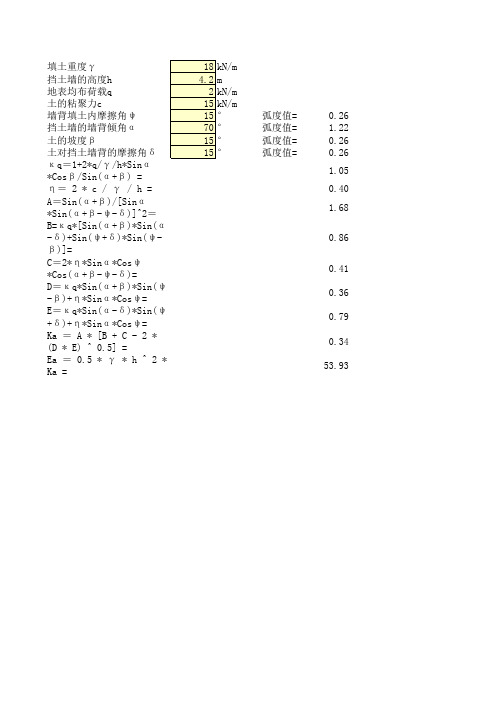
填土重度γ 18 kN/m 挡土墙的高度h 4.2 m 地表均布荷载q 2 kN/m 土的粘聚力c 15 kN/m 墙背填土内摩擦角ψ 15 ° 弧度值= 挡土墙的墙背倾角α 70 ° 弧度值= 土的坡度β 15 ° 弧度值= 土对挡土墙背的摩擦角δ 15 ° 弧度值= κq=1+2*q/γ/h*Sinα*Cosβ/Sin(α+β) = η= 2 * c / γ / h = A=Sin(α+β)/[Sinα*Sin(α+β-ψ-δ)]^2= B=κq*[Sin(α+β)*Sin(α-δ)+Sin(ψ+δ)*Sin(ψ-β)]= C=2*η*Sinα*Cosψ*Cos(α+β-ψ-δ)= D=κq*Sin(α+β)*Sin(ψ-β)+η*Sinα*Cosψ= E=κq*Sin(α-δ)*Sin(ψ+δ)+η*Sinα*Cosψ= Ka = A * [B + C - 2 * (D * E) ^ 0.5] = Ea = 0.5 * γ * h ^ 2 * Ka =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
采用朗肯土压力理论计算主动、被动土压力 朗肯土压力理论是依据半空间体的应力状态和土的极限平衡理论推出土压力强度的计算式。它的假设条件1.挡土墙背垂直;2.墙后填土表面水平;3.挡墙背面光滑即不考虑墙与土之间的摩擦力。 应用范围: 1.墙背与填土条件: (1)墙背垂直,光滑,墙后填土面水平 (2)墙背垂直,填土面为倾斜平面, (3)坦墙(工程上把出现滑裂面的挡土墙定义为坦墙)。 (4)还适应于“∠”形钢筋混凝土 挡土墙计算 2.地质条件 粘性土和无粘性土均可用,均有公式直接求解 影响土压力的因素: 作用在挡土支护结构上的土压力受以下因素制约: 1不同土类中的侧向土压力差异很大。采用同样的计算方法设计的挡土支护结构,对某些土类可能安全度很大,而对另一些土类则可能面临倒塌的危险。因此在没有完全弄清挡土支护结构土压力的性能之前,对不同土类应区别对待。 2 土压力强度的计算及其计算指标的取值与基坑开挖方式和土类有关。当剪应力超过土的抗剪强度时,背侧土体就会失去稳定,发生滑动。由于基坑用机械开挖,一般进度均较快,开挖卸荷后,土压力很快形成,为与其相适应采用直剪快剪或三轴不排水剪是合理的。但剪切前是否要固结,则根据土的渗透性而定。渗透性弱的土,由于加荷快、来不及固结即可能剪损,此时宜采用不固结即进行剪切;反之,渗透性强的土,宜固结后剪切。 3土压力是土与挡土支护结构之间相互作用的结果,它与结构的变位有着密切的关系,从而导致设计土压力值的不确定性。如经典的库仑土压力仅考虑主动与被动状态;在挡土支护结构变形很小时,要采用静止土压力(其值无统一求法);对于作用于多支点挡土支护结构的土压力则按弹塑性理论进行计算。 图1 半空间体的应力状态 (a)单元体的初始应力状态; (b)达到朗肯状态的应力路径; (c)主动朗肯状态的剪切破坏面; (d)被动朗肯状态的剪切破坏面
如图1a在半空间土体中取一竖直切面AB,在AB面上深度为Z处取一土单元体,在静止土压力状态下,作用在单元体上的大主应力1为竖直向应力z,小主应力3为水平向应力zk0,单元体处于弹性平衡状态,其应力圆1o位于强度包线下方。假定在某种原因下土体朝侧向松开,在保持大主应力1不变的条件下小主应力3不断减少,其应力圆直径随之增加,最终当应力圆2o与强度包线相切时,单元体处于主动极限平衡状态,此时的小主应力3仍在水平向,即为主动土压力强度a(图1b),土体中的两组滑移面与水平面成2/45(图1c)。当在某种原因下土体朝单元体侧向挤压时,水平向应力不断增加,应力
圆直径不断减小至一点,当水平向应力继续增大到超过竖直向应力时,水平向应力成为大主应力1,而竖直向应力变成了小主应力3,此后随着水平向应力的增加应力圆直径又不断增加,最终应力圆3o与强度包线相切,单元体处于被动极限状态,此时 大主应力1在水平向,并被认为是被动土压力强度p(图1b),土体中两组滑移面与水平面的夹角为2/45(图1d)。 朗肯认为可以用直立的挡土墙来代替上述竖直面AB左边的土体,如果满足墙背与填土界面上的剪应力为零的条件,并不改变右边土体中的应力状态。当挡土墙的变位符合上述主动或被动极限平衡条件时,作用在挡土墙墙背上的土压力即为朗肯主动土压力或朗肯被动土压力。墙背直立、光滑,墙后填土面水平的挡土墙满足这种条件。 主动土压力 由图1b可知任一深度z处的朗肯主动土压力强度a为小主应力1d,而大主应力1为上覆土压力z,根据土的极限平衡条件,则有: )2/45tan(2)2/45tan(cza
或 aaaKczK2 (1) 式中 aK—朗肯主动土压力系数,)2/45(tan2aK; —土的重度;
c、—土的粘聚力和内摩擦角。 对于无粘性土,c=0,aazK,主动土压力仅仅是由土的自重所产生,其强度随深度线性增加,呈三角形分布(图2a)。主动土压力的合力aE为三角形的面积,其值由(1)式计算;合力作用在三角形的重心处,即在挡土墙墙底以上H/3处。
aaKHE221 (2)
式中 H—挡土墙的高度。
图2 朗肯主动土压力的计算 (a)无粘性填土; (b)粘性填土
当墙后填土为粘性土时,由式(1)可知主动土压力由两部分组成,粘聚力c的存在减少了作用在墙上的土压力,并且在墙上部形成一个负侧压力区(拉应力区),见图2b中的三角形acd。由于墙背与填土在很小的拉应力下就会脱开,该区域的土中会出现拉裂缝,在计算作用在墙背上的主动土压力时应略去这部分负侧压力,而仅仅考虑三角形bce部分的土压力。此时,由土压力为零的条件可计算受拉区的高度0z: 0200KacKzazza
得到 aKcz20 (3) 0z有时也被称为土的“临界高度”,被认为是粘性土中无支挡直立开挖的最大深度。
主动土压力合力aE则为三角形bce的面积,其值由式(8-7)计算: )2)((210aaaKcHKzHE (4)
或 20)(21zHKEaa aE作用在三角形bce的形心上,即在挡土墙底面以上(H-0z)/3处。
对于粘性土的上述算法,有学者认为低估了主动土压力值。为此采用了一些修正方法。例如在墙背底面处的主动土压力值仍用式(1)计算,但墙顶处的土压力取为零值,而不是按式(1)求得的负值。作用在墙背上的主动土压力合力则为:
)21(212aaaKHcKHE。
或者仍按式(4)计算主动土压力值,但应考虑0z范围内张裂缝中从地面渗入的水压力作用。 被动土压力 由图1b可知任一深度z处的朗肯被动土压力强度p为大主应力1,而小主应力3为上覆土压力z,根据土的极限平衡条件,则有: )2/45tan(2)2/45(tan2czp
或 pppKczK2 (5) 式中 pK—朗肯被动土压力系数,)2/45(tan2pK。
图3 朗肯被动土压力的计算 (a)无粘性填土; (b)粘性填土
无粘性土的朗肯被动土压力沿深度也呈三角形分布(图3a),合力pE值由式6计算,作用在墙底以上H/3处。
ppKHE221 (6)
粘聚力c的存在增加了被动土压力,作用在墙背上的被动土压力呈梯形分布,如图3b
所示,合力pE值为梯形面积,可以用矩形abdc与三角形cde的面积之和求得:
21pppEEEpp
KHKcH2212
(7)
pE作用在梯形的形心上,也可以用分块求矩的方法计算pE距墙底的距离hz
ppphEHEHEz3221 (8)
关于朗肯条件 现以无粘性土填土和主动应力状态为例,朗肯条件的更一般情况为地面倾斜时,土体在侧向和深度上都是无限的情况(图4a)。此时如果土体有机会侧向伸展足够的量,则在土体中形成两簇滑移面(图4b),与竖直面BB的夹角分别为和,和的值为:
)sinsin(sin21)90(211 (9a)
)sinsin(sin21)90(211 (9b) 以及 90 (9c) 如果土体绕B点转动足够的量,使A点达到主动平衡条件,在土中也产生同样两簇滑移面,不过仅限制在AAB的范围内(图4c)。这两种情况在竖直面BB上都作用着朗肯主
动土压力aE,其值可用式(10)计算,方向与地面平行。而作用在AB面上的总压力等于aE与土楔BAB的重力的矢量和。
图4 土体的伸展—朗肯主动应力状态 (a)倾斜地面的原位静止土压力; (b)侧向和深度是无限的土体的伸展; (c)土楔绕B点转动产生的伸展; (d)符合朗肯条件的挡土墙
]coscoscoscoscoscos[cos2122222hEa
=aKh221 (10) 式中h是BB的高度,aK是括弧中的值,即朗肯主动土压力系数。 我们将图中BA面称为第一破裂面,将AB面称为第二破裂面。当用挡土墙时,填土中存在朗肯主动应力状态的条件是必须满足以下两个条件:①挡土墙不阻碍第二破裂面的形成,即墙背倾角>夹角。②位于第二破裂面与墙背之间的土楔CBA不沿墙背下滑,而是附在墙背上与墙一起移动,即作用在墙背上的总压力与墙背法线的夹角小于外摩擦角(图4d))。
的挡土墙称为坦墙,可知符合条件②的坦墙适用朗肯条件,此时朗肯土压力作用
在过墙踵的竖直面上。的挡土墙称为陡墙,陡墙一般不符合朗肯条件,但在墙背倾角、填土坡角、内摩擦角和外摩擦角满足式(8-14)的关系时,墙后土体仍处于简单极
限应力状态,朗肯公式仍能使用。
)sinsin(sin21)sinsin(sin2111 (11)
式(11)的关系一般不易满足,当墙背直立(=0)、光滑(=0)、填土面水平(=0)时,式(11)的关系得到满足。此时,直立墙背相当于上述竖直面BB,2/45,)2/45(tan2aK,与前述一致。
