高等传热学相变导热解(移动边界)
高等热值交换技术 边界层的流动和换热

平均
1 L tw t f tw t f L 0 温差
1 Lq q L x x dx L 0 h dx L 0 Nu dx x x
qL 平均努塞尔数: Nu tw t f Nu 0.680Re1/ 2 Pr1/ 3 偏差2.4% 1/ 2 1/3 Nu 0.664Re Pr
第三章 层流边界层的流动和换热
3-1 外掠平板层流边界层流动的相似解 h=f(u,tw,tf,λ,ρ,c,η,α,l,ψ)
流体平行外掠平板强迫对流换热的解,可以表示成特征数关联 式的形式,即
Nu=f(Re,Pr)
特征数关联式中变量个数大为减少,更突出地反映相关物理量 之间的依赖关系,及其对对流换热的综合影响。
1. 布拉修斯无量纲参数得到外掠平壁的层流边界层流 动的相似解; 2. 戈尔德斯坦研究在什么条件下,可实现相似变量的 变换而求得相似解; 3. 赛比西和布雷德肖 应用龙格-库塔法求得同样问题 的解; 4. 豪沃思用数值积分得到的结果如下表:
由上述计算得到的外掠 平壁层流边界层 流动的速度分布:
(1) 流动边界层厚度
这一结果与理论分析结果一致。附加项Prf/Prw 用以考虑物性变化和热流方向的影响。
43
作业:
1. 试证明:Prw<<1 的流体外掠平壁层流边界层流动换热的局 部努谢尔特数为:
Nu
1
Re x Pr
2
1
1
2
2. 试证明:Prw>>1 的流体外掠平壁层流边界层流动换热, 若假定速度分布与温度分布均为直线,使用积分方程求解证 明:
对有限控制容积建立动量热量平衡方程 对边界层微分方程进行积分
积分方程 25
高等热质交换技术 边界层的分析
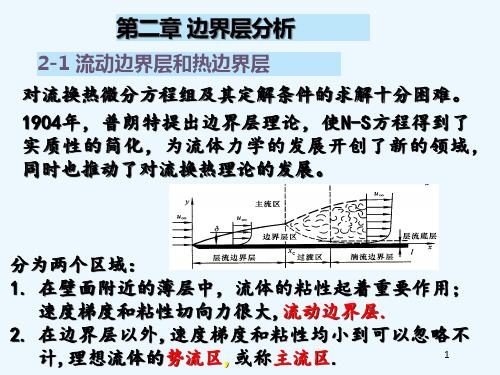
1.速度边界层(流动边界层) 速度发生明显变化 的 流体薄层。
流动边界层厚度 :
u 0.99u
流场的划分: 主流区:y< 理想流体
紊流核 心
u 边界层区: y 速度梯度存在与粘性力的作用区。
边界层的流态: 层流边界层、过渡区、紊流边界层
2
临界距离xc : 边界层从层流开始向紊流过渡的距 离。其大小取决于流体的物性、固体壁面的粗糙度等 几何因素以及来流的稳定度,由实验确定的临界雷诺 数Rc给定。
对流项 导热项
对流项进行比较分析
1.假定Δ/Δ ≥ 1,在这种情形下,导热项的系数就应 该等于 1 1 t P r Re 2 t
由于
1 Re
t
1 Re P r
Pr t
这种情形下成立的条件只能是Pr ≥ 1,意味着这样的流 体,流动边界层厚度大于或等于温度边界层厚度.
温度的无量纲参数采用: T Tw T Tw
变化范围0-1
热边界层厚度δ t度不一定等于流动边界层厚度δ, δ=LΔt , Δt是某个百分数。
无量纲参数:
x X L
y Y L
1 2 2 2 U V 2 2 2 X t Y c p Lu t X Y
导热项是偏微分方程中最高阶项,必须考虑,但 2 2 2 远小于 可以忽略不计。 2 2 X Y
无量纲能量方程
1 1 2 U V 2 X t Y Pr Re 2 Y t
有量纲边界层能量 方程
T T 2T u v x y cp p y 2
u v 0 x y
边界层对流 换热微分方 程组:
传热学(chapter7)-边界层 数量级分析

t − tw = 0.99 t f − tw
1 >> δ
∂ 2u ∂u ∂p ∂u ρ = − ∂x + µ u ∂x + v ∂y ∂y 2
∂ 2u ∂u ∂p ∂u ρ = − ∂x + µ u ∂x + v ∂y ∂y 2
∂ 2u ∂u ∂p ∂u ρ = − ∂x + µ u ∂x + v ∂y ∂y 2
∂ 2u ∂u ∂u u +v =ν 2 ∂y ∂y ∂x
∂ 2t ∂t ∂t ρc p u ∂x + v ∂y = λ ∂y 2 Fra bibliotek物理现象
(1)当粘性流体在壁面上流动时,由于粘性的作用, 在贴附于壁面的流体速度实际上等于零,即在 y=0,u=0处;。 (2)此后随 y 增加 ,u增加 。
(3)壁面法向(y 向)的速度分布,如上图所示。 经过一个薄层后u接近主流速度。 (4)
空气 u∞ = 10m / s 平壁
2mm
µ =0
第六章对流换热的基本方程1什么是边界层流动和热2为什么研究边界层流动和热变化的分布区域边界层外流动和热稳定物理现象1当粘性流体在壁面上流动时由于粘性的作用在贴附于壁面的流体速度实际上等于零即在增加u增加向的速度分布如上图所示
第六章
对流换热的基本方程
1、什么是边界层(流动和热)
2、为什么研究边界层(流动和热变化的 分布区域,边界层外流动和热稳定)
高等传热学

高等传热学
热传导是由热量从一个区域传递到另一区域的物理现象,是传热学的一个分支。
随着
科学技术的进步,许多高级应用领域需要掌握理论知识和实际技能。
传热学有两个分支:
高等传热学和低等传热学。
高等传热学是传热学的一个重要分支,主要研究物质在高温、高压、特殊流体动力学
条件下的热通量、热传导和热潜力等过程的物理和数学的研究。
高等传热学的主要研究内
容有:热传导(热通量)原理;流体动力学控制的传热现象;热导率的测定及其机理;临
界状态的热输运;紊流传热、气固耦合传热、辐射传热等。
热传导是物体内从高温处向低温处自动传递的能量形式,也是化学能反应过程中最基
本的物理方程,是传热学中最重要的理论方程之一。
热导率是表征物质热导率的物理参数,是研究物质的传热系数,可以准确的描述物质的热传导的量的变化趋势。
总的来说,高等
传热学是研究物质热运动趋势及物质本身的性状和变化的学科,是传热学中重要的理论分支。
热量的传递和相变

热量的传递和相变热量是物体内部的能量,它的传递对于我们的日常生活和工业生产来说至关重要。
热量传递的方式有三种,即传导、对流和辐射。
此外,当物体温度改变时,它可能经历相变,比如液体变成固体或气体变成液体。
本文将深入探讨热量的传递和相变,以及相关的原理和应用。
一、传导传导是通过物质内部的热能分子碰撞传递热量的过程。
根据物质的导热性能,可以分为导热体和绝热体。
导热体具有良好的导热性能,如金属、石头等,它们能够迅速传导热量。
而绝热体则是指导热性能极差的物体,如木材、绝缘材料等,它们几乎不传导热量。
在传导过程中,热量从高温区流向低温区,遵循热能传递的基本规律——热流。
热流的大小与物体的温度差、导热性能和物体的厚度有关。
而导热的速度受到物体的材料和形状、温度差、时间等因素影响。
二、对流对流是指以流体为媒介传递热量的过程。
流体可以是液体或气体,因为它们的分子之间有较大的间隙,使得热量能够通过对流传递。
对流可以分为自然对流和强制对流两种。
自然对流是指流体在温度梯度作用下,由热量较高的区域向热量较低的区域产生的对流现象。
比如,太阳辐射地表,使得地表的空气被加热,产生对流。
而强制对流是通过外界的力或设备施加的压力差来产生的,比如风扇、空调等。
三、辐射辐射是以电磁波的形式传递热量的过程,而且可以在没有传导和对流的介质中进行。
热辐射是由物体内部的分子、原子或电子的热运动产生的,常见的有红外辐射、可见光和紫外辐射。
热辐射的强度与物体的温度有关,根据斯特藩-玻尔兹曼定律,辐射功率与物体绝对温度的四次方成正比。
辐射的传递方式不需要在空间中具有介质,因此在真空中也能传递热量。
例如,太阳的热量就是通过辐射传递到地球表面。
四、相变相变是物质由一种物态转变为另一种物态的过程,常见的有固体→液体(熔化)、液体→气体(蒸发)、气体→液体(冷凝)和液体→固体(凝固)等。
相变过程中,物质的温度和压强会保持一定的恒定值。
在相变过程中,热量被吸收或释放,但温度不发生明显的变化。
高等传热学知识点总结

引言概述:在高等传热学中,掌握各种传热方式以及其基本原理是非常重要的。
本文将分析五个大点,其中包括传热方式的分类、传热边界条件、传热传导、传热对流以及传热辐射。
每个大点都将进一步分解为五到九个小点,详细阐述相关知识。
通过本文的学习和理解,读者将能够深入了解高等传热学的知识点。
正文内容:一、传热方式的分类1.传热方式的基本分类2.对流传热与传导传热的区别3.辐射传热的特点及其应用4.相变传热的机理及其实例5.传热方式在工程中的应用案例二、传热边界条件1.传热边界条件的定义及分类2.壁面传热通量的计算方法3.壁面传热系数的影响因素4.壁面传热条件的实验测定方法5.边界条件的选择与优化三、传热传导1.传热传导的基本原理2.导热系数的计算方法3.等效导热系数的定义及其应用4.传热传导方程的推导和求解方法5.传热传导的数值模拟方法及其应用四、传热对流1.对流传热的基本原理2.传热换热系数的计算方法3.流体流动与传热的耦合关系4.对流传热的实验测定方法5.传热对流的同非稳态传热问题五、传热辐射1.辐射传热的基本原理2.黑体辐射的特性和计算方法3.辐射传热过程的数学模型4.辐射系数的影响因素及其计算方法5.传热辐射的应用案例和工程实例总结:通过对高等传热学知识点的总结,我们深入了解了传热方式的分类、传热边界条件、传热传导、传热对流以及传热辐射等重要知识点。
掌握这些知识,可以帮助我们更好地理解传热现象的基本原理及其在工程实践中的应用。
同时,对于热传导与辐射换热和传热对流以及其边界条件的掌握,有助于我们解决工程中的传热问题,优化设计和提高热能利用效率。
在今后的学习和实践中,我们应不断巩固和拓展这些知识,以更好地应对传热学的挑战,并为实际工程问题提供合理的解决方案。
第5章 对流传热理论与计算-3-边界层理论
2 2v v v 1 p v u v 2 2 x y y y x
u x
v y
0
简化依据——边界层理论 方法——数量级分析法 数量级分析法—通过比较方程式中各项的数量级大小, 将数量级大的项保留下来,舍去数量级较小的项,从而 实现方程式的合理简化
50
换热充分发展的特点
(1)热边界层厚度不变 (2)局部表面传热系数为常数 (3)无量纲温度维持不变
t rx t wx t fx t wx
trx—距管轴线r、入口x处的流体温度 twx—离入口x处的管壁温度 tfx—离入口x处的截面上流体的平均温度
51
管内对流传热时的局部对流传热系数沿管长的变化
状流动
☆湍流:Re大,惯性力起主要作用,流动不规则、杂
乱无章
☆边界层内粘性力和惯性力的相对大小使边界层内也
会出现层流、紊流两种不同流态
17
平板前缘:δ小,速度梯度大,粘性力大,为层流层流 边界层(laminar boundary layer)
特点:层状、有秩序的滑动状流动,各层之间互不干扰
上节课
本章的目标——用理论或实践的方法具体给出各种场合
下h的计算关系式(经验半经验公式)
对流传热的影响因素 ——流动的起因及流动的状态 ——流体的热物理性质 ——换热面的形状、大小和位置 ——相变的影响、介质类型的影响 对流传热的分类
1
上节课
换热微分方程式——对流传热的计算式
h
t
t w t f y
| y 0
能量微分方程式——计算流体的温度场
第七讲热传导反问题
X )
4alτ
相界面的条件
tlX = t p
t p = t0 + Berf (
X )
4alτ
B
=
tp erf (
− t0 X
)
→ tl
=
t0
+
tp erf (
− t0 X
erf ( )
4alτ
4alτ
tp = const → X = k
4alτ
→
B
=
t p − t∞ erf (k)
x )
4alτ
( ) −λl
第六讲 具有移动边界的热传导 问题
——Stefan问题的解析
1 凝固问题简化的模型
t
dX
tp
O
x
tw
λ ρ
γ
X (τ )
能量平衡
t q
dX
qconduct tp
=λ
t p − tw X (τ )
qlatent
=
ργ
dX dτ
O
tw
λx
ρ γ
q = q conduct
latent
X (τ ) cp = 0
tl tp
− t∞
−
t ∞
=
4alτ
erfc k
as al
相界面的位置
λs
∂ts ∂x
− λl
∂tl ∂x
=
ρlγ
dX dτ
e−k2 + λl erf (k) λs
−k2 as
( ) as t p − t∞ e al
= kγ π
al t p − tw erfc(k as ) cpl t p − tw
第07讲相变传热
erf
x 4st erf() x 4l t
16 a 16 b
Tl (x, t) Ti Tm Ti erfc s l
erfc
2
由下式确定;
T T d s s l k k L s l x x d t
1 2b
2 s l Te e k L l sT mi e r f ( )k T T C T T e r f c s l s p mw s l mw
引起数学处理较为困难的其他因素:
在相变前、进行中和后,其物理性质依赖于温度,而温度分布是 三维的和瞬时的变化。 有时,溶解和凝结时发生的复杂又令人困惑的现象,使得传统的分 析方法无法解决。
3
热传导方程
静止的均匀物体内含有热源的各向同性物体的热传导方程
T r , t c ( k T r , t) q r , t p t
T ,t T ,t T x0,t 0 l x s x i
1 1
固液界面x=s ( t )处的耦合条件
T xt , T xt , T s l m k s T T d s s l k L l x x d t 1 2 a 1 2 b
2 k T
( 5 a ) ( 5 b ) ( 5 c )
( 6 )
h t
r V k s k = k l
h h s h h l
s = l
把原来在两个活动区域及固液界面成立的方程组转换为在一个固定 区域内成立的方程,无需跟踪界面。便于数值计算。
相变传热
+hiT=fi
r,t
Si
5
解析解
——分离变量法
平板
T
x,t
t
2T x,t
x2
T 0 x
k T hT 0 x
T F x
0 x L,t 0 x 0, t 0 x L, t 0 t 0, 0 x L
T x,t X xt
1 dt 1 d2X x t dt X x dx2
引起数学处理较为困难的其他因素:
在相变前、进行中和后,其物理性质依赖于温度,而温度分布是 三维的和瞬时的变化。
有时,溶解和凝结时发生的复杂又令人困惑的现象,使得传统的分 析方法无法解决。
2
热传导方程
静止的均匀物体内含有热源的各向同性物体的热传导方程
cp
T r,t
t
(kT
r,t
)
q& r,t
/
1/2 2
)
erfc
x
T3(x, t) Ti
41t
Tm2 Ti
erfc(2
1/2 2
/31/2
)
32
相界面的位置
s1(t) 21 1t s2 (t) 22 2t
利用相界面的能量守恒条件
Ste1
1
exp(12
)
erf ()
11
exp(121 /2 )
erf (2 ) erf (1 1 /2 )
(5 c)
h k2T
rV
(6)
t
=
s l
k=
k
s
k l
h hs h hl
把原来在两个活动区域及固液界面成立的方程组转换为在一个固定 区域内成立的方程,无需跟踪界面。便于数值计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等传热学导热理论——相变导热(移动边界问题)讨论
第五讲:相变导热(移动边界问题):
移动边界的导热问题有许多种,本讲只讲固液相变时的导热模型。
5.1 相变换热特点与分类: 特点:
(1) 相变处存在一个界面把不同相的物质分成两个区间(实际不是一个面,
而是一个区)。
(2) 相变面随时间移动,移动规律时问题的一部分。
(3) 移动面可作为边界,决定了相变问题是非线性问题。
分类:
(1) 半无限大体单区域问题(Stefan Question ) (2) 半无限大体双区域问题(Neumman Question ) (3) 有限双区域问题
5.2 相变导热的数学描述和解: 假定:固液两相内部只有导热,没有对流(适用于深空中相变)。
物性为常量。
不考虑密度变化引起的体积变化。
控制方程:
对固相:
2
21s s s t t a x
τ
∂∂=∂∂ 对液相:
2
2
1l l l t t a x
τ
∂∂=
∂∂
初值条件:0:s l t t t τ∞=== 边界条件:
0:::s l w l s l s x t ort t x t ort or
x t ort t ∞
===∞≠∞
=∆=
在相变界面,热量守恒,温度连续,Q l 为相变潜热:
()():s l s
l
l l
s l p t t d x Q and
t t t x
x
d δτδτλλρτ
∂∂==+==∂∂
5.2.1 半无限大体单区域问题(Stefan Question )的简化解:
以融解过程为例:
忽略液相显热,
2
210l l l t t a x
τ
∂∂==∂∂,方程解为一直线,由边界条件得:
()/l w p w t t t t x δ
=+-
对固相,忽略温差:w p t t t ∞==,即固相温度恒等于相变温度等于初始温度。
由相变处得换热条件求δ的变化规律:
()()():0()l l l
l l
p w l l
t d d x Q t t Q x
dx
d λδτδτδτλρρδ
τ
δ∂==+=
-+∂=
=
式中:()/l l p w l Ste c t t Q =-叫Stefan ’s Number ,物理意义是相变时液相显热和液固潜热比。
液体厚度与时间的开平方成正比。
所以:
进入物体的融解热流密度为:0
)l l
x w p t q t t x
λ=∂=-=
-∂,
热流密度与时间的开平方成反比。
5.2.2 半无限大体单区域问题(Stefan Question )的精确解:
同样以融解过程为例:
对液相,
2
21l l l t t a x
τ
∂∂=∂∂,设方程解为(满足初始条件):
(/
l t A Berf x =+
由边界温度条件得:
l w p w
t t t t -=-
对固相,忽略温差:w p t t t ∞==,即固相温度恒等于相变温度等于初始温度。
由相变处得换热条件求δ
的变化规律,设/δΩ=度也与时间的开平方成正比。
上式是关于凝固常数的方程,叫相变问题的特征方程。
进入物体的融解热流密度为:0
()l l
x t t t q x
λλ=-∂=-=
∂,热流密度同样
与时间的开平方成反比。
5.2.3 半无限大体双区域问题(Neumman Question )的精确解:
同样以融解过程为例:
对液相,
2
21l l l t t a x
τ
∂∂=∂∂,设方程解为(满足初始条件):
2
()():)0
exp()()())/l l l l
p w l w p l l l l t d x Q x d t t erf t t Q a Ste δτδτλρτ
λ∂=+∂=
-+
=ΩΩΩ=-=
(/
l w t t Aerf x =+
由边界温度条件得:
l w p w
t t t t -=
-
,t t A -=
对固相,
2
21s s s t t a x
τ
∂∂=
∂∂,设方程解为(满足初始条件):
(/
l t t Berfc x ∞=+
由边界温度条件得:
s p t t t t ∞∞
-=
-
,t t B -=
由相变处得换热条件求δ
的变化规律,设/δΩ=
度也与时间的开平方成正比,/δΩ=。
得相变问题的特征方程:
(
)
2
l x t A
x e
δ
=Ω∂=∂(
)
2
s x t B
x
e
δβ=Ω∂=-
∂
(
)
()
2
2
))
()/()/exp()()
exp()()
p w p l w p l l l s p l l l t t t t t t a Q t t a Q erf erfc λρλβρ∞∞-+
=-
----
=
ΩΩΩΩΩ
Ω
2
2
/exp()()
exp()()
l
s s l Ste Ste erf erfc βρρ-
=
ΩΩΩΩΩΩ
进入物体的融解热流密度为:0
()l l
x t t t q x
λλ=-∂=-=
∂,热流密度还是
与时间的开平方成反比。
5.2.4 非线性问题求解方法总结:
对非线性问题,直接求解难度大,一般是进行适当简化,在简化基础上构造
()():l s l
l l
s
t t d x Q x
d x
δτδτλρλτ
∂∂=+=∂∂
一个满足大多数唯一性条件的,保留部分待解常数的解函数。
将这个解函数代入余下的唯一性条件,求出待解常数,即为近似解或精确解。
5.3 关于湖水结冰问题的讨论:
几何条件假定:湖面很大,也很深,看成半无限大体。
换热条件假定:结冰前湖水均温,为t ∞,湖水主体温度一直保持t ∞。
大气环境温度为t a ,湖面与大气间的表面传热系数为常量h 1,冰层下表面与湖水间的表面传热系数也为常量h 2。
物性假定:因为在0℃附近,冰的比热c s 《Q l ,忽略冰层热容作用。
由此可得在冰层中的温度分布为直线。
设坐标原点在湖面,冰层厚度为δ,我们根据能量守恒和平壁导热规律得:
21()1//p a p s l
s
t t d h t t Q h d δρδλτ
∞-=-++ (1)
冰层温度分布:()/s w p w t t t t x δ=+- 求解δ,令
()()()()()
112
2
2
11///////s p p a s s s p a l
s s s s s h m t t t t R h h Ste Fo
Ste c t t Q Fo h c a h δδλττρλτλ∞==--===-==
代入(1)式:
()
()22
11
()1
11(1)
1p s s l
p a p
a h t t d d Q m R d h t t h t
t d d m R d λδδρδτ
τ
δδτ
δ
∞-=
+=+
+---+=
+
00,,00s t t ττδδ∞=→===→=
(
)
2
11
11(1)
0.5
/(1d d m R du m δδτ
δτ++=-+=-⎰
{ln[1/(1)]}/(,)mR mR mR f mR τδδδ=----=
讨论:当()max ,1/mR mR τδ→∞→-。
mR 一定时,冰层的最大厚度也就确定。
此时湖水对冰层的自然对流热流量等于湖面对大气散发的热流量,湖水凝结停止。
当0p t t m R ∞=→=,湖水比热无穷大,(
)2
2111τδδ=+-→=此种情况冰层没有极大值,可一直增厚。
即11)/s h δλ=。
当1m R =,冰层得到的热流量等于散出的热流量,
ln 0,c c τδδτδ=--→==-,此种情况由于厚度不能为负值,故不会结冰,尽
管t a 小于冰点。
当,p w a t t t t ∞==,湖水比热无穷大(或湖水与冰间的换热系数无穷大),湖面与大气换热系数无穷大,有:p w
p w
s
s l
s
s l
t t t t d Q d d d Q δλρλτδδ
δ
τ
ρ--=→=
δ=
=
此即Stefan 近似解。
此处的分析方法又叫做准稳态近似法。
