第四章 二元相图
第四章 二元相图

z K 0 1 CS ( z ) K 0C0 (1 ) l
z K 0 1 CS ( z ) K 0C0 (1 ) l
讨论:
• K0<1的合金随z↗,CS ↗。
K0>1的合金随z↗,CS↘。
A C0 B A C0 CS CL CS CL
B
•
CS C L K 0 1 越大,则成分不均匀性越大,在 CL
1、表示方法: 二元合金平衡相 — 成分 — 温度 可用平面图表示。 • 纵坐标:温度
• 横坐标:成分(常用质量、摩尔和原子分数)
mB wB 100% m A mB nB xB 100% n A nB
• 表相点:表示体系所处平衡状态 ★ 相图 — 也称平衡图、状态图
T℃
表相点
L
α
T TCu L L+α TNi
• 单相区:液体L、固溶体α
• 双相区:L+α
★ 相区规则:以边相邻的
x1 C u 20
α
x3 x2 60 80 Ni
相区,相数必差1。
40
特殊匀晶相图:
L L
α
A 如:CuAu B A
α
B
如:Pb-Tl
★ 极点处结晶在恒温下进行,自由度为0,而不是1。
∵ xL = xα 增加了一个约束条件 ∴ f = C-P+1-1 = 2-2+1-1 = 0
L
α 平衡
T℃
T
设: W0、Wα、WL分别为合金 系、α 相和L相的重量。 总重:W0 = Wα+ WL ①
T
L
α
溶质:W0 x0 = Wαxα+ WL xL ② ①代入②整理得: Wα(x0 - xα)= WL(xL - x0) ③ —— 杠杆定理
第四章 二元相图

铁碳相图和铁碳合金
铁-石墨相图:Fe-C; 铁-渗碳体相图:Fe-Fe3C。
1 铁碳合金中的组元和相 L, δ, A(γ), F(α), Fe3C(渗碳体)
46
2 Fe-Fe3C相图分析
点:16个。 线:两条磁性转变线;三条等温转变线; 其余三条线: GS,ES,PQ。
区:5个单相区,7个两相区,3个三相区。
5
4.1.4 二元相图的几何规律 (1)相区接触法则:两个单相区之间必定有一个由这两个相 组成的两相区,而不能以一条线接界。两个两相区必须以单 相区或三相水平线隔开。由此可以看出二元相图中相邻相区 的相数差一个(点接触除外)。 (2)在二元相图中,若是三相平衡,则三相区必为一水平 线.这条水平线与三个单相区的接触点确定了三个平衡相及 相浓度。每条水平线必与三个两相区相邻。 (3)如果两个恒温转变中有两个相同的相,则这两条水平 线之间一定是由这两个相组成的两相区。
39
2、 组元间形成化合物的相图 稳定化合物:具有一定熔点,在熔点以下不分 解的化合物。 3、具有异晶转变的相图 一个固相转变为另一个固相的转变称为异晶转 变也称同素异构转变。 4、具有固溶体形成中间相转变的相图 5、具有有序---无序转变的相图 6、具有磁性转变的相图
40
38
4.3二元相图的分析和使用 4.3.1 其他类型的二元相图 1、 其他类型的恒温转变相图 (1)熔晶转变相图 定义:一个固相在恒温下转变成一个液相和另一个固相的转 变。 (2)偏晶转变相图 定义:一个液相在恒温下分解为一个固相和另一个液相的转 变。 (3)共析转变相图 定义:一定成分的固相在恒温下生成另外两个一定成分的固 相的转变。 (4)包析转变相图 定义:两个一定成分的固相,在恒温下,转变为一个新的固 相的转变。
第四章-二元合金相图

G
t/s
70% Sn的过共晶合金的结晶过程分析
概括起来,过共晶合金平衡结晶过程为:
t1温度以上: 液态 L70 L
19
t1~ t2温度: 液相中析出 , t2温度时发生共晶反应: L61.9 t2温度以下: 初 Ⅱ
97.5
室温组织: 初 + Ⅱ + (+)共晶
一、相律
在恒压下,在纯固态或纯液态情况下,出现的相数 小于等于主元数。在液固共存(恒温)条件下出现 的相数小于等于主元数加一。因而,对二元合金, 固态下出现的相数为1或2,液固共存(恒温)条件 下恒温下出现的相数为2或3。
二、二元匀晶相图的分析
匀晶转变:在一定温度范围内由液相结 晶出单相的固溶体的结晶过程。 二元匀晶相图:指两组元在液态和固态 均无限互溶时的二元合金相图。 具有这类相图的合金系主要有Ni-Cu、 Cu-Au、Au-Ag、Mg-Cd、W-Mo等。
标注在温度— 成分坐标中 无限缓冷下测各 合金的冷却曲线 连接各相变点
确定各合金 的相变温度
确定相
如:0%Cu、20%Cu、40%Cu、60%Cu、80%Cu、100%Cu 六组合金。
Cu20% Cu60%Cu80% Cu Ni Cu40%
1600
1500
1400
1400 1300
L
(L+ )
T
Ni
WCu(%)
Cu
将铸件加热到低于固相线100~200℃的温 度,进行长时间保温,使偏析元素充分进行扩 散,以达到成分均匀化。
设A、B组元的熔点分别为1450℃和1080℃,它们 在液态和固态都无限互溶,则这两种组元组成的 二元相图叫作二元 相图;先结晶的固溶体 中含 组元多,后结晶的固溶体中含 组元多,这种成分不均匀现象称为 , 通过 工艺可以减轻或消除这种现 象。
第四章:二元相图

2.杠杆定律: 问题提出: ①当二元合金(成分已知)由两相组成时两相的相对重量是多少?
例:45钢(含C=0.45%),铁素体(F)和Fe3C两相各占多少? ②当二元合金两相相对重量已知时,合金成分是多少?
例:金相观察:F:95%; Fe3C:5%;求钢的含碳量? 杠杆定律可以解决此类问题。
纯金属结晶:在负的温度梯度下---------树枝晶。 在正的温度梯度下------平滑界面(平面长大)
固溶体合金,即使在正的温度梯度下,也会形成树枝晶-------是由于 成分过冷造成的。 (1)成分过冷概念:固溶体合金结晶时,由于液固界面前沿存在溶质 浓度梯度而改变了过冷情况,称为成分过冷。
(2) 产生原因: 以K0<1为例(图示说明) 过冷度:界面前沿液相实际温度<液相平衡结晶温 度 (3) 产生成分过冷的条件: (讨论成分过冷的影响)
④具有共晶转变的二元合金: Pb-Sn Pb-Sb Fe-C(C>2.11%) Al-Si Al-Cu Ag-Cu
第四章:二元相图
4.2.2共晶相图
1.相图分析
以Pb-Sn二元合金相图为例:
三个单相区:L、α、β α:Sn溶入Pb中固溶体 β: Pb溶入Sn中固溶体
AEB-液相线 E点:共晶合金 AMNB-固相线 ME之间:亚共晶 ; EN之间:过共晶合金 MF-Sn在Pb中溶解度曲线,随T↓,溶解度↓ NG- Pb在Sn中溶解度曲线
第四章:二元相图
4.2.2共晶相图
2.典型合金平衡结晶及组织
(2)共晶合金结晶过程(61.9%Sn) 在183℃,由61.9%Sn的液相,同时结 晶出α(19%Sn)和β(97.5%Sn)两 种固溶体。
第四章_二元相图
⒊ 相区
⑴ 五个单相区: L、、、、Fe3C
⑵ 七个两相区: L+、 L+、L+Fe3C、 +、
+Fe3C、+ 、 +Fe3C
⑶ 三个三相区:即HJB (L++)、ECF(L++ Fe3C)、 PSK(++ Fe3C)三条水平线
13
二、包晶转变(HJB)
第四章 铁碳合金
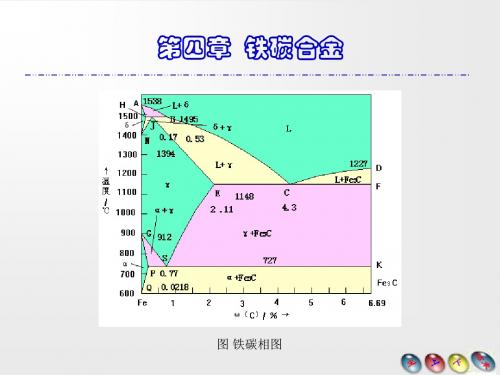
图 铁碳相图
铁碳相图
铁碳相图是研究钢和铸铁的基础,对于钢铁材料的应用 以及热加工和热处理工艺的制订也具有重要的指导意义。 铁和碳可以形成一系列化合物,如Fe3C、Fe2C、FeC等, 有实用意义并被深入研究的只是Fe- Fe3C部分,通常称其为 Fe-Fe3C相图, 此时相图的组元为Fe和Fe3C。
S P Fe3C
珠光体是铁素体和渗碳体 两相的混合物,是共析反应 的产物,用符号“P”表示。 珠光体是一种双相组织。 一般情况下,两相呈层片状 分布,强度较高、硬度适中、 有一定塑性。
7270 C
图 共析钢的室温组织
五、三条重要的特征线——ES、PQ、GS线
ES线是碳在奥氏体中的溶解度曲线。含碳量大于0.77% 的合金,从1148℃冷到727℃的过程中,将自奥氏体中析出 渗碳体,这种渗碳体称为二次渗碳体(Fe3CII)。
Q
1 2
3
4
9
25
2. 亚共析钢的结晶过程
Ⅲ
0.09~0.53%C亚共析钢
A
H J
B
冷却时发生包晶反应.
以0.45%C的钢为例
G S P
第四章 二元相图

第二节 二元匀晶相图
3 固溶体的不平衡结晶 (3)成分偏析: 晶内偏析:一个晶粒内部化学成分不均匀现象。 枝晶偏析:树枝晶的枝干和枝间化学成分不均匀 的现象。 (消除:扩散退火, 在低于固相线温度 长时间保温。)
2h
12
第 四 章 相
4 稳态凝固时的溶质分布
第二节 二元匀晶相图
( 1 )稳态凝固:从液固界面输出溶质速度等于溶 图 质从边界层扩散出去速度的凝固过程。 第 ( 2 )平衡分配系数:在一定温度下,固、液两平 二 衡相中溶质浓度的比值。 k0=Cs/Cl
(1)包晶合金的结晶
结晶过程:包晶线以下,L, α对β过饱和-界面 生成β-三相间存在浓度梯度-扩散-β长大- 全部转变为β。 室温组织:β或β+αⅡ。
35
第 四 章 相 图 第 四 节 包 晶 相 图
第四节 二元包晶相图及合金凝固
2 平衡结晶过程及其组织 (1)包晶合金的结晶 结晶过程:包晶线以下,L, α对β过饱和-界面 生成β-三相间存在浓度梯度-扩散-β长大- 全部转变为β。 室温组织:β或β+αⅡ。
36
第 四 章 相 图 第 四 节 包 晶 相 图
第四节 二元包晶相图及合金凝固
2 平衡结晶过程及其组织
(2)成分在C-D之间合金的结晶
结晶过程:α剩余;
室温组织:α+β+αⅡ+βⅡ。
37
第 四 章 相 图 第 四 节 包 晶 相 图
第四节 二元包晶相图及合金凝固
2 平衡结晶过程及其组织
38
第 四 章 相 图 第 四 节 包 晶 相 图
第三节 二元共晶相图及合金凝固
26
第三节 二元共晶相图及合金凝固
(1)伪共晶 ③ 不平衡组织 由非共晶成分的合金得到的完全共晶组织。 共晶成分的合金得到的亚、过共晶组织。(伪 共晶区偏移)
4 第四章 相图(二元)
配制合金系中几种不同成分合金 熔化后,测试其冷却曲线 根据曲线上的转折点,确定各合金的凝固温度 将上述数据引入以温度为纵轴,成分为横轴的坐标
平面中 连接意义相同的点,作出相应的曲线 曲线将图面分成若干区域----相区。经过金相组织分 析,测出各相区所含的相,将相的名称标注其中, 相图工作就完成
4,过共晶合金
★ E点以右,D点以左,为过共晶合金,与亚 共晶合金类似,白色卵形为初晶β,黑色为共 晶体(α+β)。 ★α,β,αⅡ,βⅡ,(α+β)称组织组成物 ★α,αⅡ为一个相。(α+β)两相混合物,称共晶 体。 ★求组织组成物的相对量,同样可用杠杆定理 标明各区的组织---组织分区图
四、共晶组织和初晶形貌 1,共晶组织的形貌
测试时要求合金的成分准确,纯度高,冷却
速度要慢0.5~1.5℃/min
下面是Ni-Cu合金相图,是最简单的相图之一
Ni 1500 1400 1300 1200 1100 1000 900 20% 40% Cu Cu
80% Cu 60% Cu
Cu
Ni 20 40 60 80 Cu Cu%
2.2. 使用二元合金相图的基本方法
2 > 2 ;此时 2 -2 <0
dG<0
当α相与β相彼此平衡时,在dG=0, 同理 :------------------------------
= =
1
2
2
1
1.3. 相律
相律是分析和使用相图的重要依据。凝集态
受压力影响很小,在恒压下:相平衡条件的 数学表达式:f=c-p+1 (在物理化学中也指出) 式中C为组元数,P为共存的平衡相数,f为自 由度数。 单元系(纯金属) f=1-2+1=0,自由度为1,表 明恒温下平衡熔化或凝固。 二元系C=2,当f=0,p=3,在恒定温度下处于三 相平衡;两相共存时,自由度数目为1,表明 平衡凝固或熔化就在一定温度范围
第四章+二元相图
wZr / M Zr xZr wNi / M Ni wZr / M Zr
Ni-Zr binary phase diagram
20
二元相图的建立
建立相图的方法: 1.利用已有的热力学参数,通过热力学计算和 分析建立相图;计算相图 2.依靠实验的方法建立相图;实验相图 几乎所有的相图都是通过实验得到的,最常 用的是热分析法。
Phase diagram plays an important role in researching and developing new materials, and in processing materials!
10
相律 Gibbs phase rule
相律:确定在平衡条件下,一个系统的组成物的组元数、相 数、和自由度数之间的关系规律。
Pure Fe phase diagram
Temperature-pressure
7
合金相图
对于常用的合金相图,因为压力的影响很小,况且一般都 是处在1个大气压的条件下,所以不再把压力当作变量考虑,
而采用
温度-成分相图 (temperature-composition phase diagram)。
Ω =0:eAB =(eAA+eAB)/2,能量相等,则A-B随机分布,这样的固溶体为 理想态,此时DHm=0 Ω >0:eAB >(eAA+eAB)/2,A-B能量高于A-A和B-B,则A-B结合不稳定, 28 倾向于A、B组元各自聚集,形成偏聚状态,此时DHm>0
相图
1. 相律:F=C-P+1 (pressure constant)
在保持系统平衡状态不变的条件下,没有可以独立变化的 变量。即,任何变量的变化都会造成系统平衡状态的变化。
第四章 二元相图
1.相图 相图
定义
Material
合金系中相的状态和组织与成分、温度之间的关系图称为相图(压力 恒定)。 二元合金相图的表示 相图的建立 1.实验测定法(热分析法)
热分析示意图
February 15, 2012 二元相图 第四章-4
Material Science
2.相图的建立 相图的建立
1.匀晶相图的建立
February 15, 2012
二元相图
第四章-9
Material Science
第二节 二元相图的基本类型
1.基本内容
Material
☞匀晶转变与匀晶相图 ☞共晶转变与共晶相图 ☞包晶转变与包晶相图
February 15, 2012
二元相图
第四章-10
Material Science
1.匀晶相图与匀晶转变 匀晶相图与匀晶转变
二元相图
第四章-28
Material Science
5.共晶合金的不平衡结晶及组织 共晶合金的不平衡结晶及组织
Material
伪共晶 不是共晶成分的合金获得全部共晶体的组织。 离异共晶 在共晶相数量较多而共晶体数量很少的情况下,共晶体中与初 晶相同的一相往往依附于初晶生长,而使共晶中的另一组成相留在 晶界或枝间处,从而看不出典型的共晶组织形态。把这种两相分离 的共晶组织称为离异共晶。
(3)求合金成分 杠杆定律只适合于两相区
February 15, 2012 二元相图 第四章-7
Material Science
4.相平衡与相律 相平衡与相律
Material
1.相平衡 ☞合金中各相之间不发生相变(动态平衡)。 2.相平衡的条件 ☞各组元在各相中的化学位相等。February 1 Nhomakorabea, 2012
第四章 二元相图
2) 10 %Sn合金的结晶过程 3)亚共晶合金(50% Sn,合金II) 亚共晶合金室温下的组织为:先共晶固溶体α和 共晶组织(α+β).相为: α, β. 要求计算其相对含量: 4) 过共晶合金(70% Sn,合金III) 过共晶合金的室温组织为:β+(α+β)。相为: α, β. 要求计算其相对含量:
含Ag为42.4% 的Pt-Ag合金:室温下合金的平衡组织为: β+αII 含Ag在10.5~42.4%之间的Pt-Ag合金 :室温平衡组织为: α+βII +β+αII。 含Ag在42.4~66.8%之间的Pt-Ag合金:室温平衡组织为: β+αII。 3.具有包晶转变合金的不平衡凝固
4.3二元相图分析和使用
以铂(Pt)-银(Ag)合金为例进 行分析讨论包晶相图. 相图分析: 单相区:L、α、β 二相区:L+α、L+β、α+β 三相区:L+α+β (水平线 PDC——包晶线) 成分在P、C两点之间的所 有合金在包晶温度都要发 生包晶转变。相图中的D点 称为包晶点,所对应的温 度TD称为包晶温度。
图 Pt-Ag包晶相图
相图组成:两个单相区 L 、α; 两条溶解度曲线,液相线、固相线 一个两相区 ,L + α 相图特点:二组元在液态和固态都能够完全相互溶解,具有相同的 晶体结构,相同的原子价,原子半径接近。
2.固溶体合金的平衡凝固及组织 以30%Ni, 70%Cu的合金为例说明
固溶体平衡结晶时的组织示意图
根据杠杆定律计算t2温度时的液相和固 相的相对含量: L%=(b-30%)/(b-a) α %=1- L%
1.典型合金的冷却过程分析
以10 %Sn合金, 共晶合金( 61.9 %Sn,图中合金I),亚共晶合金 (50% Sn,合金II), 过共晶合金(70% Sn,合金III)为例说明. 1)共晶合金( 61.9 %Sn,图中合金I) 共晶组织中α、β两相的相对量可以应用杠杆定理计算出来:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章二元相图相:(概念回顾)相图:描述系统的状态、温度、压力及成分之间关系的图解。
二元相图:第一节相图的基本知识1 相律相律:热力学平衡条件下,系统的组元数、相数和自由度数之间的关系。
表达式:f=c-p+2; 压力一定时,f=c-p+1。
应用可确定系统中可能存在的最多平衡相数。
如单元系2个,二元系3个。
可以解释纯金属与二元合金的结晶差别。
纯金属结晶恒温进行,二元合金变温进行。
2 相图的表示与建立状态与成分表示法状态表示:温度-成分坐标系。
坐标系中的点-表象点。
成分表示:质量分数或摩尔分数。
相图的建立方法:实验法和计算法。
过程:配制合金-测冷却曲线-确定转变温度-填入坐标-绘出曲线。
相图结构:两点、两线、三区。
3 杠杆定律平衡相成分的确定(根据相率,若温度一定,则自由度为0,平衡相成分随之确定。
)数值确定:直接测量计算或投影到成分轴测量计算。
注意:只适用于两相区;三点(支点和端点)要选准。
第二节二元匀晶相图1 匀晶相同及其分析匀晶转变:由液相直接结晶出单相固溶体的转变。
匀晶相图:具有匀晶转变特征的相图。
相图分析(以Cu-Ni相图为例)两点:纯组元的熔点;两线:L, S相线;三区:L, α, L+α。
2 固溶体合金的平衡结晶平衡结晶:每个时刻都能达到平衡的结晶过程。
平衡结晶过程分析①冷却曲线:温度-时间曲线;②相(组织)与相变(各温区相的类型、相变反应式,杠杆定律应用。
);③组织示意图;④成分均匀化:每时刻结晶出的固溶体的成分不同。
与纯金属结晶的比较相同点:基本过程:形核-长大;热力学条件:⊿T>0;能量条件:能量起伏;结构条件:结构起伏。
②不同点:合金在一个温度范围内结晶(可能性:相率分析,必要性:成分均匀化。
)合金结晶是选分结晶:需成分起伏。
3 固溶体的不平衡结晶原因:冷速快(假设液相成分均匀、固相成分不均匀)。
结晶过程特点:固相成分按平均成分线变化(但每一时刻符合相图);结晶的温度范围增大;组织多为树枝状。
成分偏析:晶内偏析:一个晶粒内部化学成分不均匀现象。
枝晶偏析:树枝晶的枝干和枝间化学成分不均匀的现象。
(消除:扩散退火,在低于固相线温度长时间保温。
)4 稳态凝固时的溶质分布(1)稳态凝固:从液固界面输出溶质速度等于溶质从边界层扩散出去速度的凝固过程。
(2)平衡分配系数:在一定温度下,固、液两平衡相中溶质浓度的比值。
k0=C s/C l(3)溶质分布:液、固相内溶质完全混合(平衡凝固)-a;固相不混合、液相完全混合-b;固相不混合、液相完全不混合-c;固相不混合、液相部分混合-d。
区域熔炼(上述溶质分布规律的应用)5 成分过冷及其对晶体生长形态的影响成分过冷:由成分变化与实际温度分布共同决定的过冷。
形成:界面溶质浓度从高到低-液相线温度从低到高。
(图示:溶质分布曲线-匀晶相图-液相线温度分布曲线-实际温度分布曲线-成分过冷区。
)(3)成分过冷形成的条件和影响因素条件:G/R<mC0(1-k0)/Dk0合金固有参数:m, k0;实验可控参数:G, R。
(4)成分过冷对生长形态的影响(正温度梯度下)G越大,成分过冷越大-生长形态:平面状-胞状-树枝状。
第三节二元共晶相图及合金凝固共晶转变:由一定成分的液相同时结晶出两个一定成分固相的转变。
共晶相图:具有共晶转变特征的相图。
(液态无限互溶、固态有限互溶或完全不溶,且发生共晶反应。
共晶组织:共晶转变产物。
(是两相混合物)1 相图分析(相图三要素)点:纯组元熔点;最大溶解度点;共晶点(是亚共晶、过共晶成分分界点)等。
线:结晶开始、结束线;溶解度曲线;共晶线等。
区:3个单相区;3个两相区;1个三相区。
2 合金的平衡结晶及其组织(以Pb-Sn相图为例)Wsn<19%的合金①凝固过程(冷却曲线、相变、组织示意图)。
②二次相(次生相)的生成:脱溶转变(二次析出或二次再结晶)。
③室温组织(α+βⅡ)及其相对量计算。
共晶合金①凝固过程(冷却曲线、相变、组织示意图)。
共晶线上两相的相对量计算。
室温组织(α+β+αⅡ+βⅡ)及其相对量计算。
亚共晶合金①凝固过程(冷却曲线、相变、组织示意图)。
②共晶线上两相的相对量计算。
③室温组织(α+βⅡ+(α+β))及其相对量计算。
组织组成物与组织图组织组成物:组成材料显微组织的各个不同本质和形态的部分。
组织图:用组织组成物填写的相图。
3 不平衡结晶及其组织伪共晶①伪共晶:由非共晶成分的合金所得到的完全共晶组织。
②形成原因:不平衡结晶。
成分位于共晶点附近。
③不平衡组织由非共晶成分的合金得到的完全共晶组织。
共晶成分的合金得到的亚、过共晶组织。
(伪共晶区偏移)不平衡共晶不平衡共晶:位于共晶线以外成分的合金发生共晶反应而形成的组织。
原因:不平衡结晶。
成分位于共晶线以外端点附件。
离异共晶离异共晶:两相分离的共晶组织。
形成原因平衡条件下,成分位于共晶线上两端点附近。
不平衡条件下,成分位于共晶线外两端点附。
消除:扩散退火。
4 共晶组织的形成共晶体的形成成分互惠-交替形核片间搭桥-促进生长两相交替分布共晶组织共晶体的形态粗糙-粗糙界面:层片状(一般情况)、棒状、纤维状(一相数量明显少于另一相)粗糙-平滑界面:具有不规则或复杂组织形态(由于两相微观结构不同)所需动态过冷度不同,金属相任意长大,另一相在其间隙长大。
可得到球状、针状、花朵状、树枝状共晶体。
非金属相与液相成分差别大。
形成较大成分过冷,率先长大,形成针状、骨骼状、螺旋状、蜘蛛网状的共晶体。
初生晶的形态:金属固溶体:粗糙界面-树枝状;非金属相:平滑界面-规则多面体。
第四节二元包晶相图包晶转变:由一个特定成分的固相和液相生成另一个特点成分固相的转变。
包晶相图:具有包晶转变特征的相图。
1 相图分析点、线、区。
2 平衡结晶过程及其组织包晶合金的结晶结晶过程:包晶线以下,L, α对β过饱和-界面生成β-三相间存在浓度梯度-扩散-β长大-全部转变为β。
室温组织:β或β+αⅡ。
成分在C-D之间合金的结晶结晶过程:α剩余;室温组织:α+β+αⅡ+βⅡ。
3 不平衡结晶及其组织异常α相导致包晶偏析〔包晶转变要经β扩散。
包晶偏析:因包晶转变不能充分进行而导致的成分不均匀现象。
〕异常β相由不平衡包晶转变引起。
成分在靠近固相、包晶线以外端点附件。
4 包晶转变的应用组织设计:如轴承合金需要的软基体上分布硬质点的组织。
晶粒细化。
第五节其它类型的二元相图自学内容第六节铁碳合金相图一二元相图的分析和使用二元相图中的几何规律①相邻相区的相数差1(点接触除外)-相区接触法则;②三相区的形状是一条水平线,其上三点是平衡相的成分点。
③若两个三相区中有2个相同的相,则两水平线之间必是由这两相组成的两相区。
④单相区边界线的延长线应进入相邻的两相区。
相图分析步骤①以稳定的化合物分割相图;②确定各点、线、区的意义;③分析具体合金的结晶过程及其组织变化注:虚线、点划线的意义-尚未准确确定的数据、磁学转变线、有序-无序转变线。
相图与合金性能的关系根据相图判断材料的力学和物理性能根据相图判断材料的工艺性能铸造性能:根据液固相线之间的距离XX越大,成分偏析越严重(因为液固相成分差别大);X越大,流动性越差(因为枝晶发达);X越大,热裂倾向越大(因为液固两相共存的温区大)。
塑性加工性能:选择具有单相固溶体区的合金。
热处理性能:选择具有固态相变或固溶度变化的合金。
二铁-碳合金相图1组元和相(1)组元:铁-石墨相图:Fe,C;铁-渗碳体相图:Fe-Fe3C。
相:L, δ, A(γ), F(α), Fe3C(K)。
(其定义)2相图分析点:16个。
线:两条磁性转变线;三条等温转变线;其余三条线:GS,ES,PQ。
区:5个单相区,7个两相区,3个三相区。
相图标注:相组成物标注的相图。
组织组成物标注的相图。
3 合金分类:工业纯钛(C%<0.0218%)、碳钢(0.0218<C%<2.11%)、铸铁(C%>2.11%)4平衡结晶过程及其组织典型合金(7种)的平衡结晶过程、组织变化、室温组织及其相对量计算。
重要问题:Fe3CⅠ, Fe3CⅡ, Fe3CⅢ的意义及其最大含量计算。
L d-L d`转变。
二次杠杆的应用。
5 含碳量对平衡组织和性能的影响对平衡组织的影响(随C%提高)组织:α+Fe3CⅢL d`+Fe3CⅠ;相:α减少,Fe3C增多;Fe3C形态:Fe3CⅢ(薄网状、点状)共析Fe3C(层片状) Fe3CⅡ(网状)共晶Fe3C(基体) Fe3CⅠ(粗大片状)。
对力学性能的影响强度、硬度升高,塑韧性下降。
对工艺性能的影响适合锻造:C%<2.11%,可得到单相组织。
适合铸造:C%~4.3%。
,流动性好。
适合冷塑变:C%<0.25%,变形阻力小。
适合热处理:0.0218~2.11,有固态相变。
第七节相图的热力学解释图示讲解第八节铸锭组织及其控制1 铸锭组织铸锭三区:表层细晶区、柱状晶区、中心等轴晶区。
组织控制:受浇铸温度、冷却速度、化学成分、变质处理、机械振动与搅拌等因素影响。
2 铸锭缺陷微观偏析宏观偏析正偏析反偏析比重偏析夹杂与气孔夹杂:外来夹杂和内生夹杂。
气孔:析出型和反应型。
缩孔和疏松形成:凝固时体积缩小-补缩不足-形成缩孔。
分类:集中缩孔(缩孔、缩管)和分散缩孔(疏松,枝晶骨架相遇,封闭液体,造成补缩困难形成。
)。
