1进制转换
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
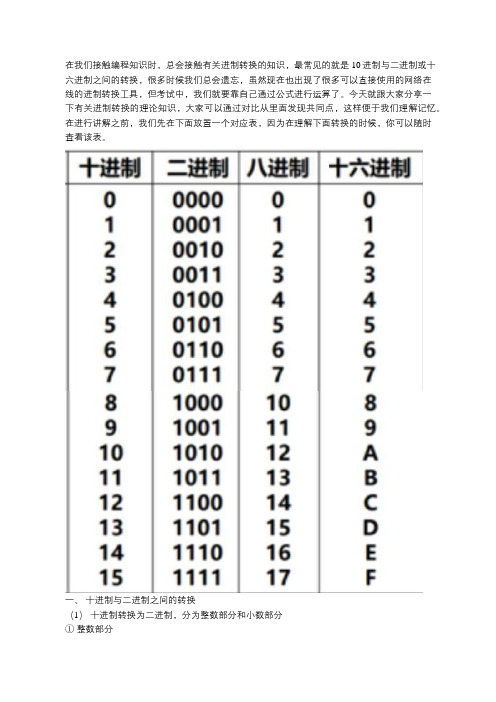
在我们接触编程知识时,总会接触有关进制转换的知识,最常见的就是10进制与二进制或十六进制之间的转换,很多时候我们总会遗忘,虽然现在也出现了很多可以直接使用的网络在线的进制转换工具,但考试中,我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识,大家可以通过对比从里面发现共同点,这样便于我们理解记忆。
在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。
一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2商84余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000②小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
进制转化公式

进制转化公式进制转化是数学中一个常见的操作,用于将数字在不同进制之间进行转换。
进制是数学表示法的一种方式,不同进制对应着不同的基数。
目前常用的进制有十进制、二进制、八进制和十六进制。
在十进制中,我们使用0-9这十个数字进行计数。
例如数字456表示的意思是4乘以100加5乘以10加6乘以1。
而在二进制中,只使用0和1进行计数。
例如数字101表示的意思是1乘以4加0乘以2加1乘以1。
八进制和十六进制则使用了更多的符号表示数值,分别使用0-7和0-9以及A-F这些字符进行计数。
进制转化的公式主要根据进制的特点来进行推导,以下是一些常见的进制转化公式:1. 十进制转二进制:将十进制数不断除以2,直到商为0,然后将每一步的余数倒序排列即可得到二进制数。
2. 二进制转十进制:将二进制数从右到左,每一位乘以2的相应指数,再将结果相加即可得到十进制数。
3. 十进制转八进制:将十进制数不断除以8,直到商为0,然后将每一步的余数倒序排列即可得到八进制数。
4. 八进制转十进制:将八进制数从右到左,每一位乘以8的相应指数,再将结果相加即可得到十进制数。
5. 十进制转十六进制:将十进制数不断除以16,直到商为0,然后将每一步的余数倒序排列,并将10-15分别用A-F表示即可得到十六进制数。
6. 十六进制转十进制:将十六进制数从右到左,每一位乘以16的相应指数,再将结果相加即可得到十进制数。
通过以上公式,我们可以在不同进制之间进行转化。
进制转化不仅在数学中有着重要的应用,同时在计算机科学和信息技术领域也扮演着重要的角色。
例如,计算机内部使用二进制进行数据存储和计算,而网络通信中常使用十六进制表示数据。
掌握进制转化公式对于进行数值计算和理解计算机科学原理非常重要。
能够灵活运用进制转化公式,不仅可以提高计算效率,还能深入理解进制的含义和应用。
因此,我们需要在数学学习的过程中,仔细掌握并灵活运用进制转化公式,以便在实际应用中取得更好的成果。
进制转换计算+ASCII表

一、二进制转化成其他进制1. 二进制(BINARY)——>八进制(OCTAL)例子1:将二进制数(10010)2转化成八进制数。
(10010)2=(010 010)2=(2 2)8=(22)8例子2:将二进制数(0.1010)2转化为八进制数。
(0.10101)2=(0. 101 010)2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
2. 二进制(BINARY)——>十进制(DECIMAL)例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
3. 二进制(BINARY)——>十六进制(HEX)例子1:将二进制数(10010)2转化成十六进制数。
(10010)2=(0001 0010)2=(1 2)16=(12) 16例子2:将二进制数(0.1010)2转化为十六进制数。
(0.10101)2=(0. 1010 1000)2=(0. A 8)16=(0.A8)16诀窍:因为每四位二进制数对应一位十六进制数,所以,以小数点为界,整数位则将二进制数从右向左每4位一隔开,不足4位的在左边用0填补即可;小数位则将二进制数从左向右每4位一隔开,不足4位的在右边用0填补即可。
进制转换方法的公式

进制转换方法的公式
数字的进制转换在我们的生活中是一种常见的操作,它能够帮助我们将一种进制的数字转换成另一种进制的数字。
进制转换方法的公式是用来计算和实现进制转换的数学方法。
一般来说,我们都知道有十进制,十六进制,八进制等不同类型的进制。
但是,他们之间的转换可以采用一种标准的公式来实现。
这就是进制转换方法的公式。
下面,我们就来详细介绍一下进制转换方法的公式。
首先,我们要将从一种进制转换到另一种进制的数字按照乘方的方式计算。
也就是说,如果我们要将十进制的数字转换为八进制的数字,首先要将该十进制数字以下列方式计算:乘方法: 10^2 8^1 4^1 2^0 1^0,等等。
其中每个乘方的指数都可以转换为另一种进制的数字,比如8^1就可以转换为8进制的数字。
然后,我们还可以用下列公式来实现数字从一种进制转换到另一种进制的运算,如从十进制转换为八进制:10^2 8^1 4^1 2^0 1^0 = (1 x 10 + 0 x 8 + 1 x 4 + 1 x 2 + 0 x 1) + 8^1。
可以看出, 8^1这一步是实现从十进制转换为八进制的关键,它把计算结果转换为八进制的数字。
最后,我们可以用一般的公式来转换一种进制的数字到另一种进制的数字,那就是将一种进制的数字经过乘方法计算后,再将每一个乘方的指数转换为另一种进制的数字,即可实现进制转换的操作。
总而言之,进制转换方法的公式可以帮助我们方便地将一种进制
的数字转换到另一种进制的数字。
它是一种简单而有效的方法,可以帮助我们快速地完成进制转换的计算。
1进制的转换与信息的编码知识点

1进制的转换与信息的编码知识点一、信息及其特征信息的载体和形态1.信息本身不是实体,必须通过载体才能体现,但不随载体的物理形式而变化。
2.语言、文字、声音、图像和视频等是信息的载体,也是信息的常见表现形态。
3.纸张可以承载文字和图像,磁带可以承载声音,电视可以承载语言、文字、声音、图像和视频,所以也把纸张、磁带、广播、电视、光盘、磁盘等称为信息的载体。
4.相同的信息,可以用多种不同的载体来表示和传播。
5.不存在没有载体的信息。
信息的五个特征1.载体依附性:信息的表示、传播、储存必须依附于某种载体,载体就是承载信息的事物。
2.可加工处理性:信息是可以加工和处理的。
信息也可以从一种形态转换成另一种形态。
3.传递性:信息可以脱离它所反映的事物被存储和保留和传播。
4.共享性:信息是可以传递和共享的。
信息可以被重复使用而不会像物质和能源那样产生损耗。
5.时效性二、信息的编码计算机只能识别和处理由“0”、“1”两个符号组成的数字代码。
或称计算机只能识别机器语言。
1.进位制的转换二进制:0、1进位规则:逢2进1二进制标识:B十进制:0、1、2、3、4、5、6、7、8、9进位规则:逢10进1十进制标识:D十六进制:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F“逢十六进一”。
不同的是用A、B、C、D、E和F分别表示10、11、12、13、14和15六个数字符号。
十六进制标识:H传递、表达信息的规则:使用1个二进制位(比特)可以表示2种信息0使用2个二进制位(比特)可以表示4种信息00011011使用3个二进制位(比特)可以表示8种信息000100第1页001101010110011111用n个二进制位最多可以表示2种不同的信息例题:下列关于信息编码的说法,正确的是()。
A.4位二进制编码可以表示15种状态B.5位二进制编码可以表示31种状态C.6位二进制编码可以表示63种状态D.7位二进制编码可以表示128种状态解:因为4位二进制编码可以表示2=16种状态5位二进制编码可以表示2=32种状态6位二进制编码可以表示26=64种状态7位二进制编码可以表示2=128种状态所以,选D。
1.1进制转换与数据、信息的概念-粤教版(2019)高中信息技术必修一课件

2
(185)10=(271)8 (185)10=(B9)16
3.r进制转换成r进制:
方法: r进制转换成十进制,十进制转换成r进制。
4.二进制与八进制、二进制与十六进制之间的互相转 变:
二进制和八进制、二进制和十六进制之间的相互转换可以直接计算。 二进制的运算首先要记住窍门:8421。 (1111)2=1×23+1×22+1×21+1×20=8+4+2+1, 即二进制数 1111 从左到右每一位分别代表十进制的 8、4、2、1。
= 64+0+16+8+0+2+1 = 91
· (356)8 = 3×82+5×81+6×80 = 192+40+6 = 238
· (2FB)16 = 2×162+15×161+11×160 = 512+240+11 = 763
2.十进制转换成r进制:
方法:除 r 取余数,直至商为零,余数倒序排序。 例:十进制 185 分别转换成二进制、八进制和十六进制。
堂 同事物的特征。(
)
练 2.数据是现实世界客观事物的符号记录,是信息的载体,不能
习 用计算机进行加工。(
)
1
3.以下关于数据的说法正确的是( )
A. 数据是计算机被发明之后产生的,所以在古代没有数据。
B. 数据的记录过程一定需要人的参与。
C. 数据就是信息,信息就是数据。
D. 数据在人们的生活中正扮演着越来越重要的作用。
个人计算 机
互联网
数据
透明电视
抬头显示屏
1进制转换

K进制数转换为十进制数
将下列数值转换为十进制数 (101.01)2 (205.4)8 (AF.8)16 解: (101.01)2= 1×22+0×21+1×20+0×2-1+1×2-2 =(5.25)10 (205.4)8 = 2×82+0×81+5×8 0+4×8–1 =(133. 5)10
1 0
视频
机读卡信息在表格中均以“涂黑”和“空白”两种方式呈
我们对卡的填涂,实际上就是一个编码的过程,
把填涂卡中的空白理解为“0”,则“涂黑”就可以理解为
“1”,这样就对信息进行了编码,转化为“0”和“1”两个
符号,从而可以方便计算机采集和存储信息。
计算机只பைடு நூலகம்识别0和1,其原因在于:计算机主 要以半导体和高速电子开关为主要元件,它们具有
1000B= 1000/1024 KB= 1000/1024/1024 MB= 1000/1024/1024/1024 GB 2GB= 2*1024 MB= 2*1024*1024 KB= 2*1024*1024*1024 B
信息的编码
(2)二进制数的特征
十、二进制对比表
①、二进制数是由0和1两个数字组成,逢二进一。
(AF.8)16
P5 进位制转换 A---10、F---15
(AF.8)16 = 10×161 +15×160+8×16-1 =(175. 5)10
十进制数转换为二进制数 短除取余法
整数部份:除以2取余数,直到商为0,余数从自下 而上排列。 【例】将(100)10 转换为二进制
2 2 2 2 2 2 2 100 余数 50 25 12 6 3 1 0 0 0 1 0 0 1 1 高位 低位 练习: (19)10 = ( 10011 )2
1进制及进制转换

位值 位权
2 二进制
2.1 什么是二进制
二进制和十进制相仿,也是一种记数制,它只使 用“0”和“1”两个不同的数字符号,采用的是 “逢二进一”。例如,二进制数(111010.1101)2。
n
NR ki Ri im
3.2 其他数制转换成二进制数
(1)十进制整数转换成二进制整数
说明:通常采用“除以2逆向取余法”
例 将(57)10转换成二进制数
余数
2 57…………………1 (低位)
2 28…………………0
2 14…………………0 2 7 ………………….1
(57)10=(111001)2
计算机中为什么采用二进制呢? 原因是: 状态稳定,容易实现; 运算规则简单; 可将逻辑处理与算术处理相结合。
3 不同进位制数之间的转换 3.1 其它进制转换成十进制
说明:通常采用按位展开、按权相乘法
(1)二进制数转换成十进制数
例(1101.01)2 =(1×23+1×22+0×21+1×20+0×2-1+1×2-2 )10 =(13.25)10
例(2AB.C)16 =(2×162+10×161+11×160+12×16-1)10
=(683.75)10 练习:将十六进制数A7D.E转换成十进制数 答案: (A7D.E)16=(10×162+7×161+13×160+14×16-1 )10
=(2685.875)10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i m n 1
上面两式中,ai=0或1, n为整数部分的位数,
m为小数部分的位数.
1.1.3 任意进制数的表示 (N) r=(an-1 an-2 … a1 a0. a-1 a-2… a-m)r
(N)r = an-1rn-1+an-2rn-2 +…+ a1r1+a0r0+a-1
1 21 0 22 1 23 16 8 2 0.5 0.125 (26.626)10
2、十进制数二进制数 • 整数部分:除2取余法 例:将(58)10转换成二进制形式
(58)10 (an 1 an 2 a1 ao )2
an 1 2n-1 an 2 2n 2 a1 21 ao 20 2(an 1 2
lnR-1=0
RC nR LnR
(
RC ) 0 LnR
R=e=2.718
1.2
数制转换
1.2.1 二进制数和十进制数的转换
1、二进制数十进制数 • 按权展开式在十进制数域中计算 例如:
(11010 .101)2 1 24 1 23 0 22 1 21 0 20
5.数字系统设计概况
1 ) 层次:从小到大,原语单元、较复杂单元、复杂单元、 更复杂单元 2)逻辑网络:以二进制为基础描述逻辑功能的网络 3)电子线路:物理构成 4)形式描述:用硬件描述语言(HDL)描述数字系统的 行为
6.为什么采用数字系统
1)安全可靠性高 2)现代电子技术的发展为其提供了可能
7.数字系统的特点
1.1
进位计数制
1.1.1 十进制数的表示
1、进位计数制
数制:用一组统一的符号和规则表示数的方法
2、记数法
• 位置计数法 例:123.45 读作 一百二十三点四五 • 按权展形式 例:123.45=1102+2101+3100+410-1+510-2 3、基与基数
用来表示数的数码的集合称为基(0—9), 集合的大小称为基数(十进制10)。
1)二值逻辑(“0”低电平、“1”高电平) 2)基本门电路及其扩展逻辑电路(组成) 3)信号间符合算术运算或逻辑运算功能 4)其主要方法为逻辑分析与逻辑设计(工具 为布尔代数、卡诺图和状态化简)
第一章 数制与码制
学习要求:
• 掌握二、十、八、十六进位计数制及相互换; • 掌握二进制数的原码、反码和补码表示及其加 减运算; • 了解定点数与浮点数的基本概念;掌握常用的 几种编码。
•短乘法:先求出的整数为高位
1.2.2 八进制数、十六进制数与二进制数的转换
例:八进制: 2
5
7 0
5
5
4
二进制:010 101 111 000 101 101 100 十六进制: A F
1
6
C
因此,(257.0554)8=(10101111.0001011011)2 =(AF.16C)16
4、权
在十进制中,10的整幂次方称为10进制数的权。
1.1.2 二进制数的表示
对于任意一个二进制数N, 用位置记 数法可表示为:
(N)2=(an-1 an-2 … a1 a0. a-1 a-2… a-m)2
用权展开式表示为 (N)2 = an-12n-1+an-22n-2 +…+ a121+a020+a-1 2-1+a-22-2+…+a-m2-m
…
则
(58)10 = (111010)2
•短除法:先求出的余数为低位。
• 小数部分:乘2取整法
例:将(0.625)10转换为二制形式
a1 1 (0.625)10 (a 2 21 a m 2 m 1) 2 2 (1.25)10 a1 (a 2 21 a m 2 m1)
得a-1=1
(0.5)10 a 2 (a3 21 a m 2 m 2 )
得a-2=0
(1.00)10 a3 (a4 2 a m 2
1 m 3
)
得a-3=1
则
(0.625)10 (0.101)2
注意:不能进行精确转换的情况
n-2
an 2 2
n 3
a1 ) ao
(29)10 an 1 2
n- 2
an 2 2
n (14 )10 an 1 2 an 2 2 a2 2 2
得a1=1
第六章 采用中,大规模集成电路的逻辑设计。
绪 论
一、数字系统 1.模拟量:连续变化的物理量 2.数字量:模拟→数字量 (A/D) 3.数字系统:使用数字量来传递、加工、处理信息 的实际工程系统 4.数字系统的任务:
1) 将现实世界的信息转换成数字网络可以理解的二进制语言 2) 仅用0、1完成所要求的计算和操作 3) 将结果以我们可以理解的方式返回现实世界
前 言
第一章 第二章 数制与码制: “数”在计算机中怎样表示。 逻辑代数基础: 逻辑代数的基本概念、逻辑函数 及其标准形式、逻辑函数的化简。
第三章 组合逻辑电路: 组合电路的分析与设计。 第四章 同步时序逻辑电路:触发器、同步时序电路的 分析与设计。 第五章 异步时序逻辑电路:脉冲异步电路的分析与设 计。
r-1+a-2r-2+…+a-mr-m
i m
n 1
ai r
i
1.1.4 二进制数的特点
• 只有两个数码, 很容易用物理器件来实现。 • 运算规则简单。 • 可使用逻辑代数这一数学工具。
• 节省设备
1)设n是数的位数 R是基数 Rn-----最大信息量 nR-----Rn个数码所需设备量 例:n=3,R=10,(R)10n=103=1000 nR=3×10=30 而Rn≥1000 R=2 2n≥1000 n=10 Rn=1024 nR=10×2=20 同样为1000的信息量,二进制比十进制节省设备。 2)唯一性证明 N=Rn (N为最大信息量) LnN=nLnR 令C=LnN C=nLnR 两边同乘R,RC=nRLnR
