初中平面几何中的定值问题
定值问题的证法
四、定值问题的证法定值问题在初中平面几何中已经多次遇到，只不过没有明确它们是“定值”而已！如：底边固定，顶点在与底边的直线上移动，则三角形的面积为定值； 点在弓形弧上移动，则对底边所张的视角为定值；过圆内一定点任意作弦，则弦被该点所分的两部分之积为定值； ……由此可见，定值问题反映出某种“动态”之下不变的量，正是这种不变的量，才使我们深刻地理解并掌握该“动态”的规律，因此，定值问题有着十分丰富的内容，由它还可以引发出一些生动的故事，引起人们对几何产生浓厚的兴趣．许多定值问题有时摇身一变，而成为我们欲定的轨迹，有些定值命题又可用来求极大、极小值，由于这多种用途，很有必要掌握它们的证法．定值问题常用的证明思路：定值问题，实质上也是一个等量问题．因此，前面介绍的各种方法，都可运用在定值问题中，但针对定值的特点，还应注意以下几个方面．1、探求有时，定值问题中并没有具体给出定值来，这时就需要以特殊位置先求这个定值．特殊情况随题而异，通常以动线处于平行、垂直的位置较易算之；对变动的三角形，则又以正的、等腰、直角为宜；涉及到圆，则圆心、切线、公共弦……又有很多性质好为我们利用．2、转化设法转化成已知的定值问题． 3、途径当定值问题不能转化时，通常可沿如下三条途径去试着论证． (1)证任一情形与某特殊情形有相同之值； (2)证任二情形有相同之值；(3)把任一情形的值用题中给定的常量表示出来．这最后一条，正是以前所讲的计算方法，不过在这里，计算之初，有时要先设一个参变量，以体现“动态”之动，然后以参变量为媒介，计算欲定之值，最后化简得出欲算之值不含该参变量，就表明它在“动态”之中确实不变．例3.12 已知⊙O 1、⊙O 2，每一圆的圆心在另一圆周上，A 、B 是二圆之交点，过B 任作一割线分别交二圆于M 、N ，B 在M 、N 之间． 试求：切圆于M 、N 之二切线间的夹角．探索：从题意看，随割线的位置不同，所求之角若变化，这样是求不出的，因此所求之角应与割线无关，故不妨以特殊位置先定其大小．相对于公共弦AB ，宜取与它垂直的割线M 0N 0，如图3-83，这时，由∠ABM 0=∠ABN 0=90o可知，AM 0、AN 0分别过各圆之圆心．故△AM 0N 0是正△，因而易知所求之角应为120o．依此证之如下：证法1：与特殊值皆等如上之探索，先作一特殊割线M 0N 0，再作任一割线MN ，如图3-84．图 3-83图 3-84∵ ∠M 0AM =∠M 0BM =∠N 0BN =∠N 0AN ，∴ ∠MAN =∠M 0AN 0=60o．由弦切角定理，∠TMN +∠TNM =∠MAB +∠NAB =∠MAN =60o．∴ ∠MTN =120o(定值)． 证法2：任二值相等将上述证法中的M 0N 0换成任意位置M 1N 1，如图3-85，则照搬上述过程，可证出∠MTN =∠M 1T 1N 1，即二切线之夹角为定值．证法3：算出任一个由每个圆心在另一圆上可知：∠AO 1B =∠AO 2B =120o． 对任一割线MN ，如图3-86，皆有：o 11602AMN AO B ∠=∠=，o 21602ANM AO B ∠=∠=，∴ △AMN 是正三角形⇒∠MAN =60o．∴ αβ+=60o ⇒∠MTN =120o(定值)．本例的三种证法，体现了上面所述的证定值问题的三种途径．不过，单凭第二种，只能肯定是定值，而未能定出具体值，但任二情形当然也包括特殊的，故如探索，即可定出．最后补充一点：如图3-87，B 不在M 、N 之间．∵ ∠AMN =180o -∠AMB =180o-∠AO 2B =180o -120o =60o，o 21602ANB AO B ∠=∠=，∴ △AMN 是正三角形⇒∠MAN =60o．又 ∠AMT =∠ABM ，∠ANT =∠ABM ，∴ A 、M 、N 、T 四点共圆⇒∠MTN =∠MAN =60o．即，如果题中省略“B 在M 、N 之间”，则二切线MT 、NT 的夹角是60o或120o．例3.13 定长的弦ST 在一个以AB 为直径的半圆周上滑动，SP ⊥AB 于P ，M 是ST 之中点．求证：不管ST 滑到什么位置，∠SPM 是一定角． 探索：题中没给出角的大小，故应以特殊位置S 0T 0探求． 相对于AB ，以S 0T 0∥AB 为宜，因为这时具有对称性，如图3-88，容易看出：∠S 0P 0M 0=∠S 0OM 012=∠S 0OT 0．图3-85图3-86图3-870图 3-88依此看来，弦长一定，所对的圆心角也定，而定角正是这弦长一定的产物．依此，可得如下两种证法．证法1：化归为圆心角如图3-89，连结OM 、OS 、OT ，则有：OM ⊥ST ⇒S 、P 、O 、M 四点共圆⇒SPM SOM ∠=∠，而 12SOM SOT ∠=∠．∴ 12SPM SOT ∠=∠=定值．证法2：化归为圆周角为使定角移至圆周角，先画出全圆周，再延长SP 交另一半圆周于Q ，再连TQ ，如图3-90，则由中位线定理知：PM ∥QT ．故 ∠SPM =∠SQT =定值．例3.14 已知：正△ABC 的边长为1，如图3-91，等腰△DBC 的顶角∠BDC =120o ，以D 为顶点任作一个60o的角，角的两边分别交AB 、AC 于M 、N ．求证：△AMN 的周长等于2．分析：因2AB BC +=，容易看出：△AMN 的周长等于2⇔MN BM CN =+， 于是，只需证后式即可．为此，在MN 上取点E ，无论是使M DE M DB ∠=∠，还是使ME MB =，或是使DE ⊥MN ，企望直接用全等形去证：E 把MN 分成的两段恰与BM 、CN 分别相等，因缺一条件而遇到困难．既然直接去证困难，我们改用间接去证．证法1：同一法如图3-92，作M D E M D B ∠=∠，且使DE DB =，则有：△MDE ≌△MDB ⇒M ED M BD ∠=∠=90o． ∵ DB DC =， ∴ DE DC =． 又 NDE MDE MDN ∠+∠=∠=60o．NDC MDB ∠+∠=120o MDN -∠=60o．∴ NDE NDC ∠=∠． ∴ △NDE ≌△NDC ⇒NED NCD ∠=∠=90o．∴ M 、E 、N 三点共线，即E 在MN 上． 再由两组全等形知：BM EM =，CN EN =， ∴ MN BM CN =+．证毕．既然把MN 分成两段去证有难度，何不反过来，把BM 、CN 合成一段！即有：证法2：作出线段和如图3-93，延长MB 至F ，使BF CN =，连结DF ．则易知：Rt △BDF ≌Rt △CDN ⇒BDF CDN ∠=∠，DF DN =．从而有 MDF MDN ∠=∠=60o．图 3-89图3-90图3-91图 3-92图 3-93∴ △MDF ≌△MDN ，∴ MN MF BM CN ==+．证毕．作出图3-93中的辅助线还有下列方式：作BDF CDN ∠=∠，使DF DN =(或使DF 交MB 的延长线于F )，或将△CDN 绕点D 逆时针旋转120o，然后去证都行的通，自行不妨一试．当然，也可在NC 的延长线上作出MB ，但无本质区别．如果一时引不出辅助线，也可采用计算的办法，因为本例中含有直角等一些特殊角．证法3：计算如图3-94，设BM a =，CN b =，在△CDN 中，由余弦定理：222o 2cos60MN AM AN AM AN =+-⋅⋅22(1)(1)(1)(1)a b a b =-+---- 221()a b a b ab =++-+-在△BDC 中，易算得BD CD ==故tan α，tan β=．又tan 60tan()o αβ==+=，∴ 1()3a b ab -+=，∴ 22222()MN a b ab a b =++=+，即 MN BM CN =+． 引申：对本例细加分析，就可看出它的来源，并加以推广．首先，从证法1中容易看出：自D 作DE ⊥MN于E ，如图3-95，则有DE DB DC ==，故以D 为圆心，以DB 为半径画圆，则BMNC 正是与此圆相切的折线，切点为B 、E 、C ．于是，原题的条件和结论：12MDN BDC ∠=∠，△AMN 的周长等于2AB ，都是十分显然的，因此，原命题之逆也是一个定值问题，即有：例3.15 已知：正△ABC 的边长为1，如图3-91，等腰△DBC 的顶角∠BDC =120o，∠MDN 的两边分别交AB 、AC 于M 、N ．若△AMN 的周长等于2，则∠MDN 为定值(60o)．从图3-95中进一步可看出，保持相切关系不变，当切点B 或C 在圆上滑动时，如图3-96，则正三角形变为等腰三角形，此时，12MDN BDC ∠=∠，△AMN 的周长等于2AB ，仍然成立．再隐去相切之圆，可得到如下推广：例3.16 已知等腰△ABC 中，AB AC =，D 与A 在BC 之异侧，且BD ⊥AB ，CD ⊥AC ，M 、N 分别在AB 、AC 上．则12MDN BDC ∠=∠⇔△AMN 的周长等于2AB ．这再一次表明：深挖一下题目的背景和来源，有利于我们加深理解并加以推广．图3-94图3-95图 3-96如前所述，定值问题也可用来解决极值问题，对此，请看一道赛题． 例3.17 设定点A 位于定圆⊙O 外，自A 引⊙O 的二切线AB 、AC ，再在劣弧 BC上任取一点P ，过P 引切线分别与AB 、AC 相交于M 、N ，如图3-97．试问：P 点在劣弧 BC上移动到何处时，△AMN 的面积最大？并证明之．证法1：利用定值 由上例可知：△AMN 的周长为定值．而周长为定值的三角形以正三角形的面积为最大．又因∠MAN 为定角，故△AMN 只能以等腰时的面积为最大，因此，当P 处于 BC的中点时，△AMN 的面积为最大． 证法2：计算如图3-97，设⊙O 的半径为r ，△AMN 的面积为S ．则：S ABOC BMNCO =-四边形的面积五边形的面积2MNO ABOC S ∆=-四边形的面积，由于四边形ABOC 的面积为定值，12MNO S r MN ∆=⋅，故当MN 最小时，S最大．记BOM α∠=，CON β∠=，则有：tan MP BM r α==，tan PN CN r β==， 所以，(tan tan )tan()(1tan tan )MN MP PN r r αβαβαβ=+=+=+-，其中，1tan()tan tan 2r r BOC r BOA αβ+=∠=∠AB =为定值，而cos cos sin sin 2cos()1tan tan cos cos cos()cos()αβαβαβαβαβαβαβ-+-==-++，故知当αβ=时，MN 达到最小值．此时易知，P 是 BC的中点． 所以，当P 滑动到 BC的中点时，△AMN 的面积最大． 进而，我们还可以求出△AMN 面积的最大值来： 如图3-98，当△AMN 的面积S 最大时，易知P 也是MN 与AO 的交点．设AO a =，则cos()cos OB rBOA OA aαβ+=∠==， ∴ 221tan tan 1r a rr a a rαβ-==++． 又tan()tan AB BOA OB αβ+=∠= ∴2r MN r a r ==+最小图 3-97图 3-98∴ 12S AP MN =⋅=最大最小 当然，MN 的最小值也可由△AMP ∽△AOB 求出：MP APBO AB =⇒BO AP MP AB ⋅===⇒2MN MP ==最小．此外，还有定位问题，即在动态之中，某些动线恒过定点等，它们也很有趣．请看下节的例3.26．。
人教版九年级数学竞赛专题：平面几何的定值问题(含答案)
（第 3 题图）
（第 4 题图）
4.如图，正△ABO 的高等于⊙O 的半径，⊙O 在 AB 上滚动，切点为 T，⊙O 交 AO，BO 于 M，N，则 弧 MTN（ ）
A.在 0°到 30°变化
B.在 30°到 60°变化
C.保持 30°不变
D.保持 60°不变
5.如图，AB 是⊙O 的直径，且 AB=10，弦 MN 的长为 8.若 MN 的两端在圆上滑动时，始终与 AB 相交， 记点 A，B 到 MN 的距离分别为 h1，h2，则∣h1-h2∣等于（ ）
A
C
(P) O
D
B
①
D
A
C P O
B D ①
D
C
PB O
D ①
O
C A
P
①
B
O
C
P
A (B)
①
O
(D)C
A(B)
P ①
（2）已知⊙O 的半径为一定值 r，若点 P 是不在⊙O 上的一个定点，请你过点 P 任作一直线交⊙O 于 不重合的两点 E，F. PE·PF 的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文 字叙述出来.
（第 7 题图）
（第 8 题图）
8.如图，设 H 是等腰三角形 ABC 两条高的交点，在底边 BC 保持不变的情况下让顶点 A 至底边 BC 的 距离变小，这时乘积 S△ABC·S△HBC 的值变小、变大，还是不变？证明你的结论.
9.如图，在平面直角坐标系 xOy 中，抛物线 y 1 x 2 4 x 10 与 x 轴的交点为点 A，与 y 轴的交点 18 9
人教版九年级数学竞赛专题：平面几何的定值问题（含答案）
【例 1】 如图，已知 P 为正方形 ABCD 的外接圆的劣弧A⌒D上任意一点.求证： PA PC 为定值. PB
人教版 初三数学竞赛专题：平面几何的定值问题(包含答案)
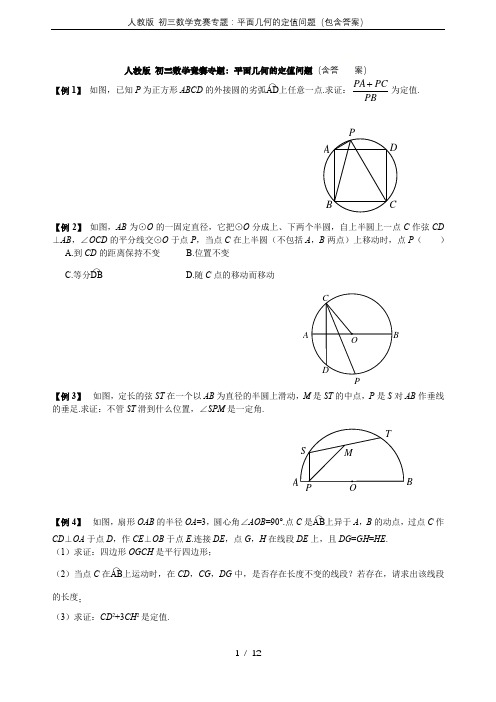
人教版 初三数学竞赛专题：平面几何的定值问题（含答案）【例1】 如图，已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证：PA PC PB为定值.【例2】 如图，AB 为⊙O 的一固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当点C 在上半圆（不包括A ，B 两点）上移动时，点P （ ） A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图，定长的弦ST 在一个以AB 为直径的半圆上滑动，M 是ST 的中点，P 是S 对AB 作垂线的垂足.求证：不管ST 滑到什么位置，∠SPM 是一定角.【例4】 如图，扇形OAB 的半径OA =3，圆心角∠AOB =90°.点C 是AB⌒上异于A ，B 的动点，过点C 作CD ⊥OA 于点D ，作CE ⊥OB 于点E .连接DE ，点G ，H 在线段DE 上，且DG =GH =HE .（1）求证：四边形OGCH 是平行四边形；（2）当点C 在AB ⌒上运动时，在CD ，CG ，DG 中，是否存在长度不变的线段？若存在，请求出该线段的长度；（3）求证：CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1，在平面直角坐标系xOy 中，点M 在x 轴的正半轴上，⊙M 交x 轴于A ，B 两点，交y 轴于C ，D 两点，且C 为弧AE 的中点，AE 交y 轴于G 点.若点A 的坐标为（-2，0），AE =8. （1）求点C 的坐标；（2）连接MG ，BC ，求证：MG ∥BC ；（3）如图2，过点D 作⊙M 的切线，交x 轴于点P .动点F 在⊙M 的圆周上运动时，PFOF的比值是否发生变化？若不变，求出比值；若变化，说明变化规律.（图1）（图2）【例6】 如图，已知等边△ABC 内接于半径为1的圆O ，P 是⊙O 上的任意一点.求证：P A 2+PB 2+PC 2为定值.【能力训练】1.如图，点A ，B 是双曲线xy 3上的两点，分别经过A ，B 两点向x 轴，y 轴作垂线段.若S 阴影=1，则BOACE HG D A=+21S S _______.（第1题图） （第3题图） （第4题图）2.从等边三角形内一点向三边作垂线段，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的面积是__________.3.如图，OA ，OB 是⊙O 任意两条半径，过B 作BE ⊥OA 于E ，又作OP ⊥AB 于P ，则定值OP 2+EP 2为_________.4.如图，在菱形ABCD 中，∠ABC =120°，F 是DC 的中点，AF 的延长线交BC 的延长线于点E ，则直线BF 与直线DE 所夹的锐角的度数为（ ）A.30°B.40°C.50°D.60°5.如图，在⊙O 中，P 是直径AB 上一动点，在AB 同侧作A A '⊥AB ，AB B B ⊥'，且A A '=AP ，B B '=BP .连接B A ''，当点P 从点A 移动到点B 时，B A ''的中点的位置（ ） A ．在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动（第5题图） （第6题图） 6.如图，A ，B 是函数xky =图象上的两点，点C ，D ，E ，F 分别在坐标轴上，且分别与点A ，B ，O 构成正方形和长方形.若正方形OCAD 的面积为6，则长方形OEBF 的面积是（ ） A.3 B.6 C.9 D.127.（1）经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ，B 和C ，D 四点，得到如图①~⑥所表示的六种不同情况.在六种不同情况下，P A ，PB ，PC ，PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子，然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'（2）已知⊙O 的半径为一定值r ，若点P 是不在⊙O 上的一个定点，请你过点P 任作一直线交⊙O 于不重合的两点E ，F . PE ·PF 的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文字叙述出来.8.在平面直角坐标系中，边长为2的正方形OABC 的两顶点A ，C 分别在y 轴，x 轴的正半轴上，点O 在原点，现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线x y =上时停止旋转.旋转过程中，AB 边交直线x y =于点M ，BC 边交x 轴于点N .（1）求OA 在旋转过程中所扫过的面积；（2）旋转过程中，当MN 与AC 平行时，求正方形OABC 旋转度数；（3）设△MBN 的周长为P ，在正方形OABC 旋转的过程中，P 值是否有变化？请证明你的结论.⑥⑤④③②①P(B )A PB9.如图，AB 是半圆的直径，AC ⊥AB ，AC =AB .在半圆上任取一点D ，作DE ⊥CD ，交直线AB 于点E ，BF ⊥AB ，交线段AD 的延长线于点F .（1）设弧AD 是x °的弧，若要点E 在线段BA 的延长线上，则x 的取值范围是_______.（2）不论点D 取在半圆的什么位置，图中除AB ＝AC 外，还有两条线段一定相等.指出这两条相等的线段，并予证明.（第9题图） （第10题图）（第11题图）10.如图，内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ，设⊙O 的半径为R .求证： （1）2222DK CK BK AK +++是定值； （2）2222DA CD BC AB +++是定值.11.如图，设P 是正方形ABCD 外接圆劣弧弧AB 上的一点，求证：DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2，H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时，面积S △ABC ·S △HBC 的值保持不变，则S △ABC ·S △HBC =________.2.已知A ，B ，C ，D ，E 是反比例函数xy 16=（x ＞0）图象上五个整数点（横、纵坐标均为整数），分别过这些点向横轴或纵轴作垂线段，以垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是__________（用含π的代数式表示）.P D CB A A折叠，使点A ，B 落在六边形ABCDEF 的内部，记∠C ＋∠D ＋ ）A. ∠1＋∠2＝900°－2α B. ∠1＋∠2＝1080°－2α C. ∠1＋∠2＝720°－α D. ∠1＋∠2＝360°－21α（第3题图） （第4题图）4.如图，正△ABO 的高等于⊙O 的半径，⊙O 在AB 上滚动，切点为T ，⊙O 交AO ，BO 于M ，N ，则弧MTN （ ）A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图，AB 是⊙O 的直径，且AB =10，弦MN 的长为8.若MN 的两端在圆上滑动时，始终与AB 相交，记点A ，B 到MN 的距离分别为h 1，h 2，则∣h 1-h 2∣等于（ ）A.5B.6C.7D.8（第5题图） 12GF EDCHBAB6.如图，已知△ABC 为直角三角形，∠ACB =90°，AC =BC ，点A ，C 在x 轴上，点B 坐标为（3，m ）（m ＞0），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B ，D . （1）求点A 的坐标（用m 表示） （2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点B 之间的一动点，连接PQ 并延长交BC 于点E ，连接BQ 并延长交AC 于点F .试证明：FC （AC +EC ）为定值.7.如图，已知等边△ABC 内接于圆，在劣弧AB 上取异于A ，B 的点M .设直线AC 与BM 相交于K ，直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.（第7题图） （第8题图）8.如图，设H 是等腰三角形ABC 两条高的交点，在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小，这时乘积S △ABC ·S △HBC 的值变小、变大，还是不变？证明你的结论.9.如图，在平面直角坐标系xOy 中，抛物线10941812--=x x y 与x 轴的交点为点A ，与y 轴的交点为点B .过点B 作x 轴的平行线BC ，交抛物线于点C ，连接AC .现有两动点P ，Q 分别从O ，C 两点同时出发，点P 以每秒4个单位的速度沿OA 向终点A 移动，点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时，点Q 也同时停止运动.线段OC ，PQ 相交于点D ，过点D 作DE ∥OA ，交CA 于E ，射线QE 交x 轴于点F .设动点P ，Q 移动的时间为t （单位：秒）. （1）求A ，B ，C 三点的坐标和抛物线的顶点坐标；（2）当t 为何值时，四边形PQCA 为平行四边形？请写出计算过程； （3）当290<<t 时，△PQF 的面积是否总是定值？若是，求出此值；若不是，请说明理由； （4）当t 为何值时，△PQF 为等腰三角形，请写出解答过程.NKMB AC HCBA（第9题图） （第10题图） 10.已知抛物线C 1：12121+-=x x y ，点F （1,1）. （1）求抛物线C 1的顶点坐标；（2）若抛物线C 1与y 轴的交点为A ，连接AF ，并延长交抛物线C 1于点B ，求证：211=+BFAF . （3）抛物线C 1上任意一点P （x P ，y P ）（0＜x P ＜1），连接PF ，并延长交抛物线C 1于点 Q （x Q ，y Q ），试判断211=+QFPF 是否成立？请说明理由.11.已知A ，B 是平面上的两个顶点，C 是位于AB 一侧的一个动点，分别以AC ，BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证：不论C 在直线AB 同一侧的任何位置，EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ，使CE ＝AP ，连结BE ，则△BCE ≌△BAP ，及△PBE 为等腰直角三角形，故PA PC CE PC PEPB PB PB++=== 例2 B 提示：连结AC ，BC ，可以证明P 为APB 的中点． 例3 ∵SP ⊥OP ，OM ⊥ST ，∴S ，M ，O ，P 四点共圆，于是∠SPM ＝∠SOM ＝12∠SOT 为定角． 例4 (1)连结OC 交DE 于M ，则OM ＝CM ， EM ＝DM ，而DG ＝ HE ，则HM ＝GM 故四边形OGCH 是平行四边形． (2)DG 不变．DE ＝OC ＝OA ＝3 .DG ＝13DE ＝13×3＝1． (3)设CD ＝x ，延长OG 交CD 于N ，则CN ＝DN ＝12 x ，229CE x =- ， 2214DN x = .∴22394ON x =-，而ON ＝32CH ，∴22143CH x =-．故CD 2＋3CH 2＝x 2＋3(4－13x 2)＝x 2＋12－x 2为定值． 例5 ⑴C (0，4) ⑵先求得AM ＝CM ＝5，连接MC 交AE 于N ，由△AO G ∽△ANM ，得OG AO MN AN =，O G ＝32，38OG OM OC OB ==，又∠BOC ＝∠G OM ，∴△G OM ∽△COB ，∠G MO ＝∠CBO ，得M G ∥BC ．⑶连结DM ，则DM ⊥PD ，DO ⊥PM ，DO 2＝OM •OP ，OP ＝163．动点F 在⊙M 的圆周上运动时，从特殊位置探求OFPF的值．当F 与点A 重合时，2316523OF AO PF AP ===-；当点F 与点B 重合时，8316583OF OB PF PB ===+；当点F 不与点A ，B 重合时，连接OF 、PF 、MF ，∴DM 2＝MO •MP ，∴FM 2＝MO •MP ，即FM MPOM FM=，又∠OMP ＝∠FMP ，∴△MFO ∽△MPF ，35OF MO PF MF ==，故OF PF 的比值不变，比值为35． 例6 ∠BPC ＝120°，在△BPC 中，由余弦定理得BC 2＝PB 2＋PC 2－2PB •PC ＝BC 2，又由上托勒密定理得BC •P A ＋PC •AB ，而AB ＝BC ＝AC ，∴P A ＝PB ＋PC ，从而P A 2＋ PB 2＋ PC 2＝ (PB ＋PC )2＋ PB 2＋ PC 2＝2 (PB 2＋PC 2＋PB •PC )＝2BC 2＝2×()23＝6．故P A 2＋PB 2＋PC 2为定值．A 级 1．4提示：∵S 1＋S 阴＝ S 2＋S 阴＝xy ＝3，∴S 1＋S 2＝2xy －2S 阴＝6－2＝4．2．273 提示：1＋3＋5＝9是等边三角形的高． 3．r 2提示：先考查OB 与OA 垂直的情形．4．D 提示：延长BF 交DE 于点M ，连接BD ，则△BCD 为等边三角形，BF 平分∠CBD ．∵F 为CD 中点，且AD ∥CE ，∴△ADF 与△ECF 关于点F 中心对称．∴CE ＝AD ＝CD ，∴∠CEM=30°，∠DMF=60°，5．D 提示：A′B′的中点均在⊙O 的上半圆的中点处． 6．B 提示：S 正方形OCAD ＝OD •OC ＝A A x y k =＝6，∴S OEBF ＝OE •OF ＝x B •y B k =＝6． 7．⑴略⑵当点P在⊙O 内时，过P 作直径CD ，则PE •PF ＝PD •PC ＝r 2－OP 2为定值；当点P 在⊙O 外时，PE •PF 为定值22OP r -．结论：过不在圆上的一个定点任作一条直线与圆相交，则这点到直线与圆相交点的两条线段长的积为定值． 8．⑴2π⑵22.5° ⑶P 值无变化．理由如下：如图，延长BA 交y 轴于E 点，可证明△OAE ≌△OCN ，得OE ＝ON ，AE ＝CN ，又∠MOE ＝∠MON ＝45°，OM ＝ON ，∴△OME ≌△OMN ，得MN ＝ME ＝AM ＋AE ＝AM ＋CN ．∴P ＝MN ＋BN ＋BM ＝AM ＋CM ＋CN ＋BN ＋BM ＝AB ＋AC ＝4．9．⑴0＜x ＜90 ⑵BE ＝BF 提示：连接BD ，可证明△BDF ∽△ADB ，△BDE ∽△ADC ． 10．⑴作OP ⊥BD 于P ，OQ ⊥AC 于Q ，连接AO ，则AO 2＝()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦，又AK •CK ＝BK •DK ，得AK 2＋BK 2＋CK 2＋DK 2＝4R 2为定值． ⑵作直径DE ，连接AE ，BE ，CE ，AB 2＋CD 2＝4R 2，AD 2＋BC 2＝4R 2，故AB 2＋BC 2＋CD 2＋DA 2＝8K 2为定值． 11．设正方形的边长为a ，根据托勒密定理，对于四边形APBC 和四边形APBD ，有CP •a ＝AP •a ＋BP •2a ，DP •a ＝BP •a ＋AP •2a ，两式相加并整理得(CP ＋DP )a ＝(AP ＋BP )(a ＋2a )，从而21AP BPCP DP+=-+为定值．B 级1．1 提示：不妨设∠A 为锐角，AD ，BE ，CF 为△ABC 的三条高，H 为垂心，由AB ＝AC 知∠HBD ＝∠HCD ＝∠HAE ，∠HDC ＝∠CDA ＝90°，故R t △CHD ∽R t △ACD ．∴AD DC DC HD =，即AD •HD ＝DC 2＝14BC 2＝1．∴S △ABC •S △HBC ＝2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭＝1．当∠A ≥90°时，结论成立．2．13π－26 提示：∵A ，B ，C ，DE 是反比例函数y ＝16x(x ＞0)图象上五个整数点，由图象可知，这些点的横坐标分别为1，2，4，8，16．∴五个正方形的边长分别为1，3，4，2，1．∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦＝5π－10＋8π－16＝13π－26． 3．B 提示：如图，设F A 的延长线与CB 的延长线交于点P ，G A ′的延长线与HB ′的延长线交于点P ′．由对称性可知∠1＝2∠APP ′，∠2＝2∠BPP ′．∴∠1＋∠2＝2∠APB ．∵∠APB ＝540°－α，∴∠1＋∠2＝1080°－2α． 4．D 5．B 提示：如图，设AB 与MN 交于点C ，过点O 作OD ⊥MN 于D ，连接FO 并延长交EB 于G ．由垂径定理，得OD ＝2254-＝3．由△AFO ≌△B G O ，得AF ＝B G ，即h 1＝B G ．由AF ⊥MN ，BE ⊥MN ，得△FOD ∽△F G E ．∴12OD FO GE FG ==．∴E G ＝2OD ＝6，∴12h h AF BE -=-＝E G ＝6． 6．⑴A (3－m ，0) ⑵y ＝x 2－2x ＋1 ⑶过点Q 作QM ⊥AC 于M ，过点Q 作QN ⊥BC 于N ，设Q 点的坐标为(x ，x 2－2x ＋1)，则QM ＝CN ＝(x －1)2，MC ＝QN＝3－x ．∵QM ∥CE ，∴PQM ∽△PEC ．∴QM PMEC PC=，即()2112x x EC--=，得EC ＝2(x －1)．∵QN ∥CF ，∴△BQN ∽△BFC ．∴QN BN FC BC =，即()24134x x FC ---=，得FC ＝41x +．又AC ＝4，∴FC (AC ＋EC )＝()44211x x +-⎡⎤⎣⎦+＝8为定值． 7．提示：易证△ABK ∽△BNA ，故AK •BN ＝AB 2为定值，即AK 与BN 的乘积与M 点的选择无关． 8．提示：S △ABC •S △HBC ＝116BC 4，由于BC 是不变的，所以当点A 至BC 的距离变小时，乘积S △ABC •S △HBC 保持不变． 9．⑴A (18，0)，B (0，－10)，顶点坐标为(4，－989)⑵若四边形PQCA 为平行四边形，由于QC ∥P A ，故只要QC ＝P A 185． ⑶即可，而P A ＝18－4t ，CQ ＝t ，故18－4t ＝t ，得t ＝设点P 运动t s ，则OP ＝4t ，CQ ＝t ，0＜t ＜4.5．说明P在线段OA 上，且不与点O ，A 重合．由于QC ∥OP 知△QDC ∽△PDO ，故144QD QC t DP OP t ===．同理QC ∥AF ，故14QC CE AF EA ==，即14t AF =，∴AF ＝4t ＝OP ．∴PF ＝P A ＋AF ＝P A ＋OP ＝18．又点Q 到直线PF 的距离d ＝10，∴S △PQF ＝12•PF •d ＝12×18×10＝90．于是S △PQF 的面积总为定值90． ⑷由前面知道，P (4t ，0)，F (18＋4t ，0)，Q (8－t ，－10)，0≤t ≤4.5．构造直角三角形后易得PQ 2＝(4t －8＋t )2＋102＝，FQ 2＝(18＋4t －8＋t )2＋102＝(5t ＋10)2＋100．①若FP ＝FQ ，即182＝(5t ＋10)2＋100，故25(t ＋2)2＝224，(t ＋2)2＝24425．∵2≤t ＋2≤6.5，∴t ＋2＝244414255=．∴t ＝ 4145－2． ②若QP ＝QF ，即(5t －8)2＋100＝(5t ＋10)2＋100，即(5t －8)2＝(5t ＋10)2，无0≤t ≤4.5的t 满足． ③若PQ ＝PF ，即(5t －8)2＋100＝182，∴(5t －8)2＝224．由于224≈15，又0≤5t ≤22.5，∴－8≤5t －8≤14.5，14.52＝22984124⎛⎫= ⎪⎝⎭＜224．故没有t (0≤t ≤4.5)满足此方程．综上所述，当t ＝4145－2时，△PQ R 为等腰三角形． 10．⑴C 1的顶点坐标为(1，12). ⑵略 ⑶作PM ⊥AB 于M ，作QN ⊥AB 交AB 延长线于N ，∴PM ＝1－y P ，FM ＝1－x P ．在R t △PMF 中，PF 2＝(1－y P )2＋(1－x P )2＝1－2y P ＋y P 2＋1－2x P ＋x P 2，又∵点P 在抛物线上，∴y P ＝12x P 2－x P ＋1，∴PF 2＝1－x P 2＋2x P －2＋y P 2＋1－2x P ＋x P 2＝y P 2，∴PF ＝y P ，同理，QF ＝y Q ，易证△PMF ∽△QNF ，则PM QN PF QF =，∴11Q P y y PF QF --=，即11PF QF PF QF --=，∴11PF QF+＝2． 11．先从特殊情况出发．当△ABC 是等腰直角三角形时，点P 与点C 重合，此时点P 的位置在AB 的中垂线上，且到AB的距离为12AB ，如图①所示．下面就一般情况来证明上面的结论(结论②所示)．过C ，E ，G 分别作直线AB 的垂线CH ，EM ，G N ，垂足分别是H ，M ，N ．容易证明△AEM ≌△ACH ，△B G N ≌△BCH ．从而有AM ＝CH ＝BN ，EM ＝AH ，G N ＝BH ．这样，线段AB 的中点O 也是线段MN 的中点，连接OP ，则OP 是梯形EMN G 的中位线，从而OP ⊥AB ，OP ＝12(EM ＋G N )＝ 12(AH ＋BH )＝12AB ．∴无论点C 在AB 同一侧的位置如何，E G 中点P 的位置不变．。
平面几何中的定值问题初探
。
:
法)
,
已知 尸 为 正 方 体对 角 线 的 六等分 点 例6 过 只点且 与 对 角 线 垂 直 的 截面
.
.
,
试画
2 ) 过M (
R
作直 线 交 A B
。
,
BC于F
G
.
则
D B
,
分析 与画 法
:
,
:
如图
,
因 截 面刁 B I C 垂直对 角 线
:
.
F 口 F 尸 确 定 的截 面 为所 画 的截 面
,
,
2
.
5尸
,
,
S Q
所确定 的 平 面
,
,
截面
,
平面ABC
,
面上三点 分析
、
试 画 过这 三 点 的 截 面
.
。
两两相交
.
画法
。
:
且 交线 易 于确 定 O ) 作 过 S 尸 S Q 的 截面 交 A B
.
E
.
令 DE
尸
Q 交于 M 〔若 尸 Q 刀 E D
,
,
读 者 考虑 作
,
C B
于0
,
若将 棱柱 理 解为 顶 点在 无 限 远 处 的 棱 淮 此 题 解 法就 与 例 4 完全 相 似 了 只 是 辅 助 平面 便 由过 R Q 作平 行 于 侧棱 的两 平行 线所 确定
,
·
·
等 于 其它 两 边 的 积
AC
·
A D = ZR A C A刀 月E A F
·
A
H
A E
·
A F = R卜 A H 二
初中数学-平面几何的定值问题
平面几何的定值问题【阅读与思考】所谓定值问题，是指按照一定条件构成的几何图形，当某些几何元素按一定的规律在确定的范围内变化时，与它有关的元素的量保持不变（或几何元素间的某些几何性质或位置关系不变）.几何定值问题的基本特点是：题设条件中都包含着变动元素和固定元素，变动元素是指可变化运动的元素，固定元素也就是“不变量”，有的是明显的，有的是隐含的，在运动变化中始终没有发生变化的元素，也就是我们要探求的定值. 解答定值问题的一般步骤是： 1.探求定值； 2.给出证明.【例题与求解】【例1】 如图，已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证：PA PC PB为定值. 解题思路：线段的和差倍分考虑截长补短，利用圆的基本性质，证明三角形全等.P AB CD【例2】 如图，AB 为⊙O 的一固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当点C 在上半圆（不包括A ，B 两点）上移动时，点P （ ） A .到CD 的距离保持不变 B .位置不变C .等分DB⌒ D .随C 点的移动而移动 解题思路：添出圆中相关辅助线，运用圆的基本性质，用排除法得出结论.AP【例3】 如图，定长的弦ST 在一个以AB 为直径的半圆上滑动，M 是ST 的中点，P 是S 对AB 作垂线的垂足.求证：不管ST 滑到什么位置，∠SPM 是一定角.解题思路：不管ST 滑到什么位置，∠SOT 的度数是定值.从探寻∠SPM 与∠SOT 的关系入手.B【例4】 如图，扇形OAB 的半径OA =3，圆心角∠AOB =90°.点C 是AB⌒上异于A ，B 的动点，过点C 作CD ⊥OA 于点D ，作CE ⊥OB 于点E .连接DE ，点G ，H 在线段DE 上，且DG =GH =HE .（1）求证：四边形OGCH 是平行四边形；（2）当点C 在AB ⌒上运动时，在CD ，CG ，DG 中，是否存在长度不变的线段？若存在，请求出该线段的长度；（3）求证：CD 2+3CH 2是定值.解题思路：延长OG 交CD 于N ，利用题中的三等分点、平行四边形和三角形中位线的性质，实现把线段ON 转化成线段CH 的倍分关系，再以Rt △OND 为基础，通过勾股定理，使问题得以解决.BOACE HGD 【例5】 如图1，在平面直角坐标系xOy 中，点M 在x 轴的正半轴上，⊙M 交x 轴于A ，B 两点，交y 轴于C ，D 两点，且C 为弧AE 的中点，AE 交y 轴于G 点.若点A 的坐标为（-2，0），AE =8. （1）求点C 的坐标；（2）连接MG ，BC ，求证：MG ∥BC ；（3）如图2，过点D 作⊙M 的切线，交x 轴于点P .动点F 在⊙M 的圆周上运动时，PFOF的比值是否发 生变化？若不变，求出比值；若变化，说明变化规律.解题思路：对于（3）从动点F 达到的特殊位置时入手探求定值.（图1） （图2）【例6】 如图，已知等边△ABC 内接于半径为1的圆O ，P 是⊙O 上的任意一点.求证：P A 2+PB 2+PC 2为定值.解题思路：当点P 与C 点重合时，P A 2+PB 2+PC 2=2BC 2为定值，就一般情形证明.A【能力训练】A 级1.如图，点A ，B 是双曲线xy 3=上的两点，分别经过A ，B 两点向x 轴，y 轴作垂线段.若S 阴影=1，则=+21S S _______.AABCDEF（第1题图） （第3题图） （第4题图）2.从等边三角形内一点向三边作垂线段，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的面积是__________.3.如图，OA ，OB 是⊙O 任意两条半径，过B 作BE ⊥OA 于E ，又作OP ⊥AB 于P ，则定值OP 2+EP 2为_________.4.如图，在菱形ABCD 中，∠ABC =120°，F 是DC 的中点，AF 的延长线交BC 的延长线于点E ，则直线BF 与直线DE 所夹的锐角的度数为（ ）A .30°B .40°C .50°D .60° 5.如图，在⊙O 中，P 是直径AB 上一动点，在AB 同侧作A A '⊥AB ，AB B B ⊥'，且A A '=AP ，B B '=BP .连接B A ''，当点P 从点A 移动到点B 时，B A ''的中点的位置（ ）A ．在平分AB 的某直线上移动 B .在垂直AB 的某直线上移动C .在弧AMB 上移动D .保持固定不移动AB'B（第5题图） （第6题图）6.如图，A ，B 是函数xky图象上的两点，点C ，D ，E ，F 分别在坐标轴上，且分别与点A ，B ，O 构成正方形和长方形.若正方形OCAD 的面积为6，则长方形OEBF 的面积是（ ） A .3 B .6 C .9 D .127.（1）经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ，B 和C ，D 四点，得到如图①~⑥所表示的六种不同情况.在六种不同情况下，P A ，PB ，PC ，PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子，然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.⑥⑤④③②①)P (B )PB（2）已知⊙O 的半径为一定值r ，若点P 是不在⊙O 上的一个定点，请你过点P 任作一直线交⊙O 于不重合的两点E ，F . PE ·PF 的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文字叙述出来.8.在平面直角坐标系中，边长为2的正方形OABC 的两顶点A ，C 分别在y 轴，x 轴的正半轴上，点O在原点，现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线x y =上时停止旋转.旋转过程中，AB 边交直线x y =于点M ，BC 边交x 轴于点N .（1）求OA 在旋转过程中所扫过的面积；（2）旋转过程中，当MN 与AC 平行时，求正方形OABC 旋转度数；（3）设△MBN 的周长为P ，在正方形OABC 旋转的过程中，P 值是否有变化？请证明你的结论.9.如图，AB 是半圆的直径，AC ⊥AB ，AC =AB .在半圆上任取一点D ，作DE ⊥CD ，交直线AB 于点E ，BF ⊥AB ，交线段AD 的延长线于点F .（1）设弧AD 是x °的弧，若要点E 在线段BA 的延长线上，则x 的取值范围是_______.（2）不论点D 取在半圆的什么位置，图中除AB ＝AC 外，还有两条线段一定相等.指出这两条相等的线段，并予证明.（第9题图） （第10题图）（第11题图）10.如图，内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ，设⊙O 的半径为R .求证： （1）2222DK CK BK AK +++是定值；（2）2222DA CD BC AB +++是定值.PD CB A A11.如图，设P 是正方形ABCD 外接圆劣弧弧AB 上的一点，求证：DPCP BPAP ++的值为定值.。
解析几何中定值和定点问题
解析几何中定值与定点问题【探究问题解决的技巧、方法】(1)定点和定值问题就是在运动变化中寻找不变量的问题，基本思想是使用参数表示要解决的问题，证明要解决的问题与参数无关．在这类试题中选择消元的方向是非常关键的．(2)解圆锥曲线中的定点、定值问题也可以先研究一下特殊情况，找出定点或定值，再视具体情况进行研究．【实例探究】题型1：定值问题:例1：已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线的焦点，离心率等于（Ⅰ）求椭圆C的标准方程；（Ⅱ）过椭圆C的右焦点作直线l交椭圆C于A、B两点，交y轴于M点，若为定值.解：（I）设椭圆C的方程为，则由题意知b= 1.∴椭圆C的方程为（II）方法一：设A、B、M点的坐标分别为易知F点的坐标为（2，0）.将A点坐标代入到椭圆方程中，得去分母整理得方法二：设A、B、M点的坐标分别为又易知F点的坐标为（2，0）.显然直线l存在的斜率，设直线l的斜率为k，则直线l的方程是将直线l的方程代入到椭圆C的方程中，消去y并整理得又例2.已知椭圆C经过点A(1,3/2),两个焦点为(-1,0),(1,0).1）求椭圆方程2）E、F是椭圆上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明：直线EF的斜率为定值，并求出这个定值（1）a²-b²=c² =1设椭圆方程为x²/（b²+1）+y²/b²=1将（1，3/2）代入整理得4b^4-9b²-9=0 解得b²=3 （另一值舍）所以椭圆方程为x²/4+y²/3=1（2）设AE斜率为k则AE方程为y-(3/2)=k(x-1)①x ²/4+y ²/3=1 ②①，②联立得出两个解一个是A （1,3/2）另一个是E （x1，y1） ①代入②消去y 得（1/4+k ²/3）x ²-（2k ²/3-k ）x+k ²/3-k-1/4=0 根据韦达定理 x1·1=（k ²/3-k-1/4）/（1/4+k ²/3）③ 将③的结果代入①式得y1=（-k ²/2-k/2+3/8）/(1/4+k ²/3)设AF 斜率为-k ，F （x2，y2） 则AF 方程为y-（3/2）=-k （x-1）④ x ²/4+y ²/3=1 ② ②④联立同样解得x2=（k ²/3+k-1/4）/（1/4+k ²/3） y2=（-k ²/2+k/2+3/8）/（1/4+k ²/3） EF 斜率为（y2-y1）/(x2-x1)=1/2所以直线EF 斜率为定值，这个定值是1/2。
初中数学培优之平面几何的定值问题
【阅读与思考】
所谓定值问题，是指按照一定条件构成的几何图形，当某些几何元素按一定的规律在确定的范围内 变化时，与它有关的元素的量保持不变（或几何元素间的某些几何性质或位置关系不变）. 几何定值问题的基本特点是：题设条件中都包含着变动元素和固定元素，变动元素是指可变化运动 的元素，固定元素也就是“不变量” ，有的是明显的，有的是隐含的，在运动变化中始终没有发生变化 的元素，也就是我们要探求的定值. 解答定值问题的一般步骤是： 1.探求定值； 2.给出证明.
5
y A M y=x B O N C
（济宁市中考试题） 9.如图，AB 是半圆的直径，AC⊥AB，AC=AB.在半圆上任取一点 D，作 DE⊥CD，交直线 AB 于点 E， BF⊥AB，交线段 AD 的延长线于点 F. （1）设弧 AD 是 x°的弧，若要点 E 在线段 BA 的延长线上，则 x 的取值范围是_______. （2）不论点 D 取在半圆的什么位置，图中除 AB＝AC 外，还有两条线段一定相等.指出这两条相等的线 段，并予证明. （江苏省竞赛试题）
解题思路：延长 OG 交 CD 于 N，利用题中的三等分点、平行四边形和三角形中位线的性质，实现把线 段 ON 转化成线段 CH 的倍分关系，再以 Rt△OND 为基础，通过勾股定理，使问题得以解决.
B
E O
C H G D A
【例 5】 如图 1，在平面直角坐标系 xOy 中，点 M 在 x 轴的正半轴上，⊙M 交 x 轴于 A，B 两点，交 y 轴于 C，D 两点，且 C 为弧 AE 的中点，AE 交 y 轴于 G 点.若点 A 的坐标为（-2，0） ，AE=8. （1）求点 C 的坐标； （2）连接 MG，BC，求证：MG∥BC； （3）如图 2，过点 D 作⊙M 的切线，交 x 轴于点 P.动点 F 在⊙M 的圆周上运动时， 生变化？若不变，求出比值；若变化，说明变化规律.
解析几何中五类定点定值问题的研究与拓展解答
专题:解析几何中五类定点定值问题的研究与拓展【问题提出】1.无论k 取任何实数，直线(1 +4k)x-(2 -3k)y+(2 -14k) =0必经过一个定点，则这个定点的坐标为2.已知直线丨：2ax +by-a +b =0 ；圆C : x 2 + y 2 - 2x-1 = 0 ,则直线I 与圆C 的位置关系为=1(a >■ b A 0)，点A,F 分别是椭圆C 的左顶点和左焦点，点P 是圆PA 若 ——为常数，则椭圆的离心率为PF过点(1, 0).若对任意的实数 m ,定直线 l 被圆C 截得的弦长为定值，则直线 I 的方程为.2x + y — 2= 0【探究拓展】2探究1：已知F 1、F 2分别为椭圆 G ：詁+詁=1(a Ab 》。
)的上、下焦点，其中F 1也是抛物线C 2：x 2=4y 的5焦点，点M是C 1与C 2在第二象限的交点，且阿七.(1) 求椭圆C 1的方程.(2)已知点P(1,3)和圆O ：X 2 +y 2 =b 2,过点P 的动直线I 与圆0相交于不同的两点 A,B ,在线段AB 上取一 点Q ,满足：AP = -A P B ,瓷=Z QB ,( A H 0且A H ±1).求证：点Q 总在某定直线上.4.平面直角坐标系 xOy 中,已知圆C ： x 2+ y 2— (6 — 2m)x — 4my + 5m 2— 6m = 0,直线 I 经 2 2x y3.已知椭圆C : —2 + —2a b2 2 2 O : x + y =b 上的动点,1 4变式1 :在平面直角坐标系 xOy 中，已知定点A( — 4,0)、B(4,0),动点P 与A 、B 两点连线的斜率之积为①求O M 的方程;直线AF i , AF 2分别交椭圆于点 (1 )求证直线BO 平分线段AC ;(2) 设点P (m , n ) ( m , n 为常数)在直线BO 上且在椭圆外，过P 的动直线(1)求点 p 的轨迹方程;(2)设点 P 的轨迹与y 轴负半轴交于点 C.半径为r 的圆M 的圆心M 在线段 AC 的垂直平分线上，且在 y轴右侧，圆 M 被y 轴截得的弦长为a②当r 变化时，是否存在定直线 I 与动圆M 均相切？如果存在，求出定直线I 的方程；如果不存在，说明理由.2 2X y 变式2 :已知椭圆E : —2 + a b= 1(a Ab >0)的离心率为 弓3 ,它的上顶点为A ,左、右焦点分别为F 1,F 2 ,MP N ,在线段MN 上取点Q ,满足—PN=器，试证明点Q 恒在一定直线上.B ,C .I 与椭圆交于两个不同点 M ,P探究2:平面直角坐标系xoy 中，圆G：(x + 3)2+(y -1)2=4和圆C2：(X-4)2+(y-5)2=4.(1)若直线I过点A(4,0)，且被圆C I截得的弦长为2J3，求直线I的方程;(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线|1和|2，它们分别与圆C1和圆C2相交，且直线|1被圆C1截得的弦长与直线12被圆C2截得的弦长相等，试求所有满足条件的点P的坐标.-- ----------- ►A H变式1：在直角坐标系xOy中，点M到点F i(-J3,0)，F2(J3,O)的距离之和为4，点M的轨迹是C，与x轴的负半轴交于点A，轨迹C上有不同的两点P和Q，且AP-AQ-O(1)求轨迹C的方程;(2)直线PQ是否过x轴上的一定点，若过定点，请给出证明，并求出该定点？若不过定点，请说明理由.变式2:已知圆C:x2+y2=9，点A(—5,0)，直线l :x-2y = 0.(1)求与圆C相切，且与直线I垂直的直线方程;PB (2)在直线OA上(O为坐标原点)，存在定点B (不同于点A),满足：对于圆C上任一点P ,都有——PA 为一常数，试求所有满足条件的点B的坐标.变式3 :在平面直角坐标系xOy中，已知直线1: 2岳—y+ 3+ 8返=0和圆C1: x2+ y2+ 8x + F= 0.若直线I被圆C i截得的弦长为2j3 .设圆C i和x轴相交于A, B两点，点P为圆C i上不同于A, B的任意一点，直线FA, PB交y轴于M, N两点.当点P变化时，以MN为直径的圆C?是否经过圆C1内一定点?请证明你的结论;变式4:如图，椭圆的中心为原点 O ,离心率e =¥，—条准线的方程为x = 2{2.(1)求该椭圆的标准方程; (2)设动点P 满足：O P = OM + 2ON ，其中M , N 是椭圆上的点，直线 0M 与ON 的斜率之积为一2,问: 是否存在两个定点 F i , F 2，使得|PFJ +|PF 2I 为定值？若存在，求出 F i , F 2的坐标；若不存在，说明理由.5:已知左焦点为F(— 1 , 0)的椭圆过点E(1 , 亜).过点P(1 , 1)分别作斜率为k i , k 2的椭圆的动弦 3 CD ，设M , N 分别为线段AB , CD 的中点. 求椭圆的标准方程； 若P 为线段AB 的中点，求k i ；若k i + k 2=1，求证直线MN 恒过定点，并求出定点坐标.变式 AB ,2 2 X y探究 3 :已知椭圆p +笃=1（a；＞bA0）的左顶点为a b+ y2+ J3x -3y -6 = 0过A, F2两点求椭圆标准的方程; A，左、右焦点分别为F1,F2，且圆X2(2) 设直线PF2的倾斜角为a,直线PF1的倾斜角为3,当a,3- a= I n时证明：点P在一定圆上;3变式设椭圆的上顶点为Q,在满足条件（2）的情形下证明: PQ = PF i + PF2 .1:在平面直角坐标系xOy中，圆C的方程为（X—1）2+ y2= 4, P为圆C上一点•若存在一个定圆过P作圆M的两条切线PA, PB,切点分别为A, B，当P在圆C上运动时，使得/ APB恒为60。
平面几何中的定值问题
心, 射线 AO 交 BC 于点 D , 动直线 l 交 AB 、 AC 于点 E 、 F . 如果 A 、 E、 D、 F 四点共圆 , 那 么, 线段 EF 在 BC 上的正射影恒为定值 . 讲 解: 如 图 6, 作 DM L AB 于 点 M , DN L AC 于 点 N , MMc L BC 于 点 Mc, NNc L BC 于点 Nc. 显然, Mc N c是定 值. 作 EE c L BC 、 FFc L BC . 易证 A 、 M、 D、 N 四点共圆 . 从而 , N DEM = N DFN . 所以 , v DEM V v DFN . EM DM sin A cos C 故 FN = DN = sin B= cos B .
2
=
3 2 2 3 ( R - r )+ Rr cos( 60 b- B) 4 2 1 Rr #2sin A + B#cos A - B 2 2 2
2 2 = 3 ( R - r ) + 3 Rr cos( 60 b- B) 4 2
3 Rr cos( 60 b- B) 2 = 3 2 2 ( R - r ) ( 定值) . 4
AB = a + b , QM = QA = QB = QD = 1 ( a- b ) . 2 1 ( a+ b ) - x . 2
2 2
1 ( a + b) , 2
令 OD = x , 则 OQ =
2 2 2
由 OQ = OD + QD , 得 1 ( a + b) - x 2 解得 x = ab . a+ b = x + 1 ( a - b) 2
PP 2 = PP 3 =
2
PA #PB , 2R PB #PC 2R .
第二十三讲 平面几何的定值与最值问题(含解答)-
第二十三讲平面几何的定值与最值问题【趣题引路】传说从前有一个虔诚的信徒,他是集市上的一个小贩.••每天他都要从家所在的点A出发,到集市点B,但是,到集市之前他必须先拐弯到圆形古堡朝拜阿波罗神像.古堡是座圣城,阿波罗像供奉在古堡的圆心点O,•而周围上的点都是供信徒朝拜的顶礼地点如图1.这个信徒想,我怎样选择朝拜点,才能使从家到朝拜点,•然后再到集市的路程最短呢?(1) (2)解析在圆周上选一点P,过P作⊙O的切线MN,使得∠APK=∠BPK,即α=β.那么朝圣者沿A→P→B的路线去走,距离最短.证明如图2,在圆周上除P点外再任选一点P′.连结BP•′与切线MN•交于R,AR+BR>AP+BP.∵RP′+AP′>AR.∴AP′+BP′=AP′+RP′+RB>AR+BP>AP+BP.不过,用尺规作图法求点P的位置至今没有解决.•“古堡朝圣问题”属于数学上“最短路线问题”,解决它的方法是采用“等角原理”.【知识延伸】平面几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题.•所谓几何定值问题就是要求出这个定值.在解决这类问题的过程中,可以直接通过计算来求出定值;也可以先考虑某一个特殊情形下的该相关值,然后证明当相应几何元素变化时,此值保持不变.例1如果△ABC的外接圆半径R一定,求证: abcS是定值.(S表示△ABC的面积)解析由三角形面积S=12absinC和正弦定理sincC=2R,∴c=2RsinC.∴abcS=2sincC=4sinsinR CC=4R是定值.点评通过正弦定理和三角形面积公式经过变形,计算出结果是4R,即为定值.平面几何中不仅有等量关系,还有不等关系,例如在变动一些几何元素时,•某一相关的值保持不大于(或不小于)某个定值,如果这个定值在某个情形下可以取得,•这就是一个几何极值.确定几何极值的问题称为几何极值问题,解决这些问题总要证明相关的几何不等式,并指明不等式成为等式的情形(或者至少证明不等式可以成为等式).例2 如图,已知⊙O的半径R=33,A为⊙O上一点,过A作一半径为r=3的⊙O′,问OO′何时最长?最长值是多少?OO′何时最短?最短值是多少?解析当O′落在OA的连线段上(即⊙A与线段OA的交点B时)OO′最短,且最短长度为33-3 ;当O′落在OA的延长线上(即⊙O与OA的延长线交点C时)OO′最长,且最长的长度为33+3 .点评⊙O′是一个动圆,满足条件的⊙O′有无数个,但由于⊙O′过A点,所以⊙O′的圆心O′在以A为圆心半径为3的⊙A上.【好题妙解】佳题新题品味例1 如图,已知P为定角O的角平分线上的定点,过O、P•两点任作一圆与角的两边分别交于A、B两点.求证:OA+OB是定值.证明连结AP、BP,由于它们为有相同圆周角的弦,AP=PB,不妨记为r.•另记x1=OA,x2=OB.对△POA应用余弦定理,得x12+OP2-2OP·cos∠AOP·x1=r2.故x1为方程x2-2OP·cos 12∠AOB·x+(O P2-r2)=0的根,同理x2亦为其根.因此x1,x2为此方程的两根,由韦达定理,得x1+x2=2OP(12∠AOB)是定值.点评当x 1=x 2时,x 1+x 2为此定值,事实上此时OP 一定是直径.例2 如图,在矩形ABCD 中,AB=8,BC=9,⊙O 与外切,且⊙O 与AB 、BC•相切.⊙O ′与AD 、CD 相切,设⊙O 的半径为x,⊙O 与⊙O ′的面积的和为S,求S•的最大值和最小值. 解析 设⊙O ′的半径为y,过O 与O ′分别作CD 与BC 的垂线OH,O ′F,•垂足分别为H,F,OH 、O ′F 交于点E,则有:O ′E=8-(x+y),OE=9-(x+y) 由勾股定理可得:(x+y)2=[8-(x+y)]2+[9-(x+y)]2. 整理,得(x+y-29)(x+y-5)=0,由题意知1≤x ≤4,∴x+y=5,y=-x+5,∴S=πx+πy=π(2x-10x+25),=2π[(x-52)2+254], 故当x=52时,S min =252π; 当x=4时,S=17π.点评先由已知求出⊙O ′的半径也⊙O 的半径x 之间的关系,然后再根据面积公式写出S 与x 之间的关系,这个关系就是一个函数关系,再通过函数的性质得解.中考真题欣赏例 (南京市中考题)如图,⊙O 1与⊙O 2内切于点P,又⊙O 1切⊙O 2•的直径BE 于点C,连结PC 并延长交⊙O 2于点A,设⊙O 1,⊙O 2的半径分别为r 、R,且R ≥2r.•求证:PC ·AC 是定值.解析 若放大⊙O 1,使⊙O 1切⊙O 2的直径于点O 2(如图), 显然此时有PC ·AC=PO 2·AO 2=2r ·R(定值). 再证明如图的情况:连结C O 1,PO 2,• 则PO 2•必过点O 1,•且O 1C ⊥BE,得CO 2=22121O O O C -=22R Rr -,从而BC=R+22R Rr -,EC=R-22R Rr -.所以PC ·AC=EC ·BC=2Rr,故PC ·AC 是定值. 点评解答几何定值问题时,可先在符合题目条件的前提下用运动的观点,从特殊位置入手,找出相应定值,然后可借助特殊位置为桥梁,完成一般情况的证明.竞赛样题展示例1 (第十五届江苏省初中数学竞赛题)如图,正方形ABCD的边长为1,•点P为边BC 上任意一点(可与点B或点C重合),分别过点B、C、D作射线AP的垂线,•垂足分别为点B′、C′、D′.求BB′+CC′+DD′的最大值和最小值.解析∵S△DPC= S△APC =12 AP·CC′,得S 四边形BCDA= S△ABP+ S△ADP+ S△DPC= 12AP(BB′+DD′+CC′),于是BB′+CC′+DD′=2 AP.又1≤AP≤2,故2≤BB′+CC′+DD•′≤2,∴BB′+CC′+DD′的最小值为2,最大值为2.点评本题涉及垂线可考虑用面积法来求.例2 (2000年“新世纪杯”广西竞赛题)已知△ABC内接于⊙O,D是BC•或其延长线上一点,AE是△ABC外接圆的一条弦,若∠BAE=∠CAD.求证:AD.AE为定值.证明如图 (1),当点D是BC上任意一点且∠BAE=∠CAD时,连结BE,则∠E=∠C,∠BAE=∠CAD,∴△ABE∽△ADC.∴AB AEAD AC=,即AD·AE=AB·AC为定值.如图 (2),当点D在BC的延长线上时,∠BAE=∠CAD.此时,∠ACD=∠AEB.∴△AEB∽△ACD,∴AB AE AD AC=即AD·AE=AB·AC为定值.综上所述,当点D在BC边上或其延长线上时,只要∠CAD=∠BAE,总有AD·AE为定值. 点评先探求定值,当AD⊥BC,AE为圆的直径时,满足∠BAE=∠CAD这一条件,•不难发现△ACD ∽△AEB,所以AD·AE=AB·AC,因为已知AB,AC均为定值.•再就一般情况分点D•在BC上,点D在BC的延长线上两种情况分别证明.全能训练A级1.已知MN是⊙O的切线,AB是⊙O的直径.求证:点A、B与MN的距离的和为定值.2.已知:⊙O与⊙O1外切于C,P是⊙O上任一点,PT与⊙O1相切于点T.求证:PC:PT是定值.3.⊙O 1与⊙O 2相交于P 、Q 两点,过P 作任一直线交⊙O 1于点E,交⊙O 2于点F.求证:∠EQF 为定值.4.以O 为圆心,1为半径的圆内有一定点A,过A 引互相垂直的弦PQ,RS.求PQ+RS 的最大值和最小值.5.如图,已知△ABC 的周长为2p,在AB 、AC 上分别取点M 和N,使MN•∥BC,•且MN 与△ABC 的内切圆相切.求:MN 的最值.CABMNA 级(答案)1.定长为圆的直径;2.利用特殊位置探求定值(当PC 构成直径时)是两圆的半径). 3.因∠E,∠F 为定角(大小固定)易得∠EQF 为定值.4.如图,设OA=a(定值),过O 作OB ⊥PQ,OC ⊥RS,B 、C 为垂足, 设OB=x,OC=y,0≤x ≤a,(0≤y ≤a),且x 2+y 2=a 2. 所以所以∴(PQ+RS)2=4(2-a 2+而x 2y 2=x 2(a 2-x 2)=-(x 2-22a )2+44a . 当x 2=22a 时,(x 2y 2)最大值=44a .此时;当x 2=0或x 2=a 2时,(x 2y 2)最小值=0,此时(PQ+RS )最小值=2（）. 5.设BC=a,BC 边上的高为h,内切圆半径为r. ∵△AMN ∽△ABC,2MN h r BC h -=,MN=a(1-2rh),• 由S △ABC =rp,∴r=2ABC S ahp p∆=, ∴MN=a(1-a p )=p ·a p (1-a p )≤p 2(1)2aa p p⎡⎤+-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=4p ,当且仅当a p =1-a p ,即a=2p 时,取等号,∴MN 的最大值为4p.B级1.如图1,已知正方形ABCD的边长为3,点E在BC上,且BE=2,点P在BD上,则PE+PC的最小值为( )A.23B. 13C. 14D.15E D CAB PSQA B PM(1) (2) (3)2.用四条线段a=14,b=13,c=9,d=7.作为四条边构成一个梯形,•则在所构成的梯形中,中位线长的最大值是__________.3.如图2,⊙O的半径为2,A、B两点在⊙O上,切线AQ和BQ相交于Q,P是AB•延长线上任一点,QS⊥OP于S,则OP·OS=_______.4.已知,如图3,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE•、•MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( •)A.定直线B.经过定点C.一定不过定点D.以上都有可能5.如图,已知⊙O的半径为R,以⊙O上一点A为圆心,以r为半径作⊙A,•又PQ与⊙A 相切,切点为D,且交⊙O于P、Q.求证:AP·AQ为定值.6.如图,⊙O 1与⊙O 2相交于A 、B 两点,经过点B•的一直线和两圆分别相交于点C 和D,设此两圆的半径为R 1,R 2.求证:AC:AD=R 1:R 2.B 级(答案)1.B.∵A 、C 关于BD 对称,连结AE 交BD 于P,此时PE+PC=AE 最短.2.11.5 (1)当上底为7,下底分别为14,13,9时,中位线长分别为10.5,10,8; (2)当上底为9和13时,均构不成梯形.3.连结OQ 交AB 于M,则OQ ⊥AB.连结OA,则OA ⊥AQ. ∵∠QMP=∠QSP=90°,∴S,P,•Q,M 四点共圆,故OS ·OP=OM ·OQ. 又∵OM ·OQ=OA 2=2,∴OS ·OP=2.4.B.由图可知直线MN 可看作⊙O 和⊙O ′的割线, 当M 在点A 时,直线MN 变为⊙O•′的切线, 当M 在点B 时,直线MN 变为⊙O 的切线.这两种情况是以AB•为直角边的等腰直角三角形的两直角边所在的直线,交点是第三个顶点M.M 是AB 的中点时,MN 是AB•的垂直平分线,也过第三个顶点,所以选B. 5.如图,作⊙O 的直径AB,连结AD. ∵PQ 切⊙A 于D,∴AD ⊥PQ, ∴AP ·AQ=AD ·AB.•而AD=r,AB=2R,∴AP ·AQ=2Rr 为定值.6.作AN ⊥CD,垂足为点N,连结AB,有AC.AB=AN.2R1,① AB ·AD=AN ·2R 2 .② ①÷②,得12R AC AD R ,∴AC:A D=R 1:R 2.。
几何模型之二图形中的最短距离定值及不等式问题
学生： 科目： 数 学 教师： 谭 前 富知识框架在平面几何问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的面积、角的度数）的最大值或最小值问题，称为最值问题。
最值问题的解决方法通常有两种： （1） 应用几何性质：① 三角形的三边关系：两边之和大于第三边，两边之差小于第三边； ② 两点间线段最短；③ 连结直线外一点和直线上各点的所有线段中，垂线段最短； ④ 定圆中的所有弦中，直径最长。
⑵运用代数证法：① 运用配方法求二次三项式的最值； ② 运用一元二次方程根的判别式。
【例题精讲】一. 最短路径和几何不等式问题： 考查知识点----：“两点之间线段最短”，“两边之和大于第三边”，“斜边大于直角边”，“垂线段最短”，“点关于线对称”，“线段的平移”。
原型----“饮马问题”，“造桥选址问题”。
考的较多的还是“饮马问题”，出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
最短路径和几何不等式问题的两种基本模型----：Ⅰ、归于函数模型：即利用一次函数的增减性和二次函数的对称性及增减性，确定某范围内函数的最大或最小值Ⅱ、归于几何模型，这类模型又分为两种情况：（1）归于“两点之间的连线中，线段最短”。
凡属于求“变动的两线段之和的最小值”时，大都应用这一模型。
（2）归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时，大都应用这一模型。
解题总思路----找点关于线的对称点实现“折”转“直”，较难的会出现“三折线”转“直”等变式问题考查。
二．最短距离中的数形结合：例：求代数式9)12(422+-++x x 的最小值.课 题几何模型之二：图形中的最短距离、定值及不等式问题教学内容三．立体几何中的最短路径问题：（1）台阶问题 如图，是一个三级台阶，它的每一级的长、宽和高分别等于5cm ，3cm 和1cm ，A 和B 是这个台阶的两个相对的端点，A 点上有一只蚂蚁，想到B 点去吃可口的食物.请你想一想，这只蚂蚁从A 点出发，沿着台阶面爬到B 点，最短线路是多少？（2）圆柱问题 有一圆形油罐底面圆的周长为24m ，高为6m ，一只老鼠从距底面1m 的A 处爬行到对角B 处吃食物，它爬行的最短路线长为多少？变式1：有一圆柱形油罐，已知油罐周长是12m ，高AB 是5m ，要从点A 处开始绕油罐一周建造梯子，正好到达A 点的正上方B 处，问梯子最短有多长？变式2： 桌上有一个圆柱形玻璃杯（无盖），高为12厘米，底面周长18厘米，在杯口内壁离杯口3厘米的A 处有一滴蜜糖，一只小虫从桌上爬至杯子外壁，当它正好爬至蜜糖相对方向离桌面3厘米的B 处时，突然发现了蜜糖。
解析几何中定值和定点问题
解析几何中的定值定点问题(一)与直线x -y 2=0相切. ⑴求椭圆C 的方程；⑵设P(4, 0) , M 、N 是椭圆C 上关于x 轴对称的任意两个不同的点，连结 PN 交椭圆C 于另一点E ，求直线PN 的斜率的取值范围；⑶在⑵的条件下，证明直线 ME 与x 轴相交于定点. 解：⑴由题意知e =£3，所以e 2 =与=a ;b=3，即玄2 =4b 2，又因为b ! 1,所以a 2a a 4J l +1222X2a =4,b =1，故椭圆C 的方程为C : - y =1 .4⑵由题意知直线 PN 的斜率存在，设直线 PN 的方程为y =k(x _4)①+y 二k(x 一4)联立 X 2 2 消去 y 得：(4k 2 -1)x 2 -32k 2x 4(16k 2-1) =0 ,4 y T由,;=(32k 2)2 _4(4k 2 1)(64k 2 —4) 0 得 12k 2 -1 ：：:0,又k =0不合题意，所以直线PN 的斜率的取值范围是3::: k ：:：0或0 :：: k 3 .6 6⑶设点 N(N ,yj E(X 2, y 2)，则 M (为，-yj ，直线 ME 的方程为 y-y ?二 一(x-x ?),X 2 —X 1令 y=0，得 x=X 2——X^) , 将 射=k(X 1 - 4), y 2 = k(X 2 - 4)代入整理，得 x = _4(XX 2). ②y 2 +y 1X 1 +血 一82 2由得①X 1 X 2二卫!J, X 1X 2二竺 4代入②整理，得X=1 ,4k -+1 4k +1 所以直线ME 与x 轴相交于定点(1, 0).【针对性练习1]在直角坐标系xOy 中，点M 到点F 1 i 、3,0 , F 2 .3,0的距离之和是4，点M 的轨 迹是C 与x 轴的负半轴交于点 A ，不过点A 的直线l : ^ kx b 与轨迹C 交于不同的两点 P 和Q . ⑴求轨迹C 的方程；⑵当AP AQ =0时，求k 与b 的关系，并证明直线l 过定点.解：⑴•••点M 到.[73,0 , . 3 ,0的距离之和是4 , ••• M 的轨迹C 是长轴为4 ,焦点在x 轴上焦中为2 32的椭圆，其方程为-y 2 =1 .、定点问题【例1 ].已知椭圆C : 2 2孚 Z =1(a b 0)的离心率为a b仝，以原点为圆心，椭圆的短半轴长为半径的圆 2AO J7—⑵将y=kx・b，代入曲线C的方程，整理得(1 4k2)x28 2kx ^0，因为直线|与曲线C交于不同的两点P 和Q，所以厶=64kb -4(1 4k )(4b — 4) =16(4k -b 1) 0 ①设P X i , y i ，Q| x2 , y2 ，则X i :' X? 2 ，X i X? 2 ②f' 1+4k 1+4k且y i y^(kX i b)(kX? ■ b^(k2X i X?) kb(X i X?)b2，显然，曲线C与X轴的负半轴交于点 A -2 , 0，所AP = X 2 , y ，AQ = X? 2 , y?.由AP AQ = 0，得(x「2)(x? 2) y y? = 0 .将②、③代入上式，整理得12k? -16kb • 5b? =0.所以(2k -b) (6k -5b) = 0 ,即b = 2k或b .经检验,5都符合条件①，当b=2k时，直线I的方程为y =kx・2k •显然，此时直线I经过定点-2 , 0点•即直线|b =6k时，直线I的方程为y = kx ■ 6k =k经过点A，与题意不符.当5 5b = @ k，且直线I经过定点5【针对性练习2】在平面直角坐标系xoy中，如图，已知椭圆? ?—-匚=1的左、右顶点为A、B，右焦点9 5为F。
九年级数学奥数知识点专题精讲---平面几何中的定值问题
知识点，重点，难点所谓定值问题，是指按照一定条件构成的几何图形，当某些几何元素按一定的规律在确定的范围内变化时，与它有关的某种几何量却始终保持不变（或几何元素间的某种几何性质或位置关系不变）。
平面几何定值一般可分为两类：一类是定量问题（如定长度、定角、定比、平方和或倒数和为定值等）；一类是定形问题（如定点、定线、定圆或弧、定方向等），它们有共同的基本特点，即给定条件中一般由固定条件和变动条件两部分组成。
一般来说，求解定值问题的方法有：图形分析法。
画出符合条件的图形后，分析图中几何元素的数量关系及位置关系，直接寻求出定值并证明。
特殊位置法。
不论图形如何变动，定值这一共性始终不变，因此可选择图形的特殊位置（如极限位置、临界位置）加以探求。
参数计算法。
图形运动中，选取其中的变量（如线段长、角度、面积等）作为参数，将要求的定值用参数表出，然后消去参数即得定值。
例题精讲例1：如图，已知⊙O 及弦AB ，P 为⊙O 上任一点，PA 、PB 分别交AB 中垂线于E 、F ，求证：OE ·OF 为定值。
分析 若在⊙O 上的点P 运动到特殊位置点Q ，则点E ，点F 都和Q 点重合，于是得到OE ·OF =OQ ，由此可推想，该定值可能为⊙O 2半径的平方。
证明 因为OE 是弦AB 的中垂线，所以，所以∠AOE=∠BOE ， AQ BQ=所以又因为∠EPB =∠PAB 1.2mAOE AB ∠= 1,2m PAB BP ∠=1,2m PBA AP ∠=＋∠ABP ，所以∠AOE = ∠EPB ，所以A 、O 、F 、P 四点共圆，所以∠OFB =∠OAE .又因为∠FOB =∠AOE ，所以△FOB ∽△OAE ，所以即OE ·OF ＝OA ·OB .因为OA =OB ，所以OE ·OF =OA （定,OF OBOA OE=2值）。
例2：如图，设AB 、CD 是圆O 的两条定直径，P 是圆周上的任一点，过P 作AB 垂线，过P 作CD 的垂线，其垂足分别为Q 、R ，DT ⊥AB ，垂足为T ，求证：QR 是定长。
解析几何中的定点和定值问题
解析几何中的定点定值问题考纲解读：定点定值问题是解析几何解答题的考查重点。
此类问题定中有动，动中有定，并且常与轨迹问题，曲线系问题等相结合，深入考查直线的圆，圆锥曲线，直线和圆锥曲线位置关系等相关知识。
考查数形结合，分类讨论，化归与转化，函数和方程等数学思想方法。
一、定点问题解题的关健在于寻找题中用来联系已知量，未知量的垂直关系、中点关系、方程、不等式，然后将已知量，未知量代入上述关系，通过整理，变形转化为过定点的直线系、曲线系来解决。
例1、已知A 、B 是抛物线y 2=2p x (p >0)上异于原点O 的两个不同点，直线OA 和OB 的倾斜角分别为α和β，当α、β变化且α+β=4π时，证明直线AB 恒过定点，并求出该定点的坐标。
解析： 设A 〔121,2y p y 〕，B 〔222,2y py 〕，则 212tan ,2tan y py p==βα，代入1)tan(=+βα得221214)(2p y y y y p -=+ 〔1〕 又设直线AB 的方程为b kx y +=，则022222=+-⇒⎩⎨⎧=+=pb py ky pxy bkx y ∴kpy y kpby y 2,22121=+=，代入〔1〕式得pk p b 22+= ∴直线AB 的方程为)2(2p x k p y +=- ∴直线AB 过定点〔-)2,2p p说明：此题在特殊条件下很难探索出定点，因此要从已知出发，把所求的定点问题转化为求直线AB ，再从AB 直线系中看出定点。
例2．已知椭圆C ：22221(0)x y a b a b+=>>，以原点为圆心，椭圆的短半轴长为半径的圆与直线0x y -相切． ⑴求椭圆C 的方程；⑵设(4,0)P ，M 、N 是椭圆C 上关于x 轴对称的任意两个不同的点，连结PN 交椭圆C 于另一点E ，求直线PN 的斜率的取值范围；⑶在⑵的条件下，证明直线ME 与x 轴相交于定点．解析：⑴由题意知c e a ==22222234c a b e a a -===，即224a b =，又因为1b ==，所以224,1a b ==，故椭圆C 的方程为C ：2214x y +=．⑵由题意知直线PN 的斜率存在，设直线PN 的方程为(4)y k x =- ① 联立22(4)14y k x x y =-⎧⎪⎨+=⎪⎩消去y 得：2222(41)324(161)0k x k x k --+-=， 由2222(32)4(41)(644)0k k k ∆=-+->得21210k -<， 又0k =不合题意，所以直线PN的斜率的取值范围是0k <<或0k <<． ⑶设点1122(,),(,)N x y E x y ，则11(,)M x y -，直线ME 的方程为212221()y y y y x x x x +-=--， 令0y =，得221221()y x x x x y y -=-+，将1122(4),(4)y k x y k x =-=-代入整理，得12121224()8x x x x x x x -+=+-． ②由得①2212122232644,4141k k x x x x k k -+==++代入②整理，得1x =， 所以直线ME 与x 轴相交于定点(1,0)．【针对性练习1】 在直角坐标系xOy 中，点M到点()1,0F，)2,0F 的距离之和是4，点M 的轨迹是C 与x 轴的负半轴交于点A ，不过点A 的直线:l y kx b =+与轨迹C 交于不同的两点P 和Q ． ⑴求轨迹C 的方程；⑵当0AP AQ ⋅=时，求k 与b 的关系，并证明直线l 过定点．解：⑴∵点M到(),0，),0的距离之和是4，∴M 的轨迹C 是长轴为4，焦点在x轴上焦中为的椭圆，其方程为2214x y +=．⑵将y kx b =+，代入曲线C的方程，整理得22(14)40k x +++= ，因为直线l 与曲线C 交于不同的两点P 和Q ，所以222222644(14)(44)16(41)0k b k b k b ∆=-+-=-+> ① 设()11,P x y ，()22,Q x y，则12x x +=，122414x x k=+ ②且2212121212()()()()y y kx b kx b k x x kb x x b ⋅=++=+++，显然，曲线C 与x 轴的负半轴交于点()2,0A -，所以()112,AP x y =+，()222,AQ x y =+．由0AP AQ ⋅=，得1212(2)(2)0x x y y +++=．将②、③代入上式，整理得22121650k kb b -+=．所以(2)(65)0k b k b -⋅-=，即2b k =或65b k =．经检验，都符合条件①，当2b k =时，直线l 的方程为2y kx k =+．显然，此时直线l 经过定点()2,0-点．即直线l 经过点A ，与题意不符．当65b k =时，直线l 的方程为6556y kx k k x ⎛⎫=+=+ ⎪⎝⎭．显然，此时直线l 经过定点6,05⎛⎫- ⎪⎝⎭点，且不过点A ．综上，k 与b 的关系是：65b k =，且直线l 经过定点6,05⎛⎫- ⎪⎝⎭点． 【针对性练习2】在平面直角坐标系xoy 中，如图，已知椭圆15922=+y x 的左、右顶点为A 、B ，右焦点为F 。
初中平面几何中的定值问题
平面几何中的定值问题开场白：同学们，动态几何类问题是近几年中考命题的热点，题目灵活、多变，能够全面考查同学们的综合分析和解决问题的能力。
这类问题中就有一类是定值问题，下面我们来看几道题：【问题1】已知一等腰直角三角形的两直角 边AB=AC=1，P 是斜边BC 上的一动点，过P 作PE ⊥AB 于E ，PF ⊥AC 于F ，则 PE+PF= 。
方法1：特殊值法：把P 点放在特殊的B 点或C点或BC 中点。
此种方法只适合小题。
方法2：等量转化法：这是绝大部分同学能够想到的方法，PF=AE,PE=BE,所以PE+PF=BE+AE 。
方法3：等面积法：连接AP ，ABC ABP APC S S S AB AC AB PE AC PF ∆∆∆=+⇒⋅=⋅+⋅AB PE PF ⇒=+总结语：这虽然是一道动态几何问题，难吗不难，在解决过程中（方法2抓住了边长AB 的不变性和PE,PF 与BE,AE 的不变关系；方法3抓住了面积的不变性），使得问题迎刃而解。
设计：大部分学生都能想到方法2，若其他两种方法学生没有想到，也不要深究，更不要自己讲掉。
此题可叫差生或中等偏下的学生回答（赛比艳，艾科）（设计意图：由简到难，让程度最差的同学也有在课堂上展示自我的机会。
）过渡：这道题太简单了，因为等腰直角三角形太特殊了，我若把等腰直角三角形换成一般的等腰三角形，问题有没有变化，又该如何解决请看：【变式1】若把问题1中的等腰直角三角形改为 等腰三角形，且两腰AB=AC=5，底边BC=6，过P 作PE ⊥AB 于E ，PF ⊥AC 于F ，则 PE+PF 还是定值吗若是，是多少 若不是，为什么 方法1：三角形相似进行量的转化 ABM PBE PCF∆∆∆,AM PE PF AM PB AM PC PE PF AB PB PC AB AB⋅⋅⇒==⇒== ()462455AM PB PC AM BC PE PF AB AB +⋅⋅⇒+==== （板书） （M 为BC 中点）（解题要点：等腰三角形中，底边上的中线是常作的辅助线，抓住这条线的长度是不变量这个特点，建立PE,PF 与AM 之间的联系，化动为静）方法2：等面积法：ABC ABP APC S S S BC AM AB PE AC PF ∆∆∆=+⇒⋅=⋅+⋅642455BC AM PE PF AB ⋅⋅⇒+===（M 为BC 中点） （板书） （解题要点：抓住三角形面积是个不变量，用等面积法求解，这是在三角形中求解与垂线段有关的量的常用方法。
定值
例：如图，已知∠POQ=900知,点 A，B分别在射线 OP,OQ上移动， ∠OAB 的平分线与∠OBA的外角平分线相交于点 C，求证： ∠ACB 的大小为定值。 证明：由于∠ACB是ABC的一个内角，所以可利用三角形的内角和定理 以及内外角平分线定义直接计算∠ACB的大小。 ∵ ∠BAC+ ∠ABC =1/2 ∠OAB+ ∠OBA + ∠OBC =1/2 ∠OAB+ ∠OBA+ 1/2(1800- ∠OBA ) = 1/2 (∠OAB+ ∠OBA)+900 = 1/2× 900+ 900 =1350 Q ∴∠ACB=1800-(∠ACB+ ∠ABC)=450 为定值
1
E B
Q
D
F
证明如图：设⊙O 切AB于点 D,切 ⊙Q于点M，显然Q,O,M 三点共线，且OD⊥AB.AD=a. BD=b (a＞b). 则AB=a + b, QM=QA=QB= 1 (a +b ), QD= 1 (a - b) 2 2 令OD=X 则OQ= 2 1 ，由 OQ 2 2 OD 2
• 例3： 如图⊙Q, 的直径AB=d(定值). ⊙o, ⊙o1
是两个动圆，它们既与⊙Q内切，又同时与AB相 切，过点B作⊙Q,的切线交射线AO,AO1于点E,F; 过点A作 ⊙Q 的切线交射线BO,BO1于点G,H.证明
不论⊙Q， ⊙o1的位置，大小怎样变化，S△AEF+S △BGH恒为定值.
G M O A H O
AM
D A E B M P
C
CM
PE MG
CP CM
MG PF ( AM MG )
F G
∴PE+PD=PF+PD=DF=AG=2AM(定值)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平面几何中的定值问题开场白：同学们，动态几何类问题是近几年中考命题的热点，题目灵活、多变，能够全面考查同学们的综合分析和解决问题的能力。
这类问题中就有一类是定值问题，下面我们来看几道题：【问题1】已知一等腰直角三角形的两直角边AB=AC=1，P 是斜边BC 上的一动点，过P 作PE ⊥AB 于E ，PF ⊥AC 于F ，则PE+PF= 。
方法1：特殊值法：把P 点放在特殊的B 点或C 点或BC 中点。
此种方法只适合小题。
方法2：等量转化法：这是绝大部分同学能够想到的方法，PF=AE,PE=BE,所以PE+PF=BE+AE 。
方法3：等面积法：连接AP ，ABC ABP APC S S S AB AC AB PE AC PF ∆∆∆=+⇒⋅=⋅+⋅AB PE PF ⇒=+总结语：这虽然是一道动态几何问题，难吗？不难，在解决过程中（方法2抓住了边长AB 的不变性和PE,PF 与BE,AE 的不变关系；方法3抓住了面积的不变性），使得问题迎刃而解。
设计：大部分学生都能想到方法2，若其他两种方法学生没有想到，也不要深究，更不要自己讲掉。
此题可叫差生或中等偏下的学生回答（赛比艳，艾科）（设计意图：由简到难，让程度最差的同学也有在课堂上展示自我的机会。
）过渡：这道题太简单了，因为等腰直角三角形太特殊了，我若把等腰直角三角形换成一般的等腰三角形，问题有没有变化，又该如何解决？请看：【变式1】若把问题1中的等腰直角三角形改为 等腰三角形，且两腰AB=AC=5，底边BC=6， 过P 作PE ⊥AB 于E ，PF ⊥AC 于F ，则PE+PF 还是定值吗？若是，是多少？若不是，为什么?方法1：三角形相似进行量的转化ABM PBE PCF∆∆∆,AM PE PF AM PB AM PCPE PF AB PB PC AB AB⋅⋅⇒==⇒==()462455AM PB PC AM BC PE PF AB AB +⋅⋅⇒+====（板书） （M 为BC 中点）（解题要点：等腰三角形中，底边上的中线是常作的辅助线，抓住这条线的长度是不变量这个特点，建立PE,PF 与AM 之间的联系，化动为静）方法2：等面积法：ABC ABP APC S S S BC AM AB PE AC PF ∆∆∆=+⇒⋅=⋅+⋅642455BC AM PE PF AB ⋅⋅⇒+===（M 为BC 中点） （板书）（解题要点：抓住三角形面积是个不变量，用等面积法求解，这是在三角形中求解与垂线段有关的量的常用方法。
）(若学生想不到，可提示：在此题中，不变的东西是什么？不变的这个量和变量PE,PF 之间有什么联系，能不能用一个等式来表示？学生会三角形的边长，角度，周长，面积等都是不变量。
（设计意图：由特殊到一般，引出求垂线段长度的常用方法：等面积法）（教师行为：出示题之后，让学生做，教师下去看。
叫用方法1的同学先站起来回答，然后再叫用方法2的同学。
以达到过渡到下一题的目的。
）问：我把题中的5改为a ，6改为b ，PE+PF 还是定值吗？你能求出这个定值吗？ 答：是定值，求解方法不变。
问：由这题，你能得出等腰三角形的一个一般性结论吗？ 结论：等腰三角形底边上任意一点到两腰的距离之和为定值PE+PF=bh a⋅(a 为腰长,b 为底边长,h 为的边上的高)（等面积法可以求解，注意当顶角为钝角的情况）（设计意图：培养学生探究的精神，养成勤总结的习惯） 问题：通过前面几题，你能说说在解答动态几何问题时解题的关键是什么？应该注意什么问题？答：不要被"动"、"变"迷惑，通过观察，分析，动中窥静，变化之中求不变，从而明确图形之间的在联系，找到不变量或不变关系，找到解题的途径。
在解题过程中要注意点或线在运动的过程中，是否需要讨论。
过渡：上面两题中的动点都是在一定线段或直线上运动，有些同学可能还是觉得不够刺激，下面再来一道刺激一点的，让点在一个区域运动，请看： 【变式2】已知P 为边长为a 的等边三角形ABC 任意一动点， P 到三边的距离分别为h 1,h 2,h 3,则P 到三边的距离之和是否为定值？为什么？（由上题的启示，学生可能很容易想到等面积法）ABC ABP ACP BCP S S S S BC AM AB PE AC PF BC∆∆∆∆=++⇒⋅=⋅+⋅+⋅PE PF PD AM ⇒++= 为定值 （M 为BC 中点）（板书）可以用几何画板度量长度，进行演示（设计意图：使学生更深一步理解等面积法的应用）过渡：研究完了P 在三角形部运动的情况，我们不防降低对P 点的约束，让这个好动的点P 动到三角形外部去，情况又会有何变化？ 【变式3】已知P 为边长为a 的等边三角形ABC 外任意一点，P 到三边的距离分别为h 1,h 2,h 3,则P 到三边的距离之间有何关系？为什么？图1 图2 图3CCC在几何画板中操作，发现当点P 移出三角形时，h 1＋h 2＋h 3发生改变，那么h 1,h 2,h 3有没有什么一定的关系呢？等面积法还可以用吗？△PAB ，△PBC ，△PAC 的面积有何关系？这三个三角形的面积和不变的三角形ABC 的面积有何关系？（直需讲解一种情况，其它让学生自己去补充）图1：ABC ABP ACP BCP S S S S BC AM AB PE AC PF BC PD ∆∆∆∆=+-⇒⋅=⋅+⋅-⋅PE PF PD AM ⇒+-=为定值 （板书）图2：ABC ACP BCP ABP S S S S BC AM AC PF BC PD AB PE ∆∆∆∆=+-⇒⋅=⋅+⋅-⋅PF PD PE AM ⇒+-=为定值 （只把结论板书）图3：ABC ABP BCP ACP S S S S BC AM AB PE BC PD AC PF ∆∆∆∆=+-⇒⋅=⋅+⋅-⋅PE PD PF AM ⇒+-=为定值 （只把结论板书）图1 图2 图3 图1：ABC ACP ABP BCP S S S S BC AM AC PE AB PF BC PD ∆∆∆∆=--⇒⋅=⋅-⋅-⋅PF PE PD AM ⇒--=为定值 （板书）图2：ABC ABP BCP ACP S S S S BC AM AB PE BC PD AC PF ∆∆∆∆=--⇒⋅=⋅-⋅-⋅PE PD PF AM ⇒--=为定值 （只把结论板书）图3：ABC BCP ABP ACP S S S S BC AM BC PD AB PE AC PF ∆∆∆∆=--⇒⋅=⋅-⋅-⋅PD PE PF AM ⇒--=为定值 （只把结论板书）（设计意图：渗透分类讨论思想在平面几何中的应用。
）（教师行为：在几何画板中作出个三角形，填充部，让学生直观地发现几个三角形之间的面积关系。
）过渡：前面我们研究的都是以三角形为背景的动态几何定值问题，下面再看一道以圆为背景的定值问题。
C【问题2】 已知：已知弧AB 为120度，在以AB 为弦的弓形劣弧上取一点M(不包括A 、B 两点)，以M 为圆心作圆M 和AB 相切，分别过A ，B 作⊙M 的切线，两条切线相交于点C. 求证：∠ACB 有定值，并求出这个定值.分析： 问：这个图形中不变的是什么？不变的角是那一个？ 答： 此题中的不变量是弧AB ，因此∠AMB 也是不变量；不变关系是相切。
问：已知直线和圆已经相切，我们会想到什么？ 答：连接圆心与切线方法1：问：要证∠ACB 有定值，可以转化为求什么为定值？ 答：要证∠ACB 有定值，只需证∠CAB+∠CBA 是定值，只需证∠MAB+∠MBA 是定值，只要∠AMB 是定值即可。
证明：在△ABC 中，∠MAB+∠MBA=180－∠AMB ， ∵M 是△ABC 的心，∴∠CAB+∠CBA=2(180－∠AMB).∴∠ACB=180－（∠CAB+∠CBA ）=180－2(180－∠AMB)= 2∠AMB －180＝60. ∴∠ACB 有定值60.方法2：问：要证∠ACB 有定值，可以转化为求什么为定值？ 答：要证∠ACB 有定值，只需证∠EMF 是定值，只需证∠EMD+∠FMD 是定值，只要∠AMD+∠BMD 即∠AMB 是定值即可。
证明：在四边形CEMF 中，∠C+∠EMF=180， ∵M 是△ABC 的心，∴∠DMA=∠EMA, ∠FMB=∠DMB ∴∠EMD+∠FMD=2∠AMB =240∴∠EMF=120∴∠C =180-∠EMF=60总结：若要证的不变量比较困难，你可以先找找题中比较容易看出的不变量，然后建立两者之间的联系。
（设计意图：多角度，多方位地研究动态几何中的定值问题，本题以圆为背景，研究角的定值问题。
）过渡：上题是道有关定值的证明题，也就是已经明确方向肯定是定值了，若不是证明题呢？【问题3】已知：O是如图同心圆的圆心,AB是大圆的直径?点P是小圆上的一动点,大小圆半径分别为R与r?问:PA2＋PB2是否有定值,若有,求出定值;若没有,说明理由.分析：这道题是探索定值的问题，可以先用特位定值法，探索以下是否可能是定值。
①点P放在直径AB上.得PA2＋PB2＝（R＋r）2＋（. R－r）2＝2（R2＋r2）.②点P放在与直径AB垂直的另一条直径上也可得PA2＋PB2＝ R2＋r2＋R2＋r2＝2（R2＋r2）.说明PA2＋PB2非常有可能是定值，而且这个值为2（R2＋r2）证明：（直角三角形计算法）PA2＋PB2＝HA2＋PH2+PH2＋HB2＝2PH2＋(OH+R)2+(R-OH)2 ＝2PH2＋2OH2+2R2=2(PH2＋OH2) +2R2=2r2＋2R2解答动态几何定值探索问题的方法，一般有两种：第一种是分两步完成：①先探求定值. 它要用题中固有的几何量表示.②再证明它能成立.探求的方法，常用特殊位置定值法，即把动点放在特殊的位置，找出定值的表达式，然后写出证明.第二种是采用综合法，直接写出证明.结束语：数学因运动不再枯燥，数学因运动而充满活力。
希望同学们能够把握动态几何的解题规律。
【小结】问：这节课我们学习了一类怎么样的问题？用什么方法解决？答：动态几何中的定值问题特点：图形中的某个元素，按某种规律在运动类型：（1）点动（2）线动（3）旋转、平移（4）形变解题思路：不要被"动"、"变"迷惑，通过观察，分析，动中窥静，变化之中求不变，从而明确图形之间的在联系，找到解题的途径。