模拟高通讲义带通滤波器设计
高通滤波器设计及仿真

信息与电气工程学院电子电路仿真及设计CDIO三级项目设计说明书(2013/2014学年第二学期)题目:高通滤波器系统仿真及设计专业班级:通信工程班目录第一章文氏桥振荡器-------------------------------------------------1 1.1振荡器的设计及要求 ---------------------------------------------1 1.2系统工作原理 ---------------------------------------------------1 1.3电路设计原理图,实物图, 参数计算及仿真 --------------------------2第二章高通滤波器---------------------------------------------------6 2.1实际滤波器的基本参数--------------------------------------------6 2.2滤波器的设计目的------------------------------------------------6 2.3设计要求--------------------------------------------------------7 2.4系统的设计方案--------------------------------------------------7 2.5系统工作原理----------------------------------------------------7 2.6滤波器设计仿真,仿真结果,实物图,实测结果----------------------7 第三章合成电路----------------------------------------------------11 3.1合成电路仿真图-------------------------------------------------11 3.2焊接成品-------------------------------------------------------12 第四章心得体会----------------------------------------------------14 附录---------------------------------------------------------------14 参考文献-----------------------------------------------------------14第一章文氏桥振荡器1.1 振荡器的设计及要求(1)设计任务:根据文氏桥原理设计一正弦波振荡器。
带通滤波电路带通滤波器

f<f1的信号可从低通滤波器通过
f>f2的信号可从高通滤波器通过
阻带宽度为f2 -fl
频率范围在fl<f<f2的信号被阻断
三、 带阻滤波电路
2. 常用带阻滤波器(BEF)
电路特征:输入信号经过一个由RC元件 组成的双T型选频网络,然后接至集成运 放的同相输入端。
工作原理:当输入信号的频率较高时,可 以认为电容短路,则高频信号从上面由两 个电容和一个电阻构成的T型支路通过;
Ui (s)
1 sC
M
1 sC
P
Uo(s)
UM (s) UP (s) UP (s)
1
R
sC
Ui (s) UM (s) UM (s) UO (s) UM (s) UP (s)
1
R
1
sC
sC
压控电压源二阶HPF电路பைடு நூலகம்
传递函数:
Au
(s)
1
[3
(sRC)2 Aup (s) Aup (s)]sRC (sRC)2
带阻滤波器的作用与带通滤波器相反,即在规定的频带内,信号被 阻断,而在此频带之外,信号能够顺利通过。带阻滤波器也常用于抗干 扰设备中阻止某个频带范围内的干扰及噪声信号通过。
从原理上说,将一个通带截止频率为fl的低通滤波器与一个通带截 止频率为f2的高通滤波器并联在一起,当满足条件fl<f2时,即可组成带 阻滤波器。
1 Q 3 AuP
A u
f f0
A u p 3 A u p
Q A u p
Q是f=f0时的电压放大倍数与通带放大倍数之比
一、高通有源滤波电路
对数幅频特性
LC带通滤波器的设计与仿真设计毕业设计(论文)

1.3.3 滤波器的前景....................................................7
1.3.4几种新型滤波器介绍..........................................8
●阻带滤波器:它的阻带限定在两个有限频率ƒ1与ƒ2之间,阻带两侧都有通带。
1.1.2 滤波器的种类
根据使用的波段和元件的不同,滤波器有很多种类,而且随着技术的发展,种类还在不断增加。总的来说,滤波器可分为两大类:无源滤波器和有源滤波器。
在无源滤波器中,所使用的是无源元件。他们在个体或组合的情况下,能够把一种形式的能量变换为另一种形式,并重新变回到原来的形式,换言之,它们必须是谐振性的。例如,在一个LC谐振电路中,在电容器的电场和电感线圈的磁场之间不断发生着能量的反复交换。因此,如果两个不同储能装置当相互偶合时,能够以很小的损耗实现能量的交换,它们就可以被利用为滤波器元件。
结束语.................................................................................43
致谢....................................................................................45
摘要
随着电子信息的发展,滤波器作为信号处理的不可缺少的部分,也得到了迅速的发展。LC滤波器作为滤波器的一个重要组成部分,它的应用相当的广泛。因此对于它的设计也受到人们的广泛关注。如何设计利用简单的方法设计出高性能的LC滤波器是人们一直研究的课题。
二阶压控型低通、高通、带通、带阻滤波器的设计.

东北石油大学课程设计课程电子线路综合课程设计题目有源滤波器设计院系电子科学学院专业班级电子信息工程14-3学生姓名陈忠昕学生学号140901140308指导教师韩建2016年7月14日东北石油大学课程设计任务书课程电子线路综合课程设计题目有源滤波器设计专业电子信息工程14-3 忠昕学号8主要容、基本要求、主要参考资料等主要容:利用运算放大器组成有源低通、高通、带通、带阻滤波器。
基本要求:1. 通频带自定义;2. 测量设计的有源滤波器的幅频特性;3. 选用通用运算放大器,运放的开环增益应在80dB以上;4. 采用Multisim软件进行仿真,验证和完善设计方案;5. 按要求完成课程设计报告,交激光打印报告和电子文档。
主要参考资料:[1] 童诗白. 模拟电子技术基础(第四版)[M]. :高等教育,2006.[2] 明义. 电子技术课程设计实用教程(第3版) [M]. :中南大学,2010.[3] 程春雨. 模拟电子技术实验与课程设计[M]. :电子工业,2016.完成期限2016年7月14日指导教师专业负责人2016 年7 月5 日一、任务技术指标1. 二阶压控型有源低通滤波器(LPF )设计一个二阶压控型有源低通滤波器,要求特征频率f 0=100kHz ,Q=1;2. 二阶压控型有源高通滤波器(HPF )设计一个二阶压控型有源高通滤波器,要求特征频率f 0=100Hz ,Q=1;3. 二阶压控型有源带通滤波器(BPF )设计一个二阶压控型有源带通滤波器,要求中心频率为f 0=5KHz ,Q=2;4. 二阶压控型有源带阻滤波器设计一个二阶压控型有源带阻滤波器,要求中心频率为f 0=100Hz ,Q=2;二、总体设计思想设计滤波电路实现,让指定频段的信号能比较顺利地通过,而对其他频段信号起衰减作用。
如低通滤波电路能使低频信号顺利通过,而使高频信号受到抑制。
常见的无源滤波有RC 滤波,但RC 滤波电路中的电阻会消耗信号能量,所以我们用放大电路和RC 网络组成有源滤波电路,以提高滤波性能。
带通滤波器设计

LC椭圆函数带通滤波器设计要求带通滤波器,在15kHz~ZOkHz的频率范围内,衰减最大变化1dB,低于14.06kHz和高于23kHz频率范围,最小衰减为50dB,Rs=RL=10kΩ。
③运行Filter Solutions程序。
点击“阻带频率”输人框,在“通带波纹(dB)”内输人0.18,在“通带频率”内输人1,在“阻带频率”内输人1.456,选中“频率单位-弧度”逻辑框。
在“源阻抗”和“负载阻抗”内输人1。
④点击“确定阶数”控制钮打开第二个面板。
在“阻带衰减(dB)”内输人50,点击“设置最小阶数”按钮并点击“关闭”,主控制面板上形式出“6阶”,选中“偶次阶模式”逻辑框。
⑤点击“电路”按钮。
Filter s。
lutions提供了两个电路图。
选择“无源滤波器1”,如图1(a)所示。
⑥这个滤波器必须变换为中心频率ω0=1的归一化带通滤波器。
带通滤波器的Q 值为:把所有的电感量和电容值都乘以Qbp°然后用电感并联每一个电容、用电容串联每一个电感使其谐振频率为ω0=1,该网络被变换为带通滤波器。
使用的谐振元仵是原元件值的倒数,如图1(b)所示。
⑦按照图1的方式转换Ⅱ型支路。
变换后的滤波器见图1(c)。
在原理图下标出了以rad/s为单位的谐振频率。
⑧用中心频率fo=17.32kHz和阻抗10kΩ对滤波器进行去归一化以完成设计。
将所有的电感乘以Z/FSF,所有的电容除以z×FSF,其中z=104,FSF=2πfe=1.0882×105。
最终的滤波器见图1(d)。
图1(c)中的归一化谐振频率直接乘以几何中心频率fo=17.32kHz即可得到谐振频率。
频率响应见图1(e)。
滤波器的主要参数滤波器的主要参数(Definitions) 中心频率(Center Frequency):滤波器通带的中心频率f 0 ,一般取f 0 =(f 1 +f 2 )/2,f 1 、f 2 为带通或带阻滤波器左、右相对下降1dB或3dB边频点。
高阶有源带通滤波器课程设计
2013级《模拟电子技术》课程设计说明书高阶有源带通滤波器课程设计评定意见学院:电气与信息工程学院适应专业:自动化、电气工程及其自动化、通信工程、电子信息工程、设计任务内容及任务,中心频率1KHZ,通频带学院:电气与信息工程学院适应专业:自动化、电气工程及其自动化、通信工程、电子信息工程摘要滤波器在现实生活中非常重要,运用广泛,在电子工程、通讯工程、自动化控制等技术领域,经常需要用到各种各样的滤波器。
随着集成电路的迅速发展,用集成运放可以很方便地构成各种滤波器。
用集成运放实现的滤波器与其他滤波器相比,稳定性和实用性等性能指标,有了很大的提高。
滤波器在电路实验和设备检测中具有十分广泛的用途,通过对滤波器的原理以及结构的认识设计一个通带为800Hz〜1200Hz增益为2〜3倍,中心频率为1000Hz的带通滤波器。
确定设计方案,设计选用UA741芯片作为电路的放大器,计算出该方案需要的电阻、电容、运算放大器参数,再用Multisim 对电路进行仿真,观察电路的幅频特性曲线,然后用AD软件制作带通滤波器电路板,制作完成后,再对电路板进行调试,误差分析,把理论值与测试值进行对比,在误差允许的范围内,证明此次设计的滤波器是成功的。
最终得到一个满足课程设计的高阶有源带通滤波器。
关键词:有源;带通;滤波器;UA741;幅频特性曲线目录1 概述. (1)1.1带通滤波器的简介和功能 ................ 错误! 未定义书签。
1.2滤波器的传递函数与频率特性 (1)1.2.1二阶RC滤波器的传递函数 (1)1.2.2 滤波器的频率特性 (3)1.3工作原理 (4)1.3.1高阶滤波器的工作原理 (4)1.3.2直流稳压电源的工作原理 (4)1.4滤波器的主要特性指标 (4)1.4.1特征频率 (4)1.4.2增益与衰减 (4)1.4.3阻尼系数与品质因数 (5)2 滤波器设计方案....................... 错误! 未定义书签。
《模拟滤波设计》课件

# 模拟滤波设计
模拟滤波是一种用于信号处理的重要技术,本课程将介绍模拟滤波器的设计 方法和电路实现。
什么是模拟滤波?
概述
模拟滤波是通过电子电路去除 信号中某些频率分量的过程。
作用
它可以用于信号处理、通信系 统、音频系统等领域。
重要性
模拟滤波在实际应用中起到了 至关重要的作用。范围的噪声。
带阻滤波器
设计一个带阻滤波器以滤除特定频率范围的信号。
总结
模拟滤波的优缺点
优点:延迟小、动态范围大。 缺点:受到噪声和干扰的影 响。
发展趋势
随着数字滤波技术的发展, 模拟滤波器的应用范围正在 逐渐减小。
学习建议
学习模拟滤波设计需要深入 了解电路理论和信号处理的 基本原理。
滤波器电路实现
1
RC低通滤波器
使用电阻和电容构成的电路来实现低通
阻容积电滤波器
2
滤波。
通过电阻、电容和电感器组合构成的电
路实现滤波。
3
LCR电路实现
利用电感、电容和电阻的相互作用来实 现滤波。
模拟滤波器设计案例
低通滤波器
设计一个低通滤波器以滤除高频噪声。
高通滤波器
设计一个高通滤波器以滤除低频噪声。
滤波器分类
• 低通滤波器 • 高通滤波器 • 带通滤波器 • 带阻滤波器
模拟滤波设计
1 滤波器设计目标
根据应用需求确定设计目标,如截止频率、通带增益等。
2 滤波器设计基本步骤
分析需求,选择适当的滤波器类型,进行电路设计和性能评估。
3 滤波器的参数选择
根据设计目标和电路实现的限制,选择适当的滤波器参数。
带通滤波器
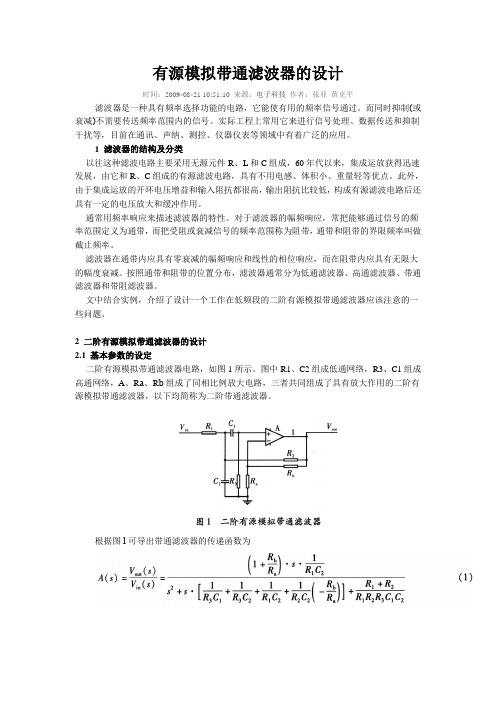
有源模拟带通滤波器的设计时间:2009-08-2110:51:10来源:电子科技作者:张亚黄克平滤波器是一种具有频率选择功能的电路,它能使有用的频率信号通过。
而同时抑制(或衰减)不需要传送频率范围内的信号。
实际工程上常用它来进行信号处理、数据传送和抑制干扰等,目前在通讯、声纳、测控、仪器仪表等领域中有着广泛的应用。
1滤波器的结构及分类以往这种滤波电路主要采用无源元件R、L和C组成,60年代以来,集成运放获得迅速发展,由它和R、C组成的有源滤波电路,具有不用电感、体积小、重量轻等优点。
此外,由于集成运放的开环电压增益和输入阻抗都很高,输出阻抗比较低,构成有源滤波电路后还具有一定的电压放大和缓冲作用。
通常用频率响应来描述滤波器的特性。
对于滤波器的幅频响应,常把能够通过信号的频率范围定义为通带,而把受阻或衰减信号的频率范围称为阻带,通带和阻带的界限频率叫做截止频率。
滤波器在通带内应具有零衰减的幅频响应和线性的相位响应,而在阻带内应具有无限大的幅度衰减。
按照通带和阻带的位置分布,滤波器通常分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
文中结合实例,介绍了设计一个工作在低频段的二阶有源模拟带通滤波器应该注意的一些问题。
2二阶有源模拟带通滤波器的设计2.1基本参数的设定二阶有源模拟带通滤波器电路,如图1所示。
图中R1、C2组成低通网络,R3、C1组成高通网络,A、Ra、Rb组成了同相比例放大电路,三者共同组成了具有放大作用的二阶有源模拟带通滤波器,以下均简称为二阶带通滤波器。
根据图l可导出带通滤波器的传递函数为令s=jω,代入式(4),可得带通滤波器的频率响应特性为波器的通频带宽度为BW0.7=ω0/(2πQ)=f0/Q,显然Q值越高,则通频带越窄。
通频带越窄,说明其对频率的选择性就越好,抑制能力也就越强。
理想的幅频特性应该是宽度为BW0.7的矩形曲线,如图3(a)所示。
在通频带内A(f)是平坦的,而通带外的各种干扰信号却具有无限抑制能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,02
lu
以及通带最大衰减 p 和阻带最小衰减 s 。
(2) 确定归一化模拟低通技术要求,即:
p1, ss2 1 s10 2,ss22 s20 2
取λs和λs的绝对值较小的λs;通带最大衰减
为 ,p 阻带最小衰减为 。s
(3) 设计归一化模拟低通G(p)。
(4) 直接将G(p)转换成带阻滤波器H(s)。
G (p)
1 p3 2 p2 2 p 1
④ 求模拟高通H(s):
s3
H(s)G(p)
pc s
s32cs222cs3c
2f
模拟带通filter的设计方法 带通滤波器的指标要求
Bu l
s1 s1 / B,s2 s2 / B l l / B,u u / B 02 lu
带通滤波器频率特性是正负对称的,故 这个变换必须是一对二的映射,它应该 是Ω的二次函数
模拟高通带通滤波器设计
4.模拟滤波器的频率变换——模拟高通、带通、带阻滤波器的 设计
1) 低通到高通的频率变换
λ和η之间的关系为
1
如 果 已 知 低 通 G(jλ) , 高 通 H(jη)则用下式转换:
H( j) G( j) 1
模拟高通filter的设计方法
H(s) G( p) pc s
Ωl=2π×905, Ωu=2π×1105; Ωs1=2π×980, Ωs2=2π×1020; Ω20=ΩlΩu=4π2×1000025, B=Ωu Ωl=2π×200;
ηl=Ωl/B=4.525, ηu=Ωu/B=5.525;
ηs1=Ωs1/B=4.9,
ηs2=5.1;
η20=ηlηu=25 (2) 归一化低通的技术要求:
C
H(s) G( p) pc s
例6.2.3 设计高通滤波器,fp=200Hz,fs=100Hz,幅度特 性 单 调 下 降 , fp 处 最 大 衰 减 为 3dB , 阻 带 最 小 衰 减 αs=15dB。
①高通技术要求:
fp=200Hz, αp=3dB;
fs=100Hz, αs=15dB
H(s) G( p)
p
sB s2 02
例6.2.5 设计模拟带阻滤波器,其技术要求为:
Ωl=2π×905rad/s,
Ωs1=2π×980rad/s,
Ωs2= 2π×1020rad/s, Ωu=2π×1105rad/s,
αp=3dB,αs=25dB。试设计巴特沃斯带阻滤波器。
解
(1) 模拟带阻滤波器的技术要求:
p s2 l u s( u l)
H ( s ) G ( p ) p s2lu s(ul )
总结模拟带通的设计步骤:
(1)确定模拟带通滤波器的技术指标,即:
带通上限频率 u ,带通下限频率 l 下阻带上限频率 s1 ,上阻带下限频率 s s21s202 4.95, p 3dB,s 25dB
s 4.95
(3)设计归一化低通滤波器G(p):
1 0 0 .1 p 1 k sp 1 0 0.1 s 1 0 .0 5 6 2
sp
s p
4 .9 5
N lg k sp 1 .8 , N 2 lg sp
G (p)
转换关系
模拟高通滤波器指标
ALF的指标
Ha(s)
转换关系
1
低通归一化的系统函数G(p)
p 1 q
高通归一化的系统函数H(q)
s q
C
模拟高通滤波器的设计步骤:
(1)确定高通滤波器的技术指标:通带下限频率 p ,阻
带上限频率 ,通s 带最大衰减 ,阻带最p 小衰减
。
s
(2)确定相应低通滤波器的设计指标:将高通滤波器的
2
2 0
指标转换公式:边界频率转换成低通的边界频率。
2
2 0
λp对应ηu λs对应ηs2
pu2u02 ul 1
s
2 s2
02
s2
模拟带通filter的设计方法
模拟带通滤波器指标
ALF的指标
Ha(s)
转换关系 2 02
低通归一化的系统函数G(p)
p
q2
2 0
q
高通归一化的系统函数H(q)
q=s/B
(4) 直接将G(p)转换成带通H(s)。
模拟带通filter的设计方法 低通与带阻滤波器的频率变换
3) 低通到带阻的频率变换
通带中心频率 02 lu ,通带宽度 Bul
为低通到带阻的频率变换公式:
2
2 0
p=jλ,并去归一化 s/B,可得
ps2sB02 ss(2 u u ll)
上式是直接由归一化低通转换成带阻的频率变换公式。
H(s) G( p)
p
sB s2 02
下面总结设计带阻滤波器的步骤:
(1)确定模拟带阻滤波器的技术要求,即:
下通带截止频率 l ,上通带截止频率 u
阻带下限频率
,阻带上限频率
s1
s2
阻带中心频率 02 lu,阻带宽度 Bul
它们相应的归一化边界频率为
s1
s1 B
,s2
s2 B
,l
l B
u
u B
通带最大衰减为 p ,阻带最小衰减为 s :
与以上边界频率对应的归一化边界频率如下:
s1
s1 B
,s2
s2 B
,l
l B
u
u B
,02
lu
(2) 确定归一化低通技术要求:
p1,ss22 s20 2,ss21 s10 2
通带最大衰减仍为αp,阻带最小衰减亦为αs。 (3) 设计归一化低通G(p)。
归一化频率 pffcp1,sffcs 0.5,
②低通技术要求:
p
1, s
1
s
2
p 3dB, s 15dB
③ 设计归一化低通G(p)。采用巴特沃斯滤波器,
k sp
1 0 0 .1 p 1 1 0 0 .1 s 1
0 .1 8
sp
s p
2
N lg k sp 2 .4 7 , N 3 lg sp
1
p2 2p 1
(4) 带阻滤波器的H(s)为
H (s) G (p )p s2 s B 0 2s42 B s 2 (s B 42 2 2 0 2 s 0 2 2 )s 2 0 42 B 0 2 s 0 4
6.5 数字高通、带通和带阻滤波器的设计
边界频率转换成低通滤波器的边界频率
①低通滤波器通带截止频率 p 1/p ;
②低通滤波器阻带截止频率 s 1/s;
③通带最大衰减仍为 p ,阻带最小衰减仍为 s 。
(3)设计归一化低通滤波器G(p)。 (4)设计归一化高通滤波器G(q)。
p 1 q
(5)求模拟高通的H(s)。 去归一化,将 q s 代入G(q)中
