向量与三角函数
三角函数,向量
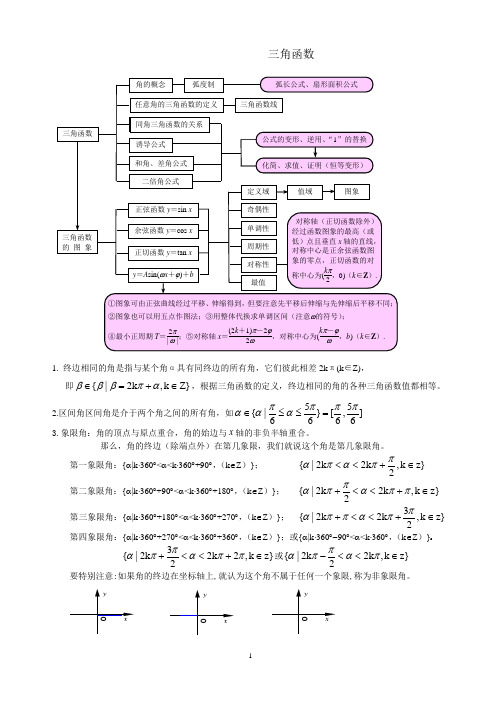
三角函数1. 终边相同的角是指与某个角α具有同终边的所有角，它们彼此相差2k π(k ∈Z)，即Z}k ,2k |{∈+=∈απβββ，根据三角函数的定义，终边相同的角的各种三角函数值都相等。
2.区间角区间角是介于两个角之间的所有角，如]65,6[}656|{πππαπαα=≤≤∈3.象限角：角的顶点与原点重合，角的始边与x 轴的非负半轴重合。
那么，角的终边（除端点外）在第几象限，我们就说这个角是第几象限角。
第一象限角：{α|k ⋅360︒<α<k ⋅360︒+90︒，（k ∈Z ）}； z}k ,22k 2k |{∈+<<ππαπα第二象限角：{α|k ⋅360︒+90︒<α<k ⋅360︒+180︒，（k ∈Z ）}； z}k ,2k 22k |{∈+<<+ππαππα第三象限角：{α|k ⋅360︒+180︒<α<k ⋅360︒+270︒，（k ∈Z ）}； z}k ,232k 2k |{∈+<<+ππαππα第四象限角：{α|k ⋅360︒+270︒<α<k ⋅360︒+360︒，（k ∈Z ）}；或{α|k ⋅360︒-90︒<α<k ⋅360︒，（k ∈Z ）}z}k ,22k 232k |{∈+<<+ππαππα或z}k ,2k 22k |{∈<<-παππα要特别注意:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限,称为非象限角。
O xyO xyO xy角的概念任意角的三角函数的定义 同角三角函数的关系三角函数 弧度制弧长公式、扇形面积公式三角函数线诱导公式 和角、差角公式 二倍角公式公式的变形、逆用、“1”的替换化简、求值、证明（恒等变形）三角函数 的 图 象 定义域奇偶性 单调性 周期性最值 对称轴（正切函数除外）经过函数图象的最高（或低）点且垂直x 轴的直线，对称中心是正余弦函数图象的零点，正切函数的对称中心为(k π2，0)（k ∈Z ）.正弦函数y ＝sin x= 余弦函数y ＝cos x 正切函数y ＝tan xy ＝A sin(ωx ＋ϕ)＋b①图象可由正弦曲线经过平移、伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同；②图象也可以用五点作图法；③用整体代换求单调区间（注意ω的符号）； ④最小正周期T ＝2π| ω |；⑤对称轴x ＝(2k ＋1)π－2ϕ2ω，对称中心为(k π－ϕω，b )（k ∈Z ）.值域图象对称性{α|α=k ⋅360︒, k ∈Z} {α|α=k ⋅360︒+180︒,k ∈Z} {α|α=k ⋅180︒,k ∈Z}O x yO x yO xy{α|α=k ⋅360︒+90︒,k ∈Z} {α|α=k ⋅360︒+270︒,k ∈Z} {α|α=k ⋅180︒+90︒,k ∈Z}O x yO x yO xy{α|α=k ⋅90︒, k ∈Z} {α|α=k ⋅90︒+45︒, k ∈Z} {α|α=k ⋅45︒, k ∈Z} 4．弧度制长度等于半径长的圆弧所对的圆心角叫做1弧度角，记作1rad ，或1弧度，或1(单位可以省略不写)。
三角函数与向量的应用
三角函数与向量的应用在数学中，三角函数和向量是两个重要的概念。
它们在各个领域中都有广泛的应用。
本文将探讨三角函数和向量的应用，并分别列举一些实际场景中的例子来说明它们的作用。
一、三角函数的应用1. 几何学中的角度测量：三角函数广泛应用于几何学中的角度测量。
我们可以使用正弦、余弦和正切函数来计算三角形中的角度。
2. 物理学中的振动和波动：三角函数在物理学中的振动和波动研究中起着重要的作用。
例如，傅里叶级数可以表示任意周期函数，而傅里叶变换可以将信号从时域转换为频域。
3. 工程学中的三维计算：在工程学中，三角函数可以用来计算转动和旋转的角度。
它们在现代计算机图形学中的应用尤为突出，可以实现逼真的三维模型和动画效果。
4. 统计学中的回归分析：在统计学中，三角函数被广泛应用于回归分析。
通过拟合三角函数的曲线，可以对观测数据进行趋势分析和预测。
二、向量的应用1. 物理学中的力学和静力学：向量在物理学中的力学和静力学研究中扮演着重要的角色。
例如，力可以表示为一个有方向和大小的向量，通过向量的合成和分解可以计算力的合成和平衡条件。
2. 计算机图形学中的矢量图形：在计算机图形学中，矢量图形使用向量的形式来描述和存储图像。
向量的性质使得图像可以无损地缩放和旋转。
3. 统计学中的因子分析：在统计学中，向量用于因子分析。
通过将多个变量表示为向量，可以将复杂的数据关系简化为向量空间中的几何关系。
4. 经济学中的资源分配：向量在经济学中的资源分配模型中得到应用。
通过定义资源向量和约束条件，可以求解最优的资源配置方案。
总结：三角函数和向量在数学、物理学、工程学、统计学等领域中都具有广泛的应用。
在几何学中，三角函数用于角度测量和三角形计算；在物理学中，三角函数用于振动和波动的分析；在工程学中，三角函数用于计算旋转角度和创建三维模型；同时，向量在力学、计算机图形学、统计学和经济学等领域发挥着重要作用。
它们的应用促进了各个领域的发展和研究，为我们理解和解决实际问题提供了有力的工具和方法。
三角函数与向量
三角函数与向量1 三角函数——连接几何与数学三角函数是连接几何和数学的关键工具之一。
正弦、余弦、正切等三角函数是用来计算角度和距离的工具。
在三角学中，角度是通过弧度来计算的，而弧度是圆的弧长与其半径之比。
三角函数中，最重要的是正弦、余弦、正切三个函数。
它们是由直角三角形的边长比值定义的。
正弦是对于直角三角形，其斜边相对于一个锐角的对边长度与斜边的比值。
余弦是同样的三角形中，斜边相对于该锐角的邻边长度与斜边的比值。
正切函数是三角形的对边与邻边的比值。
三角函数不仅在三角学中有着广泛的应用，还应用于物理学、工程学、计算机科学等领域。
它们是用来描述振动、波动、电磁波等的重要工具。
它们也经常在声音、光学等领域中出现。
2 向量——描述方向和大小的数学工具向量是一个有方向的量，它可以用箭头表示。
箭头的长度表示向量的大小，箭头的方向表示向量的方向。
向量可以被加、减、缩放等操作。
向量广泛应用于物理学、工程学、计算机科学等领域。
它们是用来描述物体的运动、力、速度等的重要工具。
它们还可以用于计算机图形、机器学习等领域中。
向量和三角函数密切相关。
向量可以用三角函数来描述和计算，而三角函数可以被表示成向量的内积和外积。
向量和三角函数一起形成了一个强大的数学工具箱，可以应用于各种领域的问题。
3 向量和三角函数的联系——使用向量描述三角形向量和三角函数之间有一个有趣的联系：可以用向量来描述三角形。
假设有一个三角形ABC，点A、B、C的坐标分别为 (x1,y1)、(x2,y2)、(x3,y3)。
可以用向量AB和AC来描述该三角形。
向量AB的坐标为 (x2-x1,y2-y1)，向量AC的坐标为 (x3-x1,y3-y1)。
可以计算出向量AB和AC的长度，然后使用三角函数来计算三角形的角度。
例如，可以使用余弦定理计算三角形的角度。
向量和三角函数是紧密相关的数学工具。
它们可以一起用来描述和计算各种物理和工程问题。
向量和三角函数的应用广泛，是数学和科学中必不可少的工具之一。
向量与三角函数专题
向量与三角函数一、解三角形例5．已知ABC △1，且sin sin A B C +=． （I ）求边AB 的长；（II ）若ABC △的面积为1sin 6C ，求角C 的度数．解：（I ）由题意及正弦定理，得1AB BC AC ++=，BC AC +=，两式相减，得1AB =．（II ）由ABC △的面积11sin sin 26BC AC C C = ，得13BC AC = ， 由余弦定理，得222cos 2AC BC AB C AC BC+-=22()2122AC BC AC BC AB AC BC +--== ，所以60C = ．例6. 如图，在ABC ∆中，2AC =，1BC =，43cos =C ．（1）求AB 的值；（2）求()C A +2sin 的值. 解答过程：（Ⅰ） 由余弦定理，得2222..cos AB AC BC AC BC C =+- 341221 2.4=+-⨯⨯⨯=那么，AB（Ⅱ）由3cos 4C =，且0,C π<<得sin C 由正弦定理，得,sin sin AB BC C A=解得sin sin BC C A AB==所以，cos A .由倍角公式sin 2sin 2cos A A A =⋅=， 且29cos 212sin 16A A =-=，故()sin 2sin 2cos cos 2sin A C A C A C +=+例7．在ABC △中，1tan 4A =，3tan 5B =． （Ⅰ）求角C 的大小；（Ⅱ）若AB，求BC 边的长．解：（Ⅰ）π()C A B =-+ ，1345tan tan()113145C A B +∴=-+=-=-- ．又0πC << ，3π4C ∴=．（Ⅱ）由22sin 1tan cos 4sin cos 1A A A A A ⎧==⎪⎨⎪+=⎩，，且π02A ⎛⎫∈ ⎪⎝⎭，，得sin A =sin sin AB BC C A =，sin sin A BC AB C ∴== 二．求三角函数的定义域、值域或最值 典型例题例8.已知函数11()(sin cos )sin cos 22f x x x x x =+--,则()f x 的值域是（ ）A.[]1,1-B.⎡⎤⎢⎥⎣⎦C.⎡-⎢⎣⎦D.1,⎡-⎢⎣⎦)),,444, 1.,,,24f x x x x f x x f x A C D x f x πππππ+-∴==--=-=解法1:(当时(故选C.11解法2:当时()=知不可能.又由时(知选C.22例9． 设函数b a x f 、=)(.其中向量2)2π(R,),1,sin 1(),cos ,(=∈+==f x x b x m a 且. （Ⅰ）求实数m 的值;（Ⅱ）求函数)(x f 的最小值.解：（Ⅰ）()(1sin )cos f x m x x ==++a b ，πππ1sin cos 2222f m ⎛⎫⎛⎫=++= ⎪ ⎪⎝⎭⎝⎭，得1m =． （Ⅱ）由（Ⅰ）得π()sin cos 114f x x x x ⎛⎫=++=++ ⎪⎝⎭，∴当πsin 14x ⎛⎫+=- ⎪⎝⎭时，()f x的最小值为1例10.已知函数1)4()cos x f x xπ-=， （Ⅰ）求()f x 的定义域；（Ⅱ）设α是第四象限的角，且4tan 3α=-，求()f α的值.解答过程：（Ⅰ） 由cos 0x≠得()2x k k Z ππ≠+∈.故()f x 的定义域为,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭， （Ⅱ） 因为43tan ,cos ,55αα=-=且第四象限的角， 所以43sin ,cos ,55αα=-=故()()21)4cos 122)22cos 1sin 2cos 2cos 2cos 2sin cos cos 2cos sin 14.5f πααααααααααααααα-==-+=-==-=例11设)0(cos sin )(>+=ωωωx b x a x f 的周期π=T ，最大值4)12(=πf ， （1）求ω、a 、b 的值；（2）的值终边不共线，求、、的两根，为方程、、若)tan(0)(βαβαβα+=x f .解答过程：(1))x sin(b a )x (f 22ϕ+ω+=， π=∴T ， 2=ω∴， 又 )x (f 的最大值4)12(f =π ， 22b a 4+=∴ ① ， 且 122cos b 122sin a 4π+π= ②， 由 ①、②解出 a=2 , b=3.(2) )3x 2sin(4x 2cos 32x 2sin 2)x (f π+=+=， 0)(f )(f =β=α∴，)32sin(4)32sin(4π+β=π+α∴，32k 232π+β+π=π+α∴， 或)32(k 232π+β-π+π=π+α， 即 β+π=αk (βα、 共线，故舍去) ， 或 6k π+π=β+α，33)6k tan()tan(=π+π=β+α∴ )Z k (∈.例12.设函数2()sin cos f x x x x a ωωω=++（其中0,a R ω>∈），且()f x 的图象在y 轴右侧的第一个最高点的横坐标为6π.（I ）求ω的值；（II ）如果()f x 在区间5,36ππ⎡⎤-⎢⎥⎣⎦a 的值.解答过程：（Ⅰ）1()2sin 22f x x x a ωω=+sin(2)3x a πω=+, 依题意得 2632πππω⋅+=， 解得 12ω=.（Ⅱ）由（Ⅰ）知，()sin()3f x x a π=+,又当5,36x ππ⎡⎤∈-⎢⎥⎣⎦时，70,36x ππ⎡⎤+∈⎢⎥⎣⎦，故11sin()123x -≤+≤，从而()f x 在5[,]36ππ-上取得最小值12a -.因此，由题设知12a -故a =例13.已知函数R x x x x f ∈++=),2sin(sin )(π（Ⅰ）求)(x f 的最小正周期；（Ⅱ）求)(x f 的最大值和最小值； （Ⅲ）若43)(=αf ，求α2sin 的值.命题目的：本题考查利用三角函数的性质, 诱导公式、同角三角函数的关系式、两角和的公式，倍角公式等基本知识，考查运算和推理能力. 解答过程：)4sin(2cos sin )2sin(sin )(ππ+=+=++=x x x x x x f（Ⅰ）)(x f 的最小正周期为ππ212==T ;（Ⅱ）)(x f 的最大值为2和最小值2-；（Ⅲ）因为43)(=αf ，即37sin cos 2sin cos .416αααα+=⇒=-即 1672sin -=α. 三．三角函数的图象和性质 典型例题 例14.已知函数22()sin 2sin cos 3cos ,f x x x x x x R =++∈.求：（Ⅰ）求函数()f x 的最大值及取得最大值的自变量x 的集合； （Ⅱ）函数()f x 的单调增区间. 解答过程：（I ）解法一： ()1cos 23(1cos 2)sin 222x f x x θ-+=++2sin 2cos 2x x =++2)4x π=+. ∴当2242x k πππ+=+，即()8x k k Z ππ=+∈时，()f x 取得最大值2因此，()f x 取得最大值的自变量x 的集合是,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭. 解法二：222()(sin cos )sin 22cos f x x x x x =+++ 1sin 21cos 2x x =+++2)4x π=+.∴当2242x k πππ+=+，即()8x k k Z ππ=+∈时，()f x 取得最大值2因此，()f x 取得最大值的自变量x 的集合是,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭.（Ⅱ）解： ()2)4f x x π=+由题意得222()242k x k k Z πππππ-≤+≤+∈，即3()88k x k k Z ππππ-≤≤+∈.因此， ()f x 的单调增区间是()3,88k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦.例15．（本小题满分12分） 已知函数2π()cos 12f x x ⎛⎫=+⎪⎝⎭，1()1sin 22g x x =+． （I ）设0x x =是函数()y f x =图象的一条对称轴，求0()g x 的值． （II ）求函数()()()h x f x g x =+的单调递增区间． 解：（I ）由题设知1π()[1cos(2)]26f x x =++． 因为0x x =是函数()y f x =图象的一条对称轴，所以0π26x +πk =， 即0 π2π6x k =-（k ∈Z ）． 所以0011π()1sin 21sin(π)226g x x k =+=+-．当k 为偶数时，01π13()1sin 12644g x ⎛⎫=+-=-= ⎪⎝⎭， 当k 为奇数时，01π15()1sin 12644g x =+=+=． （II ）1π1()()()1cos 21sin 2262h x f x g x x x ⎡⎤⎛⎫=+=++++ ⎪⎢⎥⎝⎭⎣⎦1π3113cos 2sin 2sin 2262222x x x x ⎫⎡⎤⎛⎫=+++=++⎪ ⎪⎢⎥⎪⎝⎭⎣⎦⎝⎭1π3sin 2232x ⎛⎫=++ ⎪⎝⎭． 当πππ2π22π232k x k -++≤≤，即5ππππ1212k x k -+≤≤（k ∈Z ）时， 函数1π3()sin 2232h x x ⎛⎫=++ ⎪⎝⎭是增函数， 故函数()h x 的单调递增区间是5ππππ1212k k ⎡⎤-+⎢⎥⎣⎦，（k ∈Z ） 例16.已知函数22()sin cos 2cos ,.f x x x x x x R =+∈ （I ）求函数()f x 的最小正周期和单调增区间；（II ）函数()f x 的图象可以由函数sin 2()y x x R =∈的图象经过怎样的变换得到？解答过程：（I）1cos 2()2(1cos 2)22x f x x x -=+++132cos 2223sin(2).62x x x π=++=++ ()f x ∴的最小正周期2.2T ππ== 由题意得222,,262k x k k Z πππππ-≤+≤+∈即 ,.36k x k k Z ππππ-≤≤+∈()f x ∴的单调增区间为,,.36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦（II ）方法一：先把s i n 2y x =图象上所有点向左平移12π个单位长度，得到sin(2)6y x π=+的图象，再把所得图象上所有的点向上平移32个单位长度，就得到3s i n (2)62y x π=++的图象.方法二： 把sin 2y x =图象上所有的点按向量3(,)122a π=- 平移，就得到3sin(2)62y x π=++的图象.例17.已知函数2())2sin ()().612f x x x x R ππ=-+-∈（I ）求函数()f x 的最小正周期；（II ）求使函数()f x 取得最大值的x 集合.解答过程：(Ⅰ) f(x)=3sin(2x －π6)+1－cos2(x －π12) = 2[32sin2(x －π12)－12 cos2(x －π12)]+1 =2sin[2(x －π12)－π6]+1 = 2sin(2x －π3) +1 .∴ T=2π2 =π．(Ⅱ)当f(x)取最大值时, sin(2x －π3)=1,有 2x －π3 =2k π+π2 ， 即x=k π+ 5π12 (k ∈Z) ∴所求x 的集合为{x ∈R|x= k π+ 5π12 , k ∈Z}. 四．平面向量、三角函数的图象和性质 典型例题例18.将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=- ⎪⎝⎭平移，平移后的图象如图所示，则平移后的图象所对应函数的解析式是（ ）A ．sin()6y x π=+ B ．sin()6y x π=-C ．sin(2)3y x π=+ D ．sin(2)3y x π=-解答过程：将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=- ⎪⎝⎭平移，平移后的图象所对应的解析式为sin ()6y x πω=+，由图象知，73()1262πππω+=，所以2ω=，因此选C.例19.已知向量(sin ,1),(1,cos ),.22a b ππθθθ==-<<（Ⅰ）若a b ⊥，求θ；（Ⅱ）求a b +的最大值.解：（Ⅰ）,sin cos 0a b θθ⊥若则＋＝，由此得 tan 1ππθθ=- (-<<),22所以 ;4πθ=-（Ⅱ） 由(sin ,1),(1,cos )(sin 1,1cos ),a b b b θθθθ== α+=++ α+= = =得当sin()1,,, 1.44a b a b ππθθ+=+=+时取得最大值即当时例20.已知,,A B C 是三角形ABC ∆三内角，向量((),cos ,sin m n A A =-=，且1m n ⋅=（Ⅰ）求角A ；（Ⅱ）若221sin 23cos sin BB B+=--，求tan B .解答过程：（Ⅰ）∵1m n ⋅=,∴(()cos ,sin 1A A -⋅= ,cos 1A A -=.12sin cos 12A A ⎛⎫⋅= ⎪ ⎪⎝⎭, 1sin 62A π⎛⎫-= ⎪⎝⎭. ∵50,666A A ππππ<<-<-<, ∴66A ππ-= . ∴3A π=.（Ⅱ）由题知2212sin cos 3cos sin B B B B+=--，整理得22sin sin cos 2cos 0B B B B --=∴cos 0B ≠ ∴2tan tan 20B B --=. ∴tan 2B =或tan 1B =-.而tan 1B =-使22cos sin 0B B -=，舍去. ∴tan 2B =.∴()tan tan C A B π=-+⎡⎤⎣⎦()tan A B =-+tan tan 1tan tan A B A B+=--=。
向量与三角函数的综合应用
2
解法4 解法4： 3 6 1 2 (sin θ + cos θ ) = sin θ + cos θ =± sin θ ⋅ cos θ = 2 2 ∴ ∴ 4 (sin θ − cos θ )2 = 1 sin θ − cos θ =± 2 sin 2 θ + cos 2 θ = 1 2 2 6+ 2 6− 2 sin θ = sin θ = 4 4 或 ∴ cos θ = 6 − 2 cos θ = 6 + 2 4 4 6+ 2 6− 2 sin θ = − sin θ = − 4 4 或 6− 2 cos θ = − cos θ = − 6 + 2 4 4
例2：已知 a = (cos 2α , sin α ), b = (1,2 sin α − 1), α ∈ ( , π ) ： 2 2 π a ⋅ b = , 求 cos( α + ) 解： a ⋅ b = cos 2α + sin α ( 2 sin α − 1) 2 = 1 − sin α = 5 4 π 3 ∴ sin α = ，因为 α ∈ ( , π ) ∴ cos α = − 5 2 5 π π π ∴ cos(α + ) = cos α cos − sin α sin
∴ tan θ = 2 ± 3
小结：1.向量的坐标运算。 小结：1.向量的坐标运算。 向量的坐标运算 2.三角函数的化简 计算。 三角函数的化简、 2.三角函数的化简、计算。 三角恒等变换、齐次式问题） （三角恒等变换、齐次式问题） 转化思想方法的应用。 3. 转化思想方法的应用。
本节目标： 本节目标
• 1.向量运算与三角函数求值的综合。 向量运算与三角函数求值的综合。 向量运算与三角函数求值的综合 • 2.向量运算与三角函数化简的综合。 2.向量运算与三角函数化简的综合 向量运算与三角函数化简的综合。 • 3.转化思想方法的应用。 转化思想方法的应用。 转化思想方法的应用
向量三角函数知识点归纳
向量三角函数知识点归纳向量和三角函数是高中数学中的重要内容，下面是关于这两个知识点的归纳总结。
一、向量1.向量的定义向量是有大小和方向的量，用箭头在平面或空间中表示。
向量的大小叫做模，用，a，或，a，表示；向量的方向用一个角度或另一向量表示。
2.向量的基本运算-向量的加减：向量的加减使用平行四边形法则，即将两个向量的起点相接，然后将两个向量的终点用直线连接。
- 向量的数量积：向量 a 和 b 的数量积（内积或点积）定义为abcosθ，其中θ 表示 a 和 b 之间的夹角。
-向量的数量积的性质：交换律、结合律、分配律等。
-向量的夹角：可以使用向量的点积公式计算向量之间的夹角。
-向量的投影：一个向量在另一个向量上的投影是一个标量，表示一个向量在另一个向量上的投影长度。
3.向量的应用-分解力的合力：当一个力可以分解为多个力的合力时，可以使用向量的方法表示这个过程。
-平行四边形法表示速度：当一个物体以两个向量之和的速度在平面内运动时，可以使用平行四边形法则来表示其速度。
二、三角函数1.三角函数的定义三角函数是一组用于描述角和边之间关系的函数。
常见的三角函数有正弦函数、余弦函数和正切函数。
- 正弦函数：sinθ = 对边 / 斜边- 余弦函数：cosθ = 邻边 / 斜边- 正切函数：tanθ = 对边 / 邻边2.三角函数的性质和关系-三角函数的周期性：正弦函数和余弦函数的周期都为2π，正切函数的周期为π。
-三角函数的奇偶性：正弦函数和正切函数是奇函数，余弦函数是偶函数。
-三角函数的和差化积公式：- 正弦函数的和差化积：sin(A ± B) = sinAcosB ± cosAsinB- 余弦函数的和差化积：cos(A ± B) = cosAcosB ∓ sinAsinB- 正切函数的和差化积：tan(A ± B) = (tanA ± tanB) / (1 ∓tanAtanB)-三角函数的平方和差公式：- 正弦函数的平方和差：sin²A ± sin²B = 2sinAcosA，cos²A ± cos²B = 2cosAcosB- 余弦函数的平方和差：cos²A + cos²B = 2cosAcosB，cos²A - cos²B = -2sinAsinB- 正切函数的平方和差：tan²A ± tan²B = 1 ∓ 2tanAtanB3.三角函数的应用-三角函数的性质可以用于求解各种三角形的边长和角度。
向量在三角函数中的应用
向量在三角函数中的应用一、引言向量是数学中一个重要的概念，它广泛应用于几何、物理等领域。
在三角函数中，向量同样具有重要的应用。
本文将对向量在三角函数中的应用进行详细介绍。
二、向量的基本概念1. 向量的定义向量是具有大小和方向的物理量，通常用带箭头的字母表示。
例如，$\vec{a}$表示一个向量。
2. 向量的表示方法向量可以用坐标表示，也可以用模长和方向角表示。
设$\vec{a}$是一个非零向量，则其坐标为$(x,y)$，模长为$|\vec{a}|=\sqrt{x^2+y^2}$，方向角为$\theta=\arctan\frac{y}{x}$。
3. 向量的运算向量可以进行加减乘除等运算。
其中加法和减法都是按照分量分别相加或相减；乘法有数量积和叉乘两种形式；除法则是将一个向量乘以另一个向量的倒数。
三、三角函数中的应用1. 正弦定理和余弦定理正弦定理：$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$。
余弦定理：$a^2=b^2+c^2-2bc\cos A$，$b^2=a^2+c^2-2ac\cos B$，$c^2=a^2+b^2-2ab\cos C$。
其中，$a,b,c$为三角形的边长；$A,B,C$为对应的角度；$R$为三角形外接圆半径。
这两个定理中都涉及到向量的叉乘运算。
例如，在正弦定理中，可以将$\vec{a}$、$\vec{b}$和$\vec{c}$看作三个向量，则有$\vec{a}\times\vec{b}=|\vec{a}||\vec{b}|\sin A\cdot\hat{n}$，其中$\hat{n}$为垂直于$\vec{a}$和$\vec{b}$所在平面的单位向量。
因此，正弦定理可以写成$\frac{\vec{a}}{\sin A}=\frac{\vec{b}}{\sinB}=\frac{\vec{c}}{\sin C}=2R\cdot\hat{n}$。
高一数学三角函数与向量公式
两角和公式：sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) 倍角公式：tan2A=2tanA/(1-tan 2A) cos2a=cos 2a-sin 2a=2cos 2a-1=1-2sin 2a 半角公式：sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) 和差化积：2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB 正弦定理： a/sinA=b/sinB=c/sinC=2R 注： 其中 R 表示三角形的外接圆半径 余弦定理： b 2=a 2+c 2-2accosB 注：角B 是边a 和边c 的夹角弧长公式： l=α*r ，α是圆心角的弧度数，r >0 扇形面积公式 s=1/2*l*r 乘法与因式分：a 2-b 2=(a+b)(a-b) a 3+b 3=(a+b)(a 2-ab+b 2) a 3-b 3=(a-b(a 2+ab+b 2) 一元二次方程的解: X 1=-b+√(b 2-4ac)/2a; X 2=-b-√(b 2-4ac)/2a 根与系数的关系: X 1+X 2=-b/a ；X 1*X 2=c/a （韦达定理） 判别式：b 2-4ac=0 注：方程有两个相等的实根 b 2-4ac>0 注：方程有两个不等的实根b 2-4ac<0 注：方程没有实根，有共轭复数根 降幂公式：sin 2x=1-cos2x/2 cos 2x=1-cos2x/2 万能公式：Sin2α=2 tan α/(1+ tan 2α) Cos2α=(1- tan 2α)/(1+ tan 2α) Tan2α=2tan α/(1- tan 2α) 公式一：设α为任意角，终边相同的角的同一三角函数的值相等： sin （2kπ＋α）＝sinα cos （2kπ＋α）＝cosα tan （2kπ＋α）＝tanα cot （2kπ＋α）＝cotα 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin （π＋α）＝－sinα cos （π＋α）＝－cosα tan （π＋α）＝tanα cot （π＋α）＝cotα 公式三：任意角α与 -α的三角函数值之间的关系：sin （－α）＝－sinα cos （－α）＝cosα tan （－α）＝－tanα cot （－α）＝－cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π－α）＝sinα cos （π－α）＝－cosαtan（π－α）＝－tanα cot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinα cos（2π－α）＝cosαtan（2π－α）＝－tanα cot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosα cos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotα cot（π/2＋α）＝－tanαsin（π/2－α）＝cosα cos（π/2－α）＝sinαtan（π/2－α）＝cotα cot（π/2－α）＝tanα (以上k∈Z)注意：在做题时，将a看成锐角来做会比较好做。
职高三角函数与向量知识点
职高三角函数与向量知识点在职业高中的数学学习中，三角函数和向量是相当重要的知识点。
它们不仅在数学中具有广泛应用，而且在实际问题求解中也能发挥巨大的作用。
下面我们就来仔细探讨一下职高数学中的三角函数和向量相关知识。
一、三角函数三角函数是描述角度与边长之间关系的函数。
主要包括正弦函数、余弦函数和正切函数。
它们的定义如下：1. 正弦函数：在直角三角形中，对于非直角的角A，正弦函数的定义为对边与斜边的比值，即sin A = 对边/斜边。
2. 余弦函数：在直角三角形中，对于非直角的角A，余弦函数的定义为邻边与斜边的比值，即cos A = 邻边/斜边。
3. 正切函数：在直角三角形中，对于非直角的角A，正切函数的定义为对边与邻边的比值，即tan A = 对边/邻边。
三角函数不仅有这些基本定义，还有一系列的特性和性质。
例如，关于三角函数的周期、奇偶性、增减性等。
这些特性的掌握对于进行计算和图像的解析具有重要意义。
此外，三角函数在解决实际问题中也有着广泛的应用。
例如，在测量工程中，利用正弦定理可以求解三角形的边长和角度；在物理学中，正余弦函数可以描述振动过程中的变化规律等等。
二、向量向量是指具有大小和方向的物理量，它可以用有向线段来表示。
在职高数学中，我们主要学习平面向量和空间向量。
1. 平面向量：平面向量可以用箭头表示，箭头的长度表示向量的大小，箭头的方向表示向量的方向。
平面向量的运算主要包括加法、乘法和求模等。
此外，平面向量还有一些重要的性质，例如，零向量的特点、平面向量的线性相关、平面向量的垂直等。
2. 空间向量：空间向量与平面向量类似，不同之处在于它们的表示需要通过三个坐标来描述。
空间向量的运算除了加法、乘法和求模外，还包括点积和叉积。
点积用于求两向量之间的夹角和平行关系，而叉积则能够计算两向量的乘积和垂直关系。
向量不仅在数学中有重要地位，而且在物理、工程、计算机等领域也有广泛应用。
例如，在力学中，向量可以描述物体的位移、速度和加速度等；在计算机图形学中，向量可以描述点的位置和方向等。
三角函数的基本关系与计算平面向量的共线与垂直关系
三角函数的基本关系与计算平面向量的共线与垂直关系三角函数是数学中重要的一部分，它描述了一个角度与其对应的三角比例之间的关系。
在平面向量的应用中，我们也经常需要判断向量之间的共线与垂直关系。
本文将从三角函数的基本关系和计算平面向量的共线与垂直关系两个方面进行探讨。
一、三角函数的基本关系三角函数包括正弦函数、余弦函数和正切函数，它们的定义如下：1. 正弦函数（sine）：在直角三角形中，对于一个锐角θ，其正弦值为对边与斜边的比值，记为sinθ。
2. 余弦函数（cosine）：在直角三角形中，对于一个锐角θ，其余弦值为邻边与斜边的比值，记为cosθ。
3. 正切函数（tangent）：在直角三角形中，对于一个锐角θ，其正切值为对边与邻边的比值，记为tanθ。
这三个函数之间存在基本的关系，可以通过定义和几何关系来推导，具体推导如下：1. tanθ = sinθ / cosθ；2. sin^2θ + cos^2θ = 1，两边同时除以cos^2θ，得到tan^2θ + 1 =sec^2θ，其中secθ为secant函数的值；3. cos^2θ + sin^2θ = 1，两边同时除以sin^2θ，得到1 + cot^2θ =csc^2θ，其中cscθ为cosecant函数的值。
这些基本关系在解三角方程和求解三角函数的值时非常有用。
二、计算平面向量的共线与垂直关系平面向量是在平面内具有大小和方向的量，可以通过坐标或者位移来表示。
当我们需要判断向量之间的共线与垂直关系时，可以利用向量的内积和外积来进行计算。
1. 共线关系若两个向量a和b共线，则它们的数量积等于零，即a·b = 0。
这可以通过向量的坐标表示进行计算。
假设向量a = (x1, y1)和向量b = (x2,y2)，则它们的数量积为x1 * x2 + y1 * y2。
若两个向量的数量积等于零，则它们是共线的。
2. 垂直关系若两个向量a和b垂直，则它们的数量积等于零，即a·b = 0。
三角函数与向量的综合应用
三角函数与向量的综合应用在数学领域中，三角函数与向量是两个重要的概念。
它们在各自的领域中拥有广泛的应用，并且可以相互结合，产生更强大的数学工具。
本文将讨论三角函数与向量的综合应用，并探究它们在实际问题中的应用。
一、三角函数与向量的基础知识1. 三角函数三角函数是描述角度关系的函数，其中最常用的三角函数包括正弦函数、余弦函数和正切函数。
它们可以通过三角比值或单位圆上的点坐标来定义。
三角函数在几何、物理和工程等领域中广泛应用，用于求解角度、距离、速度等问题。
2. 向量向量是具有大小和方向的量，可用于表示物体的位移、力和速度等。
向量通常用有序数组表示，其中包括了向量的分量或坐标。
向量在几何、物理、计算机图形学等领域中有重要的应用，用于描述与计算空间中的各种问题。
二、三角函数与向量的结合运用1. 正弦函数与向量的应用正弦函数可以用于求解两个向量之间的夹角。
对于给定的两个向量A和B，它们的夹角θ可以通过以下公式求得：θ = arcsin(|A × B| / (|A| |B|))其中，|A|和|B|分别表示向量A和向量B的模长，A × B表示两个向量的叉乘，|A × B|表示叉乘结果的模长。
这个夹角的计算提供了求解向量运动方向、力的方向以及判断向量共线性等问题的重要依据。
2. 余弦函数与向量的应用余弦函数可以用于求解两个向量之间的夹角以及向量在特定方向上的投影。
对于给定的两个向量A和B，它们的夹角θ可以通过以下公式求得：θ = arccos(A · B / (|A| |B|))其中，|A|和|B|分别表示向量A和向量B的模长，A · B表示两个向量的点乘。
此外，余弦函数还可以用于求解向量在特定方向上的投影长度，从而实现对向量分解和向量运动路径的分析。
3. 正切函数与向量的应用正切函数可以用于求解向量的斜率。
对于给定的向量A，它的斜率可以通过以下公式求得：m = tan(θ) = (A.y / A.x)其中，A.x和A.y分别表示向量A在x轴和y轴上的分量。
三角函数和向量的转换
三角函数和向量的转换标题：三角函数与向量的魔幻舞蹈在数学的世界里，三角函数和向量就像是一对默契的舞伴，它们相互配合，共同演绎着一场奇幻的舞蹈。
让我们跟随这对舞伴的脚步，一起探索它们的魅力。
第一幕：三角函数的旋律舞台上，一束灯光照亮了一个圆形舞池。
在这个舞池上，三角函数开始了他们的独特演绎。
正弦函数优雅地起舞，它的曲线如同一条优美的弧线，起伏着，充满了神秘感。
而余弦函数则以稳定的步伐跳着，它的曲线如同一条高低起伏的山脉，给人以安定和平和的感觉。
而正切函数则以其独特的舞姿，交织着曲线和渐近线，展现出无尽的变化和灵活性。
第二幕：向量的翩跹舞步在舞台的另一侧，向量也开始了他们的翩跹舞步。
向量的舞姿如同一支灵动的笔触，在舞池上划出了一幅美丽的图景。
位移向量像一只自由飞翔的鸟儿，轻盈地在舞池上跳跃，带给观众无限的遐想。
速度向量则像一股激流，迅猛地穿越舞池，将观众带入了瞬息万变的世界。
而加速度向量则像一阵微风，时而轻柔，时而狂暴，给人以意想不到的惊喜。
第三幕：三角函数与向量的完美融合在第三幕中，舞池上的三角函数和向量开始了一场完美的融合。
正弦函数与位移向量相互呼应，展现出一种和谐的节奏感。
余弦函数和速度向量相互交织，勾勒出一个无限延伸的空间。
而正切函数和加速度向量则相互对应，展示出一种变幻莫测的力量。
整个舞蹈以一曲动人的音乐结束，观众们沉浸在舞蹈的美妙中，仿佛置身于一个魔幻的世界。
三角函数和向量的舞蹈不仅展示了数学的美妙，更让人们感受到了数学的魔力。
在这个舞台上，数学不再是一堆枯燥的公式和计算，而是一种充满情感和生命力的艺术。
三角函数和向量的舞蹈让我们看到了数学的魅力，也让我们对数学充满了无限的向往。
让我们一起沉浸在这场魔幻舞蹈中，感受数学的魅力，享受这场数学的盛宴。
让我们用心去感受，用眼去观察，用思维去思考，让数学的世界在我们手中绽放出更加绚丽的色彩。
这是一场属于数学的独特舞蹈，也是一场属于我们的心灵盛宴。
高中数学的三角函数与向量总结
高中数学的三角函数与向量总结在高中数学学习中，三角函数与向量是两个重要的主题。
三角函数研究角的度量与各种三角关系，而向量则研究物体的位移与力的方向。
本文将总结高中数学中三角函数与向量的相关知识点，帮助读者更好地理解与应用这些概念。
一、三角函数1. 正弦函数正弦函数是三角函数中最基本的函数之一，用于研究角的正弦关系。
表示为sin(x)，其中x为角的度数。
正弦函数的定义域为全体实数，值域为[-1, 1]。
在直角三角形中，正弦函数可表示为对边与斜边之比。
2. 余弦函数余弦函数是三角函数中另一个基本的函数，用于研究角的余弦关系。
表示为cos(x)，其中x为角的度数。
余弦函数的定义域为全体实数，值域为[-1, 1]。
在直角三角形中，余弦函数可表示为邻边与斜边之比。
3. 正切函数正切函数是三角函数中较为特殊的函数，用于研究角的切线关系。
表示为tan(x)，其中x为角的度数。
正切函数的定义域为全体实数，但在某些角度上不存在值，需要注意避免这些角度。
在直角三角形中，正切函数可表示为对边与邻边之比。
4. 三角函数的基本关系三角函数之间存在一些基本的关系。
例如，sin(x)与cos(x)互为倒数，即sin(x) = 1/cos(x)。
另外，tan(x) = sin(x)/cos(x)。
通过利用这些基本关系，可以简化求解三角函数的过程。
二、向量1. 向量的定义向量是有大小和方向的量，通常用箭头表示。
在平面几何中，向量可以表示为有序数对 (a, b)，其中 a 为横坐标的变化量，b 为纵坐标的变化量。
向量也可以用矩阵表示。
2. 向量的运算向量有多种运算，包括向量的加法、减法、数量乘法和点乘法。
其中，向量的加法和减法符合平行四边形法则，数量乘法可以改变向量的大小，而点乘法可以得到两个向量的数量积，用于求夹角等相关性质。
3. 向量的模和方向角向量的模表示向量的大小，可通过勾股定理计算得出。
向量的方向角表示向量与平行于坐标轴的正方向之间的夹角。
三角函数平面向量知识与公式总结
三角函数平面向量知识与公式总结三角函数和平面向量是数学中非常重要的概念，它们在解决几何问题、物理问题和工程问题中起着重要的作用。
本文将对三角函数和平面向量的知识进行总结，并介绍常用的公式和性质。
一、三角函数2. 余弦函数：在直角三角形中，余弦函数被定义为邻边与斜边的比值。
其定义域为实数集R。
常用的余弦函数记作cos(x)。
余弦函数也具有周期性，即cos(x+2π)=cos(x)。
3. 正切函数：在直角三角形中，正切函数被定义为对边与邻边的比值。
其定义域为实数集R-{(2k+1)π/2, k∈Z}。
常用的正切函数记作tan(x)。
正切函数也具有周期性，即tan(x+π)=tan(x)。
4. 余切函数：在直角三角形中，余切函数被定义为邻边与对边的比值。
其定义域为实数集R-{kπ, k∈Z}。
常用的余切函数记作cot(x)。
余切函数也具有周期性，即cot(x+π)=cot(x)。
5. 正割函数：在直角三角形中，正割函数被定义为斜边与邻边的比值。
其定义域为实数集R-{(2k+1)π/2, k∈Z}。
常用的正割函数记作sec(x)。
正割函数也具有周期性，即sec(x+2π)=sec(x)。
6. 余割函数：在直角三角形中，余割函数被定义为斜边与对边的比值。
其定义域为实数集R-{kπ, k∈Z}。
常用的余割函数记作csc(x)。
余割函数也具有周期性，即csc(x+2π)=csc(x)。
三角函数之间有一些重要的关系：1.三角函数的互逆关系：sin(x) = 1/csc(x)cos(x) = 1/sec(x)tan(x) = 1/cot(x)cot(x) = 1/tan(x)sec(x) = 1/cos(x)csc(x) = 1/sin(x)2.三角函数的和差化积公式：sin(x+y) = sin(x)cos(y) + cos(x)sin(y)cos(x+y) = cos(x)cos(y) - sin(x)sin(y)tan(x+y) = (tan(x)+tan(y))/(1-tan(x)tan(y))3.三角函数的倍角公式：sin(2x) = 2sin(x)cos(x)cos(2x) = cos^2(x) - sin^2(x)tan(2x) = 2tan(x)/(1-tan^2(x))4.三角函数的半角公式：sin(x/2) = ±√((1-cos(x))/2)co s(x/2) = ±√((1+cos(x))/2)tan(x/2) = ±√((1-cos(x))/(1+cos(x)))二、平面向量1.平面向量的定义：平面向量是具有大小和方向的量。
平面向量与三角函数的关系
平面向量与三角函数的关系在数学中，平面向量和三角函数是两个重要的概念，并且它们之间存在着一定的关系。
本文将介绍平面向量与三角函数的相关性质和应用。
一、向量在直角坐标系中的表示在直角坐标系中，一个向量可以由其在横轴上的分量和在纵轴上的分量来表示。
假设有一个平面向量a，其水平分量为a₁，垂直分量为a₂，则可以用有序数对(a₁, a₂)表示向量a。
其中，a₁沿着横轴的正方向表示，a₂沿着纵轴的正方向表示。
二、向量的模和角度表示向量的模表示向量的长度，也叫作向量的大小。
设向量a的模为|a|，则有|a| = √(a₁² + a₂²)。
其中，a₁和a₂分别为向量a在横轴和纵轴上的分量。
另外，向量还可以用角度来表示。
假设有一个向量a，与横轴之间的夹角为θ，则有tanθ = a₂/a₁，即θ = arctan(a₂/a₁)。
其中，arctan表示反正切函数。
三、平面向量的加法和减法平面向量的加法和减法可以类比数的加法和减法。
设有两个向量a和b，分别表示为(a₁, a₂)和(b₁, b₂)。
向量的加法可以表示为a + b = (a₁ + b₁, a₂ + b₂)。
也就是将两个向量的分量对应相加。
向量的减法可以表示为a - b = (a₁ - b₁, a₂ - b₂)。
也就是将两个向量的分量对应相减。
四、向量与三角函数的关系1. 向量的模和三角函数在直角坐标系中，一个向量的模可以表示为|a| = √(a₁² + a₂²)。
根据直角三角形的性质，我们可以知道，a₁/|a| = cosθ，a₂/|a| = sinθ。
其中，θ表示向量a与横轴之间的夹角。
2. 向量的加法与三角函数设有两个向量a和b，分别表示为(a₁, a₂)和(b₁, b₂)。
根据向量的加法性质，a + b = (a₁ + b₁, a₂ + b₂)。
根据向量的模和三角函数的关系，可以得到|a + b| = √((a₁ + b₁)² + (a₂ + b₂)²) = √(a₁² + a₂² + b₁² + b₂² + 2(a₁b₁ + a₂b₂))。
三角函数与向量结合的题型
三角函数与向量结合的题型【引言】在高中数学课程中，三角函数和向量是两个重要的概念。
它们分别代表了数学的几何和代数两个方面。
三角函数帮助我们研究角度、三角形的性质，而向量则使得我们能够进行矢量运算和分析。
这两个概念的结合可以带来更加复杂和有趣的数学题型。
在本文中，我们将探讨三角函数与向量结合的题型，从简单到复杂，逐步深入地理解这个主题。
【1. 什么是三角函数】三角函数是描述角度和角度相关的性质的一组函数。
其中最常见的三角函数有正弦函数、余弦函数和正切函数。
我们通常用sin、cos和tan来表示它们。
三角函数的定义涉及到一个直角三角形的三个边长或角度，使得我们能够通过角度来研究三角形的性质。
三角函数在解决几何问题、物理问题和工程问题中起着重要的作用。
【2. 什么是向量】向量是用来表示大小和方向的量。
在数学中，向量通常用有序数对或有序数组来表示。
有向线段也可以看作是向量的几何表示。
向量在几何和代数中都有广泛的应用。
我们可以通过向量进行矢量运算，如向量加法、向量减法和数量乘法。
向量还可以用于描述力、速度和位移等物理量。
【3. 三角函数与向量的关系】三角函数和向量之间有许多密切相关的关系。
我们可以通过三角函数来表达向量的方向。
给定一个向量，我们可以计算出它与横轴的夹角，并通过三角函数来表示这个夹角的大小。
我们可以使用三角函数来计算两个向量之间的夹角。
夹角的正弦、余弦和正切值可以帮助我们理解向量之间的关系和性质。
在解决几何问题时，我们常常会遇到涉及角度和向量的复杂题目，这些题目需要我们结合三角函数和向量来求解。
【4. 三角函数与向量结合的题型举例】下面我们来看一些常见的三角函数与向量结合的题型。
4.1 题型一：求两个向量的夹角已知两个向量a和b，求它们的夹角。
解决这个问题时，我们可以使用向量的数量积和三角函数来求解。
具体步骤如下：计算向量a和b的数量积，即a·b。
计算a和b的模长，即|a|和|b|。
三角函数和向量知识点
三角函数和向量知识点
一、三角函数的定义
三角函数，即三角函数，是以角度和弧度为参数的函数。
三角函数可
以用来求出直角三角形中的各个边和角的大小。
它可以分为正弦函数，余
弦函数和正切函数。
二、三角函数的基本公式
三角函数的基本公式可以从三角形的基本定理和三角形的相关公式推出。
1、正弦函数的基本公式：sinθ=Opposite/Hypotenuse
2、余弦函数的基本公式：cosθ＝Adjacent/Hypotenuse
3、正切函数的基本公式：tanθ＝Opposite/Adjacent
三、三角函数的应用
三角函数在数学中有着广泛的应用，如绘制三角形、求解三角形的面
积和周长等。
它还可以用于计算机编程中三角函数的求值，因此在许多领
域有着重要的应用，比如地理、天文学、建筑等。
四、向量的定义
向量是由大小和方向所确定的矢量，它具有大小和方向性，也可以视
为其中一点移动的一种矢量表示。
在数学中，一个向量实际上是一个矢量，它是一组数（矢量的分量）的有序集合，这些数的每一个均表示矢量在其
中一坐标轴上的大小及其方向。
五、向量的计算
向量可以用来计算点积、叉积、矢量差、向量加法和减法等等。
1、点积：点积是两个向量的数量积，它表达了两个向量的内积。
2、叉积：叉积是两个向量的向量乘积。
高一向量三角函数知识点
高一向量三角函数知识点在高中数学中，向量和三角函数是两个重要的数学概念。
向量是具有大小和方向的量，可以用来表示力、速度、位移等物理量。
而三角函数则是通过角度来描述三角形的边长比例关系。
在高一阶段，学生将接触到向量和三角函数的基本概念和应用。
下面将介绍一些高一向量三角函数的知识点。
1. 向量的基本定义和表示方法向量可以看作是有向线段。
它有大小和方向，通常用带箭头的线段表示。
在直角坐标系中，向量可以表示为一个有序数对 (x, y) 或三元组(x, y, z)。
向量的大小可以用长度来表示，方向可以用箭头的朝向表示。
2. 向量的加法和减法向量的加法和减法是基于三角形法则的。
两个向量相加等于从第一个向量的起点出发，终点为第二个向量的终点的向量。
两个向量相减则等于从第一个向量的起点出发，终点为第二个向量的起点的向量。
3. 向量的数量积和向量积数量积，也称为点积，是两个向量之间的一种运算。
它的结果是一个标量，表示两个向量的夹角关系和相对大小。
向量积，也称为叉积，是两个向量之间的一种运算。
它的结果是一个向量，垂直于参与运算的两个向量，大小等于两个向量的模长乘以夹角的正弦值。
4. 三角函数的定义和性质三角函数是通过角度来描述三角形的边长比例关系。
主要有正弦函数、余弦函数和正切函数等。
正弦函数 sin(x) 的值等于对边与斜边的比值，余弦函数 cos(x) 的值等于邻边与斜边的比值，正切函数 tan(x) 的值等于对边与邻边的比值。
5. 三角函数的图像和周期性三角函数的图像是周期性的，它们在一个周期内的取值是重复的。
例如，正弦函数和余弦函数的周期都是2π，而正切函数的周期是π。
在坐标系中，正弦函数的图像是一条波浪形的曲线，余弦函数的图像是一条波浪形的曲线，正切函数的图像是一条无限趋近于水平线和垂直线的曲线。
6. 三角函数的基本公式和恒等式三角函数有许多基本公式和恒等式，它们在解三角方程和简化表达式中起到重要作用。
例如，正弦函数的基本公式是 sin(a ± b) =sin(a)cos(b) ± cos(a)sin(b)，正切函数的恒等式是 tan(x) = sin(x)/cos(x)。
三角函数与向量的关系
三角函数与向量的关系
《嘿，说说三角函数与向量的关系》
哎呀妈呀，这三角函数和向量，听起来是不是有点让人头大？嘿嘿，别慌，咱今天就用大白话来唠唠它们之间的关系。
我记得有一回上数学课，老师正在讲三角函数和向量。
我一开始那是听得云里雾里的，完全不知道这俩玩意儿有啥关系。
我就看着黑板上那些奇怪的符号和图形，心里直犯嘀咕：“这都是啥呀？咋这么难呢？”
老师看我们都一脸迷茫，就开始举例子。
他说啊，就好比我们在操场上跑步，我们跑步的方向和速度就可以用向量来表示。
而如果我们要计算跑步的路线和角度呢，这时候就用到三角函数了。
我一听，好像有点明白了。
然后老师又在黑板上画了一个三角形，说：“看，这个三角形的三条边可以用向量来表示，而三角形的各个角呢，就可以用三角函数来计算。
” 我看着那个三角形，脑子里开始想象自己在操场上跑步的场景。
我想，如果我知道自己跑步的速度和方向，也就是向量，那我就能用三角函数来计算我跑了多远，跑的角度是多少。
这么一想，我突然觉得三角函数和向量也不是那么难理解了。
我就开始认真听老师讲，还做了一些笔记。
下课后，我又找了几个同学一起讨论，我们互相分享自己的理解，感
觉对这两个概念越来越清楚了。
后来，我在做数学作业的时候，又遇到了关于三角函数和向量的问题。
我就想起了老师举的例子和我们讨论的内容，慢慢地就把问题给解决了。
那一刻，我心里可高兴了，觉得自己终于掌握了这两个看似很难的概念。
总之啊，三角函数和向量虽然有点复杂，但是只要我们用心去理解，多举例子，多思考，就一定能搞清楚它们之间的关系。
高中数学向量三角函数
第五讲 向量与三角函数【考点透视】1．理解任意角的概念、弧度的意义，能正确地进行弧度与角度的换算．2．掌握任意角的正弦、余弦、正切的定义，了解余切、正割、余割的定义，掌握同解三角函数的基本关系式，掌握正弦、余弦的诱导公式，理解周期函数与最小正周期的意义． 3．掌握两角和与两角差的正弦、余弦、正切公式，掌握二倍角的正弦、余弦、正切公式． 4．能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明．5．了解正弦函数、余弦函数、正切函数的图象和性质，会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+ψ)的简图，理解A 、ω、ψ的物理意义． 6．会由已知三角函数值求角，并会用符号arcsin x, arcos x,arctan x 表示．7．掌握正弦定理、余弦定理，并能初步运用它们解斜三角形，能利用计算器解决解三角形的计算问题．8．掌握向量与三角函数综合题的解法． 常用解题思想方法1．三角函数恒等变形的基本策略。
（1）常值代换：特别是用“1”的代换，如1=cos 2θ+sin 2θ=tanx ·cotx=tan45°等。
（2）项的分拆与角的配凑。
如分拆项：sin 2x+2cos 2x=(sin 2x+cos 2x)+cos 2x=1+cos 2x ；配凑角：α=（α+β）－β，β=2βα+－2βα-等。
（3）降次与升次。
即倍角公式降次与半角公式升次。
（4）化弦（切）法。
将三角函数利用同角三角函数基本关系化成弦（切）。
（5）引入辅助角。
asin θ+bcos θ=22b a +sin(θ+ϕ)，这里辅助角ϕ所在象限由a 、b 的符号确定，ϕ角的值由tan ϕ=ab确定。
（6）万能代换法。
巧用万能公式可将三角函数化成tan2θ的有理式。
2．证明三角等式的思路和方法。
（1）思路：利用三角公式进行化名，化角，改变运算结构，使等式两边化为同一形式。
（2）证明方法：综合法、分析法、比较法、代换法、相消法、数学归纳法。